The Social Cost of Sub-Soil Resource Use
Abstract
1. Introduction
2. Materials and Methods
2.1. Hotelling’s Model and the Determinants of the Market Price
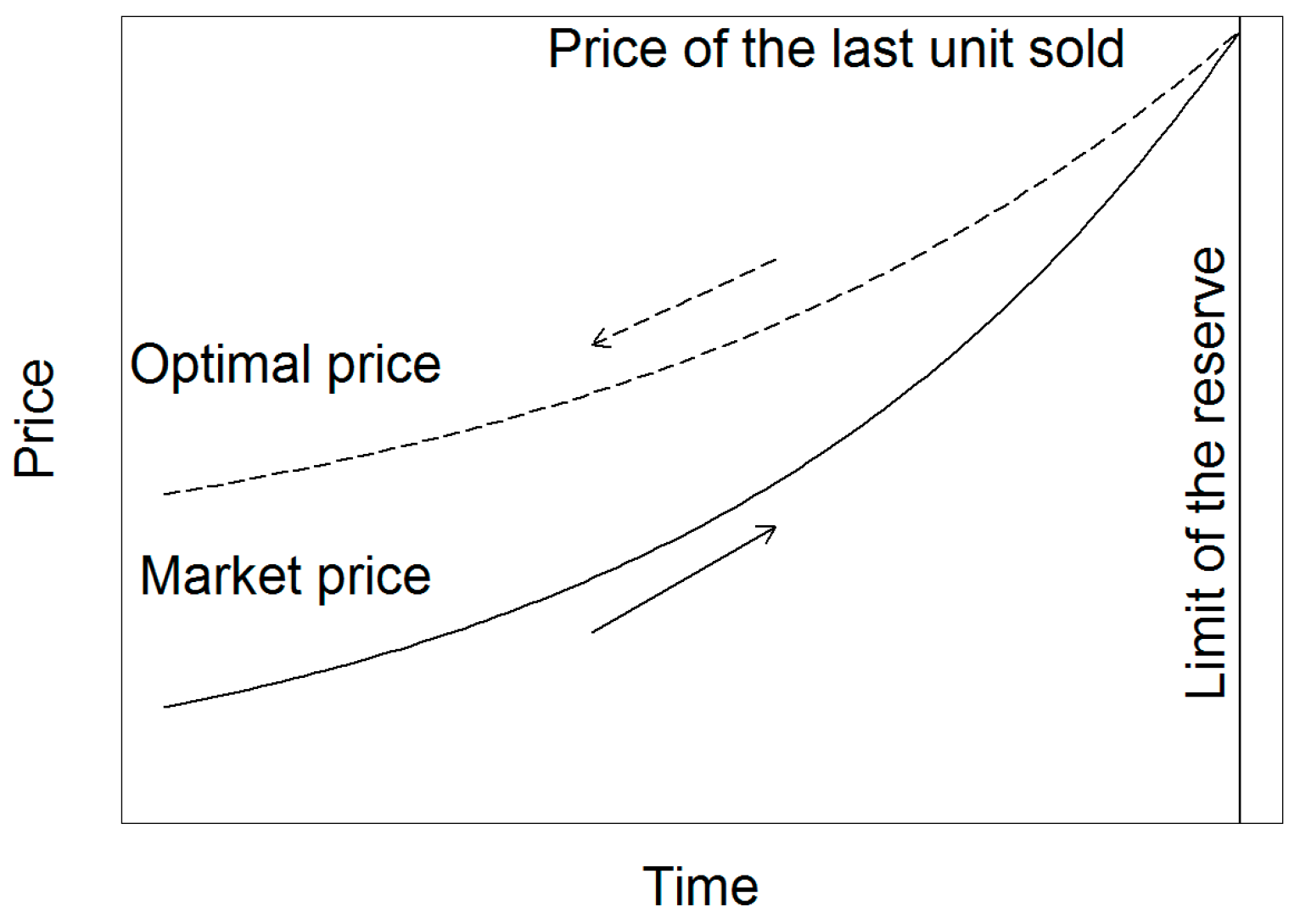
2.1.1. Time Path of the Resource Price According to Hotelling’s Model
2.1.2. Causes of Market Price Differing from Socially Optimal Price
2.2. Correcting the Market Price
2.2.1. Model 1: Principle of the Method
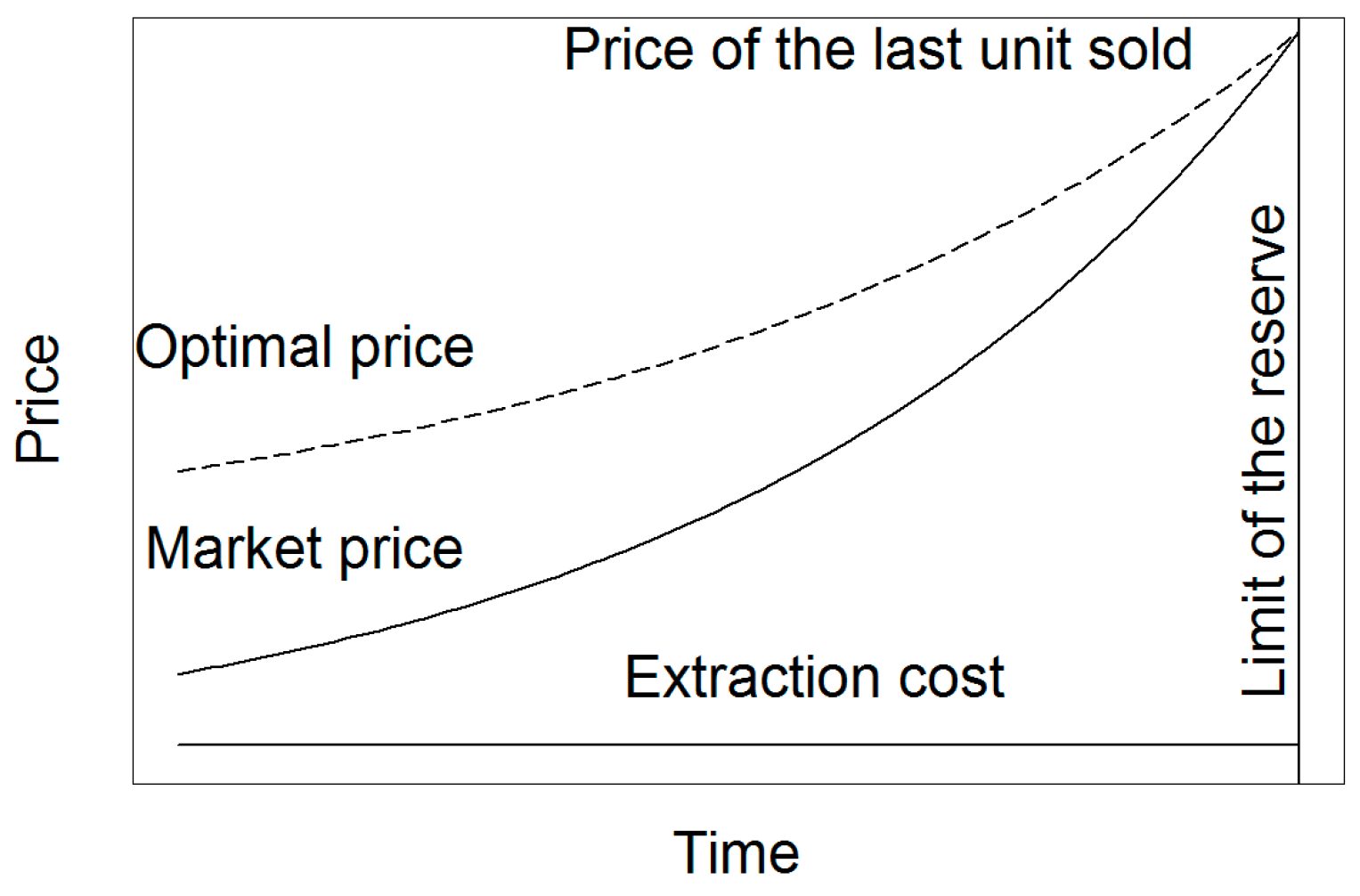
2.2.2. Model 2: Integrating Extraction Cost
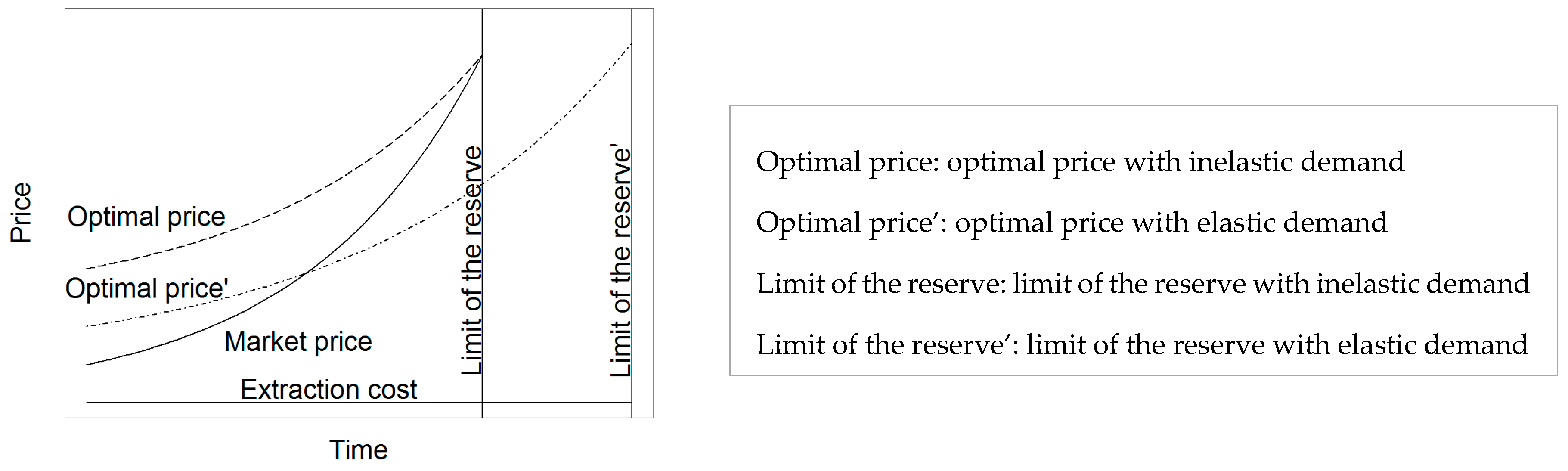
2.2.3. Model 3: Integrating Elastic Demand
2.2.4. Applied Method in Practice
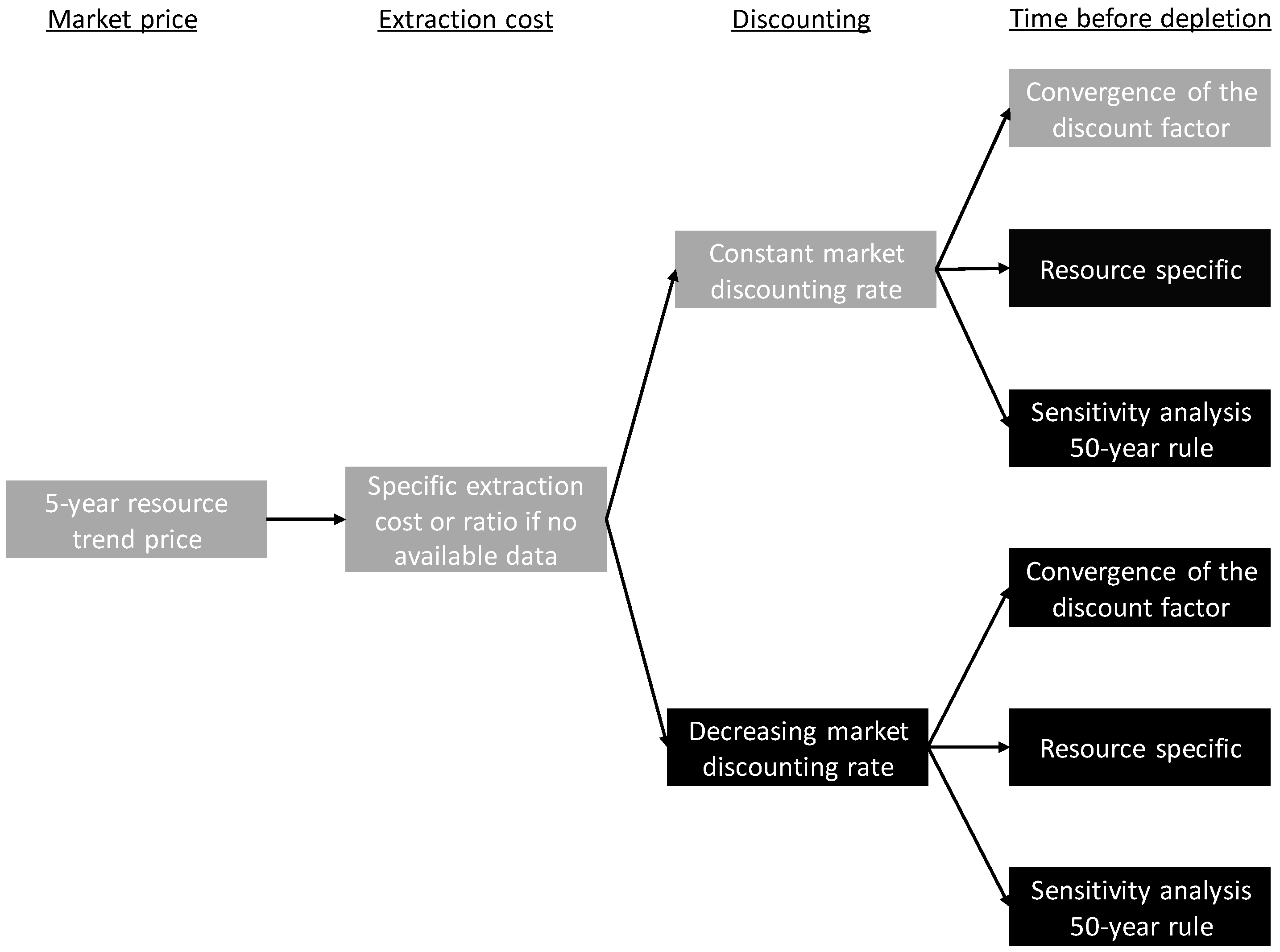
3. Data and Assumptions
3.1. Market Price Including Extraction Costs
3.2. Extraction Cost
3.3. Time before Depletion
- (1)
- t = time of convergence of the market and the social discount rates (our base case)
- (2)
- t = resource-specific estimate of time before depletion (sensitivity analysis)
- (3)
- t = resource-specific estimate of time before depletion, but not >50 years (sensitivity analysis)
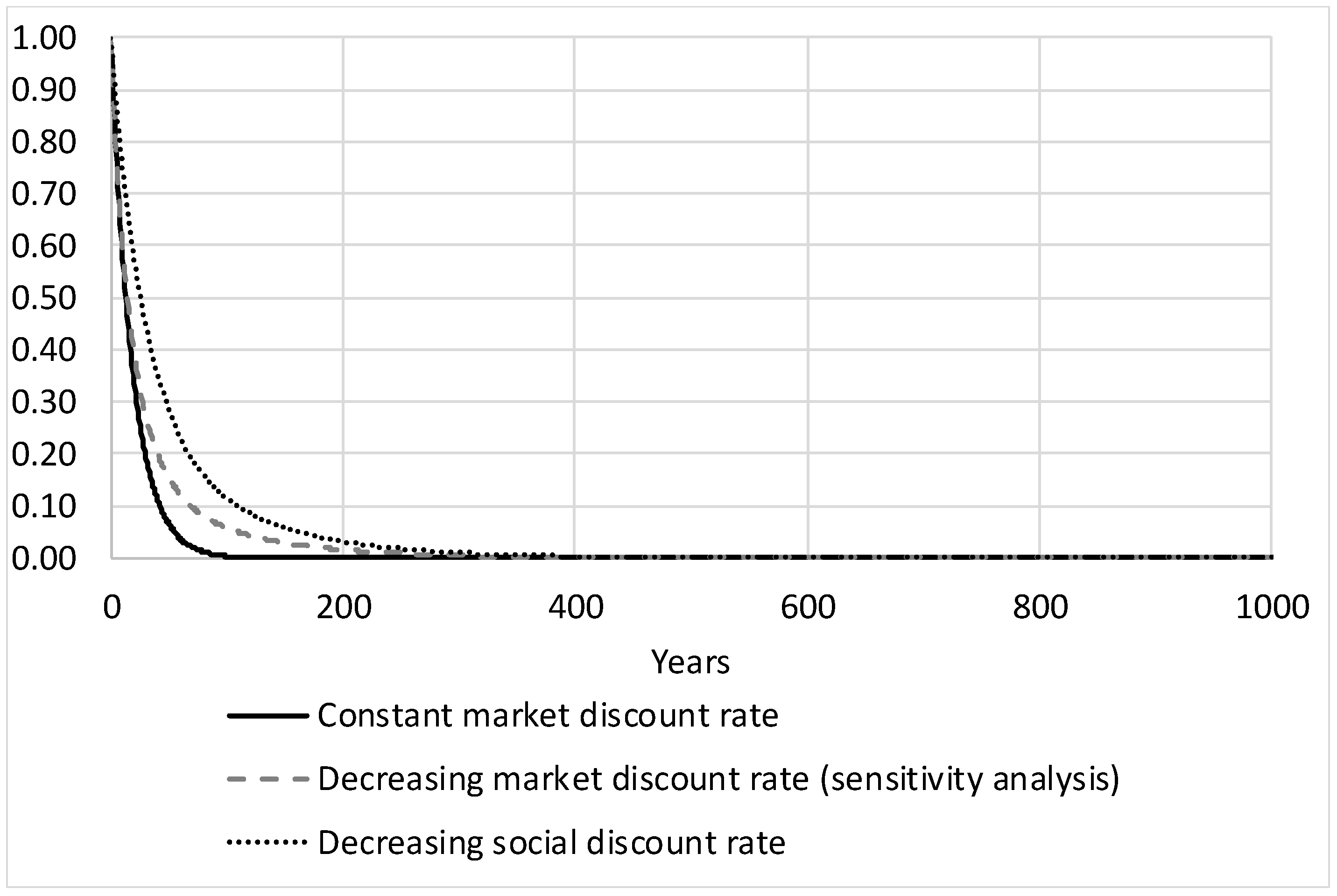
3.4. Social and Market Discount Rates
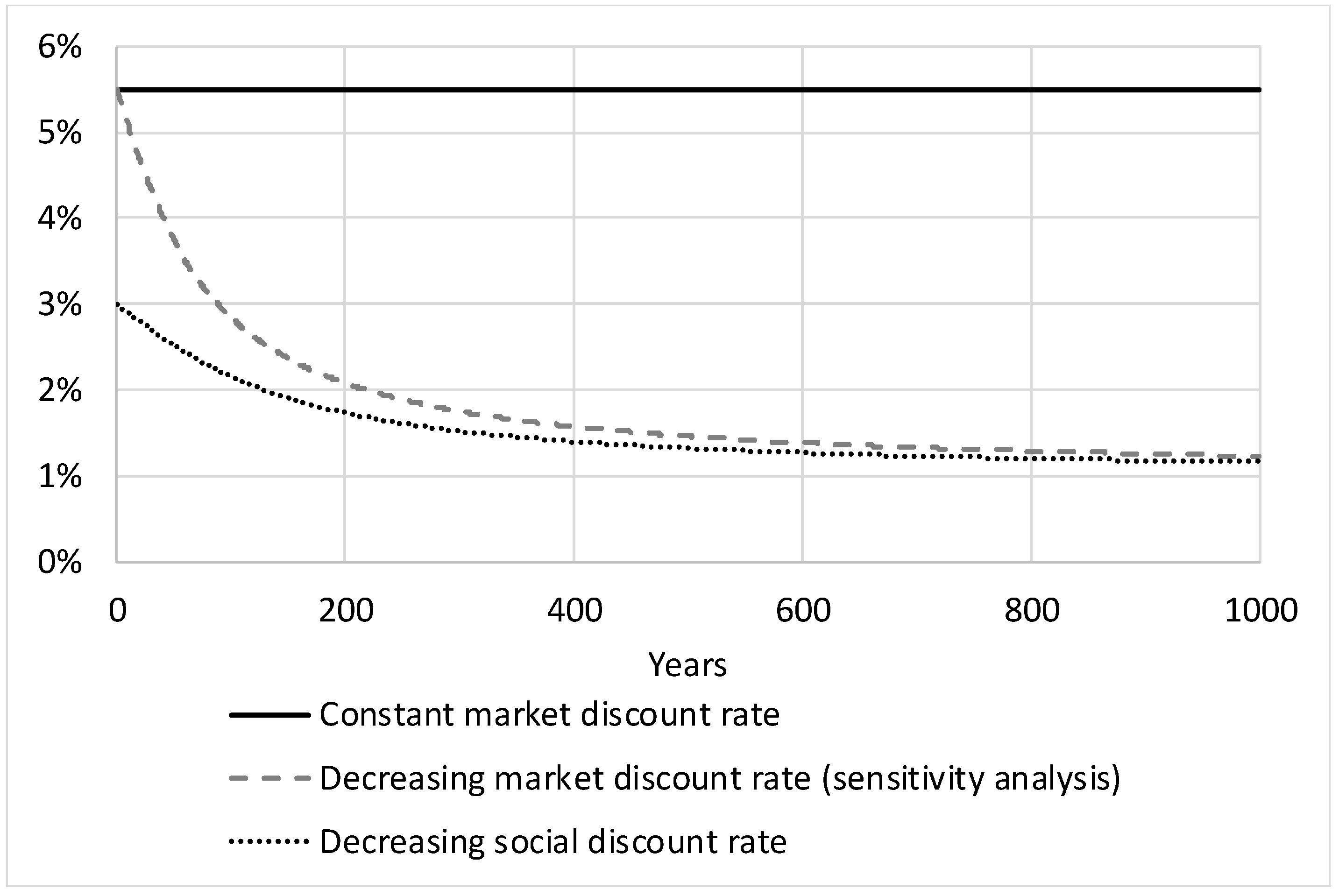
3.4.1. The Social Discount Rate
3.4.2. The Market Discount Rate
3.4.3. Evolution of the Discount Factors and Derivation of the Socially Optimal Price
4. Results
4.1. Externality Cost of Depletion of Sub-Soil Resources
4.2. Limitations
4.2.1. Modelling Assumptions Limits
4.2.2. Data Limitations
5. Comparison to Other Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Resources | 5-Year | Extraction | Estimated Time | Upper Bound Externality Cost of Depletion Relative to the Resource Prices | |||||
|---|---|---|---|---|---|---|---|---|---|
| Trend Price (€ 2017/kg) | Cost/Price | Before Depletion (Years) | Using Constant Market Discount Rate | Using Declining Market Discount Rate | |||||
| t = 300 (Base Case) | t = specific | t = specific; max. 50 | t = 300 | t = specific | t = specific; max. 50 | ||||
| Abrasives (natural) | 0.15 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Aluminium | 1.39 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Antimony | 6.29 | 75% | 13 | 0.60 | 0.29 | 0.29 | 0.39 | 0.28 | 0.28 |
| Arsenic | 0.77 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Asbestos | 1.66 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Barite | 0.12 | 75% | 51 | 0.60 | 0.40 | 0.40 | 0.39 | 0.34 | 0.34 |
| Bauxite | 0.02 | 75% | 71 | 0.60 | 0.45 | 0.40 | 0.39 | 0.36 | 0.34 |
| Beryllium | 419 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Bismuth | 16.2 | 75% | 27 | 0.60 | 0.33 | 0.33 | 0.39 | 0.31 | 0.31 |
| Boron | 0.43 | 75% | 64 | 0.60 | 0.43 | 0.40 | 0.39 | 0.35 | 0.34 |
| Bromine | 1.13 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Cadmium | 1.29 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Cement | 0.09 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Caesium | 66,000 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Chromium | 1.95 | 75% | 18 | 0.60 | 0.30 | 0.30 | 0.39 | 0.29 | 0.29 |
| Clay | 0.05 | 85% | 100 | 0.36 | 0.30 | 0.24 | 0.23 | 0.22 | 0.20 |
| Coal | 0.05 | 82% | 113 | 0.43 | 0.37 | 0.29 | 0.28 | 0.27 | 0.25 |
| Cobalt | 24.4 | 75% | 57 | 0.60 | 0.42 | 0.40 | 0.39 | 0.35 | 0.34 |
| Copper | 3.92 | 54% | 39 | 1.11 | 0.67 | 0.67 | 0.71 | 0.60 | 0.60 |
| Crude petroleum | 0.22 | 57% | 49 | 1.04 | 0.68 | 0.68 | 0.66 | 0.58 | 0.58 |
| Diamond (industrial) | 959 | 75% | 13 | 0.60 | 0.29 | 0.29 | 0.39 | 0.28 | 0.28 |
| Diatomite | 0.26 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Feldspar | 0.09 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Fluorspar | 0.21 | 75% | 40 | 0.60 | 0.37 | 0.37 | 0.39 | 0.33 | 0.33 |
| Gallium | 259 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Garnet (industrial) | 0.25 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Gemstones | 35,900 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Germanium | 1390 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Gold | 30,000 | 75% | 19 | 0.60 | 0.31 | 0.31 | 0.39 | 0.30 | 0.30 |
| Graphite (natural) | 1.01 | 75% | 193 | 0.60 | 0.58 | 0.40 | 0.39 | 0.38 | 0.34 |
| Gypsum | 0.01 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Hafnium | 516 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Helium | 18.9 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Indium | 495 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Iodine | 28 | 75% | 248 | 0.60 | 0.59 | 0.40 | 0.39 | 0.38 | 0.34 |
| Iron ore | 0.04 | 70% | 26 | 0.72 | 0.39 | 0.39 | 0.46 | 0.37 | 0.37 |
| Iron oxide pigments | 1.09 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Kyanite | 0.31 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Lead | 1.61 | 75% | 19 | 0.60 | 0.31 | 0.31 | 0.39 | 0.30 | 0.30 |
| Lime | 0.11 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Lithium | 4.02 | 75% | 431 | 0.60 | 0.61 | 0.40 | 0.39 | 0.39 | 0.34 |
| Magnesium metal | 4.11 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Manganese | 1.13 | 75% | 34 | 0.60 | 0.35 | 0.35 | 0.39 | 0.32 | 0.32 |
| Mercury | 46.6 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Mica (scrap and flake) | 2.82 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Molybdenum | 14.5 | 75% | 41 | 0.60 | 0.37 | 0.37 | 0.39 | 0.33 | 0.33 |
| Natural gas, LNG | 5.02 | 85% | 57 | 0.36 | 0.25 | 0.24 | 0.23 | 0.21 | 0.20 |
| Natural gas, US | 2.16 | 85% | 57 | 0.36 | 0.25 | 0.24 | 0.23 | 0.21 | 0.20 |
| Natural gas, Europe | 3.24 | 85% | 57 | 0.36 | 0.25 | 0.24 | 0.23 | 0.21 | 0.20 |
| Nickel | 7.44 | 75% | 31 | 0.60 | 0.35 | 0.35 | 0.39 | 0.32 | 0.32 |
| Nitrogen | 0.48 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Palladium | 20,800 | 75% | 171 | 0.60 | 0.56 | 0.40 | 0.39 | 0.38 | 0.34 |
| Peat | 0.02 | 84% | 435 | 0.39 | 0.39 | 0.26 | 0.25 | 0.25 | 0.22 |
| Perlite | 0.05 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Phosphate | 0.07 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Phosphate rocks | 0.07 | 75% | 309 | 0.60 | 0.61 | 0.40 | 0.39 | 0.39 | 0.34 |
| Platinum | 22,100 | 75% | 171 | 0.60 | 0.56 | 0.40 | 0.39 | 0.38 | 0.34 |
| Potash | 0.48 | 75% | 95 | 0.60 | 0.49 | 0.40 | 0.39 | 0.37 | 0.34 |
| Potassium chloride | 0.17 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Propane | 0.10 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Pumice | 0.03 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Rare earth | 5.43 | 75% | 1048 | 0.60 | 0.62 | 0.40 | 0.39 | 0.39 | 0.34 |
| Rhenium | 2180 | 75% | 54 | 0.60 | 0.41 | 0.40 | 0.39 | 0.34 | 0.34 |
| Salt | 0.04 | 83% | 100 | 0.41 | 0.34 | 0.27 | 0.26 | 0.25 | 0.23 |
| Sand/gravel (industrial) | 0.05 | 85% | 100 | 0.36 | 0.30 | 0.24 | 0.23 | 0.22 | 0.20 |
| Selenium | 34.3 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Silicon | 2.14 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Silver | 360 | 75% | 21 | 0.60 | 0.31 | 0.31 | 0.39 | 0.30 | 0.30 |
| Sodium carbonate | 0.13 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Sodium sulfate | 0.14 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Stone (crushed) | 0.01 | 85% | 100 | 0.36 | 0.30 | 0.24 | 0.23 | 0.22 | 0.20 |
| Stone (dimension) | 0.15 | 85% | 100 | 0.36 | 0.30 | 0.24 | 0.23 | 0.22 | 0.20 |
| Strontium | 0.32 | 75% | 21 | 0.60 | 0.32 | 0.32 | 0.39 | 0.30 | 0.30 |
| Sulfur | 0.06 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Talc and Pyrophyllite | 0.19 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Tantalum | 213 | 75% | 83 | 0.60 | 0.47 | 0.40 | 0.39 | 0.36 | 0.34 |
| Tellurium | 40.2 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Thallium | 6520 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Thorium | 249 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Tin | 14.6 | 75% | 16 | 0.60 | 0.3 | 0.30 | 0.39 | 0.29 | 0.29 |
| Titanium dioxide | 2.1 | 75% | 42 | 0.60 | 0.38 | 0.38 | 0.39 | 0.33 | 0.33 |
| Titanium metal | 9.12 | 75% | 130 | 0.60 | 0.53 | 0.40 | 0.39 | 0.37 | 0.34 |
| Tungsten | 35.3 | 75% | 38 | 0.60 | 0.36 | 0.36 | 0.39 | 0.34 | 0.33 |
| Uranium | 43 | 75% | 100 | 0.60 | 0.50 | 0.40 | 0.39 | 0.37 | 0.34 |
| Vanadium | 15.7 | 75% | 189 | 0.60 | 0.57 | 0.40 | 0.39 | 0.34 | 0.34 |
| Wollastonite | 0.19 | 75% | 164 | 0.60 | 0.56 | 0.40 | 0.39 | 0.34 | 0.34 |
| Zinc | 1.96 | 75% | 15 | 0.60 | 0.29 | 0.29 | 0.39 | 0.34 | 0.29 |
| Zirconium | 0.59 | 75% | 55 | 0.60 | 0.41 | 0.40 | 0.39 | 0.34 | 0.34 |
References
- Hicks, J.R. Value and Capital, 2nd ed.; Oxford University Press: Oxford, UK, 1946. [Google Scholar]
- El Serafy, S. The proper calculation of income from depleting natural resources. J. Energy Dev. 1981, 7, 73–88. [Google Scholar]
- Miller, M.H.; Upton, C.W. A Test of the Hotelling Valuation Principle. J. Polit. Econ. 1985, 93, 1–25. [Google Scholar] [CrossRef]
- Hotelling, H. The Economics of Exhaustible Resources. J. Polit. Econ. 1931, 39, 137–175. [Google Scholar] [CrossRef]
- Davis, G.A.; Cairns, R.D. Valuing petroleum reserves using current net price. Econ. Inq. 1999, 37, 295–311. [Google Scholar] [CrossRef]
- de Bruyn, S.; Korteland, M.; Markowska, A.; Davidson, M.; de Jong, F.; Bles, M.; Sevenster, M. Shadow Prices Handbook: Valuation and Weighting of Emissions and Environmental Impacts; CE Delft: Delft, The Netherlands, 2010. [Google Scholar]
- Sonderegger, T.; Dewulf, J.; Fantke, P.; de Souza, D.M.; Pfister, S.; Stoessel, F.; Verones, F.; Vieira, M.; Weidema, B.P.; Hellweg, S. Towards harmonizing natural resources as an area of protection in life cycle impact assessment. Int. J. Life Cycle Assess. 2017, 22, 1912–1927. [Google Scholar] [CrossRef]
- Alvarenga, R.A.F.; de Oliveira Lins, I.; de Almeida Neto, J.A. Evaluation of Abiotic Resource LCIA Methods. Resources 2013, 5, 13. [Google Scholar] [CrossRef]
- Northey, S.A.; Mudd, G.M.; Werne, T.T. Unresolved Complexity in Assessments of Mineral Resource Depletion and Availability. Nat. Resour. Res. 2018, 27, 241–255. [Google Scholar] [CrossRef]
- Mohr, S. Projection of World Fossil Fuel Production with Supply and Demand Interactions. Ph.D. Thesis, University of Newcastle, Newcastle, Australia, 2010. [Google Scholar]
- Solow, R.M. The Economics of Resources or the Resources of Economics; Palgrave Macmillan: London, UK, 1974. [Google Scholar]
- Bickel, P.; Friedrich, R. Externe. Externalities of Energy. Methodology 2005 Update; Directorate-General for Research Sustainable Energy Systems (EUR 21951); European Commission: Brussels, Belgium, 2005. [Google Scholar]
- De Caevel, B.; Standaert, S.; van Overbeke, E.; Alexandre, C. Market-based allocation of recycling benefits. Presented at the SETAC-Europe Annual Meeting, Berlin, Germany, 28 February–2 March 2011. [Google Scholar]
- Zhuang, J.; Liang, Z.; Lin, T.; De Guzman, F. Theory and Practice in the Choice of Social Discount Rate for Cost-Benefit Analysis: A Survey; ERD working paper series 94; Asian Development Bank: Mandaluyong, Philippines, 2007. [Google Scholar]
- Marshall, A. Principles of Economics: Unabridged, 8th ed.; Cosimo, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Kesler, S.E. Mineral Supply and Demand into the 21st Century. In US Geological Survey Circular 1294, Proceedings for a Workshop on Deposit Modeling, Mineral Resource Assessment, and Their Role in Sustainable Development; US Geological Survey: Reston, VA, USA, 2007; pp. 55–62. [Google Scholar]
- U.S. Geological Survey. Mineral Commodity Summaries 2015: U.S. Geological Survey; U.S. Geological Survey: Reston, VA, USA, 2015.
- Arrow, K.J.; Cropper, M.L.; Gollier, C.; Groom, B.; Heal, G.M.; Newell, R.G.; Nordhaus, W.D.; Pindyck, R.S.; Pizer, W.A.; Portney, P.R.; et al. How Should Benefits and Costs Be Discounted in an Intergenerational Context? The Views of an Expert Panel; Resources for the Future: Washington, DC, USA, 2012. [Google Scholar]
- Arrow, K.; Cropper, M.; Gollier, C.; Groom, B.; Heal, G.; Newell, R.; Nordhaus, W.; Pindyck, R.; Pizer, W.; Portney, P.; et al. Determining Benefits and Costs for Future Generations. Science 2013, 341, 349–350. [Google Scholar] [CrossRef] [PubMed]
- Weitzman, M.L. Why the far-distant future should be discounted at its lowest possible rate. J. Environ. Econ. Manag. 1998, 36, 201–208. [Google Scholar] [CrossRef]
- Lowe, J. Intergenerational Wealth Transfers and Social Discounting: Supplementary Green Book Guidance; UK HM Treasury: London, UK, 2008. [Google Scholar]
- Giglio, S.; Maggiori, M.; Stroebel, J. Very Long-Run Discount Rates (No. w20133); National Bureau of Economic Research: Cambridge, MA, USA, 2014. [Google Scholar]
- Eurostat. Annual Detailed Enterprise Statistics for Industry (NACE Rev. 2, B-E). 2018. Available online: https://ec.europa.eu/eurostat/web/products-datasets/-/sbs_na_ind_r2 (accessed on 13 March 2018).
- Steen, B. A New Impact Assessment Version for the EPS System—EPS 2015dx—Excluding Climate Impacts from Secondary Particles; Swedish Life Cycle Center Report; Chalmers University of Technology: Göteborg, Sweden, 2015. [Google Scholar]
- Steen, B. The EPS 2015d Impact Assessment Method—An Overview; Swedish Life Cycle Centre report; Chalmers University of Technology: Göteborg, Sweden, 2015. [Google Scholar]
- Vieira, M.D.M.; Ponsioen, T.C.; Goedkoop, M.; Huijbregts, M.A.J. Surplus cost potential as a life cycle impact indicator for metal extraction. Resources 2016, 5, 2. [Google Scholar] [CrossRef]

| Using Constant Market Discount Rate | Using Declining Market Discount Rates | ||
|---|---|---|---|
| t = 300 (Base Case) | t = 50 | t = 300 | t = 50 |
| 2.42 | 1.60 | 1.54 | 1.36 |
| Resources | 5-Year | Extraction | Estimated Time | Upper Bound Externality Cost of Depletion Relative to the Resource Prices | |||||
|---|---|---|---|---|---|---|---|---|---|
| Trend Price (€ 2017/kg) | Cost/Price | Before Depletion (Years) | Using Constant Market Discount Rate | Using Declining Market Discount Rate | |||||
| t = 300 (base case) | t = specific | t = specific; max. 50 | t = 300 | t = specific | t = specific; max. 50 | ||||
| Antimony | 6.29 | 75% | 13 | 0.60 | 0.29 | 0.29 | 0.39 | 0.28 | 0.28 |
| Bauxite | 0.02 | 75% | 71 | 0.60 | 0.45 | 0.40 | 0.39 | 0.36 | 0.34 |
| Bismuth | 16.2 | 75% | 27 | 0.60 | 0.33 | 0.33 | 0.39 | 0.31 | 0.31 |
| Boron | 0.43 | 75% | 64 | 0.60 | 0.43 | 0.40 | 0.39 | 0.35 | 0.34 |
| Chromium | 1.95 | 75% | 18 | 0.60 | 0.30 | 0.30 | 0.39 | 0.29 | 0.29 |
| Coal | 0.05 | 82% | 113 | 0.43 | 0.37 | 0.29 | 0.28 | 0.27 | 0.25 |
| Cobalt | 24.4 | 75% | 57 | 0.60 | 0.42 | 0.40 | 0.39 | 0.35 | 0.34 |
| Copper | 3.92 | 54% | 39 | 1.11 | 0.67 | 0.67 | 0.71 | 0.60 | 0.60 |
| Crude petroleum | 0.22 | 57% | 49 | 1.04 | 0.68 | 0.68 | 0.66 | 0.58 | 0.58 |
| Fluorspar | 0.21 | 75% | 40 | 0.60 | 0.37 | 0.37 | 0.39 | 0.33 | 0.33 |
| Gold | 30,000 | 75% | 19 | 0.60 | 0.31 | 0.31 | 0.39 | 0.30 | 0.30 |
| Graphite (natural) | 1.01 | 75% | 193 | 0.60 | 0.58 | 0.40 | 0.39 | 0.38 | 0.34 |
| Iodine | 28 | 75% | 248 | 0.60 | 0.59 | 0.40 | 0.39 | 0.38 | 0.34 |
| Iron ore | 0.04 | 70% | 26 | 0.72 | 0.39 | 0.39 | 0.46 | 0.37 | 0.37 |
| Lead | 1.61 | 75% | 19 | 0.60 | 0.31 | 0.31 | 0.39 | 0.30 | 0.30 |
| Lithium | 4.02 | 75% | 431 | 0.60 | 0.61 | 0.40 | 0.39 | 0.39 | 0.34 |
| Manganese | 1.13 | 75% | 34 | 0.60 | 0.35 | 0.35 | 0.39 | 0.32 | 0.32 |
| Molybdenum | 14.5 | 75% | 41 | 0.60 | 0.37 | 0.37 | 0.39 | 0.33 | 0.33 |
| Nickel | 7.44 | 75% | 31 | 0.60 | 0.35 | 0.35 | 0.39 | 0.32 | 0.32 |
| Palladium | 20,800 | 75% | 171 | 0.60 | 0.56 | 0.40 | 0.39 | 0.38 | 0.34 |
| Peat | 0.02 | 84% | 435 | 0.39 | 0.39 | 0.26 | 0.25 | 0.25 | 0.22 |
| Phosphate rocks | 0.07 | 75% | 309 | 0.60 | 0.61 | 0.40 | 0.39 | 0.39 | 0.34 |
| Platinum | 22,100 | 75% | 171 | 0.60 | 0.56 | 0.40 | 0.39 | 0.38 | 0.34 |
| Rhenium | 2180 | 75% | 54 | 0.60 | 0.41 | 0.40 | 0.39 | 0.34 | 0.34 |
| Silver | 360 | 75% | 21 | 0.60 | 0.31 | 0.31 | 0.39 | 0.30 | 0.30 |
| Strontium | 0.32 | 75% | 21 | 0.60 | 0.32 | 0.32 | 0.39 | 0.30 | 0.30 |
| Tantalum | 213 | 75% | 83 | 0.60 | 0.47 | 0.40 | 0.39 | 0.36 | 0.34 |
| Tin | 14.6 | 75% | 16 | 0.60 | 0.3 | 0.30 | 0.39 | 0.29 | 0.29 |
| Titanium dioxide | 2.1 | 75% | 42 | 0.60 | 0.38 | 0.38 | 0.39 | 0.33 | 0.33 |
| Titanium metal | 9.12 | 75% | 130 | 0.60 | 0.53 | 0.40 | 0.39 | 0.37 | 0.34 |
| Tungsten | 35.3 | 75% | 38 | 0.60 | 0.36 | 0.36 | 0.39 | 0.34 | 0.33 |
| Vanadium | 15.7 | 75% | 189 | 0.60 | 0.57 | 0.40 | 0.39 | 0.34 | 0.34 |
| Zinc | 1.96 | 75% | 15 | 0.60 | 0.29 | 0.29 | 0.39 | 0.34 | 0.29 |
| Zirconium | 0.59 | 75% | 55 | 0.60 | 0.41 | 0.40 | 0.39 | 0.34 | 0.34 |
| Resource | Externality Cost of Depletion | ||
|---|---|---|---|
| Results from This Study (Computed from Table A1) (EUR2017/kg) | EPS 2015 (Steen, 2015 [24,25]) (EUR2015/kg) | Surplus Cost Potential Method (Vieira et al., 2016 [26]) (USD2013/kg) | |
| Chromium | 1.2 | 59.5 | |
| Coal | 0.023 | 0.16 | |
| Cobalt | 15 | 179 | |
| Copper | 4.4 | 90.9 | 0.74 |
| Gold | 18 150 | 2 020 000 | |
| Iron Ore | 0.027 | 0.85 | 0.022 |
| Manganese | 0.7 | 4.92 | 4.42 |
| Molybdenum | 8.8 | 2 430 | 3.97 |
| Nickel | 4.5 | 107 | 5.62 |
| Palladium | 12 585 | 6 860 000 | 2480 |
| Silver | 217 | 72 800 | 114 |
| Tin | 8.8 | 482 | |
| Titanium | 5.8 | 0.89 | |
| Tungsten | 21.3 | 3 350 | |
| Uranium | 26.0 | 340 | 29 |
| Vanadium | 9.5 | 34 | |
| Crude petroleum | 0.23 | 0.47 | |
| Zinc | 1.19 | 32 | 6.69 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huppertz, T.; Weidema, B.P.; Standaert, S.; De Caevel, B.; van Overbeke, E. The Social Cost of Sub-Soil Resource Use. Resources 2019, 8, 19. https://doi.org/10.3390/resources8010019
Huppertz T, Weidema BP, Standaert S, De Caevel B, van Overbeke E. The Social Cost of Sub-Soil Resource Use. Resources. 2019; 8(1):19. https://doi.org/10.3390/resources8010019
Chicago/Turabian StyleHuppertz, Tom, Bo P. Weidema, Simon Standaert, Bernard De Caevel, and Elisabeth van Overbeke. 2019. "The Social Cost of Sub-Soil Resource Use" Resources 8, no. 1: 19. https://doi.org/10.3390/resources8010019
APA StyleHuppertz, T., Weidema, B. P., Standaert, S., De Caevel, B., & van Overbeke, E. (2019). The Social Cost of Sub-Soil Resource Use. Resources, 8(1), 19. https://doi.org/10.3390/resources8010019






