A Relationship of Causal Factors in the Economic, Social, and Environmental Aspects Affecting the Implementation of Sustainability Policy in Thailand: Enriching the Path Analysis Based on a GMM Model
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
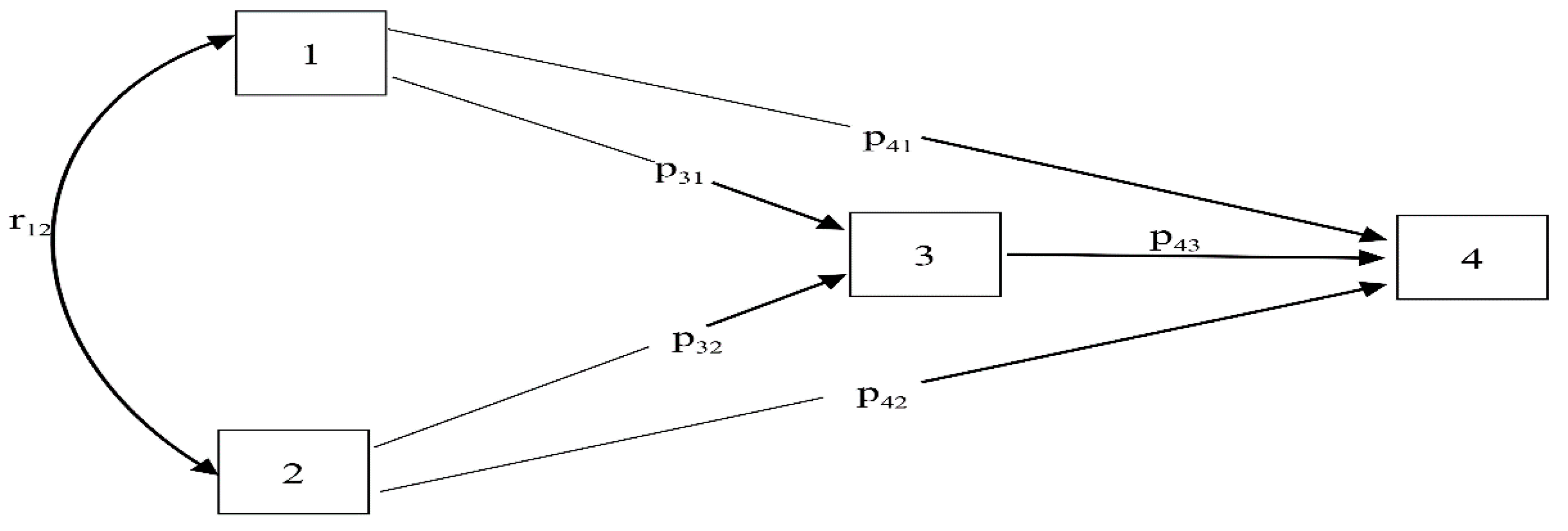
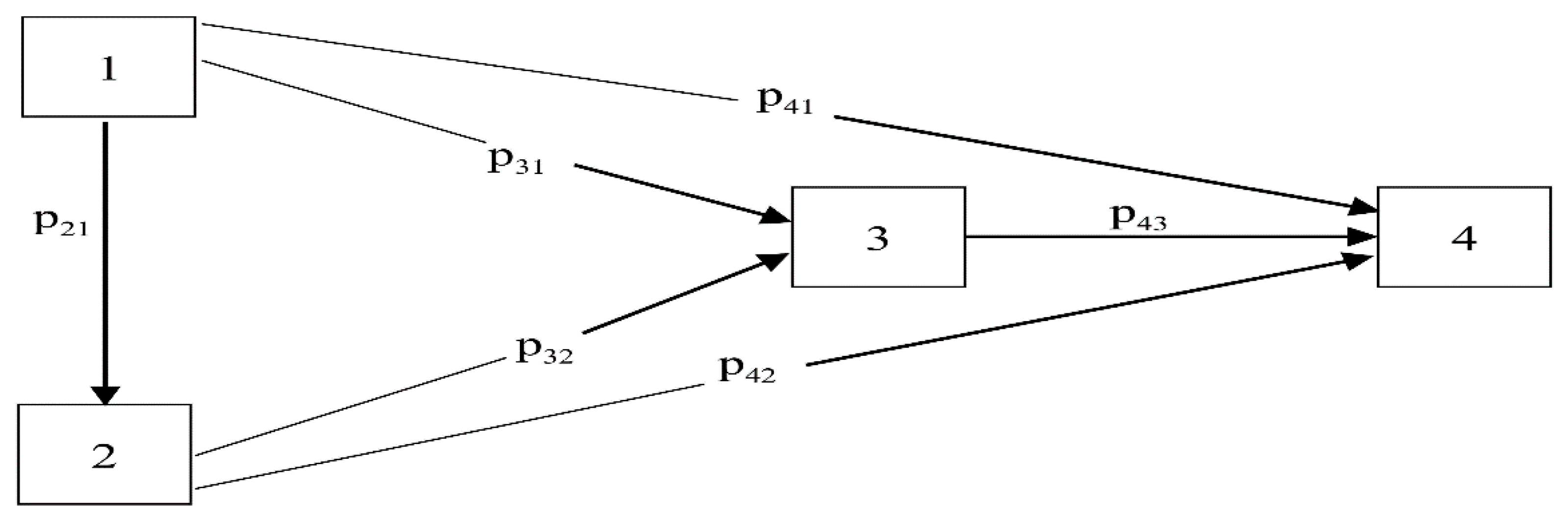
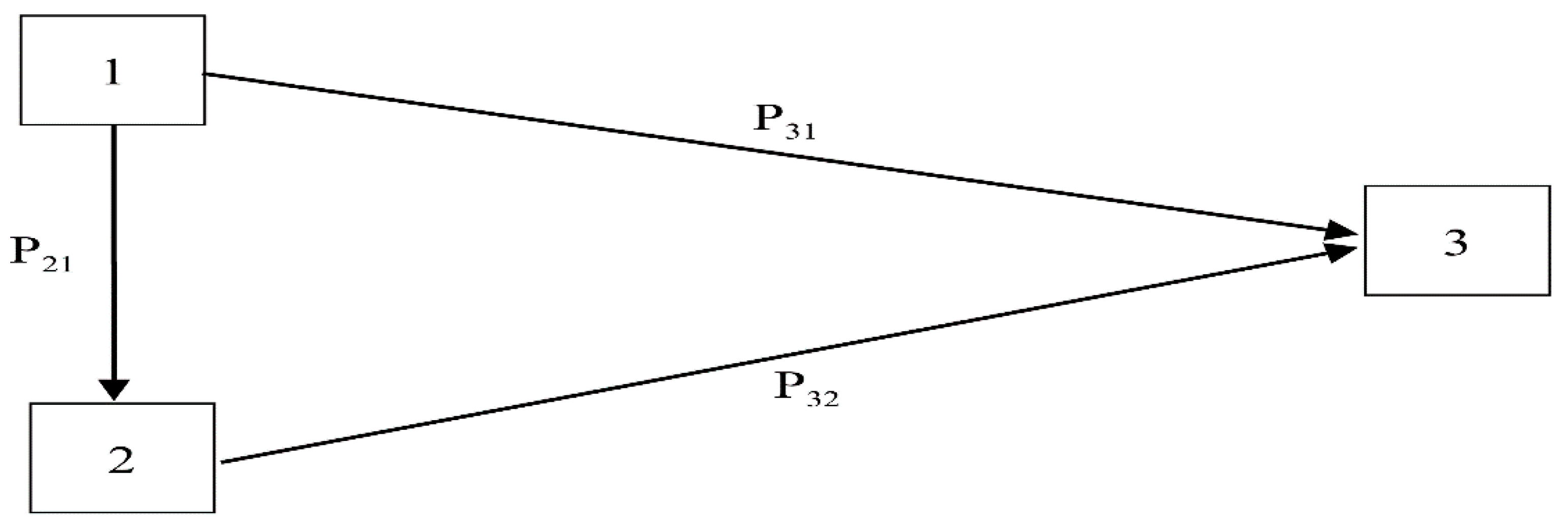
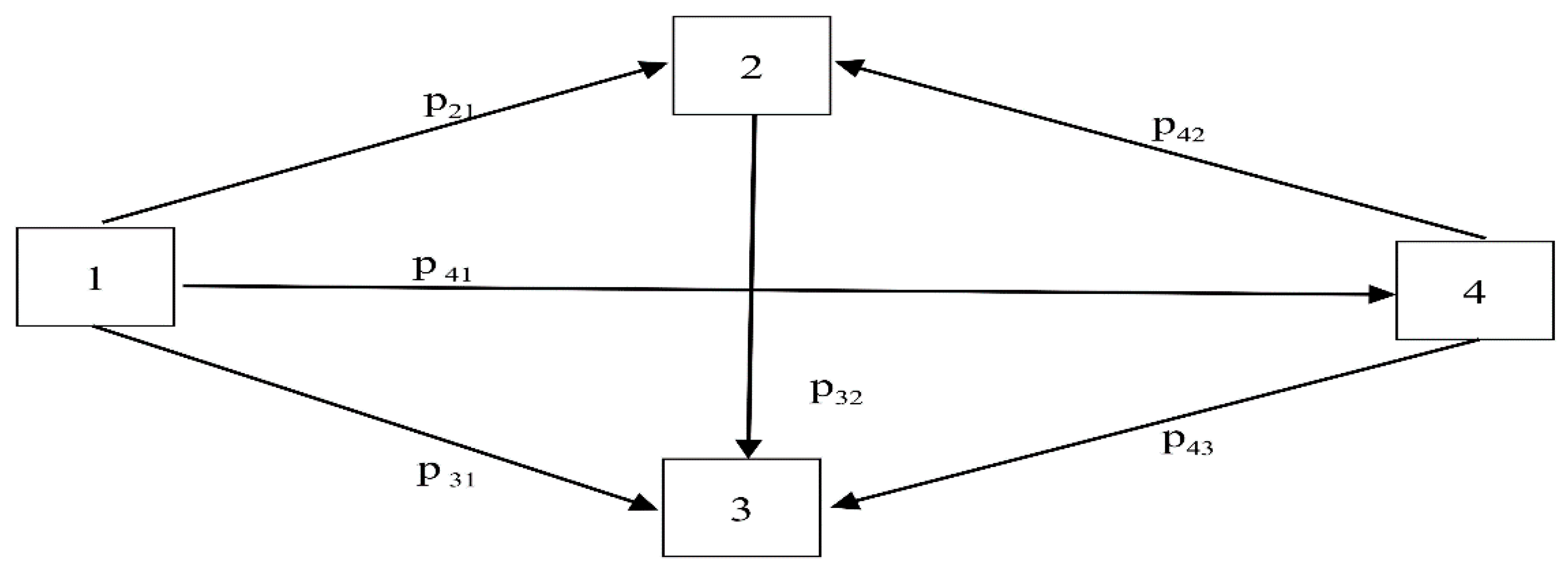
3.1. Path Analysis-GMM Model
3.2. Measurement of the Forecasting Performance
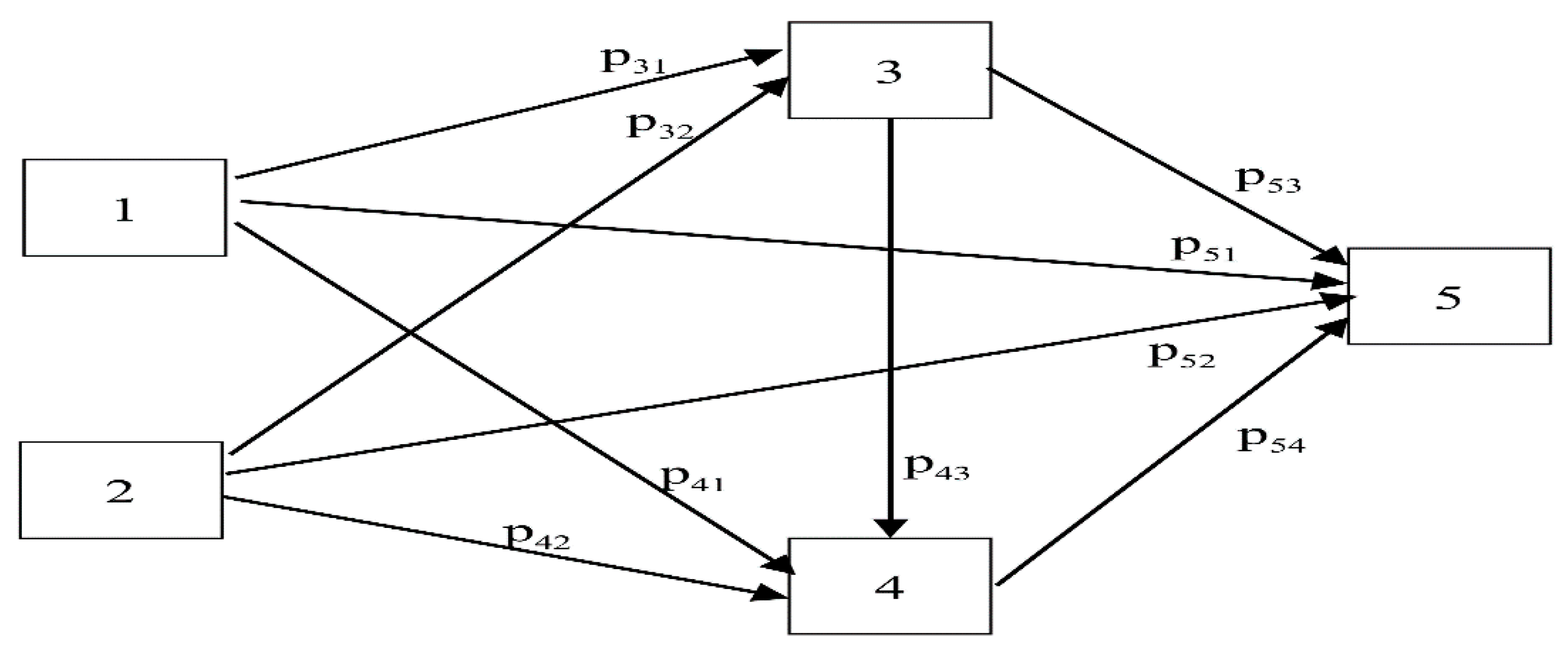
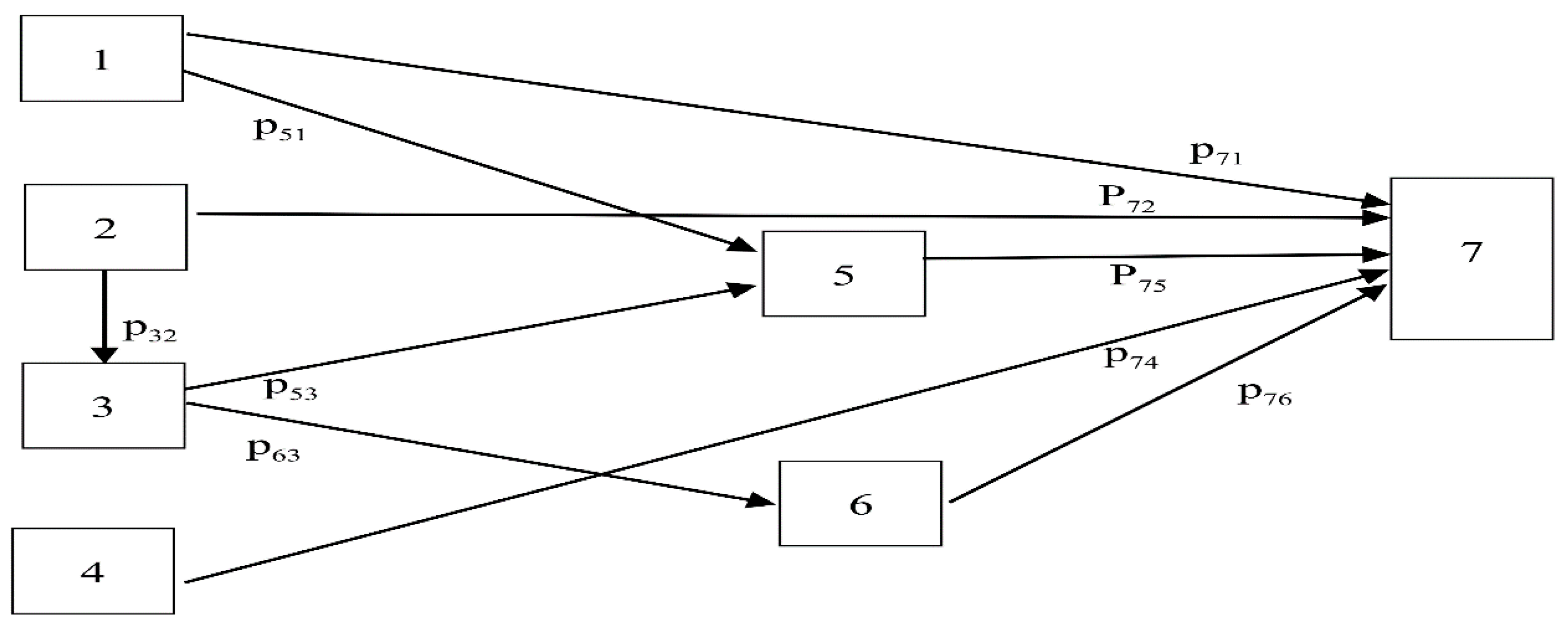
- Determine a variable framework based on the path analysis [56,57], which contains both latent variables (economic , social , and environmental , while the observed variables contained 12 factors that are economic indicators; these are per capita GDP , urbanization rate , industrial structure , net exports , and indirect foreign investment . The authors have found the data regarding these economical indicators from the Office of the National Economic and Social Development Board (NESDB) and National Statistic Office Ministry of Information and Communication Technology. For the social indicators, which are employment , health and illness , social security , and consumer protection , the authors found the data from the Office of the National Economic and Social Development Board (NESDB) and the National Statistic Office Ministry of Information and Communication Technology. For the environmental indicators, which are energy consumption , energy intensity , and carbon dioxide emissions , the authors found the data from the Department of Alternative Energy Development and Efficiency.
- Take the co-integrated variables at the same level to build a path analysis–GMM model, which features both short-term and long-term causal relationships, adding to the presentation of direct and indirect effects [61].
- Compare the effectiveness of the path analysis–GMM model with other models, including multiple regression, the grey model, ANN model, back propagation neural network (BP) model, and ARIMA model through a performance measure of MAPE and RMSE.
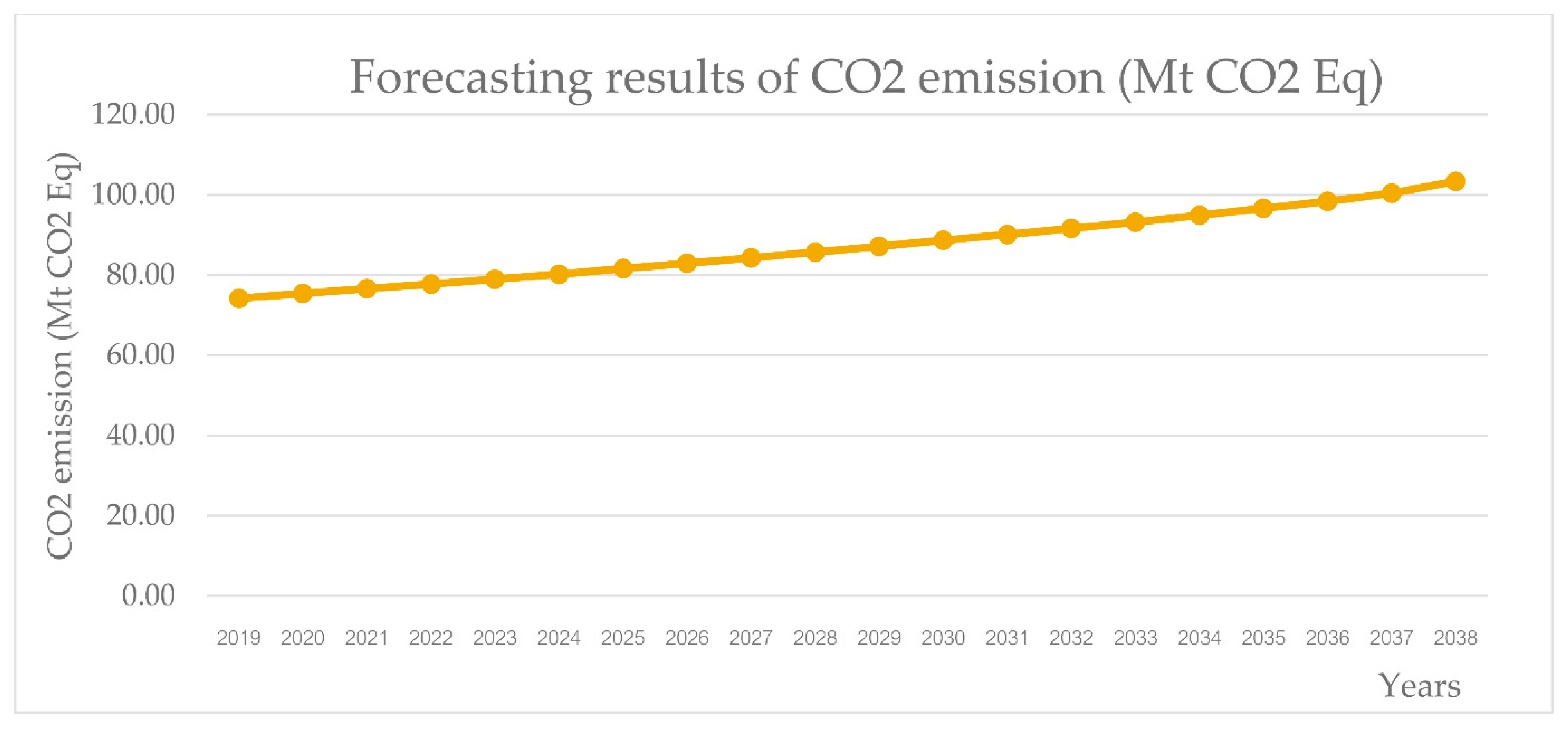
- Forecast the future economic growth and CO2 emissions by using the path analysis–GMM model from 2019 to 2038, totaling 20 years. The flowchart of the path analysis–GMM model is shown in Figure 8.
4. Empirical Analysis
4.1. Screening of Influencing Factors for Model Input
4.2. Analysis of Co-Integration
4.3. Formation of Analysis Modeling with the Path Analysis-GMM Model
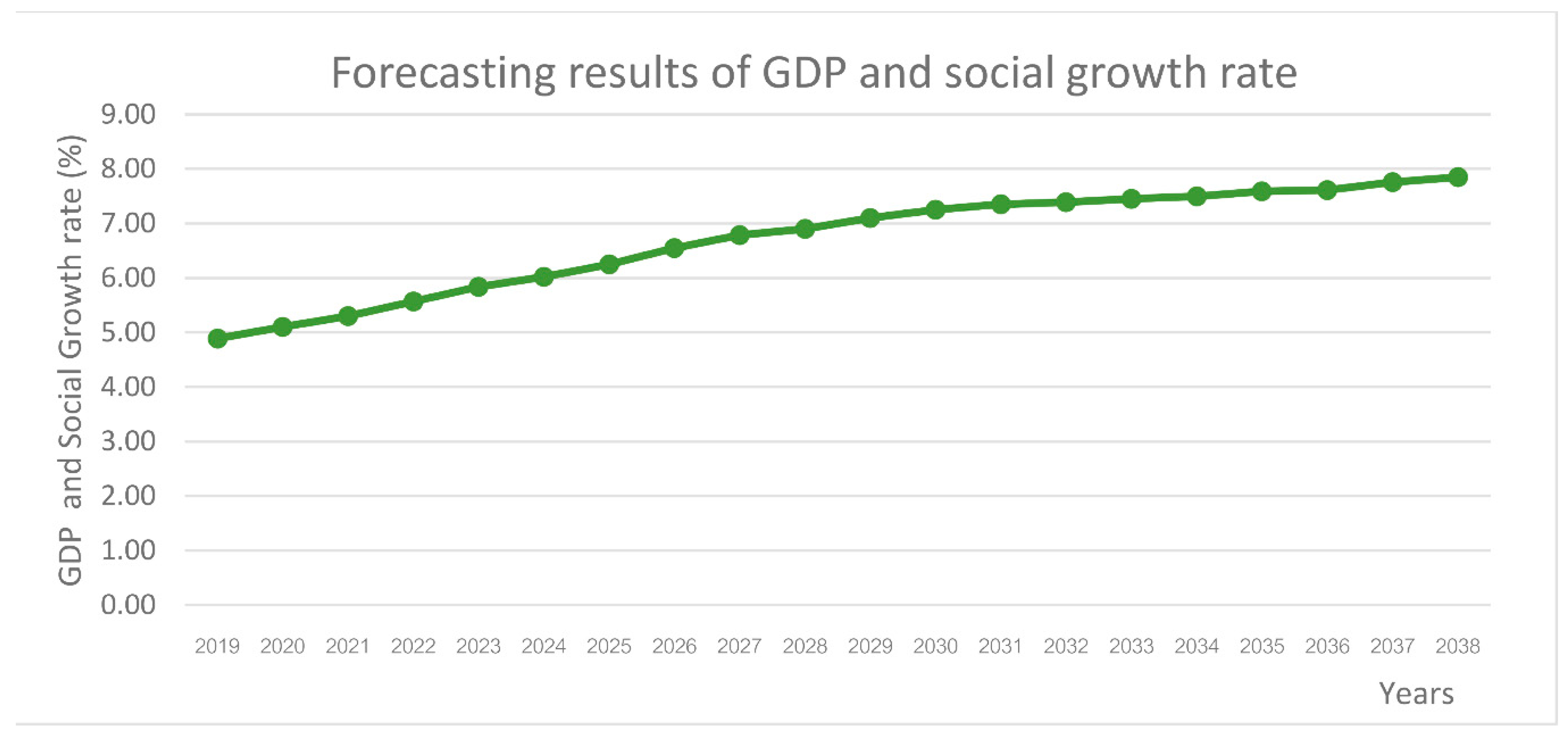
4.4. A Forecasting Model on the Changes of Economic and Social Growth and CO2 Emissions Based on the Path Analysis–GMM Model
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Achawangkul, Y. Thailand’s Alternative Energy Development Plan. Available online: http://www.unescap.org/sites/default/files/MoE%20_%20AE%20policies.pdf (accessed on 1 October 2018).
- Office of the National Economic and Social Development Board (NESDB). Available online: http://www.nesdb.go.th/nesdb_en/more_news.php?cid=154&filename=index (accessed on 1 October 2018).
- National Statistic Office Ministry of Information and Communication Technology. Available online: http://web.nso.go.th/index.htm (accessed on 2 October 2018).
- Department of Alternative Energy Development and Efficiency. Available online: http://www.dede.go.th/ewtadmin/ewt/dede_web/ewt_news.php?nid=47140 (accessed on 2 October 2018).
- Thailand Greenhouse Gas Management Organization (Public Organization). Available online: http://www.tgo.or.th/2015/thai/content.php?s1=7&s2=16&sub3=sub3 (accessed on 2 October 2018).
- Hu, Y.; Guo, D.; Wang, M.; Zhang, Z.; Wang, S. The relationship between energy consumption and economic growth: Evidence from China’s industrial sectors. Energies 2015, 8, 9392–9406. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, H.; Han, X.; He, Z.; Guo, S. Economic growth, electricity consumption, labor force and capital input: A more comprehensive analysis on North China using panel data. Energies 2016, 9, 891. [Google Scholar] [CrossRef]
- Armeanu, D.S.; Vintilă, G.; Gherghina, S.C. Does Renewable Energy Drive Sustainable Economic Growth? Multivariate Panel Data Evidence for EU-28 Countries. Energies 2017, 10, 381. [Google Scholar] [CrossRef]
- To, W.-M.; Lee, P.K.C. Energy Consumption and economic development in Hong Kong, China. Energies 2017, 10, 1883. [Google Scholar] [CrossRef]
- Gómez, M.; Ciarreta, A.; Zarraga, A. Linear and nonlinear causality between energy consumption and economic growth: The case of Mexico 1965–2014. Energies 2018, 11, 784. [Google Scholar] [CrossRef]
- Arango-Miranda, R.; Hausler, R.; Romero-Lopez, R.; Glaus, M.; Ibarra-Zavaleta, S.P. Carbon Dioxide Emissions, Energy Consumption and Economic Growth: A Comparative Empirical Study of Selected Developed and Developing Countries. “The Role of Exergy”. Energies 2018, 11, 2668. [Google Scholar] [CrossRef]
- Chang, C.-C. A multivariate causality test of carbon dioxide emissions, energy consumption and economic growth in China. Appl. Energy 2010, 87, 3533–3537. [Google Scholar] [CrossRef]
- Kivyiro, P.; Arminen, H. Carbon dioxide emissions, energy consumption, economic growth, and foreign direct investment: Causality analysis for Sub-Saharan Africa. Energy 2014, 74, 595–606. [Google Scholar] [CrossRef]
- Wesseh, P.K.; Zoumara, B. Causal independence between energy consumption and economic growth in Liberia: Evidence from a non-parametric bootstrapped causality test Energy. Policy 2012, 50, 518–527. [Google Scholar] [CrossRef]
- Yoo, S.-H.; Ku, S.-J. Causal relationship between nuclear energy consumption and economic growth: A multi-country analysis. Energy Policy 2009, 37, 1905–1913. [Google Scholar] [CrossRef]
- Chang, T.; Gatwabuyege, F.; Gupta, R.; Inglesi-Lotz, R.; Manjezi, N.C.; Simo-Kengne, B.D. Causal relationship between nuclear energy consumption and economic growth in G6 countries: Evidence from panel Granger causality tests. Nucl. Energy 2014, 77, 187–193. [Google Scholar] [CrossRef]
- Nasreen, S.; Anwar, S. Causal relationship between trade openness, economic growth and energy consumption: A panel data analysis of Asian countries. Energy Policy 2014, 69, 82–91. [Google Scholar] [CrossRef]
- Zhangm, Z.; Ren, X. Causal relationships between Energy consumption and economic growth. Energy Procedia 2011, 5, 2065–2071. [Google Scholar]
- Kasman, A.; Duman, Y.S. CO2 emissions, economic growth, energy consumption, trade and urbanization in new EU member and candidate countries: A panel data analysis. Econ. Model. 2015, 44, 97–103. [Google Scholar] [CrossRef]
- Omri, A. CO2 emissions, energy consumption and economic growth nexus in MENA countries: Evidence from simultaneous equations models. Energy Econ. 2013, 40, 657–664. [Google Scholar] [CrossRef]
- Begum, R.A.; Sohag, K.; Abdullah, S.M.S.; Jaafar, M. CO2 emissions, energy consumption, economic and population growth in Malaysia. Renew. Sustain. Energy Rev. 2015, 41, 594–601. [Google Scholar] [CrossRef]
- Ifeakachukwu, N.P. Disaggregate energy consumption and sectoral output in Nigeria. Sci. J. Energy Eng. 2017, 5, 136–145. [Google Scholar] [CrossRef]
- Yang, G.; Wang, H.; Zhou, J.; Liu, X. Analyzing and predicting the economic growth, energy consumption and CO2 emissions in Shanghai. Energy Environ. Res. 2012, 2, 83. [Google Scholar] [CrossRef]
- Soytas, U.; Sari, R. Energy consumption, economic growth, and carbon emissions: Challenges faced by an EU candidate member. Ecol. Econ. 2009, 68, 1667–1675. [Google Scholar] [CrossRef]
- Al-Mulali, U. Oil consumption, CO2 emission and economic growth in MENA countries. Energy 2011, 36, 6165–6171. [Google Scholar] [CrossRef]
- Emodi, N.V.; Emodi, C.C.; Emodi, A.S.A. Reinvestigating the Relationship between CO2 Emission, Energy Consumption and Economic Growth in Nigeria Considering Structural Breaks. Int. J. Civ. Mech. Energy Sci. 2016, 2, 075–090. [Google Scholar]
- Dagher, L.; Yacoubian, T. The causal relationship between energy consumption and economic growth in Lebanon. Energy Policy 2012, 50, 795–801. [Google Scholar] [CrossRef]
- Tang, C.F.; Abosedra, S. The impacts of tourism, energy consumption and political instability on economic growth in the MENA countries. Energy Policy 2014, 68, 458–464. [Google Scholar] [CrossRef]
- Mudarissov, B.A.; Lee, Y. The relationship between energy consumption and economic growth in Kazakhstan. Geosyst. Eng. 2014, 17, 63–68. [Google Scholar] [CrossRef]
- Yu, H.; Pan, S.-Y.; Tang, B.-J.; Mi, Z.-F.; Zhang, Y.; Wei, Y.-M. Urban energy consumption and CO2 emissions in Beijing: Current and future. Energy Effic. 2015, 8, 527–543. [Google Scholar] [CrossRef]
- Alam, M.J.; Begum, I.A.; Buysse, J.; Rahman, S.; Huylenbroeck, G.V. Dynamic modeling of causal relationship between energy consumption, CO2 emissions and economic growth in India. Renew. Sustain. Energy Rev. 2011, 15, 3243–3251. [Google Scholar] [CrossRef]
- Xiong, S.; Fu, Y.; Ray, A. Bayesian nonparametric modeling of categorical data for information fusion and causal inference. Entropy 2018, 20, 396. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, X. Nonlinear Granger causality between health care expenditure and economic growth in the OECD and major developing countries. Int. J. Environ. Res. Public Health 2018, 15, 1953. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, W.; De, G.; Ji, X.; Tan, Z. Forecasting carbon emissions related to energy consumption in Beijing-Tianjin-Hebei region based on grey prediction theory and extreme learning machine optimized by support vector machine algorithm. Energies 2018, 11, 2475. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Beljaars, A.; Panareda, A.-A.; Calvet, J.-C.; Jacobs, C.; Hurk, B.; Viterbo, P.; Lafont, S.; Dutra, E.; et al. Natural land carbon dioxide exchanges in the ECMWF integrated forecasting system: Implementation and offline validation. J. Geophys. Res. Atmos. 2013, 118, 5923–5946. [Google Scholar] [CrossRef]
- Zhu, L.; He, L.; Shang, P.; Zhang, Y.; Ma, Z. Influencing Factors and Scenario Forecasts of Carbon Emissions of the Chinese Power Industry: Based on a Generalized Divisia Index Model and Monte Carlo Simulation. Energies 2018, 11, 2398. [Google Scholar] [CrossRef]
- Khairalla, M.A.; Ning, X.; AL-Jallad, N.T.; El-Faroug, M.O. Short-Term Forecasting for Energy Consumption through Stacking Heterogeneous Ensemble Learning Model. Energies 2018, 11, 1605. [Google Scholar] [CrossRef]
- Ekonomou, L. Greek long-term energy consumption prediction using artificial neural networks. Energy 2010, 35, 512–517. [Google Scholar] [CrossRef]
- Dombayci, Ö.A. The prediction of heating energy consumption in a model house by using artificial neural networks in Denizli-Turkey. Adv. Eng. Softw. 2010, 41, 141–147. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E. Performance prediction of a solar thermal energy system using artificial neural networks. Appl. Therm. Eng. 2014, 73, 1348–1359. [Google Scholar] [CrossRef]
- Kalogiroua, S.A.; Mathioulakis, E.; Belessiotis, V. Artificial neural networks for the performance prediction of large solar systems. Renew. Energy 2014, 63, 90–97. [Google Scholar] [CrossRef]
- Liu, B.; Fu, C.; Bielefield, A.; Liu, Y.Q. Forecasting of Chinese primary energy consumption in 2021 with GRU artificial neural network. Energies 2017, 10, 1453. [Google Scholar] [CrossRef]
- Li, S.; Li, R. Comparison of forecasting energy consumption in Shandong, China using the ARIMA Model, GM Model, and ARIMA-GM Model. Sustainability 2017, 9, 1181. [Google Scholar]
- Dai, S.; Niu, D.; Li, Y. Forecasting of Energy Consumption in China Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm. Appl. Sci. 2018, 8, 678. [Google Scholar] [CrossRef]
- Zeng, B.; Zhou, M.; Zhang, J. Forecasting the Energy Consumption of China’s Manufacturing Using a Homologous Grey Prediction Model. Sustainability 2017, 9, 1975. [Google Scholar] [CrossRef]
- Nelson, R.R.; Phelps, E.S. Investment in humans, technological diffusion and Economic growth. Am. Econ. Rev. 1966, 56, 67–75. [Google Scholar]
- Scicchitano, S. On the complementarity between on-the-job training and R&D: A brief overview. Econ. Bull. 2007, 15, 1–11. [Google Scholar]
- Benhabib, J.; Spiegel, M.M. The role of human capital in economic development: Evidence from aggregate cross-country data. J. Monetary Econ. 1994, 34, 143–173. [Google Scholar] [CrossRef]
- Redding, S. Low-skill, low-quality trap: Strategic Complementarities between human capital and R&D. Econ. J. 1996, 106, 458–470. [Google Scholar]
- Scicchitano, S. Complementarity between heterogeneous human capital and R&D: Can job-training avoid low development traps? Empirica 2010, 37, 361–380. [Google Scholar]
- Janicke, M. Green growth: From a growing Eco-industry to economic sustainability. Energy Policy 2012, 48, 13–21. [Google Scholar] [CrossRef]
- Fabrizi, A.; Guarini, G.; Meliciani, V. Green patents, regulatory policies and research network policies. Res. Policy 2018, 47, 1018–1031. [Google Scholar] [CrossRef]
- Foster, A.; Rosenzweig, M. Technical Change and Human-Capital Returns and Investments: Evidence from the Green Revolution. Am. Econ. Rev. 1996, 86, 931–953. [Google Scholar]
- De Marchi, V.; Grandinetti, R. Knowledge strategies for environmental innovations: The case of Italian manufacturing firms. J. Knowl. Manag. 2013, 17, 569–582. [Google Scholar] [CrossRef]
- Cheng, C.C.J.; Yang, C.-L.; Sheu, C. The link between eco-innovation and business performance: A Taiwanese industry context. J. Clean. Prod. 2014, 64, 81–90. [Google Scholar] [CrossRef]
- Barbara, M.B. Structural Equation Modeling with Mplus: Basic Concepts, Application, and Programming; Taylor & Francis Group: New York, NY, USA, 2012. [Google Scholar]
- Shipley, B. Cause and Correlation in Biology: A User’s Guide to Path Analysis, Structural Equations and Causal Inference; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration with applications to the demand for money. Oxf. Bull. Econ. Stat. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- MacKinnon, J. Critical Values for Cointegration Test in Long-Run Economic Relationships; Engle, R., Granger, C., Eds.; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Enders, W. Applied Econometrics Time Series; Wiley Series in Probability and Statistics; University of Alabama: Tuscaloosa, AL, USA, 2010. [Google Scholar]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]

| Parameters | ||||
|---|---|---|---|---|
| Economic | 1 | 0.73 *** | –0.61 *** | |
| p-value | - | 0.00 | 0.00 | |
| Social | 0.49 *** | 1 | –0.65 *** | |
| p-value | 0.00 | - | 0.00 | |
| Environmental | –0.67 *** | −0.51 *** | 1 | |
| p-value | 0.00 | 0.00 | - | |
| Tau Test | MacKinnon Critical Value | |||
|---|---|---|---|---|
| Variables | Value | 1% | 5% | 10% |
| −5.99 *** | −4.25 | −3.05 | −2.70 | |
| −5.51 *** | −4.25 | −3.05 | −2.70 | |
| −4.95 *** | −4.25 | −3.05 | −2.70 | |
| −4.05 *** | −4.25 | −3.05 | −2.70 | |
| −5.21 *** | −4.25 | −3.05 | −2.70 | |
| −4.75 *** | −4.25 | −3.05 | −2.70 | |
| −4.31 *** | −4.25 | −3.05 | −2.70 | |
| −4.29 *** | −4.25 | −3.05 | −2.70 | |
| −4.67 *** | −4.25 | −3.05 | −2.70 | |
| −6.55 *** | −4.25 | −3.05 | −2.70 | |
| −4.90 *** | −4.25 | −3.05 | −2.70 | |
| −6.07 *** | −4.25 | −3.05 | −2.70 | |
| Variables | Hypothesized No of CE(S) | Trace Statistic Test | Max-Eigen Statistic Test | MacKinnon Critical Value | |
|---|---|---|---|---|---|
| 1% | 5% | ||||
| , , , , , , , , , , , | None ** | 210.50 ** | 235.05 ** | 15.75 | 12.50 |
| At Most 1 ** | 75.95 ** | 94.60 ** | 7.50 | 5.55 | |
| Dependent Variables | Type of Effect | Independent Variables | |||
|---|---|---|---|---|---|
| Economic | DE | - | 0.51 *** | - | −0.62 *** |
| IE | - | - | - | - | |
| Social | DE | 0.69 *** | - | - | −0.55 *** |
| IE | - | - | - | - | |
| Environmental | DE | 0.75 *** | 0.33 *** | - | −0.04 ** |
| IE | 0.21 *** | 0.27 *** | - | - | |
| Forecasting Model | MAPE (%) | RMSE (%) |
|---|---|---|
| Multiple Regression model | 18.99 | 23.07 |
| Grey model | 14.09 | 15.26 |
| ANN model | 12.05 | 14.09 |
| BP model | 9.01 | 8.87 |
| ARIMA model | 5.11 | 4.39 |
| Path analysis–GMM model | 1.01 | 1.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sutthichaimethee, P.; Dockthaisong, B. A Relationship of Causal Factors in the Economic, Social, and Environmental Aspects Affecting the Implementation of Sustainability Policy in Thailand: Enriching the Path Analysis Based on a GMM Model. Resources 2018, 7, 87. https://doi.org/10.3390/resources7040087
Sutthichaimethee P, Dockthaisong B. A Relationship of Causal Factors in the Economic, Social, and Environmental Aspects Affecting the Implementation of Sustainability Policy in Thailand: Enriching the Path Analysis Based on a GMM Model. Resources. 2018; 7(4):87. https://doi.org/10.3390/resources7040087
Chicago/Turabian StyleSutthichaimethee, Pruethsan, and Boonton Dockthaisong. 2018. "A Relationship of Causal Factors in the Economic, Social, and Environmental Aspects Affecting the Implementation of Sustainability Policy in Thailand: Enriching the Path Analysis Based on a GMM Model" Resources 7, no. 4: 87. https://doi.org/10.3390/resources7040087
APA StyleSutthichaimethee, P., & Dockthaisong, B. (2018). A Relationship of Causal Factors in the Economic, Social, and Environmental Aspects Affecting the Implementation of Sustainability Policy in Thailand: Enriching the Path Analysis Based on a GMM Model. Resources, 7(4), 87. https://doi.org/10.3390/resources7040087