Interannual Variability and Seasonal Predictability of Wind and Solar Resources
Abstract
1. Introduction
2. Methods
2.1. Reanalysis Wind and Solar Resource Fields
2.2. Wind and Solar Interannual Variability
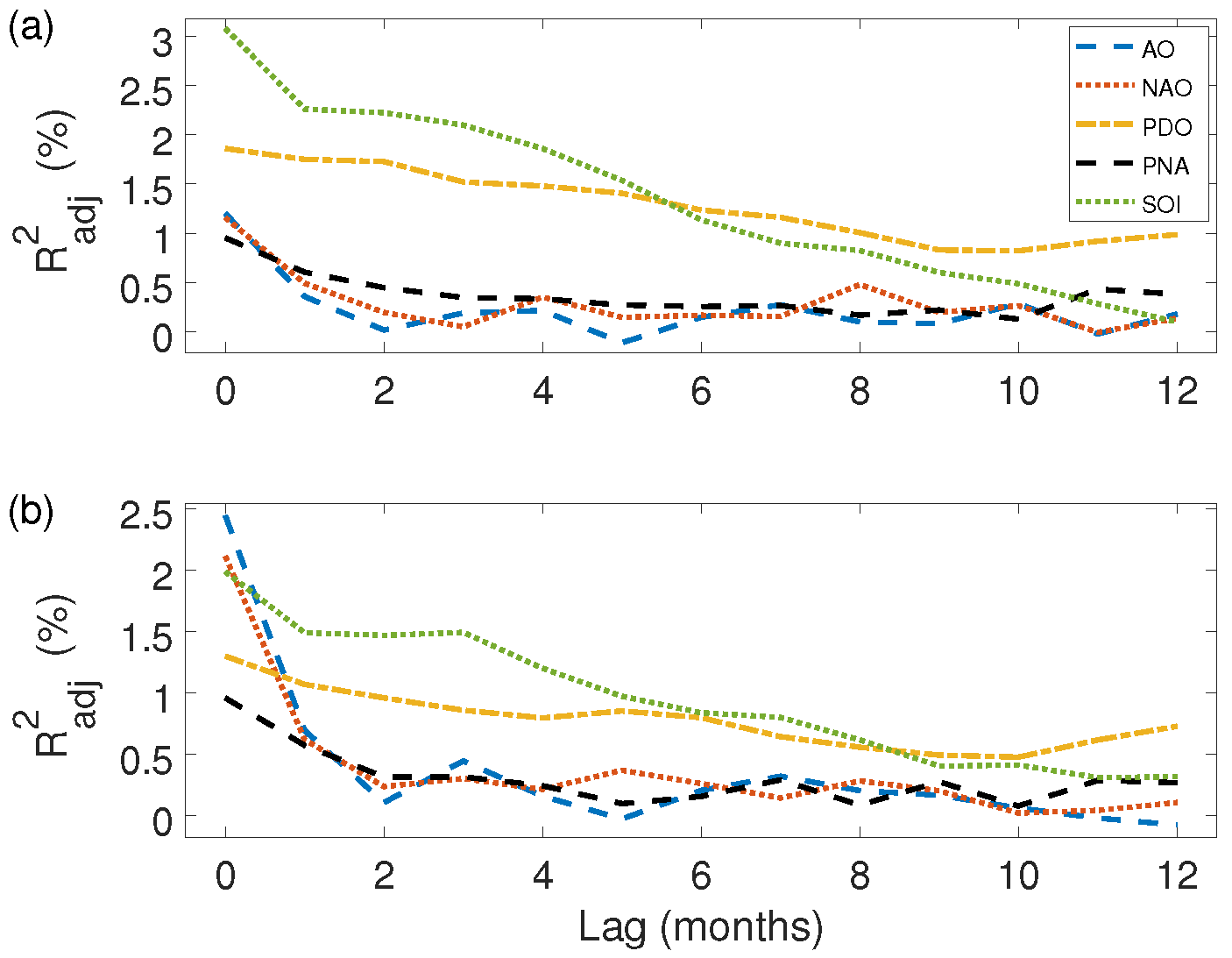
2.3. Wind and Solar Associations with Climate Modes and Potential Predictability
- Arctic Oscillation (AO), a mode of surface-pressure variability between the Arctic and North Atlantic and Pacific [52].
- North Atlantic Oscillation (NAO), a mode of 500-millibar (mb) height variability between Greenland and the central North Atlantic [53].
- Pacific Decadal Oscillation (PDO), a mode of North Pacific SST variability [54].
- Pacific-North America Index (PNA), a mode of 500-mb height variability between the North Pacific and western North America [55].
- Southern Oscillation Index (SOI), surface pressure variability across the tropical Pacific [56].
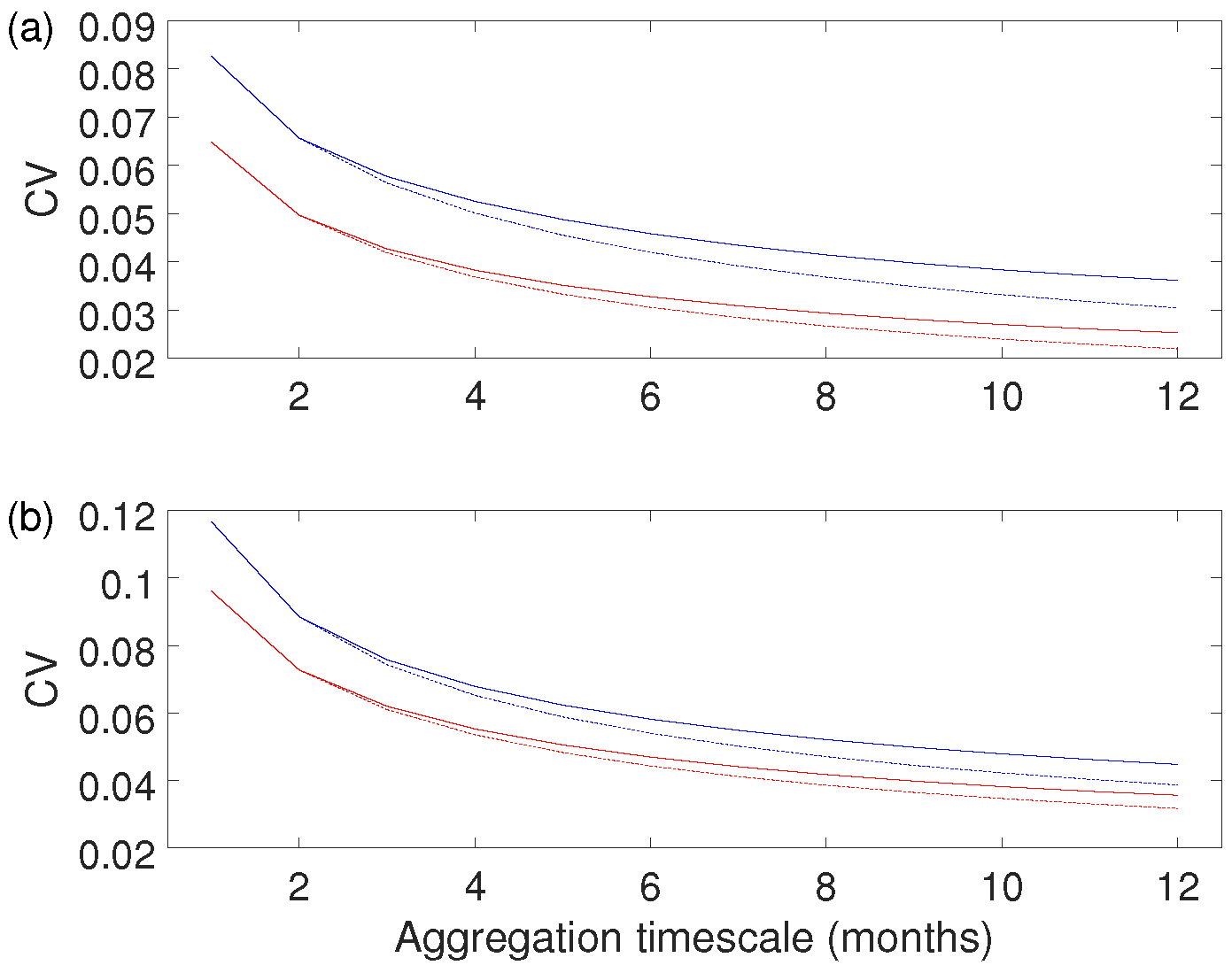
2.4. Interannual Variability over Longer Aggregation Periods
3. Results
3.1. Interannual Variability
3.2. Association with Climate Modes and Predictability
3.3. Longer Aggregation Periods
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kostylev, V.; Pavlovski, A. Solar power forecasting performance—Towards industry standards. In Proceedings of the 1st International Workshop on the Integration of Solar Power into Power Systems, Aarhus, Denmark, 24 October 2011. [Google Scholar]
- Masa-Bote, D.; Castillo-Cagigal, M.; Matallanas, E.; Caamaño-Martín, E.; Gutiérrez, A.; Monasterio-Huelín, F.; Jiménez-Leube, J. Improving photovoltaics grid integration through short time forecasting and self-consumption. Appl. Energy 2014, 125, 103–113. [Google Scholar] [CrossRef]
- Widén, J.; Carpman, N.; Castellucci, V.; Lingfors, D.; Olauson, J.; Remouit, F.; Bergkvist, M.; Grabbe, M.; Waters, R. Variability assessment and forecasting of renewables: A review for solar, wind, wave and tidal resources. Renew. Sustain. Energy Rev. 2015, 44, 356–375. [Google Scholar] [CrossRef]
- Juban, R.; Ohlsson, H.; Maasoumy, M.; Poirier, L.; Kolter, J.Z. A multiple quantile regression approach to the wind, solar, and price tracks of GEFCom2014. Int. J. Forecast. 2016, 32, 1094–1102. [Google Scholar] [CrossRef]
- Hammer, A.; Heinemann, D.; Lorenz, E.; Lückehe, B. Short-term forecasting of solar radiation: A statistical approach using satellite data. Sol. Energy 1999, 67, 139–150. [Google Scholar] [CrossRef]
- Sfetsos, A.; Coonick, A.H. Univariate and multivariate forecasting of hourly solar radiation with artificial intelligence techniques. Sol. Energy 2000, 68, 169–178. [Google Scholar] [CrossRef]
- Perez, R.; Moore, K.; Wilcox, S.; Renné, D.; Zelenka, A. Forecasting solar radiation–Preliminary evaluation of an approach based upon the national forecast database. Sol. Energy 2007, 81, 809–812. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M. A 24-h forecast of solar irradiance using artificial neural network: Application for performance prediction of a grid-connected PV plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar] [CrossRef]
- Mathiesen, P.; Kleissl, J. Evaluation of numerical weather prediction for intra-day solar forecasting in the continental United States. Sol. Energy 2011, 86, 967–977. [Google Scholar] [CrossRef]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washom, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Sol. Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Dong, Z.; Jirutitijaroen, P.; Chen, N.; Walsh, W.M. Solar irradiance forecasting using spatial-temporal covariance structures and time-forward kriging. Renew. Energy 2013, 60, 235–245. [Google Scholar] [CrossRef]
- Isvoranu, D.; Badescu, V. Preliminary WRF-ARW model analysis of global solar irradiation forecasting. Math. Model. Civ. Eng. 2014, 10, 1–8. [Google Scholar] [CrossRef]
- Chu, Y.; Li, M.; Pedro, H.T.; Coimbra, C.F. Real-time prediction intervals for intra-hour DNI forecasts. Renew. Energy 2015, 83, 234–244. [Google Scholar] [CrossRef]
- Larson, D.P.; Nonnenmacher, L.; Coimbra, C.F. Day-ahead forecasting of solar power output from photovoltaic plants in the American Southwest. Renew. Energy 2016, 91, 11–20. [Google Scholar] [CrossRef]
- Golestaneh, F.; Gooi, H.B.; Pinson, P. Generation and evaluation of space–time trajectories of photovoltaic power. Appl. Energy 2016, 176, 80–91. [Google Scholar] [CrossRef]
- Lange, M. On the uncertainty of wind power predictions–analysis of the forecast accuracy and statistical distribution of errors. J. Sol. Energy Eng. 2005, 127, 177–184. [Google Scholar] [CrossRef]
- Hering, A.S.; Genton, M.G. Powering up with space-time wind forecasting. J. Am. Stat. Assoc. 2010, 105, 92–104. [Google Scholar] [CrossRef]
- Gallego-Castillo, C.; Bessa, R.; Cavalcante, L.; Lopez-Garcia, O. On-line quantile regression in the RKHS (Reproducing Kernel Hilbert Space) for operational probabilistic forecasting of wind power. Energy 2016, 113, 355–365. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Wilcox, S.M. Assessment of spatial and temporal variability in the US solar resource from radiometric measurements and predictions from models using ground-based or satellite data. Sol. Energy 2011, 85, 1068–1084. [Google Scholar] [CrossRef]
- Correia, J.; Bastos, A.; Brito, M.; Trigo, R. The influence of the main large-scale circulation patterns on wind power production in Portugal. Renew. Energy 2017, 102 Pt A, 214–223. [Google Scholar] [CrossRef]
- Gueymard, C.A. Temporal variability in direct and global irradiance at various time scales as affected by aerosols. Sol. Energy 2012, 86, 3544–3553. [Google Scholar] [CrossRef]
- Rife, D.; Krakauer, N.Y.; Cohan, D.S.; Collier, J.C. A new kind of drought: U.S. record low windiness in 2015. Earthzine 2016. Available online: https://earthzine.org/2016/06/10/a-new-kind-of-drought-u-s-record-low-windiness-in-2015/ (accessed on 18 July 2017).
- Koster, R.D.; Suarez, M.J.; Heiser, M. Variance and predictability of precipitation at seasonal-to-interannual timescales. J. Hydrometeorol. 2000, 1, 26–46. [Google Scholar] [CrossRef]
- National Research Council. Assessment of Intraseasonal to Interannual Climate Prediction and Predictability; Technical Report; National Academies Press: Washington, DC, USA, 2010. [Google Scholar]
- Troccoli, A. Seasonal climate forecasting. Meteorol. Appl. 2010, 17, 251–268. [Google Scholar] [CrossRef]
- Smith, D.M.; Scaife, A.A.; Kirtman, B.P. What is the current state of scientific knowledge with regard to seasonal and decadal forecasting? Environ. Res. Lett. 2012, 7, 015602. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; García-Serrano, J.; Lienert, F.; Biescas, A.P.; Rodrigues, L.R.L. Seasonal climate predictability and forecasting: Status and prospects. Wiley Interdiscip. Rev. Clim. Chang. 2013, 4. [Google Scholar] [CrossRef]
- Committee on Developing a U.S. Research Agenda to Advance Subseasonal to Seasonal Forecasting; Board on Atmospheric Sciences and Climate; Ocean Studies Board; Division on Earth and Life Studies; National Academies of Sciences, Engineering, and Medicine. Next Generation Earth System Prediction: Strategies for Subseasonal to Seasonal Forecasts; National Academies Press: Washington, DC, USA, 2016. [Google Scholar]
- Barnston, A.G.; Mason, S.J.; Goddard, L.; Dewitt, D.G.; Zebiak, S.E. Multimodel ensembling in seasonal climate forecasting at IRI. Bull. Am. Meteorol. Soc. 2003, 84, 1783–1796. [Google Scholar] [CrossRef]
- Kumar, K.K.; Hoerling, M.; Rajagopalan, B. Advancing dynamical prediction of Indian monsoon rainfall. Geophys. Res. Lett. 2005, 32, L08704. [Google Scholar]
- Barnston, A.G.; Li, S.; Mason, S.J.; DeWitt, D.G.; Goddard, L.; Gong, X. Verification of the first 11 years of IRI’s seasonal climate forecasts. Appl. Meteorol. Climatol. 2010, 49, 493–520. [Google Scholar] [CrossRef]
- Barnston, A.G.; Mason, S.J. Evaluation of IRI’s seasonal climate forecasts for the extreme 15% tails. Weather Forecast. 2011, 26, 545–554. [Google Scholar] [CrossRef]
- Mwangi, E.; Wetterhall, F.; Dutra, E.; Di Giuseppe, F.; Pappenberger, F. Forecasting droughts in East Africa. Hydrol. Earth Syst. Sci. 2014, 18, 611–620. [Google Scholar] [CrossRef]
- Dutra, E.; Pozzi, W.; Wetterhall, F.; Di Giuseppe, F.; Magnusson, L.; Naumann, G.; Barbosa, P.; Vogt, J.; Pappenberger, F. Global meteorological drought—Part 2: Seasonal forecasts. Hydrol. Earth Syst. Sci. 2014, 18, 2669–2678. [Google Scholar] [CrossRef]
- Klemm, T.; McPherson, R.A. The development of seasonal climate forecasting for agricultural producers. Agric. Forest Meteorol. 2017, 232, 384–399. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Robertson, F.R.; Takacs, L.; Molod, A.; Mocko, D. Atmospheric Water Balance and Variability in the MERRA-2 Reanalysis. J. Clim. 2017. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Draper, C.S.; Mahanama, S.P.P.; Partyka, G.S. Land surface precipitation in MERRA-2. J. Clim. 2017. [Google Scholar] [CrossRef]
- Wargan, K.; Coy, L. Strengthening of the Tropopause Inversion Layer during the 2009 Sudden Stratospheric Warming: A MERRA-2 Study. J. Atmos. Sci. 2016, 73, 1871–1887. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24. [Google Scholar] [CrossRef]
- Randles, C.A.; da Silva, A.M.; Buchard, V.; Colarco, P.R.; Darmenov, A.; Govindaraju, R.; Smirnov, A.; Holben, B.; Ferrare, R.; Hair, J.; et al. The MERRA-2 Aerosol Reanalysis, 1980—Onward, Part I: System Description and Data Assimilation Evaluation. J. Clim. 2017. [Google Scholar] [CrossRef]
- Cannon, D.; Brayshaw, D.; Methven, J.; Coker, P.; Lenaghan, D. Using reanalysis data to quantify extreme wind power generation statistics: A 33 year case study in Great Britain. Renew. Energy 2015, 75, 767–778. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]
- Menne, M.; Durre, I.; Vose, R.; Gleason, B.; Houston, T. An overview of the Global Historical Climatology Network-Daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive automated quality assurance of daily surface observations. J. Appl. Meteorol. Climatol. 2010, 49, 1615–1633. [Google Scholar] [CrossRef]
- Karlsson, K.G.; Riihelä, A.; Müller, R.; Meirink, J.F.; Sedlar, J.; Stengel, M.; Lockhoff, M.; Trentmann, J.; Kaspar, F.; Hollmann, R.; et al. CLARA-A1: A cloud, albedo, and radiation dataset from 28 year of global AVHRR data. Atmos. Chem. Phys. 2013, 13, 5351–5367. [Google Scholar] [CrossRef]
- Olkin, I.; Pratt, J.W. Unbiased Estimation of Certain Correlation Coefficients. Ann. Math. Statist. 1958, 29, 201–211. [Google Scholar] [CrossRef]
- Yin, P.; Fan, X. Estimating R2 Shrinkage in Multiple Regression: A Comparison of Different Analytical Methods. J. Exp. Educ. 2001, 69, 203–224. [Google Scholar] [CrossRef]
- Skidmore, S.T.; Thompson, B. Choosing the best correction formula for the Pearson r2 effect size. J. Exp. Educ. 2011, 79, 257–278. [Google Scholar] [CrossRef]
- NOAA-NCEI. Teleconnections. Available online: https://www.ncdc.noaa.gov/teleconnections/ (accessed on 18 July 2017).
- Baldwin, M.P. Annular modes in global daily surface pressure. Geophys. Res. Lett. 2001, 28, 4115–4118. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Visbeck, M. The North Atlantic Oscillation. Science 2001, 291, 603–605. [Google Scholar] [CrossRef] [PubMed]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Horel, J.D.; Wallace, J.M. Planetary-Scale Atmospheric Phenomena Associated with the Southern Oscillation. Mon. Weather Rev. 1981, 109, 813–829. [Google Scholar] [CrossRef]
- Perez, M.J.R.; Fthenakis, V. Impacts of long-timescale variability in solar resources at high PV penetrations: Quantification. In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference (PVSC), Austin, TX, USA, 3–8 June 2012; pp. 002481–002486. [Google Scholar]
- Krishnamurti, T.N.; Chakraborty, A.; Krishnamurti, R.; Dewar, W.K.; Clayson, C.A. Seasonal prediction of sea surface temperature anomalies using a suite of 13 coupled atmosphere-ocean models. J. Clim. 2006, 19, 6069–6088. [Google Scholar] [CrossRef]
- Kumar, A.; Chen, M.; Zhang, L.; Wang, W.; Xue, Y.; Wen, C.; Marx, L.; Huang, B. An analysis of the nonstationarity in the bias of sea surface temperature forecasts for the NCEP Climate Forecast System (CFS) Version 2. Mon. Weather Rev. 2012, 140, 3003–3016. [Google Scholar] [CrossRef]
- Douville, H. Relevance of soil moisture for seasonal atmospheric predictions: Is it an initial value problem? Clim. Dyn. 2004, 22, 429–446. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, X.; Li, Y. Does a strong El Niño imply a higher predictability of extreme drought? Sci. Rep. 2017, 7, 40741. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.T.; Bett, P.E.; Thornton, H.E.; Scaife, A.A. Skilful seasonal predictions for the European energy industry. Environ. Res. Lett. 2017, 12, 024002. [Google Scholar] [CrossRef]
- Gong, D.; Wang, S. Definition of Antarctic Oscillation index. Geophys. Res. Lett. 1999, 26, 459–462. [Google Scholar] [CrossRef]
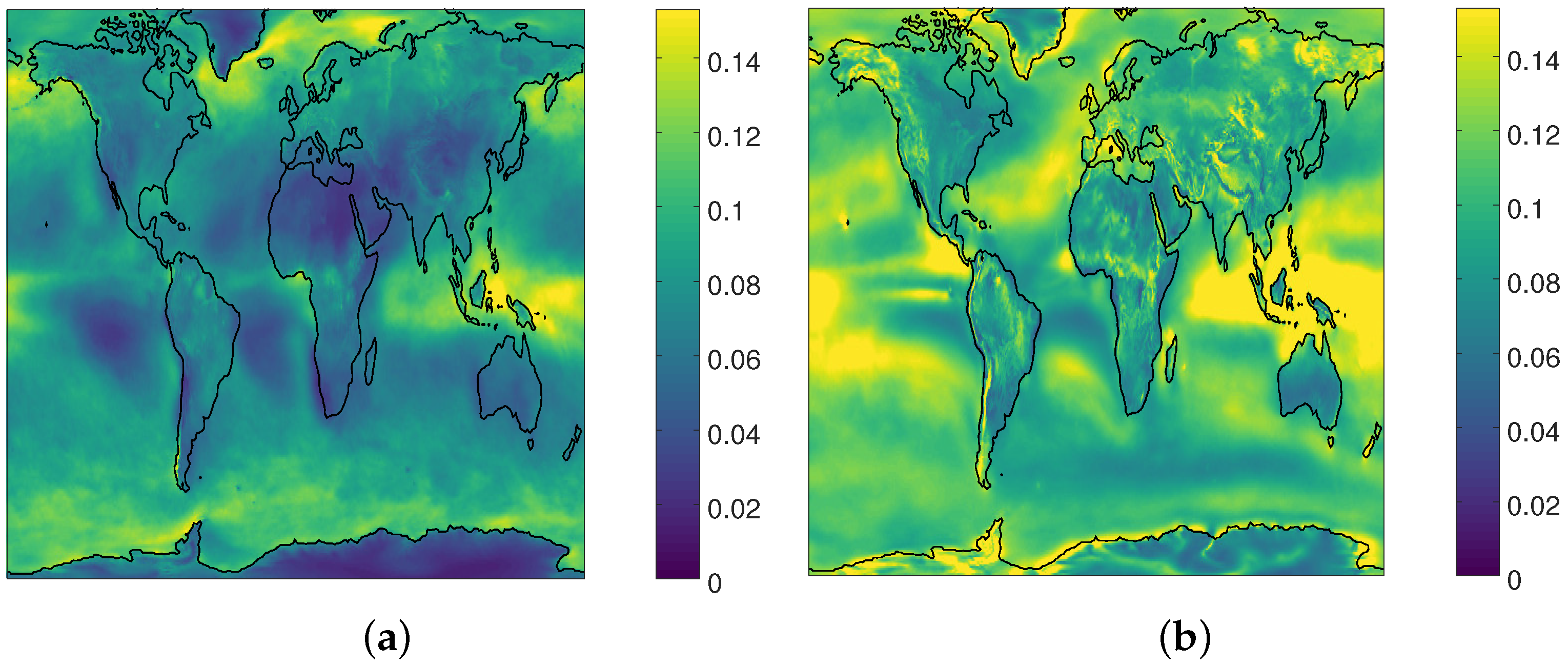
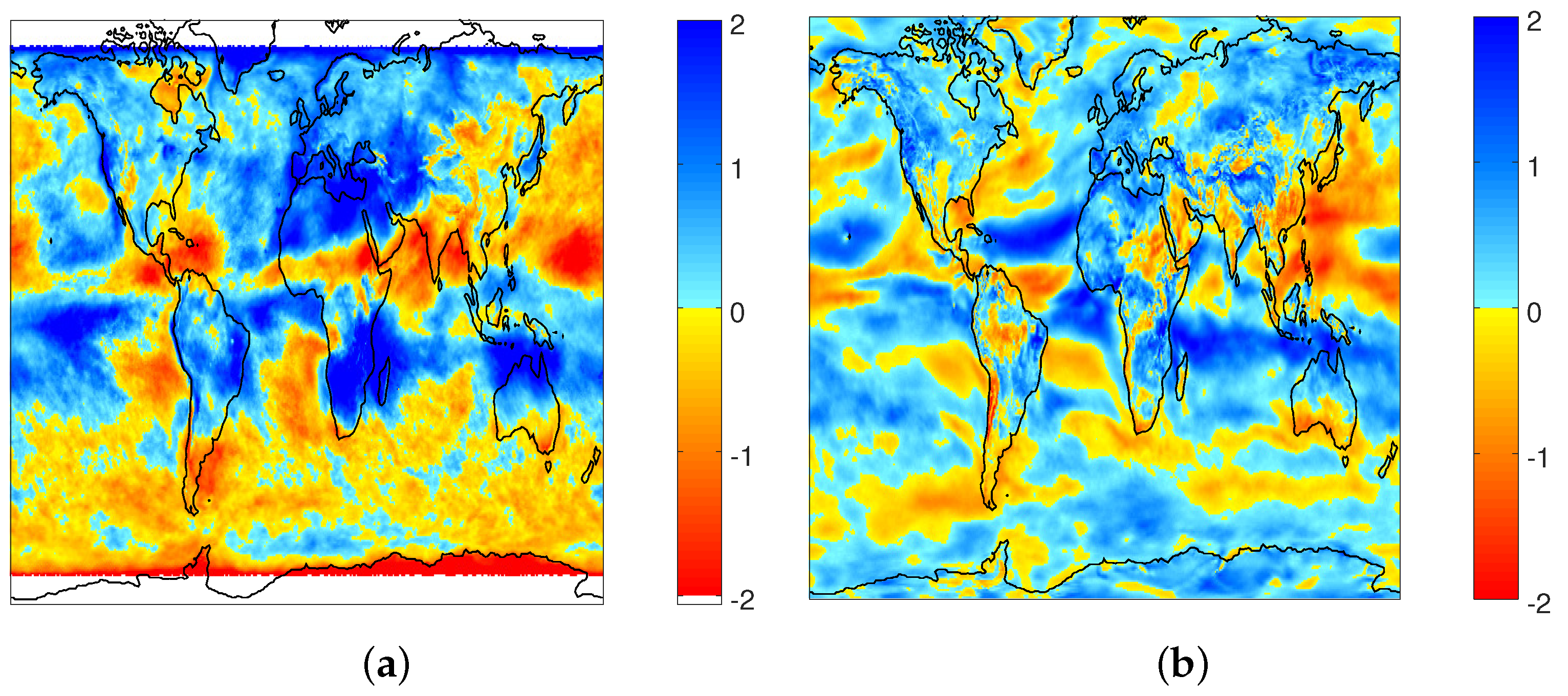
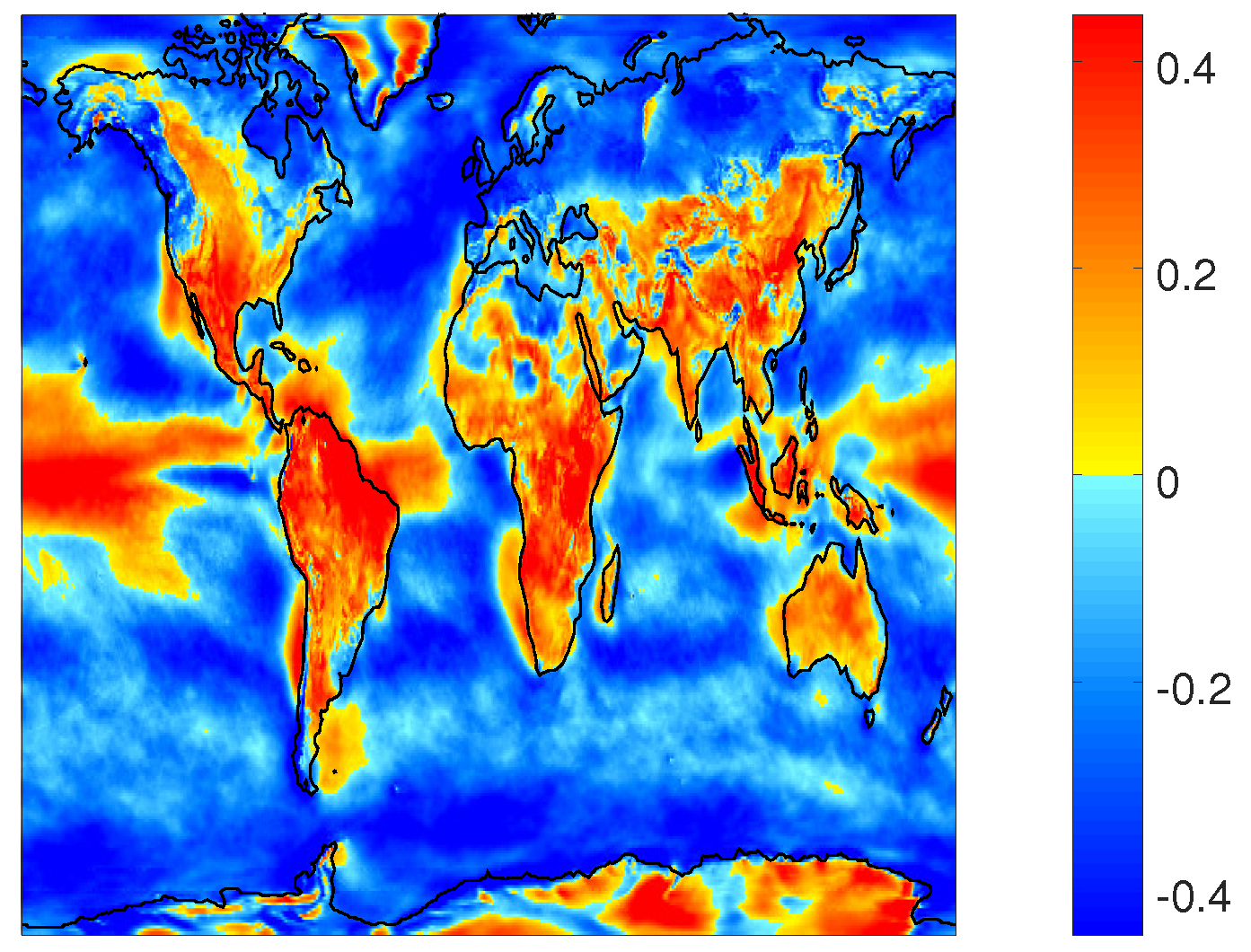
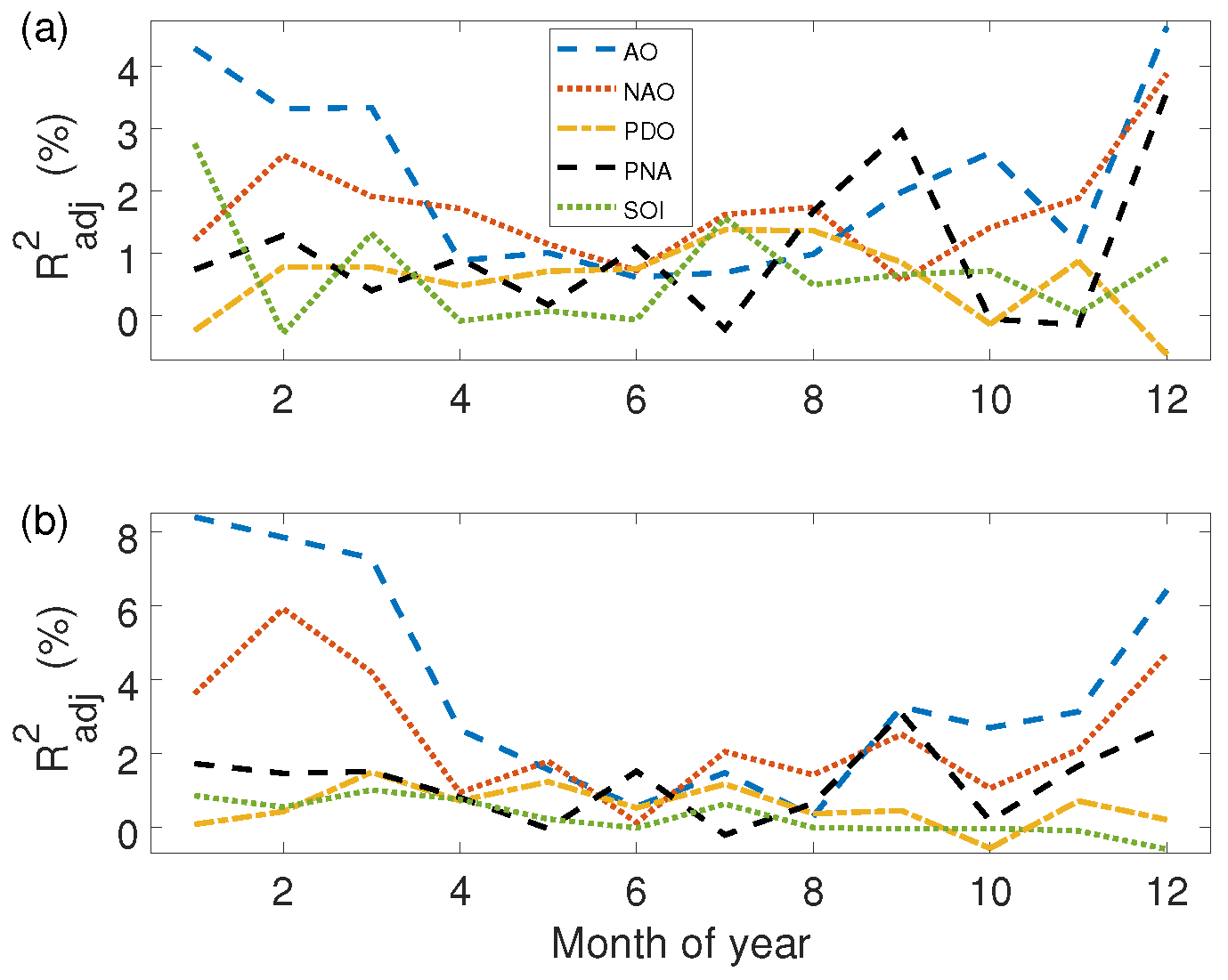
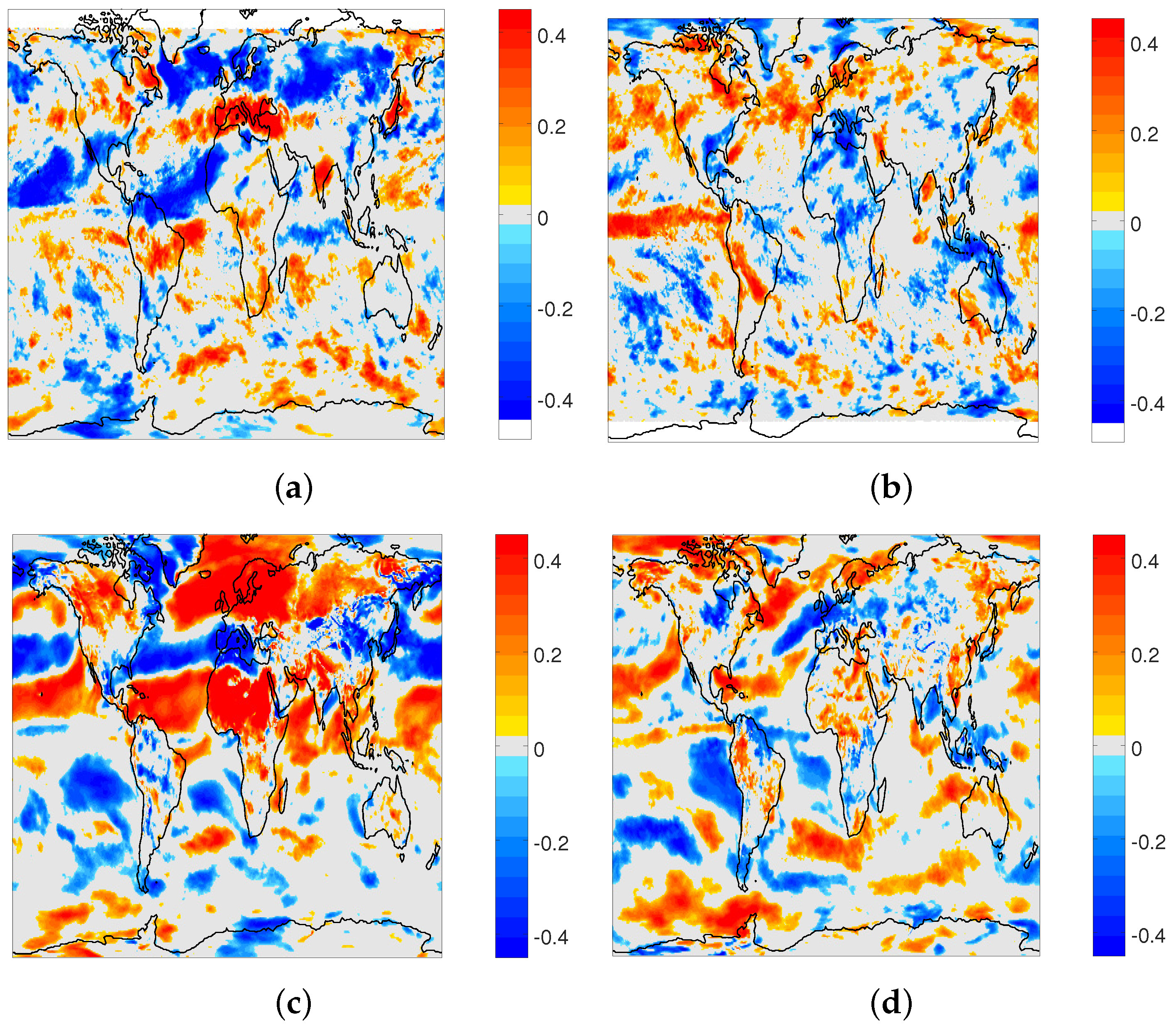
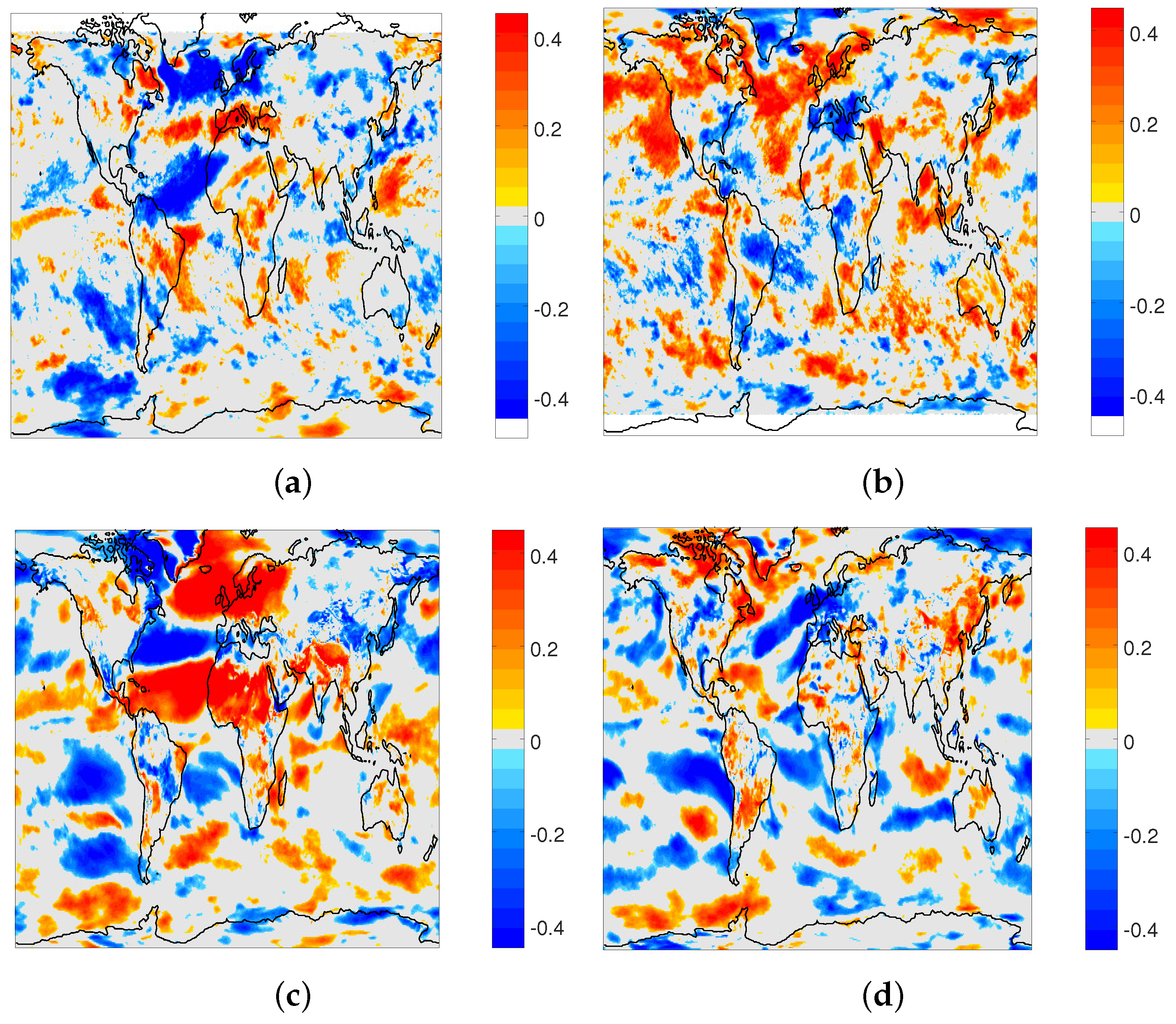
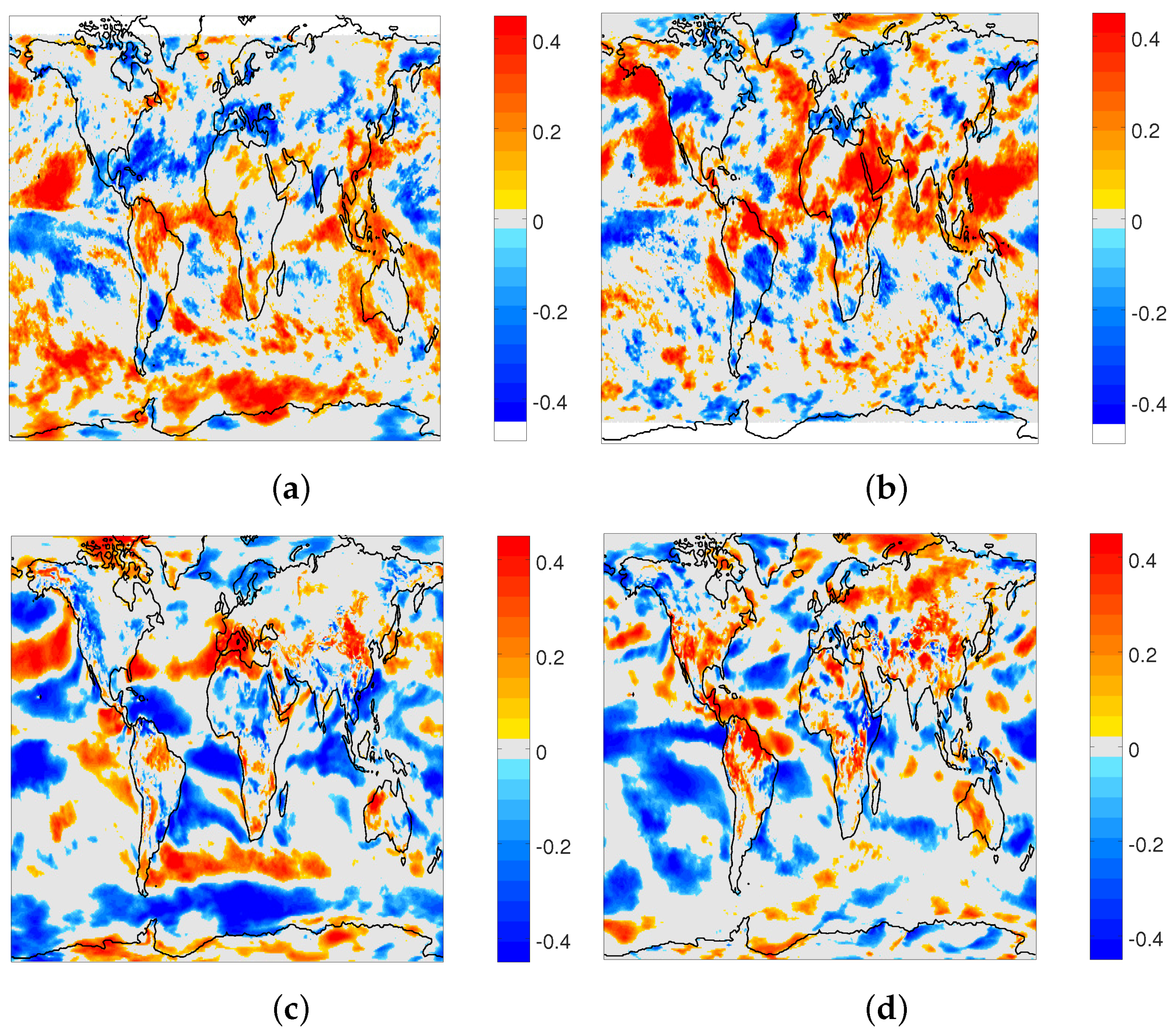

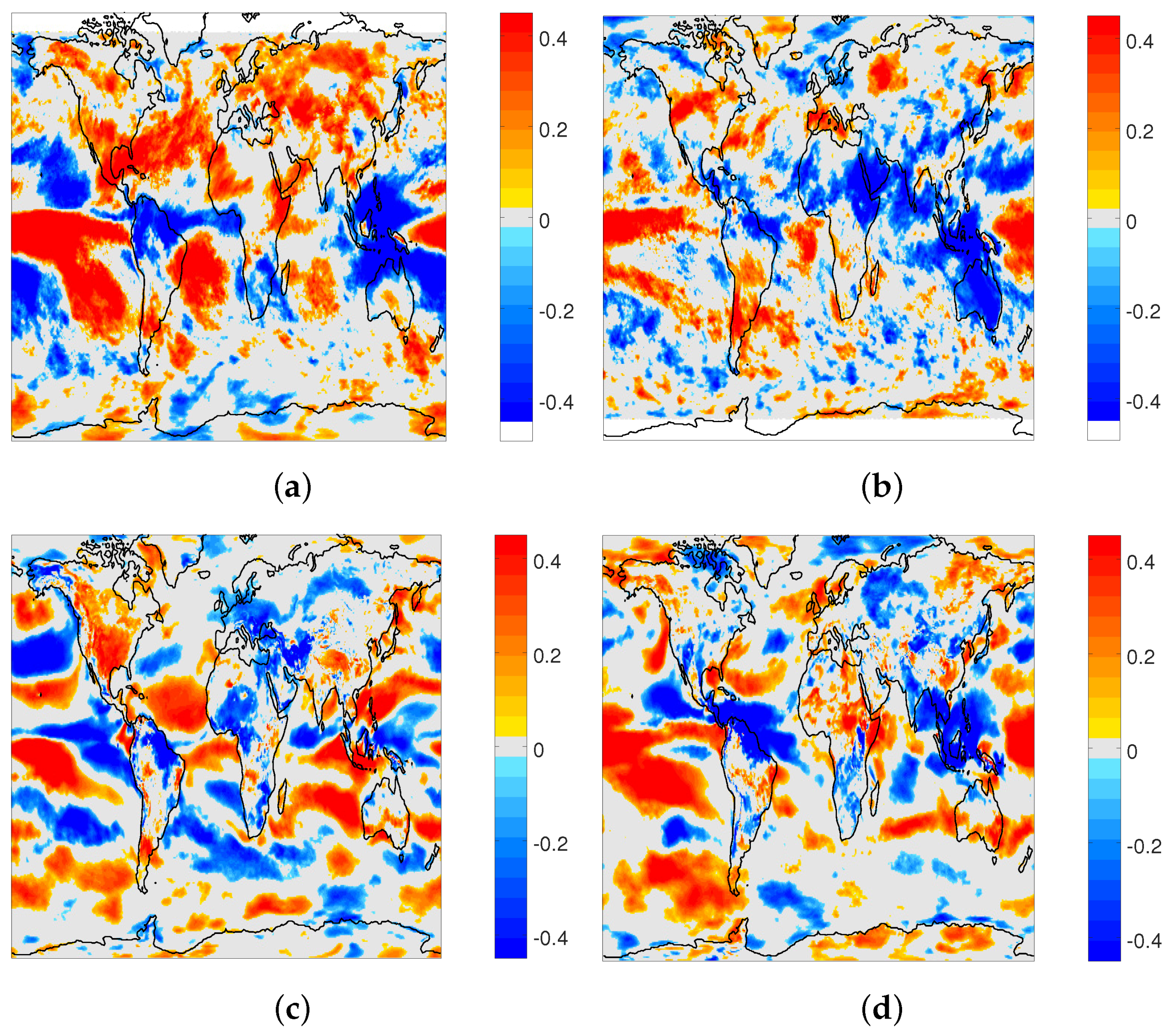
| Latitude | Land | Water | All |
|---|---|---|---|
| Solar: | |||
| Low | 6.7 | 8.3 | 7.9 |
| Mid | 5.2 | 7.1 | 6.6 |
| High | 7.5 | 9.1 | 8.7 |
| All | 6.4 | 8.2 | 7.7 |
| Wind: | |||
| Low | 9.2 | 12.6 | 11.8 |
| Mid | 8.7 | 11.7 | 10.8 |
| High | 10.3 | 10.5 | 10.4 |
| All | 9.4 | 11.6 | 11.0 |
| Latitude | Land | Water | All |
|---|---|---|---|
| Low | 0.26 | −0.02 | 0.04 |
| Mid | 0.11 | −0.21 | −0.12 |
| High | −0.14 | −0.22 | −0.20 |
| All | 0.07 | −0.15 | −0.09 |
| Solar: | Wind: | |||||
|---|---|---|---|---|---|---|
| Latitude | Land | Water | All | Land | Water | All |
| AO | ||||||
| Low | 0.51 | 0.65 | 0.62 | 1.71 | 0.80 | 1.01 |
| Mid | 0.97 | 0.75 | 0.81 | 1.84 | 1.74 | 1.77 |
| High | 2.12 | 1.20 | 1.43 | 3.81 | 1.73 | 2.25 |
| All | 1.20 | 0.86 | 0.95 | 2.44 | 1.42 | 1.68 |
| NAO | ||||||
| Low | 0.74 | 0.68 | 0.69 | 1.59 | 0.98 | 1.12 |
| Mid | 1.04 | 0.78 | 0.86 | 2.15 | 2.00 | 2.04 |
| High | 1.69 | 1.24 | 1.35 | 2.55 | 2.02 | 2.15 |
| All | 1.16 | 0.89 | 0.96 | 2.11 | 1.66 | 1.78 |
| PDO | ||||||
| Low | 3.21 | 3.98 | 3.80 | 2.13 | 3.52 | 3.19 |
| Mid | 1.89 | 2.04 | 2.00 | 1.26 | 1.34 | 1.32 |
| High | 0.58 | 0.77 | 0.72 | 0.58 | 0.86 | 0.79 |
| All | 1.86 | 2.29 | 2.18 | 1.30 | 1.92 | 1.76 |
| PNA | ||||||
| Low | 1.11 | 1.88 | 1.70 | 0.74 | 1.96 | 1.68 |
| Mid | 0.77 | 1.79 | 1.50 | 0.86 | 1.85 | 1.57 |
| High | 1.03 | 0.54 | 0.67 | 1.27 | 1.06 | 1.10 |
| All | 0.95 | 1.41 | 1.30 | 0.96 | 1.62 | 1.45 |
| SOI | ||||||
| Low | 4.83 | 7.84 | 7.14 | 4.15 | 7.78 | 6.93 |
| Mid | 3.76 | 3.46 | 3.54 | 1.73 | 2.73 | 2.45 |
| High | 0.67 | 0.59 | 0.61 | 0.28 | 1.22 | 0.99 |
| All | 3.08 | 4.03 | 3.79 | 1.99 | 3.94 | 3.44 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krakauer, N.Y.; Cohan, D.S. Interannual Variability and Seasonal Predictability of Wind and Solar Resources. Resources 2017, 6, 29. https://doi.org/10.3390/resources6030029
Krakauer NY, Cohan DS. Interannual Variability and Seasonal Predictability of Wind and Solar Resources. Resources. 2017; 6(3):29. https://doi.org/10.3390/resources6030029
Chicago/Turabian StyleKrakauer, Nir Y., and Daniel S. Cohan. 2017. "Interannual Variability and Seasonal Predictability of Wind and Solar Resources" Resources 6, no. 3: 29. https://doi.org/10.3390/resources6030029
APA StyleKrakauer, N. Y., & Cohan, D. S. (2017). Interannual Variability and Seasonal Predictability of Wind and Solar Resources. Resources, 6(3), 29. https://doi.org/10.3390/resources6030029






