Enhancing Flood Mitigation and Water Storage Through Ensemble-Based Inflow Prediction and Reservoir Optimization

Abstract

This study presents an integrated decision support system (DSS) designed to optimize real-time reservoir operation during typhoons by balancing flood control and water supply. The system combines ensemble quantitative precipitation forecasts (QPF) from WRF/MM5 models, a physically based rainfall–runoff model (KW-GIUH), and a three-stage optimization algorithm for reservoir release decisions. Eighteen ensemble rainfall members are processed to generate 6 h inflow forecasts, which serve as inputs for determining adaptive outflow strategies that consider both storage requirements and downstream flood risks. The DSS was tested using historical typhoon events—Talim, Saola, Trami, and Kong-rey—at the Tseng-Wen Reservoir in Taiwan. Results show that the KW-GIUH model effectively reproduces hydrograph characteristics, with a coefficient of efficiency around 0.80, while the optimization algorithm successfully maintains reservoir levels near target storage, even under imperfect rainfall forecasts. The mean deviation of reservoir water levels from the recorded to the target values is less than 0.18 m. The system enhances operational flexibility by adjusting release rates according to the proposed outflow index and flood-stage classification. During major storms, the DSS effectively allocates storage space for incoming floods while maximizing water retention during recession periods. Overall, the integrated framework demonstrates strong potential to support real-time reservoir management during extreme weather conditions, thereby improving both flood mitigation and water-supply reliability.

1. Introduction

Taiwan frequently experiences typhoons and severe storms that generate short-duration, high-intensity rainfall. The steep slopes of the Central Mountain Range accelerate runoff generation, resulting in limited opportunities for natural storage and rapidly increasing downstream flood hazards. Moreover, the island’s precipitation is highly uneven in both space and time, with Southern Taiwan receiving nearly 90% of its annual rainfall from May to October. This strong seasonality magnifies water scarcity during the dry months and highlights the need for deliberate water retention and storage. In recent decades, climate variability and global warming have intensified extreme rainfall and increased the frequency of prolonged drought–flood cycles, further complicating reservoir operation and regional water management [1,2,3,4,5,6]. Consequently, the ability to simultaneously mitigate flood damage and secure an adequate water supply has become a core priority, requiring improved forecasting tools and operational strategies tailored to Taiwan’s unique hydrometeorological conditions.

The Tseng-Wen Reservoir, with a current storage capacity of 491 × 10⁶ m³, is the largest and one of the most strategically important reservoirs in Taiwan. It supports irrigation in the agriculturally vital Chianan Plain, supplies domestic and industrial water, generates hydropower, and provides flood mitigation and recreational functions. Despite its multipurpose role, reservoir operation during typhoons remains highly constrained by predefined regulatory guidelines [7]. These rules aim to balance water supply stability, dam safety, and downstream flood avoidance; however, the broad operational bands and lack of real-time adaptability often lead to overly conservative or overly aggressive release decisions. Operators must frequently make judgments under extreme uncertainty, particularly when facing complex storm structures, rapidly rising inflows, or insufficient predictive information. Previous studies [2] have shown that such uncertainty can cause deviations from optimal storage levels, reduce water supply reliability, or increase downstream flood risk. Therefore, more dynamic, data-driven, and forecast-informed operational tools are urgently needed.

Enhancing reservoir performance requires not only improved flexibility in operational rules but also access to more reliable short-term rainfall and inflow forecasts. Advances in numerical weather prediction (NWP) have enabled ensemble forecasting systems to quantify atmospheric uncertainty and provide probabilistic guidance for extreme rainfall. Leading institutions such as ECMWF, NCEP, JMA, and UKMO have developed robust global and regional ensemble frameworks [8,9,10,11]. Regional-scale ensemble models provide higher spatial resolution and are particularly useful for Taiwan’s complex terrain and rapidly evolving typhoon systems [12,13,14]. These ensemble systems have demonstrated strong capability to predict storm tracks, rainfall distributions, and mesoscale features up to several days in advance [15,16,17,18]. Nevertheless, relatively few studies have integrated QPF outputs directly into real-time hydrological prediction or reservoir operating models, largely due to computational constraints, model uncertainty, or the difficulty of linking meteorological ensembles with operational decision-making [19]. This gap motivates the development of a decision support framework capable of transforming ensemble rainfall forecasts into actionable reservoir operations.

Accurate short-term inflow prediction is critical for reservoir managers, as both the magnitude and timing of inflow determine optimal release strategies. Rainfall–runoff modeling thus plays an essential role in transforming forecasted rainfall into operationally useful hydrological information. Deterministic models are advantageous because they explicitly incorporate watershed geomorphology, hydrodynamic routing, and antecedent soil moisture, allowing them to respond realistically to varying storm characteristics. Such physical representations are especially valuable in Taiwan, where steep terrain and rapid hydrologic response limit the effectiveness of purely statistical or stochastic models. Stochastic approaches, although flexible, require long-term data records to establish robust rainfall–runoff relationships and may perform poorly for rare or unprecedented storm events. Given Taiwan’s complex hydrological behavior and limited historical extreme-event data, a computationally efficient deterministic model such as the kinematic-wave-based geomorphologic instantaneous unit hydrograph modeling (KW-GIUH) [20] is well-suited for real-time inflow estimation and can effectively interface with short-term ensemble rainfall inputs.

Considering these hydrological, operational, and forecasting challenges, this study develops an integrated, computationally efficient system that couples ensemble rainfall forecasts, a physically based inflow-prediction model, and an optimal reservoir operation framework. Ensemble QPFs with a 6 h lead time are transformed into inflow predictions through the KW-GIUH model, providing real-time insights into incoming flood volumes. Based on these forecasts, an optimal programming algorithm determines reservoir releases that simultaneously address water supply objectives and downstream flood constraints. The system is tested using historical typhoon events at the Tseng-Wen Reservoir to validate its practicality under real operational conditions. The overarching goal is to design a robust, adaptive decision-support system that enhances water management resilience during typhoon-induced flooding by leveraging advances in meteorology, hydrology, and optimization.

2. Reservoir Operation Algorithm for Typhoon Storms

The following sections introduce the physical and hydrological characteristics of the Tseng-Wen Reservoir, which serve as the foundation for developing the reservoir operation algorithm evaluated in this study. A clear understanding of the watershed environment, storage limitations, and release structures is essential because these factors strongly influence reservoir response during typhoon events. After outlining these characteristics, this shifts to the governing principles of the rainfall–runoff model and the optimal programming framework adopted to support real-time operational decisions.

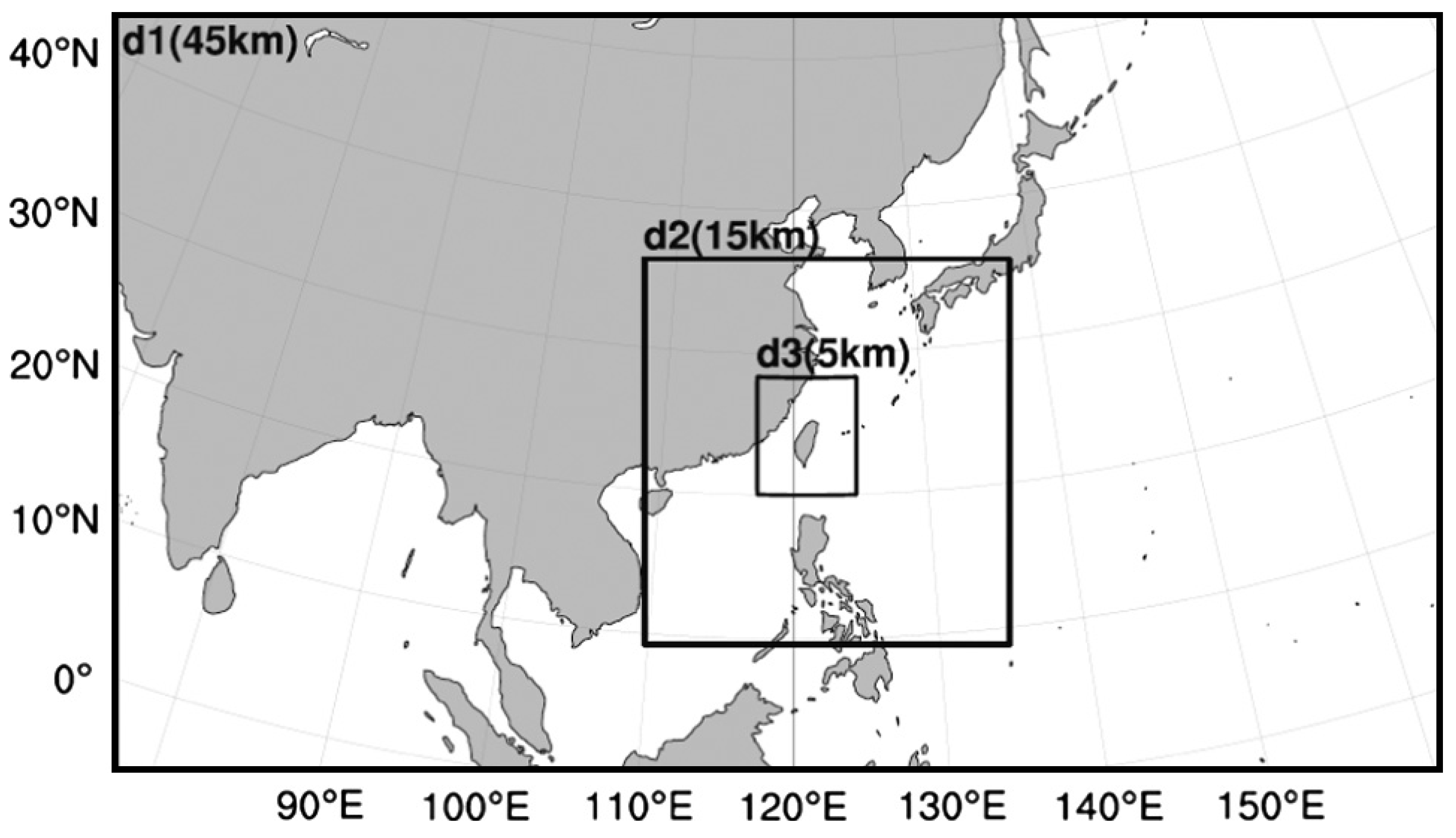
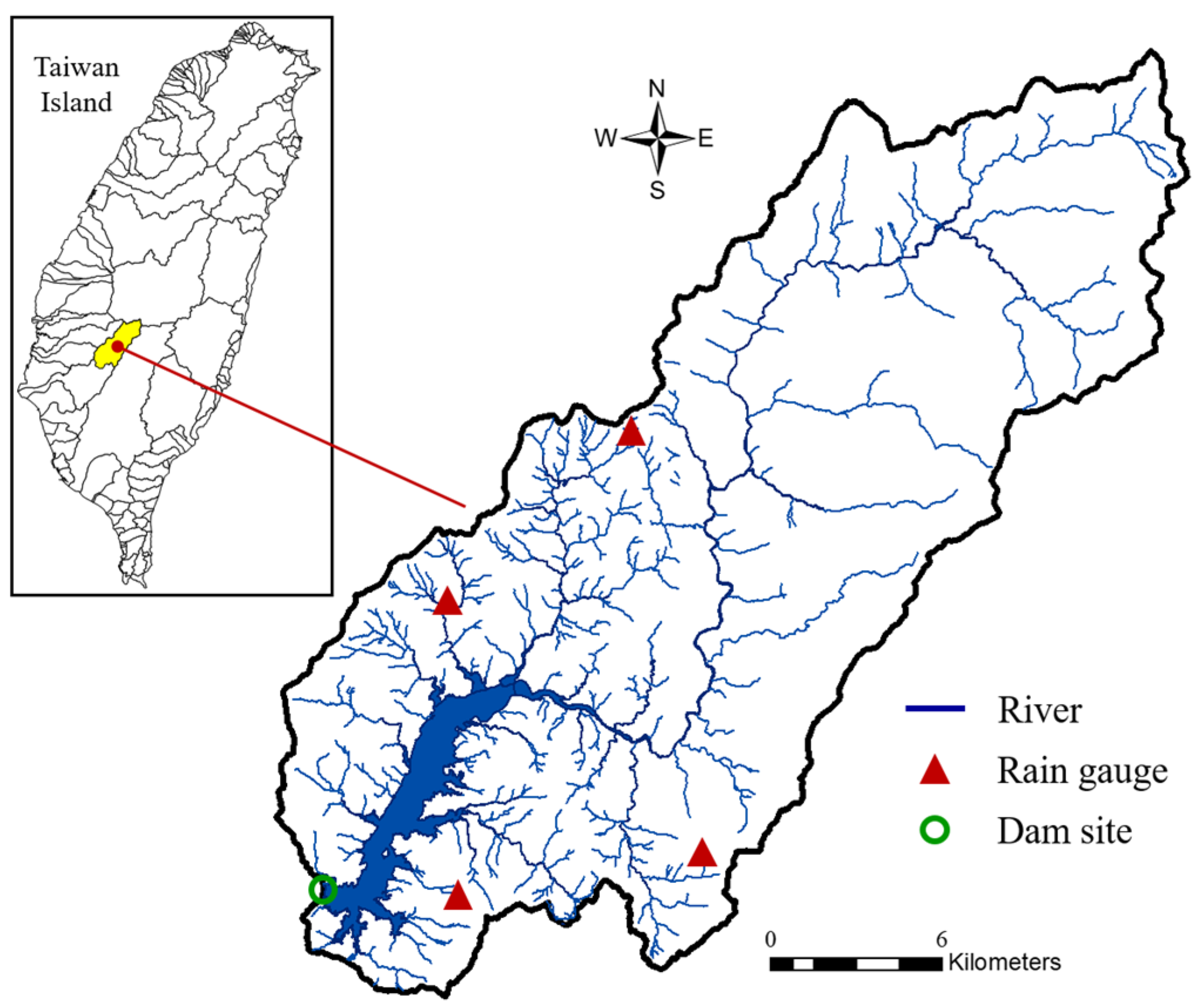
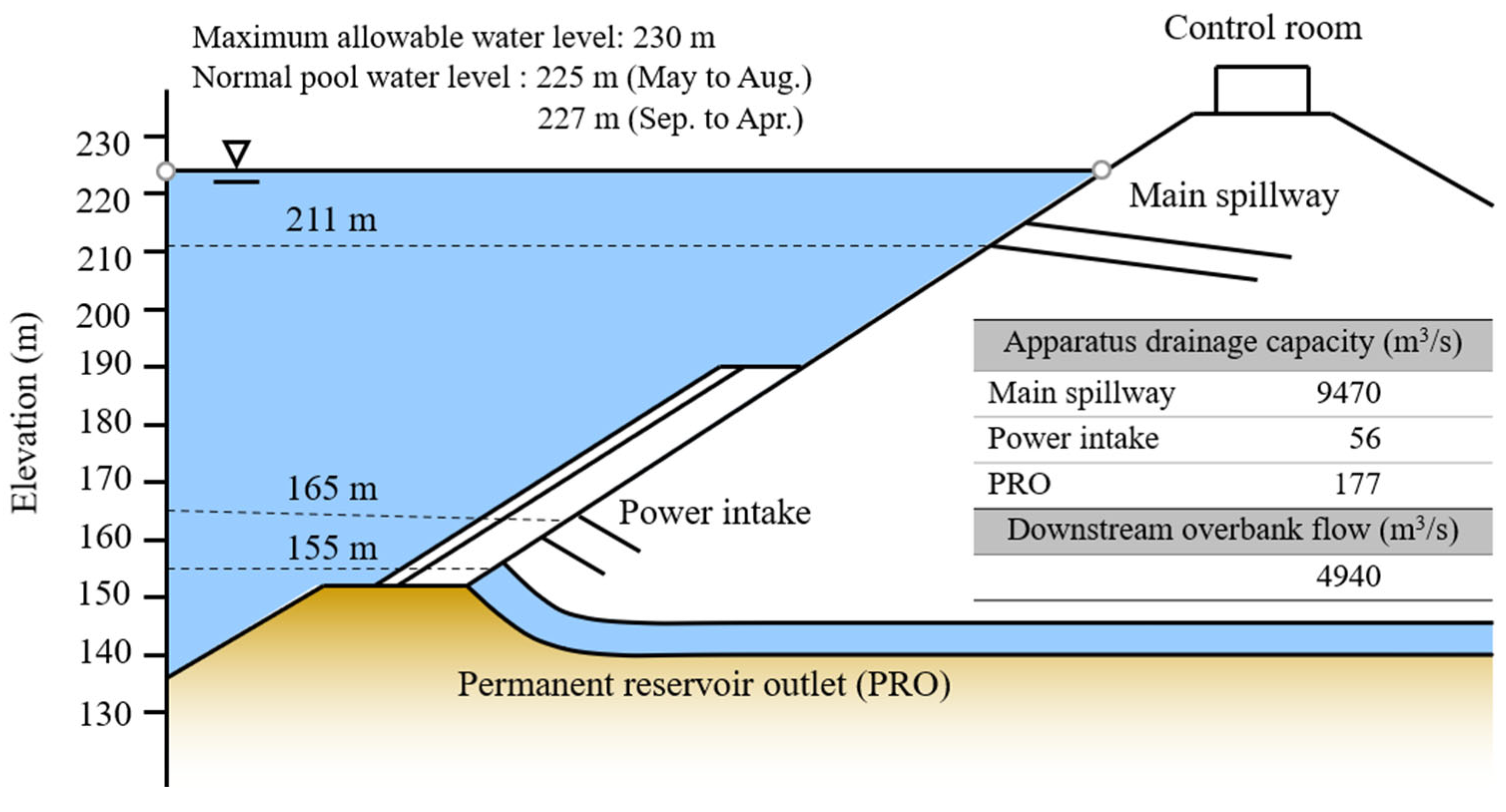
2.1. Description of the Study Watershed

As illustrated in Figure 1, the Tseng-Wen Dam is located in the upper reaches of the Tseng-Wen River—the fourth longest river system in Taiwan—extending across Tainan and Chiayi Counties with a main channel length of approximately 138.47 km. Constructed in 1973, the dam controls an upstream watershed of 481 km² characterized by steep slopes, rapid runoff generation, and highly variable rainfall patterns associated with typhoon events. These physiographic characteristics contribute to short hydrologic response times, which impose significant operational challenges for reservoir managers who must react quickly to changing inflow conditions.

Long-term sedimentation has substantially altered the reservoir’s storage characteristics, reducing the original design capacity of 708 × 10⁶ m³ to the current 491 × 10⁶ m³. This reduction not only limits the reservoir’s ability to buffer incoming floodwaters but also increases the probability of exceeding critical water levels during extreme events. As shown in Figure 2, the Tseng-Wen Reservoir is equipped with three major outlet structures: a power plant diversion canal with a discharge capacity of 56 m³/s, a permanent reservoir outlet (PRO) capable of releasing 177 m³/s, and a primary spillway for flood evacuation. The spillway consists of an overflow weir crest at Elevation 211 m and three radial gates capable of releasing up to 9470 m³/s under fully open conditions.

The operational water level typically fluctuates between Elevations 225 m and 227 m, depending on seasonal water supply requirements. During flood events, however, the reservoir may store water up to a maximum allowable flood level of Elevation 230 m. Exceeding this threshold could jeopardize dam safety. Moreover, downstream channel sections become vulnerable to overbank flooding when releases exceed approximately 4940 m³/s. These hydraulic constraints, coupled with the limited storage volume and rapid inflow fluctuations, highlight the complexity of managing Tseng-Wen Reservoir during typhoons and underscore the need for a robust real-time operation algorithm that can dynamically adjust release decisions based on forecasted hydrologic conditions.

2.2. Estimation of Reservoir Upstream Inflow

Several stochastic models have been extensively employed for predicting floodwater in reservoir upstream watersheds [3,16,21]. These models require substantial recorded data to establish the mathematical framework for transforming rainfall inputs into discharge at the watershed outlet. However, the complexity of the rainfall–runoff process depends on various factors, including watershed antecedent conditions, topographic features, land cover, and stream network structure. These diverse elements introduce variability, potentially questioning the reliability of stochastic model structures developed in the past or necessitating adjustments. In light of these considerations, this study employs a physically-based model developed by Lee and Huang [22]. This model integrates antecedent hydrological conditions and detailed watershed geomorphological factors, providing a more comprehensive approach to reservoir inflow estimation than traditional stochastic models.

The kinematic-wave-based geomorphologic instantaneous unit hydrograph modeling (KW-GIUH) adopts the perspective that a unit volume of rainfall excess comprises an infinite number of raindrops. This conceptualization enables the model to portray the rainfall–runoff process by integrating the contributions of all raindrops along various paths toward the watershed outlet, thereby forming the outflow hydrograph. The simulated results obtained by the KW-GIUH have been shown to be in good agreement with the records produced from Taiwan [20,23,24,25,26,27], the United States [28], Palestine [29], Japan [30], India [31], and Russia [32] under various climatic–topographic conditions.

The Instantaneous Unit Hydrograph (IUH) for the watershed is mathematically expressed as per the formulation proposed by Lee and Chang [33] and further developed by Lee and Huang [22].

$$\begin{array}{ll}u(t)& =u_s(t)+u_{sub}(t)\\ & ={{\displaystyle \sum _{w_s\in W_s}\left[f_{x_{o_i}}(t)\ast f_{x_i}(t)\ast f_{x_j}(t)\ast \dots \ast f_{x_{\Omega }}(t)\right]}}_{w_s}\cdot P(w_s)+\\ & {{\displaystyle \sum _{w_{sub}\in W_{sub}}\left[f_{x_{su{b}_i}}(t)\ast f_{x_i}(t)\ast f_{x_j}(t)\ast \dots \ast f_{x_{\Omega }}(t)\right]}}_{w_{sub}}\cdot P(w_{sub})\end{array}$$

(1)

where $u(t)$ denotes the total IUH of the watershed; $u_s(t)$ and $u_{sub}(t)$ represent the surface-flow and subsurface-flow IUHs, respectively; W_s is the surface-flow path space given as $W_s=\langle x_{o_i},x_i,x_j,\dots ,x_{\Omega }\rangle$; W_sub is the subsurface-flow path space given as $W_{sub}=\langle x_{su{b}_i},x_i,x_j,\dots ,x_{\Omega }\rangle$; $f_{x_j}(t)$ is the travel-time probability density function in state $x_j$ with a mean value of $T_{x_j}$; $\ast$ denotes a convolution integral; $P(w_s)$ and $P(w_{sub})$ represent the probabilities of a raindrop adopting a surface-flow path w_s or a subsurface-flow path w_sub.

Lee and Yen [20] sought to overcome the limitations associated with the application of empirical travel-time equations by employing the kinematic-wave theory to calculate mean travel times in each state, as detailed in Appendix A. Consequently, the instantaneous unit hydrograph (IUH) for a watershed, as represented in Equation (1), can be resolved analytically.

Therefore, the inflow into the reservoir watershed upstream can be expressed as the convolution of the IUH and the effective rainfall, as illustrated by the following equation:

$$I_t={\displaystyle {\int }_0^t{i}_e(\tau )\cdot u(i_e,t-\tau )d\tau }+Q_b(t)$$

(2)

where $I_t$ denotes the reservoir upstream inflow at time t; $i_e(\tau )$ denotes the effective rainfall at time τ; $u(i_e,t)$ denotes the IUH caused by effective rainfall $i_e$ at time t; $Q_b(t)$ denotes the baseflow at time t. Utilizing the KW-GIUH model offers the advantage of incorporating detailed geomorphologic characteristics of the watershed in estimating runoff travel times. Furthermore, the model allows incorporation of hydrodynamic effects arising from varying rainfall intensities, as outlined in the equations in Appendix A. In executing the model, calibration is solely required for the overland roughness coefficient (n_o) and the channel roughness coefficient (n_c). These values can be determined through either hydrological records or field investigation.

2.3. Optimization of Reservoir Operation

This study employed an optimization framework as the foundation of a decision-support system for real-time reservoir operation. The optimization approach provides a structured and quantitative means to evaluate competing operational goals under rapidly changing hydrometeorological conditions. Within this framework, objective functions and operational constraints are formulated to guide the reservoir toward an optimal release strategy that simultaneously satisfies water supply and flood control requirements.

For water supply management, the system prioritizes maximizing reservoir storage to secure sufficient water availability during dry periods, while ensuring that water levels remain safely below the maximum allowable elevation to maintain dam integrity. This objective demands careful coordination during typhoon events, when large inflows can quickly elevate water levels and reduce operational flexibility.

Conversely, flood control introduces an opposing requirement: the reservoir must release sufficient water in advance of major inflows to create adequate storage capacity for upcoming flood volumes. This must be accomplished without exceeding the downstream channel’s conveyance capacity, as excessive releases could trigger inundation and pose risks to communities and infrastructure downstream. The optimization model therefore integrates physical, hydraulic, and regulatory constraints to determine release decisions that respect downstream safety limits while maintaining enough buffer storage to attenuate peak inflows.

By embedding these considerations into a unified mathematical framework, the optimal programming approach enables dynamic, evidence-based reservoir operation that adapts to forecasted conditions and provides improved resilience during typhoon-driven hydrologic events. The continuity of flow in the reservoir is expressed as follows:

$$S_{t+1}=S_t+\Delta t\cdot (I_t-Q_t)$$

(3)

where I_t represents the reservoir inflow at time t, which can be estimated through Equation (2); O_t represents the reservoir release at time t; S_t and S_t+1 represent the reservoir storage at time t and t + 1, respectively. To efficiently mitigate flood impacts, the operational approach was divided into three distinct flood stages. Stage I corresponds to the period before the onset of the flood, Stage II encompasses the period of flood occurrence, and Stage III covers the flood recession. Flood control operations are initiated when either the average inflow discharge over the next 6 h exceeds 233 m³/s (calculated as 56 m³/s + 177 m³/s), or the water stage surpasses Ele. 223 m. In such cases, the reservoir is activated to address flood control measures. The descriptions of the objective functions and constraints for each operational flood stage are outlined below.

(1)

Before the onset of flood (Stage I):

When the incoming inflow is below 900 m³/s, the operational strategy during Stage I is to maximize water storage to fulfill water supply requirements. As a result, the objective function and constraint for the operation of spillway gates are defined as follows:

$$Objective=Min\left\{\left|S_t-S^{target}\right|\right\}$$

(4)

$$O_t\le 900{ \mathrm{m}}^3/\mathrm{s}$$

(5)

where S^target represents the reservoir target storage corresponding to the normal pool level of the reservoir. Following the operating rules and regulations outlined in the Tseng-Wen guidelines [7], the designated target water level ranges from Ele. 225 m to Ele. 227 m, varying with different seasons. The reservoir’s maximum allowable water stage is set at Ele. 230 m, corresponding to a maximum allowable water storage of 638.27 × 10⁶ m³.

(2)

Flood occurrence period (Stage II):

When the inflow exceeds 900 m³/s, it signals the onset of a significant flood, prompting a transition from Stage I to Stage II. The reason to select 900 m³/s as the threshold is that the 1.1-yr return period discharge is about 889 m³/s at the dam site. During this phase, the primary focus of reservoir operation shifts towards creating additional capacity for incoming floodwater. To pinpoint emergent flood situations, an index for water release, referred to as O_index, has been devised as follows:

$$O_{index}={\displaystyle \frac{1}{T}}(S_t+{\forall }_T-S^{max})$$

(6)

where T is the duration for determining an optimal release strategy, and it was equal to 6 h in the present study, given that ensemble forecast rainfall data is available every 6 h. ${\forall }_T$ is the cumulative estimated upstream inflow from t to t + T, and $S^{max}$ represents the maximum reservoir storage, equivalent to the storage corresponding to the maximum allowable water level of 230 m in the reservoir.

Considering that the discharge of 4940 m³/s is vulnerable to overbank flooding in downstream channel sections, if the O_index exceeds 4940 m³/s over the next 6 h, maintaining a constant release rate of 4940 m³/s would not prevent the reservoir from reaching its maximum allowable water level. Under these circumstances, the downstream flood-prevention constraint must be disregarded. Consequently, the spillway gates should be opened as wide as possible to prevent incoming floodwater from overflowing the dam site. Despite the spillway’s capacity to handle a maximum outflow of 9470 m³/s, the rate of increase is restricted to 1500 m³/s per hour by the operation of gate openings [7]. Therefore, limitations on reservoir operation at this juncture include:

$$O_t\le O_{\max }=9470 {\mathrm{m}}^3/s$$

(7)

$$\left|O_t-O_{t-1}\right|\le 1500 {\mathrm{m}}^3/\mathrm{s}$$

(8)

If the O_index is below 4940 m³/s, the outflow rate can be calculated based on optimal reservoir operation, while accounting for downstream flood control requirements. Consequently, the objective function can be formulated as:

$$Objective=Min\left\{\left|O_t-{\displaystyle \frac{1}{T}}(S_t+{\forall }_T-S^{target})\right|\right\}$$

(9)

This strategy is contingent upon the following constraints for the operation of spillway gates [7]:

$$O_t\le 4940{ \mathrm{m}}^3/\mathrm{s}$$

(10)

$$O_t\le I_t^{\max }$$

(11)

$$\left|O_t-O_{t-1}\right|\le \Delta I_t^{\max }\le 1500{\mathrm{m}}^3/\mathrm{s}$$

(12)

where $I_t^{\max }$ represents the peak inflow before time t; $\Delta I_t^{\max }$ denotes the maximum rate of increase in inflow before time t; O_t−1 represents the outflow at time t − 1. Throughout the flood event, reservoir storage is determined using the continuity equation in Equation (3). For this calculation, the time interval Δt is set to 1 h.

(3)

Flood recession period (Stage III):

If the incoming inflow at time t is less than 80% of the peak flow and the total inflow volume from t − 6 to t is less than that from t − 12 to t − 6, then the flood event is deemed to be receding. The operational strategy at Stage III aims to store more water to fulfill the water supply requirements. As a result, the objective function is formulated as:

$$Objective=Min\left\{\left|S_t-S^{target}\right|\right\}$$

(13)

The equation is identical to Equation (4). It should be noted that the constraints for Stage III can be directly acquired from those utilized in Stage II, as illustrated in Equations (10)–(12) [22].

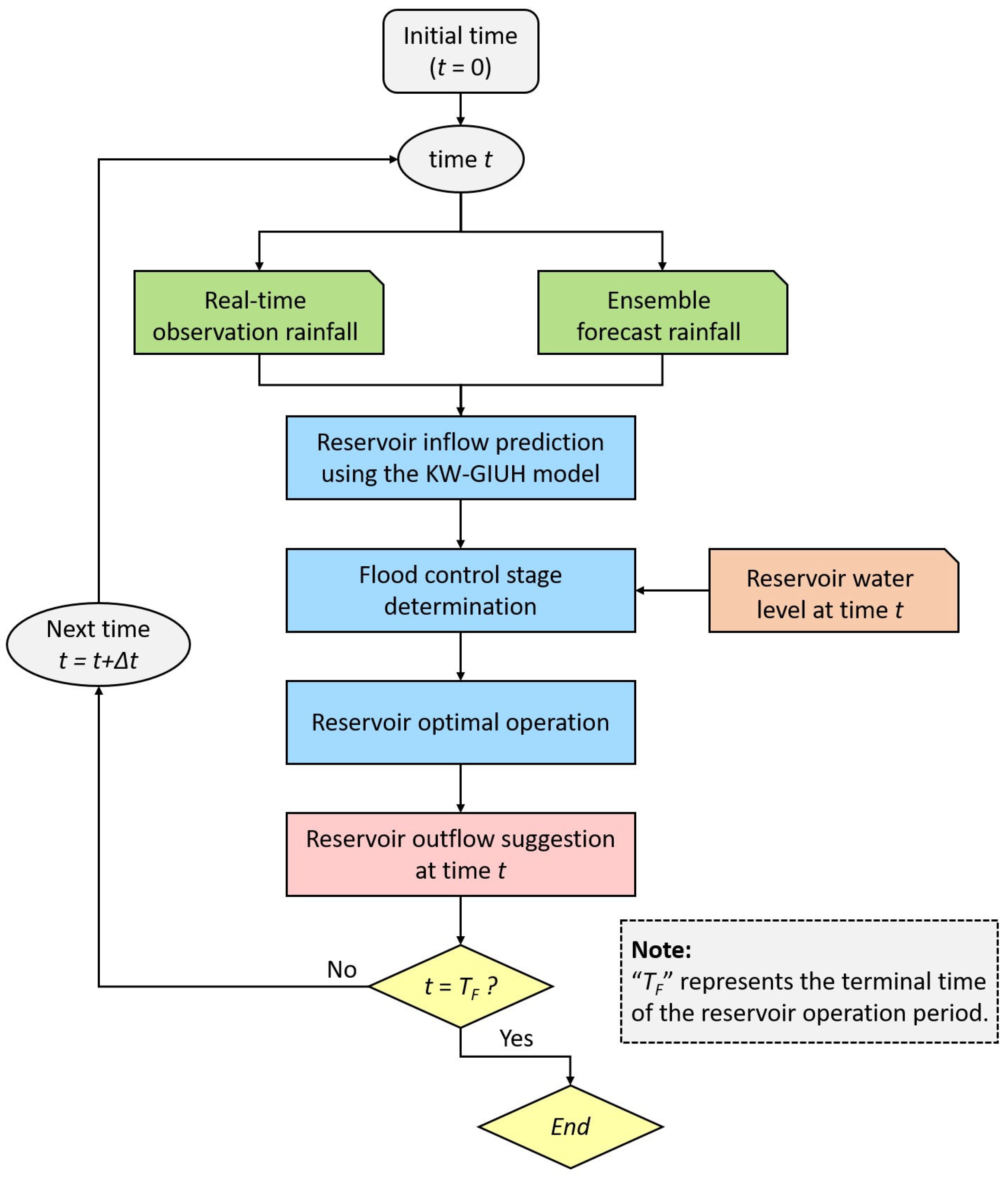
2.4. Summary of Reservoir Operation

The reservoir operation during typhoon events requires balancing water supply and flood control under rapidly changing inflow conditions. Large typhoon-induced inflows can quickly raise reservoir water levels, reducing operational flexibility. To prevent overtopping, operators must release water to create sufficient storage capacity, but releases must remain within downstream channel limits to avoid flooding. An optimal programming approach is therefore used to integrate physical, hydraulic, and regulatory constraints into a unified decision-making framework that adapts dynamically to forecasted conditions.

Reservoir water balance is governed by the continuity equation, which links inflow, outflow, and changes in storage. To efficiently manage varying hydrological conditions, the operational strategy is divided into three distinct stages. Stage I (pre-flood) applies when inflow is below 900 m³/s; the objective is to maximize storage while keeping water levels within allowable limits. Stage II (flood occurrence) begins when inflow exceeds 900 m³/s, shifting the operational goal toward creating adequate flood storage. A release index, O_index, is used to assess whether downstream constraints must be relaxed. If O_index exceeds 4940 m³/s, full spillway operation is required; otherwise, optimized releases must satisfy downstream safety constraints. Stage III (flood recession) begins when inflow decreases to 80% of the peak and continues to decline. During this stage, the reservoir again prioritizes maximizing storage, subject to the same constraints used in Stage II. The analysis procedure can be shown in Figure 3. Overall, this staged optimal operation framework enables responsive, data-driven reservoir management that enhances both flood mitigation and water supply reliability during typhoon events.

3. Ensemble Rainfall Forecast

In this study, probabilistic rainfall information is incorporated into reservoir operation through an ensemble rainfall forecasting system. Ensemble-based forecasting has become an essential tool in modern hydrometeorology because it explicitly accounts for uncertainties in atmospheric initial conditions, physical parameterizations, and numerical approximations. By combining predictions from multiple model realizations, ensemble methods provide a distribution of possible rainfall outcomes rather than a single deterministic estimate, thereby enhancing forecast robustness and supporting risk-informed decision-making for reservoir management. This is particularly important for Taiwan, where typhoon-induced rainfall is highly variable in space and time, and traditional deterministic forecasts often fail to capture extreme events accurately. The following sections present the mesoscale meteorological models used to generate the ensemble forecasts, followed by a detailed description of the ensemble configuration adopted in this study.

3.1. Mesoscale Meteorological Models

Given Taiwan’s geographical location in East Asia, where complex terrain and strong monsoon–typhoon interactions significantly influence rainfall patterns, high-resolution mesoscale numerical weather prediction (NWP) models are indispensable for improving quantitative precipitation forecasts (QPF). In this research, two widely recognized mesoscale models—the Weather Research and Forecasting (WRF) model and the fifth-generation Pennsylvania State University–National Center for Atmospheric Research Mesoscale Model (MM5)—were applied to construct the ensemble system. Using two independent modeling frameworks increases forecast diversity and reduces systematic biases associated with a single model.

(1)

Weather Research and Forecasting (WRF) model

The WRF model, particularly the Advanced Research WRF (ARW) dynamical core, is a state-of-the-art mesoscale NWP system designed for both research and operational forecasting applications. Its fully compressible, non-hydrostatic Eulerian governing equations allow accurate representation of deep convection and typhoon structure—key features for extreme rainfall prediction. The model employs a terrain-following vertical coordinate and the Arakawa-C horizontal grid arrangement, enabling stable numerical performance over Taiwan’s steep topography.

In addition, WRF incorporates a sophisticated variational data assimilation system (WRF-VAR), which can ingest various observational datasets—including radiosonde, satellite, radar, and aircraft measurements—to refine initial atmospheric conditions. The third-order Runge–Kutta time integration scheme facilitates computational stability and accuracy. WRF’s flexible physics suite and multi-level nesting capabilities (one-way, two-way, and moving nests) enable high-resolution simulations that capture fine-scale processes responsible for intense rainfall, making it highly suitable for typhoon forecasting.

(2)

Fifth-generation Mesoscale Model (MM5)

The Pennsylvania State University–National Center for Atmospheric Research (PSU–NCAR) fifth-generation Mesoscale Model (MM5) represents a major milestone in the evolution of mesoscale atmospheric modeling. Developed through a long-standing collaboration between PSU and NCAR, MM5 has become one of the most influential and widely adopted numerical weather prediction (NWP) systems in both research and operational meteorology. Its flexible architecture, robust physics options, and proven reliability have made MM5 a cornerstone for studies involving regional climate processes, severe weather systems, and typhoon simulations.

MM5 is specifically designed to simulate mesoscale atmospheric dynamics, capturing processes over spatial scales ranging from a few kilometers to several hundred kilometers—scales at which local topography, land–atmosphere interactions, and convective phenomena strongly influence weather patterns. Unlike global circulation models, which focus on large-scale atmospheric behavior, MM5 provides the fine spatial resolution needed to resolve localized features such as convective cells, orographic lifting, typhoon eyewall structures, and mesoscale rainbands. This capability is especially important for Taiwan, where steep terrain and typhoon-induced convection result in highly complex, localized rainfall distributions.

The model offers a versatile set of physical parameterizations, including various microphysics schemes, planetary boundary layer formulations, cumulus convection options, and surface–radiation interaction models. Its nested-domain system allows researchers to embed high-resolution inner domains within coarser outer domains, thereby accurately simulating both large-scale atmospheric forcing and small-scale precipitation mechanisms. These features make MM5 particularly suitable for producing quantitative precipitation forecasts (QPF) in regions with complex terrain.

A comprehensive description of MM5’s scientific foundation, numerical methods, and physical parameterizations is provided in the technical documentation by Grell et al. [34], which continues to serve as a definitive reference for the model. Given its demonstrated robustness and adaptability, MM5 plays a crucial role in this study’s ensemble rainfall forecasting framework, contributing valuable diversity and physical realism to the probabilistic prediction of typhoon-induced rainfall.

3.2. Ensemble Configuration

The ensemble meteorological modeling system adopted in this study utilizes a three-level nested-domain configuration, as illustrated in Figure 4. This nested approach allows the modeling framework to capture atmospheric processes across a broad range of spatial scales—from synoptic-scale circulation patterns affecting the broader East Asian region to fine-scale convective structures that drive localized heavy rainfall in Taiwan. The outermost domain operates at a 45 km horizontal resolution to represent large-scale atmospheric dynamics, while the intermediate 15 km domain refines the simulation of mesoscale weather systems. The innermost domain, with a 5 km resolution, is specifically designed to resolve topographic influences, mesoscale convective bands, and orographic rainfall commonly associated with typhoons. The grid dimensions of these domains are 221 × 127, 183 × 195, and 150 × 180, respectively, and forty-five vertical layers are applied throughout the system, with enhanced vertical resolution in the planetary boundary layer to improve simulation of near-surface thermodynamic and wind structures.

To generate a diverse and physically meaningful spread of predictions, 18 ensemble members were produced using various configurations of the WRF and MM5 models, as summarized in Table 1. Perturbations were introduced through multiple mechanisms, including:

(a)

Cold-start or partial-cycle initializations, which generate different atmospheric first-guess states;

(b)

Variations in data assimilation, with some members incorporating synthetic (bogus) typhoon observations while others rely solely on observational datasets; and

(c)

Different nesting strategies, including one-way and two-way interactive coupling between domains, modify feedback strength across spatial scales.

For the MM5-based members, additional perturbations were introduced through distinct statistical background error covariance matrices and the application of an outer-loop procedure within the three-dimensional variational assimilation system (3DVAR), following methodologies described by Skamarock et al. [35]. The ensemble suite also includes a four-dimensional variational assimilation (4DVAR) configuration to better capture the temporal evolution of atmospheric states, as well as a no-data-assimilation (NODA) run to preserve a fully free-running model trajectory. Together, these configurations ensure a wide and physically realistic sampling of model uncertainties.

Lateral boundary conditions for all ensemble members are updated every six hours using operational outputs from the NCEP Global Forecast System (GFS) and the Taiwan Central Weather Bureau (CWB) global model. This guarantees consistency with large-scale atmospheric forcing and facilitates accurate tracking of typhoon movement and intensity. At the Taiwan Typhoon and Flood Research Institute (TTFRI), the full 18-member ensemble is executed operationally four times per day, producing probabilistic rainfall and wind field forecasts with lead times of up to 72 h.

Figure 4. Three nested domains utilized for ensemble quantitative precipitation forecast in the WRF/MM5 model (cited from Hsiao et al. [36]).

Figure 4. Three nested domains utilized for ensemble quantitative precipitation forecast in the WRF/MM5 model (cited from Hsiao et al. [36]).

Table 1. Configuration details of ensemble members, encompassing initial conditions (ICs), lateral boundary conditions (LBCs), and a range of physical parameterizations (cited from Hsiao et al. [36]).

Ensemble Member	Model	ICs				LBCs	Cumulus Scheme	Microphysics Scheme	Boundary Layer
01	WRF	Partial cycle	3DVAR (CV5 + OL)	Bogus		NCEP GFS	GD	Goddard	YSU
02	WRF	Partial cycle	3DVAR	Bogus		NCEP GFS	G3	Goddard	YSU
03	WRF	Partial cycle	(CV5 + OL)	Bogus		NCEP GFS		Goddard	YSU
04	WRF	Partial cycle	3DVAR (CV5)	Bogus		NCEP GFS	BMJ	Goddard	YSU
05	WRF	Partial cycle	3DVAR	Bogus	Two-way interaction	NCEP GFS	KF	Goddard	YSU
06	WRF	Cold Start	(CV5 + OL)	Bogus		NCEP GFS	KF	Goddard	YSU
07	WRF	Cold Start	3DVAR	Bogus		NCEP GFS	KF	Goddard	YSU
08	WRF	Cold Start	(CV5 + OL)	Bogus		NCEP GFS	GD	Goddard	YSU
09	WRF	Cold Start	3DVAR (CV5 + OL)	Bogus		NCEP GFS	G3	Goddard	YSU
10	WRF	Partial cycle	3DVAR (CV3			NCEP GFS	BMJ	Goddard	YSU
11	WRF	Partial cycle	3DVAR (CV5 + OL)	Bogus		NCEP GFS	KF	Goddard	YSU
12	WRF	Partial cycle	3DVAR (CV3)			CWB GFS	KF	Goddard	YSU
13	WRF	Cold Start	3DVAR	Bogus		NCEP GFS	KF	Goddard	YSU
14	WRF	Cold Start	(CV3)	Bogus		NCEP GFS	KF	Goddard	YSU
15	WRF	Cold Start	3DVAR	Bogus	Two-way interaction	NCEP GFS	KF	Goddard	YSU
16	WRF	Cold Start	NODA			NCEP GFS	KF	WSM5	YSU
17	MM5	Cold Start	NODA			NCEP GFS	Grell	Goddard	MRF
18	MM5	Cold Start	4DVAR	Bogus		NCEP GFS	Grell	Goddard	MRF

Table 1. Configuration details of ensemble members, encompassing initial conditions (ICs), lateral boundary conditions (LBCs), and a range of physical parameterizations (cited from Hsiao et al. [36]).

Ensemble Member	Model	ICs				LBCs	Cumulus Scheme	Microphysics Scheme	Boundary Layer
01	WRF	Partial cycle	3DVAR (CV5 + OL)	Bogus		NCEP GFS	GD	Goddard	YSU
02	WRF	Partial cycle	3DVAR	Bogus		NCEP GFS	G3	Goddard	YSU
03	WRF	Partial cycle	(CV5 + OL)	Bogus		NCEP GFS		Goddard	YSU
04	WRF	Partial cycle	3DVAR (CV5)	Bogus		NCEP GFS	BMJ	Goddard	YSU
05	WRF	Partial cycle	3DVAR	Bogus	Two-way interaction	NCEP GFS	KF	Goddard	YSU
06	WRF	Cold Start	(CV5 + OL)	Bogus		NCEP GFS	KF	Goddard	YSU
07	WRF	Cold Start	3DVAR	Bogus		NCEP GFS	KF	Goddard	YSU
08	WRF	Cold Start	(CV5 + OL)	Bogus		NCEP GFS	GD	Goddard	YSU
09	WRF	Cold Start	3DVAR (CV5 + OL)	Bogus		NCEP GFS	G3	Goddard	YSU
10	WRF	Partial cycle	3DVAR (CV3			NCEP GFS	BMJ	Goddard	YSU
11	WRF	Partial cycle	3DVAR (CV5 + OL)	Bogus		NCEP GFS	KF	Goddard	YSU
12	WRF	Partial cycle	3DVAR (CV3)			CWB GFS	KF	Goddard	YSU
13	WRF	Cold Start	3DVAR	Bogus		NCEP GFS	KF	Goddard	YSU
14	WRF	Cold Start	(CV3)	Bogus		NCEP GFS	KF	Goddard	YSU
15	WRF	Cold Start	3DVAR	Bogus	Two-way interaction	NCEP GFS	KF	Goddard	YSU
16	WRF	Cold Start	NODA			NCEP GFS	KF	WSM5	YSU
17	MM5	Cold Start	NODA			NCEP GFS	Grell	Goddard	MRF
18	MM5	Cold Start	4DVAR	Bogus		NCEP GFS	Grell	Goddard	MRF

The resulting ensemble dataset provides a rich representation of forecast uncertainty and serves as a critical input for the hydrological and reservoir operation modules developed in this study. By leveraging multiple model realizations, the system enables more robust inflow predictions and enhances the reliability of real-time reservoir management during typhoon events.

4. Model Testing

This section presents the evaluation of the two major components of the proposed decision support system: (1) the rainfall–runoff model responsible for transforming ensemble rainfall forecasts into reservoir inflow estimates, and (2) the optimal reservoir operation algorithm designed to determine release strategies under varying hydrological conditions. Model performance was examined through controlled testing using historical typhoon events, providing insight into the robustness and operational applicability of the proposed framework.

4.1. Test of the Rainfall–Runoff Model Using Recorded Rainfall

The applicability of the KW-GIUH model for simulating reservoir inflow was assessed using rainfall data from Typhoons Talim, Saola, and Trami, and Typhoon Kong-rey, all occurring between 2012 and 2013. Hourly rainfall data from four rain-gauging stations, managed by the Central Weather Bureau of Taiwan, were processed using the Thiessen method to determine areal-averaged rainfall. The averaged rainfall data were then input into the KW-GIUH model for simulation. The recorded inflow to the reservoir was derived by analyzing variations in water level and using the reservoir’s level-volume relationship. Infiltration loss from the rainfall was calculated using Horton’s formula [37], and the initial infiltration rate (f_o) was estimated based on antecedent soil moisture, following the approach proposed by Lee and Huang [22]. The overland and channel roughness coefficients, represented by n_o and n_c, respectively, needed for the KW-GIUH modeling, were calibrated to minimize errors in estimating both peak discharge and time to peak discharge. The evaluation criteria were defined as follows:

$$E{Q}_p(\%)={\displaystyle \frac{{(Q_p)}_{sim}-{(Q_p)}_{rec}}{{(Q_p)}_{rec}}}\times 100$$

(14)

$$E{T}_p={(T_p)}_{sim}-{(T_p)}_{rec}$$

(15)

$$CE=1-{\displaystyle \frac{{\displaystyle \sum _{t=1}^n{\left[Q_{sim}(t)-Q_{rec}(t)\right]}^{ 2}}}{{\displaystyle \sum _{t=1}^n{\left[Q_{rec}(t)-{\overline{Q}}_{rec}\right]}^{ 2}}}}$$

(16)

where EQ_p (%) represents the relative error of peak discharge; ET_p denotes the error of time to peak discharge; CE stands for the coefficient of efficiency; (Q_p)_sim and (Q_p)_rec are the simulated and recorded peak discharge, respectively; (T_p)_sim and (T_p)_rec represent the simulated and recorded time to peak discharge, respectively; $Q_{rec}$ is the recorded discharge; ${\overline{Q}}_{rec}$ is the average recorded discharge.

Table 2. Performance evaluation of simulated reservoir inflow utilizing the KW-GIUH model.

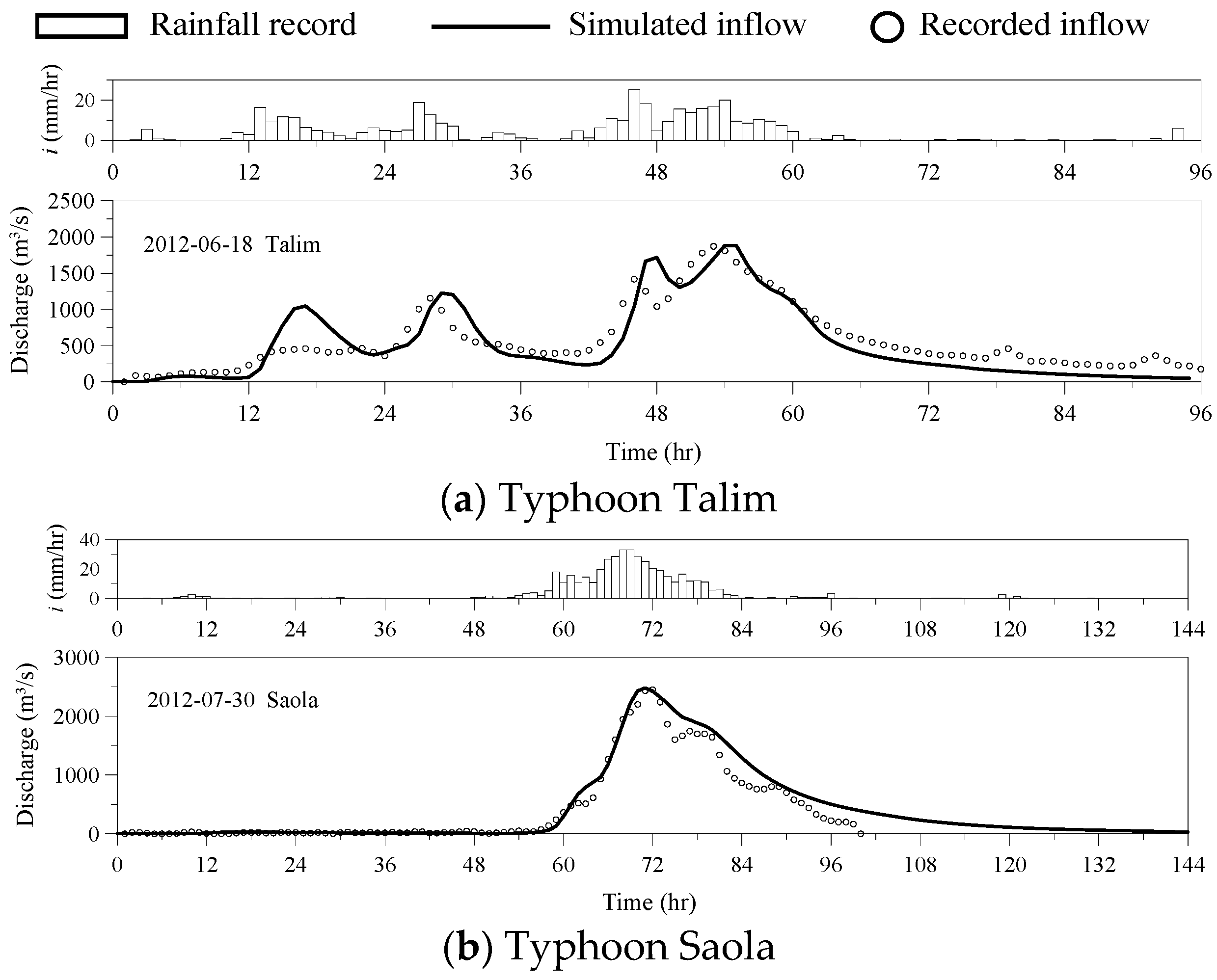
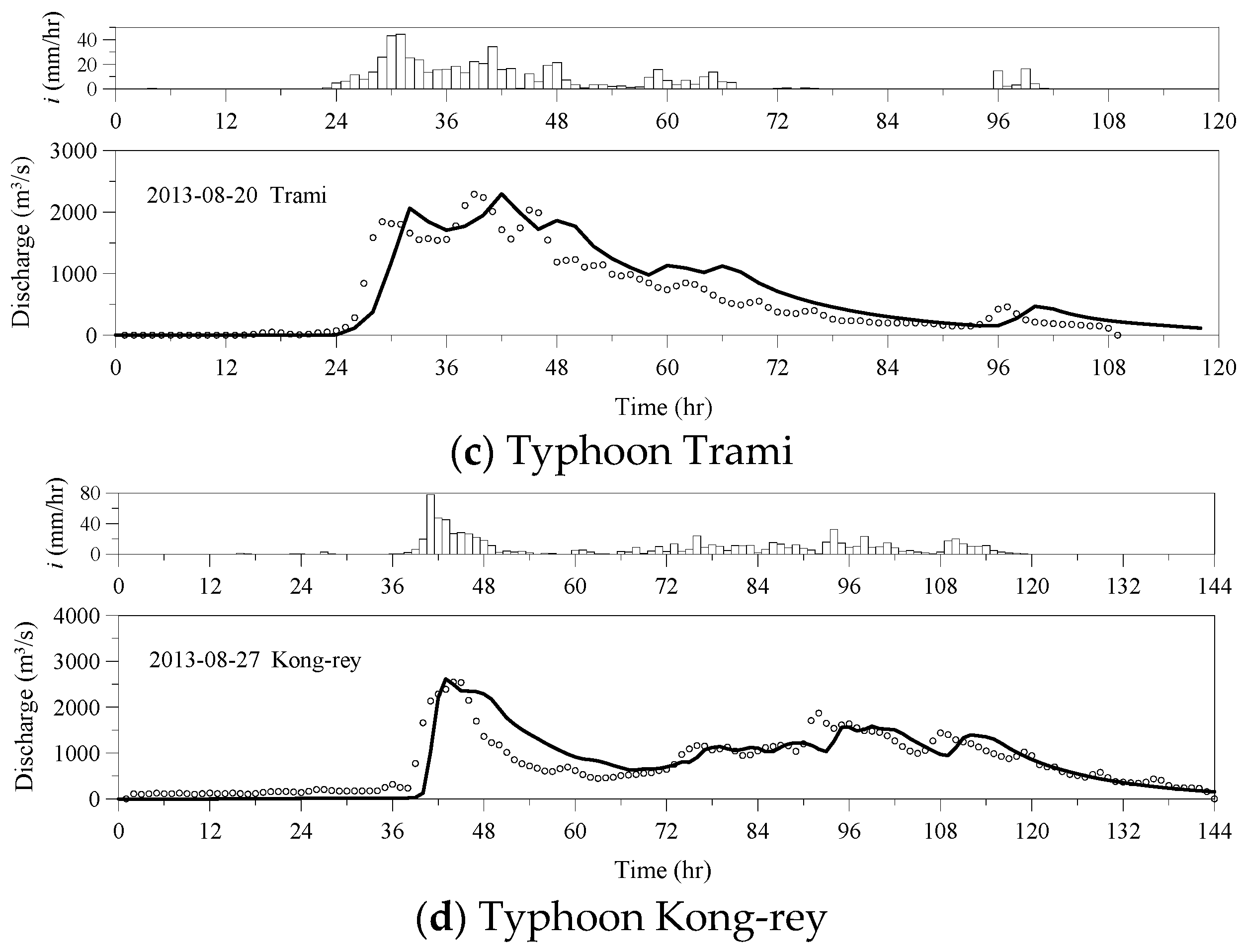
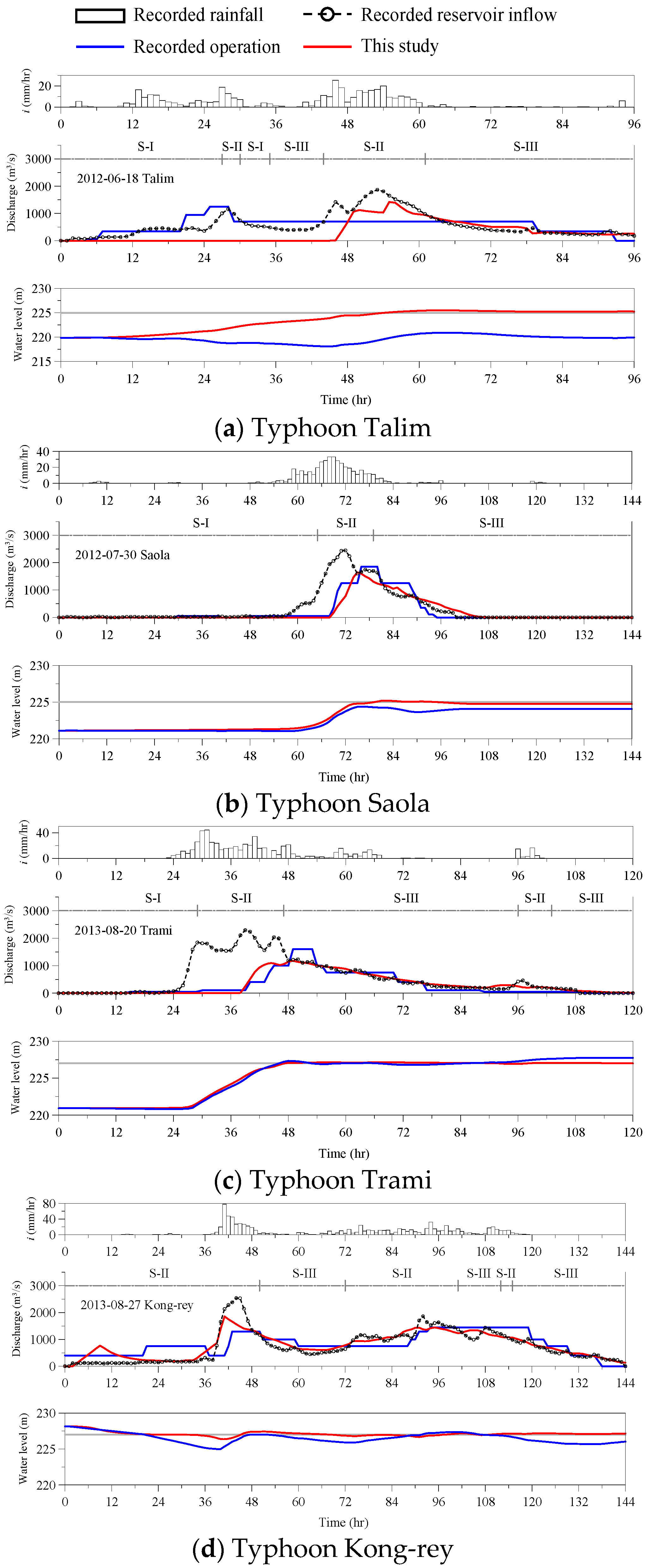
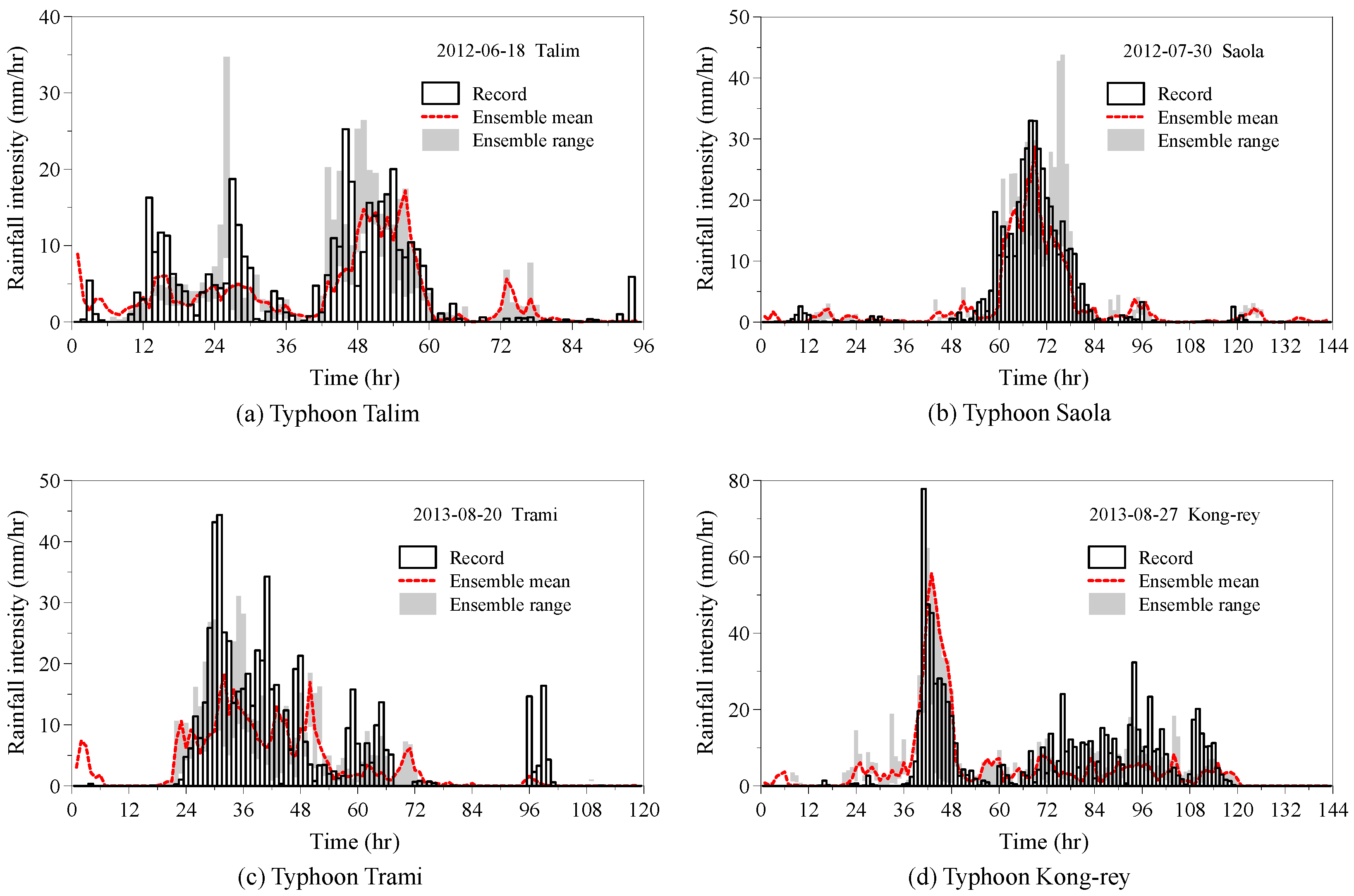
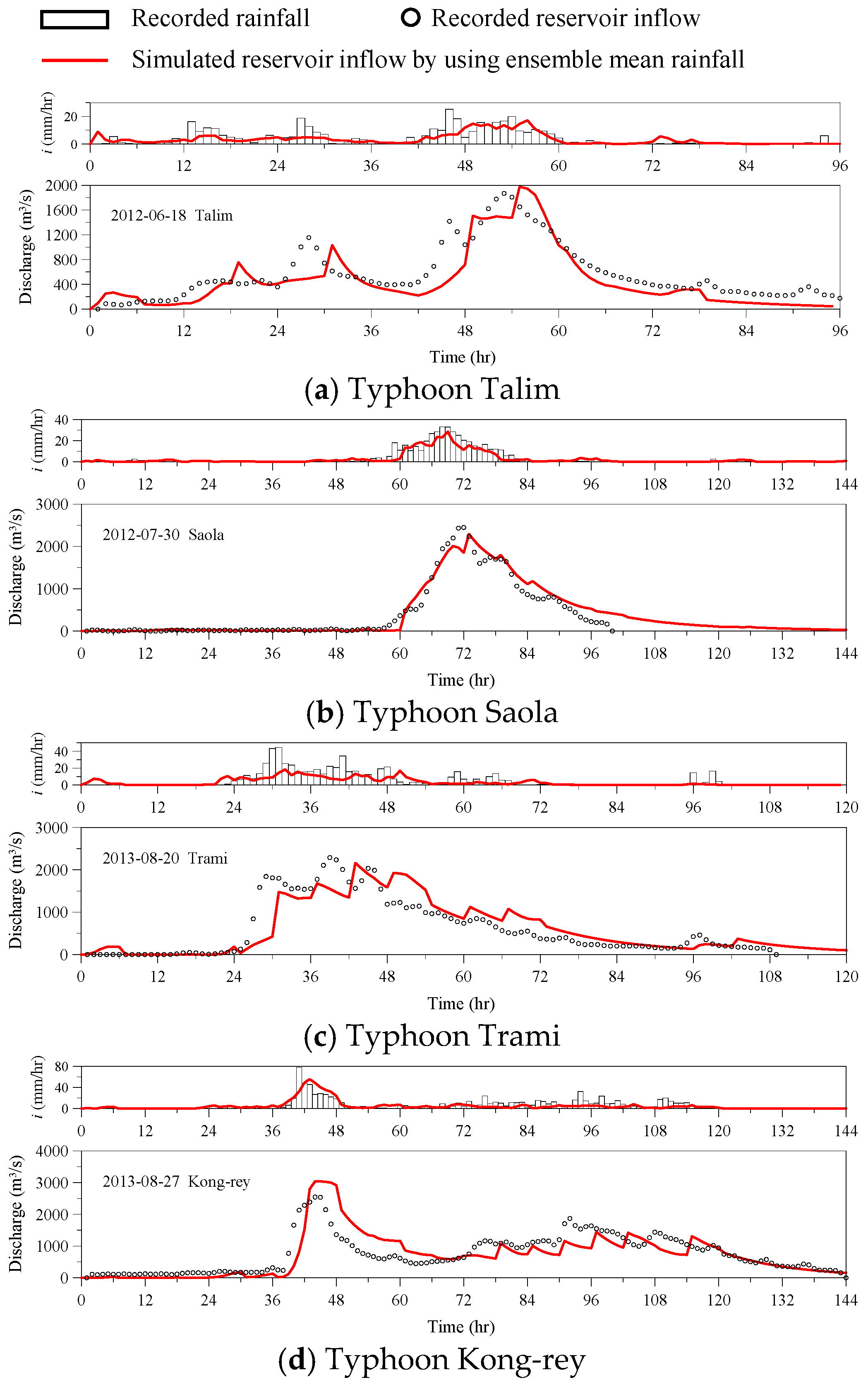
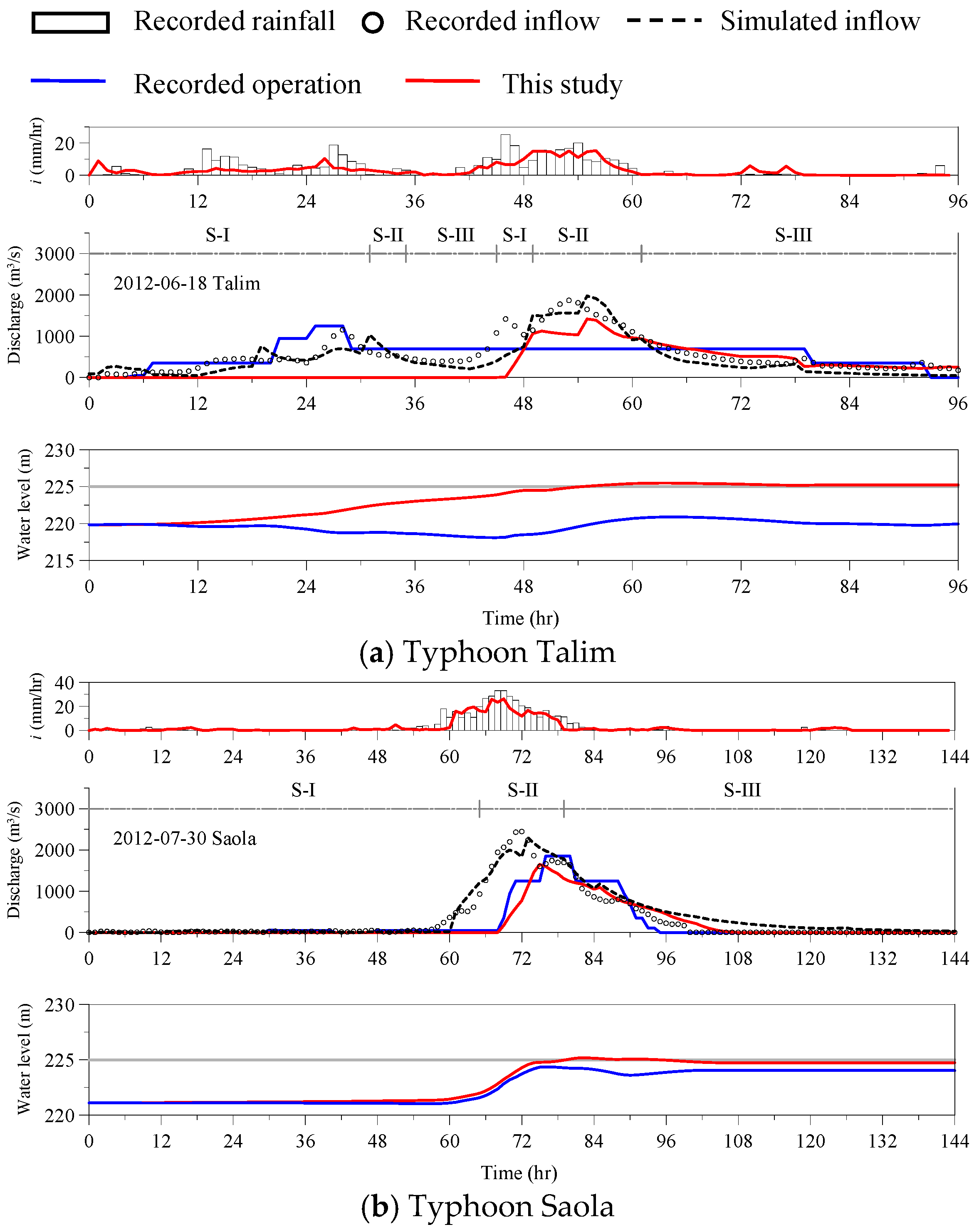
Date	Typhoon	EQp	ETp	CE
		(%)	(hr)
18 June 2012	Talim	0.67	2	0.75
30 July 2012	Saola	1.26	−1	0.95
20 August 2013	Trami	0.17	3	0.78
27 August 2013	Kong-rey	2.71	−1	0.68
	Mean value	$\pm 1.20$	$\pm 1.75$	0.79

presents the results of EQ_p, ET_p, and CE for the four typhoon events. The mean value of the relative error of peak discharge (EQ_p) is $\pm 1.20\%$. Except for Typhoon Kong-rey, which yielded a lower CE (=0.68), the other typhoons were accurately simulated and demonstrated acceptable EQ_p, ET_p, and CE values. Figure 5 displays the recorded and simulated hydrographs, which show consistent rising and recession patterns. However, in the case of Typhoon Kong-rey, the higher simulated flows observed after the peak led to a lower CE, as previously mentioned. In summary, the KW-GIUH model demonstrates competence in predicting upstream reservoir inflow.

4.2. Test of Reservoir Operation Algorithm Using Recorded Inflow

Tests of the proposed reservoir operation algorithm were conducted using recorded inflow data from the four typhoons as inputs. By concurrently considering incoming inflow and reservoir storage, the release flow rate from the reservoir was determined through an optimization process across the solution domain to maximize the corresponding objective function. The results of reservoir operation during the four typhoons are depicted in Figure 6. The figure includes references such as the normal pool level (indicated by the grey line) and the recorded operation (marked with the blue line). Additionally, labels S-I, S-II, and S-III in the figure denote the flood stages operated in the proposed algorithm.

In Figure 6a, during Typhoon Talim, recorded operations before the second inflow peak resulted in excessive water release, heightening the risk of water scarcity. This over-release occurred because the operator anticipated a subsequent major flood following an initial minor one. Consequently, a constant release rate of 700 m³/s was maintained from the 30th to the 80th hour. Conversely, our proposed algorithm prioritizes retaining water in the reservoir during Stages I and II, releasing it downstream when the reservoir approaches full capacity. During the flood recession period, the strategy transitions from Stage II to Stage III to maximize reservoir storage. As indicated in

Table 3. Reservoir water levels using both recorded reservoir inflow data and the operation algorithm proposed in this study.

Event Date	Typhoon	Initial Water Level	Target Water Level	Final Water Level
				Recorded	Simulated
		(m)	(m)	(m)	(m)
18 June 2012	Talim	219.85	225	220.01	225.24
30 July 2012	Saola	221.11	225	224.05	224.73
20 August 2013	Trami	220.91	227	227.75	227.01
27 August 2013	Kong-rey	228.14	227	226.02	227.16
			* Mean deviation	$\pm 1.92$	$\pm 0.17$

* Mean deviation = $\left|\mathrm{final} \mathrm{water} \mathrm{level} - \mathrm{target} \mathrm{water} \mathrm{level}\right|/4$.

, the deviation of reservoir water levels from the recorded to target values at the end of Typhoon Talim was 4.99 m. However, utilizing our optimization algorithm reduced this deviation significantly to only 0.24 m.

During Typhoon Saola and Trami, depicted in Figure 6b and Figure 6c, respectively, the storage level remained well controlled and closely matched the normal pool level in both the recorded and the proposed optimization results. However, a discrepancy occurred during Typhoon Saola, when the recorded storage level dropped by approximately 0.95 m below the normal pool level due to excessive outflow from the 76th to the 88th hour. Conversely, in Typhoon Trami, the recorded storage level surpassed the normal pool level by about 0.75 m after the 96th hour, attributed to subsequent heavy rainfall.

During Typhoon Kong-rey, the reservoir reached full capacity, limiting its ability to store additional water. Consequently, to ensure dam safety, a conservative approach was taken, resulting in significant water release before the 36th hour due to insufficient prediction of reservoir inflows. Subsequent dramatic adjustments in reservoir gate operations ensued, culminating in a final water level approximately 1.0 m lower than the normal pool level, as detailed in Table 3. However, the implementation of the proposed algorithm, which integrates strategies from both Stage II and Stage III, carefully balances flood control and water supply considerations. Therefore, the optimal storage level remained relatively stable and closely aligned with the normal pool level, resulting in an outflow hydrograph similar to the inflow hydrograph.

Across all cases, the algorithm consistently improved reservoir regulation by preventing both excessive releases and unnecessary storage deficits. The mean deviation of reservoir water levels from the recorded to the target values is reduced from the original operation algorithm (=$\pm 1.92$ m) to the proposal algorithm (=$\pm 0.17$ m). Even though none of the events triggered downstream overbank flooding (threshold 4940 m³/s), the framework is fully equipped to address such conditions. Overall, these results demonstrate that the proposed operation algorithm effectively balances flood control with water supply objectives, offering a more stable and efficient operational strategy than traditional rule-based approaches.

5. Results and Discussions

This section presents the evaluation of ensemble rainfall forecasts and their integration into reservoir inflow prediction and real-time operation. By applying the ensemble mean of 18 WRF/MM5 members to the KW-GIUH rainfall–runoff model, the study examines how forecast accuracy influences short-term inflow simulation during typhoon events. Furthermore, the predicted inflows are incorporated into the proposed optimal reservoir operation algorithm to assess its performance under varying hydrometeorological conditions. The following subsections discuss the effectiveness, limitations, and operational implications of these forecasting and decision-support components across four historical typhoons.

5.1. Application of Forecast Rainfall for Reservoir Inflow Prediction

For forecasting typhoon rainfall in Taiwan, an ensemble member can provide reliable guidance by providing an acceptable typhoon track [36,38,39]. Due to limited domain coverage and the complex inner-core structure at 5 km resolution, the typhoon position within this mesh is determined by locating the minimum sea-level pressure center within a 15 km mesh [39]. However, comparing typhoon tracks may be challenging when either the recorded or predicted track data are incomplete. Therefore, in this study, an ensemble mean derived from 18 WRF/MM5 members at each time step was utilized as input for the rainfall–runoff model. As reported by Hsiao et al. [36], the threat score (TS) for the 18 individual members showed that the ensemble mean rainfall had TSs exceeding 0.4.

Figure 7 illustrates the ensemble mean forecast rainfall for four typhoons, with the grey region representing the forecast rainfall range across members. To assess the performance of the forecasted rainfall against records, the error of total cumulative rainfall (ETCR) and the coefficient of efficiency (CE) were employed as evaluation criteria, defined as follows:

$$ETCR(\%)={\displaystyle \frac{{\displaystyle \sum _{t=1}^{t_d}{R}_{ens}(t)}-{\displaystyle \sum _{t=1}^{t_d}{R}_{rec}(t)}}{{\displaystyle \sum _{t=1}^{t_d}{R}_{rec}(t)}}}\times 100$$

(17)

$$CE=1-{\displaystyle \frac{{\displaystyle \sum _{t=1}^{t_d}{\left[R_{ens}(t)-R_{rec}(t)\right]}^{ 2}}}{{\displaystyle \sum _{t=1}^{t_d}{\left[R_{rec}(t)-{\overline{R}}_{rec}\right]}^{ 2}}}}$$

(18)

where t_d denotes the duration of rainfall, measured in hours; R_ens(t) represents the ensemble mean of rainfall at time t; R_rec(t) signifies the recorded rainfall at time t; ${\overline{R}}_{rec}$ denotes the average recorded rainfall. The values of ETCR and CE are presented in

Table 4. Evaluation of performance regarding the ensemble mean hyetograph and simulated reservoir inflow hydrographs during the four typhoon events.

Event Date	Typhoon	Ensemble Mean Rainfall		Reservoir Inflow Prediction
		ETCR (%)	CE	EQp (%)	ETp (hr)	CE
18 June 2012	Talim	−20.01	0.75	5.64	2	0.67
30 July 2012	Saola	−16.49	0.86	−6.18	1	0.94
20 August 2013	Trami	−35.25	0.71	−5.53	4	0.70
27 August 2013	Kong-rey	−17.99	0.76	19.57	1	0.52
	Mean value	$\pm 22.44$	0.77	$\pm 9.23$	$\pm 2$	0.71

. Negative values of ETCR in the table indicate that the ensemble mean total rainfall depths were underestimated, notably for Typhoon Trami, with a value of −35.25%.

Reservoir inflows with lead times of 1–6 h were estimated using the KW-GIUH model, which used both recorded rainfall data and the ensemble-mean rainfall for the corresponding 1–6 h periods. In Taiwan, the average lag time between the rainfall hyetograph centroid and the peak runoff ranges from 2 to 10 h; thus, a lead time of 6 h is adequate for real-time decision-making in reservoir operations.

Figure 8 depicts the predicted reservoir inflow achieved by utilizing the ensemble mean rainfall as inputs for the KW-GIUH model. Table 4 displays the EQ_P, ET_P, and CE metrics, which assess the performance of the simulated inflow with records. For Typhoon Talim, Saola, and Trami, EQ_P values are all below 10%, and CE values closely align with rainfall records (see Table 2). However, Typhoon Kong-rey exhibits a significant EQ_P and a low CE, indicating an unsatisfactory outcome primarily attributed to the overestimation of rainfall between the 24th and 48th hours (illustrated in Figure 6d). Nevertheless, the mean value of CE for the reservoir inflow prediction using the ensemble rainfall is still higher than 0.7, which demonstrates the applicability of the analysis procedure. Notably, the ensemble-mean hyetograph used here employs an equal-weighted approach. Future investigations will explore alternative weightings based on the historical prediction accuracy of individual members.

5.2. Application of Ensemble Rainfall for Real-Time Reservoir Operation

The KW-GIUH model used ensemble-mean rainfall data to predict reservoir inflow for the subsequent 6 h period. This forecasted inflow was then integrated into the proposed optimal algorithm for reservoir management. The operational outcomes during the occurrence of four typhoons are depicted in Figure 9. The graphical representations, arranged from top to bottom, include (1) the hourly rainfall hyetograph, (2) discharge hydrographs illustrating both recorded and simulated reservoir inflow, along with recorded and optimal outflow, and (3) comparisons of recorded and optimal reservoir water levels. As delineated in Section 4.2, during the Talim, Saola, and Trami typhoons, the unfilled reservoir was permitted to accumulate more upstream inflow during the initial phase of the storms to facilitate water supply needs.

As the inflow increased, the operational strategy transitioned from Stage I to Stage II, prompting the reservoir to commence water release based on the proposed outflow index O_index (as per Equation (6)), to accommodate additional space for incoming upstream inflow. Consequently, the reservoir water level rose gradually, eventually approaching the target storage level during the period of increasing flow. Following the cessation of rainfall, the focus shifted to Stage III’s objective function, which prioritized storing water for future water supply needs. However, an exception occurred during Typhoon Kong-rey, the largest typhoon among the test cases, when continuous downstream water release was required because the reservoir reached full capacity. Despite the operational water level exceeding 227 m between 76 and 114 h, the proposed algorithm effectively minimized the deviation between the operated and target storage levels during Typhoon Kong-rey.

During Typhoon Trami and Kong-rey, despite significant discrepancies between forecast rainfall and gauged records during the storms, the reservoir’s operational storage closely approached the target water level. This can be attributed to the proposed reservoir operation algorithm’s ability to promptly and intelligently adjust the release flow rate at each time step based on observed reservoir water levels and the outflow index (O_index).

Table 5. Reservoir simulated water levels using recorded rainfall and ensemble forecast rainfall.

Event Date	Typhoon	Target Water Level	Recorded Water Level	Simulated Water Level Using Recorded Rainfall	Simulated Water Level Using Ensemble Forecast Rainfall
		(m)	(m)	(m)	(m)
18 June 2012	Talim	225	220.01	225.24	225.42
30 July 2012	Saola	225	224.05	224.73	225.20
20 August 2013	Trami	227	227.75	227.01	227.08
27 August 2013	Kong-rey	227	226.02	227.16	227.01
Mean deviation				$\pm 0.17$	$\pm 0.18$

Mean deviation = $\left|\mathrm{final} \mathrm{water} \mathrm{level} - \mathrm{target} \mathrm{water} \mathrm{level}\right|/4$.

compares the simulated water levels based on recorded rainfall and ensemble forecast rainfall. It shows that the difference in mean deviations is slight, demonstrating that the proposed algorithm can achieve optimal results even when defective inputs are provided.

6. Conclusions

This study developed a comprehensive decision support system (DSS) that integrates ensemble rainfall forecasting, a physically based rainfall–runoff model, and an optimization-driven reservoir operation algorithm to enhance real-time water management during typhoon events. The system was designed to simultaneously address the competing objectives of flood control and water supply—an enduring challenge in Taiwan, where steep topography, short hydrologic response times, and increasingly extreme rainfall events heighten operational uncertainties and risks. By combining these components within a unified framework, the DSS aims to assist reservoir operators in making timely and informed decisions under rapidly evolving storm conditions. By incorporating WRF/MM5 ensemble forecasts, the DSS provides probabilistic rainfall information, which is then transformed into short-term inflow predictions using the KW-GIUH model. This hydrologic model demonstrated strong capability in reproducing inflow hydrographs for most typhoons, confirming its suitability for rapid, physically consistent estimation of upstream runoff.

The three-stage operation framework—representing pre-flood storage regulation, flood-pass routing, and post-flood recovery—proved effective across all tested storm events. Although uncertainties in ensemble rainfall forecasts persist—particularly for spatially complex or rapidly intensifying typhoons—the optimization algorithm effectively compensates for these errors. It does so by dynamically adjusting release strategies at each time step based on observed water levels, updated inflow trends, and the proposed outflow index, thereby reducing the system’s sensitivity to forecast inaccuracies. This structure allowed the reservoir to retain water before major inflows, safely pass peak floods when necessary, and restore storage once rainfall abated. Even under imperfect rainfall predictions, the DSS consistently maintained reservoir levels close to target storage and minimized deviation from ideal operation trajectories. Such performance illustrates the system’s robustness, adaptability, and ability to provide stable operational guidance despite hydrometeorological uncertainty.

This study demonstrates that integrating ensemble forecasting with hydrologic modeling and optimal programming substantially enhances reservoir resilience during extreme weather events. The developed Decision Support System (DSS) provides reservoir managers with a practical, intelligent, and adaptive framework for safer, more reliable, and efficient operations during typhoon-induced floods. The modular architecture of this system provides a foundation for advancing reservoir management research in several key directions: refining ensemble weighting strategies to improve forecast accuracy, incorporating real-time hydrologic data assimilation to enable dynamic operational adjustments, and extending the framework to multi-reservoir systems for regional flood management. These future research pathways have the potential to strengthen further the resilience and adaptability of reservoir operations in the face of increasingly variable climate conditions.