Comparison of Empirical Models to Predict Viscosity of Secondary Vacuum Gas Oils

Abstract

This work presents characterization data and viscosity of 34 secondary vacuum gas oils (H-Oil gas oils, visbreaker gas oils, and fluid catalytic cracking slurry oils) with aromatic content reaching up to 100 wt.%. Inter-criteria analysis was employed to define the secondary VGO characteristic parameters which have an effect on viscosity. Seven published empirical models to predict viscosity of the secondary vacuum gas oils were examined for their prediction ability. The empirical model of Aboul-Seud and Moharam was found to have the lowest error of prediction. A modification of Aboul-Seoud and Moharam model by separating the power terms accounting for the effects of specific gravity and average boiling point improves the accuracy of viscosity prediction. It was discovered that the relation of slope of viscosity decrease with temperature enhancement for the secondary vacuum gas oil is not a constant. This slope increases with the average boiling point and the specific gravity augmentation, a fact that has not been discussed before.

1. Introduction

Being an important input parameter in the chemical engineering design, viscosity prediction has concentrated the effort of many researchers on the development of various models that could estimate the viscosity of pure components and mixtures [1,2,3]. Whereas the prediction of pure liquid viscosity or two- or three-component mixture viscosity is a somewhat easier task, the prediction of viscosity of crude oils or petroleum fractions becomes much more complicated, because of the latter being undefined liquids. The complexity of the petroleum and its fractions has reflected in the development of different models predicting viscosity of distinct oils for the last 50 years [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Depending on how each prediction method has been developed, the methods could be categorized as theoretical, semi-theoretical or empirical. Theoretical models are based on statistical mechanics, and viscosity is related to the intermolecular potential functions [26]. Semi-theoretical models have a theoretical basis but include parameters that must be determined through fitting of experimental viscosity data. The semi-theoretical models are based on the principle of corresponding states and cubic equations of state [12,22,24]. They can be considered applied statistical mechanics models, such as the reaction rate theory, hard sphere theory, square well theory or their modifications [12,24]. The methods of corresponding states are based on one or more reference fluids and rely on the principle that under the same reduced conditions, the same reduced viscosity is obtained for any of the fluids in a group [24]. These methods predict viscosities as functions of temperature, pressure, composition, pseudo-critical properties, and the viscosity of a reference fluid at a reference temperature and pressure. As such, they can only be related to two of the following properties: the reduced temperature, reduced pressure, reduced density, or reduced volume [22]. The equation of state (EOS) concept involves a mathematical relationship between volume, pressure, and temperature that includes compositional information when dealing with mixtures. It can be used for different states of matter but is mostly used for gases, and no EOS application has been found for petroleum fluids [22]. The semi-theoretical models are usually more accurate, but they are more complex and require parameters such as critical properties, chemical composition, acentric factor or other similar properties which in many cases are not available [20]. The empirical methods include a wide variety of equations used throughout the industry involving constants calculated from experimental data by regression. Machine learning (ML) and artificial intelligence techniques (AI) have also been used to improve the prediction of oil viscosity [27,28,29,30,31,32]. The literature argues that the lowest average absolute relative error can be achieved when viscosity is predicted by AI models and the highest correlation coefficient as compared to existing empirical correlations [27,32]. The empirical models are typically simpler and only require a few basic parameters such as mid-boiling point temperature and specific gravity of the oil, or alternatively a single viscosity measurement, in order to extrapolate the viscosity to a different temperature [20]. The input oil characterization data for the empirical methods predicting viscosity include density, average boiling point or T_50% or molecular weight [4,5,10,11,13,14,15,16,17,18,20,21,22]. Al-Maamari et al. [16] and Bahadori [18] introduced the correlating parameter, that is (Sa/(Ar + Re + As)) ratio (where Sa, Ar, Re, and As are the contents of saturates, aromatics, resins, and asphaltenes, respectively); multiplied by the API to account for the effect of oil composition on viscosity. Sánchez-Minero et al. [17] account the effect of petroleum composition on its viscosity by the use of only API. As a whole, the higher the molecular weight (average boiling point or T_50%) and the higher the density of the oil the higher the viscosity is. Our earlier research [19] evaluated the available in the literature empirical models to predict viscosity of petroleum fractions originating from 244 different crude oils. The correlation of Abbott [4] was found to be the most accurate in prediction viscosity of vacuum gas oils (VGOs). The correlation of Twu [5] was the second most accurate in prediction viscosity of vacuum gas oils [12]. The correlation of Fang [14] was next in the classification of the accuracy of prediction viscosity of vacuum gas oils. The empirical models mentioned above were examined against data for vacuum gas oils from primary origin. The secondary vacuum gas oils coming from the processes of heavy oil conversion like fluid catalytic cracking (FCC), coking, and hydrocracking are more aromatic and heavier than the primary vacuum gas oils [33,34,35,36,37]. Considering that the aromatic content affects viscosity [38] one may expect that the empirical models developed on the base of data for primary vacuum gas oils could exhibit a bigger deviation in their prediction when secondary vacuum gas oils are examined. Unfortunately, information about viscosity of secondary vacuum gas oils in the literature is scarce. That is why it is very difficult, or even impossible, to verify the capability of the existing oil viscosity models to predict viscosity of the high aromatic secondary vacuum gas oils. That was the reason for us to characterize 23 secondary vacuum gas oils and a blended VGO consisting of about 70% hydrotreated straight run VGO and about 30% VGO coming from H-Oil vacuum residue hydrocracking and measure their viscosity. The content of aromatic compounds in these 24 VGOs, measured in accordance with ASTM D2549 standard, varied between 47.8% and 100%. The empirical models of Abbott [4], Twu [5], and Fang [14], which exhibited a satisfactory prediction of primary VGO viscosity were verified for their prediction ability for these 24 secondary VGOs. The models of Aboul-Seoud and Moharam [15], Sánchez-Minero et al. [17], AlMulla and Albahri [20], and Kotzakoulakis and George [21] were also examined for their capability to correctly predict the viscosity of the 24 secondary VGOs. Analyzing the results of the comparison between measured and predicted viscosity by the seven tested models, a modification of the best model was proposed and a verification with another set of 10 secondary VGOs for the new model and the best published model was performed. The aim of this work is to discuss the obtained results.

2. Materials and Methods

Properties of the secondary VGOs under study are presented in

Table 1. Properties of the secondary vacuum gas oils under study.

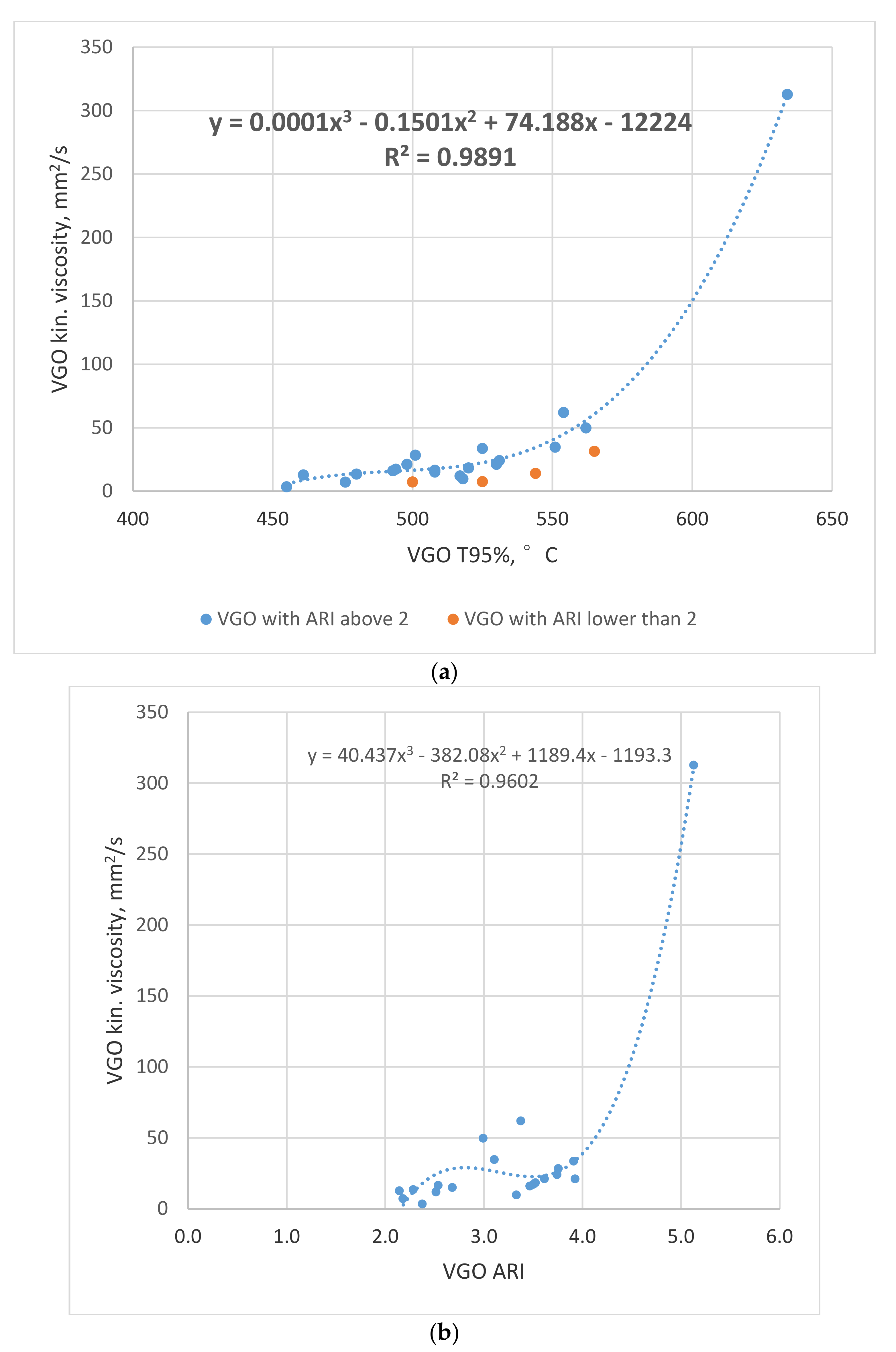
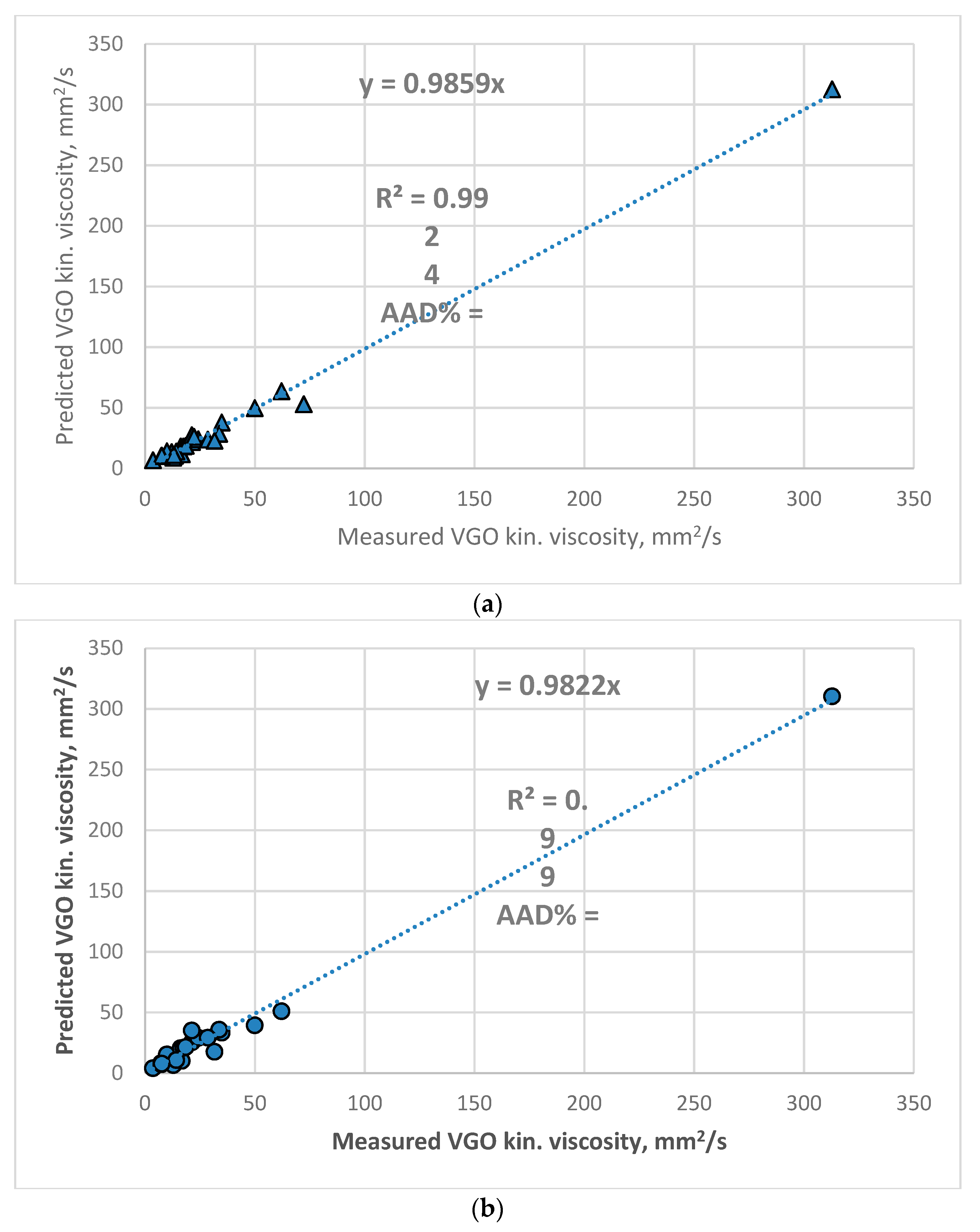
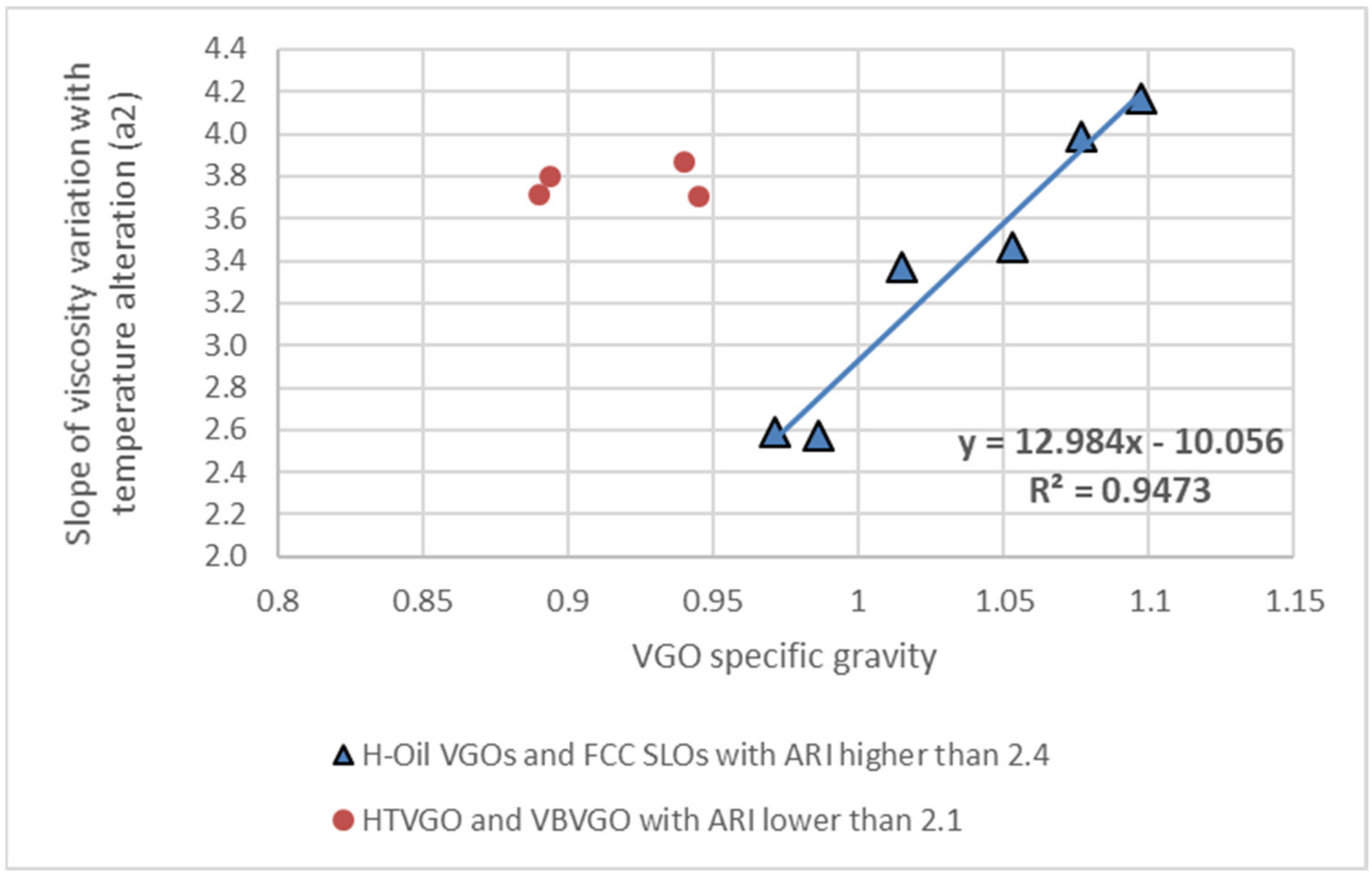
Nr	Sample	Density at 15 °C, g/cm3	SG	API	T10%	T50%	T90%	T95%	ABP, °C	Kin. vis. at 80 °C, mm2/s	Kin. vis at 98.9 °C, mm2/s	RI at 20 °C	Kw	MW, g/mol	ARI	Sat.	Aromatics
1	HAGO-1	0.9504	0.9512	17.3	343	397	455	476	398	7.3	4.6	1.5385	11.21	342	2.2	38.4	61.6
2	LVGO-1	0.9707	0.9715	14.1	343	414	493	517	417	12.1	7.1	1.5509	11.07	364	2.5	30.8	69.2
3	HVGO-1	0.9849	0.9858	12.0	426	491	548	562	488	49.9	22.9	1.5524	11.28	462	3.0	24.4	75.6
4	HAGO-2	0.9582	0.9590	16.0	335	395	458	480	396	13.6	7.9	1.5442	11.10	339	2.3	35.6	64.4
5	LVGO-2	0.9847	0.9856	12.1	330	410	488	508	409	15.2	8.6	1.5612	10.88	355	2.7	26.3	73.7
6	HVGO-2	1.0075	1.0084	8.8	430	489	540	554	486	62.1	27.4	1.5685	11.02	458	3.4	17.0	83.0
7	HAGO-3	0.9506	0.9514	17.2	323	377	439	461	380	12.9	7.5	1.5409	11.10	321	2.1	38.5	61.5
8	LVGO-3	0.9760	0.9768	13.4	324	395	482	508	400	16.7	9.3	1.5567	10.92	344	2.5	29.2	70.8
9	HVGO-3	0.9961	0.9970	10.4	405	470	534	551	470	34.8	17.1	1.5626	11.06	434	3.1	21.1	78.9
10	FCC SLO-1	0.9862	0.9871	11.9	232	282	412	455	309	3.6	2.5	1.5763	10.30	253	2.4	27.7	72.3
11	FCC SLO-2	1.054	1.0549	2.6	292	372	475	518	380	9.9	6.0	1.6140	10.01	319	3.3	8.6	91.4
12	FCC SLO-3	1.0564	1.0573	2.3	329	392	471	493	397	16.2	9.1	1.6135	10.08	338	3.5	7.4	92.6
13	FCC SLO-4	1.0662	1.0671	1.1	337	401	476	498	405	21.3	11.4	1.6194	10.02	345	3.6	5.1	94.9
14	FCC SLO-5	1.0615	1.0624	1.7	324	391	471	494	395	17.4	9.7	1.6172	10.02	335	3.5	6.4	93.6
15	FCC SLO-6	1.0943	1.0953	−2.3	331	400	491	525	407	33.8	16.7	1.6392	9.78	346	3.9	0.0	100.0
16	FCC SLO-7	1.0779	1.0788	−0.3	326	397	493	531	405	24.2	12.7	1.6280	9.92	345	3.7	2.7	97.3
17	FCC SLO-8	1.0621	1.0630	1.6	317	389	484	520	397	18.5	10.1	1.6178	10.02	337	3.5	6.2	93.8
18	FCC SLO-9	1.0826	1.0835	−0.9	327	401	480	501	403	28.5	14.5	1.6309	9.86	342	3.8	2.0	98.0
19	FCC SLO-10	1.1760	1.1770	−11.3	371	435	562	634	456	312.8	97.1	1.6927	9.31	395	5.1	0.0	100.0
20	FCC SLO-11	1.1001	1.1011	−3.0	332	394	482	530	403	21.2	11.4	1.6440	9.70	340	3.9	0.0	100.0
21	VGO blend	0.9157	0.9165	22.9	376	446	525	544	449	14.2	8.1	1.5088	11.92	404	1.7	52.2	47.8
22	HAGO-4	0.9041	0.905	24.9	357	425	489	505	424	8.0	4.9	1.5029	11.93	370	1.4	46.4	53.6
23	LVGO-4	0.9112	0.912	23.7	322	417	528	550	422	8.6	5.2	1.5088	11.83	369	1.6	51.0	49.0
24	HVGO-4	0.9211	0.922	22.0	411	486	552	568	483	27.2	13.5	1.5082	12.03	453	1.8	45.6	54.4

. The methods employed to measure their properties are given below:

• Density, g/cm³ ASTM D4052;
• High temperature simulation distillation (HTSD) Ŵ ASTM D7169;
• Engler specific viscosity ASTM D1665;
• Hydrocarbon composition ASTM D2549.

Conversion of Engler specific viscosity in kinematic viscosity was done as follows [39]:

$$Kin. vis.=7.41Engler specific viscosity$$

(1)

where Kin. vis. = kinematic viscosity, mm²/s. Engler specific viscosity = Engler specific viscosity, °E

The correlations used to estimate some of the properties of the studied secondary VGOs are summarized below.

Molecular weight was estimated by the correlation developed by Linan et al. for heavy oils[40] and shown as Equation (2).

$$M_w=284.75\left[\exp \left(0.00322\left(ABP+273.15\right)\right)\right]\left[\exp \left(-2.52SG\right)\right]\times {\left(ABP+273.15\right)}^{0.083}S{G}^{2.44}$$

(2)

The refractive index was estimated by the correlation of Stratiev et al. [41] and shown as Equation (3).

$$R{I}_{LNB}=0.702091d_{15}-0.00011T_{50}+0.91493$$

(3)

The characterization factor (Kw) was estimated by Equation (4).

$$Kw=\frac{\sqrt[3]{1.8\left[\frac{T10+T50+T90}{3}+273.15\right]}}{d_{15}}$$

(4)

The aromatic ring index (ARI), developed by Abutaqiya et al. [42,43] is estimated by Equations (5) and (6).

$$ARI=f\left(MW,F_{RI}\right)=\frac{2[\frac{MW}{F_{RI}} –\left(3.5149MW+73.1858\right]}{(3.5074MW-91.972-\left(3.5149MW+73.1858\right)}$$

(5)

where,

MW = molecular weight of EBVRHC heavy oils, g/mol;

FRI = function of refractive index.

$$F_{RI}=\frac{n_{D20}^2-1}{n_{D20}^2+2}$$

(6)

where, n_D20 = refractive index at 20 °C.

The empirical models published in the open literature and employed to predict viscosity of the studied 24 secondary vacuum gas oils are summarized in

Table 2. Empirical models to predict VGO viscosity.

Correlation Used	Equation	API	ABP, K	SG
Abbott [4]	$$\begin{gathered} {\begin{array}{c}\\ log\end{array}}_{10}VIS\left(98.89\right)=-0.463634-0.166532API \\ \begin{array}{r}+5.13447\times {10}^{-4}AP{I}^2\end{array} \\ \begin{array}{r}-8.48995\times {10}^{-3}{K}_{W}API+F\end{array} \end{gathered}$$ $F=\frac{8.0325\times {10}^{-2}{K}_W+1.24899API+0.19768AP{I}^2}{API+26.786-2.6296K_W}$	10.1°–50.3°	427.15–889.15	–
Twu [5]	$$\begin{gathered} T_C^{°}=ABP{\left(0.533272+0.191017\times {10}^{-3}ABP \\ +0.779681\times {10}^{-7}AB{P}^2 \\ -0.284376\times {10}^{-10}AB{P}^{3 }+0.959468\times \frac{{10}^{28}}{AB{P}^{13}}\right)}^{-1} \\ \begin{array}{l}\alpha =1-ABP/T_C^{°}\\ S{G}^{°}=0.843593-0.128624\alpha -3.36159{\alpha }^3-13795.5{\alpha }^{12}\\ \Delta SG=SG-S{G}^{°}\\ \ln \left(VI{S}_2^{°}+1.5\right)=4.73227-27.0975\alpha +49.4491{\alpha }^2-50.4706{\alpha }^4\\ \left|x\right|=\left|1.99873-56.7394/AB{P}^{0.5}\right|\\ f_{2 }=\left|x\right|\Delta SG-21.1141\Delta S{G}^2/AB{P}^{0.5}\\ \ln (VI{S}_{2 }+450/ABP)=\ln \left({\nu }_2^{°}+\frac{450}{ABP}\right)\left(\frac{1+2f_{2 }}{1-2f_{2 }}\right) at 98.89℃\end{array} \end{gathered}$$	–	–	–
Fang [14]	$\ln \frac{VIS}{T}=59.06AB{P}^{0.1546}{M}_W^{0.4791}\frac{\rho }{T}-\left(18.103+\ln M_W\right)$  $\rho =({\rho }_{15.6}^2-0.0011{\left(t-15.6\right)}^{0.5}$	–	363.15–727.15	0.73–0.90
Aboul-Seoud and Moharam [15]	$\ln \ln \left(VIS+0.8\right)=a_1+a_2\ln \left(T\right)$  $a_1=4.3414\times {\left(ABP\times SG\right)}^{0.2 }+6.6913$  $a_{2 }=-3.7$	–	323.15–773.15	–
AlMulla and Albahri [20]	$$\begin{gathered} VI{S}_{98.89} \\ =8.7903{\left[\frac{-31864.442+37377.083SG-14.374ABP}{-30178.282+35974.1SG-15.239ABP}\right]}^{-33.0834} \end{gathered}$$	–	450.65–883.45	0.769–0.952
Sánchez-Minero [17]	${\mu }_{od}=aexp\left(b/T^3\right)$  $a=3.9\times {10}^{-5}AP{I}^3-4.0\times {10}^{-3}AP{I}^2+0.1226API-0.7626$  $b=9.1638\times {10}^{9}AP{I}^{-1.3257}$	12.4°–43°	303.15–333.15	–
Kotzakoulakis [21]	$\ln \ln \left(VIS+0.8\right)=14.69AB{P}^{0.0684}S{G}^{0.267}-3.682\ln \left(T\right)$	–	358–873	0.806–1.024

.

3. Results

3.1. Relations of the Secondary VGO Properties to Viscosity

In order to evaluate the relations of the characteristics of the studied VGOs from Table 1 and to define these having the strongest impact on VGO viscosity, inter-criteria analysis (ICrA) was performed. The ICrA approach is specifically designed for datasets comprising evaluations, or measurements of multiple objects against multiple criteria. The building blocks of the presented ICrA for decision support are the two concepts of intuitionistic fuzziness and index matrices. Intuitionistic fuzzy sets defined by Atanassov [44,45,46,47] are one of the most popular and well investigated extensions of the concept of fuzzy sets, defined by Zadeh. Besides the traditional function of membership µA(x) defined in fuzzy sets to evaluate the membership of an element x to the set A with a real number in the [0; 1]-interval, in intuitionistic fuzzy sets (IFSs) a second function has been introduced, νA(x) defining, respectively, the non-membership of the element x to the set A, which may coexist with the membership function. More formally the IFS itself is formally denoted by

A = {‹x, µA(x), νA(x)› | x ∈ E}

and the following conditions hold:

0 ≤ µA(x) ≤ 1, 0 ≤ νA(x) ≤ 1

0 ≤ µA(x) + νA(x) ≤ 1.

Multiple relations, operations, modal and topological operators have been defined over IFS, showing that IFSs are a non-trivial extension of the concept of fuzzy sets.

The second concept, on which the proposed method is based, is the concept of index matrix, a matrix which features two index sets. The basics of the theory behind the index matrices are described in [48], and recently developed further in [49].

In the ICrA approach, the raw data for processing are put within an index matrix M of m rows {O₁, …, O_m} and n columns {C₁, …, C_n}, where for every p, q (1 ≤ p ≤ m, 1 ≤ q ≤ n), O_p in an evaluated object, C_q is an evaluation criterion, and e_OpCq is the evaluation of the p-th object against the q-th criterion, defined as a real number or another object that is comparable according to relation R with all of the remaining elements of the index matrix M.

$$\begin{array}{c}M=\\ \\ \\ \\ \\ \\ \end{array}\begin{array}{llllllll}& C_1& \dots & C_k& \dots & C_l& \dots & C_n\\ O_1& e_{O_1,C_1}& \dots & e_{O_1,C_k}& \dots & e_{O_1,C_l}& \dots & e_{O_1,C_n}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& \ddots & ⋮\\ O_i& e_{O_i,C_1}& \dots & e_{O_i,C_k}& \dots & e_{O_i,C_l}& \dots & e_{O_i,C_n}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& \ddots & ⋮\\ O_j& e_{O_j,C_1}& \dots & e_{O_j,C_k}& \dots & e_{O_j,C_l}& \dots & e_{O_j,C_n}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& \ddots & ⋮\\ O_m& e_{O_m,C_1}& \dots & e_{O_m,C_j}& \dots & e_{O_m,C_l}& \dots & e_{O_m,C_n}\end{array}\begin{array}{c},\\ \\ \\ \\ \\ \\ \end{array}$$

From the requirement for comparability above, it follows that for each i, j, k it holds the relation R (e_OiCk, e_OjCk). The relation R has dual relation, which is true in the cases when relation R is false, and vice versa.

For the needs of our decision making method, pairwise comparisons between every two different criteria are made along all evaluated objects. During the comparison, it is maintained one counter of the number of times when the relation R holds, and another counter for the dual relation.

Let $S_{k,l}^{\mu }$ be the number of cases in which the relations R (e_OiCk, e_OjCk) and R (e_{Oi Cl}, e_OjCl) are simultaneously satisfied. Let also $S_{k,l}^{\nu }$ be the number of cases in which the relations R (e_OiCk, e_OjCk) and its dual $\overline{R}$ (e_OiCl, e_OjCl) are simultaneously satisfied. As the total number of pairwise comparisons between the object is m (m − 1)/2, it is seen that there hold the inequalities:

$$0\le S_{k,l}^{\mu }+S_{k,l}^{\nu }\le \frac{m(m-1)}{2}$$

(7)

For every k, l, such that 1 ≤ k ≤ l ≤ m, and for m ≥ 2 two numbers are defined:

$${\mu }_{C_k,C_l}=2\frac{S_{k,l}^{\mu }}{m(m-1)},\hspace{0.33em}\hspace{0.33em}{\nu }_{C_k,C_l}=2\frac{S_{k,l}^{\nu }}{m(m-1)}$$

(8)

The pair, constructed from these two numbers, plays the role of the intuitionistic fuzzy evaluation of the relations that can be established between any two criteria C_k and C_l. In this way, the index matrix M that relates evaluated objects with evaluating criteria can be transformed to another index matrix M* that gives the relations among the criteria:

$$\begin{array}{c}\underset{}{M*=}\\ \\ \end{array}\begin{array}{cccc}& C_1& \dots & C_n\\ C_1& 〈{\mu }_{C_1,}{}_{C_1},{\nu }_{C_1,}{}_{C_1}〉& \dots & 〈{\mu }_{C_1,}{}_{C_n},{\nu }_{C_1,}{}_{C_n}〉\\ ⋮& ⋮& \ddots & ⋮\\ C_n& 〈{\mu }_{C_n,}{}_{C_1},{\nu }_{C_n,}{}_{C_1}〉& \dots & 〈{\mu }_{C_n,}{}_{C_n},{\nu }_{C_n,}{}_{C_n}〉\end{array}\begin{array}{c}.\\ \\ \end{array}$$

From practical considerations, it was more flexible to work with two index matrices M^μ and M^ν, rather than with the index matrix M* of IF pairs.

The final step of the algorithm is to determine the degrees of correlation between the criteria, depending on the user’s choice of µ and ν. We call these correlations between the criteria: ‘positive consonance’, ‘negative consonance’ or ‘dissonance’. Let α, β ∈ [0; 1] be the threshold values, against which we compare the values of µ_{Ck Cl} and ν_{Ck, Cl}. We call these criteria C_k and C_l in:

• (α, β)–positive consonance, if µ_Ck,Cl > α and ν_Ck,Cl < β;
• (α, β)–negative consonance, if µ_Ck,Cl < β and ν_Ck,Cl > α;
• (α, β)–dissonance, otherwise.

The approach is completely data driven, and each new application would require taking specific threshold values α, β that will yield reliable results. Various applications and suggested approaches to defining the thresholds have been discussed in a series of publications, available in [50].

Table 3. μ-value of the ICrA evaluation of relations between properties of the studied secondary vacuum gas oils.

	D15	T10%	T50%	T90%	T95%	ABP, °C	VIS 80	VIS 98.9	RI at 20 °C	Kw	MW	ARI	Sat.	Aro
D15	1.00	0.46	0.42	0.51	0.56	0.46	0.74	0.74	0.97	0.07	0.44	0.96	0.02	0.97
T10%	0.46	1.00	0.86	0.71	0.67	0.83	0.67	0.66	0.43	0.60	0.84	0.48	0.52	0.46
T50%	0.42	0.86	1.00	0.82	0.76	0.93	0.66	0.66	0.39	0.63	0.96	0.45	0.55	0.42
T90%	0.51	0.71	0.82	1.00	0.92	0.86	0.72	0.72	0.49	0.53	0.85	0.53	0.47	0.51
T95%	0.56	0.67	0.76	0.92	1.00	0.81	0.75	0.75	0.54	0.47	0.79	0.57	0.43	0.56
ABP °C	0.46	0.83	0.93	0.86	0.81	1.00	0.70	0.69	0.43	0.59	0.96	0.49	0.51	0.46
VIS 80	0.74	0.67	0.66	0.72	0.75	0.70	1.00	1.00	0.71	0.33	0.68	0.74	0.26	0.72
VIS 98.9	0.74	0.66	0.66	0.72	0.75	0.69	1.00	1.00	0.71	0.33	0.67	0.74	0.26	0.72
RI at 20 °C	0.97	0.43	0.39	0.49	0.54	0.43	0.71	0.71	1.00	0.04	0.41	0.93	0.04	0.94
Kw	0.07	0.60	0.63	0.53	0.47	0.59	0.33	0.33	0.04	1.00	0.63	0.10	0.89	0.09
MW	0.44	0.84	0.96	0.85	0.79	0.96	0.68	0.67	0.41	0.63	1.00	0.46	0.54	0.44
ARI	0.96	0.48	0.45	0.53	0.57	0.49	0.74	0.74	0.93	0.10	0.46	1.00	0.03	0.96
Sat.	0.02	0.52	0.55	0.47	0.43	0.51	0.26	0.26	0.04	0.89	0.54	0.03	1.00	0.01
Aro	0.97	0.46	0.42	0.51	0.56	0.46	0.72	0.72	0.94	0.09	0.44	0.96	0.01	1.00

Note: Green color means statistically meaningful positive relation; Red color implies statistically meaningful negative relation. The intensity of the color designates the strength of the relation. The higher the color intensity, the higher the strength of the relation is. Yellow color denotes dissonance.

and

Table 4. ν-value of the ICrA evaluation of relations between properties of the studied secondary vacuum gas oils.

	D15	T10%	T50%	T90%	T95%	ABP, °C	VIS 80	VIS 98.9	RI at 20 °C	Kw	MW	ARI	Sat.	Aro
D15	0.00	0.53	0.57	0.48	0.43	0.52	0.26	0.26	0.03	0.91	0.55	0.02	0.97	0.02
T10%	0.53	0.00	0.12	0.27	0.32	0.15	0.33	0.33	0.55	0.38	0.14	0.49	0.46	0.52
T50%	0.57	0.12	0.00	0.16	0.22	0.04	0.33	0.33	0.59	0.34	0.03	0.53	0.42	0.55
T90%	0.48	0.27	0.16	0.00	0.06	0.11	0.27	0.27	0.50	0.45	0.13	0.45	0.51	0.47
T95%	0.43	0.32	0.22	0.06	0.00	0.17	0.25	0.25	0.45	0.51	0.20	0.41	0.56	0.43
ABP °C	0.52	0.15	0.04	0.11	0.17	0.00	0.29	0.29	0.55	0.38	0.02	0.49	0.46	0.51
VIS 80	0.26	0.33	0.33	0.27	0.25	0.29	0.00	0.00	0.29	0.65	0.32	0.24	0.72	0.26
VIS 98.9	0.26	0.33	0.33	0.27	0.25	0.29	0.00	0.00	0.28	0.65	0.32	0.24	0.72	0.26
RI at 20 °C	0.03	0.55	0.59	0.50	0.45	0.55	0.29	0.28	0.00	0.94	0.58	0.05	0.94	0.04
Kw	0.91	0.38	0.34	0.45	0.51	0.38	0.65	0.65	0.94	0.00	0.35	0.88	0.09	0.89
MW	0.55	0.14	0.03	0.13	0.20	0.02	0.32	0.32	0.58	0.35	0.00	0.52	0.44	0.54
ARI	0.02	0.49	0.53	0.45	0.41	0.49	0.24	0.24	0.05	0.88	0.52	0.00	0.95	0.02
Sat.	0.97	0.46	0.42	0.51	0.56	0.46	0.72	0.72	0.94	0.09	0.44	0.95	0.00	0.99
Aro	0.02	0.52	0.55	0.47	0.43	0.51	0.26	0.26	0.04	0.89	0.54	0.02	0.99	0.00

Note: Green color means statistically meaningful positive relation; Red color implies statistically meaningful negative relation. The intensity of the color designates the strength of the relation. The higher the color intensity, the higher the strength of the relation is. Yellow color denotes dissonance.

present the statistically meaningful relations quantified by μ and ν-value of ICrA for the evaluated vacuum gas oils. It is evident from these data that the parameter that has the biggest impact on viscosity is T_95%. Figure 1a illustrates the relation of VGO viscosity to T_95%. It is in line with the empirical model proposed by Mehrota [10,12] highlighting the influence of the petroleum fraction boiling point on its viscosity. The data in Figure 1a also show that two different curves can be distinguished. The first is related to the secondary VGOs which have an aromatic ring index higher than 2. The second curve concerns the VGOs which have an ARI lower than 2. The data in Figure 1b suggest that the ARI also has a considerable impact on the VGO viscosity. These findings support the conclusion made by Redelius and Soenen [38] that both molecular weight (the molecular weight correlates with VGO boiling point) and aromaticity (expressed by ARI or density) are the main factors controlling the studied VGO viscosity. As was reported in our recent study [51] the most informative properties of a VGO are the average boiling point, or T_50%, and density, or specific gravity (SG). That is why the empirical models employed to evaluate their viscosity prediction ability in this work are based on these two VGO properties.

3.2. Evaluation of the Secondary VGO Viscosity Prediction Ability of Studied Empirical Models

To evaluate the accuracy of the employed empirical models to predict the secondary VGO viscosity the following statistical parameters were used [52]:

$$\mathrm{Error} (E): E=\left(\frac{{\upsilon }_{exp}-{\upsilon }_{calc}}{{\upsilon }_{exp}}\right)\times 100$$

(9)

$$\mathrm{Standard} \mathrm{error} (SE): S{E}_i={\left(\sum \left(\frac{{({\upsilon }_{exp}-{\upsilon }_{calc})}^2}{N-2}\right)\right)}^{\frac{1}{2}}$$

(10)

$$\mathrm{Relative} \mathrm{standard} \mathrm{error} (RSE): RS{E}_i=\frac{\mathrm{SE}}{\mathrm{mean} \mathrm{of} \mathrm{the} \mathrm{sample}}*100$$

(11)

$$\mathrm{Sum} \mathrm{of} \mathrm{square} \mathrm{errors} (SSE): SSE=\sum \frac{1}{{\upsilon }_{exp}^2}{({\upsilon }_{exp}-{\upsilon }_{calc})}^2$$

(12)

$$\mathrm{Residual} \left(R\right): R={\upsilon }_{exp}-{\upsilon }_{calc}$$

(13)

$$\mathrm{Average} \mathrm{absolute} \mathrm{deviation} (\%AAD): \%AAD=\frac{1}{N}\frac{\sum \left|v_{exp}-v_{calc}\right|}{v_{exp}}*100$$

(14)

Table 5. Statistical analysis of the seven tested empirical models to predict secondary VGO viscosity at 80 °C.

		Abbott	Twu	Al-Mulla	Aboul-Seoud	Sánchez-Minero	Fang	Kotzakoulakis
1	MIN E	−1368.7	−260.5	−1.41 × 1012	−65.5	NA	NA	−22,586.0
2	MAX E	51.3	61.8	100.0	48.9	NA	NA	76.9
3	SE	62.9	16.0	3.42 × 1010	6.3	NA	NA	15,064.7
4	RSE	190.4	110.5	1.04 × 1011	19.1	NA	NA	45,608.1
5	SSE	226.0	40.7	1.98 × 1020	1.9	NA	NA	51,789.1
6	LNR	−7.8	−13.8	−1.60 × 1011	−13.9	NA	NA	−70,656.8
7	HPR	291.5	60.0	97.1	14.0	NA	NA	24.3
8	#R−	5	23	23	12	NA	NA	12
9	#R+	19	1	1	12	NA	NA	12
10	Range R	299.3	73.8	1.60 × 1011	28.0	NA	NA	70,681.1
11	%AAD	79.3	109.7	5.87 × 1010	21.7	NA	NA	1259.9

summarizes the statistical analyses for the seven empirical models. In addition, the minimum error (min E), maximum error (max E), number of positive residuals (#R+), negative residuals (#R−), range calculated by the difference between the highest positive residual (HPR) and the lowest negative residual (LNR), are presented to provide a sound evaluation of each empirical model. It is evident from the data in Table 5 that the empirical model of Aboul-Seoud and Moharam [15] exhibited the lowest minimum and maximum error. It also showed the lowest standard error (SE), relative standard error (RSE), sum of squared error (SSE) and %AAD. The number of over- and underestimations, assessed by (#R+), and (#R−), and HPR and LNR, pointed out that the empirical model of Aboul-Seoud and Moharam [15] is the most balanced. In other words, the best prediction ability of the viscosity of the secondary VGOs from Table 1 exhibited the empirical model of Aboul-Seoud and Moharam [15]. One can see from the data in Table 5 that the empirical models of Sanchez-Minero et al. [17], and Fang and Lei [14] were found not applicable for the secondary VGO viscosity prediction.

3.3. Development of New Empirical Model

The data in Table 5 indicated that the empirical model of Aboul-Seoud and Moharam [15] best predicted the viscosity of the secondary VGOs from Table 1. In their model, however, both VGO average boiling point and specific gravity have the same power of 0.2. Kotzakoulakis and George [21] proposed an empirical model where petroleum boiling point, and specific gravity have different values of the power term. Following the suggestion to separate the power term for VGO average boiling point and the specific gravity we explored the empirical model in the form:

$$Vis=e^{e^{aAB{P}^b.D{15}^c}-d}+f$$

(15)

where,

Vis = kinematic viscosity at 80 °C, mm²/s;

ABP = VGO average boiling point, K;

D15 = VGO density at 15 °C, g/cm³;

a, b, c, d, f = regression coefficients.

Employing the data from Table 1 along with computer algebra system Maple (and Global Optimization Toolbox) the following values for the regression coefficients were found:

• a = 0.8611313197;
• b = 0.3967069960;
• c = 0.2858346574;
• d = 10.5837141796;
• f = 3.669559682208.

Figure 2 presents graphs of comparisons of measured against predicted by the empirical model developed in this work (Equation (14)) secondary VGO viscosity (Figure 2a) and that of Aboul-Seoud and Moharam [15] empirical model (Figure 2b). The data in Figure 2 show that the new empirical model distinguishes with a lower average absolute deviation (%AAD).

3.4. Validation of the New Empirical Model

Ten VGOs not included in the initial VGO database from Table 1 were examined for their viscosity at different temperatures.

Table 6. Ten VGOs employed to compare the viscosity prediction ability of the empirical model developed in this work with the empirical model of Aboul-Seoud and Moharam [15] that showed the best prediction of the tested published models.

Nr	Sample	SG	ABP °C	ARI	Kin. vis. at 80 °C, mm2/s	Predicted Viscosity at 80 °C by Aboud-Seoul and Moharam [15] Empirical Model	Predicted Viscosity at 80 °C by the Empirical Model Developed in This Work	AAD% (Aboul-Seoud and Moharam [15])	AAD% (This Work)
1	HAGO-5	0.971	397	2.4	13	10.1	11.5	22.1	11.5
2	LVGO-5	0.986	393	2.6	13	9.4	11.2	28.6	15.2
3	HVGO-5	1.015	476	3.4	57.5	45.5	53	20.8	7.8
4	FCC SLO-12	1.097	402	3.9	22.2	33	26.2	48.5	17.7
5	VBGO-1	0.940	439	2.1	14.7	12.0	14.6	18.2	0.4
6	VBGO-2	0.945	431	2.1	13.5	11.3	13.7	16.2	1.3
7	FCC SLO-13	1.053	366	3.2	14.5	12.6	12.0	13.4	17.2
8	FCC SLO-14	1.077	390	3.6	16.2	22.3	18.6	37.5	15.0
9	HTVGO-1	0.894	434	1.2	10.4	7.6	10.8	27.4	3.9
10	HTVGO-2	0.890	431	1.2	9.6	7.1	10.4	25.9	8.2
							AAD%	25.9	9.8

presents data of specific gravity, average boiling point, measured kinematic viscosity at 80 °C and predicted by Equation (15) and by the model of Aboul-Seoud and Moharam [15] for the 10 VGOs. It is evident from these data that Equation (14) predicts viscosity with 2.64 times as low % AAD as that of the model of Aboul-Seoud and Moharam [15]. The new empirical model predicts viscosity of VGOs at 80 °C. In order to predict the secondary VGO viscosity at any temperature a relation of viscosity at 80 °C to that at any temperature is required. Aboul-Seoud and Moharam [15] developed an empirical model to predict viscosity at different temperatures from one test performed at any temperature. It has the form:

$$LnLn\left(VIS+0.8\right)=LnLn\left(VI{S}_0+0.8\right)+a_{2}Ln\left(\frac{T}{T_O}\right)$$

(16)

where VIS_o is the single viscosity measurement (mm²/s) at temperature T₀ (K) and a₂ = −3.7.

Kotzakoulakis and George [21] confirmed in their study, that a₂ is almost equal to −3.7, with a small adjustment to be equal to −3.682.

In order to verify the validity of a₂ = −3.7 the viscosity of the 10 VGOs was measured in the temperature range 40–100 °C (

Table 7. Kinematic viscosity of the ten VGOs from Table 4 measured at different temperatures.

	Kinematic Viscosity, mm2/s
T °C	HAGO-5	LVGO-5	HVGO-5	FCC SLO-12	VBGO-1	VBGO-2	FCC SLO-13	FCC SLO-14	HTVGO-1	HTVGO-2
40							107.8	194.0
50	29.6	30.8		109.3	46.1	39.5	46.3	85.1	28.8	25.6
60	18.7	18.5	118.6	53.7			29.8	44.8	19.6	17.7
70	15.0	14.8	95.6	31.5			20.0	25.6	14.1	13.5
80	13.0	13.0	57.5	22.2	14.7	13.5	14.5	16.2	10.4	9.6
90	11.3	11.7	46.3	17.3	8.5	8.2
100			24.4

). By the use of Equation (15) and the data in Table 7 a₂ was calculated and it was found that a₂ is not equal to −3.7 for the 10 studied VGOs. Figure 3 indicates that a₂ varies between −2.57 and −4.17 for the 10 additionally studied VGOs. It also shows that for the VGOs having ARI equal or higher than 2.4 a₂ correlates with the VGO SG. The VGOs having ARI equal or below 2.1 a₂ is close to −3.7 and could be assumed to be −3.7. For the VGOs having ARI equal or higher than 2.4 a regression was developed to predict a₂ from data about SG and ABP. It has the form:

$$a_2=-12.0305+13.48785 * \mathrm{SG}+0.003598 * \mathrm{ABP} {\mathrm{R}}^2=0.99 \%\mathrm{AAD}=2.1$$

(17)

Equation (17) suggests that increasing both ABP and SG leads to augmentation of a₂. In other words, the heavier and higher boiling secondary VGOs will exhibit a steeper decrease in viscosity with enhancement of temperature. More data are needed to understand the relation of viscosity to temperature for VGOs having ARI lower than 2.

Another issue with the prediction of VGO viscosity at different temperatures is the accuracy of the measurement of viscosity at lower temperatures. For example, the viscosity of HVGO-5 at 50 °C was not possible to measure due to its lower fluidity.

Table 8. Kinematic viscosity measured six times at 60, 80, and 100 °C for the secondary VGOs—HVGO-5 and LVGO-5.

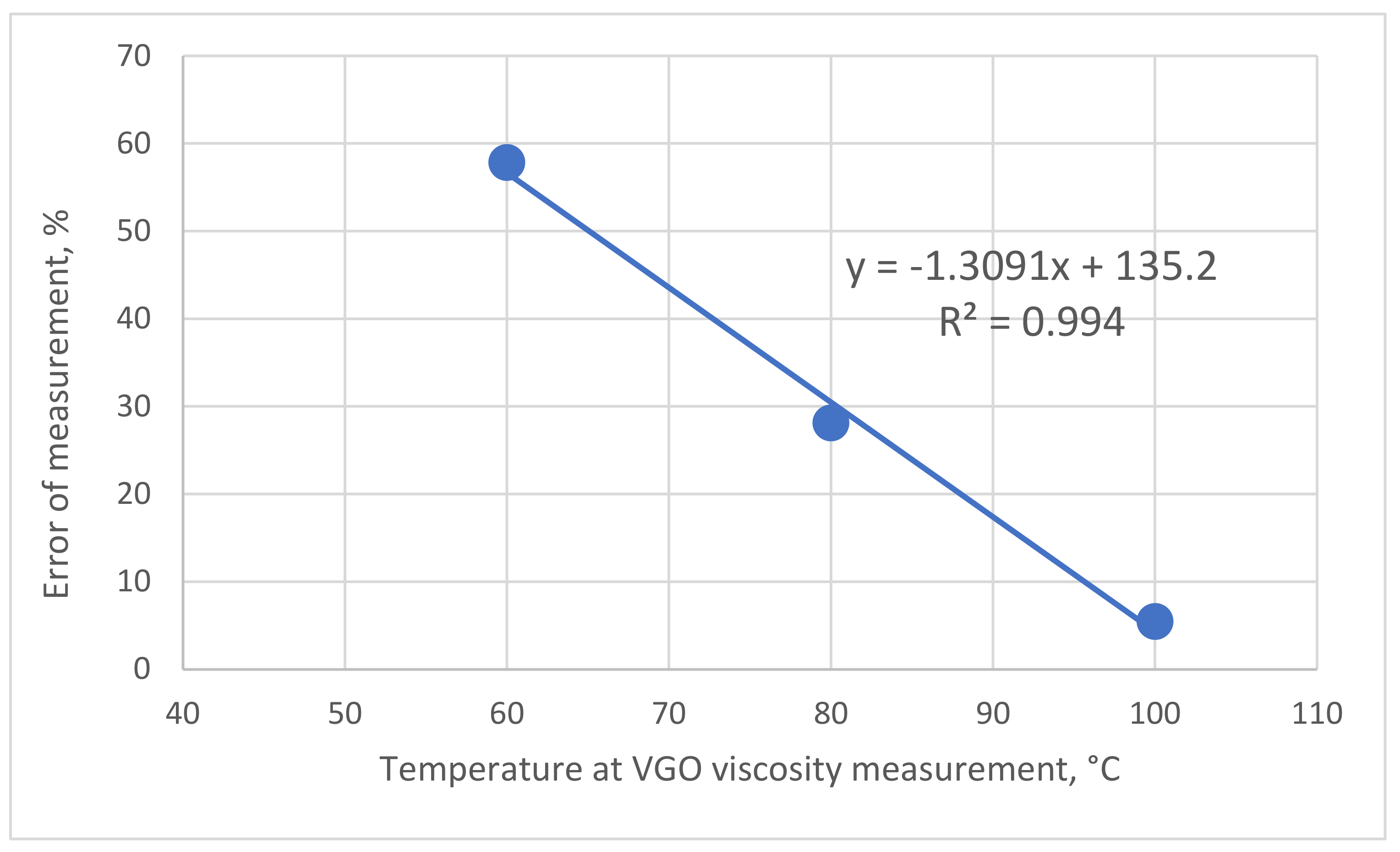
	HVGO-5		LVGO-5
Temperature °C	80	100	60
1st measurement	72.6	25.7	46.7
2nd measurement	59.3	24.1	27.8
3rd measurement	57.4	24.1	25.9
4th measurement	51.9	24.1	25.9
5th measurement	51.9	24.1	27.8
6th measurement	51.9	24.5
Average	57.5	24.4	30.8
σ2	65.4	0.4	79.4
σ	8.1	0.7	8.9
2 σ, % (error of measurement)	28.1	5.5	57.8

presents data of kinematic viscosity measured six times at 60, 80, and 100 °C for the secondary VGOs—HVGO-5 and LVGO-5. These data indicate the error of measurement linearly increases with decreasing of the temperature of measurement (Figure 4). It becomes clear from these data that prediction of viscosity of VGOs at lower temperature will suffer from a lower accuracy.

The newly developed empirical model (Equation (14)) along with Equations (15) and (16) were used to estimate viscosity of the 10 VGOs at the temperature range 40–100 °C and were compared with the empirical model of Aboul-Seoud and Moharam [15] for 42 experimental points. Table S1 (Supplementary Materials) presents data for the measured and estimated by the model developed in this work and that of Aboul-Seoud and Moharam [15] along with data for average deviation, % AAD, and standard error. These data show that the newly developed empirical model is superior with lower values for the average deviation (7.4 mm²/s for this work versus 9.4 mm²/s of Aboul-Seoud and Moharam), % AAD (13.8% versus 24.9% for Aboul-Seoud and Moharam), and standard error (18.5 versus 28.5 for Aboul-Seoud and Moharam).

4. Conclusions

This work presented characterization data and viscosity of 34 secondary VGOs with aromatics content reaching up to 100 wt.%. The secondary VGO viscosity goes up with the enhancement of average boiling point and specific gravity. The viscosity of the secondary vacuum gas oils is best predicted by the use of data for average boiling point and specific gravity (density). The empirical model of Aboul-Seoud and Moharam [15] among the seven tested empirical models was found to predict the secondary VGO viscosity with the highest accuracy. A modification of Aboul-Seoud and Moharam model by separating the power terms accounting for the distinct effects of specific gravity and average boiling point improves the accuracy of viscosity prediction. It was found out that the relation of slope of viscosity decrease with temperature enhancement for the secondary VGO is not a constant. It was discovered that this slope increases with ABP and SG augmentation, a fact that has not been discussed before. Moreover, the VGOs having different aromatic ring indexes seem to obey a different dependence of the slope of viscosity decrease with temperature enhancement. The accuracy of prediction of oil viscosity depends on the temperature of viscosity measurement. The lower the viscosity measurement temperature the higher the error of measurement can be depending on the low temperature properties of the studied oils. In this work, it was found that the error of VGO viscosity measurement linearly increases with decreasing the temperature of the measurement. Therefore, models predicting secondary VGO viscosities at temperatures lower than 80 °C can suffer from a lower accuracy.