Abstract
Supply risk assessments are an integral part of raw material criticality assessments frequently used at the country or company level to identify raw materials of concern. However, the indicators used in supply risk assessments to estimate the likelihood of supply disruptions vary substantially. Here, we summarize and evaluate the use of supply risk indicators and their normalization to supply risk scores in 88 methods published until 2020. In total, we find 618 individual applications of supply risk criteria with 98 unique criteria belonging to one of ten indicator categories. The most often used categories of supply risk indicators are concentration, scarcity, and political instability. The most frequently used criteria are the country concentration of production, depletion time of reserves, and geopolitical risk. Indicator measurements and normalizations vary substantially between different methods for the same criterion. Our results can be used for future raw material criticality assessments to screen for suitable supply risk indicators and generally accepted indicator normalizations. We also find a further need for stronger empirical evidence of widely used indicators.
1. Introduction
Raw material criticality assessments are carried out to identify materials of concern [1]. Their goals range from risk mitigation to hotspot analysis. The actors can be governments and companies alike. The scope of risk consideration ranges from physical accessibility to reputation damage. Even the material scope can differ from chemical elements to whole supply chains [2]. It is good practice to follow four phases for the design and communication of a criticality assessment, consisting of (i) goal and scope definition, (ii) indicator selection and evaluation, (iii) aggregation, (iv) interpretation and communication [2]. Most criticality assessments consider indicators in the two dimensions “supply risk” [3] and “vulnerability” [4]. Several different indicator categories are used for both, as identified by Schrijvers et al. [1]. However, there is little evidence for the general significance of individual risk aspects for raw material criticality [5]. Commodity prices are linked to changes in supply risk aspects, but the scale and significance level of this empirical evidence depends strongly on the specific raw material [6].
The present article is an update to an earlier review by Achzet and Helbig [3]. When that review was published, only 15 criticality assessments were available for a systematic review. In the past eight years, raw material criticality assessments have increased substantially in quantity, impact, and scope [7]. The International Round Table on Materials Criticality (IRTC) held a series of expert workshops and conducted a broad review of various criticality assessments, focusing on risk types, geographical scope, time horizons, and objectives of the methods [1]. However, their study did not cover the details of each criterion and the normalization and interpretation of each of the supply risk and vulnerability indicators [1].
Nevertheless, looking at such information is essential to guide future method developers and users in applying assessments. Such detailed information helps in the second criticality assessment phase, indicator selection, and evaluation [2]. Therefore, the present review focuses on indicator usage instead of the general goals of the methods or aggregation procedures. We provide an overview on supply risk indicator usage in all relevant criticality assessment schemes.
For this purpose, we distinguish indicator categories, criteria, measurements, and normalizations. Indicator categories are general supply risk aspects considered in assessments and may have multiple evaluation criteria. We identify frequently used indicator categories and, for each category, the most relevant supply risk criteria. The criteria need to be measured and consequentially normalized. We want to provide an overview on possible measurements and normalizations. Due to a lack of empirical evidence, we cannot provide a recommendation for best practice on each criterion. Normalization can happen with a continuous formula, stepwise normalization, or point-wise evaluation. For example, Graedel et al. [8] consider the country concentration of production in the criterion for concentration, measured with the Herfindahl–Hirschman Index (HHI), and apply a logarithmic normalization formula to evaluate this criterion on a shared supply risk score. Using such a procedure transparently and in a reproducible manner helps improve criticality assessments and follows good practice [2]. Our review fosters this transparency and reproducibility.
2. Method
Our review includes 88 supply risk assessment methods published from 1977 to 2020. The methods are published in peer-reviewed literature, research reports, working papers, books, book sections, or corporate or institutional websites. The previous reviews by Achzet and Helbig [3] and Schrijvers et al. [1] contributed to this collection. The list of studies was extended with citation chaining, considering only publications in English or German. The complete list of studies is included in Appendix A.
Most of the 88 methods are full criticality or supply risk assessments that follow the four good practice steps in criticality assessment [2]. Others are either a collection of indicators, which do not aggregate the results, or methods consisting of only a single supply risk indicator. The Supplementary Material spreadsheets additionally list publications that we did not include in our review because they were reviews, obsolete publications (which have been updated by the same authors or institutions by now), or applications of supply risk assessment methods without any methodological change. All of these exclusions avoid double-counting.
All methods included in the review were reviewed concerning their supply risk indicators. If the method additionally had a vulnerability or economic importance dimension, those indicators were not considered. For each of the 618 indicators used in the various supply risk assessments, we identify the overarching indicator category, the measurement (with minimum and maximum values) and the normalization type (normalization formula, stepwise supply risk levels, point-wise evaluation, or no normalization). The list of all indicators, including the normalization formula, supply risk levels, or evaluation points, can be found in Supplementary Material spreadsheets. Table 1 shows a glossary for the relevant terms contained in this data sheet.

Table 1.
Glossary of Supplementary Material spreadsheet.
The review process also included an attempt for the harmonization of terminology in supply risk assessments. For reasons of transparency, the spreadsheet in the Supplementary Material therefore also contains the original criterion name. However, in our review, harmonized criterion names are used. For example, one method may call its indicator “producer diversity”, while another calls its indicator “company concentration”, and both may be measured with the HHI. Therefore, company concentration is used in this case as the harmonized criterion name for both cases.
Category names are also harmonized always to indicate risk or problem, as shown in Figure 1. For example, many supply risk assessments consider some form of recycling in their method, but recycling itself is not a problem for supply risk—the contrary is the case. The lack of secondary production increases the dependence on primary production to maintain global material flows and supply chains. Therefore, all categories have received a name indicating that “more” in this indicator equals higher supply risk and criticality, even for those studies that initially assessed supply security or supply chain resilience rather than supply risks.
Figure 1.
Overview of supply risk categories identified in the review. Sector width is not proportional to indicator frequency.
3. Results
The review of all 88 supply risk assessments results in a list of 618 individual indicators. These indicators can be grouped into ten indicator categories with a varying number of criterions each. Risks and criterion labeling follow a single Latin letter and a two-digit numerical code, e.g., A01 for country concentration production.
The categories are (A) concentration, (B) scarcity, (C) political instability, (D) regulations, (E) by-product dependence, (F) dependence on primary production, (G) demand growth, (H) lack of substitution options, (I) price volatility, and (J) import dependence. A total of 53 additional indicators did not fit these ten categories and therefore have been allocated to the group of other indicators (X). The review results in each of these categories are described in the following subsections one by one. Table 2 shows the indicator categories and their frequency.

Table 2.
List of supply risk categories identified in the review. Categories define the leading letter (A-J, X) by order of frequency of their indicators.
Figure 2 summarizes the use of all criteria used at least three times. It shows almost all criteria are still used nowadays, with the prominent exception of criterion B07, depletion time reserve base, which is not used anymore because most data providers discontinue reserve base data.
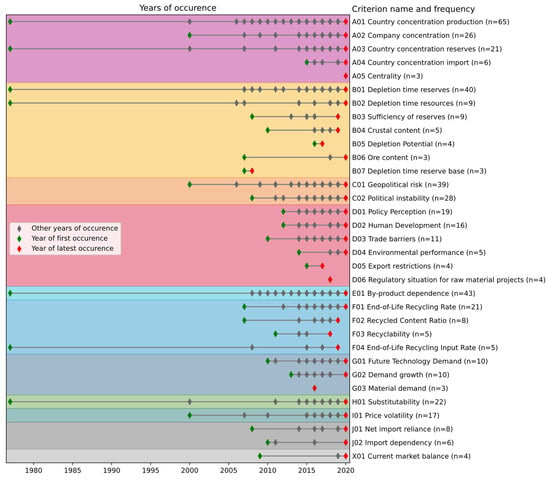
Figure 2.
Occurrence of indicators by publication year. Only indicators occurring at least three times are shown. Each rhombus represents at least one occurrence.
For each of the indicator categories, we show a graphical representation of relevant normalizations. To allow a better comparison, the original formulas are rescaled to a common “normalized supply risk score” between 0 and 100 for all categories.
3.1. Concentration (A)
The market concentration (A) is the most frequently used indicator category making up 137 of the 618 indicators (22%). The associated indicators can be grouped into a total of 18 harmonized criteria, of which the five most frequently used criteria are country concentration production (A01), company concentration (A02), country concentration reserves (A03), and country concentration import (A04). In total, these four criteria are used in 118 of 137 indicators (86%) of the concentration category.
The first appearance of concentration as a supply risk indicator dates back to 1977 when Grebe et al. [9] considered the number of countries accounting for 40%, 60%, or 80% of the global production or global reserves as a measurement of A01 and A03. These measurements were converted for both indicators into a scale from 1 to 5, indicating the extent of supply risk, whereby the exact transformation routine is not given [9]. The so-called Herfindahl–Hirschman Index (HHI) [10,11] is a much more frequent concentration measurement for criteria A01 to A04. Some publications proposed a combined indicator composed of the HHI and an indicator from another category as a weighting factor, for example, the political instability category. Another frequently used measurement is the accumulated share gathered from top countries of production or reserves, as presented by Grebe et al. [9]. Normalization approaches using the HHI measurement for A01 to A04 are presented in Figure 3. Information about the remaining harmonized criteria can be found in the Supplementary Material spreadsheets.
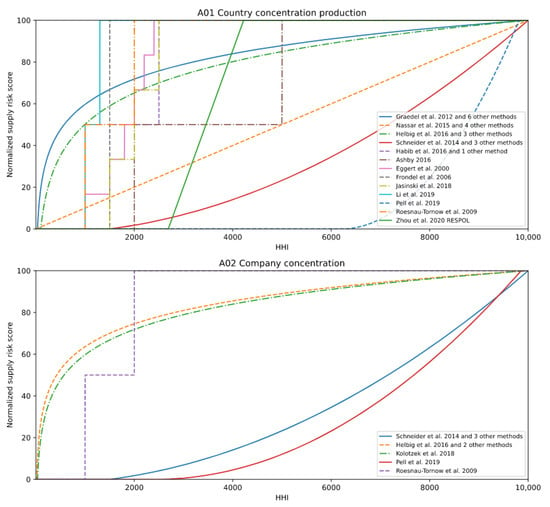
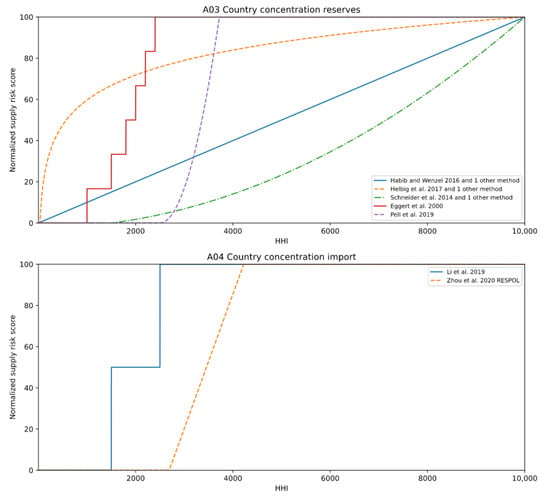
Figure 3.
Selected normalization schemes of concentration criteria: (A01) country concentration production, (A02) company concentration production, (A03) country concentration reserves, (A04) country concentration import. All four criteria are measured with the Herfindahl–Hirschman Index (HHI).
In the case of country concentration production (A01), the logarithmic transformation of the HHI (ranging from 0 to 10,000) into a normalized supply risk scale (ranging from 0 to 100) was applied by Graedel et al. [8] and other methods (cf. Equation (1)).
The values 17.5 and 61.18 in Equation (1) have been set by Graedel et al. [8] to fit the normalization so that an HHI value of 1800 results in a normalized score of 70 and an HHI value of 10,000 marks a normalized score of 100. Helbig et al. [12] adopted this approach with other fitting parameters, resulting in a slightly different normalization applied by three other publications.
Nassar et al. [13] and four other methods do not explicitly mention a normalization procedure for the HHI. We conclude that a simple linear transformation of the HHI into a score from 0 to 100 represents their interpretation of the country concentration best. Zhou et al. [14] also determine normalized scores by scaling the HHI values linearly, but they use the extreme values observed in their data set as thresholds.
Schneider et al. [15] define a threshold of 1500 for the HHI. Below this threshold, the normalized supply risk score is 0. Above 1500, the HHI is normalized by the squared ratio of the HHI value, which is also called a distance-to-target method [16]. Three other methods applied this parabolic approach. A similar approach is proposed by Pell et al. [17], but we could not fully reconstruct the normalization approach. We interpret that the HHI values were first scaled from 0 to 1 by the minimum and maximum values of the observed raw material and consequently normalized by the distance-to-target method. Based on the results, the normalization formula of Equation (2) was applied.
The remaining normalization schemes for A01 uses various stepwise functions with two [18] to seven levels [19]. Except for Habib et al. [20], the stepwise procedure only has single appearances.
For A02, we identified less variety in terms of measurements and normalization schemes. The most frequently used is the method of Schneider et al. [15] which was already explained for A01. The threshold of 1500 is once again used, which results in an identical normalization curve. Three other publications applied this approach. Pell et al. [17] applied the same normalization scheme with extreme values of HHI observed for A02 and the distance-to-target approach. Helbig et al. [12] adopted their normalization formula from A01 for A02 with different key points, leading to a slightly different formula (cf. Equation (3)).
The same formula is also applied in two other publications. Kolotzek et al. [21] stuck to the key points used by Helbig et al. [12] for A01 and applied a logarithmic transformation for A02. The work from Rosenau-Tornow et al. [22] is the only study involving a level-based normalization on the HHI for A02.
A03 is also dominated by normalizations based on normalization formulas. Habib and Wentzel [23] and Nassar et al. [13] applied no transformation. Therefore, we assigned an HHI of 0 to the normalized supply risk score of 0 and an HHI of 10,000 to a score of 100. Helbig et al. [24] applied the same logarithmic transformation as Helbig et al. [12] for A01. Schneider et al. [15] also used the distance-to-target method with an HHI threshold of 1500 as for A01 and A02. Each of the three approaches is applied in one other publication. Pell et al. [17] proceeded as in A01, A02 scaling the HHI values according to the observed minimum and maximum values for A03 followed by the distance-to-target method. Eggert et al. [19] also use the same levels as in A01 to assign HHI values to supply risk levels.
For A04, only two different normalization approaches for the HHI are identified. Zhou et al. [14] applied the same curve to A04 as for A01. Li et al. [25] decreased the number of levels from four for A01 to three for A04, using thresholds of HHI 1500 and 2500. The limits of the levels applied in this approach are identical to those from Rosenau-Tornow et al. [22] for A01 and A02.
3.2. Scarcity (B)
The second-most frequently occurring indicator category is scarcity (B), for which we identified 25 different harmonized criteria. The four most common criteria are the depletion time of reserves (B01) and resources (B02), the sufficiency of reserves (B03), and the crustal content (B04). Figure 4 visualizes the normalization approaches for B01, B02, and B04. Information about the remaining harmonized criteria can be found in the Supplementary Material spreadsheets.
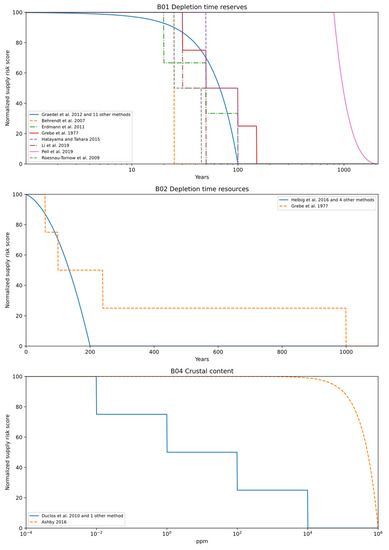
Figure 4.
Selected normalization schemes of scarcity criteria: (B01) depletion time reserves, (B02) depletion time resources, and (B04) crustal content. Both depletion times are quantified in years, crustal content in parts per million (ppm). The criterion B03, the sufficiency of reserves, is not shown due to a lack of evident normalization and measurement in the respective assessments.
Both depletion time of reserves (B01) and depletion time of resources (B02) first appeared in the work of Grebe et al. [9]. The ratio between the available deposits and the current (primary) production rate determines the depletion time. Some authors also use terms such as the static reach for these criteria. No matter the name, the ratio is typically expressed in years. For B01, the considered deposits are available reserves, meaning the deposits are identified, and extraction is techno-economically viable. Graedel et al. [8] presented the most frequently used normalization scheme adopted by 11 other methods (cf. Equation (4)).
A parabolic function is used to assign high depletion time (DT) to low supply risk scores. Three key points are used to determine the shape of the parabola in Equation (4): A DT of 0 years leads to a normalized supply risk score of 100, whereas a value of 50 years is assigned to a score of 70 and a DT of 100 years results in a score of 0. Depletion times above 100 years are interpreted with no supply risk by Graedel et al. [8].
Pell et al. [17] applied their approach already presented for concentration criteria A01 to A03 by rescaling the inverted DT to a score from 0 to 1 with the observed minimum and maximum values and applying the distance-to-target method. The remaining publications presented for B01 in Figure 4 developed individual level-based normalization approaches. The number of levels varies from just two proposed by Behrendt et al. [26] to five in the work of Grebe et al. [9].
The depletion time of resources (B02) shows more consensus in the normalization approach. Resources, in contrast to reserves, also include inferred and sub-economic deposits; therefore, the depletion time of resources is larger than the depletion time of reserves. In most cases, the normalization of B02 is similar to that of B01. Helbig et al. [12] proposed a parabolic transformation comparable to the approach of Graedel et al. [8] for B01. For the DT of the resources, they suggest different key points by doubling the periods: A DT value of 200 years is considered as causing no supply risk at all, resulting in a supply risk score of 0, and a value of 100 years results in a score of 70. Four other publications followed this approach. The only different normalization approach found was the level-based normalization by Grebe et al. [9], consisting of five levels. Here, a DT exceeding 1000 years yields a supply risk score of 0. However, this method has never been applied by another study in our review.
For the crustal content (B04), the “abundance in earth’s crust” was identified as the mainly used indicator. Two different approaches were found for normalization. Ashby [27] considers a high supply risk for materials with rare abundance in the earth’s crust, but it does not propose a specific transformation into a normalized supply risk score. Nevertheless, we want to display Ashby’s intention of assigning a high supply risk score to a low abundance [27]. Therefore, we conducted a simple linear transformation considering a value of ppm as no supply risk and a value of 0 ppm as a normalized score of 100. An alternative method of normalization was applied by Duclos et al. [28] and one other method subdividing abundance values into five levels of supply risk.
3.3. Political Instability (C)
The third most used supply risk category is political instability (C), which is dominated by two harmonized criteria, namely geopolitical risk (C01) and political instability (C02). These two criteria make up 67 out of 75 cases (89%) for this category. Each of the eight remaining criteria identified is applied only once.
C01 appeared for the first time in the work of Eggert et al. [19] in 2000. To evaluate the geopolitical risk, they used the political country risk evaluation of Hermes/BMWi classification on a scale from 1 to 7. They use this classification three times for indicators in this category, each with a different weighting: the production shares, the export shares, and the reserve shares of the countries, respectively.
In contrast, C02 appeared first in the method of Morley and Eatherley [29] in 2008. They classified the percentile rank of the Worldwide Governance Indicator “Political Stability and Absence of Violence/Terrorism” () [30] of the largest producer into a supply risk score using a three-level normalization function. In addition, the World Bank developed five other Worldwide Governance Indicators, which are updated yearly: Government Effectiveness (, Voice and Accountability, Control of Corruption, Regulatory Quality, and Rule of Law. They are available as WGI score and WGI percentile rank [30].
The classification displays the normalization schemes used for the criteria of political instability according to their measurement: WGI score and WGI percentile rank (cf. Figure 5). In most cases, the WGI scores or ranks are weighted by production share. Other weighing factors are import shares [31] or the consideration of the largest producers [32]. The composition of a WGI dimension in combination with the HHI is described in Section 3.1. Other schemes are expressed in the Supplementary Material.
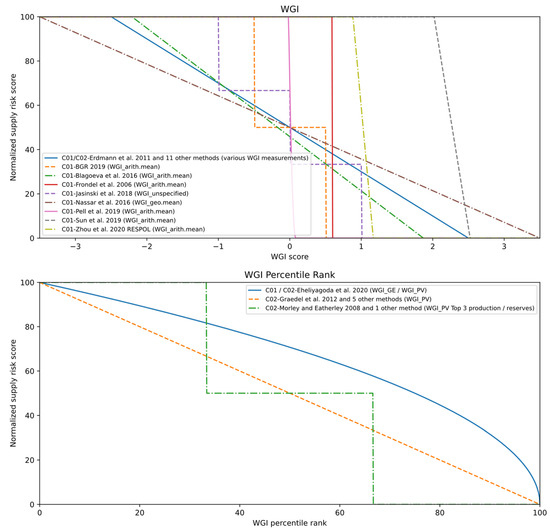
Figure 5.
Selected normalization schemes of political instability criteria: (C01) Geopolitical risk and (C02) Political instability. Indicators use either the score or the percentile rank of the Worldwide Governance Indicators (WGI).
The WGI indicators in the default unit usually range from −2.5 to 2.5 [30], where a low value indicates bad governance. Consequently, the most frequently used normalization approach for both C01 and C02 is the linear transformation of WGI scores based on a hypothetical lower bound of −2.5 and upper bound of 2.5, as presented in Equation (5). After the conversion, values of −2.5 in WGI units and lower yield the highest supply risk score. Twelve other methods have adopted this transformation.
Diverging from this are Nassar et al. [33], who instead assume a range from −3.5 to 3.5 (cf. Figure 5). Three methods use the observed minimum and maximum WGI scores for normalizing them to supply risk scores: Blagoeva et al. [34] and Zhou et al. [14] based on the arithmetic mean of all six WGI dimensions, and Nassar et al. [13] based on the geometric mean of all six WGI dimensions. DERA [35] and Jasinski et al. [36] presented a level-based normalization with three and four levels, respectively. In addition to the approach of Erdmann et al. [32], none of the above-presented methods has been taken up so far. Sun et al. [37] used the function presented in Equation (6) to normalize the weighted arithmetic mean of the WGI-dimensions.
For the normalization of the percentile rank of the WGI dimensions, four different methods were identified. Graedel et al. [8] simply inverted the percentile rank (on a scale from 0 to 100) by assigning the highest political stability with the lowest supply risk (cf. Equation (7)). This approach was adopted by five other methods, whereas other methods did not take up the remaining approaches for the normalization of WGI percentile ranks.
Eheliyagoda et al. [38] developed a proceeding for both C01 and C02 using Equation (8) to invert and rescale the weighted respectively (Governance and Effectiveness).
3.4. Regulations (D)
The fourth most often mentioned category is regulations (D), which is used in 68 out of 618 indicators (11%). We identify policy perception (D01), human development (D02), trade barriers (D03), and environmental performance (D04) as the most prominent harmonized criteria. In contrast to most other categories, the risk from regulations has emerged more recently in the work of Thomason et al. [39] in 2010. They determined the percentage of produced goods expressed in U.S. market shares that a country intends to supply to the U.S. as a measurement of D03. In 2012, Graedel et al. [8] developed a measure to determine D01 and D02 for the first time.
It is worth mentioning that three dominant measurements of regulations have been developed within the criteria: The Policy Perception Index (PPI) in D01 is provided by the Fraser Institute and captures the influence of policies on mining activities in a country [40]. The Human Development Indicator (HDI) in D02 has been developed by the UNDP and evaluates the living conditions of a country [41]. The Environmental Performance Index (EPI) in D04 is provided by Yale University and rates the ability of a country to cope with environmental challenges [42]. All three measurements are updated annually. The associated normalization schemes are displayed in Figure 6.
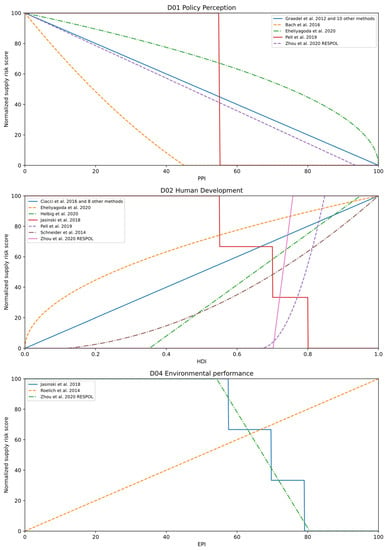
Figure 6.
Selected normalization schemes of regulations criteria: (D01) policy perception, (D02) human development, and (D04) environmental performance. Policy perception is measured with the Policy Perception Index (PPI), human development with the Human Development Indicator (HDI), and environmental performance with the Environmental Performance Index (EPI).
Graedel et al. [8] weighted the PPI of mining regions by the respective production share. They normalized this measurement by a simple inversion subtracting the PPI from 100 according to Equation (9). The PPI ranges from 0, indicating low policy attractiveness, to 100, displaying high policy attractiveness for mining activities. Ten other methods adopted this approach in the same way.
Bach et al. [43] applied the distance-to-target method as described in Section 3.1 on the inverted and weighted PPI values using a threshold of 55. Eheliyagoda et al. [38] applied the same approach for the WGI percentile ranks of D01 and D02 (cf. Equation (8)) on the weighted PPI values. Both Zhou et al. [14] and Pell et al. [17] adopted their previously presented approaches. Zhou et al. [14] applied the normalization based on the minimum and maximum observed values of the PPI, whereas Pell et al. [17] first applied a rescaling from 0 to 1 according to the minimum and maximum observed values followed by the distance-to-target approach.
For D02, the HDI weighted by production shares of mining countries was the most often used measurement. The HDI evaluates the three dimensions of life expectancy, educational standard, and standard of living on a scale from 0 to 1 [44]. Ciacci et al. [45] rescaled the weighted HDI values as presented in Equation (10) by a scaling factor of 100, which was followed by eight other methods.
Eheliyagoda et al. [38], Zhou et al. [14], as well as Pell et al. [17] applied their approaches on the HDI as conducted for previous criteria: Eheliyagoda et al. [38] applied the normalization formula shown in Equation (8) on HDI values, Zhou et al. [14] normalized according to the observed minimum and maximum values, Pell et al. [17] applied their combination of a normalization to a scale from 0 to 1 based on minimum and maximum values and the distance-to-target method. Schneider et al. [15] also stuck to their distance-to-target method already performed for A01–A03 with a threshold for the weighted HDI of 0.12. Helbig et al. [46] applied the formula presented in Equation (11) to normalize the weighted HDI values, resulting in 0 to 100. All of the previously mentioned studies deem high values of the HDI as high supply risk.
An opposite interpretation of the HDI was proposed by Jasinski et al. [36], resulting in an alternative normalization. They consider countries with low human development as critical because of the high probability of improving social conditions by introducing policies that disrupt mining activities. In other words, high weighted HDI values lead to a low supply risk in their study. Therefore, a stepwise normalization consisting of four levels is conducted.
The discrepancy in the interpretation of indicators continues for D04 with the EPI as a single measurement. Roelich et al. [47] used the production-weighted EPI as a measurement of D04 for the first time to describe the risk that a country has or introduces environmental policies that might restrict mining activities. Thus, an EPI value of 100 yields a high potential for restrictions in mining activities due to environmental policies. Since an EPI of 100 indicates high supply risk, no further normalization needs to be applied.
In contrast, Zhou et al. [14] and Jasinski et al. [36] oppositely interpreted the EPI. According to their normalization approaches, a higher EPI value leads to lower supply risk scores. They are less vulnerable to incidents and related supply failures because of their environmental standards [36]. While Zhou et al. [14] applied the same method as previously used for A by scaling the weighted EPI according to the minimum and maximum values observed, Jasinski et al. [36] used a four-level normalization applied for D02 with slightly different limits.
3.5. By-Product Dependence (E)
The fifth most often occurred category is by-product dependence (E), which is used in 44 out of 618 indicators (7%). We have found one dominant criterion giving the same name as the category by-product dependence (E01), which first appeared in the work of Grebe et al. [9]. A qualitative approach was used to assign the observed raw materials to a supply risk score ranging from 1 to 5. More information about the classification can be found in the Supplementary Material spreadsheets. However, the most commonly used measurement for E01 is companionality developed by Nassar et al. [13] and the companion metal fraction (CMF), which is the percentage share of a raw material produced as a by-product. Companionality (CP) evaluates the contribution of raw material to the profitability of a mine in contrast to other raw materials sourced from the same mine for all sourcing locations. The CP values are usually rescaled by a factor of 100, as shown in Equation (12) to result in a supply risk score from 0 for no risk by independent raw materials to 100 for high supply risk posed by full dependence of raw materials from other mined materials.
The normalization schemes of CMF are displayed in Figure 7. Same as for companionality, the most common approach is a multiplication by 100 to create a supply risk score ranging from 0, indicating a raw material is not produced as a by-product to 100, meaning a raw material is entirely made as a by-product. This method is used by Graedel et al. [8], followed by six other methods. Schneider et al. [15] applied the same distance-to-target approach for the categories above using a threshold of 0.2. BGS [48] and Jasinski et al. [36] proposed a stepwise three-level respectively four-level normalization. Other methods have not adopted either approach.
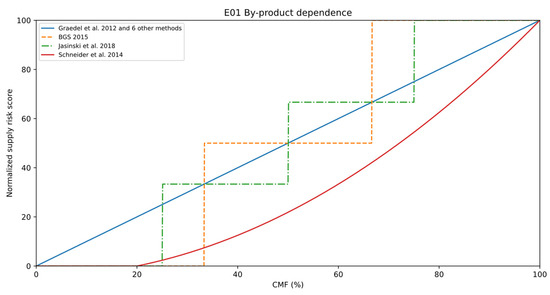
Figure 7.
Normalization schemes for the by-product dependence criterion (E01) relying on the Companion Metal Fraction (CMF), given in percentages.
3.6. Dependence on Primary Production (F)
The sixth supply risk indicator category is the dependence on primary production. This terminology inverts the typically used original category name of recycling or recyclability. The inversion reflects that it is precisely the lack of recycling that increases the supply risk. The two most often used criteria in this category are the end-of-life recycling rate (F01) and the recycled content ratio (F02). The UNEP report on recycling of metals a decade ago has given a good overview on the terminology on metal cycles, including differentiation between old scrap and new scrap, and the importance of collection rates, remelting yields, and growing material demands for the measurements of recycling in global cycles [49]. The report is still often used as the data source for various supply risk assessments.
The argument for why dependence on primary production and thus a lack of secondary production, i.e., recycling, causes higher supply risk is the following: Secondary raw materials are a raw material source independent of the primary production route, in particular mining; it is available without geological exploration, with its availability depending predominantly on past material use, and it is known locally in the countries of utilization. Therefore, the availability of secondary raw materials makes shortages of primary raw materials and high market concentrations less likely.
In general, there are two schools of thought on how recycling should be measured as a criterion for dependence on primary production: Either method uses the end-of-life recycling rate (EoLRR) as the measurement or they use the recycling content ratio (RCR). Figure 8 shows the normalization schemes applied in these two measurements.
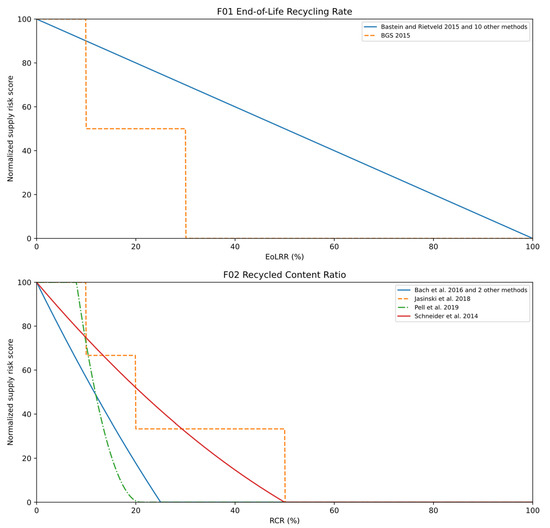
Figure 8.
Selected normalization schemes for criteria for dependence on primary production: (F01) end-of-life recycling rate and (F02) recycled content ratio. Both end-of-life recycling rate (EoLRR) and recycled content ratio (RCR) are given in percentages.
The EoLRR measures the share of end-of-life wastes collected and recycled so that the material can enter a new fabrication or manufacturing stage. Since there will always be waste flows that are not collected and thermodynamic limits to remelting yields, this EoLRR will always be smaller than 100%. The predominant normalization formula applied to the EoLRR is the naïve approach to linearly rescale the values of 0% to 100% to scores of 100 to 0 points.
In contrast, the RCR measures the share of recycled content in fabricated or manufactured goods. Since these goods can only consist of primary or secondary materials, this ratio will also be between 0% and 100%. However, because raw material markets have been growing for most materials over the past decades, the RCR will often be lower than the EoLRR. Therefore, methods already attribute no supply risk scores for any RCR over 50%.
Both EoLRR and RCR have their flaws as measurements for primary production dependence. For the EoLRR, there may be high recycling rates at end-of-life; however, these are irrelevant if the supply risks are emerging from rapidly growing future technology demand. As the EoLRR considers only recycling from old scrap, which is only formed after the use phase, there is a natural time lag between demand growth and growth of end-of-life wastes. For the RCR measurement, the ratio of recycled content may be high in a fabricated product. Still, if this all came from new scrap recycling, recycling before the use phase does not alter the primary material demand. One should be cautious that high prompt scrap formation rates with high recycling rates for prompt scrap might artificially increase the RCR without providing any risk-reducing alternative raw material source.
3.7. Demand Growth (G)
The seventh supply risk category is that of expected demand growth, in particular from future technologies. The most common approach is to relate the expected additional demand in the future and relate it to current production volumes. Angerer et al. [50] have first utilized this approach, which is a study that has been excluded from our dataset because it has been updated by Marscheider-Weidemann et al. [51].
This approach to calculate the future technology demand as a ratio between additional demand growth and current production typically needs a base year (for current production) and reference year (for future technology demand). For example, Angerer et al. originally calculated the raw material demand for various future technologies for 2030 and used 2006 as the base year. Using the ratio rather than, e.g., the quantity or value of future technology demand also allows comparing different raw materials produced in orders of varying magnitude. Not the absolute amount of material production is problematic, but rather the required relative demand growth. Since base years and reference years differ between supply risk assessments naturally, depending on their publication date and goal and scope of the evaluations, normalizations can only be compared based on the annualized additional demand growth, given in percentages (cf. Figure 9).
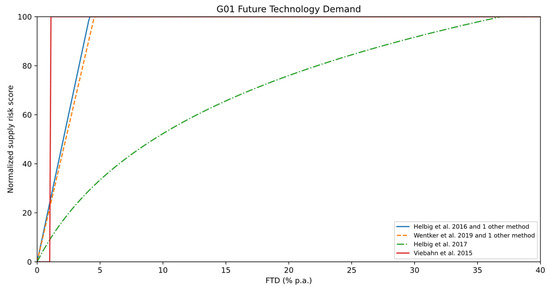
Figure 9.
Normalization schemes for the future technology demand criterion (G01). Underlying measurements are annualized in future technology demand (FTD) growth per year (% p.a.).
3.8. Lack of Substitution Options (H)
The eighth indicator category for supply risk is that of lack of substitution options. A lack of viable substitutes for a material or product creates a dependency in the supply chains, reducing the system’s resilience. In 22 out of 26 cases (84 %), the substitutability of raw material is used as a criterion in this category. Substitutability can happen on a material, component, assembly, or conceptual level as described by Habib and Wenzel [23] at the example of wind turbines. In particular, for high-tech applications, the substitution of materials is often limited, as developed by Nassar [52] for platinum-group metals. The most prominent evaluation of substitutability for a large set of raw materials has been published by Graedel et al. [53], who set out to identify the main applications of each element, identify possible substitute materials in each of these applications, and then evaluate the performance of that substitute. As a result of the heterogeneity of applications, these are difficult to quantify. Therefore, experts’ judgment on a multi-point scale is used to conclude the substitutability score. Application shares are afterwards used to calculate a weighted average of the scores [53]. Graedel et al. were not the first and not the only ones to use such an approach for evaluating the lack of substitution options. The first to use the lack of substitution options as an indicator for supply risk was again Grebe et al. [9], however only with the straightforward classification of raw materials with “no substitution”, “hardly any substitution”, and “substitution” and no differentiation of application shares. The European Commission [54] and Erdmann et al. [32] also applied this concept of a weighted average of expert assessment for the main applications of the raw material. A shift from substitutability to substitution has been used for the later updates of the EU Critical Raw Materials list [55]. While this may seem to be quibbling, the difference is substantial, as substitution only considers proven and readily available substitutes. Consequentially, the supply risk scores of many raw materials in the EU criticality study increased due to this change [56,57].
The normalization scheme for lack of substitution options is trivial: typically, a linear scale is used, with no further rescaling. Therefore, no figure is shown for this indicator category.
3.9. Price Volatility (I)
The ninth indicator category for supply risk is price volatility. It was impossible to identify different criteria for this category, so all 17 cases are assigned to the same criterion I01. In detail, the measurements vary between the price volatility, the variation coefficient, and the relative price change within a specific period. All methods use a stepwise normalization of price volatility measurements to supply risk scores. Most studies use four-level to five-level normalization functions in which higher price volatility leads to higher supply risks. The only exception is the method by Eggert et al. [19], who use a seven-level decreasing normalization function. The authors were among the early supply risk assessments, and they did not explain why they evaluated low price volatility with high supply risk. Figure 10 shows the different level choices of the four methods. Other methods’ schemes are shown in the Supplementary Material spreadsheets.
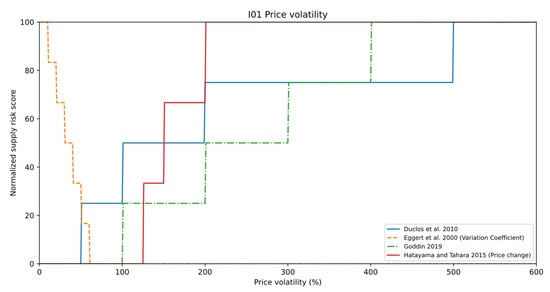
Figure 10.
Normalization schemes for the price volatility criterion (I01). Price volatility is either used directly, in percentage, or calculated as variation coefficient or price change, also in percentages.
According to economic theory, the interpretation of the criterion price volatility is ambiguous, because a price increase should result from a supply–demand gap, not the reason. It is also questionable if one can anticipate future supply risks by the analysis of historical price development. Therefore, it is not surprising that this indicator category has only been used in very selected supply risk assessments and not been used consecutively by a series of methods.
3.10. Import Dependency (J)
The tenth indicator category for supply risks is import dependency. This indicator category is specifically designed for a national perspective. This category is measured with the net import reliance criterion in eight out of 16 cases (50%) (J01). The net import reliance (NIR) is calculated as the ratio between net imports and apparent consumption, as shown in Equation (13).
The rationale behind using this indicator for supply risk assessments is to identify materials for which the upstream supply chain is out of the hands of domestic policy and trade. If a country has to rely on foreign exploration, extraction, or processing, it can consider their continuous operation, or the access to the materials, as less reliable. Therefore, higher net import reliance is considered with higher supply risks.
Most methods, starting with Goe and Gaustad [58], use the simple linear normalization approach where no net imports result in no supply risk, and 100% NIR results in a supply risk score of 100. Only Li et al. [59] define the steps at 40% and 70% NIR as thresholds for their three-level normalization function. Figure 11 shows the normalization functions for J01. Other criteria are shown in the Supplementary Material spreadsheets.
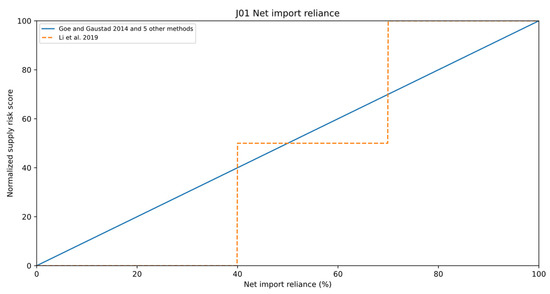
Figure 11.
Normalization schemes for the net import reliance criterion (J01), which is measured in percent.
3.11. Other Indicators
Our review found an additional 67 cases of indicator uses that could not be grouped into indicator categories. Therefore, these “other” indicators are a collection of 53 widely differing criteria, none of them used more than four times in total. Those that are at least used twice are the current market balance (X01), stock keeping (X02), purchasing potential (X03), supply adequacy (X04), natural disasters (X05), economic importance (X06), the Sector Competition Index (X07), the economy of storage and transport (X08), storage complexity (X09), investment potential (X10), material cost impact (X11), and material dependency (X12).
If one wants to find patterns in this loose collection of indicators, three areas of interest may occur: stocks and storage patterns, price and cost aspects, as well as total demand and market size. However, due to the high variation in indicator application and measurements and a lack of repeated implementation in supply risk assessments, we will refrain from discussing these indicators in detail. All individual indicators are listed with their respective measurement and normalization scheme in the Supplementary Material spreadsheets.
4. Discussion and Conclusions
The variety in supply risk indicator usage is impressive. It is understandable because of the different goals and scopes of studies in our review. For example, omitting physical scarcity as a risk factor makes sense when the assessment is focused on short-term risks. Likewise, companies will be much less concerned about import dependence than nations. Therefore, even after another “five years of criticality assessments”, the harmonization that Graedel and Reck asked for has not taken place [7]. However, many of Graedel and Reck’s other “desirable aspects” are covered nowadays by the methods in this review.
The material scope often includes various chemical elements and biotic raw materials and minerals [60,61]. The risk factors also include geology (scarcity, by-product dependence), regulations, and geopolitics (political instability, import dependence). For example, even cultural aspects are used, the “conformity of ideological values” by Nassar et al. [62]. The substitutability or the lack thereof, the dependence on primary production, and the by-product dependence are three of the ten indicator categories. However, these categories often rely on previous assessments such as Graedel et al. [49,53] or Nassar et al. [13]. In contrast to the studies reviewed by Achzet and Helbig [3], in 2013, most of the methods in this review are now published in peer-reviewed journals, not as technical reports. Similar to the European Commission or the United States, some governmental reports undertake the split path of publishing the technical report and a peer-reviewed methodological paper in parallel [62,63].
However, the periodical update that Graedel and Reck [7] also asked for is a rare feature. Many studies are carried out by researchers at universities or other academic institutes without permanent funding for such updates. The EU and US criticality lists, updated every three to four years, are exceptions [60,64].
The transparency of some methods is hampered by the non-disclosure of data [15,65,66,67,68]. While we understand the importance of confidentiality, particularly for company reports, from a scientific perspective, this reduces the transparency and accessibility of corporate supply risk assessment reports [28,69]. Some other methods used sophisticated intermediate scores, thresholds, and renormalizations up to the point that results turned out to be irreproducible or the quantitative results simply contradict the textual explanations [17,34,62,70].
Some methods such as Zhou et al. [14], Pell et al. [17], and Bach et al. [71] use normalizations based on the specific material scope, for example setting the bounds by looking at the minimum and maximum observed measurement, leading to a distortion of the supply risk score since the score is dependent on the raw materials selected for the assessment. In other words, the supply risk score of the observed raw materials varies depending on the investigated raw materials. The integration of individual bounds depending on the values in the normalization function leads to different supply risk scores for the same indicator value. Therefore, results in between studies are not comparable, and the overall results are weakened. Adjusting indicator calculation or normalization schemes may be viable for specific purposes of custom methods. However, in these cases, full transparency and reproducibility are even more important.
The supply risk assessments in the review still often do not adequately report data uncertainties and sensitivity to methodological choices. Only very few authors undertake the effort of doing Monte Carlo simulation or other error propagation methods [8,12,31,72]. Variations of indicator choices and normalizations, which have been discussed by Erdmann and Graedel [73], are also rare.
Concluding, we want to highlight two efforts by individual researchers and one general recommendation which, in our view, would improve future supply risk assessments. Firstly, the effort from Mayer and Gleich [6] (and in many other publications from this working group) to link commonly used supply risk indicators with price variations, as the theoretical result of supply shortages through multiple regression analysis is a practical approach. One of their results was that impacts of supply risk aspects vary between chemical elements and, therefore, no universal indicator set will be found. Secondly, Hatayama and Tahara [5] established a list of supply disruption events, which, if continued, extended to global coverage, and further evaluated could be an excellent basis for event studies. Such event studies could be used to statistically assess the likelihood of supply disruptions at various levels of supply risk indicators. For example, this would eventually allow identifying a non-linear normalization formula instead of naïve approaches or single threshold values. However, the normalization formula and thresholds are still better than the semi-quantitative approach of point-wise or step-wise normalizations used in many assessments. Supply risk indicators can be measured and should be interpreted quantitatively.
We strongly recommend updating some of the data sources commonly used in supply risk assessments. While the USGS provides annual updates to production and reserves data, and while the various political and regulatory indices are also updated annually, the data sources for by-product dependence, dependence on primary production, and lack of substitution options by now are up to a decade old. Given increasing efforts to implement a circular economy, ongoing technological development, and rapid material extraction growth, the values of these data sources are at risk of becoming outdated.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/resources10080079/s1, Table S1: List of studies, Table S2: Indicators summary, Table S3: Normalization and Thresholds, Tables S4–S7: Data for Figure 2, Tables S8–S10: Data for Figure 3, Tables S11 and S12: Data for Figure 4, Tables S13–S15: Data for Figure 5, Table S16: Data for Figure 6, Tables S17 and S18: Data for Figure 7, Table S19: Data for Figure 8, Table S20: Data for Figure 9, Table S21: Data for Figure 10.
Author Contributions
Conceptualization, C.H. and A.T. (Andrea Thorenz); formal analysis, C.H. and M.B.; data curation, M.B.; writing—original draft preparation, C.H. and M.B.; writing—review and editing, A.T. (Andrea Thorenz) and A.T. (Axel Tuma); visualization, C.H.; supervision, A.T. (Andrea Thorenz) and A.T. (Axel Tuma). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All underlying data is available in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
List of studies. Additional information is provided in the Supplementary Material spreadsheet.
Table A1.
List of studies. Additional information is provided in the Supplementary Material spreadsheet.
| Short Name | Year | Type | Ref. |
|---|---|---|---|
| Adibi et al. 2017 | 2017 | assessment | [74] |
| Alonso et al. 2007 | 2007 | collection of indicators | [75] |
| Althaf and Babbit 2020 | 2020 | assessment | [70] |
| Apple 2019 | 2019 | collection of indicators | [69] |
| Ashby 2016 | 2016 | collection of indicators | [27] |
| Bach et al. 2016 | 2016 | assessment | [43] |
| Bach et al. 2017 RESPOL | 2017 | assessment | [71] |
| Bach et al. 2017 Sustainability | 2017 | assessment | [76] |
| Bach et al. 2018 | 2018 | assessment | [61] |
| Bastein and Rietveld 2015 | 2015 | assessment | [77] |
| Bauer et al. 2011 | 2011 | assessment | [78] |
| Behrendt et al. 2007 | 2007 | assessment | [26] |
| Beylot and Villeneuve 2015 | 2015 | assessment | [79] |
| BGS 2015 | 2015 | assessment | [48] |
| Blagoeva et al. 2016 | 2016 | assessment | [34] |
| Blengini et al. 2017 RESPOL | 2017 | assessment | [55] |
| Brown 2018 | 2018 | assessment | [80] |
| Buchert et al. 2009 | 2009 | assessment | [81] |
| Calvo et al. 2018 | 2018 | assessment | [82] |
| Ciacci et al. 2016 | 2016 | assessment | [45] |
| Cimprich et al. 2017 | 2017 | assessment | [83] |
| Cimprich et al. 2018 | 2018 | assessment | [84] |
| Coulomb et al. 2015 | 2015 | assessment | [85] |
| Daw 2017 | 2017 | assessment | [86] |
| DERA 2019 | 2019 | assessment | [35] |
| Duclos et al. 2010 | 2010 | assessment | [28] |
| European Commission 2014 | 2014 | assessment | [56] |
| Eggert et al. 2000 | 2000 | assessment | [19] |
| Eheliyagoda et al. 2020 | 2020 | assessment | [38] |
| Erdmann et al. 2011 | 2011 | assessment | [32] |
| Frenzel et al. 2017 RESPOL | 2017 | assessment | [87] |
| Frondel et al. 2006 | 2006 | single indicator | [18] |
| Fu et al. 2019 | 2019 | assessment | [88] |
| Gemechu et al. 2016 | 2016 | assessment | [31] |
| Glöser-Chahoud et al. 2016 | 2016 | assessment | [89] |
| Goddin 2019 | 2019 | assessment | [90] |
| Goe and Gaustad 2014 | 2014 | assessment | [58] |
| Graedel et al. 2012 | 2012 | assessment | [8] |
| Graedel et al. 2015 | 2015 | assessment | [91] |
| Grebe et al. 1977 | 1977 | assessment | [9] |
| Habib and Wenzel 2016 | 2016 | assessment | [23] |
| Habib et al. 2016 | 2016 | single indicator | [20] |
| Hatayama and Tahara 2015 | 2015 | assessment | [92] |
| Helbig et al. 2016 | 2016 | assessment | [12] |
| Helbig et al. 2017 | 2017 | assessment | [24] |
| Helbig et al. 2018 | 2018 | assessment | [72] |
| Helbig et al. 2020 | 2020 | assessment | [46] |
| Ioannidou et al. 2019 | 2019 | assessment | [93] |
| Jasinski et al. 2018 | 2018 | assessment | [36] |
| Kim et al. 2019 | 2019 | assessment | [94] |
| Kolotzek et al. 2018 | 2018 | assessment | [21] |
| Kosmol et al. 2018 | 2018 | assessment | [95] |
| Li et al. 2019 | 2019 | assessment | [59] |
| Malinauskiene et al. 2018 | 2018 | assessment | [65] |
| Marscheider-Weidemann et al. 2016 | 2016 | single indicator | [51] |
| Martins and Castro 2019 | 2019 | assessment | [96] |
| Mayer and Gleich 2015 | 2015 | assessment | [6] |
| Miyamoto et al. 2019 | 2019 | assessment | [97] |
| Morley and Eatherley 2008 | 2008 | assessment | [29] |
| Moss et al. 2013 | 2013 | assessment | [98] |
| Nansai et al. 2015 | 2015 | assessment | [99] |
| Nansai et al. 2017 | 2017 | assessment | [100] |
| Nassar et al. 2015 | 2015 | collection of indicators | [13] |
| Nassar et al. 2016 | 2016 | assessment | [33] |
| Nassar et al. 2020 | 2020 | assessment | [62] |
| NRC 2008 | 2008 | assessment | [101] |
| Parthemore 2011 | 2011 | assessment | [102] |
| Pell et al. 2019 | 2019 | assessment | [17] |
| Pfleger et al. 2015 | 2015 | assessment | [68] |
| Roelich et al. 2014 | 2014 | assessment | [47] |
| Rosenau-Tornow et al. 2009 | 2009 | assessment | [22] |
| Schneider et al. 2014 | 2014 | assessment | [15] |
| Shammugam et al. 2019 | 2019 | assessment | [103] |
| Simon et al. 2014 | 2014 | assessment | [104] |
| Spörri et al. 2017 | 2017 | assessment | [105] |
| Sun et al. 2019 | 2019 | assessment | [37] |
| Thomason et al. 2010 | 2010 | assessment | [39] |
| Tuma et al. 2014 | 2014 | assessment | [106] |
| van den Brink 2020 | 2020 | assessment | [107] |
| Viebahn et al. 2015 | 2015 | assessment | [108] |
| Wentker et al. 2019 | 2019 | assessment | [109] |
| Yan et al. 2020 | 2020 | assessment | [110] |
| Yuan et al. 2019 | 2019 | assessment | [111] |
| Zepf et al. 2014 | 2014 | assessment | [112] |
| Zhou et al. 2019 | 2019 | assessment | [66] |
| Zhou et al. 2020 JCLEPRO | 2020 | assessment | [67] |
| Zhou et al. 2020 RESPOL | 2020 | assessment | [14] |
References
- Schrijvers, D.; Hool, A.; Blengini, G.A.; Chen, W.-Q.; Dewulf, J.; Eggert, R.; van Ellen, L.; Gauss, R.; Goddin, J.; Habib, K.; et al. A review of methods and data to determine raw material criticality. Resour. Conserv. Recycl. 2020, 155, 104617. [Google Scholar] [CrossRef]
- Helbig, C.; Schrijvers, D.; Hool, A. Selecting and prioritizing material resources by criticality assessments. One Earth 2021, 4, 339–345. [Google Scholar] [CrossRef]
- Achzet, B.; Helbig, C. How to evaluate raw material supply risks—An overview. Resour. Policy 2013, 38, 435–447. [Google Scholar] [CrossRef]
- Helbig, C.; Wietschel, L.; Thorenz, A.; Tuma, A. How to evaluate raw material vulnerability—An overview. Resour. Policy 2016, 48, 13–24. [Google Scholar] [CrossRef]
- Hatayama, H.; Tahara, K. Adopting an objective approach to criticality assessment: Learning from the past. Resour. Policy 2018, 55, 96–102. [Google Scholar] [CrossRef]
- Mayer, H.; Gleich, B. Measuring Criticality of Raw Materials: An Empirical Approach Assessing the Supply Risk Dimension of Commodity Criticality. Nat. Resour. 2015, 6, 56–78. [Google Scholar] [CrossRef] [Green Version]
- Graedel, T.E.; Reck, B.K. Six Years of Criticality Assessments: What Have We Learned So Far? J. Ind. Ecol. 2016, 20, 692–699. [Google Scholar] [CrossRef]
- Graedel, T.E.; Barr, R.; Chandler, C.; Chase, T.; Choi, J.; Christoffersen, L.; Friedlander, E.; Henly, C.; Jun, C.; Nassar, N.T.; et al. Methodology of Metal Criticality Determination. Environ. Sci. Technol. 2012, 46, 1063–1070. [Google Scholar] [CrossRef] [PubMed]
- Grebe, W.H.; Krauß, U.; Kurszona, M.; Schmidt, H.; Kamphausen, D.; Liebrucks, M.; Rumberger, M.; Wettig, E.; Bäse, K.; Jägeler, F.; et al. Ausfallrisiko bei 31 Rohstoffen: Bergwirtschaftliche und Rohstoffwirtschafliche Kriterien für das Angebot und die Nachfrage wichtiger Rohstoffe; Bundesanstalt Für Geowissenschaften und Rohstofe, Deutsches Institut für Wirtschaftforschung, Institut zur Erforschung Technologischer Entwicklungslinien: Berlin, Germany, 1977. [Google Scholar]
- Herfindahl, O.C. Concentration in the US Steel Industry. Ph.D. Thesis, Columbia University, New York, NY, USA, 1950. [Google Scholar]
- Hirschman, A.O. National Power and the Structure of Foreign Trade; University of California Press: Berkeley, CA, USA, 1980; ISBN 9780520040823. [Google Scholar]
- Helbig, C.; Bradshaw, A.M.; Kolotzek, C.; Thorenz, A.; Tuma, A. Supply risks associated with CdTe and CIGS thin-film photovoltaics. Appl. Energy 2016, 178, 422–433. [Google Scholar] [CrossRef]
- Nassar, N.T.; Graedel, T.E.; Harper, E.M. By-product metals are technologically essential but have problematic supply. Sci. Adv. 2015, 1, e1400180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, N.; Wu, Q.; Hu, X.; Zhu, Y.; Su, H.; Xue, S. Synthesized indicator for evaluating security of strategic minerals in China: A case study of lithium. Resour. Policy 2020, 69, 101915. [Google Scholar] [CrossRef]
- Schneider, L.; Berger, M.; Schüler-Hainsch, E.; Knöfel, S.; Ruhland, K.; Mosig, J.; Bach, V.; Finkbeiner, M. The economic resource scarcity potential (ESP) for evaluating resource use based on life cycle assessment. Int. J. Life Cycle Assess. 2014, 19, 601–610. [Google Scholar] [CrossRef]
- Frischknecht, R.; Steiner, R.; Jungbluth, N. The Ecological Scarcity Method—Eco-Factors 2006. A Method for Impact Assessment in LCA; Federal Office for the Environment: Bern, Switzerland, 2009. [Google Scholar]
- Pell, R.S.; Wall, F.; Yan, X.; Bailey, G. Applying and advancing the economic resource scarcity potential (ESP) method for rare earth elements. Resour. Policy 2019, 62, 472–481. [Google Scholar] [CrossRef]
- Frondel, M.; Angerer, G.; Buchholz, P. Trends der Angebots-und Nachfragesituation bei Mineralischen Rohstoffen; BMWi: Berlin, Germany, 2006. [Google Scholar]
- Eggert, P.; Haid, A.; Wettig, E.; Dahlheimer, M.; Kruszona, M.; Wagner, H. Auswirkungen der Weltweiten Konzentration in der Bergbauproduktion auf die Rohstoffversorgung der Deutschen Wirtschaft; Deutsches Institut für Wirtschaftsforschung: Berlin, Germany, 2000; Volume 184, ISBN 3428102738. [Google Scholar]
- Habib, K.; Hamelin, L.; Wenzel, H. A dynamic perspective of the geopolitical supply risk of metals. J. Clean. Prod. 2016, 133, 850–858. [Google Scholar] [CrossRef]
- Kolotzek, C.; Helbig, C.; Thorenz, A.; Reller, A.; Tuma, A. A company-oriented model for the assessment of raw material supply risks, environmental impact and social implications. J. Clean. Prod. 2018, 176, 566–580. [Google Scholar] [CrossRef]
- Rosenau-Tornow, D.; Buchholz, P.; Riemann, A.; Wagner, M. Assessing the long-term supply risks for mineral raw materials-a combined evaluation of past and future trends. Resour. Policy 2009, 34, 161–175. [Google Scholar] [CrossRef]
- Habib, K.; Wenzel, H. Reviewing resource criticality assessment from a dynamic and technology specific perspective—using the case of direct-drive wind turbines. J. Clean. Prod. 2016, 112, 3852–3863. [Google Scholar] [CrossRef]
- Helbig, C.; Kolotzek, C.; Thorenz, A.; Reller, A.; Tuma, A.; Schafnitzel, M.; Krohns, S. Benefits of resource strategy for sustainable materials research and development. Sustain. Mater. Technol. 2017, 12, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Y.; Ge, J.P.; Chen, W.Q.; Wang, P. Scenarios of rare earth elements demand driven by automotive electrification in China: 2018–2030. Resour. Conserv. Recycl. 2019, 145, 322–331. [Google Scholar] [CrossRef]
- Behrendt, S.; Scharp, M.; Kahlenborn, W.; Feil, M.; Dereje, C.; Bleischwitz, R.; Delzeit, R. Maßnahmen und Konzepte zur Lösung des Problems konfliktverschärfender Rohstoffausbeutung am Beispiel Coltan; Umweltbundesamt: Berlin, Germany, 2007. [Google Scholar]
- Ashby, M.F. Materials and Sustainable Development; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Duclos, S.J.; Otto, J.P.; Konitzer, D.G. Design in an Era of Constrained Resources: As Global Competition for Materials strains the Supply Chain, Companies must know where a Shortage can hurt and then plan around it. Mech. Eng. 2010, 132, 36–40. [Google Scholar] [CrossRef] [Green Version]
- Morley, N.; Eatherley, D. Material Security—Ensuring Resource Availability for the UK Economy; C-Tech Innovations: Chester, UK, 2008. [Google Scholar]
- Kaufmann, D.; Kraay, A.; Mastruzzi, M. The Worldwide Governance Indicators: Methodology and Analytical Issues. World Bank Policy Res. Work. Pap. 2010, 5430, 1–31. [Google Scholar] [CrossRef]
- Gemechu, E.D.; Helbig, C.; Sonnemann, G.; Thorenz, A.; Tuma, A. Import-based Indicator for the Geopolitical Supply Risk of Raw Materials in Life Cycle Sustainability Assessments. J. Ind. Ecol. 2016, 20, 154–165. [Google Scholar] [CrossRef]
- Erdmann, L.; Behrendt, S.; Feil, M. Kritische Rohstoffe für Deutschland; KfW Bankengruppe: Berlin, Germany, 2011. [Google Scholar]
- Nassar, N.T.; Xun, S.; Fortier, S.M.; Schoeberlein, D. Assessment of Critical Minerals: Screening Methodology and Initial Application; Executive Office of the President of the United States: Washington, DC, USA, 2016. [Google Scholar]
- Blagoeva, D.T.; Alves Dias, P.; Marmier, A.; Pavel, C.C. Assessment of Potential Bottlenecks along the Materials Supply Chain for the Future Deployment of Low-Carbon Energy and Transport Technologies in the EU. Wind Power, Photovoltaic and Electric Vehicles Technologies, Time Frame: 2015–2030; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- DERA. DERA-Rohstoffliste 2019; Deutsche Rohstoffagentur in der Bundesanstalt für Geowissenschaften und Rohstoffe: Berlin, Germany, 2019.
- Jasiński, D.; Cinelli, M.; Dias, L.C.; Meredith, J.; Kirwan, K. Assessing supply risks for non-fossil mineral resources via multi-criteria decision analysis. Resour. Policy 2018, 58, 150–158. [Google Scholar] [CrossRef]
- Sun, X.; Hao, H.; Hartmann, P.; Liu, Z.; Zhao, F. Supply risks of lithium-ion battery materials: An entire supply chain estimation. Mater. Today Energy 2019, 14, 100347. [Google Scholar] [CrossRef]
- Eheliyagoda, D.; Zeng, X.; Li, J. A method to assess national metal criticality: The environment as a foremost measurement. Humanit. Soc. Sci. Commun. 2020, 7, 43. [Google Scholar] [CrossRef]
- Thomason, S.J.; Atweill, R.; Bajraktari, Y.; Bell, J.; Barnett, D.; Karvonides, N.; Niles, M.; Schwartz, E. From National Defense Stockpile (NDS) to Strategic Materials Security Program (SMSP): Evidence and Analytic Support; Institute for Defense Analysis: Washington, DC, USA, 2010. [Google Scholar]
- Yunis, J.; Elmira, A. Survey of Mining Companies 2020. Fraser Inst. Annu. 2018. Available online: http://www.fraserinstitute.org (accessed on 3 August 2021).
- UNDP. The Next Frontier: Human Development and the Anthropocene; UNDP: New York, NY, USA, 2020; ISBN 9789211264425. [Google Scholar]
- Wendling, Z.A.; Emerson, J.W.; de Sherbinin, A.; Esty, D.C. 2020 Environmental Performance Index; Yalce Center for Environmental Law & Policy: New Haven, CT, USA, 2020. [Google Scholar]
- Bach, V.; Berger, M.; Henßler, M.; Kirchner, M.; Leiser, S.; Mohr, L.; Rother, E.; Ruhland, K.; Schneider, L.; Tikana, L.; et al. Integrated method to assess resource efficiency—ESSENZ. J. Clean. Prod. 2016, 137, 118–130. [Google Scholar] [CrossRef] [Green Version]
- UNDP. 2020 Human Development Report: Technical Notes; UNEP: Nairobi, Kenya, 2020. [Google Scholar]
- Ciacci, L.; Nuss, P.; Reck, B.K.; Werner, T.T.; Graedel, T.E. Metal Criticality Determination for Australia, the US, and the Planet—Comparing 2008 and 2012 Results. Resources 2016, 5, 29. [Google Scholar] [CrossRef]
- Helbig, C.; Bradshaw, A.M.; Thorenz, A.; Tuma, A. Supply Risk Considerations for the Elements in Nickel-Based Superalloys. Resources 2020, 9, 106. [Google Scholar] [CrossRef]
- Roelich, K.; Dawson, D.A.; Purnell, P.; Knoeri, C.; Revell, R.; Busch, J.; Steinberger, J.K. Assessing the dynamic material criticality of infrastructure transitions: A case of low carbon electricity. Appl. Energy 2014, 123, 378–386. [Google Scholar] [CrossRef] [Green Version]
- BGS Risk. List 2015—An Update to the Supply Risk Index for Elements or Element Groups that are of Economic Value; British Geological Survey: Keyworth, UK, 2015. [Google Scholar]
- Graedel, T.E.; Allwood, J.M.; Birat, J.-P.; Reck, B.K.; Sibley, S.F.; Sonnemann, G.; Buchert, M.; Hagelüken, C. Recycling Rates of Metals—A Status Report, A Report of the Working Group on the Global Metal Flows to the International Resource Panel; UNEP: Nairobi, Kenya, 2011. [Google Scholar]
- Angerer, G.; Marscheider-Weidemann, F.; Lüllmann, A.; Erdmann, L.; Scharp, M.; Handke, V.; Marwede, M. Raw Materials for Emerging Technologies; Frauenhofer IRB Verlag: Stuttgart, Germany, 2009. [Google Scholar]
- Marscheider-Weidemann, F.; Langkau, S.; Hummen, T.; Erdmann, L.; Tercero Espinoza, L.A.; Angerer, G.; Marwede, M.; Benecke, S. Rohstoffe für Zukunftstechnologien 2016; Deutsche Rohstoffagentur (DERA): Berlin, Germany, 2016. [Google Scholar]
- Nassar, N.T. Limitations to elemental substitution as exemplified by the platinum-group metals. Green Chem. 2015, 17, 2226–2235. [Google Scholar] [CrossRef]
- Graedel, T.E.; Harper, E.M.; Nassar, N.T.; Reck, B.K. On the materials basis of modern society. Proc. Natl. Acad. Sci. USA 2015, 112, 6295–6300. [Google Scholar] [CrossRef] [Green Version]
- European Commission. Critical Raw Materials for the EU; European Commission: Brussels, Belgium, 2010. [Google Scholar]
- Blengini, G.A.; Nuss, P.; Dewulf, J.; Nita, V.; Peirò, L.T.; Vidal-Legaz, B.; Latunussa, C.; Mancini, L.; Blagoeva, D.; Pennington, D.; et al. EU methodology for critical raw materials assessment: Policy needs and proposed solutions for incremental improvements. Resour. Policy 2017, 53, 12–19. [Google Scholar] [CrossRef] [Green Version]
- European Commission. Report on Critical Raw Materials for the EU: Report of the Ad hoc Working Group on Defining Critical Raw Materials; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- European Commission. Study on the Review of the List of Critical Raw Materials; European Commission: Brussels, Belgium, 2017; ISBN 978-92-79-47937-3. [Google Scholar]
- Goe, M.; Gaustad, G.G. Identifying critical materials for photovoltaics in the US: A multi-metric approach. Appl. Energy 2014, 123, 387–396. [Google Scholar] [CrossRef]
- Li, S.; Yan, J.; Pei, Q.; Sha, J.; Mou, S.; Xiao, Y. Risk Identification and Evaluation of the Long-term Supply of Manganese Mines in China Based on the VW-BGR Method. Sustainability 2019, 11, 2683. [Google Scholar] [CrossRef] [Green Version]
- Blengini, G.A. European Commission Study on the EU’s List of Critical Raw Materials-Final Report; European Commission: Brussels, Belgium, 2020; ISBN 978-92-79-72119-9. [Google Scholar]
- Bach, V.; Berger, M.; Forin, S.; Finkbeiner, M. Comprehensive approach for evaluating different resource types—Case study of abiotic and biotic resource use assessment methodologies. Ecol. Indic. 2018, 87, 314–322. [Google Scholar] [CrossRef]
- Nassar, N.T.; Brainard, J.; Gulley, A.; Manley, R.; Matos, G.; Lederer, G.; Bird, L.R.; Pineault, D.; Alonso, E.; Gambogi, J.; et al. Evaluating the mineral commodity supply risk of the U.S. manufacturing sector. Sci. Adv. 2020, 6, eaay8647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blengini, G.; Blagoeva, D.; Dewulf, J.; Torres De Matos, C.; Nita, V.; Vidal-Legaz, B.; Latunussa, C.; Kayam, Y.; Talens Peiró, L.; Baranzelli, C.; et al. Assessment of the Methodology for Establishing the EU List of Critical Raw Materials; European Commission: Brussels, Belgium, 2017; ISBN 9789279696114. [Google Scholar]
- Nassar, N.T.; Fortier, S.M. Methodology and Technical Input for the 2021 Review and Revision of the U.S.; Unites States Geological Survey: Reston, VA, USA, 2021.
- Malinauskienė, M.; Kliopova, I.; Hugi, C.; Staniškis, J.K. Geostrategic Supply Risk and Economic Importance as Drivers for Implementation of Industrial Ecology Measures in a Nitrogen Fertilizer Production Company. J. Ind. Ecol. 2018, 22, 422–433. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.; Wang, G.; Chen, S.; Xing, W.; Li, T. Assessing the short-to medium-term supply risks of clean energy minerals for China. J. Clean. Prod. 2019, 215, 217–225. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.; Rechberger, H.; Wang, G.; Chen, S.; Xing, W.; Li, P. Dynamic criticality of by-products used in thin-film photovoltaic technologies by 2050. J. Clean. Prod. 2020, 263, 121599. [Google Scholar] [CrossRef]
- Pfleger, P.; Lichtblau, K.; Bardt, H.; Bertenrath, R. Rohstoffsituation der Bayerischen Wirtschaft; Vereinigung der Bayerischen Wirtschaft: München, Germany, 2015. [Google Scholar]
- Apple. Material Impact Profiles; Apple Inc.: Los Altos, CA, USA, 2019. [Google Scholar]
- Althaf, S.; Babbitt, C.W. Disruption risks to material supply chains in the electronics sector. Resour. Conserv. Recycl. 2020, 167, 105248. [Google Scholar] [CrossRef]
- Bach, V.; Finogenova, N.; Berger, M.; Winter, L.; Finkbeiner, M. Enhancing the assessment of critical resource use at the country level with the SCARCE method—Case study of Germany. Resour. Policy 2017, 53, 283–299. [Google Scholar] [CrossRef] [Green Version]
- Helbig, C.; Bradshaw, A.M.; Wietschel, L.; Thorenz, A.; Tuma, A. Supply risks associated with lithium-ion battery materials. J. Clean. Prod. 2018, 172, 274–286. [Google Scholar] [CrossRef]
- Erdmann, L.; Graedel, T.E. Criticality of Non-Fuel Minerals: A Review of Major Approaches and Analyses. Environ. Sci. Technol. 2011, 45, 7620–7630. [Google Scholar] [CrossRef]
- Adibi, N.; Lafhaj, Z.; Yehya, M.; Payet, J. Global Resource Indicator for life cycle impact assessment: Applied in wind turbine case study. J. Clean. Prod. 2017, 165, 1517–1528. [Google Scholar] [CrossRef]
- Alonso, E.; Gregory, J.; Field, F.R.; Kirchain, R. Material availability and the supply chain: Risks, effects, and responses. Environ. Sci. Technol. 2007, 41, 6649–6656. [Google Scholar] [CrossRef] [Green Version]
- Bach, V.; Berger, M.; Finogenova, N.; Finkbeiner, M. Assessing the availability of terrestrial Biotic Materials in Product Systems (BIRD). Sustainability 2017, 9, 137. [Google Scholar] [CrossRef] [Green Version]
- Bastein, T.; Rietveld, E. Materials in the Dutch Economy: A Vulnerability Assessment; TNO: Delft, The Netherlands, 2015. [Google Scholar]
- Bauer, D.; Diamond, D.; Li, J.; McKittrick, M.; Sandalow, D.; Telleen, P.U.S. Department of Energy Critical Materials Strategy; Diane Publishing: Collingdale, PA, USA, 2011. [Google Scholar]
- Beylot, A.; Villeneuve, J. Assessing the national economic importance of metals: An Input-Output approach to the case of copper in France. Resour. Policy 2015, 44, 161–165. [Google Scholar] [CrossRef]
- Brown, T. Measurement of mineral supply diversity and its importance in assessing risk and criticality. Resour. Policy 2018, 58, 202–218. [Google Scholar] [CrossRef]
- Buchert, M.; Schüler, D.; Bleher, D. Critical Metals for Future Sustainable Technologies and Their Recycling Potential; United Nations Environment Programme: Berlin, Germany, 2009.
- Calvo, G.; Valero, A.; Valero, A. Thermodynamic Approach to Evaluate the Criticality of Raw Materials and Its Application through a Material Flow Analysis in Europe. J. Ind. Ecol. 2018, 22, 839–852. [Google Scholar] [CrossRef] [Green Version]
- Cimprich, A.; Young, S.B.; Helbig, C.; Gemechu, E.D.; Thorenz, A.; Tuma, A.; Sonnemann, G. Extension of geopolitical supply risk methodology: Characterization model applied to conventional and electric vehicles. J. Clean. Prod. 2017, 162, 754–763. [Google Scholar] [CrossRef] [Green Version]
- Cimprich, A.; Karim, K.S.; Young, S.B. Extending the geopolitical supply risk method: Material “substitutability” indicators applied to electric vehicles and dental X-ray equipment. Int. J. Life Cycle Assess. 2018, 23, 2024–2042. [Google Scholar] [CrossRef]
- Coulomb, R.; Dietz, S.; Godunova, M.; Nielsen, T.B. Critical Minerals Today and in 2030: An Analysis for OECD Countries. OECD Environ. Work. Pap. 2015, 91, 49. [Google Scholar] [CrossRef]
- Daw, G. Security of mineral resources: A new framework for quantitative assessment of criticality. Resour. Policy 2017, 53, 173–189. [Google Scholar] [CrossRef]
- Frenzel, M.; Mikolajczak, C.; Reuter, M.A.; Gutzmer, J. Quantifying the relative availability of high-tech by-product metals—The cases of gallium, germanium and indium. Resour. Policy 2017, 52, 327–335. [Google Scholar] [CrossRef]
- Fu, X.; Polli, A.; Olivetti, E. High-Resolution Insight into Materials Criticality: Quantifying Risk for By-Product Metals from Primary Production. J. Ind. Ecol. 2019, 23, 452–465. [Google Scholar] [CrossRef]
- Glöser-Chahoud, S.; Tercero Espinoza, L.A.; Walz, R.; Faulstich, M. Taking the Step towards a More Dynamic View on Raw Material Criticality: An Indicator Based Analysis for Germany and Japan. Resources 2016, 5, 45. [Google Scholar] [CrossRef] [Green Version]
- Goddin, J.R.J. Identifying Supply Chain Risks for Critical and Strategic Materials. In Critical Materials-Underlying Causes and Sustainable Mitigation Strategies; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2019; pp. 117–150. [Google Scholar]
- Graedel, T.E.; Harper, E.M.; Nassar, N.T.; Nuss, P.; Reck, B.K. Criticality of metals and metalloids. Proc. Natl. Acad. Sci. USA 2015, 112, 4257–4262. [Google Scholar] [CrossRef] [Green Version]
- Hatayama, H.; Tahara, K. Criticality Assessment of Metals for Japan’s Resource Strategy. Mater. Trans. 2015, 56, 229–235. [Google Scholar] [CrossRef] [Green Version]
- Ioannidou, D.; Pommier, R.; Habert, G.; Sonnemann, G. Evaluating the risks in the construction wood product system through a criticality assessment framework. Resour. Conserv. Recycl. 2019, 146, 68–76. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Kim, B.; Kim, J. Raw material criticality assessment with weighted indicators: An application of fuzzy analytic hierarchy process. Resour. Policy 2019, 60, 225–233. [Google Scholar] [CrossRef]
- Kosmol, J.; Müller, F.; Keßler, H. The Critical Raw Materials Concept: Subjective, Multifactorial and Ever-Developing. In Factor X; Lehmann, H., Ed.; Springer: Cham, Germany, 2018; pp. 71–92. ISBN 9783319500799. [Google Scholar]
- Martins, F.; Castro, H. Significance ranking method applied to some EU critical raw materials in a circular economy—Priorities for achieving sustainability. Procedia CIRP 2019, 84, 1059–1062. [Google Scholar] [CrossRef]
- Miyamoto, W.; Kosai, S.; Hashimoto, S. Evaluating Metal Criticality for Low-Carbon Power Generation Technologies in Japan. Minerals 2019, 9, 95. [Google Scholar] [CrossRef] [Green Version]
- Moss, R.L.; Tzimas, E.; Willis, P.; Arendorf, J.; Tercero Espinoza, L.A. Critical Metals in the Path towards the Decarbonisation of the EU Energy Sector; Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Nansai, K.; Nakajima, K.; Kagawa, S.; Kondo, Y.; Shigetomi, Y.; Suh, S. Global Mining Risk Footprint of Critical Metals Necessary for Low-Carbon Technologies: The Case of Neodymium, Cobalt, and Platinum in Japan. Environ. Sci. Technol. 2015, 49, 2022–2031. [Google Scholar] [CrossRef]
- Nansai, K.; Nakajima, K.; Suh, S.; Kagawa, S.; Kondo, Y.; Takayanagi, W.; Shigetomi, Y. The role of primary processing in the supply risks of critical metals. Econ. Syst. Res. 2017, 29, 1–22. [Google Scholar] [CrossRef] [Green Version]
- U.S. National Research Council. Minerals, Critical Minerals, and the U.S. Economy; The National Academies Press: Washington, DC, USA, 2008.
- Parthemore, C. Elements of Security: Mitigating the Risks of U.S. Dependence on Critical Minerals; Center for a New American Security: Washington, DC, USA, 2011. [Google Scholar]
- Shammugam, S.; Rathgeber, A.; Schlegl, T. Causality between metal prices: Is joint consumption a more important determinant than joint production of main and by-product metals? Resour. Policy 2019, 61, 49–66. [Google Scholar] [CrossRef]
- Simon, B.; Ziemann, S.; Weil, M. Criticality of metals for electrochemical energy storage systems—Development towards a technology specific indicator. Metall. Res. Technol. 2014, 111, 191–200. [Google Scholar] [CrossRef]
- Spörri, A.; Wäger, P. Metal Risk Check. Available online: https://www.metal-risk-check.ch/ (accessed on 2 March 2021).
- Tuma, A.; Reller, A.; Thorenz, A.; Kolotzek, C.; Helbig, C. Nachhaltige Ressourcenstrategien in Unternehmen: Identifikation kritischer Rohstoffe und Erarbeitung von Handlungsempfehlungen zur Umsetzung einer Ressourceneffizienten Produktion; Deutsche Bundesstiftung Umwelt: Augsburg, Germany, 2014. [Google Scholar]
- van den Brink, S.; Kleijn, R.; Sprecher, B.; Tukker, A. Identifying supply risks by mapping the cobalt supply chain. Resour. Conserv. Recycl. 2020, 156, 104743. [Google Scholar] [CrossRef]
- Viebahn, P.; Soukup, O.; Samadi, S.; Teubler, J.; Wiesen, K.; Ritthoff, M. Assessing the need for critical minerals to shift the German energy system towards a high proportion of renewables. Renew. Sustain. Energy Rev. 2015, 49, 655–671. [Google Scholar] [CrossRef] [Green Version]
- Wentker, M.; Greenwood, M.; Asaba, M.C.; Leker, J. A raw material criticality and environmental impact assessment of state-of-the-art and post-lithium-ion cathode technologies. J. Energy Storage 2019, 26, 101022. [Google Scholar] [CrossRef]
- Yan, W.; Cao, H.; Zhang, Y.; Ning, P.; Song, Q.; Yang, J.; Sun, Z. Rethinking Chinese supply resilience of critical metals in lithium-ion batteries. J. Clean. Prod. 2020, 256, 120719. [Google Scholar] [CrossRef]
- Yuan, Y.; Yellishetty, M.; Muñoz, M.A.; Northey, S.A. Toward a dynamic evaluation of mineral criticality: Introducing the framework of criticality systems. J. Ind. Ecol. 2019, 23, 1264–1277. [Google Scholar] [CrossRef]
- Zepf, V.; Simmons, J.; Reller, A.; Ashfield, M.; Rennie, C. Materials Critical to the Energy Industry. An Introduction, 2nd ed.; BP p.l.c.: London, UK, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).