Toward a Faster Screening of Faulty Digital Chips via Current-Bound Estimation Based on Device Size and Threshold Voltage

Abstract

Observations of peak and average currents are important for designed circuits, as faulty circuits have abnormal peaks and average currents. Using current bounds to detect faulty chips is a comparatively innovative idea, and many advanced schemes without them use it as a component in statistical outlier analysis. However, these previous research works have focused on the discussion of the testing impact without a proposed method to define reference current bounds to find faulty chips. A software framework is proposed to synthesize high-performance, power-performance optimized, noise-immune, and low-power circuits with current-bound estimations for testing. This framework offers a rapid methodology to quickly screen potential faulty chips by using the peak and average current bounds for different purposed circuits. The proposed estimation technique generates suitable reference current bounds from transistor threshold voltage and size adjustments. The SPICE-level simulation leads to the most accurate estimations. However, such simulations are not feasible for a large digital circuit. Hence, this work proposes constructing a feasible gate-level software framework for large digital circuits that will serve all of simulation purposes. In comparison with transistor-level Nanosim simulations, the proposed gate-level simulation framework has a margin of error of less than 2% in the peak current, and the computation time is 334 times faster.

1. Introduction

The general power consumption equation can be divided into three parts: dynamic, static, and leakage power consumption, which is represented as follows: P_total = I_totalV_dd = P_dynamic + P_static + P_leakage. The first part, P_dynamic = I_avgV_dd = C_loadV_dd²F_CK, represents dynamic power consumption, where I_avg is the average current consumption, C_load is the circuit output loading, V_dd is the supply voltage, and F_CK is the circuit working clock frequency. The second part is the static power consumption of P_static = I_peakV_dd = T_SCI_peakV_ddF_CK, where T_SC is the short current duration time, and I_peak is the peak current during circuit transition time. The P_leakage is the leakage power consumption that includes the leakage current of I_leakage and V_dd.

From the equation P_dynamic = I_avgVdd = C_loadVdd²F_CK, it can be seen that the chip’s power consumption is directly related to supply voltage (Vdd), the chip’s work frequency (F_CK), and the chip’s load (C_load). The chip power consumption is directly related to the average current. Hence, the measurement current value (I_avg) will increase when accelerating the working frequency or increasing the supply voltage to the chip.

The I_peak of a gate is dependent on two factors. The first factor is the input signal transition time. For the same output loading, the input signal with a large transition time (fast signal transition) results in a lower I_peak. The second factor is that, for two signals with the same transition time, the circuit with the large output loading has a smaller I_peak than the one with the small output loading. Most of the I_avg comes from the working frequency and the loading of the circuit.

The I_peak and I_avg values can then be used as the tightened current bounds during the circuit testing phase. If the test circuit is functioning, the current consumption is over the setting bound and the voltage drop increases the circuit delay, which results in test circuit performance degradation. Accordingly, the upper bound is set for the test chip working at a target clock frequency, and the good chip outputs should all be functionally correct. By applying the lower bound to set a power supply current bound under the original design target clock frequency, the test chip output responses should be mostly incorrect. If the test clock frequency is degraded in this situation, there should be fewer incorrect output responses. The functions of the failed chip can then be quickly found by applying this screening technique.

This paper focuses on I_peak and I_avg issues. This leakage issue is outside the scope of this discussion. The supply voltage (V_dd) and clock frequency (F_CK) are not altered in the following discussion. As the V_dd and F_CK are not altered, the I_peak and I_avg current consumptions are not correlated with the supply voltage or clock frequency.

Using the I_avg and I_peak to quickly detect faulty chips is a comparatively new idea. However, previous research has focused on discussing the testing impact without upper or lower current bounds to screen for faulty chips or use them as components in a statistical outlier analysis.

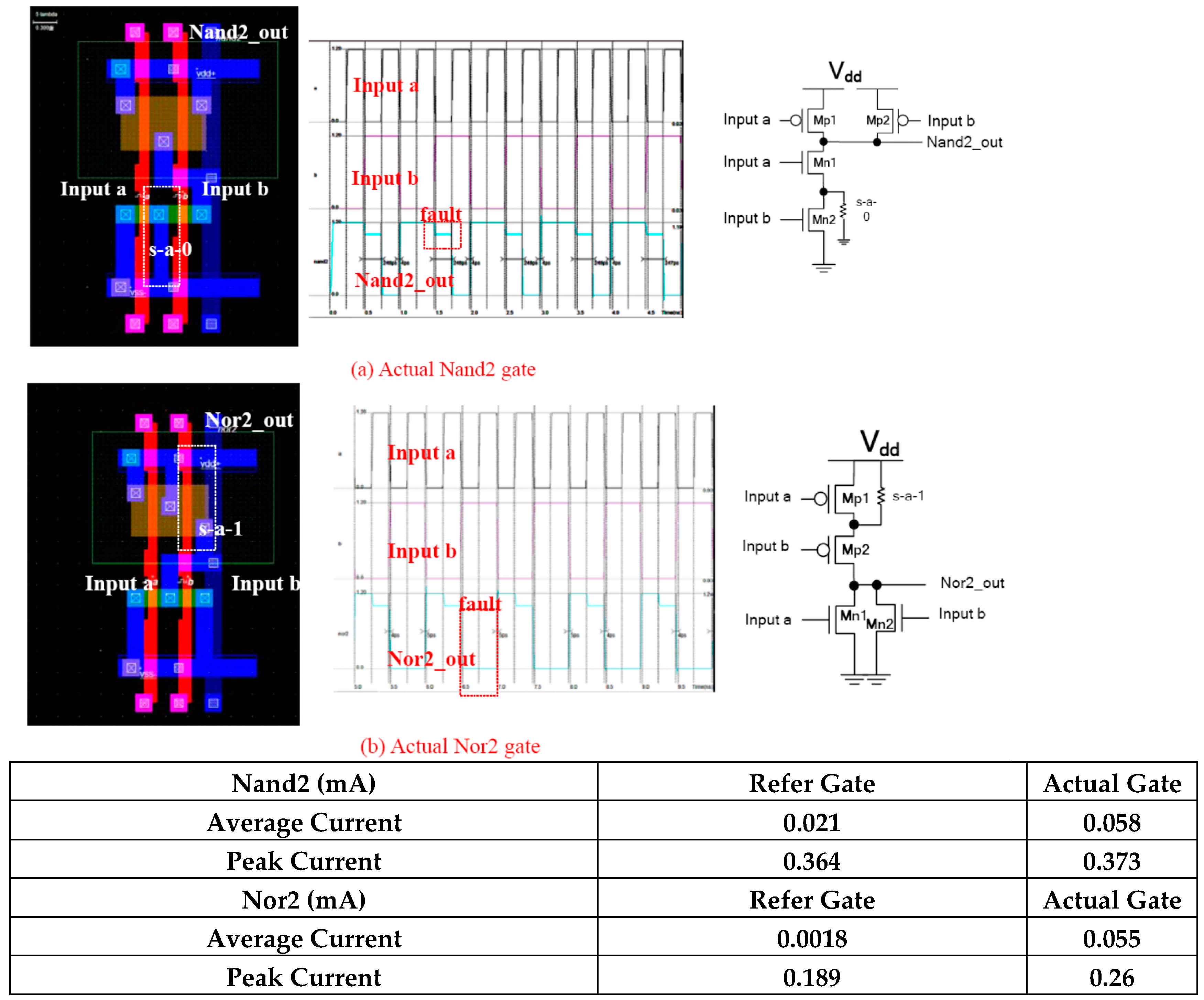
For example, to apply a stuck-fault in a generic CMOS logic gate, Figure 1a shows a NAND gate with an NMOS transistor connection stuck-on-Vss (s-a-0). The referenced gate functions are without an obvious failure phenomenon. However, there is a nearly three times larger than average current consumption. Figure 1b shows a NOR gate with a PMOS transistor connection stuck-on-Vdd (s-a-1). This referenced gate has failure functions, and there is a 30-fold larger than average current. The above simulations are based on 0.12-µm technology provided by Microwind [1]. Although the SPICE-level simulation is in fact accurate, such simulations are not feasible for a large digital circuit.

The above simulations are used to demonstrate the motivation for this current research. Whenever some logic gates fail, they cannot operate and do not consume a normal current in faulty situations. As the above gate demonstrates in the simulation results, all of the functional logic gates in the circuit are activated simultaneously. Hence, the I_avg and I_peak values are large. There is either a small or large amount of current consumption in abnormal functions. Hence, judging from the I_avg and I_peak current value comparisons, the good and faulty chips can be detected.

For industry designed chips, faulty chips have abnormal (too large or small) current consumptions in comparison with good chips.

Table 1. Comparison of good/faulty chip current values.

NO.	Chip Measurement	Peak Current (mA)	Average Current (mA)	Power (µW)
1	Failed Chip IO Pad Fail (333 MHz)	71	13	1534
2	Failed Chip IO Pad Fail (83 MHz)	71	2	361
3	Failed Chip Function Fail (33 MHz)	1717	6	13024
4	Good Chip (333 MHz)	1532	289	520634

shows an example of a large test chip evaluation. From the I_avg and I_peak values, the faulty and good chips show significant differences.

Defective chips exhibit abnormal currents, possibly due to failed or unrealizable designed circuits. This means that, for most normally tested chips, I_peak and I_avg values are within the designed emulation bounds. Hence, using the designed chip’s emulated I_avg and I_peak, functionally failed chips can be screened quickly.

It is difficult to accurately measure the I_avg and I_peak in real time. Hence, there are two monitoring approaches that can be used after setting the limitation of maximum supplied current for the test chip. The first approach entails the monitoring of voltage variance, and the second entails the monitoring of the circuit delay time or functionalities of the circuit under testing.

The voltage drop level can be used to determine whether the designed chip’s consuming current is over the threshold during normal work status. This situation also occurs when the consumed current exceeds the power-rails limitation of the designed chip. Abnormal current consumption is due to the stuck-open and stuck-short faults when the CMOS circuit opens or shorts in relation to the Vdd and Vss (power sources). However, the voltage drops are not easily evaluated when there is an abnormal I_avg and I_peak during the chip testing phase.

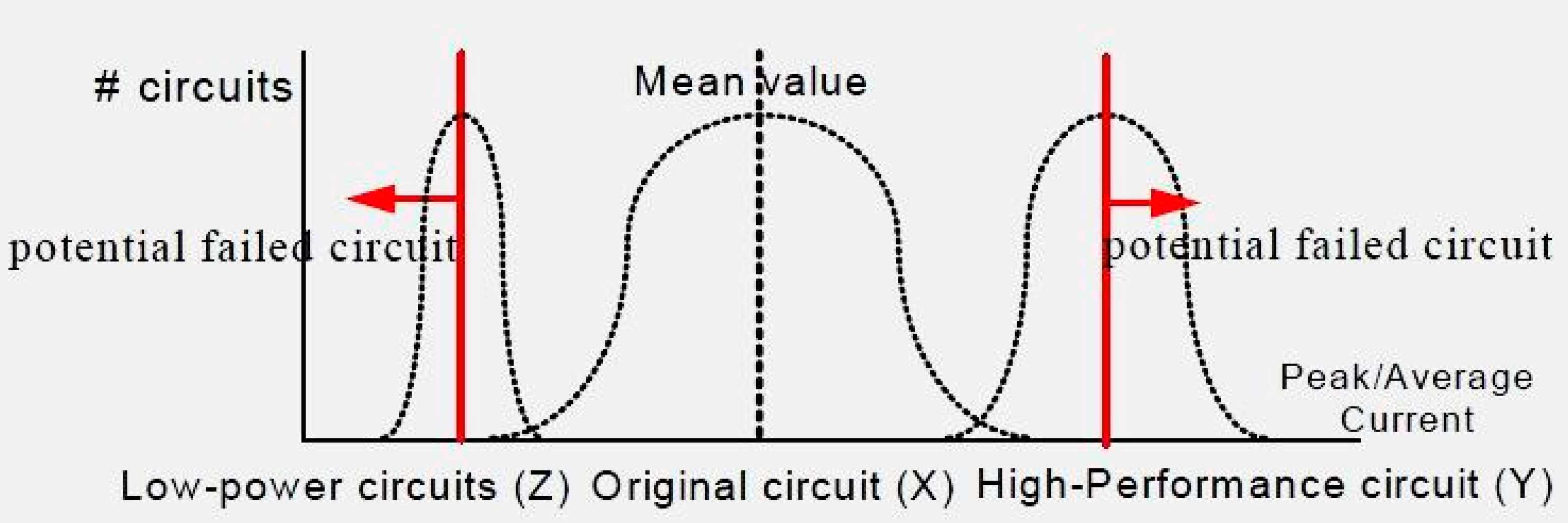
The current values may be in a uniform distribution waveform for most chips, and the waveforms differ for different chips. In order to clarify the current information for monitoring abnormal test chips, there needs to be a distribution waveform (outlier) with defined bounds. This is the current outlier for each design, and the ±3ó or ±6 deviation tolerance is considered during chip testing, as shown in Figure 2. For such chips, the measured I_peak and I_avg are closed to the current outlier. A detailed retest is required to prevent the chip-testing quality problem.

The I_peak and I_avg screen concept is introduced in Figure 2. The low-power design (LP-circuit) can be a lower bound of the original design (ORI-circuit). The high-performance design (HP-circuit) can be an upper bound of the original design (ORI-circuit). The current value of ORI-circuit is X, and its normal current value should not exceed the Y value of an HP-circuit, nor should it be less than the Z value of the LP-circuit reported value. The Y and Z values are the upper-bound and lower-bound references, respectively. The measured values I_peak (or I_avg) are between Y and Z.

Assuming that the current consumption is within the normal distribution range for the test chips, closed bounds need to be determined to screen the failed chips more accurately (to prevent over/under kill results). The proposed pretest stage technique can determine the current bounds for different types of designed circuits.

Our proposed technique provides reference bounds of the I_avg and I_peak. As chips’ current consumption falls along a distribution, the referenced current-bound gap is not absolutely isolated. This means the current-bound regions might overlap. This type of situation leads potentially faulty results for the test chip, and therefore, it is necessary to carefully evaluate chips’ measurement results that are located in the boundary region of the distributed curve.

Before the chip testing phase, the I_peak and I_avg information (values) may be obtained from the chip designer. However, when considering the fault coverage issue, the designer designated verification patterns might not be the same as the test patterns used during the chip testing stage. Hence, the I_peak and I_avg need to be re-evaluated during the chip testing phase to identify abnormal peak and average currents of faulty chips.

The V_T is the dominant source of circuit power consumption and circuit performance. The I_peak and I_avg increases are linearly dependent on the quantity of normal V_T gates. Multiple threshold voltage (MTCMOS) is a well-known, broadly-used design technique. Generic design technique proposes the gate V_T-adjusting technique for low power consumption. The MTCMOS technique controls the thickness of the gate oxide (SiO₂) of the CMOS transistor. This allows the transistor threshold voltage to be adjusted. There have not been any studies concerning the application of multiple threshold voltage CMOS (MTCMOS) circuit current consumption as bounds in order to evaluate other designed circuits under testing.

The drain-to-source current (I_DS) formula is shown in Equation (1). From the threshold voltage-adjusted technique, the lower V_T causes a higher I_DS for a shorter circuit delay time and higher power consumption designs. The higher V_T allows for the use of a lower I_DS current for lower power and longer circuit delay times. The high-threshold voltage can be used to design low-power and noise-immune circuits [2]. Equation (1) shows that, by increasing the threshold voltage, the peak and average current values can be effectively reduced. Hence, the MTCMOS technique can be effectively used to reduce I_peak and I_avg:

$$I_{DS}=\frac{1}{2}{\mathsf{\mu }}_n{C}_{OX}\frac{W}{L}{(V_{GS}-V_T)}^2(1+\mathsf{\lambda }{V}_{DS})$$

(1)

The observations show that, when most of the logic gates use the normal-threshold voltage (V_T) in the circuit, the current consumption increases and the circuit delay time decreases. When T_size decreases, there are large current saving gains and the delay time increases. However, fewer gates using normal V_T dominate the circuit performance (operation frequency). When most of the gates use high V_T, the circuit current consumption is determined by these gates. Hence, the whole circuit current consumption is lower for most of the gates in an IE-circuit using high V_T with small T_size.

The circuit re-synthesis technique is adopted under a performance constraint in this proposed framework. The I_peak and I_avg can be effectively reflected by adjusting the V_T with gate transistor’s sizing (T_SIZE) techniques. From the threshold voltage-adjusting and gate-resizing techniques, the I_avg, I_peak, and area can all be reduced. The V_T-adjusting and gate sizing techniques are under a positive delay slack time, and the circuit delay time does not increase.

The gate transistor’s resizing technique uses the greedy algorithm. By defining the logic gate slack time symbol as φ during the gate-resizing process, the gate with the largest φ is selected for replacement with a small driving gate in noncritical paths. The gate with the lowest φ is resized to a large driving gate in critical paths. This process maintains the circuit performance and decreases the transition current value. We show that the threshold voltage-adjusting and gate-resizing techniques can effectively estimate the I_avg and I_peak.

The objective of the proposed software framework is to find an efficient methodology with in-house tools to analyze and degrade the I_peak and I_avg concurrently. For example, if the synthesized circuit uses a low V_T with a large transistor size, the I_peak and I_avg currents increase. This framework has two purposes. For the test purpose, by applying dual threshold voltage and gate-resizing techniques, this proposed methodology can also be utilized to generate the peak and average current bounds while considering the circuit delay time and area. The second purpose is utilized to generate IE-circuit optimized design, which lowers the short, dynamic, and static leakage power consumptions without sacrificing system performance.

Each power rail can provide a limited current. When the gates consume a maximum current over the power rail design, then the power supply provides less current. This results in a voltage drop, and thus creates a gate delay. We propose that the circuit total I_avg and I_peak need to be calculated from logic gates that transition at the same time interval, so accurate I_avg and I_peak calculations should take the gate delay into consideration.

By using a quick incremental static timing analysis (STA), the slack time calculation speed increases. Nonlinear static or dynamic timing analysis techniques along with a dual V_T cell library provide two kinds of accurate delay time calculation methods that are examined in this paper. The proposed technique has been divided into two parts: analysis and alleviation processes for I_peak and I_avg.

Accurate I_peak and I_avg information is needed for a transistor-level circuit simulation. However, this type of simulation requires a great deal of time and cannot be applied to large test circuits. The proposed frameworks can be used to solve the above problem for a large test chip. From gate-level estimation, this software framework has been proven to be highly accurate in comparison to a Nanosim (a transistor-level simulation tool).

The proposed methodology tries to toggle the logic gates as much as possible for emulating the real circuit operations. The input patterns are not as random as those of most conventional tools. Using this exhaustive technique to drive the tested circuit is unnecessary, as this is excessively time-consuming. In this proposed technique, the automatic test pattern generation (ATPG) is used to generate the essential and representative test patterns. This technique applies the generated evaluation patterns using the stuck-fault model from the ATPG and then applies the I_peak and I_avg evaluated patterns into the circuit.

The reference current bound values need to cover the functional mode’s corner cases in order to be applied during testing phases. It also suggested that the test engineer needs to cooperate with the designer and apply the circuit’s functional test patterns during the testing phase. This method has the same design phase behavior as applying the circuit simulation pattern during the chip testing stage.

The static leakage current issue is not covered in this paper. However, the leakage current is an issue of genuine concern during chip testing. The leakage current measurement is found to be insufficiently accurate during the circuit simulation phase. The leakage current is postponed, while applying management requires a period of time when applying test patterns to the circuit during the practical chip testing stage. The duration depends on the characteristics of the circuit and applied process technology.

The focus of this framework is a rapid methodology for quickly estimating the I_avg and I_peak current for normal chips. These proposed software tools effective screen potentially faulty chips and reduce the lengthy testing time for large circuits.

For deep submicron technology, manufacturing variation has a major impact on circuit performance and current consumption. When threshold voltage and transistor size are altered from the process variation, and the current distribution outlier is changed. The proposed reference circuit applies these variations to the simulation by altering the transistor high-/low-threshold voltage assignment and gate-resizing. Future work needs to integrate this consideration into simulations.

2. Literature Review

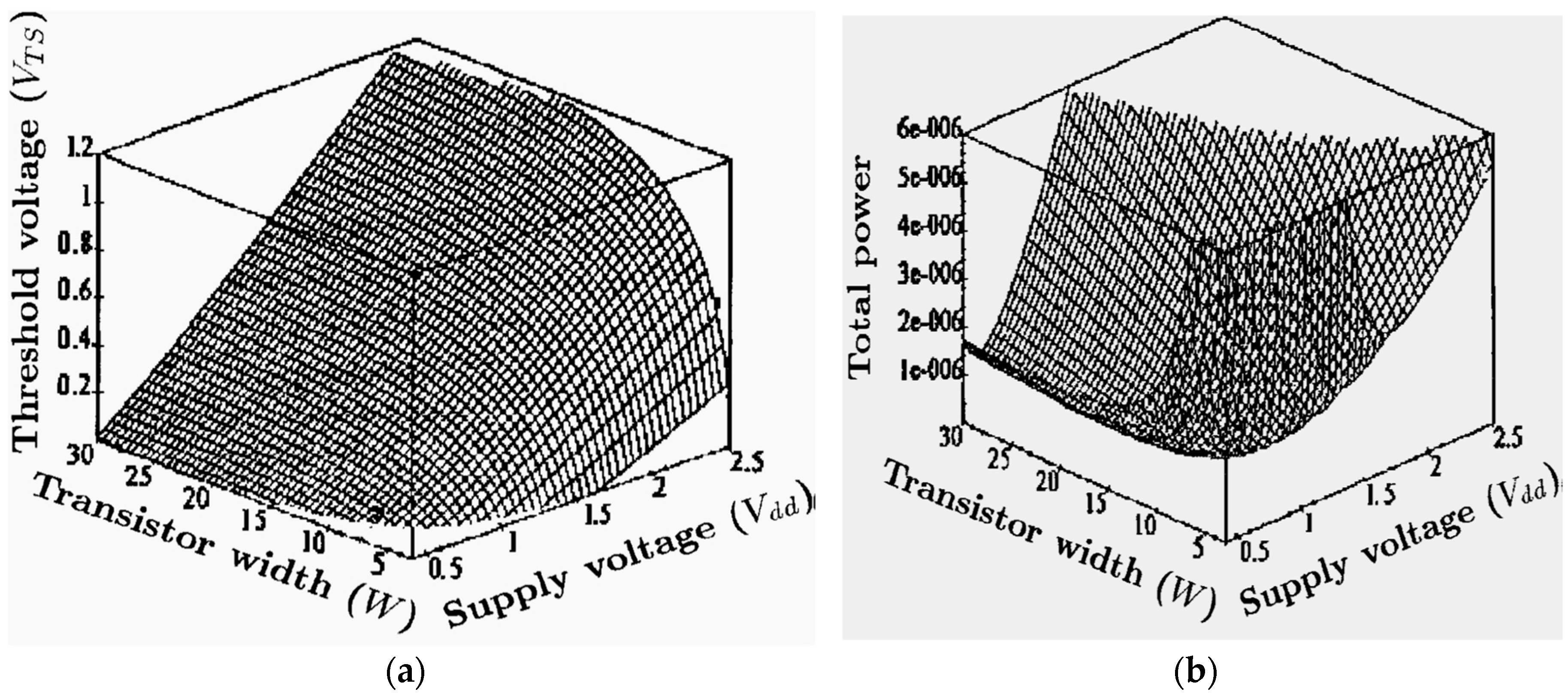
Figure 3 illustrates the function with respect to altering the transistors’ V_T and T_size for the 0.18-μm technology [3].

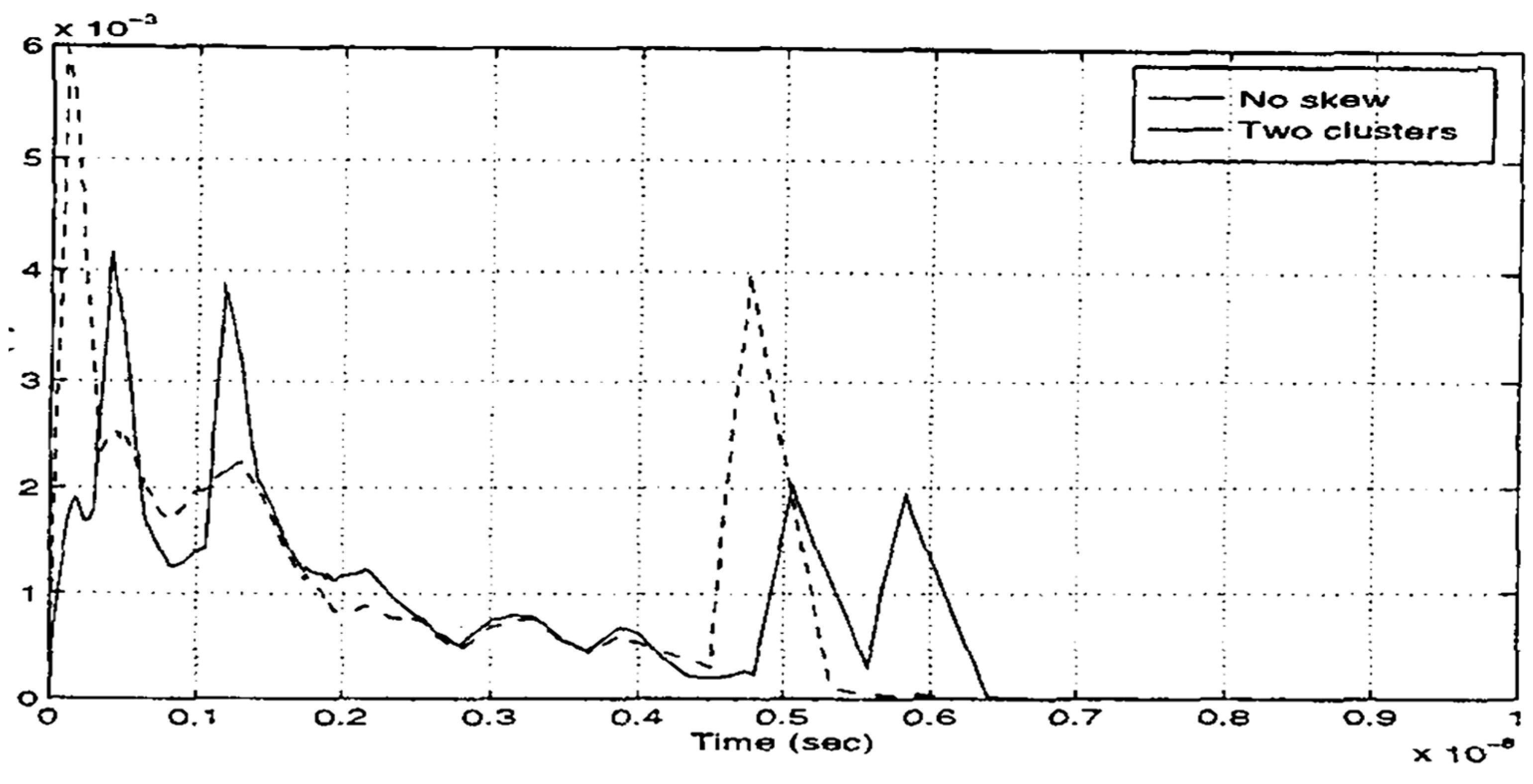
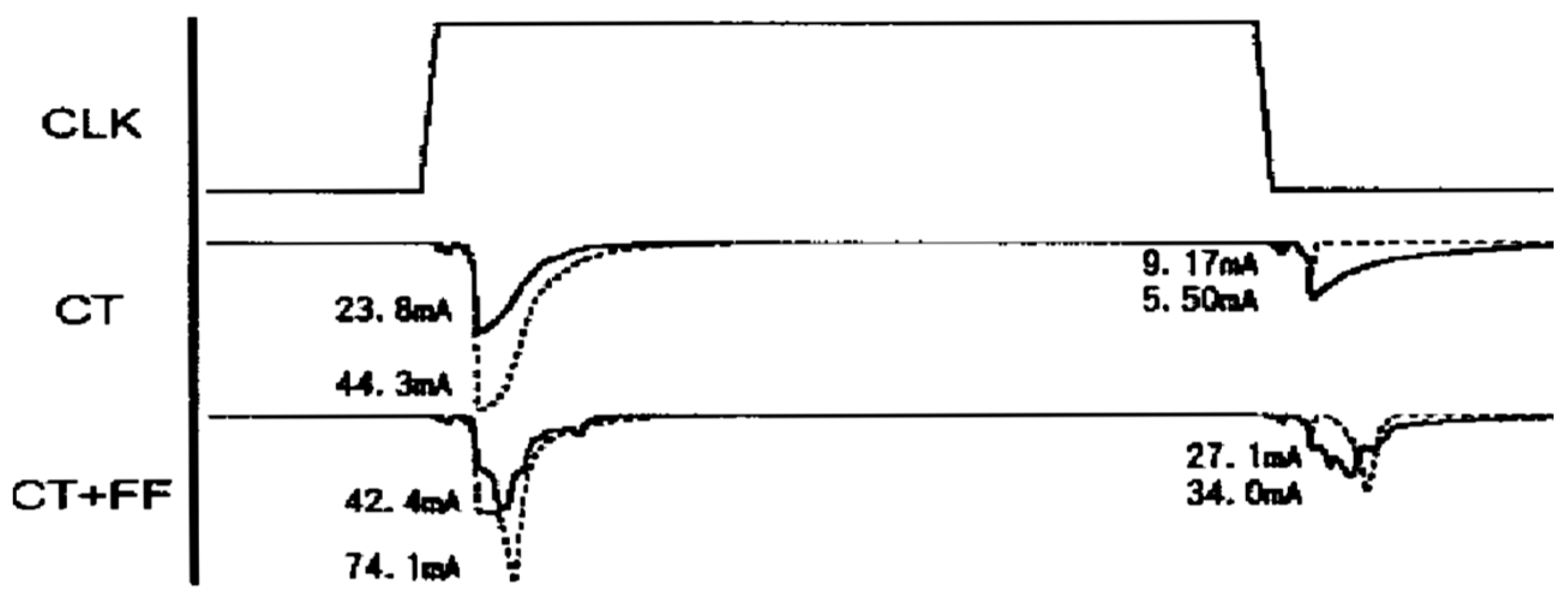
An algorithm [2] was proposed that determines the clock arrival time at each flip-flop in order to minimize the current peaks while respecting timing constraints, as shown in Figure 4. Benchmark circuits show that current peaks can be reduced by more than a factor of two without penalty in terms of cycle time and average power dissipation.

An opposite-phase scheme for peak current reduction was proposed in [4]. The basic idea is to divide the clock buffers at each level of the clock tree into two sets: Half the clock buffers operate at the same phase as the clock source, while the other half operate at the opposite phase of the clock source. Consequently, this technique can reduce the I_peak of the clock tree by nearly 50%, with the current waveforms shown in Figure 5.

References [2,4] proposed an efficient I_peak reduction technique that uses the useful clock skew to shift the I_peak generation location. This technique does not take into account that the waveform dimension magnitude is similar. This leads to a reduction in the highest peak current, but not in power reduction.

Literature sources define CLUSTVAR (Cluster Inclined Supply and Threshold Voltage Scaling with Gate Resizing) [5] as an algorithmic platform for power optimization by using dual supply voltages, gate sizing, and dual threshold voltages. CLUSTVAR can find a circuit status with the lowest dynamic and leakage power consumption on the premise that the circuit will not reduce performance or violate timing constraints. By demonstrating combinational circuits in the MCNC′85 benchmark suite, the savings of dynamic and leakage power are up to 42% and 67%, respectively.

The CLUSTVAR contributes to further power reduction. In CLUSTVAR, the algorithm is developed based on a maximal-weight independent set. However, the CLUSTVAR only considers the combinational circuit. The CLUSTVAR technique is STA-based. Conventional STA tools often provide pessimistic results and are only suitable for general-application designs. The traditional STA computations would require that all of the nodes in this circuit be recomputed due to the circuit delay time global impact, as shown in Figure 6. This is due to the fact that simplifying the STA calculation reduces the gate-delay re-computation time.

In [6], the methodology includes an explanation of how to set the quiescent current (IDDQ) bound to detect defective parts without rejecting defect-free parts. The proposed methodology increases design efforts for accurate standard cell library characterization with respect to power. The study does not consider that the accurate value is difficult to obtain, as the physical implementation issues (delay time, gate loading) cannot be accurately computed in the early design stage.

In [7], tests for input threshold voltages are used to distinguish the characteristics of a device during validation, as well as the quality of a device during production testing. The paper focuses on the input threshold voltage issue, but does not take the internal core circuit into consideration.

Reference [8] provides a survey of several outlier analysis techniques and compares their effectiveness in the context of delay testing.

A method is elucidated in [9], in which the combinational circuit simultaneous switching operations are minimized. The delay slack times of the paths and clustered paths have similar slack values. The proposed register-transfer level (RTL) method takes advantage of the logic-path timing slack to reschedule circuit activities, thereby minimizing value within timing intervals.

Spreading the clock-tree drivers’ switching activity while maintaining a low clock skew at the clocked tree’s sink-nodes is proposed in [10]. The clock-tree driver’s switching characterization has been used for fast computation of peak currents. A mix of high-threshold voltage and low-threshold voltage clock-drivers to minimize clock skew is employed in [1].

In [9], the objective is to reduce the number of glitches from the clock skew scheduling in a circuit, thus reducing dynamic power. The scheduling is formulated according to an integer linear programming problem, and the vector-independent clock skew schedule is derived to reduce glitches.

The studies [9,10,11] are related to the proposed technique. However, their motivations are different. Contributions to the power reduction are made in [9] and [11], but not for the peaking current.

The above techniques most commonly used in the past only focus on I_peak or I_avg reduction, i.e. one target in a circuit optimization stage. The generic low I_avg technique decreases the current waveform dimensions. However, the I_peak reduction technique reduces the highest current value. Hence, the generic low I_avg technique cannot effectively reduce the I_peak. The generic I_peak reduction technique also cannot effectively reduce the I_avg.

For the I_avg and I_peak estimation issues, the proposed technique is different from the above-mentioned studies and has several advantages. The proposed gate-level is approached after the circuit has finished the back-end synthesis stage and the gate-level information is extracted and calculated. This methodology will be more accurate if it is compared to the higher (RTL) design phase. Hence, the increased accuracy and computation time reduction targets are both achieved through the proposed framework.

3. The Proposed Current-Bound References Generation Technique

Circuit-testing engineers require an accurate and fast estimation tool to reprocess designed circuits into five reference circuits to find appropriate current bounds. In this paper, the proposed framework can quickly estimate the current bounds to support a fast screening technique to identify potentially faulty chips.

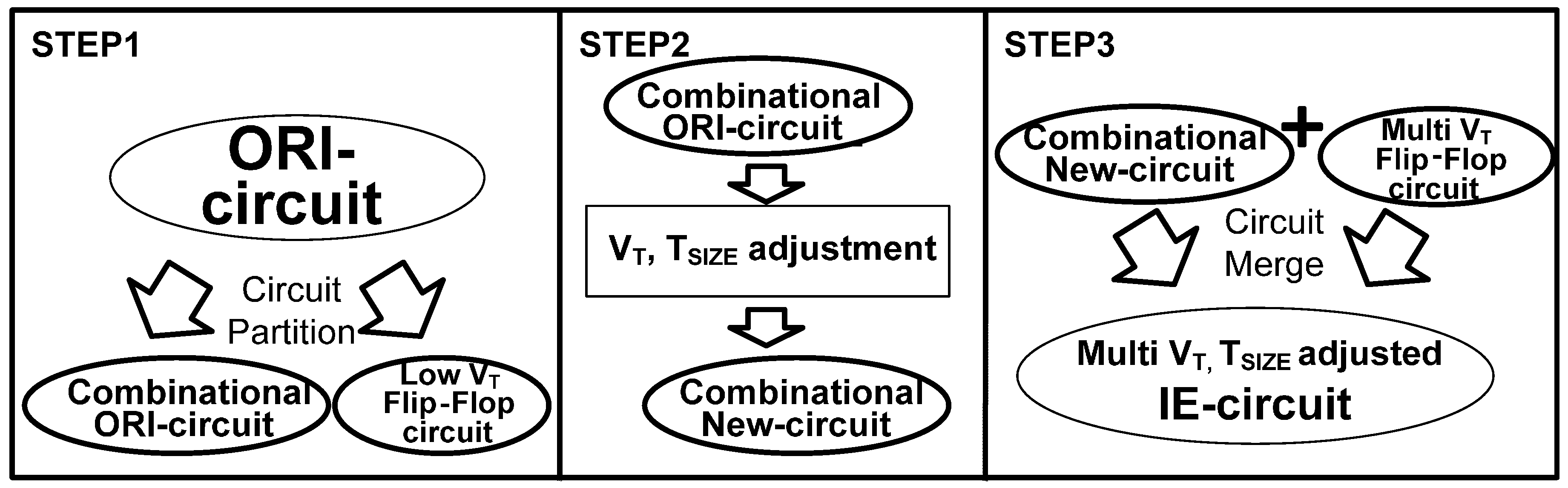
The proposed framework adopts threshold voltage-adjusting and gate-resizing techniques to re-synthesize five reference circuits, which are high-performance (HP-circuit). The large-T_SIZE and low-V_T transistors are used in this circuit. The ORI-circuit is an original-designed power-performance optimized circuit that uses best-T_SIZE and low-V_T transistors. The current reference design (IE-circuit) is a reference circuit for I_peak and I_avg estimation, which is designed by using both T_SIZE- and V_T-adjusted transistors.

The re-synthesized IE-circuit can accurately estimate the I_peak and I_avg and effectively perform I_peak and I_avg reduction, using the threshold voltage (V_T) adjustment with transistor sizing (T_size) techniques under the same circuit’s performance constraint. The noise-immune design (NI-circuit) uses the best-T_SIZE and high-V_T transistors. The low-power design (LP-circuit) is a low-power designed circuit, which uses the small-T_SIZE and high-V_T transistors.

The low V_T or high V_T means the transistor is designed for low- or high-threshold voltage, respectively. The used T_SIZE represents the circuit’s area; best-T_SIZE means that the synthesized circuit uses the area-optimal constraint for a small area. Based on this synthesis methodology, if we design an LP-circuit, the IE-circuit’s reported value can serve as the reference upper bound, and the measured currents of the LP-circuit are not higher than the reported IE-circuit values. The I_peak and I_avg closed lower bounds are the lowest I_peak and I_avg values of the ORI-circuit working at the same clock frequency.

They are re-synthesized from the ORI-circuit. Once the original design (ORI-circuit) is ready, the test engineer utilizes the proposed framework to re-synthesize the ORI-circuit to the IE-circuit HP-circuit, NI-circuit, and LP-circuit. The IE-circuit is an adjusted V_T and T_SIZE circuit by adopting the MTCMOS approach from the ORI-circuit, IE-circuit current consumption serves as a reference for the other four designed circuits. After determining the I_avg and I_peak current values of the IE-circuit from simulations, the obtained current values can then be used as a comparison value of the designed chips during the testing stage.

The IE-circuit is a power-performance optimized reference circuit. In IE-circuits, the gates that do not dominate performance are replaced with gates that have high-V_T and small-T_SIZE for lower I_peak and I_avg. This technique uses the longest circuit delay time as the constraint. As the IE-circuit has low I_peak and I_avg, without performance degradation, it can be applied as a closed lower bound for the ORI-circuit. The proposed IE-circuit with the V_T and T_SIZE adjustment technique does not increase the circuit delay time, and I_peak and I_avg decreases concurrently.

In this paper, the proposed IE-circuit can be used during chip testing to classify faulty chips. The IE-circuit has the same performance as the original designed circuit under testing. Only the threshold voltage and transistor size are altered from NI, LP, or HP reference circuits.

4. The Current-Bound Reference Circuits Generation Method

The characteristics of the proposed framework are twofold. The first is a quick and accurate I_avg/I_peak estimation technique. The second is the designed circuit I_peak and I_avg alleviation technique to reduce the I_avg/I_peak current values. The proposed dynamic timing incremental analysis methodology can quickly and accurately identify the I_peak and I_avg of an application circuit.

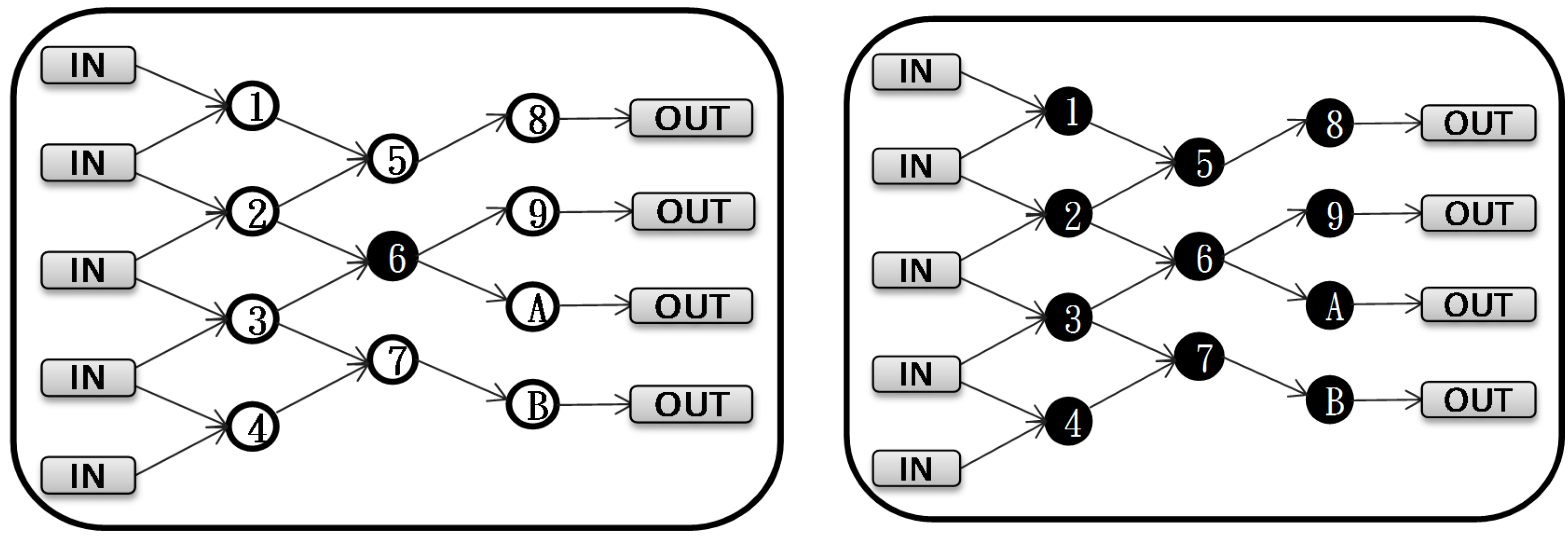
There are five types of circuits adopted in this paper. The ORI-circuit is the original circuit synthesized by using generic cells based on design flow. All gates use low-V_T and simplified logic circuits with optimal driving capabilities. The HP-circuit is designed for high performance. It is synthesized by using low-V_T for all logic gates while enlarging the gate size for higher driving strength. The LP-circuit with all high-V_T and minimized T_SIZE cells has the least power consumption and a low peak current. The NI-circuit uses the best-T_SIZE and high-V_T transistors for higher signal noise tolerate ability. These circuits are shown in Figure 7.

LP-circuit is designed with high-V_T and uses a small driving ability gate (small-T_SIZE) for the lowest I_peak and I_avg consumption. NI-circuits use High-V_T with the same T_SIZE as ORI-circuits. The NI-circuit uses High-V_T gates that have best-T_SIZE. The I_peak and I_avg decrease, and circuit delay time increases. The LP-circuit, in contrast to the NI-circuit, minimizes the T_SIZE for lower I_peak and I_avg, but also increases the delay time. The difference between the NI-circuit and the LP-circuit is T_SIZE.

For the proposed technique, the first target is I_avg and I_peak current estimations, and lowering the average power has also been taken into consideration. The proposed software framework target is to generate (re-synthesize) several reference NI-, LP- and HP-circuits as the measurement reference bounds to the original designed circuit (ORI-circuit) during the test-circuit testing stage.

The gate-resizing method is adopted to choose different driving capability cells in the library. The threshold voltage reassignment and gate-resizing techniques are executed from the ORI-circuit, and are then re-synthesized by applying the proposed framework.

We focus on the IE-circuit generation method in this paper. The IE-circuit is a multi-V_T designed circuit that uses adjustable V_T and gate sizes. The IE-circuit has optimal performance with I_peak and I_avg consumption. The proposed framework is used to synthesize all of the above circuits for comparison purposes.

The V_T- and T_SIZE-adjusted technique impacts the I_peak, I_avg, and power consumption. The IE-circuit uses the V_T-adjusting and T_SIZE sizing techniques. IE-circuits have larger-T_SIZE than NI-circuits and LP-circuits under a certain delay requirement. Thus, the I_peak and I_avg are larger.

As

Table 2. Comparison of five circuit types.

Property	Generic Circuit Type
	HP Low-VT Max-TSIZE	ORI Low-VT Best-TSIZE	IE Adj-VT Adj-TSIZE	NI High-VT Best-TSIZE	LP High-VT Min-TSIZE
Peak Current	1	2	3	4	5
Average Current	1	2	3	4	5
Delay Time	5	4	3	2	1

shows, the peak current and power consumption of IE-circuits are in the middle range of the five circuit types. The IE-circuit does not change the critical circuit path delay times. The IE-circuit is a good reference circuit under the same ORI-circuit performance constraint, but with the lower I_peak and I_avg current consumption.

After determining the average measured current from the sample’s physical ORI-designed test chip, simulation bound values can then be used to set the bounds for chip testing equipment. The software framework reported values are used as references to set the upper and lower current bounds during the chip testing phase.

The Reference IE-Circuit Generation

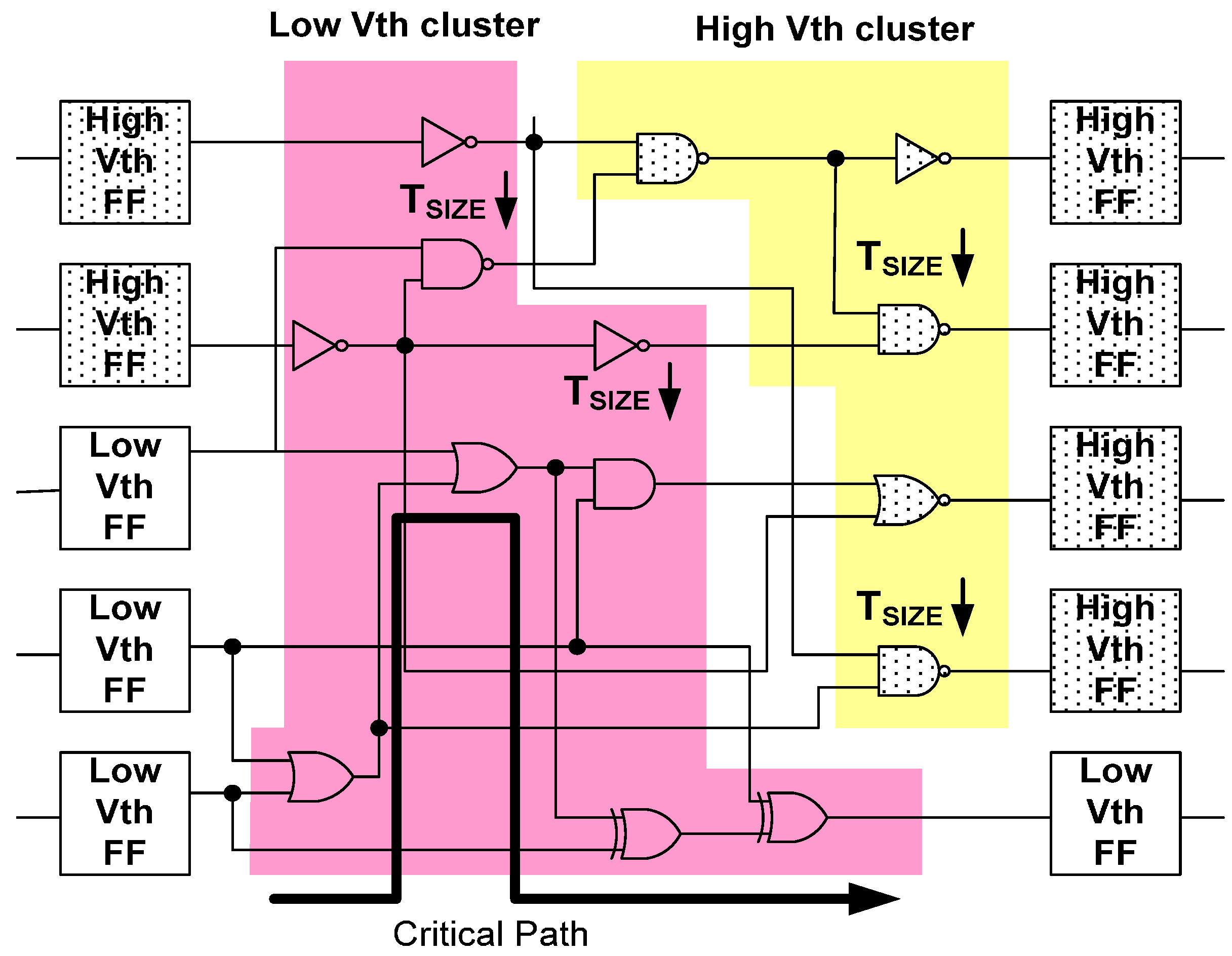
Most of the I_peak and I_avg comes from the flip-flop (FF) state transition. In this proposed technique, both the FF and logic gate V_T are simultaneously adjusted to reduce the I_peak and I_avg.

This proposed efficient framework of peak-current alleviation with a power delay and area reduction uses adjusted transistor threshold voltage and gate-resizing. The largest I_peak is generated from the flip-flops with prior stages of the logic gates’ input transitions at the same time. A high V_T gate has a higher circuit delay time with a lower I_peak than a normal V_T gate. The IE-circuit allows the logic gates in a noncritical path with positive slack time to replace the high V_T gate, as shown in Figure 8.

The IE-circuit uses both the gate-resizing and threshold voltage (V_T)-adjusting techniques to simultaneously attain I_peak and I_avg reduction, power savings, and a smaller area. I_avg and I_peak can be effectively reduced by changing MTCMOS gates or by changing MTCMOS gates, which have the same function but different driving capabilities (T_size). The nonlinear dynamic timing analyses with incremental delay time calculation techniques can quickly and accurately estimate I_peak and I_avg.

5. The IE-Circuit Delay Time Calculation

We propose the circuit total I_avg and I_peak need to be calculated from logic gates that transition at the same time interval, so accurate I_avg and I_peak calculations should take the gate delay into consideration. This technique has considered the different gate delays when there are varying V_T.

Most traditional circuit delay time evaluation techniques are computed using STA. The traditional STA is pattern-independent from the worst-case estimation technique. However, this STA technique provides an excessively pessimistic evaluation of the circuit delay times. It is not suitable for designs used in specific applications.

The conventional STA counts the path delay by summation of all individual gate delays. This conventional STA calculates the circuit delay by summation of all of the gates’ delays based on a single threshold voltage source. This is referred to as the linear STA, which does not consider the gate delay difference from the threshold voltage variance of each gate.

The traditional STA computations would require that all the nodes in this circuit be recomputed because of the circuit delay time global impact. Hence, most conventional STA tools provide overly pessimistic results and are only suitable for general-application designs.

The circuit’s consuming current is related to the timing of the gate’s transitions. Accurate timing analysis can efficiently estimate the consuming current. The proposed technique simplifies the STA calculation and reduces the gate-delay re-computation time. Compared with the other gate-level tools, the proposed incremental nonlinear STA was used for quick and accurate estimates.

In a traditional design strategy, the circuit performance analysis relies on the longest path delay calculation by using STA/DTA. The voltage drop may not induce circuit delays, as not all gates in the circuit are affected by voltage drops. The path delay will not increase if the consumed currents of all gates do not exceed the power supply. Moreover, the circuit total delay will not increase if the increasing gate delay (due to lower voltage) is not located on the critical path. Thus, repeat timing recalculation by STA/DTA is not necessary for all paths. The proposed incremental STA/DTA technique focuses on the paths of concern to avoid the re-computation of many path delay times.

Two timing calculations are proposed in this framework. The first nonlinear STA (NLSTA) uses the table-lookup method to estimate the gate delay time, which is pattern-dependent. As the NLSTA technique is based on real circuit transition times, the estimation results are more accurate than STA by specific dependent applications. The NLSTA technique is needed to design a reliable chip without specific applications, such as for a CPU.

The dynamic time analysis (DTA) estimation results are close to the real application results. The second proposed nonlinear dynamic time analysis (NLDTA) technique is used for the pattern-dependent delay time calculation. NLDTA achieves the highest accurate estimations in comparison with the STA, NLSTA, and DTA techniques. However, the calculation time is the longest. The accurate voltage induced delay is a dynamic behavior that is pattern-dependent. NLDTA is a real application transition current. It is suitable for specific application designs. The NLDTA verification input patterns provided by a circuit designer may have lower logic state transitions than those of NLSTA.

From comparisons with the conventional STA technique, the proposed NLSTA and NLDTA have good computation time saving results. The nonlinear STA and DTA need more time to compute the circuit delay. However, the incremental technique can save a great deal of re-computation time.

For a generic designed circuit, the I_peak and I_avg are pattern- or timing-dependent. The proposed NLSTA and NLDTA are pattern-dependent estimation techniques. This can solve the problem of the pessimistic estimation of the traditional STA.

5.1. The Proposed NLSTA and NLDTA Delay Time Calculation Techniques

The proposed IE-circuit technique applies threshold voltage-adjusting and gate-resizing to reduce I_avg and I_peak. The gate delay, I_avg and I_peak need to be re-computed for accurate estimation when threshold voltage varies. Moreover, the proposed technique uses the estimation of the current bound setting and then induces a supply voltage drop and a circuit delay time increase. Hence, an accurate and quick delay calculation technique is an integral element of our approach.

Good I_peak and I_avg estimation input patterns (testbench) can activate a large number of gate switches (transitions) at the same time. These patterns trigger the circuit to generate the largest voltage drop. Our proposed methodology can quickly estimate the worst-case I_peak/I_avg of the circuit using NLSTA/NLDTA.

The first step in the process is to define the circuit level from the topological sort and then sort the level according to I_peak and I_avg. This is followed by computation and sorting by cost (COST) for all gates at each level. The gate-resizing and V_T-adjusting processes are applied using the cost function of each gate. The cost function of each gate is defined by the equation COST_g = (I_peak-before − I_peak-after)/(Slack_before − Slack_after). The computation formula is the same for the average current process. This cost function is also applied by changing I_peak to I_avg when calculating average current.

The large cost function means that the gate contributes more to I_peak (I_avg) reduction, and needs to be processed first. I_peak-before (I_avg-before) and I_peak-after (I_avg-after) denote the I_peak (I_avg) of this gate before and after sizing, respectively. Slack_before and Slack_after denote the slack time of this gate before and after sizing, respectively.

The procedure for the I_peak (I_avg) reduction process is as follows:

• Divide the circuit into a multi-level structure.
• Compute the I_peak (I_avg) of each level.
• For the circuit:

  (1)

  Select the highest I_peak (I_avg) level;

  a

  compute the cost function of those gates in this level and sort the cost function by using heap sort;

  b

  re-compute the cost of this gate after resizing and V_T-adjusting process to select the gate that has the highest cost; and

  c

  assign suitable sizing and V_T to this gate.

  (2)

  Re-compute the circuit slack time using the incremental STA technique.

  (3)

  Repeat (1) until all gates in the same level are processed.

Repeat the process for the highest remaining value among the remaining levels until all levels are processed.

5.2. The Incremental Calculation Technique for the Proposed NLSTA and NLDTA

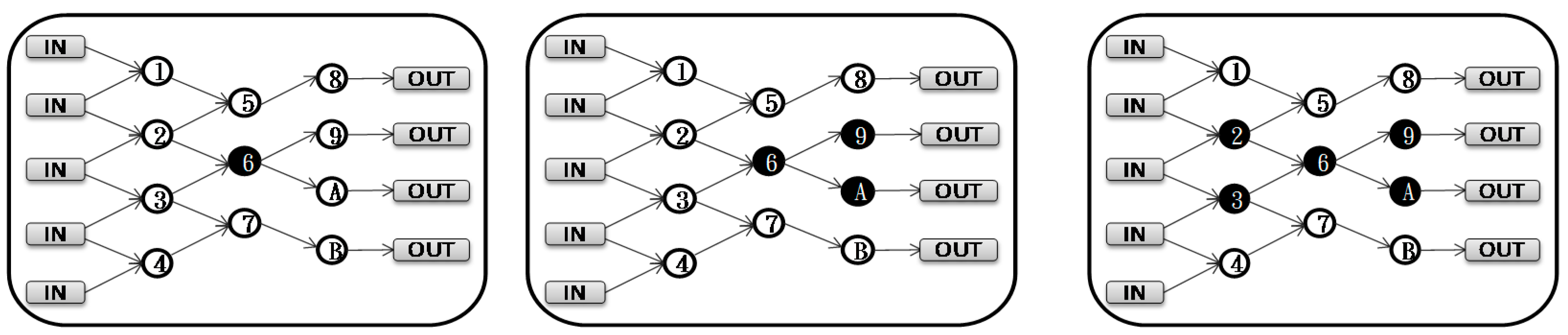
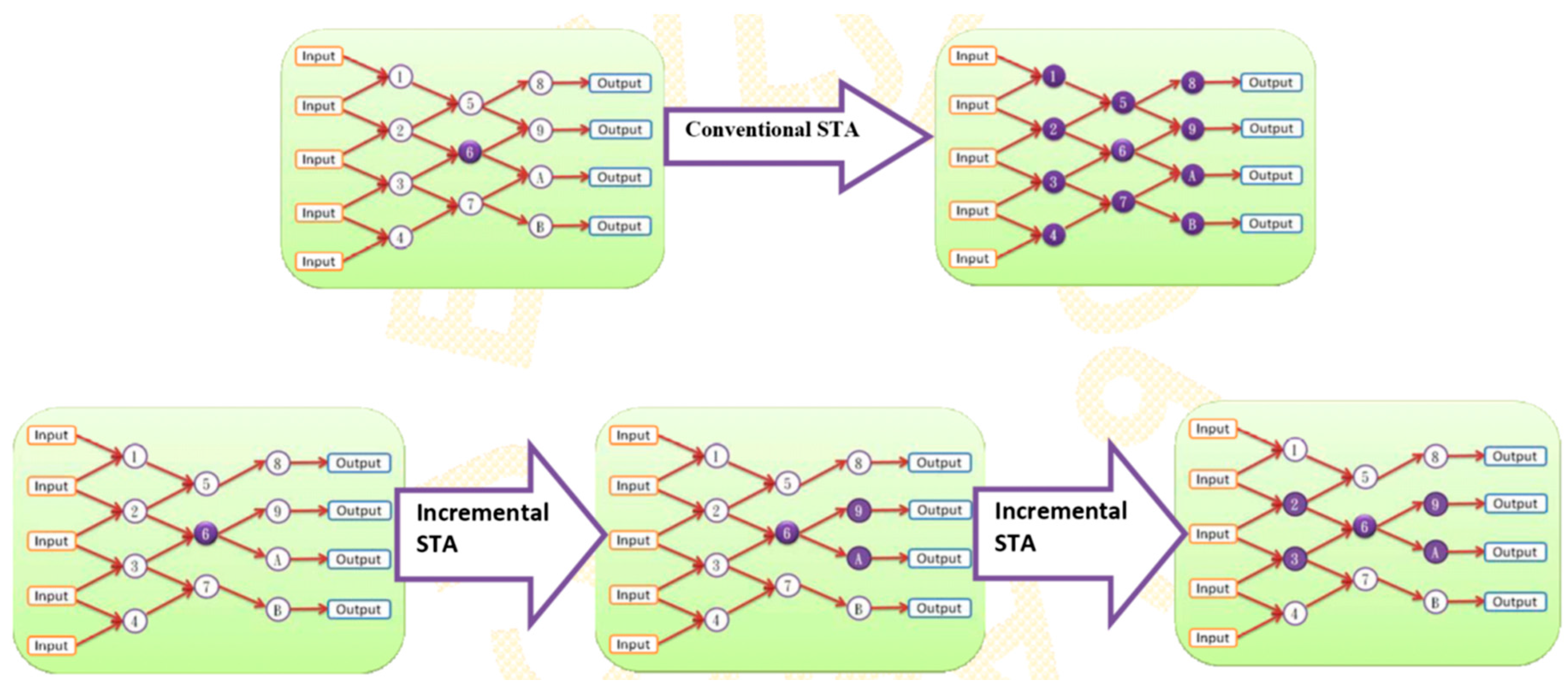
In conventional STA delay, timing re-computation is required if the node-6 gate information is changed. Due to the circuit delay time global impaction, the traditional STA computation modifies all nodes in this circuit that need to be recomputed. For the following incremental STA, the impaction is only on the fan-in and fan-out cones of this node, as shown in Figure 9.

It is complex to dynamically recalculate the circuit’s delay by considering all gates using varied threshold voltage. This is due to the fact that V_T adjustment will result in different gate delays. Then, the former estimated I_peak and I_avg should be re-calculated due to the different gate delays (from varying V_T). The re-computing process should be repeated until all of the gates are processed.

Dynamic timing analysis is required in order to consider the floating gate delay value under varying V_T and T_size. Dynamically re-calculating the circuit performance is time-consuming because of the high computation effort involved. This calculation time can be reduced by using the incremental NLSTA and NLDTA.

The proposed framework uses the non-linear STA to compute the accurate slack time, and the delay time can be found in the tables. From the execution time comparisons, there is less computation time for the large circuit.

The circuit tree data structure is mapped according to the timing-based gate topology. This tree can then be used for easy path tracing. The affected longer delay path can be easily found from the lowest leaf of the tree.

The proposed increment nonlinear DTA technique uses the table lookup technique to compute an accurate delay time. The proposed incremental technique only impacts the fan-in and fan-out cones of this node. Moreover, the dynamic nonlinear STA saves significant computation effort. The computation time comparisons are shown in Figure 10.

6. The Proposed Software Framework of the IE-Circuit

IE-circuit is the only detailed discussed reference in this section. The functions of IE framework include the I_peak and I_avg alleviation process, which came from the close relationship between the I_peak, I_avg, and the gate delay. The V_T- and T_SIZE-adjusted techniques are used to reduce the current consumption with a lower I_peak, I_avg, and area, as demonstrated in Section 5. After locating those logic gate levels with the largest I_peak and I_avg within the circuit gate forest, fast path delay calculation is carried out by combining NLSTA/NLDTA and the path sensitization algorithm. The largest I_peak and I_avg contributed gates are located by using Heap-Sort. When any gate V_T is varied or resized, the new path delay times are recomputed by applying an incremental timing analysis technique to the circuit hierarchy.

The I_peak and I_avg alleviation and analysis tool includes two major functions. This software framework is written with C, sis, and Perl. The tools also combine the common interface with commercial tools, such as Synopsys and Nanosim.

The analysis feature includes the following functions:

• gate-level function simulation;
• consumption current report;
• circuit delay timing report;
• power consumption report; and
• voltage/current waveforms.

The optimization feature includes the following techniques:

• gate (T_size) resizing; and
• threshold voltage (V_T)-adjusting.

In this framework, the synthesis/analysis process of the cell delay uses the threshold voltage from the cell library, which is characterized from the TSMC 0.18-μm standard cell library. It is modified by calibrating the calculation formula and HSPICE simulation results. The intrinsic delay time is characterized by the gate simulation with no output load. The normal- and high-threshold voltages are 0.23 V and 0.44 V, respectively.

In Figure 11, for a sequential circuit, the expanded combinational circuit part from the timing window and repeat the calculation process. Because the IE-circuit considers the delay time optimization of flip-flops, the circuit delay times do not increase after the flip-flop (high-V_T) replacement process.

For example, the LP-circuit is obtained from replacing the high-V_T and small-T_size logic gates for a lower I_peak and I_avg. An optimization process is performed to minimize the I_peak and the I_avg by substituting logic gates that have low V_T and large T_size instead of having logic gates that have a high V_T and a small T_size. High-V_T and small-T_size logic gates dissipate less I_peak and I_avg, but also operate more slowly than low-V_T and large-T_size logic gates. Hence, multi-V_T and T_size optimizations are a trade-off between I_peak, I_avg, and path timing.

As the I_peak, I_avg computations have recursive relationships, they conform to the circuit’s path delay time. The optimization process is finished when the I_peak and I_avg values are in a stable state. There is an approach utilized: When all circuit levels are evaluated and the range of delay times lies below a threshold (5%), the optimization recursive process is then halted.

The proposed software tool is not used to report the accurate values for the designed circuits. It is difficult to accurately compute the I_peak and I_avg from a higher-level model. The software framework proposes the gate-level estimation and reduction methodology. This technique can also reduce the I_peak and I_avg without the circuit delay time or area increase penalty. The proposed framework includes quick gate-level estimation functionality with transistor-level accuracy.

7. Experimental Results Analysis

The current-induced voltage drop not only induces circuit delay and power, but also reduces the circuit noise margin from a lower supply voltage and raises the issue of reliability from electro-migration. The framework proposes a fast gate-level estimation and reduction technique, which merges the I_avg, I_peak, and nonlinear static/dynamic timing analysis. From the proposed framework, fast and accurate estimation results are determined for five types of re-synthesized circuits. There are ten test circuits used to demonstrate the efficiency of IE methodology. Among nine of the ISCAS89 benchmark circuits, the VLD circuit is the variable-length video decoder design.

The sizes of the tested circuits are listed in

Table 3. The sizes of the tested circuits.

Circuit Name	Inputs	Outputs	DFFs	Logic Gates
S27	5	1	3	9
S349	10	11	15	109
S9234	37	39	145	759
S5378	36	49	176	1054
S13207	63	152	625	2348
S15850	78	150	513	3003
VLD	69	43	222	6773
S38417	29	106	1564	8009
S38584	39	304	1275	8596
S35932	36	320	1728	8666

. The experimental circuits are optimally synthesized by circuit synthesis tools (sis and Synopsys). The sizes are different for all circuit logic gates.

The commercial circuit simulation tools are included as a reference for comparison and to allow us to evaluate our tool’s accuracy. The computation time information is shown in

Table 4. The computational time for each circuit.

Circuit Name	Gates #	Execution Time (s)			Execution Time Per Gate #
		Clustvar [5]	NLSTA	NLDTA	Clustvar	NLSTA	NLDTA
S27	12	0.00	0.00	9.07	0	0	0.75583
S349	124	2.02	1.01	53.40	0.01629	0.00815	0.43065
S9234	904	59.28	4.01	347.61	0.06558	0.00444	0.38452
S5378	1230	110.15	5.00	512.72	0.08955	0.00407	0.41685
S13207	2973	873.29	23.01	1492.15	0.29374	0.00774	0.5019
S15850	3516	2776.30	55.00	1327.09	0.78962	0.01564	0.37744
VLD	6995	36893.43	196.04	3241.92	5.27426	0.02803	0.08105
S38417	9573	32631.15	231.00	4501.48	3.40866	0.02413	0.47023
S38584	9871	43618.51	651.00	4949.41	4.41885	0.06595	0.50141
S35932	10394	31764.37	325.00	5567.53	3.05603	0.03127	0.53565
Average Execution time per Gate #					1.74126	0.01894	0.44555

; the computation time is very short when using our proposed tool.

Table 5. Peak current comparisons.

Circuit Name	Ipeak (mA) for Multiple Type Reference Circuits
	HP Low-VT Max-TSIZE	ORI Low-VT Best-TSIZE	IE Adj-VT Adj-TSIZE	NI High-VT Best-TSIZE	LP High-VT Min-TSIZE
S27	× 2.21	1.26	× 0.64	× 0.57	× 0.31
S349	× 2.23	4.52	× 0.61	× 0.54	× 0.41
S9234	× 1.78	33.69	× 0.61	× 0.60	× 0.35
S5378	× 1.70	62.81	× 0.55	× 0.45	× 0.37
S13207	× 1.41	133.40	× 0.61	× 0.54	× 0.31
S15850	× 1.26	100.45	× 0.62	× 0.53	× 0.42
VLD	× 1.09	37.12	× 0.61	× 0.60	× 0.42
S38417	× 2.10	282.41	× 0.61	× 0.60	× 0.42
S38584	× 2.11	366.61	×0.62	× 0.50	× 0.32
S35932	× 2.11	557.30	× 0.61	× 0.55	× 0.33
Average	× 1.80	157.96	× 0.61	× 0.55	× 0.37

and

Table 6. Power consumption comparisons.

Circuit Name	Ipeak (mA) for Multiple Type Reference Circuits
	HP Low-VT Max-TSIZE	ORI Low-VT Best-TSIZE	IE Adj-VT Adj-TSIZE	NI High-VT Best-TSIZE	LP High-VT Min-TSIZE
S27	× 1.43	0.008	× 0.90	× 0.75	× 0.40
S349	× 1.96	0.045	× 0.87	× 0.73	× 0.43
S9234	× 1.50	0.301	× 0.88	× 0.67	× 0.38
S5378	× 1.93	0.528	× 0.78	× 0.61	× 0.47
S13207	× 1.29	1.273	× 0.86	× 0.71	× 0.49
S15850	× 1.51	1.186	× 0.85	× 0.67	× 0.37
VLD	× 1.46	0.370	× 0.84	× 0.73	× 0.47
S38417	× 1.41	3.621	× 0.89	× 0.65	× 0.39
S38584	× 2.00	4.260	× 0.84	× 0.66	× 0.46
S35932	× 1.31	5.378	× 0.87	× 0.64	×0.41
Average	× 1.58	1.697	× 0.86	× 0.68	× 0.43

show the gate-level circuit estimation results of peak and average current consumption for the five types of circuits. Based on the TSMC 0.18-μm process, the clock frequency is 20 MHz for all circuits. Two thousand ATPG test patterns are used for the test circuit.

Column 3 in Table 5 and Table 6 shows the peak current and power consumption of the ORI-circuit, respectively. Columns 2, 4, 5, and 6 show the ratios of comparisons for the four types of circuits with an ORI-circuit. These results are used as the basis for the following comparisons with the ORI-circuit. The following values mean that the specific circuit reference values are multiplied by the values of the ORI-circuit. As shown in the example in Table 5, the reference I_peak for HP-S27, IE-S27, NI-S27, and LP-S27 are 2.78 mA (2.21 × 1.26 mA), 0.81 mA (0.64 × 1.26 mA), 0.72 mA (0.57 × 1.26 mA), and 0.39 mA (0.31 × 1.26 mA), respectively. The major contribution of this tool is to provide the tightened lower reference bound for the current outliers in the designed circuit.

Table 5 and Table 6 indicate that the HP-circuit is a high-performance one. Its I_peak and I_avg current consumptions are larger than those of the other proposed circuits. These values can be referred to as the upper bounds of different circuits. IE-circuit optimization technique reduces the circuit I_peak and I_avg current consumption. The IE-circuit is closer in value to an ORI-circuit. For low-power (LP) and noise immune (NI) MTCMOS circuits, the IE-circuit can serve as the upper reference values of the I_peak and I_avg currents.

Table 5 and Table 6 also indicate that the IE-circuit is the median value of the five types of circuits. IE-circuits can be good a reference during a circuit test phase and can quickly filter out the failed chips. The IE-circuit uses dual threshold voltage with gate-resizing for I_avg, I_peak, power, delay time, and area reductions without increasing overhead delay time.

The Nanosim circuit simulation results are taken as the golden values. Although the IE-circuit uses the gate-level estimation method, we show high accuracy in comparison to Nanosim, as presented in

Table 7. The error comparisons of Nanosim and IE.

Circuit Name	MAX Peak Current (mA)			Average Power (μW)
	Nanosim	IE	Error	Nanosim	IE	Error
s27	−1.263	−1.260	−0.20%	13.479	11.902	−11.70%
S349	−4.523	−4.465	−1.30%	81.384	72.421	−11.01%
s9234	−33.694	−34.546	2.53%	543.176	494.048	−9.04%
S5378	−62.813	−62.114	−1.11%	949.860	862.956	−9.15%
S13207	−133.398	−127.825	−4.18%	2290.972	2101.525	−8.27%
S15850	−100.447	−96.135	−4.29%	2134.741	1966.001	−7.90%
VLD	−37.116	−36.705	−1.11%	665.922	605.615	−9.06%
S38417	−282.405	−273.937	−3.00%	6517.099	5897.327	−9.51%
S38584	−366.605	−358.809	−2.13%	7667.985	6864.462	−10.48%
S35932	−557.3	−535.546	−3.90%	9681.069	8667.232	−10.47%
Average error			−1.87%			−9.66%

. The software framework provides good estimations. The I_peak and I_avg consumption estimations are 1.87% and 9.66% lower than Nanosim estimations, respectively. An efficient I_peak and I_avg reduction methodology and accurate in-house EDA analysis tools are proposed in this paper.

As shown in

Table 8. Nanosim and IE execution time comparisons.

Execution Time (s)	Nanosim	IE	Times(X)
s27	2268.12	8.20	276.60
S349	16789.01	59.98	279.91
s9234	173108.72	352.11	491.63
S5378	201476.46	720.84	279.50
S13207	681476.33	1601.11	425.63
S15850	558466.99	1396.23	399.98
VLD	222593.30	530.11	419.90
S38417	716073.10	4682.41	152.93
S38584	1566344.48	5796.95	270.20
S35932	2659931.09	7747.44	343.33
		Average	333.96

, the computation time of the IE-circuit is 334 times faster on average than that of Nanosim. The quick and accurate estimation results help designers to quickly predict a circuit voltage drop.

In this work, several benchmark circuits’ evaluation results have been provided. Practical chip measurement results are not shown in this manuscript. It is recommended that physical chip validations be examined in detail in a separate future study.

8. Discussion of Test Application Using the Proposed Techniques

A complicated preparation process is required to test the chip and to evaluate whether the chip is functionally workable. Furthermore, the proposed technique assists the test engineer to quickly screen out the failed chips from using the chip’s consuming current values and to determine the lower and higher current values for normal chips during the chip measurements. The proposed method can also be used for the chip binning situations.

In this research, both the I_peak and I_avg values can serve as effective references for judging a failed chip during testing. Thus, current consumption observations can be helpful for quick screening of potentially failed chips in the testing phase. The current estimation technique generates current bounds suitable for reference from transistor threshold voltage and size adjustment. The feasibility of the proposed bounds will require further detailed examination, which could be addressed in a future work.

An abnormally large I_avg and I_peak current induces a voltage-drop and impacts the circuit delay time and reliability. This paper presents I_avg and I_peak estimation and reduction techniques based on T_SIZE and V_T selection. As a chip’s current consumption is a distribution, the proposed technique provides reference bounds for the I_avg and I_peak, and these referenced current-bound gaps are not absolutely isolated within the HP-, NI-, and LP-circuits. This means that the current-bound region might overlap. This type of situation leads to potentially faulty results for the test chip; therefore, it is necessary to carefully evaluate chips’ measurement results that are located in the boundary region.

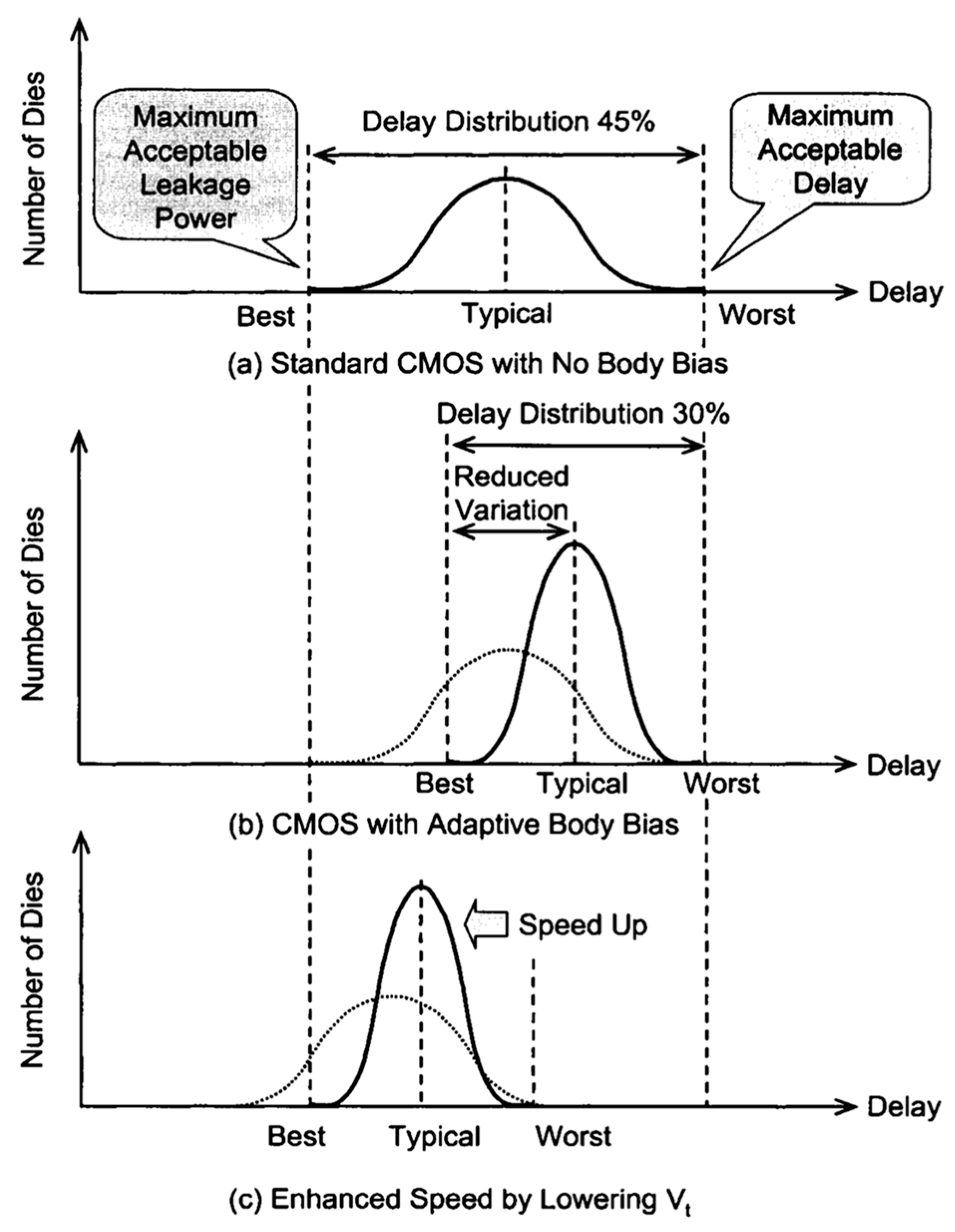
When the transistor’s body-bias is altered, there is the V_T disparity in the process variation, the wafer’s die-to-die delay time variations are shown in Figure 12. Our study does not take the process variation into simulations. This also leads to the inaccuracy estimation, and a feasible methodology is needed to add ±3σ statistic variation parameters into the emulations.

The leakage should be accommodated for advanced process in a future study. The manufacturing variations in the circuit’s simulation have not been included here. These factors need to be included in a future study.

There are several claims addressed in this paper:

(1)

The proposed technique identifies the transition gate and includes the gate’s timing and average- and peak-current in the calculation. When calculating the I_avg and I_peak, the proposed method partitions a circuit level by level, and then sums the I_peak at every level. However, due to the different delays of various gate types, gates of the same level do not necessarily switch at the same time.

(2)

There are two steps during the testing chip operation with the proposed technique. In the first step, ATE quickly screens the tested chips by using current bounds. For chips that fail during the first step, the second step is conducted manually. We can view and retest the chips by monitoring the circuit function and current in detail to accurately recover any potentially good chips.

(3)

In general, using T_SIZE and V_T change as a means of current reduction is more easily evaluated than other competing design constraints in low-power objectives, and it is suitable for advanced design technology. The input signal with a lower transition time (fast signal transition) has a lower I_peak.

(4)

The generic static timing analysis tool does not consider gate dual-delay for dual-V_T cells for the path delay time calculation.

9. Conclusions

As the testing of chips requires a longer period of time, the proposed technique can assist an engineer in quickly screening for as many failed chips as possible. Using current bounds to screen for faulty chips is a comparatively novel idea, and the proposed schemes use it as a component in statistical outlier analysis. Observations of the I_peak and I_avg currents are important for testing a circuit. However, previous research has focused on the discussion of the testing impact on power consumption, without upper or lower current bounds to screen for faulty chips. This paper proposes using the peak and average current bounds as the mechanism for a fast screening of potentially failed chips during the testing stage. The five proposed reference circuits provide I_peak and I_avg references for an original designed circuit under testing. The IE-circuit shows that, from applications of the V_T and T_SIZE-adjusting techniques, the closed current bounds can be determined. There are less than 2% and 10% estimation errors, respectively, in the I_peak and power (I_avg), with respect to the Nanosim (transistor-level) simulation results. The computation time of the proposed framework is 334 times faster on average than Nanosim. The software framework is a rapid methodology to estimate I_peak and I_avg to solve the lengthy testing time problems for large circuits. The effectiveness of the proposed method for screening faulty chips needs to be justified in future studies.