A Survey of Neural Front End Amplifiers and Their Requirements toward Practical Neural Interfaces
Abstract
:1. Introduction
2. Physiology and Action Potentials, a Brief Review
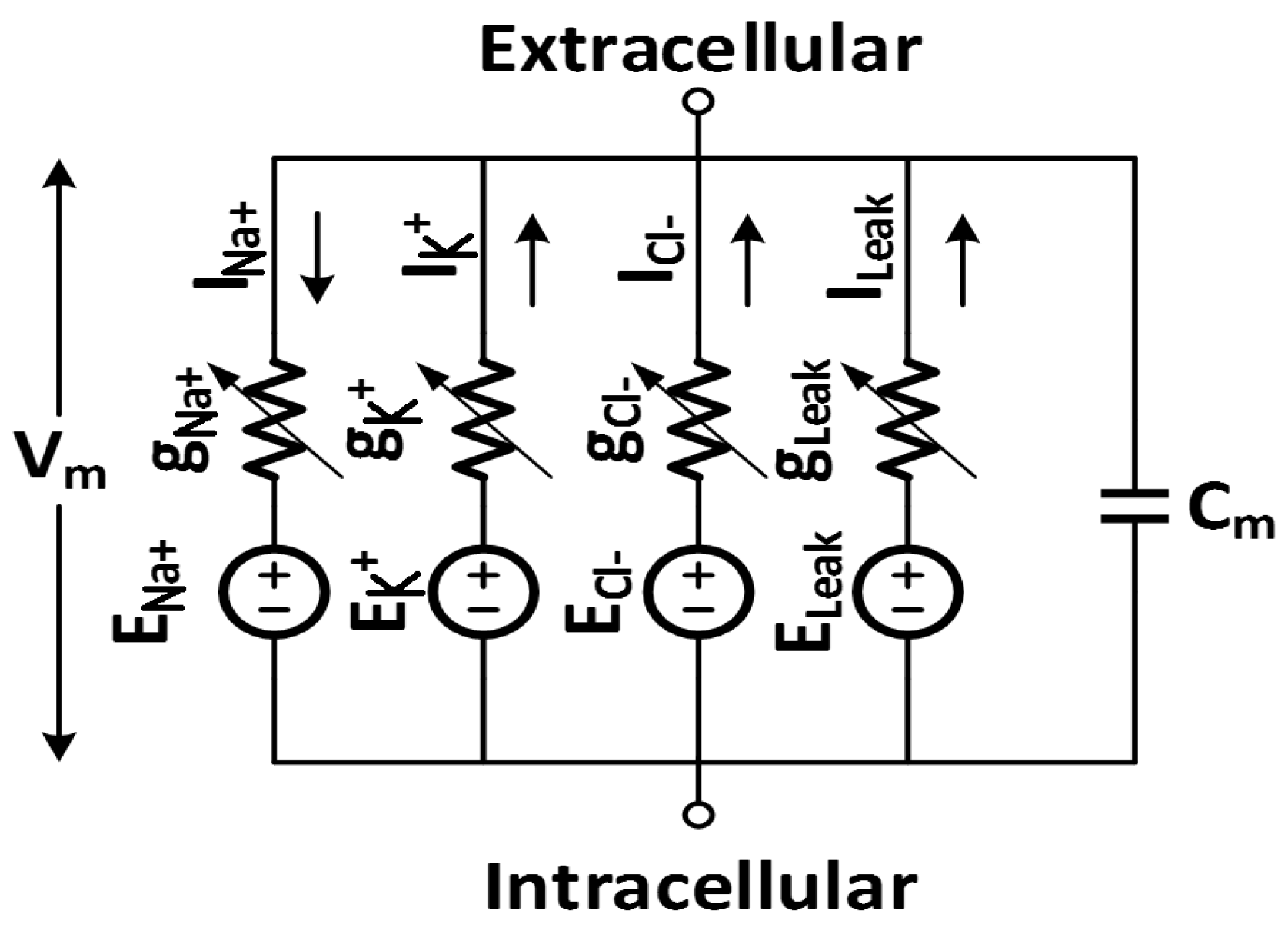
3. Neural Amplifiers Specifications
4. System Level Specifications
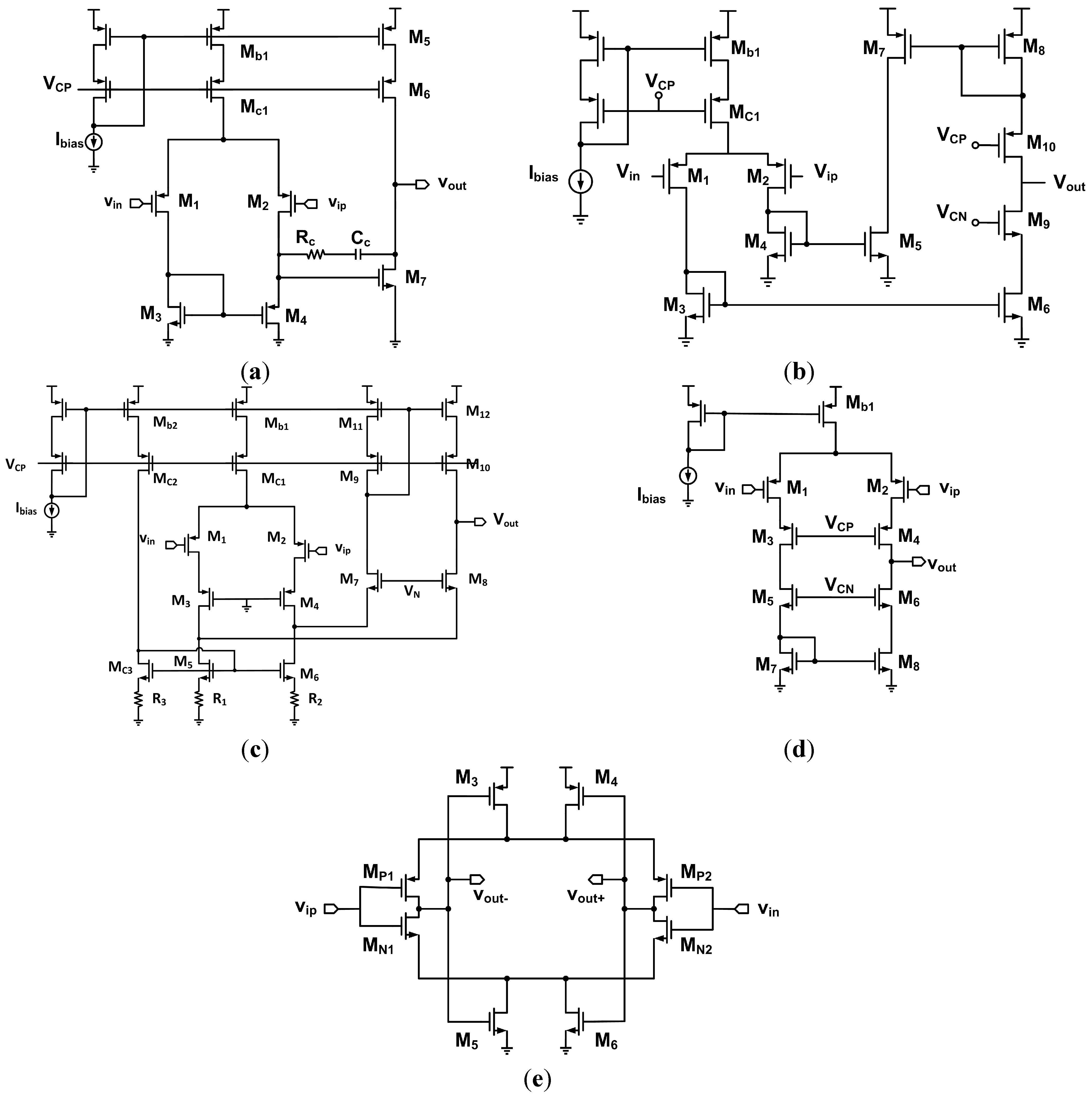
5. Circuit Topologies
| Architecture | NEF | Power consumption (μw) | Mid band gain (dB) | Area (mm2) |
|---|---|---|---|---|
| Telescopic-cascode Closed-loop Amplifier | 4.5 | 12.5 | 40.5 | 0.047 |
| Complementary-input Open loop Amplifier | 1.9 | 0.8 | 36 | 0.046 |
| Complementary-input Closed-loop Amplifier | 2.9 | 12.1 | 40 | 0.072 |

6. System Architectures
6.1. Open-Loop Amplifiers

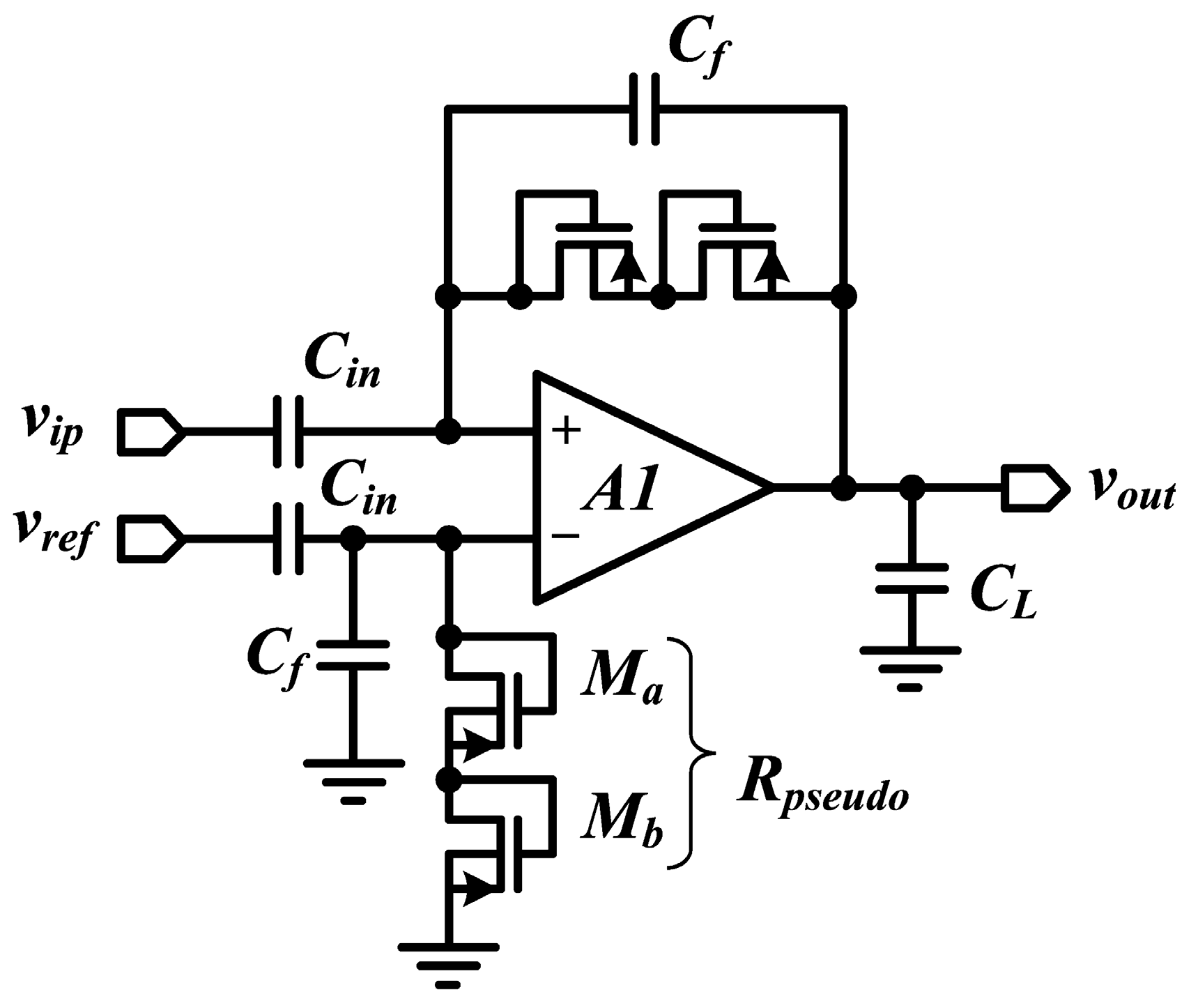
6.2. Capacitive Feedback Topology
6.3. Active Feedback Topology
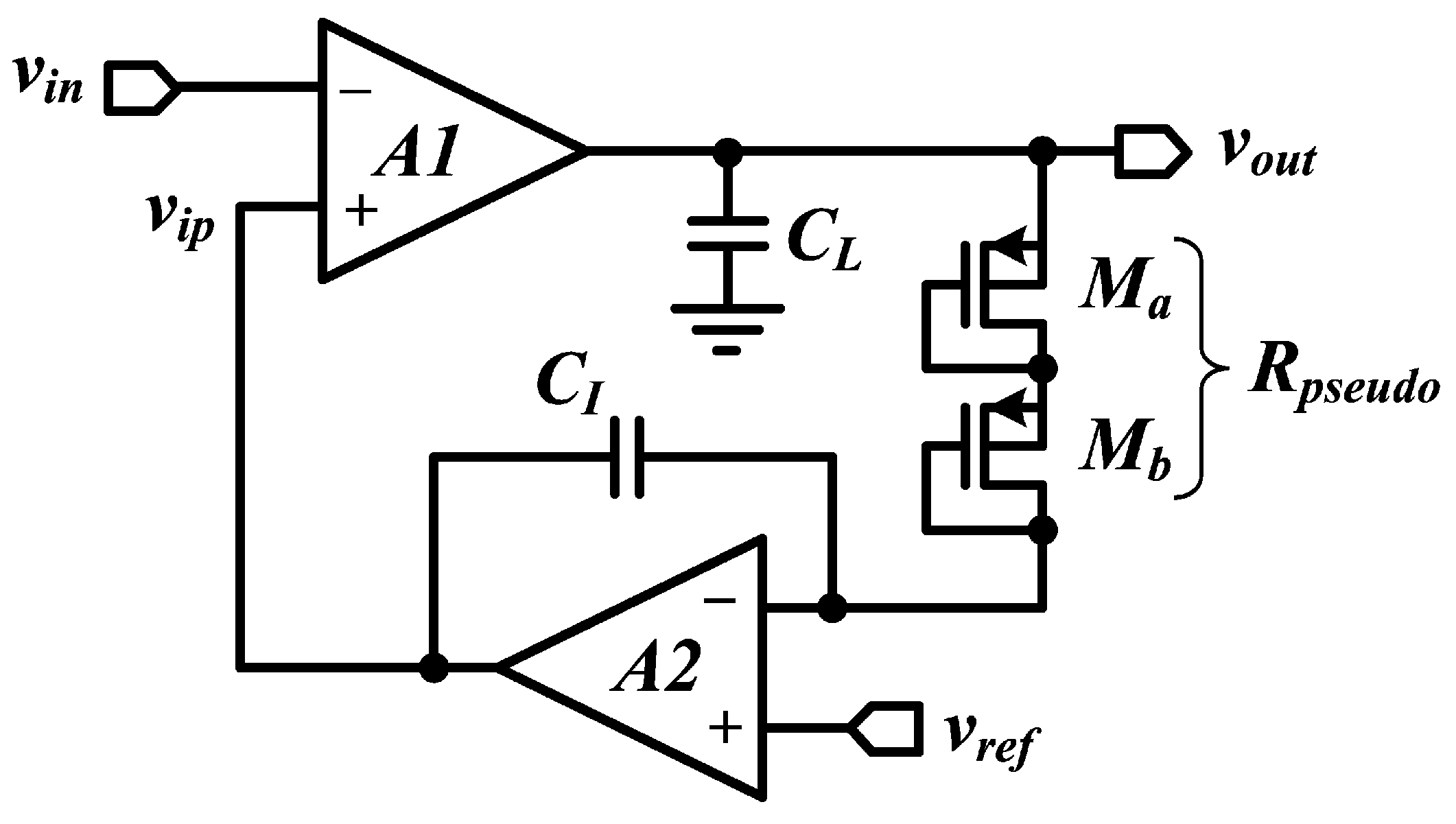
6.4. Pseudo-Resistors
6.5. Adaptive Topology
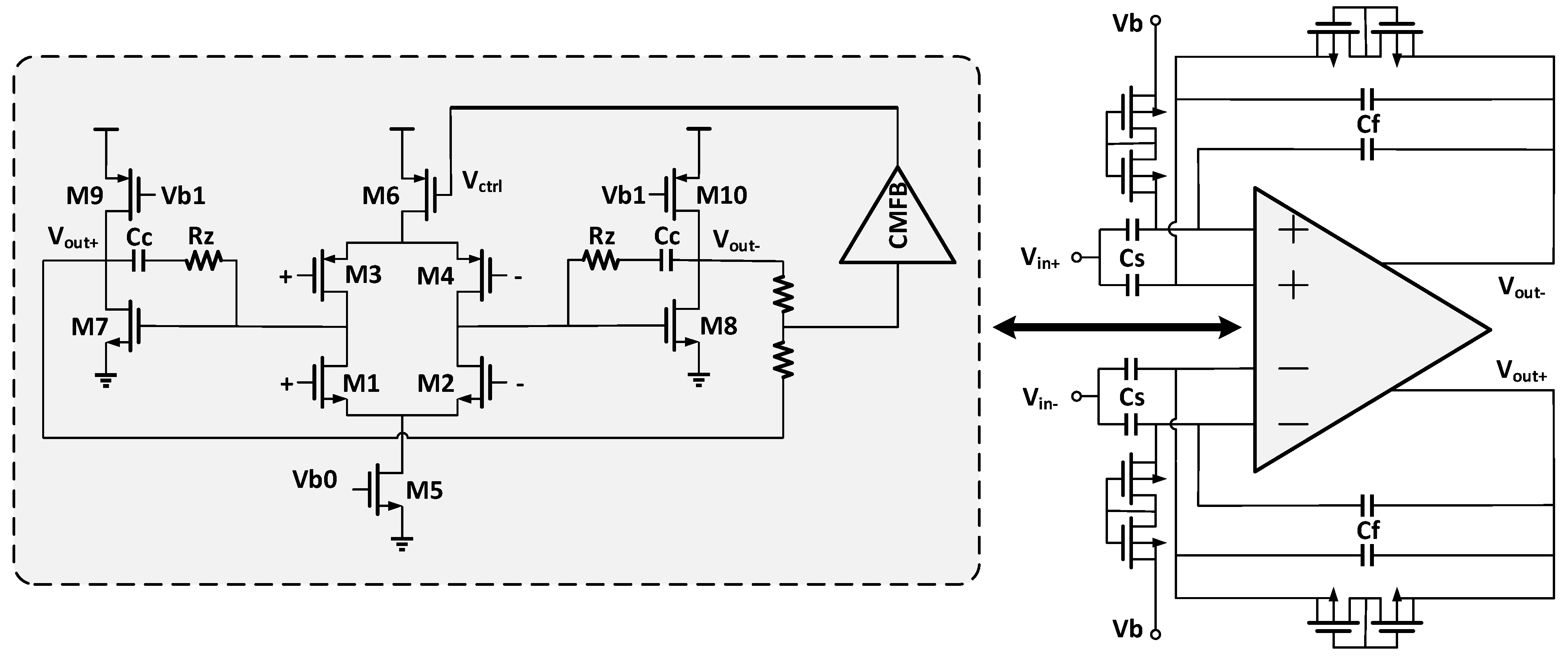
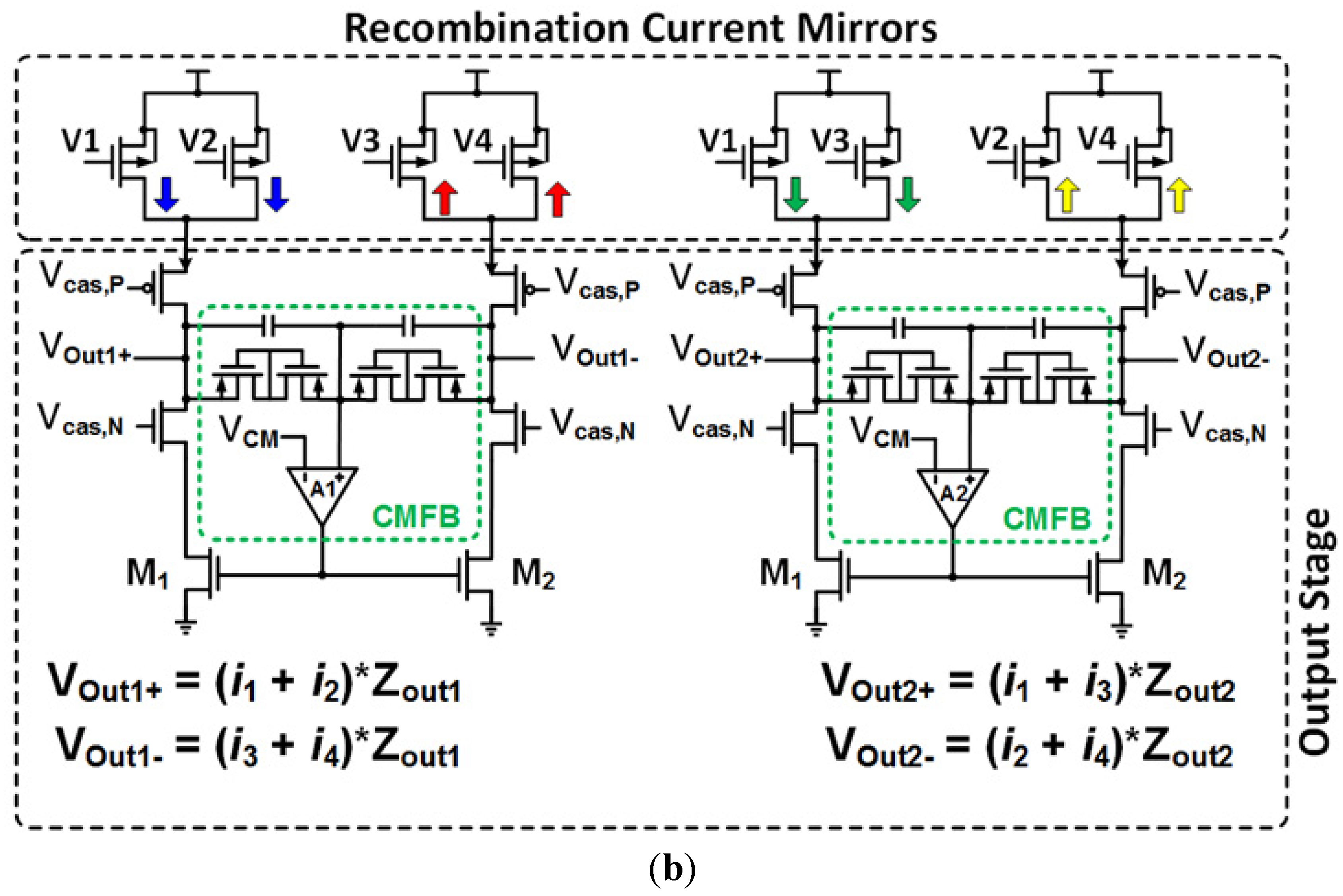
7. Integrated Systems Based on Neural Amplifiers
8. Discussion
9. Conclusions
| Author | Year of publication | Circuit topology/Architecture | Number of channels | Gain (dB) | NEF | Frequency range (Hz) | Noise (µVrms) | Supply voltage (V) | Supply current (µA) | CMRR (dB) | Power consumption per Ch. (Front-end only) or * entire chip (µW) | Area per Ch./Entire chip (mm2) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Harrison [67] | 2007 | Two-stage with added gm-C HP filter/Capacitive feedback | 100 | 60 | 10.47 | 300–5 k | 5.1 | N/A | 12.8 | N/A | 13500 * | N/A/5.9 × 4.7 |
| Chae [61] | 2008 | Two-stage/Capacitive feedback differential | 128 | 40 | 8 | 0.1–20 k | 4.9 | 1.65 | 40.0 | 90 | 6000* | N/A/8.8 × 7.2 |
| Aziz [60] | 2009 | Two-stage/Capacitive feedback + transconductance LNA | 256 | 48–68 | 4.6 | 0.01–5 k | 7 | 3 | 5.0 | N/A | 15 | 0.04/3.5 × 4.5 |
| Gosselin [68] | 2009 | Active feedback/Multiple stage | 16 | 70 | 4.9 | 100–9.2 k | 5.4 | 1.8 | 4.8 | 45 | 8.6 | 0.05/2.304 |
| Mollezadeh [41] | 2009 | Two stage/Capacitive feedback | 16 | 39.6 | 2.9* | 0.2–8.2 k | 1.94 | 3.3 | 8.0 | 70 | 26.4 | 0.107/N/A |
| Sodagar [64] | 2009 | Two stage/Capacitive feedback | 64 | 59.5 | 21.3 | 24m–9.1 k | 8 | 1.8 | 41.7 | N/A | 75 | 0.072/N/A |
| Liew [69] | 2009 | Two-stage/Capacitive feedback | 16 | 45.7–60.5 | 2.16 | 0.23–7.8 k | 4.43 | 1 | 3.8 | 58 | 3.77 | N/A |
| Miranda [70] | 2010 | N/A | 32 | N/A | N/A | 1–4.5 k | 5 | N/A | N/A | N/A | 142000 * | N/A/24000 |
| Perlin [71] | 2010 | Two-stage/Capacitive feedback | 64 | 60 | 11.42 | <10–9.1 k | 4.8 | 1.5 | 33.3 | N/A | 50 | 0.098/N/A |
| Shahrokhi [20] | 2010 | Fully differential/Telescopic | 128 | 33 | 5.55 | 10–5 k | 6.08 | 3 | 2.8 | N/A | 8.4 | 0.02/N/A |
| Greenwald [72] | 2011 | Two-stage with Common mode feedback/Differential | 16 | 40 | 4.61 | N/A–8.2 k | 3 | 3.3 | 12.5 | N/A | 41.25 | N/A/(3.4 × 2.5) |
| Aceros [73] | 2011 | Two stage/Capacitive feedback | 32 | 45.6 | 115.66 | 0.1–7.8 k | 8.5 | 3 | 14.5 | N/A | 43.8 | N/A |
| Al-Ashmouny [17] | 2011 | Two stage/Capacitive feedback | 16 | 52.4–79.8 | 2.9 | 0.1–17 k | 6.76 | 0.9 | 3.7 | 60 | 3.3 | 0.07/N/A |
| Jo-Yu [74] | 2011 | Two stage/Capacitive feedback | 4 | 51.9 | 2.79 | 2.38–12.9 k | 4.7 | –0.9/+0.9 | 2.9 | N/A | 5.22 | N/A |
| Lopez [75] | 2011 | Folded Cascode OTA multiple stages/Capacitive Feedback | 16 | 40–60 | 12.12 | 2.6–6.2 k | 2.9 | 3.3 | 70.0 | >63 | 231 | N/A/25.2 |
| Majidzadeh [11] | 2011 | Shared reference structure/Capacitive feedback | N/A | 39.4 | 3.35 | 10–7.2 k | 3.5 | 1.8 | 4.4 | 70.1 | 7.92 | 0.065/N/A |
| Rouse [76] | 2011 | N/A | 96 | variable | N/A | 5 k | N/A | 1.7–2.2 | 2.5 | >80 | 4.25–5.5 | N/A |
| Szuts [77] | 2011 | N/A | 64 | 65 | N/A | 10–4.5 k | 4 | 3 | N/A | N/A | N/A | N/A |
| Wattanapanitch [78] | 2011 | Three-stage—Source degenerate active loads/Capacitive feedback | 32 | 49–66 | 4.4–5.9 | 350–11.6 k | 5.4–11.2 | 1.8 | 3–11.11 | 62 | 5.4–20 | 0.03/N/A |
| Lo [79] | 2011 | Two stage/Capacitive feedback | 64 | 47–59 | 3 | 0.5–12 k | 3.8 | 1.2 | 5.0 | N/A | 6 | N/A/(3 × 4) |
| Zoladz [80] | 2011 | Two stage—folded cascode/Capacitive feedback | 64 | 60 | 21.28 | 0.1–12 k | 3.7 | 1.65 | 15.2 | 48 | 25 | N/A/(5 × 5) |
| Yin [81] | 2012 | Two-stage/Capacitive feedback | 100 | 46 | 3.3 | 0.1–7.8 k | 2.83 | 3 | 20 | 60 | 60 | N/A/(5.2 × 4.9) |
| Gao [82] | 2012 | Fully differential/Capacitive feedback, with switch-cap filtering | 96 | 40–56 | 6.62 | 1–10 k | 2.2 | 1.2 | 56.7 | N/A | 68 | 0.26/(5 × 5) |
| Dong [83] | 2013 | Two-stage/Capacitive Feedback—fully differential | 100 | 52 | 1.57 | 1–10 k | 3.2 | 0.45 | 162.2 | 73 | 73 | N/A/25 |
| Johnson [34] | 2013 | Orthogonal Current-Reuse/Capacitive feedback | 4 | 40 | 1.64 | 19.9 k BW | 3.7 | 1.5 | 2.6 | 78 | 3.9 | 0.125/N/A |
| Kmon [56] | 2013 | Two stage—folded cascode/Capacitive feedback | 8 | 48/60 | 4.6 | 0.3–9 k | 5 | 1.8 | 6.1 | 48 | 11 | 0.065/N/A |
| Zou [55] | 2013 | Low Noise OTA/Capacitive feedback multi-stage | 100 | – | 1.9 | 0.001–5.1 k | 4 | 1.8 | 6.4 | 60+ | 11.6 | N/A/28.2 |
| Yin, [84] | 2013 | Two-stage/Capacitive feedback | 100 | 46 | 3.3 | 0.1–7.8 k | 2.83 | 3 | 20 | 60 | 60 | N/A/(5.2 × 4.9) |
| Lopez [62] | 2014 | Two-stage/Capacitive feedback | 55/455 | 29.5/72 | 3.08 | 0.2–6 k | 3.2 | 1.8 | 3.9 | 60 | 7.02 | 0.19/N/A |
| Sepehrian [35] | 2014 | Orthogonal Current-Reuse/Capacitive feedback | 4 | 45.2–59.7 | 4.37 | 10.02 k BW | 3.28 | 1.8 | 2.27 | 76 | 4.1 | 0.035/N/A |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jochum, T.; Denison, T.; Wolf, P. Integrated circuit amplifiers for multi-electrode intracortical recording. J. Neural Eng. 2009, 6. [Google Scholar] [CrossRef]
- Shepherd, G.M. Neurobiology, 2nd ed.; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Majidzadeh, V. A Micropower Neural Recording Amplifier with Improved Noise Efficiency Factor. In Proceedings of the European Conference on Circuit Theory and Design, Antalya, Turkey, 23–27 August 2009; pp. 319–322.
- Ruiz-Amaya, J. A Review of Low-Noise Amplifiers for Neural Applications. In Proceedings of the 2nd Circuits and Systems for Medical and Environmental Applications Workshop (CASME’10), Merida, Mexico, 13–15 December 2010.
- Krasteva, V.; Papazov, S. Estimation of current density distribution under electrodes for external defibrillation. BioMed. Eng. OnLine 2002, 1. [Google Scholar] [CrossRef]
- Ackermann, D.M.; Bhadra, N.; Foldes, E.L.; Wang, X.F.; Kilgore, K.L. Effect of nerve cuff electrode geometry on onset response firing in high-frequency nerve conduction Block. IEEE Trans. Biomed. Circuits Syst. 2010, 18, 658–665. [Google Scholar]
- Ackermann, D.M.; Foldes, E.L.; Bhadra, N.; Kilgore, K.L. Electrode Design for High Frequency Block: Effect of Bipolar Separation on Block Thresholds and the Onset Response. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’09), Minneapolis, MN, USA, 3–6 September 2009; pp. 654–657.
- Agnew, W.F.; McCreery, D.B. Neural Prostheses: Fundamental Studies; Prentice Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Baker, R.J. CMOS: Circuit Design, Layout, and Simulation; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Steyaert, M.S.J.; Sansen, W.M.C. A micropower low-noise monolithic instrumentation amplifier for medical purposes. IEEE J. Solid State Circuits 1987, 22, 1163–1168. [Google Scholar] [CrossRef]
- Majidzadeh, V.; Schmid, A.; Leblebici, Y. Energy efficient low-noise neural recording amplifier with enhanced noise efficiency factor. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 262–271. [Google Scholar] [CrossRef] [PubMed]
- Harrison, R.R.; Charles, C. A low-power low-noise CMOS amplifier for neural recording applications. IEEE J. Solid Stare Circuits 2003, 38, 958–965. [Google Scholar] [CrossRef]
- British Standards Institution. Active Implantable Medical Devices. General Requirements For Safety, Marking and Information to Be Provided by the Manufacturer; British Adopted European Standard, B. EN45502–1:1998; BSI: London, UK, 1998. [Google Scholar]
- Seese, T.M.; Harasaki, H.; Saidel, G.M.; Davies, C.R. Characterization of tissue morphology, angiogenesis, and temperature in the adaptive response of muscle tissue to chronic heating. Lab. Investig. 1998, 78, 1553. [Google Scholar] [PubMed]
- IEEE. IEEE Standard for Safety Levels With Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 3 kHz to 300 GHz; IEEE Std C95.1–2005 (Revision of IEEE Std C95.1–1991); IEEE: Piscataway, NJ, USA, 2006; pp. 1–238. [Google Scholar]
- Silay, K.M.; Dehollain, C.; Declercq, M. Numerical Analysis of Temperature Elevation in the Head Due to Power Dissipation in a Cortical Implant. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’08), Vancouver, BC, USA, 20–25 August 2008; pp. 951–956.
- Al-Ashmouny, K.; Sun-Il, C.; Euisik, Y. A 4 mW/Ch Analog Front-End Module with Moderate Inversion and Power-Scalable Sampling Operation for 3-D Neural Microsystems. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS'11), San Diego, CA, USA, 10–12 November 2011; pp. 1–4.
- Olsson, R.H.; Wise, K.D. A three-dimensional neural recording microsystem with implantable data compression circuitry. IEEE J. Solid State Circuits 2005, 40, 2796–2804. [Google Scholar] [CrossRef]
- Urs, F. An 11k-Electrode 126-Channel High-Density Microelectrode Electrode to Interact with Electrogenic Cells. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC’07), San Francisco, CA, USA, 11–15 February 2007; pp. 158–593.
- Shahrokhi, F.; Abdelhalim, K.; Serletis, D.; Carlen, P.L.; Genov, R. The 128-channel fully differential digital integrated neural recording and stimulation interface. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 149–161. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Holleman, J.; Otis, B.P. Design of ultra-low power biopotential amplifiers for biosignal acquisition applications. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 344–355. [Google Scholar] [CrossRef] [PubMed]
- Saberhosseini, S.S.; Zabihian, A.; Sodagar, A.M. Low-Noise OTA for Neural Amplifying Applications. In Proceedings of the 8th International Caribbean Conference on Devices, Circuits and Systems (ICCDCS’12), Playa del Carmen, Mexico, 14–17 March 2012; pp. 1–4.
- Wattanapanitch, W.; Fee, M.; Sarpeshkar, R. An energy-efficient micropower neural recording amplifier. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 136–147. [Google Scholar] [CrossRef] [PubMed]
- Chae, M.; Kim, J.; Liu, W. Fully-differential self-biased bio-potential amplifier. Electron. Lett. 2008, 44, 1390–1391. [Google Scholar] [CrossRef]
- Gosselin, B. Recent advances in neural recording microsystems. Sensors 2011, 11, 4572. [Google Scholar] [PubMed]
- Qinwen, F.; Huijsing, J.H.; Makinwa, K.A. A 21 nV/ Hz−1/2 Chopper-Stabilized Multipath Current-Feedback Instrumentation Amplifier with 2 mV Offset. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC’10), San Francisco, CA, USA, 7–11 February 2010; pp. 80–81.
- Wu, R.; Makinwa, K.A.A.; Huijsing, J.H. A chopper current-feedback instrumentation amplifier with a 1 mHz 1/f noise corner and an AC-coupled ripple reduction loop. IEEE J. Solid State Circuits 2009, 44, 3232–3243. [Google Scholar] [CrossRef]
- Wei, T.; Chenxi, H.; Dongsoo, K.; Martini, B.; Culurciello, E. 4-Channel Asynchronous Bio-Potential Recording System. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; pp. 953–956.
- Wu, R.; Huijsing, J.H.; Makinwa, K.A.A. A current-feedback instrumentation amplifier with a gain error reduction loop and 0.06% untrimmed gain error. IEEE J. Solid State Circuits 2011, 46, 2794–2806. [Google Scholar] [CrossRef]
- Belloni, M.; Bonizzoni, E.; Fornasari, A.; Maloberti, F. A Micropower chopper-CDS operational amplifier. IEEE J. Solid Stare Circuits 2010, 45, 2521–2529. [Google Scholar] [CrossRef]
- Kusuda, Y. A 5.9 nV/Hz−1/2 Chopper Operational Amplifier with 0.78 mV Maximum Offset and 28.3 nV/°C Offset Drift. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC’11), San Francisco, CA, USA, 20–24 February 2011; pp. 242–244.
- Burt, R.; Zhang, J. A micropower chopper-stabilized operational amplifier using a SC notch filter with synchronous integration inside the continuous-time signal path. IEEE J. Solid Stare Circuits 2006, 41, 2729–2736. [Google Scholar] [CrossRef]
- Qinwen, F.; Huijsing, J.; Makinwa, K. A Capacitively Coupled Chopper Instrumentation Amplifier with a +/−30 V Common-Mode Range, 160 dB CMRR and 5 mV Offset. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC’12), San Francisco, CA, USA, 19–23 February 2012; pp. 374–376.
- Johnson, B.; Molnar, A. An orthogonal current-reuse amplifier for multi-channel sensing. IEEE J. Solid Stare Circuits 2013, 48, 1487–1496. [Google Scholar] [CrossRef]
- Sepehrian, H.; Mirbozorgi, A.; Gosselin, B. A Low-Power Current-Reuse Analog Front-End for Multi-Channel Neural Signal Recording. In Proceedings of the 12th IEEE International NEWCAS conference (NEWCAS’14), Trois-Rivieres, Quebec, Canada, 22–25 June 2014.
- Liu, L.; Zou, X.; Goh, W.L.; Je, M. Comparative Study and Analysis of Noise Reduction Techniques for Front-End Amplifiers. In Proceedings of the 13th International Symposium on Integrated Circuits (ISIC’11), Singapore, Singapore, 12–14 December 2011; pp. 555–558.
- Baru Fassio, M.D. Implantable Signal Amplifying Circuit for Electroneurographic Recording. U.S. Patent 6996435, 2006. [Google Scholar]
- Rieger, R.; Schuettler, M.; Pal, D.; Clarke, C.; Langlois, P.; Taylor, J.; Donaldson, N. Very low-noise ENG amplifier system using CMOS technology. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 427–437. [Google Scholar] [CrossRef] [PubMed]
- Holleman, J.; Otis, B. A Sub-Microwatt Low-Noise Amplifier for Neural Recording. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’07), Lyon, France, 22–26 August 2007; p. 3930.
- Demosthenous, A.; Pachnis, I.; Jiang, D.; Donaldson, N. An integrated amplifier with passive neutralization of myoelectric interference from neural recording tripoles. IEEE Sens. J. 2013, 13, 3236–3248. [Google Scholar] [CrossRef]
- Mollazadeh, M.; Murari, K.; Cauwenberghs, G.; Thakor, N.V. Wireless micropower instrumentation for multimodal acquisition of electrical and chemical neural activity. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 388–397. [Google Scholar] [CrossRef] [PubMed]
- Kazerouni, I.A.; Dehrizi, H.G.; Isfahani, S.M.M.; Zhuo, Z.; Baghaei-Nejad, M.; Li-Rong, Z. A 77 nW Bioamplifier with a Tunable Bandwidth for Neural Recording Systems. In Proceedings of the IEEE Asia Pacific Conference on Circuits and Systems (APCCAS’10), Kuala Lumpur, Malaysia, 6–9 December 2010; pp. 36–39.
- Kim, J.; Chae, M.S.; Liu, W. A 220 nW Neural Amplifier for Multi-Channel Neural Recording Systems. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS’09), Taipei, Taiwan, 24–27 May 2009; pp. 1257–1260.
- Gosselin, B.; Sawan, M.; Chapman, C.A. A low-power integrated bioamplifier with active low-frequency suppression. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Muller, R.; Gambini, S.; Rabaey, J.M. A 0.013 mm(2), 5 mu W, DC-coupled neural signal acquisition IC with 0.5 v supply. IEEE J. Solid Stare Circuits 2012, 47, 232–243. [Google Scholar] [CrossRef]
- Wei, Z.; Li, H.; Youguang, Z. A Low-Noise Integrated Bioamplifier with Active DC Offset Suppression. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS’09), Beijing, China, 26–28 November 2009; pp. 5–8.
- Castro, P.; Silveira, F. High CMRR Power Efficient Neural Recording Amplifier Architecture. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS’11), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1700–1703.
- Chung-Yu, W.; Wei-Ming, C.; Liang-Ting, K. A CMOS power-efficient low-noise current-mode front-end amplifier for neural signal recording. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, G.; Gozzini, F.; Molari, A.; Sampietro, M. Transimpedance amplifier for high sensitivity current measurements on nanodevices. IEEE J. Solid State Circuits 2009, 44, 1609–1616. [Google Scholar] [CrossRef]
- Rezaee-Dehsorkh, H.; Ravanshad, N.; Lotfi, R.; Mafinezhad, K. A Linear Tunable Amplifier for Implantable Neural Recording Applications. In Proceedings of the IEEE 54th International Midwest Symposium on Circuits and Systems (MWSCAS'11), Seoul, South Korea, 7–10 August 2011; pp. 1–4.
- Zou, X.D.; Xu, X.Y.; Yao, L.B.; Lian, Y. A 1-V 450-nW fully integrated programmable biomedical sensor interface chip. IEEE J. Solid Stare Circuits 2009, 44, 1067–1077. [Google Scholar] [CrossRef]
- Chaturvedi, V.; Amrutur, B. A Low-Noise Low-Power Noise-Adaptive Neural Amplifier in 0.13 um CMOS Technology. In Proceedings of the 24th International Conference on VLSI Design (VLSI Design’11), Chennai, India, 2–7 January 2011; pp. 328–333.
- Yao, K.-W. Design of A Neural Recording Amplifier with Tunable Pseudo Resistors. In Proceedings of the IEEE International SOC Conference, Taipei, Taiwan, 26–28 September 2011; pp. 376–379.
- Yin, M.; Ghovanloo, M. A Low-Noise Preamplifier with Adjustable Gain and Bandwidth for Biopotential Recording Applications. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS’07), New Orleans, LA, USA, 27–30 May 2007; pp. 321–324.
- Zou, X.; Liu, L.; Cheong, J.H.; Yao, L.; Li, P.; Cheng, M.-Y.; Goh, W.L.; Rajkumar, R.; Dawe, G.S.; Cheng, K.-W.; et al. A 100-channel 1-mW implantable neural recording IC. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2584–2596. [Google Scholar] [CrossRef]
- Kmon, P.; Grybos, P. Energy efficient low-noise multichannel neural amplifier in submicron CMOS process. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1764–1775. [Google Scholar] [CrossRef]
- Al-Ashmouny, K.; Sun-Il, C.; Euisik, Y. A 8.6 mW 3-bit Programmable Gain Amplifier for Multiplexed-Input Neural Recording Systems. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’11), Boston, MA, USA, 30 August–3 September 2011; pp. 2945–2948.
- Gosselin, B. Approaches for the Efficient Extraction and Processing of Neural Signals in Implantable Neural Interfacing Microsystems. In Proceedings of the 33th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’11), Boston, MA, USA, 30 August–3 September 2011; pp. 5855–5859.
- Park, H.; Kiani, M.; Hyung-Min, L.; Jeonghee, K.; Block, J.; Gosselin, B.; Ghovanloo, M. A wireless magnetoresistive sensing system for an intraoral tongue-computer interface. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 571–585. [Google Scholar] [CrossRef] [PubMed]
- Aziz, J.N.Y.; Abdelhalim, K.; Shulyzki, R.; Genov, R.; Bardakjian, B.L.; Derchansky, M.; Serletis, D.; Carlen, P.L. 256-channel neural recording and delta compression microsystem with 3D electrodes. IEEE J. Solid Stare Circuits 2009, 44, 995–1005. [Google Scholar] [CrossRef]
- Chae, M.; Liu, W.; Zhi, Y.; Chen, T.; Kim, J.; Sivaprakasam, M.; Yuce, M. A 128-Channel 6 mW Wireless Neural Recording IC with On-the-Fly Spike Sorting and UWB Tansmitter. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC’08), San Francisco, CA, USA, 3–7 February 2008; pp. 146–603.
- Lopez, C.M.; Andrei, A.; Mitra, S.; Welkenhuysen, M.; Eberle, W.; Bartic, C.; Puers, R.; Yazicioglu, R.F.; Gielen, G. An Implantable 455-Active-Electrode 52-Channel CMOS Neural Probe. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC’13), San Francisco, CA, USA, 17–21 February 2013; pp. 288–289.
- Gosselin, B.; Sawan, M. A low-power integrated neural interface with digital spike detection and extraction. Analog Integr. Circuits Signal Process. 2009, 64, 3–11. [Google Scholar] [CrossRef]
- Sodagar, A.M.; Perlin, G.E.; Ying, Y.; Najafi, K.; Wise, K.D. An implantable 64-channel wireless microsystem for single-unit neural recording. IEEE J. Solid State Circuits 2009, 44, 2591–2604. [Google Scholar] [CrossRef]
- Gosselin, B.; Sawan, M. Adaptive Detection of Action Potentials Using Ultra Low-Power CMOS Circuits. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS’08), Baltimore, MD, USA, 20–22 November 2008; pp. 209–212.
- Gosselin, B.; Sawan, M.; Kerherve, E. Linear-phase delay filters for ultra-low-power signal processing in neural recording implants. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 171–180. [Google Scholar] [CrossRef] [PubMed]
- Harrison, R.R.; Watkins, P.T.; Kier, R.J.; Lovejoy, R.O.; Black, D.J.; Greger, B.; Solzbacher, F. A low-power integrated circuit for a wireless 100-electrode neural recording system. IEEE J. Solid State Circuits 2007, 42, 123–133. [Google Scholar] [CrossRef]
- Gosselin, B.; Ayoub, A.E.; Roy, J.F.; Sawan, M.; Lepore, F.; Chaudhuri, A.; Guitton, D. A mixed-signal multichip neural recording interface with bandwidth reduction. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 129–141. [Google Scholar] [CrossRef] [PubMed]
- Liew, W.-S.; Zou, X.; Yao, L.; Lian, Y. A 1-V 60 mW 16-Channel Interface Chip for Implantable Neural Recording. In Proceedings of the IEEE Custom Integrated Circuits Conference (CICC’09), San Jose, CA, USA, 13–16 September 2009; pp. 507–510.
- Miranda, H.; Gilja, V.; Chestek, C.A.; Shenoy, K.V.; Meng, T.H. HermesD: A high-rate long-range wireless transmission system for simultaneous multichannel neural recording applications. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Perlin, G.E.; Wise, K.D. An ultra compact integrated front end for wireless neural recording microsystems. J. Microelectromechanical Syst. 2010, 19, 1409–1421. [Google Scholar] [CrossRef]
- Greenwald, E.; Mollazadeh, M.; Hu, C.; Tang, W.; Culurciello, E.; Thakor, N. A VLSI neural monitoring system with ultra-wideband telemetry for awake behaving subjects. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Aceros, J.; Ming, Y.; Borton, D.A.; Patterson, W.R.; Nurmikko, A.V. A 32-Channel Fully Implantable Wireless Neurosensor for Simultaneous Recording from Two Cortical Regions. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’11), Boston, MA, USA, 30 August–3 September 2011; pp. 2300–2306.
- Jo-Yu, W.; Kea-Tiong, T. A Band-Tunable, Multichannel Amplifier for Neural Recording with AP/LFP Separation and Dual-Threshold Adaptive AP Detector. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’11), Boston, MA, USA, 30 August–3 September 2011; pp. 1847–1850.
- Lopez, C.M.; Braeken, D.; Bartic, C.; Puers, R.; Gielen, G.; Eberle, W. A 16-Channel Low-Noise Programmable System for the Recording of Neural Signals. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS’11), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1451–1454.
- Rouse, A.G.; Stanslaski, S.R.; Cong, P.; Jensen, R.M.; Afshar, P.; Ullestad, D.; Gupta, R.; Molnar, G.F.; Moran, D.W.; Denison, T.J. A chronic generalized bi-directional brain-machine interface. J. Neural Eng. 2011, 8, 036018. [Google Scholar] [CrossRef] [PubMed]
- Szuts, T.A.; Fadeyev, V.; Kachiguine, S.; Sher, A.; Grivich, M.V.; Agrochao, M.; Hottowy, P.; Dabrowski, W.; Lubenov, E.V.; Siapas, A.G.; et al. A wireless multi-channel neural amplifier for freely moving animals. Nat. Neurosci. 2011, 14, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Wattanapanitch, W.; Sarpeshkar, R. A low-power 32-channel digitally programmable neural recording integrated circuit. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 592–602. [Google Scholar] [CrossRef] [PubMed]
- Lo, Y.-K.; Liu, W.; Chen, K.; Tsai, M.-H.; Hsueh, F.-L. A 64-Channel Neuron Recording System. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC'11), Boston, MA, USA, 30 August–3 September 2011; pp. 2862–2865.
- Zoladz, M.; Kmon, P.; Grybos, P.; Szczygiel, R.; Kleczek, R.; Otfinowski, P.; Rauza, J. Design and Measurements of Low Power Multichannel Chip for Recording and Stimulation of Neural Activity. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’12), San Diego, CA, USA, 28 August–1 September 2012; pp. 4470–4474.
- Ming, Y.; Borton, D.A.; Aceros, J.; Patterson, W.R.; Nurmikko, A.V. A 100-Channel Hermetically Sealed Implantable Device for Wireless Neurosensing Applications. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS’12), Seoul, Korea, 20–23 May 2012; pp. 2629–2632.
- Gao, H.; Walker, R.M.; Nuyujukian, P.; Makinwa, K.A.A.; Shenoy, K.V.; Murmann, B.; Meng, T.H. HermesE: A 96-channel full data rate direct neural interface in 0.13 µm CMOS. IEEE J. Solid Stare Circuits 2012, 47, 1043–1055. [Google Scholar] [CrossRef]
- Dong, H.; Yuanjin, Z.; Rajkumar, R.; Dawe, G.; Minkyu, J. A 0.45 V 100-Channel Neural-Recording IC with Sub-mW/Channel Consumption in 0.18 mm CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC’13), San Francisco, CA, USA, 17–21 February 2013; pp. 290–291.
- Yin, M.; Borton, D.A.; Aceros, J.; Patterson, W.R.; Nurmikko, A.V. A 100-channel hermetically sealed implantable device for chronic wireless neurosensing applications. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 115–128. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bharucha, E.; Sepehrian, H.; Gosselin, B. A Survey of Neural Front End Amplifiers and Their Requirements toward Practical Neural Interfaces. J. Low Power Electron. Appl. 2014, 4, 268-291. https://doi.org/10.3390/jlpea4040268
Bharucha E, Sepehrian H, Gosselin B. A Survey of Neural Front End Amplifiers and Their Requirements toward Practical Neural Interfaces. Journal of Low Power Electronics and Applications. 2014; 4(4):268-291. https://doi.org/10.3390/jlpea4040268
Chicago/Turabian StyleBharucha, Eric, Hassan Sepehrian, and Benoit Gosselin. 2014. "A Survey of Neural Front End Amplifiers and Their Requirements toward Practical Neural Interfaces" Journal of Low Power Electronics and Applications 4, no. 4: 268-291. https://doi.org/10.3390/jlpea4040268
APA StyleBharucha, E., Sepehrian, H., & Gosselin, B. (2014). A Survey of Neural Front End Amplifiers and Their Requirements toward Practical Neural Interfaces. Journal of Low Power Electronics and Applications, 4(4), 268-291. https://doi.org/10.3390/jlpea4040268





