Compact Modeling Solutions for Oxide-Based Resistive Switching Memories (OxRAM)
Abstract
:1. Introduction

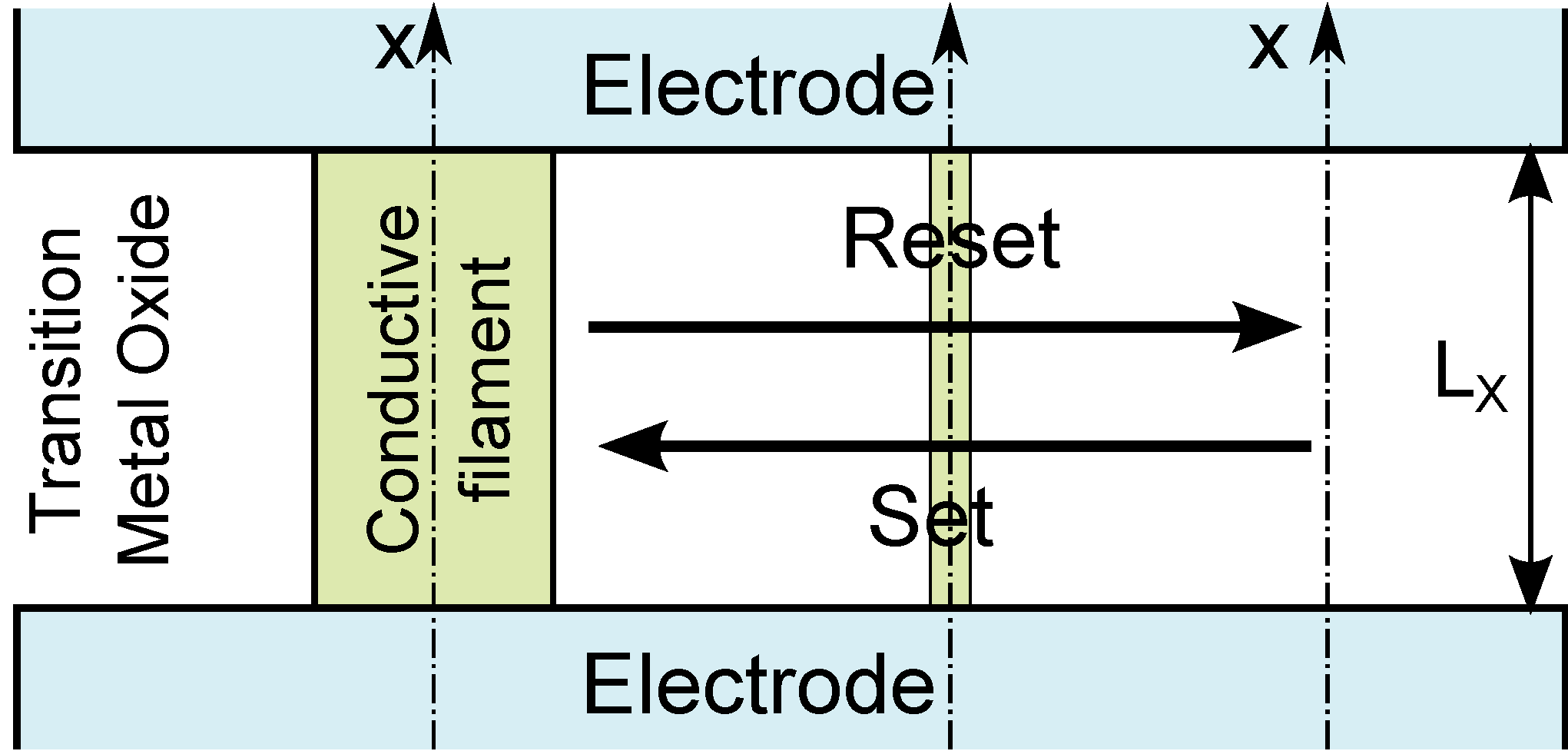
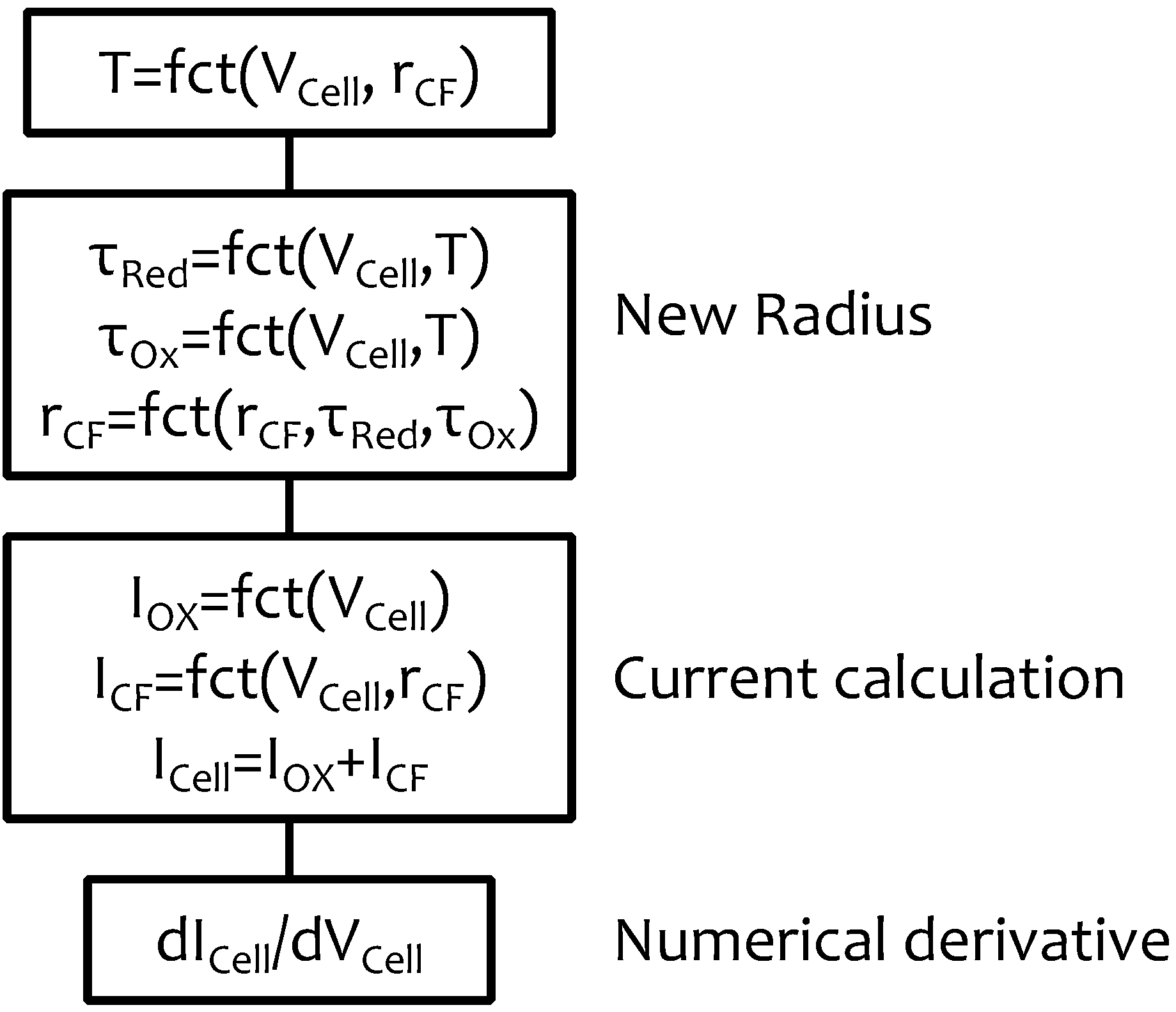
2. Compact Model for OxRAM Cells
3. Model Validation
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 2 | |||
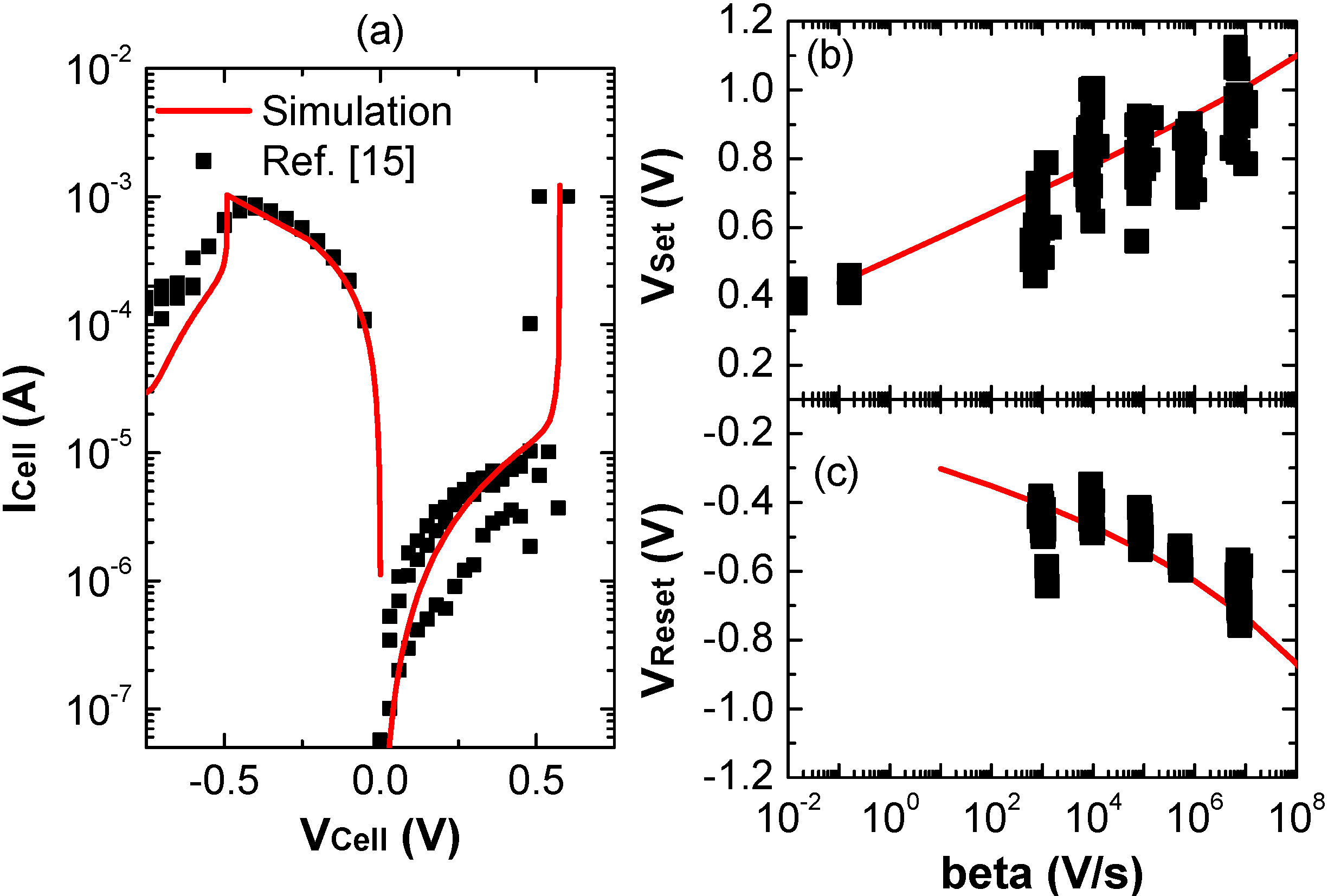
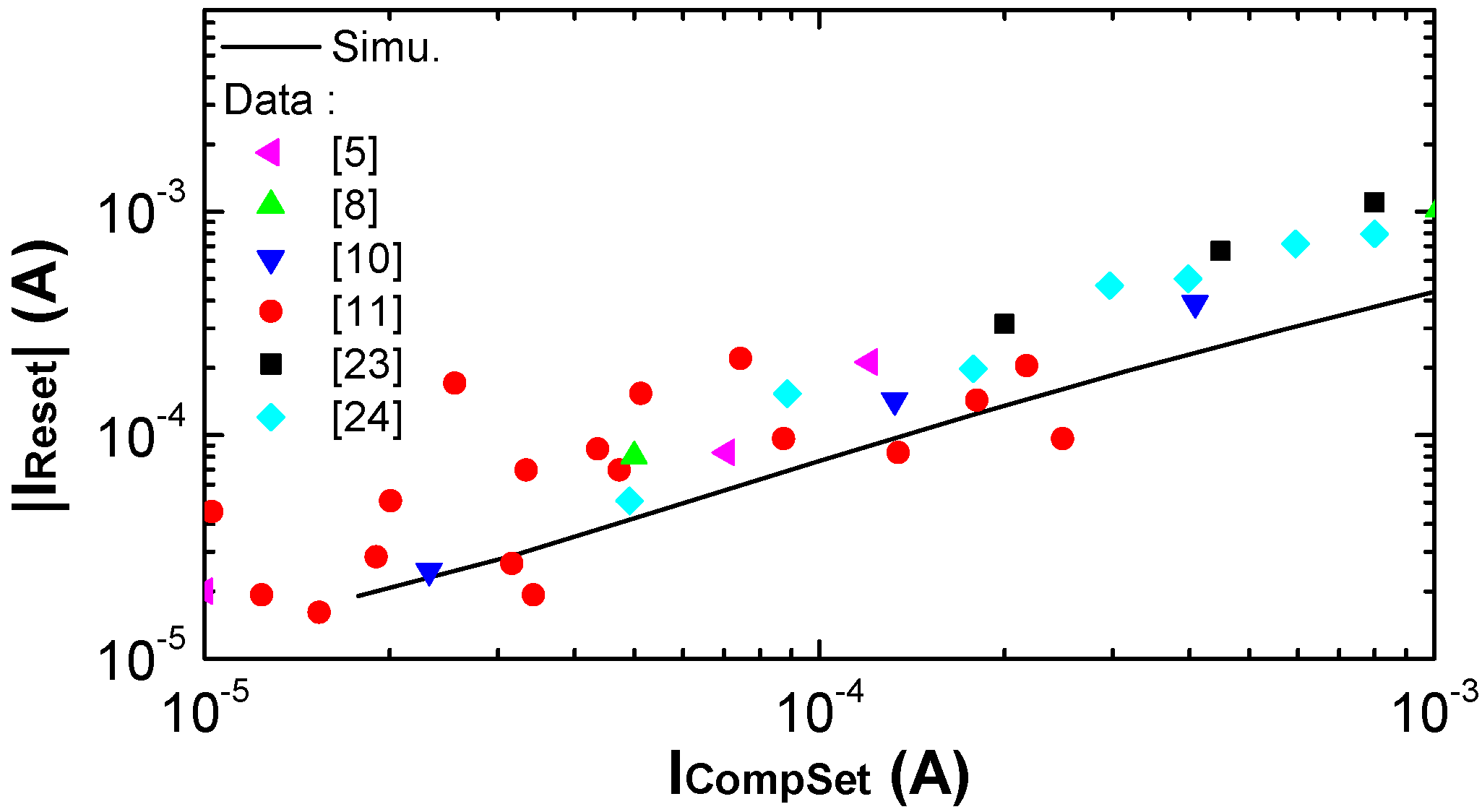
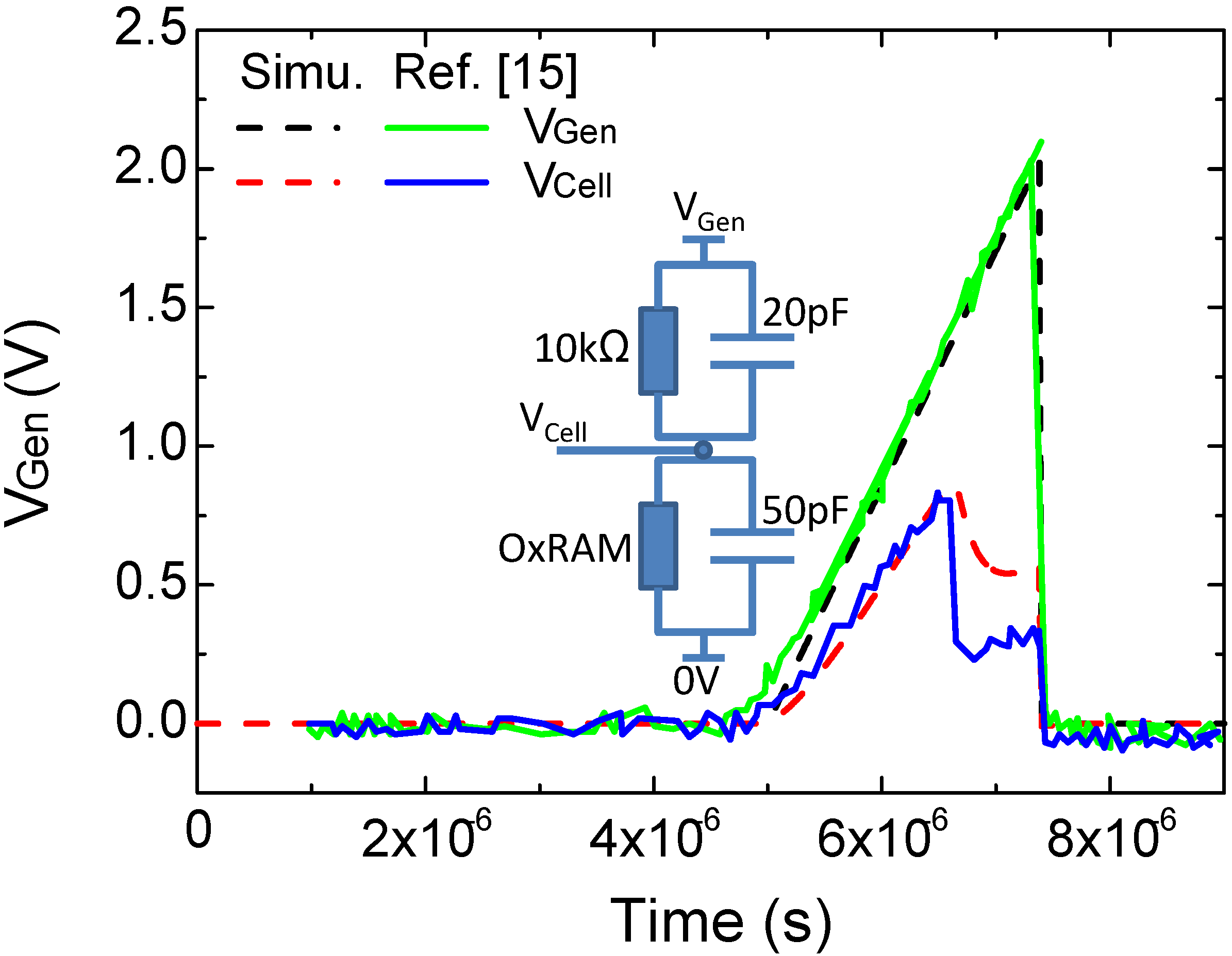
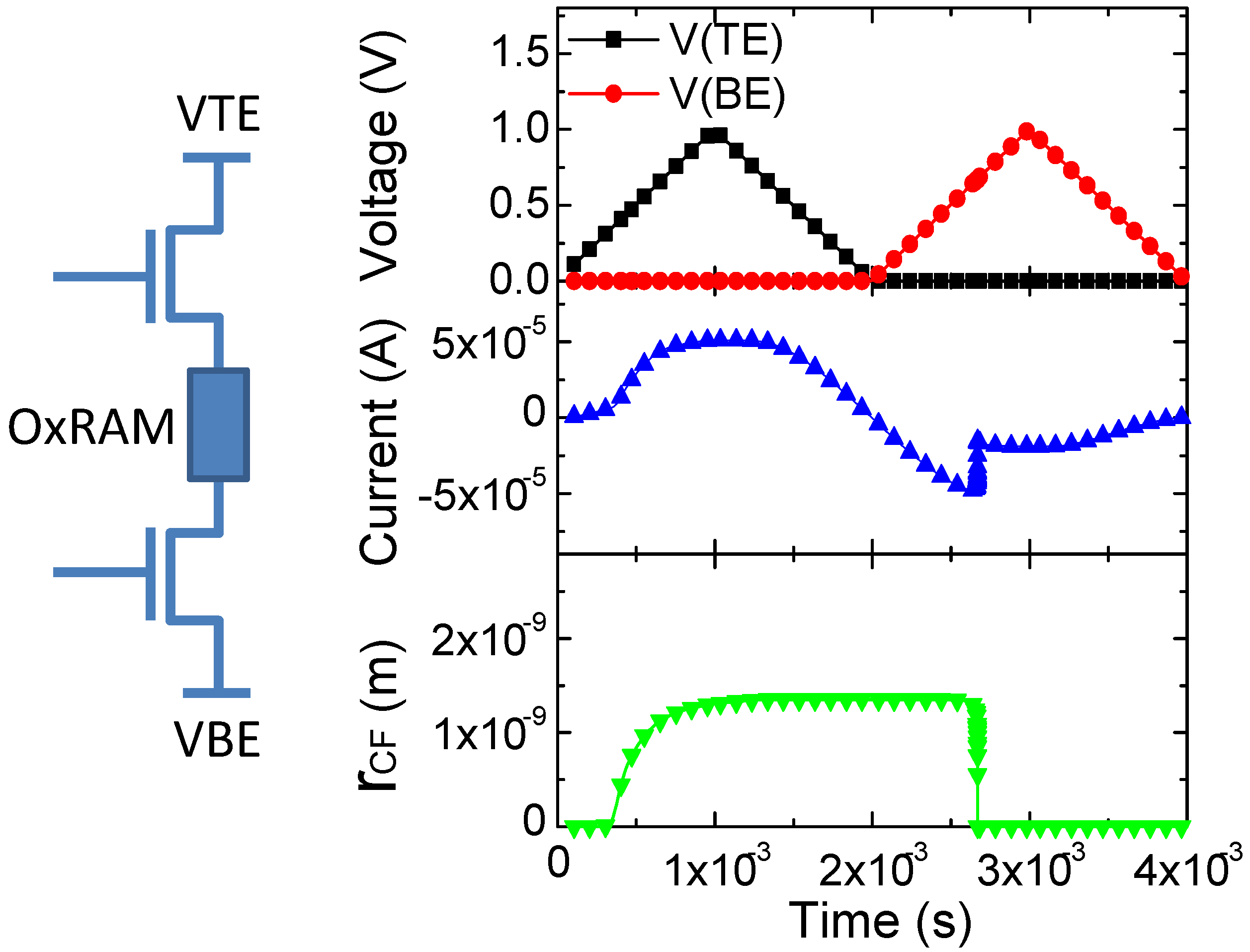
4. Model Application
4.1. OxRAM Reliability Evaluation versus OxRAM Variability [16]
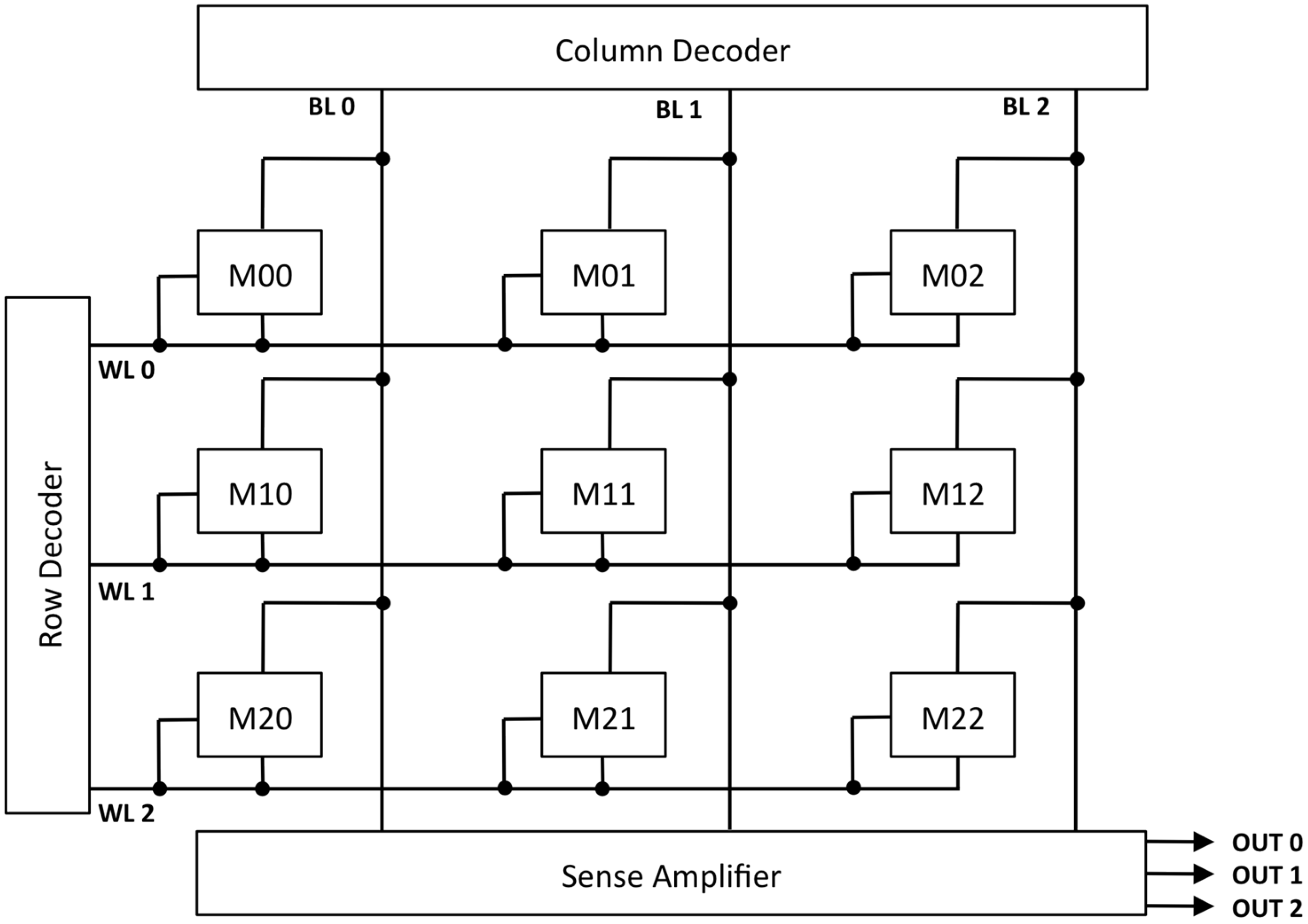
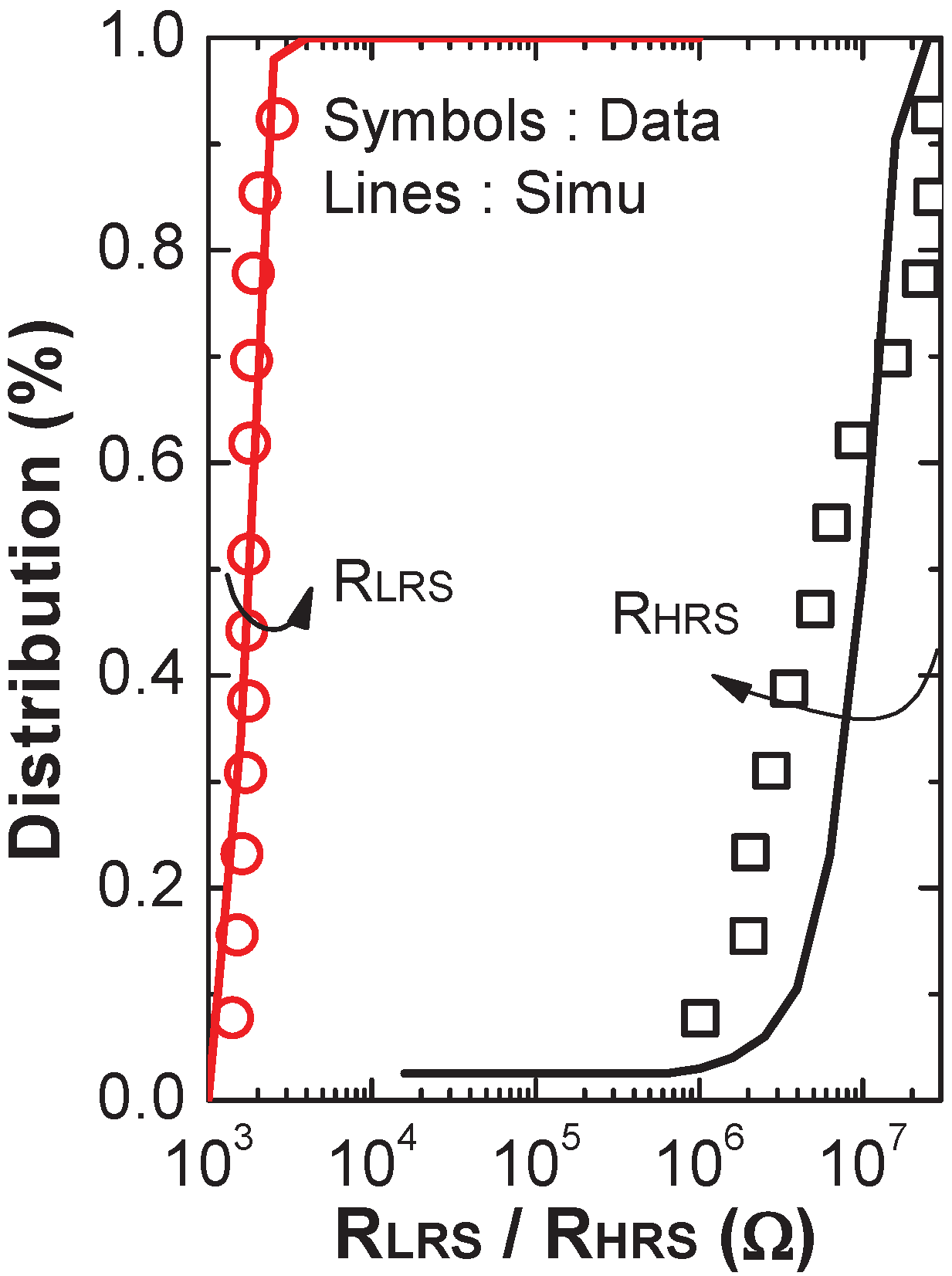
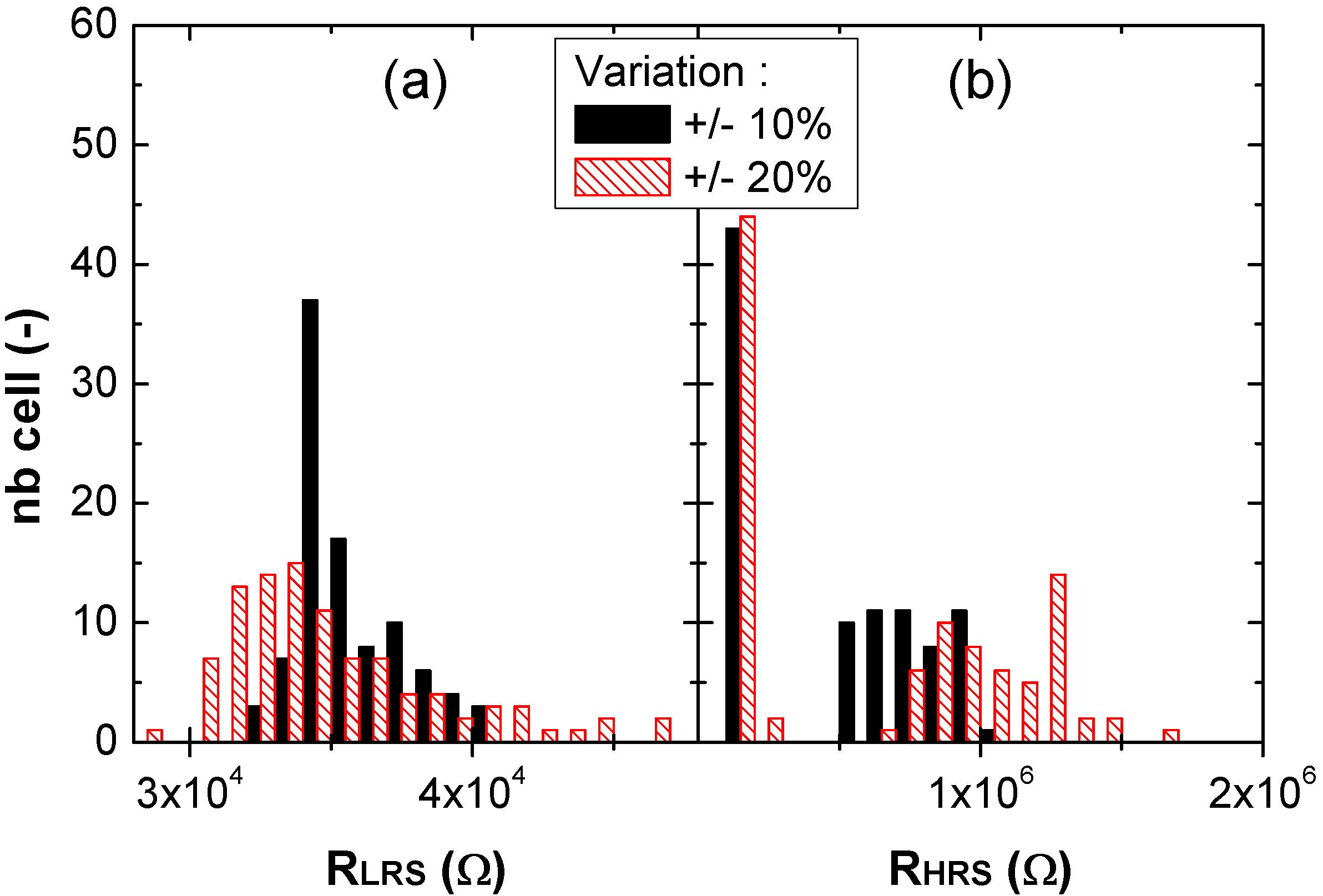
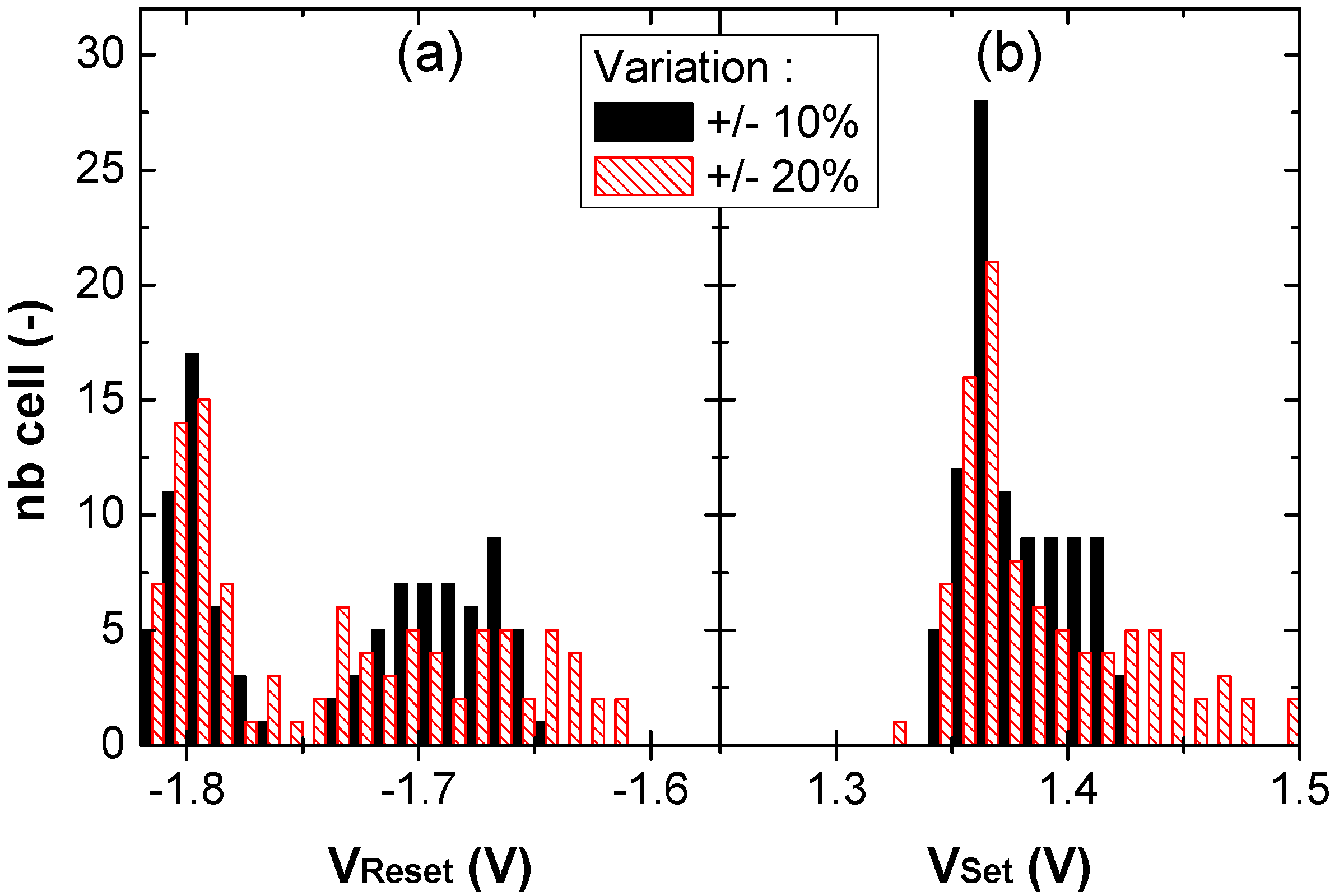
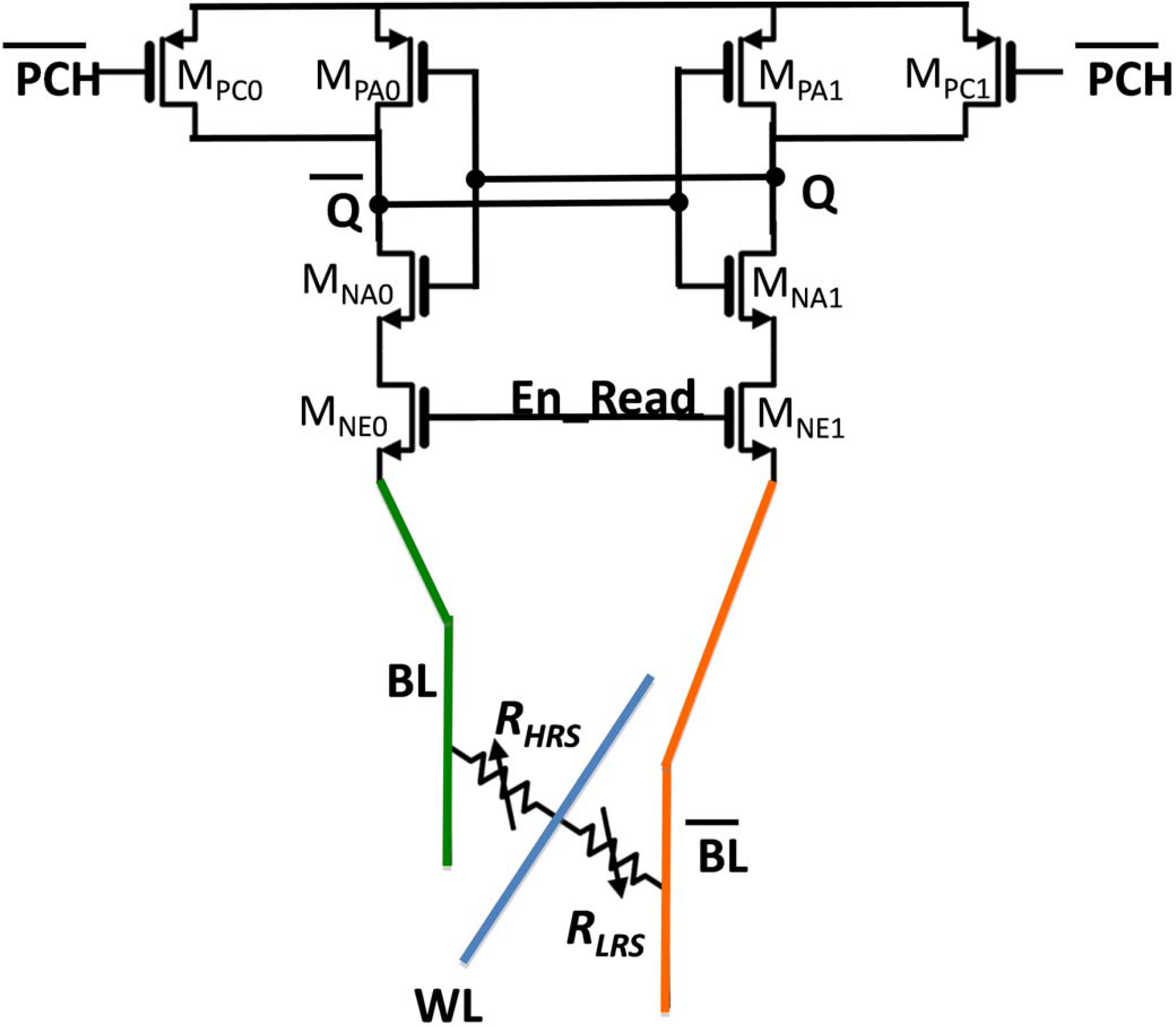
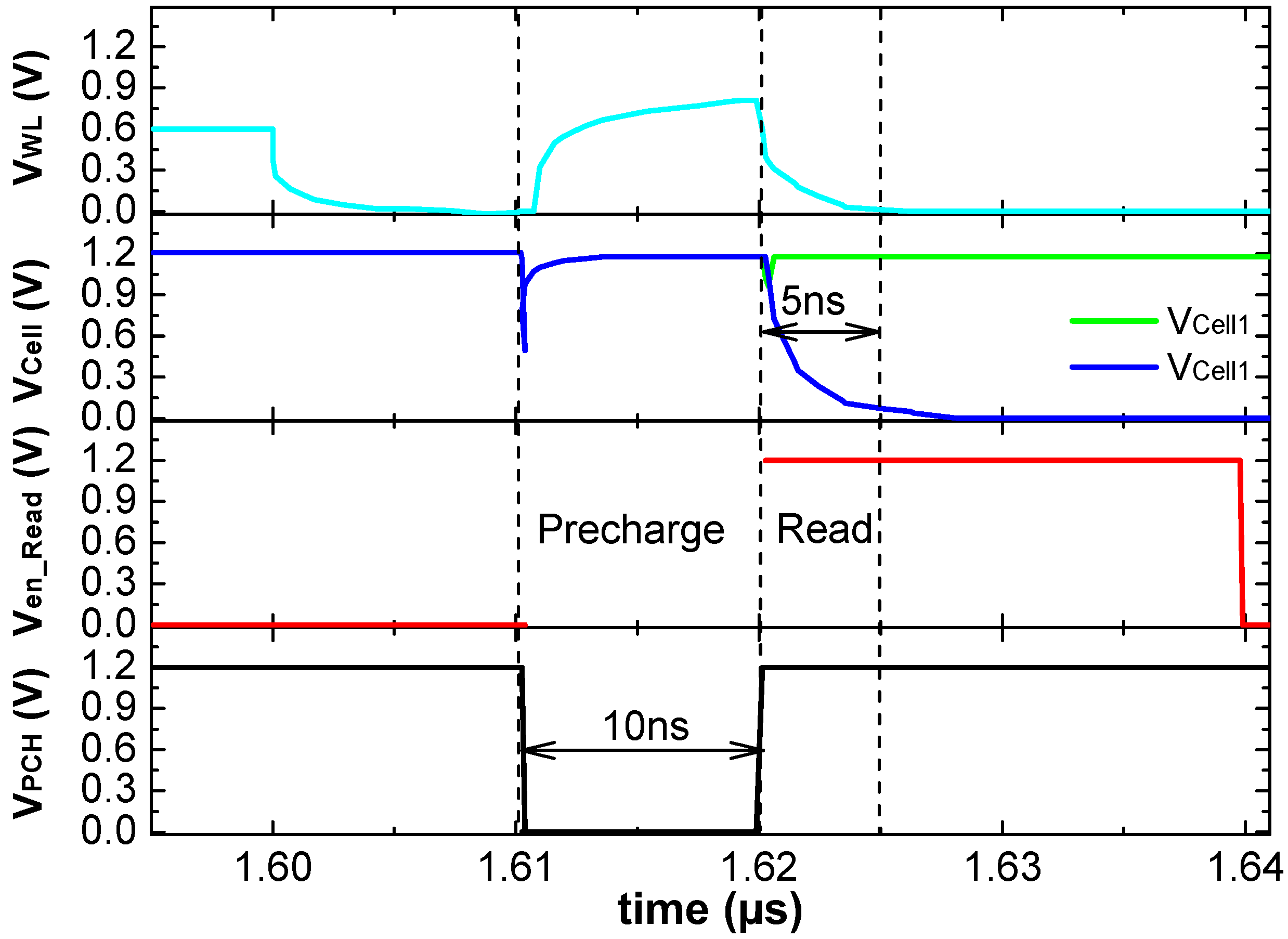
4.2. Diffrential Precharge Sense Amplifier for CRS Bitcell [26]
- 1st Phase: The sense amplifier is first connected to the bit-line of the selected word with SEN set to “1” and the circuit is pre-charged with PCH equals “0”;
- 2nd Phase: The data stored in the 2R cell can be evaluated to logic level at the output Q as PCH is changed to “1” and WL is pulled down to “0”.
5. Conclusions
Acknowledgements
Conflicts of Interest
References
- Hong, S. Memory Technology Trend and Future Challenges. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 6–8 December 2010; pp. 292–295.
- Govoreanu, B.; Kar, G.S.; Chen, Y.Y.; Paraschiv, V.; Kubicek, S.; Fantini, A.; Radu, I.P.; Goux, L.; Clima, S.; Degraeve, R.; et al. 10 × 10 nm2 Hf/HfOx Crossbar Resistive RAM with Excellent Performance, Reliability and Low-Energy Operation. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 729–732.
- Higuchi, K.; Iwasaki, T.O.; Takeuchi, K. Investigation of Verify-Programming Methods to Achieve 10 Million Cycles for 50 nm HfO2 ReRAM. In Proceedings of the 2012 4th IEEE International Memory Workshop, Milan, Italy, 20–23 May 2012; pp. 119–122.
- Kund, M.; Beitel, G.; Pinnow, C.U.; Rohr, T.; Schumann, J.; Symanczyk, R.; Ufert, K.D.; Muller, G. Conductive Bridging RAM (CBRAM): An Emerging Non-Volatile Memory Technology Scalable to Sub 20 nm. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5 December 2005; pp. 754–757.
- Lee, H.Y.; Chen, P.S.; Wu, T.Y.; Chen, Y.S.; Wang, C.C.; Tzeng, P.J.; Lin, C.H.; Chen, F.; Lien, C.H.; Tsai, M.J. Low Power and High Speed Bipolar Switching with a Thin Reactive Ti Buffer Layer in Robust HfO2 Based RRAM. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008; pp. 1–4.
- Baek, I.G.; Lee, M.S.J.; Seo, S.; Seo, D.H.; Suh, D.S.; Park, J.C.; Park, S.O.; Kim, H.S.; Yoo, I.K.; Chung, U.I.; et al. Highly Scalable Nonvolatile Resistive Memory Using Simple Binary Oxide Driven by Asymmetric Unipolar Voltage Pulses. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 13–15 December 2004; pp. 587–590.
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833–840. [Google Scholar] [CrossRef] [PubMed]
- Seo, S.; Lee, M.J.; Seo, D.H.; Jeoung, E.J.; Suh, D.S.; Joung, Y.S.; Yoo, I.K.; Hwang, I.R.; Kim, S.H.; Byun, I.S.; et al. Reproducible resistance switching in polycrystalline NiO films. Appl. Phys. Lett. 2004, 85, 5655–5657. [Google Scholar] [CrossRef]
- Kim, W.G.; Sung, M.G.; Kim, S.J.; Kim, J.Y.; Moon, J.W.; Yoon, S.J.; Kim, J.N.; Gyun, B.G.; Kim, T.W.; Kim, C.H.; et al. Dependence of the Switching Characteristics of Resistance Random Access Memory on the Type of Transition Metal Oxide. In Proceedings of the IEEE European Solid State Device Research Conference, Sevilla, Spain, 14–16 September 2010; pp. 400–403.
- Fang, T.N.; Kaza, S.; Haddad, S.; Chen, A.; Wu, Y.C.; Lan, Z.; Avanzino, S.; Liao, D.; Gopalan, C.; Choi, S.; et al. Erase Mechanism for Copper Oxide Resistive Switching Memory Cells with Nickel Electrode. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 11–13 December 2006; pp. 1–4.
- Nardi, F.; Larentis, S.; Balatti, S.; Gilmer, D.C.; Ielmini, D. Resistive switching by voltage-driven ion migration in bipolar RRAM—Part I: Experimental study. IEEE Trans. Electron Devices 2012, 59, 2461–2467. [Google Scholar] [CrossRef]
- Fang, Z.; Yu, H.Y.; Singh, N.; Lo, G.Q.; Kwong, D.L. HfOx/TiOx/HfOx/TiOx Multilayer-based sith excellent uniformity. IEEE Electron Device Lett. 2011, 32, 566–568. [Google Scholar] [CrossRef]
- Kim, W.; Park, S.I.; Zhang, Z.; Yang-liauw, Y.; Sekar, D.; Wong, H.P.; Wong, S.S. Forming-Free Nitrogen-Doped AlOX RRAM with Sub-μA Programming Current. In Proceedings of the 2011 Symposium on VLSI Technology (VLSIT), Honolulu, HI, USA, 14–16 June 2011; pp. 22–23.
- Gao, B.; Yu, S.; Xu, N.; Liu, L.F.; Sun, B.; Liu, X.Y.; Han, R.Q.; Kang, J.F.; Yu, B.; Wang, Y.Y. Oxide-Based RRAM Switching Mechanism: A New Ion-Transport-Recombination Model. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008; pp. 1–4.
- Bocquet, M.; Deleruyelle, D.; Muller, C.; Portal, J.M. Self-consistent physical modeling of set/reset operations in unipolar resistive-switching memories. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
- Aziza, H.; Bocquet, M.; Portal, J.M.; Muller, C. Evaluation of OxRAM Cell Variability Impact on Memory Performances through Electrical Simulations. In Proceedings of the 11th Annual Non-Volatile Memory Technology Symposium (NVMTS), Shanghai, China, 7–9 November 2011; pp. 1–5.
- Aziza, H.; Bocquet, M.; Portal, J.M.; Muller, C. Bipolar OxRRAM Memory Array Reliability Evaluation Based on Fault Injection. In Proceedings of the 2011 IEEE 6th International Design and Test Workshop (IDT), Beirut, Lebanon, 11–14 December 2011; pp. 78–81.
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 92–100. [Google Scholar]
- Akinaga, H.; Shima, H. Resistive Random Access Memory (ReRAM) based on metal oxides. Proc. IEEE 2010, 98, 2237–2251. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Lee, H.Y.; Yu, S.; Chen, Y.S.; Wu, Y.; Chen, P.S.; Lee, B.; Chen, F.T.; Tsai, M.J. Metal-oxide RRAM. Proc. IEEE 2012, 100, 1951–1970. [Google Scholar] [CrossRef]
- Cagli, C.; Buckley, J.; Jousseaume, V.; Cabout, T.; Salaun, A.; Grampeix, H.; Nodin, J.F.; Feldis, H.; Persico, A.; Cluzel, J.; et al. Experimental and Theoretical Study of Electrode Effects in HfO2 Based RRAM. In Proceedings of the 2011 International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 28.7.1–28.7.4.
- Nardi, F.; Ielmini, D.; Cagli, C.; Spiga, S.; Fanciulli, M.; Goux, L.; Wouters, D.J. Control of filament size and reduction of reset current below 10 μA in NiO resistance switching memories. Solid-State Electron. 2011, 58, 42–47. [Google Scholar] [CrossRef]
- Kinoshita, K.; Tsunoda, K.; Sato, Y.; Noshiro, H.; Yagaki, S.; Aoki, M.; Sugiyama, Y. Reduction in the reset current in a resistive random access memory consisting of NiOx brought about by reducing a parasitic capacitance. Appl. Phys. Lett. 2008, 93. [Google Scholar] [CrossRef]
- Tsunoda, K.; Kinoshita, K.; Noshiro, H.; Yamazaki, Y.; Iizuka, T.; Ito, Y.; Takahashi, A.; Okano, A.; Sato, Y.; Fukano, T.; et al. Low Power and High Speed Switching of Ti-Doped NiO ReRAM under the Unipolar Voltage Source of Less than 3V. In Proceedings of the IEEE International Electron Devices Meeting (IEDM 2007), Washington, DC, USA, 10–12 December 2007; pp. 767–770.
- Portal, J.M.; Bocquet, M.; Deleruyelle, D.; Muller, C. Non-volatile flip-flop based on unipolar ReRAM for power-down applications. J. Low Power Electron. 2012, 8, 1–10. [Google Scholar] [CrossRef]
- Aziza, H.; Makosiej, A.; Palma, G.; Portal, J.M.; Bocquet, M.; Thomas, O.; Clermidy, F.; Reyboz, M.; Onkaraiah, S.; Muller, C.; et al. Operation and stability analysis of bipolar OxRRAM-based non-volatile 8T2R SRAM as solution for information back-up. Solid-State Electron. 2013, 90, 99–106. [Google Scholar]
- Zhao, W.S.; Zhang, Y.; Klein, J.O.; Querlioz, D.; Chabi, D.; Ravelosona, D.; Chappert, C.; Portal, J.M.; Bocquet, M.; Aziza, H.; et al. Crossbar Architecture Based on 2R Complementary Resistive Switching Memory Cell. In Proceedings of the 2012 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Amsterdam, the Netherlands, 4–6 July 2012; pp. 85–92.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bocquet, M.; Aziza, H.; Zhao, W.; Zhang, Y.; Onkaraiah, S.; Muller, C.; Reyboz, M.; Deleruyelle, D.; Clermidy, F.; Portal, J.-M. Compact Modeling Solutions for Oxide-Based Resistive Switching Memories (OxRAM). J. Low Power Electron. Appl. 2014, 4, 1-14. https://doi.org/10.3390/jlpea4010001
Bocquet M, Aziza H, Zhao W, Zhang Y, Onkaraiah S, Muller C, Reyboz M, Deleruyelle D, Clermidy F, Portal J-M. Compact Modeling Solutions for Oxide-Based Resistive Switching Memories (OxRAM). Journal of Low Power Electronics and Applications. 2014; 4(1):1-14. https://doi.org/10.3390/jlpea4010001
Chicago/Turabian StyleBocquet, Marc, Hassen Aziza, Weisheng Zhao, Yue Zhang, Santhosh Onkaraiah, Christophe Muller, Marina Reyboz, Damien Deleruyelle, Fabien Clermidy, and Jean-Michel Portal. 2014. "Compact Modeling Solutions for Oxide-Based Resistive Switching Memories (OxRAM)" Journal of Low Power Electronics and Applications 4, no. 1: 1-14. https://doi.org/10.3390/jlpea4010001