Dynamics of a Neuromorphic Circuit Incorporating a Second-Order Locally Active Memristor and Its Parameter Estimation
Abstract
1. Introduction
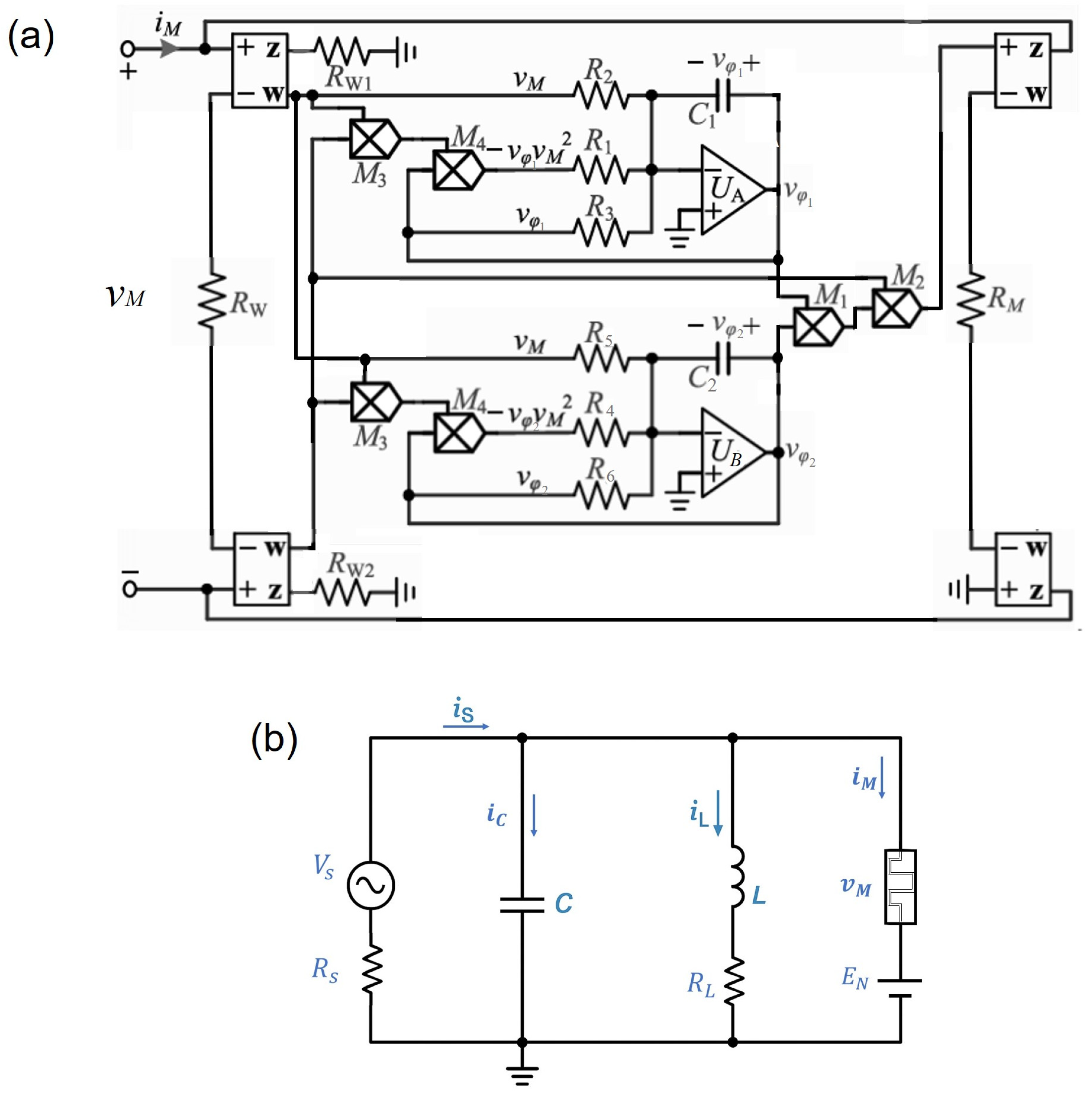
2. Circuit Modeling
2.1. Description of the Second-Order LAM
2.2. The Neuromorphic Circuit Using the Second-Order LAM
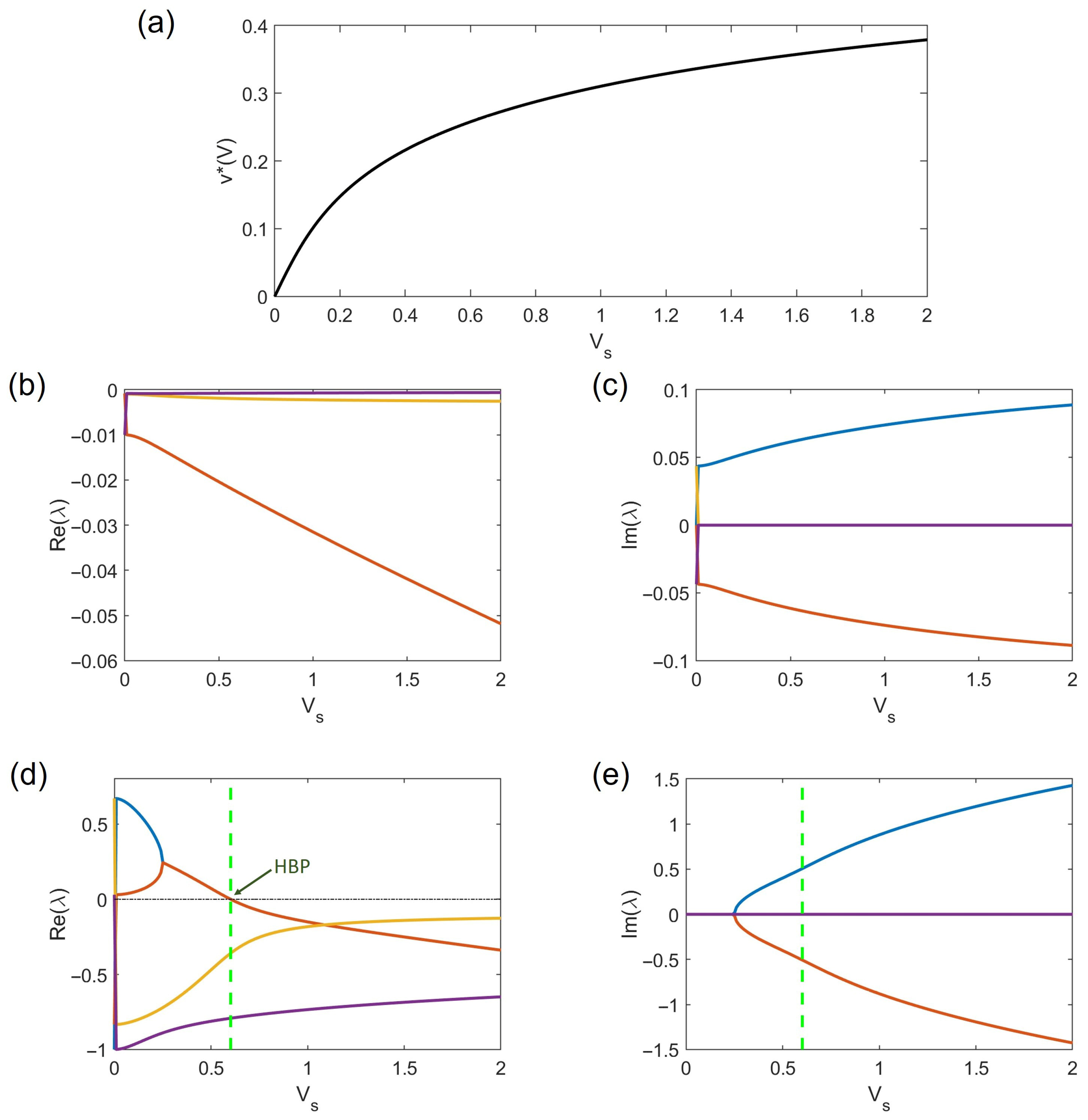
2.3. Equilibrium Analysis
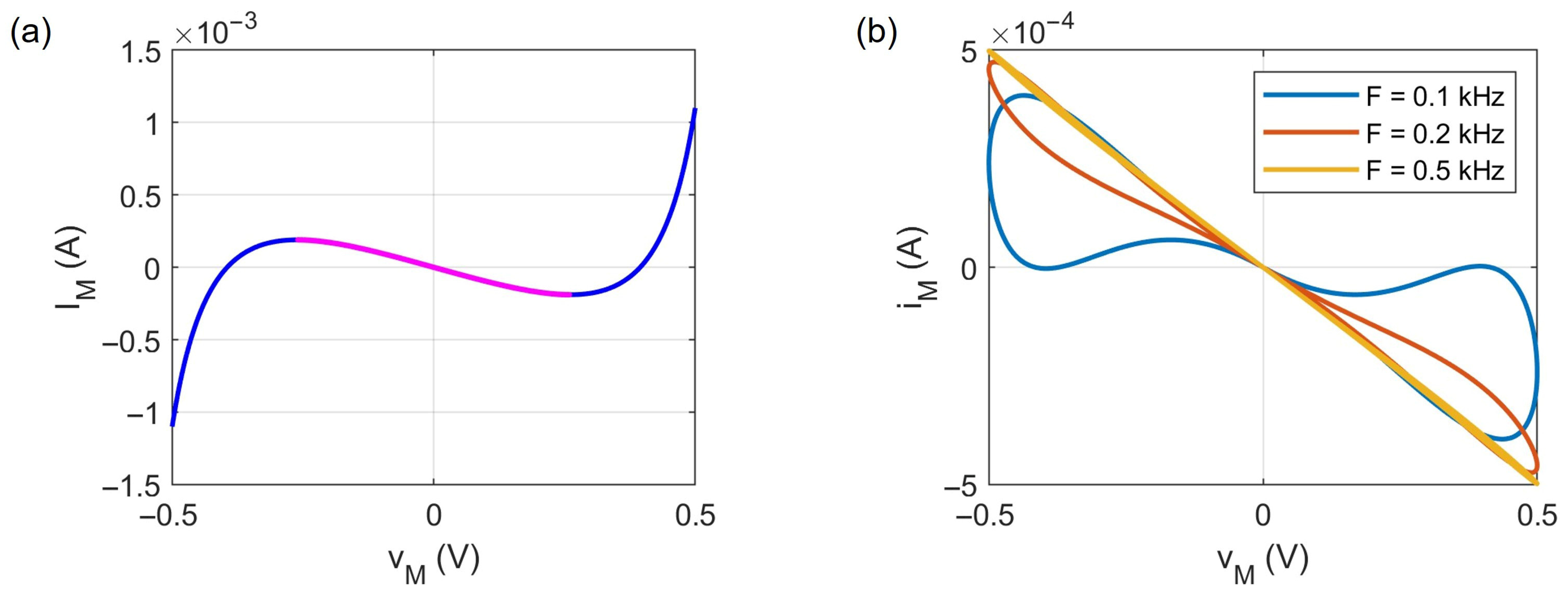
3. Dynamical Behaviors
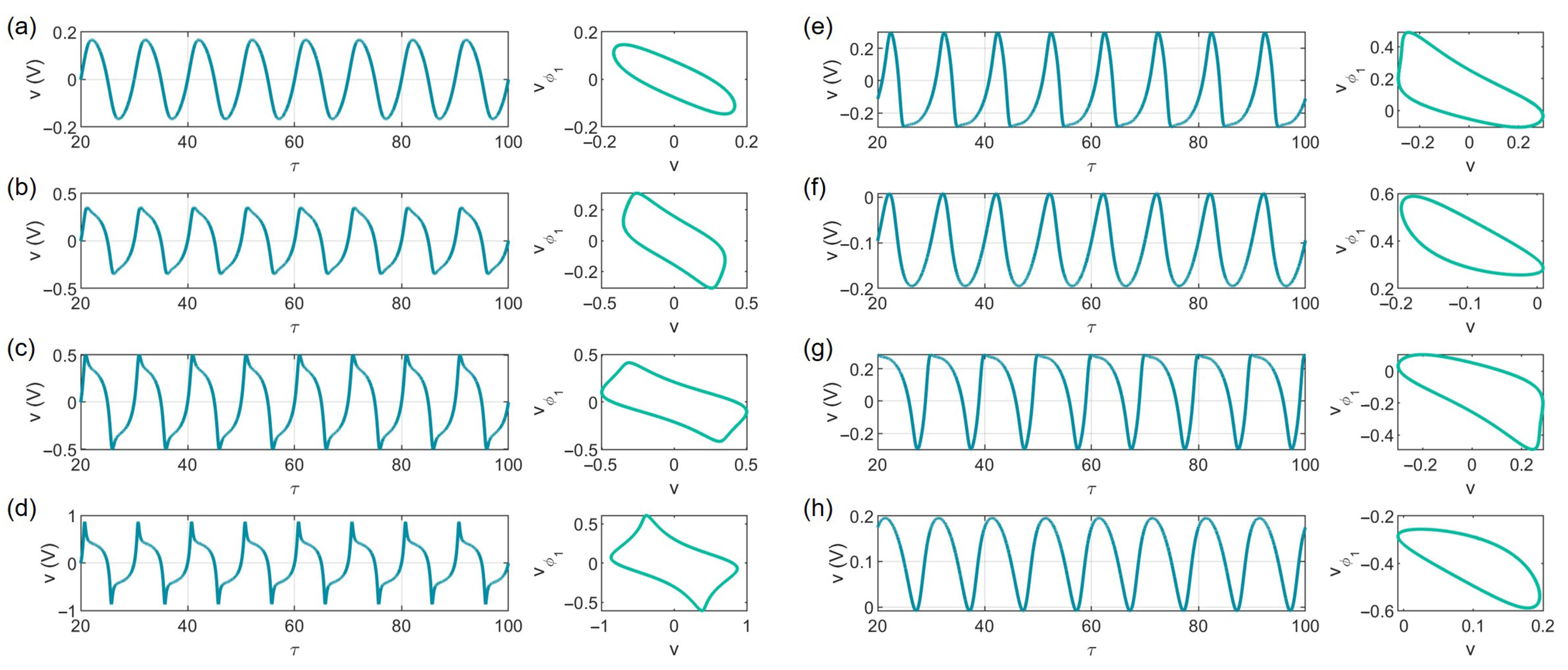
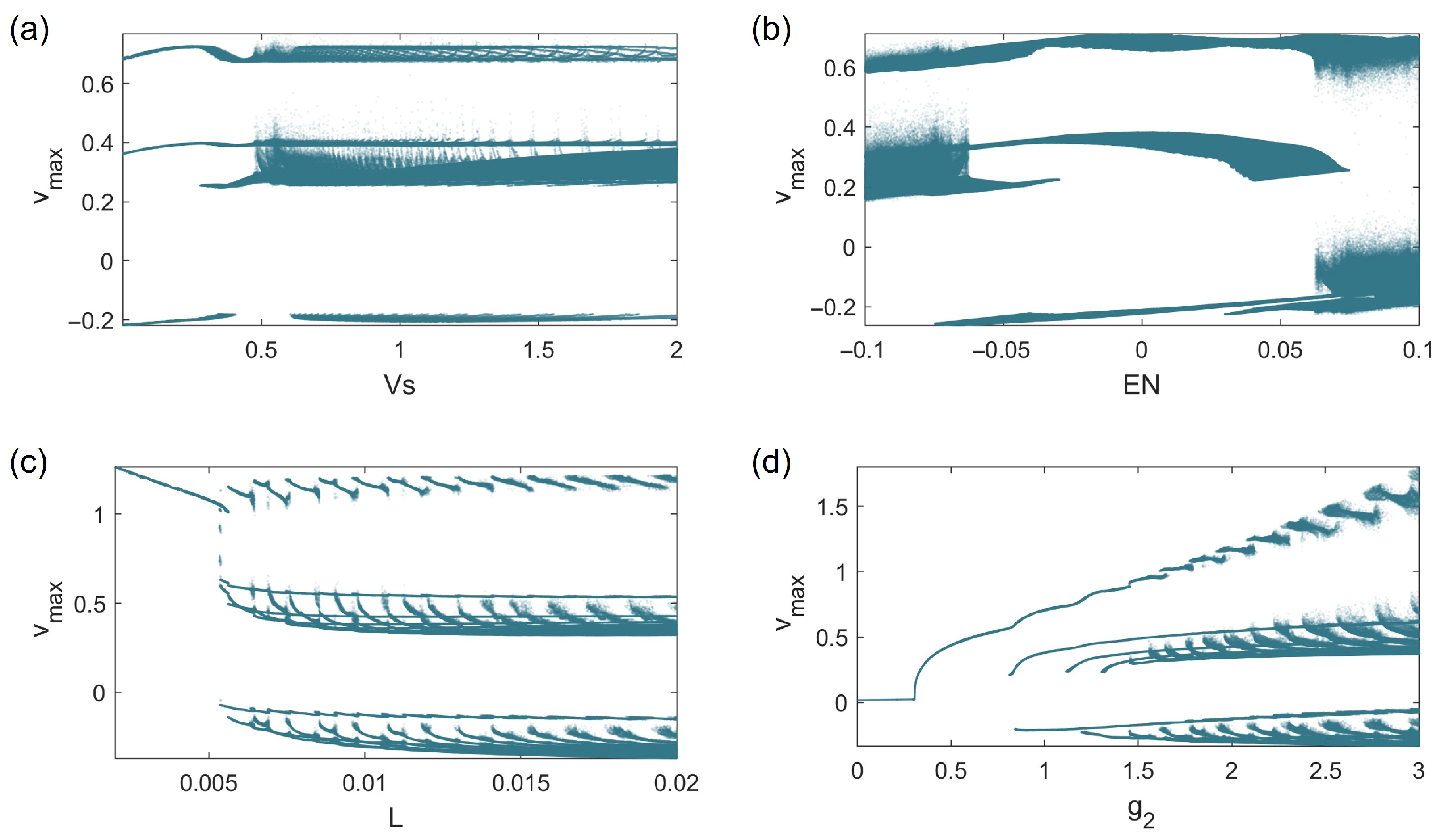
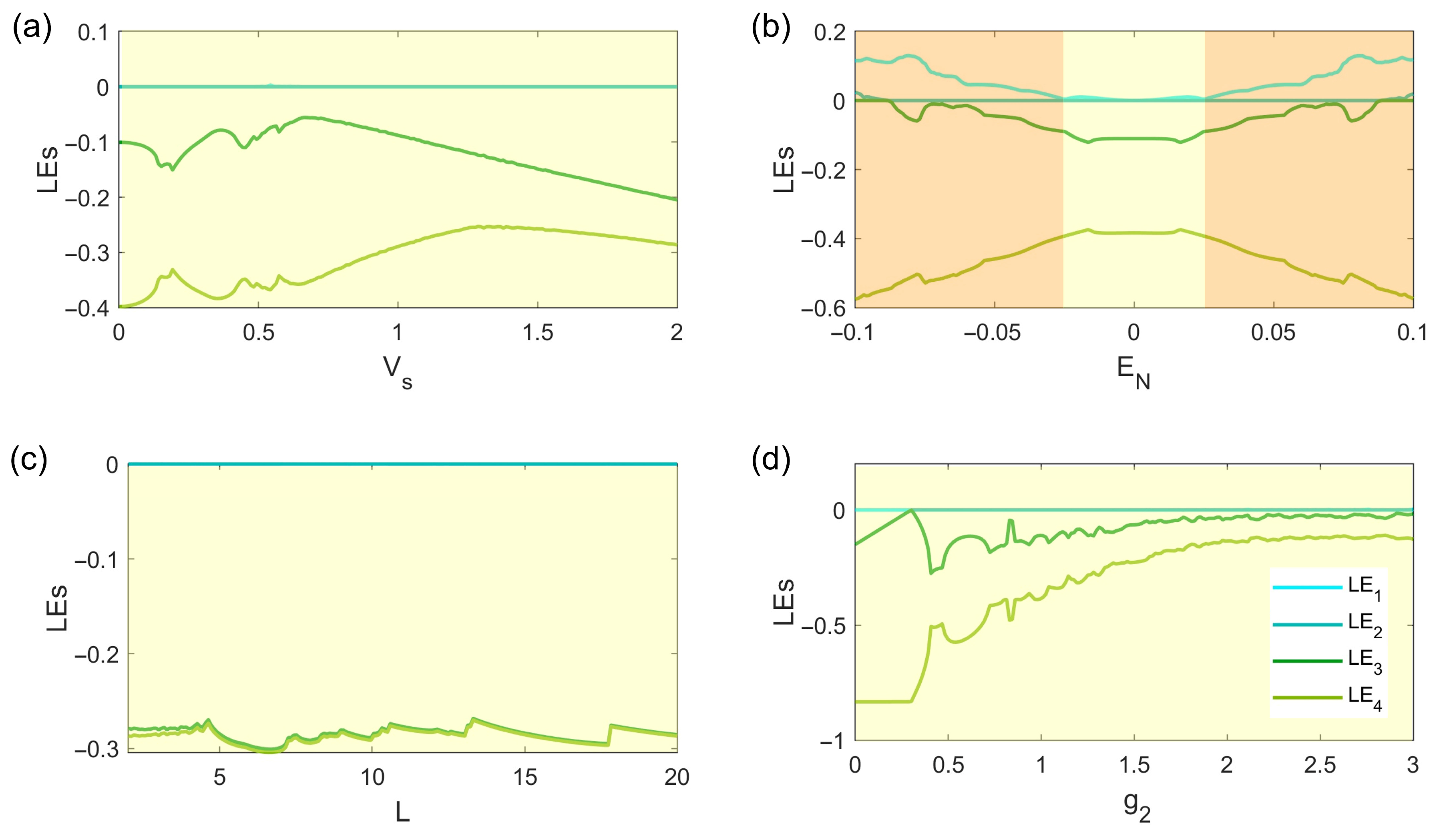
3.1. DC External Stimulation
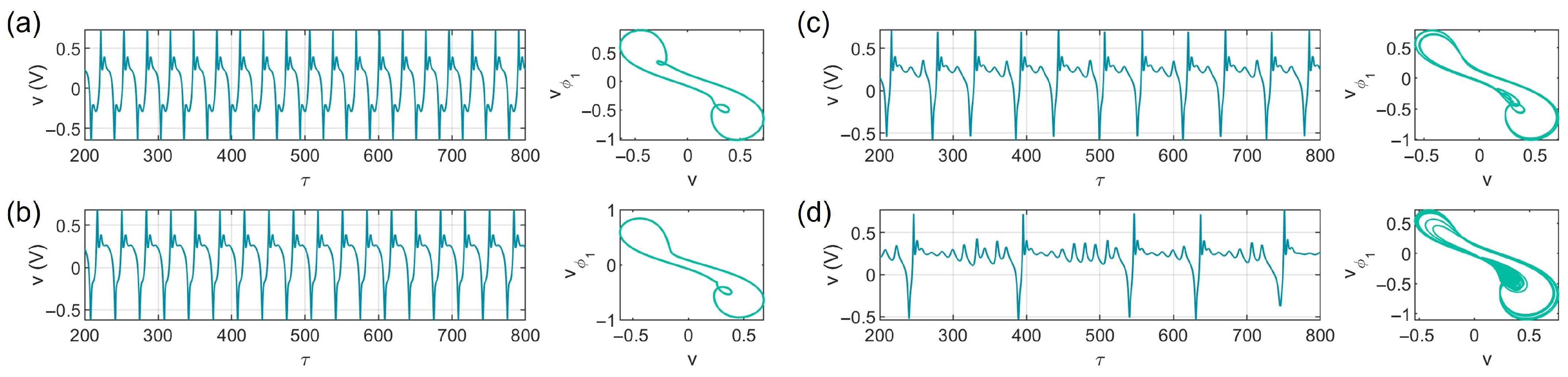
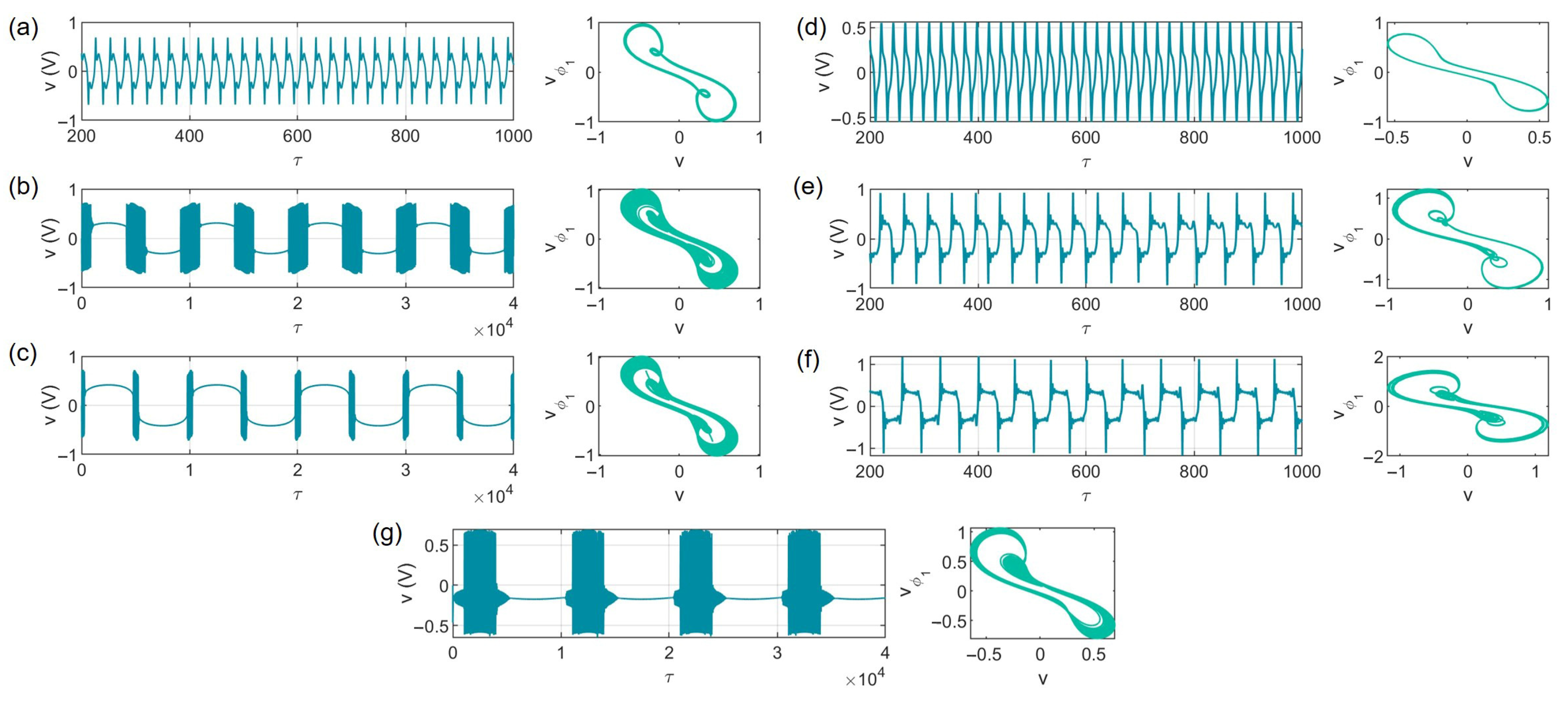
3.2. AC External Stimulation
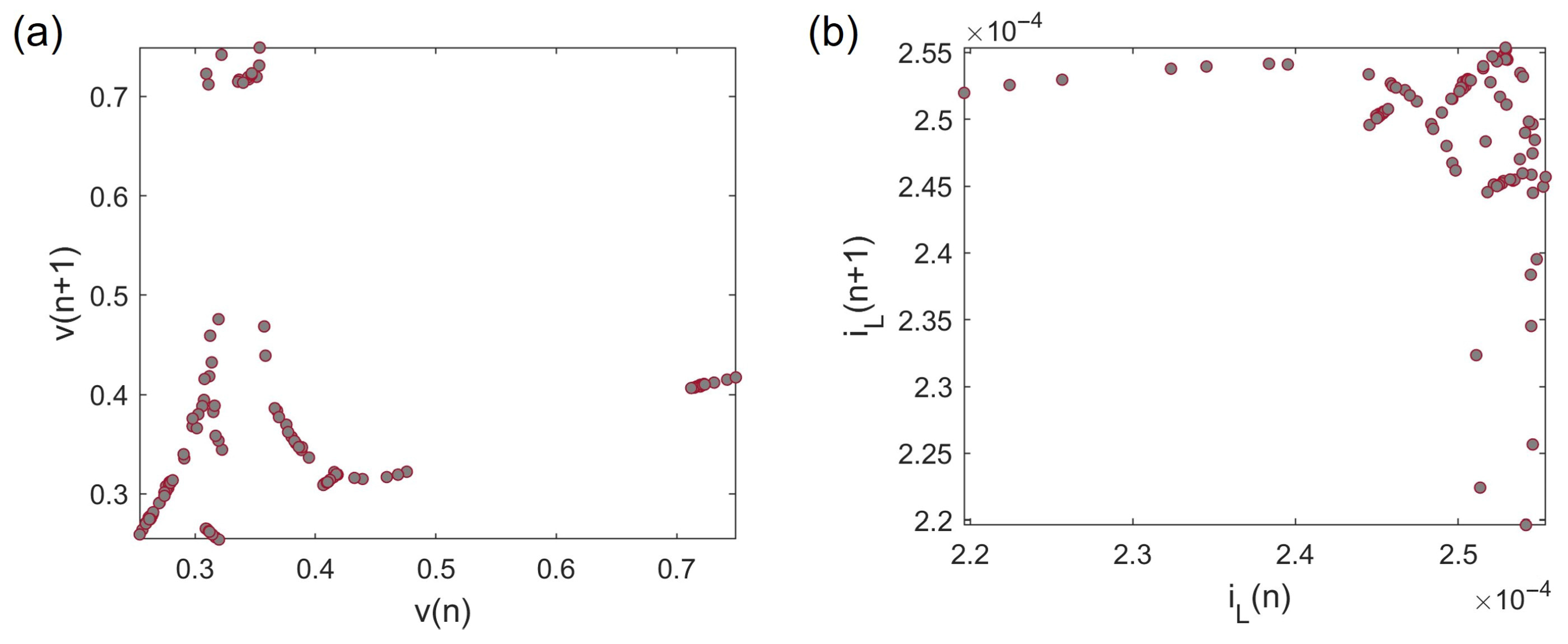
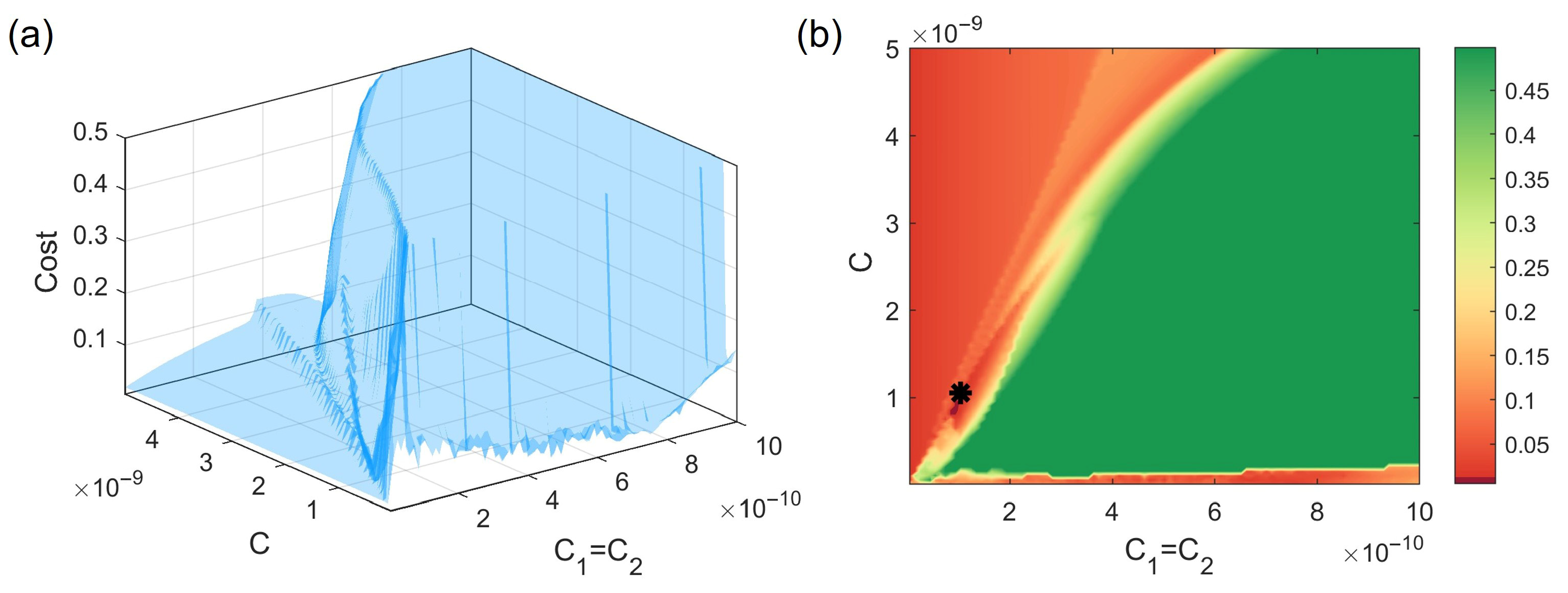
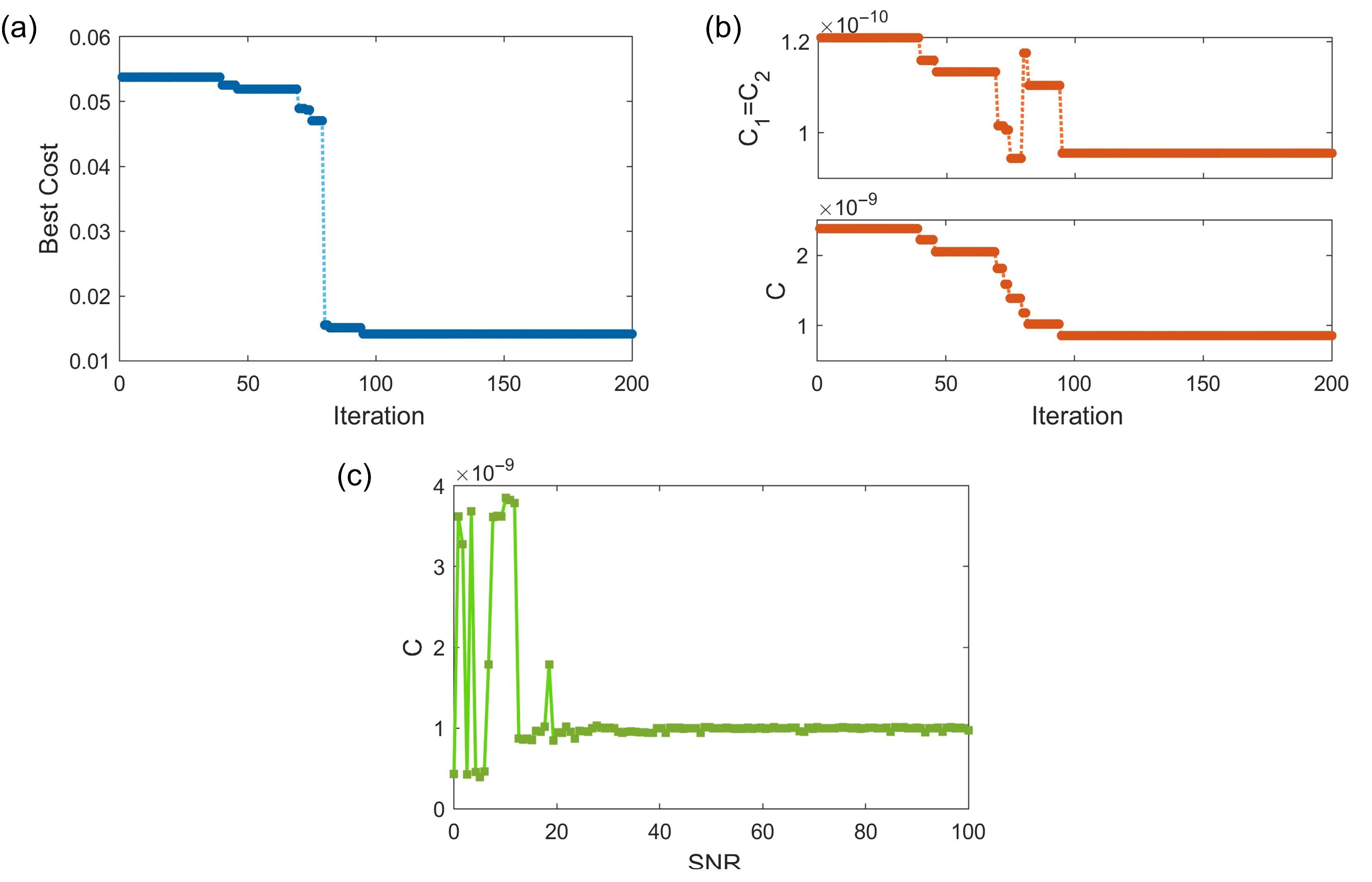
4. Parameter Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- MacGregor, R. Neural Modeling: Electrical Signal Processing in the Nervous System; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Shlyonsky, V.; Dupuis, F.; de Prelle, B.; Erneux, T.; Osee, M.; Nonclercq, A.; Gall, D. Compact hybrid type electronic neuron and computational model of its dynamics. Nonlinear Dyn. 2024, 112, 14343–14362. [Google Scholar] [CrossRef]
- Tang, H.; Tan, K.C.; Yi, Z. Neural Networks: Computational Models and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Xu, Q.; Ding, X.; Chen, B.; Parastesh, F.; Iu, H.H.-C.; Wang, N. A universal configuration framework for mem-element-emulator-based bionic firing circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4120–4130. [Google Scholar] [CrossRef]
- Schuman, C.D.; Kulkarni, S.R.; Parsa, M.; Mitchell, J.P.; Date, P.; Kay, B. Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci. 2022, 2, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Marković, D.; Mizrahi, A.; Querlioz, D.; Grollier, J. Physics for neuromorphic computing. Nat. Rev. Phys. 2020, 2, 499–510. [Google Scholar] [CrossRef]
- Li, H.; Min, F. Cross-Hemispheric Memristive Neural Network with Discrete Corsage Memristor for Telemedicine Encryption Application. IEEE Internet Things J. 2025, 12, 29018–29031. [Google Scholar] [CrossRef]
- Wang, Y.; Tao, K.; Wang, Z.; Sun, J. Memristor-based GFMM neural network circuit of biology with multiobjective decision and its application in industrial autonomous firefighting. IEEE Trans. Ind. Inform. 2025, 21, 5777–5786. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Zheng, Y.; Li, Y.; Li, C.; Wang, Y.; Ding, X.J.I.I.o.T.J. Tri-Memristor Hyperchaotic Ring Neural Network with Hidden Firings: Dynamic Analysis, Hardware Implementation and Application to Image Encryption. IEEE Internet Things J. 2025, in press. [Google Scholar] [CrossRef]
- Vazquez-Guerrero, P.; Tuladhar, R.; Psychalinos, C.; Elwakil, A.; Chacron, M.J.; Santamaria, F. Fractional order memcapacitive neuromorphic elements reproduce and predict neuronal function. Sci. Rep. 2024, 14, 5817. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Lei, T.; Iu, H.H.-C.; Kapitaniak, T. Coexisting Hyperchaos in a Memristive Neuromorphic Oscillator. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2025, 44, 3179–3188. [Google Scholar] [CrossRef]
- Wei, Q.; Gao, B.; Tang, J.; Qian, H.; Wu, H. Emerging memory-based chip development for neuromorphic computing: Status, challenges, and perspectives. IEEE Electron Devices Mag. 2023, 1, 33–49. [Google Scholar] [CrossRef]
- Burr, G.W.; Shelby, R.M.; Sebastian, A.; Kim, S.; Kim, S.; Sidler, S.; Virwani, K.; Ishii, M.; Narayanan, P.; Fumarola, A. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2017, 2, 89–124. [Google Scholar] [CrossRef]
- Milo, V.; Malavena, G.; Monzio Compagnoni, C.; Ielmini, D. Memristive and CMOS devices for neuromorphic computing. Materials 2020, 13, 166. [Google Scholar] [CrossRef] [PubMed]
- Yammenavar, B.D.; Gurunaik, V.R.; Bevinagidad, R.N.; Gandage, V.U. Design and analog VLSI implementation of artificial neural network. Int. J. Artif. Intell. Appl. 2011, 2, 96–109. [Google Scholar] [CrossRef]
- Chen, X.; Byambadorj, Z.; Yajima, T.; Inoue, H.; Inoue, I.H.; Iizuka, T. CMOS-based area-and-power-efficient neuron and synapse circuits for time-domain analog spiking neural networks. Appl. Phys. Lett. 2023, 122, 074102. [Google Scholar] [CrossRef]
- Khanday, F.A.; Kant, N.A.; Dar, M.R.; Zulkifli, T.Z.A.; Psychalinos, C. Low-voltage low-power integrable CMOS circuit implementation of integer-and fractional–order FitzHugh–Nagumo neuron model. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2108–2122. [Google Scholar] [CrossRef]
- Khanday, F.A.; Dar, M.R.; Kant, N.A.; Zulkifli, T.Z.A.; Psychalinos, C. Ultra-low-voltage integrable electronic implementation of delayed inertial neural networks for complex dynamical behavior using multiple activation functions. Neural Comput. Appl. 2020, 32, 8297–8314. [Google Scholar] [CrossRef]
- Aguirre, F.; Sebastian, A.; Le Gallo, M.; Song, W.; Wang, T.; Yang, J.J.; Lu, W.; Chang, M.-F.; Ielmini, D.; Yang, Y. Hardware implementation of memristor-based artificial neural networks. Nat. Commun. 2024, 15, 1974. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Wang, Y.; Wu, H.; Chen, M.; Chen, B. Periodic and chaotic spiking behaviors in a simplified memristive Hodgkin-Huxley circuit. Chaos Solitons Fractals 2024, 179, 114458. [Google Scholar] [CrossRef]
- Jeong, H.; Shi, L. Memristor devices for neural networks. J. Phys. D 2018, 52, 023003. [Google Scholar] [CrossRef]
- Indiveri, G.; Linares-Barranco, B.; Legenstein, R.; Deligeorgis, G.; Prodromakis, T. Integration of nanoscale memristor synapses in neuromorphic computing architectures. Nanotechnology 2013, 24, 384010. [Google Scholar] [CrossRef]
- Ye, L.; Gao, Z.; Fu, J.; Ren, W.; Yang, C.; Wen, J.; Wan, X.; Ren, Q.; Gu, S.; Liu, X. Overview of memristor-based neural network design and applications. Front. Phys. 2022, 10, 839243. [Google Scholar] [CrossRef]
- He, S.; Liu, J.; Wang, H.; Sun, K. A discrete memristive neural network and its application for character recognition. Neurocomputing 2023, 523, 1–8. [Google Scholar] [CrossRef]
- Li, F.; Chen, Z.; Zhang, Y.; Bai, L.; Bao, B. Cascade tri-neuron hopfield neural network: Dynamical analysis and analog circuit implementation. AEU-Int. J. Electron. Commun. 2024, 174, 155037. [Google Scholar] [CrossRef]
- Lai, Q.; Lai, C.; Zhang, H.; Li, C. Hidden coexisting hyperchaos of new memristive neuron model and its application in image encryption. Chaos Solitons Fractals 2022, 158, 112017. [Google Scholar] [CrossRef]
- Ma, M.; Xiong, K.; Li, Z.; He, S. Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk. Chin. Phys. B 2024, 33, 028706. [Google Scholar] [CrossRef]
- Bao, H.; Zhang, Y.; Liu, W.; Bao, B. Memristor synapse-coupled memristive neuron network: Synchronization transition and occurrence of chimera. Nonlinear Dyn. 2020, 100, 937–950. [Google Scholar] [CrossRef]
- Kozma, R.; Pino, R.E.; Pazienza, G.E. Advances in Neuromorphic Memristor Science and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 4. [Google Scholar]
- Zhang, X.; Huang, A.; Hu, Q.; Xiao, Z.; Chu, P.K. Neuromorphic computing with memristor crossbar. Phys. Status Solidi 2018, 215, 1700875. [Google Scholar] [CrossRef]
- Weilenmann, C.; Ziogas, A.N.; Zellweger, T.; Portner, K.; Mladenović, M.; Kaniselvan, M.; Moraitis, T.; Luisier, M.; Emboras, A. Single neuromorphic memristor closely emulates multiple synaptic mechanisms for energy efficient neural networks. Nat. Commun. 2024, 15, 6898. [Google Scholar] [CrossRef]
- Bao, H.; Fan, J.; Hua, Z.; Xu, Q.; Bao, B. Discrete Memristive Hopfield Neural Network and Application in Memristor-State-Based Encryption. IEEE Internet Things J. 2025, 12, 31843–31855. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y.; Wang, Y.; Wang, Y. A Memristor-Based Neural Network Circuit with Retrospective Revaluation Effect and Application in Intelligent Household Robots. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 11466–11478. [Google Scholar] [CrossRef]
- Chua, L. If it’s pinched it’sa memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, C. A simple locally active memristor and its application in HR neurons. Chaos 2020, 30, 053118. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, C.; He, S. Locally active memristor with variable parameters and its oscillation circuit. Int. J. Bifurc. Chaos 2023, 33, 2350032. [Google Scholar] [CrossRef]
- Xu, Q.; Fang, Y.; Wu, H.; Bao, H.; Wang, N. Firing patterns and fast–slow dynamics in an N-type LAM-based FitzHugh–Nagumo circuit. Chaos Solitons Fractals 2024, 187, 115376. [Google Scholar] [CrossRef]
- Lu, R.; Ying, J.; Min, F.; Wang, G. Neurodynamics of Different Neurons Based on a Memristor with S-Type and N-Type Locally Active Domains. Int. J. Bifurc. Chaos 2025, 35, 2530008. [Google Scholar] [CrossRef]
- Xu, Q.; Fang, Y.; Feng, C.; Parastesh, F.; Chen, M.; Wang, N. Firing activity in an N-type locally active memristor-based Hodgkin–Huxley circuit. Nonlinear Dyn. 2024, 112, 13451–13464. [Google Scholar] [CrossRef]
- Ding, X.; Fan, W.; Wang, N.; Su, Y.; Chen, M.; Lin, Y.; Xu, Q. Dynamical behaviors and firing patterns in a fully memory-element emulator-based bionic circuit. Chaos Solitons Fractals 2025, 199, 116658. [Google Scholar] [CrossRef]
- Mou, J.; Cao, H.; Zhou, N.; Cao, Y. An FHN-HR neuron network coupled with a novel locally active memristor and its DSP implementation. IEEE Trans. Cybern. 2024, 54, 7333–7342. [Google Scholar] [CrossRef]
- Tabekoueng Njitacke, Z.; Sriram, G.; Rajagopal, K.; Karthikeyan, A.; Awrejcewicz, J. Energy computation and multiplier-less implementation of the two-dimensional FitzHugh–Nagumo (FHN) neural circuit. Eur. Phys. J. E 2023, 46, 60. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Ramadoss, J.; Takembo, C.N.; Rajagopal, K.; Awrejcewicz, J. An enhanced FitzHugh–Nagumo neuron circuit, microcontroller-based hardware implementation: Light illumination and magnetic field effects on information patterns. Chaos Solitons Fractals 2023, 167, 113014. [Google Scholar] [CrossRef]
- Chen, L.; Bao, H.; Zhang, X.; Zhang, Y.; Bao, B. DC-bias induced chaotic dynamics and periodic bursting in Chua’s diode-based FitzHugh-Nagumo circuit. Chaos Solitons Fractals 2025, 199, 116739. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Pham, V.-T.; Golpayegani, S.M.R.H.; Jafari, A.H. A new cost function for parameter estimation of chaotic systems using return maps as fingerprints. Int. J. Bifurc. Chaos 2014, 24, 1450134. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajagopal, S.; Pham, V.-T.; Parastesh, F.; Rajagopal, K.; Jafari, S. Dynamics of a Neuromorphic Circuit Incorporating a Second-Order Locally Active Memristor and Its Parameter Estimation. J. Low Power Electron. Appl. 2025, 15, 62. https://doi.org/10.3390/jlpea15040062
Rajagopal S, Pham V-T, Parastesh F, Rajagopal K, Jafari S. Dynamics of a Neuromorphic Circuit Incorporating a Second-Order Locally Active Memristor and Its Parameter Estimation. Journal of Low Power Electronics and Applications. 2025; 15(4):62. https://doi.org/10.3390/jlpea15040062
Chicago/Turabian StyleRajagopal, Shivakumar, Viet-Thanh Pham, Fatemeh Parastesh, Karthikeyan Rajagopal, and Sajad Jafari. 2025. "Dynamics of a Neuromorphic Circuit Incorporating a Second-Order Locally Active Memristor and Its Parameter Estimation" Journal of Low Power Electronics and Applications 15, no. 4: 62. https://doi.org/10.3390/jlpea15040062
APA StyleRajagopal, S., Pham, V.-T., Parastesh, F., Rajagopal, K., & Jafari, S. (2025). Dynamics of a Neuromorphic Circuit Incorporating a Second-Order Locally Active Memristor and Its Parameter Estimation. Journal of Low Power Electronics and Applications, 15(4), 62. https://doi.org/10.3390/jlpea15040062





