Accurate Analysis and Design of Integrated Single Input Schmitt Trigger Circuits

Abstract

Schmitt trigger (ST) circuits are widely used integrated circuit (IC) blocks with hysteretic input/output (I/O) characteristics. Like the I/O characteristics of a living neuron, STs reject noise and provide stability to systems that they are deployed in. Indeed, single-input/single-output (SISO) STs are likely candidates to be the core unit element in artificial neural networks (ANNs) due not only to their similar I/O characteristics but also to their low power consumption and small silicon footprints. This paper presents an accurate and detailed analysis and design of six widely used complementary metal-oxide-semiconductor (CMOS) SISO ST circuits. The hysteresis characteristics of these ST circuits were derived for hand calculations and compared to original design equations and simulation results. Simulations were carried out in a well-established, 0.35 μm/3.3 V, analog/mixed-signal CMOS process. Additionally, simulations were performed using a wide range of supplies and process variations, but only 3.3 V supply results are presented. Most of the new design equations provide better accuracy and insights, as broad assumptions of original derivations were avoided.

1. Introduction

Artificial neural networks (ANNs) are the core of artificial intelligence (AI) in next generation systems that mimic the parallel processing capabilities of the human brain. One important characteristic of the distributed processing element of the brain, the neuron, is to deal with chaos through its hysteretic I/O response [1]. It is shown that this characteristic of a neuron makes ANNs stable [2] and converge more rapidly [3]. Additionally, the artificial neuron has to be small and consume minimal power to be able to be integrated into mass numbers [4].

The Schmitt trigger (ST) has been used in both analog and digital domains to improve the noise immunity of circuits, thanks to its programmable or hard-wired hysteresis characteristics [5,6,7,8,9,10,11]. This characteristic has been utilized in many CMOS circuit blocks including oscillators [12,13,14,15], input/output pads of integrated circuits [16,17], image sensors [18,19,20,21,22,23,24], triangular carrier-based PWM modulators [25], subthreshold SRAMs [26,27,28,29], CMOS transceivers [30,31,32,33,34], impedance-to-frequency converters [35], digital to analog converters (DACs) [36], neuron-based analog to digital converters (ADCs) [37,38,39], powerline communication systems [40], binary logic circuits (i.e., adders [41] and gates [42]), and sensors [43,44].

CMOS STs can be categorized based on their mode of operation (voltage or current), inputs (single or differential input), outputs (inverting or noninverting), and hysteresis controls (fixed or programmable). The simplest and most compact STs are the ones with fixed hysteresis, and single voltage input and single voltage output types. Six well known single input/single output ST topologies are investigated in this paper: Dokic [5] (three types: N, P, and CMOS), Steyaert [6], Pedroni [7], and Al-Sarawi [8]. In this paper, we show how to derive the hysteresis voltages accurately for these STs, and determine their design limitations and sensitivities to process variations. For the analysis and design of an ST circuit, three fundamental input-output (I/O) parameters are considered: high-to-low switching voltage (V_HL), low-to-high switching voltage (V_LH), and hysteresis voltage (ΔV_H = V_HL − V_LH), as shown in Figure 1. The hysteresis offset (V_HO) in Figure 1 can be calculated as (V_HO = V_LH + ΔV_H/2).

Detailed analysis and the hand calculation equations of each topology are presented in Section 2. Each topology is extensively simulated at different corners of the selected CMOS process. The simulation results are presented in Section 3, as are the comparisons between hand calculations and the simulation results of each topology, in addition to the comparisons between the six topologies. The conclusion is presented in Section 4.

2. Analysis of Schmitt Trigger (ST) Circuits

Six well known single input and single output ST topologies and their variants are analyzed in this section, providing transistor level and more accurate and intuitive design equations. They are Dokic [5] (three types), Steyaert [6], Pedroni [7], and Al-Sarawi [8] STs. We used long-channel MOSFET models and high supply voltage process in this section. Equations (1) and (2) are the quadratic MOSFET transistor model equations that were used for the analysis in saturation (SAT) and linear/triode (LIN) regions, respectively [45]. The threshold voltage equation was modified slightly, linearizing bulk-to-source voltage dependency as V_thx = V_th0 + ψ∙V_SB. Here, ψ is defined as ψ = n∙GAMMA∙PHI, where GAMMA is the back-gate effect parameter, PHI is the surface potential, and n is a fitting parameter (0.3 < n < 0.5) which is determined through the simulation.

$$I_{DS}=\beta {\left(V_{GS}-V_{TH}\right)}^2 \mathrm{for} V_{DS}\ge V_{GS}-V_{TH \left(\mathrm{Saturation}\right)}$$

(1)

$$I_{DS}=\beta \left(2\left(V_{GS}-V_{TH}\right)V_{DS}-V_{DS}^2\right) \mathrm{for} V_{DS}<V_{GS}-V_{TH \left(\mathrm{Linear}\right)}$$

(2)

where

$$\beta =\frac{1}{2}KP\left(\frac{W}{L}\right)$$

(3)

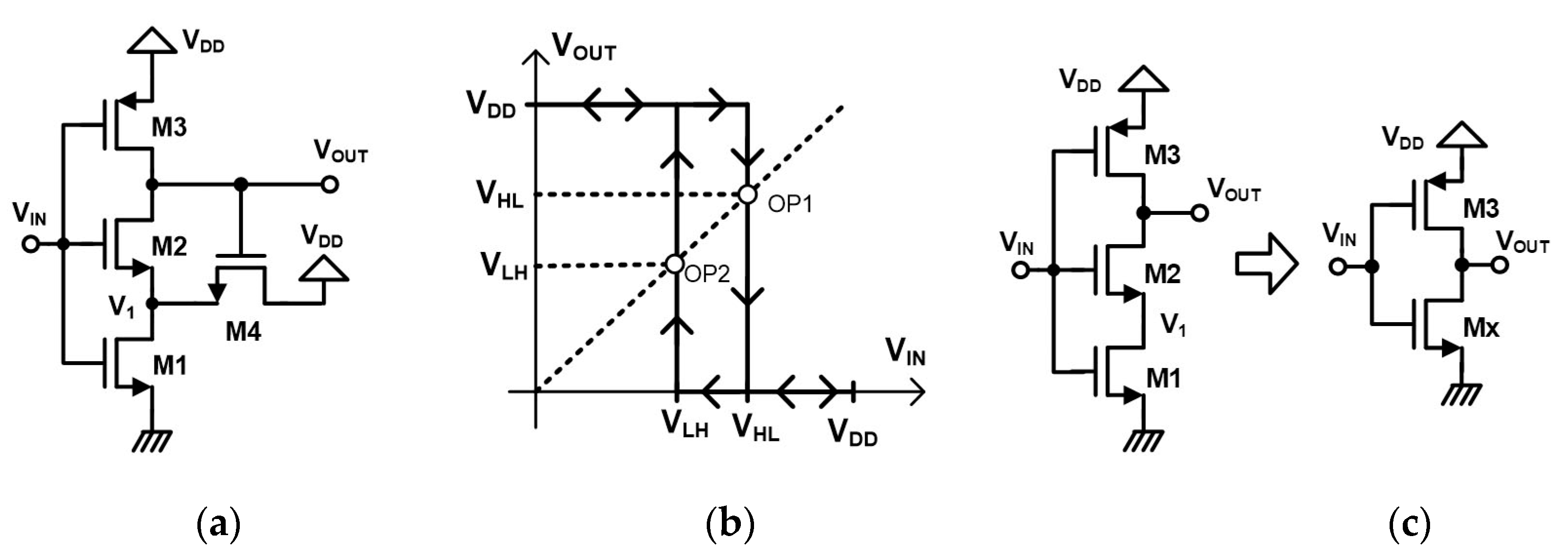
2.1. Dokic Schmitt Trigger Circuits

Dokic proposed three ST topologies in [5]: N-type, P-type, and CMOS-type. These topologies are investigated and detailed, and more accurate design equations for V_HL, V_LH, and ΔV_H are derived.

2.1.1. N-Type ST by Dokic

Figure 2a shows the N-type Dokic ST [5]. It is composed of four transistors and its hysteresis is shown in Figure 2b. Depending on how the input signal changes, two I/O characteristics can be observed. If the input goes from low (0) to high (V_DD), the output changes from high to low at V_HL. If the input goes from high (V_DD) to low (0), the output changes from low (0) to high (V_DD) at V_LH. The V_HL and V_LH can be found when the input and output voltages are equal to each other at operating points OP1 and OP2, respectively, as marked in Figure 2b.

V_HL Voltage

From Figure 2a, in the steady-state and when input is 0 V, the transistors M1 and M2 are OFF, M3 is in the deep LIN region where V_ds3 is close to 0 V, and M4 can be considered in the subthreshold region, where V_gs4 < V_thn4 while the output is V_DD. The node voltage V₁ would be (V_DD – V_thn4) and rising. When the input is increased and greater than V_thn0, M1 turns ON, discharging V₁ to a switching point. Since V_sb2 = V_sb4 > V_thn0, M2 is still OFF and M4 is in SAT. M2 turns ON only when V_in is V_thn0 above the V₁ voltage. Before M2 turns on, the V₁ can be found by equating the drain currents of transistors M1 and M4. The general V₁ equation, including body-effect where V_thn4 ≈ V_thn0 + ψ∙V₁, is:

$$V_1=\frac{V_{DD}-V_{thn0}\cdot \left(1-{\alpha }_{1n}\right)-{\alpha }_{1n}{V}_{in}}{\left(1+\Psi \right)}$$

(4)

where

$${\alpha }_{1n}=\sqrt{\frac{{\beta }_1}{{\beta }_4}}$$

(5)

When V_in further increases, V₁ drops further, and finally, M2 turns ON. Then, the output node starts discharging, first turning M4 OFF and then turning M3 ON during this high to low transition. M2 turns ON when V_in(min) > V₁ + V_thn2. V_in(min) could be considered as the threshold voltage of the series combination of M1 and M2, or V_thnx. Using (4), it can be found as follows:

$$V_{in\left(min\right)}\ge V_1+V_{thn2}=V_1+V_{thn0}+\Psi \cdot V_1=V_{DD}+{\alpha }_{1n}{V}_{thn0}-{\alpha }_{1n}{V}_{in\left(min\right)}$$

(6)

$$V_{thn\mathrm{x}}=V_{in\left(min\right)}\ge \frac{V_{DD}+{\alpha }_{1n}\cdot V_{thn0}}{\left(1+{\alpha }_{1n}\right)}$$

(7)

When V_in = V_HL, Dokic [5] assumes that M1 works in LIN, and M2 and M3 are in SAT regions, while M4 is OFF. However, series transistors M1 and M2 (Figure 2c) work in two different operation regions (M1 in LIN, M2 in SAT) that could be simplified into a single NMOS (M_x) transistor working in SAT with an equivalent threshold voltage of V_thnx, and β = β_xn, as follows:

$$I_{ds1}={\beta }_1\cdot \left(2\cdot \left(V_{in}-V_{thn0}\right)\cdot V_1-V_1^2\right)$$

(8)

$$V_1=+\left(V_{in}-V_{thn0}\right)\pm \sqrt{{\left(V_{in}-V_{thn0}\right)}^2-\frac{I_{ds1}}{{\beta }_1}}$$

(9)

$$I_{ds2}=\frac{1}{2}{KP}_n{\left(\frac{W}{L}\right)}_2{\left(V_{in}-V_1-V_{thn2}\right)}^2={\beta }_2{\left(V_{in}-V_1-V_{thn0}-\Psi \cdot V_1\right)}^2$$

(10)

using (9) in (10):

$$I_{ds2}={\beta }_2\cdot {\left(V_{in}-\left(1+\Psi \right)\cdot \left[+\left(V_{in}-V_{thn0}\right)\pm \sqrt{{\left(V_{in}-V_{thn0}\right)}^2-\frac{I_{ds1}}{{\beta }_1}}\right]-V_{thn0 }\right)}^2$$

(11)

and assuming that V_thn1 ≅ V_thn2 = V_thn0, where ψ = 0, and I_ds1 = I_ds2 = I_dsx, Equation (11) becomes,

$$I_{dsx}={\beta }_2\cdot \left[{\left(V_{in}-V_{thn0}\right)}^2-\frac{I_{dsx}}{{\beta }_1}\right]$$

(12)

$$I_{ds1}=I_{ds2}=I_{dsx}=\left[\frac{{\beta }_1\cdot {\beta }_2}{{\beta }_1+{\beta }_2}\right] {\left(V_{in}-V_{thn0}\right)}^2={\beta }_{xn}\cdot {\left(V_{in}-V_{thn0}\right)}^2$$

(13)

where

$${\beta }_{xn}=\left[\frac{{\beta }_1\cdot {\beta }_2}{{\beta }_1+{\beta }_2}\right]$$

(14)

The V_HL of the N-type Dokic ST can now be found by equating the drain currents of the transistors M3 and Mx shown in Figure 2c, assuming that both are working in SAT region at OP1:

$$V_{HL}=\frac{V_{DD}-\left|V_{thp0}\right|+{\alpha }_{2n}\cdot V_{thn0}}{\left(1+{\alpha }_{2n}\right)}+\frac{{\alpha }_{2n}\cdot \left(V_{DD}-V_{thn0}\right)}{\left(1+{\alpha }_{1n}\right)\left(1+{\alpha }_{2n}\right)}$$

(15)

$$\mathrm{where},{\alpha }_{1n}=\sqrt{\frac{{\beta }_1}{{\beta }_4}}\mathrm{and}{\alpha }_{2n}=\sqrt{\frac{{\beta }_{xn}}{{\beta }_3}}$$

(16)

V_LH Voltage

The V_LH can be found by considering M4 as being OFF right before the output transition from low to high which occurs at OP2 (V_in = V_out = V_LH), and by equating the drain current of M3 to that of M_x, which both work in SAT. It is important to note here that the current of M_x is equal to that of M2 (as in (13)) in which β_xn, V_thn0, and α_1n, and α_2n from Equation (16) are used.

$$V_{LH}=\frac{V_{DD}-\left|V_{thp0}\right|+{\alpha }_{2n}\cdot V_{thn0}}{\left(1+{\alpha }_{2n}\right)}$$

(17)

Hysteresis Voltage

The hysteresis voltage of the N-type Dokic ST can then be derived by using (15) and (17) as:

$$\Delta V_H=V_{HL}-V_{LH}=\frac{{\alpha }_{2n}\cdot \left(V_{DD}-V_{thn0}\right)}{\left(1+{\alpha }_{1n}\right)\left(1+{\alpha }_{2n}\right)}$$

(18)

Compared to Dokic’s original hysteresis equation (Equation (7) in [5]), (18) provides a transistor-level design strategy, that the hysteresis voltage could be maximized by minimizing α_1n and by maximizing α_2n parameters while ensuring that the individual transistor parameters satisfy β₄ > β₁ and β₃ < β_xn.

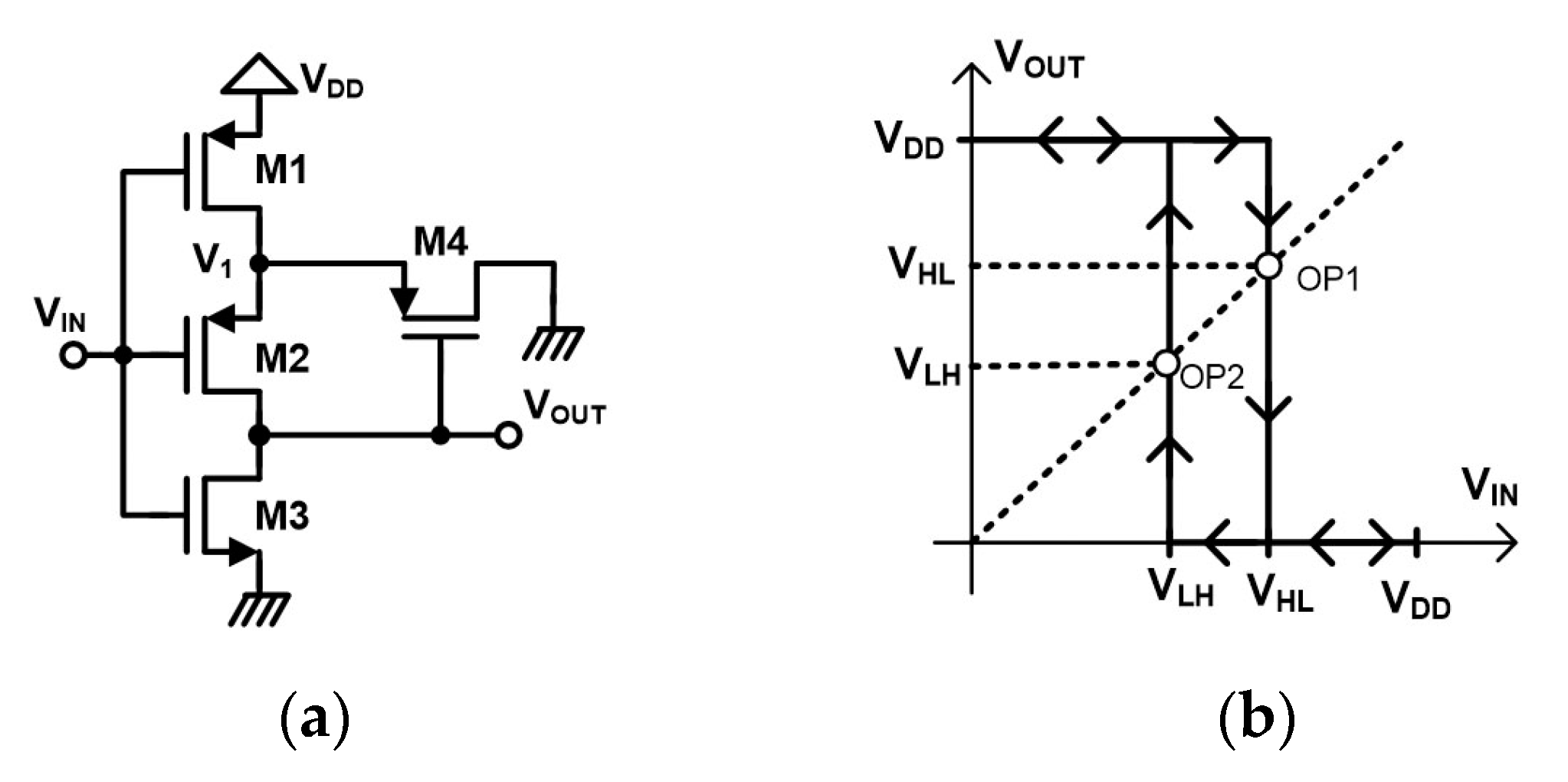
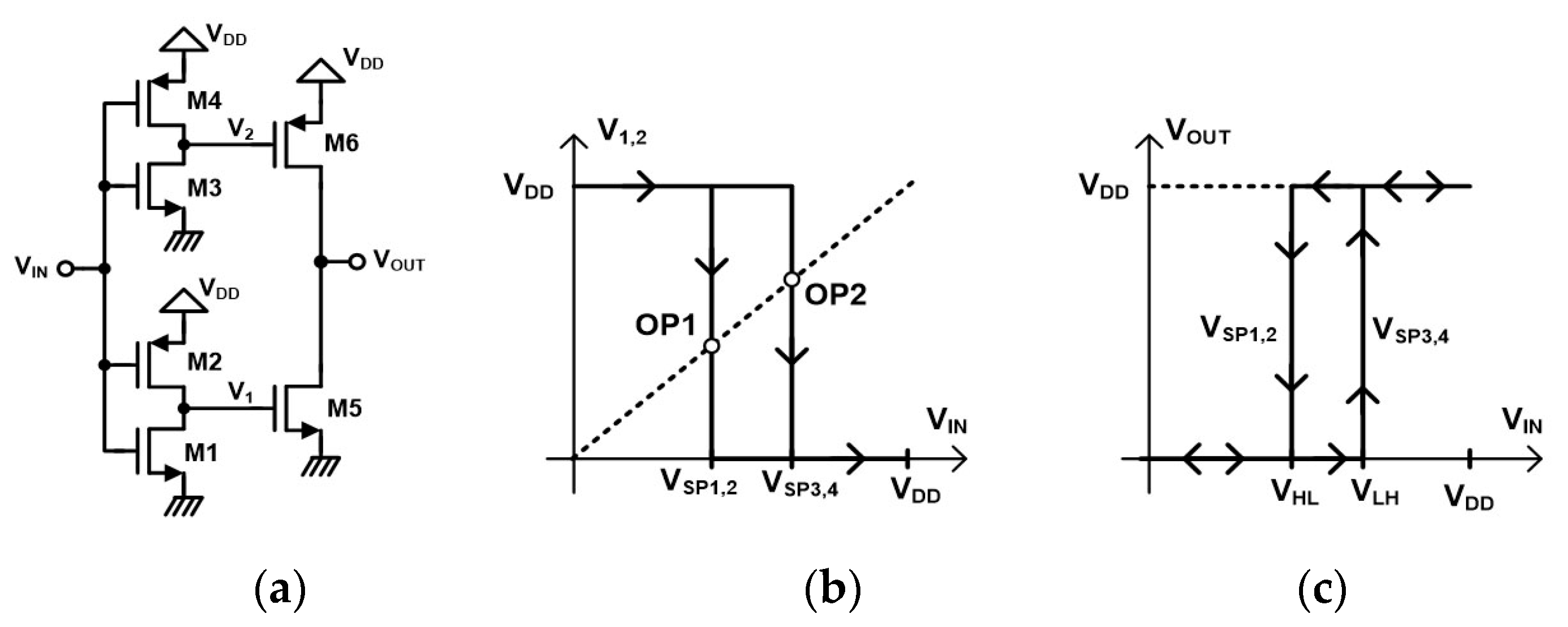
2.1.2. P-Type ST by Dokic

Figure 3 shows the P-type Dokic ST [5]. It is the complementary version of the N-type and has the same hysteresis characteristics. Transistors are numbered the same as the N-type as shown in Figure 2 and the analysis is carried out following the same process presented in the previous section. The V_HL and V_LH of the P-type Dokic ST can be found when input and output voltages are equal at operating points OP1 and OP2 as shown in Figure 3.

The design equations and parameters for the P-type Dokic ST can be derived as:

$$V_{LH}=\frac{{\alpha }_{2p}\cdot V_{thn0}}{\left(1+{\alpha }_{2p}\right)}+\frac{{\alpha }_{1p}\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)}{\left(1+{\alpha }_{1p}\right)\left(1+{\alpha }_{2p}\right)}$$

(19)

$$V_{HL}=\frac{V_{DD}-\left|V_{thp0}\right|+{\alpha }_{2p}\cdot V_{thn0}}{\left(1+{\alpha }_{2p}\right)}$$

(20)

and the hysteresis voltage:

$$\Delta V_H=V_{HL}-V_{LH}=\frac{\left(V_{DD}-\left|V_{thp0}\right|\right)}{\left(1+{\alpha }_{1p}\right)\left(1+{\alpha }_{2p}\right)}$$

(21)

where

$${\alpha }_{1p}=\sqrt{\frac{{\beta }_1}{{\beta }_4}} , {\alpha }_{2p}=\sqrt{\frac{{\beta }_3}{{\beta }_{xp}}}, {\beta }_{xp}=\left[\frac{{\beta }_1\cdot {\beta }_2}{{\beta }_1+{\beta }_2}\right], \mathrm{and} \left|V_{thpx}\right|=V_{DD}-\frac{{\alpha }_{1p}\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)}{\left(1+{\alpha }_{1p}\right)}$$

(22)

Compared to Dokic’s original hysteresis equation (Equation (13) in [5]), (21) provides a transistor-level design strategy, that the hysteresis voltage could be maximized by minimizing both α_1p and α_2p parameters while ensuring the individual transistor parameters satisfies β₄ > β₁ and β_xp < β₃ conditions.

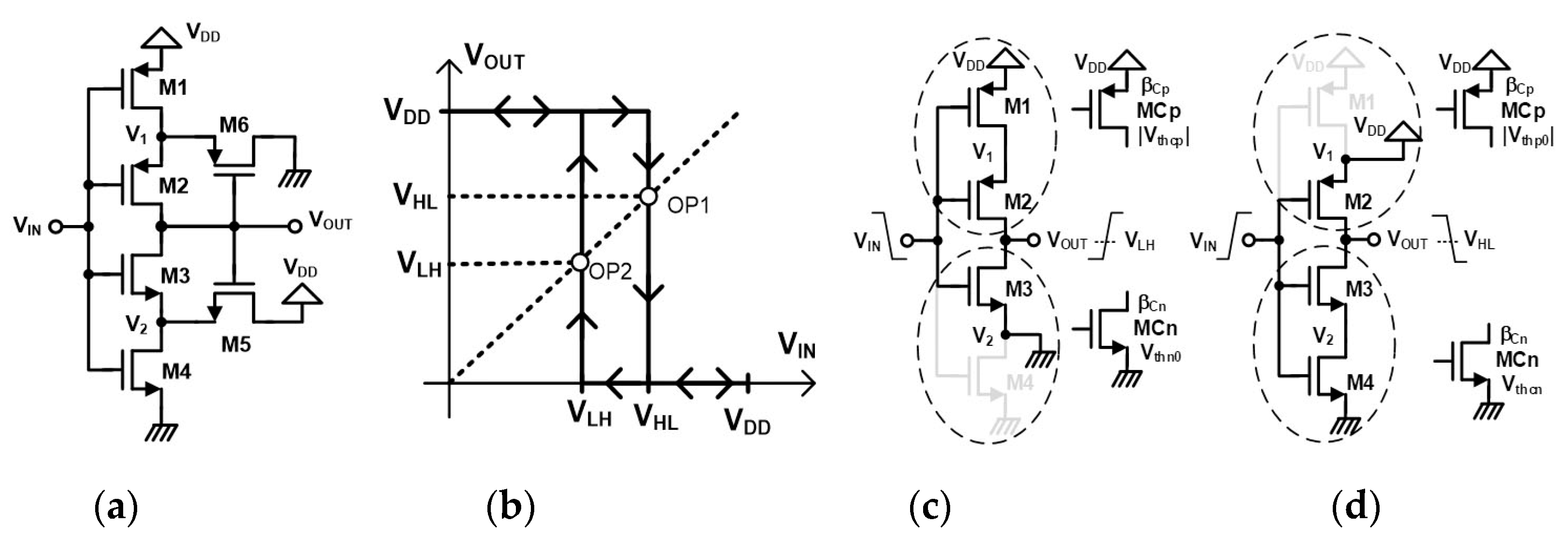
2.1.3. CMOS-Type ST by Dokic

Figure 4 shows the CMOS type Dokic ST circuit [5]. It is composed of six transistors and its hysteresis is shown in Figure 4b. Depending on how the input signal changes, two I/O characteristics can be observed. If the input goes from low (0) to high (V_DD) voltage level, the output state is changed at V_HL where the output goes from high (V_DD) to low (0) and vice versa, it switches from low (0) to high (V_DD) at V_LH. The V_HL and V_LH can be found when the input and output voltages are equal at operating points OP1 and OP2, as shown in Figure 4b.

V_LH Voltage

When the input is V_DD, the output is close to 0 V and M1, M2, and M5 are OFF, while M6 operates in the subthreshold region. M3 and M4 are in the deep LIN region where V_ds3,4 ≈ 0, and I_ds3,4 ≈ 0. V₁ approaches but remains below |V_thp6| and is continuously discharged by the subthreshold current of M6. When V_in drops a |V_thcp| below V_DD, the series combination of M1 and M2 (MCp) turns ON and works in the SAT region. During this time, M3 still works in SAT, while M5 is OFF and M4 is in LIN, which keeps V₂ voltage close to 0 V. Thus, the V_LH voltage could be determined by equating the SAT current of the transistor MCp to that of MCn formed by the series combination of M3 and M4, while assuming V₂ = 0. This means that MCn will have V_thn0 as the threshold voltage, while the threshold voltage of MCp will be |V_thcp|, the same as |V_thpx| in Equation (22). Thus, the V_LH can be derived as:

$$V_{LH}=\frac{{\alpha }_2\cdot V_{thn0}}{\left(1+{\alpha }_2\right)}+\frac{{\alpha }_1\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)}{\left(1+{\alpha }_1\right)\left(1+{\alpha }_2\right)}$$

(23)

where

$${\alpha }_1=\sqrt{\frac{{\beta }_1}{{\beta }_6}}, {\alpha }_2=\sqrt{\frac{{\beta }_{cn}}{{\beta }_{cp}}}, {\beta }_{cp}=\left[\frac{{\beta }_1\cdot {\beta }_2}{{\beta }_1+{\beta }_2}\right],\mathrm{and} {\beta }_{cn}=\left[\frac{{\beta }_3\cdot {\beta }_4}{{\beta }_3+{\beta }_4}\right]$$

(24)

V_HL Voltage

When the input is 0 V, the output is close to V_DD and transistors M3, M4, and M6 are OFF, while M5 operates in the subthreshold region. Transistors M1 and M2 are in the deep LIN region where V_sd1,2 ≈ 0, and I_sd1,2 ≈ 0. V₂ approaches but remains below V_DD and is continuously charged by the subthreshold current of M5. When V_in increases a V_thcn above 0 V, the series combination of M3 and M4 (MCn) turns ON and into the SAT region. During this time, M2 still works in SAT, while M6 is OFF and M1 is in the LIN region, which keeps V₁ voltage close to V_DD. Thus, the V_HL voltage could be determined by equating the SAT current of transistor MCn to that of MCp formed by the series combination of M1 and M2, while assuming V₁ = V_DD. This means that MCp will have |V_thp0| as threshold voltage, while the threshold voltage of MCn will be V_thcn, the same as V_thnx in Equation (7). Thus, V_HL can be derived as:

$$V_{HL}=\frac{V_{DD}-\left|V_{thp0}\right|+{\alpha }_2\cdot V_{thn0}}{\left(1+{\alpha }_2\right)}+\frac{{\alpha }_2\cdot \left(V_{DD}-V_{thn0}\right)}{\left(1+{\alpha }_2\right)\left(1+{\alpha }_3\right)}$$

(25)

where

$${\alpha }_3=\sqrt{\frac{{\beta }_4}{{\beta }_5}} \mathrm{and}{V}_{thcn}=\frac{V_{DD}+{\alpha }_3\cdot V_{thn0}}{\left(1+{\alpha }_3\right)}$$

(26)

Hysteresis Voltage

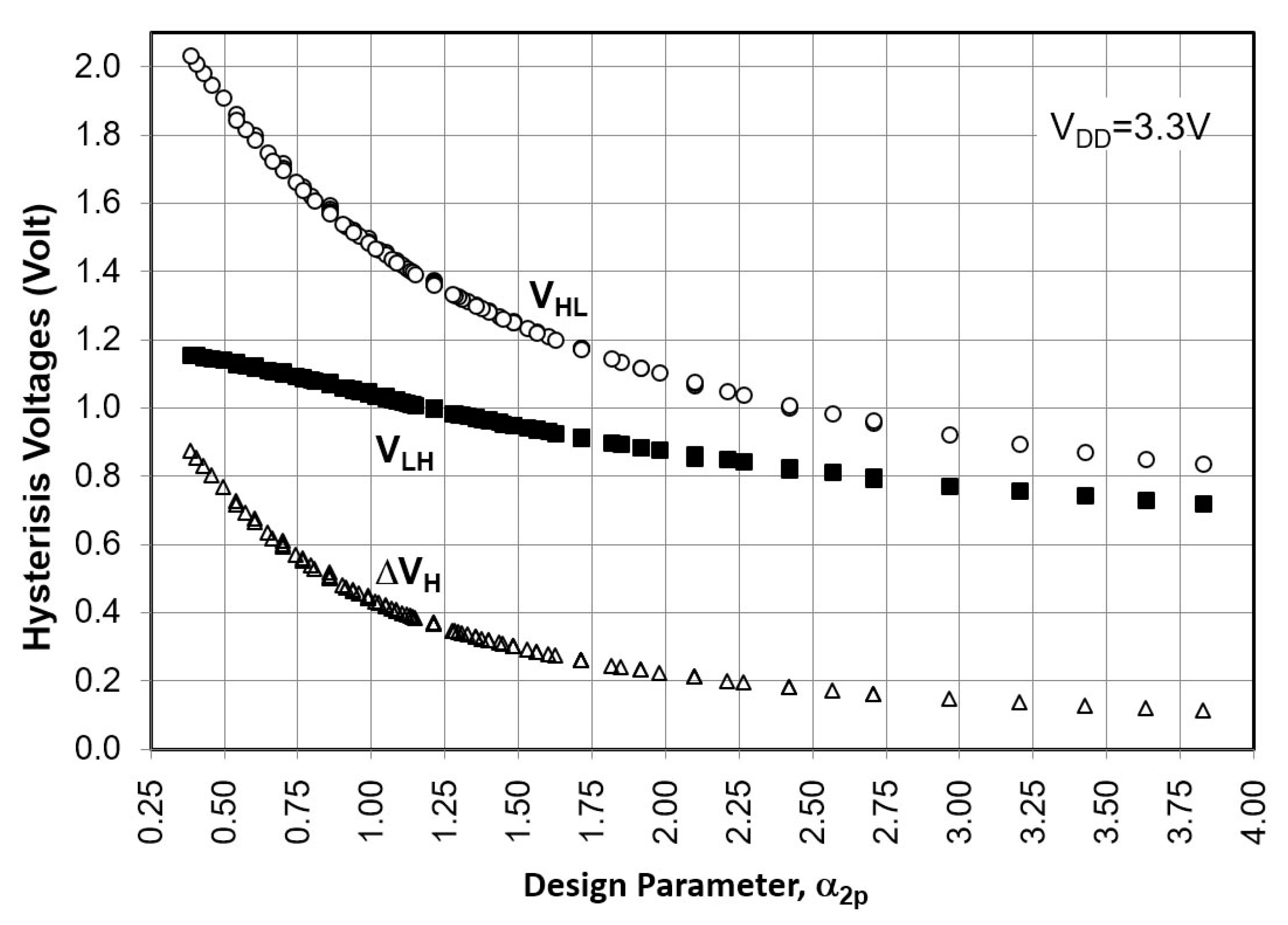
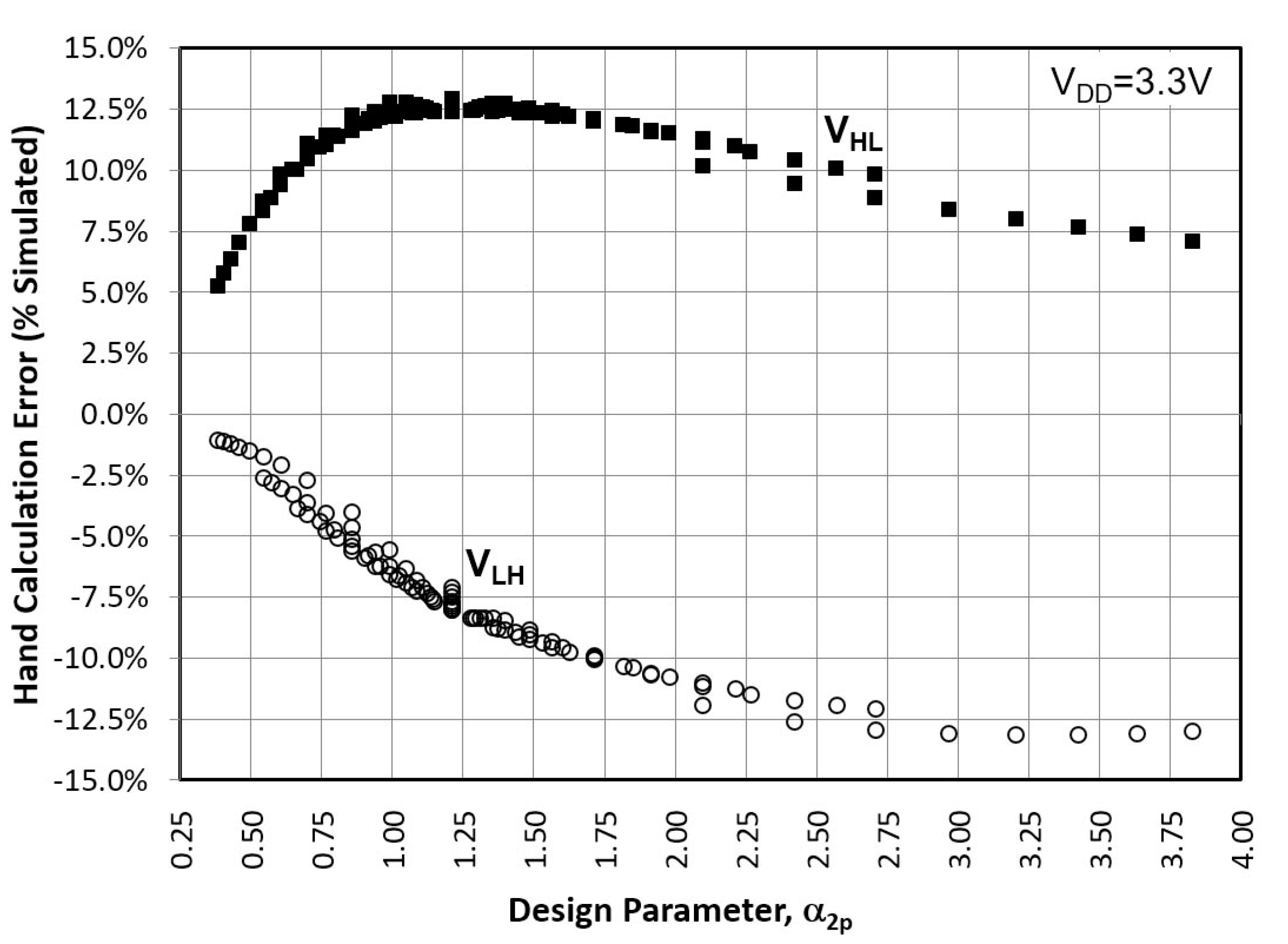
The hysteresis voltage can then be derived by using Equations (23) and (25), as follows:

$$\Delta V_H=\frac{1}{\left(1+{\alpha }_2\right)}\left(\frac{{\alpha }_2\cdot \left(V_{DD}-V_{thn0}\right)}{\left(1+{\alpha }_3\right)}+\frac{V_{DD}-\left|V_{thp0}\right|}{\left(1+{\alpha }_1\right)}\right)$$

(27)

Compared to Dokic’s original hysteresis equation (Equation (16) in [5]), (27) provides a transistor-level design strategy, that hysteresis voltage could be adjusted accordingly. The design parameters sensitivity (V_HL, V_LH, and ΔV_H) in terms of the individual transistor parameters (α_1, α_2, α₃) can also be determined by using the new design Equations (23), (25) and (27), which provides better insight for the design of CMOS-type Dokic ST.

The new design equations for N-, P-, and CMOS-type Dokic ST presented in this section also provides better hand calculation accuracy in the wide process, supply, and device parameters variation as presented in the next section.

2.2. CMOS-Type Schmitt Trigger by Steyaert

Figure 5a shows the CMOS type ST circuit by Steyaert [6]. It is composed of five transistors and has the hysteresis that is shown in Figure 5b. Depending on how the input signal changes, two I/O characteristics can be observed. If the input goes from low (0) to high (V_DD), the output state changes at V_LH, where the output goes from low (0) to high (V_DD) supply voltage. If the input goes from high (V_DD) to (0) low, in this case, the output changes its value at V_HL, where the output value goes from high (V_DD) to (0) low. The V_HL and V_LH can be found when input and output voltages are equal at the operating points OP1 and OP2, as shown in Figure 5b. During the analysis, we will assume that, without M5, the switching voltages of the two inverters are the same. Thus, the device sizes of M1 and M3 and M1 and M3 are the same. We also assume that there is a slight delay between voltages V_in and V_out due to the loading at the V₁ and output nodes.

2.2.1. V_LH Voltage

When the input is low (0 V), V₁ is high (V_DD). Transistors M2 and M3 are ON while M1, M4, and M5 are OFF. At OP1, the V_LH voltage is determined by equating the SAT currents of M1 and M2, like a regular CMOS inverter. Thus, the V_LH can be derived as:

$$V_{LH}=\frac{{\alpha }_1\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)+V_{thn0}}{\left(1+{\alpha }_1\right)}$$

(28)

where

$${\alpha }_1=\sqrt{\frac{{\beta }_2}{{\beta }_1}}$$

(29)

This formulation is the same as the one presented by Steyaert as Equation (1) in [6].

2.2.2. V_HL Voltage

When the input is high (V_DD), V₁ is low (0 V). Transistors M2 and M3 are OFF while M1, M4, and M5 are ON. At OP2, M2 turns ON, and the V_HL voltage could be determined by equating the SAT currents of M1, M2, and M5 while ignoring the channel-length modulation parameter (λ) of the transistors as follows:

$$V_{HL}=V_{HLA}\left(1+\sqrt{1-\frac{V_{HLB}}{V_{HLA}}}\right)$$

(30)

where

$${\alpha }_2=\sqrt{\frac{{\beta }_5}{{\beta }_1}}$$

(31)

and

$$V_{HLA}=\frac{\alpha _1^2·\left(V_{DD}-\left|V_{thp0}\right|\right)-V_{thn0}}{\left({\alpha }_1^2-1\right)} V_{HLB}=\frac{\alpha _1^2{\left(V_{DD}-\left|V_{thp0}\right|\right)}^2-V_{thn0}^2-{\alpha }_2^2{\left(V_{DD}-V_{thn0}\right)}^2}{\left({\alpha }_1^2-1\right)}$$

(32)

The formulation presented by Steyaert (Equation (2) in [6]) is given below, which is much simpler than Equation (30) above, but inaccurate for hand calculations as discussed in the next section.

$$V_{HL}=V_{LH}-\frac{{\alpha }_2\cdot \left(V_{DD}-V_{thn0}\right)}{2\cdot \left(1+{\alpha }_1\right)}$$

(33)

2.2.3. Hysteresis Voltage

The hysteresis voltage can then be derived by using Equations (28) and (30) as:

$$\Delta V_H=V_{HL}-V_{LH}=V_{HLA}\left(1+\sqrt{1-\frac{V_{HLB}}{V_{HLA}}}\right)-\frac{{\alpha }_1\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)+V_{thn0}}{\left(1+{\alpha }_1\right)}$$

(34)

Compared with the Steyaert’s formula, Equation (34) is more accurate, but less intuitive in designing the ST circuit. More accurate hysteresis voltage could be derived if we include the channel-length modulation mechanism, but the equation becomes more complicated and less intuitive.

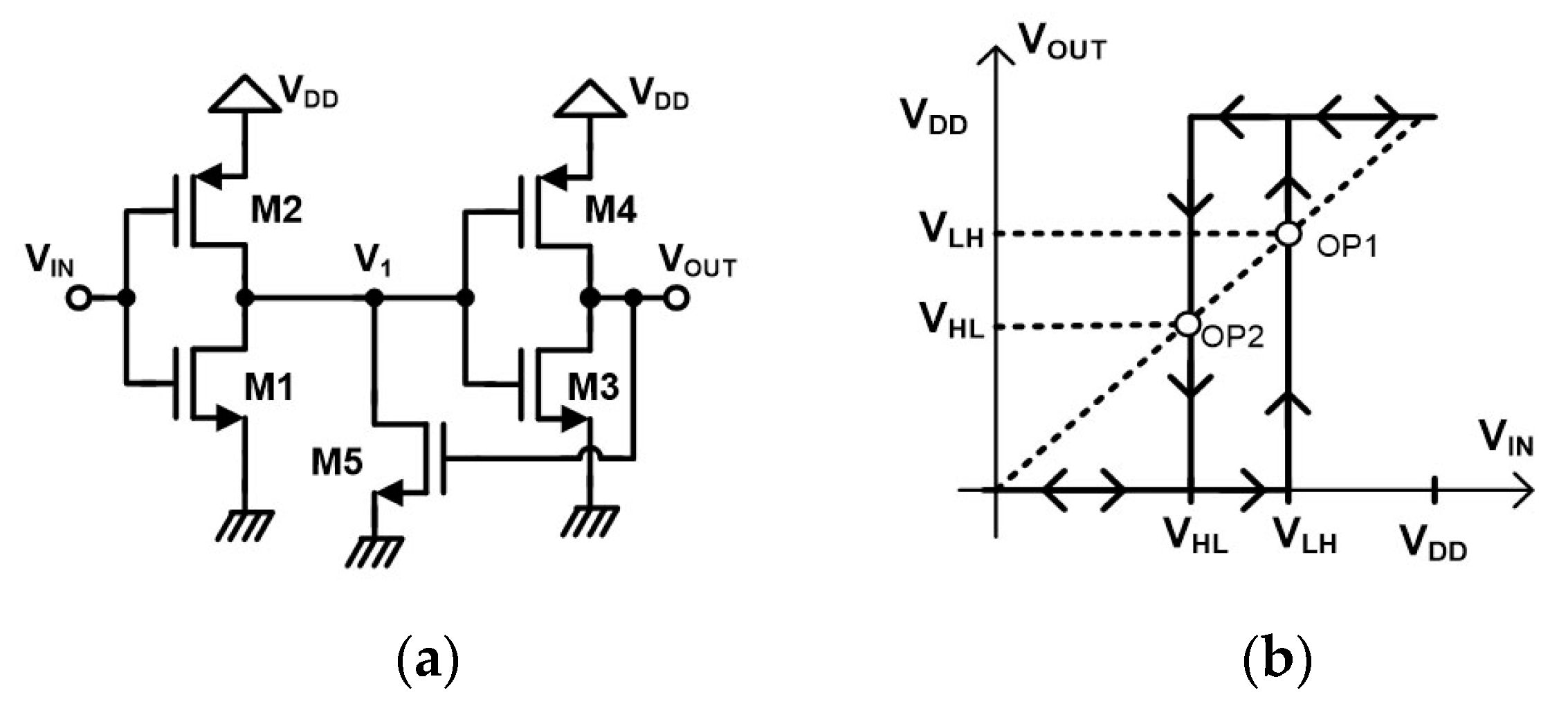
2.3. Non-Inverting Schmitt Trigger by Pedroni

Figure 6 shows the non-inverting ST by Pedroni [7]. It is composed of six transistors and its hysteresis is shown in Figure 6a. When the input goes from low (0) to high (V_DD) voltage level, the output state changes at V_LH where the output goes from low (0) to high (V_DD). If the input goes from high (V_DD) to (0) low, the output changes at V_HL, where the output goes from high (V_DD) to (0) low. The V_HL is defined by the switching point of the inverter composed of M1 and M2 and the V_LH is set by the inverter transistors M3 and M4, as shown in Figure 6b. Besides, the hysteresis exists only if V_SP3,4 > V_SP1,2.

Hysteresis Voltages

When the input is low (0 V), V₁ and V₂ are high (V_DD). M2, M4, and M5 are ON while M1, M3, and M6 transistors are OFF, and the output is 0 V. At OP1, V₁ becomes 0 V which turns off M5, and then the output floats maintaining its last state which is 0 V. The output only changes when V₂ becomes 0 V at OP2 where M6 turns ON and charges the output to V_DD. Thus, VLH occurs at the switching point (V_SP) of the upper inverter composed of transistors M3 and M4. Thus, V_LH = V_SP3,4 can be derived as follows:

$$V_{HL}=\frac{{\alpha }_1\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)+V_{thn0}}{\left(1+{\alpha }_1\right)}$$

(35)

where

$${\alpha }_1=\sqrt{\frac{{\beta }_4}{{\beta }_3}}$$

(36)

Similarly, the V_HL can be found as:

$$V_{HL}=\frac{{\alpha }_2\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)+V_{thn0}}{\left(1+{\alpha }_2\right)}$$

(37)

where

$${\alpha }_2=\sqrt{\frac{{\beta }_2}{{\beta }_1}}$$

(38)

The hysteresis voltage could then be derived as:

$$\Delta V_H=V_{HL}-V_{LH}=-\frac{(V_{DD}-\left|V_{thp0}\right|+V_{thn0})({\alpha }_1-{\alpha }_2)}{\left(1+{\alpha }_1\right)\left(1+{\alpha }_2\right)}$$

(39)

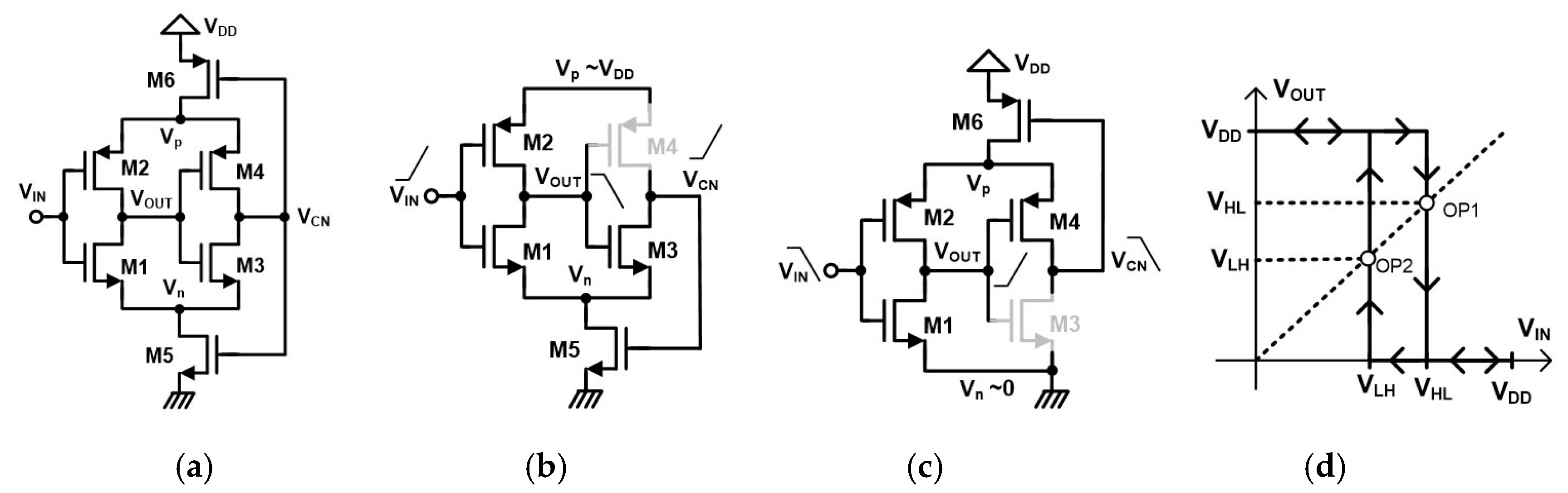
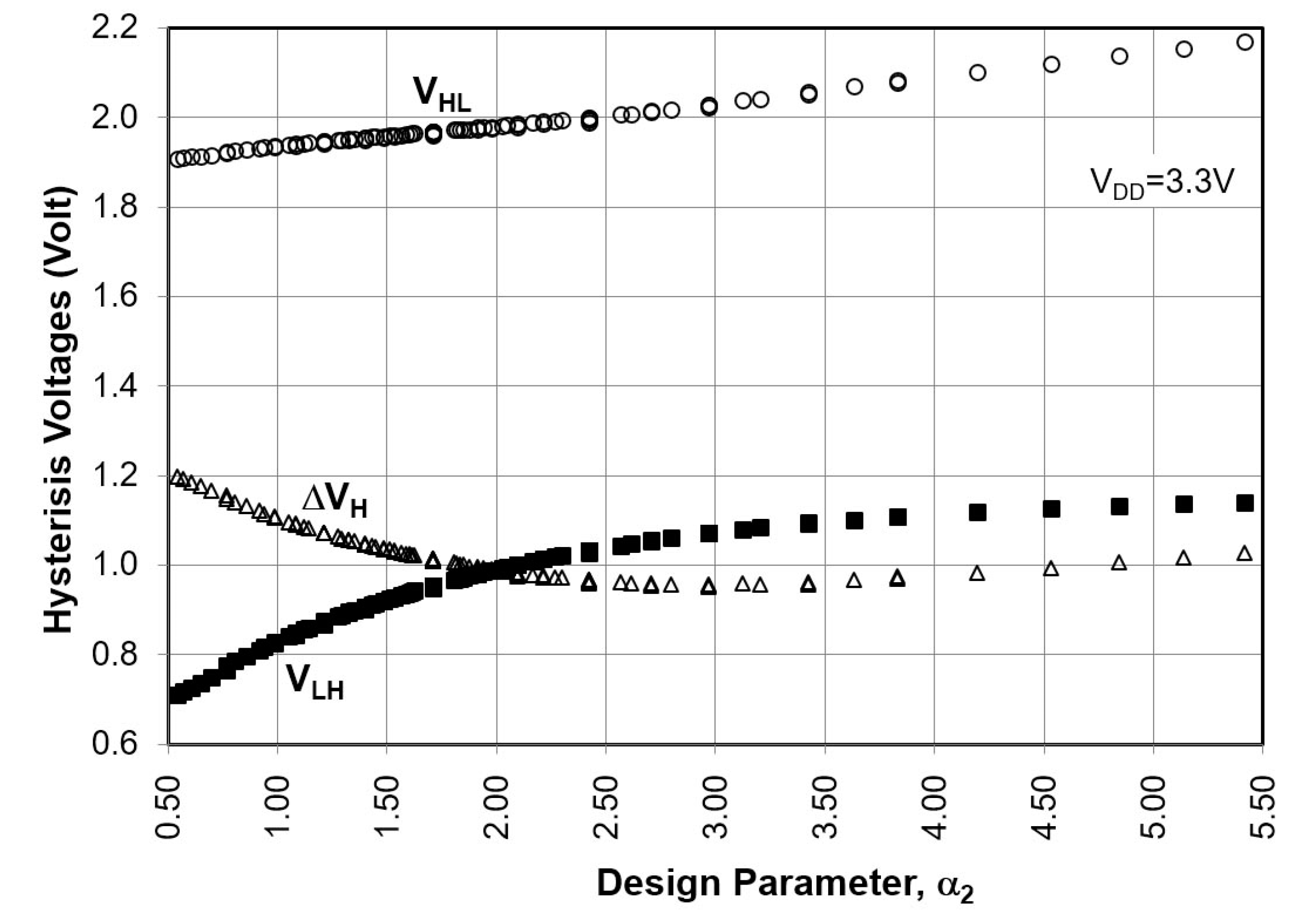
2.4. Low-Power CMOS-Type Schmitt Trigger by Al-Sarawi

Figure 7 shows the low-power CMOS-type ST by Al-Sarawi [8]. It is composed of six transistors and its hysteresis is shown in Figure 7d. Depending on how the input signal changes, two I/O characteristics can be observed: If the input goes from low (0) to high (V_DD) voltage level, the output state changes at V_HL where the output goes from high (V_DD) to low (0). If the input goes from high (V_DD) to low (0), in this case, the output changes at V_LH, where the output goes from low (0) to high (V_DD). The V_HL and V_LH can be found when the input and the output voltages are equal at the operating points OP1 and OP2, as shown in Figure 7b,c. For the analysis, the switching voltage of the two inverters is assumed to be the same. Thus, the device sizes of M1 and M3, and M2 and M4 are the same.

2.4.1. V_HL Voltage

When the input is low (0 V), V_out is high (V_DD). Since V_out is a high impedance node and M1 is OFF, V_CN drifts towards low (0) potential through the diode-connected M5 that works in the subthreshold region. While M3 works in the deep LIN region that V_DS3 is close to 0. As a result, M6 turns fully ON which pulls the node voltage V_P to V_DD. Thus, when input is low (0) at steady state, transistors M2, M6, and M3 are ON, M5 is in subthreshold and, other transistors are fully OFF. Assuming V_HL is larger than the threshold voltage of M1 at OP1, the V_HL switching voltage could be determined by equating the SAT currents of M1 and M2, like a regular CMOS inverter with finite V_n that keeps M5 on the edge of SAT and OFF regions.

$$V_{HL}=\frac{V_n+{\alpha }_1\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)+V_{thn0}}{\left(1+{\alpha }_1\right)}$$

(40)

where

$${\alpha }_1=\sqrt{\frac{{\beta }_2}{{\beta }_1}}$$

(41)

V_n could be found by using the equivalent circuit shown in Figure 7b. Here, it is assumed that the V_out node voltage is close to V_DD, and M3 shorts V_cn to V_n effectively connecting the gate of M5 to its drain, which keeps it in the SAT region. Thus, using SAT currents of transistors M1 and M5, we can determine the V_n voltage as follows:

$$V_n=\frac{V_{in}}{\left(1+{\alpha }_2\right)}+\frac{\left({\alpha }_2-1\right)\cdot V_{thn0}}{\left(1+{\alpha }_2\right)}$$

(42)

where

$${\alpha }_2=\sqrt{\frac{{\beta }_5}{{\beta }_1}}$$

(43)

Using (42) in (40) for V_in = V_HL, we can find the V_HL as follows.

$$V_{HL}=\frac{2·{\alpha }_2·V_{thn0}+{\alpha }_1·\left(1+{\alpha }_2\right)\cdot \left(V_{DD}-\left|V_{thp0}\right|\right)}{{\alpha }_1+{\alpha }_2·\left(1+{\alpha }_1\right)}$$

(44)

Compared to Al-Sarawi’s equation, Equations (42) and (44) are different than his V_n and V_HL equations (Equations (2) and (3) in [8]) due to his broad assumption of V_thn0 = |V_thp0| = V_th.

2.4.2. V_LH Voltage

When the input is high (V_DD), V_out is low (0 V). As a result, M4 is ON shorting drain and gate of M6 that keeps M6 at the edge of SAT and OFF regions. Thus, when the input is high (V_DD), transistors M1, M5, M4, and M6 are ON and the other transistors are OFF. At OP2, the V_LH voltage can be determined by equating the SAT currents of M1 and M2. Here, V_p could be considered as finite and less than V_DD, where M6 is on the edge of the SAT and OFF regions.

$$V_{LH}=\frac{{\alpha }_1\cdot \left(V_p-\left|V_{thp0}\right|\right)+V_{thn0}}{\left(1+{\alpha }_1\right)}$$

(45)

V_p could be found by using the equivalent circuit as shown in Figure 7c. Here, it is assumed that the V_out node voltage is approximately equal to 0 V, and M4 shorts V_cn to V_p effectively connecting the gate of M6 to its drain, which keeps it in SAT region. Thus, using SAT currents of transistors M2 and M6, we can determine the V_p voltage as follows:

$$V_p=\frac{V_{in}+{\alpha }_3\cdot V_{DD}+\left(1-{\alpha }_3\right)\left|V_{thp0}\right|}{\left(1+{\alpha }_3\right)}$$

(46)

where

$${\alpha }_3=\sqrt{\frac{{\beta }_6}{{\beta }_2}}$$

(47)

Using (46) in (45) for V_in = V_LH, we can derive the V_LH as follows:

$$V_{LH}=\frac{\left(1+{\alpha }_3\right)\cdot V_{thn0}+{\alpha }_1\cdot {\alpha }_3\cdot \left(V_{DD}-2\cdot \left|V_{thp0}\right|\right)}{1+{\alpha }_3\cdot \left(1+{\alpha }_1\right)}$$

(48)

Al-Sarawi derived the V_LH equation (Equation (4) in [8]) rather differently, which assumes V_LH = V_DD − V_HL as well as V_thn0 = |V_thp0| = V_th. This assumption results in a simple but inaccurate V_LH design equation. Additionally, his V_LH equation has a typographical error that causes gross calculation error larger than 200% of simulated values. The corrected equation that gives reasonable hand calculation error (<20% of simulated values) is given below. We used this corrected equation instead of Equation (4) in [8] to compare our new equation.

$$V_{LH}=V_{DD}\times \frac{\left(R+1\right)}{R_p\left(R+1\right)+1}-V_{th}\times \frac{R_p\left(2R-1\right)-1}{R_p\left(R+1\right)+1}$$

(49)

where

R = 1/α₁, and R_p = α₃

(50)

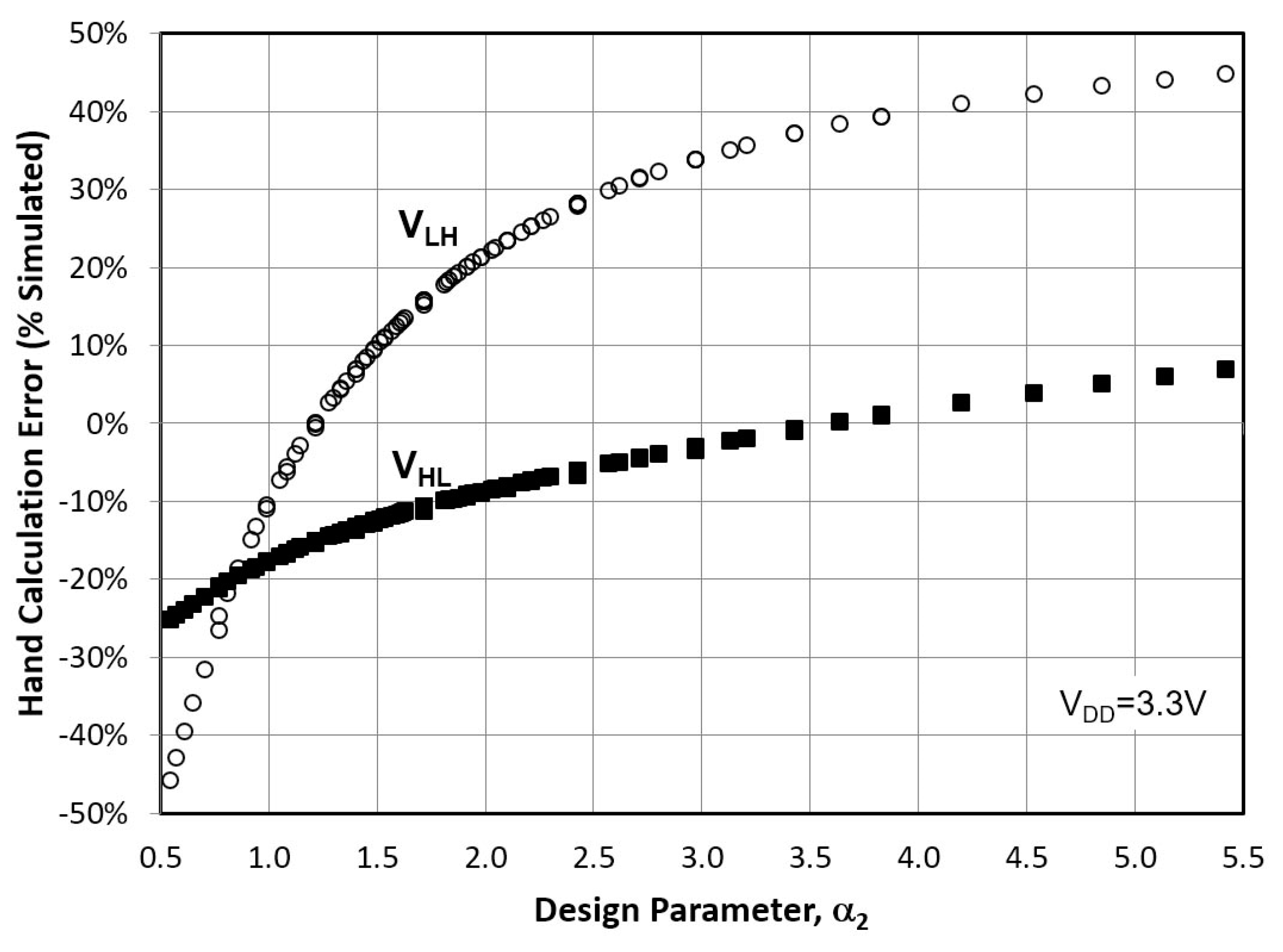
2.4.3. Hysteresis Voltages

Formulation provided by Al-Sarawi (Equations (2)–(4) in [8]) assumes that the threshold voltages of the NMOS and PMOS devices are the same and do not cover all design and process variations. Thus, the equations given in (44) and (48) are more detailed and useful for hand calculations and design for the hysteresis voltage (ΔV_H = V_HL − V_LH).

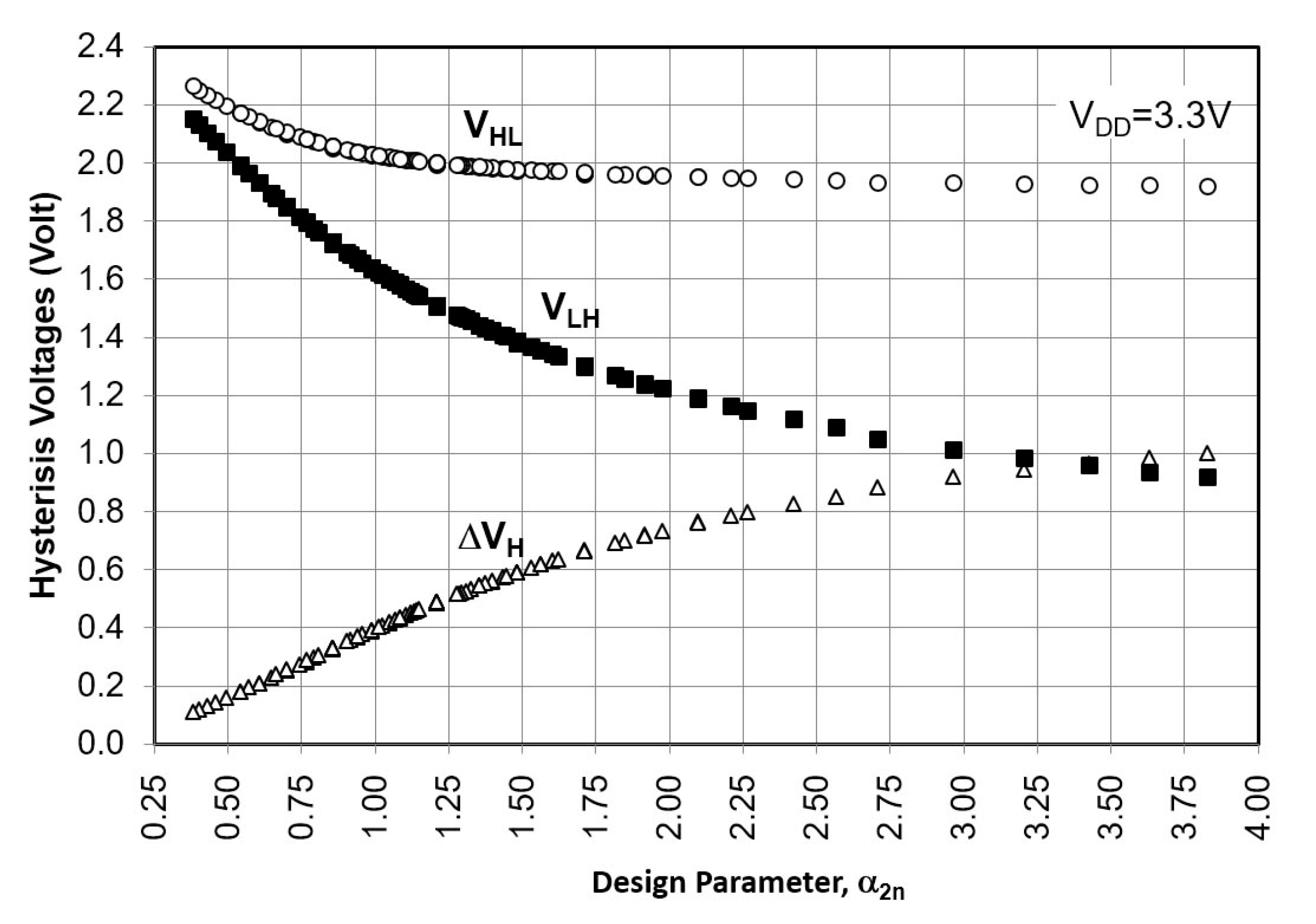
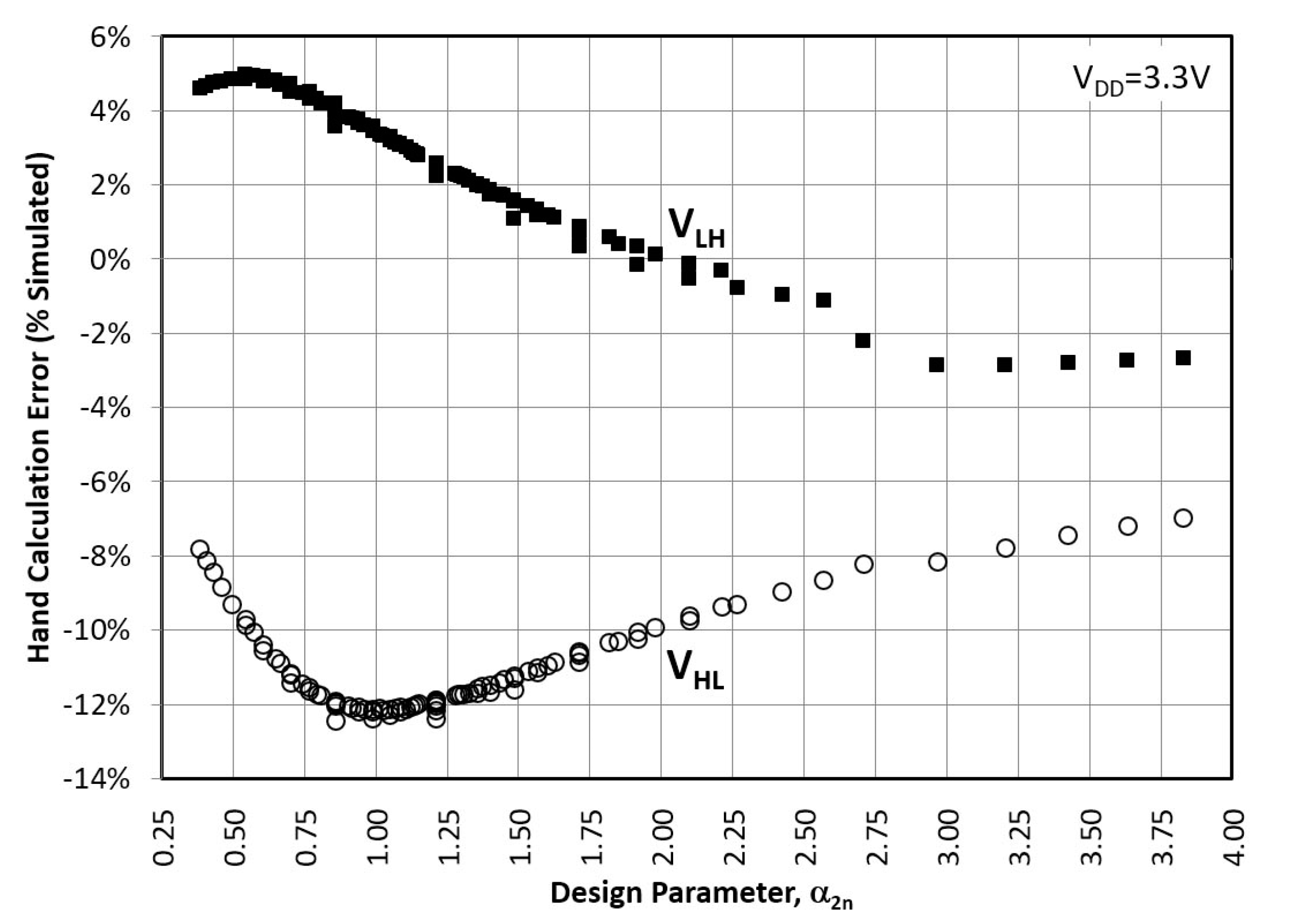
3. Comparison of Simulation and Hand Calculations

Simulations of all ST circuits were performed using a well established, analog/mixed-signal, 0.35 μm CMOS, 3.3 V, CMOS process with BSIM3v3 Spice models. The process has device characteristics listed in

Table 1. 0.35 μm CMOS process parameters for hand calculations.

Parameter	NMOS	PMOS
Transconductance (KP) (μA/V2)	170	58
Threshold Voltage (Vth0) (V)	0.50	−0.65

. This process allows a fair comparison with literature that used long channel MOSFET models and high supply voltages. We used a minimum channel length (L_min) of 0.35 μm and changed widths of transistors to cover a wide range of design spaces. In addition, Monte-Carlo, corner/parameter, or both, sweep simulations were run to find hysteresis voltages (V_LH and V_HL) under various conditions. Here, we only reported 3.3 V supply results at room temperature (T = 300 K), while similar trends were observed for other supply voltages.

3.1. Dokic ST Circuits

For the simulations of Dokic’s circuits, transistor widths were changed between 2 L_min and 20 L_min with 2 L_min steps such that channel widths of transistors M1, M2, and M4 were set equal to each other and M3 varied separately for P-type and N-type ST circuits. For CMOS type ST, widths of M1, M2, M6 and widths of M3, M4, M5 were set equal, respectively. Since minimum channel length was used for all transistors, setting α_1n, α_1p, α₁, and α₃ to 1.0 for all ST types, while α_2n and α_2p were varied between 0.383 and 3.83 for N-type and P-type circuits. For CMOS ST, α₂ was changed between 0.54 and 5.4. The bulk of all NMOS transistors were connected to ground and the bulk of all PMOS transistors were connected to V_DD.

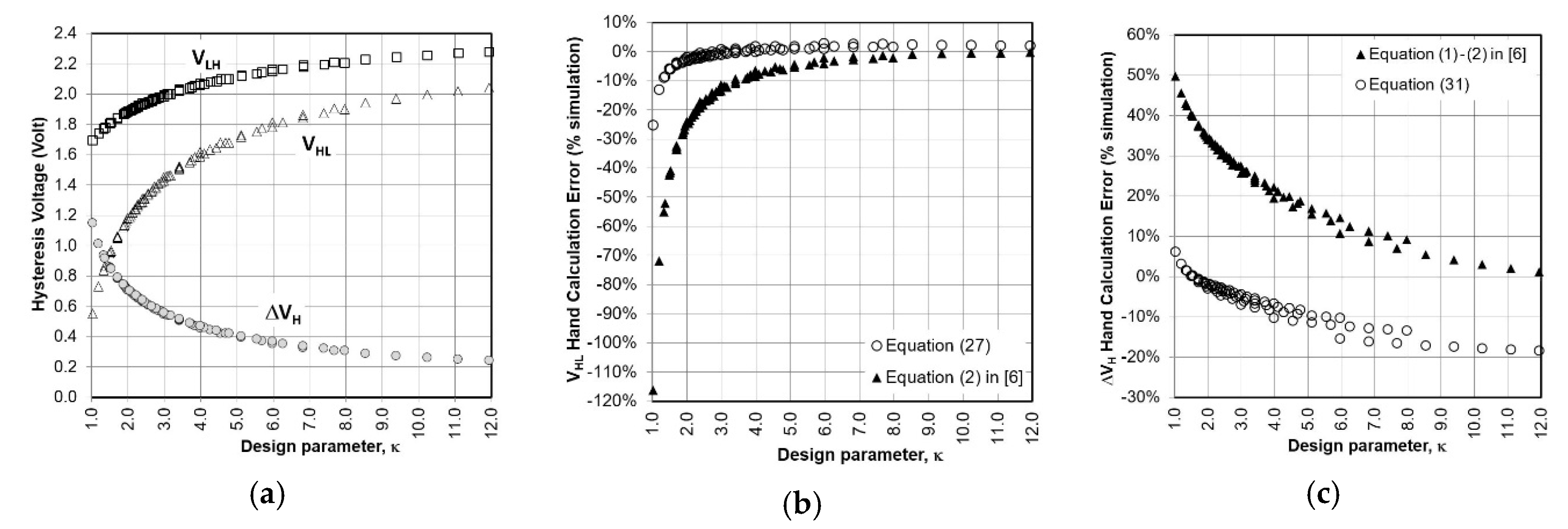
3.1.1. N-Type ST by Dokic

Figure 8 shows the simulation results for N-type Dokic ST. Hysteresis voltage (ΔV_H) as large as 1 V could be achieved for α_2n = 3.83. Moreover, smaller hysteresis voltages close to 0.1 V are also possible with N-type Dokic ST. Although they are not the same, Equations (15) and (17) result in the same V_HL and V_LH hand calculation values as the original Dokic equations (Equations (5) and (6) in [5]). Hand calculation accuracy compared to the simulation results are shown in Figure 9. Hand calculations result in lower than −13 and +5% errors for V_HL and V_LH, respectively. Wide hysteresis voltage can be achieved by choosing (W/L)_1,2,4 = 20 (α_1n = 1.0), and (W/L)₃ = 2 (α_2n = 3.83).

3.1.2. P-Type ST by Dokic

For P-type Dokic ST, the channel length of M3 is set to 4 L_min and the bulk of M4 is connected to the node V₁ while the dimensions of other transistors and bulk connections are kept the same as N-type Dokic ST. Figure 10 shows the simulation results of P-type Dokic ST for 3.3 V supply voltage. Hysteresis voltage (ΔV_H) as large as 0.9 V could be achieved for α_2p = 0.383. Moreover, hysteresis voltages close to 0.1 V are also possible with P-type Dokic ST for larger α_2p values. The simulation results for the hysteresis voltages for different device sizes and supply voltages show that, typically, the V_HL voltage is widely controlled by the design parameters. Figure 11 shows the hand calculation errors of the hysteresis voltages for the design parameter α_2p using Equations (19) and (20) (or with Equations (8) and (12) in [5]). The error could be less than ±13%.

3.1.3. CMOS-Type ST by Dokic

For CMOS-type Dokic ST circuit simulations, the bulk of M6 is connected to the node V₁. Figure 12 shows the simulation results for the 3.3 V supply voltage. Hysteresis voltage (ΔV_H) as large as 1.2 V could be achieved for α₂ = 0.54. The simulation results show that a smaller hysteresis voltage is not possible. Additionally, hand calculation equations (Equations (23) and (25)) and original Dokic equations (Equations (14) and (15) in [5]) do not provide good approximations that result in up to ±50% error for V_HL and between +10% and −25% error for V_LH, as shown in Figure 13.

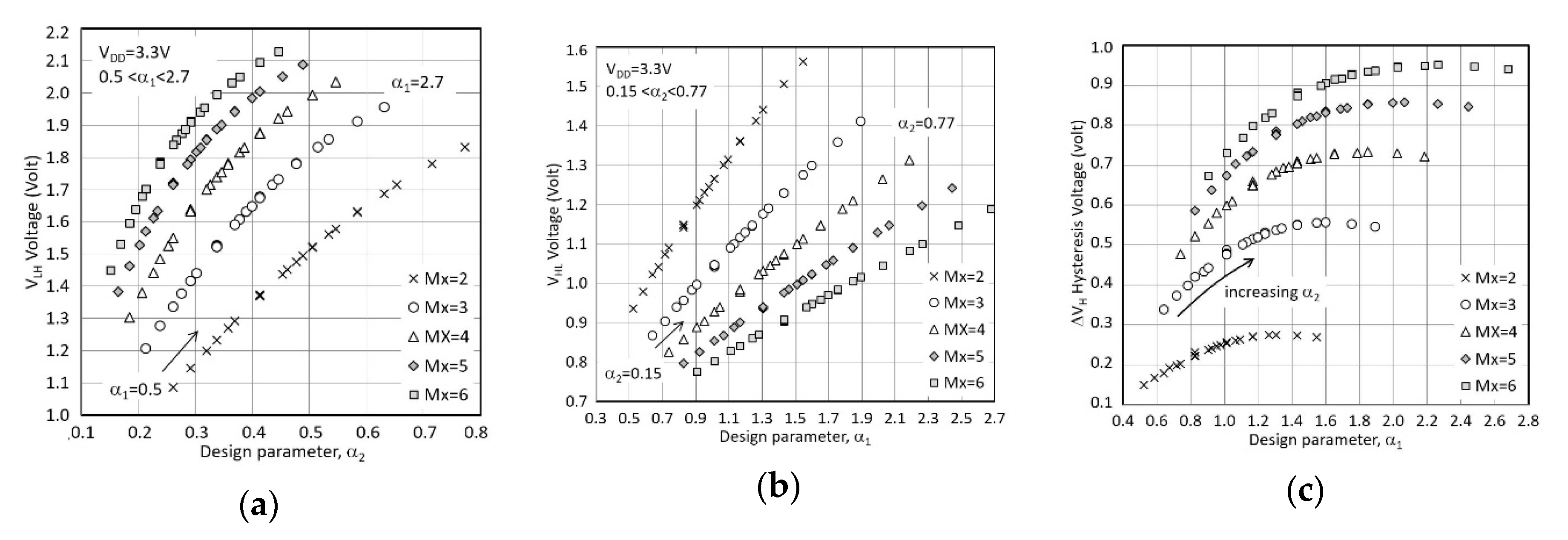
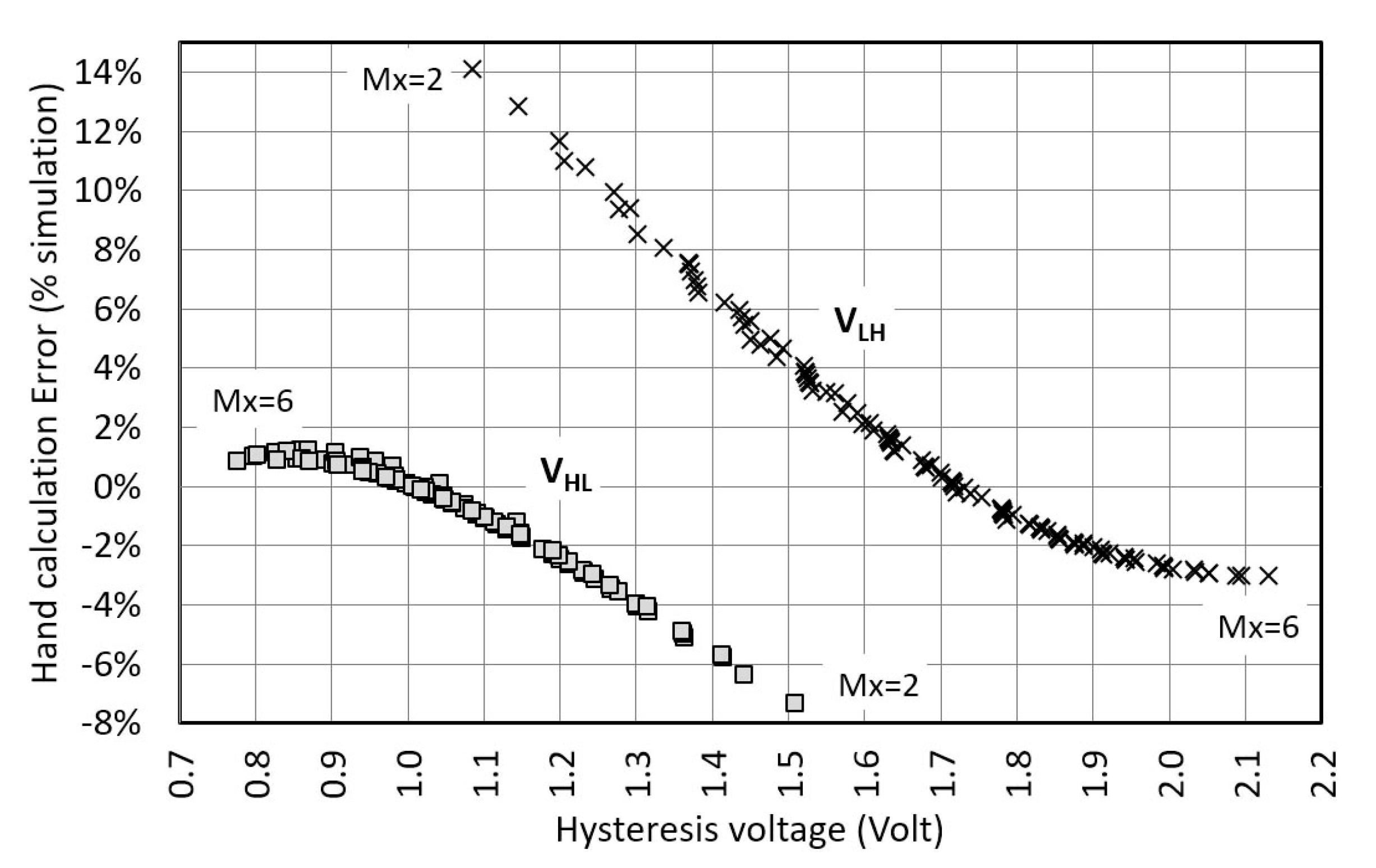
3.2. CMOS-Type ST by Steyaert

Transistor widths were changed between 2 L_min and 10 L_min with L_min steps for transistors M1, M3, and M5, and between 7 L_min and 14 L_min with 4 L_min steps for transistors M2 and M4 during the simulation. The channel lengths of NMOS and PMOS transistors were set to 10 L_min and L_min, respectively. As a result, a wide design space was covered for simulations and calculations. A new design parameter, the transconductance factor ratio (κ) which is defined as the ratio between β₂ (M2) and β₁ + β₅ (M1 and M5 combination) represents the design space. κ was set between 1.0 and 12. This results in the V_HL voltage being between 0.55 and 2.04 V, the V_LH between 1.7 and 2.30 V, and the hysteresis voltage between 0.24 and 1.15 V for 3.3 V supply voltage, as shown in Figure 14a.

Derived V_LH equation in this work, Equation (28), and the original Steyaert equation ((1) in [6]) are the same, resulting in a maximum −4% hand calculation error. Steyaert’s V_HL equation ((2) in [6]), on the other hand, results in gross hand calculation errors up to −120% for smaller κ values, while Equation (30) presented in this work results in less than −25% as shown in Figure 14b. As a result, overall hand calculation error for the hysteresis voltage ΔV_H by Equation (34) is lower than that of the original Steyaert equation, (Equations (1) and (2) in [6]), as shown in Figure 14c.

3.3. Non-Inverting ST by Pedroni

The hysteresis voltages of Pedroni ST can be set by modifying the sizes of NMOS (M1, M3, M5) or PMOS (M2, M4, M6) transistors. For simulation, NMOS transistor widths were changed between 2 L_min and 10 L_min with 2 L_min steps. The multiplication factor (M) of M1 is set to M_x and M3 and M5 is to unity, respectively. Similar widths and steps used for the PMOS transistors while setting the multiplication factor of M4 to be Mx, and keeping the multiplication factor of M2 and M6 to be unity. The channel length of NMOS and PMOS transistors were set to L_min or 0.35 μm. Multiplication factor of transistor M1, M4, the M_x, varied from 2 to 6 while other Ms were kept constant at unity so that a wide range of V_HL and V_LH voltages were achieved.

Design parameter M_x, α₁, and α₂ can be used for setting hysteresis voltages (V_HL, V_LH, and ΔV_H) as shown in Figure 15. Hysteresis voltage as large as 1 V can be achieved by increasing all design parameters, however, this will result in a large silicon footprint. Equations (35) and (37) predict the hysteresis voltages, V_HL, and V_LH with +14% to −8% calculation errors as shown in Figure 16.

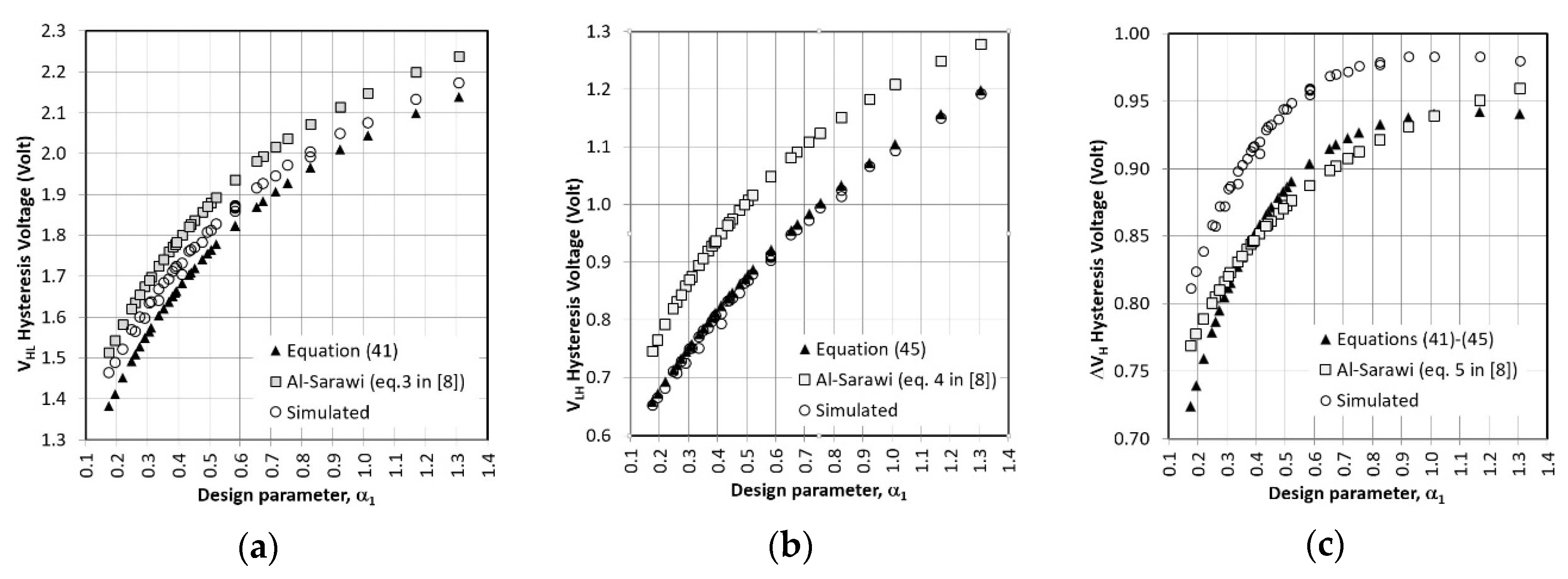
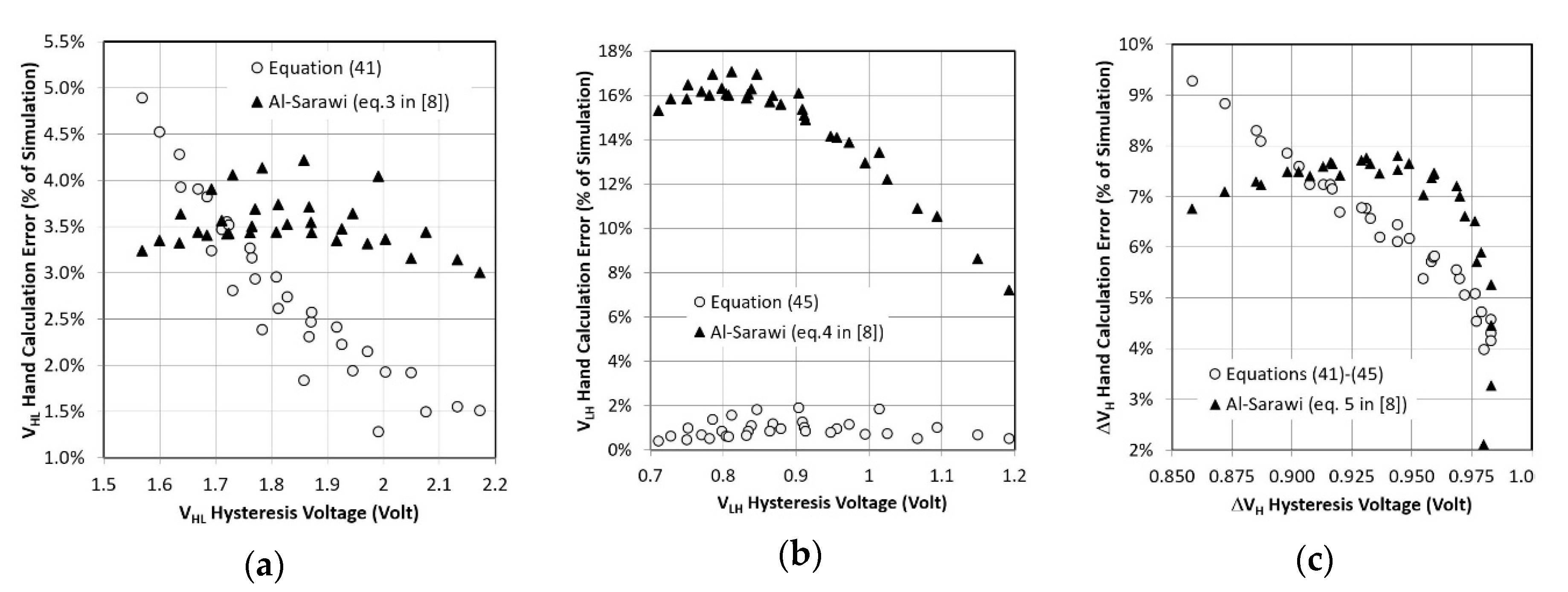
3.4. CMOS-Type ST by Al-Sarawi

The sensitivity of the V_HL to α₁ parameter, which can be derived from Equation (44), is much higher than the α₂ and α₃ parameters. Thus, for simulation and evaluation of the design equation accuracies, α₁ parameter varied from 0.15 to 1.3 while α₂ and α₃ were set to 1.41 and 2, respectively. We proposed new hysteresis design equations for the Al-Sarawi ST. Figure 17 shows the simulated and calculated values by using Al-Sarawi’s original design equation and the proposed design Equation (44) of the hysteresis voltages V_HL, V_LH, and ΔV_H versus α₁ parameter. The simulation results show that the ΔV_H reaches 0.98 V (Figure 17c), which is larger than Al-Sarawi’s original design equation. However, it saturates around these values even if α₁ parameter is increased.

Figure 18 illustrates the hand calculation errors of proposed design equations in Section 2.4 as well as Al-Sarawi’s original design equations related to the simulated values of V_HL, V_LH, and ΔV_H. It can be noticed from Figure 18b that V_LH hand calculation error of the proposed design Equation (48) is less than 2% while it could be as large as 17% for Al-Sarawi’s original design equation. Additionally, hand calculation errors of V_HL and ΔV_H by the proposed design equations are always inversely proportional to V_HL and ΔV_H, respectively, and are lower than the calculation errors of Al-Sarawi’s original design equations.

3.5. Comparison of All Circuits

Table 2. Performance comparison of the six ST circuits.

ST Circuit	Trise (ns)	Tfall (ns)	Area(μm)	Power (μW)	ΔVH (V)	FoM
Dokic (N) [5]	1.636	0.109	7.60	58.51	1.110	1.43
Dokic (P) [5]	0.412	1.507	6.86	61.58	0.855	1.05
Dokic (CMOS) [5]	1.239	0.372	7.80	75.31	1.015	1.07
Steyaert [6]	1.308	3.043	38.20	186.48	1.150	0.04
Pedroni [7]	0.425	0.338	13.70	63.20	0.952	1.44
Al-Sarawi [8]	1.320	1.185	5.40	43.23	0.983	1.68

summarizes a comparison between Dokic [5], Steyaert [6], Pedroni [7], and Al-Sarawi [8] ST circuits in terms of total area, simulated power consumption, transition delays, and maximum hysteresis voltage based on the variation of device dimensions. There are tradeoffs among these parameters that the larger ΔV_H design may have the higher-power consumption or the larger footprint or the lower speed. By design, it is desirable to have larger ΔV_H, and smaller delay, area, and power consumption. Thus, we propose a figure of merit (FoM) based on these parameters. FoM for ST circuits can be calculated using the following equation:

$$FoM=\frac{10000\times \Delta V_H\left(V\right)}{Area\left(\mathsf{\mu }{m}^2\right) \times Power consumtion\left(\mathsf{\mu }W\right)\times Delays\left(ns\right)}$$

(51)

This equation is scaled by a multiplying factor of 10,000 for better number representation. Delay was measured at 50% of the supply voltage level when a 100 fF loading is added at the output of each ST design. The sum of rising (t_rise) and falling times (t_fall) was calculated as the delay.

From Table 2, if the large hysteresis voltage is the main requirement, the Steyaert ST circuit is the best, yet it has the lowest FoM due to large power consumption and area. Overall, Al-Sarawi’s ST circuit offers the best FoM. However, it is slower than Pedroni’s ST, which is the second-best choice among the investigated topologies.

4. Conclusions

In this paper, detailed reviews of Dokic [5], Steyaert [6], Pedroni [7], and Al-Sarawi [8] SISO ST circuits are presented. The paper starts with the detailed derivation of the hysteresis voltages (V_HL, V_LH, and ΔV_H) for each topology. Then, we propose some new design equations which result in a more intuitive, and accurate design through hand calculations. Simulations were run to verify that the derived and the original design equations are accurate. The simulations were carried out in a well-established 0.35 μm/3.3 V analog/mixed-signal CMOS process. For each ST circuit, hysteresis voltages (V_HL, V_LH, and ΔV_H) were calculated with respect to different device sizes, which cover wide design space at a process supply voltage of 3.3 V. The hand calculation results derived from both the original and the new design equations were presented for each ST circuit and are compared with simulation results. The comparisons show that the new design equations are better than the original ones in terms of accuracy and intuition. Finally, the proposed FoM in Equation (51) can work as a criterion to compare different ST circuits. It is found that Al-Sarawi’s ST circuit offers the best FoM of the investigated topologies.