Abstract
Ultra-low-voltage operation improves energy efficiency of logic circuits by a factor of 10×, at the expense of speed, which is acceptable for applications with low-to-medium performance requirements such as RFID, biomedical devices and wireless sensors. However, in 65/45 nm CMOS, variability and short-channel effects significantly harm robustness and timing closure of ultra-low-voltage circuits by reducing noise margins and jeopardizing gate delays. The consequent guardband on the supply voltage to meet a reasonable manufacturing yield potentially ruins energy efficiency. Moreover, high leakage currents in these technologies degrade energy efficiency in case of long stand-by periods. In this paper, we review recently published techniques to design robust and energy-efficient ultra-low-voltage circuits in 65/45 nm CMOS under relaxed yet strict timing constraints.
1.Introduction
Low power consumption is nowadays paramount for digital integrated circuits. High-performance chips such as multi-core processors for servers are power constrained by the die temperature limit and by both the cooling and electricity costs [1]. Portable applications such as smart phones obviously have an even tighter power budget for battery life concern, which drove innovation during the last decade in advanced power management techniques [2]. Besides these mainstream designs stands another chip category: ultra-low power circuits for applications such as RFID, biomedical devices and sensor networks [3]. These application have in common a minute power budget as the circuits should operate either on tiny batteries (<1 cm3 [4]) or harvest energy from their environment [5]: from a few nW to hundreds of μW. Fortunately, these applications feature low-to-medium speed requirements with target clock frequencies ftarget from 10 kHz to 50 MHz, depending on the application and circuit topology. These relaxed speed constraints give room for power savings beyond simple frequency scaling or duty-cycled operation. Indeed, the supply voltage Vdd can be scaled down to reduce the energy required to switch on-chip capacitances at each clock cycle
as the associated delay penalty is acceptable given the relaxed cycle time Tcycle at low-to-medium ftarget. Ultra-low-voltage operation is the extreme case where Vdd is aggressively scaled down to 0.3–0.5 V with potential energy savings above 10× when compared to nominal-Vdd operation at 1–1.2 V
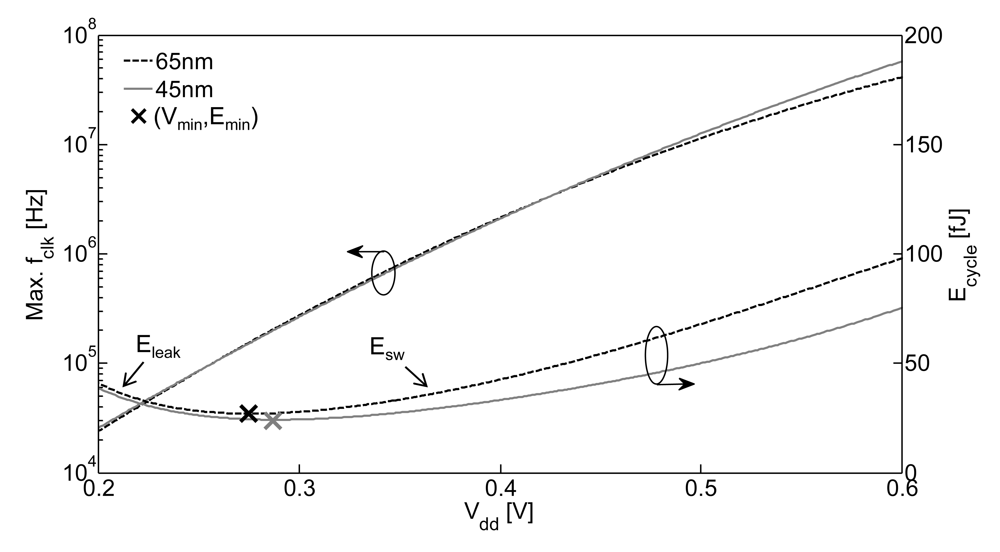
Ultra-low-voltage (ULV) operation was proposed in the 1970s [7,8] and put back in light for digital circuits in 1999 at the Int. Symp. on Low-Power Electronics and Design [9]. When Vdd is reduced to or below the threshold voltage Vt, MOSFETs start to operate in near-threshold or subthreshold regime [8,9]. As the subthreshold Ion current is exponentially dependent on Vdd, the gate delay dramatically increases. As shown in Figure 1, it significantly reduces the maximum clock frequency for digital circuits. The resulting Tcycle penalty also has a detrimental side effect on the total energy per cycle composed by switching and leakages contributions: Ecycle = Esw + Eleak. Indeed, the leakage energy increases when reaching subthreshold regime as it results from the integration of leakage power over Tcycle: Eleak = VddIleak × Tcycle. There is thus an optimum supply voltage Vmin, which minimizes the energy to an Emin level [10], as depicted in Figure 1. The Vmin level is often comprised between 0.25 and 0.5 V depending on the ratio between Esw and Eleak, which varies accordingly to circuit parameters and technology characteristics through total leakage current Ileak, average switched capacitance per cycle CL, gate delay and number of gates in the critical path [11]. This concept known as the minimum-energy point has received a lot of attention in the research community during the last decade [3,12] with numerous successful ULV chip implementations: microcontrollers for biomedical applications [13,14] for wireless sensor nodes [5,15] as well as dedicated ASICs for biomedical applications [16,17], communication [18], image processing [19,20] or RFIDs [21].
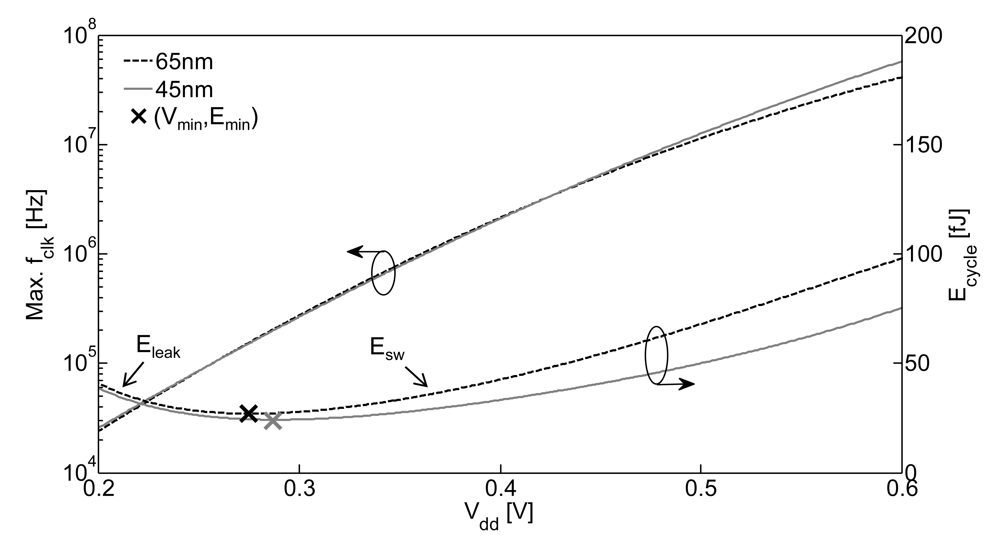
Figure 1.
Maximum clock frequency fclk and corresponding energy per cycle Ecycle at ultra-low voltage (SPICE simulations of an 8-bit multiplier [6] in 65 and 45 nm LP CMOS technologies, at 25 °C, nominal results).
Along with this ULV trend, new CMOS technology nodes have been introduced to maintain the historical increase in on-chip device density. Unfortunately in nanometer CMOS technologies, reaching Emin in practice raises important challenges because ULV operation magnifies the sensitivity of circuits against MOSFET variability, short-channel effects and leakage currents [6,12]. Several design solutions have recently been proposed to reliably operate nanometer CMOS logic circuits at ultra-low voltage under relaxed yet strict timing constraints: gate length upsize [6], process flavor [22] and MOSFET selection [23], circuit adaptation [22] and power gating [24]. In this paper, we provide for the first time a unified review of:
- The pitfalls of nanometer ULV circuits limiting their minimum Vdd for functional robustness and timing closure;
- The detrimental impact of stand-by periods on energy efficiency;
- The proposed techniques to overcome these limitations.
We specifically target 65 and 45 nm CMOS nodes as they share many characteristics: multiple process flavors, std-κ oxide/poly-Si gate stack and strained-Si, which give similar behaviors at ultra-low voltage as shown in Figure 1. To illustrate the findings, we combine chip measurements in 65 nm and simulation results in 45 nm. The results are based on the work carried out in this field at UCLouvain and more specifically on papers [6,22,24,25].
The paper is organized as follows. In Section 2, we recall the impact of CMOS technology scaling on ULV circuits and set up a framework for evaluating energy-efficiency under robustness and timing constraints. We then address the impact of these constraints on the minimum ultra-low Vdd: the speed limit and the functional limit in Sections 3 and 4, respectively. Existing solutions are also presented. Section 5 finally deals with the impact of stand-by periods on energy efficiency, given these constraints on minimum Vdd.
2. Energy Efficiency of ULV Circuits in Nanometer CMOS Technologies
CMOS technology scaling driven by Moore's law increases MOSFET density on a chip by a factor of two every 18–24 months. This is particularly useful for increasing the functionality of CMOS circuits without increasing die area and thereby by keeping manufacturing costs acceptable. It also boosts speed performances at each technology generation while reducing the energy required to perform a given function [26]. ULV circuits for ultra-low-power applications similarly benefit from these enhancements. Indeed, Esw is effectively reduced thanks to lower on-chip capacitances CL while gate delay at ultra-low voltage is improved thanks to a higher subthreshold Ion current resulting from the scaled Vt [12]. This leads to boosted speed performances at the minimum-energy point.
However, CMOS technology scaling also comes with severe drawbacks when reaching nanometer CMOS nodes: leakage currents including subthreshold Ioff current and gate tunneling leakage [27], short-channel effects [27] and variability [28]. The impact of these nanometer MOSFET effects are magnified at ultra-low voltage [12]. A first consequence at device level is a reduction of the effective Ion/Ioff ratio due to lower Vt values and short-channel increase of the subthreshold swing and of the drain-induced barrier lowering (DIBL) effect. A major consequence at circuit level is on the minimum-energy level Emin which stopped scaling from 90 nm node and actually increases significantly at 45 nm node because of the combined effects of subthreshold swing, DIBL, gate leakage and statistical variability [29]. Fortunately, this Emin increase can be limited by choosing the optimum MOSFET (medium gate length and low Vt) within a versatile yet standard CMOS technology menu with good speed performances and negligible area penalty [23]. Moreover, fully-depleted Silicon-on-Insulator (SOI) technology can further save 60% of Emin [29] although this technology is not yet commercially available for industrial circuit design.
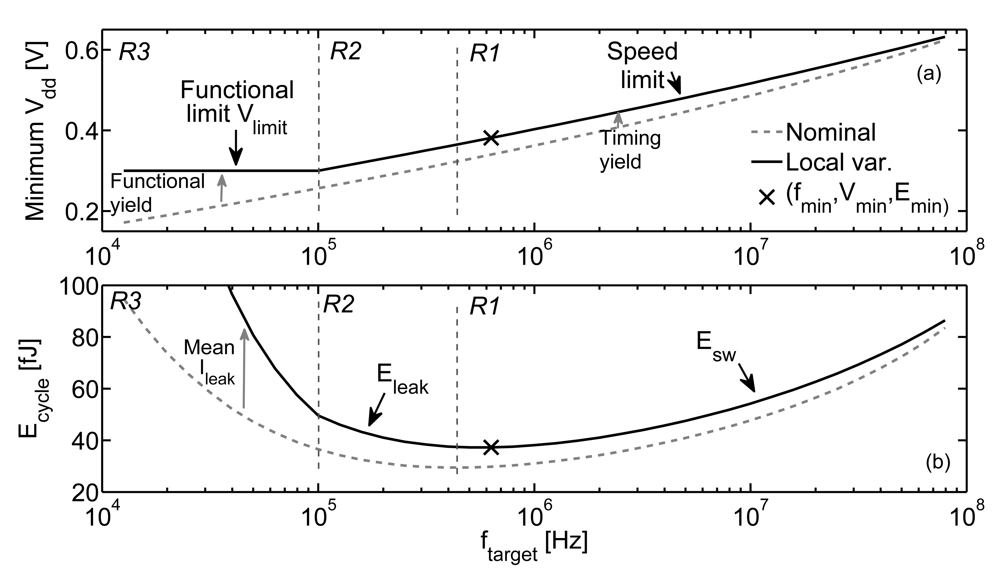
Beyond Emin scaling trend, a key challenge for ULV circuit design in nanometer CMOS technologies is to reliably operate at the corresponding supply voltage Vmin of the minimum-energy point. Indeed, as shown in Figure 2(a), the minimum Vdd for a logic circuit is given by both timing and robustness constraints [6]. Speed must be sufficient to meet the timing constraint associated with the target frequency ftarget of the application. The delay of the critical path has to be shorter than the cycle time Tcycle = 1/ ftarget. Moreover, even if safe timing closure is achieved, there is a functional limit Vlimit on Vdd, which is independent from ftarget. We set up a framework for evaluating energy efficiency under timing and robustness constraints in [6], illustrated in Figure 2. This framework shows that the ftarget range of ultra-low-power applications can be divided into 3 regions for ULV circuits:
- R1 region where Esw dominates and minimum Vdd is speed limited,
- R2 region where Eleak dominates and minimum Vdd is speed limited,
- R3 region where Eleak dominates and minimum Vdd is limited by functionality.
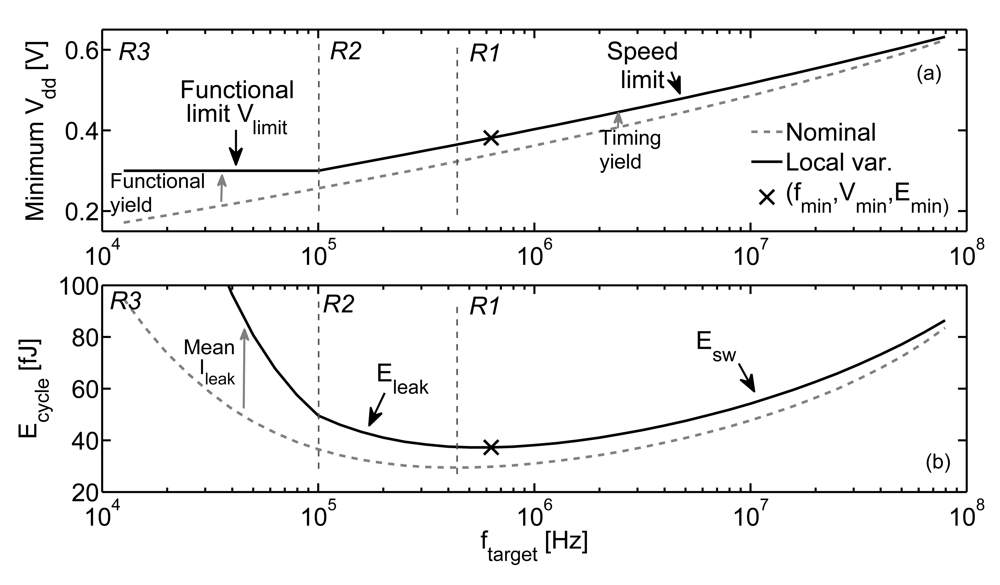
Figure 2.
Minimum Vdd and energy per cycle Ecyclevs. the target frequency of the application ftarget (SPICE simulations of an 8-bit multiplier [6] in 45 nm LP CMOS technology, at 25 °C, Monte-Carlo simulations addresses local variations through statistical extraction of worst-case speed and functional limits as well as mean Ileak).
Within this framework, it is obvious that Emin is only reached at one particular clock frequency fmin corresponding to a Tcycle equal to the critical path delay at Vmin. fmin is in R1 region as Eleak accounts for 30% of Ecycle at the minimum-energy point. Emin can thus only be reached for one particular target frequency. If ftarget is higher than fmin, switching energy is wasted because Vdd is higher than Vmin and, if ftarget is below fmin, leakage energy is wasted because leakage power is integrated over a prohibitively long Tcycle. For example, Emin of an 8-bit multiplier in a 45 nm LP (Low-Power) CMOS technology is reached at Vmin = 0.38 V and fmin = 630 kHz, as shown in Figure 2. Ecycle is within Emin + 10% between 200 kHz and 2 MHz. For ftarget outside this range, Figure 2 shows that practical energy under robustness and timing constraints can thus significantly differ from Emin [6].
As the minimum-energy point (Vmin,fmin,Emin) varies with technology generations according to technological characteristics [12], there is an optimum CMOS technology node for each ftarget that minimizes Ecycle under timing and robustness constraints [12,30]. However, using an older CMOS technology is not optimum regarding die area and thus high-volume manufacturing costs. For this reason, we focus in this paper on techniques to reliably operate ULV logic at the minimum-energy point in 65/45 nm CMOS technologies.
Finally, let us introduce here that statistical MOSFET variations in nanometer CMOS technologies due to random dopant fluctuations, line edge roughness, oxide thickness variations, etc. have an important impact on energy efficiency. Indeed, these variability sources induce local within-die random Vt variations that exponentially affect subthreshold Ion and Ioff [31]. The consequences at circuit level are [6]:
- A guardband on Tcycle or on the minimum Vdd for sufficient timing (parametric) yield because worst-case delay of critical paths has to be considered given its large statistical distribution;
- Increase in functional limit Vlimit voltage to ensure sufficient functional yield for large chips;
- Increase in mean leakage Ileak because Ileak is a lognormal distribution (exponentially dependent on the normally-distributed Vt) with a mean value higher than the typical one.
It has further been reported that Esw is also statistically distributed in nanometer ULV circuits because local gate delay distribution introduces random glitches with Esw penalties [32]. However, for the sake of simplicity we do not consider this effect in this paper.
As shown in Figure 2, statistical variability leads to energy penalties. As local variations can hardly be compensated by circuit adaption due to their randomness from a MOSFET to another, it is important to consider statistical variability when designing ULV circuits in nanometer CMOS technologies. In next sections, we review the constraints on minimum Vdd to ensure circuit robustness given this high local variability in nanometer CMOS technologies.
3. Speed Limit on Vdd
3.1. Timing Constraint and the Minimum-Energy Point
The first constraint on minimum Vdd is a timing constraint on the critical path delay, which have to be lower than Tcycle given by the ftarget of the application. Typical ftarget for ultra-low-power circuits ranges from 10 kHz to 50 MHz. As explained in Section 2, minimum energy of ULV circuits can only be reached at a single clock frequency fmin. The challenge for the designers is thus to tune the circuit to make fmin meet the ftarget of the application. This can be done by changing the Vt of MOSFETs in the circuit. Indeed, reducing Vt will exponentially boost speed performances at ultra-low voltage through an exponential increase of subthreshold Ion which can be expressed from the subthreshold drain current expression [6]:
where I0 is a reference current proportional to the MOSFET size W/Lg that exponentially depends on Vt, S is the subthreshold swing, Uth the thermal voltage and ηDIBL the drain-induced barrier lowering (DIBL) factor. The impact of Vt reduction on Eleak at a given ultra-low Vdd is not significant [11]. Indeed, as Ileak is often dominated by subthreshold leakage in 65/45 nm CMOS, the exponential Ileak increase from a Vt reduction through I0 parameter is compensated by the shorter critical path delay and thus Tcycle, as long as the MOSFETs remain in subthreshold regime:
where LD is the logic depth (number of gates in the critical path) and gate delay is modeled with CV/I approximation. By changing I0 reference current through Vt tuning, the voltage Vmin and energy level Emin of the minimum-energy point are thus not modified while fmin can be exponentially tuned to make it corresponds to the ftarget of the application.
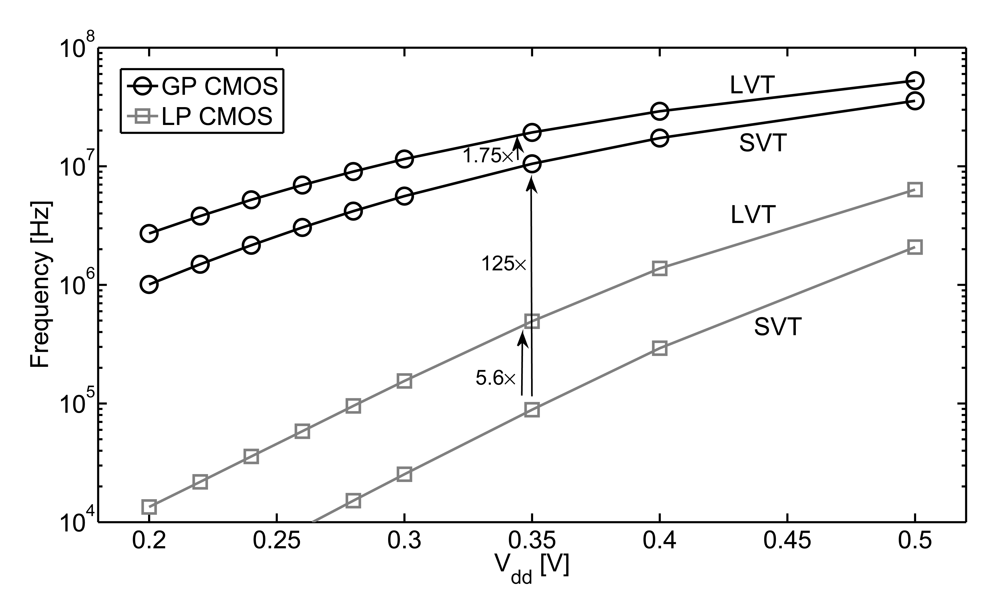
Standard nanometer CMOS technologies feature a versatile technology menu with several process flavors targeting different applications: General-purpose (GP) also called generic (G) process targets high-performance applications with short gate delay and relaxed leakage constraints while low-power (LP) process targets portable applications with relaxed speed and tight leakage constraints [22]. GP flavor features short gate length, low Vt and thin oxide for maximizing Ion at nominal Vdd whereas LP flavor feature longer gate length and higher Vt for subthreshold leakage concern and thicker oxide for gate leakage concern. As a result, subthreshold current varies by several orders of magnitude between GP and LP flavor through I0 reference current. Figure 3 illustrates this fact with the measured frequency of 65 nm ring oscillators in GP and LP flavors. At 0.35 V for example, GP flavor frequency (11 MHz) is 125 × higher than LP flavor frequency (88 kHz). Notice that this speed difference is much higher than at nominal 1–1.2 V Vdd because of the exponential dependence of subthreshold current on Vt at ultra-low voltage.
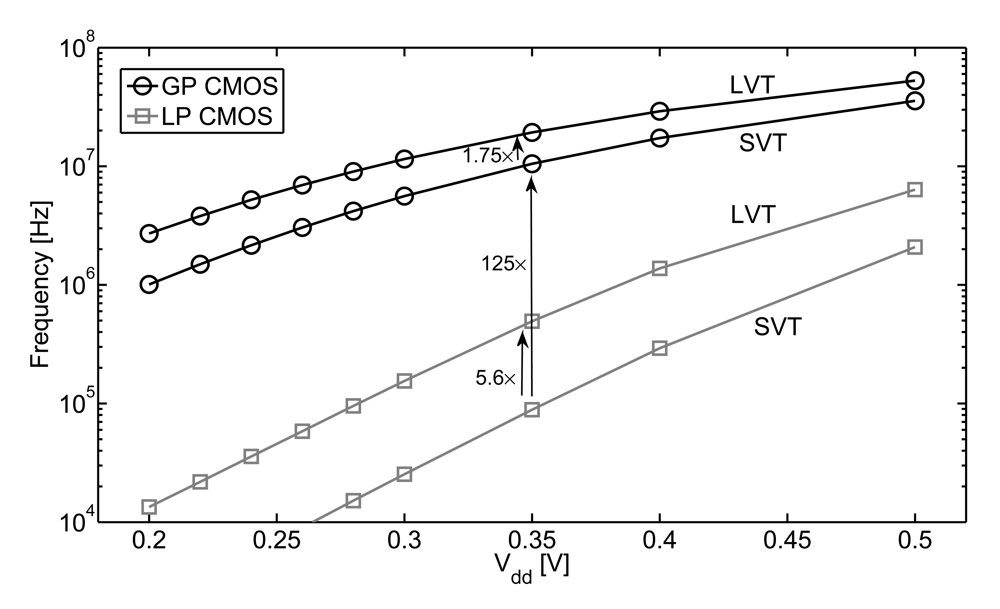
Figure 3.
Measured speed for different CMOS flavors and Vt's (measurements of 251-stage ring oscillators with FO1 inverters [25] in 65 nm LP/GP CMOS technology, at 25 °C, mean frequency of 20 measured dies).
We thus showed in [22] that process flavor selection can effectively be used to operate at the minimum-energy point (Vmin, Emin) for a wide ftarget range. LP flavor can be used for frequencies between 10 kHz and 1 MHz, and GP flavor can be used for frequencies between 1 and 50 MHz. Moreover, nanometer CMOS technologies feature MOSFETs with two or three different Vt values within each flavor. Fine fmin tuning to meet ftarget can thus further be achieved by proper Vt selection for the MOSFETs. As shown in Figure 3, moving from standard-Vt (SVT) to low-Vt (LVT) devices in 65 nm boosts frequency and thus fmin by factors of 5.6× and 1.75× in LP and GP flavors, respectively. The frequency difference between SVT and LVT is lower in GP flavor because at 0.35 V, GP MOSFETs operate more in the near-threshold regime (Vt ≈ 350 mV) than in subthreshold regime and the Ion dependence on Vt is not fully exponential. Let us mention here that the curve of energy vs. ftarget is quite flat in the vicinity of the minimum-energy point, as shown in Figure 2. Therefore, once a proper process flavor and Vt selection has been performed to bring fmin close to ftarget, fine tuning of Vdd by a few tens of mV can be used for meeting exactly the timing constraint with negligible energy overhead [22].
3.2. Timing Constraint and Process/Temperature Variations
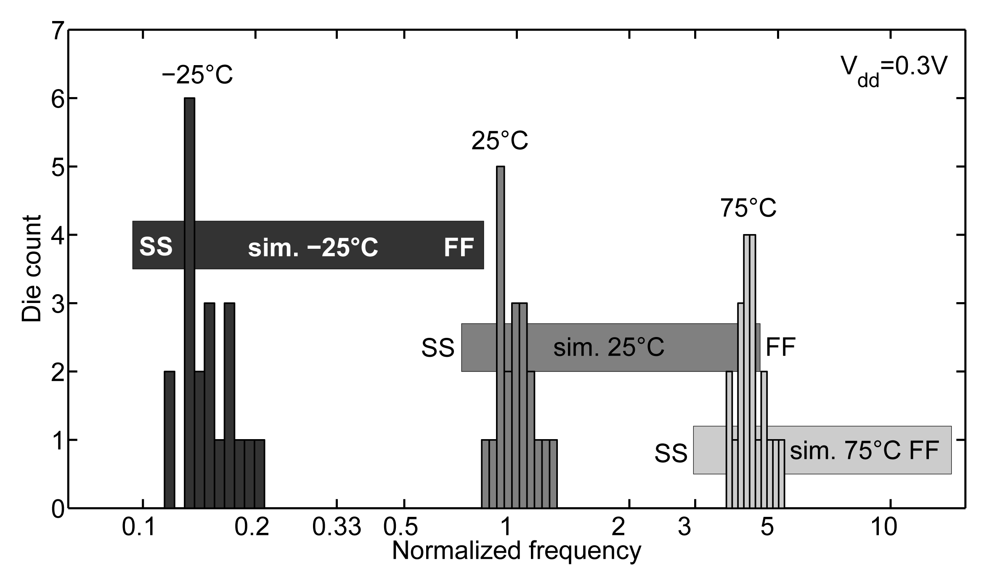
As MOSFETs in ULV circuits operate in the near- or sub-threshold regime, not only their Ioff but also their Ion current depend exponentially on Vt through I0 parameter from Equation (1). Gate delay is thus very sensitive to Vt variations [31] coming either from local random variations, global process corners or temperature variations. The frequency distribution of a ring oscillator at 0.3 V on 20 dies in 65 nm LP CMOS is plotted in Figure 4 for three different operating temperatures. This figure also compares the results with simulations at extreme SS (Slow NMOS/Slow PMOS) and FF (Fast NMOS/Fast PMOS) process corners. At 25 °C, the frequency at SS corner is 6.5× lower than typical frequency, which induces a large Tcycle guardband to ensure sufficient timing (parametric) yield regarding the ftarget timing constraint. However, we showed in [25] that the main concern regarding timing constraint in ULV circuits comes from low-temperature operation. Indeed, low-temperature operation dramatically reduces subthreshold Ion due to Vt increase and subthreshold swing reduction. The measured impact of a −40 °C operation on speed is a 8.5× delay increase at 0.3 V. The Tcycle guardband to ensure safe timing closure over the standard temperature range from −40 to +85 °C is thus more important than the guardband for handling global process variations. This obviously implies energy penalties as minimum Vdd for speed constraint has to be increased to handle low-temperature operation. The simulated combined effect of SS corner and −40 °C operation on speed is a degradation of gate delay by a factor of 40×. Notice that the speed of ULV circuits in GP flavor suffer less from process/temperature variations [25]. Indeed, their near-threshold operation limits the exponential dependence of gate delay on Vt.
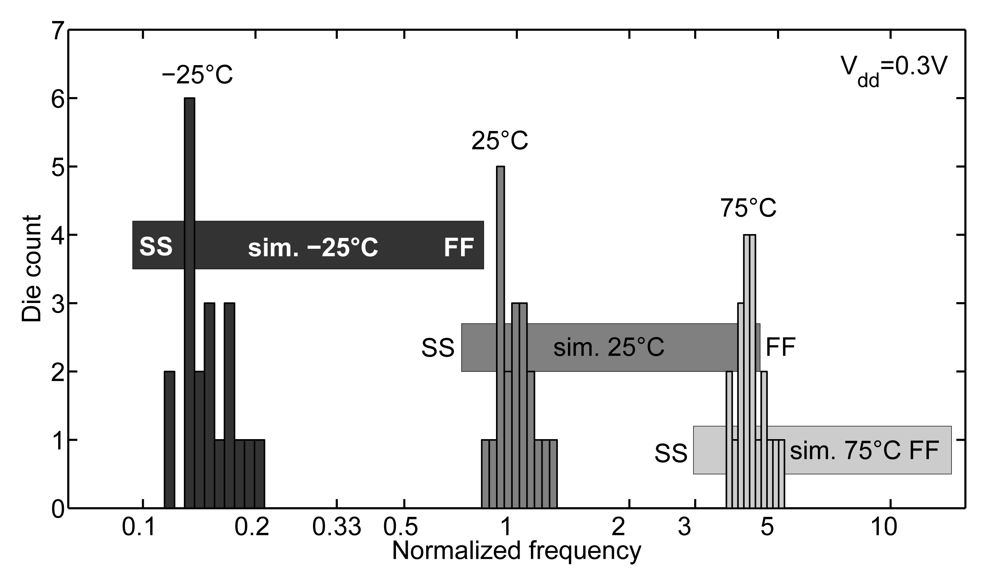
Figure 4.
Distribution of maximum frequency with process and temperature variations (measurements of 251-stage ring oscillators with FO1 inverters [25] in 65 nm LP CMOS technology with simulation results of global process corners, Lg = 60 nm).
Although local variations have a strong impact on gate delay as mentioned in Section 2, the consequence on speed performances is smaller than the effect of global process/temperature variations. Indeed, gate delay variability is averaged out over the high number of gates in critical paths [31] and the guardband on Tcycle is thus reduced. For example, simulations of the 8-bit multiplier from Section 2 in 45 nm LP at 0.3 V show a 3σ worst-case delay due to local variations 2.3 × higher than the typical delay. This is further mitigated by the use of an upsized Lg required to improve noise margins, as will be explained in Section 4.1.
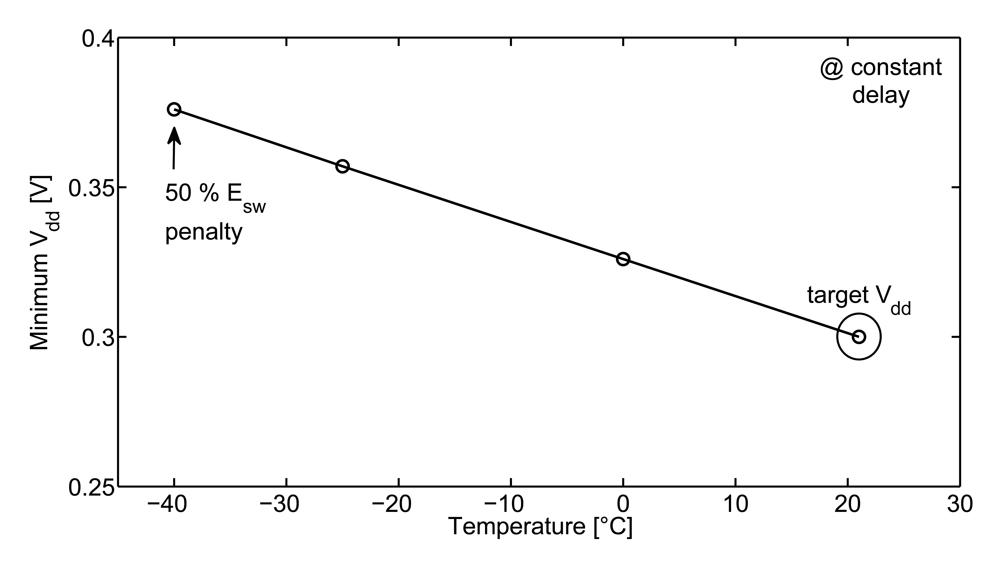
In order to limit Tcycle guardbands and Ecycle penalties due to process/temperature variations, adaptive techniques can be used. Assuming that clock frequency is fixed at ftarget by the application, adaptation can be achieved through either Vdd scaling or body biasing. We showed in [22] that adaptive body biasing is potentially more energy-efficient than adaptive voltage scaling as it exactly compensates Vt variations while the circuit is constantly operated at Vmin. However, adaptive body biasing raises practical implementation issues. Indeed, the body bias voltages to compensate process/temperature variations are quite high in 65/45 nm CMOS technologies due to the vanishing body effect in short-channel thin-oxide MOSFETs [22]. Measurement results of ring oscillators in 65 nm LP CMOS at 0.3 V show that forward body biasing by 300 mV only reduces gate delay by a factor of 5×, which is not sufficient when compared to the 8.5× delay increase due to −40 °C operation only. Adaptive voltage scaling is more efficient to mitigate delay increase at low temperature. Figure 5 shows the measured minimum Vdd to keep the delay constant vs. temperature. A 75 mV Vdd boost is capable of fully compensating the −40 °C delay increase. This comes at the expense of a 50% Esw penalty at such a low temperature.
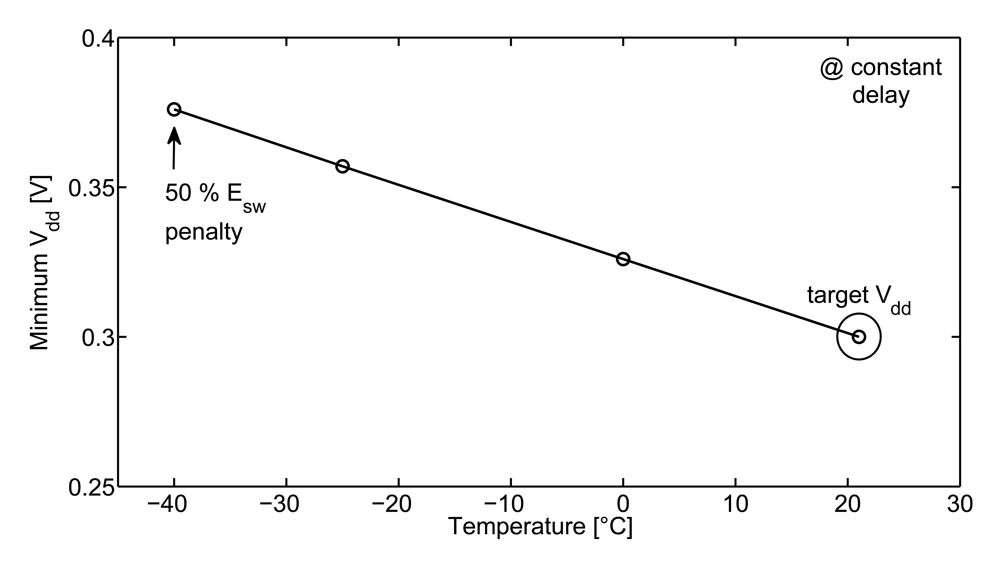
Figure 5.
Minimum Vdd for compensating temperature-induced speed variations (measurements of 251-stage ring oscillators with FO1 inverters [25] in 65 nm LP CMOS technology).
4. Functional Limits on Vdd
4.1. Noise Margin Constraint
When Vdd is reduced from 1–1.2V to ultra-low values, the Ion reduction leads to lower Ion/Ioff ratio for subthreshold MOSFETs. The impact on ULV logic is not only a speed penalty but also a strong reduction of noise margins [33,34]. The vanishing noise margins can lead to soft errors due to a higher sensitivity to transient noise from crosstalk [35] or radiations [36]. In 65/45 nm CMOS, local Vt variations further degrade output logic levels of ULV circuits, which can even lead to hard “stuck-at” faults and thus a functional failure of several manufactured chips [33,37]. When the number of gates in a circuit increases, the probability of a hard fault increases and the minimum Vdd for functionality Vlimit increases fast. Measurement of 90 nm ring oscillators in [38] show that the mean Vlimit between 1 k and 1 M gates is increased from 0.2 to 0.35 V. Robust ULV operation can thus only be achieved by taking Vlimit into account, which might significantly degrade energy efficiency if Vlimit gets close to the minimum-energy voltage Vmin.
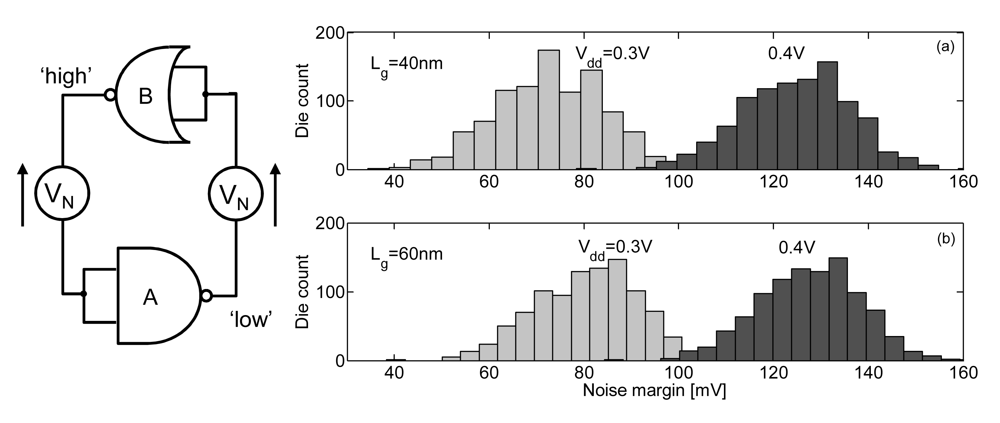
A convenient way to evaluate noise margins of ULV logic was proposed in [33] with the simulation of a NAND gate cross-coupled with a NOR gate, similarly to SRAM static noise margin extraction. This benchmark circuit represents an infinite chain of alternating NAND/NOR gates, which is a worst case regarding noise margins as the NAND (resp. NOR) gate features the highest Vih (resp. lowest Vil) level with the highest Vol (resp. lowest Voh) due to stacking of on transistors and parallel combination of off transistors [33]. Let us mention that precise noise margin extraction for a given circuit can be performed according to the method from [39] but for the sake of generality, we stick to the NAND/NOR method in this paper. Figure 6(a) shows the noise margins of ULV logic in 45 nm LP technology from statistical Monte-Carlo simulation with this benchmark circuit at 0.3 and 0.4 V. The wide noise margin distribution implies that many gates with low noise margins exhibit a high susceptibility to transient noise. The probability of gates with a negative noise margin is even not null, which means that hard errors might be encountered in a large ULV chip with many gates. At 0.4 V, noise margins are higher, which decreases the susceptibility to transient noise and the probability of hard errors but might also degrade energy efficiency.
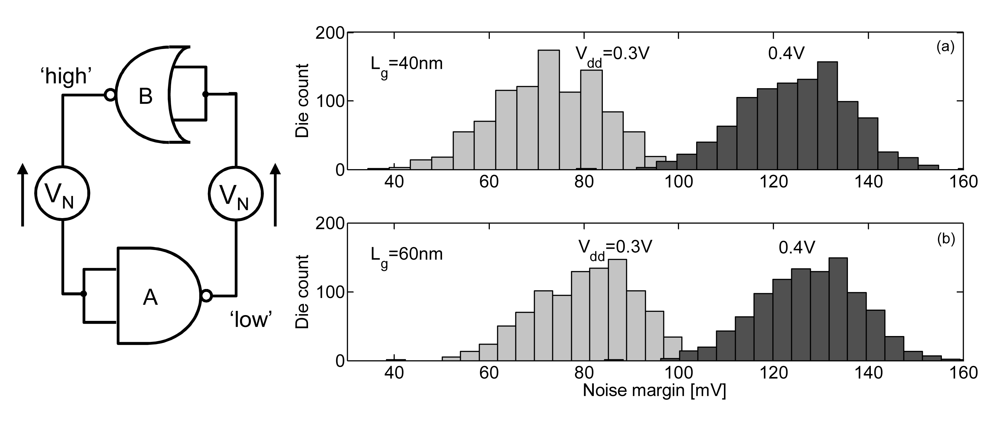
Figure 6.
Noise margin distribution of ULV logic (SPICE simulations of NAND2/NOR2 gates [33] in 45 nm LP CMOS technology, at 25 °C, 1 k Monte-Carlo runs).
In order to reliably operate at Vmin, several techniques have been proposed to increase noise margins and thereby improve Vlimit. In [33], the authors propose to upsize the transistor width of critical gates to improve their resilience to local Vt variations and thereby limit their worst-case noise margins. However, this comes at the cost of energy penalties due to high CL and Ileak in the circuit [6]. A widespread technique for robust ULV operation consists in the restriction of logic gates from the standard-cell library [20]. Indeed, gates with large transistors stacks or a large number of parallel branches such as NAND/NOR gates with 4 inputs feature worse noise margins. Eliminating these cells for ULV operation is thus very efficient to improve circuit robustness at the cost of slight area overhead. Another solution was proposed in [40,41]: Vt balancing also called adaptive β ratio. This technique can be used to match the subthreshold current between NMOS and PMOS devices in case of “crossed” process corners with slow NMOS/fast PMOS or the opposite. Implemented with an adaptive body biasing scheme, this technique can only address global process variations as the area overhead for compensating statistical local variations would be unacceptable. Therefore, this technique significantly improves nominal noise margins but is not capable of mitigating local noise margin variations.
We showed in [6,12] that both the degradation of the subthreshold swing and the increase of DIBL factor due to short-channel effects in nanometer CMOS technologies threatens ULV circuit robustness by further degrading output logic levels and thereby increasing Vlimit. Therefore, upsizing the gate length Lg of MOSFETs in ULV logic is able to significantly improve noise margins [6,12]. As shown in Figure 6(b), an upsize of the drawn Lg by 20 nm in 45 nm LP CMOS tightens noise margins distributions. The impact on functional die yield is computed for 0.3 V logic circuits with a varying number of gates Ngates from 1 k to 1000 M. We constrained the minimum noise margins to 20 mV for robustness against transient noise and extrapolated die yield with a simple model:
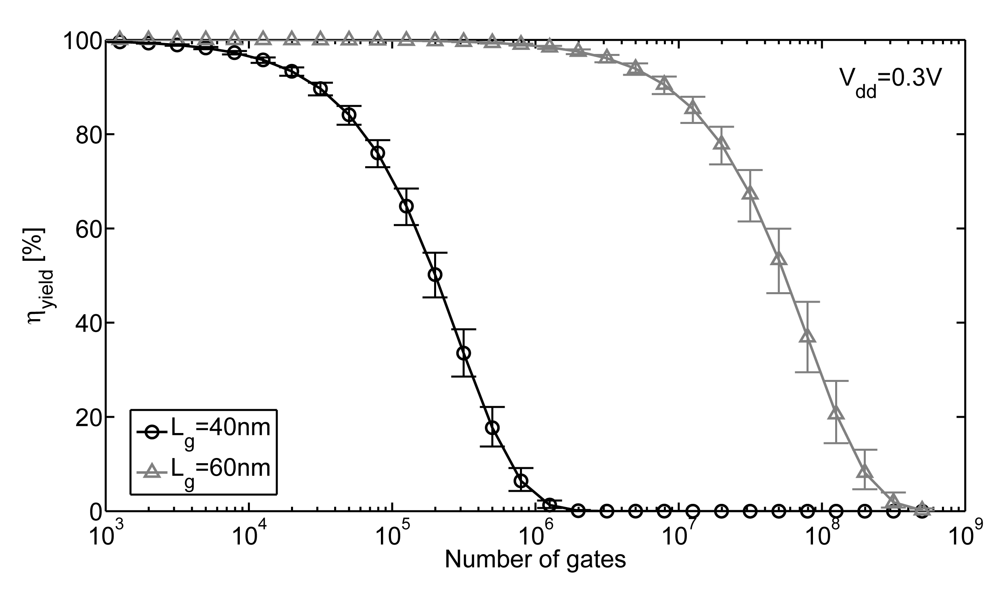
with ηgate the functional yield with a 20 mV noise margin constraint for the NAND2/NOR2 benchmark circuit (2 gates). Notice that this is quite a pessimistic assumption as it considers a logic circuit with only alternating NAND2/NOR2 gates. The resulting die yield is plotted for both 40 and 60 nm drawn Lg in Figure 7. It shows that the maximum number of logic gates in a circuit for 95% die yield is increased from 15 k at the minimum Lg to 4 M logic gates at the upsized Lg. This technique is thus very efficient to improve Vlimit for robust ULV operation. Moreover, it does not bring energy penalty as the CL increase due to an upsized Lg is significantly compensated by Eleak reduction thanks to reduced subthreshold swing, DIBL and variability [23,29].
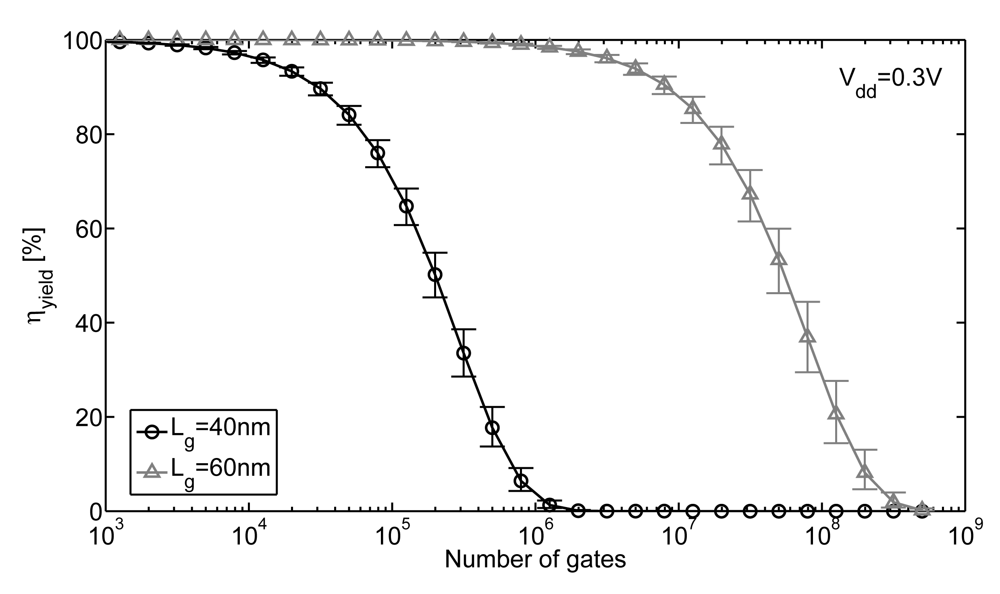
Figure 7.
Functional yield at 0.3 V with a 20 mV constraint on minimum noise margin (SPICE simulations of NAND2/NOR2 gates in 45 nm LP CMOS technology, at 25 °C, 50 k Monte-Carlo runs with 95% confidence interval plotted).
4.2. Hold Time Constraint
As ULV logic features a magnified sensitivity against local Vt variations, the statistical distribution of gate delay is quite large. It not only limits speed due to Tcycle guardband reported in Section 2 but also threatens functionality of ULV circuits due to potential hold time failures [37]. Indeed, local delay variations in the clock tree of ULV circuits might lead to large clock skew values between two branches of the clock tree and short logic paths might thus exhibit timing violations of hold constraint [42]. This is a critical point as hold time violations cannot be fixed by relaxing the clock frequency and generate a fault each time the path is triggered. Hold time failures thus sets another limit on the minimum Vdd for functionality Vlimit.
We further showed in [25] that low-temperature operation magnifies the sensitivity of ULV gate delay to Vt variations because of the steeper subthreshold swing. Low temperature thus increases the probability of hold time violations due to this variability-induced clock skew. As this raises Vlimit with potential energy penalties, low temperature has to be carefully addressed when checking the timing closure of hold constraints in ULV logic.
Although this problem can be addressed by upsizing the width or length of MOSFETs within the clock tree, it comes with Esw penalty from CL increase because the clock tree has a high activity factor. Another technique was recently proposed in [42]. The idea comes from the fact that RC interconnect delays are less important than gate delays at ultra-low voltage [43]. Therefore, the distributed buffering of a standard H-type clock tree at each level in the tree can be replaced by a single yet stronger bufferization stage at the clock root without incurring delay penalties within the clock tree. In this case, all leaf flip-flops in the tree share a common buffer stage, which can be composed of several series-connected buffers, and delay variations in this buffer thus do not introduce clock skew. This significantly reduces the probability of hold time failures. For circuits with more than a few kgates, a single bufferization stage might not be practical due to the prohibitively large dimension of buffers. In this case, the approach can be extended to a clock tree with a reduced depth of 2–4 buffer stages.
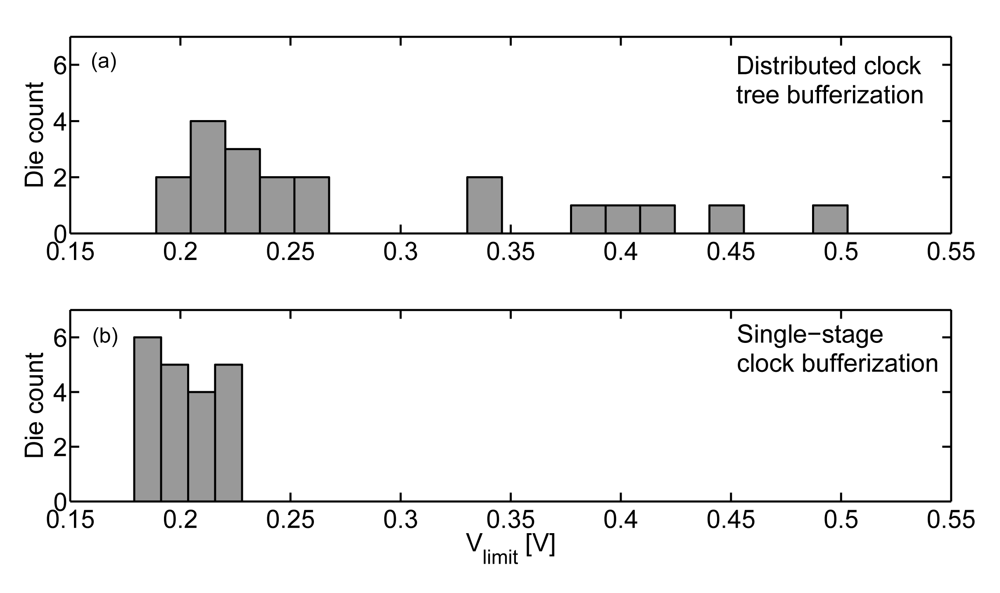
To validate this technique, we measured Vlimit of two versions of a small logic circuit presented in [21]: one version with a standard distributed clock tree bufferization and a second with a single bufferization stage at the clock root: two large series-connected buffers. The Vlimit histograms are plotted in Figure 8. The use of a single bufferization stage allows safe operation down to 0.23 V, whereas several dies of the circuit with standard distributed bufferization fail below 0.5 V. Let us recall here that ULV circuits in GP process flavor exhibit less delay variations as MOSFETs operate in near-threshold regime. They are thus less sensitive to variability-induced hold time violations.
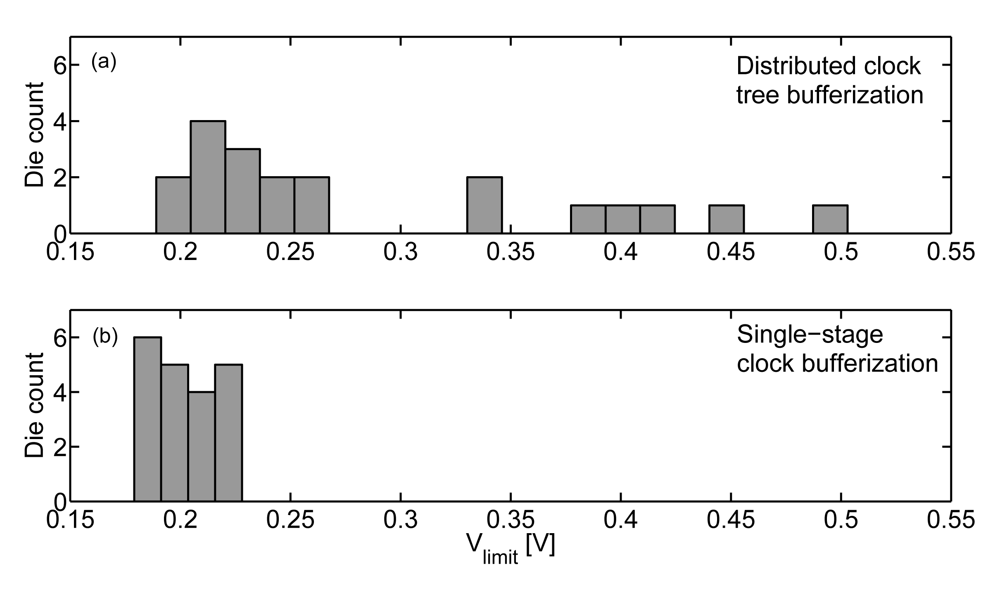
Figure 8.
Vlimit distribution for two versions of a small logic circuit (measurements of an 8-bit AES coprocessor with 3500 gates [21] in 65 nm LP CMOS technology, at 25 °C. Hold time violations due to clock tree variability prevent from reliably operating below 0.5 V. The use of a clock tree with a single bufferization stage significantly improves Vlimit thanks to mitigation of hold time violations.
5. Energy Efficiency and Stand-By Periods
Many ultra-low-power applications such as data logging in environmental [44] or biomedical [5] domains typically operate on a duty-cycled basis with long stand-by. Power consumed in stand-by mode degrades energy efficiency by adding an overhead to the effective energy per active cycle Ecycle [45]. When assuming ideal clock gating for eliminating switching power during stand-by periods, the effective Ecycle can be expressed as [45]:
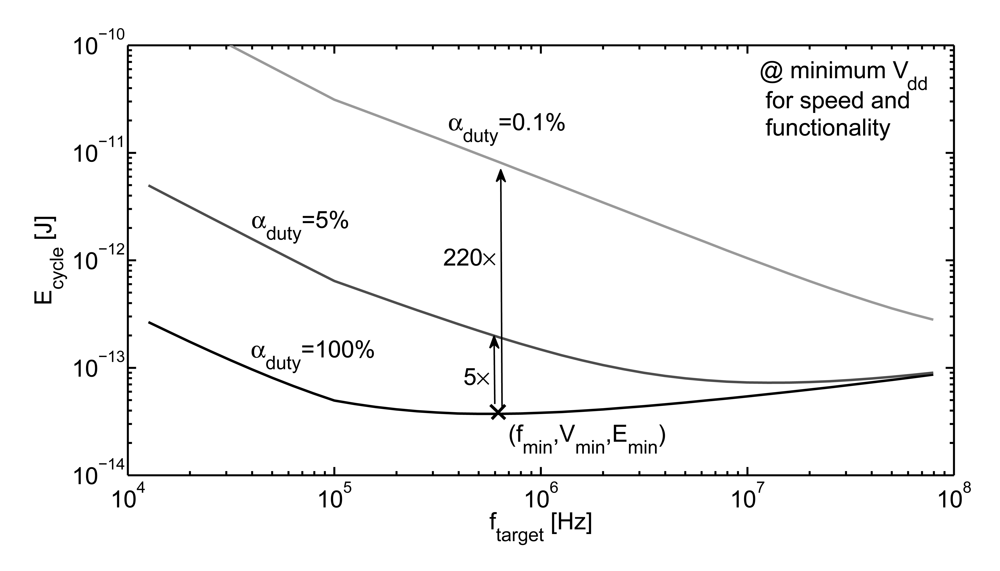
where αduty is the duty cycle i.e., the percentage of time that the circuit spends in active mode. As illustrated in Figure 9, an αduty of 0.1% increases the effective Ecycle by a factor of 220× at the minimum-energy point.
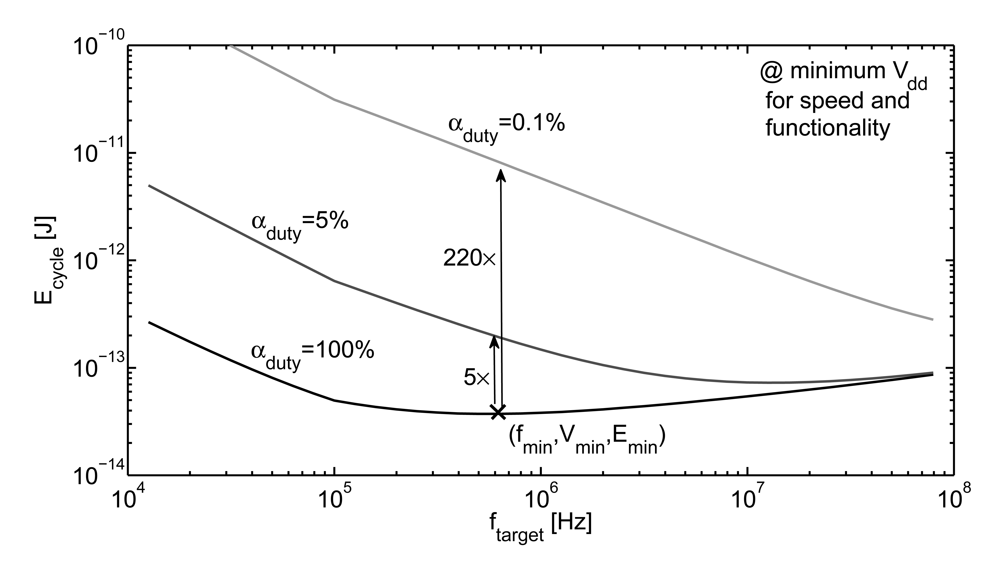
Figure 9.
Impact of stand-by periods on effective energy per cycle Ecycle (SPICE simulations of an 8-bit multiplier [6] 45 nm LP CMOS technology, at 25 °C.
To mitigate the Ecycle overhead, Pleak can be reduced either with an active-mode reduction technique or with a sleep-mode reduction technique [6]. Active-mode leakage reduction techniques relies on a Vt increase either globally in the whole circuit or selectively in gates from non-critical paths. At ultra-low voltage, a global Vt increase induces an exponential delay increase that requires a subsequent Vdd increase to maintain speed. If the Vt was already properly selected for making fmin meet the ftarget of the application as proposed in Section 3, a global Vt assignment will make the minimum Vdd for speed deviate from Vmin and in turn increase Ecycle [6]. Moreover, a selective Vt increase in non-critical paths is not efficient at ultra-low voltages because the exponential delay dependence on Vt due to MOSFET subthreshold operation limits the high- Vt assignment to a few logic gates in very short paths [22]. Besides Vt increase, serial operation was proposed in [46] to limit the number of gates and thereby reduce Pleak. This is an efficient technique which comes at the cost of more complex architectural design. In any case, active-mode leakage reduction techniques can only cut Pleak by a factor of 3–10× [6], which is not sufficient with αduty values below 5%.
Therefore, a sleep-mode leakage reduction technique is preferred. Amongst them, power gating relies on the addition of a high-Vt sleep transistor to cut off the leakage path in sleep mode. The effective Ecycle can thus be expressed as [24]:
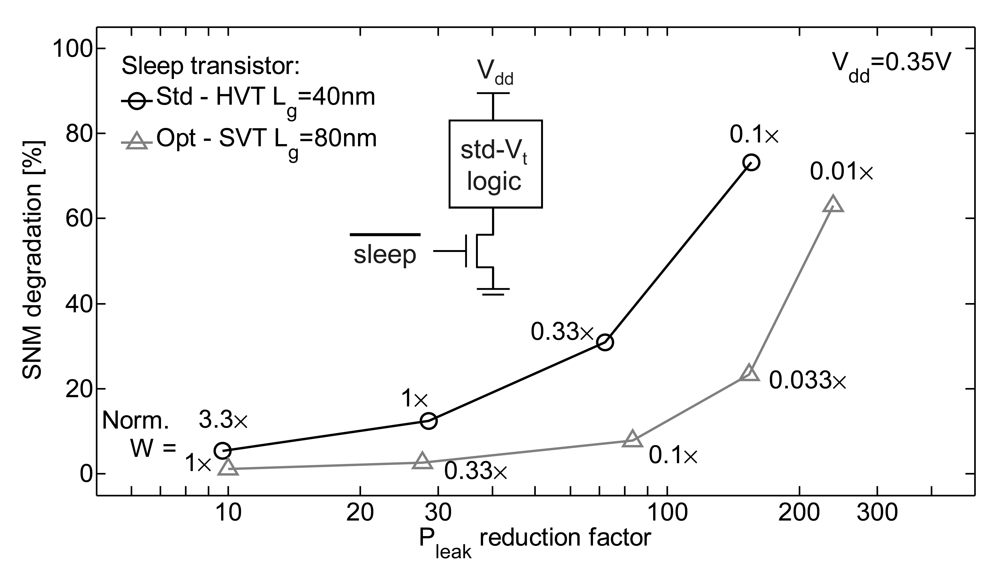
where Psleep is the leakage power in stand-by mode, Ewake-up the energy required to wake up from sleep mode and Ncycles the number of cycles in active mode between two stand-by periods in sleep mode. Notice that both wake-up and sleep-mode energies are amortized over Ncycles to calculate the effective energy per active cycle Ecycle. For sleep-mode energy, this is done through the (1 – αduty) /αduty term, which also corresponds to the ratio between cycles in sleep and active modes. Wake-up energy can usually be neglected when Ncycles is high (e.g., above 80 cycles in [24]). As in nominal-Vdd operation, the sleep transistor introduces a series resistance on the supply rails, which degrades ULV logic delay [45]. Sizing the sleep transistor thus results from a trade-off between large Psleep reduction for narrow sleep transistors and small delay overhead for wide sleep transistors. Indeed, the delay overhead need a subsequent Vdd increase to meet the speed constraint with a subsequent Ecycle penalty [45]. Moreover, we showed in [24] that the series resistance of the sleep transistor also reduces noise margins of ULV logic. The consequence on Vlimit for functional robustness is even worse than on minimum Vdd for speed. Figure 10 shows the impact of the sleep transistor sizing on Pleak reduction and the noise margin degradation at 0.35 V. A Pleak reduction by a factor of 100× reduces the noise margins by more than 50%, which makes ULV logic prone to functional failures. The impact of the sleep transistor on noise margin should thus carefully be addressed when designing a power-gated ULV circuit.
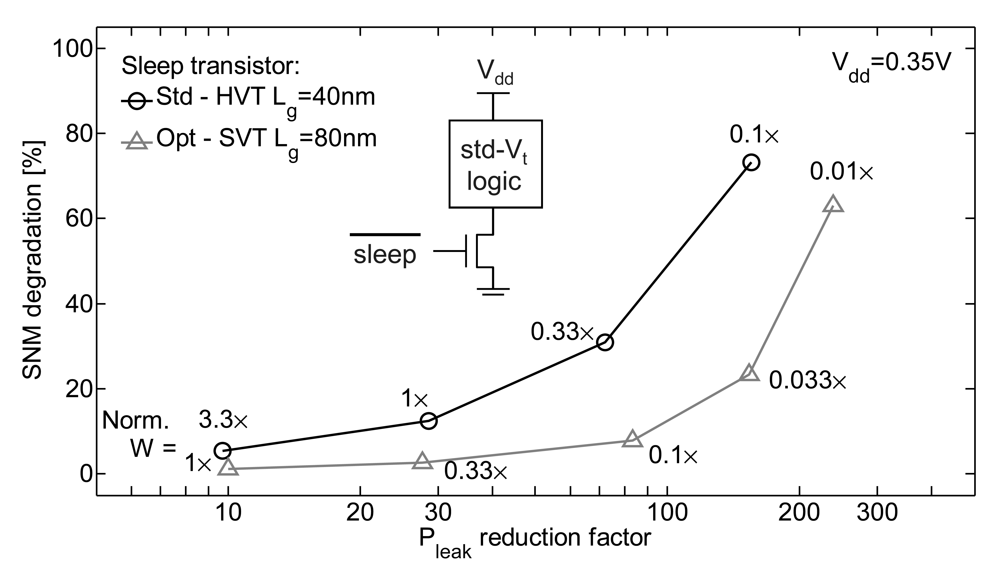
Figure 10.
Degradation of noise margins with sleep transistor sizing (SPICE simulations of an 8-bit multiplier for the leakage reduction [6] and NAND2/NOR2 circuit for noise margins ([33]) 45 nm LP CMOS technology, at 25 °C, sleep transistor width is normalized to the total width of parallel NMOS branches.
In order to limit this noise margin degradation, we showed in [24] that standard-Vt (SVT) MOSFETs with an upsized gate length should be preferred as they usually shows better subthreshold characteristics than high-Vt MOSFETs in 65/45 nm LP CMOS. As shown in Figure 10, this optimum sleep transistor in 45 nm LP CMOS degrades the noise margins by less than 20% for a Pleak reduction of 100×. These results with optimum sleep transistor further show that power gating is much more efficient than dynamic reverse body biasing in ULV circuits with long stand-by periods as dynamic reverse body biasing only enable 10× Pleak reduction [6].
6. Conclusions
Ultra-low-voltage (ULV) operation between 0.3 and 0.5 V leads to minimum-energy consumption at the expense of speed for ultra-low-power applications. However, ensuring robust and energy-efficient ULV operation in nanometer CMOS technologies raises a number of design challenges due to high short-channel effects, leakage currents and variability of these technologies. In this paper, we reviewed these challenges and the potential circuit solutions, as summarized in Table 1.

Table 1.
Design challenges for robust and energy-efficient ULV operation under timing constraints in 65/45 nm CMOS technologies.
First, we set up a general framework for analyzing energy efficiency under timing and robustness constraints for the whole range of target clock frequencies ftarget in ultra-low-power applications. We specifically took the impact local Vt variations into account in this framework through statistical circuit simulation.
We then reported that the frequency of the minimum-energy point fmin can significantly differ from ftarget with large Ecycle energy penalties. Process flavor and Vt selection in a versatile yet standard CMOS technology menu can be used to operate at the minimum-energy point under the timing constraint of the considered application, i.e., make fmin meet ftarget. We investigated the impact of global process/temperature variations on the timing constraint set by ftarget. Low-temperature operation was shown to be a primary concern as it dramatically degrades delay and thereby involves large cycle time Tcycle guardbands. Adaptive voltage scaling was shown to be able to fix this at reasonable energy penalty.
We then analyzed how the minimum supply voltage for functionality Vlimit is set by degraded noise margins and variability-induced clock skew. The first phenomenon induces soft errors due to increased noise sensitivity and even hard errors due to “stuck-at” faults. This can be fixed by gate length upsize and restriction of the logic gates within the standard-cell library to only low fan-in gates. The second phenomenon can lead to hold time violations and can be addressed by single-stage bufferization in the clock tree.
We finally analyzed the impact of stand-by periods on effective Ecycle. Application with low duty cycles need a leakage reduction technique to reduce leakage power in stand-by mode. Power-gating technique is preferred thanks to its high leakage power reduction capability. However, the addition of the sleep transistor harms noise margins and thereby increases Vlimit. This side effect can be effectively mitigated by the choice of an optimum sleep transistor.
Acknowledgments
Dr. Bol is with UCLouvain as a postdoctoral researcher from the National Foundation for Scientific Research (FNRS) of Belgium. Chip manufacturing was supported by the Walloon region of Belgium under TABLOID and E.USER projects. The author would like to thank C. Hocquet from UCLouvain for his precious help with chip measurements.
References
- Bianchini, R.; Rajamony, R. Power and energy management for server systems. Computer 2004, 37, 68–76. [Google Scholar]
- Gammie, G.; Wang, A.; Mair, H.; Lagerquist, R.; Chau, M.; Royannez, P.; Gururajarao, S.; Ko, U. SmartReflex Power and Performance Management Technologies for 90 nm, 65 nm, and 45 nm Mobile Application Processors. Proc. IEEE 2010, 98, 144–159. [Google Scholar]
- Wang, A.; Calhoun, B.; Chandrakasan, A. Sub-Threshold Design for Ultra-Low-Power Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Warneke, B.; Pister, K. An ultra-low energy microcontroller for Smart Dust wireless sensor networks. Proceedings of the 2004 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA; 2004; pp. 316–317. [Google Scholar]
- Chen, G.; Fojtik, M.; Kim, D.; Fick, D.; Park, J.; Seok, M.; Chen, M.T.; Foo, Z.; Sylvester, D.; Blaauw, D. Millimeter-scale nearly perpetual sensor system with stacked battery and solar cells. Proceedings of the 2010 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA; 2010; pp. 288–289. [Google Scholar]
- Bol, D.; Ambroise, R.; Flandre, D.; Legat, J.D. Analysis and minimization of practical energy in 45nm subthreshold logic circuits. Proceedings of the 2008 IEEE International Conference on Computer Design, Lake Tahoe, CA, USA; 2008; pp. 294–300. [Google Scholar]
- Swanson, R.; Meindl, J. Ion-implanted complementary MOS transistors in low-voltage circuits. IEEE J. Solid-State Circuits 1972, 7, 146–153. [Google Scholar]
- Vittoz, E.; Fellrath, J. CMOS analog integrated circuits based on weak inversion operations. IEEE J. Solid-State Circuits 1977, 12, 224–231. [Google Scholar]
- Soeleman, H.; Roy, K. Ultra-low power digital subthreshold logic circuits. Proceedings of the 1999 ACM/IEEE International Symposium on Low Power Electronics and Design, San Diego, CA, USA; 1999; pp. 94–96. [Google Scholar]
- Kao, J.; Miyazaki, M.; Chandrakasan, A. A 175-mV multiply-accumulate unit using an adaptive supply voltage and body bias architecture. IEEE J. Solid-State Circuits 2002, 37, 1545–1554. [Google Scholar]
- Calhoun, B.; Wang, A.; Chandrakasan, A. Modeling and sizing for minimum energy operation in subthreshold circuits. IEEE J. Solid-State Circuit 2005, 40, 1778–1786. [Google Scholar]
- Bol, D.; Ambroise, R.; Flandre, D.; Legat, J.D. Interests and limitations of technology scaling for subthreshold logic. IEEE Trans. VLSI Syst. 2009, 17, 1508–1519. [Google Scholar]
- Kwong, J.; Ramadass, Y.; Verma, N.; Chandrakasan, A. A 65 nm sub-Vt microcontroller with integrated SRAM and switched capacitor DC-DC converter. IEEE J. Solid-State Circuits 2009, 44, 115–126. [Google Scholar]
- Sridhara, S.; DiRenzo, M.; Lingam, S.; Lee, S.J.; Blazquez, R.; Maxey, J.; Ghanem, S.; Lee, Y.H.; Abdallah, R.; Singh, P.; Goe, M. Microwatt embedded processor platform for medical system-on-chip applications. Proceedings of the 2010 IEEE Symposium on VLSI Circuits (VLSIC), Honolulu, HI, USA; 2010; pp. 15–16. [Google Scholar]
- Zhai, B.; Nazhandali, L.; Olson, J.; Reeves, A.; Minuth, M.; Helfand, R.; Pant, S.; Blaauw, D.; Austin, T. A 2.60 pJ/Inst Subthreshold Sensor Processor for Optimal Energy Efficiency. Proceedings of the 2006 IEEE Symposium on VLSI Circuits (VLSIC), Honolulu, HI, USA; 2006. [Google Scholar]
- Kim, C.I.; Soeleman, H.; Roy, K. Ultra-low-power DLMS adaptive filter for hearing aid applications. IEEE Trans. VLSI Syst. 2003, 11, 1058–1067. [Google Scholar]
- Jocke, S.C.; Bolus, J.F.; Wooters, S.N.; Jurik, A.D.; Weaver, A.C.; Blalock, T.N.; Calhoun, B.H. A 2.6-μW sub-threshold mixed-signal ECG SoC. Proceedings of the 2009 IEEE Symposium on VLSI Circuits (VLSIC), Kyoto, Japan; 2009; pp. 60–61. [Google Scholar]
- Sze, V.; Chandrakasan, A. A 0.4-V UWB baseband processor. Proceedings of the 2007 ACM/IEEE International Symposium on Low Power Electronics and Design, Portland, OR, USA; 2007; pp. 262–267. [Google Scholar]
- Sze, V.; Finchelstein, D.; Sinangil, M.; Chandrakasan, A. A 0.7-V 1.8-mWH.264/AVC 720p Video Decoder. IEEE J. Solid-State Circuits 2009, 44, 2943–2956. [Google Scholar]
- Pu, Y.; Pineda de Gyvez, J.; Corporaal, H.; Ha, Y. An Ultra-Low-Energy Multi-Standard JPEG Co-Processor in 65 nm CMOS With Sub/Near Threshold Supply Voltage. IEEE J. Solid-State Circuits 2010, 45, 668–680. [Google Scholar]
- Hocquet, C.; Kamel, D.; Regazzoni, F.; Legat, J.D.; Flandre, D.; Bol, D.; Standaert, F.-X. Harvesting the potential of nano-CMOS for lightweight cryptography: An ultra-low-voltage 65 nm AES coprocessor for passive RFID tags. J. Cryptogr. Eng. 2011, 1, 8. [Google Scholar]
- Bol, D.; Flandre, D.; Legat, J.D. Technology flavor selection and adaptive techniques for timing-constrained 45 nm subthreshold circuits. Proceedings of the 2009 ACM/IEEE International Symposium on Low Power Electronics and Design, San Francisco, CA, USA; 2009; pp. 21–26. [Google Scholar]
- Bol, D.; Kamel, D.; Flandre, D.; Legat, J.D. Nanometer MOSFET effects on the minimum-energy point of 45 nm subthreshold logic. Proceedings of the 2009 ACM/IEEE International Symposium on Low Power Electronics and Design, San Francisco, CA, USA; 2009; pp. 3–8. [Google Scholar]
- Bol, D.; Hocquet, C.; Flandre, D.; Legat, J.D. Robustness-aware sleep transistor engineering for power-gated nanometer subthreshold circuits. Proceedings of the 2010 IEEE International Symposium on Circuits and System, Paris, France; 2010; pp. 1484–1487. [Google Scholar]
- Bol, D.; Hocquet, C.; Flandre, D.; Legat, J.D. The detrimental impact of negative Celsius temperature on ultra-low-voltage CMOS logic. Proceedings of the 2010 European Solid-State Circuit Research Conference, Seville, Spain; 2010; pp. 522–525. [Google Scholar]
- Dennard, R.; Gaensslen, F.; Rideout, V.; Bassous, E.; LeBlanc, A. Design of ion-implanted MOSFET's with very small physical dimensions. IEEE J. Solid-State Circuits 1974, 9, 256–268. [Google Scholar]
- Roy, K.; Mukhopadhyay, S.; Mahmoodi-Meimand, H. Leakage current mechanisms and leakage reduction techniques in deep-submicrometer CMOS circuits. Proc. IEEE 2003, 91, 305–327. [Google Scholar]
- Asenov, A.; Brown, A.; Davies, J.; Kaya, S.; Slavcheva, G. Simulation of intrinsic parameter fluctuations in decananometer and nanometer-scale MOSFETs. IEEE Trans. Electron Device 2003, 50, 1837–1852. [Google Scholar]
- Bol, D.; Flandre, D.; Legat, J.D. Nanometer MOSFET Effects on the Minimum-Energy Point of Sub-45 nm Subthreshold Logic—Mitigation at Technology and Circuit Levelsc. ACM Trans. Design Autom. Electr. Syst. 2010, 16, 2–26. [Google Scholar]
- Seok, M.; Sylvester, D.; Blaauw, D. Optimal technology selection for minimizing energy and variability in low voltage applications. Proceedings of the 2008 ACM/IEEE International Symposium on Low Power Electronics and Design, Bangalore, India; 2008; pp. 9–14. [Google Scholar]
- Zhai, B.; Hanson, S.; Blaauw, D.; Sylvester, D. Analysis and mitigation of variability in subthreshold design. Proceedings of the 2005 ACM/IEEE International Symposium on Low Power Electronics and Design, San Diego, CA, USA; 2005; pp. 20–25. [Google Scholar]
- Kamel, D.; Hocquet, C.; Standaert, F.X.; Flandre, D.; Bol, D. Glitch-induced within-die variations of dynamic energy in voltage-scaled nano-CMOS circuits. Proceedings of the 2010 European Solid-State Circuit Research Conference, Seville, Spain; 2010; pp. 518–521. [Google Scholar]
- Kwong, J.; Chandrakasan, A. Variation-Driven Device Sizing for Minimum Energy Sub-threshold Circuits. Proceedings of the 2006 ACM/IEEE International Symposium on Low Power Electronics and Design, Tegernsee, Germany; 2006; pp. 8–13. [Google Scholar]
- Alioto, M. Understanding DC Behavior of Subthreshold CMOS Logic Through Closed-Form Analysis. IEEE Trans. Circuits Syst. I 2010, 57, 1597–1607. [Google Scholar]
- Nanua, M.; Blaauw, D. Investigating Crosstalk in Sub-Threshold Circuits. Proceedings of the 8th International Symposium on Quality Electronic Design, San Jose, CA, USA; 2007; pp. 639–646. [Google Scholar]
- Dhillon, Y.; Diril, A.; Chatterjee, A.; Singh, A. Analysis and optimization of nanometer CMOS circuits for soft-error tolerance. IEEE Trans. VLSI Syst. 2006, 14, 514–524. [Google Scholar]
- Verma, N.; Kwong, J.; Chandrakasan, A. Nanometer MOSFET variation in minimum energy subthreshold circuits. IEEE Trans. Electron Device 2008, 55, 163–174. [Google Scholar]
- Niiyama, T.; Piao, Z.; Ishida, K.; Murakata, M.; Takamiya, M.; Sakurai, T. Increasing minimum operating voltage (VDDmin) with number of CMOS logic gates and experimental verification with up to 1 Mega-stage ring oscillators. Proceedings of the 2008 ACM/IEEE International Symposium on Low Power Electronics and Design, Bangalore, India; 2008; pp. 117–122. [Google Scholar]
- Pu, Y.; de Gyvez, J.; Corporaal, H.; Ha, Y. Statistical noise margin estimation for sub-threshold combinational circuits. Proceedings of the 13th Asia and South Pacific Design Automation Conference, Seoul, Korea; 2008; pp. 176–179. [Google Scholar]
- Pu, Y.; de Jesus Pineda de Gyvez, J.; Corporaal, H.; Ha, Y. Vt balancing and device sizing towards high yield of sub-threshold static logic gates. Proceedings of the 2007 ACM/IEEE International Symposium on Low Power Electronics and Design, Portland, OR, USA; 2007; pp. 355–358. [Google Scholar]
- Hwang, M.E.; Roy, K. ABRM: Adaptive β-Ratio Modulation for Process-Tolerant Ultradynamic Voltage Scaling. IEEE Trans. VLSI Syst. 2010, 18, 281–290. [Google Scholar]
- Seok, M.; Blaauw, D.; Sylvester, D. Clock network design for ultra-low power applications. Proceedings of the 2010 ACM/IEEE International Symposium on Low Power Electronics and Design, Austin, DX, USA; 2010; pp. 271–276. [Google Scholar]
- Hanson, S.; Zhai, B.; Seok, M.; Cline, B.; Zhou, K.; Singhal, M.; Minuth, M.; Olson, J.; Nazhandali, L.; Austin, T.; Sylvester, D.; Blaauw, D. Exploring Variability and Performance in a Sub-200-mV Processor. IEEE J. Solid-State Circuits 2008, 43, 881–891. [Google Scholar]
- Hanson, S.; Seok, M.; Lin, Y.S.; Foo, Z.Y.; Kim, D.; Lee, Y.; Liu, N.; Sylvester, D.; Blaauw, D. A Low-Voltage Processor for Sensing Applications With Picowatt Standby Mode. IEEE J. Solid-State Circuits 2009, 44, 1145–1155. [Google Scholar]
- Seok, M.; Hanson, S.; Sylvester, D.; Blauw, D. Analysis and optimization of sleep modes in subthreshold circuit design. Proceedings of the 44th ACM/IEEE Design Automation Conference, San Diego, CA, USA; 2007; pp. 604–699. [Google Scholar]
- Khanna, S.; Calhoun, B.H. Serial sub-threshold circuits for ultra-low-power systems. Proceedings of the 14th ACM/IEEE International Symposium on Low Power Electronics and Design, New York, NY, USA; 2009; pp. 27–32. [Google Scholar]
© 2011 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)