COVID-19 Case Rates in the UK: Modelling Uncertainties as Lockdown Lifts
Abstract
:1. Introduction
- to investigate the likely effects of lockdown easing on the UK pandemic, exploring the remaining uncertainties on vaccine efficacy and post-infection immunity;
- to estimate the unknown proportion of COVID-19 cases in the UK and the role of unknown cases in the spread of the disease;
- to increase the transparency of the modelling and analysis process, by focusing on containing the model detail complexity and clearly establishing the implications of different assumptions.
2. Background
2.1. Recovered and Post-Vaccination Immunity
2.2. Transmissibility after Vaccination
2.3. Known, Unknown and Asymptomatic Cases
3. Method and Data Sources
3.1. Model Development
3.2. Model Data Sources
- For parameters where reliable data was available from published research, e.g., virus incubation time, the median values from the research were used;
- For parameters where data was either unavailable or considered unreliable, the Powell optimisation method was used to calibrate the model and confirm a narrow spread of 95% confidence intervals.
3.3. Lockdown Effectiveness Timeline Estimation
3.4. Model Calibration and Optimisation
- The ‘new susceptible’ and ‘recovered susceptible’ stocks in the model were validated against UK COVID-19 antibody prevalence studies to ensure that the population fraction of people with antibodies, who can be presumed to have recovered from COVID-19, aligns with the modelled fraction [4];
- Modelled UK case fatality rates were compared with historical data to ensure broad alignment [36];
- The reproduction number Rt, calculated by the model over time, was compared with studies of the initial R0 and the ongoing COVID-19 Rt values to check consistency [45];
- The relative infectivity increases at two points in time due to the new Alpha and Delta variants;
- Vaccination proceeds at a steady daily rate in all scenarios and is offered to the total eligible population irrespective of whether an individual is known to have recovered from COVID-19;
- The maximum achievable population immunity fraction of 70% is capped by ineligible population sectors (pregnant women and most children under 18), vaccine hesitancy [37] and logistical difficulties;
- The second dose of a vaccine is given 12 weeks after the first dose;
- The protective effect of the first dose of the vaccine is established 21 days after administration, and increased protection is established 7 days after the second dose;
- The average time lag between symptom onset and the reporting of a positive case to the data source is 4 days.
3.5. Uncertainty Modelling
4. Results
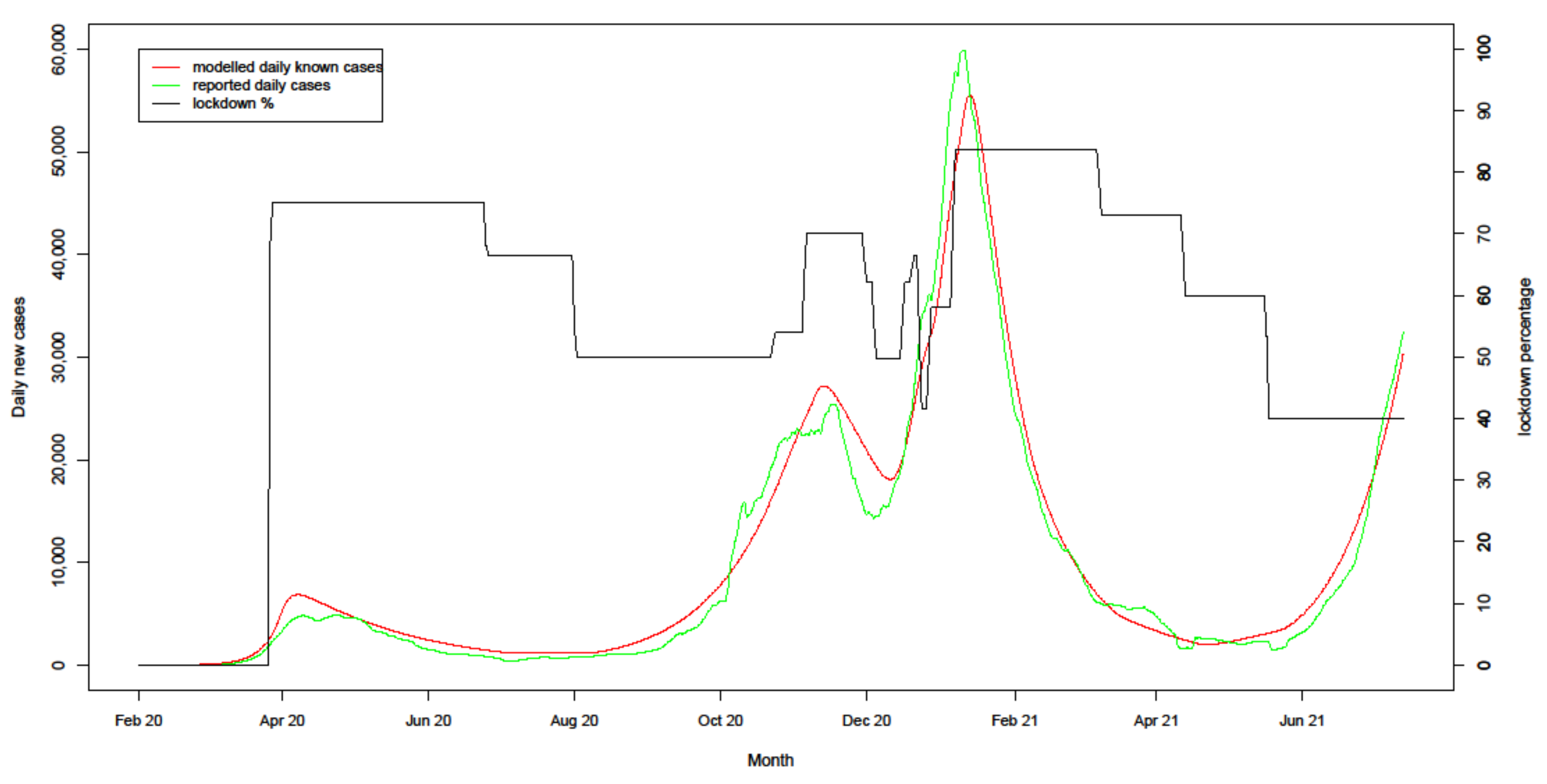
4.1. Model Fit to Actuals
4.2. Exploring Uncertainty
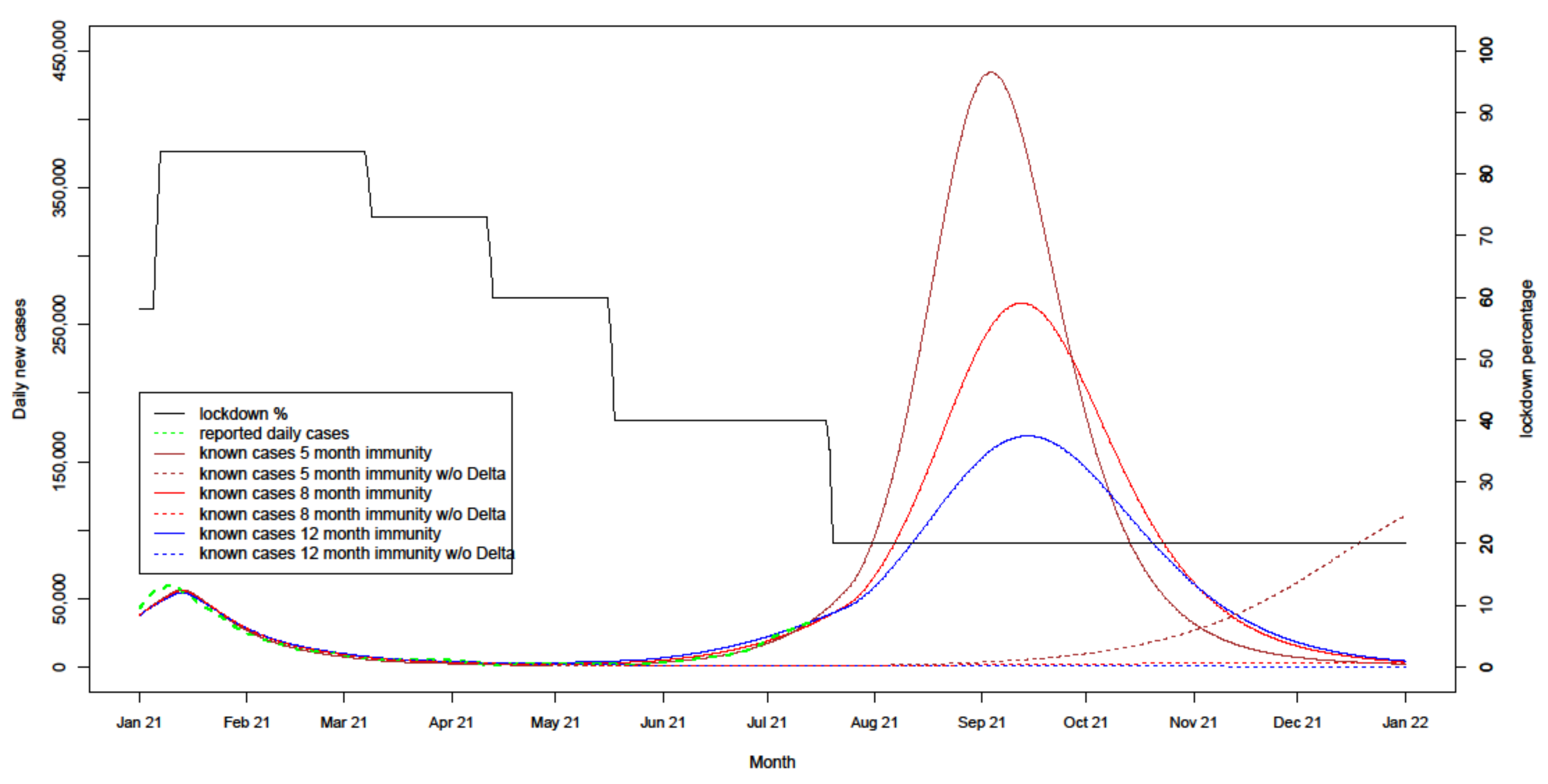
4.2.1. Uncertain Immunity Length
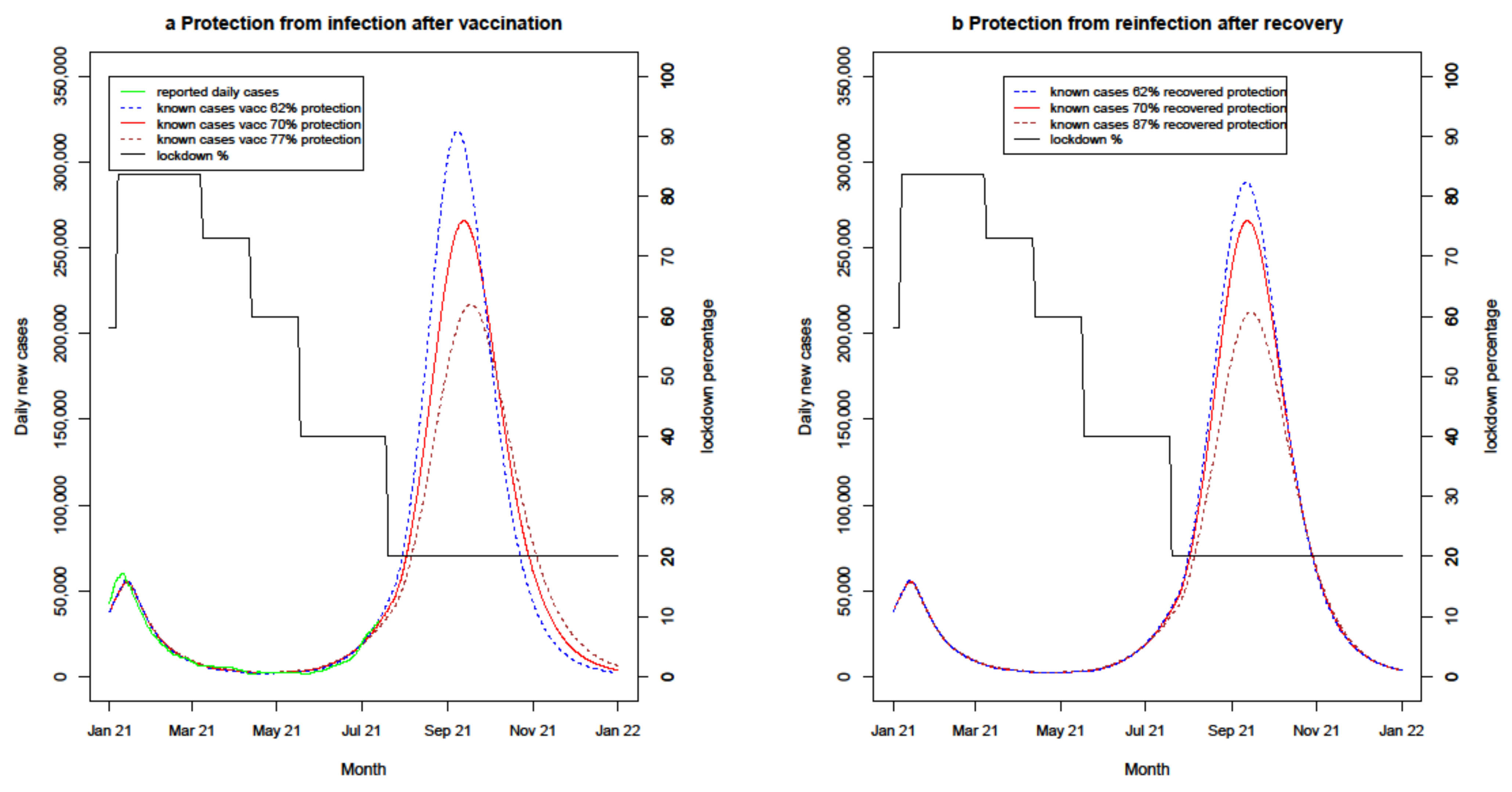
4.2.2. Uncertain Immunity Effectiveness
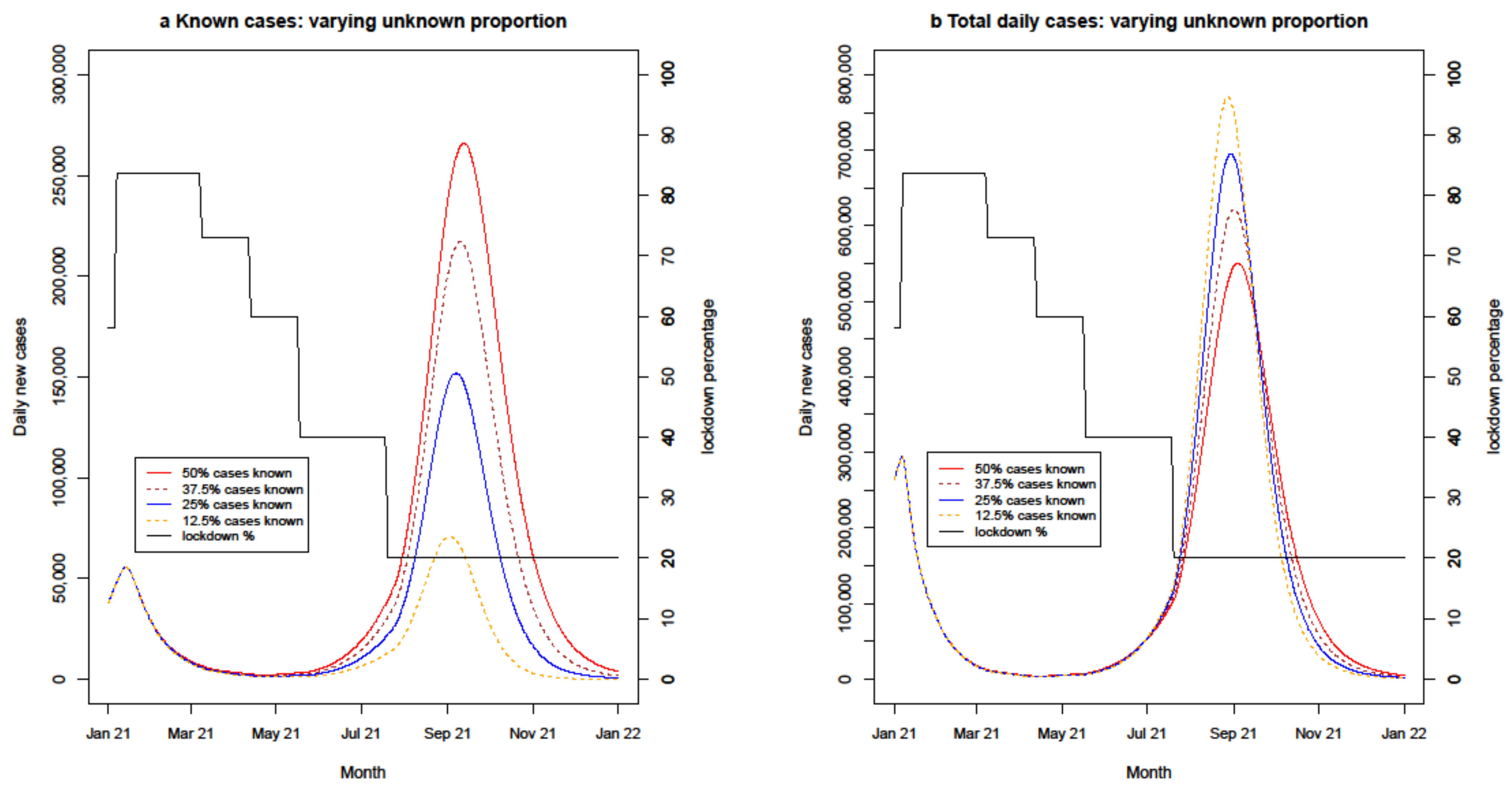
4.2.3. Uncertain Known Proportion
4.2.4. Modelling the Effect of Interventions
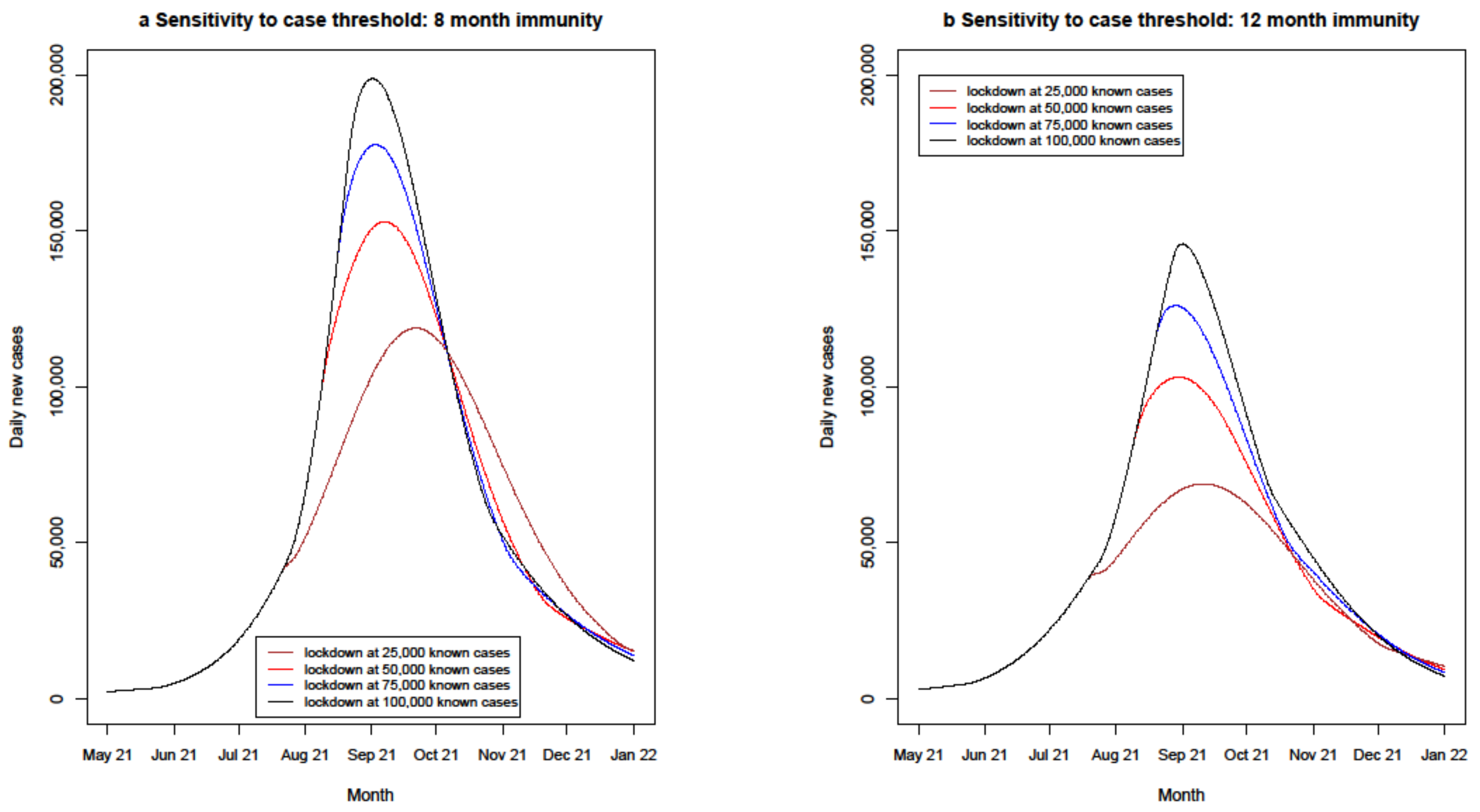
4.2.5. Lockdown Policy Sensitivities
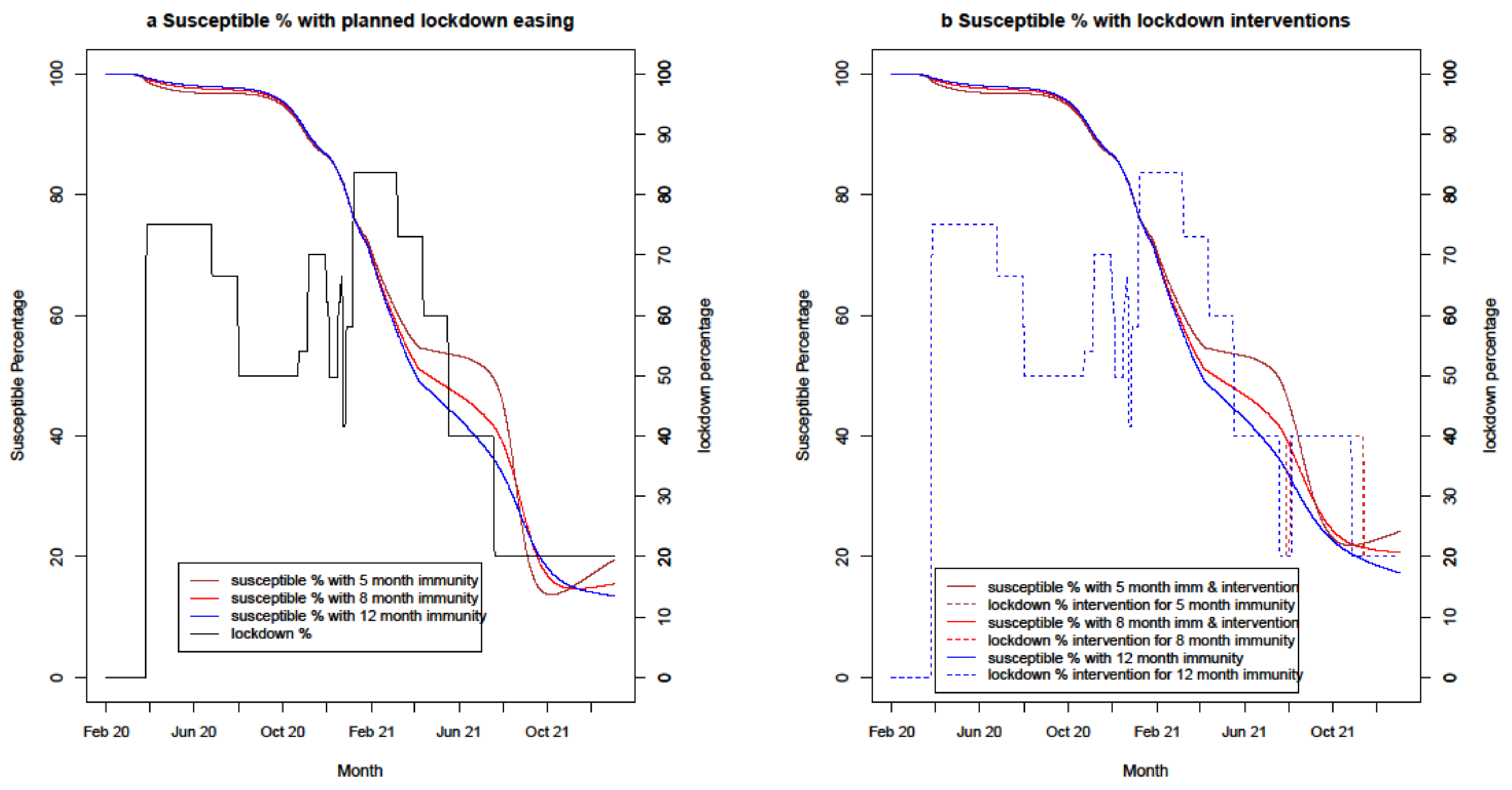
4.2.6. Change in Susceptible Percentage
5. Discussion
5.1. Implications of Findings
5.2. Modelling Discussion
5.2.1. Uncertainty
- length of recovered immunity;
- vaccine efficacy in reducing transmission;
- duration and relative infectiousness of asymptomatic and mildly symptomatic cases;
- ongoing uncertainty on the proportion of unknown cases which continue to drive infections.
5.2.2. Confidence in the Results for Given Assumptions
5.2.3. Comparison with Other Models
5.2.4. Generalisation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Godlee, F.; Silberner, J. The BMJ interview: Anthony Fauci on covid-19. BMJ 2020, 370, m3703. [Google Scholar] [CrossRef]
- How Epidemiological Models of COVID-19 Help Us Estimate the True Number of Infections. Available online: https://ourworldindata.org/covid-models (accessed on 30 June 2021).
- Rahmandad, H.; Lim, T.Y.; Sterman, J. Behavioral dynamics of COVID-19: Estimating under-reporting, multiple waves, and adherence fatigue across 91 nations. medRxiv 2020. [Google Scholar] [CrossRef]
- Ward, H.; Cooke, G.; Atchison, C.; Whitaker, M.; Elliott, J.; Moshe, M. Spiral: Antibody prevalence for SARS-CoV-2 in England following first peak of the pandemic: REACT2 study in 100,000 adults. bioRxiv 2020. [Google Scholar] [CrossRef]
- COVID-19 Pandemic Planning Scenarios. Available online: https://www.cdc.gov/coronavirus/2019-ncov/hcp/planning-scenarios.html (accessed on 30 March 2021).
- We Scientists Said Lock Down. But UK Politicians Refused to Listen. Available online: https://www.theguardian.com/commentisfree/2020/apr/15/uk-government-coronavirus-science-who-advice (accessed on 30 March 2021).
- Hancock, M. An Update on the Coronavirus Vaccine, 2 December 2020. Available online: https://www.gov.uk/government/speeches/an-update-on-the-coronavirus-vaccine-2-december-2020 (accessed on 30 March 2021).
- Covid-19: Oxford-AstraZeneca Vaccine Approved for Use in UK. Available online: https://www.bbc.com/news/health-55280671 (accessed on 30 March 2021).
- COVID-19 Response—Spring 2021. Available online: https://www.gov.uk/government/publications/covid-19-response-spring-2021 (accessed on 30 March 2021).
- Imperial College COVID-19 Reports. Available online: https://mrc-ide.github.io/global-lmic-reports/ (accessed on 30 June 2021).
- Holmdahl, I.; Buckee, C. Wrong but Useful—What Covid-19 Epidemiologic Models Can and Cannot Tell Us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef]
- IHME COVID-19 Projections. Available online: https://covid19.healthdata.org/global?view=cumulative-deaths&tab=trend (accessed on 30 June 2021).
- SPI-M-O: Summary of Modelling on Scenarios for Easing Restrictions. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/975909/S1182_SPI-M-O_Summary_of_modelling_of_easing_roadmap_step_2_restrictions.pdf (accessed on 30 April 2021).
- Cohen, J.I.; Burbelo, P.D. Reinfection with SARS-CoV-2: Implications for Vaccines. Clin. Infect. Dis. 2020, cia1866. [Google Scholar] [CrossRef]
- Dan, J.M.; Mateus, J.; Kato, Y.; Hastie, K.M.; Yu, E.D.; Faliti, C.E.; Grifoni, A.; Ramirez, S.I.; Haupt, S.; Fraizer, A.; et al. Immunological memory to SARS-CoV-2 assessed for up to eight months after infection. bioRxiv 2020. [Google Scholar] [CrossRef]
- Seow, J.; Graham, C.; Merrick, B.; Acors, S.; Steel, K.J.A.; Hemmings, O.; O’Bryne, A.; Kouphou, N.; Pickering, S.; Galao, R.P.; et al. Longitudinal evaluation and decline of antibody responses in SARS-CoV-2 infection. medRxiv 2020. [Google Scholar] [CrossRef]
- Wajnberg, A.; Amanat, F.; Firpo, A.; Altman, D.R.; Bailey, M.J.; Mansour, M.; McMahon, M.; Meade, P.; Mendu, D.R.; Muellers, K.; et al. SARS-CoV-2 infection induces robust, neutralizing antibody responses that are stable for at least three months. medRxiv 2020. [Google Scholar] [CrossRef]
- Mumoli, N.; Vitale, J.; Mazzone, A. Clinical immunity in discharged medical patients with COVID-19. Int. J. Infect. Dis. 2020, 99, 229–230. [Google Scholar] [CrossRef] [PubMed]
- Mahase, E. Covid-19: Past infection provides 83% protection for five months but may not stop transmission, study finds. BMJ 2021, 372, n124. [Google Scholar] [CrossRef]
- Pritchard, E.; Matthews, P.C.; Stoesser, N.; Eyre, D.W.; Gethings, O.; Vihta, K.-D.; Jones, J.; House, T.; VanSteenHouse, H.; Bell, I.; et al. Impact of vaccination on SARS-CoV-2 cases in the community: A population-based study using the UK’s COVID-19 Infection Survey. medRxiv 2021. [Google Scholar] [CrossRef]
- Hodgson, S.H.; Mansatta, K.; Mallett, G.; Harris, V.; Emary, K.R.W.; Pollard, A.J. What defines an efficacious COVID-19 vaccine? A review of the challenges assessing the clinical efficacy of vaccines against SARS-CoV-2. Lancet Infect. Dis. 2021, 21, e26–e35. [Google Scholar] [CrossRef]
- Rivett, L.; Sridhar, S.; Sparkes, D.; Routledge, M.; Jones, N.K.; Forrest, S.; Young, J.; Pereira-Dias, J.; Hamilton, W.L.; Ferris, M.; et al. Screening of healthcare workers for SARS-CoV-2 highlights the role of asymptomatic carriage in COVID-19 transmission. eLife 2020, 9, e58728. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Meyler, P.; Mozel, M.; Tauh, T.; Merchant, R. Asymptomatic carriage and transmission of SARS-CoV-2: What do we know? Can. J. Anesth. 2020, 67, 1424–1430. [Google Scholar] [CrossRef]
- Altmann, D.M.; Douek, D.C.; Boyton, R.J. What policy makers need to know about COVID-19 protective immunity. Lancet 2020, 395, 1527–1529. [Google Scholar] [CrossRef]
- Johansson, M.A.; Quandelacy, T.M.; Kada, S.; Prasad, P.V.; Steele, M.; Brooks, J.T.; Slayton, R.B.; Biggerstaff, M.; Butler, J.C. SARS-CoV-2 Transmission from People without COVID-19 Symptoms. JAMA Netw. Open 2021, 4, e2035057. [Google Scholar] [CrossRef] [PubMed]
- Pollock, A.M.; Lancaster, J. Asymptomatic transmission of Covid-19. BMJ 2020, 371, m4851. [Google Scholar] [CrossRef]
- Byambasuren, O.; Cardona, M.; Bell, K.; Clark, J.; McLaws, M.-L.; Glasziou, P. Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: Systematic review and meta-analysis. Off. J. Assoc. Med. Microbiol. Infect. Dis. Can. 2020, 5, 223–234. [Google Scholar] [CrossRef]
- Lau, H.; Khosrawipour, T.; Kocbach, P.; Ichii, H.; Bania, J.; Khosrawipour, V. Evaluating the massive underreporting and undertesting of COVID-19 cases in multiple global epicenters. Pulmonology 2021, 27, 110. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.; Mckendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A Math. Phys. Eng. Ser. 1927, 115, 700–721. [Google Scholar]
- Ward, H.; Graham, C.; Atchison, C.; Whitaker, M.; Elliot, J.; Moshe, M.; Brown, J.C.; Flower, B.; Daunt, A.; Ainslie, K.; et al. Declining prevalence of antibody positivity to SARS-CoV-2: A community study of 365,000 adults. bioRxiv 2020. [Google Scholar] [CrossRef]
- Volz, E.; Mishra, S.; Chand, M.; Barrett, J.; Johnson, R.; Geidelberg, L.; Hinsley, W.R.; Laydon, D.J.; Dabrera, G.; O’Toole, A.; et al. Transmission of SARS-CoV-2 Lineage B.1.1.7 in England: Insights from linking epidemiological and genetic data. medRxiv 2020. [Google Scholar] [CrossRef]
- Graham, M.S.; Sudre, C.H.; May, A.; Antonelli, M.; Murray, B.; Varsavsky, T.; Kläser, K.; Canas, L.S.; Molteni, E.; Modat, M.; et al. Changes in symptomatology, reinfection, and transmissibility associated with the SARS-CoV-2 variant B.1.1.7: An ecological study. Lancet Public Health 2021, 6, 335–380. [Google Scholar] [CrossRef]
- Moss, R.; Wood, J.; Brown, D.; Shearer, F.; Black, A.J.; Cheng, A.C.; McCaw, J.M.; McVernon, J. Modelling the impact of COVID-19 in Australia to inform transmission reducing measures and health system preparedness. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Byrne, A.W.; McEvoy, D.; Collins, A.B.; Hunt, K.; Casey, M.; Barber, A.; Butler, F.; Griffin, J.; Lane, E.A.; McAloon, C.; et al. Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open 2020, 10, e039856. [Google Scholar] [CrossRef] [PubMed]
- UK Government. Joint Committee on Vaccination and Immunisation: Advice on Priority Groups for COVID-19 Vaccination, 30 December 2020. Available online: https://www.gov.uk/government/publications/priority-groups-for-coronavirus-covid-19-vaccination-advice-from-the-jcvi-30-december-2020/joint-committee-on-vaccination-and-immunisation-advice-on-priority-groups-for-covid-19-vaccination-30-december-2020 (accessed on 30 March 2021).
- Ritchie, H.; Ortiz-Ospina, E.; Beltekian, D.; Mathieu, E.; Hasell, J.; Macdonald, B.; Giattino, C.; Appel, C.; Rodés-Guirao, L.; Roser, M. Coronavirus Pandemic (COVID-19). Available online: https://ourworldindata.org/coronavirus (accessed on 12 July 2021).
- Robertson, E.; Reeve, K.S.; Niedzwiedz, C.L.; Moore, J.; Blake, M.; Green, M.; Katikireddi, S.V.; Benzeval, M.J. Predictors of COVID-19 vaccine hesitancy in the UK Household Longitudinal Study. Brain Behav. Immun. 2021, 94, 41–50. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, J.W.; Lam, T.T.Y. Transmission dynamics of the COVID-19 epidemic in England. Int. J. Infect. Dis. 2021, 104, 132–138. [Google Scholar] [CrossRef]
- Noh, J.Y.; Yoon, J.G.; Seong, H.; Choi, W.S.; Sohn, J.W.; Cheong, H.J.; Kim, W.J.; Song, J.Y. Asymptomatic infection and atypical manifestations of COVID-19: Comparison of viral shedding duration. J. Infect. 2020, 81, 816–846. [Google Scholar] [CrossRef]
- Zhou, R.; Li, F.; Chen, F.; Liu, H.; Zheng, J.; Lei, C.; Wu, X. Viral dynamics in asymptomatic patients with COVID-19. Int. J. Infect. Dis. 2020, 96, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Increased Household Transmission Of COVID-19 Cases Associated with SARS-Cov-2 Variant of Concern B.1.617.2: A National Case-Control Study. Available online: https://khub.net/documents/135939561/405676950/Increased+Household+Transmission+of+COVID-19+Cases+-+national+case+study.pdf/7f7764fb-ecb0-da31-77b3-b1a8ef7be9aa (accessed on 31 March 2021).
- Atalan, A. Is the lockdown important to prevent the COVID-9 pandemic? Effects on psychology, environment and economy-perspective. Ann. Med. Surg. 2020, 56, 38–42. [Google Scholar] [CrossRef] [PubMed]
- Prime Minister Sets Out Roadmap to Cautiously Ease Lockdown Restrictions. Available online: https://www.gov.uk/government/news/prime-minister-sets-out-roadmap-to-cautiously-ease-lockdown-restrictions (accessed on 30 April 2021).
- Wright, L.; Fancourt, D. Do predictors of adherence to pandemic guidelines change over time? A panel study of 21,000 UK adults during the COVID-19 pandemic. medRxiv 2020. [Google Scholar] [CrossRef]
- Sanche, S.; Lin, Y.T.; Xu, C.; Romero-Severson, E.; Hengartner, N.; Ke, R. High Contagiousness and Rapid Spread of Severe Acute Respiratory Syndrome Coronavirus 2. Emerg. Infect. Dis. 2020, 26, 1470–1477. [Google Scholar] [CrossRef]
- Subsidizing the Spread of COVID19: Evidence from the UK’s Eat-Out-to-Help-Out Scheme. Available online: https://ideas.repec.org/p/wrk/warwec/1310.html (accessed on 31 January 2021).
- Prime Minister Confirms Move to Step 4. Available online: https://www.gov.uk/government/news/prime-minister-confirms-move-to-step-4 (accessed on 12 July 2021).
- Rise in Covid Cases Will Put Intense Pressure on NHS, Bosses Warn. Available online: https://www.theguardian.com/world/2021/jul/12/rise-in-covid-cases-will-put-intense-pressure-on-nhs-bosses-warn (accessed on 14 July 2021).
- Britton, T.; Ball, F.; Trapman, P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science 2020, 369, 846–849. [Google Scholar] [CrossRef] [PubMed]
- Fontanet, A.; Cauchemez, S. COVID-19 herd immunity: Where are we? Nat. Rev. Immunol. 2020, 20, 583–584. [Google Scholar] [CrossRef]
- Wang, M.; Flessa, S. Modelling Covid-19 under uncertainty: What can we expect? Eur. J. Health Econ. 2020, 21, 665–668. [Google Scholar] [CrossRef] [PubMed]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef] [Green Version]
- Struben, J. The coronavirus disease (COVID-19) pandemic: Simulation-based assessment of outbreak responses and postpeak strategies. Syst. Dyn. Rev. 2020, 36, 247–293. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Parr, T.; Zeidman, P.; Razi, A.; Flandin, G.; Daunizeau, J.; Hulme, O.J.; Biling, A.J.; Litvak, J.; Price, C.J.; et al. Tracking and tracing in the UK: A dynamic causal modelling study. Wellcome Open Res. 2021, 5, 144. [Google Scholar] [CrossRef]
- Phipps, S.J.; Grafton, R.Q.; Kompas, T. Robust estimates of the true (population) infection rate for COVID-19: A backcasting approach. R. Soc. Open Sci. 2020, 7, 200909. [Google Scholar] [CrossRef]
- Böhning, D.; Rocchetti, I.; Maruotti, A.; Holling, H. Estimating the undetected infections in the Covid-19 outbreak by harnessing capture–recapture methods. Int. J. Infect. Dis. 2020, 97, 197–201. [Google Scholar] [CrossRef]




| Parameter | Value | Unit | Source |
|---|---|---|---|
| Incubation duration (non-infectious latent period) | 3.5 | Days | [33] |
| Disease duration stage 1 unknown | 2 | Days | [33,34] |
| Disease duration stage 2 known | 8 | Days | [33,34] |
| Disease duration stage 2 unknown | 5 | Days | [33,34] |
| Time from known disease till death | 11 | Days | [34] |
| Vaccine rollout speed PB/AZ | 130,000/380,000 | Doses/day | [35,36] |
| Vaccine protection against onwards transmission 21 days after dose 1 PB/AZ | 65% $ | - | [20] |
| Vaccine protection against onwards transmission 7 days after dose 2 PB/AZ | 70% $ | - | [20] |
| Length of immunity after vaccination or recovery | 8 $ | Months | [15] |
| Maximum population immunity | 70% | - | [37] |
| Average immunity protection post recovery | 70% $ | - | [20] |
| Unknown infectiousness ratio * | 72% $ | - | [5,26,27,38,39,40] and model optimisation |
| Unconstrained infecting daily contact rate unknown | 0.56 $ | - | model optimisation |
| Unconstrained infecting daily contact rate known | 0.14 $ | - | model optimisation |
| Known proportion estimate February 2021 | 21% $ | - | [2] and model optimisation |
| Relative infectivity after alpha variant identified | 1.32 $ | - | [32] and model optimisation |
| Relative infectivity after delta variant identified | 2.0 $ | [41] |
| Event | Date |
|---|---|
| First two UK COVID-19 cases confirmed | 1 February 2020 |
| UK Government Coronavirus action plan | 3 March 2020 |
| First COVID-19 death | 3 March 2020 |
| Contact tracing abandoned | 12 March 2020 |
| UK-wide lockdown effected | 26 March 2020 |
| Prime Minister admitted to hospital with COVID-19 symptoms | 4 April 2020 |
| COVID-19 alert levels system announced | 1 May 2020 |
| Lockdown eased, workers return, outdoor exercise with another | 13 May 2020 |
| Lockdown eased, non-essential shops reopen | 15 June 2020 |
| Restaurants and pubs open | 4 July 2020 |
| Restaurant ‘eat out to help out’ campaign | 3 August 2020 |
| One of every three cases in 20–29-year-olds, fast growth in younger people | 7 September 2020 |
| England—‘Rule of Six’ announced to curb social gatherings | 14 September 2020 |
| England—three-tier alert framework implemented | 14 October 2020 |
| Northern Ireland—4-week ‘circuit breaker’ lockdown starts | 16 October 2020 |
| Wales—3-week ‘firebreak’ lockdown starts | 23 October 2020 |
| Scotland—5-tier alert system starts | 2 November 2020 |
| England—4-week national lockdown starts at new tier 4 | 5 November 2020 |
| New COVID-19 strain (Alpha variant) B.1.1.7 detected in UK | 13 November 2020 |
| England—4-week lockdown ends | 3 December 2020 |
| PB immunisation rollout starts | 8 December 2020 |
| London and Scotland, new tier 4 lockdown | 20 December 2020 |
| Christmas one day lockdown relaxation | 25 December 2020 |
| AZ immunization rollout starts | 4 January 2021 |
| England, Scotland—tier 5 lockdown to 22 February | 6 January 2021 |
| England—lockdown extended to 8 March | 27 January 2021 |
| Schools return | 8 March 2021 |
| Non-essential retail, outdoor hospitality and attractions reopen | 12 April 2021 |
| New COVID-19 strain (Delta variant) B.1.617.2 detected in UK | 15 April 2021 |
| Indoor hospitality and sporting events with limited capacity reopen | 17 May 2021 |
| Planned England and Scotland ‘Freedom day’ 21 June deferred to 19 July | 14 June 2021 |
| FUTURE CHANGES: | |
| England—mandatory mask rules lifted, nightclubs reopen, full capacity events | 19 July 2021 |
| Scotland—level zero, up to 10 people meet indoors, nightclubs remain closed | 19 July 2021 |
| Scenario | Immunity Length Post Vaccination and Post Recovery | Protection from Infection Given by Recovered Immunity | Vaccine Protection 3 Weeks after 1st Dose | Vaccine Transmission Protection 1 Week after 2nd Dose | Future Known Proportion of Cases | Lockdown Characteristics |
|---|---|---|---|---|---|---|
| Base Case | 8 months [15] | 70% [20] | PB/AZ 65% [20] | PB/AZ 70% [20] | 50% | - |
| Recovered immunity protection variations | 8 months | 62%/70%/87% [15,16,17,19,20] | PB/AZ 65% | PB/AZ 70% | 50% | - |
| Vaccine protection variations | 8 months | 70% | PB/AZ 60%/65%/70% [20] | PB/AZ 62%/70%/77% [20] | 50% | - |
| Known proportion of cases variations | 8 months | 70% | PB/AZ 65% | PB/AZ 70% | 50%/37.5%/25%/12.5% | - |
| Lockdown sensitivity variations | 8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | 50% | Delays from 3.5 to 21 days, Case thresholds from 5000 to 25,000, Lockdown increase from 25% to 50% |
| Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 3 Weeks after 1st Dose | Vaccine Protection 1 Week after 2nd Dose | Future Known Cases |
|---|---|---|---|---|---|
| Immunity length variations | 5/8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | 50% |
| Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 3 Weeks after 1st Dose | Vaccine Protection 1 Week after 2nd Dose | Future Known Cases |
|---|---|---|---|---|---|
| Vaccine protection variations | 8 months | 70% | PB/AZ 60%/65%/70% | PB/AZ 62%/70%/77% | 50% |
| Recovered immunity protection variations | 8 months | 62%/70%/87% | PB/AZ 65% | PB/AZ 70% | 50% |
| Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 3 Weeks after 1st Dose | Vaccine Protection 1 Week after 2nd Dose | Future Known Cases |
|---|---|---|---|---|---|
| Known proportion variations | 8 months | 70% | PB/AZ 65% | PB/AZ 70% | 50%/37.5%/25%/12.5% |
| Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 1st Dose | Vaccine Protection 2nd Dose | Future Known Cases | Lockdown Daily Case Threshold | Lockdown% |
|---|---|---|---|---|---|---|---|
| Lockdown effects for varying immunity lengths | 5/8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | 7 days | 50,000 | 20% addition |
| Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 1st Dose | Vaccine Protection 2nd Dose | Delay before Lockdown | Lockdown Daily Case Threshold | Lockdown% |
|---|---|---|---|---|---|---|---|
| Lockdown delay variations | 8 months | 70% | PB/AZ 65% | PB/AZ 70% | 3.5, 7, 10.5, 14, 17.5, 21 days | 5000 | 25% addition |
| 5 months | 70% | PB/AZ 65% | PB/AZ 70% | 3.5, 7, 10.5, 14, 17.5, 21 days | 5000 | 25% addition |
| Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 1st Dose | Vaccine Protection 2nd Dose | Delay before Lockdown | Lockdown Daily Case Threshold | Lockdown% |
|---|---|---|---|---|---|---|---|
| Lockdown case threshold variations | 8 months | 70% | PB/AZ 65% | PB/AZ 70% | 7 days | 25,000, 50,000, 75,000, 100,000 | 20% addition |
| 12 months | 70% | PB/AZ 65% | PB/AZ 70% | 7 days | 25,000, 50,000, 75,000, 100,000 | 20% addition |
| Figure | Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 1st Dose | Vaccine Protection 2nd Dose | Delay before Lockdown | Lockdown Daily Case Threshold | Lockdown% |
|---|---|---|---|---|---|---|---|---|
| 9a | Long delay & high case threshold | 8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | 21 days | 100,000 | 20% addition |
| 9b | Severe lockdown | 8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | 7 days | 50,000 | 40% addition |
| Figure | Scenario | Immunity Length | Recovered Immunity Protection | Vaccine Protection 1st Dose | Vaccine Protection 2nd Dose | Delay before Lockdown | Lockdown Daily Case Threshold | Lockdown% |
|---|---|---|---|---|---|---|---|---|
| 10a | Immunity variations | 5/8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | - | - | - |
| 10b | Immunity variations with lockdown intervention | 5/8/12 months | 70% | PB/AZ 65% | PB/AZ 70% | 7 days | 50,000 | 20% addition |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brereton, C.; Pedercini, M. COVID-19 Case Rates in the UK: Modelling Uncertainties as Lockdown Lifts. Systems 2021, 9, 60. https://doi.org/10.3390/systems9030060
Brereton C, Pedercini M. COVID-19 Case Rates in the UK: Modelling Uncertainties as Lockdown Lifts. Systems. 2021; 9(3):60. https://doi.org/10.3390/systems9030060
Chicago/Turabian StyleBrereton, Claire, and Matteo Pedercini. 2021. "COVID-19 Case Rates in the UK: Modelling Uncertainties as Lockdown Lifts" Systems 9, no. 3: 60. https://doi.org/10.3390/systems9030060
APA StyleBrereton, C., & Pedercini, M. (2021). COVID-19 Case Rates in the UK: Modelling Uncertainties as Lockdown Lifts. Systems, 9(3), 60. https://doi.org/10.3390/systems9030060







