1. Introduction
Personalized medicines, or customized pharmaceutical products, is an emerging field to enhance the therapeutic outcome with patientcentricity in mind, i.e., providing the patient with a safe and effective treatment [
1,
2,
3]. Patientcentricity implies customizing the pharmaceutical product according to design requirements complying with individual patient needs. These individual product design requirements include active pharmaceutical ingredient (API), dose strength, target release profile, appearance (including treatment size and shape, for example), sensory properties, and composition [
4].
However, the large-scale deployment of customized pharmaceutical products is currently inadequate. The dominating production context is mass production, where the product design embraces a one-size-fits-all design, which means that four-to-six dose strengths are produced in large volumes [
5]. A shift toward a pharmaceutical product customization context leads to the inevitable consequence and challenge of a vast increase in the number of product variants produced in smaller volumes. However, a product variety exceeding six dose strengths has been argued as infeasible in the current mass production paradigm [
5]. Thus, uneconomical production will challenge the provision of customized pharmaceutical products, and in the end, if the product does not reach the patient, the therapeutic outcome cannot be enhanced.
Mass customization, as a production paradigm, has the intent of increasing business performance by serving a wide range of customers with customized products, through efficient production [
6]. Three mass customization principles described by Hu et al. [
7] incorporate product family architecture, reconfigurable manufacturing systems, and delayed differentiation. Govender et al. [
4] projected these into the pharmaceutical context as product modularization, process reconfiguration, and postponement. Product modularization in a pharmaceutical context is, to some extent, present in the literature. Siiskonen et al. [
8] have suggested an initial approach to product modularization of pharmaceutical products using function modeling, by which two product design requirements, originating from patient needs, were integrated into the product: a scalable dose strength and product size. For these modular product designs, cost and benefit studies were conducted. Govender et al. [
9] and Govender et al. [
10] experimentally showed the realization of a modular product design for a pharmaceutical product with a scalable dose strength and flexible, but controlled, target release profile. Building on the studies by Siiskonen et al. [
8], Govender et al. [
9], and Govender et al. [
10], the novelty of this paper is a theoretical modeling approach to generate modular product designs for pharmaceutical products for cost-efficient customization. The earlier work is extended by integrating three product design requirements into a customized pharmaceutical product: scalable dose strength, target release profile flexibility, and scalable treatment size. The scope of this study considers pharmaceutical products embracing the dosage form of a tablet, which is the most common dosage form [
5,
11,
12]. This study will not consider the design of the molecules of the active pharmaceutical ingredients or excipients. Furthermore, to assess the value to the patient of these modular product designs, models for benefit and cost are suggested and applied. The research questions guiding this study are RQ1:
How can individual product design requirements be realized in a pharmaceutical product for customization? and RQ2:
How can the cost and benefit of customized pharmaceutical product designs be assessed?The remainder of this paper is organized as follows:
Section 2 presents essential literature and concepts upon which this study has been built and describes the research gap addressed in this paper.
Section 3 describes the collection of methods used in the study, and the results of applying these are presented and discussed in
Section 4.
Section 5 answers the research questions posed in
Section 1 and discusses the study’s methods.
Section 6 concludes the paper and offers suggestions for future research directions.
4. Results
This section presents the resulting CC model of a pharmaceutical product integrating three product design requirements. Furthermore, the product platform development procedure and the resulting treatment portfolios generated through platform execution are described. Finally, the performance metrics constructed are presented along with the final performance assessment of the generated treatment portfolios.
4.1. CC Model of a Pharmaceutical Product Integrating Three Design Requirements
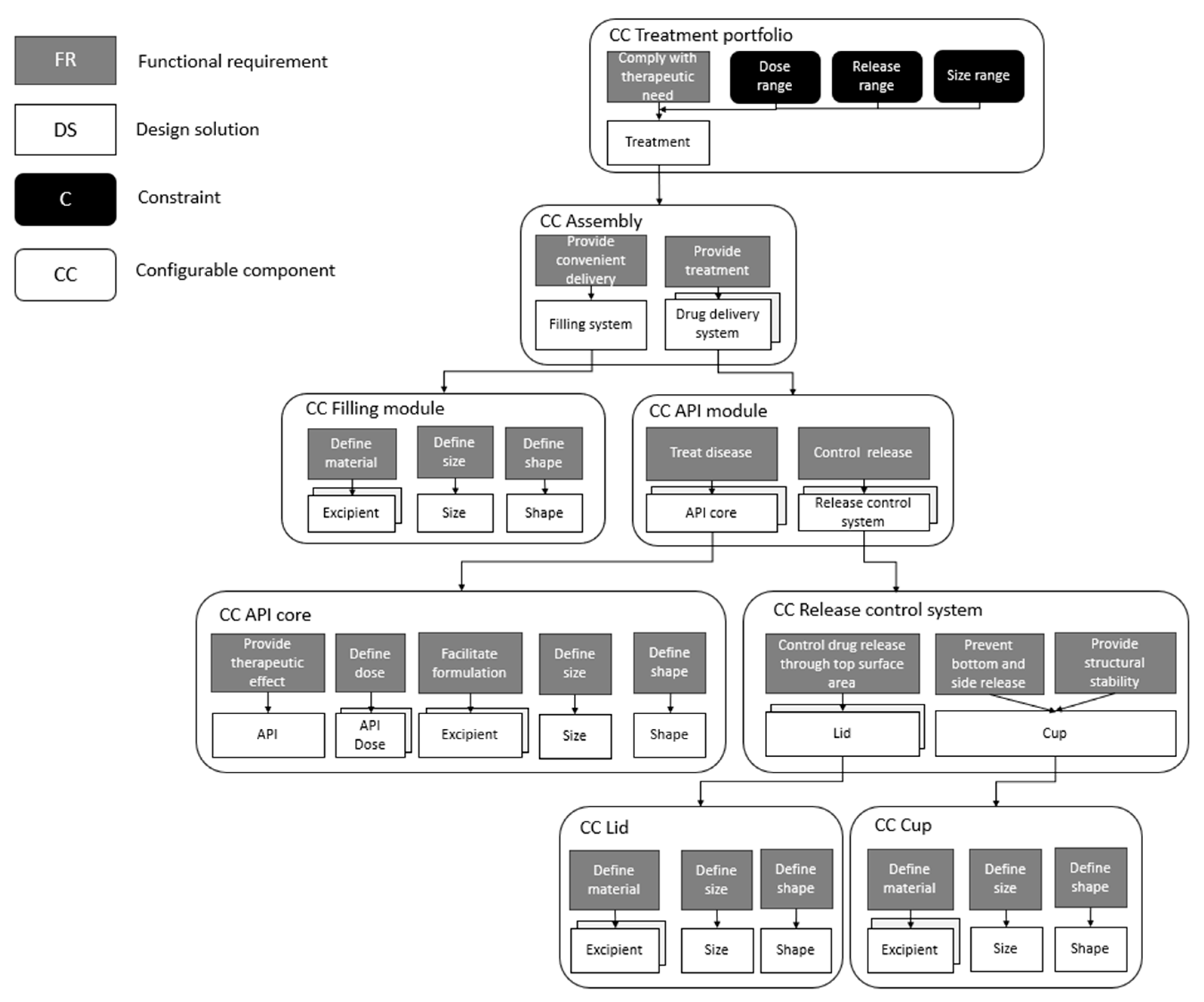
The resulting CC model of a treatment portfolio integrating the three design requirements of interest in this study (dose strength, target release profile, and size) is displayed in
Figure 1. Note that this CC model only displays three product design requirements and not the exhaustive set of design requirements required for a pharmaceutical product or customization of the pharmaceutical product.
The main FR of a treatment portfolio is to comply with the therapeutic need of any patient, and this FR is solved by the DS treatment. This treatment is aimed to comply with product design requirements originating from patient needs: dose strength, target release profile, and size. The CC assembly, which essentially comprises the treatment, embodies two FRs: provide convenient delivery and provide treatment. The first FR, provide convenient delivery, regards processes occurring before administration to support the administration process, whereas the second FR, provide treatment, relates to processes occurring within the body after administration. These FRs are solved through the DSs filling system and drug delivery system, which are further composed using lower-level CC objects, filling module and API module. These provide the means for the independent realization of the FRs provide convenient delivery and provide treatment.
The CC API module is further composed using the CCs API core and release control system. Within the CC API core, the product design requirement dose strength has been denoted as the FRs provide therapeutic effect and define dose, to which the DSs API and API dose have been assigned, respectively. Within the CC API core, additional FRs are defined that are essential for the final realization of the API core, but not explicitly required by the design requirement dose strength; for example, although not crucial for the dose strength, an API core must contain excipients (DSs to the FR facilitate formulation) for enabling the formulation of the core and, in the end, ensuring the core to be producible. Furthermore, the API core must be defined concerning its geometrical properties, leading to the inclusion of the FRs define size and define shape and their respective DSs, size and shape.
The product design requirement target release profile is achieved through the CC release control system. This CC object contains the FR control drug release through top surface area, for which the DS lid is defined. The DS lid is further described within a CC object of its own. Depending on how the CC object lid is defined during physical realization, different release properties can be obtained. The CC object release control system further incorporates the FRs prevent bottom and side release and provide structural stability, which are solved through a single DS cup. This DS is likewise described within a CC object of its own, cup, and the physical realization of this will result in a component preventing any API release from the sides and bottom of the API core. The FR provide structural stability aims at giving the API core a structure into which it can be placed for controlled release.
Two types of release mechanisms, dose-dependent release and dose-independent release, are provided through the product model. The dose-independent release scenario is achieved using the CC object release control system. In a scenario where this CC object is nonexistent, the dose-dependent release scenario is obtained instead. The dose-dependent release is simply performed through the inherent release properties of the API cores, a result of the formulation of the cores (i.e., the API to excipient ratio, size, and shape of the cores).
The final product design requirement, size, is categorized as a property of the CC assembly and is translated into the FR provide convenient delivery. To this FR, the DS filling system is assigned to further be composed using the CC filling module as an autonomous CC object.
On the highest hierarchical level, i.e., within the CC treatment portfolio, the Cs dose range and release range describe the viable range of both properties and, hence, essentially define the dose strength scalability and release flexibility of the treatment portfolio. The C size range informs the allowed sizes of any treatment and thus describes the extent of size scalability.
4.2. Component Tree and Platform Execution for Physical Realization
Figure 2 displays the realization of the respective CC object, defined in the CC model in
Figure 1, as COs within the component tree. The DSs on the lowest hierarchical level of the CC model are connected to the COs in the component tree through is-realized-in (iri) relationships; however, in
Figure 2, only the CCs have, for the sake of brevity, been displayed (not the breakdown of the CCs into FRs and DSs). For detailed descriptions of the CCs, the reader is referred to
Figure 1. It should be noted that several CCs are provided with a depth, such as the CC
API module. The depths describe alternative CC objects originating from assigning alternative DSs to FRs within that CC (see
Figure 1). When executing the CC model and generating the various product variants, the results are various physical realizations of the CC object, as components, depending on the assigned DS during the instance of execution. For example, in
Figure 2, for the CO
API module, six variants of
API modules are displayed; these correspond to the alternative DSs defined in the CC model before execution. The physical realizations of the CCs
API core,
lid,
cup, and
assembly have likewise been displayed in the component tree in
Figure 2. These are described in detail in the subsequent sections. For each CO in the tree, a figure has been provided to give the reader a visual idea of the realized COs. It should be noted that for the CO
tablet, several examples of final assemblies configured from the set of COs are displayed, not the exhaustive set of possible variants.
4.3. Product Platform Design for Treatment Portfolio Generation
As described in
Section 3, a model treatment, an SSRI product, has been selected as a case example. For this model treatment, modular product designs are proposed based on the outlined CC model of a treatment described throughout
Section 4.1. Through platform modeling and execution of the CC model, treatment portfolios containing sets of modular product variants are generated. The platform is also used to generate the treatment portfolios for the reference case. Their performance is assessed to evaluate the impact of various levels of modularity that these treatment portfolios embrace on the benefit for the patient and the cost of the product.
4.3.1. Reference Case Design
The reference case, based on the commercial SSRI treatment, is produced in two dose strengths: 50 and 100 mg.
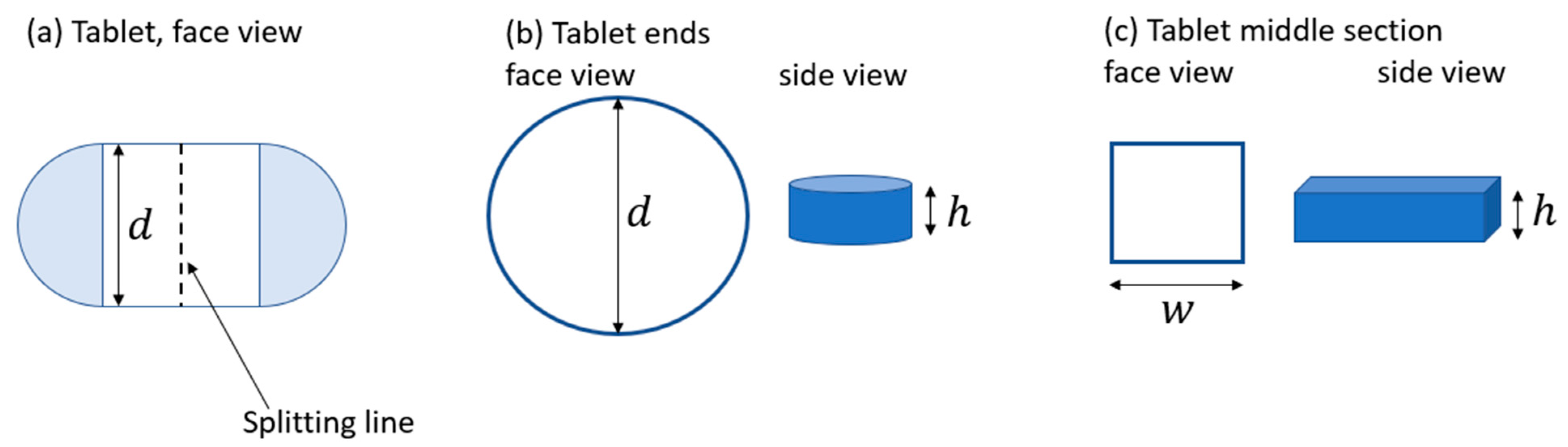
Figure 3 displays an illustration of the commercial treatment with a dose strength of 50 mg. This treatment has the approximate geometrical properties illustrated in
Figure 3: an oval-formed body assuming flat faces where the body can be divided into two end parts and a middle part (see
Figure 3a). The end parts are assumed to form a perfect cylinder with a diameter of 5 mm and height of 2 mm,
d and
h, respectively, in
Figure 3b. The middle part is assumed to form a cuboid with the width,
w, of 4 mm and height,
h, of 2 mm (see
Figure 3c). From these geometrical properties, the approximate volume of the commercial treatment is calculated to 81.4 mm
3. In this study, an assumption is made that a tablet can be split, generating the additional dose strengths 25 and 75 mg; the splitting line is marked in
Figure 3a. A single release profile is assumed for each dose strength. In theory, a 50 mg treatment could be established by a single 50 mg tablet or half a 100 mg tablet. Likewise, a 75 mg treatment can be established by one and a half 50 mg tablets or half a 50 mg and half a 100 mg tablet. The preferable approach, however, is to administer a single 50 mg tablet rather than splitting a 100 mg tablet due to the challenges with tablet splitting (see, for example, Wening and Breitkreutz [
17]); thus, the viable approach for creating the dosages 50 and 75 mg is to minimize the number of tablet splits. A single treatment variant is assumed for each dose strength, making the reference case consist of, in total, four dose strengths, four release profiles, and four treatment sizes.
4.3.2. Modular Product Designs
To configure modular product designs, elements are proposed to provide for the various design requirements (these elements are denoted COs in the component tree,
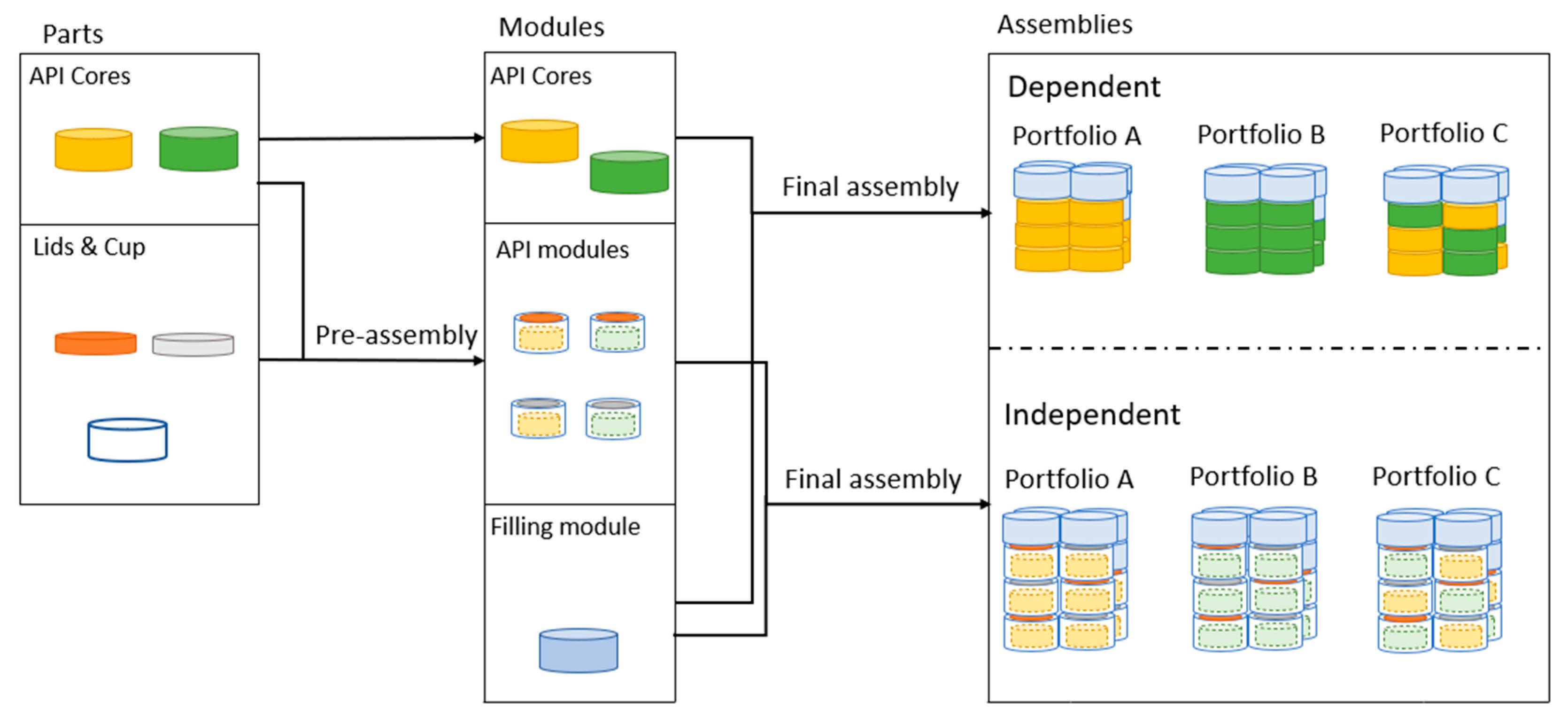
Figure 2). These elements are divided into parts, modules, and assemblies, see visualizations in
Figure 4. A modular product design must be assembled through an assembly process to generate an administrable treatment (i.e., an assembly). Parts are transferred through a preassembly process into modules, and then modules are transferred through a final assembly process into an assembly, see
Figure 4.
In this study, parts are the smallest elements of a treatment that serve as inputs into the preassembly process, where these are transformed into modules. Parts include the
API cores lids and cups. The
API cores comply with the design requirement dose strength (i.e., the cores are physical entities containing a specific dose of a specific API). Dose strength scalability is achieved through two cores, A and B, that are smaller in size concerning dose content than the commercial tablets. These cores are a cylindric shape and are displayed in
Figure 4, core A as yellow and core B as green. The dose content of core A is selected as one-fifth of the smaller-sized commercial treatment, which has a dose content of 50 mg, i.e., the dose of core A is 10 mg. Core B is selected to contain half of the dose content of core A, i.e., 5 mg. To define the geometrical size of core A, the same ratio of material content as in the commercial treatment of 50 mg is assumed. Furthermore, given that the approximate volume of the commercial treatment is 81.4 mm
3, and knowing the dose of the commercial treatment as well as the dose of core A, the volume of core A is calculated as 16.3 mm
3.
Govender et al. [
10] produced
API cores experimentally using hot-melt extrusion and melt molding. The geometrical shape of the core is a cylinder, and the diameter of the cylinder is given as 3.81 ± 0.11 mm. The core in this study is aimed at imitating these experimentally realized cores by Govender et al. [
10]; the core diameter is defined as 2.4 mm. A smaller core diameter is assigned in this study due to the volume restrictions of an assembled treatment. This is discussed further below in
Assemblies and treatment portfolios. The
API cores can resemble commercially available mini-tablets that have a diameter of 2–3 mm or even smaller [
45], verifying the manufacturability of the core with a diameter of 2.4 mm. Selecting the diameter of the core, and defining the geometric shape as a cylinder, the height can be calculated as 3.6 mm.
For core B, despite, dose-wise, being half the size of core A, the geometrical size and shape are assumed to be equal to core A. This means that the excipient content of core B is higher than for core A.
The design requirement of target release profile is realized by two distinct approaches. Either a dose-dependent release is generated, which relies on the inherent release properties of the
API cores (i.e., no additional elements are introduced to realize this), or a dose-independent release is generated by the means of a release system consisting of
lids and a
cup. Two lids with different release properties, lids A and B, are considered; however, the drug-release mechanism generated by these is outside the thesis scope. Govender et al. [
10] produced lids and cups by fused deposition modeling with a thickness of 0.5 mm, which is used as a geometrical property in this study.
Modules are defined as elements that serve as an input into the final assembly step and are to be transformed into assemblies. The assemblies are the treatments provided to patients. Modules are API cores, API modules, and filling modules. It must be noted that API cores are considered both parts and modules since these can either be used for generating API modules or can be directly transferred into assemblies.
API modules are configured through the preassembly process by placing a core into a cup and sealing with a lid (see a visual representation of
API modules in
Figure 4). The
filling module has the aim of complying with the product design requirement size. The filling module is, by itself, inert and serves the purpose of providing filling material to be able to generate product variants of different sizes, enabling size scalability of treatments. The geometry of the filling module is assumed to be a cylinder, and the size is assumed to be equal to the
API modules.
- —
Assemblies and treatment portfolios
Assemblies, or treatments, are configured through the final assembly process, where modules are assembled into desired constellations. As displayed in
Figure 4, three treatment portfolios, A, B, and C, are generated through platform execution for two scenarios, dose-dependent and dose-independent release. The treatment portfolios are initially defined through the
API cores used for product variant configuration. Portfolio A uses core A in both dose-dependent and -independent release scenarios. Portfolio B uses core B, and portfolio C uses cores A and B for both dose-dependent and -independent release scenarios.
Figure 4 displays a product variant (assembly) of each treatment portfolio; it should be noted, however, that only a single product variant is displayed and not the exhaustive set of product variants within each treatment portfolio.
The approach to assemble the modules into desired constellations forming the final assemblies follows several assumptions. The assumed final allowed assembly size and shape are in accordance with those described in the study by Siiskonen et al. [
8] but modified for the convenience of this study. In the study by Siiskonen et al. [
8], a capsule of size 00 was used as a reference into which a cuboid was placed. The volume of this cuboid gave the maximum volume for the final assembly. The geometries of this capsule and cuboid are used in this study to define the boundary conditions of a final assembled treatment size.
Figure 5a displays a redrawn 3D view of the cuboid that constituted the total volume to be used by the modules in an assembly. The cuboid embraces the length,
, defined as the maximum length of a 00 capsule, which is 23.3 mm. Hence, a limit of stacking five modules on top of each other (in the
dimension) was set, which allows for a total length of 23 mm, since the height of a module is 4.6 mm (core height of 3.6 mm and the thicknesses of the cup and lid, 0.5 mm, respectively). Thus, the size of a treatment variant within a product portfolio can range from a single
API module to 20 modules (consisting of both
API modules and filling modules in different ratios depending on the treatment variant). The cuboid diagonal,
, aligns with the diameter of a 00 capsule, i.e., 8.18 mm. The capsule periphery is displayed in
Figure 5b with a dashed red line.
At the bottom of the cuboid, the modules are packed in arrangements of four, as displayed in
Figure 5b. This type of arrangement is called a
module stack for convenience. The arrangement of a module stack fit within the periphery of the capsule, verified by calculations based on the diameter of the core, 2.4 mm, and adding the thickness of the walls of the cup (i.e., 2 × 0.5 mm). The module stacks are stacked on top of each other along the length,
, dimension of the cuboid (see
Figure 5c).
4.3.3. Product Variety
Through platform execution, the exhaustive set of product variants, for the complete dose range 25 to 100 mg, within each treatment portfolio and both dose-dependent and -independent scenarios is generated. The resulting number of product variants are displayed in
Table 1.
Table 1 shows that by product modularization, and thus, by the introduction of a few smaller components to configure the treatments from, a vast increase in product variety can be achieved. To exemplify, instead of producing two tablets of 50 mg and 100 mg, respectively, (reference case) generating in total four product variants, producing a single core containing 10 mg and a single filling module (portfolio A for the dose-dependent scenario) generates in total 116 product variants, not only due to the dose strength scalability but also, due to the size scalability. It should be noted that in both cases two elements were produced, however, due to modularization, the number of product variants can be significantly increased.
The product variety is created by two approaches; the first is a scaled functional bandwidth of a function within the product but keeping the number of functions provided by the product intact. The result of scaling the bandwidth is evident when comparing the number of product variants of different treatment portfolios for the same scenario. For example, the API core is scaled dose-wise, portfolio A uses a core of 10 mg, portfolio B a core of 5 mg, and portfolio C uses both the 5 and 10 mg cores. The smaller the dose content of the core the smaller increments of dose strengths can be obtained between the treatment variants generating an increased number of product variants (compare for example portfolio A and B for the dose-dependent scenario, the number of product variants resulting for the respective scenario in 116 and 136). A smaller core can generate an increased number of dose strengths; however, this also means that an increased number of cores are required to configure a treatment. An increased number of cores in a treatment might, for higher doses, pose size restrictions implying a lower degree of size scalability. Hence, using two cores for treatment variant configuration, as for portfolio C, can give an advantage concerning size scalability and dose strength scalability, thus the number of product variants is further increased when comparing to portfolios A and B. However, for the dose-dependent scenario, portfolio C can configure 1540 product variants, which is not solely a consequence of the higher degree of dose strength and size scalability. Portfolio C, using two cores with different inherent release properties for treatment configuration, will provide target release profile flexibility for a fixed dose; a treatment configured from three cores, each containing 10 mg, has a different target release profile than a treatment configured from two cores containing 10 mg and two cores containing 5 mg, even though the dose for both cases is the same.
The second approach to establish product variety is to introduce modules with different functions to satisfy design requirements. This is seen in
Table 1 by comparing the product variety of the dose-dependent and -independent release scenarios for the same treatment portfolio. In the dose-independent release scenario lids and cups have been introduced for the means of controlling the release providing for a vast increase in the target release profile flexibility.
4.4. Treatment Portfolio Performance
Product variety, although giving some indication, cannot alone describe the value for the patient. This section will thus present the results of each treatment portfolio in terms of value generated for the patient.
Patient Segmentation
As described in
Section 3.3.2, the treatment population is divided into segments, illustrated in
Figure 6, both for the reference case (above) and the treatment portfolios embracing modular product designs (below). The segment dose for the modular product designs denoted in
Figure 6 by A, B, M, N, and so forth, is decided according to the dose strengths that each treatment portfolio embracing modular product designs can offer. It should be mentioned that the illustration in
Figure 6 is purely conceptual, and the sizes of the segments, concerning the number of patients, are not correct ratios. The optimal dose of each patient is a result on a continuous scale generated by MATLAB random number generator. The patient is categorized into the segment offering the next available dose from the patient’s optimal dose offered by the treatment portfolio (i.e., if the patient requires 27 mg, but the treatment portfolio can only provide a dose strength of 30 mg, the patient will receive 30 mg and belong to the 30 mg segment).
4.5. Benefit
This section describes the suggested benefit metrics, , and , to assess the treatment portfolio performance from a benefit perspective and the outcome of calculating these for each treatment portfolio.
4.5.1.
- —
Dose strength scalability
Siiskonen et al. [
20] proposed an approach to assess the benefit of a treatment portfolio concerning dose scalability by suggesting the concept of
quality decay. This concept describes the distance between the dose received by the patient, decided through the patient segmentation process, and the patient’s optimal dose. Reformulating the quality decay concept suggested by Siiskonen et al. [
20],
aims to assess how close the dose offered by a treatment portfolio is to the patient’s optimal dose.
To assess the benefit from a dose strength scalability perspective,
is calculated through Equation (1). In this equation,
is the optimal dose of each patient
m,
is the dose received by the patient decided through the patient’s segment, and
denotes the size of the population.
Figure 7 depicts the increase in the
metric in percentage when comparing each treatment portfolio embracing modular product designs, A to C, to the reference case. It is inevitable that, through product modularization, the dose strength of the treatment offered to the patient is better matched with the patient’s optimal dose. If studying the raw numbers for
, displayed in
Table A1 in
Appendix A, the match of the received dose to the optimal dose of the patient is 0.92 for portfolio A and 0.96 for portfolios B and C. The reference case results in 0.79, and 1.0 denotes a perfect match. This substantial improvement in dose match might not be as evident if solely displaying the increase from the reference to the modular product designs in percentage.
The driver for improved quality from a dose strength perspective is the dose content of the API core as this decides the dose strength increments between each treatment variant in a portfolio. The smaller the dose content of the API core, the better the dose strength received by the patient can be matched to the patient’s optimal dose, and, hence, the performance of is increased. Portfolios B and C show the same level of increase in the metric. The reason is that, even though the level of scalability is higher for portfolio C than B (i.e., using API cores of two dose strengths for generating product variants), it is still the smallest core that, dose-wise, decides the final performance on this metric. The smallest core decides the smallest dose increments that can be obtained.
4.5.2.
- —
Target release profile flexibility
The target release profile flexibility,
, is assessed through Equation (2). Patient segmentation decides the dose that a patient receives, and given this dose strength, the number of release profiles a patient can choose from is assessed. In Equation (2),
describes the number of release variants each treatment portfolio can configure for each patient segment, and
describes the ratio of patients within each segment, which is obtained through Equation (3). In this equation,
describes the number of patients within a segment, and
describes the size of the whole treatment population.
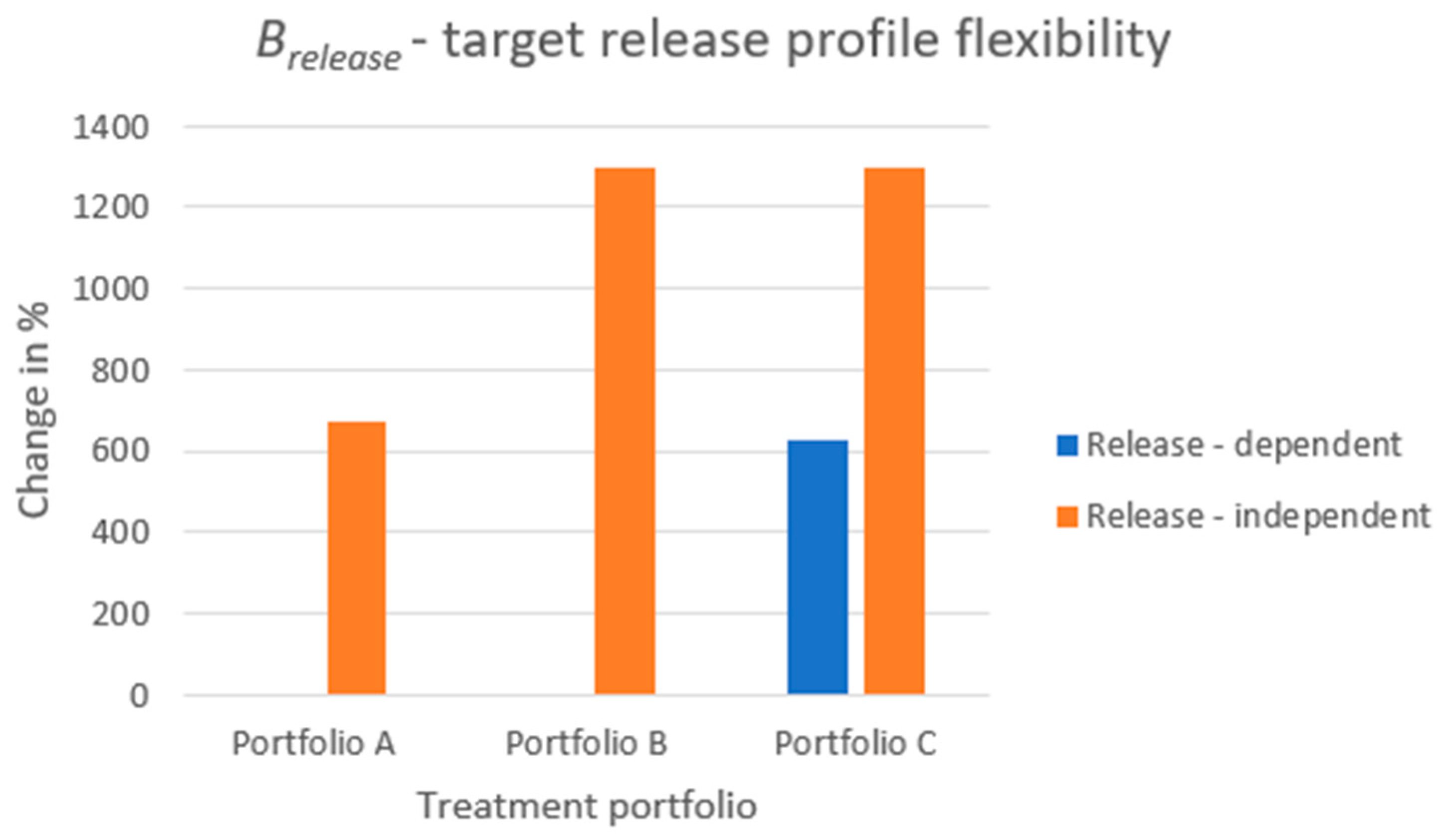
The results of the
metric is displayed in
Figure 8. The increase in percentage when comparing the modular product designs to the reference case is depicted. The increase in target release profile flexibility is shown for both the dose-dependent scenario (i.e., relying on the inherent release properties of the
API cores) and the dose-independent scenario (i.e., controlling the release through the release control system). By modularizing the product and only introducing a few different parts to it, the number of release profiles can be substantially increased. When studying portfolio C for dose-dependent release, solely relying on the inherent properties of the
API cores, the number of release profiles a patient can choose from is increased by more than 600% when compared to the reference case. Studying the raw numbers of
(see
Table A1 in
Appendix A), the reference case can generate a single release profile for each dose strength, whereas portfolio C can generate an average of 7.23 release profiles. This increase in release profiles is achieved by using two
API cores for product variant configuration instead of a single core. When studying the independent-release scenarios, portfolio A can generate, on average, 7.75 release profiles, and portfolios B and C can generate 14.0 release profiles, on average. These increases correspond to 675% and 1300% and are achieved entirely by either introducing two additional types of components, a lid and a cup (portfolio A) or three additional types of components, two lids and a cup (portfolios B and C).
It should be noted that for portfolios A and B, for the dose-dependent scenario, there is no increase in the metric. The reason is that, even though portfolio B can, from a dose-strength perspective, provide an increased number of product variants compared to portfolio A, these portfolios can, when fixing the dose, from a release perspective, solely configure a single target release profile. For dose-dependent release, the release profile relies solely on the API core combination creating the product variants, and portfolios A and B use a single API core, in the respective case, for the creation of the product variants for each dose strength.
Portfolios B and C are different from a dose-dependent release perspective, even though, from a dose-independent perspective, they are identical. From a dose-independent perspective, the lids control the release rate. This means that it does not matter if one configures one’s treatment of 25 mg consisting, API core-wise, of five 5 mg cores or two 10 mg cores and a single 5 mg core. Only the unique combinations of the lids for each dose strength act as the driver of the product variety in the dose-independent release scenario.
4.5.3.
The third metric, , is calculated through Equation (4) and assesses the size scalability of a treatment portfolio. As an indicator for size scalability, the number of treatment sizes, given a fixed dose and target release profile of the patient, is used. In Equation (4), denotes the average number of different sizes that a treatment variant can be configured as when the dose strength and target release profile are fixed. Several treatment sizes are obtained for each variant within a patient segment with different target release profiles; thus, the average number of size variants is calculated. For example, for portfolio C, a dose strength of 25 mg can be obtained by the means of different cores. Regardless of whether a dose-dependent or -independent scenario is considered, several target release profiles can be configured for the dose strength 25 mg, and for all these, different-sized treatments can be configured. To obtain a single value representing the number of size variants for each segment, the average of the number of size variants for each segment is calculated.
The number of treatment sizes is constrained concerning the shape and volume of the final assembly, as described in
Section 4.3.2. In Equation (4),
describes the ratio of patients within each segment and is obtained through Equation (3).
The results of the
metric are displayed in
Figure 9, where, as with the preceding benefit metrics, the percentage increase is presented when comparing the modular product designs to the reference case. Overall, similarly to the
metric, substantial increases in the number of product variants offered for the patient to choose from can be obtained simply by just introducing an additional module, a filling module, to provide size scalability. Studying the raw data of
(see
Table A1 in
Appendix A), the reference case can offer a single treatment size for each dose strength, whereas portfolio A can, on average, offer 14.25, portfolio B 8.0, and portfolio C 11.13. These numbers correspond to increases of 1330%, 700%, and 1010%, respectively.
Portfolio B shows the smallest increase in . The reason is that the geometrical size of API core B, which is used for configuring the product variants of portfolio B, is the same as for API core A (used in portfolios A and C), however, API core B contains only half the dose content of the API core A. Thus, the configured treatments of portfolio B are larger in size compared with, especially, portfolio A when configuring treatments of the same dose strength. In addition, since there is an upper limit in treatment size, the size scalability by the means of filling modules is much lower for portfolio B than for A since the remaining volume to fill by filling modules for treatments of portfolio B is much smaller. The same reason applies when considering the size scalability of portfolio C compared to portfolio A. Portfolio C poses some increased level of size scalability compared to portfolio B due to using both API cores A and B for product variant configuration. Hence, for a fixed dose, portfolio C can configure several sizes of treatment variants by varying the API cores A and B; on average, the remaining volume of the treatments within which to vary the filling modules is larger for portfolio C than portfolio B.
4.5.4. Patient Benefit Exemplification
To describe the meaning of an increased patient benefit by the means of modular product designs, an exemplification is offered in
Figure 10.
In
Figure 10, the example of treatments that a patient requiring the dose strength of 34.3 mg can be offered in the respective scenario is illustrated. The reference case displays the current mass production paradigm, where the patient receives a dose of 50 mg. The resulting treatment outcome from a dose perspective,
, is 0.54. Furthermore, this patient is limited to a single target release profile and treatment size, i.e., the values for
and
are 1.
The selection of treatments offered to the patient from portfolio C for both the dose-dependent and -independent scenarios are displayed in
Figure 10. Note that not the exhaustive set of treatment choices have been illustrated. For both scenarios, the benefit from a dose perspective,
, can be increased to 0.98. For the dose-dependent scenario, the patient has eight target release profiles to select from. In a dose-independent scenario, the selection of the number of target release profiles is increased to 40. Furthermore, portfolio C can at an average offer the patient a selection of 15.5 treatment sizes. An average number for treatment sizes is displayed since the treatment variants posing different release properties, i.e., D1 to D8 or I1 to I40 poses different size scalability properties. For example, the degree of size scalability of treatment D8 is not as large as for treatment D1 due to the former configuring a larger treatment from the
API cores alone before the filling modules for size scalability is introduced.
4.6. Cost Model
Equation (5) displays the total cost,
, of a treatment portfolio. In this equation,
is the preassembly cost, and
is the final assembly cost; both these expressions are based on the complexity factor by Pugh [
41].
4.6.1. Preassembly Cost
The preassembly cost,
, is only applicable in the dose-independent scenario since the preassembly process is therein used to transform
API cores, lids and cups, into
API modules (see
Figure 4). The preassembly cost,
, is obtained through Equation (6), where
is the number of parts in an
API module,
is the number of interfaces between the parts, and
is the number of types of parts in an
API module.
4.6.2. Final Assembly Cost
The final assembly cost,
, is obtained through Equation (7) and is applicable to the process of transforming modules into assemblies (see
Figure 4).
In Equation (7), , , and are the number of modules, interfaces between the modules, and types of modules, respectively, calculated for each unique product variant within each patient segment for each treatment portfolio, both for dose-dependent and -independent scenarios. The expression is averaged by the number of product variants, , within each segment. Finally, for each treatment portfolio, a weighted average is calculated for using the patient segment fraction of the total treatment population, , obtained through Equation (3).
In Equations (6) and (7), K is the constant of convenience, and f is the number of functions within the assembly for which the cost is evaluated.
4.6.3. Cost Assessment
The cost assessment is performed for both the reference case and the respective portfolio embracing modular product designs. The result is displayed as a change in cost when comparing each portfolio embracing modular product designs to the reference case, respectively, for both dose-dependent and -independent scenarios.
- —
Reference case cost assessment
As mentioned, the reference case is based on a commercial treatment providing two tablets containing the dose strengths 50 and 100 mg. A split tablet not only generates additional dose strengths, but also an imaginary interface is introduced to perform cost estimates on the commercial treatment by using Equation (7). This imaginary interface aligns with the splitting line, displayed in
Figure 3a. If this imaginary interface were not introduced, Equation (7) could not be used for cost assessment since the number of interfaces,
Ni, would be equal to zero, making the expression in Equation (7) zero. Hence, the result of the reference case would not be comparable with the cost of the treatment portfolios embracing modular product designs.
- —
Modular product design cost assessment
The preassembly cost, , obtained through Equation (6), is equal for each treatment portfolio (for the dose-independent scenario); since each API module consists of three parts (an API core, a lid, and a cup), the assembly of the parts is fixed, and, in this study, three interfaces are assumed (one between each part). Finally, the API module is configured of three types of parts since each part in the API module is a type of its own.
To perform a final cost assessment, the sets of product variants in each treatment portfolio obtained through platform execution are used. The output from platform execution describes the
and
for each product variant within each treatment portfolio. To calculate the number of interfaces,
, within each assembly (product variant) of each treatment portfolio, the final configuration of the assembled treatment must be known. In
Section 4.3.2, the approach of assembling the treatments into desired module constellations is described. Based on the module constellations in an assembly, the number of interfaces between the modules is calculated by Equation (8).
In Equation (8),
NMS is the number of modules in a stack, and
NSS is the number of saturated stacks (a full arrangement of four modules) placed on top of each other, as displayed in
Figure 5c.
NMPNS is the number of modules in any non-saturated stack.
According to Pugh [
41], the product
, in both Equations (6) and (7), is the cost driver; thus, the focus is directed to this product in the modeling. Hence,
K, which, in Equations (6) and (7), is a constant of convenience, is set to one.
denotes the number of functions of the product; thus, the complexity factor essentially indicates the cost per function. However, in this study, the number of functions is set to one when using Equations (6) and (7). The reason is that the functions embedded by any treatment portfolio will be the same, since the idea is to propose treatment portfolios complying with each of the design requirements: dose strength scalability, target release profile flexibility, and size scalability. These design requirements are the primary functions embodied by the product design, providing value for the patient.
Figure 11 displays the resulting increase in the cost of each treatment portfolio for both dose-dependent and -independent scenarios. Since the cost of any treatment portfolio embracing modular product designs is calculated as a change compared to the reference case, it is evident that portfolios consisting of modular product designs will increase the cost of production. In addition, an increased level of modularization will increase the cost of production. For example, when comparing portfolio A to portfolio B, the
API core in portfolio B entails a smaller dose than the
API core of portfolio A. The consequence is that portfolio B requires more
API cores in an assembly to generate product variants of the same dose strength as portfolio A, hence increasing the value of
in Equation (7). When comparing portfolios B and C, portfolio C does not necessarily require as many
API cores for generating a specific dose strength as portfolio B since portfolio C has two
API core sizes to use for configuration. However, due to portfolio C using two cores for configuration, the value for
in Equation (7) is increased, and thus, overall, the final cost of portfolio C is higher than that for portfolio B. The difference in cost when comparing the dose-dependent and dose-independent scenarios for the respective treatment portfolio is due to the preassembly cost, which is added in the dose-independent scenario.
4.7. Value Model
Overall, when studying the benefit and cost metrics, the cost increases for the treatment portfolios are between ~450 and 800% compared to the reference case, whereas the increase in benefit metrics, especially for and , can approach and exceed values of ~1300%. This might give some indication that the benefit of modular product designs increases faster than their production cost. However, the benefit and cost metrics are not directly comparable as they currently stand.
To enable weighing the cost to benefit, an approach to assess the value of each treatment portfolio is suggested. Based on the concept scoring method by Ulrich and Eppinger [
24], the final value,
V, of each treatment portfolio is calculated through Equation (9).
In Equation (9),
is the sum of each benefit metric and is, in Equation (9), described for each treatment portfolio by a score on a scale of 1 to 5. Similarly,
is a score on a scale of one to five. To distribute scores for the
benefit and
cost metrics in Equation (9), a scale for each performance metric has been constructed. These scales are based on raw data obtained when calculating the performance metrics for each treatment portfolio. This raw data can be found in
Table A1 in
Appendix A. For each performance metric, the highest and lowest performances, across the treatment portfolios, have been used in between to establish a linear relationship. To exemplify a scale,
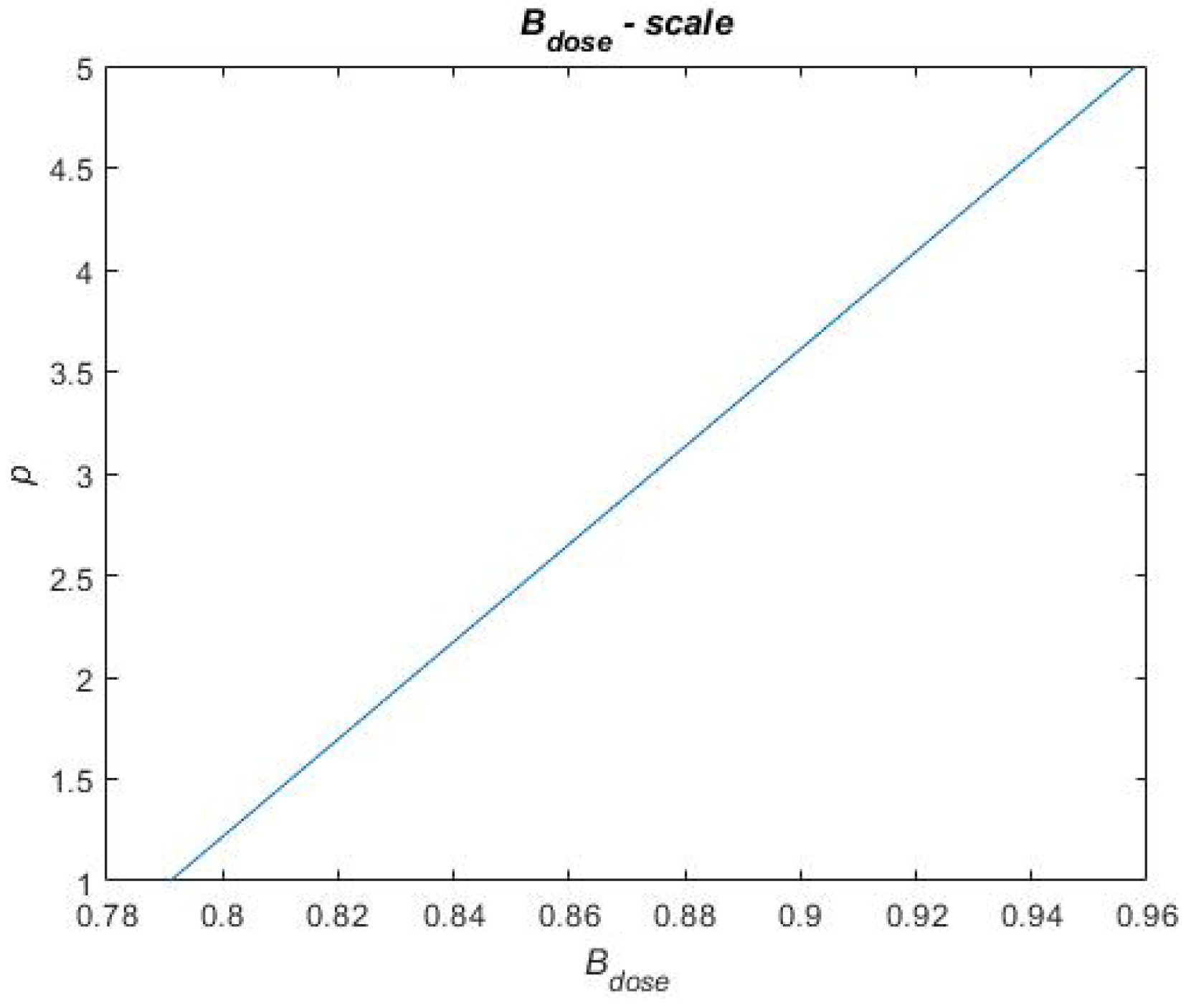
Figure 12 presents the scale for the
metric. The reference case performs the worst on this metric, i.e.,
= 0.7909 for which the score
p = 1 is assigned. Portfolios B and C perform the best on this metric, i.e.,
= 0.9581 for which the score
p = 5 is assigned. A linear relationship is established in between these metric values and scores (see
Figure 12), and the remaining portfolio performances are evaluated on this linear scale to be assigned a score. Thus, the final score on each performance metric that each treatment portfolio obtains depends on how well the treatment portfolios perform (i.e., where they end up on the scale). The remaining scales for the performance metrics and the final scores of each treatment portfolio on each performance metric are found in
Figure A1,
Figure A2,
Figure A3 and
Figure A4 in
Appendix B and
Table A2 in
Appendix C, respectively.
The scores obtained for the benefit and cost metrics that each treatment portfolio achieves are divided by the number of either benefit or cost metrics (i.e.,
or
), respectively, to obtain an average score of both benefit and cost. Furthermore, the benefit and cost metrics are weighted to explore cases where either the benefit and cost are weighted equally or where either the benefit or the cost is emphasized. The weighting is determined through the weight factors in Equation (9),
and
. The cases explored are illustrated in
Table 2 where, in the Value 50–50 case, the cost and benefit are weighted equally; in the Value 67–33 case, the benefit is emphasized; and, finally, in the Value 33–67 case, the cost is emphasized.
Value Assessment
Table 3 presents the value of each treatment portfolio for both dose-dependent and -independent release scenarios. Furthermore, based on the resulting value of each treatment portfolio, to get a quick sense of how the treatment portfolios compare to each other, a ranking has been assigned when comparing the resulting values.
When the cost and benefit are equally emphasized (i.e., Value 50–50 case), the reference case is resulting in the highest value followed by portfolios A and C for the dose-dependent release scenario. Portfolio A and C performs well on the and metrics but poorly on the cost metric, whereas the reference case maximizes the cost metric but performs poorly on the benefit metrics. Since the benefit term of the value equation is an average of each benefit metric, the overall benefit term will suffer when the performance is not maximized on each of the benefit metric. For example, portfolios A and C for the dose-dependent release scenario maximizes or performs well on the and metrics, but since the performance on the metric is worse, the overall benefit term suffers noticeably even though the and metrics are significantly better for portfolios A and C compared to the reference case.
An increased modularization (moving from portfolio A to portfolio C) can result in a benefit exceeding the cost, however, the benefit must be emphasized prior to cost (i.e., Value 67–33 case). The reason for this can be seen in
Figure 7,
Figure 8 and
Figure 9, where an evident increase in benefits can be obtained through modular product designs. Especially when comparing portfolios A, B, and C, in the dose-independent release scenario, an increased value can be seen by increased degree of modularization. Even the dose-independent release scenario of portfolio C exceeds the dose-dependent scenario of portfolio A in value due to the vast increase in benefit resulting from product modularization.
When emphasizing cost prior to benefit (i.e., Value 33–67 case) a low degree of modularization is suggestively resulting in higher value. When, for example, comparing portfolios A to C for the dose-independent release scenario, the final value of portfolio C is lower than for A and B, which could suggest that the cost of increased modularization exceeds its benefits.
5. Discussion
To answer the research question RQ1: How can individual product design requirements be realized in a pharmaceutical product for customization? the CC method was proposed as an approach to integrate product design requirements as functions into the pharmaceutical product. The usability of this approach has been demonstrated by developing a CC model of a treatment integrating the design requirements of dose strength, target release profile, and size. By using the independently operating CC objects, these separate design requirements have been incorporated as functions in the overall product. As these CC objects operate independently, a modular approach to variety has been presented, i.e., an overall treatment can be configured by using or not using each CC object depending on the design requirements to which the treatment must comply.
The API core was introduced to satisfy the design requirement dose strength. To incorporate the design requirement target release profile, two approaches to realization were discussed; the first relies on the inherent release properties of the API cores (dose-dependent release), and the second approach introduces a release control system by means of lids and cups (dose-independent release). Finally, the filling module was introduced to satisfy the design requirement size.
Not only were these design requirements incorporated, but so were the desired properties of these design requirements, i.e., a scalable dose strength, a flexible target release profile, and a scalable treatment size. Achieving flexibility in these design requirements enables the customization of the treatment according to the individual needs of the patients. The flexibility of the design requirements has been realized through the scalable approach to product variety. For example, a scalable dose strength is achieved by introducing API cores with a low dose content, and by varying the number of API cores in a treatment, the dose strength of the treatments can be varied. Furthermore, different sizes of API cores were introduced to further increase product variety. A decreased dose content of the API core increases the dose strength scalability. Lowering the dose content raises two considerations, though. If the dose content is decreased but the overall material content of the treatment remains fixed, the API core size decreases in proportion, and this means that the manufacturability of these must be verified. The second consideration is to keep the API core size to ensure their manufacturability. Hence, the material content of the core is changed, resulting in a decreased dose content. The case study in this paper is, however, purely theoretical and serves the purpose of testing the usability of the proposed method of generating modular product designs for pharmaceutical products, and rather describes the approach to increase the scalability of the treatment dose strength. API core design concerning limits in sizes and dose content, the manufacturability of these as well as the resulting dose strength scalability is product specific and depends on the API to excipient ratio. Thus, the dose strength scalability shall be investigated for each product separately. The challenge of configuring treatments (final assemblies) embracing higher dose contents arises since, for the convenience of administering any treatment, an upper size limit exists. This study did, however, only explore two different sizes of API cores to determine any indication of the benefit and cost of the resulting treatments. This study did not, by any means, aim to optimize the size(s) of the API cores or the number of different-sized API cores that should be incorporated in a treatment portfolio for the optimized benefit and cost.
Target release profile flexibility is obtained by two approaches. The first scenario is relying on the dose dependency of the release (i.e., depending on the API-to-excipient ratio of the API core) as well as the size and the shape. The resulting release mechanism has not been studied and is left for future work. The other scenario is dose-independent release, which is controlled, and the product variety can be increased vastly, since this approach relies on the release properties of lids. The lids ensure that the release is slower than through the cores, meaning that the lids control the release. This study has only explored the consequence on benefit and cost of introducing lids with two different release properties. This study did not study the explicit manufacturing process of the lids, the release mechanism of the lids and the obtained release window of treatment through varying the lids but should be in future studies.
The scalable size property was realized by scaling the number of filling modules. A single size of a filling module was used, and the number was varied within the limits of a maximum treatment volume, described in
Section 4.3.2. This study aimed to explore the size scalability property and suggest an approach to achieve this. The preferred size or shape of a treatment for any specific patient is outside the scope of this research.
This study demonstrated the applicability of the method by integrating three design requirements, dose strength, target release profile, and treatment size, for the means of pharmaceutical product customization. This study has not integrated the exhaustive set of design requirements; however, the CC method is general and can be used to integrate any desired design requirement by translating the design requirement into a functional requirement and searching for design solutions to this. This way the CC method can likewise be used to develop function models of pharmaceutical products, beyond the dosage form of a tablet, by focusing on the functions required for the specific dosage form of interest. CCM was used to develop a platform basing on the CC model of the pharmaceutical product. CCM is a research tool and due to its limitations support was brought from MATLAB to, for example, eliminate unfeasible solutions and to perform benefit, cost, and value assessments. Hence, this approach to platform modeling does not offer a complete solution applicable in the industry yet, however, a basis and a concept is presented to be further developed into a robust tool for usage in the industry.
To answer the second research question,
How can the cost and benefit of customized pharmaceutical product designs be assessed?, this study proposed three categories of performance metrics—benefit, cost, and value—to assess the value for the patient when redesigning the pharmaceutical product to comply with patient design requirements. To assess the performance, the CC model was developed into a platform based on a commercial SSRI treatment, and through platform execution treatment, portfolios A, B, and C, embracing modular product designs, were generated. Three metrics were proposed within the benefit category:
,
, and
.
complies to the design requirement of dose strength scalability and adapts the concept of
quality decay, which was initially suggested by Siiskonen et al. [
20]. This metric describes how closely the dose received by the patient matches the patient’s optimal dose. How to define the optimal dose of the patient is a question that belongs to the diagnostic field of research and is outside the scope of this study. However, in this study, based on the selected model treatment, a fictitious treatment population was generated following a normal distribution between 25 mg and 100 mg for the means of illustrating the usability of the described model.
The second benefit metric, , was proposed to assess the target release profile flexibility of the treatment portfolios. This metric assesses the unique number of release profiles a patient with a predefined dose can choose from. As an initial suggestion, this term can indicate the improved treatment quality concerning target release profiles by using the increase in the number of release profiles. However, future work should be conducted to, for example, construct a metric that can describe the release profile window that it is possible to create from the components of the treatments and then assess the distance between the optimal release profile of the patient and the release profile that actually can be generated for the patient by the treatment portfolios.
The third benefit metric, , was an initial suggestion to assess the size scalability of treatments within a treatment portfolio; for this, the number of treatment sizes that a patient, given a preselected dose and target release profile, can choose from is used as an indication for improved treatment quality. Future work should, however, incorporate the design of an assessment procedure where the optimal size and shape of treatment for the patient and the size and shape received by the patient can be compared.
To assess the cost of the treatment portfolio, the complexity factor by Pugh [
41] was used as a proxy. This factor indicated additional costs arising from the manufacturing of more complex product designs (i.e., modular products instead of fully integral products, as the reference case represents). In this study, the reference case (a fully integral product, meaning it is not composed of several parts or modules) does not entail any interfaces between the modules, since no modules exist to create any interfaces. Hence, the cost estimate using the complexity factor in Equation (7) cannot directly be used to give a comparative number to which modular product designs can be compared since the resulting complexity factor for a fully integral product is zero. By introducing an imaginary interface to the product design of the reference case, the complexity factor was used as an estimate indicating cost; however, with this approach, the complexity factor is overestimated, which might indicate an overestimation of the cost. On the other hand, the inclusion of the imaginary interface also allows for tablet splitting, which generates additional dose strengths for the reference case; similarly, this overestimates the benefit of the reference treatment portfolio. As an initial suggestion of cost assessment, this overestimation of both the cost and benefit was accepted; however, the complexity factor is an initial pragmatic estimate for design concepts to indicate the cost. The complexity factor by Pugh [
41] is based on discrete part products. In the current mass production context, pharmaceutical products embrace a composite type of nature rather than being discrete part products. However, the approach to product modularization for pharmaceutical products is inspired by discrete part products, especially modular product architectures that have been established for product customization purposes. Thus, the complexity factor, likewise inspired by assessments performed on discrete part products, has been used to assess the increase in cost when generating modular architectures for pharmaceutical products. The complexity factor has been used as an indicative measure, measuring a change when comparing the reference case to any modular product design case. The complexity factor has not been used to describe any absolute increase in cost. To determine if the complexity factor is the right approach to assess the cost of modular pharmaceutical products is not further discussed. Detailed cost models should, however, be constructed when more knowledge about the product is acquired, the material selections are made, and the manufacturing processes are outlined and so forth. The scope of this study, however, extended to modular product design; hence, the consideration of actual material selection, the selection of manufacturing processes from a cost-efficiency and technical realizability perspective has not been incorporated; however, this shall be addressed in future research.
The value assessment approach for each treatment portfolio has been suggested to weigh the benefits to the cost. Scales were created based on the raw performance data of each treatment portfolio on the respective performance metric. The scales were established to follow a purely linear scoring system between the lowest- and highest-performing portfolio on the respective metric. Whether the scales should be designed to follow linear relationships was not further studied; however, for sensitivity purposes, future experiments could be conducted to determine if any other type of scales (for example, following multiplicative or exponential relationships) will change the resulting value assessment.
The expression for value consists of two distinct terms: benefit and cost. The benefit term consisted of the three performance metrics , and . These have in this study been equally weighted in the expression for value. However, future studies can consider the weighting of these benefit metrics in relation to each other depending on the patient preference; this can provide the basis for the selection of the most suitable treatment for that patient.
Since the cost term only consists of a single metric, no inherent weighting must be considered for this term. Nonetheless, the benefit and cost terms were weighted against each other to create cases that either weigh the benefit and cost equally or emphasize either the benefit or the cost (i.e., the cases Value 50–50, Value 67–33, and Value 33–67). These cases have been created for the sole purpose of testing the impact in the resulting value metrics of the respective treatment portfolio. To determine whether the correct weights have been assigned was not the objective of this study. The value model was kept general, and essentially the stakeholders responsible for designing the products must choose the weighting to suit their respective business models.
Overall, to increase the value for the patient, modular product designs could be used to integrate desired design requirements into treatments, resulting in substantially increased performance concerning the benefit metrics, especially and . However, these benefit metrics measured the number of variants for the patient to choose from while fixing the dose of the patient. Clarifying the optimal target release profile and treatment size of the patient, as well as the offered target release profile and the treatment sizes by their portfolios, would allow to investigate the match between the optimal and the offered target release profile and size, respectively. This match would better reveal the actual increase in the benefit metrics and and reveal if the increase in performance, magnitude-wise, can reach the values that resulted from the approach to assess the performance in this study. In addition, the cost of producing modular products, posing increased benefits, increases in a similar trend. Thus, further studies should consider the tradeoff between the increased benefit for the patient and the increased cost of production. Ultimately, a better treatment could cost more due to its benefits, but the question remains of how much more is viable from a business perspective.
In this study, the benefit for the patient has solely considered benefits from a single treatment perspective. Product modularization offers another significant opportunity, combination therapeutics. Polypharmacy, i.e., administering multiple medications in a day, has been discussed as a reason for nonadherence especially for an ageing population [
46]. Modular pharmaceutical product designs could offer a solution to nonadherence from polypharmacy since instead of administering multiple treatments, the treatments could be combined as modules into a single treatment and thus, improve the adherence rate.
Increased modularity (i.e., from portfolio A to C) displayed an overall improved performance concerning benefits, mainly from a dose strength and target release profile perspective. However, when regarding the benefit from a size scalability perspective a lower degree of modularization is preferable due to the size restriction of the final treatment. The key is to consciously design the modules to find the balance that results in a degree of modularization that, from a cost and benefit perspective, provides the best outcome. To develop this optimal design will probably be a case-by-case consideration, and any further discussion of this is outside the scope of this paper. Not only is the trade-off between benefit for the patient and the cost of production a key consideration when modularizing products; pharmaceutical production is a highly regulated environment that currently poses strict approaches for the quality control of any commercial pharmaceutical product. The approaches to quality control today generally imply an off-line quality control of each batch produced. Employing current quality control approaches with increased product modularity and the resulting increase in complexity of production logically implies an increased degree of quality control activities. The management of the required increase of quality control activities remains a challenge. Hence, the challenge of quality control for customized pharmaceutical products is researched and for notable research initiatives on the topics such as quality by design and process analytical technology for real-time quality control the reader is referred to [
47].
6. Conclusions and Future Work
This paper presented an approach to integrate three product design requirements—dose strength, target release profile, and size—to customize pharmaceutical products according to patient needs. The CC method enabled the integration of these design requirements as functions to which design solutions were assigned and, further, which were developed into independently operating CC objects. These CC objects were further realized as components that generated modular product designs.
The API core was introduced to satisfy the design requirement of dose strength, the lid and cup were used to meet the design requirement of target release profile, and the filling module was employed to fulfill the design requirement of size. To achieve the desired flexibility of these design requirements, scalable parameters of the design solutions were defined. For example, by introducing an API core with low dose content, the number of these cores could be scaled to generate treatments of different dose strengths.
An SSRI treatment was selected as a model treatment for which a platform was developed, based on the CC model of a treatment. Through platform execution, treatment portfolios were generated. Portfolios A, B, and C embraced modular product designs, with varying degrees of modularization, and the design of the reference case was based on the model treatment. Furthermore, a patient population for this model treatment described by patient needs was developed. The value of the treatment portfolios for the patient was assessed through three categories of performance metrics: benefit, cost, and value. From a benefit perspective, three metrics were suggested to comply with the three product design requirements: dose strength scalability, target release profile flexibility, and size scalability, respectively. The results showed that
- —
Increased degree of modularization can substantially increase the ability to match the offered treatment to the patient’s optimal dose.
- —
By introducing a few components to increase target release profile flexibility, there is a substantial increase in the number of target release profiles from which the patient can choose.
- —
Maximizing the dose content of the API core offers the best conditions for maximizing treatment size scalability.
To assess the cost of each treatment portfolio, the complexity factor by Pugh [
41] was applied. The results indicated that the cost of modularization does not increase as fast as the improvement obtained in the benefit metrics. However, as the
benefit and
cost metrics are not directly comparable,
value has been suggested as an approach to compare the treatment portfolios concerning the benefit for the patient and the cost of producing the various product variants within a treatment portfolio. Overall, the results showed that
- —
An increased degree of modularization (moving from portfolio A to portfolio C) can result in faster increasing benefits compared to the increasing costs from modularization.
However, several tradeoffs between design choice concerning the degree of product modularization and the performance metrics could be detected. A decreasing API core dose strength promotes dose strength scalability; however, the size scalability of a treatment portfolio suffers. Introducing additional components such as lids and cups substantially improves the target release profile flexibility, but the cost of production increases. Further studies should account for which design requirement is the most important to support decisions regarding modular product designs and/or to conduct module design optimization by maximizing the benefit and cost tradeoff.
This study only considered modular product designs. Process flexibility (i.e., the feasible approach to producing increased product variety) as well as a profitable provision (i.e., the ability to supply the customized pharmaceutical products to the patients) should be studied along with product modularization. Ultimately, if the customized pharmaceutical product cannot be produced and supplied profitably, it will not reach the patient, and thus the treatment outcome cannot be enhanced.