Efficient and Equitable Climate Change Policies
Abstract
1. Introduction
2. The Energy Model TIAM
2.1. The Reference Energy System (RES)
2.2. Technology Data
2.3. LAP Emissions and External Costs
- Power Sector. Emissions for each technology follow either the NEEDS data with end-of-pipe measures included in the cost, or the U.S. Environmental Protection Agency (EPA) data [21] for the missing NEEDS technologies.
- Transport. The transport sector is quite detailed and is based on NEEDS for each technology, explicitly following model activities rather than being on a fuel-consumption basis.
- In all other sectors, the calibrated emission coefficients for the base year take into account exogenous future improvement via policies and end-of-pipe technologies and are generic. In the reference development (BASE) scenario presented in this report, emission coefficients in 2020 are lower by 10% relative to 2005, by 20% in 2030, by 30% in 2050, and by 55% in 2100. In addition, extra desulfurization measures in the industrial sectors of China and India are implemented. This approach simulates emission standards following technological change without extra investment costs in the model (see also [15] for scenario PROG, where specific emission reductions are defined between stabilization in the levels of 2010 and the best possible available technology).
2.4. Macro Stand Alone (MSA)
- Cr,t: annual consumption (variable)
- Yr,t: annual production (variable)
- Kr,t: total capital (variable)
- INVr,t: annual investments (variable)
- DEMr,t,k: annual demand in Macro for commodity k (variable)
- DETr,t,k: annual demand in TIMES for commodity k (variable)
- ECr,t: annual energy system costs in Macro (variable)
- Aklr: production function constant
- ampr,t: constant term to account for the full annualized investment cost of existing capacities in the starting period.
- Br,k: demand coefficient for demand commodity k
- aeeifacr,t,k: autonomous energy efficiency improvement
- dt: duration of period t in years
- ddfr,t,k demand decoupling factor (calibration parameter)
- deprr: depreciation rate
- dfactr,t: utility discount factor
- growvr,t: growth rate (calibration parameter)
- kpvs: capital value share
- lr,t: annual labor growth index
- nwtr: Negishi weight for region r
- pwt: period-length-dependent weights in the utility function (these multipliers are introduced to in cases where the period lengths are not equal)
- qar,t: constant term of the quadratic supply cost function
- qbr,t,k: coefficient for demand k in the quadratic supply cost function
- tsrvr,t: capital survival factor between periods t and t + 1
- ρr: substitution constant
- T: number of periods in the model horizon
3. Scenarios Analyzed
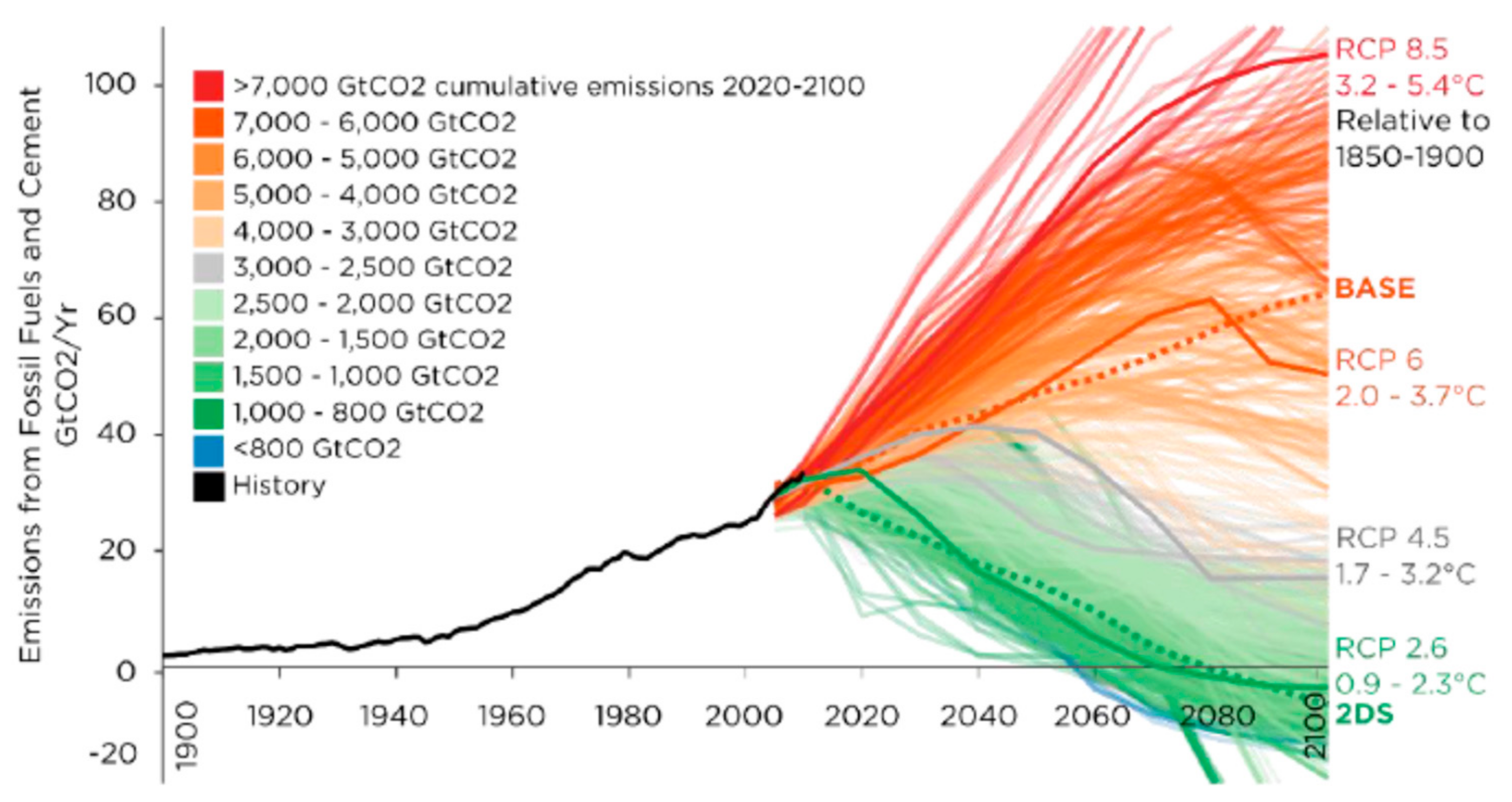
- The reference scenario (BASE) generated in the ETSAP project refers to the calibration year of 2005, describes the development of the global energy system in agreement with all other valid policies (including the nuclear phase out where it has been decided), and provides a baseline for comparing policy scenarios. The “BASE” scenario solves for least cost predicated on available resources and technologies under existing macroeconomic projections, which are consistent with the projections of the GEM-E3 [23] growth model. Total CO2 emissions related to energy and cement production are similar to the short-term reductions resulting from the National Determined Contributions (NDCs) and follow the pathways of the Representative Concentration Pathways (RCP) 4.5 scenario up to 2030 (Figure 1). The BASE case economic projection does not take into account environmental damage costs to ecosystem services in the global economy due to climate change or health and other damages related to local atmospheric pollutants (LAP).
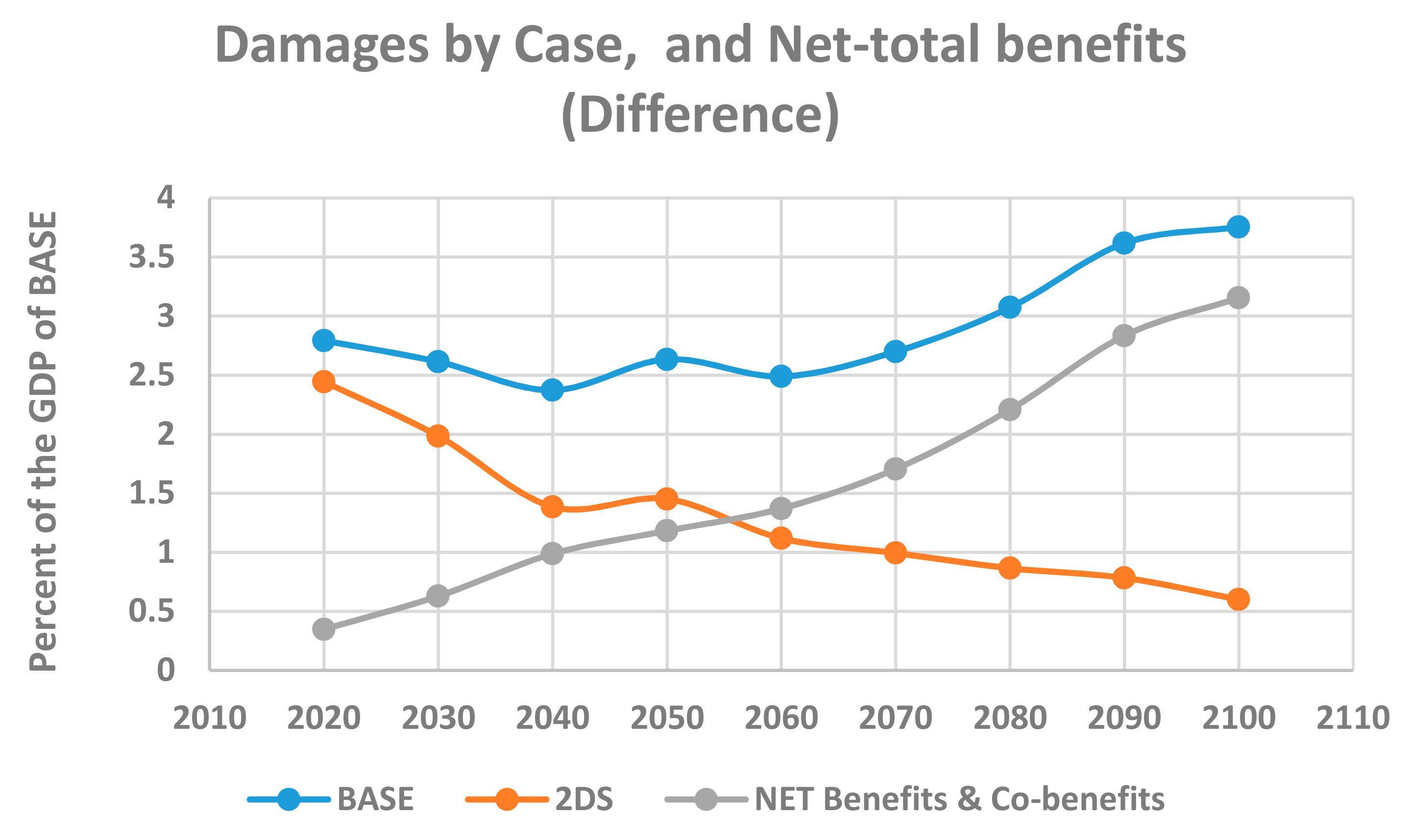
- Then, we assess the 2 °C (2DS) climate policy postulating a global cumulative CO2eq budget compatible with the long-term target of 2 °C. The 2DS scenario begins with the same macroeconomic structure as the BASE scenario and a cumulative GHG budget of 1850 GtCO2eq applied between 2020 and 2100 with a 50% confidence level to remain below 2 °C [24]. The emissions of the 2DS case, shown in Figure 1, are initially below those of the RCP2.6 case, which are starting to fall in 2020. The 2DS trajectory intercepts the RCP2.6 case in 2040, and follows a higher path afterwards to join again this trajectory at the end of the time horizon such that both integrals of emissions are quite the same.
- Finally, we define ex-post damages related to climate change and to the ambient air pollution for each scenario such that their differences (reduction of climate damages) and co-benefits (reduction of LAP damages) induced by climate policies are defined as the net benefits of the 2DS case over the BASE case. The cost of such policy (GDP losses of the 2DS scenario relative to BASE) is also evaluated, while this ex-post assessment presents a kind of alternative cost/benefit analysis.
4. Main Results and Discussion
4.1. Emission Pathways
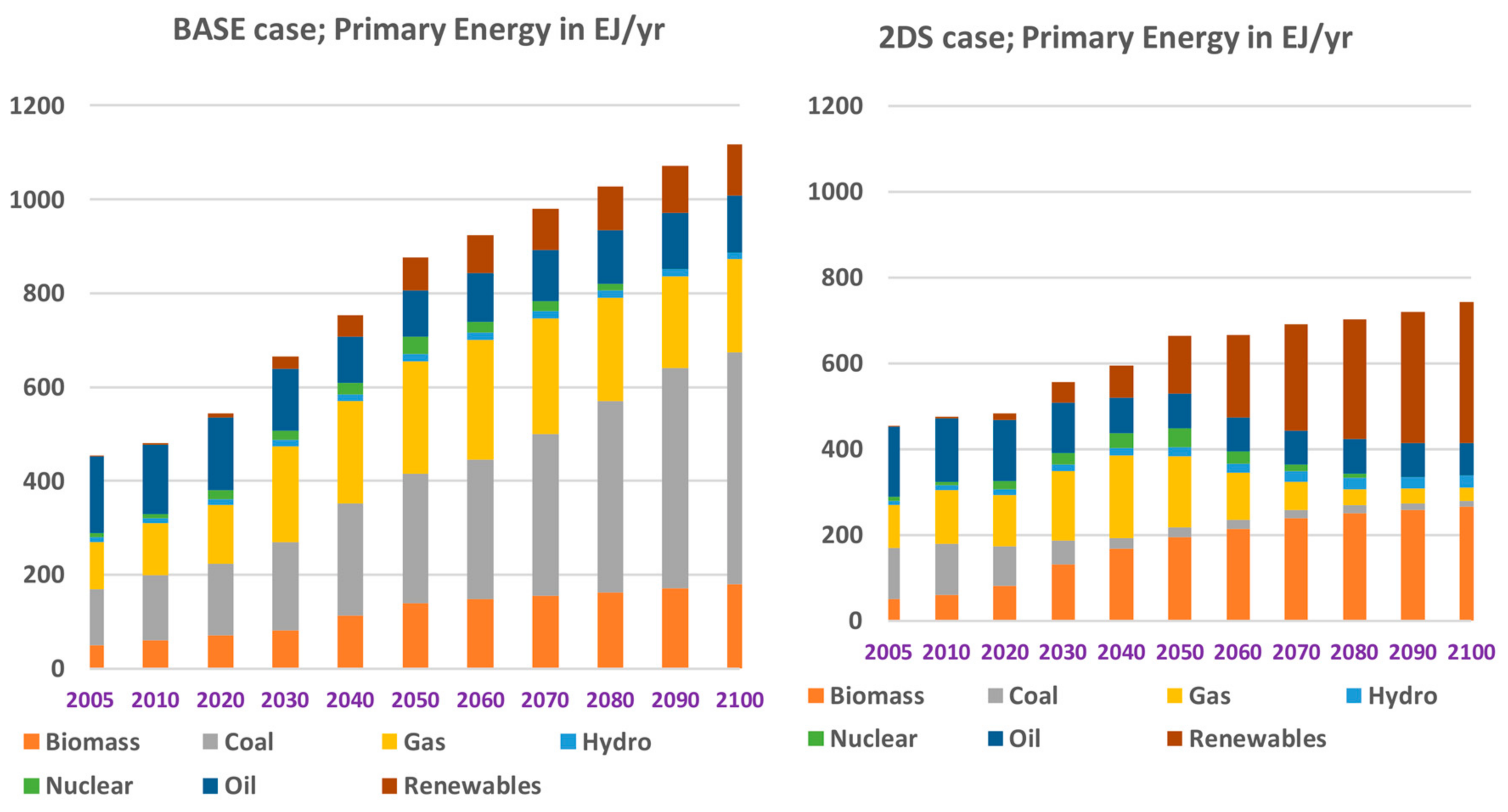
4.2. Primary Energy Consumption
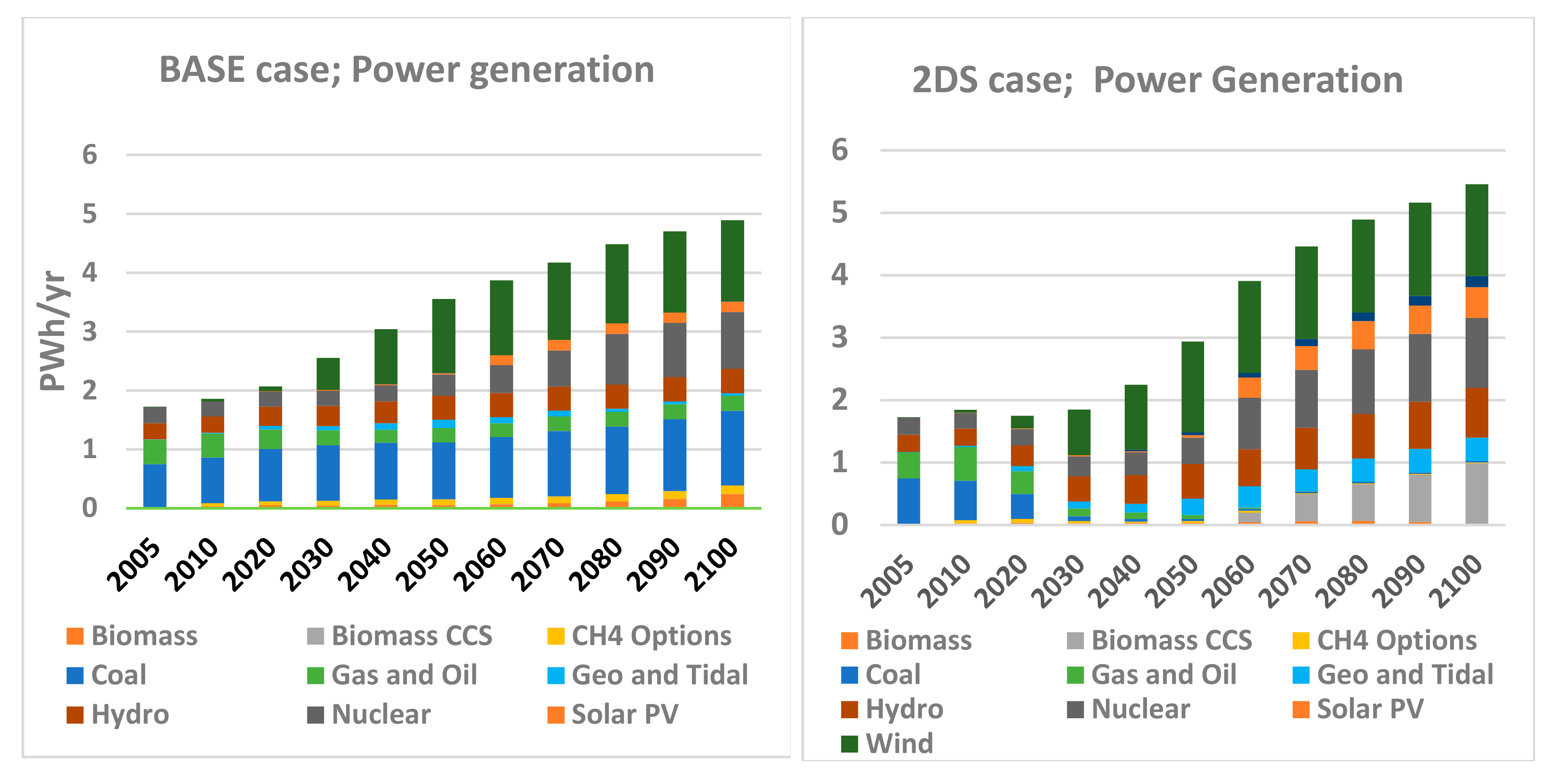
4.3. Electricity Generation
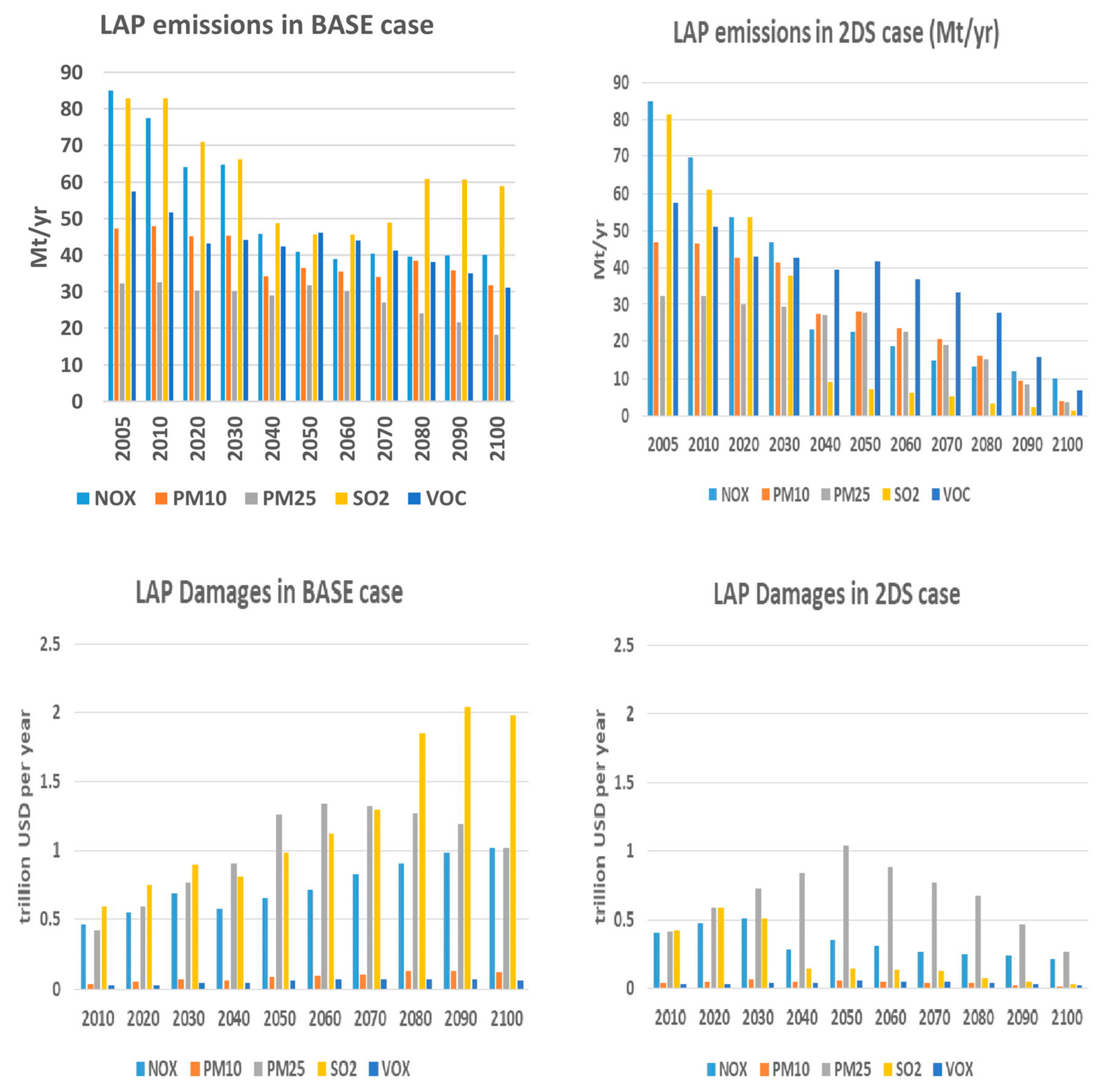
4.4. LAP Emissions
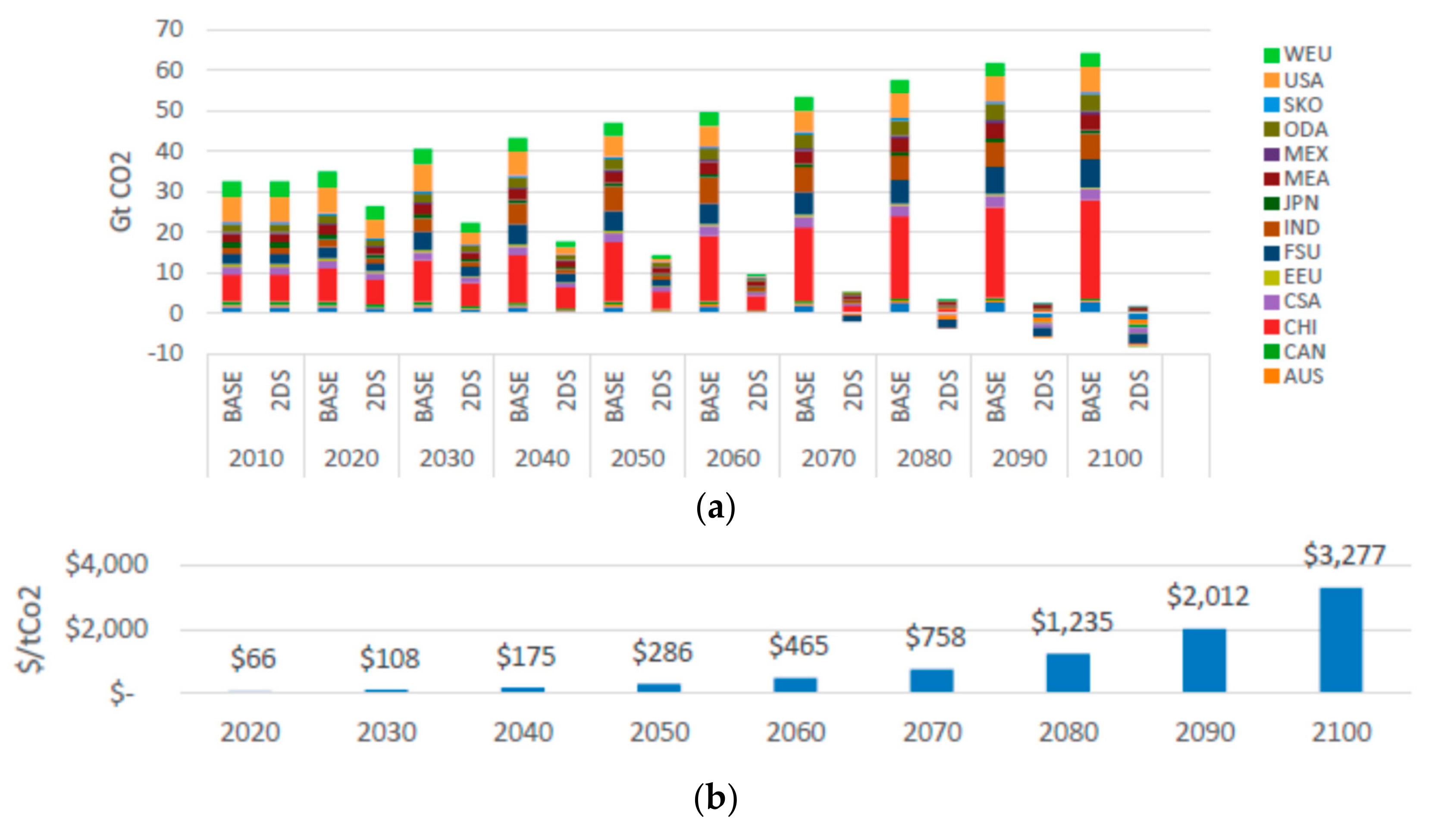
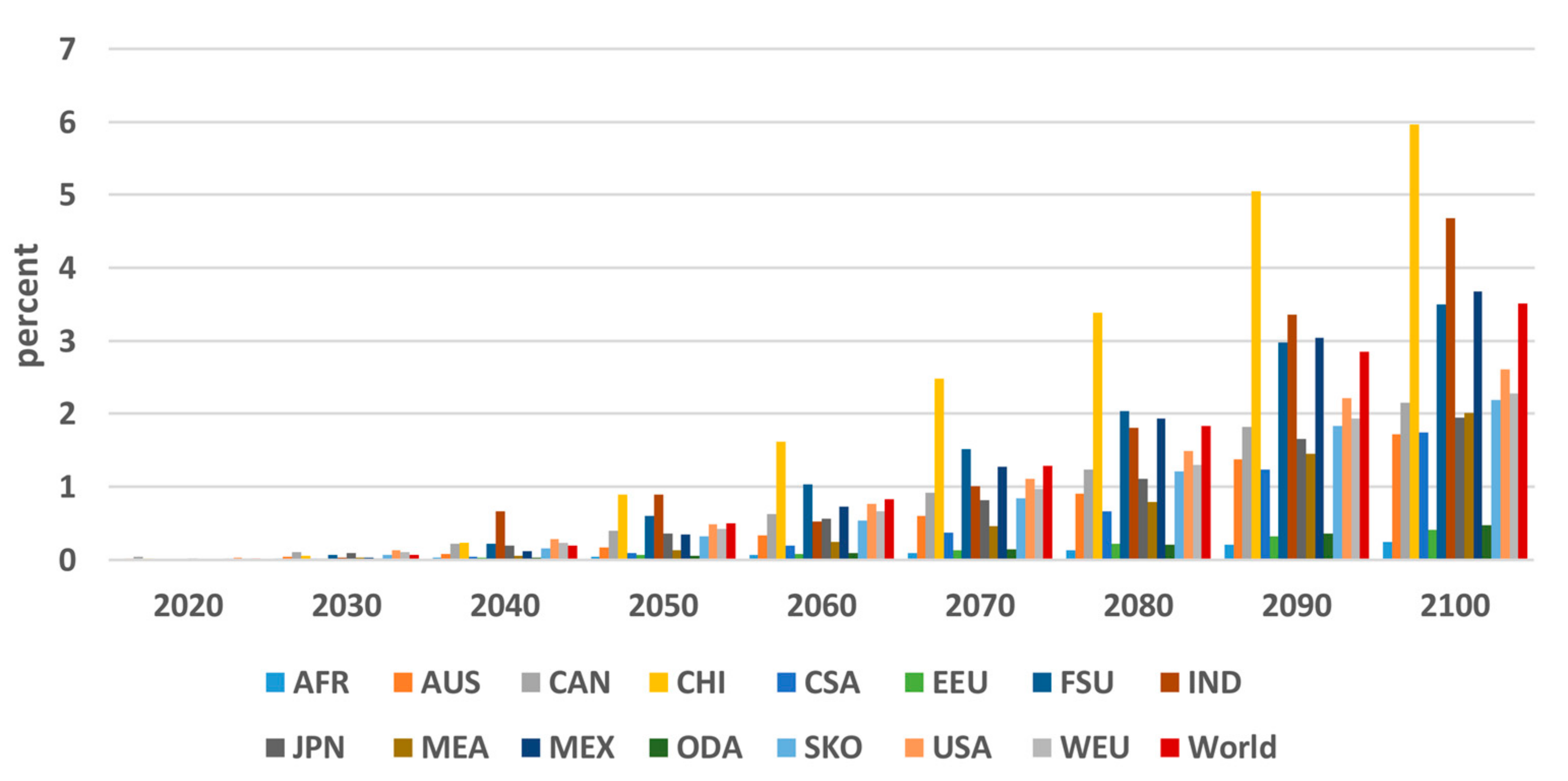
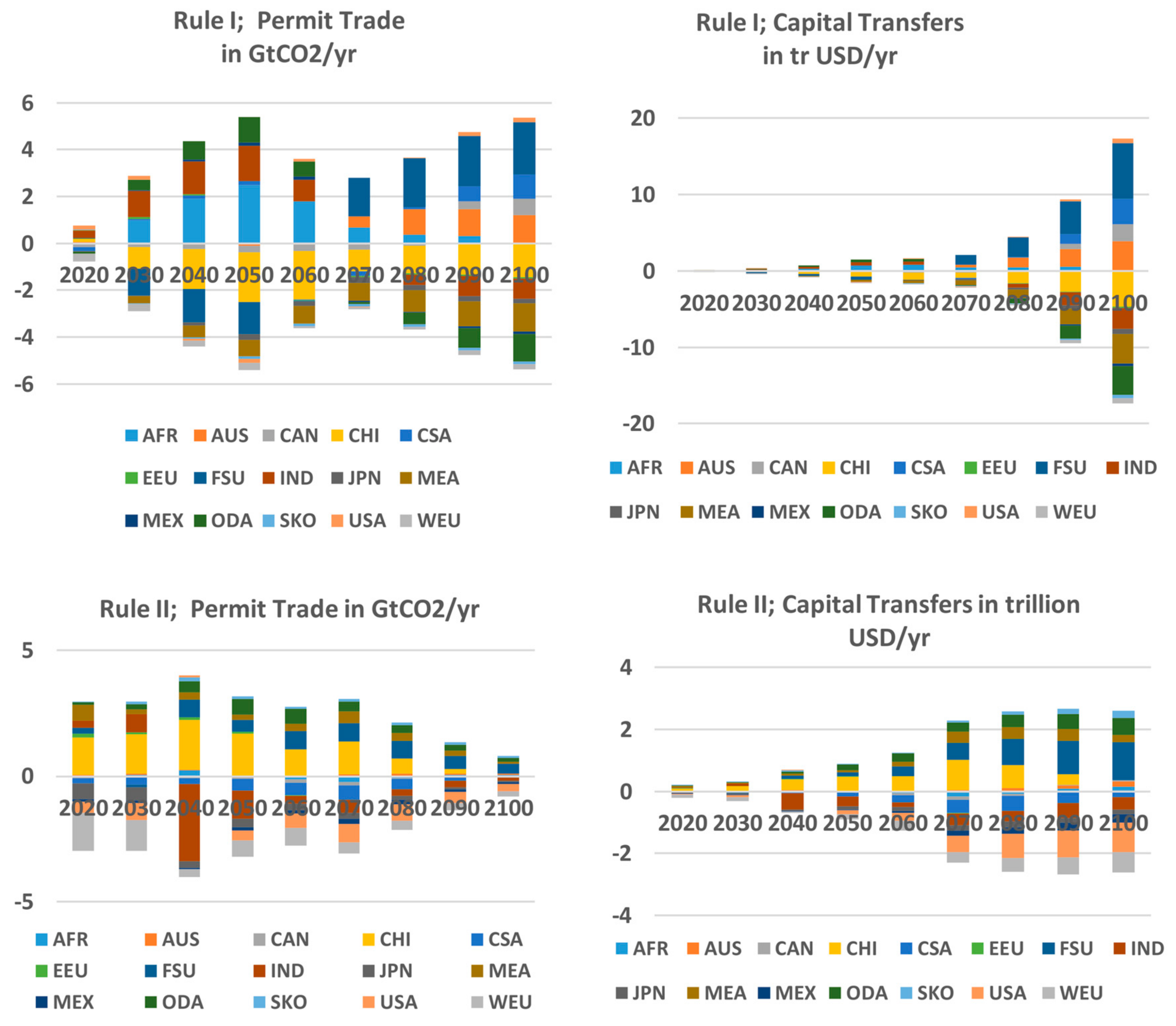
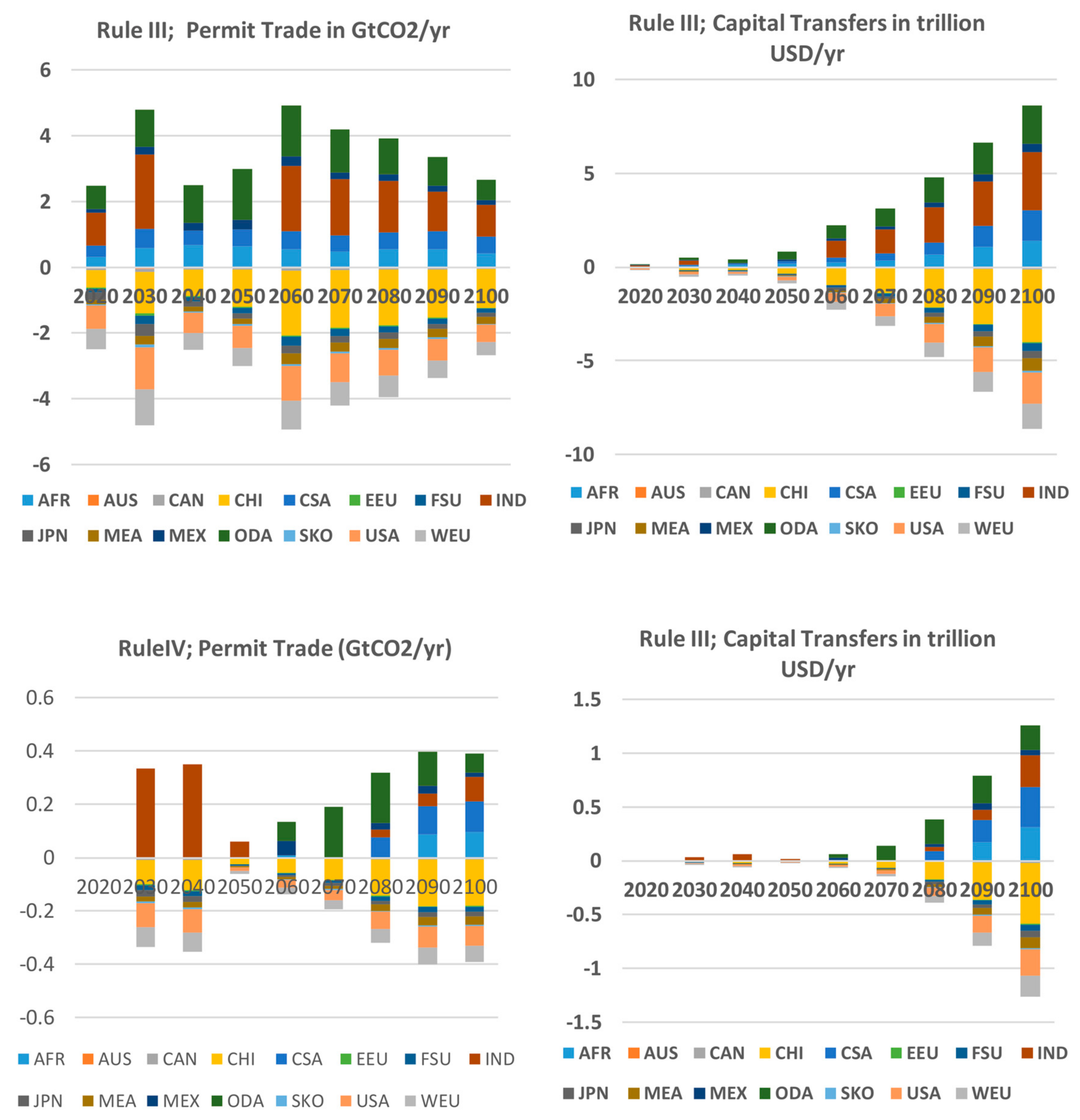
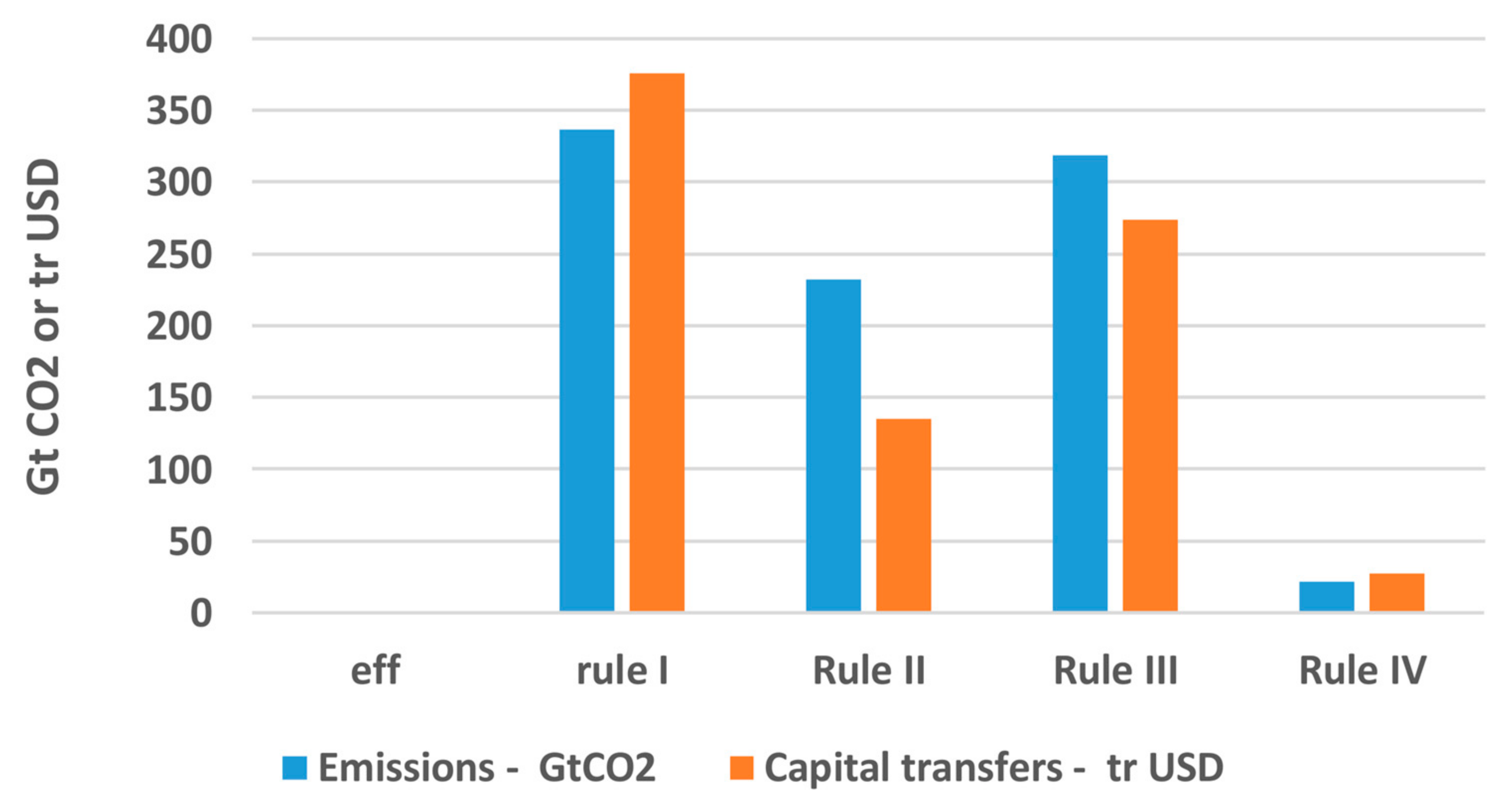
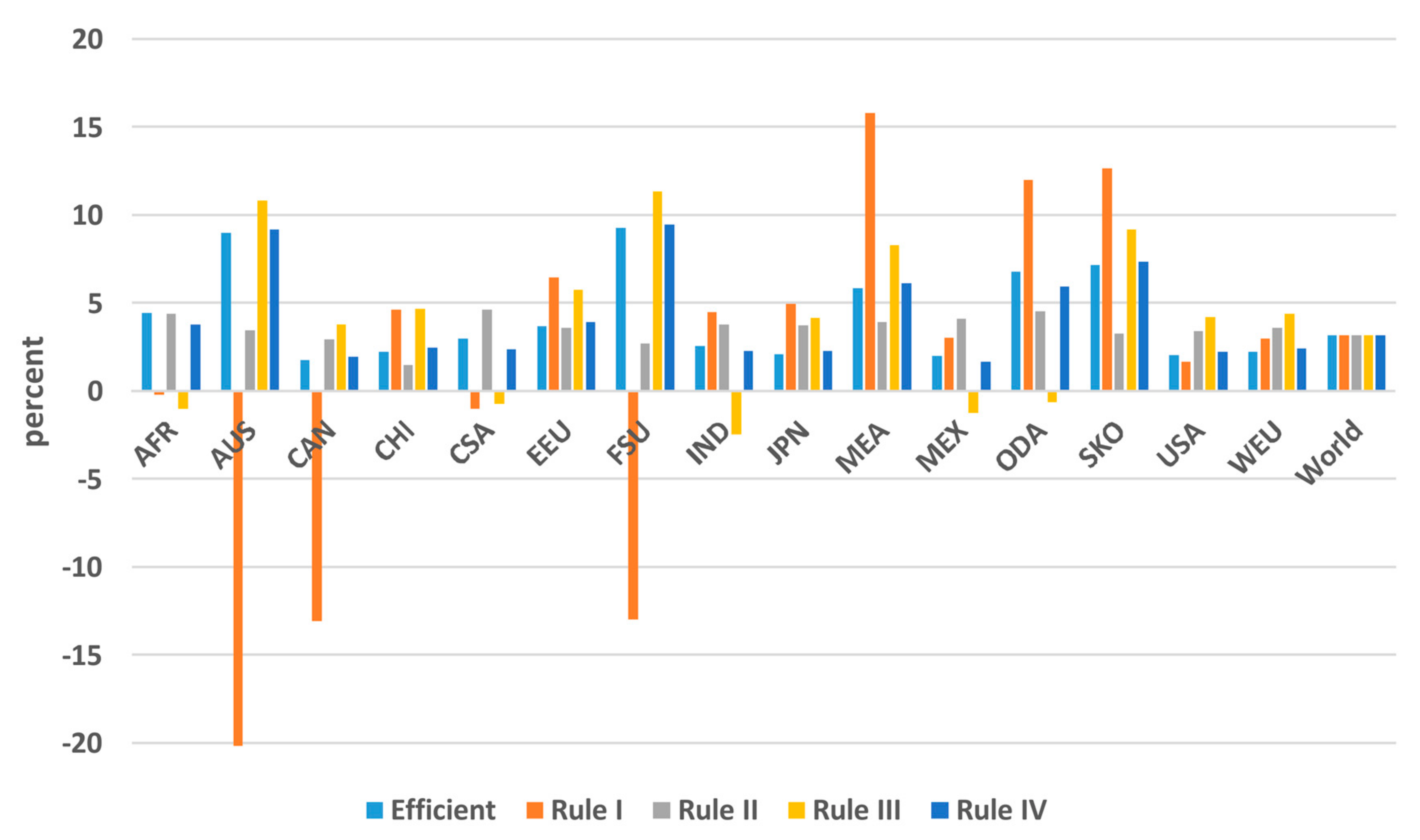
5. Burden Sharing (BS)
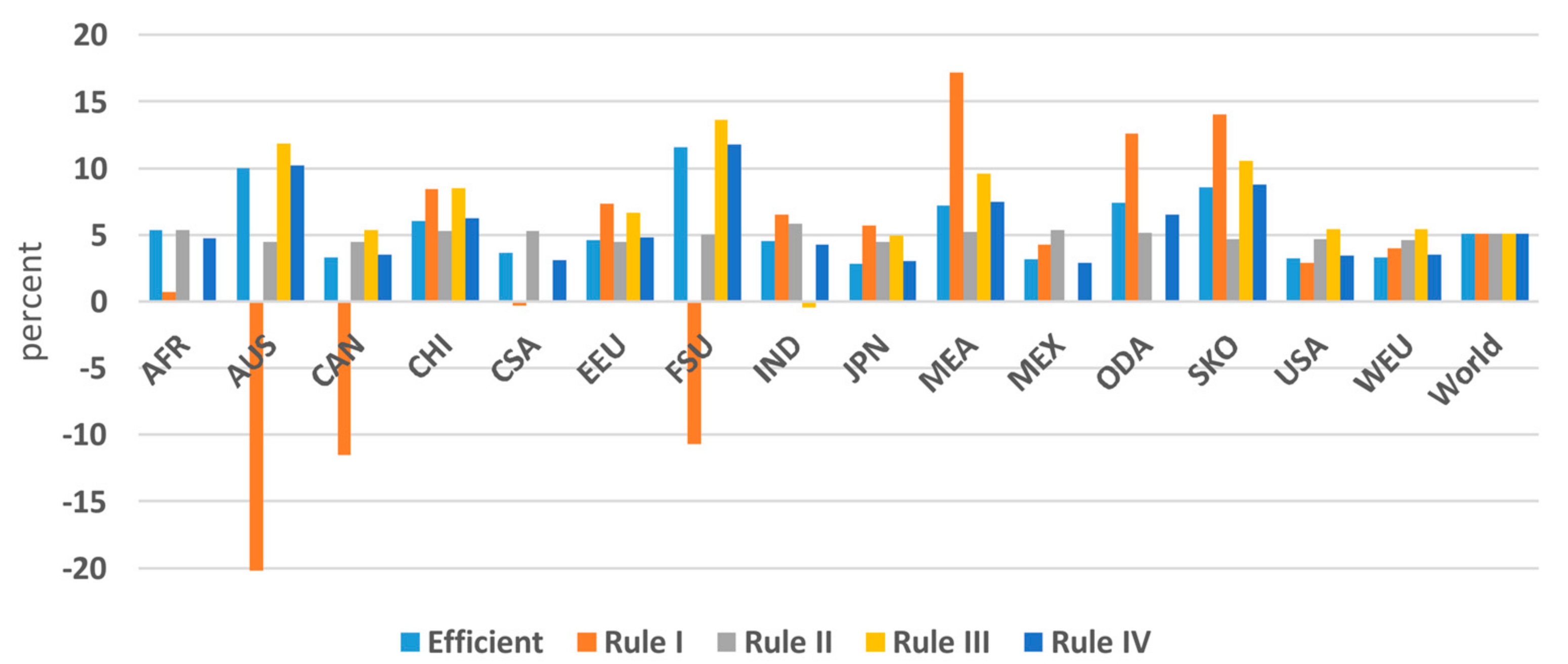
6. BS Net of Global Climate Change (GCC) Damages and LAP Externalities
7. Conclusions
- The 2 °C policy is technically feasible and accepting burden sharing redistribution rules can be equitable. However, total cumulative (2020–2100) and undiscounted GDP losses are high (5.15% compared to the GDP integral of the BASE case). This cost is within the economy and the energy system exclusive of the side benefits, i.e., it is an economically efficient second best solution.
- However, the pre-conditions of technical feasibility for the 2DS case are related to the assumptions underlying the calculations, such as a universal determination of industrialized nations to proceed first with their own commitments, second with assisting LDCs to materialize the transition of their energy systems, and finally with increasing Research & Development & Demonstration (R&D&D) spending of public and private resources for the development of advanced technology, such as BECCS, and for supporting related infrastructures.
- The climate policy brings also ancillary benefits that reduce damage from local pollutants (SO2, NOx, PM, VOC) by exploiting synergies. Carbon mitigation policies reduce global climate change damages and improve ambient air quality; therefore, they compensate for part of the cost of mitigating climate change.
- The analysis quantifies the avoided climate damages and the co-benefits of LAP control always under the reservation of uncertainties in the climate science, in the ambient air quality and damages, and in the economics of climate change. Both benefits result in a net benefit of about two percentage points (p. p.) of the BASE case’s GDP integral. Nevertheless, the mitigation cost of climate change for the 2DS policy case is not fully balanced and remains higher than the benefits by three percentage points.
- These benefits address part of all of the potential benefits of climate policies. Co-benefits in TIAM do not account for indoor pollution and ecosystem services nor for natural capital conserved via climate mitigation policy. We do not consider also the improvement of air quality as a consequence of climate change control that could significantly reduce health impacts [16].
- The consideration of burden sharing between regions defines equitable scenarios. Equal relative GDP losses is a balanced burden sharing allocation rule but is less appropriate for LDCs. The full compensation of the energy system cost increase requires low capital transfers to LDCs for their investments in favor of a carbon-free technology switch. The capital transfers of Rule IV in favor of LDCs are low and therefore one could argue to fully support investments via technology transfer protocols towards a decarbonized economy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chiodi, A.; Donnellan, T.; Breen, J.; Deane, P.; Hanrahan, K.; Gargiulo, M.; Ó Gallachóir, B.P. Integrating agriculture and energy to assess GHG emissions reduction: A methodological approach. Clim. Policy 2015, 16, 215–236. [Google Scholar] [CrossRef]
- Fricko, O.; Havlik, P.; Rogelj, J.; Klimont, Z.; Gusti, M.; Johnson, N.; Ermolieva, T. The marker quantification of the Shared Socioeconomic Pathway 2: A middle-of-the-road scenario for the 21st century. Glob. Environ. Chang. 2017, 42, 251–267. [Google Scholar] [CrossRef]
- Kriegler, E.; Bauer, N.; Popp, A.; Humpenöder, F.; Leimbach, M.; Strefler, J.; Mouratiadou, I. Fossil-fueled development (SSP5): An energy and resource intensive scenario for the 21st century. Glob. Environ. Chang. 2017, 42, 297–315. [Google Scholar] [CrossRef]
- Emmerling, J.; Drouet, L.; Reis, L.A.; Bevione, M.; Berger, L.; Bosetti, V.; Malpede, M. The WITCH 2016 Model-Documentation and Implementation of the Shared Socioeconomic Pathways. FEEM Working Paper 42. 2016. Available online: http://www.feem.it/getpage.aspx?id=8521 (accessed on 11 April 2018).
- Kypreos, S.; Lehtilä, A. Decomposing TIAM-MACRO to Assess Climatic Change Mitigation. Environ. Model. Assess. 2015, 20, 1–11. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Energy Technology Perspectives-Scenarios & Strategies to 2050; International Energy Agency: Paris, France, 2006. [Google Scholar]
- US-EIA. Energy Outlook; International Energy Agency: Paris, France, 2007. [Google Scholar]
- Howells, M.; Rogner, H.; Strachan, N.; Heaps, C.; Huntington, H.; Kypreos, S.; Roehrl, A. OSeMOSYS: The Open Source Energy Modeling System: An introduction to its ethos, structure and development. Energy Policy 2011, 39, 5850–5870. [Google Scholar] [CrossRef]
- PRIMES. 2016. Available online: www.e3mlab.ntua.gr (accessed on 11 April 2018).
- IEA Statistics. Available online: https://www.iea.org/statistics/ (accessed on 11 March 2018).
- IEA/ETSAP Project. Available online: https://iea-etsap.org/ (accessed on 8 March 2018).
- Loulou, R.; Labriet, M. ETSAP-TIAM: The TIMES integrated assessment model Part I: Model structure. Comput. Manag. Sci. 2008, 5, 7–40. [Google Scholar] [CrossRef]
- Loulou, R. ETSAP-TIAM: The TIMES integrated assessment model, part II: Mathematical formulation. Comput. Manag. Sci. 2008, 5, 41–66. [Google Scholar] [CrossRef]
- IEA-WEO. Special Issue on Energy and Air Pollution; International Energy Agency: Paris, France, 2016. [Google Scholar]
- Kitous, A.; Keramidas, K.; Vandyck, T.; Saveyn, B.; Van Dingenen, R.; Spadaro, J.; Holland, M. Global Energy and Climate Outlook 2017: How Climate Policies Improve Air Quality; JRC107944, EUR 28798 EN; European Commission, Joint Research Centre: Seville, Spain, 2017; pp. 71–72. [Google Scholar]
- Garcia-Menendez, F.; Saari, R.K.; Monier, E.; Selin, N.E. US Air Quality and Health Benefits from Avoided Climate Change under Greenhouse Gas Mitigation. Environ. Sci. Technol. 2015, 49, 7580–7588. [Google Scholar] [CrossRef] [PubMed]
- Volkart, Integration of Energy-Economic System Modelling and Multi-Criteria Analysis. Ph.D. Thesis, ETH Zurich/Paul Scherrer Institute, Switzerland, Europe, 2016.
- NEEDS. New Energy Externalities Developments for Sustainability. 2009. Available online: http://www.needs-project.org (accessed on 11 April 2018).
- EMEP/EEA. Air Pollutant Emission Inventory Guidebook. 2013. Available online: https://www.eea.europa.eu/themes/air/emep-eea-air-pollutant-emission-inventory-guidebook (accessed on 11 April 2018).
- EDGAR. Emission Database for Global Atmospheric Research (EDGAR) for the Year 2005. Available online: http://edgar.jrc.ec.europa.eu/overview.php?v=42 (accessed on 11 April 2018).
- Shay, C.; DeCarolis, J.; Loughlin, D.; Gage, C.; Yeh, S.; Vijay, S.; Wright, E.L. EPA U.S. National MARKAL Database: Database Documentation; EPA-600/R-06/057; Environmental Protection Agency: Washington, DC, USA, 2006.
- Manne, A.; Mendelsohn, R.; Richels, R. MERGE: A model for evaluating regional and global effects of GHG reduction policies. Energy Policy 1995, 23, 17–34. [Google Scholar] [CrossRef]
- GEM-E3. Manual and Documentation of the GEM-E3 Model. 2016. Available online: https://ec.europa.eu/jrc/en/gem-e3/model (accessed on 11 April 2018).
- Kriegler, E.; Tavoni, M.; Aboumahboub, T.; Luderer, G.; Calvin, K.; Demaere, G.; Van Vuuren, D.P. What does the 2 °C target imply for a global climate agreement in 2020? The limits study on Durban platform scenarios. Clim. Chang. Econ. 2013, 4, 1340008. [Google Scholar] [CrossRef]
- Socrates Kypreos: Equitable Burden Sharing: Modelling the Macroeconomic Impacts of the Carbon Constrained Energy System in ETSAP-TIAM-MACRO, International Energy Workshop in Cork, Ireland in 2016. Available online: https://www.ucc.ie/en/iew2016/presentations/ (accessed on 8 March 2018).
- Tavoni, M.; Kriegler, E.; Riahi, K.; Van Vuuren, D.P.; Aboumahboub, T.; Bowen, A.; Luderer, G. Post-2020 climate agreements in the major economies assessed in the light of global models. Nat. Clim. Chang. 2015, 5, 119–126. [Google Scholar] [CrossRef]
- ISCHESS—Integration of Stochastic Renewables in the Swiss Electricity Supply System. Available online: https://www.psi.ch/lea/HomeEN/Final-Report-ISCHESS-Project.pdf (accessed on 11 March 2018).
| 1 | Naturally, the methodology followed in TIAM-MACRO for the cost of local pollutants is simple as it is based on emission inventories only. On the contrary, the approach described in [16] follows the causality chain and concludes about the atmospheric quality of each scenario. According to [16], climate change, exclusive of changes in air pollutant emissions, can significantly impact ozone (O3) and fine particulate matter (PM2.5) pollution across the U.S. and increases the associated health effects. Clearly, by excluding such analysis concerning the impacts of climate change to air quality, we underestimate health impacts. Figure 3, page 7585, in [16] indicates that such improved air quality could offset the cost of climate policy by 11–14.5%, which for our case corresponds roughly to another 0.8 p.p. of the estimated climate change mitigation cost. |
| 2 | It is quite easy to integrate in TIAM the MACRO Stand-Alone (MSA) module. One has to just include Equations (2)–(11) (excluding Equation (8)) into the set of equations modelling TIAM and to solve the overall model maximizing Equation (2). The result will be a non-linear model with about a million linear equations that is not tractable even with the best available personal computer. |
| 3 | The values shown in Figure 2b correspond to an exponential growth factor of 1.6289 = (1.05)10 per decade, induced by the cumulative CO2 constraint, and start from 66 $/tCO2 in 2020. 5% per year is the discount factor applied in TIMES. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kypreos, S.; Glynn, J.; Panos, E.; Giannakidis, G.; Ó Gallachóir, B. Efficient and Equitable Climate Change Policies. Systems 2018, 6, 10. https://doi.org/10.3390/systems6020010
Kypreos S, Glynn J, Panos E, Giannakidis G, Ó Gallachóir B. Efficient and Equitable Climate Change Policies. Systems. 2018; 6(2):10. https://doi.org/10.3390/systems6020010
Chicago/Turabian StyleKypreos, Socrates, James Glynn, Evangelos Panos, George Giannakidis, and Brian Ó Gallachóir. 2018. "Efficient and Equitable Climate Change Policies" Systems 6, no. 2: 10. https://doi.org/10.3390/systems6020010
APA StyleKypreos, S., Glynn, J., Panos, E., Giannakidis, G., & Ó Gallachóir, B. (2018). Efficient and Equitable Climate Change Policies. Systems, 6(2), 10. https://doi.org/10.3390/systems6020010



