Model-Based Design and Formal Verification Processes for Automated Waterway System Operations
Abstract
:1. Introduction
2. System View of Narrow Waterways
- A.
- Boundary: This is the physical perimeter of the waterway that separates it from its external environment. This is defined based on the specificity of the given waterway, taking into account the traffic, physical constraints, security and operation parameters. Geopolitical and environmental considerations may play important roles in delimiting the boundaries of the waterway system. We note, in particular, that most of the world’s straits are shared by two or more countries, while the majority of canals are inland.
- B.
- Inputs and outputs: Ships are physical entities that enter and exit the waterway through the above-mentioned boundaries. From a component and component assembly perspective, flows of ships are the inputs and outputs of our system. Whether they navigate the waterway by their own or with some help, they need and use information provided by the system controller (traffic management system) to complete the crossing.
- C.
- Subsystems and components: Straits and canals have subsystems and components that are distinct. In the former, they are the “zoning” naturally created by the shape and width of the strait. In the latter, sets of lock chambers are subsystems distributed along the canal. The waterway control system regulates the traffic and/or commands the crossing operation as a core subsystem of the waterway. Depending on the analysis need, subsystems can be decomposed recursively into low-level components having well-defined repeatable functionality. We will illustrate this decomposition process in the case study section below.
- D.
- Connectivity: System connectivities are defined by the physical (wired) and non-physical (wireless) connections between components. For our purposes, connectivities allow for the coordination and sequencing of actions necessary to achieve efficient and safe execution of the ship crossing process. In modernized waterway systems, connectivity can be achieved through the use of geographical information systems (GIS) and communication between the distributed set of locks in canal systems or check points in straits [11,12].
- E.
- Surrounding environment: This comprises elements that are external to the system, but that might influence its functioning and/or performance. Extreme weather events, such as heavy rain, are environmental elements that can potentially affect the navigability of the waterway.
3. Pathway of Development for Model-Based Design
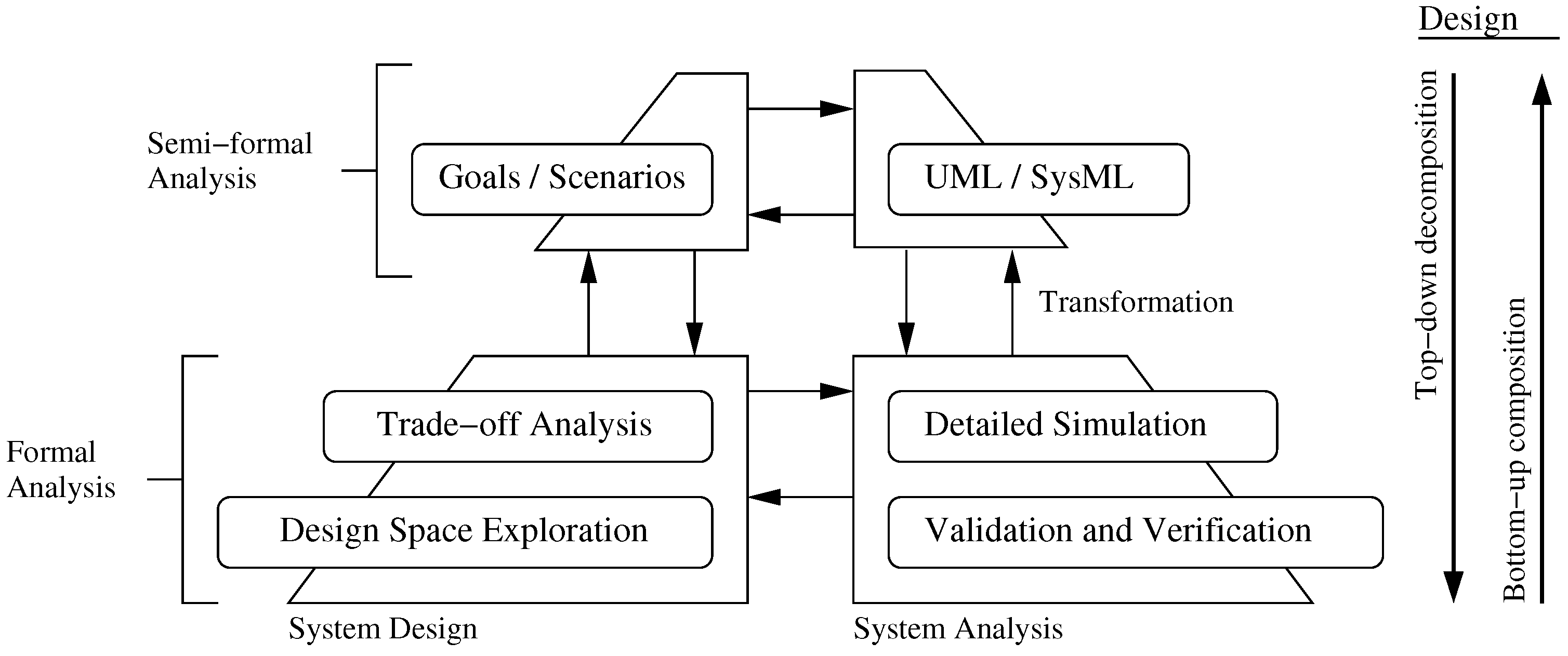
3.1. Multi-Level Approach Model-Based System Design
3.2. Pathway of Development
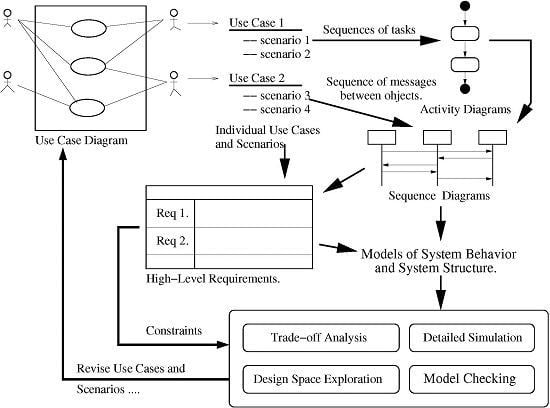
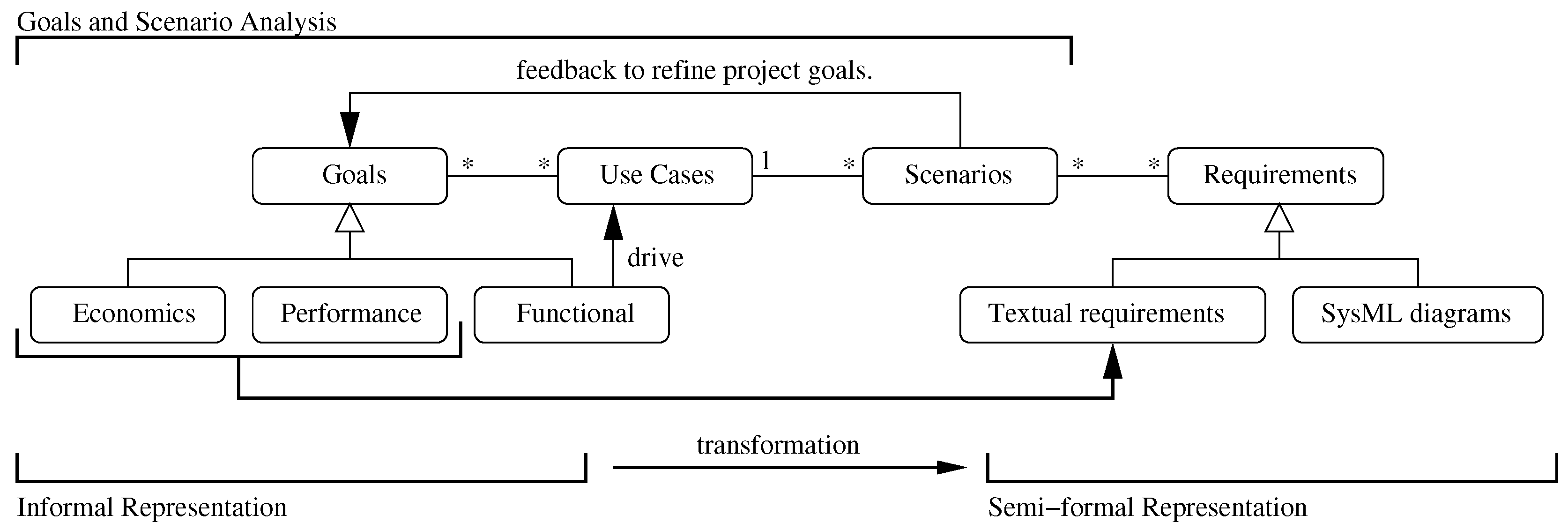
3.3. Goals and Scenario Analysis
4. Related Theory for Engineering System Behavior and Formal Verification Processes
4.1. Mathematical Modeling of the Fluid System
4.2. System Behavior Modeling with Networks of Timed Automata
4.3. Model Checking
4.4. Model Checking with UPPAAL
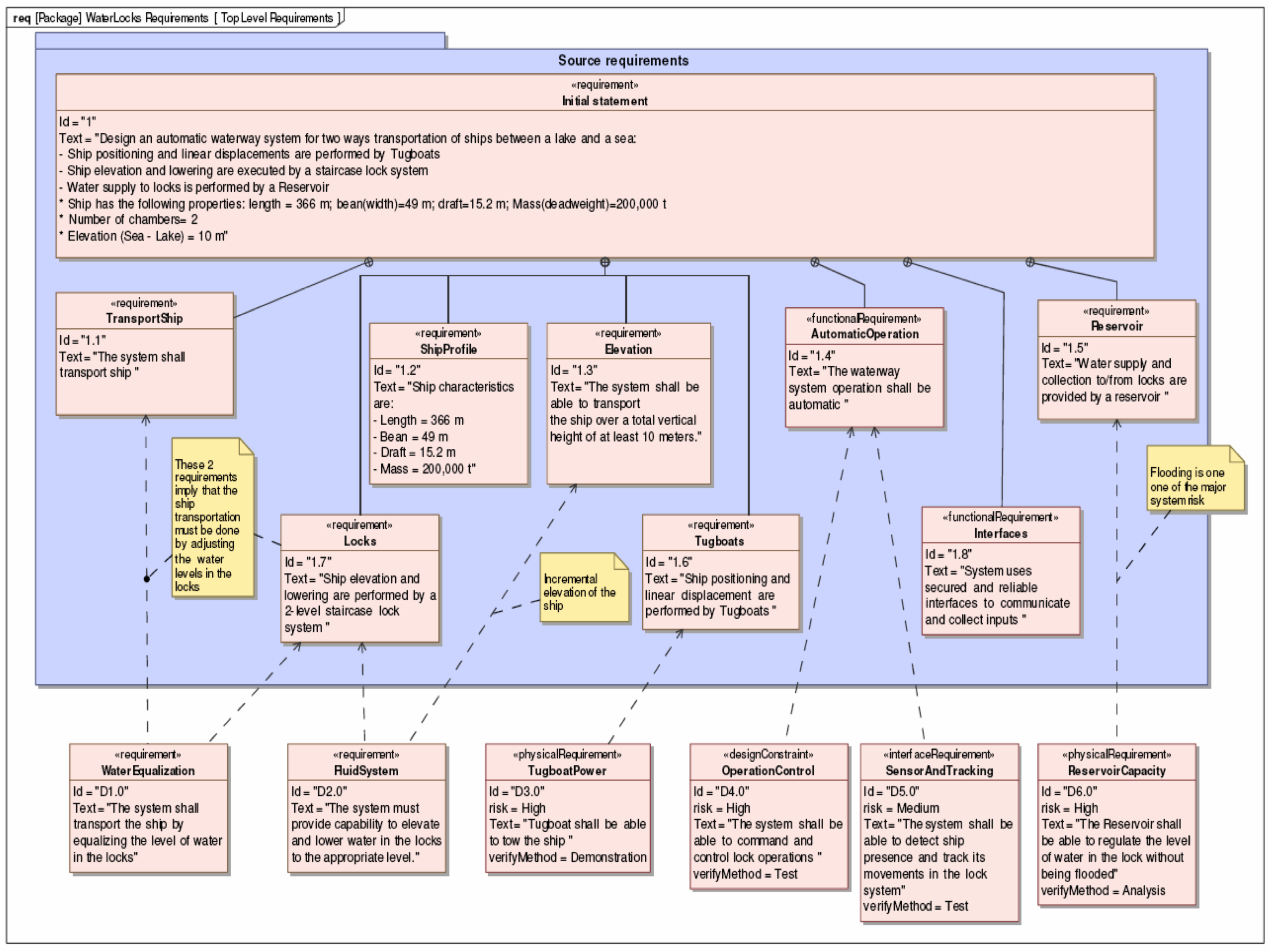
5. Case Study: Model-Based Design and Formal Validation of a Canal Water Lock
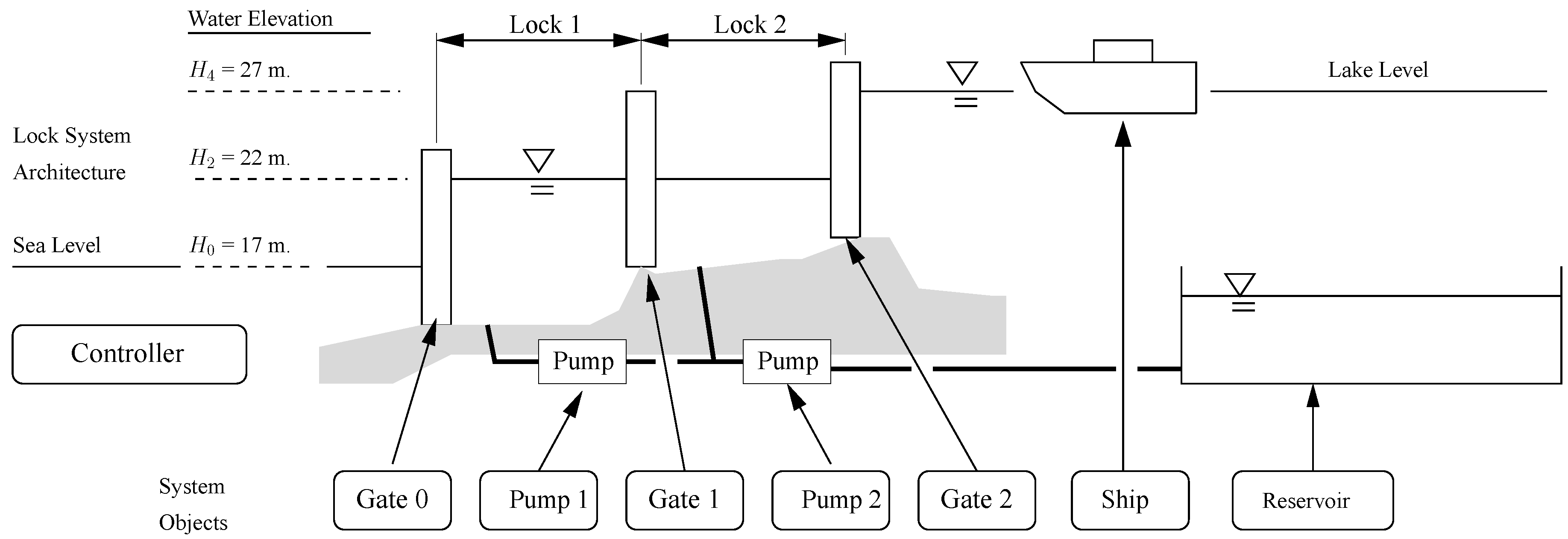
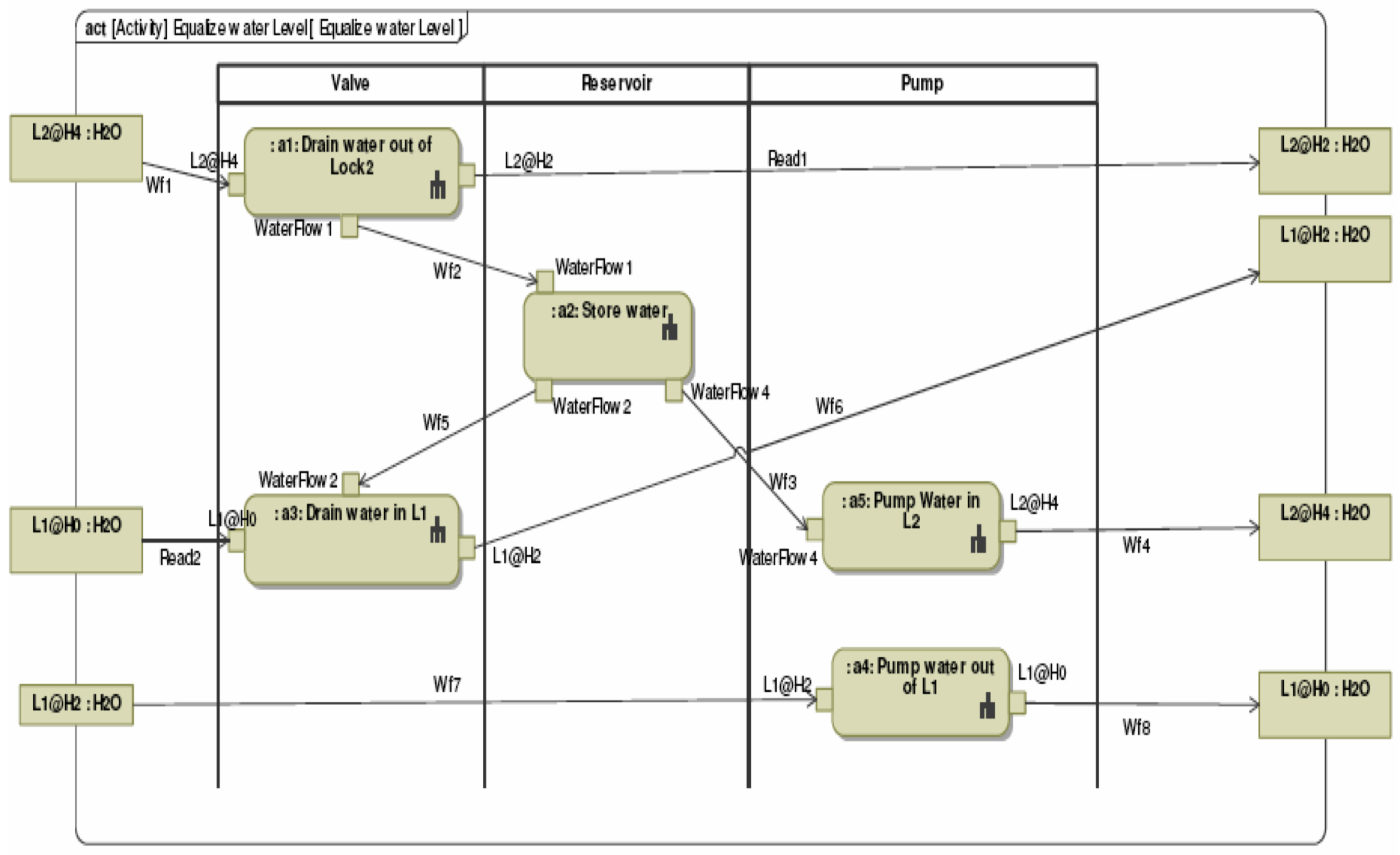
5.1. Water Lock Operations and Fluid System Design
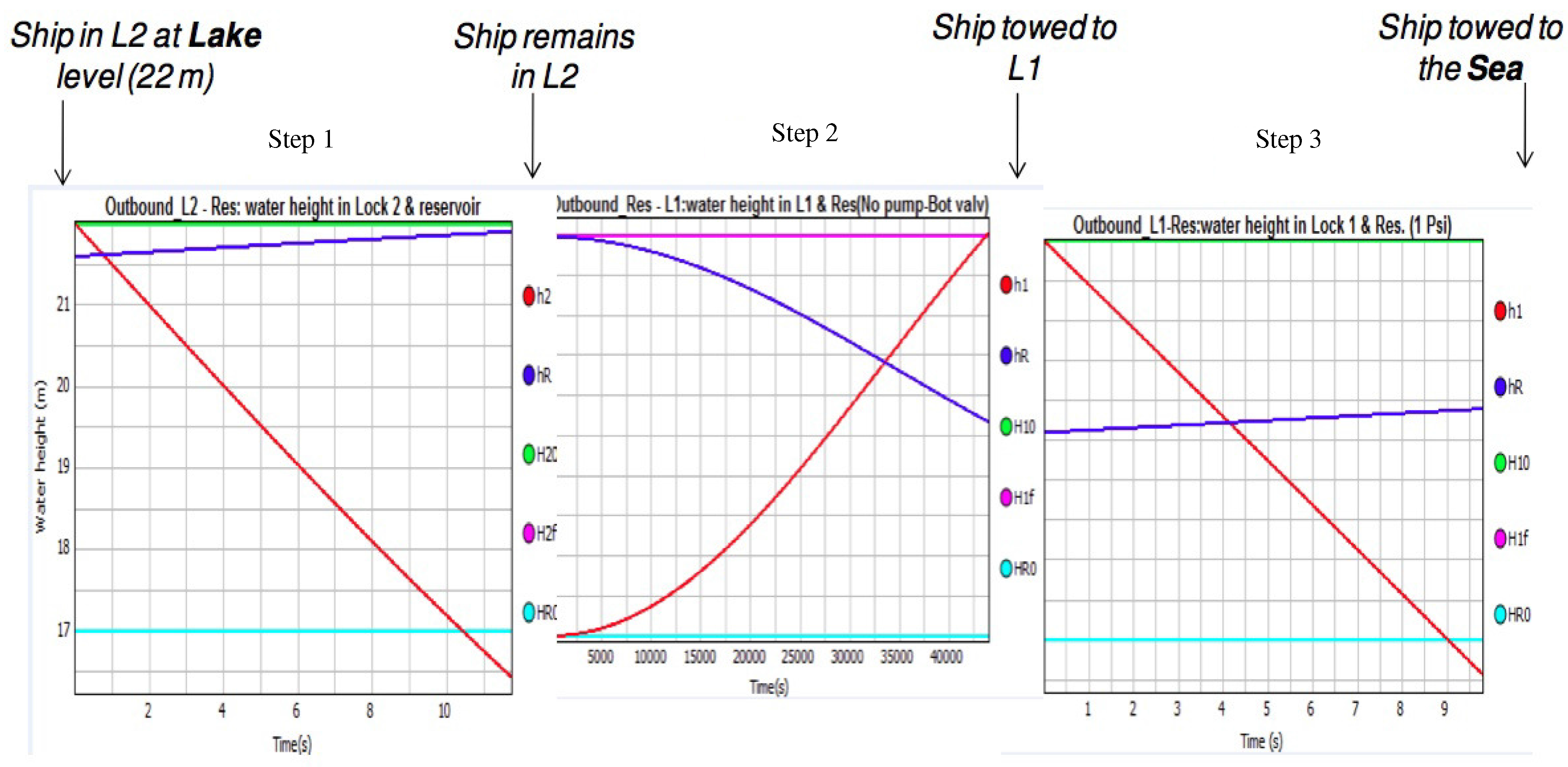
- Step 1.
- Water is transferred from Lock 2 to the reservoir (R), then,
- Step 2.
- Water is transferred from the reservoir (R) to Lock 1 (L1) for equalization with L2.
- Step 3.
- Water is transferred from L1 back to the reservoir R, thereby allowing the ship to be lowered to sea level, then towed out.
- 1.
- Water equalization between locks during towing,
- 2.
- Fluid system operation i.e., elevate and lower ships, and,
- 3.
- Limited reservoir capacity.
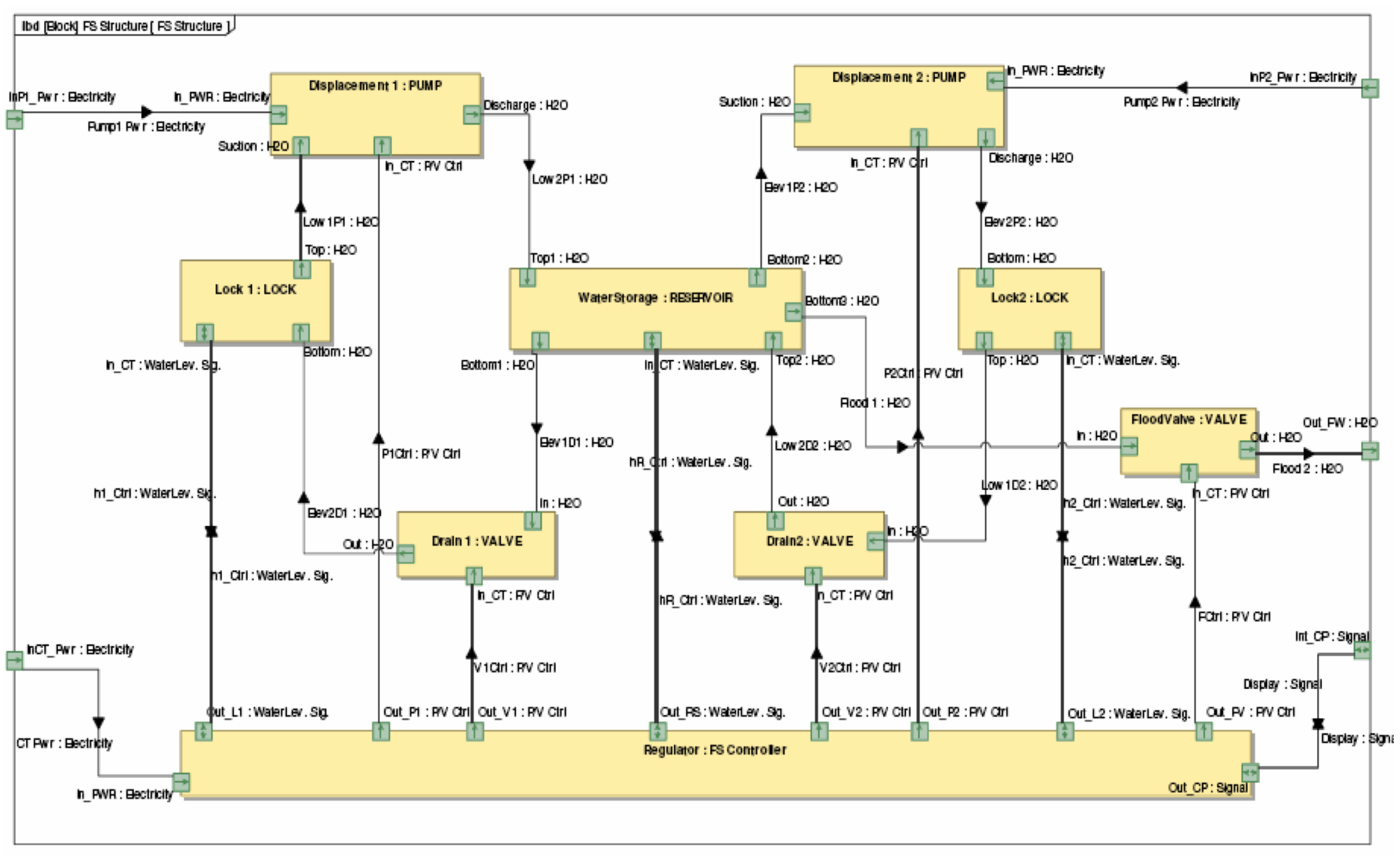
5.2. System Architecture and Modeling
- •
- Six goals covering the desired functionality, performance, maintenance, security and economics of the waterway system operation. For convenience, the corresponding use-cases can be organized into four viewpoints: ship, humans, computer system and system engineer.
- •
- Thirteen use-cases stemming from the six goals. The interactions between the water lock system and external actors in each use-case are described in more detail by a textual scenario.
- •
- A use-case (UC) task interaction matrix and model.
- •
- Scenario specifications with a step-by-step description of the expected functionality, with a traceability back to individual use-cases and individual goals.
- Goal 1: The lock system must allow large container ships to traverse the lock system.
- Use-case 01: Operate the lock system.
- Scenario 1.1: A large container ship crosses the lock system inbound in a small amount of time.
- Scenario 1.2: A large container ship crosses the lock system outbound in a small amount of time.
- Scenario 1.3: The system accomplishes its operations with a minimal amount of water usage.
- •
- FS controller: control and regulate the portion of crossing operations performed by FS,
- •
- Lock (x2): provide room and a road (water) to the ship during crossing process,
- •
- Valve (x3): drain water from/to the locks to/from the reservoir,
- •
- Pump (x2): displace water from/to the locks to/from the reservoir to the required elevation and
- •
- Reservoir: store reusable water for crossing operations.
5.3. Time-History Simulation
5.4. Design Space Exploration
5.5. System Controller Design and Verification Approach
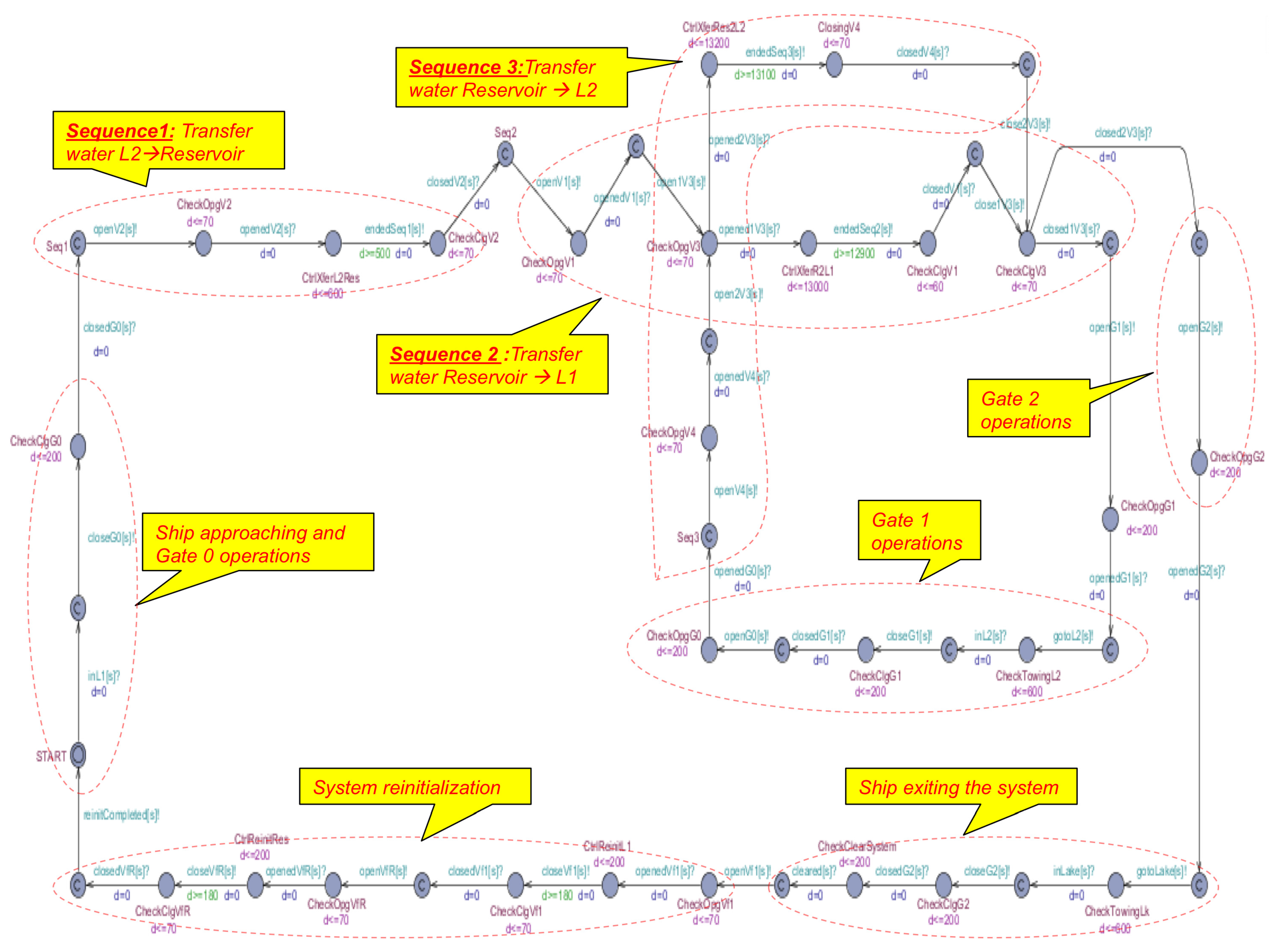
- 1.
- Transfer water from Lock 2 to the reservoir.
- 2.
- Transfer water from the reservoir to Lock 1.
- 3.
- Transfer water from the reservoir to Lock 2.
- 4.
- The ship leaves the lock system.
- 5.
- Reinitialize the lock system.
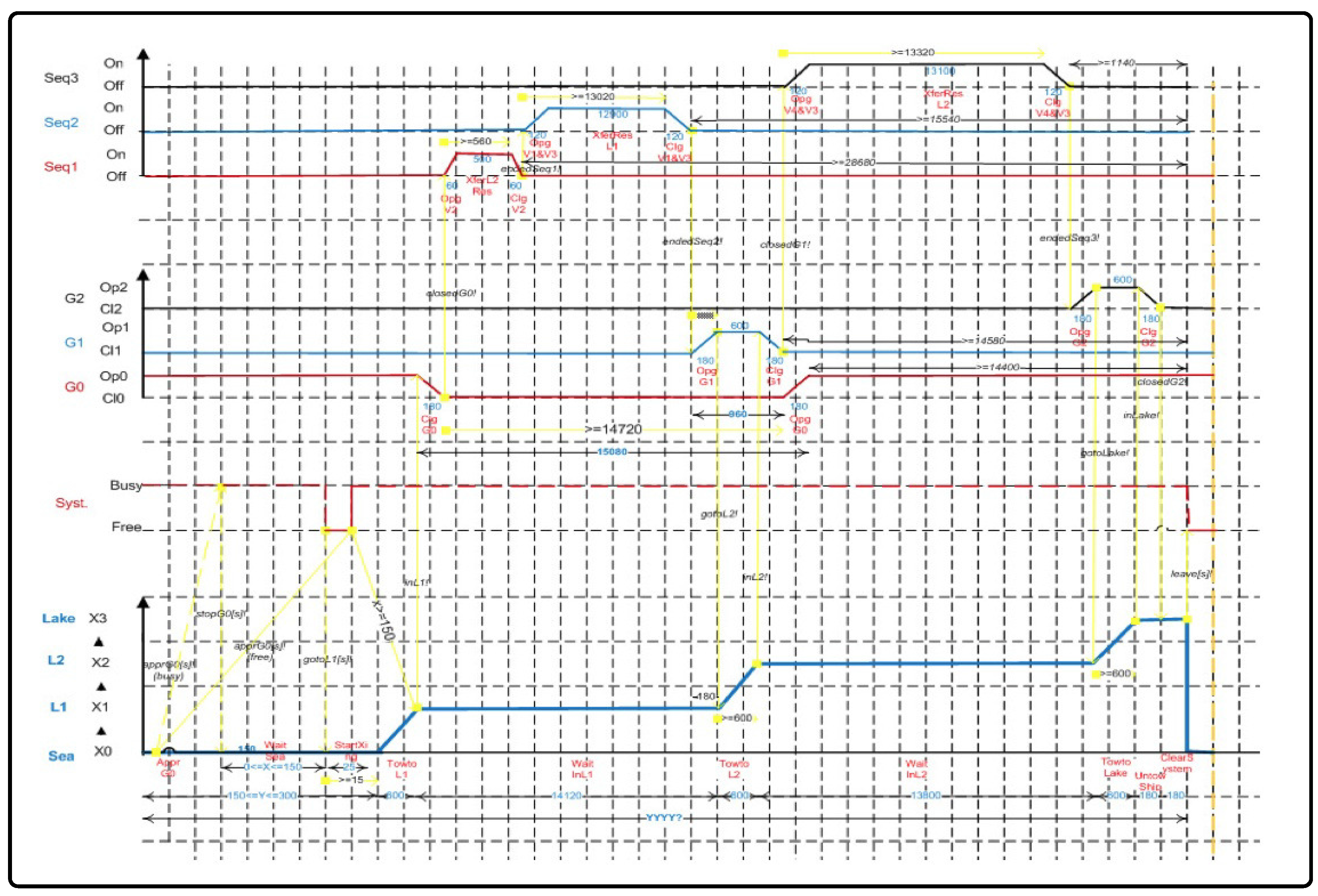
5.6. Controller Modeling and Verification
- 1.
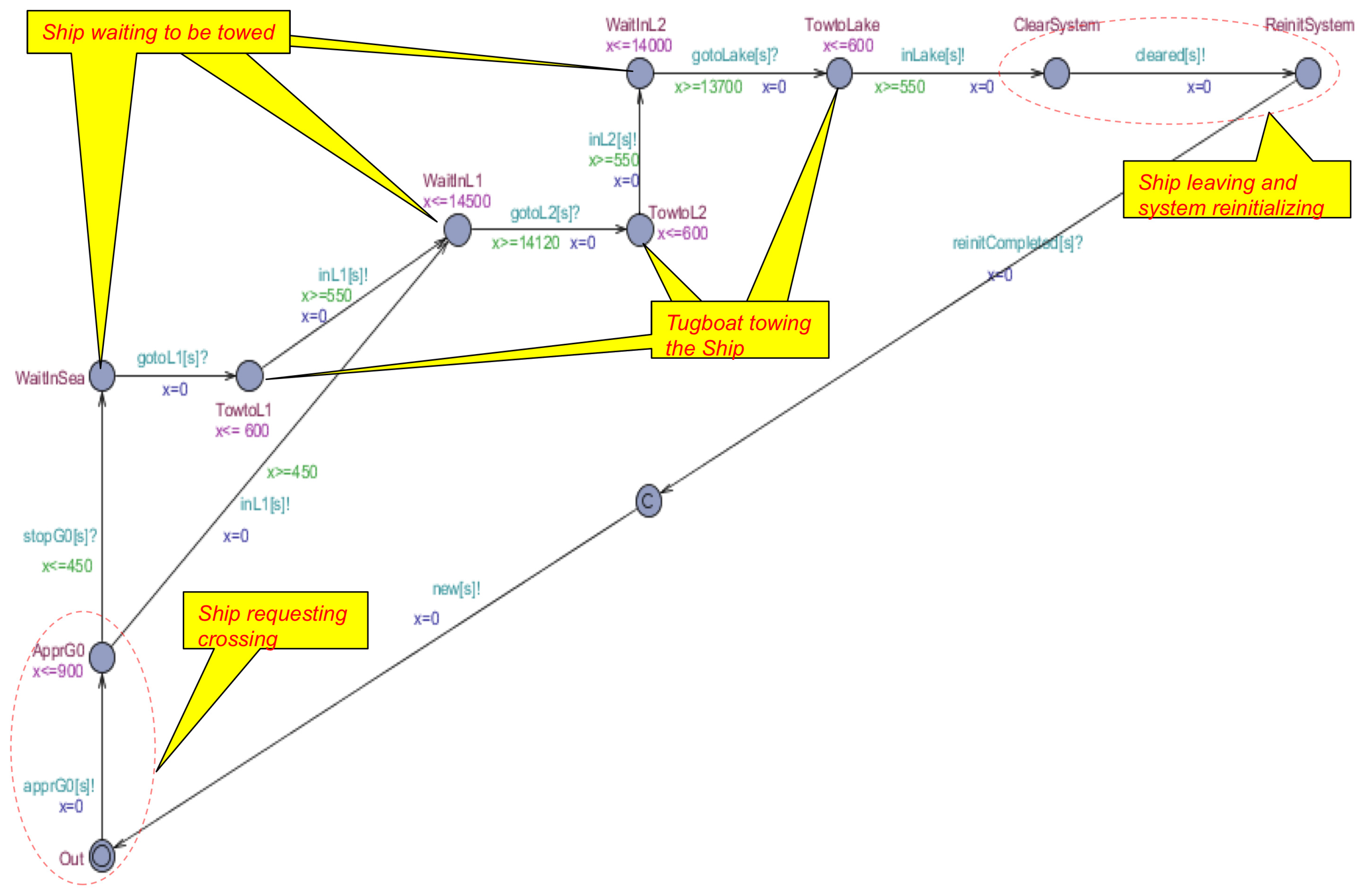
- The ship approaches the lock system and requests crossing (automatic detection by a sensor). If the system is free, i.e., there are no other ships in the water lock system, it will be towed directly into the lock ahead i.e., Lock 1 for inbound crossing and Lock 2 for outbound crossing. Otherwise, it waits in the sea/lake for the signal from the controller to proceed.
- 2.
- The ship waits in the lock for the water to be raised/lowered up to the level of the water in lock ahead (equalization).
- 3.
- When the water in the actual lock is the same as the one in the lock ahead, the ship is towed to the lock ahead.
- 4.
- For inbound crossing, when the lake is reached, the ship is released and can leave the system, which has to be reinitialized before another ship can proceed.
- 5.
- For outbound crossing, the water in Lock 1 is lowered to the sea level, and the ship is towed in the sea and released; then, the system is reinitialized.
- 1.
- After the scheduler frees a space in the queue, the ship requesting the crossing gets into Lock 1, and the controller oversees the Hate 0 closing process.
- 2.
- The controller sends the proper signal (opening and closing) to the valve actuators in order to start Sequences 1 and 2, which correspond to water equalization between Lock 1 and 2. It controls the opening and closing of valves, as well as the durations of sequences.
- 3.
- Once Step 2 is completed, it opens Gate 1 to let the ship get into Lock 2 and also performs the closing of Gate 0.
- 4.
- It now commands actuators of valves and to perform Step 3 (water equalization between Lock 2 and the lake). It controls both the time and proper execution of the sequence.
- 5.
- Having reached the lake, the ship can now exit the system. The controller first ensures the Gate 2 is closed and oversees the ship clearing the water lock system.
- 6.
- In the last step, the controller reinitializes the system by activation of reservoir and Lock 1 flooding valves to bring the water in those containers at the appropriate level prior to the beginning of the next crossing cycle.
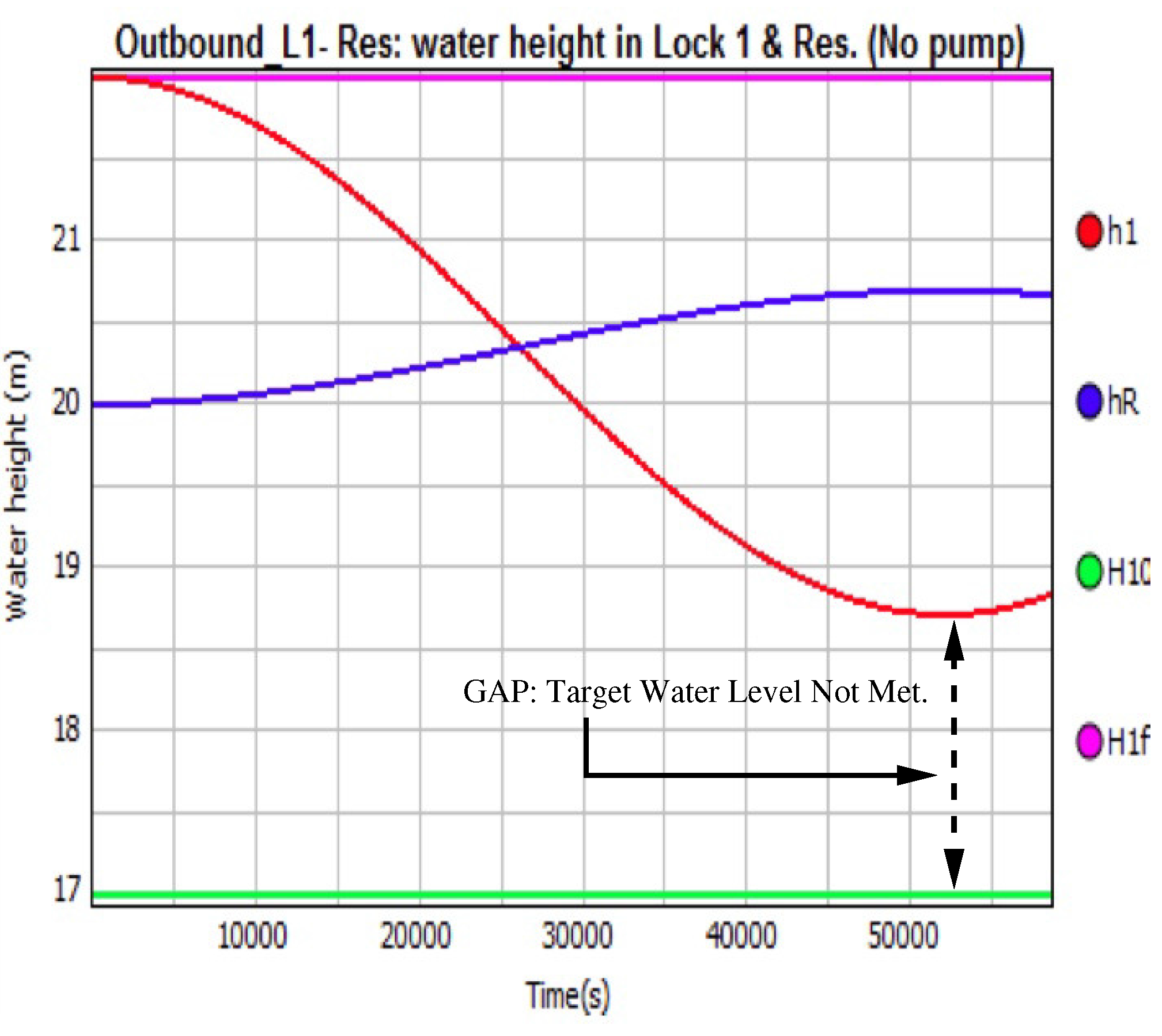
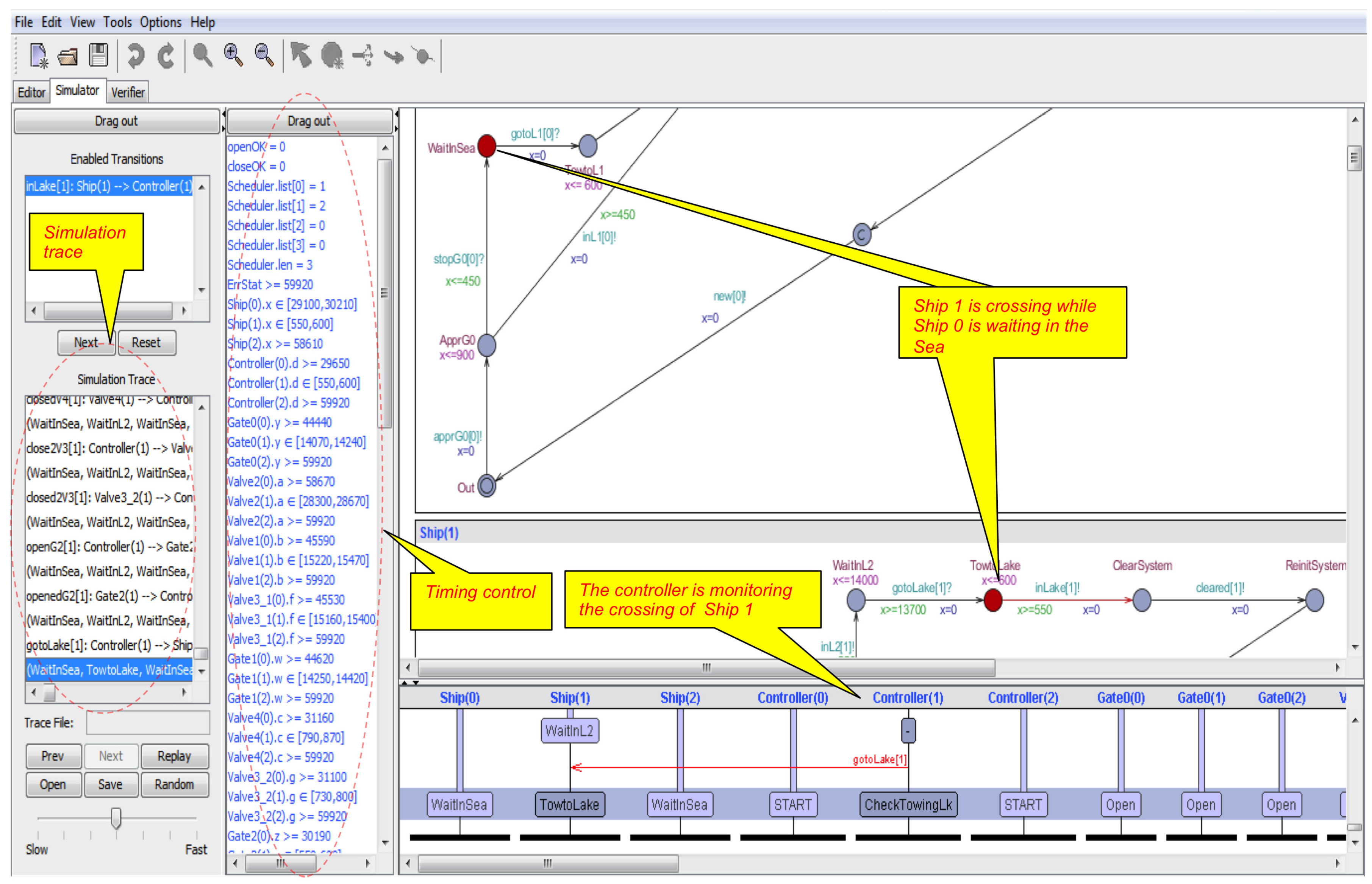
5.7. Model Simulation and Verification
6. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grier, D.V. The Declining Reliability of the U.S. InlandWaterway System; U.S. Army Corps of Engineers, Institute for Water Resources: Alexandria, VA, USA, 2005.
- Jackson, D.E., Jr. Leveraging the Strategic Value of the U.S. Inland Waterway System, USAWC Strategy Research Project; US Army War College, Carlisle Barracks: Carlisle, PA, USA, 2007. [Google Scholar]
- Iowa Department of Transportation. U.S. Inland Waterway Modernization: A Reconnaissance Study; HDR Engineering Inc.: Ames, IA, USA, 2013.
- Schexnayder, C.J. Firms Eye Billions in Expansion Work At Panama Canal. ENR Eng. News-Rec. 2007. Available online: http://panama-guide.com/ (accessed on 1 June 2016). [Google Scholar]
- James, T. All Locked Up. Comput. Control Eng. 2006, 17, 16–21. [Google Scholar] [CrossRef]
- Kaisar, E.; Austin, M.A.; Papadimitriou, S. Formal Development and Evaluation of Narrow Passageway System Operations. Eur. Transp. 2006, 34, 88–104. [Google Scholar]
- Kaisar, E.; Austin, M.A. Synthesis and Validation of High-Level Behavior Models for Narrow Waterway Management Systems. J. Comput. Civ. Eng. ASCE 2007, 21, 373–378. [Google Scholar] [CrossRef]
- UPPAAL: An integrated tool environment for modeling, validation and verification of real-time systems modeled as networks of timed automata. 2004. Available online: http://www.uppaal.com/ (accessed on 1 June 2016).
- SysML Plugin, No Magic Inc. Available online: http://www.nomagic.com/products/magicdraw-addons/sysml-plugin.html (accessed 30 January 2014).
- Fritzson, P. Principles of Object-Oriented Modeling and Simulation with Modelical 2.1; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Gribar, J.C.; Bocanegro, J.A. Passage to 2000: Modernization of the Panama Canal. Civ. Eng. Mag. 1999; 69, 48–53. [Google Scholar]
- Moore, M. The Bosporus: A Clogged Artery. The Washington Post. Available online: http://www.washingtonpost.com/ (accessed on 1 June 2016).
- Wieringa, R. Design Methods for Reactive Systems: Yourdon, Statemate, and the UML; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2003; p. 457. [Google Scholar]
- Dai, M.D.; Schonfeld, P. Metamodels for Estimating Waterway Delays Through a Series of Queues. Transport. Res. 1998, 32, 1–19. [Google Scholar] [CrossRef]
- DeSalvo, J.S.; Lave, L.B. An Analysis of Towboat Delays. J. Transp. Econ. Policy 1968, 2, 232–241. [Google Scholar]
- Ting, C.J.; Schonfeld, P. Integrated Control For Series of Waterway Locks. ASCE J. Waterw. Port Coast. Ocean Eng. 1998, 124, 199–206. [Google Scholar] [CrossRef]
- Zhu, L.; Schonfeld, P.; Kim, Y.; Flood, I.; Ting, C.J. Queuing Network Analysis for Waterways with Artificial Neural Networks. Artif. Intell. Eng. Des. Anal. Manuf. 1998, 13, 365–275. [Google Scholar] [CrossRef]
- Austin, M.A.; Baras, J.S.; Kositsyna, N.I. Combined Research and Curriculum Development in Information-Centric Systems Engineering. In Proceedings of the Twelth Annual International Symposium of the International Council on Systems Engineering (INCOSE), Las Vegas, NV, USA, 28 July–1 August 2003.
- Austin, M.A.; Mayank, V.; Shmunis, N. PaladinRM: Graph-Based Visualization of Requirements Organized for Team-Based Design. Syst. Eng. 2006, 9, 129–145. [Google Scholar] [CrossRef]
- Jackson, D. Dependable Software by Design. Sci. Am. 2006, 294, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Mosteller, M.; Austin, M.A.; Yang, S.; Ghodssi, R. Platforms for Engineering Experimental Biomedical Systems. IEEE Syst. J. 2014, 9, 1–11. [Google Scholar] [CrossRef]
- Fridenthal, S.; Moore, A.; Steiner, R. A Practical Guide to SysML; The MK-OMG Press: Burlington, MA, USA, 2008. [Google Scholar]
- Unified Modeling Language (UML). 2003. Available online: http://www.omg.org/uml (accessed on 1 June 2016).
- Wellstead, P.E. Introduction to Physical System Modelling. Control Systems Principles; Academic Press Ltd: London, UK, 2000; p. 256. [Google Scholar]
- Hooman, J. Introduction to Timed Systems; University of Nijmegen: Nijmegen, The Netherlands, 2001. [Google Scholar]
- Slind, K. Class Notes on Theory of Computation; Department of Computer Science, University of Utah: Salt Lake City, UT, USA, 2004. [Google Scholar]
- Baier, C.; Katoen, J.P. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Graves, H. Integrating Reasoning with SysML. In Proceedings of the INCOSE International Symposium, Rome, Italy, 9–12 July 2012.
- Eppinger, S.D.; Browning, T.D. Design Structure Matrix Methods and Applications; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- MagicDraw. 2016. Available online: http://www.nomagic.com/products/magicdraw.html (accessed on 4 May 2016).
- The Jython Project. 2016. Available online: http://www.jython.org (accessed on 4 May 2016).
- Functional Mock-up Interface Standard for Model Exchange and Tool Coupling. 2016. Available online: https://www.fmi-standard.org (accessed on 4 May 2016).
- Brauer, J.; Moller, O. Techniques for Abstraction of Continuous-Time Models into Finite Discrete-Event Models for Model Checking. Technical Note D5.1c, Version: 0.3, Horizon 2020: Integrated Tool Chain for Model-Based Design of CPSs. 2015. Available online: http://into-cps.au.dk (accessed on 1 June 2016).


| ID | Property | Type | Query (UPPAAL) | Satisfied? |
|---|---|---|---|---|
| The system is deadlock free. | S | not deadlock | Yes | |
| There is never more than one ship crossing the lock. | S | forall (i : ) forall (j : ) Ship(i).TowtoL2 && Ship(j).TowtoL2 imply i == j | Yes | |
| There can never be N ships (>1) in the queue (thus the array will not overflow). | S | Scheduler.list[N] == 0 | Yes | |
| Whenever a ship approaches the system, it will eventually cross. | L | Ship(0).ApprG0 → Ship(0).TowtoL2 | No | |
| A ship approaching the system will ultimately find a way to cross. | L | Ship(0).ApprG0 imply Ship(0).TowtoL2 | Yes | |
| Whenever a gate opens, it will eventually close later. | L | Gate1(1).Open → Gate1(1).Closed | Yes | |
| Whenever a gate closes, it will eventually open later. | L | Gate1(1).Close → Gate1(1).Opened | Yes | |
| Whenever a sequence start, it will finish at a certain point in time. | L | Controller(0).Seq2Start → Controller(0).Seq2End | Yes | |
| Whenever a sequence finish, it will start over at a certain point in time. | L | Controller(1).Seq2End → Controller(1).Seq2Start | No | |
| Whenever the system is busy, will system free eventually hold?. | L | Scheduler.Busy → Scheduler.Free | No | |
| A busy system will ultimately become free. | L | Scheduler.Busy imply Scheduler.Free | Yes | |
| Any ship can reach at least Lock 2. | R | Ship(1).WaitInL2 | Yes | |
| Any ship crossing inbound can reach the lake. | R | Ship(0).ClearSystem | Yes | |
| Ship 0 can be crossing the lock system, while Ship 1 is waiting to cross. | R | Ship(0).TowtoL2 and Ship(1).WaitInSea | Yes | |
| Ship 0 can cross the lock system while the other ships are waiting to cross. | R | Ship(0).TowtoL2 and (forall (i : ) i 0 imply Ship(i).WaitInSea) | Yes |
| Use Cases | Source Requirements | Derived Requirements | Fluid System | ||||
|---|---|---|---|---|---|---|---|
| ID | Name | ID | Name | ID | Name | Spec. | Components |
| Operates the lock system | 1.4 | Automation | , | Operation control; sensors and tracking | Controller | ||
| 1.3 | Elevation | Fluid system | UR1-5, VR1-6, PR1-5, RR1-5 | Pump, valve, pipe, reservoir | |||
| Provides water to locks | 1.5 | Reservoir | Reservoir capacity | VR1-6; PR1-5; RR1-5 | Reservoir, pipe, valve | ||
| 1.1 | Transportation | Water equalization | LR1-4; UR1-5; VR1-6; PR1-5; RR1-5 | Lock, reservoir, pump, valve, pipe | |||
| Provides system health information | 1.8 | Interfaces | |||||
| Logs into the system | 1.8 | Interfaces | |||||
| Monitors lock operations | 1.7 | Locks | , | Water equalization; fluid system | LR1-4; UR1-5; VR1-6; PR1-5; RR1-5 | Lock, reservoir, pump, valve, pipe | |
| 1.8 | Interfaces | ||||||
| Navigates lock system | 1.2 | Ship profile | |||||
| 1.6 | Tugboats | Tugboat Power | |||||
| 1.8 | Interfaces | ||||||
| Stores reusable water | 1.5 | Reservoir | Reservoir capacity | RR1-5 | Reservoir | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petnga, L.; Austin, M. Model-Based Design and Formal Verification Processes for Automated Waterway System Operations. Systems 2016, 4, 23. https://doi.org/10.3390/systems4020023
Petnga L, Austin M. Model-Based Design and Formal Verification Processes for Automated Waterway System Operations. Systems. 2016; 4(2):23. https://doi.org/10.3390/systems4020023
Chicago/Turabian StylePetnga, Leonard, and Mark Austin. 2016. "Model-Based Design and Formal Verification Processes for Automated Waterway System Operations" Systems 4, no. 2: 23. https://doi.org/10.3390/systems4020023
APA StylePetnga, L., & Austin, M. (2016). Model-Based Design and Formal Verification Processes for Automated Waterway System Operations. Systems, 4(2), 23. https://doi.org/10.3390/systems4020023