A Possibilistic Approach for Aggregating Customer Opinions in Product Development
Abstract
:1. Introduction
2. Preliminaries
2.1. State of a Product Feature
2.2. Numerical and Linguistic Truth-Value or Degree of Belief of a Feature
3. Logical Aggregation Process
3.1. The Kano Model
3.2. Probability-Possibility Transformation
3.3. Logical Transformation
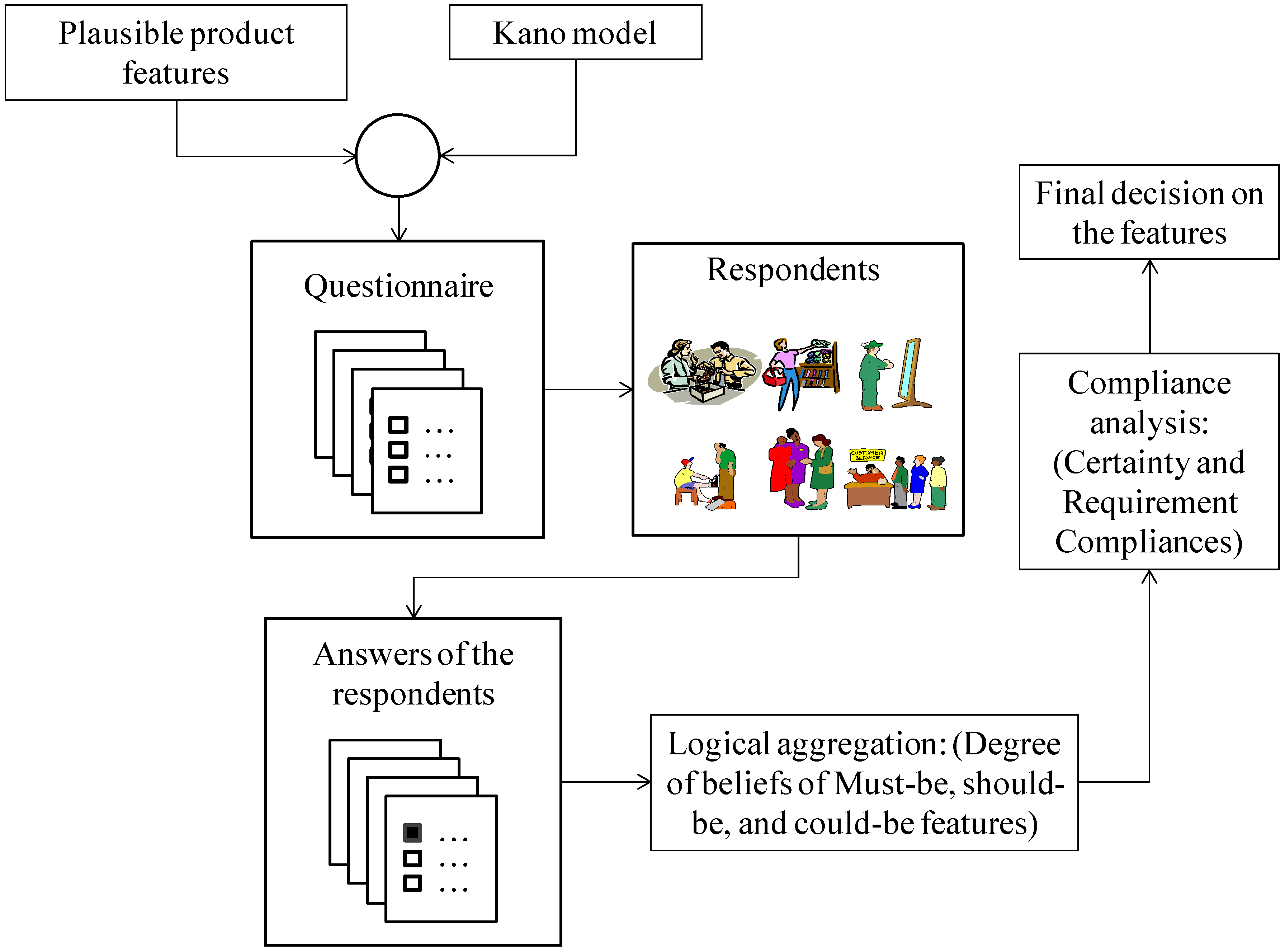
4. Results and Discussions
- Step 1
- Considering plausible product features (e.g., the features called Sedan, SUV, and Van for a product called car) and a customer needs model (e.g., the Kano model)
- Step 2
- Developing a questionnaire
- Step 3
- Sending the developed questionnaire to certain respondents
- Step 4
- Collecting the respondents’ opinions based on the developed questionnaire
- Step 5
- Performing logical aggregation through the Degree of Belief (DoB) of all features in terms of must-be, should-be, and could-be features
- Step 6
- Ranking the features based on the compliance analysis using the quantity called certainty and requirement compliances denoted as CC and RC, respectively
- Step 7
- Making final decision on the features
4.1. Implementation
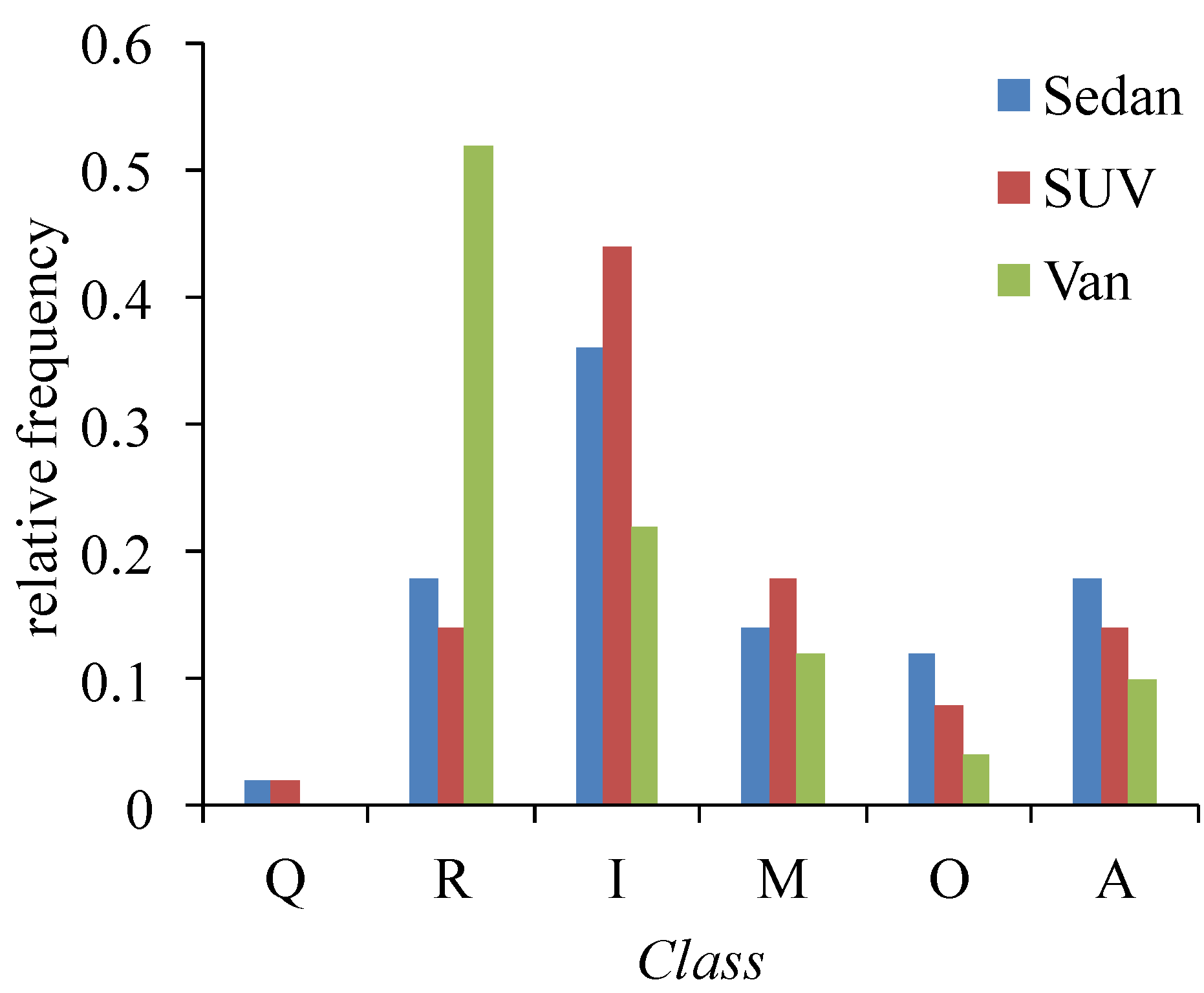
4.1.1. Execution of Steps 1–5
4.1.2. Execution of Steps 6–7
5. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Dieter, G.E.; Schmidt, L.C. Engineering Design, 4th ed.; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Kahn, K.B. The PDMA Handbook of New Product Development, 2nd ed.; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Ming, X.G.; Yan, J.Q.; Lu, W.F.; Ma, D.Z. Technology Solutions for Collaborative Product Lifecycle Management Status Review and Future Trend. Concurr. Eng. 2005, 13, 311–319. [Google Scholar] [CrossRef]
- Jiao, J.; Zhang, L.; Pokharel, S. Process Platform Planning for Variety Coordination from Design to Production in Mass Customisation Manufacturing. IEEE Trans. Eng. Manag. 2007, 54, 112–129. [Google Scholar] [CrossRef]
- Jiao, J.; Helander, M. Development of an Electronic Configure-to-Order Platform for Customised Product Development. Comput. Ind. 2006, 57, 231–244. [Google Scholar] [CrossRef]
- Jiao, J.; Zhang, Y. Product Portfolio Planning with Customer-Engineering Interaction. IIE Trans. 2005, 37, 801–814. [Google Scholar] [CrossRef]
- Jin, J.; Ji, P.; Kwong, C.P. What makes consumers unsatisfied with your products. J. Eng. Appl. Artif. Intell. 2016, 47, 38–48. [Google Scholar] [CrossRef]
- Kong, F.; Ming, X.G.; Wang, L.; Wang, P.; Zuo, H.; He, L. An integrated modularity approach for green product development. Int. J. Environ. Technol. Manag. 2011, 14, 397–416. [Google Scholar] [CrossRef]
- Kano, N.; Seraku, N.; Takahashi, F.; Tsuji, S. Attractive quality and must-be quality. Hinshitsu 1984, 14, 39–48. (In Japanese) [Google Scholar]
- Meng, Q.L.; Jiang, X.; Bian, L.L. A Decision-Making Method for Improving Logistics Services Quality by Integrating Fuzzy Kano Model with Importance-Performance Analysis. J. Serv. Sci. Manag. 2015, 8, 322–331. [Google Scholar] [CrossRef]
- Meng, Q.L.; Jiang, X.; He, L.; Guo, X. Integrating Fuzzy Theory into Kano Model for Classification of Service Quality Elements: A Case Study of Machinery Industry in China. J. Ind. Eng. Manag. 2015, 8, 1661–1675. [Google Scholar]
- Rashid, M.M.; Tamaki, J.; Ullah, A.M.M.S.; Kubo, A. A Numerical Kano Model for Compliance Customer Needs with Product Development. Ind. Eng. Manag. Syst. Int. J. 2011, 10, 140–153. [Google Scholar] [CrossRef]
- Rashid, M.M.; Tamaki, J.; Ullah, A.M.M.S.; Kubo, A. A Virtual Customer Needs System for Product Development. In Proceedings of the 2010 Annual Meeting of Japan Society for Precision Engineering, Sapporo, Japan, 4 September 2010; pp. 53–54.
- Rashid, M.M.; Ullah, A.M.M.S.; Sarker, M.A.R.; Tamaki, J.; Kubo, A. Logical Aggregation of Customer Needs Assessment. In Proceedings of the Fifth International Symposium on Computational Intelligence and Industrial Applications (ISCIIA2012), Sapporo, Japan, 20–26 August 2012.
- Rashid, M.M.; Ullah, A.M.M.S.; Tamaki, J.; Sarker, M.A.R. Epistemic Uncertainty Study of the Conceptual Phase of Product Development by Multi-Valued Logic and Information Content. In Proceedings of the International Conference on Mechanical, Industrial and Materials Engineering 2013 (ICMIME2013), RUET, Rajshahi, Bangladesh, 1–3 November 2013.
- Ullah, A.M.M.S.; Tamaki, J. Analysis of Kano-Model-Based Customer Needs for Product Development. Syst. Eng. 2011, 14, 154–172. [Google Scholar] [CrossRef]
- Wang, P.; Ming, X.G.; Li, D.; Wu, Z.; Xu, Z.; Song, W. Achieving sustainability through product-service life cycle management. Int. J. Environ. Technol. Manag. 2011, 14, 516–530. [Google Scholar] [CrossRef]
- Xu, Q.; Jiao, R.J.; Yang, X.; Helander, M.; Khalid, H.M.; Opperud, A. An analytical Kano model for customer need analysis. Des. Stud. 2009, 30, 87–110. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility Theory: An Approach to Computerized Processing of Uncertainty; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Dubois, D.; Foulloy, L.; Mauris, G.; Prade, H. Probability-Possibility Transformations, Triangular Fuzzy Sets, and Probabilistic Inequalities. Reliab. Comput. 2004, 10, 273–294. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Shamsuzzaman, M. Fuzzy Monte Carlo Simulation using Point-Cloud-Based Probability-Possibility Transformation. Simulation 2013, 89, 860–875. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Klir, G.J. On fuzzy-set interpretation of possibility theory. Fuzzy Sets Syst. 1999, 108, 263–273. [Google Scholar] [CrossRef]
- Mauris, G. Possibility distributions: A unified representation of usual direct-probability-based parameter estimation methods. Int. J. Approx. Reason. 2011, 52, 1232–1242. [Google Scholar] [CrossRef]
- Yamada, K. A Study on Probability-Possibility Transformation Methods Based on Evidence Theory. J. Jpn. Soc. Fuzzy Theory Syst. 2001, 13, 302–312. (In Japanese) [Google Scholar]
- Ullah, A.M.M.S.; Harib, K.H. An Intelligent Method for Selecting Optimal Materials and Its Application. Adv. Eng. Inform. 2008, 22, 473–483. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Harib, K.H.; Al-Awar, A. Minimizing Information Content of a Design using Compliance Analysis; SAE Technical Paper 2007-01-1209; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Ullah, A.M.M.S.; Rashid, M.M.; Tamaki, J. On Some Unique Features of C-K Theory of Design. CIRP J. Manuf. Sci. Technol. 2012, 5, 55–66. [Google Scholar] [CrossRef]

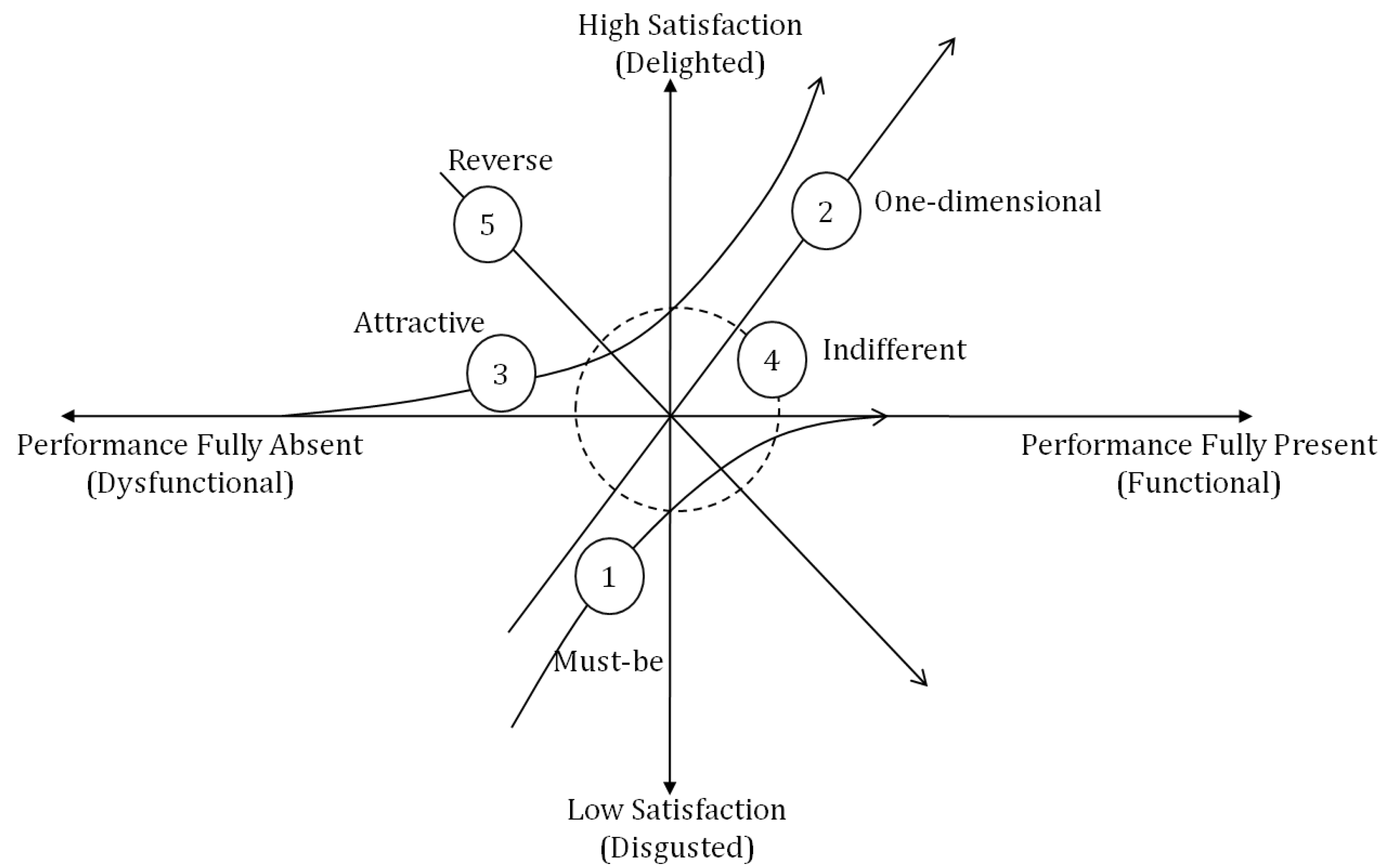


| Present (↓) | Not Present | ||||
|---|---|---|---|---|---|
| Like | Must-be | Neutral | Live-with | Dislike | |
| Like | Q | A | A | A | O |
| Must-be | R | I | I | I | M |
| Neutral | R | I | I | I | M |
| Live-with | R | I | I | I | M |
| Dislike | R | R | R | R | Q |
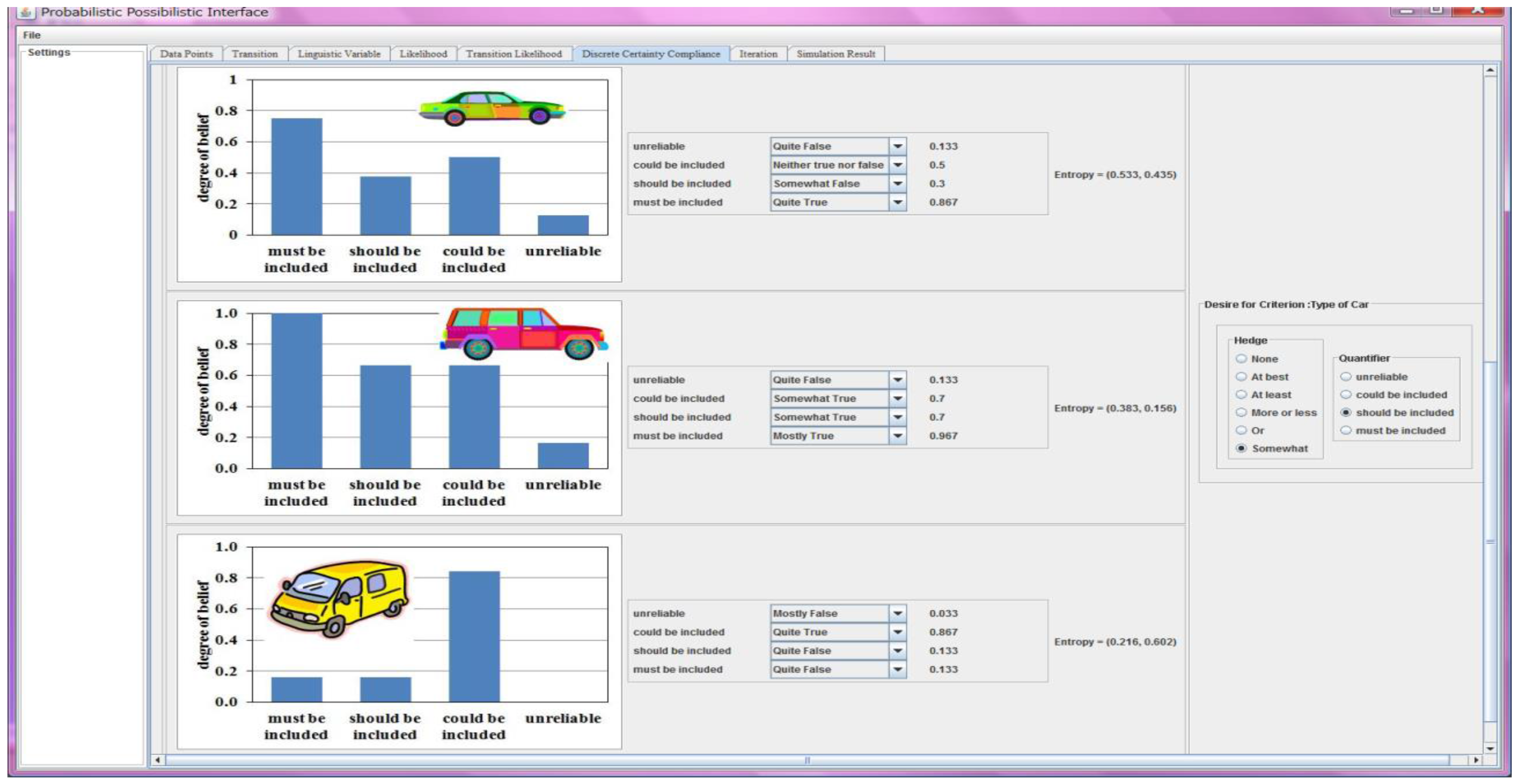
| Requirement (RE) | X | ||
|---|---|---|---|
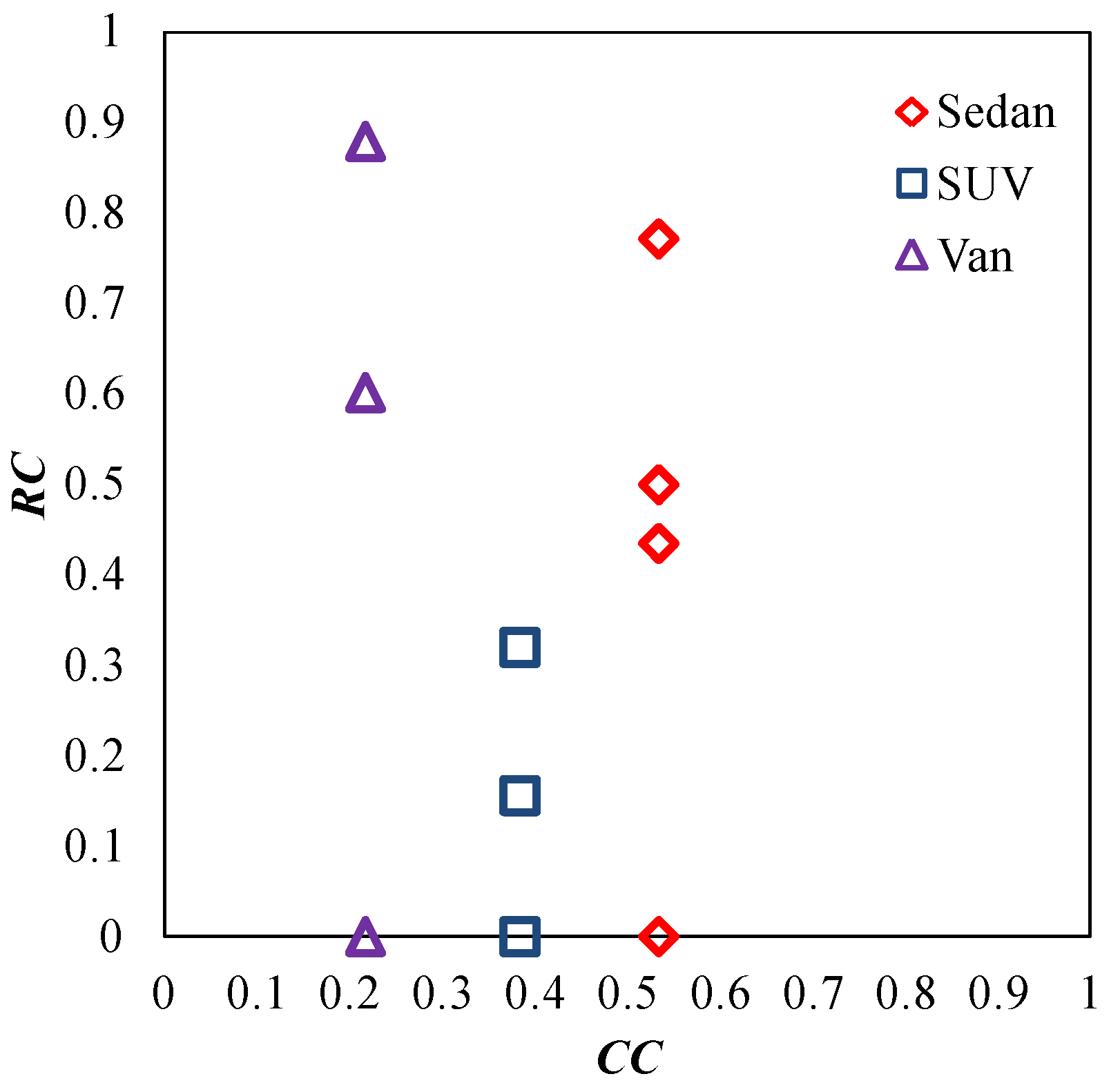
| Sedan | SUV | Van | |
| X must be included | (0.533, 0) | (0.383, 0) | (0.216, 0.88) |
| X should be included | (0.533, 0.772) | (0.383, 0.32) | (0.216, 0.88) |
| X could be included | (0.533, 0.5) | (0.383, 0.32) | (0.216, 0) |
| X somewhat should be included | (0.533, 0.435) | (0.383, 0.156) | (0.216, 0.602) |
| X must be or should be included | (0.533, 0.0) | (0.383, 0) | (0.216, 0.88) |
| - | (CC, RC) | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, M.M.; Ullah, A.S. A Possibilistic Approach for Aggregating Customer Opinions in Product Development. Systems 2016, 4, 17. https://doi.org/10.3390/systems4020017
Rashid MM, Ullah AS. A Possibilistic Approach for Aggregating Customer Opinions in Product Development. Systems. 2016; 4(2):17. https://doi.org/10.3390/systems4020017
Chicago/Turabian StyleRashid, Md. Mamunur, and AMM Sharif Ullah. 2016. "A Possibilistic Approach for Aggregating Customer Opinions in Product Development" Systems 4, no. 2: 17. https://doi.org/10.3390/systems4020017
APA StyleRashid, M. M., & Ullah, A. S. (2016). A Possibilistic Approach for Aggregating Customer Opinions in Product Development. Systems, 4(2), 17. https://doi.org/10.3390/systems4020017







