Metabolic Scaling in Complex Living Systems
Abstract
1. Introduction
2. A Systems View of Metabolic Scaling
3. Major Theoretical Approaches: A Historical Perspective
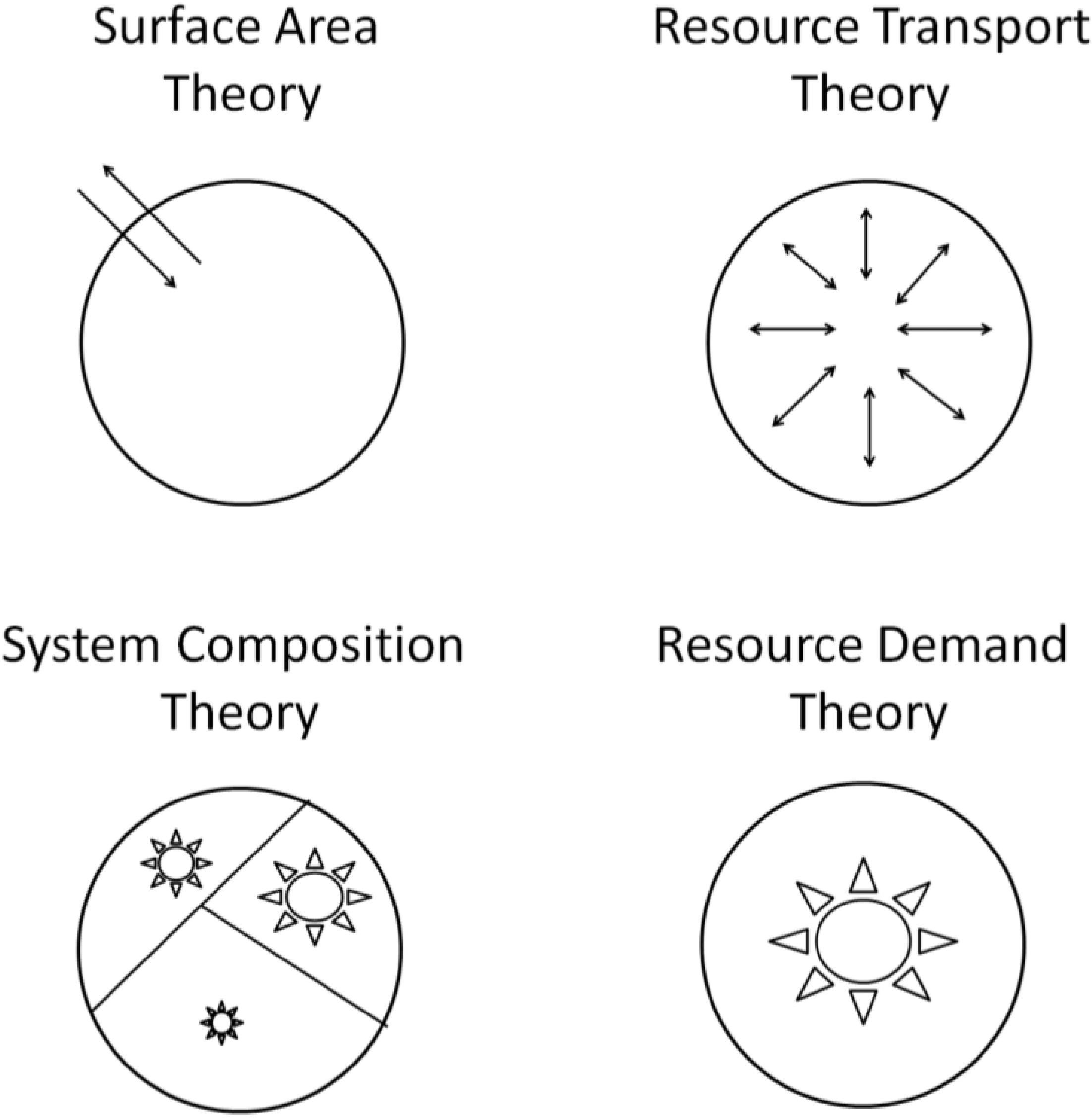
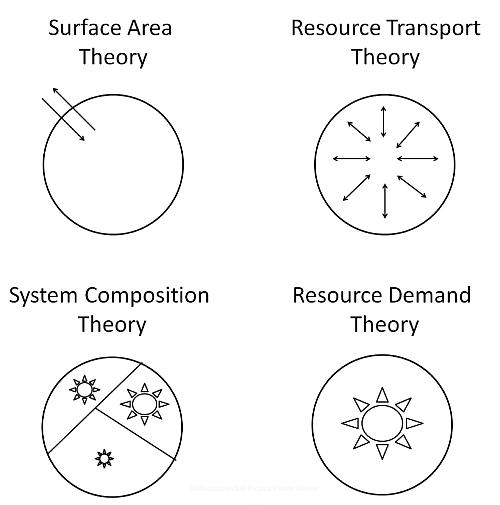
3.1. Surface Area (SA) Models
3.2. Resource Transport (RT) Models
3.3. System Composition (SC) Models
3.4. Resource Demand (RD) Models
4. Major Theoretical Approaches: Applicability to Different Hierarchical Levels of Biological Organization
4.1. Models of Cells or Subcellular Processes
4.1.1. Surface Area (SA) Models
4.1.2. Resource Transport (RT) Models
4.1.3. System Composition (SC) Models
4.1.4. Resource Demand (RD) Models
4.2. Models of Whole Organisms
4.3. Models of Colonies and Other Social Groups of Organisms
4.3.1. Surface Area (SA) Models
4.3.2. Resource Transport (RT) Models
4.3.3. System Composition (SC) Models
4.3.4. Resource Demand (RD) Models
4.4. Models of Populations, Communities and Ecosystems
4.4.1. Surface Area (SA) Models
4.4.2. Resource Transport (RT) Models
4.4.3. System Composition (SC) Models
4.4.4. Resource Demand (RD) Models
5. Major Theoretical Approaches: Evidence For and Against
5.1. Surface Area Theory
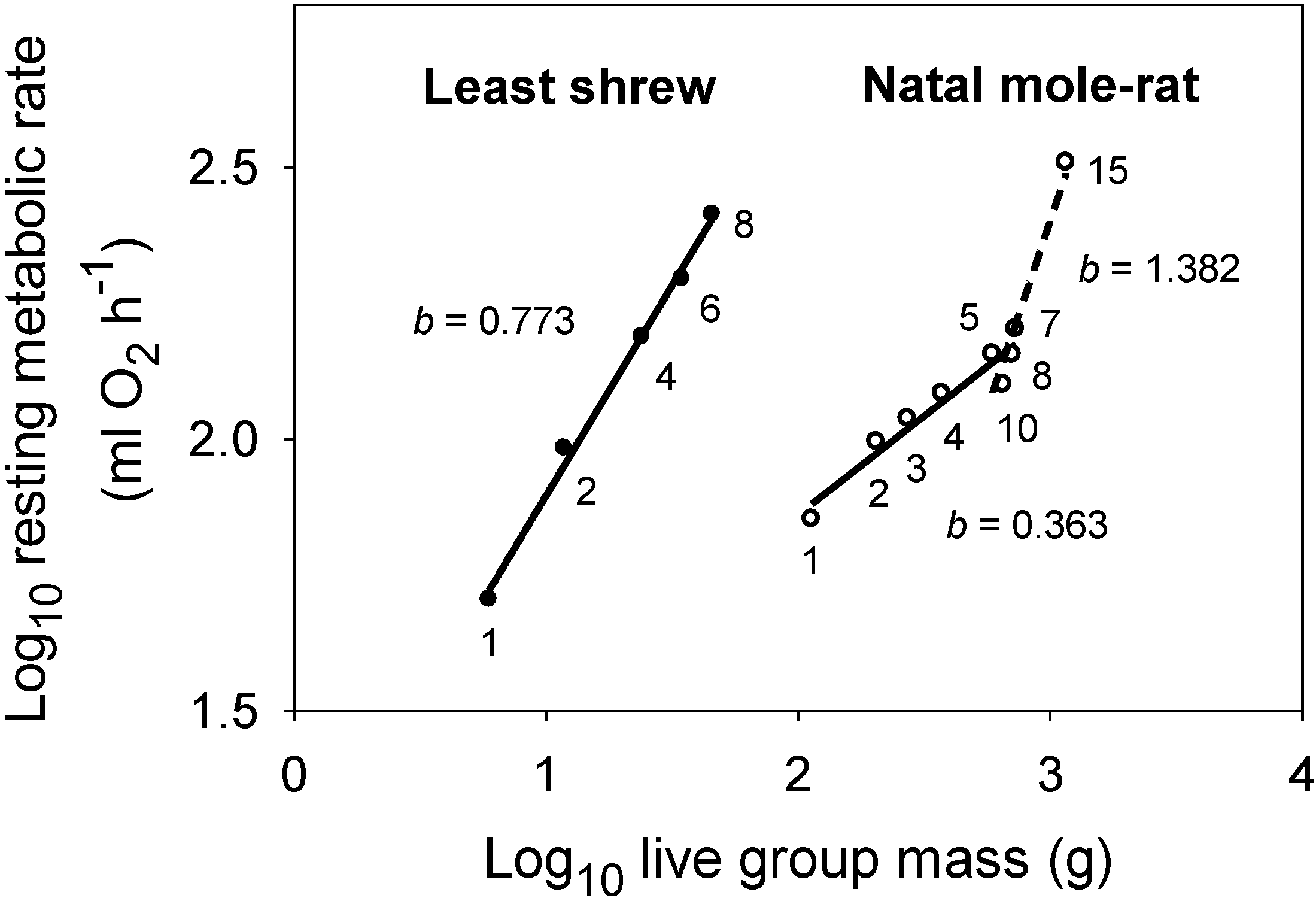
5.2. Resource Transport Theory
5.3. System Composition Theory
5.4. Resource Demand Theory
5.5. Comparison of Evidence for the Four Theories
| Evidence | |||
|---|---|---|---|
| Direct | |||
| Theory | Indirect | Correlational | Experimental |
| Surface Area (SA) | X | X | X |
| Resource Transport (RT) | X | ||
| System Composition (SC) | X | X | |
| Resource Demand (RD) | X | X | X |
6. Resource Supply and Demand and Their Biological Regulation
7. Relative Effects of Internal and External Constraints and Processes
8. Toward a Synthetic Theory of Metabolic Scaling
8.1. General Approach and Perspective
| Subtheories Used | ||||
|---|---|---|---|---|
| Model | SA | RT | SC | RD |
| Metabolic-level boundaries hypothesis (MLBH) [19] | X | X | x | X |
| Dynamic energy budget (DEB) theory [66] | X | X | X | |
| Resource-transport network (RTN) models 1 | x | X | x | |
| Allometric cascade model [167] | X | X | ||
| Constructal theory [296] | X | X | ||
| Cell-size model [68,69] | X | x | ||
| Classic surface law and related heat-loss models 2 | X | |||
| Mass-transfer model [103] | X | |||
| Membrane pacemaker model [70,191] | X | |||
| Quantum metabolism model (QMM) [21,71,72] | X | |||
| Biomechanical support model [454] | X | |||
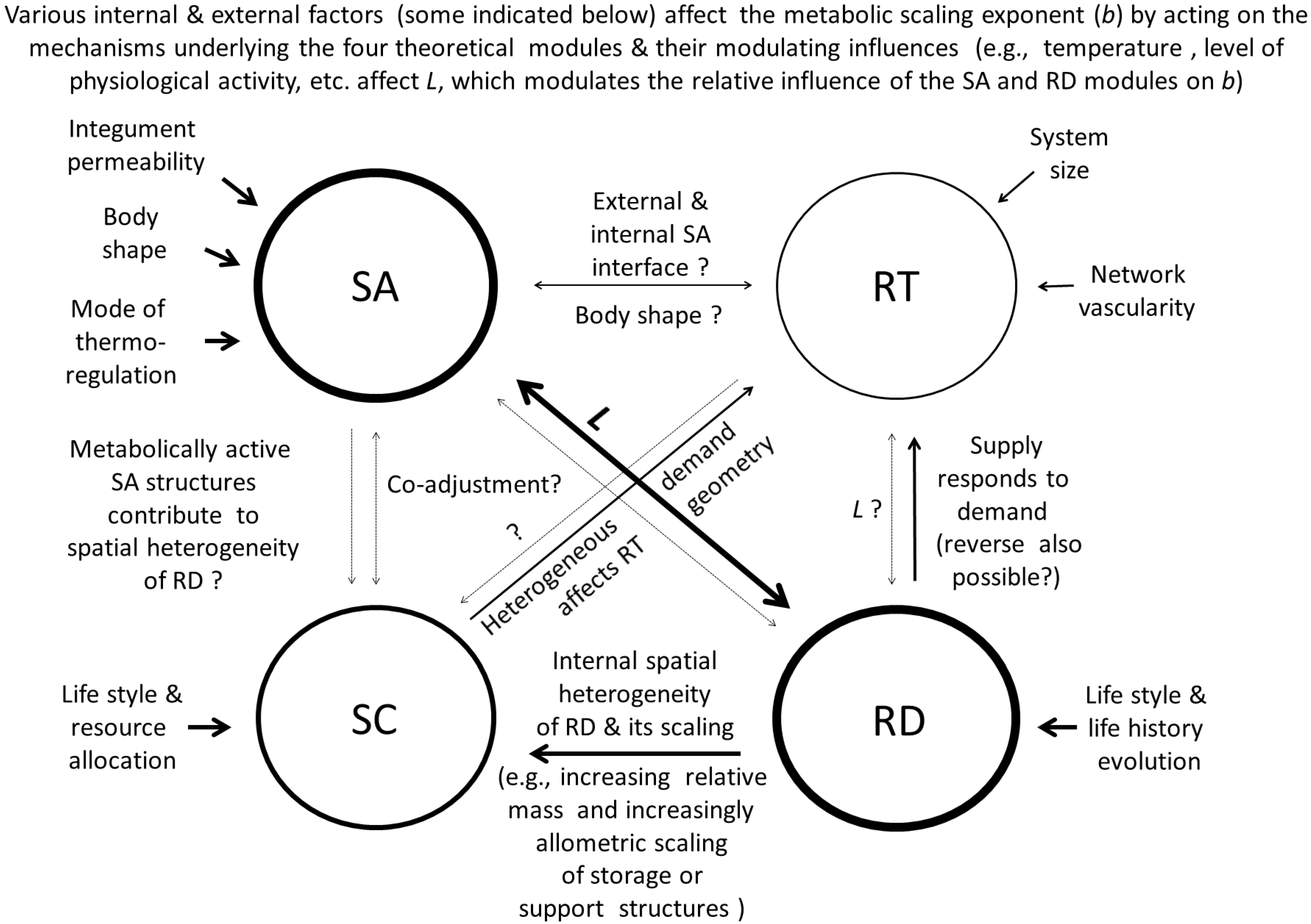
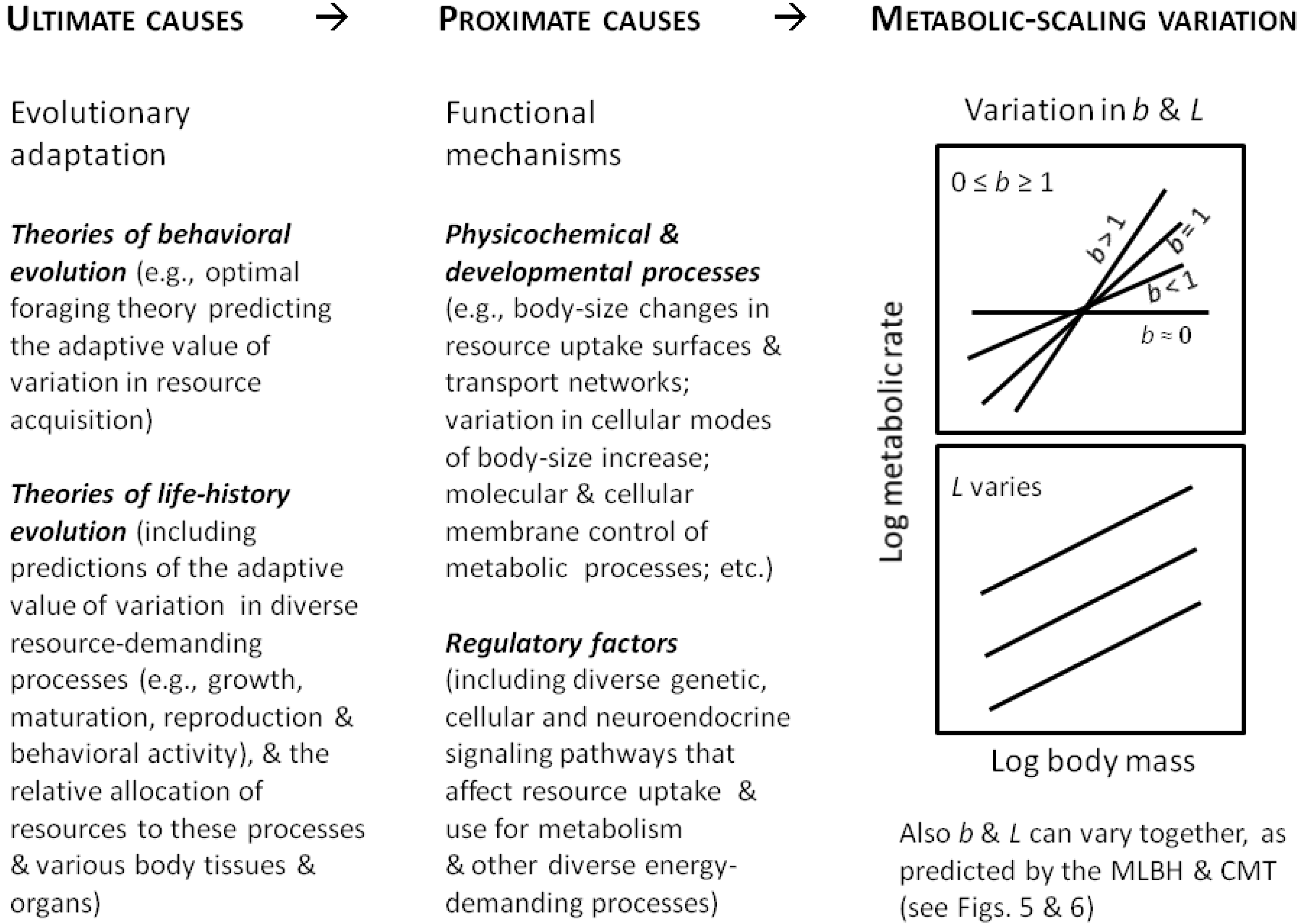
8.2. Specific Details of the Contextual Multimodal Theory (CMT)
8.2.1. How the Contextual Multimodal Theory (CMT) Can Explain Variation in the Slope (b) of Metabolic Scaling Relationships
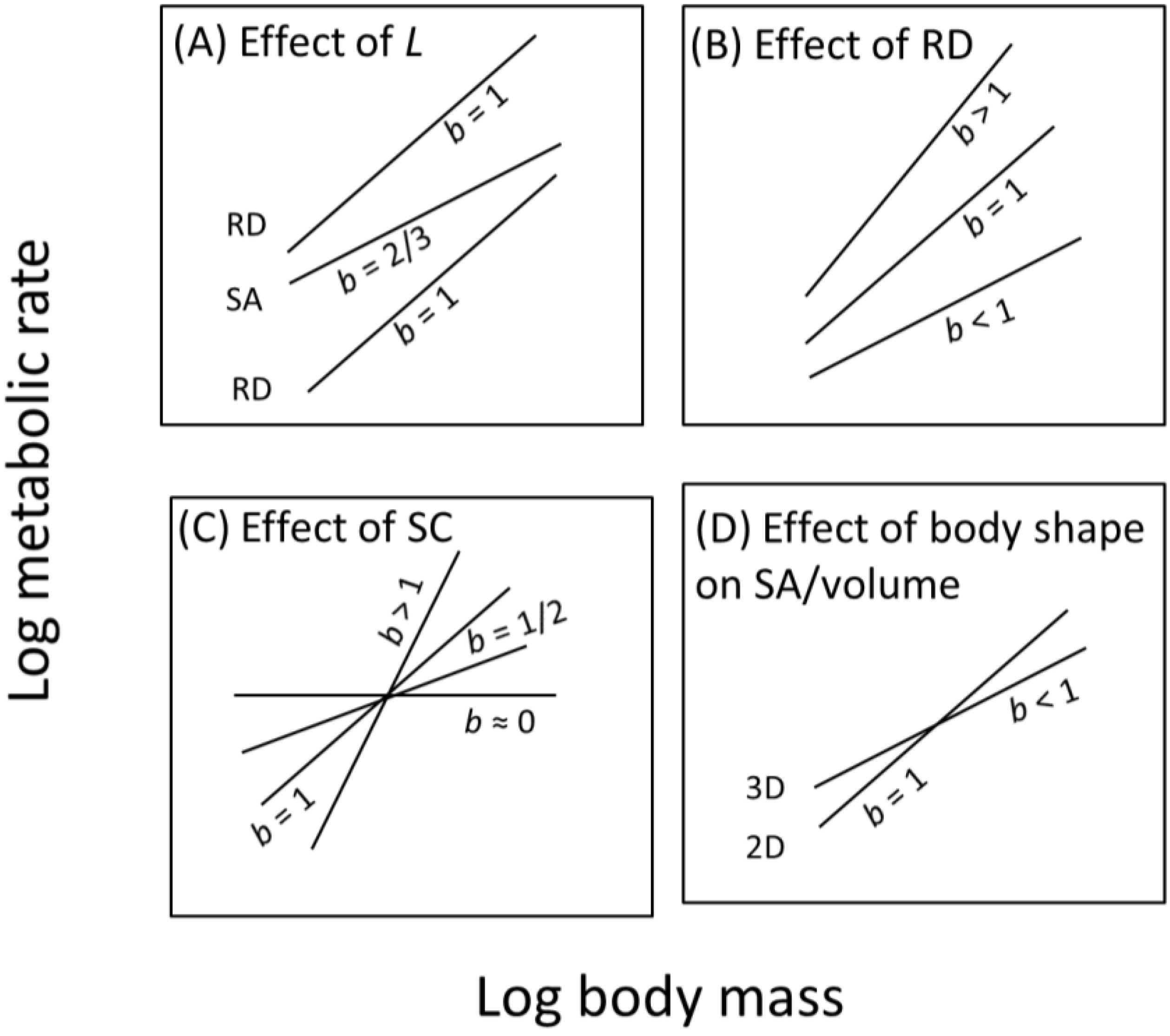
8.2.2. How the Contextual Multimodal Theory (CMT) Can Explain Variation in the Elevation (L) of Metabolic Scaling Relationships
8.3. Application of the Contextual Multimodal Theory (CMT) to Various Levels of Biological Organization
8.3.1. Application of CMT to Cellular Level
8.3.2. Application of CMT to Groups of Organisms
8.3.3. Upward and Downward Causation and Other Hierarchical Effects
8.4. General Outlook for the Contextual Multimodal Theory (CMT)
9. General Implications for Biological Scaling and a Metabolic Theory of Biology
9.1. Metabolic Rate and the Pace of Life
9.2. Metabolism Is Not Monolithic: A Plea for Exploring the Scaling of the Multiple Components of Metabolism and the Various Factors Affecting Them
9.3. The Role of Biological Regulation of Supply and Demand in a Metabolic Theory of Biology (MTB)
9.4. Essential Elements of a Comprehensive Metabolic Theory of Biology (MTB)
9.5. Practical Applications of the CMT and a Holistic MTB
10. A Methodological Epilogue
10.1. Power Functions and Least-Squares Regression (LSR) Analyses of Log-Transformed Data
10.2. Phylogenetically and Ecologically Informed Analyses
10.3. Standard Scaling Analyses are Useful for Constructing General Theory
11. Conclusions
Acknowledgments
Conflicts of Interest
References
- Lotka, A.J. Contribution to the energetics of evolution. Proc. Natl. Acad. Sci. USA 1922, 8, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Odum, H.T.; Pinkerton, R.C. Time’s speed regulator: The optimum efficiency for maximum power output in physical and biological systems. Am. Sci. 1955, 43, 331–343. [Google Scholar]
- McNab, B.K. Food habits, energetics, and the population biology of mammals. Am. Nat. 1980, 116, 106–124. [Google Scholar] [CrossRef]
- Schneider, E.D.; Sagan, D. Into the Cool: Energy Flow, Thermodynamics, and Life; University of Chicago Press: Chicago, IL, USA, 2005. [Google Scholar]
- Milewski, A.V.; Mills, A.J. Does life consistently maximise energy intensity? Biol. Rev. 2010, 85, 859–879. [Google Scholar]
- Banavar, J.R.; Cooke, T.J.; Rinaldo, A.; Maritan, A. Form, function, and evolution of living organisms. Proc. Natl. Acad. Sci. USA 2014, 111, 3332–3337. [Google Scholar] [CrossRef] [PubMed]
- Kleiber, M. Body size and metabolism. Hilgardia 1932, 6, 315–353. [Google Scholar] [CrossRef]
- Kleiber, M. The Fire of Life; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Hemmingsen, A.M. Energy metabolism as related to body size and respiratory surfaces, and its evolution. Rep. Steno Mem. Hosp. Nord. Insulin Lab. 1961, 9, 1–110. [Google Scholar]
- Peters, R.H. The Ecological Implications of Body Size; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Schmidt-Nielsen, K. Scaling: Why Is Animal Size So Important? Cambridge University Press: New York, NY, USA, 1984. [Google Scholar]
- Savage, V.M.; Gillooly, J.F.; Woodruff, W.H.; West, G.B.; Allen, A.P.; Enquist, B.J.; Brown, J.H. The predominance of quarter-power scaling in biology. Funct. Ecol. 2004, 18, 257–282. [Google Scholar] [CrossRef]
- Whitfield, J. In the Beat of a Heart: Life, Energy, and the Unity of Nature; John Henry Press: Washington, DC, USA, 2006. [Google Scholar]
- Moses, M.E.; Hou, C.; Woodruff, W.H.; West, G.B.; Nekola, J.C.; Zuo, W.; Brown, J.H. Revisiting a model of ontogenetic growth: Estimating model parameters from theory and data. Am. Nat. 2008, 171, 632–645. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Sibly, R.M.; Brown, J.H.; Kodric-Brown, A. Metabolic Ecology: A Scaling Approach; Wiley-Blackwell: Oxford, UK, 2012. [Google Scholar]
- Agutter, P.S.; Wheatley, D.N. Metabolic scaling: Consensus or controversy? Theor. Biol. Med. Model. 2004, 1. [Google Scholar] [CrossRef]
- Glazier, D.S. Beyond the “3/4-power law”: Variation in the intra- and interspecific scaling of metabolic rate in animals. Biol. Rev. 2005, 80, 611–662. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. A unifying explanation for diverse metabolic scaling in animals and plants. Biol. Rev. 2010, 85, 111–138. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, M.P.; Kemp, S.J.; Agosta, S.J.; Hansen, F.; Sieg, A.E.; Wallace, B.P.; McNair, J.N.; Dunham, A.E. Reconsidering the mechanistic basis of the metabolic theory of ecology. Oikos 2007, 116, 1058–1072. [Google Scholar] [CrossRef]
- Agutter, P.S.; Tuszynski, J.A. Analytic theories of metabolic scaling. J. Exp. Biol. 2011, 214, 1055–1062. [Google Scholar] [CrossRef] [PubMed]
- Price, C.A.; Weitz, J.S.; Savage, V.M.; Stegen, J.; Clarke, A.; Coomes, D.A.; Dodds, P.S.; Etienne, R.S.; Kerkhoff, A.J.; McCulloh, K.; et al. Testing the metabolic theory of ecology. Ecol. Lett. 2012, 15, 1465–1474. [Google Scholar] [CrossRef] [PubMed]
- McMahon, B.R.; Wilkens, J.L.; Smith, P.J.S. Invertebrate circulatory systems. Compr. Physiol. 2011, 931–1008. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. The fourth dimension of life: Fractal geometry and allometric scaling of organisms. Science 1999, 284, 1677–1679. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Moses, M.E.; Brown, J.H.; Damuth, J.; Rinaldo, A.; Sibly, R.M.; Maritan, A. A general basis for quarter-power scaling in animals. Proc. Natl. Acad. Sci. USA 2010, 107, 15816–15820. [Google Scholar] [CrossRef] [PubMed]
- Dodds, P.S.; Rothman, D.H.; Weitz, J.S. Re-examination of the “3/4-law” of metabolism. J. Theor. Biol. 2001, 209, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Kozłowski, J.; Konarzewski, M. Is West, Brown and Enquist’s model of allometric scaling mathematically correct and biologically relevant? Funct. Ecol. 2004, 18, 283–289. [Google Scholar]
- Kozłowski, J.; Konarzewski, M. West, Brown and Enquist’s model of allometric scaling again: The same questions remain. Funct. Ecol. 2005, 19, 739–743. [Google Scholar] [CrossRef]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.-L. Revising the distributive network models of West, Brown & Enquist (1997) and Banavar, Maritan & Rinaldo (1999). Metabolic inequity of living tissues provides clues for the observed allometric scaling rules. J. Theor. Biol. 2005, 237, 291–307. [Google Scholar] [CrossRef] [PubMed]
- Painter, P.R. The fractal geometry of nutrient exchange surfaces does not provide an explanation for 3/4-power metabolic scaling. Theor. Biol. Med. Model. 2005, 2, 30. [Google Scholar] [PubMed]
- Chaui-Berlinck, J.G. A critical understanding of the fractal model of metabolic scaling. J. Exp. Biol. 2006, 209, 3045–3054. [Google Scholar] [CrossRef] [PubMed]
- Chaui-Berlinck, J.G. Response to “Comment on ‘A critical understanding of the fractal model of metabolic scaling’”. J. Exp. Biol. 2007, 210, 3875–3876. [Google Scholar] [CrossRef]
- Apol, M.E.F.; Etienne, R.S.; Olff, H. Revisiting the evolutionary origin of allometric metabolic scaling in biology. Funct. Ecol. 2008, 22, 1070–1080. [Google Scholar] [CrossRef]
- White, C.R.; Frappell, P.B.; Chown, S.L. An information-theoretic approach to evaluating the size and temperature dependence of metabolic rate. Proc. R. Soc. B 2012, 279, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Painter, P.R. Data from necropsy studies and in vitro studies lead to a model for allometric scaling of basal metabolic rate. Theor. Biol. Med. Model. 2005, 2. [Google Scholar] [CrossRef]
- Killen, S.S.; Costa, I.; Brown, J.A.; Gamperl, A.K. Little left in the tank: Metabolic scaling in marine teleosts and its implications for aerobic scope. Proc. R. Soc. Lond. B 2007, 274, 431–438. [Google Scholar] [CrossRef]
- Moran, D.; Wells, R.M.G. Ontogenetic scaling of fish metabolism in the mouse-to-elephant mass magnitude range. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2007, 148, 611–620. [Google Scholar] [CrossRef] [PubMed]
- Clarke, A.; Rothery, P.; Isaac, N.J.B. Scaling of basal metabolic rate with body mass and temperature in mammals. J. Anim. Ecol. 2010, 79, 610–619. [Google Scholar] [CrossRef] [PubMed]
- Kolokotrones, T.; Savage, V.; Deeds, E.J.; Fontana, W. Curvature in metabolic scaling. Nature 2010, 464, 753–756. [Google Scholar] [CrossRef] [PubMed]
- Mori, S.; Yamaji, K.; Ishida, A.; Prokushkin, S.G.; Masyagina, O.V.; Hagihara, A.; Rafiqul Hoque, A.T.M.; Suwa, R.; Osawa, A.; Nishizono, T.; et al. Mixed-power scaling of whole-plant respiration from seedlings to giant trees. Proc. Natl. Acad. Sci. USA 2010, 107, 1447–1451. [Google Scholar] [CrossRef] [PubMed]
- Ehnes, R.B.; Rall, B.C.; Brose, U. Phylogenetic grouping, curvature and metabolic scaling in terrestrial invertebrates. Ecol. Lett. 2011, 14, 993–1000. [Google Scholar] [CrossRef] [PubMed]
- Streicher, J.W.; Cox, C.L.; Birchard, G.F. Non-linear scaling of oxygen consumption and heart rate in a very large cockroach species (Gromphadorhina portentosa): Correlated changes with body size and temperature. J. Exp. Biol. 2012, 215, 1137–1143. [Google Scholar] [CrossRef] [PubMed]
- Price, C.A.; Enquist, B.J.; Savage, V.M. A general model for allometric covariation in botanical form and function. Proc. Natl. Acad. Sci. USA 2007, 104, 13204–13209. [Google Scholar] [CrossRef] [PubMed]
- Savage, V.M.; Deeds, E.J.; Fontana, W. Sizing up allometric scaling theory. PLoS Comp. Biol. 2008, 4. [Google Scholar] [CrossRef]
- Dodds, P.S. On the optimal form of branching supply and collection networks. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Hirst, A.G.; Glazier, D.S.; Atkinson, D. Body shape-shifting during growth permits tests that distinguish between competing geometric theories of metabolic scaling. Ecol. Lett. 2014, 17, 1274–1281. [Google Scholar] [CrossRef] [PubMed]
- Enquist, B.J.; Allen, A.P.; Brown, J.H.; Gillooly, J.F.; Kerkhoff, A.J.; Niklas, K.J.; Price, C.A.; West, G.B. Biological scaling: Does the exception prove the rule? Nature 2007, 445, E9–E10. [Google Scholar] [CrossRef]
- DeLong, J.P.; Okie, J.G.; Moses, M.E.; Sibly, R.M.; Brown, J.H. Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. USA 2010, 107, 12941–12945. [Google Scholar] [CrossRef] [PubMed]
- White, C.R.; Kearney, M.R. Determinants of inter-specific variation in basal metabolic rate. J. Comp. Physiol. B 2013, 183, 1–26. [Google Scholar] [CrossRef]
- White, C.R.; Kearney, M.R. Metabolic scaling in animals: Methods, empirical results, and theoretical explanations. Compr. Physiol. 2014, 4, 231–256. [Google Scholar] [PubMed]
- Isaac, N.J.; Carbone, C. Why are metabolic scaling exponents so controversial? Quantifying variance and testing hypotheses. Ecol. Lett. 2010, 13, 728–735. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S.; Butler, E.M.; Lombardi, S.A.; Deptola, T.J.; Reese, A.J.; Satterthwaite, E.V. Ecological effects on metabolic scaling: Amphipod responses to fish predators in freshwater springs. Ecol. Monogr. 2011, 81, 599–618. [Google Scholar] [CrossRef]
- White, C.R.; Kearney, M.R.; Matthews, P.G.D.; Kooijman, S.A.L.M.; Marshall, D.J. Manipulative test of competing theories for metabolic scaling. Am. Nat. 2011, 178, 746–754. [Google Scholar] [CrossRef] [PubMed]
- Kearney, M.R.; White, C.R. Testing metabolic theories. Am. Nat. 2012, 180, 546–565. [Google Scholar] [CrossRef] [PubMed]
- Gifford, M.E.; Clay, T.A.; Peterman, W.E. The effects of temperature and activity on intraspecific scaling of metabolic rates in a lungless salamander. J. Exp. Zool. A 2013, 319, 230–236. [Google Scholar] [CrossRef]
- Watson, S.-A.; Morley, S.A.; Bates, A.E.; Clark, M.S.; Day, R.W.; Lamare, M.; Martin, S.M.; Southgate, P.C.; Tan, K.S.; Tyler, P.A.; et al. Low global sensitivity of metabolic rate to temperature in calcified marine invertebrates. Oecologia 2014, 174, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Chamberlin, T.C. The method of multiple working hypotheses. Science 1965, 148, 754–759. [Google Scholar] [CrossRef] [PubMed]
- Martínez del Rio, C. Metabolic theory or metabolic models? Trends Ecol. Evol. 2008, 23, 256–260. [Google Scholar]
- Levins, R. The strategy of model building in population biology. Am. Sci. 1966, 54, 421–431. [Google Scholar]
- Scheiner, S.M. Toward a conceptual framework for biology. Q. Rev. Biol. 2010, 85, 293–318. [Google Scholar] [CrossRef] [PubMed]
- von Bertalanffy, L. Quantitative laws in metabolism and growth. Q. Rev. Biol. 1957, 32, 217–231. [Google Scholar] [CrossRef] [PubMed]
- von Bertalanffy, L. Basic concepts in quantitative biology of metabolism. Helgol. Wiss. Meeresunters. 1964, 9, 5–37. [Google Scholar] [CrossRef]
- von Bertalanffy, L. General System Theory: Foundations, Development, Applications; George Braziller: New York, NY, USA, 1968. [Google Scholar]
- von Bertalanffy, L.; Pirozynski, W.J. Tissue respiration, growth, and basal metabolism. Biol. Bull. 1953, 105, 240–256. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H. The origin of allometric scaling laws in biology from genomes to ecosystems: Towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef] [PubMed]
- Kooijman, S.A.L.M. Dynamic Energy Budget Theory for Metabolic Organization; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Maino, J.L.; Kearney, M.R.; Nisbet, R.M.; Kooijman, S.A.L.M. Reconciling theories for metabolic scaling. J. Anim. Ecol. 2014, 83, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Davison, J. Body weight, cell surface, and metabolic rate in anuran Amphibia. Biol. Bull. 1955, 109, 407–419. [Google Scholar] [CrossRef]
- Kozłowski, J.; Konarzewski, M.; Gawelczyk, A.T. Cell size as a link between noncoding DNA and metabolic rate scaling. Proc. Natl. Acad. Sci. USA 2003, 100, 14080–14085. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, A.J.; Else, P.L. Membranes and the setting of energy demand. J. Exp. Biol. 2005, 208, 1593–1599. [Google Scholar] [CrossRef] [PubMed]
- Demetrius, L. The origin of allometric scaling laws in biology. J. Theor. Biol. 2006, 243, 455–467. [Google Scholar] [CrossRef] [PubMed]
- Demetrius, L.; Tuszynski, J.A. Quantum metabolism explains the allometric scaling of metabolic rates. J. R. Soc. Interface 2010, 7, 507–514. [Google Scholar] [CrossRef] [PubMed]
- Suarez, R.K.; Darveau, C.-A. Multi-level regulation and metabolic scaling. J. Exp. Biol. 2005, 208, 1627–1634. [Google Scholar] [CrossRef] [PubMed]
- Suarez, R.K. Energy and metabolism. Compr. Physiol. 2012, 2, 2527–2539. [Google Scholar] [PubMed]
- Simon, H.A. The architecture of complexity. Proc. Am. Philos. Soc. 1962, 106, 467–482. [Google Scholar]
- Weiss, P.A. The Living System: Determinism Stratified. In Beyond Reductionism: New Perspectives in the Life Sciences; Koestler, A., Smythies, J.R., Eds.; Macmillan: New York, NY, USA, 1969; pp. 3–55. [Google Scholar]
- Campbell, D.T. Downward Causation in Hierarchically Organized Biological Systems. In Studies in the Philosophy of Biology; Dobzhansky, T., Ayala, F.J., Eds.; Macmillan: New York, NY, USA, 1974; pp. 85–90. [Google Scholar]
- Salthe, S.N. Evolving Hierarchical Systems: Their Structure and Representation; Columbia University Press: New York, NY, USA, 1985. [Google Scholar]
- Noble, D. Claude Bernard, the first systems biologist, and the future of physiology. Exp. Physiol. 2008, 93, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Winther, R.G. Systemic Darwinism. Proc Natl. Acad. Sci. USA 2008, 105, 11833–11838. [Google Scholar] [CrossRef] [PubMed]
- Saetzler, K.; Sonnenschein, C.; Soto, A.M. Systems biology beyond networks: Generating order from disorder through self-organization. Semin. Cancer Biol. 2011, 21, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Bose, B. Systems biology: A biologist’s viewpoint. Prog. Biophys. Mol. Biol. 2013, 113, 358–368. [Google Scholar] [CrossRef] [PubMed]
- Sarrus, F.; Rameaux, J.F. Application des sciences accessoires et principalement des mathématiques à la physiologie générale (Rapport sur une mémoire adressé à l’Académic royale de Médecine, séance du 23 juillet 1839). Bull. Acad. R. Méd. (Paris) 1839, 3, 1094–1100. [Google Scholar]
- Rubner, M. Über den Einfluss der Körpergrösse auf Stoff- und Kraftwechsel. Z. Biol. 1883, 19, 535–562. [Google Scholar]
- Richet, C.R. La Chaleur Animale; Bibliothèque Scientifique Internationale, Felix Alcan: Paris, France, 1889. [Google Scholar]
- Voit, E. Über die Grösse des Energiebedarfs der Tiere in Hungerzustande. Z. Biol. 1901, 41, 113–154. [Google Scholar]
- Brody, S.; Procter, R.C. Relation between basal metabolism and mature body weight in different species of mammals and birds. Univ. Mo. Agric. Exp. Stat. Res. Bull. 1932, 116, 89–101. [Google Scholar]
- Thompson, D.W. On Growth and Form, Volume I, 2nd ed.; Cambridge University Press: Cambridge, UK, 1942. [Google Scholar]
- Brody, S. Bioenergetics and Growth; Hafner: New York, NY, USA, 1945. [Google Scholar]
- Lehmann, G. Energetik des organismus. In Oppenheimer’s Handb. Biochem., 2nd ed.; Fischer: Jena, Germany, 1926; pp. 564–608. [Google Scholar]
- Ellenby, C. Relation between body size and metabolism. Nature 1937, 140, 853. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Monin, A.S. Similarity principles for the biology of pelagic animals. Proc. Natl. Acad. Sci. USA 1983, 80, 3540–3542. [Google Scholar] [CrossRef] [PubMed]
- Pfaundler, M. Über die energetische Flächenregel. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 1921, 188, 273–280. [Google Scholar] [CrossRef]
- Rubner, M. Betrachtungen er die Resorptionsvorgge der Organzellen. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 1913, 180, 240–258. [Google Scholar]
- Ellenby, C. Oxygen consumption of prepupae of Drosophila melanogaster Meigen, in relation to the surface area of the puparium. J. Exp. Biol. 1945, 21, 39–45. [Google Scholar]
- Krogh, A. The Respiratory Exchange of Animals and Man; Longmans, Green: London, UK, 1916. [Google Scholar]
- Bartholomew, G.A. Energy Metabolism. In Animal Physiology: Principles and Adaptations; Gordon, M.S., Ed.; Macmillan: New York, NY, USA, 1982; pp. 46–93. [Google Scholar]
- Seymour, R.; White, C. Can the basal metabolic rate of endotherms be explained by biophysical modeling? Response to “A new model for the body size–metabolism relationship”. Physiol. Biochem. Zool. 2011, 84, 107–110. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Effects of metabolic level on the body size scaling of metabolic rate in birds and mammals. Proc. R. Soc. B 2008, 275, 1405–1410. [Google Scholar]
- Porter, W.P.; Kearney, M. Size, shape, and the thermal niche of endotherms. Proc. Natl. Acad. Sci. USA 2009, 106, 19666–19672. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.F.; Lightfoot, E.N.; Porter, W.P. A new model for the body size–metabolism relationship. Physiol. Biochem. Zool. 2010, 83, 395–405. [Google Scholar] [CrossRef] [PubMed]
- Speakman, J.R.; Król, E. Maximal heat dissipation capacity and hyperthermia risk: Neglected key factors in the ecology of endotherms. J. Anim. Ecol. 2010, 79, 726–746. [Google Scholar] [PubMed]
- Patterson, M.R. A mass transfer explanation of metabolic scaling relations in some aquatic invertebrates and algae. Science 1992, 255, 1421–1423. [Google Scholar] [CrossRef] [PubMed]
- Kooijman, S.A.L.M. Dynamic Energy and Mass Budgets in Biological Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wirtz, K.W. How fast can plankton feed? Maximum ingestion rate scales with digestive surface area. J. Plankton Res. 2013, 35, 33–48. [Google Scholar] [CrossRef]
- Okie, J.G. General models for the spectra of surface area scaling strategies of cells and organisms: Fractality, geometric dissimilitude, and internalization. Am. Nat. 2013, 181, 421–439. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. The scaling of metabolic scaling within physical limits. Systems 2014, in press. [Google Scholar]
- Hoesslin, H.von. Über die Ursache der scheinbaren Abhängigkeit des Umsatzes von der Grösse der Körperoberfläche. Arch. Anat. Physiol. Physiol. Abth. 1888, 11, 323–379. [Google Scholar]
- Read, J.M. Correlation of basal metabolic rate with pulse rate and pulse pressure. J. Am. Med. Assoc. 1922, 78, 1887–1889. [Google Scholar] [CrossRef]
- Henderson, Y. Volume changes of the heart. Physiol. Rev. 1923, 3, 165–208. [Google Scholar]
- Read, J.M.; Barnett, C.W. New formulae for prediction of basal metabolism from pulse rate and pulse pressure. Proc. Soc. Exp. Biol. Med. 1934, 31, 723–725. [Google Scholar] [CrossRef]
- Green, J.A. The heart rate method for estimating metabolic rate: Review and recommendations. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2011, 158, 287–304. [Google Scholar]
- Currie, S.E.; Körtner, G.; Geiser, F. Heart rate as a predictor of metabolic rate in heterothermic bats. J. Exp. Biol. 2014, 217, 1519–1524. [Google Scholar] [PubMed]
- Sernetz, M.; Willems, H.; Bittner, H.R. Fractal Organization of Metabolism. In Energy Transformations in Cells and Organisms; Wieser, W., Gnaiger, E., Eds.; Georg Thieme Verlag: Stuttgart, Germany, 1989; pp. 82–90. [Google Scholar]
- Spatz, H.C. Circulation, metabolic rate, and body size in mammals. J. Comp. Physiol. B 1991, 161, 231–236. [Google Scholar] [CrossRef] [PubMed]
- Krogh, A. The Anatomy and Physiology of Capillaries; Yale University Press: New Haven, CT, USA, 1929. [Google Scholar]
- Santillán, M. Allometric scaling law in a simple oxygen exchanging network: Possible implications on the biological allometric scaling laws. J. Theor. Biol. 2003, 223, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Maritan, A.; Rinaldo, A. Size and form in efficient transportation networks. Nature 1999, 399, 130–132. [Google Scholar] [CrossRef] [PubMed]
- Dreyer, O.; Puzio, R. Allometric scaling in animals and plants. J. Math. Biol. 2001, 43, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R.; Hoppeler, H. Exercise-induced maximal metabolic rate scales with muscle aerobic capacity. J. Exp. Biol. 2005, 208, 1635–1644. [Google Scholar] [CrossRef] [PubMed]
- Dawson, T.H. Scaling laws for capillary vessels of mammals at rest and in exercise. Proc. R. Soc. B 2003, 270, 755–763. [Google Scholar] [CrossRef] [PubMed]
- Hou, C.; Mayo, M. Pulmonary diffusional screening and the scaling laws of mammalian metabolic rates. Phys. Rev. E 2011, 84. [Google Scholar] [CrossRef]
- Reitsma, W. Formation of new capillaries in hypertrophic skeletal muscle. Angiology 1973, 24, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Bloor, C.M. Angiogenesis during exercise and training. Angiogensis 2005, 8, 263–271. [Google Scholar] [CrossRef]
- Helm, B.R.; Davidowitz, G. Mass and volume growth of an insect tracheal system within a single instar. J. Exp. Biol. 2013, 216, 4703–4711. [Google Scholar] [CrossRef] [PubMed]
- Benedict, F.G. Factors affecting basal metabolism. J. Biol. Chem. 1915, 20, 263–299. [Google Scholar]
- Blank, H. Tiergrösse und Stoffwechsel. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 1934, 234, 310–317. [Google Scholar] [CrossRef]
- Kestner, O. Über die Oberflächenregel des Stoffwechsels. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 1934, 234, 290–301. [Google Scholar] [CrossRef]
- Kestner, O. Metabolism and size of organs. J. Physiol. 1936, 87, 39P–41P. [Google Scholar]
- Crile, G.W. Intelligence, Power and Personality; Wittlesey: New York, NY, USA, 1941. [Google Scholar]
- Martin, R.D. Relative brain size and basal metabolic rate in terrestrial vertebrates. Nature 1981, 293, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Mink, J.W.; Blumenschine, R.J.; Adams, D.B. Ratio of central nervous system to body metabolism in vertebrates: Its constancy and functional basis. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1981, 241, R203–R212. [Google Scholar]
- McNab, B.K.; Eisenberg, J.F. Brain size and its relation to the rate of metabolism in mammals. Am. Nat. 1989, 133, 157–167. [Google Scholar] [CrossRef]
- Nilsson, G. Brain and body oxygen requirements of Gnathonemus petersii, a fish with an exceptionally large brain. J. Exp. Biol. 1996, 199, 603–607. [Google Scholar] [PubMed]
- Isler, K.; van Schaik, C.P. Metabolic costs of brain size evolution. Biol. Lett. 2006, 2, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Barton, R.A.; Capellini, I. Maternal investment, life histories, and the costs of brain growth in mammals. Proc. Natl. Acad. Sci. USA 2011, 108, 6169–6174. [Google Scholar] [CrossRef] [PubMed]
- Itazawa, Y.; Oikawa, S. A quantitative interpretation of the metabolism-size relationship in animals. Experientia 1986, 42, 152–153. [Google Scholar] [CrossRef]
- Oikawa, S.; Itazawa, Y. Relationship between summated tissue respiration and body size in a marine teleost, the porgy Pagrus major. Fish. Sci. 2003, 69, 687–694. [Google Scholar] [CrossRef]
- Wang, Z.; O’Connor, T.P.; Heshka, S.; Heymsfield, S.B. The reconstruction of Kleiber’s law at the organ-tissue level. J. Nutr. 2001, 131, 2967–2970. [Google Scholar] [PubMed]
- Wang, Z.; Zhang, J.; Ying, Z.; Heymsfield, S.B. Organ-tissue level model of resting energy expenditure across mammals: New insights into Kleiber’s Law. ISRN Zool. 2012. [Google Scholar] [CrossRef]
- Spaargaren, D.H. Metabolic rate and body size. Acta Biotheor. 1994, 42, 263–269. [Google Scholar] [PubMed]
- Bishop, R.E.; Torres, J.J. Leptocephalus energetics: Metabolism and excretion. J. Exp. Biol. 1999, 202, 2485–2493. [Google Scholar] [PubMed]
- Šustr, V.; Pižl, V. Oxygen consumption of the earthworm species Dendrobaena mrazeki. Eur. J. Soil Biol. 2009, 45, 478–482. [Google Scholar] [CrossRef]
- Cheng, D.L.; Li, T.; Zhong, Q.L.; Wang, G.X. Scaling relationship between tree respiration rates and biomass. Biol. Lett. 2010, 6, 715–717. [Google Scholar] [CrossRef] [PubMed]
- Kutschera, U.; Niklas, K.J. Ontogenetic changes in the scaling of cellular respiration with respect to size among sunflower seedlings. Plant Signal. Behav. 2011, 6, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Kutschera, U.; Niklas, K.J. Organ-specific rates of cellular respiration in developing sunflower seedlings and their bearing on metabolic scaling theory. Protoplasma 2012, 249, 1049–1057. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.J.; Langemann, D.; Gehrke, I.; Later, W.; Heller, M.; Glüer, C.C.; Heymsfield, S.B.; Bosy-Westphal, A. Effect of constitution on mass of individual organs and their association with metabolic rate in humans—A detailed view on allometric scaling. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Wels, P. Der Einfluss der Tiergrösse auf die Oxydationsgeschwindigkeit im überlebenden Gewebe. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 1925, 209, 32–48. [Google Scholar] [CrossRef]
- Terroine, E.F.; Roche, J. La respiration des tissus. I. Production calorique des homéothermes et intensité de la respiration in vitro des tissus homologues. Arch. Intern. Physiol. 1925, 24, 356–399. [Google Scholar]
- Grafe, E.; Reinwein, H.; Singer, F. Studien über Gewebsatmung. II. Die Atmung der überlebenden Warmblüterorgane. Biochem. Z. 1925, 165, 102–117. [Google Scholar]
- Kleiber, M. Body size and metabolism of liver slices in vitro. Proc. Soc. Exp. Biol. Med. 1941, 48, 419–423. [Google Scholar] [CrossRef]
- Krebs, H.A. Body size and tissue respiration. Biochim. Biophys. Acta 1950, 4, 249–269. [Google Scholar] [CrossRef] [PubMed]
- Holmes, W.N.; Stott, G.H. Studies of the respiration rates of excretory tissues in the Cutthroat Trout (Salmo clarki clarki) I. Variations with body weight. Physiol. Zool. 1960, 33, 9–14. [Google Scholar]
- Oikawa, S.; Itazawa, Y. Allometric relationship between tissue respiration and body mass in the carp. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1984, 77, 415–418. [Google Scholar] [CrossRef]
- Oikawa, S.; Itazawa, Y. Allometric relationship between tissue respiration and body mass in a marine teleost, porgy Pagrus major. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1993, 105, 129–133. [Google Scholar] [CrossRef]
- Couture, P.; Hulbert, A.J. Relationship between body mass, tissue metabolic rate, and sodium pump activity in mammalian liver and kidney. Am. J. Physiol. 1995, 268, R641–R650. [Google Scholar] [PubMed]
- Porter, R.K.; Brand, M.D. Causes of differences in respiration rate of hepatocytes from mammals of different body mass. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1995, 269, R1213–R1224. [Google Scholar]
- Else, P.L.; Brand, M.D.; Turner, N.; Hulbert, A.J. Respiration rate of hepatocytes varies with body mass in birds. J. Exp. Biol. 2004, 207, 2305–2311. [Google Scholar] [PubMed]
- West, G.B.; Woodruff, W.H.; Brown, J.H. Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc. Natl. Acad. Sci. USA 2002, 99, 2473–2478. [Google Scholar] [PubMed]
- Brown, M.F.; Gratton, T.P.; Stuart, J.A. Metabolic rate does not scale with body mass in cultured mammalian cells. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 292, R2115–R2121. [Google Scholar] [CrossRef] [PubMed]
- Robb, E.L.; Maddalena, L.A.; Dunlop, V.A.; Foster, T.; Stuart, J.A. Absence of metabolic rate allometry in an ex vivo model of mammalian skeletal muscle. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2012, 162, 157–162. [Google Scholar] [CrossRef] [PubMed]
- Wheatley, D.N. Convergence of metabolic rate of cultured cells from animals of different sizes. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 292, R2113–R2114. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Is metabolic rate a universal “pacemaker” for biological processes? Biol. Rev. 2014. [Google Scholar] [CrossRef]
- Teissier, G. Recherches Morphologiques et Physiologiques Croissance des Insectes: Thèses Presentees a la Faculte des Sciences de L’Université de Paris pour obtenir le Grade de Docteur ès Sciences Naturelles. Les Presses Universitaires de France: Paris, France, 1931. [Google Scholar]
- Riddle, O.; Nussmann, T.C.; Benedict, F.G. Metabolism during growth in a common pigeon. Am. J. Physiol. 1932, 101, 251–259. [Google Scholar]
- Kibler, H.H.; Brody, S. Metabolism and growth rate of rats. J. Nutr. 1942, 24, 461–468. [Google Scholar]
- Darveau, C.-A.; Suarez, R.K.; Andrews, R.D.; Hochachka, P.W. Allometric cascade as a unifying principle of body mass effects on metabolism. Nature 2002, 417, 166–170. [Google Scholar] [CrossRef]
- Hochachka, P.W.; Darveau, C.A.; Andrews, R.D.; Suarez, R.K. Allometric cascade: A model for resolving body mass effects on metabolism. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2003, 134, 675–691. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Activity affects intraspecific body-size scaling of metabolic rate in ectothermic animals. J. Comp. Physiol. B 2009, 179, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Zeuthen, E. Oxygen uptake as related to body size in organisms. Quart. Rev. Biol. 1953, 28, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Phillipson, J. Bioenergetic Options and Phylogeny. In Physiological Ecology: An Evolutionary Approach to Resource Use; Townsend, C.R., Calow, P., Eds.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 20–45. [Google Scholar]
- Finkel, Z.V.; Irwin, A.J.; Schofield, O. Resource limitation alters the 3/4 size scaling of metabolic rates in phytoplankton. Mar. Ecol. Prog. Ser. 2004, 273, 269–279. [Google Scholar] [CrossRef]
- Glazier, D.S. Metabolic level and size-scaling of rates of respiration and growth in unicellular organisms. Funct. Ecol. 2009, 23, 963–968. [Google Scholar] [CrossRef]
- Lewis, W.M. Surface/volume ratio: Implications for phytoplankton morphology. Science 1976, 192, 885–887. [Google Scholar] [CrossRef] [PubMed]
- Raven, J.A. The role of vacuoles. New Phytol. 1987, 106, 357–422. [Google Scholar] [CrossRef]
- Niklas, K.J. The evolution of plant body plans—A biomechanical perspective. Ann. Bot. 2000, 85, 411–438. [Google Scholar] [CrossRef]
- Dao, M.H. Reassessment of the cell surface area limitation to nutrient uptake in phytoplankton. Mar. Ecol. Prog. Ser. 2013, 489, 87–92. [Google Scholar] [CrossRef]
- Davison, J. An analysis of cell growth and metabolism in the crayfish (Procambrus alleni). Biol. Bull. 1956, 110, 264–273. [Google Scholar] [CrossRef]
- Glazier, D.S.; Powell, M.G.; Deptola, T.J. Body-size scaling of metabolic rate in the trilobite Eldredgeops rana. Paleobiology 2013, 39, 109–122. [Google Scholar] [CrossRef]
- Else, P.L.; Hulbert, A.J. Mammals: An allometric study of metabolism at tissue and mitochondrial level. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1985, 248, R415–R421. [Google Scholar]
- Porter, R.K. Allometry of mammalian cellular oxygen consumption. Cell. Mol. Life Sci. 2001, 58, 815–822. [Google Scholar] [CrossRef] [PubMed]
- Snelling, E.P.; Seymour, R.S.; Runciman, S.; Matthews, P.G.; White, C.R. Symmorphosis and the insect respiratory system: Allometric variation. J. Exp. Biol. 2011, 214, 3225–3237. [Google Scholar] [CrossRef] [PubMed]
- Krogh, A. The Comparative Physiology of Respiratory Mechanisms; University of Philadelphia Press: Philadelphia, PA, USA, 1941. [Google Scholar]
- Fenchel, T. Protozoa and oxygen. Acta Protozool. 2012, 52, 11–20. [Google Scholar]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.L. Energetics of the smallest: Do bacteria breathe at the same rate as whales? Proc. R. Soc. Lond. B 2005, 272, 2219–2224. [Google Scholar] [CrossRef]
- Johnson, M.D.; Völket, J.; Moeller, H.V.; Breslauer, K.J.; Falkowski, P.G. Universal constant for heat production in protists. Proc. Natl. Acad. Sci. USA 2009, 106, 6696–6699. [Google Scholar] [CrossRef] [PubMed]
- Sweetlove, L.J.; Fernie, A.R. The spatial organization of metabolism within the plant cell. Ann. Rev. Plant Biol. 2013, 64, 723–746. [Google Scholar]
- Norland, S.; Heldal, M.; Tumyr, O. On the relation between dry matter and volume of bacteria. Microb. Ecol. 1987, 13, 95–101. [Google Scholar] [PubMed]
- Menden-Deuer, S.; Lessard, E.J. Carbon to volume relationships for dinoflagellates, diatoms, and other protist plankton. Limnol. Oceanogr. 2000, 45, 569–579. [Google Scholar] [CrossRef]
- Fujiwara, N. Origin of the scaling rule for fundamental living organisms based on thermodynamics. BioSystems 2003, 70, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, A.J.; Else, P.L. Membranes as possible pacemakers of metabolism. J. Theor. Biol. 1999, 199, 257–274. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, A.J.; Pamplona, R.; Buffenstein, R.; Buttemer, W.A. Life and death: Metabolic rate, membrane composition, and life span of animals. Physiol. Rev. 2007, 87, 1175–1213. [Google Scholar] [CrossRef] [PubMed]
- Radzinskaya, L.I.; Nikol’skaya, I.S.; Alekseeva, T.A.; Vladimirova, I.G.; Kovalenko, P.I.; Ozernyuk, N.D. Changes in the intensity of respiration during ontogenesis of some invertebrates. Russ. J. Dev. Biol. 2003, 34, 317–320. [Google Scholar] [CrossRef]
- Blossman-Myer, B.L.; Burggren, W.W. Metabolic allometry during development and metamorphosis of the silkworm Bombyx mori: Analyses, patterns, and mechanisms. Physiol. Biochem. Zool. 2010, 83, 215–231. [Google Scholar] [PubMed]
- Burpee, J.L.; Bardsley, E.L.; Dillaman, R.M.; Watanabe, W.O.; Kinsey, S.T. Scaling with body mass of mitochondrial respiration from the white muscle of three phylogenetically, morphologically and behaviorally disparate teleost fishes. J. Comp. Physiol. B 2010, 180, 967–977. [Google Scholar] [CrossRef] [PubMed]
- Martínez, I.; Gómez, M.; Packard, T.T. Potential respiration is a better respiratory predictor than biomass in young Artemia salina. J. Exp. Mar. Biol. Ecol. 2010, 390, 78–83. [Google Scholar] [CrossRef]
- Norin, T.; Malte, H. Intraspecific variation in aerobic metabolic rate of fish: Relations with organ size and enzyme activity in Brown Trout. Physiol. Biochem. Zool. 2012, 85, 645–656. [Google Scholar] [CrossRef] [PubMed]
- Schoombie, R.E.; Boardman, L.; Groenewald, B.; Glazier, D.S.; van Daalen, C.E.; Clusella-Trullas, S.; Terblanche, J.S. High metabolic and water-loss rates in caterpillar aggregations: Evidence against the resource-conservation hypothesis. J. Exp. Biol. 2013, 216, 4321–4325. [Google Scholar] [CrossRef] [PubMed]
- Broly, P.; Devigne, L.; Deneubourg, J.L.; Devigne, C. Effects of group size on aggregation against desiccation in woodlice (Isopoda: Oniscidea). Physiol. Entomol. 2014, 39, 165–171. [Google Scholar] [CrossRef]
- Pearson, O.P. The rate of metabolism of some small mammals. Ecology 1947, 28, 127–145. [Google Scholar] [CrossRef]
- Contreras, L. Bioenergetics of huddling: Test of a psycho-physiological hypothesis. J. Mammal. 1984, 65, 256–262. [Google Scholar] [CrossRef]
- Canals, M.; Rosenmann, M.; Bozinovic, F. Energetics and geometry of huddling in small mammals. J. Theor. Biol. 1989, 141, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Canals, M.; Rosenmann, M.; Bozinovic, F. Geometrical aspects of the energetic effectiveness of huddling in small mammals. Acta Theriol. 1997, 42, 321–328. [Google Scholar] [CrossRef]
- Hayes, J.; Speakman, J.; Racey, P. The contributions of local heating and reducing exposed surface area to the energetic benefits of hudding by short-tailed field voles (Microtus agrestis). Physiol. Zool. 1992, 65, 742–762. [Google Scholar]
- Davies, P.S. Respiration in some Atlantic reef corals in relation to vertical distribution and growth form. Biol. Bull. 1980, 158, 187–194. [Google Scholar] [CrossRef]
- Gillooly, J.F.; Hou, C.; Kaspari, M. Eusocial insects as superorganisms: Insights from metabolic theory. Commun. Integr. Biol. 2010, 3, 360–362. [Google Scholar] [CrossRef] [PubMed]
- Southwick, E.E.; Moritz, R.F. Social control of air ventilation in colonies of honey bees, Apis mellifera. J. Insect Physiol. 1987, 33, 623–626. [Google Scholar] [CrossRef]
- Turner, J.S. On the mound of Macrotermes michaelseni as an organ of respiratory gas exchange. Physiol. Biochem. Zool. 2001, 74, 798–822. [Google Scholar] [CrossRef] [PubMed]
- Hughes, D.J.; Hughes, R.N. Metabolic implications of modularity: Studies on the respiration and growth of Electra pilosa. Philos. Trans. R. Soc. Lond. B 1986, 313, 23–29. [Google Scholar] [CrossRef]
- Peck, L.S.; Barnes, D.K. Metabolic flexibility: The key to long-term evolutionary success in Bryozoa? Proc. R. Soc. Lond. B 2004, 271, S18–S21. [Google Scholar] [CrossRef]
- Biggs, D.C. Respiration and ammonium excretion by open ocean gelatinous zooplankton. Limnol. Oceanogr. 1977, 22, 108–117. [Google Scholar]
- Cetta, C.M.; Madin, L.P.; Kremer, P. Respiration and excretion by oceanic salps. Mar. Biol. 1986, 91, 529–537. [Google Scholar] [CrossRef]
- Iguchi, N.; Ikeda, T. Metabolism and elemental composition of aggregate and solitary forms of Salpa thompsoni (Tunicata: Thaliacea) in waters off the Antarctic Peninsula during austral summer 1999. J. Plankton Res. 2004, 26, 1025–1037. [Google Scholar] [CrossRef]
- Nakaya, F.; Saito, Y.; Motokawa, T. Switching of metabolic-rate scaling between allometry and isometry in colonial ascidians. Proc. R. Soc. Lond. B 2003, 270, 1105–1113. [Google Scholar] [CrossRef]
- Sebens, K.P. Coelenterata. In Animal Energetics, Volume 1; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; pp. 55–120. [Google Scholar]
- Vollmer, S.V.; Edmunds, P.J. Allometric scaling in small colonies of the scleractinian coral Siderastrea siderea (Ellis and Solander). Biol. Bull. 2000, 199, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Calow, P. Life Cycles: An Evolutionary Approach to the Physiology of Reproduction, Development and Ageing; Chapman and Hall: London, UK, 1978. [Google Scholar]
- Starkweather, P.L. Rotifera. In Animal Energetics, Volume 1; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; pp. 159–183. [Google Scholar]
- Tuck, S. The control of cell growth and body size in Caenorhabditis elegans. Exp. Cell Res. 2014, 321, 71–76. [Google Scholar] [CrossRef] [PubMed]
- Stemberger, R.S.; Gilbert, J.J. Rotifer threshold food concentrations and the size-efficiency hypothesis. Ecology 1987, 68, 181–187. [Google Scholar] [CrossRef]
- Schiemer, F. Nematoda. In Animal Energetics, Volume 1; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; pp. 185–215. [Google Scholar]
- Hou, C.; Kaspari, M.; Vander Zanden, H.B.; Gillooly, J.F. Energetic basis of colonial living in social insects. Proc. Natl. Acad. Sci. USA 2010, 107, 3634–3638. [Google Scholar] [CrossRef] [PubMed]
- Shik, J.Z. The metabolic costs of building ant colonies from variably sized subunits. Behav. Ecol. Sociobiol. 2010, 64, 1981–1990. [Google Scholar] [CrossRef]
- Waters, J.S.; Holbrook, C.T.; Fewell, J.H.; Harrison, J.F. Allometric scaling of metabolism, growth, and activity in whole colonies of the seed-harvester ant Pogonomyrmex californicus. Am. Nat. 2010, 176, 501–510. [Google Scholar] [CrossRef] [PubMed]
- Cao, T.T.; Dornhaus, A. Larger laboratory colonies consume proportionally less energy and have lower per capita brood production in Temnothorax ants. Insectes Sociaux 2013, 60, 1–5. [Google Scholar] [CrossRef]
- Lighton, J.R.B. Individual and whole-colony respiration in an African formicine ant. Funct. Ecol. 1989, 3, 523–530. [Google Scholar] [CrossRef]
- Fonck, C.; Jaffé, K. On the energetic cost of sociality. Physiol. Behav. 1996, 59, 713–719. [Google Scholar] [CrossRef] [PubMed]
- Jun, J.; Pepper, J.W.; Savage, V.M.; Gillooly, J.F.; Brown, J.H. Allometric scaling of ant foraging trail networks. Evol. Ecol. Res. 2003, 5, 297–303. [Google Scholar]
- Bruce, A.I.; Burd, M. Allometric scaling of foraging rate with trail dimensions in leaf-cutting ants. Proc. R. Soc. Lond. B 2012, 279, 2442–2447. [Google Scholar] [CrossRef]
- Bengston, S.E.; Dornhaus, A. Colony size does not predict foraging distance in the ant Temnothorax rugatulus: A puzzle for standard scaling models. Insectes Sociaux 2013, 60, 93–96. [Google Scholar] [CrossRef]
- Waters, J.S. Theoretical and empirical perspectives on the scaling of supply and demand in social insect colonies. Entomol. Exp. Appl. 2014, 150, 99–112. [Google Scholar]
- Nakaya, F.; Saito, Y.; Motokawa, T. Experimental allometry: Effect of size manipulation on metabolic rate of colonial ascidians. Proc. R. Soc. B 2005, 272, 1963–1969. [Google Scholar] [CrossRef] [PubMed]
- Damuth, J. Interspecific allometry of population density in mammals and other animals: The independence of body mass and population energy-use. Biol. J. Linn. Soc. 1987, 31, 193–246. [Google Scholar] [CrossRef]
- Enquist, B.J.; Economo, E.P.; Huxman, T.E.; Allen, A.P.; Ignace, D.D.; Gillooly, J.F. Scaling metabolism from organisms to ecosystems. Nature 2003, 423, 639–642. [Google Scholar] [CrossRef] [PubMed]
- Ernest, S.K.; Enquist, B.J.; Brown, J.H.; Charnov, E.L.; Gillooly, J.F.; Savage, V.M.; White, E.P.; Smith, F.A.; Hadly, E.A.; Haskell, J.P.; et al. Thermodynamic and metabolic effects on the scaling of production and population energy use. Ecol. Lett. 2003, 6, 990–995. [Google Scholar] [CrossRef]
- Hechinger, R.F.; Lafferty, K.D.; Dobson, A.P.; Brown, J.H.; Kuris, A.M. A common scaling rule for abundance, energetics, and production of parasitic and free-living species. Science 2011, 333, 445–448. [Google Scholar] [CrossRef] [PubMed]
- Salcido Guevara, L.A.; Arreguín Sánchez, F.; Palmeri, L.; Barausse, A. Metabolic scaling regularity in aquatic ecosystems. CICIMAR Oceán. 2012, 27, 13–26. [Google Scholar]
- Hechinger, R.F. A metabolic and body-size scaling framework for parasite within-host abundance, biomass, and energy flux. Am. Nat. 2013, 182, 234–248. [Google Scholar] [PubMed]
- Sewall, B.J.; Freestone, A.L.; Hawes, J.E.; Andriamanarina, E. Size-energy relationships in ecological communities. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
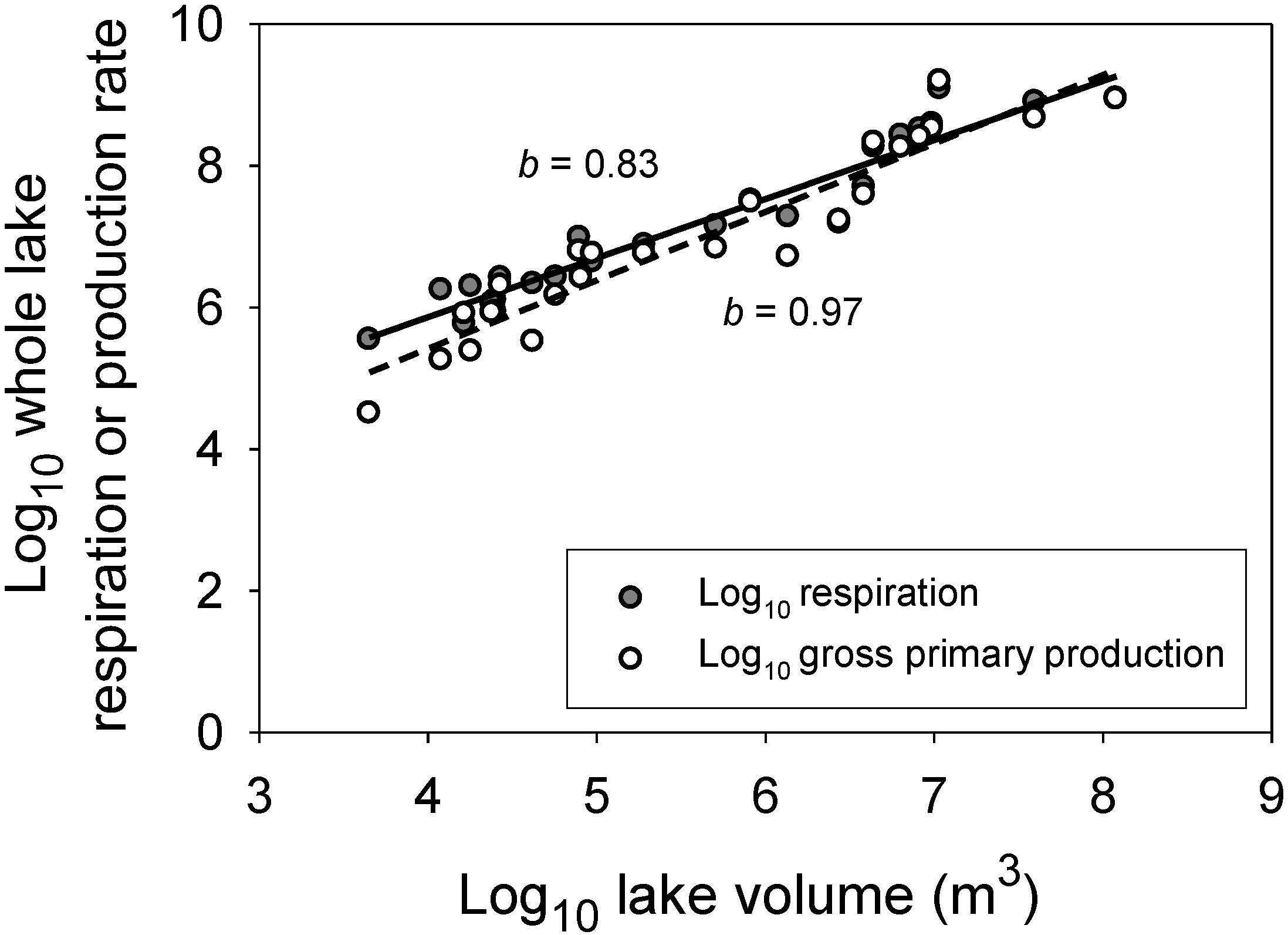
- Sand-Jensen, K.; Staehr, P.A. Scaling of pelagic metabolism to size, trophy and forest cover in small Danish lakes. Ecosystems 2007, 10, 128–142. [Google Scholar] [CrossRef]
- Staehr, P.A.; Baastrup-Spohr, L.; Sand-Jensen, K.; Stedmon, C. Lake metabolism scales with lake morphometry and catchment conditions. Aquat. Sci. 2012, 74, 155–169. [Google Scholar] [CrossRef]
- Yvon-Durocher, G.; Allen, A.P. Linking community size structure and ecosystem functioning using metabolic theory. Philos. Trans. R. Soc. Lond. B 2012, 367, 2998–3007. [Google Scholar] [CrossRef]
- Hoellein, T.J.; Bruesewitz, D.A.; Richardson, D.C. Revisiting Odum (1956): A synthesis of aquatic ecosystem metabolism. Limnol. Oceanogr. 2013, 58, 2089–2100. [Google Scholar]
- Horn, H.S. Adaptive Geometry of Trees; Princeton University Press: Princeton, NJ, USA, 1971. [Google Scholar]
- Rüger, N.; Condit, R. Testing metabolic theory with models of tree growth that include light competition. Funct. Ecol. 2012, 26, 759–765. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Caldarelli, G.; Pietronero, L. Universal scaling relations in food webs. Nature 2003, 423, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Energy flows in complex ecological systems: A review. J. Syst. Sci. Complex. 2009, 22, 345–359. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L. Scaling behaviors of weighted food webs as energy transportation networks. J. Theor. Biol. 2010, 264, 760–770. [Google Scholar] [CrossRef] [PubMed]
- Warren, P.H. Variation in food-web structure: The determinants of connectance. Am. Nat. 1990, 136, 689–700. [Google Scholar] [CrossRef]
- Montoya, J.M.; Solé, R.V. Topological properties of food webs: From real data to community assembly models. Oikos 2003, 102, 614–622. [Google Scholar] [CrossRef]
- Brown, L.E.; Edwards, F.K.; Milner, A.M.; Woodward, G.; Ledger, M.E. Food web complexity and allometric scaling relationships in stream mesocosms: Implications for experimentation. J. Anim. Ecol. 2011, 80, 884–895. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.E.; Briand, F. Trophic links of community food web. Proc. Natl. Acad. Sci. USA 1984, 81, 4105–4109. [Google Scholar] [CrossRef] [PubMed]
- Martinez, N.D. Constant connectance in community food webs. Am. Nat. 1992, 139, 1208–1218. [Google Scholar]
- Pimm, S.L. Food Webs; Chapman and Hall: London, UK, 1982. [Google Scholar]
- Warren, P.H. Making connections in food webs. Trends Ecol. Evol. 1994, 9, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.M.; Dunne, J.A.; Woodward, G. Freshwater food webs: Towards a more fundamental understanding of biodiversity and community dynamics. Freshw. Biol. 2012, 57, 1329–1341. [Google Scholar] [CrossRef]
- McNab, B.K. Minimizing energy expenditure facilitates vertebrate persistence on oceanic islands. Ecol. Lett. 2002, 5, 693–704. [Google Scholar] [CrossRef]
- Maurer, B.A.; Brown, J.H.; Rusler, R.D. The micro and macro in body size evolution. Evolution 1992, 46, 939–953. [Google Scholar] [CrossRef]
- Marquet, P.A.; Taper, M.L. On size and area: Patterns of mammalian body size extremes across landmasses. Evol. Ecol. 1998, 12, 127–139. [Google Scholar] [CrossRef]
- Burness, G.P.; Diamond, J.; Flannery, T. Dinosaurs, dragons, and dwarfs: The evolution of maximal body size. Proc. Natl. Acad. Sci. USA 2001, 98, 14518–14523. [Google Scholar] [CrossRef] [PubMed]
- Okie, J.G.; Brown, J.H. Niches, body sizes, and the disassembly of mammal communities on the Sunda Shelf islands. Proc. Natl. Acad. Sci. USA 2009, 106, 19679–19684. [Google Scholar] [CrossRef] [PubMed]
- Millien, V.; Gonzalez, A. The maximal body mass-area relationship in island mammals. J. Biogeogr. 2011, 38, 2278–2285. [Google Scholar] [CrossRef]
- McNab, B.K. The influence of food habits on the energetics of eutherian mammals. Ecol. Monogr. 1986, 56, 1–19. [Google Scholar] [CrossRef]
- Glazier, D.S. Relationship between metabolic rate and energy expenditure for lactation in Peromyscus. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1985, 80, 587–590. [Google Scholar] [CrossRef]
- Mueller, P.; Diamond, J. Metabolic rate and environmental productivity: Well-provisioned animals evolved to run and idle fast. Proc. Natl. Acad. Sci. USA 2001, 98, 12550–12554. [Google Scholar] [CrossRef] [PubMed]
- DeLong, J.P.; Hanley, T.C.; Vasseur, D.A. Competition and the density dependence of metabolic rates. J. Anim. Ecol. 2013, 83, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Bennett, A.F.; Harvey, P. Active and resting metabolism in birds: Allometry, phylogeny and ecology. J. Zool. 1987, 213, 327–363. [Google Scholar] [CrossRef]
- Daan, S.; Masman, D.; Groenewold, A. Avian basal metabolic rates: Their association with body composition and energy expenditure in nature. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1990, 259, R333–R340. [Google Scholar]
- Reynolds, P.S.; Lee, R.M. Phylogenetic analysis of avian energetics: Passerines and nonpasserines do not differ. Am. Nat. 1996, 147, 735–759. [Google Scholar]
- Tieleman, B.I.; Williams, J.B. The adjustment of avian metabolic rates and water fluxes to desert environments. Physiol. Biochem. Zool. 2000, 73, 461–479. [Google Scholar] [CrossRef] [PubMed]
- McKechnie, A.E.; Wolf, B.O. The allometry of avian basal metabolic rate: Good predictions need good data. Physiol. Biochem. Zool. 2004, 77, 502–521. [Google Scholar] [CrossRef] [PubMed]
- White, C.R.; Phillips, N.F.; Seymour, R.S. The scaling and temperature dependence of vertebrate metabolism. Biol. Lett. 2006, 2, 125–127. [Google Scholar] [CrossRef] [PubMed]
- McNab, B.K. Ecological factors affect the level and scaling of avian BMR. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2009, 152, 22–45. [Google Scholar] [CrossRef] [PubMed]
- Lovegrove, B.G. The zoogeography of mammalian basal metabolic rate. Am. Nat. 2000, 156, 201–219. [Google Scholar] [CrossRef] [PubMed]
- White, C.R.; Seymour, R.S. Mammalian basal metabolic rate is proportional to body mass2/3. Proc. Natl. Acad. Sci. USA 2003, 100, 4046–4049. [Google Scholar] [CrossRef] [PubMed]
- McNab, B.K. An analysis of the factors that influence the level and scaling of mammalian BMR. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2008, 151, 5–28. [Google Scholar] [PubMed]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.L. A note on metabolic rate dependence on body size in plants and animals. J. Theor. Biol. 2003, 221, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Duncan, R.P.; Forsyth, D.M.; Hone, J. Testing the metabolic theory of ecology: Allometric scaling exponents in mammals. Ecology 2007, 88, 324–333. [Google Scholar] [CrossRef] [PubMed]
- White, C.R.; Blackburn, T.M.; Seymour, R.S. Phylogenetically informed analysis of the allometry of mammalian basal metabolic rate supports neither geometric nor quarter-power scaling. Evolution 2009, 63, 2658–2667. [Google Scholar] [CrossRef] [PubMed]
- Sieg, A.E.; O’Connor, M.P.; McNair, J.N.; Grant, B.W.; Agosta, S.J.; Dunham, A.E. Mammalian metabolic allometry: Do intraspecific variation, phylogeny, and regression models matter? Am. Nat. 2009, 174, 720–733. [Google Scholar] [CrossRef]
- Capellini, I.; Venditti, C.; Barton, R.A. Phylogeny and metabolic scaling in mammals. Ecology 2010, 91, 2783–2793. [Google Scholar] [CrossRef] [PubMed]
- Hayssen, V.; Lacy, R.C. Basal metabolic rates in mammals: Taxonomic differences in the allometry of BMR and body mass. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1985, 81, 741–754. [Google Scholar] [CrossRef]
- Packard, G.C.; Birchard, G.F. Traditional allometric analysis fails to provide a valid predictive model for mammalian metabolic rates. J. Exp. Biol. 2008, 211, 3581–3587. [Google Scholar] [CrossRef] [PubMed]
- White, C.R.; Seymour, R.S. Does basal metabolic rate contain a useful signal? Mammalian BMR allometry and correlations with a selection of physiological, ecological, and life-history variables. Physiol. Biochem. Zool. 2004, 77, 929–941. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.W.; Codron, D.; Werner, J.; Fritz, J.; Hummel, J.; Griebeler, E.M.; Clauss, M. Dichotomy of eutherian reproduction and metabolism. Oikos 2012, 121, 102–115. [Google Scholar] [CrossRef]
- Heldmaier, G. Seasonal Acclimatization of Energy Requirements in Mammals: Functional Significance of Body Weight Control, Hypothermia, Torpor and Hibernation. In Energy Transformations in Cells and Organisms; Wieser, W., Gnaiger, E., Eds.; Georg Thieme: Stuttgart, Germany, 1989; pp. 130–139. [Google Scholar]
- Degen, A.A.; Kam, M.; Khokhlova, I.S.; Krasnov, B.R.; Barraclough, T.G. Average daily metabolic rate of rodents: Habitat and dietary comparisons. Funct. Ecol. 1998, 12, 63–73. [Google Scholar] [CrossRef]
- Speakman, J.R. The cost of living: Field metabolic rates of small mammals. Adv. Ecol. Res. 1999, 30, 177–297. [Google Scholar]
- McNab, B.K. Standard energetics of phyllostomid bats: The inadequacies of phylogenetic-contrast analyses. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2003, 135, 357–368. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.F.; Lightfoot, E.N.; Porter, W.P. Basal metabolic rate of endotherms can be modeled using heat-transfer principles and physiological concepts: Reply to “Can the basal metabolic rate of endotherms be explained by biophysical modeling?”. Physiol. Biochem. Zool. 2011, 84, 111–114. [Google Scholar] [CrossRef]
- Neess, D.; Bek, S.; Bloksgaard, M.; Marcher, A.B.; Færgeman, N.J.; Mandrup, S. Delayed hepatic adaptation to weaning in ACBP−/− mice is caused by disruption of the epidermal barrier. Cell Rep. 2013, 5, 1403–1412. [Google Scholar] [CrossRef] [PubMed]
- Mortola, J.P. Thermographic analysis of body surface temperature of mammals. Zool. Sci. 2013, 30, 118–124. [Google Scholar] [CrossRef] [PubMed]
- Lovegrove, B.G. The influence of climate on the basal metabolic rate of small mammals: A slow-fast metabolic continuum. J. Comp. Physiol. B 2003, 173, 87–112. [Google Scholar] [PubMed]
- McNab, B.K. The Physiological Ecology of Vertebrates: A View from Energetics; Cornell University Press: Ithaca, NY, USA, 2002. [Google Scholar]
- McNab, B.K. Extreme Measures: The Ecological Energetics of Birds and Mammals; University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Bejan, A. The tree of convective heat streams: Its thermal insulation function and the predicted 3/4-power relation between body heat loss and body size. Int. J. Heat Mass Transf. 2001, 44, 699–704. [Google Scholar] [CrossRef]
- Killen, S.S.; Atkinson, D.; Glazier, D.S. The intraspecific scaling of metabolic rate with body mass in fishes depends on lifestyle and temperature. Ecol. Lett. 2010, 13, 184–193. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Ontogenetic body-mass scaling of resting metabolic rate covaries with species-specific metabolic level and body size in spiders and snakes. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2009, 153, 403–407. [Google Scholar] [CrossRef] [PubMed]
- McEdward, L.R. Morphometric and metabolic analysis of the growth and form of an echinopluteus. J. Exp. Mar. Biol. Ecol. 1984, 82, 259–287. [Google Scholar] [CrossRef]
- Seibel, B.A. On the depth and scale of metabolic rate variation: Scaling of oxygen consumption rates and enzymatic activity in the Class Cephalopoda (Mollusca). J. Exp. Biol. 2007, 210, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Shick, J.M.; Brown, W.I.; Dolliver, E.G.; Kayar, S.R. Oxygen uptake in sea anemones: Effects of expansion, contraction, and exposure to air and the limitations of diffusion. Physiol. Zool. 1979, 52, 50–62. [Google Scholar]
- Gray, I.E. Comparative study of the gill area of marine fishes. Biol. Bull. 1954, 107, 219–225. [Google Scholar] [CrossRef]
- Gray, I.E. A comparative study of the gill area of crabs. Biol. Bull. 1957, 112, 34–42. [Google Scholar] [CrossRef]
- Johnson, L.; Rees, C.J.C. Oxygen consumption and gill surface area in relation to habitat and lifestyle of four crab species. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1988, 89, 243–246. [Google Scholar] [CrossRef]
- Wegner, N.C.; Sepulveda, C.A.; Bull, K.B.; Graham, J.B. Gill morphometrics in relation to gas transfer and ram ventilation in high-energy demand teleosts: Scombrids and billfishes. J. Morphol. 2010, 271, 36–49. [Google Scholar] [PubMed]
- Post, J.R.; Lee, J.A. Metabolic ontogeny of teleost fishes. Can. J. Fish. Aquat. Sci. 1996, 53, 910–923. [Google Scholar] [CrossRef]
- Hughes, G.M.; Al-Kadhomiy, N.K. Changes in scaling of respiratory systems during the development of fishes. J. Mar. Biol. Assoc. UK 1988, 68, 489–498. [Google Scholar]
- Shield, J.W.; Bentley, P.J. Respiration of some urodele and anuran amphibia—I. In water, role of the skin and gills. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1973, 46, 17–28. [Google Scholar] [CrossRef]
- Bentley, P.J.; Shield, J.W. Respiration of some urodele and anuran amphibia—II. In air, role of the skin and lungs. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1973, 46, 29–38. [Google Scholar] [CrossRef]
- Heath, A.G. Respiratory responses to hypoxia by Ambystoma tigrinum larvae, paedomorphs, and metamorphosed adults. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1976, 55, 45–49. [Google Scholar] [CrossRef]
- Ultsch, G.R. Respiratory surface area as a factor controlling the standard rate of O2 consumption of aquatic salamanders. Respir. Physiol. 1976, 26, 357–369. [Google Scholar] [CrossRef] [PubMed]
- Brown, W.I.; Shick, J.M. Bimodal gas exchange and the regulation of oxygen uptake in holothurians. Biol. Bull. 1979, 156, 272–288. [Google Scholar] [CrossRef]
- Fenchel, T.; Finlay, B.J. Respiration rates in heterotrophic, free-living protozoa. Microb. Ecol. 1983, 9, 99–122. [Google Scholar] [CrossRef] [PubMed]
- Huete-Ortega, M.; Cermeño, P.; Calvo-Díaz, A.; Marañón, E. Isometric size-scaling of metabolic rate and the size abundance distribution of phytoplankton. Proc. R. Soc. Lond. B 2012, 279, 1815–1823. [Google Scholar]
- Prothero, J. Scaling of energy metabolism in unicellular organisms: A re-analysis. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1986, 83, 243–248. [Google Scholar] [CrossRef]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.L.; Chown, S.L. Size-and temperature-independence of minimum life-supporting metabolic rates. Funct. Ecol. 2006, 20, 83–96. [Google Scholar] [CrossRef]
- Kotze, J.; Bennett, N.C.; Scantlebury, M. The energetics of huddling in two species of mole-rat (Rodentia: Bathyergidae). Physiol. Behav. 2008, 93, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Merritt, J.F.; Zegers, D.A. Social thermoregulation in least shrews, Cryptotis parva. Mammalia 2014, 78, 11–22. [Google Scholar] [CrossRef]
- Hanson, P.C.; Bade, D.L.; Carpenter, S.R. Lake metabolism: Relationships with dissolved organic carbon and phosphorus. Limnol. Oceanogr. 2003, 48, 1112–1119. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar]
- Glazier, D.S. The 3/4-power law is not universal: Evolution of isometric, ontogenetic metabolic scaling in pelagic animals. BioScience 2006, 56, 325–332. [Google Scholar] [CrossRef]
- Riveros, A.J.; Enquist, B.J. Metabolic scaling in insects supports the predictions of the WBE model. J. Insect Physiol. 2011, 57, 688–693. [Google Scholar] [CrossRef] [PubMed]
- Chown, S.L.; Marais, E.; Terblanche, J.S.; Klok, C.J.; Lighton, J.R.B.; Blackburn, T.M. Scaling of insect metabolic rate is inconsistent with the nutrient supply network model. Funct. Ecol. 2007, 21, 282–290. [Google Scholar] [CrossRef]
- Barvitenko, N.N.; Aslam, M.; Filosa, J.; Matteucci, E.; Nikinmaa, M.; Pantaleo, A.; Saldanha, C.; Baskurt, O.K. Tissue oxygen demand in regulation of the behavior of the cells in the vasculature. Microcirculation 2013, 20, 484–501. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B.; Tjoelker, M.G.; Machado, J.L.; Oleksyn, J. Universal scaling of respiratory metabolism, size and nitrogen in plants. Nature 2006, 439, 457–461. [Google Scholar] [CrossRef] [PubMed]
- Hammond, S.T.; Niklas, K.J. Computer simulations support a core prediction of a contentious plant model. Am. J. Bot. 2012, 99, 508–516. [Google Scholar] [PubMed]
- Huang, Q.; Zhang, Y.; Liu, S.; Wang, W.; Luo, Y. Intraspecific scaling of the resting and maximum metabolic rates of the Crucian Carp (Carassius auratus). PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Holliday, M.A.; Potter, D.; Jarrah, A.; Bearg, S. The relation of metabolic rate to body weight and organ size. Pediatr. Res. 1967, 1, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Oikawa, S.; Itazawa, Y.; Gotoh, M. Ontogenetic change in the relationship between metabolic rate and body mass in a sea bream Pagrus major (Temminck & Schlegel). J. Fish Biol. 1991, 38, 483–496. [Google Scholar] [CrossRef]
- Kamler, E. Early Life History of Fish: An Energetics Approach; Chapman and Hall: London, UK, 1992. [Google Scholar]
- Gaitán-Espitia, J.D.; Bruning, A.; Mondaca, F.; Nespolo, R.F. Intraspecific variation in the metabolic scaling exponent in ectotherms: Testing the effect of latitudinal cline, ontogeny and transgenerational change in the land snail Cornu aspersum. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2013, 165, 169–177. [Google Scholar] [CrossRef]
- Peng, Y.; Niklas, K.J.; Reich, P.B.; Sun, S. Ontogenetic shift in the scaling of dark respiration with whole-plant mass in seven shrub species. Funct. Ecol. 2010, 24, 502–512. [Google Scholar]
- Glazier, D.S. Separating the respiration rates of embryos and brooding females of Daphnia magna: Implications for the cost of brooding and the allometry of metabolic rate. Limnol. Oceanogr. 1991, 36, 354–362. [Google Scholar]
- Simčič, T.; Brancelj, A. Estimation of the proportion of metabolically active mass in the amphipod Gammarus fossarum. Freshw. Biol. 2003, 48, 1093–1099. [Google Scholar] [CrossRef]
- Ultsch, G.R. The allometric relationship between metabolic rate and body size: Role of the skeleton. Am. Midl. Nat. 1974, 92, 500–504. [Google Scholar] [CrossRef]
- Reynolds, W.W.; Karlotski, W.J. The allometric relationship of skeleton weight to body weight in teleost fishes: A preliminary comparison with birds and mammals. Copeia 1977, 1977, 160–163. [Google Scholar]
- Calder, W.A. Size, Function and Life History; Harvard University Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Franz, R.; Hummel, J.; Kienzle, E.; Kölle, P.; Gunga, H.C.; Clauss, M. Allometry of visceral organs in living amniotes and its implications for sauropod dinosaurs. Proc. R. Soc. Lond. B 2009, 276, 1731–1736. [Google Scholar] [CrossRef]
- Lease, H.M.; Wolf, B.O. Lipid content of terrestrial arthropods in relation to body size, phylogeny, ontogeny and sex. Physiol. Entomol. 2011, 36, 29–38. [Google Scholar] [CrossRef]
- Finkel, Z.V.; Beardall, J.; Flynn, K.J.; Quigg, A.; Rees, T.A.V.; Raven, J.A. Phytoplankton in a changing world: Cell size and elemental stoichiometry. J. Plankton Res. 2010, 32, 119–137. [Google Scholar]
- Vleck, C.M.; Hoyt, D.F.; Vleck, D. Metabolism of avian embryos: Patterns in altricial and precocial birds. Physiol. Zool. 1979, 52, 363–377. [Google Scholar]
- Riisgärd, H.U. No foundation of a “3/4 power scaling law” for respiration in biology. Ecol. Lett. 1998, 1, 71–73. [Google Scholar] [CrossRef]
- Montes, L.; le Roy, N.; Perret, M.; de Buffrenil, V.; Castanet, J.; Cubo, J. Relationships between bone growth rate, body mass and resting metabolic rate in growing amniotes: A phylogenetic approach. Biol. J. Linn. Soc. 2007, 92, 63–76. [Google Scholar] [CrossRef]
- Rombough, P. The energetics of embryonic growth. Respir. Physiol. Neurobiol. 2011, 178, 22–29. [Google Scholar] [PubMed]
- Kempes, C.P.; Dutkiewicz, S.; Follows, M.J. Growth, metabolic partitioning, and the size of microorganisms. Proc Natl. Acad. Sci. USA 2012, 109, 495–500. [Google Scholar] [PubMed]
- Woodland, D.J.; Hall, B.K.; Calder, J. Gross bioenergetics of Blattella germanica. Physiol. Zool. 1968, 41, 424–431. [Google Scholar]
- Czarnołęski, M.; Kozłowski, J.; Dumiot, G.; Bonnet, J.C.; Mallard, J.; Dupont-Nivet, M. Scaling of metabolism in Helix aspersa snails: Changes through ontogeny and response to selection for increased size. J. Exp. Biol. 2008, 211, 391–400. [Google Scholar] [CrossRef] [PubMed]
- Snelling, E.P.; Seymour, R.S.; Matthews, P.G.D.; Runciman, S.; White, C.R. Scaling of resting and maximum hopping rate throughout the life cycle of the locust Locusta migratoria. J. Exp. Biol. 2011, 214, 3218–3224. [Google Scholar] [CrossRef] [PubMed]
- Niven, J.E.; Scharlemann, J.P. Do insect metabolic rates at rest and during flight scale with body mass? Biol. Lett. 2005, 1, 346–349. [Google Scholar]
- Clarke, A.; Pörtner, H.-O. Temperature, metabolic power and the evolution of endothermy. Biol. Rev. 2010, 85, 703–727. [Google Scholar] [PubMed]
- Dlugosz, E.M.; Chappell, M.A.; Meek, T.H.; Szafrańska, P.A.; Zub, K.; Konarzewski, M.; Jones, J.H.; Bicudo, J.E.P.W.; Nespolo, R.F.; Careau, V.; et al. Phylogenetic analysis of mammalian maximal oxygen consumption during exercise. J. Exp. Biol. 2013, 216, 4712–4721. [Google Scholar] [PubMed]
- Brett, J.R. The relation of size to rate of oxygen consumption and sustained swimming speed of sockeye salmon (Oncorhynchus nerka). J. Fish. Res. Board Can. 1965, 22, 1491–1501. [Google Scholar] [CrossRef]
- Gillooly, J.F.; Allen, A.P. Changes in body temperature influence the scaling of and aerobic scope in mammals. Biol. Lett. 2007, 3, 100–103. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Q.; Liu, S.; He, D.; Wei, G.; Luo, Y. Intraspecific mass scaling of metabolic rates in grass carp (Ctenopharyngodon idellus). J. Comp. Physiol. B 2014, 184, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Secor, S.M. Specific dynamic action: A review of the postprandial metabolic response. J. Comp. Physiol. B 2009, 179, 1–56. [Google Scholar] [CrossRef] [PubMed]
- Gilman, S.E.; Wong, J.W.; Chen, S. Oxygen consumption in relation to body size, wave exposure, and cirral beat behavior in the barnacle Balanus glandula. J. Crustac. Biol. 2013, 33, 317–322. [Google Scholar] [CrossRef]
- McClure, P.A.; Randolph, J.C. Relative allocation of energy to growth and development of homeothermy in the eastern wood rat (Neotoma floridana) and hispid cotton rat (Sigmodon hispidus). Ecol. Monogr. 1980, 50, 199–219. [Google Scholar] [CrossRef]
- Hulbert, A.J. Membrane fatty acids as pacemakers of animal metabolism. Lipids 2007, 42, 811–819. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, A.J. Metabolism and longevity: Is there a role for membrane fatty acids? Integr. Comp. Biol. 2010, 50, 808–817. [Google Scholar] [CrossRef]
- Brookes, P.S.; Buckingham, J.A.; Tenreiro, A.M.; Hulbert, A.J.; Brand, M.D. The proton permeability of the inner membrane of liver mitochondria from ectothermic and endothermic vertebrates and from obese rats: Correlations with standard metabolic rate and phospholipid fatty acid composition. Comp. Biochem. Physiol. B Biochem. Mol. Biol. 1998, 119, 325–334. [Google Scholar] [PubMed]
- Hulbert, A.J.; Else, P.L. Mechanisms underlying the cost of living in animals. Ann. Rev. Physiol. 2000, 62, 207–235. [Google Scholar] [CrossRef]
- Porter, R.K.; Hulbert, A.J.; Brand, M. Allometry of mitochondrial proton leak: Influence of membrane surface area and fatty acid composition. Am. J. Physiol. 1996, 271, R1550–R1560. [Google Scholar] [PubMed]
- Brand, M.D.; Turner, N.; Ocloo, A.; Else, P.L.; Hulbert, A.J. Proton conductance and fatty acyl composition of liver mitochondria correlates with body mass in birds. Biochem. J. 2003, 376, 741–748. [Google Scholar] [PubMed]
- Valencak, T.G.; Ruf, T. N-3 polyunsaturated fatty acids impair lifespan but have no role for metabolism. Aging Cell 2007, 6, 15–25. [Google Scholar] [CrossRef] [PubMed]
- Haggerty, C.; Hoggard, N.; Brown, D.S.; Clapham, J.C.; Speakman, J.R. Intra-specific variation in resting metabolic rate in MF1 mice is not associated with membrane lipid desaturation in the liver. Mech. Ageing Dev. 2008, 129, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Brzęk, P.; Bielawska, K.; Książek, A.; Konarzewski, M. Anatomic and molecular correlates of divergent selection for basal metabolic rate in laboratory mice. Physiol. Biochem. Zool. 2007, 80, 491–499. [Google Scholar] [CrossRef] [PubMed]
- Wone, B.W.; Donovan, E.R.; Cushman, J.C.; Hayes, J.P. Metabolic rates associated with membrane fatty acids in mice selected for increased maximal metabolic rate. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2013, 165, 70–78. [Google Scholar] [PubMed]
- Polymeropoulos, E.T.; Heldmaier, G.; Frappell, P.B.; McAllan, B.M.; Withers, K.W.; Klingenspor, M.; White, C.R.; Jastroch, M. Phylogenetic differences of mammalian basal metabolic rate are not explained by mitochondrial basal proton leak. Proc. R. Soc. Lond. B 2012, 279, 185–193. [Google Scholar]
- Rodríguez, E. Variation in Membrane Composition Associated with Body Mass and Body Temperature in Tropical and North American Bees. Dissertation, University of Ottawa, Ottawa, ON, Canada, 2013. [Google Scholar]
- Ruf, T.; Arnold, W. Effects of polyunsaturated fatty acids on hibernation and torpor: A review and hypothesis. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, R1044–R1052. [Google Scholar] [CrossRef] [PubMed]
- Arnold, W.; Ruf, T.; Frey-Roos, F.; Bruns, U. Diet-independent remodeling of cellular membranes precedes seasonally changing body temperature in a hibernator. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Geiser, F.; Klingenspor, M.; McAllan, B.M. A functional nexus between photoperiod acclimation, torpor expression and somatic fatty acid composition in a heterothermic mammal. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Gillooly, J.F.; Allen, A.P.; Savage, V.M.; Charnov, E.L.; West, G.B.; Brown, J.H. Response to Clarke and Fraser: Effects of temperature on metabolic rate. Funct. Ecol. 2006, 20, 400–404. [Google Scholar]
- Fell, D. Understanding the Control of Metabolism; Portland Press: London, UK, 1997. [Google Scholar]
- Hofmeyr, J.H.S.; Rohwer, J.M. Supply-demand analysis: A framework for exploring the regulatory design of metabolism. Meth. Enzymol. 2011, 500, 533–554. [Google Scholar]
- Morandini, P. Control limits for accumulation of plant metabolites: Brute force is no substitute for understanding. Plant Biotechnol. J. 2013, 11, 253–267. [Google Scholar] [PubMed]
- Clarke, A.; Fraser, K.P.P. Why does metabolism scale with temperature? Funct. Ecol. 2004, 18, 243–251. [Google Scholar]
- Koebmann, B.J.; Westerhoff, H.V.; Snoep, J.L.; Nilsson, D.; Jensen, P.R. The glycolytic flux in Escherichia coli is controlled by the demand for ATP. J. Bacteriol. 2002, 184, 3909–3916. [Google Scholar] [PubMed]
- Suarez, R.K.; Darveau, C.A.; Childress, J.J. Metabolic scaling: A many-splendoured thing. Comp. Biochem. Physiol. B Biochem. Mol. Biol. 2004, 139, 531–541. [Google Scholar] [CrossRef] [PubMed]
- Ebert, B.E.; Kurth, F.; Grund, M.; Blank, L.M.; Schmid, A. Response of Pseudomonas putida KT2440 to increased NADH and ATP demand. Appl. Environ. Microbiol. 2011, 77, 6597–6605. [Google Scholar] [CrossRef]
- Paul, M.J.; Foyer, C.H. Sink regulation of photosynthesis. J. Exp. Bot. 2001, 52, 1383–1400. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, S.B.; Richter, E.A.; Wojtaszewski, J.F.P. Role of AMPK in skeletal muscle metabolic regulation and adaptation in relation to exercise. J. Physiol. 2006, 574, 17–31. [Google Scholar] [CrossRef] [PubMed]
- Stitt, M.; Sulpice, R.; Keurentjes, J. Metabolic networks: How to identify key components in the regulation of metabolism and growth. Plant Physiol. 2010, 152, 428–444. [Google Scholar] [CrossRef] [PubMed]
- Broach, J.R. Nutritional control of growth and development in yeast. Genetics 2012, 192, 73–105. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Tu, B.P. Driving the cell cycle through metabolism. Annu. Rev. Cell Dev. Biol. 2012, 28, 59–87. [Google Scholar] [CrossRef] [PubMed]
- Ward, P.S.; Thompson, C.B. Signaling in control of cell growth and metabolism. Cold Spring Harb. Perspect. Biol. 2012, 4. [Google Scholar] [CrossRef]
- Smeekens, S.; Ma, J.; Hanson, J.; Rolland, F. Sugar signals and molecular networks controlling plant growth. Curr. Opin. Plant Biol. 2013, 13, 274–279. [Google Scholar]
- Banavar, J.R.; Damuth, J.; Maritan, A.; Rinaldo, A. Supply-demand balance and metabolic scaling. Proc. Natl. Acad. Sci. USA 2002, 99, 10506–10509. [Google Scholar] [CrossRef] [PubMed]
- Chaui-Berlinck, J.G.; Navas, C.A.; Monteiro, L.H.A.; Bicudo, J.E.P.W. Control of metabolic rate is a hidden variable in the allometric scaling of homeotherms. J. Exp. Biol. 2005, 208, 1709–1716. [Google Scholar] [CrossRef] [PubMed]
- Bradley, S.R.; Deavers, D.R. A re-examination of the relationship between thermal conductance and body weight in mammals. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1980, 65, 465–476. [Google Scholar] [CrossRef]
- Riek, A.; Geiser, F. Allometry of thermal variables in mammals: Consequences of body size and phylogeny. Biol. Rev. 2013, 88, 564–572. [Google Scholar] [CrossRef] [PubMed]
- Bronson, F.H. Mammalian Reproductive Biology; University of Chicago Press: Chicago, IL, USA, 1989. [Google Scholar]
- Ricklefs, R.E.; Wikelski, M. The physiology/life-history nexus. Trends Ecol. Evol. 2002, 17, 462–468. [Google Scholar] [CrossRef]
- Glazier, D.S. Trade-offs. In Resource Allocation Theory Applied to Farm Animals; Rauw, W.M., Ed.; CAB International: Wallingford, UK, 2009; pp. 44–60. [Google Scholar]
- Rowell, L.B. Ideas about control of skeletal and cardiac muscle blood flow (1876–2003): Cycles of revision and new vision. J. Appl. Physiol. 2004, 97, 384–392. [Google Scholar] [CrossRef] [PubMed]
- Segal, S.S. Regulation of blood flow in the microcirculation. Microcirculation 2005, 12, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Duncker, D.J.; Bache, R.J. Regulation of coronary blood flow during exercise. Physiol. Rev. 2008, 88, 1009–1086. [Google Scholar] [CrossRef] [PubMed]
- McArdle, W.D.; Katch, F.I.; Katch, V.L. Exercise Physiology: Nutrition, Energy, and Human Performance, 7th ed.; Lippincott Williams and Wilkins: Baltimore, MD, USA, 2010. [Google Scholar]
- Sarelius, I.; Pohl, U. Control of muscle blood flow during exercise: Local factors and integrative mechanisms. Acta Physiol. 2010, 199, 349–365. [Google Scholar] [CrossRef]
- González-Alonso, J. ATP as a mediator of erythrocyte-dependent regulation of skeletal muscle blood flow and oxygen delivery in humans. J. Physiol. 2012, 590, 5001–5013. [Google Scholar] [CrossRef]
- Golub, A.S.; Pittman, R.N. A paradigm shift for local blood flow regulation. J. Appl. Physiol. 2014, 116, 703–705. [Google Scholar] [CrossRef] [PubMed]
- Prior, B.M.; Yang, H.T.; Terjung, R.L. What makes vessels grow with exercise training? J. Appl. Physiol. 2004, 97, 1119–1128. [Google Scholar] [CrossRef]
- Fraisl, P.; Mazzone, M.; Schmidt, T.; Carmeliet, P. Regulation of angiogenesis by oxygen and metabolism. Dev. Cell 2009, 16, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Guarani, V.; Potente, M. SIRT1—A metabolic sensor that controls blood vessel growth. Curr. Opin. Pharmacol. 2010, 10, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Huber-Abel, F.A.; Gerber, M.; Hoppeler, H.; Baum, O. Exercise-induced angiogenesis correlates with the up-regulated expression of neuronal nitric oxide synthase (nNOS) in human skeletal muscle. Eur. J. Appl. Physiol. 2012, 112, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Djonov, V.; Andres, A.-C.; Ziemiecki, A. Vascular remodelling during the normal and malignant life cycle of the mammary gland. Microsc. Res. Tech. 2001, 52, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Andres, A.-C.; Djonov, V. The mammary gland vasculature revisited. J. Mammary Gland Biol. Neoplasia 2010, 15, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Newsholme, E.A.; Start, C. Regulation in Metabolism; Wiley: London, UK, 1973. [Google Scholar]
- Storey, K.B.; Heldmaier, G.; Rider, M.H. Mammalian Hibernation: Physiology, Cell Signaling, and Gene Controls on Metabolic Rate Depression. In Dormancy and Resistance in Harsh Environments; Lubzens, E., Cerda, J., Clark, M., Eds.; Springer: Berlin, Germany, 2010; pp. 227–252. [Google Scholar]
- Norris, D.O.; Carr, J.A. Vertebrate Endocrinology; Academic Press: London, UK, 2013. [Google Scholar]
- Heldmaier, G. Life on low flame in hibernation. Science 2011, 331, 866–867. [Google Scholar] [CrossRef] [PubMed]
- Heldmaier, G.; Ortmann, S.; Elvert, R. Natural hypometabolism during hibernation and daily torpor in mammals. Respir. Physiol. Neurobiol. 2004, 141, 317–329. [Google Scholar] [CrossRef] [PubMed]
- Heldmaier, G.; Ruf, T. Body temperature and metabolic rate during natural hypothermia in endotherms. J. Comp. Physiol. B 1992, 162, 696–706. [Google Scholar] [CrossRef] [PubMed]
- Tøien, Ø.; Blake, J.; Edgar, D.M.; Grahn, D.A.; Heller, H.C.; Barnes, B.M. Hibernation in black bears: Independence of metabolic suppression from body temperature. Science 2011, 331, 906–909. [Google Scholar] [CrossRef] [PubMed]
- Grimpo, K.; Legler, K.; Heldmaier, G.; Exner, C. That’s hot: Golden spiny mice display torpor even at high ambient temperatures. J. Comp. Physiol. B 2013, 183, 567–581. [Google Scholar] [CrossRef] [PubMed]
- Singer, D.; Bach, F.; Bretschneider, H.J.; Kuhn, H.-J. Metabolic Size Allometry and the Limits to Beneficial Metabolic Reduction: Hypothesis of a Uniform Specific Minimal Metabolic Rate. In Surviving Hypoxia; Hochachka, P.W., Lutz, P.L., Sick, T., Rosenthal, M., van den Thillart, G., Eds.; CRC Press: Boca Raton, FL, USA, 1993; pp. 447–458. [Google Scholar]
- Tomasi, T.E. Utilization rates of thyroid hormones in mammals. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1991, 100, 503–516. [Google Scholar] [CrossRef]
- Hulbert, A.J. Thyroid hormones and their effects: A new perspective. Biol. Rev. 2000, 75, 519–631. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, A.J.; Else, P.L. Basal metabolic rate: History, composition, regulation, and usefulness. Physiol. Biochem. Zool. 2004, 77, 869–876. [Google Scholar] [CrossRef] [PubMed]
- Stuart, J.A.; Page, M.M. Plasma IGF-1 is negatively correlated with body mass in a comparison of 36 mammalian species. Mech. Ageing Dev. 2010, 131, 591–598. [Google Scholar] [CrossRef] [PubMed]
- Swanson, E.M.; Dantzer, B. Insulin-like growth factor-1 is associated with life-history variation across Mammalia. Proc. R. Soc. B 2014, 281. [Google Scholar] [CrossRef] [PubMed]
- Moyes, C.D.; LeMoine, C.M. Control of muscle bioenergetic gene expression: Implications for allometric scaling relationships of glycolytic and oxidative enzymes. J. Exp. Biol. 2005, 208, 1601–1610. [Google Scholar] [CrossRef] [PubMed]
- Yeoh, A.J.; Davis, K.; Vela-Mendoza, A.V.; Hartlaub, B.A.; Gillen, C.M. Effect of body size on expression of Manduca sexta midgut genes. J. Exp. Zool. A Ecol. Genet. Physiol. 2012, 317, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Greenlee, K.J.; Montooth, K.L.; Helm, B.R. Predicting performance and plasticity in the development of respiratory structures and metabolic systems. Integr. Comp. Biol. 2014. [Google Scholar] [CrossRef]
- Glazier, D.S. Resource Allocation Patterns. In Resource Allocation Theory Applied to Farm Animals; Rauw, W.M., Ed.; CAB International: Wallingford, UK, 2009; pp. 22–43. [Google Scholar]
- Allen, A.P.; Gillooly, J.F. The mechanistic basis of the metabolic theory of ecology. Oikos 2007, 116, 1073–1077. [Google Scholar] [CrossRef]
- Carey, N.; Sigwart, J.D.; Richards, J.G. Economies of scaling: More evidence that allometry of metabolism is linked to activity, metabolic rate and habitat. J. Exp. Mar. Biol. Ecol. 2013, 439, 7–14. [Google Scholar] [CrossRef]
- Duerr, F.G. Changes in the size-metabolic rate relationship of Lymnaea stagnalis appressa Say produced by digenetic trematode parasitism. Comp. Biochem. Physiol. 1967, 20, 391–398. [Google Scholar] [CrossRef] [PubMed]
- Roy, A. Analyse des facteurs du taux de metabolisme chez la limace Arion circumscriptus. Rev. Can. Biol. 1969, 28, 33–43. [Google Scholar] [PubMed]
- Xie, X.; Sun, R. The bioenergetics of the southern catfish (Silurus meridionalis Chen). I. Resting metabolic rate as a function of body weight and temperature. Physiol. Zool. 1990, 63, 1181–1195. [Google Scholar]
- Ohlberger, J.; Staaks, G.; Holker, F. Effects of temperature, swimming speed and body mass on standard and active metabolic rate in vendace (Coregonus albula). J. Comp. Physiol. B 2007, 177, 905–916. [Google Scholar] [CrossRef] [PubMed]
- Hoque, A.T.M.R.; Sharma, S.; Suwa, R.; Mori, S.; Hagihara, A. Seasonal variation in the size-dependent respiration of mangroves Kandelia obovata. Mar. Ecol. Prog. Ser. 2010, 404, 31–37. [Google Scholar] [CrossRef]
- Weldon, C.W.; Daniels, S.R.; Clusella-Trullas, S.; Chown, S.L. Metabolic and water loss rates of two cryptic species in the African velvet worm genus Opisthopatus (Onychophora). J. Comp. Physiol. B 2012, 183, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Vaca, H.F.; White, C.R. Environmental modulation of metabolic allometry in ornate rainbowfish Rhadinocentrus ornatus. Biol. Lett. 2010, 6, 136–138. [Google Scholar] [CrossRef] [PubMed]
- Farmer, G.J.; Beamish, F.W.H. Oxygen consumption of Tilapia nilotica in relation to swimming speed and salinity. J. Fish. Board Can. 1969, 26, 2807–2821. [Google Scholar] [CrossRef]
- Finn, R.N.; Ronnestad, I.; van der Meeren, T.; Fyhn, H.J. Fuel and metabolic scaling during the early life stages of Atlantic cod Gadus morhua. Mar. Ecol. Prog. Ser. 2002, 243, 217–234. [Google Scholar] [CrossRef]
- Chen, X.; Li, B.-L. Testing the allometric scaling relationships with seedlings of two tree species. Acta Oecol. 2003, 24, 125–129. [Google Scholar] [CrossRef]
- Navarro, E.; Ortega, M.M.; Iglesias, J.I.P. An analysis of variables affecting oxygen consumption in Actinia equina L. (Anthozoa) from two shore positions. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1987, 86, 233–240. [Google Scholar] [CrossRef]
- McFeeters, B.J.; Xenopoulos, M.A.; Spooner, D.E.; Wagner, N.D.; Frost, P.C. Intraspecific mass-scaling of field metabolic rates of a freshwater crayfish varies with stream land cover. Ecosphere 2011, 2. [Google Scholar] [CrossRef]
- Mayr, E. This Is Biology: The Science of the Living World; Harvard University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Witting, L. The body mass allometries as evolutionarily determined by the foraging of mobile organisms. J. Theor. Biol. 1995, 177, 129–137. [Google Scholar] [CrossRef]
- Kozłowski, J.; Weiner, J. Interspecific allometries are by-products of body size optimization. Am. Nat. 1997, 149, 352–380. [Google Scholar] [CrossRef]
- Law, R. Optimal life histories under age-specific predation. Am. Nat. 1979, 114, 399–417. [Google Scholar]
- Reznick, D.A.; Bryga, H.; Endler, J.A. Experimentally induced life-history evolution in a natural population. Nature 1990, 346, 357–359. [Google Scholar] [CrossRef]
- Charlesworth, B. Evolution in Age-Structured Populations, 2nd ed.; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Ivleva, I.V. The dependence of crustacean respiration rate on body mass and habitat temperature. Int. Rev. Gesamten Hydrobiol. 1980, 65, 1–47. [Google Scholar] [CrossRef]
- Hirst, A.G. Intraspecific scaling of mass to length in pelagic animals: Ontogenetic shape change and its implications. Limnol. Oceanogr. 2012, 57, 1579–1590. [Google Scholar]
- Pawar, S.; Dell, A.I.; Savage, V.M. Dimensionality of consumer search space drives trophic interaction strengths. Nature 2012, 486, 485–489. [Google Scholar] [PubMed]
- McCauley, E.; Murdoch, W.W.; Nisbet, R.M.; Gurney, W.S.C. The physiological ecology of Daphnia: Development of a model of growth and reproduction. Ecology 1990, 71, 703–715. [Google Scholar] [CrossRef]
- Bradley, M.C.; Perrin, N.; Calow, P. Energy allocation in the cladoceran Daphnia magna Straus, under starvation and refeeding. Oecologia 1991, 86, 414–418. [Google Scholar] [CrossRef]
- Nogueira, A.J.A.; Baird, D.J.; Soares, A.M.V.M. Testing physiologically-based resource allocation rules in laboratory experiments with Daphnia magna Straus. Ann. Limnol. 2004, 40, 257–267. [Google Scholar] [CrossRef]
- Glazier, D.S.; Calow, P. Energy allocation rules in Daphnia magna: Clonal and age differences in the effects of food limitation. Oecologia 1992, 90, 540–549. [Google Scholar] [CrossRef]
- Lika, K.; Kooijman, S.A. The comparative topology of energy allocation in budget models. J. Sea Res. 2011, 66, 381–391. [Google Scholar]
- McMahon, T.A. Size and shape in biology. Science 1973, 179, 1201–1204. [Google Scholar] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. Growth models based on first principles or phenomenology? Funct. Ecol. 2004, 18, 188–196. [Google Scholar]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Brown, J.H.; Sibly, R.M. The Metabolic Theory of Ecology and its Central Equation. In Metabolic Ecology: A Scaling Approach; Sibly, R.M., Brown, J.H., Kodric-Brown, A., Eds.; Wiley-Blackwell: Chichester, UK, 2012; pp. 21–33. [Google Scholar]
- Bokma, F. Evidence against universal metabolic allometry. Funct. Ecol. 2004, 18, 184–187. [Google Scholar] [CrossRef]
- White, C.R.; Cassey, P.; Blackburn, T.M. Allometric exponents do not support a universal metabolic allometry. Ecology 2007, 88, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Parker, G.A.; Maynard Smith, J. Optimality theory in evolutionary biology. Nature 1990, 348, 27–33. [Google Scholar] [CrossRef]
- Orzack, S.H.; Sober, E. Optimality models and the test of adaptationism. Am. Nat. 1994, 143, 361–380. [Google Scholar] [CrossRef]
- De Vos, M.G.; Poelwijk, F.J.; Tans, S.J. Optimality in evolution: New insights from synthetic biology. Curr. Opin. Biotechnol. 2013, 24, 797–802. [Google Scholar] [CrossRef] [PubMed]
- Hartikainen, H.; Humphries, S.; Okamura, B. Form and metabolic scaling in colonial animals. J. Exp. Biol. 2014, 217, 779–786. [Google Scholar] [CrossRef]
- Lighton, J.R.; Fielden, L.J. Mass scaling of standard metabolism in ticks: A valid case of low metabolic rates in sit-and-wait strategists. Physiol. Zool. 1995, 68, 43–62. [Google Scholar]
- Heusner, A.A. Size and power in mammals. J. Exp. Biol. 1991, 160, 25–54. [Google Scholar] [PubMed]
- Niklas, K.J. Plant allometry: Is there a grand unifying theory? Biol. Rev. 2004, 79, 871–889. [Google Scholar]
- Kaitaniemi, P. How to derive biological information from the value of the normalization constant in allometric equations. PLoS ONE 2008, 3. [Google Scholar] [CrossRef] [PubMed]
- Kiørboe, T.; Hirst, A.G. Shifts in mass scaling of respiration, feeding, and growth rates across life-form transitions in marine pelagic organisms. Am. Nat. 2014, 183, E118–E130. [Google Scholar] [CrossRef] [PubMed]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.L.; Chown, S.L.; Reich, P.B.; Gavrilov, V.M. Mean mass-specific metabolic rates are strikingly similar across life’s major domains: Evidence for life’s metabolic optimum. Proc. Natl. Acad. Sci. USA 2008, 105, 16994–16999. [Google Scholar] [PubMed]
- Robinson, W.R.; Peters, R.H.; Zimmermann, J. The effects of body size and temperature on metabolic rate of organisms. Can. J. Zool. 1983, 61, 281–288. [Google Scholar]
- Childress, J.J. Are there physiological and biochemical adaptations of metabolism in deep-sea animals? Trends Ecol. Evol. 1995, 10, 30–36. [Google Scholar]
- Reinhold, K. Energetically costly behaviour and the evolution of resting metabolic rate in insects. Funct. Ecol. 1999, 13, 217–224. [Google Scholar]
- Seibel, B.A.; Drazen, J.C. The rate of metabolism in marine animals: Environmental constraints, ecological demands and energetic opportunities. Philos. Trans. R. Soc. Lond. B 2007, 362, 2061–2078. [Google Scholar]
- Else, P.L.; Hulbert, A.J. Comparison of the “mammal machine” and the “reptile machine”: Energy production. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1981, 240, R3–R9. [Google Scholar]
- Else, P.L.; Hulbert, A.J. An allometric comparison of the mitochondria of mammalian and reptilian tissues: The implications for the evolution of endothermy. J. Comp. Physiol. B 1985, 156, 3–11. [Google Scholar] [PubMed]
- Wiersma, P.; Nowak, B.; Williams, J.B. Small organ size contributes to the slow pace of life in tropical birds. J. Exp. Biol. 2012, 215, 1662–1669. [Google Scholar] [CrossRef]
- Drazen, J.C. Depth related trends in proximate composition of demersal fishes in the eastern North Pacific. Deep-Sea Res. 2007, 54, 203–219. [Google Scholar] [CrossRef]
- Drazen, J.C.; Seibel, B.A. Depth-related trends in metabolism of benthic and benthopelagic deep-sea fishes. Limnol. Oceanogr. 2007, 52, 2306–2316. [Google Scholar] [CrossRef]
- McClain, C.R.; Allen, A.P.; Tittensor, D.P.; Rex, M.A. Energetics of life on the deep seafloor. Proc. Natl. Acad. Sci. USA 2012, 109, 15366–15371. [Google Scholar] [CrossRef] [PubMed]
- Jetz, W.; Freckleton, R.P.; McKechnie, A.E. Environment, migratory tendency, phylogeny and basal metabolic rate in birds. PLoS ONE 2008, 3. [Google Scholar] [CrossRef] [PubMed]
- Rosa, R.; Trueblood, L.; Seibel, B.A. Ecophysiological influence on scaling of aerobic and anaerobic metabolism of pelagic gonatid squids. Physiol. Biochem. Zool. 2009, 82, 419–429. [Google Scholar] [PubMed]
- Gavrilov, V.M. Energy expenditures for flight, aerodynamic quality, and colonization of forest habitats by birds. Biol. Bull. (Russ.) 2011, 38, 779–788. [Google Scholar]
- Gavrilov, V.M. Origin and development of homoiothermy: A case study of avian energetics. Adv. Biosci. Biotechnol. 2013, 4, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Kölsch, G.; Krause, A. Oxygen consumption of the aquatic leaf beetles Macroplea mutica and Macroplea appendiculata is low and not influenced by salinity. Physiol. Entomol. 2011, 36, 111–119. [Google Scholar] [CrossRef]
- Vignes, F.; Fedele, M.; Pinna, M.; Mancinelli, G.; Basset, A. Variability of Lekanesphaera monodi metabolic rates with habitat trophic status. Acta Oecol. 2012, 41, 58–64. [Google Scholar] [CrossRef]
- Feng, P.; Zhao, H.; Lu, X. Evolution of mitochondrial DNA and its relation to basal metabolic rate. Mitochondrial DNA 2014. [Google Scholar] [CrossRef]
- Gillooly, J.F.; Brown, J.H.; West, G.B.; Savage, V.M.; Charnov, E.L. Effects of size and temperature on metabolic rate. Science 2001, 293, 2248–2251. [Google Scholar] [PubMed]
- Box, G.E. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar]
- Darwin, C. On the Origin of Species by Means of Natural Selection; Murray: London, UK, 1859. [Google Scholar]
- Gilbert, S.F. Mechanisms for the environmental regulation of gene expression: Ecological aspects of animal development. J. Biosci. 2005, 30, 65–74. [Google Scholar] [PubMed]
- Evans, M.R.; Grimm, V.; Johst, K.; Knuuttila, T.; de Langhe, R.; Lessells, C.M.; Merz, M.; O’Malley, M.A.; Orzack, S.H.; Weisberg, M.; et al. Do simple models lead to generality in ecology? Trends Ecol. Evol. 2013, 28, 578–583. [Google Scholar]
- West, G.B.; Brown, J.H. Life’s universal scaling laws. Phys. Today 2004, 57, 36–43. [Google Scholar]
- Enquist, B.J.; Stark, S.C. Follow Thompson’s map to turn biology from a science into a Science. Nature 2007, 446. [Google Scholar] [CrossRef]
- Haeckel, E. Generelle Morphologie der Organismen: Allgemeine Grundzüge der Organischen Formen-Wissenschaft, mechanisch begründet durch die von Charles Darwin reformirte Descendenz-Theorie; Georg Reimer: Berlin, Germany, 1866. [Google Scholar]
- Gould, S.J. Ontogeny and Phylogeny; Harvard University Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Frankino, W.A.; Zwaan, B.J.; Stern, D.L.; Brakefield, P.M. Natural selection and developmental constraints in the evolution of allometries. Science 2005, 307, 718–720. [Google Scholar] [CrossRef] [PubMed]
- Ketola, T.; Kotiaho, J.S. Inbreeding depression in the effects of body mass on energy use. Biol. J. Linn. Soc. 2012, 105, 309–317. [Google Scholar] [CrossRef]
- Ketola, T.; Kotiaho, J.S.; Mazzi, D.; Puurtinen, M. Inbreeding depression in intraspecific metabolic scaling. Anim. Biol. 2013, 63, 357–367. [Google Scholar]
- Voje, K.L.; Hansen, T.F.; Egset, C.K.; Bolstad, G.H.; Pélabon, C. Allometric constraints and the evolution of allometry. Evolution 2013, 68, 866–885. [Google Scholar] [PubMed]
- Needham, J. On the dissociability of the fundamental processes in ontogenesis. Biol. Rev. 1933, 8, 180–223. [Google Scholar] [CrossRef]
- Smith, B.H. Life history and the evolution of human maturation. Evol. Anthropol. Issues News Rev. 1992, 1, 134–142. [Google Scholar] [CrossRef]
- Glazier, D.S.; Newcomer, S.D. Allochrony: A new way of analysing life histories, as illustrated with mammals. Evol. Ecol. Res. 1999, 1, 333–346. [Google Scholar]
- Gerstner, G.E.; Gerstein, J.B. Chewing rate allometry among mammals. J. Mammal. 2008, 89, 1020–1030. [Google Scholar] [CrossRef]
- Clark, T.D.; Farrell, A.P. Effects of body mass on physiological and anatomical parameters of mature salmon: Evidence against a universal heart rate scaling exponent. J. Exp. Biol. 2011, 214, 887–893. [Google Scholar]
- Clauss, M.; Dittmann, M.T.; Müller, D.W.H.; Zerbe, P.; Codron, D. Low scaling of a life history variable: Analyzing eutherian gestation periods with and without phylogeny-informed statistics. Mamm. Biol. 2013, 79, 9–16. [Google Scholar]
- Dillon, M.E.; Frazier, M.R. Thermodynamics constrains allometric scaling of optimal development time in insects. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Lemaître, J.F.; Müller, D.W.; Clauss, M. A test of the metabolic theory of ecology with two longevity data sets reveals no common cause of scaling in biological times. Mamm. Rev. 2014. [Google Scholar] [CrossRef]
- Laland, K.N.; Sterelny, K.; Odling-Smee, J.; Hoppitt, W.; Uller, T. Cause and effect in biology revisited: Is Mayr’s proximate-ultimate dichotomy still useful? Science 2011, 334, 1512–1516. [Google Scholar]
- Bauman, D.E.; Eisemann, J.H.; Currie, W.B. Hormonal effects on partitioning of nutrients for tissue growth: Role of growth hormone and prolactin. Fed. Proc. 1982, 41, 2538–2544. [Google Scholar] [PubMed]
- Leggatt, R.A.; Raven, P.A.; Mommsen, T.P.; Sakhrani, D.; Higgs, D.; Devlin, R.H. Growth hormone transgenesis influences carbohydrate, lipid and protein metabolism capacity for energy production in coho salmon (Oncorhynchus kisutch). Comp. Biochem. Physiol. B Biochem. Mol. Biol. 2009, 154, 121–133. [Google Scholar] [PubMed]
- Møller, N.; Jørgensen, J.O.L. Effects of growth hormone on glucose, lipid, and protein metabolism in human subjects. Endocr. Rev. 2009, 30, 152–177. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, D.; Sibly, R.M. Why are organisms usually bigger in colder environments? Making sense of a life history puzzle. Trends Ecol. Evol. 1997, 12, 235–239. [Google Scholar] [CrossRef] [PubMed]
- Somero, G.N.; Childress, J.J. A violation of the metabolism-size scaling paradigm: Activities of glycolytic enzymes in muscle increase in larger-size fish. Physiol. Zool. 1980, 53, 322–337. [Google Scholar]
- Emmett, B.; Hochachka, P.W. Scaling of oxidative and glycolytic enzymes in mammals. Respir. Physiol. 1981, 45, 261–272. [Google Scholar] [PubMed]
- Hochachka, P.W.; Emmett, B.; Suarez, R.K. Limits and constraints in the scaling of oxidative and glycolytic enzymes in homeotherms. Can. J. Zool. 1988, 66, 1128–1138. [Google Scholar]
- Childress, J.J.; Somero, G.N. Metabolic scaling: A new perspective based on scaling of glycolytic enzyme activities. Am. Zool. 1990, 30, 161–173. [Google Scholar]
- Goolish, E.M. Aerobic and anaerobic scaling in fish. Biol. Rev. 1991, 66, 33–56. [Google Scholar] [CrossRef]
- Goolish, E.M. The Metabolic Consequences of Body Size. In Biochemistry and Molecular Biology of Fishes, Volume 4 Metabolic Biochemistry; Hochachka, P.W., Mommsen, T.P., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; pp. 335–366. [Google Scholar]
- Thuesen, E.V.; Childress, J.J. Oxygen consumption rates and metabolic enzyme activities of oceanic California medusae in relation to body size and habitat depth. Biol. Bull. 1994, 187, 84–98. [Google Scholar] [CrossRef]
- Baldwin, J.; Gupta, A.; Iglesias, X. Scaling of anaerobic energy metabolism during tail flipping behaviour in the freshwater crayfish, Cherax destructor. Mar. Freshw. Res. 1999, 50, 183–187. [Google Scholar] [CrossRef]
- Burness, G.P.; Leary, S.C.; Hochachka, P.W.; Moyes, C.D. Allometric scaling of RNA, DNA, and enzyme levels: An intraspecific study. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1999, 277, R1164–R1170. [Google Scholar]
- Thuesen, E.V.; McCullough, K.D.; Childress, J.J. Metabolic enzyme activities in swimming muscle of medusae: Is the scaling of glycolytic activity related to oxygen availability? J. Mar. Biol. Assoc. UK 2005, 85, 603–611. [Google Scholar] [CrossRef]
- Jessen, G.L.; Quinones, R.A.; González, R.R. Aerobic and anaerobic enzymatic activity and allometric scaling of the deep benthic polychaete Hyalinoecia artifex (Polychaeta: Onuphidae). J. Mar. Biol. Assoc. UK 2009, 89, 1171–1175. [Google Scholar] [CrossRef]
- Moyes, C.D.; Genge, C.E. Scaling of muscle metabolic enzymes: An historical perspective. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2010, 156, 344–350. [Google Scholar]
- Kirkton, S.D.; Nyberg, E.T.; Fox, K.M. Ontogenetic changes in citrate synthase and lactate dehydrogenase activity in the jumping muscle of the American locust (Schistocerca americana). Comp. Biochem. Physiol. B Biochem. Mol. Biol. 2011, 160, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Zamer, W.E.; van Dorp, W. Body size and performance of pathways of carbohydrate metabolism in the sea anemone Metridium senile L. Physiol. Zool. 1994, 67, 925–943. [Google Scholar]
- Simčič, T.; Pajk, F.; Vrezec, A.; Brancelj, A. Size scaling of whole-body metabolic activity in the noble crayfish (Astacus astacus) estimated from measurements on a single leg. Freshw. Biol. 2012, 57, 39–48. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, W.; Zhang, Y.; Huang, Q. Effect of body size on organ-specific mitochondrial respiration rate of the largemouth bronze gudgeon. Fish Physiol. Biochem. 2013, 39, 513–521. [Google Scholar] [PubMed]
- Baldwin, J.; Seymour, R.S.; Webb, G.J.W. Scaling of anaerobic metabolism during exercise in the estuarine crocodile (Crocodylus porosus). Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1995, 112, 285–293. [Google Scholar] [CrossRef]
- Franz, R.; Soliva, C.R.; Kreuzer, M.; Steuer, P.; Hummel, J.; Clauss, M. Methane production in relation to body mass of ruminants and equids. Evol. Ecol. Res. 2010, 12, 727–738. [Google Scholar]
- Clauss, M.; Hummel, J.; Streich, W.J.; Sudekum, K. Mammalian metabolic rate scaling to 2/3 or 3/4 depends on the presence of gut contents. Evol. Ecol. Res. 2008, 10, 153–154. [Google Scholar]
- Waterlow, J.C.; Garlick, P.J.; Millward, D.J. Protein Turnover in Mammalian Tissues and in the Whole Body; Elsevier/North-Holland Biomedical Press: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Hellerstein, M.K. In vivo measurement of fluxes through metabolic pathways: The missing link in functional genomics and pharmaceutical research. Annu. Rev. Nutr. 2003, 23, 379–402. [Google Scholar] [CrossRef] [PubMed]
- Sauer, U. High-throughput phenomics: Experimental methods for mapping fluxomes. Curr. Opin. Biotechnol. 2004, 15, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Doherty, M.K.; Beynon, R.J. Protein turnover on the scale of the proteome. Expert Rev. Proteomics 2006, 3, 97–110. [Google Scholar] [PubMed]
- Kohlstedt, M.; Becker, J.; Wittmann, C. Metabolic fluxes and beyond—Systems biology understanding and engineering of microbial metabolism. Appl. Microbiol. Biotechnol. 2010, 88, 1065–1075. [Google Scholar] [CrossRef] [PubMed]
- Rolfe, D.F.S.; Brown, G.C. Cellular energy utilization and molecular origin of standard metabolic rate in mammals. Physiol. Rev. 1997, 77, 731–758. [Google Scholar] [PubMed]
- Chen, Q.; Vazquez, E.J.; Moghaddas, S.; Hoppel, C.L.; Lesnefsky, E.J. Production of reactive oxygen species by mitochondria central role of complex III. J. Biol. Chem. 2003, 278, 36027–36031. [Google Scholar] [CrossRef] [PubMed]
- Balaban, R.S.; Nemoto, S.; Finkel, T. Mitochondria, oxidants, and aging. Cell 2005, 120, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Navarro, A.; Boveris, A. The mitochondrial energy transduction system and the aging process. Am. J. Physiol. Cell Physiol. 2007, 292, C670–C686. [Google Scholar] [CrossRef] [PubMed]
- Breitenbach, M.; Rinnerthaler, M.; Hartl, J.; Stincone, A.; Vowinckel, J.; Breitenbach-Koller, H.; Ralser, M. Mitochondria in ageing: There is metabolism beyond the ROS. FEMS Yeast Res. 2014, 14, 198–212. [Google Scholar] [CrossRef]
- Selman, C.; Blount, J.D.; Nussey, D.H.; Speakman, J.R. Oxidative damage, ageing, and life-history evolution: Where now? Trends Ecol. Evol. 2012, 27, 570–577. [Google Scholar]
- Bratic, A.; Larsson, N.G. The role of mitochondria in aging. J. Clin. Investig. 2013, 123, 951–957. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, A.G.; van Brocklyn, J.; Wortman, M.; Williams, J.B. Cellular metabolic rate is influenced by life-history traits in tropical and temperate birds. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.J.; Holford, N.H.G. Mechanism-based concepts of size and maturity in pharmokinetics. Ann. Rev. Pharmocol. Toxicol. 2008, 48, 303–332. [Google Scholar] [CrossRef]
- Hu, T.-M.; Hayton, W.L. Allometric scaling of xenobiotic clearance: Uncertainty versus universality. AAPS Pharm. Sci. 2001, 3. [Google Scholar] [CrossRef]
- McLeay, S.C.; Morrish, G.A.; Kirkpatrick, C.M.; Green, B. The relationship between drug clearance and body size. Clin. Pharmacokinet. 2012, 51, 319–330. [Google Scholar] [PubMed]
- Holford, N.; Heo, Y.A.; Anderson, B. A pharmacokinetic standard for babies and adults. J. Pharm. Sci. 2013, 102, 2941–2952. [Google Scholar] [PubMed]
- Mahmood, I. Prediction of drug clearance in children 3 months and younger: An allometric approach. Drug Metab. Drug Interact. 2010, 25, 25–34. [Google Scholar] [CrossRef]
- Mahmood, I. Theoretical versus empirical allometry: Facts behind theories and application to pharmacokinetics. J. Pharm. Sci. 2010, 99, 2927–2933. [Google Scholar] [PubMed]
- Wang, C.; Peeters, M.Y.M.; Allegaert, K.; Blussé van Oud-Alblas, H.J.; Krekels, E.H.J.; Tibboel, D.; Danhof, M.; Knibbe, C.A.J. A bodyweight-dependent allometric exponent for scaling clearance across the human life-span. Pharm. Res. 2012, 29, 1570–1581. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Allegaert, K.; Peeters, M.Y.M.; Tibboel, D.; Danhof, M.; Knibbe, C.A. The allometric exponent for scaling clearance varies with age: A study on seven propofol datasets ranging from preterm neonates to adults. Br. J. Clin. Pharm. 2014, 77, 149–159. [Google Scholar]
- Warton, D.I.; Wright, I.J.; Falster, D.S.; Westoby, M. Bivariate line-fitting methods for allometry. Biol. Rev. 2006, 81, 259–291. [Google Scholar] [CrossRef] [PubMed]
- Hui, C.; Terblanche, T.S.; Chown, S.L.; McGeoch, M.A. Parameter landscapes unveil the bias in allometric estimation. Meth. Ecol. Evol. 2010, 1, 69–74. [Google Scholar]
- Packard, G.C.; Birchard, G.F.; Boardman, T.J. Fitting statistical models in bivariate allometry. Biol. Rev. 2011, 86, 549–563. [Google Scholar] [CrossRef] [PubMed]
- White, C.R. Allometric estimation of metabolic rates in animals. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2011, 158, 346–357. [Google Scholar] [CrossRef]
- White, E.P.; Xiao, X.; Isaac, N.J.B.; Sibly, R.M. Methodological Tools. In Metabolic Ecology: A Scaling Approach; Sibly, R.M., Brown, J.H., Kodric-Brown, A., Eds.; Wiley-Blackwell: Chichester, UK, 2012; pp. 9–20. [Google Scholar]
- LaBarbera, M. Analyzing body size as a factor in ecology and evolution. Annu. Rev. Ecol. Syst. 1989, 20, 97–117. [Google Scholar] [CrossRef]
- Smith, R.J. Use and misuse of the reduced major axis for line-fitting. Am. J. Phys. Anthropol. 2009, 140, 476–486. [Google Scholar] [CrossRef] [PubMed]
- McArdle, B.H. The structural relationship—Regression in biology. Can. J. Zool. 1988, 66, 2329–2339. [Google Scholar] [CrossRef]
- Al-Wathiqui, N.; Rodríguez, R.L. Allometric slopes not underestimated by ordinary least squares regression: A case study with Enchenopa treehoppers (Hemiptera: Membracidae). Ann. Entomol. Soc. Am. 2011, 104, 562–566. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Biometry; Freeman: New York, NY, USA, 1995. [Google Scholar]
- Harvey, P.H.; Pagel, M.D. The Comparative Method in Evolutionary Biology; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Darlington, R.B.; Smulders, T.V. Problems with residual analysis. Anim. Behav. 2001, 62, 599–602. [Google Scholar]
- Freckleton, R.P. On the misuse of residuals in ecology: Regression of residuals vs. multiple regression. J. Anim. Ecol. 2002, 71, 542–545. [Google Scholar] [CrossRef]
- Freckleton, R.P. The seven deadly sins of comparative analyses. J. Evol. Biol. 2009, 22, 1367–1375. [Google Scholar] [CrossRef] [PubMed]
- Huxley, J.S. Problems of Relative Growth; Dover Publications: New York, NY, USA, 1932. [Google Scholar]
- Packard, G.C. Is logarithmic transformation necessary in allometry? Biol. J. Linn. Soc. 2013, 109, 476–486. [Google Scholar]
- Gingerich, P.D. Arithmetic or geometric normality of biological variation: An empirical test of theory. J. Theor. Biol. 2000, 204, 201–221. [Google Scholar] [CrossRef] [PubMed]
- Kerkhoff, A.J.; Enquist, B.J. Multiplicative by nature: Why logarithmic transformation is necessary in allometry. J. Theor. Biol. 2009, 257, 519–521. [Google Scholar] [CrossRef]
- Glazier, D.S. Log-transformation is useful for examining proportional relationships in allometric scaling. J. Theor. Biol. 2013, 334, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Yang, B.; Lin, D.; Kerkhoff, A.J.; Ma, K. The allometry of coarse root biomass: Log-transformed linear regression or nonlinear regression? PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Mascaro, J.; Litton, C.M.; Hughes, R.F.; Uowolo, A.; Schnitzer, S.A. Is logarithmic transformation necessary in allometry? Ten, one-hundred, one-thousand-times yes. Biol. J. Linn. Soc. 2014, 111, 230–233. [Google Scholar] [CrossRef]
- Garland, T.; Bennett, A.F.; Rezende, E.L. Phylogenetic approaches in comparative physiology. J. Exp. Biol. 2005, 208, 3015–3035. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, M.P.; Agosta, S.J.; Hansen, F.; Kemp, S.J.; Sieg, A.E.; McNair, J.N.; Dunham, A.E. Phylogeny, regression, and the allometry of physiological traits. Am. Nat. 2007, 170, 431–442. [Google Scholar] [CrossRef] [PubMed]
- Revell, L.J. Phylogenetic signal and linear regression on species data. Meth. Ecol. Evol. 2010, 1, 319–329. [Google Scholar] [CrossRef]
- Rezende, E.L.; Diniz-Filho, J.A.F. Phylogenetic analyses: Comparing species to infer adaptations and physiological mechanisms. Compr. Physiol. 2012, 2, 639–674. [Google Scholar] [PubMed]
- Dame, R.F. The ecological energies of growth, respiration and assimilation in the intertidal American oyster Crassostrea virginica. Mar. Biol. 1972, 17, 243–250. [Google Scholar] [CrossRef]
- Elliott, J.M. The energetics of feeding, metabolism and growth of brown trout (Salmo trutta L.) in relation to body weight, water temperature and ration size. J. Anim. Ecol. 1976, 45, 923–948. [Google Scholar] [CrossRef]
- Caulton, M.S. The effect of temperature and mass on routine metabolism in Sarotherodon (Tilapia) mossambicus (Peters). J. Fish Biol. 1978, 13, 195–201. [Google Scholar]
- Ware, D.M. Bioenergetics of pelagic fish: Theoretical change in swimming speed and ration with body size. J. Fish. Board Can. 1978, 35, 220–228. [Google Scholar] [CrossRef]
- DeMont, M.E.; O’Dor, R.K. The effects of activity, temperature and mass on the respiratory metabolism of the squid, Illex illecebrosus. J. Mar. Biol. Assoc. UK 1984, 64, 535–543. [Google Scholar]
- Ikeda, T. Metabolic rates of epipelagic marine zooplankton as a function of body mass and temperature. Mar. Biol. 1985, 85, 1–11. [Google Scholar] [CrossRef]
- Wright, J.C. Effects of body temperature, mass and activity on aerobic and anaerobic metabolism in juvenile Crocodylus porosus. Physiol. Zool. 1986, 59, 505–513. [Google Scholar]
- Kurmaly, K.; Yule, A.B.; Jones, D.A. Effects of body size and temperature on the metabolic rate of Penaeus monodon. Mar. Biol. 1989, 103, 25–30. [Google Scholar] [CrossRef]
- Müller, H.; Geller, W. Maximum growth rates of aquatic ciliated protozoa: The dependence on body size and temperature reconsidered. Arch. Hydrobiol. 1993, 126, 315–327. [Google Scholar]
- Dorcas, M.E.; Hopkins, W.A.; Roe, J.H. Effects of body mass and temperature on standard metabolic rate in the Eastern Diamondback Rattlesnake (Crotalus adamanteus). Copeia 2004, 145–151. [Google Scholar]
- Spanopoulos-Hernández, M.; Martínez-Palacios, C.A.; Vanegas-Pérez, R.C.; Rosas, C.; Ross, L.G. The combined effects of salinity and temperature on the oxygen consumption of juvenile shrimps Litopenaeus stylirostris (Stimpson, 1874). Aquaculture 2005, 244, 341–348. [Google Scholar] [CrossRef]
- Glover, D.C.; DeVries, D.R.; Wright, R.A. Effects of temperature, salinity and body size on routine metabolism of coastal largemouth bass Micropterus salmoides. J. Fish Biol. 2012, 81, 1463–1478. [Google Scholar] [CrossRef]
- Patterson, J.T.; Mims, S.D.; Wright, R.A. Effects of body mass and water temperature on routine metabolism of American paddlefish Polyodon spathula. J. Fish Biol. 2013, 82, 1269–1280. [Google Scholar] [CrossRef] [PubMed]
- Ohlberger, J.; Mehner, T.; Staaks, G.; Hölker, F. Intraspecific temperature dependence of the scaling of metabolic rate with body mass in fishes and its ecological implications. Oikos 2012, 121, 245–251. [Google Scholar]
- Blum, J.J. On the geometry of four-dimensions and the relationship between metabolism and body mass. J. Theor. Biol. 1977, 64, 599–601. [Google Scholar] [PubMed]
- Speakman, J.R. On Blum’s four-dimensional geometric explanation for the 0.75 exponent in metabolic allometry. J. Theor. Biol. 1990, 144, 139–141. [Google Scholar] [PubMed]
- Da Silva, J.K.L.; Garcia, G.J.; Barbosa, L.A. Allometric scaling laws of metabolism. Phys. Life Rev. 2006, 3, 229–261. [Google Scholar]
- Ginzburg, L.; Damuth, J. The space-lifetime hypothesis: Viewing organisms in four dimensions, literally. Am. Nat. 2008, 171, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Ma, C.X.; Littell, R.C.; Casella, G. A statistical model for the genetic origin of allometric scaling laws in biology. J. Theor. Biol. 2002, 219, 121–135. [Google Scholar] [CrossRef] [PubMed]
- West, D.; West, B.J. Statistical origin of allometry. Europhys. Lett. 2011, 94. [Google Scholar] [CrossRef]
- West, D.; West, B.J. On allometry relations. Int. J. Mod. Phys. B 2012, 26. [Google Scholar] [CrossRef]
- Weathers, W.W. Energetics of Postnatal Growth. In Avian Energetics and Nutritional Ecology; Carey, C., Ed.; Chapman & Hall: New York, NY, USA, 1996; pp. 461–496. [Google Scholar]
- Economos, A.C. Gravity, metabolic rate and body size of mammals. Physiologist 1979, 22, S71–S72. [Google Scholar] [PubMed]
- Parry, G.D. The influence of the cost of growth on ectotherm metabolism. J. Theor. Biol. 1983, 101, 453–477. [Google Scholar] [CrossRef] [PubMed]
- Rau, A.R.P. Biological scaling and physics. J. Biosci. 2002, 27, 475–478. [Google Scholar] [PubMed]
- Vickery, W.L.; Millar, J.S. The energetics of huddling by endotherms. Oikos 1984, 43, 88–93. [Google Scholar] [CrossRef]
Appendix
Other Metabolic Scaling Models
Fourth Dimensional Models
Foraging Models
Whole Organism Optimization Models
Statistical Models
| HLBO | Subtheory | Model/Hypothesis/Mechanism | b | Sources | |
|---|---|---|---|---|---|
| Cell | SA theory | Cell SA effects | 2/3 (C) | [93,171] | |
| (MLBH) | [173] | ||||
| Cell-size and number model | 2/3 to 1 (O) | [68,69,178] | |||
| SA elaboration due to cell-shape change | >2/3 (C) | [106,171,173] | |||
| Mitochondrial SA | Variable (C & O) | [120,180,181,182] | |||
| Photosynthetic pigment light reception | 2/3 (C) | [172] | |||
| RT theory | RTN models | 3/4 (C) | [159,172] | ||
| SC theory | %MSC (e.g., vacuolar space) increases as cell size increases | <1 (C) | [106,173] | ||
| RD theory | Cell membrane pacemaker model | Variable | [70,191] | ||
| Thermodynamics model | 3/4 (O) | [190] | |||
| Amount of metabolic machinery (e.g., number of enzymes or mitochondria) | Variable | [120,146,181] | |||
| Quantum statistics model (C & O) | 2/3, 3/4 1/2 to 1 | [71] [72] | |||
| Cell V effects (MLBH) | 1 (C) | [173] | |||
| Organism | SA theory | Thermoregulatory models: Compensation for heat loss | 2/3 | [83,84,101,292] | |
| (MLBH) | 2/3 | [19] | |||
| Heat dissipation | 0.63 | [102] | |||
| Resource & waste flux models/hypotheses: | 2/3 | [61,90,91] | |||
| DEB theory | 2/3 | [66,104] | |||
| Fractal SA of respiratory organs | 2/3 to 1 (assumed) | [92] | |||
| Mass-transfer model | 1/2 to 5/4 | [103] | |||
| MLBH | 2/3 | [19] | |||
| RT theory | Blood flow models | 2/3 | [108] | ||
| 3/4 | [7,8] | ||||
| RTN models | 3/4 | [15,118,119] | |||
| 2/3, 3/4 | [24,388,602] | ||||
| 5/6, 1 | [26] | ||||
| 7/9 | [117] | ||||
| 3/5 to 6/7 | [594] | ||||
| 1/2 to 3/4 1 | [43] | ||||
| 0.6 to 1 2 | [43] | ||||
| 1 | [33] | ||||
| 0.81 | [44] | ||||
| 0 to 2/3 | [45] | ||||
| 1/4 to 3/4 | [24,25,46] | ||||
| Constructal theory | 1/3, 2/3, 3/4 | [296] | |||
| SC theory | %MSC increases as body size increases | <1 | [18,29,35,40,89,127,129,137,138,139,140,141,142,143,144,145,146,147,155,333,599] | ||
| (DEB theory) | <1 | [66,104] | |||
| %MSC (inert nutrient reserves) decrease during early development | >1 | Present paper | |||
| RD theory | Maintenance demand: Intrinsic cellular/tissue energy costs | Variable | [8,70,71,72,148,168,191] | ||
| Body V effects | |||||
| Neuro-endocrine control | Variable | [8,64,84,150] | |||
| Locomotor demand: Support/anti-gravity costs | 3/4 | [454,600] | |||
| Costs of muscular exertion | >3/4 | [167] | |||
| Growth (production) demand | 1 | [18,66,67,89,104,164,165,166,332,342,347,601] | |||
| Food processing (SDA) demand | 1 | [19,355] | |||
| Increasing costs of developmental maturation (including thermoregulation) | >1 | [18]; | |||
| Colony/other social groups | SA theory | Resource (e.g., energy & water conservation models) | 2/3 | [200] | |
| RT theory | RTN models | 3/4 | [222] | ||
| SC theory | %MSC (e.g., % inert materials or relatively in-active individuals increases as colony size inc.) | <1 | [216,223,224,225] | ||
| RD theory | Additive model (Colony MR = simple sum of individual MRs) | 1 | [209,214,224] | ||
| Larger individual body sizes in larger colonies | <1 | [225] | |||
| Lower activity level of all individuals in colony | <1 | [225] | |||
| Neural/chemical stimulation among close individuals | >1 | [198] |
| Subtheories Linked | Mechanisms | Sources |
|---|---|---|
| SA, RD & RT | Metabolic-level boundaries hypothesis (see text) | [19] |
| SA, RD & SC | Dynamic energy budget theory (see text) | [66,104] |
| SA & RT | Matching of scaling of SA & blood circulation | [108] |
| Matching of metabolic rate to both SA-related heat loss and internal RT | [8] | |
| Internal geometry of SA and RT | [24] | |
| Heat flow across external SA and within body | [296] | |
| SA and RT effects depend on resource level | [172] | |
| Relative effects of SA & RT depend on body size | [38] | |
| SA & RD | Cell size & SA/V affect whole organism RD scaling | [68,69,178] |
| Variation in relative influence of SA- and V(RD)-related processes | [49] | |
| SC & RD | Allometric cascade model | [73,167,168] |
| RT & SC | RT theory adjusted to ontogenetic changes in water content (SC) | [455] |
| RT predictions adjusted for differences in tissue metabolic rates (SC) | [29] |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glazier, D.S. Metabolic Scaling in Complex Living Systems. Systems 2014, 2, 451-540. https://doi.org/10.3390/systems2040451
Glazier DS. Metabolic Scaling in Complex Living Systems. Systems. 2014; 2(4):451-540. https://doi.org/10.3390/systems2040451
Chicago/Turabian StyleGlazier, Douglas S. 2014. "Metabolic Scaling in Complex Living Systems" Systems 2, no. 4: 451-540. https://doi.org/10.3390/systems2040451
APA StyleGlazier, D. S. (2014). Metabolic Scaling in Complex Living Systems. Systems, 2(4), 451-540. https://doi.org/10.3390/systems2040451