Scaling of Metabolic Scaling within Physical Limits

Abstract

Both the slope and elevation of scaling relationships between log metabolic rate and log body size vary taxonomically and in relation to physiological or developmental state, ecological lifestyle and environmental conditions. Here I discuss how the recently proposed metabolic-level boundaries hypothesis (MLBH) provides a useful conceptual framework for explaining and predicting much, but not all of this variation. This hypothesis is based on three major assumptions: (1) various processes related to body volume and surface area exert state-dependent effects on the scaling slope for metabolic rate in relation to body mass; (2) the elevation and slope of metabolic scaling relationships are linked; and (3) both intrinsic (anatomical, biochemical and physiological) and extrinsic (ecological) factors can affect metabolic scaling. According to the MLBH, the diversity of metabolic scaling relationships occurs within physical boundary limits related to body volume and surface area. Within these limits, specific metabolic scaling slopes can be predicted from the metabolic level (or scaling elevation) of a species or group of species. In essence, metabolic scaling itself scales with metabolic level, which is in turn contingent on various intrinsic and extrinsic conditions operating in physiological or evolutionary time. The MLBH represents a “meta-mechanism” or collection of multiple, specific mechanisms that have contingent, state-dependent effects. As such, the MLBH is Darwinian in approach (the theory of natural selection is also meta-mechanistic), in contrast to currently influential metabolic scaling theory that is Newtonian in approach (i.e., based on unitary deterministic laws). Furthermore, the MLBH can be viewed as part of a more general theory that includes other mechanisms that may also affect metabolic scaling.

1. Introduction

For decades, a major tenet of comparative biology has been that the rate of life-giving metabolism (R) scales with body mass (M) to the 3/4-power (R = aM^b, where a is the scaling coefficient and b is the scaling exponent or slope in log-log space [1,2,3,4,5]). According to this 3/4-power law (also called Kleiber’s law) as log body mass increases 4-fold, log metabolic rate should increase 3-fold. As a result, smaller organisms tend to have higher rates of metabolism and of other energy-dependent processes per unit body mass than larger organisms. This law, one of the few that appears to be well established in biology, has attracted much attention from both biological and physical scientists. Not surprisingly, frequent attempts have been made to use the quantitative methods of physics, a field which focuses largely on natural laws, to explain Kleiber’s law (e.g., [6,7,8,9,10,11,12,13,14,15,16,17]). However, these mostly deterministic explanations (but see [18,19,20]) have failed to explain fully the marked diversity of metabolic scaling relationships that actually exists in the living world (b ranging between ~0 to >1, but mostly between 2/3 and 1 [21,22,23,24,25]). Thus, there has been a need for new theoretical approaches to explain this diversity. This is an important objective because typically most of the variation in metabolic rate observed in various groups of organisms is related to body size (see e.g., [26,27]), and the rates of many other kinds of biological processes are in turn related to metabolic rate [3,28,29].

In a companion review, I argue that theory based on multiple mechanisms, each of which acts contingently, rather than deterministically in response to various internal (system) and external (environmental) factors, shows the most promise for explaining the rich diversity of metabolic scaling [23]. To illustrate the potential power of this “meta-mechanistic” approach, I developed the “contextual multimodal theory” (CMT), which is based on four subtheories, including surface area (SA), resource transport (RT), system composition (SC) and resource demand (RD) related mechanisms, whose expression is modulated by various internal and external influences (for further details see [23]). Central to this theory is the recently proposed “metabolic-level boundaries hypothesis” (MLBH) [21,22,30], which posits that metabolic level (the vertical elevation of a metabolic scaling relationship) modulates the relative influence of the SA and RD modules (and possibly the RT module as well) on the metabolic scaling exponent.

The purpose of this essay is to give an updated account of the MLBH, including its current status and future prospects in the field of metabolic scaling. First, I provide a brief overview of the MLBH, including its conceptual foundation and predictive power. Second, I review evidence that appears to support or contradict the MLBH. Third, I describe how the predictions of the MLBH may be altered by various modulating influences on the SA, SC and RD modules of the CMT. Taking into account these effects helps to explain why the predictions of the MLBH do not always match empirical data. The CMT and MLBH are both meta-mechanistic, and as such their predictions of the metabolic scaling exponent (b) are strongly context-dependent. Fourth, I discuss some potentially useful lines of future research involving the testing and further theoretical development of the MLBH.

2. Overview of the Metabolic-Level Boundaries Hypothesis (MLBH)

In this section I describe the conceptual foundation of the MLBH and the nature of its predictive power. At the outset, it is important to emphasize that I do not regard the MLBH as a complete, all-encompassing theory, but rather as a hypothetical conceptual framework that shows promise for helping us to understand much, but not all of the variation in intra- and interspecific metabolic scaling that has been observed (also see [22]). This hypothesis can be considered part of a larger more general theory (e.g., the CMT [23]) that shows how all or nearly all existing variation in metabolic scaling may be explained at least potentially (including b values outside the range of 2/3 to 1 that is emphasized by the MLBH; also see Section 2.1.1 and Section 4). In addition, the MLBH is a “work in progress”; it is being further developed, especially to make it more quantitative (also see Section 2.2 and Section 5.2). Furthermore, the MLBH is designed to help us understand not only variation in resting metabolic rate (a common focus of metabolic scaling theory), but also variation in all kinds of metabolic rate under various conditions, including torpor or diapause, free-living field conditions, thermally challenging environments, and various levels of behavioral activity.

2.1. Conceptual Foundation of the MLBH

The MLBH posits that body volume (V) and surface area (SA) act as important physical boundary limits within which the metabolic scaling exponent (b) can vary as a result of various physiological, developmental and ecological influences. Metabolic level (L, the vertical elevation of a metabolic scaling relationship, estimated here as the mass-specific metabolic rate at the midpoint of a log body-mass range [22]) modulates the relative influences of SA and V-related RD on b. In this section, I briefly describe the general importance of body V and SA in allometric scaling, as well as explain why b is expected to covary with L, which in turn is affected by various internal and external factors, according to the MLBH. More details about the MLBH can be found in an earlier review [22].

2.1.1. Body Volume and Surface Area as Physical Boundary Limits

Recognition of the importance of body V and SA, two basic geometric properties of all organisms, pervades the history of biological scaling. As Thompson ([31], p. 25) wrote over 70 years ago “A common effect of scale is due to the fact that, of the physical forces, some act either directly at the surface of the body, or otherwise in proportion to its surface or area; while others exert a force which is proportional to the mass, and so usually to the volume of the body”. Hemmingsen ([2], p. 94) also remarked that metabolic scaling appears to be the result of a “struggle between proportionality of metabolism to body weight and proportionality to surface functions” (also see [32,33,34]. These physical properties continue to receive prominent attention in metabolic scaling theory at the cellular [21,23,35,36,37], organismal [23,25,38], and social group levels [23,39]. In particular, V- and SA-related processes play an essential role in dynamic energy budget (DEB) theory, which has been applied to many kinds of species and ecological systems [38,40]. This is not surprising because fluxes of resources and metabolic wastes (including heat) between a cell, organism or huddle of organisms and its environment are expected to be related to its exposed SA, and production of metabolic energy is expected to be related to total cell or tissue volume.

However, V and SA effects on metabolic scaling have typically been invoked in an overly simplistic, deterministic way. For example, SA theory (in particular the “surface law” of Rubner [41]) was initially used to explain why resting metabolic rate tended to be proportional to SA, thus scaling to near the 2/3-power within many species of birds and mammals (see discussion and references cited in [23]). According to SA theory, this is because endotherms can maintain a constant body temperature only by balancing their SA-related heat loss by an equal amount of metabolic heat production. Since heat loss is expected to scale as M^2/3, so should metabolic rate. However, when several interspecific analyses in mammals and other ectothermic organisms with variable body temperatures revealed near 3/4 (not 2/3) power scaling, the death of SA theory was proclaimed (e.g., [3,5]), although not by Kleiber [1,33], who was among the first to report 3/4-power metabolic scaling in mammals (see [23]). A major problem with this premature obituary is that it did not recognize that the application of SA theory may be context dependent, including the specific value of b that it predicts. First, body SA may not always scale to the 2/3-power as expected in isomorphic organisms, but may scale differently with b values as high as 1 in organisms that grow mainly in one or two dimensions ([23,42,43]; also see Section 4). Second, the relevant SA may not be external but internal (e.g., respiratory and alimentary surfaces), which may scale with various b values (not just 2/3), as well [21,42]. Third, the relative influence of SA on metabolic scaling may vary among taxa and physiological states [22,23]. For example, the thermoregulation of homeothermic (endothermic) animals is more affected by SA-related heat loss than that of poikilothermic (ectothermic) animals, and thus as expected, recent interspecific analyses show that b is often near 2/3 in the former, but >2/3 (sometimes approaching 1) in the latter (reviewed in [21,22,23]). In addition, as postulated by the MLBH, SA effects on b may be stronger at high resting L when resource and waste fluxes are more influential, than at low L when V-related RD effects are stronger. In short, SA and RD effects on metabolic scaling should not be considered as being deterministic in a simple all-or-none sense, but as being contingent on various internal and external contexts.

Given the above SA- and V-related boundary limits, the MLBH predicts that b should vary between 2/3 and 1. However, these represent idealized boundaries that strictly apply only to isomorphic organisms with homogenous internal resource demands that are isometric with body mass. These boundary limits may be transgressed if size differences in organisms are associated with changes in body shape (thus altering SA/V) or the relative intensity or heterogeneity of tissue resource demand (thus altering how RD relates to V) ([22,23]; also see Section 4).

The boundary approach of the MLBH contrasts sharply with currently influential resource transport network (RTN) models that focus on the average tendency of metabolic rate to scale near a 3/4-power [9,12]. The MLBH allows b to vary within broad physical limits, whereas RTN models invoke physical limits that cause tight clustering of b around a central value. Both approaches can explain why the average value of b in many taxa is between 2/3 and 1, but between them only the MLBH successfully predicts variation in b that is related to differences in physiological state [21,22,30] and ecological lifestyle [21,22,44,45] (also see [8,18,21,23,25] for other approaches that can explain variation in b related to physiological and ecological differences).

2.1.2. Covariation of the Elevation (L) and Slope (b) of Metabolic Scaling Relationships

Most metabolic scaling models focus on the scaling exponent (b), while either ignoring or explaining in a separate way the scaling coefficient (a) or elevation (L) of a scaling relationship ([22,23]; but see [46]). The MLBH is the first model to propose that b and L are linked in biologically meaningful ways (rather than their association being merely a statistical artifact [3,34,47]). According to the MLBH, b for inactive metabolic rate should decrease as L increases. At low L, the metabolic demand of an organism is lower than its resource-supply capacity. When energy demand is low, SA- or RT-related resource supply and waste removal are not limiting, and therefore b should be near 1 because metabolic rate is now mainly dictated by total tissue RD, which is proportional to body V or M. This should be especially apparent in low-L organisms that are sedentary, torpid or in diapause. However at high L, the metabolic demand of an inactive organism becomes closer to its sustainable resource-supply or waste-loss capacity. As a result, b should approach 2/3 in isomorphic organisms because of the increased influence of SA-related fluxes of metabolic resources and/or wastes (including heat). This should be especially apparent in high-L endothermic animals with high rates of heat loss requiring compensating heat production either in cold or thermoneutral environments. In contrast, b for active metabolic rate should increase as L increases. As activity increases, animal metabolism becomes increasingly dominated by muscular power production, which scales isometrically (b ~ 1) with V or M. However, this isometric scaling of maximally active metabolism is temporary because it depends on finite body stores of oxygen and energy, limited tolerance to metabolic waste accumulation, and an unsustainable up-regulation of respiratory and circulatory activity. Considering all L levels for both inactive and active metabolic rates, b is predicted to show a V- or U-shaped relationship with L [22,30]. No other current mechanistic model makes this prediction (but for a possible explanation based on fractional probability calculus, see [19,20]).

2.1.3. Internal and External Influences on L and b

Traditional explanations of the metabolic scaling slope (especially b = 3/4) have focused on internal factors (e.g., body design). This focus has stemmed from a belief that b is universally 3/4 or nearly so, independently of environmental conditions. According to RTN models, environmental factors act only on the scaling coefficient a, not b [5,48,49]. However, numerous studies have reported variation in b that is associated with various ecological factors, both biotic and abiotic (reviewed in [21,23,24,50]). Clearly, a comprehensive explanation of metabolic scaling must include both internal and external factors. The MLBH and CMT attempt to provide such a synthesis. The MLBH in particular shows how ecological factors may affect b via their effect on L, but within V- and SA-related boundary limits. Any physiological or ecological factor that increases L is predicted to decrease b. In addition, any factor that directly affects the relative contribution of a SA or V-related process to metabolic scaling should also affect b.

2.2. Predictive Power of the MLBH

The MLBH is sometimes misunderstood as being merely descriptive (phenomenological) rather than mechanistically predictive. This misunderstanding may arise because the MLBH is based not on obligatory deterministic mechanisms, as are many metabolic scaling models, but rather on facultative contingent mechanisms. The MLBH is not mechanistic in the traditional (deterministic) sense, but is meta-mechanistic. A meta-mechanistic theory is composed of multiple specified mechanisms, each of which is expressed contingently based on various modulating contextual factors (see [23]). Major “modal mechanisms” in the MLBH include V-related power production and SA-related resource supply and metabolic waste disposal. The relative influence of these mechanisms is modulated by L, which in turn depends on various internal and external factors that act as “modulating mechanisms”. Note that the MLBH does not rely on any possible mechanism, which would make it unfalsifiable, but rather invokes specific mechanisms that affect L and the relative influence of SA and V-related processes on b. These mechanisms include the effects of increases in temperature and various energy-using processes, such as growth, food processing, heat production and behavioral activity (also see Section 4).

Given its contingent nature, the MLBH does not make a single prediction for b, like some theoretical models, but rather makes multiple predictions that depend on various contextual factors. For example, any factor that increases L for inactive metabolic rate is predicted to cause a decrease in b from a maximum of 1 to a minimum of 2/3. Moreover, if one knows how b is related to L in a specific group of species, one can make a quantitative prediction of b for a species in that group by only knowing its L (i.e., its metabolic rate at geometric mean body mass). Consider that in a sample of 89 teleost fish species, b = 1.377–0.145 (ln L) [44]. Using this predictive equation, it is possible to predict b for any teleost species, if its L is known, as has been done [51]. Quantitative predictions of b can also be made if one knows the habitat temperature (T) of a species (also see Section 3.3). Using the above equation describing the inverse relationship between b and L, and an additional quantitative relationship describing the positive relationship between L and T [44], one can easily predict b for a teleost species by knowing T. One can also make qualitative predictions of b if one knows the ecological lifestyle of a species. For example, high-L pelagic teleosts exhibit low b values near 2/3 (mean = 0.698), whereas medium-L benthopelagic and benthic species have higher b values (means = 0.776 and 0.802, respectively), and low-L bathyal species even higher b values approaching 1 (mean = 0.856) [44]. Therefore, one can predict the b value of any teleost species, at least approximately, if one knows whether it has a pelagic, benthic or bathyal lifestyle, because these lifestyles are related to L, which in turn modulates b. Similar quantitative and qualitative predictions can also be made for active metabolic rates, if one knows L and the activity level of a species (also see Section 5.2).

In short, the MLBH allows for “if, then” predictions, which is useful given that b is highly variable and sensitive to the internal state of an organism and its environmental conditions. Other models that do not have this flexibility may successfully predict modal values of b, but not variation around these values (e.g., some RTN models [9,11,17]). Although recent analyses show that RTN models can be modified to permit predictions of multiple b values (i.e., by making the predicted b values contingent on specific geometric and physical properties of RTNs [12,49]), no evidence directly supporting these modified effects on metabolic scaling has yet been collected (also see [23]), unlike that for the MLBH, which I discuss next.

3. Evidence Appearing to Support or Contradict the MLBH

Numerous (but not all) lines of evidence appear to support the MLBH. These lines of evidence are grouped into three categories, including how metabolic level (L) and the metabolic scaling exponent (b) are affected by differences in (1) physiological or developmental state; (2) ecological lifestyle or taxonomic affiliation; and (3) environmental conditions.

3.1. Effects of Physiological or Developmental State

The MLBH predicts that an increase in the influence of any V-related RD process on whole body metabolism should result in the metabolic scaling exponent (b) increasing toward 1 [22]. This prediction is supported by several studies examining the effects of increased behavioral activity, growth and food processing on b. Most notably, many intra- and interspecific analyses have shown that higher activity results in increases in both L and b (the latter approaching 1 at maximal activity levels) [21,22,30,52,53,54,55,56,57,58,59,60,61,62], as predicted by the MLBH. An excellent example of this is the classic study of Brett [59], who showed that b increases from 0.78 at rest to near 1 (0.97) in sockeye salmon (Oncorhynchus nerka) swimming at increasing speeds. Similar effects of activity level have been observed in many other fish species (Figure 1). However, in some relatively sedentary or slow-moving fish, increased activity does not increase b significantly, perhaps because it entails relatively small increases in muscular power production [23,51,63]. The MLBH also predicts that b should increase toward 1 at minimal metabolic levels during torpor, hibernation or diapause, which has been shown to occur in insects, birds and mammals [22,30]. Tegu lizards (Tupinambis merianae) similarly show higher b values during winter torpor (1.12) than during the summer active period (b = 0.75) [64]. Moreover, as predicted, a concave upward relationship between b and L has been revealed when a wide range of metabolic levels is examined not only for interspecific scaling relationships in insects, birds and mammals [22,30], but also even intraspecific metabolic scaling relationships, as recently revealed in chitons [45]. In addition, an examination of the effects of temperature and swimming activity on metabolic rate in the fish Coregonus albula reveals a concave upward relationship as well (Figure 2). These patterns clearly show that metabolic scaling itself scales with activity level and within the predicted boundary limits of 2/3 and 1. However, although these studies have shown that differences in activity level can induce a wide range of b values (~2/3 to 1), in some ectothermic species with low resting L less substantial changes in b in response to increases in activity level may be observed [52,61]. Relatively small differences in b between resting and active ectotherms may also be seen at low ambient temperatures, because b is already near the maximum level (i.e., near 1) in the resting state, as observed in C. albula (Figure 2).

Other processes, such as growth and food processing that have body-wide effects and thus are V related, also cause b to increase to 1. This prediction is consistent with numerous studies showing that b is near 1 in rapidly growing organisms, either during early development, as observed in various plants and animals (reviewed in [21,23]), or throughout life, as seen in many pelagic invertebrates [21,50]. Experimental manipulations, based on artificial selection or nutritional enhancement, have further shown that increased growth rates result in steeper metabolic scaling (reviewed in [23,29]). Enhanced body-wide metabolism associated with food processing (i.e., specific dynamic action) results in b approaching 1, as well [65].

The above studies provide some of the strongest evidence for the MLBH, but analyses of field metabolic rates (FMR) presently do not provide a clear picture. Although the data of Nagy [66] support the MLBH by showing that FMRs that include various behavioral activities have higher b values than basal metabolic rates (BMR) in birds and mammals [22], other recent analyses suggest that mammalian FMR may scale with an exponent equal to or even lower than that of BMR [67,68,69]. These patterns may be due in part to FMR being affected by both the costs of thermoregulation (scaling to the 2/3-power) and activity (scaling to the 1-power), which may vary among species depending on environmental temperature and activity demands. Further studies of FMR scaling are needed to resolve this issue.

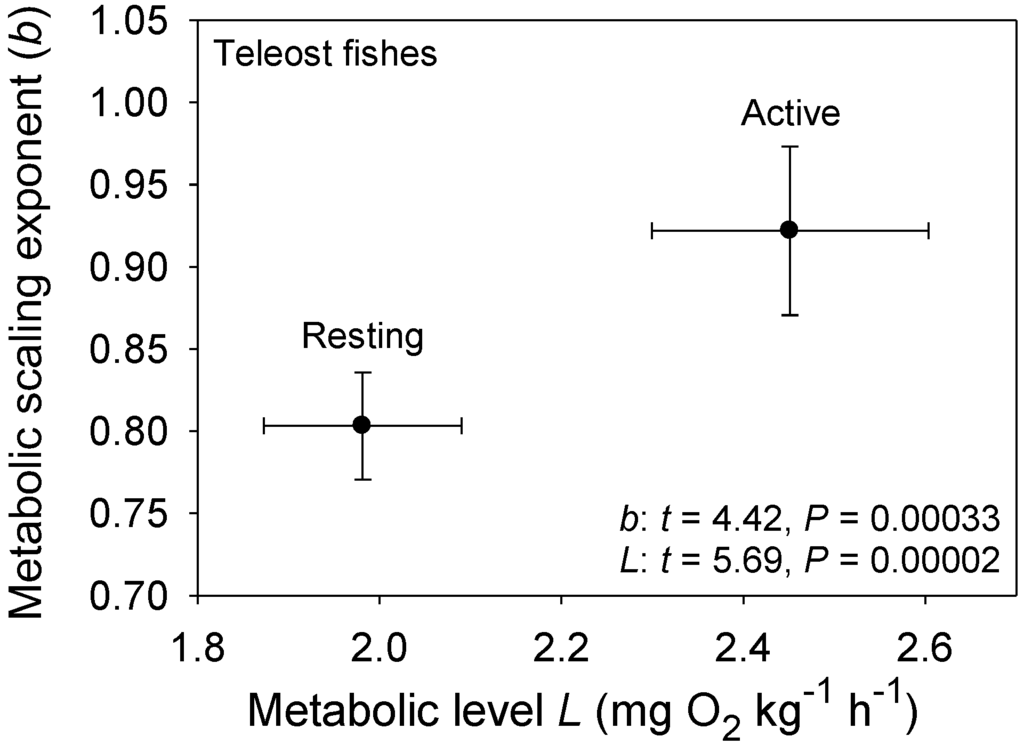
Figure 1. Mean scaling exponents (b) and elevations (L) (±95% confidence intervals) for resting and active (maximal) metabolism of 10 teleost fishes: Carassius auratus [51], Coregonus albula ([54]; and additional data from J. Ohlberger), Ctenopharyngodon idellus [63], Cyclopterus lumpus [52], Esox lucius [62], Macrozoarces americanus [52], Myoxocephalus scorpius [52], Oncorhynchus nerka [59], Salmo gairdneri [60] and Stizostedion vitreum [61]. As predicted by the metabolic-level boundaries hypothesis (MLBH), b is significantly higher (approaching 1) for fishes in an active high-L state, than for those in an inactive low-L state (results of t-tests are shown). Note also that b for resting metabolic rate is quite high (significantly greater than 3/4) as would be expected in ectotherms with a low inactive L, according to the metabolic-level boundaries hypothesis (MLBH).

Figure 1. Mean scaling exponents (b) and elevations (L) (±95% confidence intervals) for resting and active (maximal) metabolism of 10 teleost fishes: Carassius auratus [51], Coregonus albula ([54]; and additional data from J. Ohlberger), Ctenopharyngodon idellus [63], Cyclopterus lumpus [52], Esox lucius [62], Macrozoarces americanus [52], Myoxocephalus scorpius [52], Oncorhynchus nerka [59], Salmo gairdneri [60] and Stizostedion vitreum [61]. As predicted by the metabolic-level boundaries hypothesis (MLBH), b is significantly higher (approaching 1) for fishes in an active high-L state, than for those in an inactive low-L state (results of t-tests are shown). Note also that b for resting metabolic rate is quite high (significantly greater than 3/4) as would be expected in ectotherms with a low inactive L, according to the metabolic-level boundaries hypothesis (MLBH).

3.2. Effects of Taxonomic or Ecological Lifestyle Differences

For resting metabolic rate (RMR), many, but not all differences in b between major taxonomic groups are consistent with the MLBH. For example, recent interspecific analyses reveal that high-L endothermic birds and mammals usually have relatively low b values near 2/3 (0.64 to 0.72), whereas low-L ectothermic fish, amphibians and reptiles exhibit significantly higher b values (0.76 to 0.88) [30,70], as predicted [22]. In addition, as expected, a comparison of various higher taxa of invertebrates shows a significant negative relationship between b and L [22]. Similar negative relationships between b and L occur among various vertebrate orders [21] and echinoderm classes [71], and for other comparisons of various groups of arthropods [21,72], birds [73] and unicellular organisms [74]. However, although low-L termites, scorpions and turtles exhibit b values near 1 [72,75,76], as predicted, low-L ticks unexpectedly show a very low b value (0.57 [77]). The apparently contradictory tick data may be explained by confounding effects of changes in body composition (see Section 4).

Other studies have reported taxonomic variation in b values that appears to be unrelated to L. For example, the scaling exponents for various taxonomic groups of marine gastropods are not significantly different and apparently unrelated to L, though L varied over less than 1/2 of an order of magnitude [78]. Another broader analysis of various taxonomic groups of animals revealed no significant relationships between b and L [79], but unfortunately the method used to calculate L was flawed, as one of the authors of this study has later acknowledged [69]. Their measure of L was not appropriate because it was body-size dependent, as can be seen clearly in their Figure 2: large-bodied orders of birds and mammals (e.g., Proboscidea, Perissodactyla, Artiodactyla, Struthioniformes and Sphenisciformes) have higher calculated L values than small-bodied orders (e.g., Chiroptera, Rodentia, Insectivora, Apodiformes and Passeriformes) despite the fact that the latter actually have higher mass-specific metabolic rates.

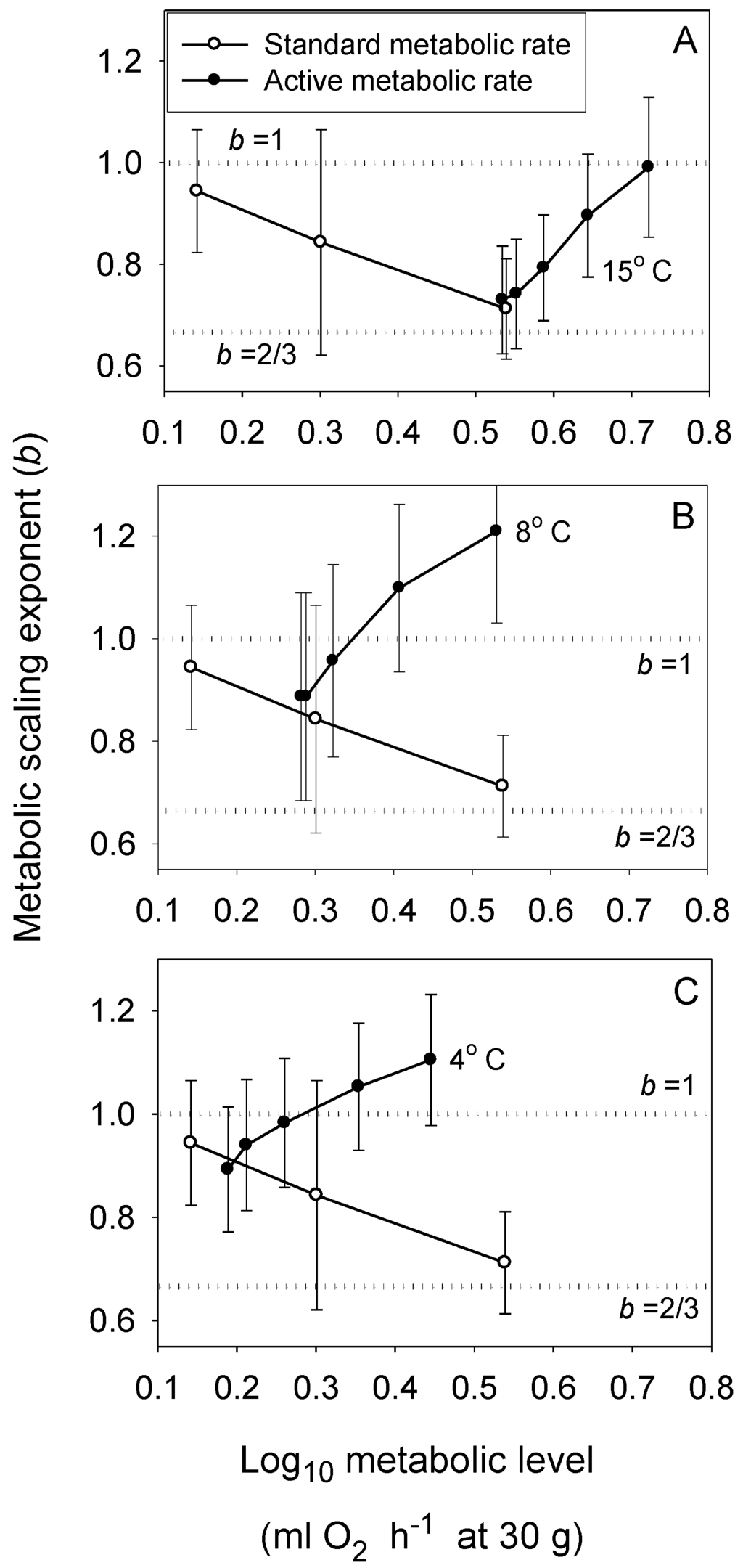
Figure 2. Scaling exponents (b ± 95% confidence intervals) in relation to metabolic level (L) for standard (resting) metabolism at three temperatures (open circles: 4, 8 and 15 °C from left to right in each panel [54]) and for active metabolism at five swimming speeds and three temperatures (solid circles: A: 15 °C; B: 8 °C; C: 4 °C; calculated from [54] and additional data provided by J. Ohlberger, personal communication). The scaling exponent b varies mainly between 2/3 and 1, and shows concave upward relationships with L that become narrower at lower temperatures, as predicted by the metabolic-level boundaries hypothesis. The dotted horizontal lines indicate scaling in relation to volume (b = 1) and surface area (b = 2/3).

Figure 2. Scaling exponents (b ± 95% confidence intervals) in relation to metabolic level (L) for standard (resting) metabolism at three temperatures (open circles: 4, 8 and 15 °C from left to right in each panel [54]) and for active metabolism at five swimming speeds and three temperatures (solid circles: A: 15 °C; B: 8 °C; C: 4 °C; calculated from [54] and additional data provided by J. Ohlberger, personal communication). The scaling exponent b varies mainly between 2/3 and 1, and shows concave upward relationships with L that become narrower at lower temperatures, as predicted by the metabolic-level boundaries hypothesis. The dotted horizontal lines indicate scaling in relation to volume (b = 1) and surface area (b = 2/3).

Several intraspecific RMR analyses have revealed further evidence for the MLBH. For example, significant negative correlations between b and L have been found among species of spiders, snakes and teleost fishes [44,80]. Recent studies of low-L hagfish [81] and insect species (e.g., silverfish, firebrats, bed bugs and aquatic leaf beetles) also reveal that they have b values near 1 [82,83,84], as predicted by the MLBH.

Figure 3. (A) Scaling of log resting (endogenous) metabolic rate in relation to log wet body mass in various groups of uni- and multicellular organisms (based on data from [22,74]). The symbols at the ends of each least squares regression line denote the minimum and maximum body masses for each sample (◊ unicellular prokaryotes; ♦ unicellular algae and protozoans; ● invertebrates: winged insects, wingless insects, crustaceans, spiders, gastropods, bivalves and polychaetes; ○ diapausing insects; ■ vertebrates: birds, mammals, reptiles, amphibians and fishes; □ hibernating mammals; ▲ vascular plants (tree saplings): from approximately left to right, and for each symbol in approximate descending order of metabolic level. The slopes (scaling exponents, b) of thick solid lines are not significantly different from 1, whereas the slopes of thick dashed lines are not significantly different from 2/3 (b values are indicated). (B) Whole organism metabolic scaling exponents (b ± 95% confidence limits) vs. metabolic level (L = mass-specific metabolic rate at the midpoint of each log-log regression shown in panel A among all of the groups of organisms analyzed; following [22,44]). The solid diagonal line represents the regression for multicellular organisms (b = 0.665–0.167 (L), r = −0.901, P < 0.00001, N = 15), whereas the dashed diagonal line represents the regression for unicellular organisms (b = 0.949–0.271 (L), r = −0.846, P = 0.357, N = 3). These negative relationships are predicted by the metabolic-level boundaries hypothesis, which may also explain why multicellular organisms show metabolic scaling slopes approaching 2/3 at lower metabolic levels than do unicellular organisms because multicellular organisms are much larger and thus typically have significantly smaller body surface area to volume ratios. Dotted lines in panels A and B represent scaling in proportion to body-surface area (b = 2/3) and body mass (b = 1), and according to the 3/4-power law. The elevations of the dotted lines in panel A are arbitrary; these lines are meant only to show specific theoretical slopes for visual comparison with those of the empirical scaling relationships.

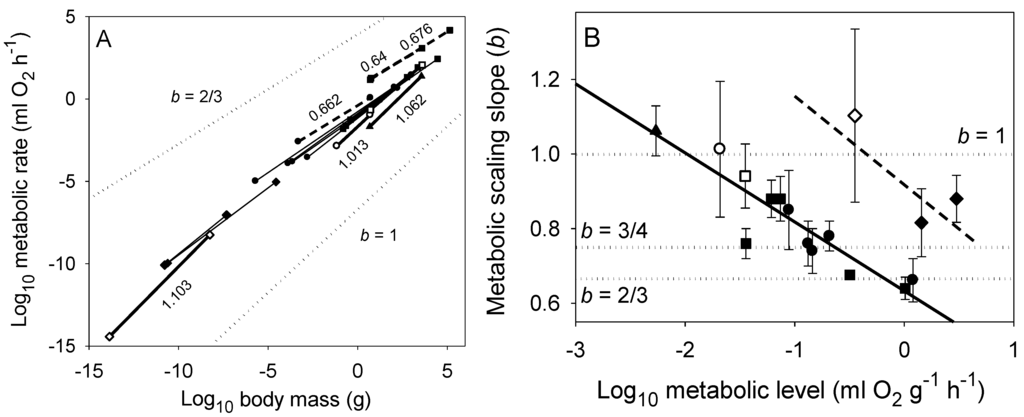
Figure 3. (A) Scaling of log resting (endogenous) metabolic rate in relation to log wet body mass in various groups of uni- and multicellular organisms (based on data from [22,74]). The symbols at the ends of each least squares regression line denote the minimum and maximum body masses for each sample (◊ unicellular prokaryotes; ♦ unicellular algae and protozoans; ● invertebrates: winged insects, wingless insects, crustaceans, spiders, gastropods, bivalves and polychaetes; ○ diapausing insects; ■ vertebrates: birds, mammals, reptiles, amphibians and fishes; □ hibernating mammals; ▲ vascular plants (tree saplings): from approximately left to right, and for each symbol in approximate descending order of metabolic level. The slopes (scaling exponents, b) of thick solid lines are not significantly different from 1, whereas the slopes of thick dashed lines are not significantly different from 2/3 (b values are indicated). (B) Whole organism metabolic scaling exponents (b ± 95% confidence limits) vs. metabolic level (L = mass-specific metabolic rate at the midpoint of each log-log regression shown in panel A among all of the groups of organisms analyzed; following [22,44]). The solid diagonal line represents the regression for multicellular organisms (b = 0.665–0.167 (L), r = −0.901, P < 0.00001, N = 15), whereas the dashed diagonal line represents the regression for unicellular organisms (b = 0.949–0.271 (L), r = −0.846, P = 0.357, N = 3). These negative relationships are predicted by the metabolic-level boundaries hypothesis, which may also explain why multicellular organisms show metabolic scaling slopes approaching 2/3 at lower metabolic levels than do unicellular organisms because multicellular organisms are much larger and thus typically have significantly smaller body surface area to volume ratios. Dotted lines in panels A and B represent scaling in proportion to body-surface area (b = 2/3) and body mass (b = 1), and according to the 3/4-power law. The elevations of the dotted lines in panel A are arbitrary; these lines are meant only to show specific theoretical slopes for visual comparison with those of the empirical scaling relationships.

Further support for the MLBH comes from comparing organisms with different ecological lifestyles. Animals with active, high L lifestyles tend to exhibit lower b values than those with relatively sedentary, low L lifestyles, as predicted. This pattern is seen for comparisons of endothermic vs. ectothermic vertebrates [21,22], euthermic vs. heterothermic mammals [21], birds and mammals from mesic vs. xeric habitats [21], pelagic vs. benthic fishes [44], winged vs. flightless insects [22], epigeic vs. endogeic earthworm species [85], intertidal vs. subtidal marine gastropods [78], and non-burrowing vs. burrowing marine crustaceans [86].

The above studies clearly show that the classic, widely accepted view of Hemmingsen [2] that the metabolic scaling relationships of unicells, ectotherms and endotherms differ only in scaling elevation, and not scaling slope (b ~ 3/4) should be abandoned (also see [74,87]). Not only do both b and L vary among taxonomic groups, ecological lifestyles and physiological states of both unicellular and multicellular organisms, but also they often covary, as predicted by the MLBH (Figure 3).

3.3. Effects of Environmental Conditions

Various environmental factors (both biotic and abiotic) may influence the scaling of metabolic rate [21,22,24,88]. Here I emphasize ambient temperature (T) because more studies have examined its effects than that of any other environmental factor [21]. The MLBH predicts that b for resting metabolic rate should decrease with increasing T (by increasing L), which is often, but not always observed [21,44,89,90]. Mixed results may be caused by T having multiple effects on various metabolic and physiological processes that have different thermal sensitivities [29]. When interpreting these results, at least two important questions should be asked: (1) were the observed patterns due to differences in native or artificially changed T (i.e., chronic vs. acute T differences); and (2) did the T differences (especially those that were acute) cause changes in activity or other energy-dependent processes and stress responses that were size-specific? The best systems for testing the MLBH prediction of an inverse correlation between b and T (and thus L) are those that involve comparisons of species at their native mean T (thus minimizing stress responses), and those where temperature-induced differences in activity have been minimized or controlled (note that the MLBH predicts positive correlations between b and L for active metabolism, which is the opposite of that predicted for resting metabolism [22]).

So far only two studies have been carried out that compared b and T among species or groups of species at their respective native mean temperatures. Both support the MLBH. An extensive analysis of interspecific relationships between metabolic rate and wet body mass of marine crustaceans at three native temperatures (20, 25 and 29 °C) revealed an inverse correlation between T and b (means ± 95% confidence intervals = 0.781 ± 0.016, 0.725 ± 0.086 and 0.664 ± 0.026, respectively; N = 247, 249 and 212 [91]). Similarly, another major analysis showed an inverse correlation between b and native T for intraspecific scaling relationships among 89 species of teleost fishes [44]. Also supportive of the MLBH is the finding that tropical fish in their native warm water tend to show b values near 2/3 (0.59–0.73 [92]).

Other studies that have controlled for activity have also revealed negative associations between b and T, as predicted by the MLBH. Plants and algae that are incapable of active movement are especially useful for this kind of study. As predicted, in a field study of a mangrove population, b was found to be inversely correlated with T during various seasons (Figure 4 [93]). Unicellular algae also show a negative relationship between b and T [74]. In a laboratory study of the fish C. albula where resting metabolic rate was determined by extrapolating an empirical relationship between metabolic rate and swimming activity to zero, b was again found to decrease with increasing T (Figure 2 [54]). Many other intraspecific studies on various kinds of aquatic and terrestrial animals have revealed negative associations between b and T [21,94,95,96,97,98,99,100,101,102,103,104,105,106,107], but some studies have reported no significant relationship [21,89,90,108,109,110], or more rarely positive [111], concave upward [112,113] or concave downward [114,115] relationships. Apparent exceptions to the inverse b-T pattern predicted by the MLBH may be attributed to (1) some species having metabolic rates with relatively low thermal sensitivity (leading to small changes in L and thus b); (2) temperature induced increases in activity or other energy-demanding processes and stress responses that may affect various size classes equally or unequally (leading to absent, positive or other b-T relationships, depending on the level and size-specificity of the thermally induced activity or stress); (3) thermal induction of activity and or other energy demanding processes that varies over different T ranges (leading to concave b-T patterns); and (4) insufficient acclimation to experimental temperature regimes, thus causing spurious results. These hypotheses require testing.

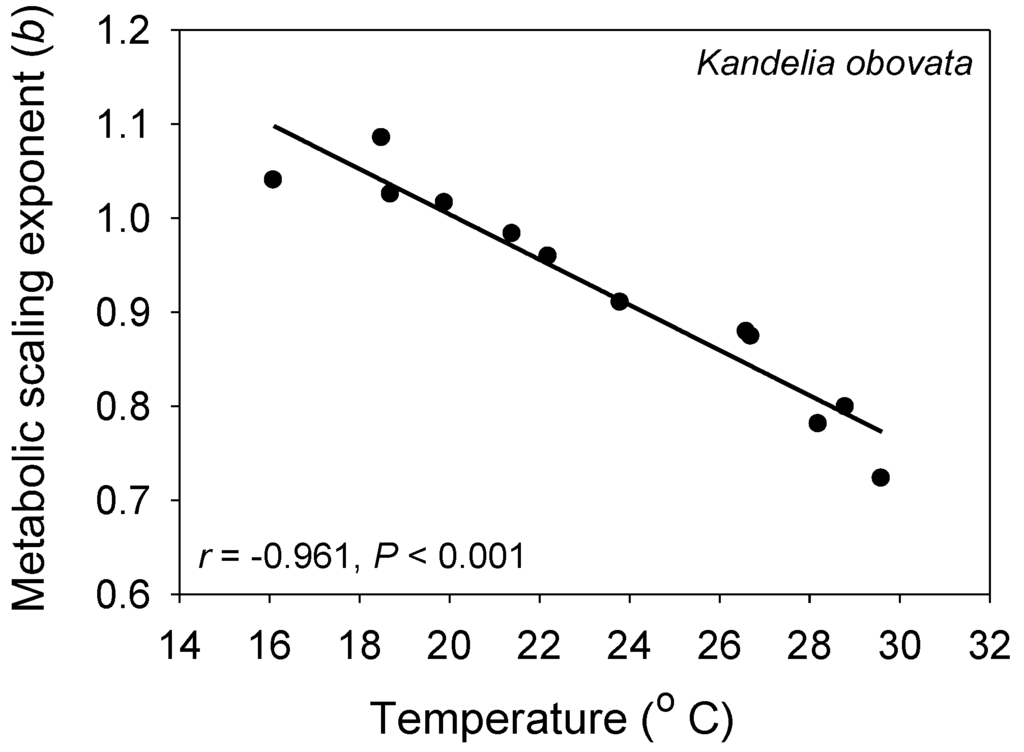
Figure 4. The metabolic scaling exponent (b) of the mangrove tree Kandelia obovata is significantly negatively related to air temperature during different seasons (data from [93]), as predicted by the metabolic-level boundaries hypothesis [21,22].

Figure 4. The metabolic scaling exponent (b) of the mangrove tree Kandelia obovata is significantly negatively related to air temperature during different seasons (data from [93]), as predicted by the metabolic-level boundaries hypothesis [21,22].

T effects on b may be complex because of differential thermal effects on different components of metabolism. Metabolism is not monolithic [23]. T changes can also dissociate the rates of metabolism and other biological processes [29]. Differences in thermal sensitivities among various biological processes and kinds of species [29,116,117,118] suggest that different fitness-related strategies of adaptation or acclimation underlie the variation in b-T relationships that have been observed. For example, it is possible that some animals may respond to increasing T either by remaining motionless to conserve energy (thus resulting in a negative b-T relationship) or by increasing activity in an attempt to escape thermal stress (thus resulting in an absent or positive b-T relationship). Therefore, I feel that we can learn much about the causes of metabolic scaling by further research on T effects, which may not only be of theoretical importance, but also of practical value (e.g., for better understanding the biological and ecological consequences of climate change: also see [89]).

According to the MLBH, other environmental factors that influence L may also affect b. For example, decreased food availability reduces L and increases b in some animal species [21]. Other unfavorable conditions (e.g., pollution, hypoxia or suboptimal seasons) that lower L may also increase b [103,119,120]. However, the fishes Fundulus grandis and Galaxias maculatus show a concave downward relationship between b and oxygen level (and L) [121,122]. By lowering L, mild hypoxia may increase the importance of V-related tissue maintenance demand, but more severe hypoxia may not only lower L still further, but also directly affect the ability of the organism to uptake oxygen through body surfaces, thus increasing the importance of SA on metabolic scaling. The b values for G. maculatus conform nicely to this interpretation (b ~ 1 at mild hypoxia, and b ~ 2/3 at severe hypoxia; see Figure 5), but the b values for F. grandis are quite low at all oxygen levels (0.37 to 0.62 [121]). Oxygen levels may also differentially affect the relative importance of aerobic vs. anaerobic metabolism in small vs. large individuals with relatively high vs. low SA/V ratios, respectively (also see [121,122]).

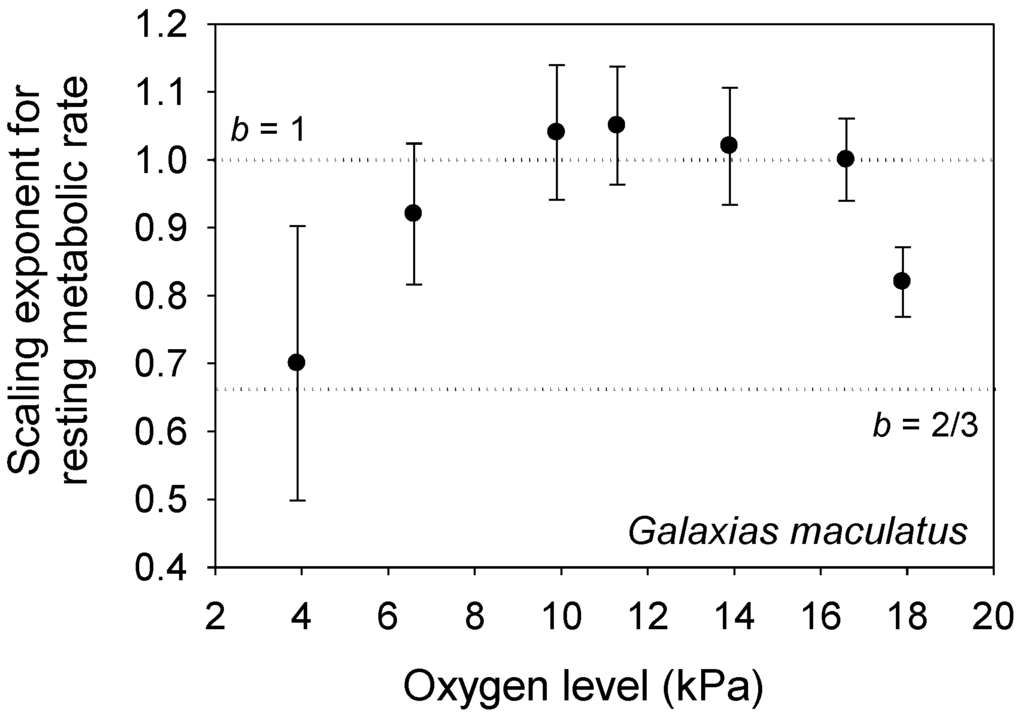
Figure 5. The metabolic scaling exponent (b ± 95% confidence intervals) of the fish Galaxias maculatus shows a concave downward relationship with oxygen level (data from [122] and M. Urbina, personal communication), as predicted by the metabolic-level boundaries hypothesis (see text). The dotted horizontal lines indicate scaling in relation to volume (b = 1) and surface area (b = 2/3).

Figure 5. The metabolic scaling exponent (b ± 95% confidence intervals) of the fish Galaxias maculatus shows a concave downward relationship with oxygen level (data from [122] and M. Urbina, personal communication), as predicted by the metabolic-level boundaries hypothesis (see text). The dotted horizontal lines indicate scaling in relation to volume (b = 1) and surface area (b = 2/3).

4. Reassessing Predictions of the MLBH in the Context of the CMT

Although numerous lines of evidence support the MLBH (Section 3), its predictions are not always upheld. Why? Here I suggest that many, if not all, of the apparent exceptions to the predictions of the MLBH may be explained by viewing the MLBH in the larger framework of the contextual multimodal theory (CMT) proposed in a companion paper [23]. The MLBH focuses on how metabolic level (L) modulates the relative expression of two major kinds of mechanisms involving surface area (SA) related fluxes of resources and wastes vs. volume related resource demand (RD). However, the CMT posits that not only may other factors besides L affect the SA and RD mechanisms, but also two other major kinds of mechanisms involving internal resource transport (RT) and system composition (SC, which concerns the relative contribution that different parts or tissues of an organism make to total metabolic rate) may have important effects as well. Here I highlight some examples of how these contextual effects can alter the predictions of MLBH in significant ways (for further details see [23]).

First, any changes in the permeability of SA or its magnitude relative to volume may affect how b for resting metabolic rate should vary with L. For example, the idealized version of the MLBH predicts that b should approach 2/3 at high resting L, but if body shape changes with increasing body size (thus altering how SA scales with body volume or mass), then other values of b may be predicted. For example, if an organism grows mainly in one or two dimensions, then SA will scale near the 1-power. If so, such an organism should show b values near 1 regardless of L. This prediction could be tested in many kinds of pelagic animals where it is most likely to apply ([43,123]; but see [104]).

Second, if a large proportion of the metabolism of an animal is due to growth or muscular power production, each of which scales near the 1-power, then temperature-related changes in L may have no discernable effect on b (remaining near a constant 1), as has been observed in rapidly growing fish larvae [124] and swimming fish [54,125] and pelagic krill [126].

Third, if metabolic demands of different tissues within an organism are heterogeneous and scale differently with body size (as specified by SC theory), then total body resource demand (RD) may not scale isometrically (as assumed in the idealized version of the MLBH), but may in fact scale with negative allometry (b < 1) regardless of L. Therefore, SC theory predicts that b may be <1 even at low L. This prediction may explain why adult trees show negatively allometric metabolic scaling despite their low L. Trees accumulate increasing proportions of “dead wood” as they grow, thus causing their b values to be <1 in mature trees, but ~1 in immature seedlings and saplings that contain no dead wood (see [23,127,128]). A similar explanation may apply to low-L ticks that also exhibit negatively allometric metabolic scaling [77]. Much of the body mass of ticks consists of metabolically inert exoskeleton, thus allowing for substantial body distension during blood meals [77]). If larger ticks have disproportionately greater exoskeleton masses than smaller ticks, then b values less than 1 should result, a hypothesis requiring testing [23].

Fourth, RD and SC theory may also explain why b values may occur outside the range of 2/3 to 1 predicted by the idealized version of the MLBH. Low b values (<2/3) may result if a metabolically dependent (RD) process scales with strongly negative allometry. For example, populations of the freshwater amphipod Gammarus minus that inhabit springs with fish predators exhibit shallow scaling of energy-expensive growth, which is in turn linked to relatively low b values for resting metabolic rate (0.54–0.62 [88]). In contrast, the thermoregulatory maturation of developing birds and mammals results in steep increases in heating costs, thus causing b values to exceed 1 [21]. Any escalation of RD costs during ontogenetic development may cause b > 1 [23]. SC theory may also explain the positive allometry of metabolic rate observed in embryonic ectothermic organisms that rapidly replace inert storage materials (e.g., yolk) with actively metabolizing tissues [23].

This discussion makes clear that future tests of the MLBH should be made with appropriate consideration of the context-dependency of its predictions. The MLBH focuses on only a portion (albeit an important portion) of the multiple factors and mechanisms that can affect metabolic scaling (see [21,22,23]).

5. Outlook for the MLBH: Future Research Directions

Here I briefly consider important avenues for future research involving the further testing and development of the MLBH.

5.1. Factors Affecting L and b and Their Mechanistic Basis

There is a need to increase our understanding of the various developmental, physiological and ecological factors that can affect L and thus b. Some of these factors have been identified [21,22,23,24,26,27,129,130], but it is likely that many more remain to be discovered. The mechanisms underlying the effects of various factors on L and b also require further investigation. Both proximate (functional) and ultimate (evolutionary) causes of variation in L and b should be identified and explained. Exploration of the effects of temperature (T) on metabolic scaling appears to be an especially promising area for further research given the diversity of relationships between b and T that have been discovered (see Section 3.3). Such studies may result in a modification of the MLBH or the development of new theory.

5.2. Quantitative Extensions of the MLBH

It would be useful to develop a quantitative extension of the MLBH (a QMLBH), which allows for predictions of b based on knowledge of L and body mass (M). This kind of theory is sorely needed for supplying b values to energetic models of various kinds of organisms that previously depended on the now falsified assumption of a universal 3/4 value. The QMLBH could have practical value for predicting the biological and ecological consequences of environmental (e.g., climate) change.

5.3. Hierarchical Expansion of the MLBH

The MLBH was originally devised to help explain the diversity of metabolic scaling at the organismal level [21,22]. Can the MLBH be applied to other hierarchical levels of biological organization? Data showing that b and L are negatively correlated in various groups of unicellular organisms [74] suggests that the MLBH is applicable at the cellular level. It remains to be seen whether the MLBH can also be applied to the cellular, tissue and organ levels within multicellular organisms. In mammals, some organs and tissues with high metabolic levels (e.g., brain, kidney and liver) tend to show lower whole organ metabolic scaling exponents (b = 0.60–0.77) than those with low resting metabolic rates (e.g., skeletal muscle: b = 0.84 [131]), as predicted by the MLBH. The high-L heart appears to be an exception to this pattern (b = 0.86), but since it is always active, its metabolic scaling is actually consistent with the MLBH prediction that b should approach 1 for active metabolism.

Recent findings that b is inversely correlated with L in ascidean colonies with different physiological states [132] and among different species of colonial bryozoans [133] suggests that the MLBH may even be applied to the colony level of organization. However, the inverse b-L pattern observed in bryozoans may be explained in other ways: e.g., by invoking SC theory (i.e., high-L colonies with high growth rates may show disproportionately greater increases in numbers of low-metabolizing zooids with increasing colony size than do low-L colonies with low growth rates (see [23,133]).

5.4. Synthesizing the MLBH with Other Models and Theories

The most obvious models to unite with the MLBH include those focusing on SA and RD theory, which not only lie at the core of the MLBH, but also have the most empirical support of the four major theories recognized by the CMT [23]. Examples of these models include those that show how body-shape changes may affect the scaling of SA and by association resting or routine metabolic rate [42,43], and those that invoke the effects of specific lifestyles on the ontogeny of various energy demanding processes, including growth, reproduction, developmental maturation and behavioral activity [22,23,29,88]. SC theory also helps to explain deviations from the predictions of the MLBH by invoking the effects of differential scaling of the metabolism of high- vs. low-energy tissues or organs (see Section 4). Furthermore, as mentioned in Section 5.3, the MLBH may be used to predict inter-organ differences in metabolic scaling, thus possibly helping to explain SC effects at the whole organism level. RT theory was included in the original version of the MLBH [21,22], but it has yet to provide further explanatory power beyond that already supplied by the modulation of the SA and RD related mechanisms by L [22,23].

Another promising approach may be to unite cell-size theory with the MLBH. According to this theory, small cells can have higher mass-specific metabolic rates than larger cells because their larger SA/V ratio enables more metabolic resources and wastes to be exchanged between a unit volume of cytoplasm and the environment, and because many metabolic activities are linked to cell membranes [35,36,37,134]. On the other hand, large cells may be able to sustain themselves with less energy expenditure per unit volume because of relatively lower costs of maintaining ionic balance [134]. Therefore, one can hypothesize that organisms with small cells should have higher L values than those of related organisms with large cells, as has been observed [51,63,135,136,137]. According to the MLBH, small-celled organisms should also have lower b values than related large-celled organisms. This prediction is confirmed by a comparison of 22 species of non-polyploid teleost fishes: red blood cell (RBC) size is significantly negatively correlated with L, but positively correlated with b (Figure 6). Although RBC size is positively correlated with genome size, genome size is not significantly correlated with either L or b (Figure 6). These data suggest that the surface geometry of cells, rather than their DNA content, is related to L and b. Another possible explanation for the observed associations between RBC size, L and b is that smaller RBCs are better able to exchange oxygen with surrounding tissues than larger RBCs, thus supporting higher levels of aerobic metabolism [138].

The MLBH may also provide insight into why the cell-size model cannot explain all patterns of metabolic scaling, especially those involving organisms with a very high or low L. The cell-size model predicts that b should be 2/3 when an organism grows by cell enlargement (because cell SA scales with body volume or mass to the 2/3-power), but should be 1 when an organism grows by cell multiplication (because cell SA now scales to the 1-power). Intermediate b values should result if growth involves both cell enlargement and multiplication [35,36]. This hypothesis has been tested in insects by using eye-facet size as a proxy for cell size (following [72,139]). The scaling of eye-facet size in insects predicts that b for resting metabolic rate should be 0.776 (±0.022 95% CI) [37], which is not significantly different from the b value based on actually measured metabolic rates (0.75, following phylogenetic correction [72,140]). However, the cell-size model cannot account for why b is near 1 in diapausing insects with a very low L, and in actively flying insects with a very high L [22]. These deviations may occur because at very low and very high L, cell-SA related processes no longer have a significant influence on metabolic scaling. At low inactive L, minimal levels of metabolism are more related to tissue volume than to cellular or organismal SA (thus b is near 1). Similarly, at high active L, maximal levels of metabolism are mostly a function of muscular power production, which also scales to the 1-power (thus again b is near 1).

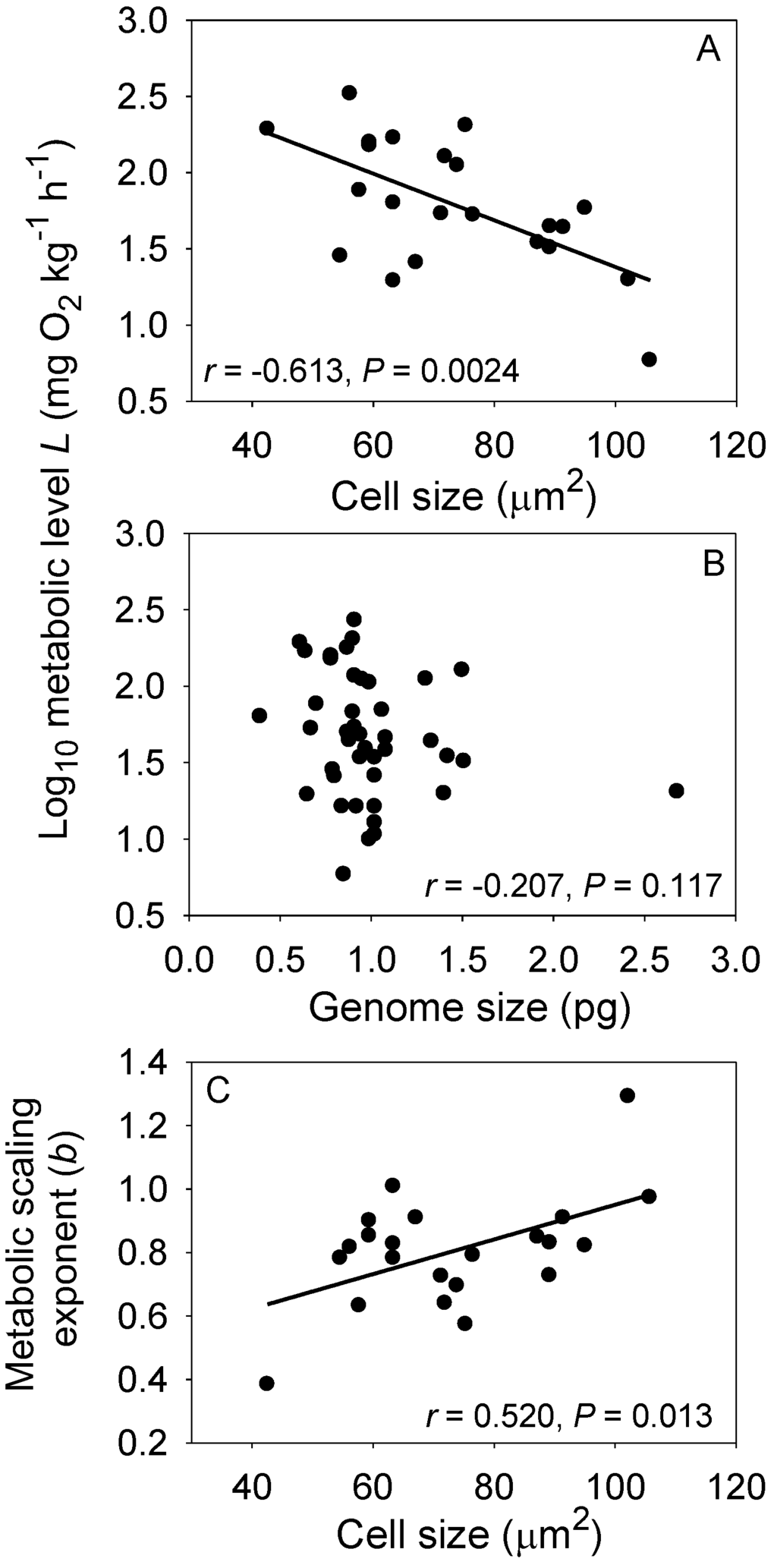
Figure 6. Relationships among resting metabolic level (L), the metabolic scaling exponent (b), cell size (CS: mean red blood cell area) and genome size (GS: DNA content) in 22 non-polyploid teleost fishes (data from Table S1 of [44] and the Animal Genome Size DataBase and Cell Size Database compiled by [141]). Cell size was indexed as the elliptical area (μm²) per red blood cell measured by image analysis or calculated as π(CLD/2)(CSD/2), where CLD is cell long diameter, and CSD is cell short diameter. Genome size was estimated as the haploid DNA contents (C-value, pg) per red blood cell. When multiple values for cell size or genome size were available, the mean of these values was used. In addition, in a few cases when species values for cell size or genome size were not available, values from conspecific species were used. (A) L is significantly negatively correlated with CS; (B) L is unrelated to GS, even though GS is significantly positively correlated with CS (r = 0.602, p = 0.0050); (C) The scaling exponent b is significantly positively correlated with CS, as would be expected because b is inversely related to L [44], a major prediction of the metabolic-level boundaries hypothesis.

Figure 6. Relationships among resting metabolic level (L), the metabolic scaling exponent (b), cell size (CS: mean red blood cell area) and genome size (GS: DNA content) in 22 non-polyploid teleost fishes (data from Table S1 of [44] and the Animal Genome Size DataBase and Cell Size Database compiled by [141]). Cell size was indexed as the elliptical area (μm²) per red blood cell measured by image analysis or calculated as π(CLD/2)(CSD/2), where CLD is cell long diameter, and CSD is cell short diameter. Genome size was estimated as the haploid DNA contents (C-value, pg) per red blood cell. When multiple values for cell size or genome size were available, the mean of these values was used. In addition, in a few cases when species values for cell size or genome size were not available, values from conspecific species were used. (A) L is significantly negatively correlated with CS; (B) L is unrelated to GS, even though GS is significantly positively correlated with CS (r = 0.602, p = 0.0050); (C) The scaling exponent b is significantly positively correlated with CS, as would be expected because b is inversely related to L [44], a major prediction of the metabolic-level boundaries hypothesis.

As another example, b values for mammalian resting metabolism are often near 2/3 (see reviews of [21,22,23,30]), despite the fact that species differences in body size are mainly due to variation in cell number rather than size (b for cell size is only ~0.03–0.05 in mammals [3,142,143]). Once again the cell-size model may not apply because body-SA related heat loss is more important in affecting the metabolic scaling of these endotherms than is cell-SA related processes. As emphasized here and in a companion review [23], the relative expression of various mechanisms causing metabolic scaling depends on the context. The cell-size model appears to be no exception.

5.5. Applying the MLBH to Other Biological Processes

Can the MLBH or a similar boundary approach be applied to the scaling of other biological processes that depend on metabolic energy? Data on algal growth rates support this possibility because they show a negative relationship between their cell- or colony-size scaling slope and elevation similar to that seen for resting metabolic rate [74,144]. Other comparisons of various behavioral, physiological and life-history processes show that their body-mass scaling often differs significantly between endothermic and ectothermic animals in ways that are consistent with similar differences in metabolic scaling predicted by the MLBH [22,145]. For example, rates of reproductive investment (g·individual⁻¹·year⁻¹) scale with slopes that are inversely related to L, which increases successively in plants (b = 0.834), lizards (b = 0.805), mammals (b = 0.63 or 0.685, based on two estimates) and birds (b = 0.48 to 0.77 in a single curvilinear relationship) (data from [146,147,148,149]). Therefore, I believe that the MLBH can contribute to the formulation of a general metabolic theory of biology (also see [23]). However, in doing so, it should be recognized that metabolic rate may not necessarily drive the rates of other biological processes, but may also respond to them in a supportive, co-adjusted way [29].

6. Conclusions

In my opinion, the MLBH shows much promise for continuing to provide insight into the diversity of metabolic scaling relationships existing in the living world, especially if viewed in the context of the CMT [23]. Major features of the MLBH include an emphasis on (1) physical or geometric (SA and V) properties possessed by all organisms and how processes related to them underlie boundary limits on the range of metabolic scaling exponents (b); (2) covariance between the slopes and elevations (L) of metabolic scaling relationships; and (3) the contingent influence of both internal and external factors on both L and b. In essence, the MLBH and the more encompassing CMT view the scaling of metabolic rate as being scaled itself in relation to metabolic level and other modulating factors (thus along multiple dimensions). Metabolic scaling does not follow a universal physical law, but is a product of many contextual influences. Multifaceted, contextual (meta-mechanistic) theories are more likely to provide a comprehensive understanding of diverse patterns of allometric scaling than can unitary, deterministic theories. As I also argue in a companion review [23], the commonly employed “Newtonian” (physical, mechanistic, universal law) approach to metabolic scaling theory should be replaced by a “Darwinian” (adaptive, meta-mechanistic, contingency) approach. In short, my recommendation for biological scaling theory is to become contextualized.