A CNN-LSTM-GRU Hybrid Model for Spatiotemporal Highway Traffic Flow Prediction

Abstract

The rapid growth in the number of motor vehicles has exacerbated traffic congestion. The occurrence of congestion not only poses significant challenges for traffic management authorities but also severely impacts residents’ travel and daily routines. Against this backdrop, predicting traffic flow can provide crucial insights for anticipating changing traffic patterns. Therefore, this paper proposes a novel hybrid deep learning architecture (CNN-LSTM-GRU) for highway traffic flow prediction that integrates spatiotemporal and meteorological dimensions. Our approach constructs a multidimensional feature matrix encompassing temporal sequences, spatial correlations, and weather conditions. Convolutional Neural Networks (CNN) are employed to capture spatial patterns, while Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) networks jointly model temporal dependencies. Through systematic hyperparameter tuning and step-length optimization, we validate the model using real-world traffic data from a provincial highway network. The experimental evaluation analyzes the following two critical dimensions: (1) holiday vs. non-holiday traffic patterns, and (2) the impact of weather data integration. Comparative analysis reveals that our hybrid model demonstrates superior prediction accuracy over standalone LSTM, GRU, and their CNN-based counterparts (CNN-LSTM, CNN-GRU).

1. Introduction

The development of highway infrastructure constitutes a pivotal component in national modernization efforts and serves as the backbone of contemporary transportation networks. Amidst the exponential growth in motor vehicle ownership, highway congestion has emerged as a pressing challenge, with traffic volumes having reached critical thresholds during holiday periods. This phenomenon not only undermines public mobility efficiency but also constrains service quality enhancement, thereby impeding regional economic integration and societal advancement.

Traffic flow dynamics exhibit complex spatiotemporal patterns influenced by multifactorial factors. Crucially, holiday periods and meteorological conditions have been identified as primary determinants of traffic volatility, resulting in nonlinear relationships that traditional prediction models struggle to capture. In response to these challenges, this paper proposes a novel framework for highway traffic prediction that integrates key contextual factors, such as holiday-induced travel patterns and weather conditions, into multidimensional analytics.

In recent years, with the rapid development of deep learning algorithms, an increasing number of models have been employed for traffic flow prediction research. To enhance model accuracy, this paper proposes a hybrid CNN-LSTM-GRU model. This model extracts spatial features from data using Convolutional Neural Networks (CNN) and subsequently captures temporal features through Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) networks. The advantages of this approach are twofold. (1) Spatial Feature Enhancement: By constructing two-dimensional feature matrices of highway network topologies, the CNN effectively captures spatial correlations between adjacent road segments, addressing the limitation of traditional time-series models that often overlook spatial dependencies. (2) Temporal Feature Synergy: The dual-path architecture combining LSTM and GRU preserves LSTM’s strength in long-term memory retention while leveraging the GRU’s computational efficiency, creating a complementary mechanism for temporal sequence analysis. This integrated framework enables more accurate traffic flow prediction by simultaneously modeling spatial dependencies and temporal dynamics, offering a robust solution for modern highway management challenges.

2. Literature Review

Currently, research on short-term traffic flow prediction is diverse, and with the continuous advancement of technology, prediction levels and accuracy are also improving. This section summarizes traffic flow prediction methods based on a review of the existing literature.

Firstly, the most common methods are those based on mathematical statistics, which include both linear and nonlinear models. Linear models include Kalman filtering and historical average models, while nonlinear methods include non-parametric regression models and chaos theory. Guo et al. [1] proposed using Kalman filtering to achieve real-time data processing capabilities, employing process variance to handle real-world data. Wang and Papageorgiou [2] used a macroscopic traffic flow model along with the measurement model, which is designed by use of the extended Kalman-filtering method. Some other researches relied on time series analysis, such as autoregressive integrated moving average models (ARIMA) and their variants (SARIMA), to capture periodic patterns through linear assumptions. The ARIMA method was first proposed in 1979, by Ahmed et al. [3] and applied to traffic flow prediction research. Smith et al. [4] conducted an investigation into the theoretical underpinnings of nonparametric regression, with the dual objectives of establishing its methodological framework and evaluating whether heuristically optimized forecast generation techniques in nonparametric regression could attain traffic flow prediction accuracy comparable to seasonal ARIMA models in single-interval forecasting scenarios. Kumar et al. [5] developed a predictive framework utilizing the Seasonal Autoregressive Integrated Moving Average (SARIMA) model for short-term traffic flow forecasting, achieving reliable performance even when constrained by limited input data. However, this type of method has weak adaptability to nonlinear and unexpected events, and it ignores spatial correlation. For the nonlinearity of complicated urban traffic flow, Chen and Xiao [6] proposed a switching autoregressive integrated moving average (ARIMA) model and employed it to explore how traffic flow varies with time.

There are also many studies that use machine learning algorithms to conduct traffic flow prediction research. Algorithms such as Support Vector Machine (SVM), Random Forest (RF), and k-Nearest Neighbor (k-NN) enhance predictive ability through nonlinear mapping. Zhang et al. [7] developed a high-precision multi-step traffic flow prediction model using Support Vector Machine (SVM) methodology. The framework incorporates actual traffic volume data as input vectors, with a systematic comparison of four distinct input vector configurations conducted to evaluate their comparative predictive performance. Hou et al. [8] developed four traffic flow forecasting models—Random Forest, regression tree, multilayer feed-forward neural network, and nonparametric regression—specifically for planned work zone events. Concurrently, Zhang et al. [9] proposed a short-term traffic flow prediction method using k-Nearest Neighbor (KNN)-based nonparametric regression, systematically analyzing how key parameter configurations influence model performance. Building on these efforts, Lu et al. [10] introduced a hybrid traffic flow prediction framework combining signal decomposition and machine learning. The improved complete ensemble empirical mode decomposition with adaptive noise (ICEEMDAN) was applied to decompose traffic sequences into multiple intrinsic mode functions (IMFs), which were then processed by machine learning algorithms for enhanced predictive accuracy. Nevertheless, traditional machine learning approaches often necessitate extensive manual feature engineering and demonstrate limited capacity in processing high-dimensional spatiotemporal datasets.

In recent years, deep learning has garnered significant attention and has been widely applied to the research of traffic flow prediction. The application of foundational models, such as CNN, enables the effective utilization of spatial convolution to capture topological relationships in road networks. For instance, Zhang et al. [11] proposed ST-ResNet, which models the spatiotemporal correlation of urban traffic flow through residual CNN. LSTM, with its gating mechanism addressing long-range dependencies, has become a benchmark for processing temporal data. Ma et al. [12] were the first to apply LSTM to traffic prediction, demonstrating its superiority over traditional methods. Additionally, numerous studies have integrated various models for traffic flow prediction. The spatiotemporal fusion architecture, constructed by combining CNN and LSTM [13], extracted the temporal dependencies of spatial features and models. Mackenzie et al. [14] used HTM (Hierarchical Temporal Memory) to integrate and evaluate data from the adaptive traffic system on the main roads of Sydney and Adelaide. The results showed that HTM achieved comparable prediction outcomes to the LSTM model. Tian et al. [15] proposed using multi-scale temporal smoothing to infer missing data and conducted comparisons on the PEMS dataset and their own dataset. Experiments demonstrated that this method achieved high accuracy. Feng et al. [16] proposed the AMSVM-STC model based on support vector machines to accurately predict traffic congestion. They used an adaptive particle swarm optimization algorithm to find optimal parameters. The validation of datasets showed that, even during periods of abnormal traffic flow fluctuations, the model could provide accurate and timely predictions, outperforming the results of other mentioned models. This has further evolved into a combination of 3D convolution (C3D) and Transformer [17], enhancing multi-scale feature extraction. For the non-Euclidean structure of road networks, Graph Neural Networks (GNNs), such as GCN and GAT, capture inter-node relationships through graph convolution. The DCRNN model proposed by Li et al. [18], which combines graph diffusion convolution with sequence modeling, has become a classic framework.

In the research on predicting traffic flow on highways, due to the periodicity of highway traffic flow, a certain section of road has a relatively stable flow and change trajectory at the same time period in different historical times. Therefore, historical time is considered an important entry point for predicting traffic flow. Fang et al. [19] added an attention mechanism to the LSTM model, effectively assigning different weights to different inputs of the model and focusing on filtering important information. After, four datasets were used as examples to prove that this model has good accuracy. Shuai et al. [20] decomposed the traffic flow components through SSA, predicted the traffic flow through LSTM and SVR, and finally combined their respective prediction results to obtain the final prediction results. Through the verification of the traffic flow data of the Guizhou expressway, it was concluded that the combined model based on component decomposition was superior to the single model. Bing et al. [21] proposed a multi-step prediction method consisting of VMD and LSTM. The VMD algorithm decomposes traffic flow into IMF components, and each LSTM predicts one component before integrating the predictions. Xu et al. [22] proposed using the whale optimization algorithm to optimize the structure of the BiLSTM-Attention network, and using this algorithm to find the best parameters to input into the network structure, they formed the WOA_BiLSTM-Attention model.

At the same time, during the process of reading the literature, it was found through induction and summary that traffic flow prediction considering time and space has also formed quite rich results. Due to the high degree of closure of highways, the traffic flow of a certain section will be affected by the upper and lower nodes; thus, it is necessary to consider the spatial impact of highways. Zheng et al. [23] considered spatiotemporal correlation in the prediction of urban road network traffic flow, selected similar and target road segments as independent and dependent variables, and finally used them as inputs for CNN-LSTM traffic flow prediction. The final results showed that, compared with other models, this model has higher accuracy. Zheng et al. [24] proposed using an attention mechanism on the basis of Conv LSTM to solve the problem of poor spatial feature capture, and using multi-layer architecture for feature extraction to improve the capturing power of Bi LSTM on temporal features, they thereby improved the overall prediction accuracy of the model. Some combination models have also been proposed for short-term traffic flow prediction research, i.e., Bi-LSTM-CNN [25] and GTO-CNN-LSTM [26].

Traffic flow prediction is influenced by a multitude of factors. Beyond the inherent temporal and spatial characteristics of traffic flow itself, it is also affected by fundamental elements such as driver behavior and road conditions. These conventional factors can generally be categorized as routine influences, as their impact on traffic flow tends to remain relatively stable. This study, however, places particular emphasis on analyzing the effects of dynamic factors—including weather conditions, holidays, and other time-varying elements—on traffic flow. For instance, adverse weather such as rain or snow can render road surfaces slippery to varying degrees, compromising driver control, reducing vehicle speeds, and ultimately leading to congestion. Similarly, holidays often induce significant fluctuations in highway traffic flow, with notable surges observed before and after holiday periods. Hence, this research aims to integrate these dynamic factors (weather, holidays, etc.) with the intrinsic temporal and spatial attributes of traffic flow to develop a more comprehensive predictive framework.

In terms of prediction methods, the combination model can better utilize the advantages of each model and fully explore data features. Therefore, in this study, a combination model based on LSTM-GRU is constructed. CNN is used to better extract spatial features of the data and to complete the prediction.

3. Data Sources and Characteristics Analysis

3.1. Data Sources and Preprocessing

The dataset used in this study consists of traffic flow data and weather data collected from toll stations on a provincial highway from 19 July 2016 to 24 October 2016. The traffic flow data include entry and exit traffic data from three toll stations, labeled as Station 1, Station 2, and Station 3. Each toll station has two directions (0 and 1), where 0 represents the entrance and 1 represents the exit. Station 2 was only allowed to enter the highway due to maintenance, which is a one-way passage. The weather data span from 19 July 2016, 00:00, to 24 October 2016, 24:00, and includes the following seven fields: atmospheric pressure, sea-level pressure, wind direction, wind speed, temperature, humidity, and rainfall.

The raw traffic flow data were collected at a frequency of 20 min. Specifically, the entrance of toll Station 1 contains 2084 records, the exit of toll Station 1 contains 2084 records, the exit of toll Station 2 contains 1725 records, the entrance of toll Station 2 is 0 in this dataset, the exit of toll Station 3 contains 2086 records, and the entrance of toll Station 3 contains 2085 records.

The weather data consist of 231 records collected at a frequency of every 3 h.

Preprocessing raw data is an essential and critical step in data mining, machine learning, and artificial intelligence. Data collected directly often lack quality assurance, with missing values being a common issue due to machine malfunctions or human errors. Missing data can lead to errors during feature extraction, thereby affecting prediction accuracy. Linear interpolation, the simplest form of algebraic interpolation, is widely used for handling nonlinear functions. Therefore, this study employs linear interpolation to fill in missing values.

The traffic flow data for direction 1-0 from 19 July 2016 to 24 October 2016 contain four missing values. The traffic flow data for direction 2-0 during the same period contain 362 missing values. The traffic flow data for direction 3-0 contain two missing values. The traffic flow data for direction 1-1 contain four missing values, and the traffic flow data for direction 3-1 contain three missing values. Below is a portion of the raw traffic flow data table for direction 1-0, which includes one missing value, as shown in

Table 1. The original data of the 1-0 station entrance direction somewhere missing value and its filling value processing.

Tollgate_ID	Time_Window	Direction	Volume
1	[2016-10-01 22:40:00, 2016-10-01 23:00:00]	0	41
1	[2016-10-01 23:00:00, 2016-10-01 23:20:00]	0	35
1	[2016-10-01 23:20:00, 2016-10-01 23:40:00]	0	16
1	[2016-10-01 23:40:00, 2016-10-02 00:00:00]	0
1	[2016-10-02 00:00:00, 2016-10-02 00:20:00]	0	13
1	[2016-10-02 00:20:00, 2016-10-02 00:40:00]	0	7
1	[2016-10-02 00:40:00, 2016-10-02 01:00:00]	0	3

. The missing value is filled using the mean imputation method. Since the data represent the number of vehicles passing through at 20 min intervals, the repaired data are rounded to 14.5. Due to the large number of missing values in direction 2-0, likely caused by detector malfunctions, linear interpolation is used for filling.

Since the weather data collection frequency differs from the traffic flow data, linear interpolation is applied to align the weather data frequency to 20 min, resulting in a total of 2088 weather data records. A portion of the filled weather data is shown in

Table 2. Weather data linear interpolation filling result table.

Time_Window	Pressure (hPa)	Sea_Pressure (hPa)	$\mathbf{Wind}\text{\_}\mathbf{Direction}$ (°)	Wind_Speed (m/s)	Temperature (°C)	Rel_Humidity (%)	Precipitation (mm)
[2016-09-19 00:00:00, 2016-09-19 00:20:00]	1008.2	1013.2	329	2.8	22.2	76	0
[2016-09-19 00:20:00, 2016-09-19 00:40:00]	1008.213	1013.213	289.75	3.0125	22.475	74.875	0
[2016-09-19 00:40:00, 2016-09-19 01:00:00]	1008.225	1013.225	250.5	3.225	22.75	73.75	0
[2016-09-19 01:00:00, 2016-09-19 01:20:00]	1008.238	1013.238	211.25	3.4375	23.025	72.625	0
[2016-09-19 01:20:00, 2016-09-19 01:40:00]	1008.25	1013.25	172	3.65	23.3	71.5	0
[2016-09-19 01:40:00, 2016-09-19 02:00:00]	1008.263	1013.263	132.75	3.8625	23.575	70.375	0

.

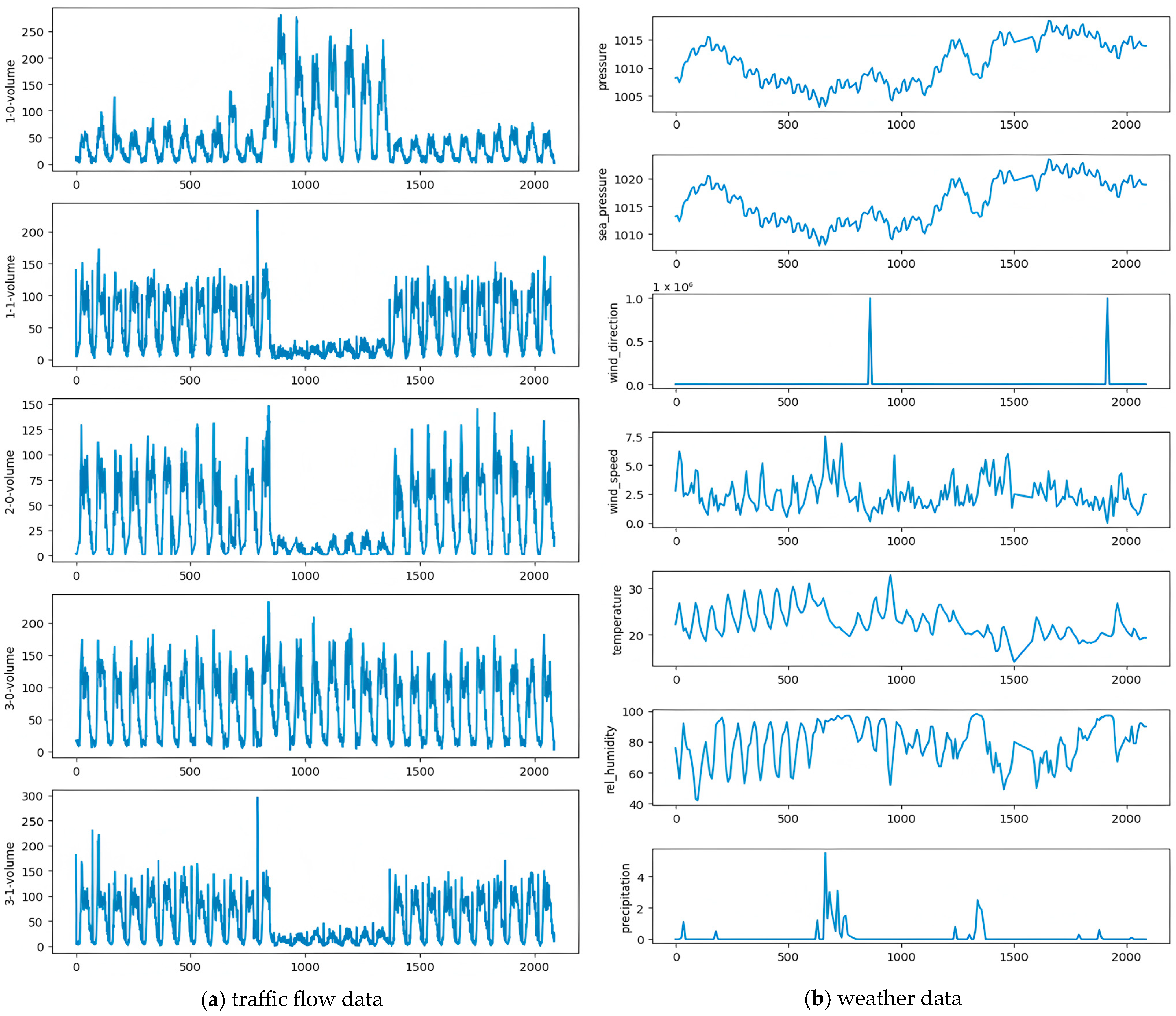
Data visualization is crucial for in-depth analysis and trend prediction. By presenting traffic flow and weather data in graphical form, it helps uncover patterns over time and space, explore correlations between the two, analyze long-term traffic demand trends, and provide scientific references for future traffic flow predictions and traffic management under extreme weather conditions.

Therefore, to better observe the characteristics of the data, visualizations of the features of traffic flow data and weather data are provided, as shown in Figure 1 below.

From the figure, it can be observed that the traffic flow trends at each station are similar over certain periods. When studying traffic flow prediction, integrating data from all stations can be considered. Additionally, understanding traffic flow trends can help traffic management departments to allocate resources more effectively and to simplify management models.

Based on the previous analysis, periodic changes in traffic flow, holidays, and weather are key factors influencing traffic flow. Therefore, the weather and traffic flow data are integrated here, with a portion of the data shown in

Table 3. Traffic flow and weather data integration table.

Time_Window	Pressure (hPa)	Sea_Pressure (hPa)	Wind_Direction (°)	Wind_Speed (m/s)	Temperature (°C)	Rel_Humidity (%)	Precipitation (mm)	Tollgate_ID	Direction	Volume
[2016-09-19 00:00:00, 2016-09-19 00:20:00]	1008.2	1013.2	329	2.8	22.2	76	0	1	0	3
[2016-09-19 00:20:00, 2016-09-19 00:40:00]	1008.213	1013.213	289.75	3.0125	22.475	74.875	0	1	0	6
[2016-09-19 00:40:00, 2016-09-19 01:00:00]	1008.225	1013.225	250.5	3.225	22.75	73.75	0	1	0	9
[2016-09-19 01:00:00, 2016-09-19 01:20:00]	1008.238	1013.238	211.25	3.4375	23.025	72.625	0	1	0	0
[2016-09-19 01:20:00, 2016-09-19 01:40:00]	1008.25	1013.25	172	3.65	23.3	71.5	0	1	0	4
[2016-09-19 01:40:00, 2016-09-19 02:00:00]	1008.263	1013.263	132.75	3.8625	23.575	70.375	0	1	0	10

below.

After integration, this study finds that the data features are not on the same scale, which could affect prediction accuracy. Therefore, before analysis, the obtained data were normalized. This study employs the commonly used min–max method for data normalization, scaling the data to a range between 0 and 1. The min–max method is shown in Formula 1 below:

$$x{’}_i={\displaystyle \frac{x_i-x_{min}}{x_{max}-x_{min}}}$$

(1)

where $x_i$ represents the original data, ${x_i}^{\prime }$ represents the normalized data, $x_{min}$ is the minimum value, and $x_{max}$ is the maximum value.

3.2. Analysis of Highway Traffic Flow Characteristics

Highway traffic flow, as a crucial indicator reflecting the operational status of road transportation systems, is shaped and driven by a series of complex internal conditions and external environments. Therefore, to better predict traffic flow, it is necessary to analyze both internal and external characteristics.

(1)

Analysis of Internal Traffic Flow Characteristics

(a).

Periodicity

The periodicity analysis of highway traffic flow focuses on temporal characteristics, primarily manifested in daily and weekly cycles, exhibiting both complexity and regularity. As shown in Figure 2, the data represent traffic flow from 00:00 on 7 October 2016 to 00:00 on 8 October 2016 in Figure 2a. It can be observed that the traffic flow exhibits significant fluctuations within a single day, indicating strong complexity. Figure 2b shows the traffic flow data from 19 September 2016 to 25 September 2016, revealing a high degree of similarity in traffic flow trends over a week, with peak commuting times being largely consistent. Figure 2c displays traffic flow data from 21 September 2016 to 11 October 2016, including both workdays and holidays. The data show two distinct patterns, but within individual workdays or holiday periods, the trends remain similar.

By leveraging long-term accumulated highway traffic data, these periodic phenomena can be precisely quantified, and the patterns can be used to predict future traffic conditions. This, in turn, guides the optimal allocation of traffic resources and the design of more accurate and efficient traffic management and control measures. Additionally, the results of the periodicity analysis provide indispensable scientific support for highway system expansion plans and the development of emergency response strategies for unexpected events.

(b).

Spatial Correlation

In the highway system, the spatial correlation of traffic flow refers to the inherent connections and influencing mechanisms between traffic volume, density, and speed across different road segments. Understanding this characteristic allows for a global analysis of the operational patterns of the traffic system. This not only provides recommendations for optimizing existing traffic management models but also enables better allocation of road resources to alleviate congestion. In the long term, grasping the spatial correlation of highway traffic flow helps in designing more forward-looking and adaptable road network layouts, thereby enhancing the operational efficiency and service quality of the road transportation system.

Figure 3 shows the traffic flow trends from 20 September 2016 to 29 September 2016 for the 0-direction of the three adjacent toll stations (Station 1, Station 2 and Station 3). It can be observed that the traffic flow changes at adjacent stations are highly correlated, with consistent trends.

(2)

Analysis of External Traffic Flow Characteristics

Traffic flow has uncertainty, which means that the influence of other factors outside the transportation system can cause dynamic changes in traffic flow. According to daily experience, the occurrence of unconventional congestion is usually due to factors such as commuting time, holidays, and weather. In order to achieve a more accurate prediction of highway traffic flow, this article integrates the impact of key factors on traffic flow and conducts research.

The Pearson correlation analysis method is used to calculate the correlation between dynamic weather factors and traffic flow. The Pearson correlation coefficient is calculated using Formula (2) as follows:

$$r={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(X_i-\overline{X}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}}$$

(2)

The strength of the correlation results is judged based on the range shown in

Table 4. Correlation coefficient value and intensity correspondence table.

$\mathbf{Correlation} \mathbf{Coefficient} (\left|\mathit{r}\right|$) Range	Strength of Correlation
$0.8\le \left|r\right|\le 1$	Very Strong
$0.6\le \left|r\right|\le 0.8$	Strong
$0.4\le \left|r\right|\le 0.6$	Moderate
$0.2\le \left|r\right|\le 0.4$	Weak
$0\le \left|r\right|\le 0.2$	Very Weak or No Correlation

below.

The calculation results are shown in Figure 4.

As shown in Figure 4, we found that the correlations between Station 1-0 and other stations are 0.65, 0.74, 0.64, and 0.60, all above 0.6, indicating strong correlations between the traffic flows at different stations. Therefore, when predicting traffic flow at a target station, the traffic flow data from other stations should also be considered.

Taking Station 1-0 as an example, the correlations between traffic flow and weather factors such as atmospheric pressure (pressure), sea-level pressure (sea_pressure), wind direction (wind_direction), wind speed (wind_speed), temperature (temperature), and relative humidity (rel_humidity) are −0.14, −0.017, 0.09, 0.03, 0.039, and 0.14, respectively, all below 0.2. This indicates that these factors have almost no correlation with the traffic flow data at this station. However, the correlation between precipitation (precipitation) and traffic flow data is 0.35, indicating a strong correlation. This also proves that natural factors like weather do indeed influence traffic flow.

4. Methodology

LSTM (Long Short-Term Memory) and GRU (Gated Recurrent Unit) are models developed to address the vanishing gradient problem encountered by recurrent neural networks (RNNs) when processing continuous and lengthy data. Both models introduce gating mechanisms to more effectively regulate the flow and storage of information, thereby improving the processing of time-series data. While LSTM can finely handle long-term dependencies, its structure is complex. On the other hand, GRU has a simpler structure but sacrifices some prediction accuracy. Therefore, this study adopts an integrated LSTM-GRU approach to leverage the strengths of both models in handling long-term dependencies. However, neither model can process the spatial features in traffic flow data. To address this, the study incorporates CNN (Convolutional Neural Network) to extract spatial features and validates the model using highway traffic flow data and weather data from a specific province.

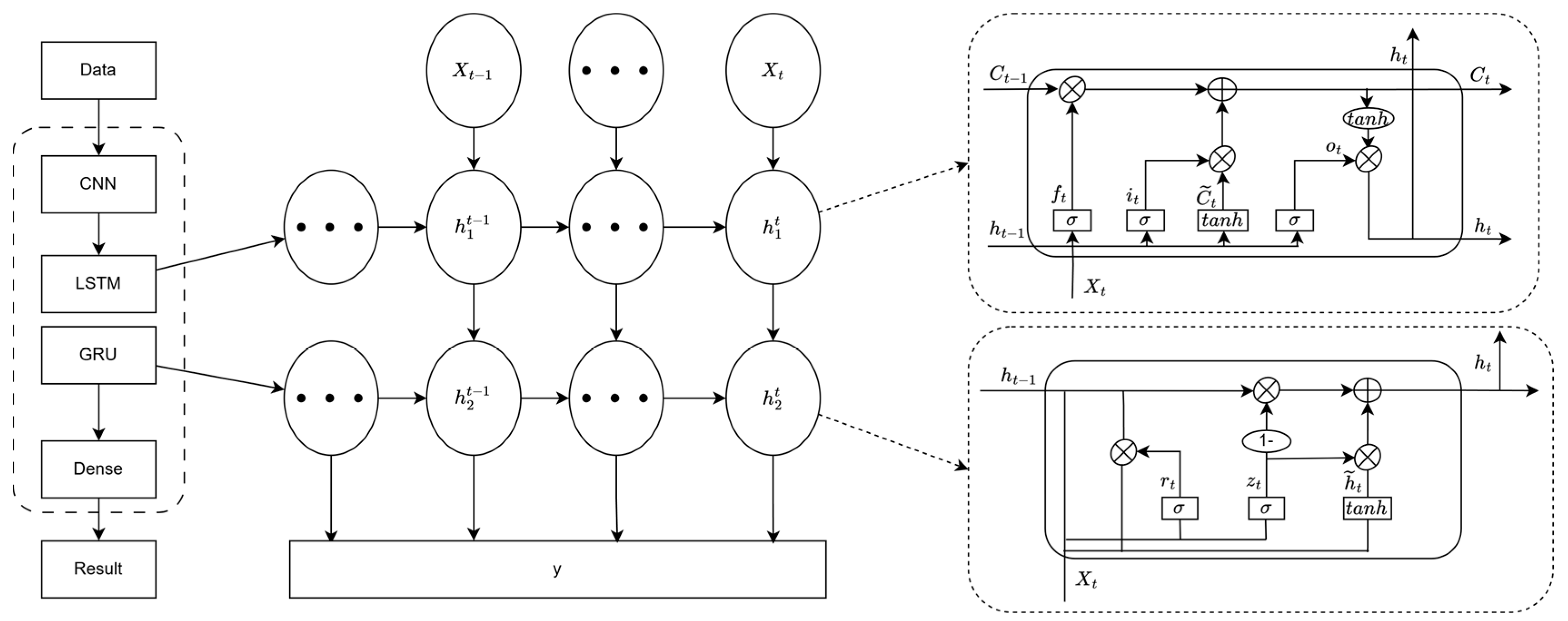
4.1. Model Architecture Design

The architecture mainly consists of three parts, which are data preprocessing, feature matrix construction, and model building. First, missing values in the raw traffic flow and weather data are filled, and the data are normalized. Then, the processed data are constructed into a matrix containing time, space, and weather features, which serves as the input to the model. In the model phase, the CNN is used to extract spatial features, while a combination of LSTM and GRU layers processes the temporal features. Finally, a fully connected layer (Dense) is used to output the results. The main architecture of the model is shown in Figure 5 below.

When extracting temporal features using LSTM-GRU, the Keras Sequential model is first used, with an LSTM layer embedded using the add function. The parameter return_sequences is set to True. Then, a GRU layer is added, using the output of the LSTM layer as its input. Finally, a fully connected layer (Dense) and an output layer are appended to obtain the final prediction. The specific structure is shown in Figure 6 below.

(1)

The LSTM layer mainly includes structures such as the forget gate, input gate, and output gate. The calculation process is shown in Formulas (3)–(8) below:

$$f_t=\sigma \left(f_t\right)=\sigma \left(W_{xf}{x}_t+W_{hf}{h}_{t-1}+b_f\right)$$

(3)

$$i_t=\sigma \left(i_t\right)=\sigma \left(W_{xi}{x}_t+W_{hi}{h}_{t-1}+b_i\right)$$

(4)

$${\tilde{C}}_t=\mathit{tanh}\left(c_t\right)=\mathit{tanh}\left(W_{xg}{x}_t+W_{hg}{h}_{t-1}+b_g\right)$$

(5)

By integrating the above formulas, the following calculation formula is derived:

$$c_t=c_{t-1}\ast f_t+{\tilde{C}}_t\ast i_t$$

(6)

where $x_t$ represents the input variable at the current time step. $h_{t-1}$ represents the hidden state at the previous time step. $c_{t-1}$ represents the cell memory at time $t-1$. $c_t$ represents the cell memory at time $t$. $\widetilde{C_t}$ represents the candidate cell memory. $W$ represents the weight matrices for the input state and hidden state. $b$ represents the value of bias.

$$m_t=\mathit{tanh}\left(c_t\right)$$

(7)

$$h_t=o_t\ast m_t$$

(8)

The hidden state $h_{t-1}$ and input $x_t$ are processed through the output gate’s Sigmoid function to calculate $o_t$. The cell memory $c_t$ is activated using the tanh function, ultimately yielding the updated hidden state $h_t$.

(2)

The GRU layer mainly includes the reset gate and update gate. The calculation process is shown in Formulas (9)–(13) below:

$$r_t=\delta \left(W_r\cdot \left[h_{t-1},x_t\right]\right)$$

(9)

$$z_t=\delta \left(W_z\cdot \left[h_{t-1},x_t\right]\right)$$

(10)

$${\tilde{h}}_t=\mathit{tanh}\left(W\cdot \left[r_t\ast h_{t-1},x_t\right]\right)$$

(11)

$${\tilde{h}}_{t-1}=r_t\ast h_{t-1}$$

(12)

$$h_t=\left(1-z_t\right)\ast h_{t-1}+z_t\ast {\tilde{h}}_t$$

(13)

where $r_t$ represents the portion of the hidden state from the previous time step that needs to be reset. $\delta$ is a Sigmoid activation function ranging from 0 to 1, quantifying the degree of selective forgetting. $h_{t-1}$ represents the hidden state from the previous time step. $x_t$ is the current input. $W_r$ is the relevant weight matrix.

$z_t$ represents the degree of retention for the current data, ranging from 0 to 1. A value closer to 0 indicates more forgetting, while a value closer to 1 indicates more retention.

During the calculation of $\widetilde{h_t}$, the reset data are first combined with $h_{t-1}$ to obtain ${\tilde{h}}_{t-1}$. Then, ${\tilde{h}}_{t-1}$ is combined with $x_t$ and scaled using the tanh function.

Finally, the updated hidden state $h_t$ is obtained.

4.2. Construction of the Two-Dimensional Matrix

As mentioned earlier, highway traffic flow is influenced by both internal and external factors. Specifically, since traffic flow is time-series data, historical data are required for traffic flow prediction to forecast future traffic based on historical trends. Additionally, traffic flow at adjacent stations and upstream/downstream stations can also impact the target station’s traffic flow. External dynamic factors can cause fluctuations in traffic as well. Therefore, considering these aspects, a matrix containing time, space, and weather features is constructed.

The specific calculation method is shown in Formula (14) below:

$$D=\left[\begin{array}{l}\begin{array}{c}{S}_1\\ S_2\\ S_3\\ ⋮\\ W_1\\ W_2\\ ⋮\end{array}\\ Wm\end{array}\right]=\left[\begin{array}{cccc}{S}_{11}& S_{12}& \dots & S_{1\mathrm{t}}\\ S_{21}& S_{22}& \dots & S_{2t}\\ S_{31}& S_{32}& \dots & S_{3t}\\ & & ⋮& \\ S_{m1}& S_{m2}& \dots & S_{mt}\\ & & ⋮& \\ W_{11}& W_{12}& \dots & W_{1t}\\ W_{21}& W_{22}& \dots & W_{2t}\\ & & ⋮& \\ W_{m1}& W_{m2}& \dots & W_{mt}\end{array}\right]$$

(14)

where $S_1,S_2,S_3\dots$ represent the traffic flow data, $W_1,\dots ,W_m$ represent the weather data for the same time period. $S_1,S_2,S_3\dots$ contain two types of data; one is the historical traffic flow data of the station itself, and the other is the traffic flow data from adjacent stations. The horizontal data in the matrix are sorted in chronological order, representing $t$ historical data points.

4.3. Model Parameter Settings

The configuration of the model’s network structure significantly impacts its predictive performance. For the highway toll station traffic flow data in this study, parameters such as the number of filters, convolution kernels, pooling layers, LSTM layers and units, GRU layers and units, learning rate, and optimizer are determined to suit the model.

First, the learning rate and step size are determined. The fixed parameter method is used to find the optimal learning rate.

Table 5. Model error value under different learning rates.

Learning Rates	0.001	0.002	0.003	0.004	0.005	0.006
MAE	5.016	5.992	6.043	4.940	4.965	6.278
RMSE	6.798	8.086	8.022	7.297	6.542	7.984

shows the model’s MAE and RMSE values under different learning rates.

From the table, it can be observed that, when the learning rate is 0.005, the model’s error values are relatively the smallest. Therefore, the learning rate is set to 0.005.

Next, with the learning rate fixed at 0.005,

Table 6. Model error value under different iteration times.

Epoch	1	25	50	100	150	200	250	300
MAE	23.947	9.389	7.441	5.270	5.873	5.370	4.795	5.767
RMSE	31.151	13.062	12.005	7.170	9.014	7.185	6.801	9.890

shows the MAE and RMSE values of the model under different iteration counts.

From the table, it can be concluded that, when the iteration count is 250, the model’s error values are relatively the smallest. Thus, the iteration count is set to 250.

The number of filters is set to 3, with values of 224, 104, and 72. The number of convolution kernels is set to 3, with values of 6, 5, and 6. The pooling layers are set to 2. The LSTM layers and units are set to 1 and 128, respectively. The GRU layers and units are set to 1 and 96, respectively. The learning rate is fixed at 0.005, and the Adam optimizer is chosen. Other parameter settings are shown in

Table 7. Parameter setting table.

Parameter Name	Value
Number of maxpool	2
Number of dropout	3
Number of LSTM layers	1
Number of GRU layers	1
Number of con_filters	224, 104, 72
Number of con_kernels	6, 5, 6
Number of dropouts	0.2, 0.3, 0.4
Unit number of each LSTM layer	128
Unit number of each GRU layer	96
Learning rate (lr)	0.005
Optimizer	Adam

below.

4.4. Sliding Window and Evaluation Metrics

When handling time-series data prediction tasks, the model’s prediction accuracy is indeed influenced by the sequence length setting. Given this, this study adopts the sliding window technique to select an appropriate sequence length. The sliding window method is an effective approach for processing array or sequence data structures by setting a fixed window size, which can simplify multiple loops into a single loop in specific scenarios, thereby reducing computational complexity.

The choice of window size directly affects the number of generated samples and the number of time-step features included in the samples. In other words, in a given dataset, a smaller window means capturing shorter time segments, resulting in more independent samples. Conversely, a larger window captures longer time spans, resulting in fewer samples. Therefore, selecting an appropriate window size is crucial for accurately predicting traffic flow.

In terms of evaluation metrics, with reference to the approaches in [27,28], the study employs MAE (Mean Absolute Error) and RMSE (Root Mean Square Error) to evaluate the predictive performance of the regression model. RMSE is sensitive to extreme values in the data and measures the gap between predicted results and actual observations. MAE calculates the average of the absolute errors between predicted values and true values, intuitively reflecting the average level of model prediction bias. The mathematical formulas for these two evaluation metrics are as follows:

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum }_{i=1}^n\left|y_i-y_i^{\ast }\right|$$

(15)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum }_{i=1}^n{\left(y_i-y_i^{\ast }\right)}^2}$$

(16)

where $y_i$ and ${y_i}^{\mathrm{*}}$ represent the true values and predicted values, respectively.

Given the above reasons, it is necessary to calculate the appropriate time step size for the highway dataset of the province. The step sizes were set to 72 (1 day), 144 (2 days), 216 (3 days), 288 (4 days), 360 (5 days), 432 (6 days), 504 (7 days), and 576 (8 days), and the MAE and RMSE values are calculated for each. The specific results are shown in

Table 8. Values of MAE and RMSE under different window sizes.

Window Size	MAE	RMSE
72 (1 day)	13.310	19.230
144 (2 day)	11.681	15.638
216 (3 day)	10.148	13.487
288 (4 day)	10.108	13.255
360 (5 day)	9.363	12.581
432 (6 day)	6.393	8.949
504 (7 day)	4.761	6.250
576 (8 day)	5.283	7.456

below.

From the table, it can be observed that, when the window size is 504 (7 days), the MAE and RMSE values are the lowest, indicating that the model’s prediction results are better under this window size. Based on these results, the window size is ultimately set to 504.

5. Results Comparison and Analysis

The experimental results in this section are analyzed from the following two perspectives: whether it is a holiday and whether weather factors are included. To better demonstrate the predictive performance of the proposed model, this study compares it with four other models, which are LSTM, GRU, CNN-LSTM, and CNN-GRU. The following presents the comparison of prediction results.

5.1. Comparison and Analysis of Workday Traffic Flow Prediction Results

This study takes 11–17 October 2016 as the prediction target for workdays and calculates the prediction errors of the model for each station, direction, and date, as shown in

Table 9. Prediction error of the CNN-LSTM-GRU model for seven-day working days.

Date	Toll Station and Direction
	1-0		1-1		2-0		3-0		3-1
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
11	3.767	4.781	7.097	10.198	3.202	4.765	5.873	8.048	8.865	12.889
12	3.284	4.462	6.291	9.283	3.512	4.791	5.780	7.988	7.099	9.786
13	3.894	4.871	6.912	10.305	3.492	5.710	5.953	9.778	8.133	10.867
14	4.515	5.842	7.460	10.392	4.576	7.345	6.473	10.089	7.914	11.410
15	4.346	6.468	5.928	8.135	4.156	6.807	5.655	9.319	8.706	14.579
16	4.492	5.992	7.228	10.142	4.682	6.978	8.656	12.995	8.432	11.772
17	5.955	7.857	10.929	16.878	5.676	7.870	7.892	10.558	10.170	14.542
Average	4.322	5.860	7.406	11.073	4.185	6.427	6.612	9.951	8.474	12.379

below.

To better evaluate the model’s prediction accuracy,

Table 10. Average prediction error of the 5 models for seven-day working days.

Date	Models
	LSTM		GRU		CNN-LSTM		CNN-GRU		CNN-LSTM-GRU
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
1-0	5.125	7.103	5.125	7.103	4.611	6.525	4.476	6.040	4.322	5.860
1-1	9.427	14.457	10.032	16.379	7.784	11.744	8.138	12.626	7.407	11.073
2-0	6.480	9.377	6.551	9.434	5.617	8.175	5.711	8.206	4.185	6.427
3-0	8.643	12.592	8.523	12.426	7.239	10.193	6.966	10.067	6.612	9.951
3-1	9.008	17.222	10.865	16.977	10.511	16.819	10.522	15.931	8.474	12.379

provides a comparison of the average prediction errors of the five models for 11–17 October 2016.

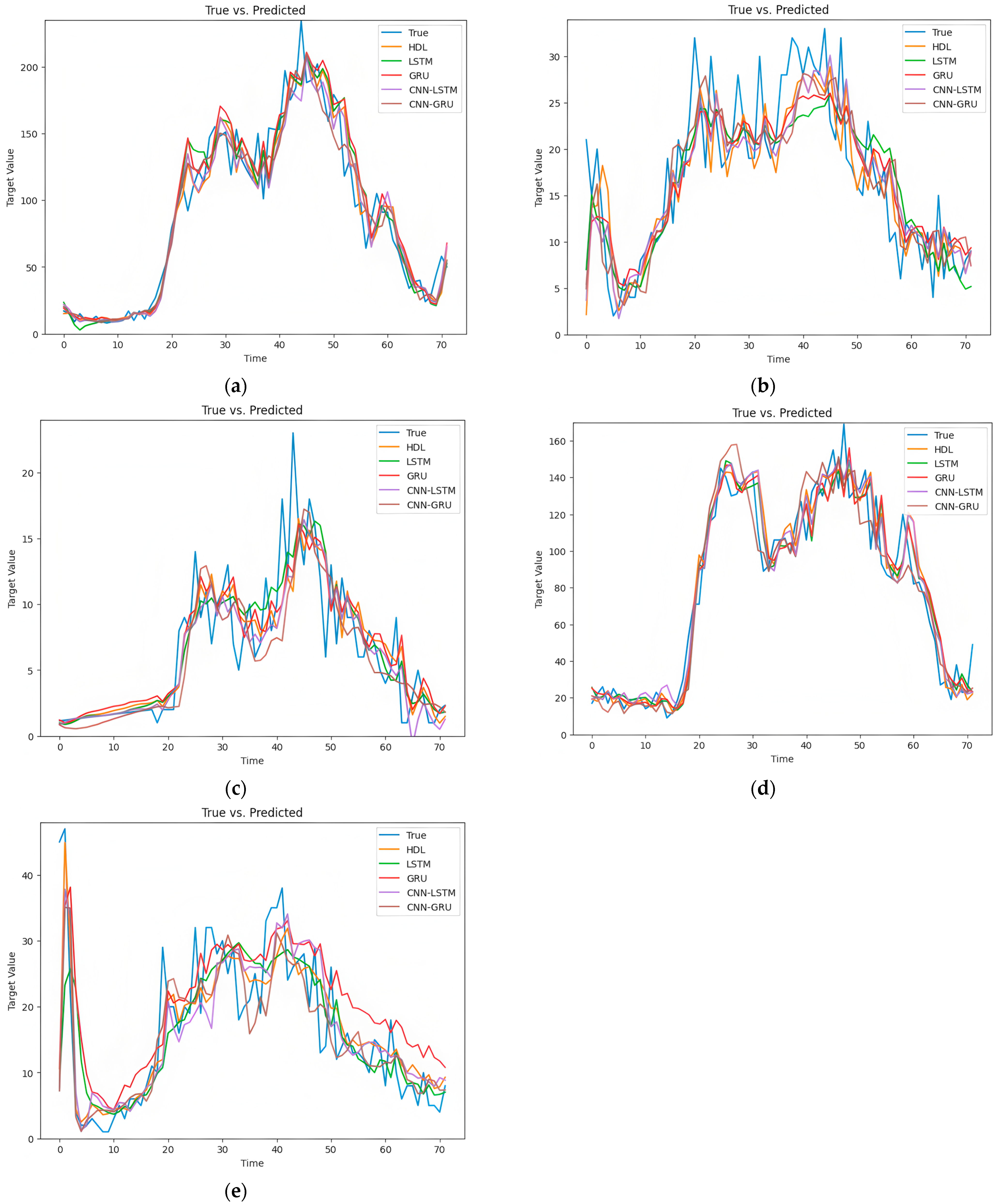
From the table above, it can be observed that, when predicting workday traffic flow, the proposed model achieves the lowest MAE and RMSE values, indicating superior prediction accuracy.

To more clearly demonstrate the prediction accuracy of the model, Figure 7 presents the prediction results of the proposed model (HDL) compared to LSTM, GRU, CNN-LSTM, and CNN-GRU for 11 October 2016, as shown in the following figures.

In the previous analysis, it was noted that weather factors can impact the entire traffic system, causing fluctuations in traffic flow. Therefore, this study incorporates weather factors into the model. Using 11–17 October 2016 as the prediction target, the average prediction errors for each station are calculated and compared with the other four models. The comparison results are shown in

Table 11. Comparison of forecast errors of five models during working days after adding external factors.

Date	Model
	LSTM		GRU		CNN-LSTM		CNN-GRU		CNN-LSTM-GRU
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
1-0	5.266	7.335	5.017	6.858	4.411	6.017	4.198	5.706	2.905	4.229
1-1	9.573	13.755	8.384	12.552	8.601	13.495	7.128	10.977	6.303	9.829
2-0	6.232	9.009	6.348	9.167	5.768	8.437	5.065	7.409	4.105	6.271
3-0	8.488	12.292	8.506	12.506	8.235	11.859	8.013	11.264	6.333	9.279
3-1	10.918	18.150	10.304	15.793	9.845	15.949	10.403	16.056	5.395	8.567

below.

After incorporating external factors, it can be observed that the model’s prediction results have significantly improved. For the CNN-LSTM-GRU predictions at each station, the MAE and RMSE decreased by 32.8% and 27.8%, 14.9% and 11.23%, 1.91% and 2.42%, 4.22% and 6.75%, and 36.3% and 30.79%, respectively. This indicates that including weather factors effectively enhances prediction accuracy.

5.2. Comparison and Analysis of Holiday Traffic Flow Prediction Results

In this section, 1–7 October 2016 is taken as the prediction target for holidays. The prediction errors of the model for each station, direction, and date are calculated, as shown in

Table 12. Prediction error of the CNN-LSTM-GRU model for seven-day holidays.

Date	Toll Station and Direction
	1-0		1-1		2-0		3-0		3-1
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
1	16.946	21.963	2.847	3.545	1.507	2.188	7.090	9.467	2.174	2.770
2	14.258	20.021	2.690	3.554	1.238	1.883	6.269	10.575	2.556	3.845
3	12.073	21.151	2.739	3.601	0.916	1.338	5.707	11.003	2.873	4.635
4	11.047	15.398	2.880	3.689	1.339	1.921	6.745	10.695	3.029	4.571
5	15.745	21.591	3.268	4.496	1.644	2.322	6.623	10.929	2.909	4.635
6	11.566	15.373	3.694	4.966	1.667	2.654	6.700	10.328	3.079	4.847
7	5.955	7.857	4.574	5.612	1.943	2.800	9.624	13.328	4.516	7.284
Average	13.496	19.333	3.242	4.278	1.464	2.207	6.966	10.947	3.019	4.824

below.

To better evaluate the model’s prediction accuracy,

Table 13. Average prediction error of the 5 models for seven-day holidays.

Date	Model
	LSTM		GRU		CNN-LSTM		CNN-GRU		CNN-LSTM-GRU
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
1-0	33.250	49.627	29.083	44.224	14.634	21.506	14.326	20.909	13.496	19.333
1-1	3.685	4.998	4.269	5.672	3.689	4.886	3.345	4.346	3.242	4.278
2-0	1.819	2.646	1.828	2.779	2.003	2.982	1.647	2.433	1.465	2.207
3-0	15.387	23.101	14.568	21.588	12.032	16.479	10.737	15.229	6.966	10.947
3-1	3.561	4.911	3.901	5.499	3.994	5.691	3.624	5.069	3.019	4.824

provides a comparison of the average prediction errors of the five models for 1–7 October 2016.

From Table 13, it can be seen that, when predicting holiday traffic flow, the proposed model achieves the lowest MAE and RMSE values, indicating superior prediction accuracy.

In the previous analysis, it was noted that weather factors can impact the entire traffic system, causing fluctuations in traffic flow. Therefore, this section incorporates weather factors into the model. Using 1–7 October 2016 as the prediction target, the average prediction errors for each station are calculated and compared with the other four models. The comparison results are shown in

Table 14. Comparison of prediction errors of the 5 models during holidays after adding external factors.

Date	Model
	LSTM		GRU		CNN-LSTM		CNN-GRU		CNN-LSTM-GRU
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
1-0	31.937	48.243	28.348	44.403	14.437	20.825	14.453	21.049	12.958	17.987
1-1	3.105	4.479	4.027	5.429	3.370	4.609	3.143	4.446	3.194	4.434
2-0	1.672	2.282	1.980	2.521	1.766	2.941	1.422	2.274	1.211	2.175
3-0	14.586	23.567	14.518	21.351	12.801	14.943	10.230	15.042	6.805	10.498
3-1	3.055	4.439	3.408	4.995	3.457	5.252	3.223	4.699	2.970	4.373

below.

After incorporating external factors, the model’s prediction results show improvement. For the CNN-LSTM-GRU predictions at each station, the MAE and RMSE decreased by 7.08% and 6.96%, 1.48% and 3.65%, 17.3% and 1.45%, 2.31% and 4.10%, and 1.62% and 9.35%, respectively. This indicates that including weather factors also improves the prediction accuracy for holiday traffic flow. However, compared to workday prediction accuracy, there is a noticeable gap. This is because the data volume for the National Day holiday is smaller than that for workdays, and the traffic flow during the holiday is influenced by more uncontrollable factors and exhibits greater fluctuations, resulting in lower prediction accuracy for holiday traffic flow.

Based on the above analysis, after conducting two sets of comparisons, the results indicate that incorporating weather factors and holiday factors leads to smaller prediction errors for the integrated model compared to individual models, both on workdays and holidays. The proposed model in this study demonstrates superior prediction accuracy for highway traffic flow over the other four typical deep learning models. The performance of the model has improved to varying degrees.

The recent literature using relevant datasets for traffic flow prediction was collected, and the prediction results are shown in

Table 15. Prediction results of highway traffic flow in existing literature.

Model	MAE	RMSE
CNN-LSTM-GRU	2.905/(vehicles·ehiclesG-1)	4.229/(vehicles·ehiclesG-1)
CEEMD-CNN-LSTM-Attention	3.488/(vehicles·ehiclesN-1)	4.512/(vehicles·ehiclesN-1)

below.

From the table, it can be concluded that, within the same dataset used in this study, the proposed model outperforms the CEEMD-CNN-LSTM-Attention model.

6. Conclusions

The main work of this paper included two aspects. Firstly, a deep learning model based on CNN-LSTM-GRU was proposed. Although LSTM could effectively handle long-term dependencies in data, its structure was complex; GRU had the advantage of a simpler structure but sacrificed some prediction accuracy. Therefore, this paper adopted an integrated LSTM and GRU framework to combine their respective strengths in managing long-term dependencies. However, both models were unable to capture spatial features in traffic flow data. To address this, our study integrated LSTM-GRU with CNN to extract spatial features and validated the model using highway traffic flow data from a certain province.

Additionally, in the experimental analysis, considering factors affecting traffic flow prediction, this paper incorporated temporal factors and weather data and analyzed the results from the following two perspectives: whether holidays were included and whether weather data had been added. The findings showed that the proposed model exhibited better prediction performance compared to LSTM, GRU, CNN-LSTM, and CNN-GRU, indicating that incorporating temporal and weather elements could further enhance the model’s prediction accuracy.

However, there are still some limitations in the research process of this paper, which need to be further optimized in future studies. For example, in terms of dataset, the dataset used in the paper is relatively limited and outdated. In order to verify the applicability of the algorithm, experiments will need to be conducted on more and updated datasets in the future. In addition, in the study, the impact of road conditions and driver’s own reasons on traffic flow was not taken into account. In future research, a more comprehensive indicator system of influencing factors can be established.