Evaluation of the Dynamic Behavior and Vibrations of the Operator-Vehicle Assembly in Electric Agricultural Tractor Operations: A Simulation Approach for Sustainable Transport Systems

Abstract

This study presents an advanced simulation-based methodology for evaluating the dynamic vibrational behavior of the operator–vehicle assembly in autonomous electric agricultural tractors. Using the TE-0 electric tractor as the experimental platform, the research is structured into three integrated stages. In the first stage, a seated anthropometric virtual model of the human operator is developed based on experimental data and biomechanical validation. The second stage involves a detailed modal analysis of the TE-0 electric tractor using Altair Sim Solid, with the objective of determining the natural frequencies and vibration modes in the [0–80] Hz range, in compliance with ISO 2631-1. This analysis captures both the structural-induced frequencies—associated with the chassis, wheelbase, and metallic frame—and the operational-induced frequencies, influenced by the velocity and terrain profile. Subsequently, the modal analysis of the “Grammer Cabin Seat” is conducted to assess its dynamic response and identify critical vibration modes, highlighting how the seat behaves under vibrational stimuli from the tractor and terrain. The third stage extends the analysis to the virtual operator model seated on the tractor seat, investigating the biomechanical response of the human body and the operator–seat–vehicle interaction during simulated motion. Simulations were carried out using SolidWorks 2023 and Altair Sim Solid over a frequency range of [0–80] Hz, corresponding to operation on unprocessed soil covered with grass, at a constant forward speed of 7 km/h. The results reveal critical resonance modes and vibration transmission paths that may impact operator health, comfort, and system performance. The research contributes to the development of safer, more ergonomic, and sustainable autonomous agricultural transport systems. By simulating real-world operation scenarios and integrating a rigorously validated experimental protocol—including vibration data acquisition, biomechanical modeling, and multi-stage modal analysis—this study demonstrates the importance of advanced modeling in optimizing system-level performance, minimizing harmful vibrations, and supporting the transition toward resilient and eco-efficient electric tractor platforms in smart agricultural mobility.

1. Introduction

The agricultural sector, in continuous evolution, is becoming increasingly reliant on advanced technologies and precise data analysis, surpassing the traditional boundaries of conventional farming practices. Although agricultural processes are well understood, the integration of state-of-the-art technologies for monitoring and managing agricultural operations is essential for optimizing the performance of agricultural vehicles and ensuring operator safety. The agricultural industry significantly benefits from the implementation of advanced systems for the acquisition and processing of experimental data, which enable the monitoring of operator-exposed vibrations, thereby contributing to more effective management of ergonomic and health-related risks.

An important aspect in this context is the use of high-precision sensors, which can be integrated into various specific agricultural processes, such as soil preparation and processing, as well as the assessment of vibration levels within the integrated vehicle–seat–operator system. These technologies enable the optimization of agricultural vehicle operation from the perspective of vibrational behavior, which directly impacts operator comfort and equipment durability. Vibration analysis is essential and involves a complex approach that includes the appropriate selection of the type of self-propelled agricultural vehicle, the integration of the operator’s anthropometric data, the evaluation of terrain characteristics, and the analysis of the interaction between the vehicle, the operator, and the environment.

With regard to the evolution of agricultural vehicles, recent research has focused on the development of innovative systems that replace internal combustion engines with hybrid and electric solutions. A major challenge in the automation of self-propelled agricultural vehicles lies in their ability to perceive and effectively adapt to the uncertainties inherent in the agricultural domain, particularly under real operating conditions, where environmental factors and terrain variability play a critical role [1].

In this context, the present study focuses on the analysis of the dynamic behavior of the operator-vehicle assembly in a self-propelled electric agricultural tractor, using advanced modeling and simulation techniques to evaluate the impact of vibrations on the operator under real operating conditions on variable agricultural terrain. The proposed approach contributes to the development of more resilient and ergonomic autonomous agricultural vehicles, supporting the transition toward sustainable solutions by optimizing both vehicle performance and operator protection within agricultural transport systems.

Self-propelled agricultural vehicles such as tractors are essential equipment for agricultural production; however, their use is associated with high fuel consumption and a significant impact on soil and air pollution. In this context, the development and implementation of sustainable technologies represent an important step toward reducing their environmental footprint. One of the emerging technological pathways involves the hybridization of propulsion systems, wherein an electric drive unit operates in conjunction with a traditional internal combustion engine to enhance energy efficiency and reduce environmental impact. The transformation of agricultural transport systems through digitalization, automation, and electrification requires a reassessment of the interaction between the operator and the vehicle, especially in the case of autonomous electric tractors.

Given the increasing integration of electric propulsion and automation in agricultural machinery, understanding the vibrational dynamics of the operator–vehicle system is fundamental for improving performance, extending equipment longevity, and ensuring the operator’s physical safety under real-world working conditions.

Recent research underlines the relevance of monitoring vibration exposure in self-propelled agricultural machinery, particularly tractors, with the dual objective of safeguarding operator health and enhancing the durability of mechanical components.

Notably, vibration mode and natural frequency analyses of the coupled operator–seat system, performed in compliance with ISO 2631-1 standards, have yielded essential data that inform ergonomic improvements and help mitigate operator fatigue and discomfort during extended periods of fieldwork [2].

In the specific case of electric agricultural vehicles, economic evaluations increasingly rely on the Total Cost of Ownership (TCO) framework to assess long-term viability. This model has gained traction as a reliable method for comparing initial and operational costs across different vehicle types. Since 2021, advancements in battery technology and charging infrastructure have contributed to narrowing the cost gap, enabling small- and medium-sized electric tractors to reach a level of competitiveness previously reserved for conventional models [3].

In the context of agricultural modernization, autonomous electric tractors such as the TE-0 model provide an efficient and sustainable solution. This study contributes through an advanced vibrational analysis of the operator–seat–vehicle assembly, employing three-dimensional modeling and modal analysis methods to optimize performance and reduce operator exposure to harmful vibrations. Within this evolving landscape, it becomes increasingly important to investigate the transmission of vibrations from the vehicle to the operator through the seating interface. Such analyses support the development of improved comfort criteria and health-oriented design measures for next-generation agricultural equipment.

The practical impact of these vibrations on agricultural operations is directly reflected in the health and performance of tractor operators, negatively affecting the efficiency of mechanized agricultural processes. Vertical vibrations transmitted through the seat, particularly in the 4–12 Hz range, coincide with the natural frequencies of the human body, amplifying biomechanical effects on the spinal column and internal organs [4]. Chronic exposure to such vibrations is associated with the development of musculoskeletal disorders, especially lower back pain and postural discomfort [5,6]. These consequences lead to reduced optimal operating time, decreased concentration, and an increased risk of accidents or human error, ultimately impacting the overall productivity of agricultural tasks [7]. Moreover, international standards such as ISO 2631-1 and European regulations (Directive 2002/44/EC) [2,8] set strict limits for permissible vibration exposure, which influence working time durations and may require interruptions or the reorganization of field operations [9,10]. Therefore, accurate evaluation and advanced simulation of this type of exposure are essential for optimizing modern agricultural systems and protecting the health of operators in the context of the transition toward sustainable mechanization.

Recent studies have investigated the weighted average levels of seat-transmitted vibrational accelerations and their effects on electric tractor operators. By performing a modal analysis using Altair Sim Solid software, critical frequencies (within the 0–80 Hz range) and vibration modes that significantly contribute to discomfort were identified, including lateral and torsional oscillations of the electric tractor structure [11].

In various fields of activity, vibrations originating from the surrounding environment can constitute a significant source of discomfort for operators, having temporary effects on their health status [12,13,14,15]. However, in certain professional sectors, chronic and continuous exposure to vibrations may lead to the development of severe and irreversible physiological disorders, affecting the long-term health of operators, particularly those who interact with high-speed equipment or complex mechanical systems [16,17,18].

These risks are associated with the transmission of vibrations through mechanical structures and their effects on the human musculoskeletal and neurological systems.

As a result, international regulations and safety standards have been adopted to establish precise limits for vibration exposure levels, with the aim of protecting operator health and ensuring a safe and sustainable working environment.

Electric tractors have been the subject of research since the 19th century, with the first such vehicle built in the United States [19,20].

Subsequent developments of this type of equipment have been largely driven by significant advances in battery technology, which have enabled improvements in their performance and operational autonomy.

In addition to well-established research on the performance and stability of agricultural vehicles such as tractors [21,22,23,24], the improvement of agricultural work efficiency is strongly influenced by soil characteristics, which represent an essential factor that cannot be overlooked [25,26,27].

Moreover, numerous studies address aspects related to autonomous driving [28,29,30,31,32]; however, research focused on self-propelled electric agricultural vehicles, particularly electric tractors, that includes a detailed analysis of operator-vehicle vibration and its impact on the operator remains relatively limited. Operators of agricultural vehicles such as tractors are frequently exposed to mechanical vibrations transmitted to the whole body while seated, especially during driving operations on various surface types, which can have significant health implications [33,34]. According to ISO 2631-1:1997, the human body in a seated position is particularly sensitive to vibrations in the frequency range of 0.4–100 Hz. In particular, vibrations between 1 and 2 Hz can induce temporary discomfort effects, such as motion sickness, while vibrations in the 2–20 Hz range may lead to musculoskeletal disorders, including lower back injuries and spinal trauma. It is well established that the critical frequencies for such injuries lie between 3 and 10 Hz [35].

Vehicle seats, including those used in electric tractors, are subjected to vibrations that vary significantly depending on the type of vehicle, travel speed, surface characteristics, and other factors specific to the operational environment. The operator, being in direct contact with the seat, is primarily exposed to vibrations transmitted through it, making the analysis of seat dynamics essential for assessing vibration exposure levels and their impact on operator health and comfort. In order to reduce the operator’s adverse response to vibrations generated by the interaction with the agricultural tractor and the terrain type, the seat must be equipped with a suspension system that ensures optimal dynamic characteristics.

The effectiveness of such a seat is determined by the interaction of three fundamental factors: the vibrational environment (representing vehicle motion over different types of terrain at a constant speed), the vibration isolation capability provided by the seat suspension, and the physiological response of the human body to these vibrations. The vehicle seat exhibits a natural resonance frequency in the range of 2–4 Hz, while the frequency range between 4–8 Hz represents a critical zone in which human sensitivity to vertical vibrations reaches significantly high levels [36,37,38,39,40].

The main objective of this set of advanced modal analyses is to support the development of innovative and sustainable solutions for autonomous electric agricultural vehicles, within a scientific framework that aligns closely with the scope of the journal, which focuses on the modeling, simulation, and optimization of transport systems. By conducting detailed analyses of the vibrational behavior of the electric agricultural vehicle, its seat, and the virtual mannequin (operator) seated on the seat, this study explores the complex interactions among these components, simulating the tractor’s operating conditions on unprocessed grass-covered terrain at a constant speed of 7 km/h.

The multidisciplinary approach adopted, encompassing advanced simulation techniques and vibration analysis, aims not only to optimize the performance of the electric tractor but also to protect the operator by reducing harmful vibrations, thereby contributing to the development of greener, safer, and more ergonomic electric agricultural vehicles. By integrating these advanced analyses, this study addresses the objectives of this special issue, focusing on improving the performance and efficiency of autonomous agricultural transport systems and promoting sustainable solutions in vehicle design to meet current challenges in agricultural mobility. In this context, the analysis of the dynamic behavior of the entire tractor-seat-operator assembly through advanced simulations contributes to increasing awareness of the importance of such vibrational assessments, having a significant impact on optimizing the design of autonomous agricultural vehicles and strengthening their sustainability and safety.

2. Methodology

Presentation of the Modal Analysis of the Integrated Vehicle-Seat-Virtual Mannequin (Operator) Assembly

• Stage 1—Modal analysis of the TE-0 electric tractor

In the present research, the analysis of the vibrational behavior of the self-propelled electric agricultural tractor, model TE-0, represents a critical step in evaluating the impact of vibrations on the operator. Figure 1 shows the TE-0 electric tractor during operation on unprocessed grass-covered terrain, a typical agricultural work environment, which was used in the advanced, complex simulation. This advanced simulation enables the investigation of the interaction between vehicle-generated vibrations and their effects on operator comfort and health, contributing significantly to the advancement of more efficient and ergonomic solutions for electric agricultural vehicles [41].

The selection of a grass-covered terrain for the vibration tests conducted in this study, as illustrated in Figure 1, was based on both practical and statistical considerations, grounded in the predominant characteristics of surfaces commonly encountered in agricultural activities, such as greenhouses and farm fields. Grass-covered or short-vegetation terrains—similar to those found in protected agricultural environments (e.g., greenhouses)—provide a natural testbed that realistically simulates the operational conditions of a self-propelled agricultural vehicle (tractor type) used in delicate field operations.

According to several studies in the literature, grass-covered surfaces tend to generate lower levels of vibration, primarily due to the vegetation layer acting as a natural damping medium. Compared to hard surfaces such as asphalt or gravel, grass-covered terrain is capable of absorbing a significant portion of the vibrational energy, thereby reducing the transmission of vibrations to the vehicle and, consequently, to the operator.

For the purpose of this study, an uneven dirt road covered with grass was selected, characterized by a surface roughness value—determined using the sand patch method (Height of Sand, HS)—falling within the range of [0.2–0.6 mm]. This corresponds to a satisfactory rolling surface condition for conducting the experimental tests.

This electric tractor, a prototype developed by the research team of the National Institute of Agricultural Machinery (INMA) in Bucharest, was selected to explore the vibrational dynamics of electric vehicles in the context of emerging technologies and the transition toward more sustainable transport solutions.

Physical measurements were conducted on unprocessed soil terrain covered with grass, at a constant travel speed of 7 km/h, using triaxial accelerometer sensors mounted at the seat cushion level, seat backrest, tractor steering wheel, cabin floor, and operator’s head, as shown in Figure 2.

The TE-0 electric tractor model was created using SolidWorks software [42], and upon completion of the design process, it was imported into the advanced simulation software Altair Sim Solid [43].

The modal analysis of the TE-0 electric tractor model was selected in order to understand and evaluate the vibrational behavior of this vehicle in the context of operator exposure to mechanical vibrations. Given current technological trends and the transition toward electric vehicles, it is essential to investigate how the TE-0 electric tractor behaves from a vibrational standpoint, in order to identify the natural frequencies and vibration modes that may affect the comfort and health of the driver.

This type of analysis allows for the identification of potential resonance phenomena and amplification effects that could increase the risk of discomfort and musculoskeletal disorders, thus providing a foundation for optimizing the vehicle design and protecting the operator.

The TE-0 electric tractor was designed using SolidWorks software.

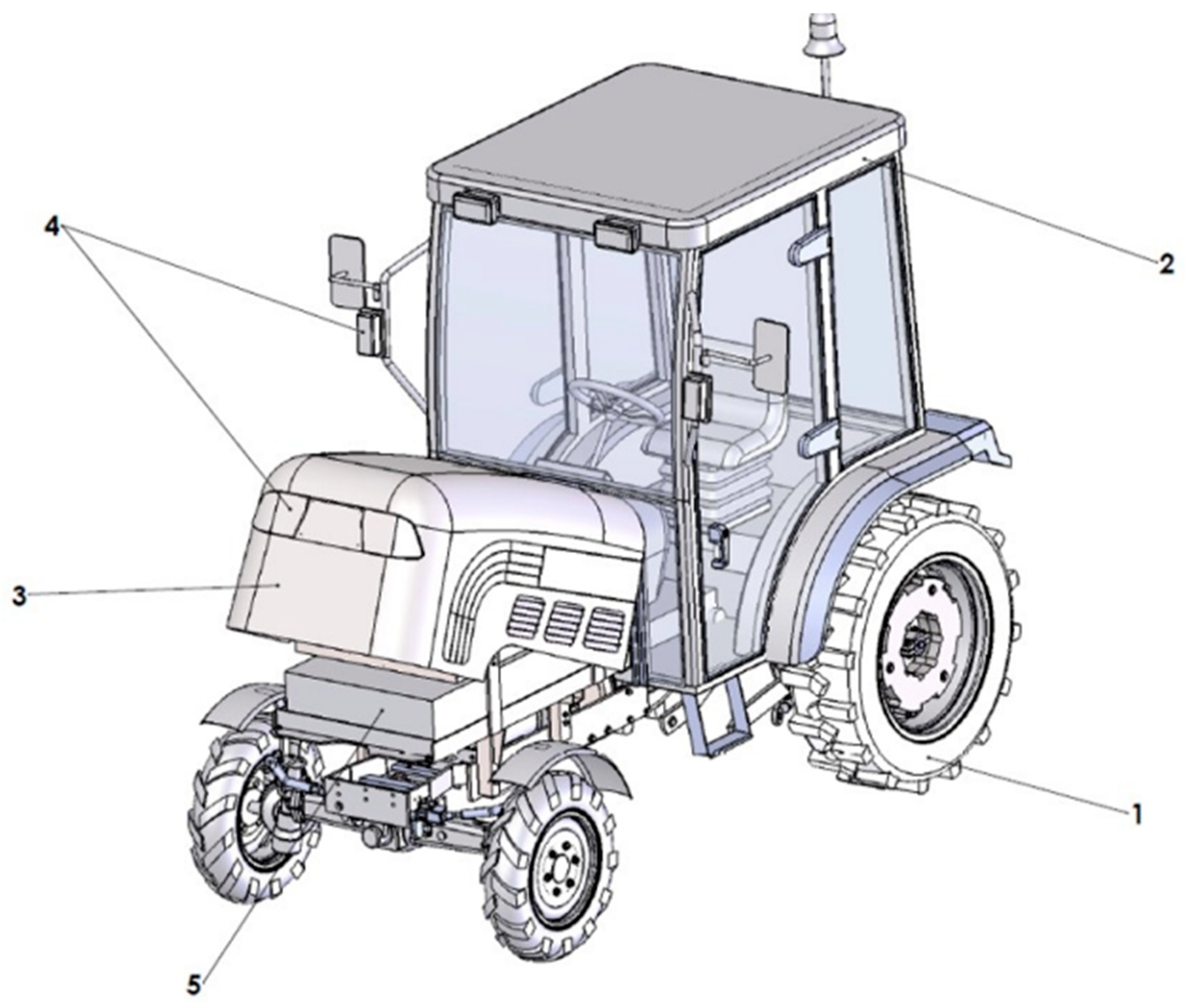
The main assemblies of the electric tractor are shown in Figure 3, as follows:

1—Running gear; 2—Cabin; 3—Engine hood; 4—Lighting and signaling system; 5—Electric drive system.

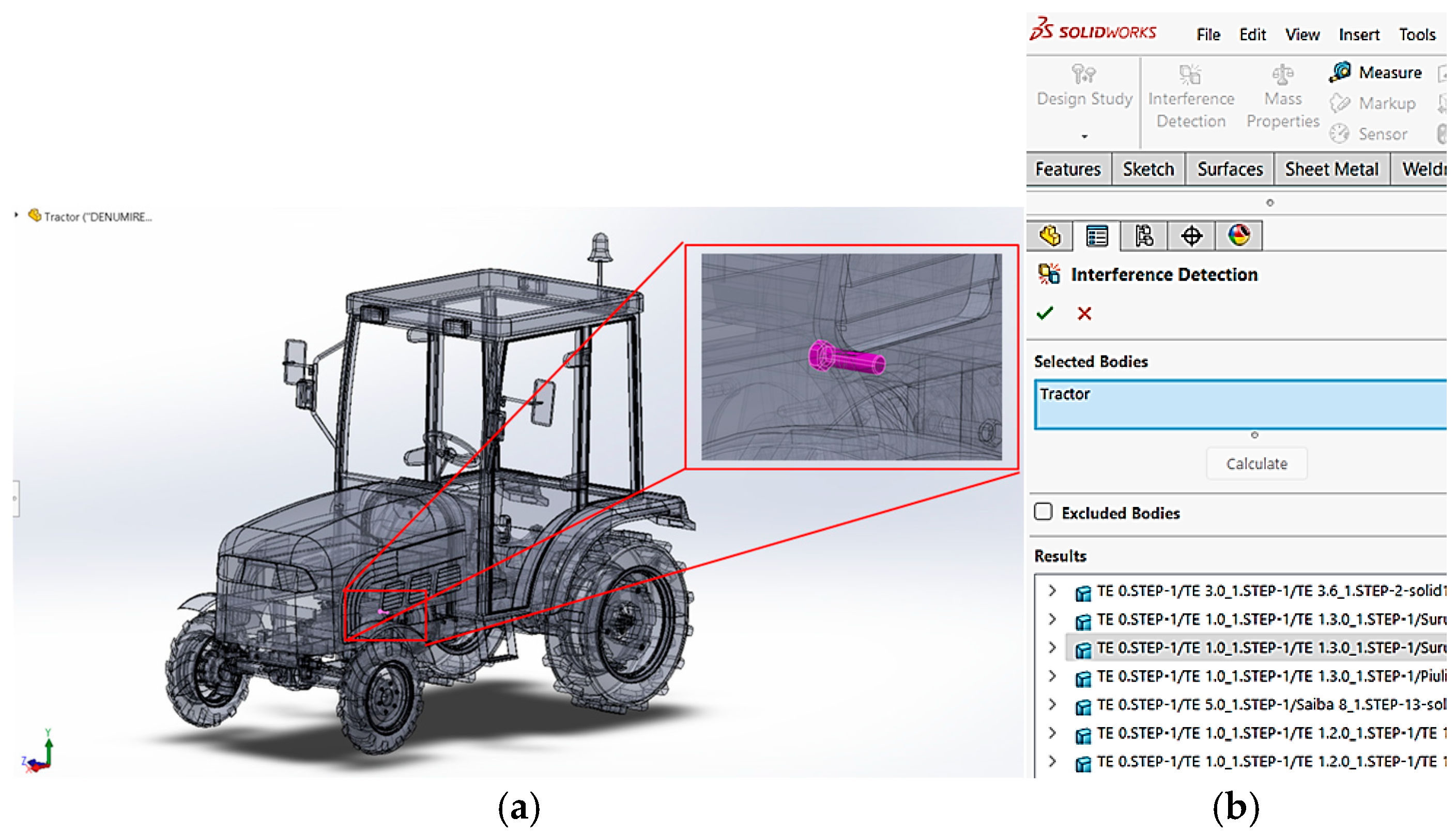
To initiate the modal analysis, the electric tractor model was carefully checked for interferences and clearances between parts in SolidWorks using the “Evaluate” tab, specifically the “Interference Detection” and “Clearance Verification” tools.

An example of interference detection is shown in Figure 4, where (a) illustrates the interference detection result, and (b) shows the selection of the part for which the interference check was performed.

Minor errors identified in the model were corrected, and certain components—such as window seals, glass elements, and headlamp lenses—were excluded from the analysis. These components were omitted in order to avoid post-processing errors and to reduce the overall processing time, without compromising the accuracy of the results.

The virtual model of the TE-0 electric tractor was exported from SolidWorks to Altair Sim Solid, one of the most advanced simulation platforms based on the finite element method, recently developed by Altair.

This modern solution enables accurate and efficient analyses without the need for generating a traditional finite element mesh, thus allowing fast and complex simulations of large structures and detailed geometries.

Altair Sim Solid is an advanced simulation software capable of performing static, dynamic, and thermal analyses of complex structural systems. Unlike traditional methods, Sim Solid works directly with fully detailed solid geometry models, eliminating the need for geometry simplification and the generation of a finite element mesh.

The computational algorithm used by Altair Sim Solid is illustrated in Figure 5 and is based on innovative extensions of the theory of external approximations, which represents an advanced generalization of the finite element method (FEM) because:

Arbitrary geometric shapes can be used as “finite elements.”

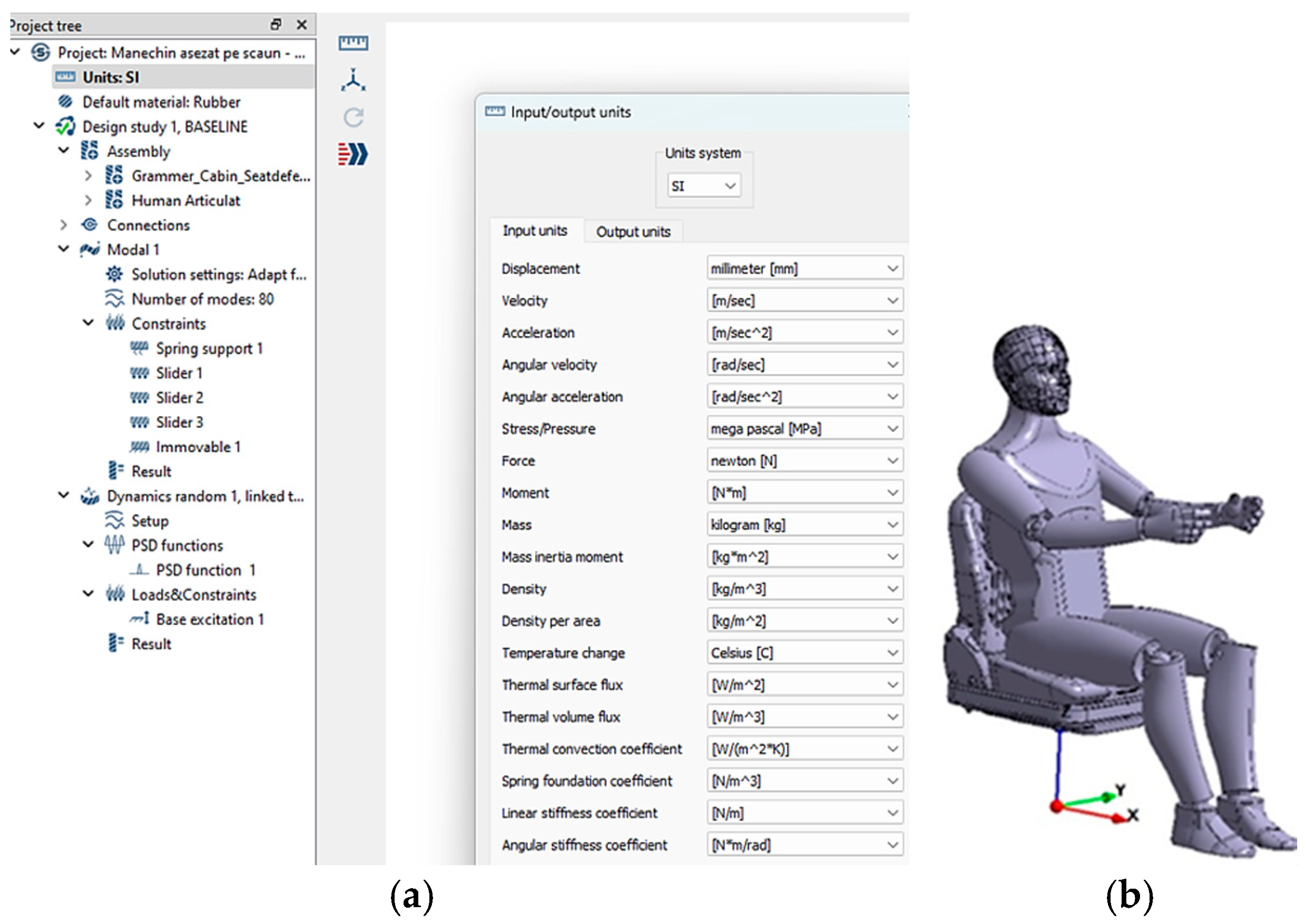
After a brief functional description, Figure 6 illustrates the practical application of the Altair Sim Solid software, highlighting the essential elements of the user interface. These illustrations present the main functionalities, including the main menu structure, the project tree, and the user interaction workflow within the simulation environment, providing a clear understanding of the simulation setup and execution process.

The definition and analysis of connections is a crucial step in ensuring the structural integrity and coherence of the virtual model of the electric tractor. During this process, all components of the assembly are analyzed to determine the mechanical interactions between them. A total of 2480 connections were identified and verified, ensuring that each part of the model functions correctly within the context of the simulations.

In Figure 7, the Altair Sim Solid software displays the visualization of all connections within the TE-0 electric tractor assembly.

This graphical representation allows the user to quickly and efficiently verify how the tractor components are interconnected and to identify potential critical points or structural inconsistencies.

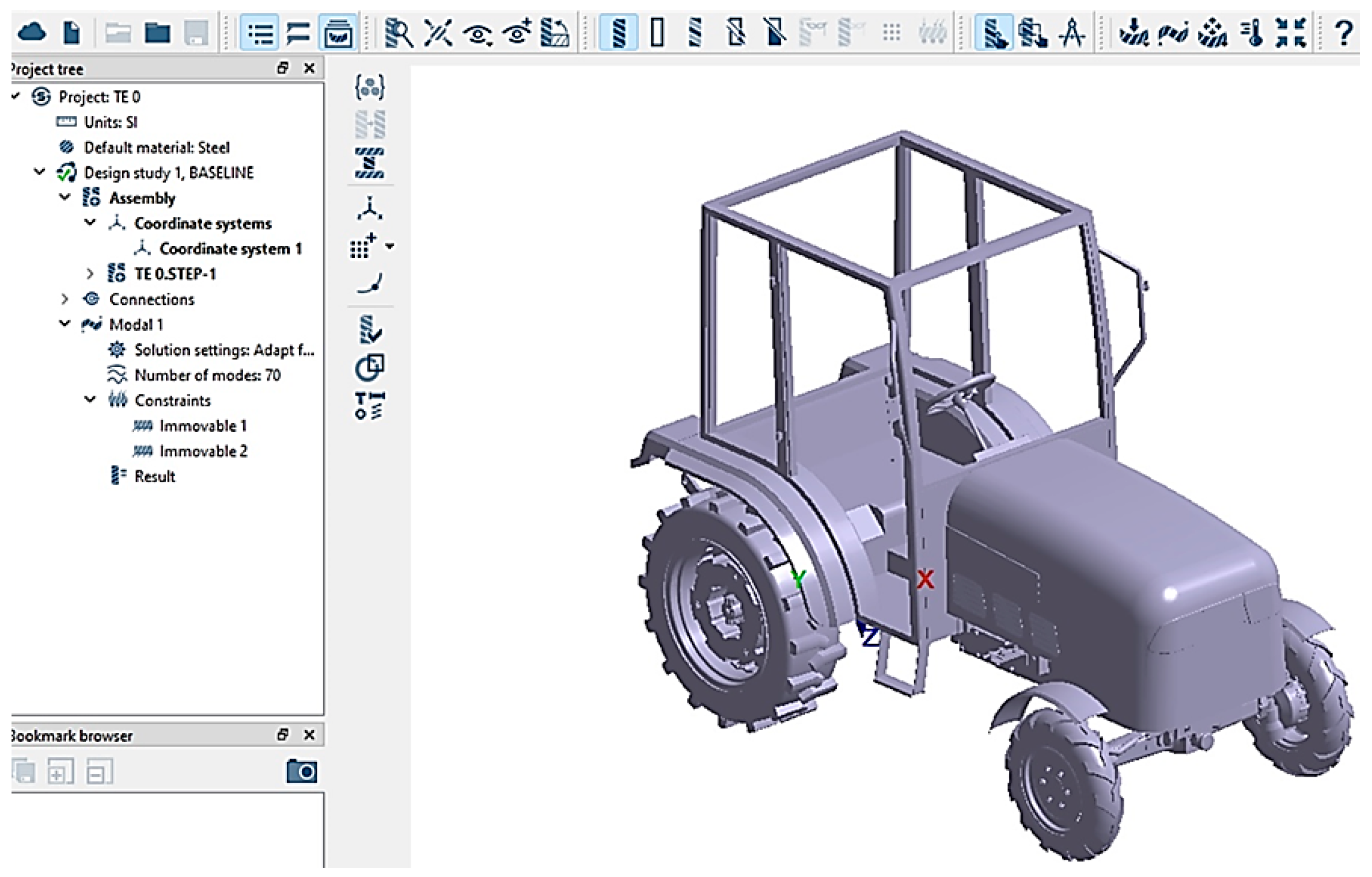
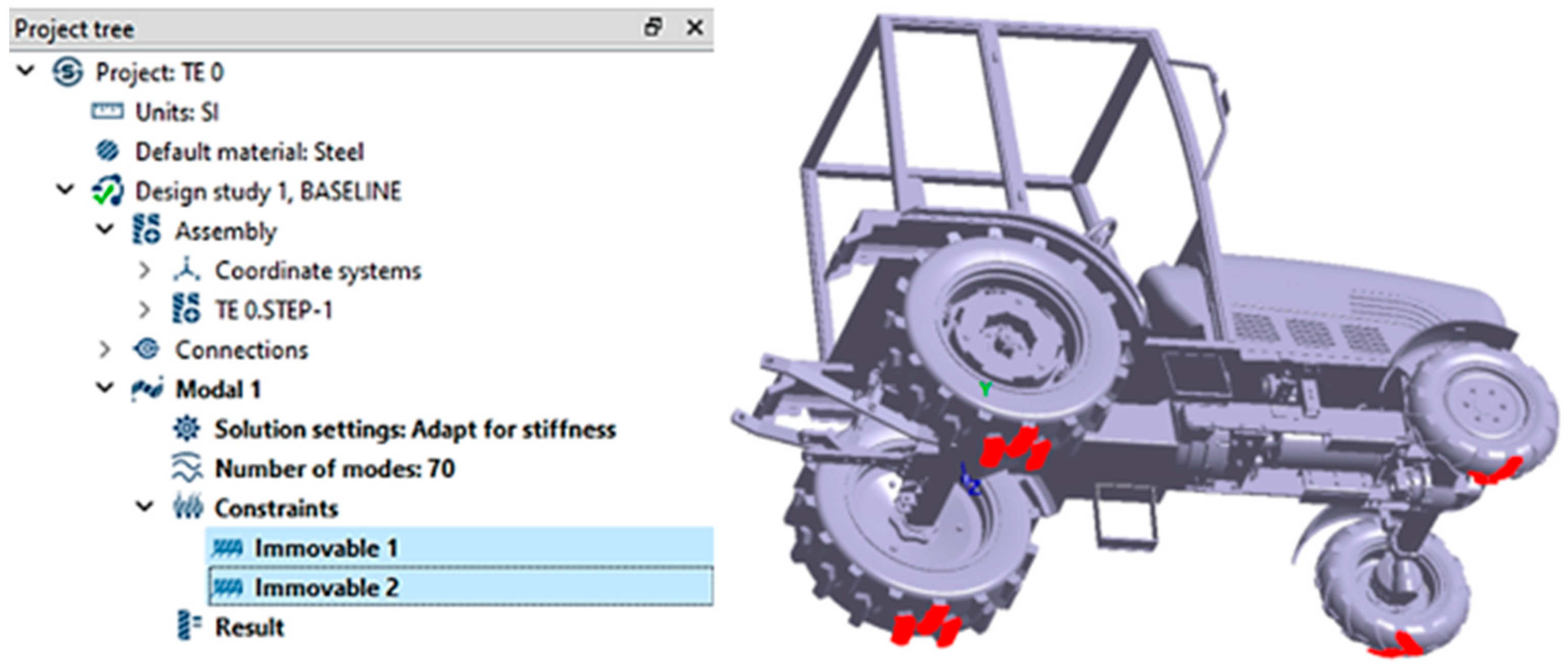
The definition of constraints was carried out under stationary conditions, simulating the position of the tractor on a virtual horizontal plane representing the ground. In this context, fixed supports were assigned to each tire at the contact points with the ground, in order to accurately reflect the real operating conditions of the tractor. This step is essential for ensuring the stability of the model and enabling an accurate modal analysis.

Figure 8 illustrates the placement of these constraints within the simulation environment.

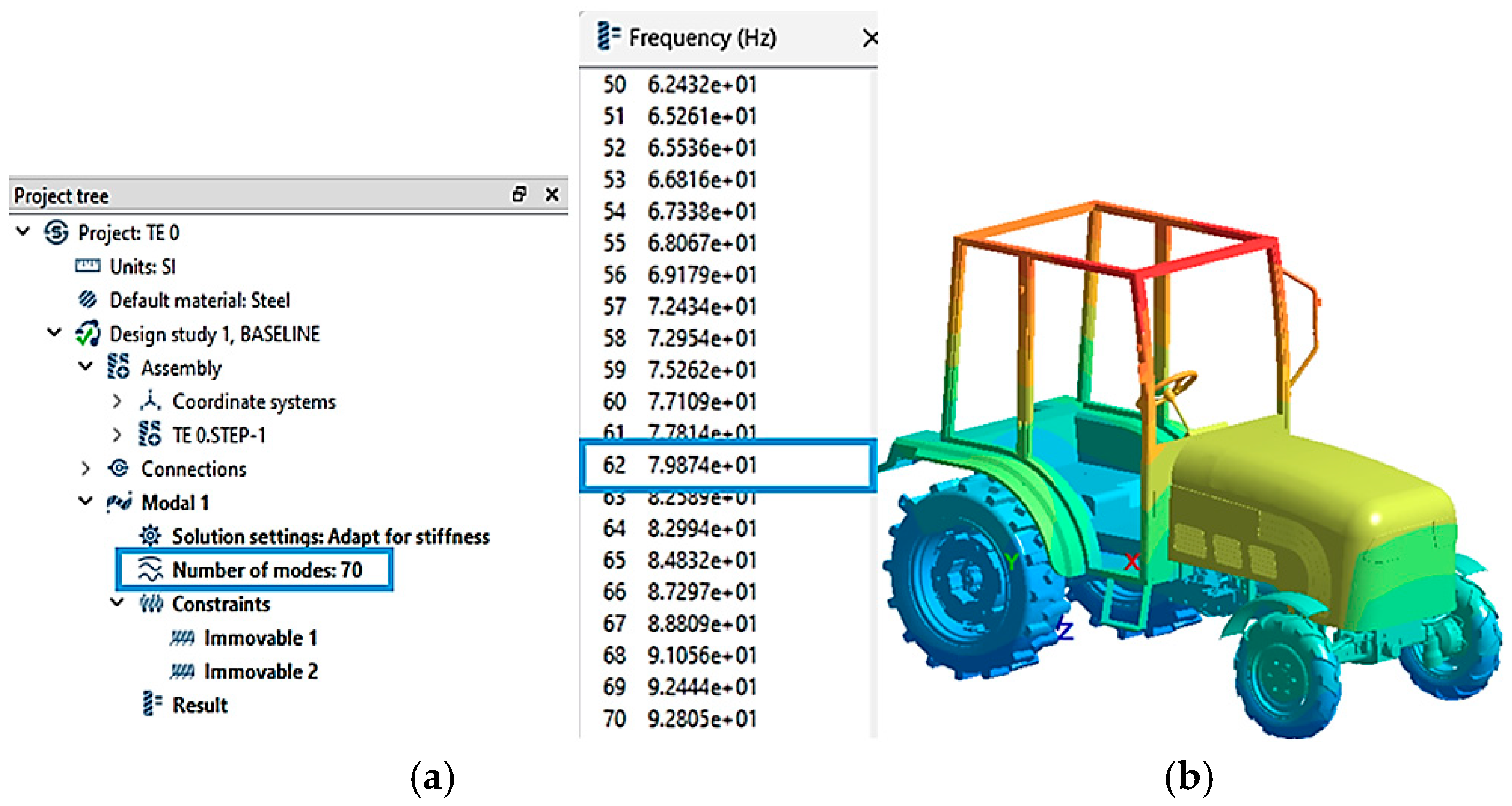
For the modal simulation of the TE-0 electric tractor, a maximum of 70 vibration modes was selected in Altair Sim Solid, within a frequency range of [0–80] Hz, in accordance with ISO 2631-1. As a result of the modal analysis performed within this frequency interval, 62 distinct vibration modes were identified and are presented in Figure 9.

This selection is essential for evaluating the natural frequencies of the tractor and understanding how it responds to external excitations. Identifying the vibration modes allows for a detailed understanding of the dynamic behavior of the tractor and helps prevent resonance phenomena, thereby minimizing the vibrations transmitted to the operator.

The most relevant vibration modes of the TE-0 electric tractor model are presented in Figure 10, representing the distinct vibration patterns exhibited by the tractor structure at its natural frequencies, which may have a significant impact on the operator’s health.

This methodological approach enabled the identification of natural frequencies and vibration modes that affect operator comfort, playing an important role in preventing resonance phenomena and reducing vibrations transmitted to the operator’s seat. Furthermore, the detailed vibrational analysis of the TE-0 electric tractor supports the optimization of vehicle design to ensure ergonomic and safe operating conditions, which are essential for the development of high-performance and sustainable autonomous systems in the agricultural sector.

This first stage of the vibrational analysis of the TE-0 electric tractor is closely connected to the following stage, which will involve a detailed modal analysis of the tractor seat, an essential component in assessing the operator’s level of vibration exposure.

• Stage 2—Modal analysis of the electric tractor seat

In this study, the second stage focuses on the detailed modal analysis of the electric tractor seat, an essential component of the operator-vehicle assembly, for the purpose of assessing the impact of vibrations on the operator. The 3D virtual model of the seat, available in the online library Grabcad.com, is named “Grammer Cabin Seat,” and is designed for off-road vehicles [44]. It consists of a robust steel structure, rubber-foam elements for vibration damping, and plastic components that provide comfort and functionality. These components are illustrated in Figure 11.

The experimental protocol specifies the type of seat suspension, which is mechanical, with adjustable suspension height. For the test case, the suspension was set to its maximum height (S2), corresponding to 20 cm, as illustrated in Figure 12a. Additionally, the seat backrest was adjusted to a right angle of 90 degrees.

To acquire the necessary data, two accelerometer sensors were mounted on the seat surface and on the seat backrest, as shown in Figure 12b. During the entire test, the operator remained in continuous contact with both sensors—mounted at the base of the seat and on the backrest, respectively Figure 12c—in accordance with the specifications of ISO 2631-1. This setup ensured a detailed and accurate analysis of the vibrations transmitted to the human operator.

The calculation and numerical simulation of the seat suspension behavior were carried out in SolidWorks by accurately assigning material properties to each component of the 3D model. The total mass of the seat was estimated at 27.553 kg, based on the density and volume of the modeled components. Figure 13 illustrates the mass properties of the assembly, including total volume, surface area, center of gravity coordinates, and moments of inertia along the X, Y, and Z axes of the coordinate system.

The suspension stiffness of the seat was experimentally determined for the configuration used in the vibration analysis, defined as a “rigid suspension.”

Table 1. Compilation of data required for the suspension stiffness study.

Subject No.	Mass [Kg]	Weight [N]	A [mm]	B [mm]	C [mm]	C–A [mm]	C–B [mm]
Subject 1	68	667.08	451	393	497	46	104
Subject 2	75	735.75	445	391	497	52	106
Subject 3	72	706.32	448	392	497	49	105
Subject 4	92	902.52	432	387	497	65	110
Subject 5	78	765.18	444	390	497	53	107
Subject 6	77	755.37	445	391	497	52	106
Subject 7	65	637.65	455	393	497	42	104

summarizes all relevant parameters obtained through physical testing, including applied forces, resulting displacements, and stiffness coefficients, which are essential for the dynamic characterization of the suspension system in this study.

“A” represents the distance from the ground to the base of the seat when the suspension is “rigid” and the operator is seated.

“B” represents the distance from the ground to the base of the seat when the suspension is “soft” and the operator is seated.

“C” represents the distance from the ground to the base of the seat when no operator is seated.

For each of the A, B, and C conditions, five measurements were performed. The values recorded in Table 1 represent the arithmetic mean of the five measurements.

A rigid suspension tends to transmit vibrations more directly to the vehicle structure and the operator, providing better stability on uneven terrain but at the cost of reduced comfort. In contrast, a soft suspension absorbs a greater portion of the vibrations, thereby reducing the discomfort experienced by the operator, although it may compromise stability under certain operating conditions.

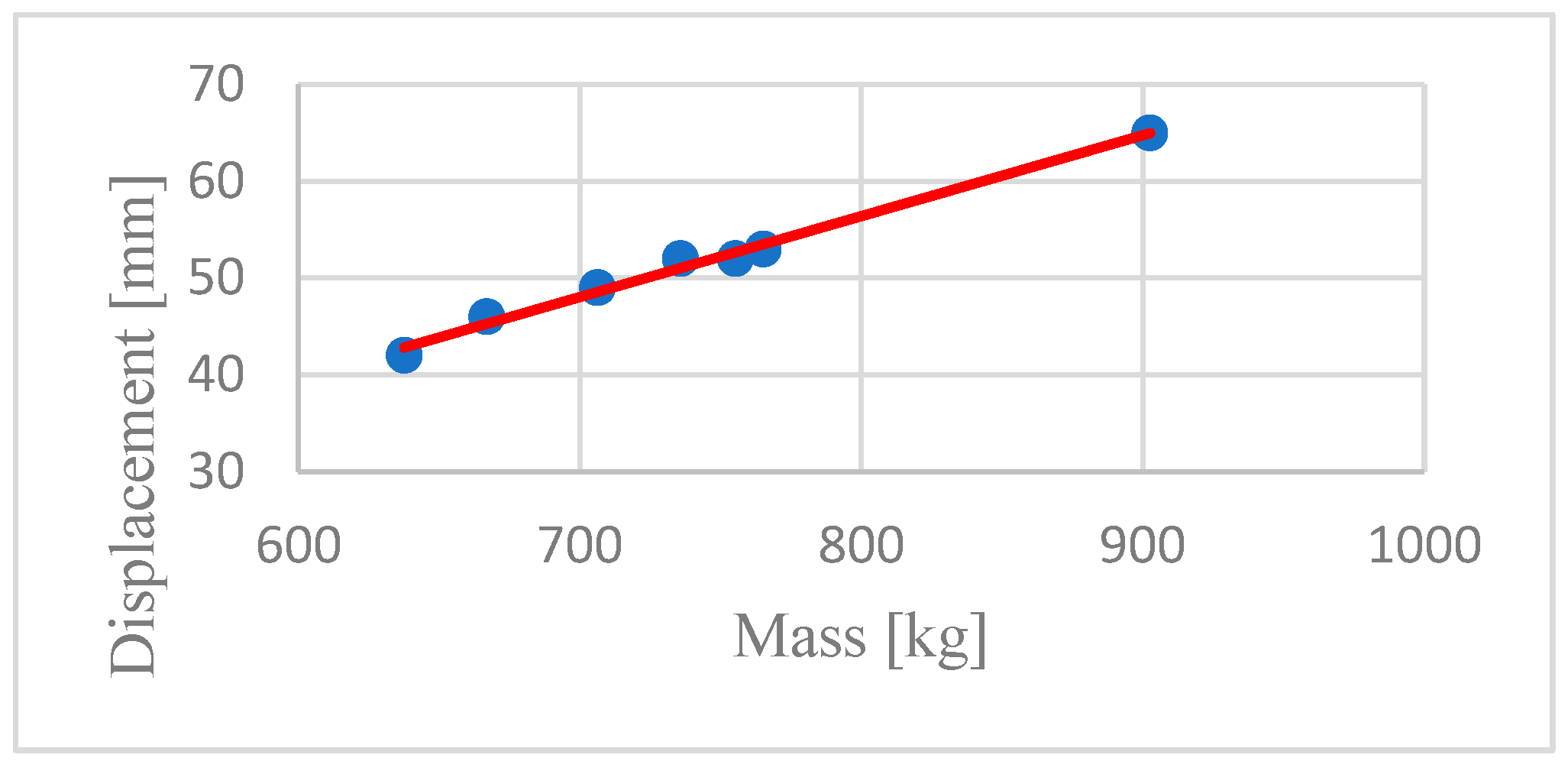
By applying a linear interpretation of the system’s vibration response, it is possible to assess how each suspension type influences the transmission of vibrations to the vehicle structure and, consequently, to the operator.

The linear interpolation of the suspension is illustrated in Figure 14, based on the data collected from the sample of human subjects who participated in the experimental vibration tests.

Using the data from Table 1, it can be observed that the suspension exhibits linear behavior, and the equation derived from relation (1) shows a precision of 99%.

Y = A + B * X

(1)

where:

A = −1.96637, B = 0.06855, X = operator’s weight expressed in [N]

Md (Driver mass) + Ms (Seat mass) = 75 kg + 27.53 kg = 102.53 kg = 1005 N

The suspension stiffness is calculated as:

1005 N/(0.06855 × 1005 − 1.96637) = 15.0 N/mm

Thus, the maximum suspension stiffness is:

15.0 N/mm

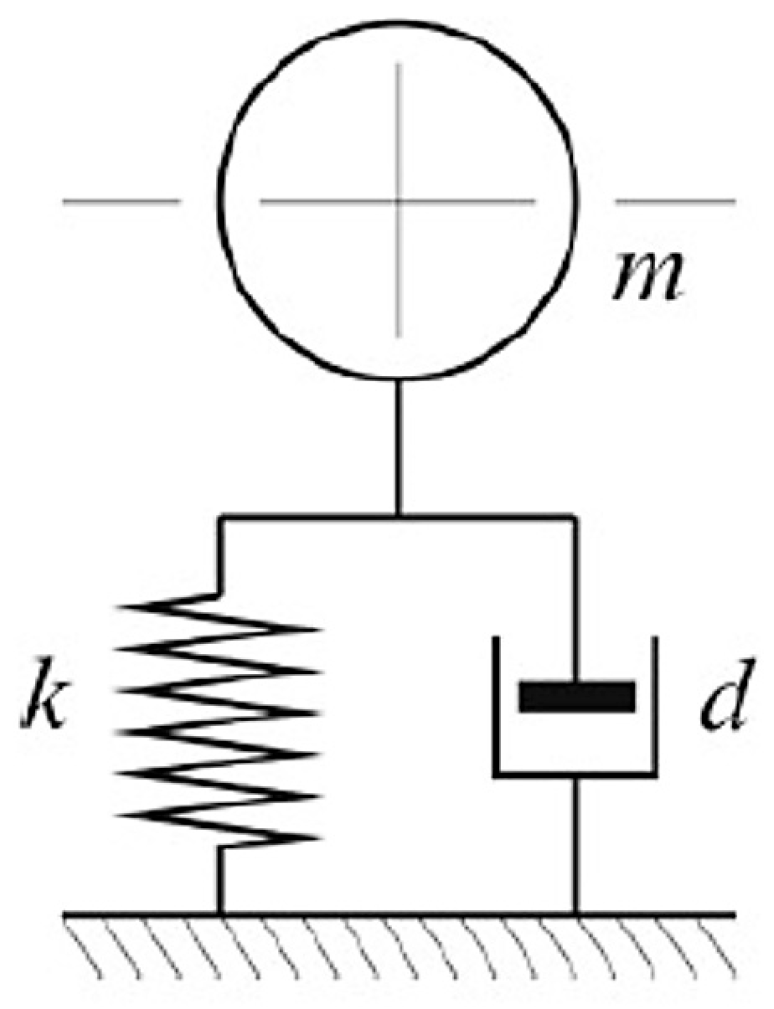
In order to account for the damping of the seat suspension, the mathematical calculation of the natural frequency of the seat suspension was carried out using the standard formula for the natural frequency of a mass–spring system. This formula allows for the determination of the natural frequency, which is essential for evaluating the dynamic behaviour of the suspension and for preventing resonance phenomena, which could amplify the vibrations transmitted to the operator. Figure 15 presents a schematic model of the suspension adopted for this study.

For the mathematical calculation of the natural frequency of Suspension, the frequency was determined using the formula given in Equation (2):

$$\mathrm{f}={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}-{\left({\displaystyle \frac{d}{2m}}\right)}^2}$$

(2)

where:

f is the natural frequency of the damped harmonic oscillator, expressed in hertz [Hz];

k is the stiffness constant of the system, expressed in [N/m];

m is the mass of the object, expressed in [kg];

d is the damping coefficient, expressed in [Ns/m];

π is the mathematical constant pi (approximately 3.14159);

k = 15 [N/mm] = 15.000 [N/m];

d = 0.6 [Ns/mm] = 600 [Ns/m];

m = 27.53 [kg].

Thus, Equation (3) represents the value of the natural frequency of the seat suspension:

$$\mathrm{f}=({\displaystyle \frac{\sqrt{\left(\frac{15000}{27.53}\right)-{\left(\frac{600}{2\ast 27.53}\right)}^2}}{2\ast 3.14159}}) = 3.285 \mathrm{H}\mathrm{z}$$

(3)

In our research, the seat was mounted on the TE-0 electric tractor used for experimental vibration analyses. The modal analysis of the seat was performed to evaluate its vibrational behavior under the actual operating conditions of the electric tractor. The seat plays an important role in transmitting vibrations to the operator, and identifying its natural frequencies and vibration modes is essential for understanding how these factors influence operator comfort and safety. In this context, the modal analysis of the seat is directly related to the main objective of our research, which focuses on evaluating the dynamic behavior of the operator-vehicle assembly and identifying optimal solutions for protecting the operator from harmful vibrations.

The seat mounted on the TE-0 electric tractor is a key factor in the development of sustainable and ergonomic design solutions for electric agricultural vehicles. The data obtained from this modal analysis are fundamental for optimizing the seat design, thus contributing to reducing the operator’s risk of exposure to harmful vibrations. After processing the model in SolidWorks software, it was exported to the advanced simulation software Altair Sim Solid, which enabled a precise finite element analysis.

The model preparation, meshing strategies, and boundary condition settings for the tractor seat in the simulation software followed the same steps as those used for modeling the electric tractor. In Figure 16a, Altair Sim Solid highlights all connection analyses within the seat assembly, while Figure 16b shows the virtual model of the seat with all connection points between its constituent components.

These connections play a critical role in the structural behavior of the seat under vibrational and mechanical loads. They determine how forces and vibrations are distributed and absorbed by the seat components, thereby influencing the durability, stability, and comfort provided to the operator.

In the modal analysis of the seat, 8 relevant vibration modes were identified within the [0–80] Hz frequency range, in accordance with ISO 2631-1 standards, with a maximum of 10 vibration modes selected.

This selection is essential for capturing the vibration modes that could significantly affect seat performance and comfort, thereby playing a key role in the comprehensive and rigorous evaluation of its dynamic behavior. This aligns with the article’s objective of assessing and optimizing operator exposure to vibrations during the operation of electric agricultural tractors. The distribution of the seat’s vibration modes within the specified frequency range is presented in Figure 17 and illustrates the different vibration patterns the seat may exhibit depending on its natural frequencies.

Following the first stage of vibrational analysis of the TE-0 electric tractor, in which the vehicle’s vibration modes were identified, the second stage of the analysis focused on the tractor seat. The modal analysis of the seat was conducted to identify the vibration modes within the [0–80] Hz frequency range, providing a detailed understanding of the seat’s vibrational behavior and its interaction with the vehicle. Participation factors were determined along the three axes (X, Y, Z), and cumulative participation factors were obtained by aggregating them. A high value of these factors indicates the significant importance of the corresponding vibration modes, highlighting those that have a major impact on the dynamic behavior of the seat and, consequently, on operator comfort.

It is essential to verify the seat’s modal frequencies in correlation with the modal frequencies of the tractor and those of the virtual mannequin, which represents the operator seated on the seat. The overlap of these frequencies can lead to the phenomenon of resonance, a process that amplifies the vibrations transmitted to the operator. Resonance is particularly important, as it can have significant effects on the operator’s health by increasing the risk of discomfort and the development of musculoskeletal disorders.

At a frequency of 23.77 Hz, the third vibration mode exhibits a total participation factor of 0.33, as shown in Figure 18. This mode is of particular interest due to its relatively high frequency, indicating a faster seat movement, but with lower influence compared to the first vibration modes. Frequencies above 20 Hz are essential for characterizing the vibrational behavior at higher speeds or when operating on uneven terrain.

Thus, the modal analysis of the seat is a key factor in understanding the dynamics of the operator-seat-vehicle assembly and in reducing the risks of exposure to harmful vibrations. This stage of seat modal analysis is directly connected to the first stage, in which the vibrational behavior of the TE-0 electric tractor was analyzed, and it serves as the foundation for the next stage of the research—the comprehensive analysis of the electric tractor-seat-virtual mannequin (operator) assembly.

• Stage 3—Modal analysis of the virtual mannequin (operator) seated on the tractor seat

In the third stage of our research, a modal analysis of the virtual mannequin (operator) seated on the electric tractor model TE-0 was conducted to evaluate the behavior of the human body under the influence of vibrations transmitted through the seat during operation.

Considering the aim of the article and the overall focus of the study, this simulation allows for an accurate representation of how vibrations affect different parts of the operator’s body. The modal analysis of the virtual mannequin is essential for understanding the impact of vibrations on operator health and comfort, complementing the vibrational analysis of the vehicle and the seat from the previous stages of the research.

To ensure the accuracy of the virtual mannequin model, average anthropometric dimensions of the subjects were used in accordance with the experimental protocol, as presented in

Table 2. Average anthropometric dimensions of the subject sample.

Participant Sample	Mass [kg]	Height [cm]	Shank Length [cm]	Thigh Length [cm]	Upper Limb Length [cm]	Spinal Column Length in Seated Position [cm]
Average	75	175	48	49	72	70

.

In the development of the virtual human operator model, in addition to the dimensional parameters derived from the anthropometric data presented in Table 2, a validated biomechanical human model was integrated to enhance the accuracy of the vibration analysis simulation. This biomechanical model, designed with nine degrees of freedom, was specifically developed and validated to enable both static and dynamic testing in the context of operator interaction with an agricultural vehicle of the tractor type.

The model enables the simulation of the complex three-dimensional behavior of the human body in a seated posture on the vehicle seat and accurately reflects the interactions between body segments and the seat suspension system.

The nine biomechanical segments—head (m₁), neck (m₂), torso (m₃), upper arms (m₄), forearms (m₅), hands (m₆), thighs (m₇), lower legs (m₈), and feet (m₉)—are modeled as lumped masses connected by spring–damper elements, which simulate the mechanical characteristics of human tissues and joints. The vehicle seat is modeled as a separate mass (m_s), directly interacting with the human model.

The dynamic parameters and mechanical properties of this model are presented in

Table 3. Mechanical properties of the 9-degree-of-freedom model.

Segment	Mi Initial Mass [Kg]	CS Segment Coefficient	No of Pieces	MS Segment Mass [kg]	Stiffness Coefficient [KN/m]	Damping Coefficient (C) [KNs/m]
Head	72.15	0.081	1	5.84	120.00	1.50
Neck		0.04	1	2.89	120.00	1.50
Torso		0.497	1	35.86	105.00	1.80
Upper arms		0.028	2	4.04	50.00	1.00
Forearms		0.016	2	2.31	50.00	1.00
Hands		0.006	2	0.87	50.00	1.00
Thighs		0.1	2	14.43	50.00	1.10
Lower legs		0.0465	2	6.71	50.00	1.00
Feet		0.0145	2	2.09	50.00	1.00
MT Total Mass				75.04

and were selected based on validated biomechanical data and relevant literature, in order to ensure high fidelity in the simulation of the operator’s vibrational response during the operation of the TE-0 electric vehicle.

Figure 19 presents the equivalent system of the biomechanical model of the seated driver. The segments comprising the model are denoted as [m_{1 −} m₉ + m_seat]. Each segment of the human body is associated with a system consisting of springs and dampers, labeled K_i and C_i, respectively. These elements are placed beneath each mass to represent the deformable properties of the body segments, as well as to simulate the vibrations transmitted from the floor through the seat to the entire body. The total mass of the model is 75 kg.

Based on the development of the biomechanical model of the seated vehicle operator, designed with nine degrees of freedom, an advanced and detailed analysis of the dynamic behavior of the human body was made possible, particularly regarding the manner in which vibrations are transmitted through the vehicle seat during motion. This biomechanical model—composed of body segments represented by lumped masses interconnected via spring–damper elements—enabled a three-dimensional simulation of the operator’s vibrational response under real working conditions.

The integration of these features into the virtual model, constructed using average anthropometric dimensions of the vehicle operator, led to a realistic and rigorous representation of the interaction between the operator, the seat, and the tractor.

Consequently, the analysis became more comprehensive, providing relevant results for identifying the natural vibration modes that may directly influence the comfort, health, and safety of the operator during operation on unprepared terrain.

SolidWorks provides a clear and methodical framework for accurately modeling the central segment of the human body, commonly referred to as the torso. The modeling process is structured into several essential stages, each playing an important role in ensuring the geometrical and functional accuracy of the torso, which is a critical component in the structure of the virtual mannequin.

Figure 20 presents an exploded view of the virtual mannequin, offering a detailed visual representation of each individual component and their assembly. This graphical representation visually separates the main components—such as the head, torso, arms, legs, and other body segments—highlighting their interconnection within a coherent assembly.

The metric system is selected by default to ensure the consistency and accuracy of all numerical values used in the analysis, as illustrated in Figure 21a. The main coordinate system is attached to the center of mass of the mannequin, with the X-axis oriented longitudinally, the Y-axis transversely, and the Z-axis vertically, as shown in Figure 21b.

The model is graphically represented in Figure 22, providing a detailed visualization of the human body structure in the context of vibrational analysis. This simulation stage is in full alignment with the objective of our article, which focuses on analyzing the dynamic interaction between the operator, the seat, and the electric vehicle. It contributes significantly to the development of more efficient and ergonomic design solutions aimed at protecting operators from the harmful effects of vibrations under real operating conditions.

Altair Sim Solid allows for the detailed visualization and management of all connections (joints, contact surfaces, or other types of mechanical interfaces), as shown in Figure 23a, ensuring that all physical interactions between components are accurately considered in order to obtain precise and reliable results in simulating the dynamic behavior of the mannequin seated on the chair under vibrational conditions.

In Figure 23b, Altair Sim Solid highlights the virtual model of the mannequin seated on the chair, showing all connection points between its constituent components.

The modal analysis of the mannequin seated on the chair was configured to display all natural frequencies and vibration modes within the [0–80] Hz range, in accordance with ISO 2631-1. Within this frequency range, a total of 80 vibration modes were identified.

In Figure 24a, the software displays the total number of vibration modes of the mannequin, while Figure 24b shows the virtual model of the mannequin with the corresponding natural frequencies highlighted for each vibration mode.

To simulate the seat suspension, an elastic support with a vertical (Z-axis) stiffness of 15 N/mm was applied at the base of the seat. The longitudinal and transverse axes at the base of the seat were considered fixed. The tractor floor was simulated by applying a “slider” support to the flat surface of the mannequin’s feet. An “immovable” support was applied to the palms of the mannequin, thus simulating a fixed contact between the palm surfaces and the steering wheel, as shown in Figure 25.

This detailed modal analysis, along with comparative discussions of the vibration modes and frequency values, enables a deeper understanding of how each vibration mode contributes to the dynamic behavior of the mannequin.

The participation factors calculated for each vibration mode provide essential insights into the influence of each frequency on the overall operator-seat-vehicle system. Through this process, critical frequencies can be identified which, in the event of resonance, may amplify vibrations and lead to operator discomfort or health risks.

Thus, the analysis of vibration modes is a fundamental component in the comprehensive assessment of the impact of vibrations on the operator and in optimizing the design of the electric vehicle to ensure safe and ergonomic operating conditions.

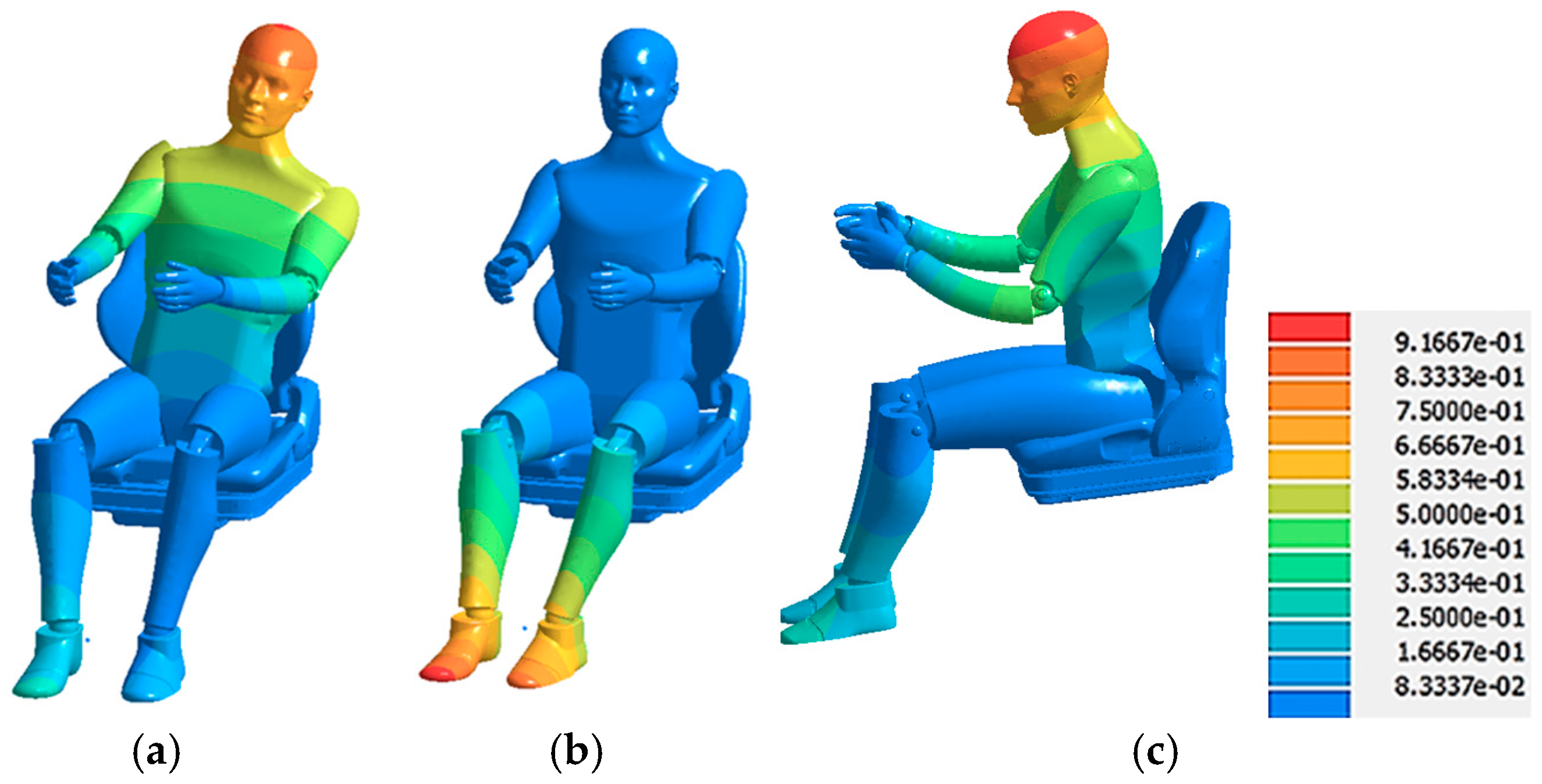
The most important and relevant vibration modes of the mannequin seated on the chair are shown in Figure 26, specifically modes 2, 3, and 5.

Vibration mode 2, at a frequency of 2.80 Hz with a participation factor of 62.12, shows a decrease in influence compared to the first mode, but still plays a significant role in vibration transmission, indicating its importance in the assessment of comfort and the mannequin’s dynamic behavior. Vibration mode 3, at 2.99 Hz with a participation factor of 39.88, reflects a gradual reduction in the influence of the modes on the overall response of the mannequin. Vibration mode 5, at 4.03 Hz with a participation factor of 70.55, indicates a resurgence in modal influence, suggesting a strong interaction with vibrational excitations.

3. Discussion

In this study, the analysis of the vibration modes of the integrated assembly—electric tractor, seat, and virtual mannequin (operator) provides a detailed perspective on the interaction between the vehicle component, the seat, and the operator in terms of the impact of vibrations on operator comfort and health. By comparing the modal frequencies obtained from the analyses of the electric tractor, the seat, and the virtual mannequin, the relationships among these elements and their implications within the context of an autonomous and sustainable agricultural transport system can be highlighted.

In the case of the TE-0 electric tractor, the predominant vibrations were identified within the [0–10] Hz frequency range, with a significant peak at 39 Hz, corresponding to the nominal operating speed of the electric motor.

The correlation between the calculated modal frequencies and those determined experimentally validates the models used, confirming their accuracy in predicting the dynamic behavior of the electric tractor-seat-virtual mannequin system. This validation suggests that simulation models can be employed to anticipate the effects of vibrations on the operator under various operating conditions and to optimize the vehicle design, thereby reducing the risks associated with exposure to harmful vibrations. Thus, the vibrational analysis of the electric tractor, together with the assessment of its impact on the operator, serves as an important tool for the development of sustainable, safe, and ergonomic agricultural transport solutions. A relevant example from the analysis is presented in Figure 27, which illustrates the vibrational behavior of the integrated vehicle–seat-operator system under simulated real-world operating conditions on unprocessed grass-covered terrain at a predefined speed.

The frequency of 10.22 Hz corresponds to vibration mode 3 of the tractor and is manifested as a torsional deformation of the chassis along the longitudinal axis. This can be described as an opposing twist between the two axles (the rear axle and the front axle) as illustrated in Figure 27a. This tractor frequency is very close to modal frequency 2 of the seat, located at 10.75 Hz, which is manifested by a rotational motion of the seat backrest around the transverse Y-axis, as shown in Figure 27b.

The mentioned frequency is also observed in the modal analysis of the mannequin seated on the seat, corresponding to vibration mode 11. This frequency originates from the tractor’s structure and is transmitted through the seat to the seated mannequin, as illustrated in Figure 27c. This transmission of vibrations suggests a strong correlation between the tractor’s structural behavior and the dynamic response of the seat and mannequin, highlighting the importance of harmonizing the modal frequencies of the components in order to avoid undesirable vibrational effects and to ensure operator comfort and safety.

The frequency of 10.66 Hz, with a deviation of ±0.372, was measured at the level of the tractor cabin floor with an incidence of 37.5%. This frequency was also detected by the triaxial accelerometer sensors mounted on the seat, at a slightly different frequency of 10.35 Hz, with a deviation of ±0.374 and an incidence of 31.25%. These data indicate that vibrations at this frequency are significantly transmitted from the tractor structure (floor) to the seat, highlighting the potential impact of these vibrations on operator comfort and health.

The consistency between the frequencies measured at the tractor cabin floor and those at the seat level suggests a direct transmission of vibrations, which amplifies the discomfort experienced by the operator.

An experimental study published in 2025 [11], investigated the vibrations transmitted through the seat of an electric tractor prototype similar to the TE-0 model, using triaxial accelerometers and experimental modal analysis methods.

The results indicated that vibrations in the 0–20 Hz range—particularly lateral and torsional modes—are most strongly associated with operator discomfort and may lead to long-term musculoskeletal disorders. The same study demonstrated that comfort could be significantly improved through appropriate adjustment of the seat suspension.

A comparative analysis within the same study [36] assessed the vibration isolation efficiency between a diesel tractor and an electric one, including the TE-0 model. Vibration transmissibility from the seat to the operator’s head was monitored, and the electric tractor achieved up to 98% isolation efficiency in the critical 4–12 Hz frequency range, clearly highlighting its advantage in safeguarding operator health.

Furthermore, other studies on conventional (non-electric) tractors have shown that prolonged exposure to similar frequency ranges results in fatigue, lower back pain, and reduced productivity, posing serious risks during extended agricultural operations.

Therefore, our focus on vibrations in the context of optimizing the operator–seat–vehicle system is well-grounded in clear evidence of the impact on comfort, health, and efficiency in agricultural applications. The referenced studies support the need for advanced simulation approaches and provide a solid foundation for our contribution: identifying problematic vibration modes and increasing awareness—among researchers and operators alike—about the risks associated with prolonged whole-body vibration exposure under real-life driving scenarios.

The findings of this research offer relevant insights into the intricate dynamics between the human operator and the electric vehicle when operating in real-life agricultural conditions. The TE-0 electric tractor was tested while maintaining a steady speed of 7 km/h over unprocessed soil, representative of standard working environments in the agricultural sector. This testing setup allowed for the collection of empirical data reflecting the vehicle’s behavior under actual field conditions, with particular focus on the vibrations generated during use.

The dynamic analysis of the operator–seat–tractor system highlighted the crucial role that optimized structural design plays in reducing harmful vibration levels and enhancing operator comfort. The results emphasize that integrating appropriate seat suspension mechanisms and maintaining vibration control through design refinement can effectively mitigate health risks caused by prolonged exposure to vibration.

These comparative results clearly illustrate that transitioning to electric-powered tractors not only reduces emissions and dependence on fossil fuels but also contributes to a healthier work environment by lowering vibration and noise levels. Consequently, the adoption of electric technologies in agricultural transport aligns with broader global initiatives aimed at reducing pollution and advancing sustainable mobility.

Through the application of advanced modeling and simulation methods, this study delivers valuable observations concerning the vibrational characteristics of electric tractors and their impact on the operator. These simulations allowed for the identification of vibration modes with potential ergonomic and health implications, facilitating the development of design strategies that minimize exposure to harmful mechanical stimuli. Moreover, the real-world evaluation of vibration effects reinforces the case for sustainable transport solutions, with relevance not only to agriculture but also to other domains where human–machine interaction plays a critical role.

In this sense, the present study directly supports the thematic objectives of this Systems special issue, which promotes research at the intersection of modeling, simulation, and sustainability in transport systems. By employing interdisciplinary tools and simulation-driven approaches, the research contributes to the advancement of more efficient, ergonomic, and environmentally responsible vehicles—offering a forward-looking perspective on sustainable innovation in agricultural transport.

4. Conclusions

In the context of the transition toward autonomous and sustainable agricultural mechanization, this study proposes an advanced methodology for the vibrational analysis of the operator–seat–electric tractor system by integrating three-dimensional modeling, finite element modal analysis, and validation through experimental data. Structured in three stages, the research highlights, through detailed simulations and correlation with real-world measurements, the critical natural vibration modes that directly impact operator comfort and safety.

The results indicate that the natural frequencies of the analyzed system occasionally coincide with dangerous resonance zones (below 5 Hz), confirming the direct transmission of vibrations between the vehicle, seat, and operator. The electric tractor model TE-0, tested on unprocessed soil terrain, demonstrated high vibration isolation efficiency, significantly reducing the risk of musculoskeletal disorders.

This research supports the development of ergonomically oriented and resilient design solutions, providing a strong scientific foundation for improving the performance of autonomous electric agricultural vehicles. The proposed approach aligns with current trends in intelligent transport systems engineering, contributing to the development of sustainable and human-centered transportation systems.

Future research will focus on expanding the vibroacoustic analysis by integrating noise transmission modeling and whole-body vibration exposure, as well as validating the findings across a broader set of terrain conditions and operator profiles. Additionally, coupling the vibrational data with real-time sensor feedback will enhance the development of adaptive suspension systems for electric agricultural vehicles.