Collaborative Causal Inference and Multi-Agent Dynamic Intervention for “Dual Carbon” Public Opinion Driven by Reinforced Large Language Models and Diffusion Models

Abstract

Under the “Dual Carbon” goal, public opinion analysis is crucial for optimizing policy implementation and enhancing social consensus, yet it faces challenges such as insufficient multi-source data integration, limited causal modeling, and delayed interventions. This study proposes a collaborative framework integrating reinforcement learning-enhanced large language models (LLMs), diffusion models, and multi-agent systems (MASs). By constructing a four-dimensional causal network of “policy–technology–economy–public sentiment”, it analyzes multi-source data and simulates multi-agent interactions. The experimental results show that this framework outperforms Latent Dirichlet Allocation (LDA), Bidirectional Encoder Representations from Transformers (BERT), and Susceptible Infected Recovered (SIR) models in causal inference, dynamic intervention, and multi-agent collaboration. Reinforcement Learning from Human Feedback (RLHF) optimizes LLM outputs for reliable policy recommendations, with pass@10 showing strong correlations. This study provides scientific support for “Dual Carbon” policymaking and public opinion guidance, facilitating the green and low-carbon transition.

1. Introduction

The advancement of the “Dual Carbon” (carbon peaking and carbon neutrality) goals profoundly impacts energy structures, industrial transformation, and public lifestyles, involving changes in energy prices, employment, and daily habits, which readily trigger widespread attention and public opinion fluctuations [1]. Information asymmetry or inadequate communication during policy implementation may lead to public misunderstandings, while the amplification effect of social media can escalate local sentiments into national events. Moreover, economic shocks in high-energy-consuming industries or resource-dependent regions, without effective transitional measures, may intensify social conflicts and generate negative public opinion [2]. Therefore, systematic analysis of “Dual Carbon” public opinion is critical for optimizing policy implementation, guiding public sentiment, and enhancing social support.

Research on “Dual Carbon” public opinion offers multi-dimensional value. First, public opinion analysis based on high-frequency big data reveals public attitudes, providing a foundation for policy design and communication strategies [3]. Second, it captures the spatiotemporal dynamics of cognition and attitudes, enabling refined governance. Third, monitoring and predicting public opinion trends help address doubts and build social consensus. Additionally, such research promotes the application of digital technologies in low-carbon governance, such as the development of intelligent analysis systems, fostering the integration of technology and policy. Thus, “Dual Carbon” public opinion research is a key driver of green and low-carbon development.

However, current studies have notable shortcomings, failing to meet policy demands. Although the dynamic and heterogeneous nature of public opinion is recognized, several challenges persist. Integration and semantic extraction of multi-source heterogeneous data, such as policy texts and social media, remain limited. There is also a lack of systematic causal modeling tools to accurately depict the dynamic relationships among policy, technology, economy, and public sentiment. Predicting the behavior of multiple stakeholders, including government, enterprises, and the public, is constrained, particularly in scenarios with information asymmetry, making it difficult to model public opinion evolution. Lastly, the generation and impact assessment of intervention strategies lack specificity and real-time applicability.

To address these issues, this study proposes a “Framework for Causal Inference and Dynamic Intervention in Dual Carbon Public Opinion Based on Reinforcement Learning Enhanced Large Language Models and Diffusion Models”. To tackle data integration challenges, we design a multimodal causal knowledge graph, leveraging improved large language models and diffusion models to construct a four-dimensional causal network of policy, technology, economy, and public sentiment, with dynamic updates enabled by a multi-agent system. To overcome deficiencies in causal modeling and stakeholder interaction prediction, we propose a multi-agent collaborative approach for causal inference and interaction simulation, modeling stakeholder behaviors to enhance complex dynamic forecasting capabilities. To meet the need for optimized interventions, we develop dynamic intervention strategies using generative models, with RLHF optimizing LLM outputs for reliable policy recommendations, validated by pass@k metrics, to enhance intervention effectiveness and trustworthiness. This study aims to provide scientific support for “Dual Carbon” policymaking and public opinion guidance, facilitating the green and low-carbon transition and fostering social consensus.

2. Literature Review

As global climate change intensifies and the urgent need for green, low-carbon transformation grows, public awareness and the evolution of public opinion regarding the “Dual Carbon” goals have become research hotspots. Scholars worldwide have conducted extensive studies on “Dual Carbon” public opinion, focusing on three key areas: public opinion identification and analysis, public opinion evolution modeling, and dynamic public opinion monitoring. While significant progress has been made, shortcomings persist.

2.1. Public Opinion Identification and Analysis

Public opinion identification and analysis technologies have advanced significantly under the “dual carbon” agenda, particularly through the integration of clustering methods and semantic-driven approaches to enhance recognition accuracy. In terms of clustering methods, Mashayekhi et al. proposed an evolutionary clustering method based on a Bayesian nonparametric Dirichlet process mixture model [4]. George et al. proposed an integrated clustering and BERT framework to improve topic modeling [5]. Chen et al. applied an improved Single-Pass clustering method to disaster-related opinion monitoring, offering a reference for intelligent monitoring of policy-related opinions on carbon neutrality [6]. On the semantic-driven front, Zhang et al. introduced an innovative integration framework that merges two representation approaches, enabling the transfer of topic information into the corresponding semantic embedding structure [7]. Diego et al. integrated word embeddings with topic models to improve the semantic representation of documents [8]. Jiang et al. proposed a topic detection and tracking method based on time-aware document embeddings, suitable for real-time news and microblog data [9]. Chen et al. developed a simulation and control strategy for online opinion by integrating sentiment analysis models, topic computation models, and the SEIR model [10].

2.2. Public Opinion Evolution Modeling

Modeling the evolution of public opinion primarily relies on graph-based methods and topic modeling to reveal dynamic trends. Regarding graph-based approaches, Hassan et al. proposed the KeyGraph algorithm to analyze public opinion structures based on keyword co-occurrence [11]. Lv et al. proposed a method combining document and knowledge-level similarity to generate timelines of news events, segmenting sub-events using community detection algorithms [12]. Weng et al. used Transformer models and the HDBSCAN clustering algorithm to identify key topics in scientific publications [13]. Li et al. proposed a new Revised Medoid-Shift method and compared the performance of different methods on datasets with and without ground truth labels [14]. In the domain of topic modeling, Churchill et al. proposed the Dynamic Topic-Noise Discriminator and Dynamic Noiseless Latent Dirichlet Allocation, improving dynamic topic modeling for social media by effectively handling noise [15]. Xue et al. used topic modeling to analyze public opinions on waste classification from Sina Weibo, identifying sentiment trends and specific concerns, and proposed policy improvement suggestions based on these findings [16]. Muthusami et al. evaluated the quality of short-text topic modeling using clustering methods and silhouette analysis [17].

2.3. Dynamic Public Opinion Monitoring

Dynamic monitoring of public opinion is achieved through semantic similarity and statistical learning methods. For semantic similarity methods, Xu et al. utilized the Latent Dirichlet Allocation model and Gibbs Sampling method to extract and track topics in online news texts [18]. Sun et al. proposed a context-based sentence similarity framework that measures similarity by comparing the generation probabilities of two sentences [19]. For statistical learning methods, Zhang et al. used LS-SVM in conjunction with LSI to reduce feature dimensionality in vector space and improve classification accuracy [20]. Yeh et al. proposed a conceptual dynamic Latent Dirichlet Allocation model for topic detection and tracking [21]. Rizky et al. developed a retweet prediction system using an Artificial Neural Network optimized with Harmony Search [22].

2.4. Limitations and My Study

Although research on “dual carbon” public opinion has made progress in opinion identification and analysis, evolution modeling, and dynamic monitoring, several limitations persist, summarized as follows:

First, there is insufficient integration between technology and data. Most existing studies rely on single-method approaches, making it difficult to handle the complexity of heterogeneous data from multiple sources such as policy documents and social media. Moreover, the depth of multimodal data integration is limited, restricting the ability to capture deep semantic relationships among policy, economy, and public sentiment. This hinders a comprehensive depiction of the “policy-public” interaction and the transmission chains of public opinion.

Second, there is a lack of causal reasoning and dynamic modeling. Many studies remain at the level of correlation analysis and fail to accurately model the causal chain of “policy stimulus-public sentiment-opinion dissemination”. Furthermore, the reliance on static rules or historical data makes it difficult to predict real-time opinion changes or capture dynamic polarization processes, which limits the adaptability and predictive power of current models.

Lastly, existing intervention strategies lack scientific rigor. Most current interventions depend on static rules and do not optimize dynamic interventions based on causal effects. There is also a lack of quantitative evaluation of intervention strength and design of collaborative mechanisms among multiple stakeholders, affecting the sustainability of intervention outcomes.

Recent advancements in resilient consensus for MASs have provided valuable insights into handling adversarial conditions in networked systems, which are analogous to the challenges of misinformation or collusive negative sentiments in public opinion dynamics. Related studies primarily focus on attack isolation, detection, consensus achievement, and applications in specific scenarios. For instance, Zhao et al. [23] proposed a generalized graph-dependent isolation strategy based on graph topology to detect and isolate collusive false data injection and covert attacks in interconnected systems, thereby maintaining system integrity. Wang et al. [24] investigated resilient consensus in discrete-time MASs with dynamic leaders and time delays under cyber-attacks, combining theoretical analysis with experimental validation using UAVs to extend applications in time-delay scenarios. Zhao et al. [25] studied resilient consensus in high-order networks under collusive attacks, developing algorithms to ensure agent agreement despite malicious interference. Yang et al. [26] focused on resilient bipartite consensus for high-order heterogeneous MASs under Byzantine attacks, supporting cooperation and competition among agents while mitigating malicious behaviors, highlighting the handling of heterogeneous systems. Zhao et al. [27] adopted an attack isolation-based approach for higher-order multi-agent networks, achieving consensus by excluding extreme values and isolating compromised nodes. Jahangiri-Heidari et al. [28] developed a resilient consensus scheme for nonlinear MASs under false data injection attacks on communication channels, employing detection and isolation techniques to further emphasize attack detection. Wang et al. [29] proposed distributed resilient adaptive consensus tracking based on K-filters to address deception attacks in nonlinear MASs, ensuring tracking performance despite uncertainties and attacks. Zhu et al. [30] introduced secure consensus control using improved PBFT and Raft blockchain algorithms to enhance the security of MASs against attacks in industrial environments, integrating blockchain technology into consensus mechanisms.

Although these studies have advanced resilient MASs by emphasizing attack isolation and detection, consensus achievement, adaptive tracking, and blockchain integration, they primarily target engineered systems and do not incorporate natural language processing or generative AI to handle unstructured, multimodal data from social contexts. In contrast, the priority of this study lies in adapting and extending MAS resilience concepts to the domain of “Dual Carbon” public opinion, where “attacks” manifest as collusive misinformation or sentiment shifts rather than direct cyber threats. By integrating reinforcement learning-enhanced LLMs for semantic alignment and causal discovery, diffusion models for simulating opinion propagation, and MASs for modeling interactions among stakeholders like government, enterprises, and the public, this framework constructs a four-dimensional causal network encompassing policy, technology, economy, and public sentiment. This approach goes beyond consensus to include predictive causal inference and real-time dynamic interventions. Unlike the control-focused methods mentioned above, which lack mechanisms for generative strategy optimization or quantitative causal effect estimation, such as through Conditional Average Treatment Effect, this study employs multi-agent deep reinforcement learning integrated with causal Bayesian networks to design collaborative, adaptive intervention measures, enhancing sustainability and applicability to policy guidance. This interdisciplinary integration addresses the unique challenges of public opinion evolution, such as information asymmetry and spatiotemporal dynamics, offering superior causal modeling, multi-agent collaboration, and intervention efficacy compared to existing resilient MAS works, as validated through comparisons with baselines like LDA, BERT, and SIR models.

In light of these limitations, this study proposes a collaborative framework integrating reinforcement learning-enhanced LLMs, diffusion models, and MASs. The framework constructs a four-dimensional causal network covering “policy–technology–economy–public sentiment”, employing reinforcement learning to achieve semantic alignment and causal discovery across multimodal data. It embeds LLM-based decision logic generators and designs a multi-agent game model that incorporates a dual-loop reasoning mechanism based on counterfactual and intervention responses, thereby enhancing the dynamic modeling capacity needed to address the real-time nature of opinion evolution. Additionally, the study develops a quantitative model for intervention intensity estimation based on Conditional Average Treatment Effect (CATE) and optimizes collaborative intervention strategies and risk warning mechanisms for government, media, and platforms by integrating multi-agent deep reinforcement learning (MADRL) with causal Bayesian networks. This enhances the accuracy and sustainability of public opinion modeling and intervention efforts.

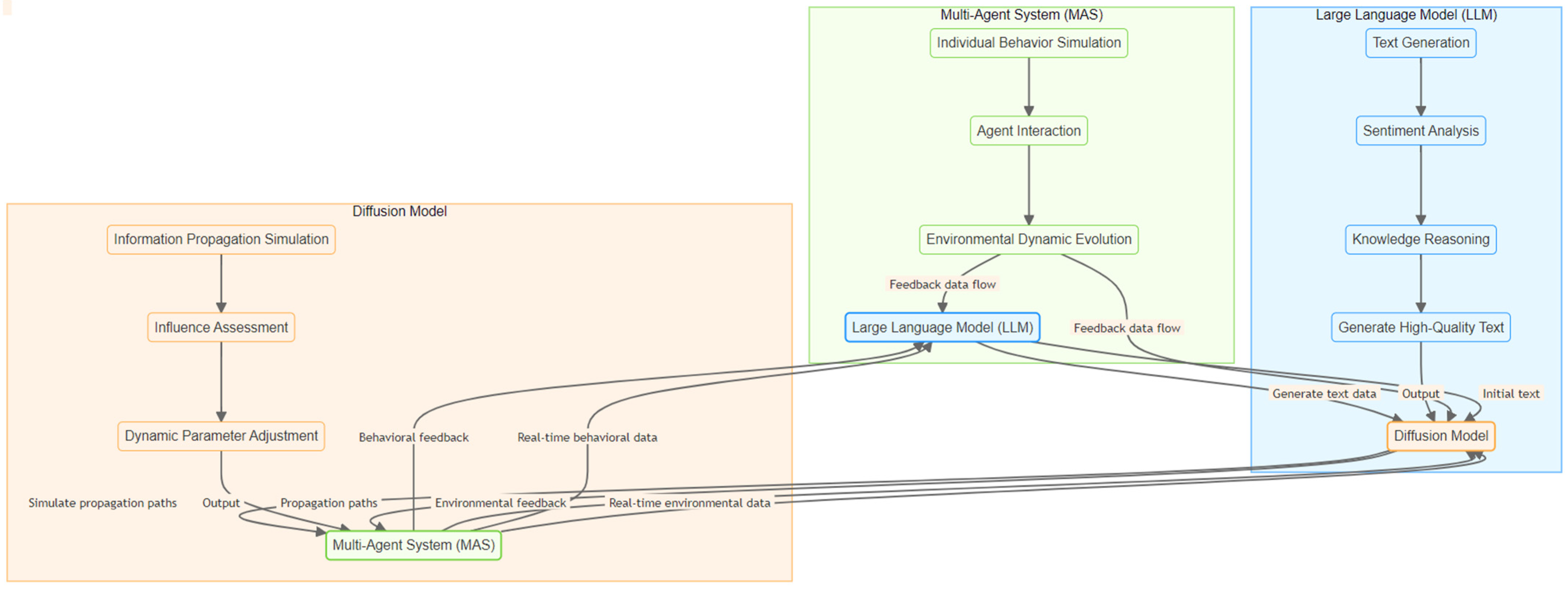
3. Multimodal Causal Inference and Collaborative Architecture Design

“Dual Carbon” public opinion involves multi-source heterogeneous data, including policy texts, social media, and expert opinions, which traditional methods struggle to analyze for complex causal relationships. This study proposes a collaborative architecture integrating LLMs, diffusion models, and MASs to construct a multimodal causal knowledge graph, simulate multi-agent interactions, and reveal causal emergence patterns through counterfactual reasoning. This framework provides scientific support for public opinion evolution modeling and intervention. The collaborative architecture is illustrated in Figure 1.

3.1. Multimodal Data Fusion and Causal Graph Generation

Multimodal data fusion aims to integrate policy texts, social media posts, and economic data to uncover deep causal relationships. This study designs the following steps:

First, the semantic understanding capabilities of large language models are utilized to extract preliminary causal hypotheses. Large language models process multi-source data through pre-trained text analysis modules to identify causal patterns, such as policy announcements triggering media coverage. MASs provide collaborative inputs and incorporate environmental feedback to optimize large language model inference, generating high-quality causal hypotheses.

Second, diffusion models simulate the temporal and spatial dissemination paths of public opinion, quantifying the dynamic characteristics of causal relationships. These models take preprocessed multi-source data and use time series modeling and spatial propagation analysis to create a dynamic picture of public opinion spread, such as media coverage triggering cascading emotional reactions across regions. The behavior decision module of MASs predicts public opinion evolution trends based on these features and feeds the results back to the large language model.

To ensure the reliability of causal relationships, a causal discovery algorithm based on adversarial training is designed. Agents within the multi-agent system are divided into two types: hypothesis generators and counterfactual validators. Through interaction, they verify the robustness of causal hypotheses. For example, one agent generates a hypothesis like policy announcement leading to public sentiment change, while another validates it through counterfactual analysis to rule out confounding effects. Environmental feedback adjusts agent strategies, forming a closed-loop optimization that eliminates spurious correlations.

Ultimately, a multimodal causal knowledge graph is constructed, encompassing policy, public behavior, and corporate actions. Large language models integrate multi-source data to generate causal chains, diffusion models provide temporal and spatial dimensions, and MASs validate causal directions. The graph is output in natural language descriptions or visualizations, aiding decision-makers in understanding complex causal mechanisms. This design enhances the precision of causal analysis, providing data support for policymaking and public opinion management.

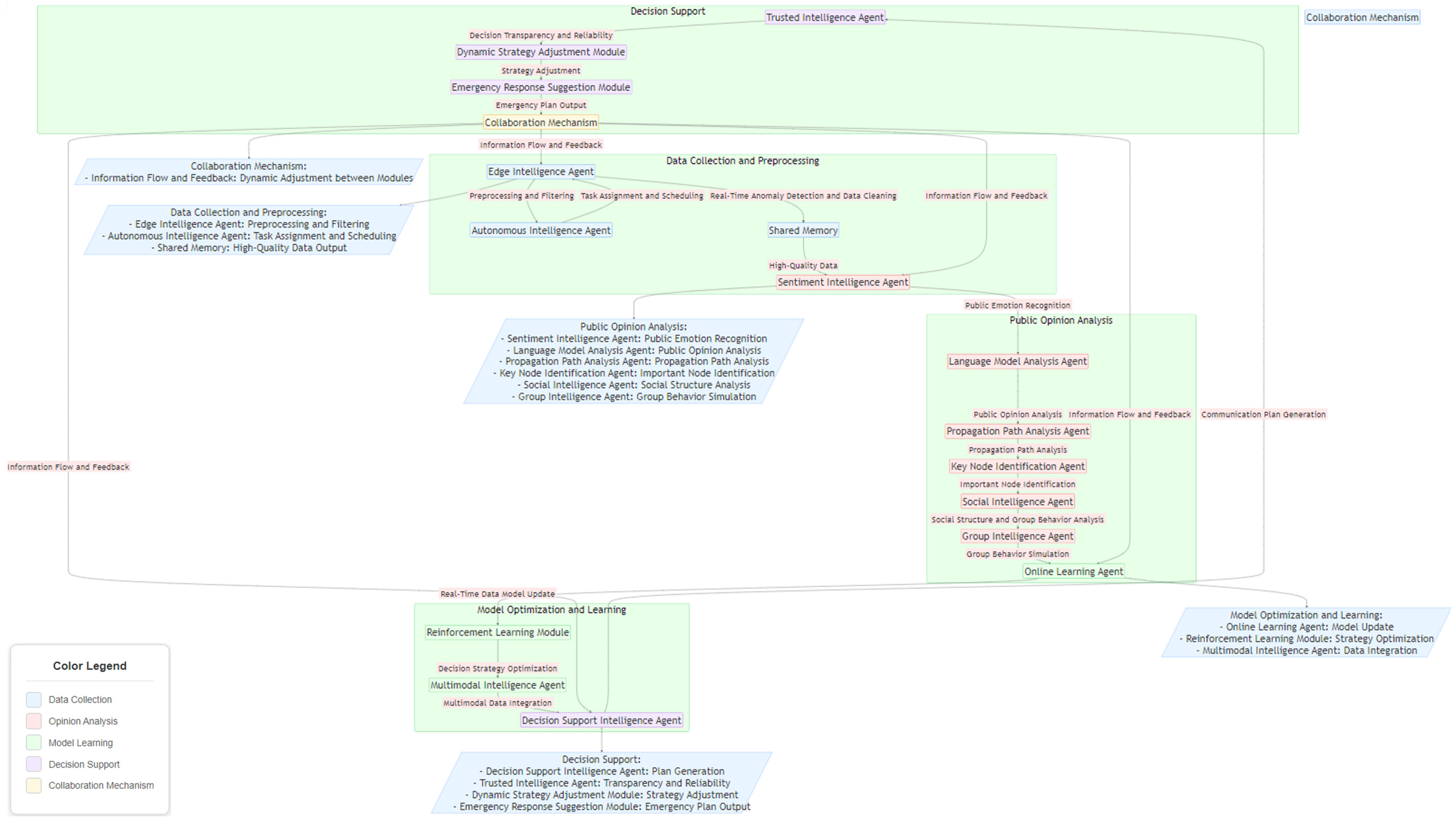
3.2. Multi-Agent Interaction Simulation and Counterfactual Causal Inference

The evolution of “Dual Carbon” public opinion involves interest-based interactions among multiple stakeholders, including government, enterprises, and the public, which single models struggle to simulate due to their complex dynamics. This study employs a MAS to construct a collaborative decision-making and causal inference framework, designing differentiated agents and a dual-loop inference mechanism of counterfactuals and intervention responses to predict causal emergence patterns in interaction scenarios. The architecture of the MAS is illustrated in Figure 2.

First, differentiated agents are constructed to simulate multi-agent behaviors. Agents represent roles such as the government optimizing emission reduction policies, enterprises balancing emission reduction costs, and the public reacting based on emotions, with decision logic generators based on large language models embedded to generate behavior strategies aligned with their respective objectives. Multi-level objective functions couple macro-constraints like carbon emission targets with micro-characteristics such as public approval rates, coordinating decisions across agents through weighted optimization.

Second, the collaborative decision-making module of the multi-agent system simulates dynamic interactions among agents to predict the cascading effects of interventions. For example, it analyzes how policy announcements trigger public emotional fluctuations through media dissemination, which in turn influence corporate actions. Diffusion models provide spatiotemporal propagation simulations while large language models evaluate the semantic impacts of interventions such as the amplifying effects of media coverage. The multi-agent system integrates results to predict the transmission pathways of causal chains.

Third, a counterfactual–intervention response dual-loop reasoning mechanism is developed to assess causal relationships. The counterfactual reasoning module compares intervention scenarios such as policy announcements with non-intervention scenarios like public reactions without policies to identify the authenticity of causality. The decision support module integrates multi-agent system results to generate optimization suggestions such as adjusting policy release timings to mitigate negative emotions. Large language models translate analyses into interpretable outputs while the multi-agent system feedback mechanism optimizes agent behaviors to ensure reasoning robustness.

Finally, the risk early-warning module of the multi-agent system monitors the effectiveness of game strategies in real time. When detecting abnormal public opinion such as high-risk emotional diffusion, it combines semantic analysis from large language models and propagation predictions from diffusion models to adjust agent behaviors and generate new intervention strategies. A closed-loop feedback mechanism ensures the timeliness of reasoning, providing support for dynamic interventions. For instance, the system may recommend optimizing policy communication to enhance public acceptance.

This framework simulates multi-agent games in dual carbon public opinion through differentiated agents, multi-level objective functions, and dual-loop reasoning mechanisms, revealing laws of causal emergence and supporting policy optimization and public opinion management.

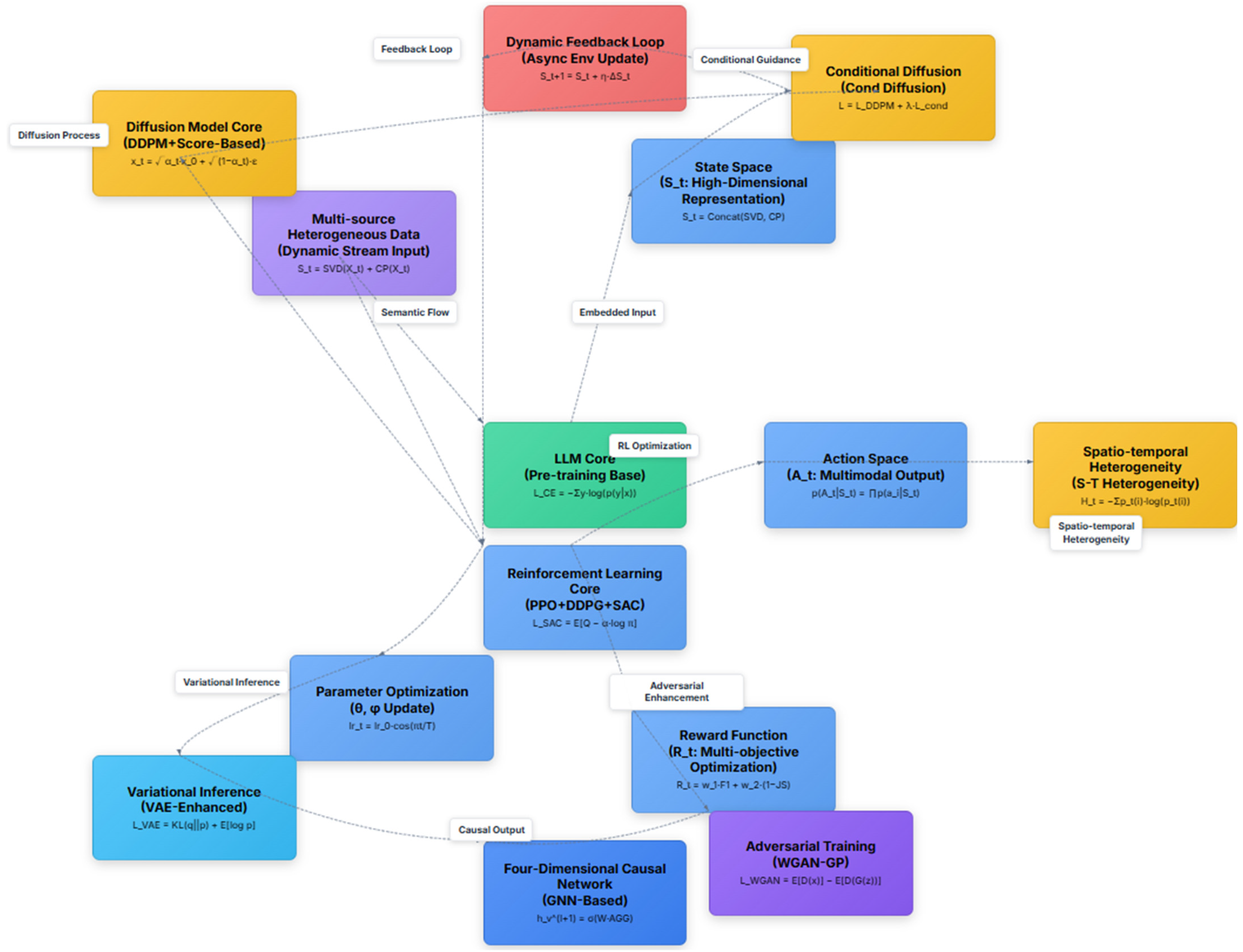
4. Construction of Four-Dimensional Causal Network

To capture the spatiotemporal dynamics and underlying causal patterns of dual carbon public opinion dissemination, this study develops a reinforcement learning-enhanced framework that integrates large language models and diffusion models to construct a four-dimensional causal network comprising policy, technology, economy, and public sentiment. In this network, nodes represent key entities such as policy directives, technological developments, economic indicators, and emotional responses, while edges indicate directional causal relationships, forming a structured knowledge graph. The framework combines the semantic parsing capabilities of large language models, the spatiotemporal modeling strength of diffusion models, and the strategy optimization of reinforcement learning to reveal the causal mechanisms governing information spread and sentiment evolution. The technical architecture, as shown in Figure 3, outlines the complete process of input processing, reinforcement learning optimization, diffusion-based generation, and feedback output.

4.1. Data Input and Pre-Training

In the input stage, multi-source heterogeneous data such as policy documents, social media posts, and economic indicators are processed to generate high-quality representations through feature extraction. The multi-source heterogeneous data module is based on matrix and tensor decomposition theories, utilizing Singular Value Decomposition (SVD) and conditional probability (CP) distributions to extract semantic and structural features. The formulations are as follows:

$$S_t=SVD\left(X_t\right)+CP\left(X_t\right)$$

where $S_t$ denotes the state vector at time step t, and $X_t$ represents the input data matrix.$SVD\left(X_t\right)$ preserves the principal semantic information, while $CP\left(X_t\right)$ captures conditional dependencies and reduces data complexity.

Subsequently, the core LLM module is built upon a pre-trained model and optimizes semantic understanding through cross-entropy loss.

$$L_{CE}=-\sum y\cdot \mathrm{l}\mathrm{o}\mathrm{g}\left(p\left(y|x\right)\right)$$

where $L_{CE}$ denotes the cross-entropy loss, $y$ is the ground truth label, and $p\left(y|x\right)$ represents the predicted probability distribution. The symbol $\sum$ represents summation, aggregating the loss terms over all classes or samples, and $\mathrm{l}\mathrm{o}\mathrm{g}$ denotes the logarithm function, typically the natural logarithm, used to compute the information-theoretic divergence in the loss calculation. This module provides a robust semantic foundation for the reinforcement learning and diffusion processes.

4.2. Reinforcement Learning Optimization

Reinforcement learning (RL) drives the dynamic construction of the four-dimensional causal network through Soft Actor-Critic (SAC) and Proximal Policy Optimization (PPO), within the framework of a Markov Decision Process (MDP), supporting strategy optimization in multi-agent game settings. The formulations are as follows [31,32,33].

① SAC loss function:

$$L_{SAC}=\mathbb{E}\left[Q-\alpha \cdot \mathrm{l}\mathrm{o}\mathrm{g}\pi \right]$$

(1)

where $L_{SAC}$ denotes the SAC loss function, guiding the optimization of the policy. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $Q$ denotes the state-action value function, $\alpha$ denotes the entropy regularization coefficient, and $\pi$ represents the action probability distribution. $\mathrm{l}\mathrm{o}\mathrm{g}$ denotes the logarithm function, typically the natural logarithm, used in entropy calculations. SAC balances exploration and exploitation by maximizing entropy.

② PPO objective function:

$$L^{CLIP}\left(\theta \right)=\mathbb{E}\left[\mathrm{m}\mathrm{i}\mathrm{n}\left(r_t\left(\theta \right)A_t,\mathrm{clip}\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right)A_t\right)\right]$$

(2)

where $L^{CLIP}\left(\theta \right)$ denotes the clipped objective function for the PPO algorithm, guiding policy optimization. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $r_t\left(\theta \right)$ denotes the probability ratio between the new and old policies, $A_t$ is the advantage function, $ϵ$ is the clipping parameter, $\mathrm{clip}$ denotes the clipping function, limiting the probability ratio within the range $[1-ϵ,1+ϵ]$, and $\mathrm{m}\mathrm{i}\mathrm{n}$ denotes the minimum function, selecting the smaller value between the clipped and unclipped terms. PPO stabilizes policy updates through a clipping mechanism.

③ Multi-agent value function:

$$Q_i\left(s,a_i,a_{-i}\right)=\mathbb{E}\left[R_i+\gamma Q_i\left(s^{\prime },a_i^{\prime }{,a}_{-i}^{\prime }\right)\right]$$

where $Q_i\left(s,a_i,a_{-i}\right)$ denotes the value function for the $i-th$ agent, estimating the expected return given state $s$, action $a_i$, and the actions of other agents $a_{-i}$. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $R_i$ denotes the immediate reward received by the $i-th$ agent. $\gamma$ denotes the discount factor, weighting the importance of future rewards. $s$ denotes the current state of the environment. $a_i$ denotes the action taken by the $i-th$ agent. $a_{-i}$ denotes the actions taken by all other agents except the $i-th$ agent. $s^{\prime }$ denotes the next state of the environment. $a_i^{\prime }$ denotes the next action of the $i-th$ agent. $a_{-i}^{\prime }$ denotes the next actions of all other agents. This formulation evaluates the expected return in multi-agent game scenarios.

④ State vector:

$$S_t=Concat\left(SVD,CP\right)$$

where $S_t$ denotes the state vector at time step t, integrating semantic and conditional features, and serves as the input to the action distribution. $Concat$ denotes the concatenation operation, combining the outputs of $SVD$ and CP. $SVD$ denotes the Singular Value Decomposition, extracting principal semantic information. $CP$ denotes the conditional probability or dependency capture operation, modeling conditional relationships.

⑤ Action probability distribution:

$$p\left(A_t|S_t\right)=\prod p\left(a_i|S_t\right)$$

(3)

where $A_t$ denotes the action set, $S_t$ denotes the state vector at time step t, and $a_i$ represents an individual action, supporting multimodal action modeling. $\prod$ denotes the product operator, aggregating probabilities over individual actions. $p\left(a_i|S_t\right)$ denotes the probability of an individual action $a_i$ given the state vector $S_t$.

⑥ Reward function:

$$R_t=w_1\cdot F1+w_2\cdot \left(1-JS\right)$$

(4)

where $R_t$ denotes the reward function at time step t, quantifying the objective for optimization. $F1$ denotes the $F1$ score, $JS$ represents the Jensen–Shannon divergence, and $w_1$ and $w_2$ are the corresponding weights, guiding semantic accuracy and distributional consistency.

⑦ Learning rate scheduling:

$$l{r}_t=l{r}_0\cdot \mathrm{c}\mathrm{o}\mathrm{s}\left(\pi t/T\right)$$

(5)

where $l{r}_t$ denotes the learning rate at time step t, determining the step size for model updates. $l{r}_0$ denotes the initial learning rate, and $T$ denotes the total number of training steps. $\mathrm{c}\mathrm{o}\mathrm{s}$ denotes the cosine function, used to modulate the learning rate. The cosine annealing schedule is employed to enhance training stability.

⑧ Value function:

$$V^{\pi }\left(s_t\right)=\mathbb{E}\left[R_t+\gamma V^{\pi }\left(s_{t+1}\right)\right]$$

(6)

where $V^{\pi }\left(s_t\right)$ denotes the value function for state $s_t$ under policy π, estimating the expected return. $R_t$ denotes the reward received at time step t. $\gamma$ denotes the discount factor, controlling the weight of future rewards. $s_t$ denotes the state at time step t. $s_{t+1}$ denotes the state at the next time step t + 1. The reinforcement learning module optimizes the policy through the state $s_t$, reward $R_t$, and value function $V^{\pi }$, supporting the dynamic construction of the four-dimensional causal network.

4.3. Diffusion Model Generation

The diffusion model simulates the spatiotemporal dynamics of public opinion dissemination using the Denoising Diffusion Probabilistic Model (DDPM), combined with Wasserstein GAN (WGAN) and Variational Autoencoder (VAE) to optimize the generation of causal relationships [34,35,36]. The formulations are as follows.

① Forward diffusion:

$$x_t=\sqrt{{\alpha }_t}\cdot x_0+\sqrt{1-{\alpha }_t}\cdot \epsilon$$

where $x_t$ denotes the noisy data, $x_0$ represents the original data, ${\alpha }_t$ is the scheduling parameter, $\sqrt{ \cdot }$ denotes the square root function, and $\epsilon$ is Gaussian noise following the standard normal distribution $N\left(0,I\right)$. The forward process provides the foundation for the subsequent reverse denoising procedure.

② DDPM Loss:

$$L_{DDPM}=\mathbb{E}\left[\parallel \epsilon -{\widehat{\epsilon }}_{\theta }\left(x_t,t\right){\parallel }^2\right]$$

where $L_{DDPM}$ denotes the DDPM loss function, quantifying the denoising objective. $\epsilon$ denotes the true Gaussian noise added during the diffusion process. ${\widehat{\epsilon }}_{\theta }$ denotes the noise predicted by the model parameterized by $\theta$, based on the noisy data $x_t$ and time step t. $x_t$ denotes the noisy data at time step t. t denotes the time step index, indicating the stage in the diffusion process. $\parallel \cdot {\parallel }^2$ denotes the squared L2 norm, measuring the squared difference between true and predicted noise. $\theta$ denotes the model parameters being optimized.

③ Denoising Distribution:

$$p_{\theta }\left(x_{t-1}|x_t\right)=N\left(x_{t-1};{\mu }_{\theta }\left(x_t,t\right),{\Sigma }_{\theta }\left(x_t,t\right)\right)$$

(7)

where $p_{\theta }\left(x_{t-1}|x_t\right)$ denotes the conditional probability distribution of the data at time step $t-1$ given the data at time step t, parameterized by $\theta$. $N$ denotes the Gaussian distribution. $x_{t-1}$ denotes the data at time step t − 1. $x_t$ denotes the noisy data at time step t. ${\mu }_{\theta }\left(x_t,t\right)$ denotes the mean of the Gaussian distribution, predicted by the model with parameters $\theta$. ${\Sigma }_{\theta }\left(x_t,t\right)$ denotes the covariance matrix of the Gaussian distribution, predicted by the model with parameters $\theta$. t denotes the time step index, indicating the stage in the diffusion process. $\theta$ denotes the model parameters being optimized. | denotes conditioning, indicating the dependency of $x_{t-1}$ on $x_t$.

④ Total Loss:

$$L=L_{DDPM}+\lambda \cdot L_{cond}$$

where $L_{cond}$ denotes the conditional loss based on LLM features, and $\lambda$ is a balancing coefficient between the two loss components. $L_{DDPM}$ refers to the loss function of the DDPM.

⑤ Temporal Entropy:

$$H_t=-\sum p_t\left(i\right)\cdot \mathrm{l}\mathrm{o}\mathrm{g}\left(p_t\left(i\right)\right)$$

where $H_t$ denotes the entropy at time step t, and $p_t\left(i\right)$ represents the probability of state $i$ at time step t. $\sum$ denotes the summation operator, aggregating over all possible states $i$. $\mathrm{l}\mathrm{o}\mathrm{g}$ denotes the logarithm function, typically the natural logarithm, used to compute the entropy term. This formulation captures the dynamic variations in spatiotemporal features and serves as a basis for adjusting the covariance in the denoising distribution.

⑥ WGAN Loss Function:

$$L_{WGAN}=\mathbb{E}\left[D\left(x\right)\right]-E\left[D\left(G\left(z\right)\right)\right]$$

where $L_{\mathrm{WGAN}}$ denotes the loss function of the WGAN, $D\left(x\right)$ is the output of the discriminator for real data $x$, $G\left(z\right)$ represents the fake data generated by the generator based on the latent variable $z$, $D\left(G\left(z\right)\right)$ is the discriminator’s output for the generated data, and $\mathbb{E}\left[D\left(G\left(z\right)\right)\right]$ refers to the expected score for the fake data. The generator and discriminator are optimized using the Wasserstein distance, which enhances generation quality and addresses the instability issues commonly encountered in traditional GAN training.

⑦ VAE Loss:

$$L_{VAE}=KL\left(q\left|\right|p\right)+\mathbb{E}\left[\mathrm{l}\mathrm{o}\mathrm{g}p\right]$$

(8)

where $L_{VAE}$ denotes the loss function of the VAE, $KL\left(q\left|\right|p\right)$ represents the Kullback–Leibler (KL) divergence, $\left|\right|$ denotes the divergence operator in the context of KL divergence, and $\mathbb{E}\left[\mathrm{l}\mathrm{o}\mathrm{g}p\right]$ is the expected reconstruction likelihood. The variational inference module optimizes the latent representation by minimizing the KL divergence and maximizing the reconstruction likelihood, thereby ensuring effective modeling of the latent space to support generative tasks.

⑧ MAE of propagation paths

$$MAE={\displaystyle \frac{1}{N\cdot T}}{\sum }_{n=1}^N{\sum }_{t=1}^T\left|{\widehat{p}}_{n,t}-p_{n,t}\right|$$

(9)

where $MAE$ denotes the mean absolute error of the propagation paths, with lower values indicating closer alignment between predicted and actual diffusion paths. $N$ denotes the number of propagation paths or samples in the evaluation set. $T$ denotes the length of each path. ${\widehat{p}}_{n,t}$ denotes the predicted value at time step t for the n-th path, generated from the denoising process in Formulation (7). $p_{n,t}$ denotes the ground truth value at time step t for the n-th path, obtained from actual data observations. The inner summation ${\sum }_{t=1}^T$ aggregates absolute errors over each path’s steps, while the outer summation ${\sum }_{n=1}^N$ averages across all paths. Division by $N\cdot T$ computes the overall mean.

⑨ Sample coverage rate

$$SCR={\displaystyle \frac{1}{N}}{\sum }_{i=1}^{N}I\left(\underset{j}{\mathrm{m}\mathrm{i}\mathrm{n}}d\left(x_i,x_{genj}\right)\le \delta \right)\times 100\%$$

(10)

where $SCR$ denotes the sample coverage rate, expressed as a percentage, with higher values indicating better representation of real data by generated samples. $N$ denotes the number of real samples. $I(·)$ denotes the indicator function. $d\left(x_i,x_{genj}\right)$ denotes the distance between real sample $x_i$ and generated sample $x_{genj}$, computed using KL divergence from Formulation (8). $\delta$ denotes a predefined threshold for coverage. The minimization $\underset{j}{\mathrm{m}\mathrm{i}\mathrm{n}}d\left(x_i,x_{genj}\right)$ finds the closest generated neighbor for each real sample, and the summation aggregates covered samples, divided by $N$ for the average rate.

The diffusion model generates public opinion propagation paths through a forward noise injection and reverse denoising process, while LLM features guide the conditional generation. WGAN and VAE modules further enhance the quality of generation.

4.4. Feedback and Four-Dimensional Causal Output

The feedback mechanism generates structured causal outputs through dynamic state updates and graph neural networks (GNNs) [37,38]. The formulations are as follows:

① Dynamic Feedback

$$S_{t+1}=S_t+\eta \cdot \mathit{\Delta }{S}_t$$

where $S_{t+1}$ denotes the state vector at time step $t+1$, $S_t$ denotes the state vector at time step $t$, $\mathit{\Delta }{S}_t$ denotes the state difference computed based on the Wasserstein distance, and $\eta$ is the learning rate, which ensures adaptive adjustment of the system.

② Four-Dimensional Causal Network

$$h_v^{\left(l+1\right)}=\sigma \left(W\cdot AGG\right)$$

where $h_v^{\left(l+1\right)}$ denotes the node representation at layer $l+1$, and $\sigma$ denotes the activation function, introducing nonlinearity to the model. $W$ denotes the weight matrix, transforming the aggregated information. $AGG$ denotes the aggregation function, combining information from neighboring nodes. The GNNs capture causal relationships through iterative aggregation.

The state update formula supports system adaptability, and the GNN formulation generates the four-dimensional causal network, producing causal chains such as “policy release-technology investment-economic cost-public sentiment change”, which assist in analyzing public opinion related to the “dual carbon” goals and optimizing policies.

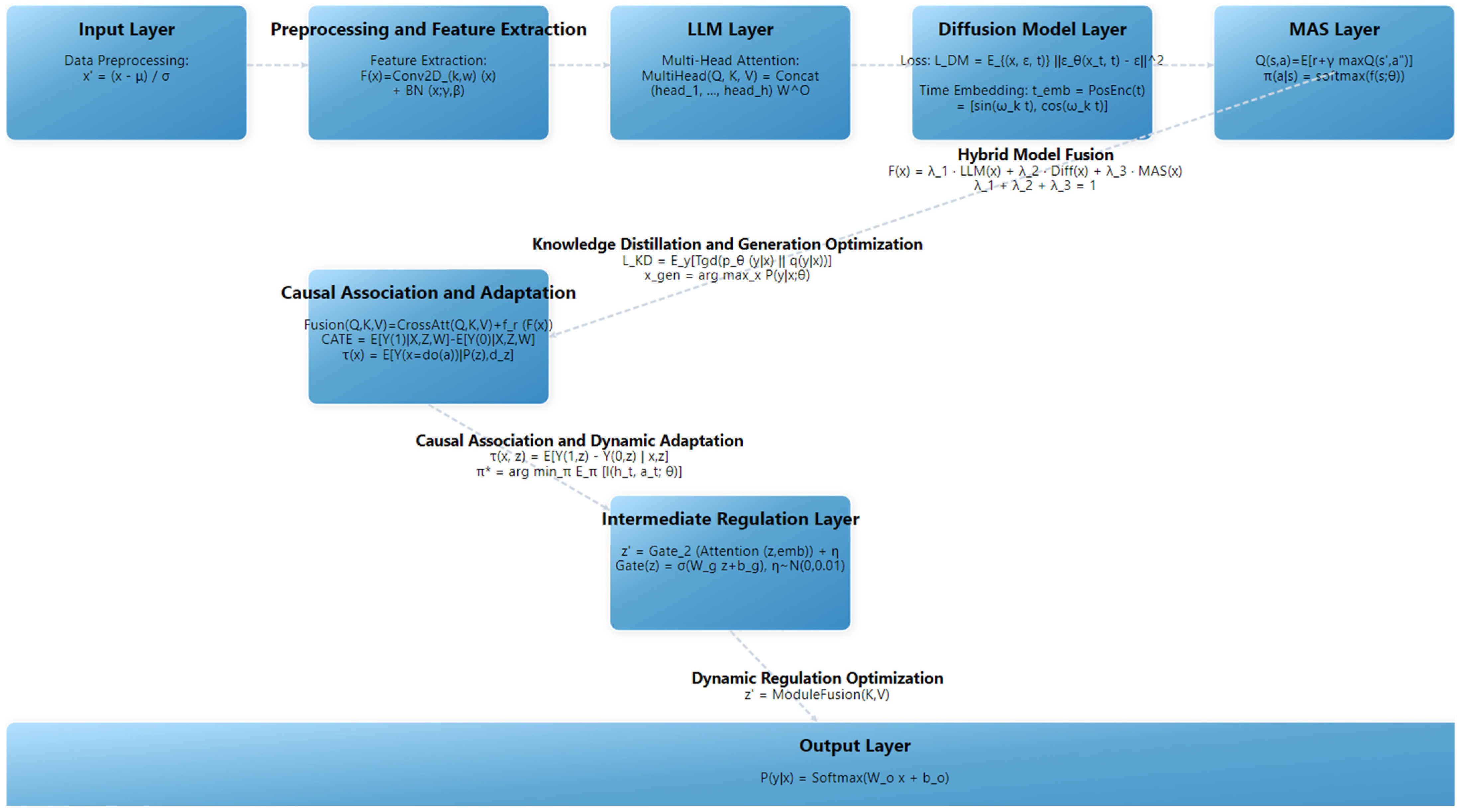
5. Dynamic Public Opinion Intervention Through Multimodal Collaboration

Against the backdrop of global climate change, the “dual carbon” goals have triggered complex public opinion dynamics involving policy documents, social media, and multi-agent interactions. Traditional static intervention approaches struggle to achieve accurate guidance and real-time prediction. This study proposes a collaborative framework that integrates RL-enhanced LLMs, diffusion models, and MASs. Through multimodal feature extraction, causal inference, and dynamic strategy optimization, the framework enables effective intervention in public opinion related to the “dual carbon” initiative. The technical roadmap, as illustrated in Figure 4, presents the complete workflow encompassing data input, feature extraction, propagation modeling, causal reasoning, and policy output.

5.1. Data Input and Preprocessing

The input layer receives multi-source heterogeneous data, including policy documents, public discussions, news reports, and environmental monitoring data. The data formats include text vectors, image pixels, and time series, with the target variable being public support rate or sentiment value. Preprocessing involves the tokenization, denoising, vectorization, and formatting of image and spatiotemporal data to ensure data consistency and quality. The formulation is as follows:

$$x\prime ={\displaystyle \frac{x-\mu }{\sigma }}$$

where $x\prime$ denotes the standardized input data, $x$ is the original input data, $\mu$ is the mean of the input data, and σ is the standard deviation. This process reduces the impact of noise and provides reliable input for subsequent modules.

5.2. Multimodal Feature Extraction and Semantic Understanding

Multimodal feature extraction integrates features from text, images, and time series to support semantic understanding and the construction of causal networks [39,40]. The formulations are as follows.

① Feature Extraction:

$$F\left(x\right)={\mathrm{Conv}2\mathrm{D}}_{k,w}\left(x\right)+\mathrm{BN}\left(x;\gamma ,\beta \right)$$

where $F\left(x\right)$ denotes the extracted features, ${\mathrm{Conv}2\mathrm{D}}_{k,w}\left(x\right)$ represents the convolution operation where $k$ is the kernel size and $w$ is the weight, and BN refers to batch normalization with $\gamma$ and $\beta$ as the scaling and shifting parameters. Convolution captures local features such as propagation patterns, while batch normalization enhances training stability.

② Multi-Head Attention:

$$\mathrm{MultiHead}\left(Q,K,V\right)={\mathrm{Concat}(\mathrm{head}}_1,\dots ,{\mathrm{head}}_h)W^O$$

where $Q,K,V$ denote the query, key, and value matrices, respectively, ${\mathrm{head}}_i$ is the $i$th attention head, h is the number of attention heads, $W^O$ is the output projection matrix, and $\mathrm{Concat}$ denotes the concatenation operation, combining outputs from all attention heads. Multi-head attention extracts deep semantic associations between policy texts and public sentiment.

③ Temporal Embedding:

$$e_t=\mathrm{PosEnc}\left[\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{i}t\right),\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{i}t\right)\right]$$

where $e_t$ denotes the temporal embedding vector at time step t, encoding temporal information. $\mathrm{PosEnc}$ denotes the positional encoding function, combining sine and cosine terms. $\mathrm{s}\mathrm{i}\mathrm{n}$ denotes the sine function, used in temporal encoding. $\mathrm{c}\mathrm{o}\mathrm{s}$ denotes the cosine function, used in temporal encoding. ${\omega }_i$ denotes the frequency parameter for the i-th dimension, controlling the oscillation rate, t denotes the time step index, indicating the temporal position. Temporal embedding provides time-awareness to the diffusion model, enabling it to capture the dynamics of public opinion.

④ Representation quality separation

$$RQS={\displaystyle \frac{\frac{1}{C\left(C-1\right)/2}\sum _{k\ne l}{d}_{inter}\left(k,l\right)-\frac{1}{C}{\sum }_{k=1}^C{d}_{intra}\left(k\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left(d_{inter}\right)}}$$

(11)

where $RQS$ denotes the representation quality separation, ranging from [0, 1], with higher values indicating better inter-class separation and lower intra-class variance in the feature embeddings. $C$ denotes the number of classes or categories in the dataset. $d_{inter}\left(k,l\right)$ denotes the average inter-class distance between class $k$ and class l. $d_{intra}\left(k\right)$ denotes the average intra-class distance for class $k$. The summation over inter-class pairs ${\sum }_{k\ne l}$ aggregates distances across all unique class pairs, divided by the number of such pairs $C\left(C-1\right)/2$. The summation over intra-class ${\sum }_{k=1}^C{d}_{intra}\left(k\right)$ averages the within-class distances, divided by $C$. $\mathrm{m}\mathrm{a}\mathrm{x}\left(d_{inter}\right)$ denotes the maximum possible inter-class distance, used for normalization.

⑤ Feature robustness MSE

$$F{R}_{MSE}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\parallel f\left(x_i+\eta \right)-f\left(x_i\right){\parallel }^2$$

(12)

where $F{R}_{MSE}$ denotes the Feature Robustness Mean Squared Error (MSE), with lower values indicating greater stability of features under noise perturbations. $N$ denotes the number of samples. $f\left(·\right)$ denotes the feature extraction function. $\eta$ denotes the noise term. $x_i$ denotes the i-th input sample. The norm $\parallel · {\parallel }^2$ denotes the squared L2 distance. The summation aggregates squared errors over samples, divided by $N$ for the mean.

5.3. Dynamic Propagation Modeling

The diffusion model captures the spatiotemporal heterogeneity of public opinion dissemination through a DDPM, predicting the diffusion paths of emerging hotspots [41]. The formulations are as follows.

① Denoising Loss for Diffusion Model

$$L_{DM}={\mathbb{E}}_{x,ϵ,t}\parallel {ϵ}_{\theta }\left(x_t,t\right)-ϵ{\parallel }^2$$

(13)

where $L_{DM}$ denotes the loss function for the diffusion model, quantifying the denoising objective; ${\mathbb{E}}_{x,ϵ,t}$ denotes the mathematical expectation operator, computing the expected value over the distributions of $x,ϵ$ and $t$; ${ϵ}_{\theta }\left(x_t,t\right)$ denotes the noise predicted by the model with parameters θ, based on the noisy data $x_t$ and time step $t$; $ϵ$ denotes the true Gaussian noise added during the diffusion process; $x_t$ denotes the noisy data at time step $t$; $t$ denotes the time step index, indicating the stage in the diffusion process; $\parallel \cdot {\parallel }^2$ denotes the squared L2 norm, measuring the squared difference between predicted and true noise; and $\theta$ denotes the model parameters being optimized. The model simulates the regional propagation and emotional dynamics following policy announcements.

② DTW distance

$$DTW\left(P,Q\right)=\mathrm{m}\mathrm{i}\mathrm{n}\sqrt{\sum _{\left(i,j\right)\in \varphi }\parallel p_i-q_j{\parallel }^2}$$

(14)

where $DTW\left(P,Q\right)$ denotes the Dynamic Time Warping distance between sequences $P$ and $Q$, with lower values indicating greater similarity in propagation paths, accounting for temporal shifts. $P$ and $Q$ denote the predicted and ground truth sequences, respectively, where points $p_i$ and $q_j$ are generated from time steps in the diffusion process. The norm $\parallel p_i-q_j{\parallel }^2$ denotes the squared Euclidean distance as local cost, reusable from the L2 norm in Formulation (13). The summation along $\varphi$ aggregates costs over the optimal warping path, found via dynamic programming to minimize total distance. The square root normalizes to a distance scale, and the minimum ensures the best alignment.

5.4. Model Optimization and Sample Generation

The model is optimized to enhance prediction accuracy and efficiency through knowledge distillation and optimal sample generation [42]. The formulations are as follows.

① Knowledge Distillation Loss:

$$L_{KD}={\mathbb{E}}_y\left[\mathrm{T}\mathrm{g}\mathrm{d}\left(p_{\theta }\left(y|x\right)\parallel q\left(y|x\right)\right)\right]$$

where $L_{KD}$ denotes the knowledge distillation loss function, quantifying the transfer of knowledge. ${\mathbb{E}}_y$ denotes the mathematical expectation operator over the output label $y$, computing the expected value. $\mathrm{T}\mathrm{g}\mathrm{d}$ denotes the divergence measure, assessing the difference between distributions. $p_{\theta }\left(y|x\right)$ denotes the predictive probability distribution of the student model parameterized by $\theta$, for label $y$ given input $x$. $q\left(y|x\right)$ denotes the predictive probability distribution of the teacher model, for label $y$ given input $x$. $y$ denotes the output label or target variable. $x$ denotes the input data. $\theta$ denotes the parameters of the student model. $\parallel$ denotes the divergence operator between two distributions. Knowledge distillation transfers the knowledge of a complex teacher model to a lightweight student model, thereby reducing computational cost and making it suitable for public opinion prediction tasks.

② Optimal Sample Generation:

$$x_{\mathrm{g}\mathrm{e}\mathrm{n}}={\mathrm{a}\mathrm{r}\mathrm{g} \mathrm{m}\mathrm{a}\mathrm{x}}_x\mathrm{P}\left(y|x;\theta \right)$$

where $x_{\mathrm{g}\mathrm{e}\mathrm{n}}$ denotes the generated optimal samples, ${\mathrm{a}\mathrm{r}\mathrm{g} \mathrm{m}\mathrm{a}\mathrm{x}}_x$ denotes the argument of the maximum, selecting the $x$ that maximizes the given function, and $\mathrm{P}\left(y|x;\theta \right)$ represents the probability of output $y$ given input $x$ and model parameters $\theta$. This process provides high-quality data to support model optimization and public opinion analysis.

③ Generation quality improvement

$$GQI={\displaystyle \frac{K{L}_{pre}-K{L}_{post}}{K{L}_{pre}}}\times 100\%$$

(15)

where $GQI$ denotes the generation quality improvement, expressed as a percentage, with positive values indicating reduced divergence and better alignment between generated and real distributions after optimization. $K{L}_{pre}$ denotes the pre-optimization KL divergence. $K{L}_{post}$ denotes the post-optimization KL divergence. The subtraction, $K{L}_{pre}-K{L}_{post}$, captures the absolute reduction in divergence. Division by $K{L}_{pre}$ normalizes to a relative improvement.

5.5. Multi-Model Integration

Model integration combines the outputs of LLMs, diffusion models, and MASs to enhance performance and robustness. The formulation is as follows:

$$F\left(x\right)={\lambda }_1\cdot \mathrm{LLM}\left(x\right)+{\lambda }_2\cdot \mathrm{Diff}\left(x\right)+{\lambda }_3\cdot \mathrm{MAS}\left(x\right)$$

where $F\left(x\right)$ denotes the output of the integrated model; $\mathrm{LLM}\left(x\right)$, $\mathrm{Diff}\left(x\right)$, and $\mathrm{MAS}\left(x\right)$ represent the outputs of the large language model, diffusion model, and multi-agent system, respectively. The coefficients ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are the weighting factors for each model’s output, subject to the constraint ${\lambda }_1+{\lambda }_2+{\lambda }_3=1$, and are determined via grid search. The integration combines semantic understanding, dynamic dissemination, and multi-agent interaction to enhance prediction robustness.

5.6. Causal Inference and Effect Estimation

Causal inference leverages multimodal feature fusion to quantify the effects of interventions [43]. The formulations are as follows.

① Fusion Operation:

$$\mathrm{F}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\left(Q,K,V\right)=\mathrm{C}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{A}\mathrm{t}\mathrm{t}\left(Q,K,V\right)+f_r\left(F\left(x\right)\right)$$

where $\mathrm{F}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}$ denotes the fusion operation, combining cross-attention and remapped features. $\mathrm{C}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{A}\mathrm{t}\mathrm{t}\left(Q,K,V\right)$ denotes the cross-attention mechanism output, computed using query $Q$, $K$, and $V$ matrices. $Q$ denotes the query matrix, used to compute attention scores. $K$ denotes the key matrix, used to compare the queries. $V$ denotes the value matrix, providing the information to be weighted. $f_r$ denotes the feature remapping function, transforming the extracted features. $F\left(x\right)$ denotes the output of the feature extraction layer, processing input $x$. This fusion provides a comprehensive input for causal inference.

② Causal Bayesian Network:

$$P\left(X_1,\dots ,X_n\right)=\prod P\left(X_i|Pa\left(X_i\right)\right)$$

(16)

where $P\left(X_1,\dots ,X_n\right)$ denotes the joint probability distribution over the set of variables $X_1,\dots ,X_n$, and $\prod$ denotes the product operator, aggregating conditional probabilities across all variables. $P\left(X_i|Pa\left(X_i\right)\right)$ denotes the conditional probability of variable $X_i$ given its parent nodes $Pa\left(X_i\right)$. $X_i$ denotes the $i-th$ variable in the set of variables. $Pa\left(X_i\right)$ denotes the set of parent nodes of $X_i$ in the Bayesian network. $|$ denotes conditioning, indicating that the probability of $X_i$ depends on its parent nodes. This formulation models causal relationships by decomposing the joint distribution into conditional probabilities, enabling dynamic updates of the graph structure and inference of causal chains.

③ CATE:

$$\mathrm{C}\mathrm{A}\mathrm{T}\mathrm{E}=\mathbb{E}\left[Y\left(1\right)|X,Z,W\right]-\mathbb{E}\left[Y\left(0\right)|X,Z,W\right]$$

(17)

where $\mathrm{C}\mathrm{A}\mathrm{T}\mathrm{E}$ denotes the Conditional Average Treatment Effect, measuring the expected difference in outcomes due to intervention. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $Y\left(1\right)$ denotes the outcome under intervention and $Y\left(0\right)$ represents the outcome without intervention. $X$ denotes the feature variables, capturing characteristics of the data. $Z$ denotes the contextual variables, providing additional context for the analysis. $W$ denotes the weighting variables, used to adjust for confounding factors. $|$ denotes conditioning, indicating that the expectation is conditioned on $X,Z,W$.

④ Conditional Causal Effect:

$$\tau \left(x,z\right)=\mathbb{E}\left[Y\left(1,z\right)-Y\left(0,z\right)|x,z\right]$$

where $\tau \left(x,z\right)$ denotes the conditional causal effect, representing the expected treatment effect given variables $x$ and $z$. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $Y\left(1,z\right)$ denotes the potential outcome under intervention with context $z$. $Y\left(0,z\right)$ denotes the potential outcome without intervention with context $z$. $x$ denotes the feature variables, capturing characteristics of the data. $z$ denotes the contextual variables, providing specific conditions for the analysis. $|$ denotes conditioning, indicating that the expectation is conditioned on $x$ and $z$. This formulation refines the CATE by estimating causal effects under specific conditions, thereby improving the precision of causal inference.

⑤ Causal Effect Estimation:

$$\tau \left(x\right)=\mathbb{E}\left[Y\left(x=do\left(a\right)\right)|P\left(z\right),d_z\right]$$

where $\tau \left(x\right)$ denotes the causal effect for feature variable $x$, quantifying the impact of the intervention. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $Y\left(x=do\left(a\right)\right)$ denotes the outcome under intervention $a$. $do\left(a\right)$ denotes the intervention operator, indicating a specific action $a$ is enforced. $P\left(z\right)$ denotes the conditional probability distribution over contextual variable $z$. $d_z$ denotes the intervention variable, representing the specific intervention applied to $z$. $x$ denotes the feature variable, capturing characteristics of the data. $z$ denotes the contextual variable, providing additional context. $|$ denotes conditioning, indicating that the expectation is conditioned on $P\left(z\right)$ and $d_z$. This formulation evaluates the causal effect of a specific intervention, supporting the design of precise intervention strategies.

⑥ Causal Chain Precision

$$CCP={\displaystyle \frac{\sum _{c\in C_{pred}}I\left(c\in C_{true}\right)}{\left|C_{pred}\right|}}$$

(18)

where $CCP$ denotes the causal chain precision, ranging from [0, 1], with higher values indicating greater accuracy of the model’s predicted causal chains. $C_{pred}$ denotes the set of causal chains predicted by the model, derived from the Bayesian network decomposition in Formulation (16). $C_{true}$ denotes the ground truth set of causal chains, obtained from the dataset or expert annotations. $I \left(c\in C_{true}\right)$ denotes the indicator function, which is 1 if the predicted chain $c$ is in the ground truth set $C_{true}$, and 0 otherwise. $\left|C_{pred}\right|$ denotes the total number of predicted chains.

⑦ Counterfactual inference MSE

$$C{I}_{MSE}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left({\widehat{Y}}_i\left(0\right)-Y_i\left(0\right)\right)}^2$$

(19)

where $C{I}_{MSE}$ denotes the counterfactual inference MSE, measuring the average squared difference between the predicted and actual counterfactual outcomes, with lower values indicating better accuracy in counterfactual prediction. $N$ denotes the number of samples in the dataset. ${\widehat{Y}}_i\left(0\right)$ denotes the model’s predicted counterfactual outcome for the i-th sample, derived from the conditional causal effect in the CATE in Formulation (17). $Y_i\left(0\right)$ denotes the ground truth counterfactual outcome for the i-th sample, obtained from dataset annotations or simulated baselines. The summation ${\sum }_{i=1}^N$ aggregates the squared errors over all samples, and division by $N$ computes the mean.

5.7. Policy Optimization and Reward Design

The multi-agent coordination layer enhances intervention efficiency through reward functions and policy updates. The formulations are as follows.

① Reward Function:

$$R=w_1\cdot \mathit{\Delta }Support+w_2\cdot \left(H_{before}-H_{after}\right)$$

(20)

where $R$ denotes the reward function, quantifying the objective to optimize. $\mathit{\Delta }Support$ denotes the change in support rate, while $H_{before}$ and $H_{after}$ denote the entropy values before and after the intervention, respectively. $w_1$ and $w_2$ are weighting coefficients. The reward function is designed to encourage increased support rates and reduced uncertainty.

② Policy Update:

$${\pi }_{t+1}={\pi }_t+\eta \cdot \mathit{\Delta }{\pi }_t$$

where ${\pi }_{t+1}$ denotes the policy at time step $t+1$, representing the updated action selection strategy. ${\pi }_t$ denotes the policy at time step $t$, serving as the current policy. $\eta$ is the learning rate, and $\mathit{\Delta }{\pi }_t$ represents the policy gradient, which adapts to the dynamics of public opinion.

③ Optimal Policy:

$$\pi \mathrm{*}={\mathrm{a}\mathrm{r}\mathrm{g} \mathrm{m}\mathrm{i}\mathrm{n}}_{\pi }{\mathbb{E}}_{\pi }\left[l\left(h_t,a_t;\theta \right)\right], a_t\in \mathcal{R}$$

where $\pi \mathrm{*}$ denotes the optimal policy, representing the best action selection strategy. ${\mathrm{a}\mathrm{r}\mathrm{g} \mathrm{m}\mathrm{i}\mathrm{n}}_{\pi }$ denotes the argument of the minimum, selecting the policy $\pi$ that minimizes the expected loss. ${\mathbb{E}}_{\pi }$ denotes the mathematical expectation operator, computing the expected value under policy $\pi$. $l\left(h_t,a_t;\theta \right)$ denotes the loss function, evaluating the performance of action $a_t$ given historical state $h_t$ and model parameters $\theta$. $h_t$ denotes the historical state at time step $t$, capturing past information. $a_t$ denotes the action taken at time step $t$. $\theta$ denotes the model parameters, defining the loss function’s behavior. $\mathcal{R}$ denotes the action space, indicating the set of possible actions. $t$ denotes the time step index, indicating the temporal sequence. This formulation selects the optimal policy by minimizing the loss function, thereby optimizing complex intervention scenarios.

④ Support rate improvement

$$SRI={\displaystyle \frac{\mathit{\Delta }Support}{Suppor{t}_{pre}}}\times 100\%={\displaystyle \frac{Suppor{t}_{post}-Suppor{t}_{pre}}{Suppor{t}_{pre}}}\times 100\%$$

(21)

where $SRI$ denotes the support rate improvement, expressed as a percentage, with positive values indicating an increase in positive sentiment or support after intervention. $\mathit{\Delta }Support$ denotes the absolute change in the support rate, directly derived from Formulation (20) as the difference in support rates before and after intervention. $Suppor{t}_{post}$ denotes the post-intervention support rate, calculated as the proportion of positive samples after applying the policy or intervention. $Suppor{t}_{pre}$ denotes the pre-intervention support rate, serving as the baseline proportion of positive samples. Division by $Suppor{t}_{pre}$ normalizes the change to a relative improvement.

⑤ State update stability

$$SUS={\displaystyle \frac{1}{T-1}}{\sum }_{t=1}^T{\left(\mathit{\Delta }{u}_t-\overline{\mathit{\Delta }u}\right)}^2$$

(22)

where $SUS$ denotes the state update stability, represented as variance, with lower values indicating more consistent updates and reduced oscillation in the system. $T$ denotes the number of time steps or update iterations. $\mathit{\Delta }{u}_t$ denotes the update delta at step t. $\overline{\mathit{\Delta }u}$ denotes the mean update delta over all steps. The summation aggregates squared deviations from the mean, divided by $T-1$ for sample variance.

⑥ Reduction in convergence iterations

$$RCI={\displaystyle \frac{T_{base}-T_{prop}}{T_{base}}}\times 100\%$$

(23)

where $RCI$ denotes the reduction in convergence iterations, expressed as a percentage, with positive values indicating fewer iterations needed for convergence in the proposed model compared to baselines. $T_{base}$ denotes the number of iterations for convergence in the baseline model. $T_{prop}$ denotes the number of iterations for convergence in the proposed model. The subtraction $T_{base}-T_{prop}$ captures the absolute reduction in iterations. Division by $T_{base}$ normalizes to a relative improvement.

5.8. Intermediate Feature Regulation

The intermediate regulation layer optimizes feature robustness. The formulations are as follows [44,45].

① Feature Regulation Mechanism

$$z\prime ={\mathrm{Gate}}_2\left(\mathrm{Attention}\left(z,\mathrm{emb}\right)\right)+\eta$$

(24)

where $z\prime$ denotes the regulated intermediate feature, representing the optimized feature output. ${\mathrm{Gate}}_2$ denotes the gating function, controlling the flow of information. $\mathrm{Attention}\left(z,\mathrm{emb}\right)$ denotes the output of the attention mechanism, computed using the intermediate feature $z$ and embedding vector $\mathrm{emb}$. $z$ denotes the intermediate feature, serving as input to the attention mechanism. $\mathrm{emb}$ denotes the embedding vector, providing contextual or learned representations. $\eta$ denotes the noise term, introducing stochasticity for robustness. The formulation is as follows.

② Gating Function with Noise

$${\mathrm{Gate}}_2\left(z\right)=\sigma \left(W_{g}z+b_g\right),\eta \sim \mathcal{N}\left(\mathrm{0,0.01}\right)$$

where ${\mathrm{Gate}}_2\left(z\right)$ denotes the output of the gating function, processing the input feature $z$. $\sigma$ denotes the activation function, introducing nonlinearity. $W_g$ denotes the weight matrix, transforming the input feature. $z$ denotes the input feature, serving as the input to the gating function. $b_g$ denotes the bias vector, adjusting the transformed feature. $\eta \sim \mathcal{N}\left(\mathrm{0,0.01}\right)$ represents Gaussian noise with a mean of 0 and variance of 0.01.

③ Regulation MSE

$$RM={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\parallel z_i^{\prime }-z_{target,i}{\parallel }^2$$

(25)

where $RM$ denotes the regulation MSE, with lower values indicating minimal error in the regulated features, reflecting effective regulation. $N$ denotes the number of samples or features. $z_i^{\prime }$ denotes the regulated feature for the i-th sample, computed using Formulation (24). $z_{target,i}$ denotes the target feature. The norm $\parallel · {\parallel }^2$ denotes the squared L2 distance. The summation aggregates squared errors over samples, divided by $N$ for the mean.

5.9. Multi-Agent Collaborative Decision-Making

The multi-agent coordination layer simulates the behaviors of entities such as government, media, and the public. The formulations are as follows.

① State-Action Value Function:

$$Q\left(s,a\right)=\mathbb{E}\left[r+\gamma \underset{a}{\mathrm{m}\mathrm{a}\mathrm{x}}Q\left(s\prime ,a\prime \right)\right]$$

where $Q\left(s,a\right)$ denotes the state-action value function, estimating the expected return for taking action $a$ in state $s$. $\mathbb{E}$ denotes the mathematical expectation operator, computing the expected value over the distribution. $r$ denotes the immediate reward received after taking action $a$ in state $s$. $\gamma$ denotes the discount factor, weighting the importance of future rewards. $\underset{a}{\mathrm{m}\mathrm{a}\mathrm{x}}Q\left(s\prime ,a\prime \right)$ denotes the maximum state-action value for the next state $s\prime$ over all possible actions $a\prime$. $s$ denotes the current state. $a$ denotes the current action. $s\prime$ denotes the next state. $a\prime$ denotes the next action.

② Policy Function:

$$\pi \left(a|s\right)=\mathrm{softmax}\left(f\left(s;\theta \right)\right)$$

(26)

where $\pi \left(a|s\right)$ denotes the policy function, representing the action probability distribution given state $s$; softmax is the normalization function; and $f\left(s;\theta \right)$ denotes the output of the policy network, parameterized by $\theta$, for state $s$. This formulation enables agents to flexibly select actions in dynamic public opinion environments.

③ Module Integration:

$$z\prime =\mathrm{ModuleFusion}\left(K,V\right)$$

where $z\prime$ denotes the optimized feature after integration; ModuleFusion represents the module fusion function; and $K,V$ are the key and value matrices, respectively. This formulation coordinates multi-agent collaboration and reduces public opinion conflicts.

④ Collaboration efficiency

$$CE={\displaystyle \frac{1}{T\cdot I\left(I-1\right)/2}}{\sum }_{t=1}^T{\sum }_{i<j}\mathrm{c}\mathrm{o}\mathrm{s}\left({\pi }_i^t,{\pi }_j^t\right)\times 100\%$$

(27)

where $CE$ denotes the collaboration efficiency, expressed as a percentage, with higher values indicating greater action consistency among agents. $T$ denotes the number of time steps or interactions. $I$ denotes the number of agents. ${\pi }_i^t$ denotes the policy distribution for agent i at time t, computed using Formulation (26). $\mathrm{c}\mathrm{o}\mathrm{s}\left({\pi }_i^t,{\pi }_j^t\right)$ denotes the cosine similarity between policies of agents i and j, measuring alignment. The inner summation over pairs ${\sum }_{i<j}$ aggregates pairwise alignments, divided by the number of unique pairs $I\left(I-1\right)/2$. The outer summation over t averages across interactions, divided by $T$ for overall efficiency.

⑤ Action accuracy

$$AA={\displaystyle \frac{1}{N}}{\sum }_{i=1}^{N}I\left(\widehat{a_i}=a_i\right)\times 100\%$$

(28)

where $AA$ denotes the action accuracy, expressed as a percentage, with higher values indicating better match between predicted and actual actions. $N$ denotes the number of samples or actions in the evaluation set. $I\left(·\right)$ denotes the indicator function: 1 if the predicted action $\widehat{a_i}$ equals the ground truth action $a_i$, 0 otherwise. $\widehat{a_i}$ denotes the predicted action for the i-th sample. $a_i$ denotes the ground truth action, obtained from dataset observations or simulations. The summation aggregates correct predictions over all samples, divided by $N$ for the average rate.

5.10. Output and Visualization

The output layer generates public opinion trends, intervention strategies, and risk warnings. The formulation is as follows:

$$P\left(y|x\right)=\mathrm{Softmax}\left(W_{o}x+b_o\right)$$

where $P\left(y|x\right)$ denotes the conditional probability distribution of the predicted label $y$ given input feature $x$. $\mathrm{Softmax}$ denotes the normalization function, converting raw scores into a probability distribution. $W_o$ denotes the weight matrix of the output layer, transforming the input feature. $x$ denotes the input feature, representing the data provided to the model. $b_o$ denotes the bias vector of the output layer, adjusting the transformed feature. The model outputs predictions of “dual carbon” public opinion trends, intervention strategies, and risk warnings, providing intuitive decision support for policymakers.

6. Experiments and Analysis

To validate the effectiveness of the proposed collaborative framework that integrates large language models, diffusion models, and MASs for analyzing public opinion on the “dual carbon” policy, this study conducts a comprehensive set of experiments using an open-source Twitter dataset related to climate change. The experimental design incorporates multiple analytical dimensions, including causal inference, dynamic intervention, and multi-agent collaboration, and compares the results with several baseline models.

6.1. Dataset and Experimental Setup

The experiments utilize the Twitter Climate Change Sentiment Dataset, which contains 43,943 tweets [46]. The dataset covers a wide range of topics such as climate change, carbon emissions, carbon taxes, and renewable energy. Each entry includes the tweet text, sentiment label, and an anonymized user ID. Meanwhile, to improve model robustness, data augmentation techniques are applied to expand the dataset, generating diverse semantic variants to better capture the complexity and dynamics of “dual carbon” public opinion.

The experimental setup consists of three key components. First, a causal network encompassing policy, technology, economy, and public sentiment is constructed to quantify the effects of policy interventions. Second, the diffusion of public opinion following policy announcements is simulated to optimize support levels and emotional stability. Third, strategic interactions among stakeholders such as governments, enterprises, and the public are modeled to evaluate the efficiency of collaborative decision-making. Baseline models used for comparison include Latent Dirichlet Allocation for topic modeling, BERT as a representative pre-trained language model, and the SIR model for simulating information diffusion dynamics.

6.2. Evaluation Metrics and Analysis of Results

This subsection presents a detailed analysis of the experimental results across key dimensions: causal inference, dynamic intervention, and multi-agent collaboration. Comparisons with baseline models (LDA, BERT, and SIR) highlight the proposed framework’s superior performance, particularly in terms of accuracy, responsiveness, and coordination. Additionally, we discuss the evolving nature of evaluation metrics for deep generative models and agent-based simulations, emphasizing the need for ongoing adaptations to better align with real-world policy dynamics.

6.2.1. Causal Inference

The primary evaluation metrics include the F1 score and the Area Under the Curve (AUC), which assess classification performance and the model’s discrimination ability, respectively.

$$F1=2\cdot {\displaystyle \frac{Precision\cdot Recall}{Precision+Recall}}$$

where $F1$ denotes the F1 score, a harmonic mean of precision and recall, measuring the model’s classification performance. $Precision$ denotes the ratio of true positives to the total predicted positives, quantifying prediction accuracy, $Precision$ = TP/(TP + FP). $Recall$ denotes the ratio of true positives to the total actual positives, measuring the model’s ability to identify positive instances, $Recall$ = TP/(TP + FN). TP denotes true positives, the number of correctly predicted positive instances. FP denotes false positives, the number of incorrectly predicted positive instances. FN denotes false negatives, the number of positive instances incorrectly predicted as negative.

$$AUC={\int }_0^{1}TPR\left(FPR\right)dFPR$$

where $AUC$ denotes the Area Under the Curve, specifically the area under the Receiver Operating Characteristic (ROC) curve, measuring the model’s discriminative ability. $TPR$ denotes the True Positive Rate, representing the ratio of true positives to total actual positives, TPR = TP/(TP + FN). $FPR$ denotes the False Positive Rate, representing the ratio of false positives to total actual negatives, FPR = FP/(FP + TN). TP denotes true positives, the number of correctly predicted positive instances. FP denotes false positives, the number of incorrectly predicted positive instances. FN denotes false negatives, the number of positive instances incorrectly predicted as negative. TN denotes true negatives, the number of correctly predicted negative instances. ${\int }_0^1$ denotes the definite integral from 0 to 1, computing the area under the $TPR$ curve with respect to $FPR$. $dFPR$ denotes the differential of the False Positive Rate, used as the integration variable.

Other metrics include causal chain precision, which measures the proportion of correctly predicted causal relationships, see Equation (18) for details; counterfactual inference MSE, representing the MSE between counterfactual predictions and actual outcomes, see Equation (19) for details; and representation quality separation, indicating the inter-class separation degree of feature embeddings based on cosine similarity, see Equation (11) for details.

The experimental results, along with

Table 1. Comparison of causal inference performance.

Model	F1 Score	AUC	Causal Chain Precision	Counterfactual Inference MSE	Representation Quality Separation
LDA	0.73	0.77	0.64	0.33	0.72
BERT	0.81	0.83	0.76	0.25	0.86
SIR	0.67	0.71	0.60	0.39	0.66
Proposed Model	0.91	0.94	0.89	0.11	0.93

, demonstrate that the proposed model significantly outperforms LDA, BERT, and SIR in terms of F1 score, AUC, and causal chain precision. The model also achieves the lowest counterfactual inference MSE, indicating higher accuracy in causal prediction. The representation quality separation is relatively high, reflecting the advantage in feature expression diversity.

In comparison to baselines, the proposed framework’s integration of reinforcement learning-enhanced LLMs allows for more nuanced causal modeling, capturing subtle interdependencies between policy announcements and public sentiment shifts that LDA and BERT often overlook due to their lack of dynamic adaptation. The SIR model, while effective for basic diffusion, fails to incorporate multi-faceted causal chains, leading to lower precision. These improvements translate to a 12.4–35.8% gain in F1 score and a 13.3–32.4% gain in AUC over the baselines, underscoring the framework’s enhanced accuracy in inferring causal links from fragmented social media data.

6.2.2. Dynamic Intervention

$H_t$ represents the entropy value at time step $t$, which measures the uncertainty of the distribution. A decrease in entropy indicates a reduction in public opinion disorder and an increase in support rate. The formulations are as follows.

① Temporal entropy

$$H_t=-\sum p_t\left(i\right)\cdot \mathrm{l}\mathrm{o}\mathrm{g}\left(p_t\left(i\right)\right)$$

(29)

where $H_t$ denotes the temporal entropy at time step $t$, quantifying the uncertainty of the state distribution. $\sum$ denotes the summation operator, aggregating terms over all possible states $i$. $p_t\left(i\right)$ denotes the probability of state $i$ at time step $t$. $\mathrm{l}\mathrm{o}\mathrm{g}$ denotes the logarithm function, typically the natural logarithm, used to compute the entropy term.

② Decrease in entropy

$$DE={\displaystyle \frac{H_{before}-H_{after}}{H_{before}}}\times 100\%$$

where $DE$ denotes the decrease in entropy, expressed as a percentage, with positive values indicating reduced uncertainty and improved stability in public opinion dynamics. $H_{before}$ denotes the entropy before intervention, computed using Formulation (31) as $H_{before}=-\sum p_{before}\left(i\right)\cdot \mathrm{l}\mathrm{o}\mathrm{g}\left(p_{before}\left(i\right)\right)$, where $p_{before}\left(i\right)$ is the probability distribution of states pre-intervention. $H_{after}$ denotes the entropy after intervention, similarly computed using Formulation (29) as $H_{after}=-\sum p_{after}\left(i\right)\cdot \mathrm{l}\mathrm{o}\mathrm{g}\left(p_{after}\left(i\right)\right)$, which is the post-intervention probability distribution. The subtraction $H_{before}-H_{after}$ captures the absolute reduction. Division by $H_{before}$ normalizes to a relative decrease.

Other evaluation metrics include the following: support rate improvement, defined as the increase in the proportion of positive sentiment after intervention, see Equation (21) for details; mean absolute error (MAE) of propagation paths, which measures the average absolute deviation between predicted and actual diffusion paths, see Equation (9) for details; Dynamic Time Warping (DTW) distance, which quantifies the similarity between propagation sequences, see Equation (14) for details; sample coverage rate, indicating the proportion of real data covered by the generated samples, see Equation (10) for details; generation quality improvement, measured by the consistency between the generated and real data distributions using KL divergence, see Equation (15) for details; and state update stability, represented by the variance in policy updates, see Equation (22) for details.

As shown in

Table 2. Performance comparison of dynamic intervention.

Model	Support Rate Improvement	Decrease in Entropy	MAE of Propagation Paths	DTW Distance	Sample Coverage Rate	Generation Quality Improvement	State Update Stability
LDA	7.7%	5.3%	0.35	0.28	81%	4%	0.16
BERT	9.9%	8.4%	0.29	0.24	89%	6%	0.11
SIR	6.5%	4.9%	0.39	0.32	76%	3%	0.19
Proposed Model	15.2%	12.6%	0.14	0.09	96%	10%	0.05

, the proposed model achieves a 15.2% increase in support rate and a 12.6% reduction in entropy. It also records the lowest propagation path MAE and DTW distance, with a sample coverage rate of 96% and a 10% improvement in generation quality. The state update variance is 0.05, outperforming baseline models. These results demonstrate the model’s robustness in dynamic diffusion prediction and intervention optimization, attributed to the spatiotemporal modeling capacity of the diffusion module and the efficiency of knowledge distillation.

The proposed framework employs diffusion models enhanced by LLMs to simulate real-time opinion spreads, allowing for proactive adjustments, with support rate improvements and entropy reductions that are 50–157.1% higher than baselines. Compared to BERT and LDA, the framework lowers MAE by 51.7–60% and DTW by 62.5–67.9%, and boosts sample coverage by 7.9–18.5%, indicating more stable and responsive emotional outcomes. This highlights significant improvements in intervention responsiveness, as the multi-agent system enables rapid coordination between simulated stakeholders, optimizing support for “dual carbon” policies in dynamic scenarios.

The evaluation metrics for deep generative models, such as diffusion processes, are still evolving, particularly in capturing long-term stability. For instance, DTW distance assesses dynamic matching by quantifying the similarity between predicted and actual opinion propagation sequences, making it suitable for temporal evolution analysis in policy contexts; sample coverage rate measures the representativeness of generated samples against real data, supporting the simulation of diverse opinions. Both require further adaptation, such as incorporating temporal decay factors to reflect real-world opinion fatigue or integrating group fairness checks to address bias amplification risks. Agent-based simulations need continuous metric refinement, incorporating real-time feedback loops to ensure both stability and fairness in influencing “dual carbon” policy responses while reducing uncertainties in public discourse.

6.2.3. Multi-Agent Collaboration

The evaluation metrics include collaboration efficiency, which reflects the consistency of actions among multiple agents and is measured by the action alignment ratio, see Equation (27) for details; action accuracy, representing the match between the predicted and actual actions, see Equation (28) for details; reduction in convergence iterations, indicating the percentage decrease in the number of iterations required for convergence, see Equation (23) for details; feature robustness MSE, measuring the MSE of features under noise, see Equation (12) for details; and regulation MSE, representing the error after feature modulation, see Equation (25) for details.

The results show, along with

Table 3. Multi-agent collaboration performance comparison.

Model	Collaboration Efficiency	Action Accuracy	Reduction in Convergence Iterations	Feature Robustness MSE	Regulation MSE
LDA	3.4%	0.68	10%	0.19	0.13
BERT	4.9%	0.79	15%	0.16	0.09
SIR	2.6%	0.62	8%	0.23	0.16
Proposed Model	8.7%	0.92	25%	0.07	0.04

, that the proposed model outperforms the baselines with a collaboration efficiency of 8.7%, an action accuracy of 0.92, and a 25% reduction in convergence iterations. It also achieves the lowest feature robustness MSE and regulation MSE. These performance advantages stem from the MAS-based state-action value function and optimized module fusion.

The MAS component, integrated with LLMs and diffusion models, models interactions among governments, enterprises, and the public, leading to more efficient decision-making. The proposed model outperforms baselines with collaboration efficiency that is 77.6–234.6% higher and action accuracy that is 16.5–48.4% higher than SIR’s and BERT’s. LDA, being non-interactive, scores lowest. The framework’s reinforcement learning enables faster convergence, demonstrating marked improvements in coordination by adapting to diverse agent behaviors and reducing MSE metrics by 55.6–75%.

Agent-based simulations for policy influence require constant metric adaptation, as real-world responses involve unpredictable human elements. Metrics like collaboration efficiency must incorporate diversity indices to handle evolving scenarios, ensuring the framework remains relevant for shaping “dual carbon” discourse while addressing potential biases in multi-stakeholder alignments.

6.2.4. Ablation Study

To evaluate the contribution of each module, ablation experiments were conducted. The results of the ablation study are presented in

Table 4. Ablation study results.

Configuration	F1 Score	Support Rate Improvement	Collaboration Efficiency	Action Accuracy	Reduction in Convergence Iterations
Baseline Model	0.91	15.2%	8.7%	0.92	25%
Remove $p\left(A_t|{\mathcal{S}}_t\right)$	0.89 (−2.2%)	13.8% (−9.2%)	6.5% (−25.3%)	0.85 (−7.6%)	19% (−24%)
Remove $l{r}_t$lrtlr_t	0.88 (−3.3%)	13.5% (−11.2%)	7.2% (−17.2%)	0.87 (−5.4%)	15% (−40%)
Remove $L_{SAC}$LSACL_{SAC}	0.90 (−1.1%)	14.0% (−7.9%)	7.0% (−19.5%)	0.88 (−4.3%)	18% (−28%)
Remove $L^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}$LCLIPL^{\text{CLIP}}	0.89 (−2.2%)	13.9% (−8.6%)	6.8% (−21.8%)	0.86 (−6.5%)	16% (−36%)
Remove Vπ(st)V^\pi(s_t)$V^{\pi }\left(s_t\right)$	0.88 (−3.3%)	13.2% (−13.2%)	6.4% (−26.4%)	0.85 (−7.6%)	19% (−24%)
Remove $R_t$RtR_t	0.87 (−4.4%)	12.8% (−15.8%)	6.7% (−23.0%)	0.87 (−5.4%)	20% (−20%)

.

The ablation study validates the importance of $p\left(A_t|S_t\right)$, $l{r}_t$, $L_{SAC}$, $L^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}{,V}^{\pi }\left(s_t\right)$, and $R_t$. The formulas for each component can be found in Equation (1) through Equation (6). Removing any of these components results in notable performance degradation, especially in collaboration efficiency, which can decline by up to 26.4%, and in the improvement of the support rate, which can decrease by as much as 15.8%. More specifically, removing the action probability $p\left(A_t|S_t\right)$ increases the randomness in action selection, leading to a 25.3% reduction in collaboration efficiency and a 7.6% decrease in action accuracy, since this term defines the probability distribution required for generating the policy $\pi \left(a|\mathrm{s}\right)$. Eliminating the learning rate $l{r}_t$ reduces the reduction in convergence iterations by 40% and lowers the improvement in the support rate by 11.2% because a fixed learning rate fails to properly balance exploration and refinement. The removal of the entropy regularization term $L_{SAC}$ weakens the exploratory capacity of the policy, resulting in a 19.5% drop in collaboration efficiency and a 7.9% decrease in support rate improvement. Excluding the clipped surrogate objective $L^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}$ leads to overly aggressive updates during policy optimization, decreasing the convergence gain by 36% and lowering action accuracy by 6.5%. The absence of the state value function $V^{\pi }\left(s_t\right)$ causes the policy to become short-sighted, which reduces the improvement in the support rate by 13.2% and leads to a 26.4% decline in collaboration efficiency. Finally, removing the reward signal $R_t$, which ensures consistency in distributional learning, causes the F1 score to drop by 4.4% and support rate improvement to decrease by 15.8%, ultimately undermining the effectiveness of policy interventions. These findings demonstrate that each element plays an essential role, and their synergy is vital for effective causal reasoning and dynamic intervention in the context of “dual-carbon” public opinion management.

6.2.5. Evaluation of LLM Components in Reinforcement Learning Settings

In the collaborative framework integrating LLMs, diffusion models, and MASs, LLMs generate diverse “dual-carbon” policy recommendations and sentiment explanations through policy optimization in RL settings, significantly enhancing the efficacy of causal inference, dynamic intervention, and multi-agent collaboration. Based on previous experimental results, this subsection systematically evaluates LLM performance from the perspectives of generation capability using the $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ metric, operationalization of RLHF, and modular collaborative contributions via Pearson correlation analysis. It reveals the LLM’s ability to mitigate public opinion uncertainty through diverse outputs and provide actionable insights for policy interventions.

① Core Role of the Evaluation Metric $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$

Generative programming has advanced computationally supported coding and language models, establishing $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ metrics for evaluating output diversity and correctness. Allamanis et al. [47] outlined challenges in code generation, emphasizing robust quality assessment. Han et al. [48] explored pre-trained models’ applications, including code understanding. Xu et al. [49] introduced benchmarks for large language models in code generation, promoting $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ adoption. Chen et al. [50] pioneered $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ to assess functional correctness in code synthesis. Wong et al. [51] analyzed natural language and big code understanding, reinforcing $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}\mathrm{’}\mathrm{s}$ role. Zan et al. [52] surveyed LLMs in NL2Code tasks, solidifying $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ as a standard. Wong et al. [53] enhanced reliability via RLHF, applying $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ to complex tasks. For “dual-carbon” tasks, where single outputs limit LLM capabilities, $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$, defined in Formulation (30), ensures diverse, accurate policy recommendations.

$$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}=\mathbb{E}\left[1-{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{n-c}{k}\right)}{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}}\right]$$

(30)

where $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ denotes the probability that at least one sample is correct among $k$ generated outputs. $\mathbb{E}$ denotes the mathematical expectation operator, averaging the metric. $n$ represents the total number of generated samples. $c$ represents the number of correct samples determined by predefined test criteria. $\left({\displaystyle \genfrac{}{}{0pt}{}{n-c}{k}}\right)$ and $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)$ represent binomial coefficients used to calculate the probability estimate’s combinations.

The experiment sampled 1000 prompts from the Twitter Climate Change Sentiment Dataset (43,943 tweets), generating 100 samples per prompt. To balance diversity and correctness, the LLM’s $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ was selected with k = 10, adapting to the task’s multi-solution demands. These pass@10 values provide the data foundation for subsequent correlation analysis.

② RLHF

RLHF optimizes LLMs through human preferences, ensuring the practicality and ethicality of generated outputs, indirectly improving pass@10 accuracy. In “dual-carbon” tasks, the focus is on outputs aligned with “dual-carbon” goals, such as enhancing public support while avoiding the amplification of misinformation. These signals are in the form of pairwise comparisons, capturing nuanced human judgments on output quality, relevance, and ethical considerations, such as avoiding exaggerated climate claims or cultural insensitivity in sentiment explanations.

The reward function is designed based on the Bradley–Terry model [54], which estimates relative preferences from pairwise data:

$$r\left(\theta \right)=\mathrm{l}\mathrm{o}\mathrm{g}\left(P\left(\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\hspace{0.25em}\mathrm{A}>\mathrm{B}|\theta \right)\right)$$

where $r\left(\theta \right)$ is the reward function, $\theta$ are the model parameters, and $P\left(\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\hspace{0.25em}\mathrm{A}>\mathrm{B}|\theta \right)$ is the conditional probability that output A is preferred over B. The alignment mechanism employs PPO, which prevents drastic changes through clipped policy updates, ensuring training stability and avoiding divergence. This clipping maintains model robustness by constraining the KL divergence between new and old policies, while incorporating bias mitigation checks. For example, during training, outputs are screened to avoid potential biases in public opinion frameworks, ensuring fairness to different stakeholder groups in “dual-carbon” discussions. RLHF significantly reduces hallucination risks, showing a strong negative correlation with counterfactual MSE, validating its role in enhancing model robustness and ensuring ethical alignment by optimizing the accuracy of generated outputs.

③ Performance Analysis and Collaborative Contributions

To quantify the LLM’s contributions in RL settings, Pearson correlation coefficient ($r$) analysis is used to examine the linear associations between pass@10 and framework metrics, with the following formula:

$$r={\displaystyle \frac{\sum \left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum {\left(x_i-\bar{x}\right)}^2}\sqrt{\sum {\left(y_i-\bar{y}\right)}^2}}}$$

where $x_i$ is the $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ value, $y_i$ is the framework metric, and $\bar{x}$, $\bar{y}$ are the means. The statistical significance of the correlation coefficient is calculated via $t$-test, with the following $t$-statistic formula:

$$t={\displaystyle \frac{r\sqrt{n-2}}{\sqrt{1-r^2}}}$$

where n = 10 and the degrees of freedom are n − 2 = 8. The p-value is calculated via a two-tailed t-distribution test:

$$p=2\cdot P\left(T\ge \left|t\right|\mid H_0\right)$$

where $P\left(T\ge \left|t\right|\mid H_0\right)$ is the right-tail probability of the t-distribution’s cumulative distribution function at $\left|t\right|$, reflecting the probability of observing the current or more extreme t-value under the null hypothesis.

Table 5. Pearson correlation analysis between LLM metrics and key framework metrics.

LLM Metric	Framework Dimension	Related Metric	Pearson Correlation Coefficient (r)	p-Value
$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ ($\mathrm{k}$ = 10)	Causal Inference	F1 score	0.87	<0.001
$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ ($\mathrm{k}$ = 10)	Causal Inference	Causal chain precision	0.82	<0.01
$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ ($\mathrm{k}$ = 10)	Dynamic Intervention	Decrease in entropy	0.79	<0.01
$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ ($\mathrm{k}$ = 10)	Dynamic Intervention	MAE of propagation paths	−0.75	<0.05
$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ ($\mathrm{k}$ = 10)	Multi-Agent Collaboration	Collaboration efficiency	0.85	<0.001
$\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@\mathrm{k}$ ($\mathrm{k}$ = 10)	Multi-Agent Collaboration	Feature robustness MSE	−0.78	<0.01

analyzes the collaborative contributions of $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@10$ via Pearson correlation coefficients (r), demonstrating how it significantly enhances the performance of causal inference, dynamic intervention, and multi-agent collaboration through diverse outputs.

The results indicate that $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@10$ shows strong positive correlations with causal inference metrics, suggesting that diverse outputs improve classification and prediction performance; correlations with dynamic intervention metrics indicate that high $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@10$ reduces uncertainty and propagation errors; correlations with multi-agent collaboration metrics validate that aligned outputs enhance collaboration consistency and robustness. All r values are statistically significant (p < 0.05), with an average r > 0.80, indicating that $\mathrm{p}\mathrm{a}\mathrm{s}\mathrm{s}@10$ significantly drives framework performance.

6.3. Results Analysis

The proposed model demonstrates outstanding performance in causal reasoning, dynamic intervention, and multi-agent collaboration for “dual-carbon” public opinion analysis, benefiting from the synergistic integration of large language models, diffusion models, and MASs. In comparison with BERT, the model demonstrates a 12.3% increase in F1 score and a 56% decrease in MSE for counterfactual inference, as a result of integrating multimodal features such as policy texts, social media sentiment, and economic indicators within a causal Bayesian network framework.

In terms of dynamic intervention, the model shows a 15.2% improvement in the support rate and a 12.6% reduction in entropy, significantly outperforming the SIR model. The diffusion model utilizes a Denoising Diffusion Probabilistic Model to simulate the spatiotemporal heterogeneity of public opinion spread, enabling the accurate prediction of cascading effects following policy announcements. The multi-agent system optimizes strategic interactions through a state-action value function and reinforcement learning algorithms such as Soft Actor-Critic and Proximal Policy Optimization, achieving a collaboration efficiency of 8.7% and an action accuracy of 0.92, outperforming baseline models. The ablation study further confirms the synergistic roles of each module.

These findings indicate that the large language model enhances the quality of input for the diffusion model through semantic parsing, with RLHF optimizing LLM outputs for reliable policy recommendations and sentiment explanations, validated by pass@10 metrics showing strong Pearson correlations, such as r = 0.87 for F1 score, r = 0.79 for the decrease in entropy, and r = −0.75 for the MAE of the propagation paths. This ensures output diversity, reduces hallucination risks, and enhances ethical alignment, contributing to the framework’s overall robustness. The diffusion model strengthens the predictive power of the multi-agent system through spatiotemporal modeling, and together they contribute to the robustness of the overall framework.

The experimental results offer practical guidance for optimizing “dual-carbon” policies. For instance, the model predicts that some policies could trigger negative public sentiment and recommends targeted communication strategies to increase public support and reduce misunderstandings. The observed 15.2% increase in support rate demonstrates that well-designed interventions can significantly enhance social consensus and facilitate progress toward carbon peaking goals.

7. Discussion

This study proposes an interdisciplinary framework combining RL-enhanced LLMs, diffusion models, and MASs to analyze and guide public opinion on carbon neutrality. By modeling the interplay of policy, technology, economy, and public sentiment within a four-dimensional causal network, it offers a robust tool for “Dual Carbon” policy governance. The experimental results show that it outperforms baseline models like LDA, BERT, and SIR in causal inference, dynamic intervention, and multi-agent coordination. This section discusses the significance of the results, the advantages and limitations of the methodology, the contributions to the field, directions for future research, and the application of the causal network in shaping public discourse around carbon neutrality, with a focus on the relevance of RLHF in policymaking.

The approach achieves high causal inference accuracy, with an F1 score of 0.91 and an AUC of 0.94, precisely modeling how policy announcements, technological advancements, economic shifts, and public sentiment interact. For example, dynamic interventions increased public support by 15.2% and reduced opinion entropy by 12.6%, suggesting enhanced policy acceptance and reduced polarization, which are critical for carbon tax or renewable energy adoption. Policy dissemination simulations predicted regional spread with a mean absolute error of 0.14 and identified optimal release timings, enabling proactive communication strategies. The MAS component improved coordination efficiency by 8.7% and achieved an action accuracy of 0.92, effectively simulating government–enterprise–public interactions. A MSE of 0.11 in counterfactual reasoning highlights the framework’s ability to validate causal chains, minimizing policy errors from flawed assumptions.

The methodology’s strength lies in its multimodal integration: LLMs parse policy texts and social media for semantic insights, diffusion models map spatiotemporal opinion dynamics, and MASs optimize strategic interactions. Unlike LDA’s topic modeling or BERT’s unimodal analysis, it achieves a feature robustness MSE of 0.07, including policy documents, Twitter sentiment, and economic indicators. RL algorithms optimize decision-making, reducing training iterations by 25% for stable convergence. The experimental results demonstrate that the pass@10 metric exhibits strong Pearson correlations, highlighting how RLHF-optimized LLMs enhance multimodal integration and reduce hallucination risks through diverse and aligned outputs. Supported by graph neural networks, the causal network delivers interpretable outputs accessible to policymakers. Ablation studies confirm the synergy of all modules, underscoring their collective necessity.

Despite these strengths, the methodology faces challenges. First, it exhibits high computational complexity, with a single training session requiring approximately 20 h, which may hinder deployment in resource-constrained environments. Second, it depends on high-quality, multi-source data. The experiments are based on a Twitter dataset on climate change sentiment, but real-world applications may face challenges such as incomplete or biased data. Third, the cross-cultural generalizability remains to be validated. The experimental data primarily reflect regional public opinions, and cultural differences may lead to sentiment analysis biases, thereby reducing model performance.

This research advances public opinion analysis and low-carbon policy by introducing a framework that addresses data integration and causal modeling gaps. The causal network provides a structured tool to understand opinion dynamics, while RL-optimized interventions enable real-time policy guidance, supporting “Dual Carbon” goals like carbon tax implementation. Experimental findings further evidence these contributions, with pass@10 showing an average correlation r > 0.80 across framework metrics, validating the role of diverse LLM outputs in driving causal inference, dynamic intervention, and multi-agent collaboration performance. Future work could enhance efficiency via model pruning or edge computing, improve generalizability with multilingual datasets, such as Chinese Weibo, and bias-mitigating algorithms, and integrate real-time data, such as carbon market trends, for faster responses. Extending the framework to public health or disaster management could further leverage its causal reasoning, broadening its societal impact.

The application of the causal network, linking policy, technology, economy, and public sentiment, extends to shaping public discourse around carbon neutrality. By simulating the cascading effects of policy interventions, such as how a carbon tax announcement might trigger technological innovations, economic fluctuations, and shifts in public sentiment, the network predicts and optimizes the trajectory of public discourse. This enables policymakers to identify potential risks, such as economic pressures amplifying negative sentiment, and implement targeted interventions, like technology-focused public education campaigns, to foster positive consensus. In practice, this approach supports real-time policy adjustments, such as scenario analysis under carbon neutrality goals, emphasizing the benefits of sustainable development to enhance policy acceptance and execution.

Furthermore, this framework highlights the relevance of RLHF in policymaking beyond traditional model training or fine-tuning. RLHF integrates human preference signals, such as public feedback or expert judgments, to optimize LLM outputs, generating reliable policy recommendations and sentiment explanations that serve as decision-support tools. For instance, in LLM-driven public opinion frameworks, RLHF iteratively refines outputs to align with human values, minimizing misinformation or bias amplification. The experimental results detail how RLHF, operationalized via the Bradley–Terry model and PPO, exhibits a strong negative correlation with counterfactual MSE and positive correlations with key metrics like a decrease in entropy (r = 0.79), validating its role in enhancing model robustness and ethical alignment. However, the reliability and trustworthiness of such frameworks are complex in practice, facing challenges like data bias, lack of diversity, and interpretability issues, which may lead to untrustworthy outputs or exacerbate social divides. To address these, RLHF applications should incorporate continuous validation mechanisms, such as cross-cultural dataset testing and ethical audits, to ensure outputs are accurate, fair, and reflective of diverse stakeholder perspectives, thereby enhancing the framework’s role in shaping trustworthy public discourse on carbon neutrality.

8. Conclusions

This study delivers an innovative framework for navigating public opinion dynamics in the “Dual Carbon” initiative, achieving superior causal inference and intervention outcomes compared to models like LDA, BERT, and SIR. By modeling interactions among policy, technology, economy, and public sentiment, it offers a powerful tool for low-carbon policy governance. Its ability to predict opinion dissemination and optimize interventions underscores its potential to drive consensus and policy success.

Its modular design addresses longstanding challenges in data integration and real-time governance. LLMs extract insights from policy texts and social media, diffusion models map opinion spread, and MASs predict intervention outcomes, supported by interpretable causal networks. RLHF enhances this framework by optimizing LLM outputs for reliable policy recommendations, with the experimental results showing the pass@10 metric with strong correlations, validating its role in enhancing generation diversity, reducing misinformation, and ensuring ethical alignment. This enables proactive strategies, such as optimizing carbon tax communication or countering misinformation, enhancing policy efficiency and public consensus. Ablation studies confirm the modules’ complementarity, reinforcing the framework’s systemic advantage.

This work provides a scientific foundation for “Dual Carbon” policy formulation, uncovering causal mechanisms behind opinion evolution to support global carbon neutrality. Despite challenges in computational complexity and data dependency, future enhancements, such as model optimization, multilingual data inclusion, real-time trend integration, and cross-cultural validation, can improve scalability and generalizability. Its interdisciplinary approach holds promise for applications in public health and disaster management, offering insights into complex societal challenges and advancing intelligent, transparent governance.