TSGformer: A Unified Temporal–Spatial Graph Transformer with Adaptive Cross-Scale Modeling for Multivariate Time Series

Abstract

Multivariate time series forecasting requires modeling complex and evolving spatio-temporal dependencies as well as frequency-domain patterns; however, the existing Transformer-based approaches often struggle to effectively capture dynamic inter-series correlations and disentangle relevant spectral components, leading to limited forecasting accuracy and robustness under non-stationary conditions. To address these challenges, we propose TSGformer, a Transformer-based architecture that integrates multi-scale adaptive graph learning, adaptive spectral decomposition, and cross-scale interactive fusion modules to jointly model temporal, spatial, and spectral dynamics in multivariate time series data. Specifically, TSGformer constructs dynamic graphs at multiple temporal scales to adaptively learn evolving inter-variable relationships, applies an adaptive spectral enhancement module to emphasize critical frequency components while suppressing noise, and employs interactive convolution blocks to fuse multi-domain features effectively. Extensive experiments across eight benchmark datasets show that TSGformer achieves the best results on five datasets, with an MSE of 0.354 on Exchange, improving upon the best baselisnes by 2.4%. Ablation studies further verify the effectiveness of each proposed component, and visualization analyses reveal that TSGformer captures meaningful dynamic correlations aligned with real-world patterns.

1. Introduction

Multivariate time series (MTS) consist of multiple interdependent variables recorded sequentially over time and have become fundamental in domains such as healthcare [1], traffic systems [2], and financial markets [3]. In medical applications, MTS data commonly includes measurements like body temperature, heart rate, and blood pressure collected continuously from patients [4]. Urban traffic monitoring includes vehicle flow volumes, average speeds, and congestion levels observed across multiple junctions [5]. Accurately forecasting target variables based on temporally aligned multi-dimensional signals is critical in decision-making and resource allocation. However, real-world MTS often exhibit complex temporal dynamics, latent inter-variable correlations, and non-stationary behaviors that pose significant challenges for effective modeling and prediction. These challenges necessitate the development of forecasting models that can capture both global patterns and local variations flexibly and adaptively.

With the growing complexity and volume of time series data, deep learning models have emerged as powerful tools for MTS forecasting [6]. These models surpass traditional statistical approaches by capturing nonlinear dynamics and latent dependencies. Among them, three prominent classes of methods have been widely studied. The first class leverages recurrent neural networks (RNNs) capable of modeling sequential dependencies through gated memory mechanisms [7,8]. The second class utilizes convolutional neural networks (CNNs) to extract local temporal patterns and reduce noise sensitivity [9,10]. More recently, a third class based on Transformer architectures has attracted considerable attention due to its ability to model long-range dependencies and global interactions through self-attention mechanisms [11,12]. Transformer-based models have shown promising performance in MTS forecasting by capturing temporal dependencies and inter-variable relationships across extended horizons.

Despite the advances in Transformer-based methods, which have demonstrated superior capability in modeling long-range dependencies, their original design for natural language or univariate tasks limits their effectiveness in multivariate time series forecasting. These models often struggle to capture the complex and dynamic structural dependencies and spectral patterns inherent in real-world MTS data. One major difficulty lies in the dynamic nature of correlations among variables. Most existing models assume fixed or slowly changing dependencies, failing to reflect inter-series relationships’ temporal evolution in practical settings [13]. Furthermore, MTS data often exhibit strong non-stationarity [14]. Distributional shifts and structural transitions over time can significantly degrade model robustness unless adaptation mechanisms are explicitly integrated. Another key challenge arises from the spectral characteristics of multivariate time series. Many real-world signals possess critical frequency-domain patterns such as seasonal trends and periodic oscillations. However, noise often contaminates these informative components, which may be unevenly distributed across the frequency spectrum and overlap with signal bands [15]. In such cases, conventional models may mistakenly amplify noise or misinterpret spurious frequency components as meaningful patterns. In addition [16,17], cross-variable noise coupling can introduce false correlations between variables, which leads to inaccurate predictions and poor generalization. These issues are further complicated by the non-stationarity of noise characteristics, which requires forecasting models to maintain adaptability over time in both the time and frequency domains.

To address the aforementioned limitations, we propose TSGformer, a unified architecture for robust multivariate time series forecasting. The model integrates temporal modeling, structural dependency learning, and spectral representation enhancement into a coherent framework. First, TSGformer employs a dynamic graph learning module that infers evolving inter-variable relationships, serving as a structural prior for downstream representation learning. Second, the model applies temporal attention to extract salient time-dependent features, which are then transformed into the frequency domain for adaptive decomposition. A spectral enhancement module amplifies informative low-frequency components while suppressing high-frequency noise. Finally, an adaptive feature fusion module integrates temporal, graph-based, and frequency-domain representations to improve forecasting accuracy and generalizability. By jointly capturing temporal dynamics, structural correlations, and spectral patterns, TSGformer is designed to overcome the limitations of the existing approaches and provide a principled solution for accurate and robust MTS forecasting across diverse application domains.

The main contributions of this work are summarized as follows:

• We introduce TSGformer, a multi-scale Transformer architecture that incorporates dynamic graph learning into the self-attention framework, enabling adaptive modeling of evolving inter-series dependencies in multivariate time series.
• We design an adaptive multi-domain processing pipeline, which combines temporal attention, graph-structured representation, and spectral decomposition. This pipeline enhances signal expressiveness and mitigates the impact of non-stationary noise and false correlations.
• We conduct extensive experiments on real-world datasets, demonstrating that TSGformer consistently outperforms state-of-the-art baselines in terms of forecasting accuracy and robustness across diverse application scenarios.

2. Related Works

2.1. Transformer-Based Models for Time Series Forecasting

Transformer architectures have emerged as a dominant framework in time series forecasting due to their capacity to model long-range dependencies and flexible input representations [18,19]. The early adaptations primarily focused on transferring the self-attention mechanism to temporal modeling, offering improvements over recurrent models constrained by limited memory and sequential computation [20,21]. To improve scalability, some models adopt sparse or probabilistic attention mechanisms that reduce the computational overhead of standard self-attention [22]. Others focus on improving temporal representation by explicitly decomposing time series into trend and seasonal components, enabling more effective modeling of structured temporal patterns. Additionally, hierarchical temporal encoding strategies have been introduced to capture both local variations and global dynamics across multiple time scales [23,24,25], further enhancing the model’s expressiveness over extended forecasting horizons.

Some recent designs have explored patch-level tokenization and segment-wise encoding, enabling the model to process time series data in a more structured and localized manner [26,27,28,29]. While these approaches have substantially improved robustness and forecasting accuracy, they typically operate under the assumption that temporal dependencies dominate, with limited consideration of the evolving interactions across multiple variables. As a result, their performance may degrade when inter-variable relationships shift over time or when the forecasting task involves heterogeneous temporal behaviors across dimensions. This limitation leads to suboptimal performance in complex multivariate scenarios where inter-variable dependencies dynamically change over time, a gap our proposed TSGformer explicitly addresses by integrating adaptive graph learning to capture these evolving structural relationships alongside temporal patterns.

2.2. Graph- and Frequency-Aware Enhancements for MTS Modeling

More studies have incorporated graph structures into MTS forecasting to capture interdependencies beyond time [30,31]. These methods represent each variable as a node within a graph and apply relational aggregation techniques to model interactions, often assuming spatial or semantic connectivity among variables [32]. Graph-based encoders have demonstrated strong performance in scenarios where variable dependencies are known or approximately static. However, in real-world settings where relationships among time series evolve dynamically, models with fixed or pre-defined graph topologies become insufficient due to regime shifts or latent processes [33]. Attempts to learn graph structures adaptively have emerged, but many still rely on static assumptions or fail to integrate graph dynamics tightly with temporal modeling.

In parallel, frequency-domain modeling has gained attention as an effective means to isolate meaningful signal components from noise [34]. Some forecasting models decompose input series into low- and high-frequency components, allowing the model to focus on smoother long-term trends [35,36]. Others implicitly integrate frequency sensitivity through tailored attention mechanisms, highlighting periodic patterns [37,38]. Despite these innovations, the current methods often lack adaptability in non-stationary noise or overlapping frequency bands. Moreover, few approaches unify temporal attention, graph-based structural reasoning, and frequency-domain processing within a single framework. This gap motivates the development of architectures that can dynamically adjust to structural shifts and spectral variations while preserving high expressiveness for long-horizon and high-dimensional forecasting tasks. Our work bridges this critical gap by proposing a unified architecture that jointly learns dynamic graph structures, adapts spectral representations, and fuses these multi-domain features, thereby enhancing the model’s robustness and expressiveness in complex non-stationary multivariate forecasting tasks.

This integration allows TSGformer to simultaneously address temporal evolution, structural dynamics, and spectral variability, which existing methods typically treat in isolation, thereby providing a more comprehensive and flexible solution for real-world multivariate time series forecasting challenges.

3. Preliminaries

3.1. Problem Definition

MTS forecasting aims to predict the future evolution of multiple temporally aligned variables based on their historical observations. Formally, let the input sequence be denoted as

$$\mathrm{X}=\left[{\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{T}}\right]\in {\mathbb{R}}^{\mathrm{T}\times \mathrm{N}},$$

(1)

where $\mathrm{T}$ denotes the length of the input sequence, and $\mathrm{N}$ is the number of variables. Each time step ${\mathrm{x}}_{\mathrm{T}}\in {\mathbb{R}}^{\mathrm{N}}$ is a vector containing the values of all variables at time step $\mathrm{t}$.

The forecasting objective is to predict the values of all variables over a future horizon $\mathsf{\tau }$, denoted as

$${\widehat{\mathrm{X}}}_{\mathrm{T}+1:\mathrm{T}+\mathsf{\tau }}=\mathrm{f}\left({\mathrm{X}}_{1:\mathrm{T}}\right),$$

(2)

where $\mathrm{f}$ is the forecasting model, and ${\widehat{\mathrm{X}}}_{\mathrm{T}+1:\mathrm{T}+\mathsf{\tau }}\in {\mathbb{R}}^{\mathsf{\tau }\times \mathrm{N}}$ represents the predicted sequence.

3.2. Notations and Representations

To capture the interdependencies among the $\mathrm{N}$ variables, we represent the variable-wise structure as a graph:

$$\mathcal{G}=\left(\mathcal{V},\mathcal{E}\right),$$

(3)

where $\mathcal{V}$ is the set of nodes corresponding to variables, and $\mathcal{E}$ is the set of edges denoting their interactions. The adjacency matrix of the graph is defined as

$$\mathrm{A}\in {\mathbb{R}}^{\mathrm{N}\times \mathrm{N}},$$

(4)

where each entry encodes the strength of the connection between a pair of variables.

In addition to modeling in the temporal domain, we also consider frequency-domain representations to capture periodic patterns and reduce the impact of high-frequency noise. For a univariate time series $\mathrm{x}\in {\mathbb{R}}^{\mathrm{N}}$, the discrete Fourier transform (DFT) is defined as

$$\widehat{\mathrm{x}}=\mathcal{F}\left(\mathrm{x}\right),$$

(5)

where $\widehat{\mathrm{x}}\in {\mathbb{C}}^{\mathrm{T}}.$ denotes the frequency-domain representation. The inverse transformation is given by

$$\mathrm{x}={\mathcal{F}}^{-1}\left(\widehat{\mathrm{x}}\right).$$

(6)

4. Methodology

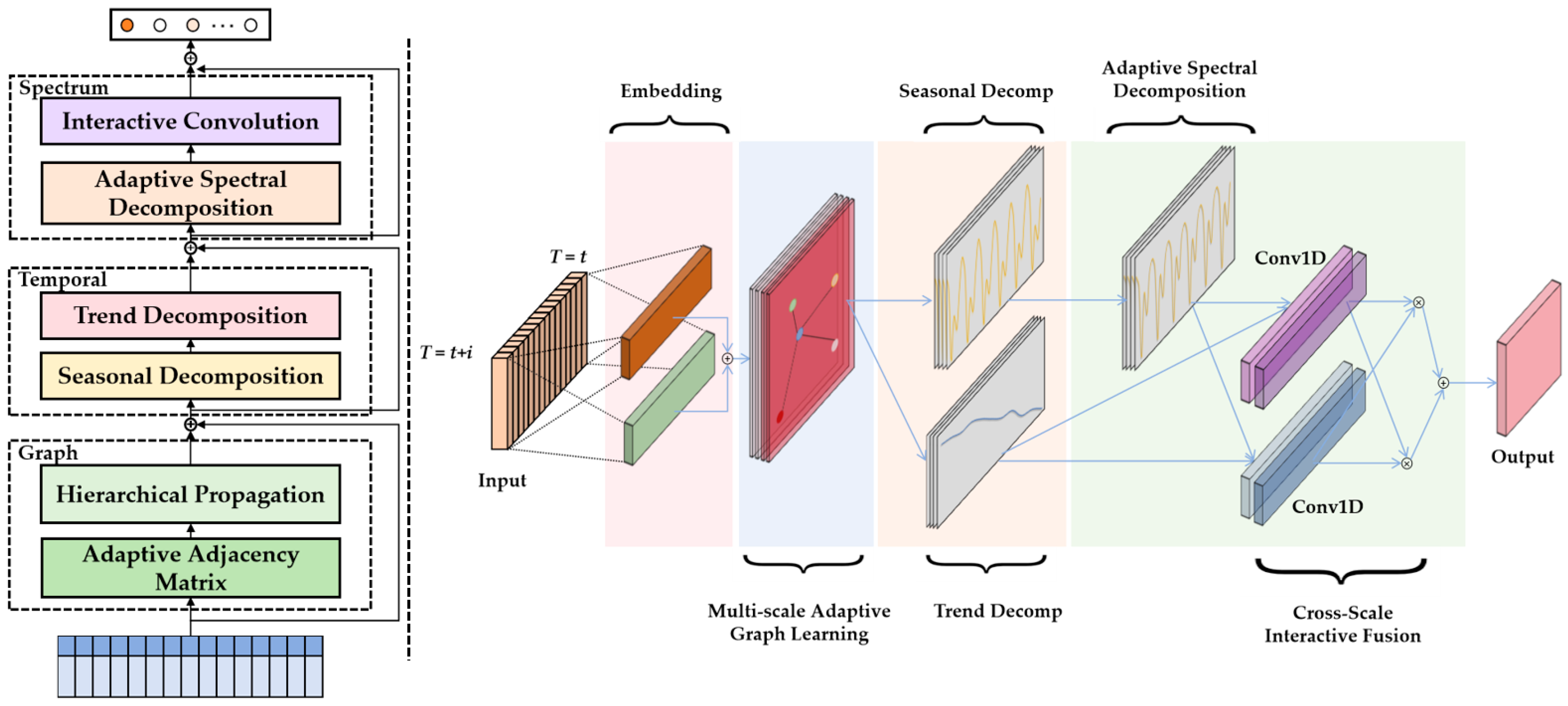
TSGformer is a Transformer-based architecture designed for multivariate time series forecasting, which unifies dynamic modeling of inter-variable dependencies, temporal patterns, and frequency-aware features, as illustrated in Figure 1. Given a multivariate time series input, TSGformer constructs embeddings that integrate the observed variable values and relevant time attributes. The resulting embedded sequence is fed into successive layers that simultaneously model dynamic spatial graphs, temporal dependencies, and spectral characteristics. This allows the model to generate accurate forecasts for future time steps across all variables. The specific algorithm is described in Algorithm 1.

Algorithm 1 Overall TSGformer Procedure.

Input: Original time series $\mathrm{X}=({\mathrm{x}}_1,{\mathrm{x}}_2,...,{\mathrm{x}}_{\mathrm{n}})$, input sequence length H, forecasting horizons T, binary mask θ. Output: Predicted results $\widehat{Y}$ for i ∈ epoch do   X ← {X, value embedding, temporal feature embedding};   for k ∈ Layers do     Obtain adaptive adjacency matrix A;     X ← {X, A} Hierarchical propagation;     for l = 1,2,…,n do       Z1 ← {X} Seasonal decomposition;       Z1 ← {Z1} Adaptive spectral decomposition;     end     for l = 1,2,…,n do       Z2 ← {H} Trend decomposition;     end     O1 ← {Z1} Local feature extraction;     O2 ← {Z2} Global feature extraction;     $\widehat{Y}$ ← {O1,O2} Cross-Scale interactive fusion;   end   Calculate loss of TSGformer   Backpropagate to update model parameters;   end

4.1. Input Representation

The input sequence is encoded into a unified representation by combining value embeddings and temporal feature embeddings. A one-dimensional convolution is applied along the temporal dimension to each variable, projecting the raw series into a shared feature space with hidden dimension ${\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}$, given by

$${\mathrm{E}}_{\mathrm{value}}=\mathrm{Conv}1\mathrm{D}{\left({\mathrm{X}}^{\mathrm{T}}\right)}^{\mathrm{T}},$$

(7)

where ${\mathrm{E}}_{\mathrm{value}}\in {\mathbb{R}}^{\mathrm{T}\times \mathrm{N}\times {\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$. Temporal attributes extracted from timestamps, including month, day, weekday, hour, and minute, are encoded separately using fixed embeddings, aggregated as

$${\mathrm{E}}_{\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}}{=\mathrm{E}}_{\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}}+{\mathrm{E}}_{\mathrm{d}\mathrm{a}\mathrm{y}}+{\mathrm{E}}_{\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{d}}+{\mathrm{E}}_{\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{r}}+{\mathrm{E}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{u}\mathrm{t}\mathrm{e}},$$

(8)

where ${\mathrm{E}}_{\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}}\in {\mathbb{R}}^{\mathrm{T}\times \mathrm{N}\times {\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$. The final input embedding fed into the model is obtained by summing both components:

$${\mathrm{X}}_{\mathrm{emb}}={\mathrm{E}}_{\mathrm{value}}+{\mathrm{E}}_{\mathrm{temporal}}.$$

(9)

4.2. Multi-Scale Adaptive Graph Learning

Capturing the dynamic and often nonlinear relationships among multiple time series variables is a fundamental challenge in multivariate forecasting. To address this problem, we propose a dynamic multi-scale graph convolution module that adaptively learns the inter-variable dependencies at different temporal resolutions. Unlike conventional static graph-based approaches, our module constructs scale-specific adjacency matrices in a data-driven manner, allowing the model to represent evolving connectivity patterns that reflect the temporal context.

Specifically, for each temporal scale $\mathrm{i}$, we initialize trainable matrices ${\mathrm{V}}_{\mathrm{i}}^1$, ${\mathrm{V}}_{\mathrm{i}}^2\in {\mathbb{R}}^{\mathrm{N}\times \mathrm{h}}$ and construct an adaptive adjacency matrix as

$${\mathrm{A}}_{\mathrm{i}}=\mathrm{Softmax}\left(\mathrm{ReLU}\left({\mathrm{V}}_{\mathrm{i}}^1({\mathrm{V}}_{\mathrm{i}}^2{)}^{\mathrm{\top }}\right)\right),$$

(10)

which encodes the pairwise variable correlations unique to the given temporal scale. The embeddings are then projected to scale-aware spaces, and a hierarchical propagation is performed via an iterative update rule:

$${\mathrm{H}}_{\mathrm{k}}=\mathsf{\alpha }{\mathrm{X}}_{\mathrm{i}}+\left(1-\mathsf{\alpha }\right){\mathrm{A}}_{\mathrm{i}}{\mathrm{H}}_{\mathrm{k}-1},$$

(11)

where $\mathsf{\alpha }$ balances contributions from self-information and neighboring variables. By updating both node features and adjacency structures simultaneously during training, our approach enables a flexible representation of cross-variable dynamics, essential for modeling real-world time series where dependency patterns frequently shift due to external or endogenous factors.

4.3. Adaptive Spectral Decomposition

Multivariate time series often exhibit complex frequency characteristics, including underlying periodic patterns interspersed with non-stationary noise. To robustly extract meaningful components while suppressing misleading fluctuations, we design an adaptive spectral decomposition module that leverages frequency-domain analysis as an integral part of the forecasting pipeline.

Our module first decomposes the input time series into trend and seasonal components, then transforms the seasonal component into the frequency domain using the fast Fourier transform (FFT), formulated as

$${\mathrm{X}}_{\mathrm{fft}}=\mathrm{FFT}\left({\mathrm{X}}_{\mathrm{in}}\right),$$

(12)

which reveals the distribution of energy across frequency bands. An adaptive threshold $\mathsf{\theta }$ is then learned to generate a binary mask $\mathrm{y}$ based on the power spectrum $\mathrm{P}={\left|{\mathrm{X}}_{\mathrm{fft}}\right|}^2$, effectively distinguishing relevant low- or mid-frequency signals from high-frequency noise:

$$\mathrm{y}=\mathbb{I}\left[\mathrm{P}\le \mathsf{\theta }\right],{\mathrm{F}}_{\mathrm{adaptive}}={\mathrm{X}}_{\mathrm{fft}}\odot \mathrm{y}.$$

(13)

The module combines the adaptively filtered and original frequency components through learnable reweighting and reconstructs the enhanced time-domain signal using inverse FFT to enhance spectral expressiveness. This dynamic sample-specific frequency filtering improves the model’s ability to capture consistent periodicities while discarding spurious fluctuations, reinforcing temporal patterns critical to forecasting.

4.4. Cross-Scale Interactive Fusion

To effectively capture hierarchical temporal dependencies, we design a cross-scale interactive convolution block that models the interaction between local and global temporal features through element-wise modulation and aggregation in a compact mathematical form. Given the embedded input sequence $\mathrm{X}\in {\mathbb{R}}^{\mathrm{B}\times \mathrm{L}\times \mathrm{C}}$, we first extract multi-scale temporal representations via two convolutional pathways:

$${\mathrm{H}}_1=\mathsf{\varphi }\left({\mathrm{Conv}}_{\mathrm{local}}\right(\mathrm{X}\left)\right),{\mathrm{H}}_2=\mathsf{\varphi }\left({\mathrm{Conv}}_{\mathrm{global}}\right(\mathrm{X}\left)\right),$$

(14)

where $\mathsf{\varphi }$ denotes the activation function GELU, and ${\mathrm{Conv}}_{\mathrm{local}}$ and ${\mathrm{Conv}}_{\mathrm{global}}$ represent convolutions with small and large receptive fields, respectively. Cross-scale feature interaction is formulated by element-wise modulation with dropout regularization:

$${\mathrm{O}}_1={\mathrm{H}}_1\odot \mathrm{Dropout}\left({\mathrm{H}}_2\right),{\mathrm{O}}_2={\mathrm{H}}_1\odot \mathrm{Dropout}\left({\mathrm{H}}_1\right),$$

(15)

where $\odot$ denotes the element-wise product. Finally, the interactive features are aggregated and refined through a fusion operation:

$$\mathrm{Y}=\mathsf{\Psi }\left({\mathrm{O}}_1+{\mathrm{O}}_2\right),$$

(16)

where $\mathsf{\Psi }$ is the fusion convolution layer, serving as a projection layer that consolidates the modulated cross-branch features into a unified temporal representation.

This interaction mechanism allows complementary patterns extracted at different temporal scales to modulate each other adaptively, enhancing the model’s capacity to focus on salient temporal dynamics while suppressing irrelevant fluctuations. The formulation enables a principled and interpretable way to combine multi-scale temporal cues, providing richer representations for accurate long-horizon forecasting.

5. Results and Discussion

5.1. Datasets

We evaluate TSGformer on eight widely used multivariate time series benchmark datasets (

Table 1. Datasets for multivariate time series prediction tasks.

Dataset	Length	Variates	Frequency
ETTh1	17,421	8	1 h
ETTh2	17,421	8	1 h
ETTm1	69,681	8	15 min
ETTm2	69,681	8	15 min
Electric	26,304	321	1 h
Traffic	17,544	862	1 h
Exchange	7588	8	1 day
Flight	26,305	8	1 h

), following previous studies [34,39,40], covering various domains with diverse temporal dynamics and correlation structures. Specifically, the ETT benchmark includes ETTh1, ETTh2, ETTm1, and ETTm2, industrial load datasets containing hourly and minute-level measurements of electric power consumption and voltage. Additionally, we use Electric, a dataset of hourly electricity consumption across multiple clients; Traffic, which records hourly occupancy rates from 862 sensors on California highways; Exchange, a dataset of daily exchange rates of eight major currencies; and Flight, a dataset of flight data related to the COVID-19 pandemic. These datasets collectively present challenges, including complex inter-series dependencies, periodic patterns, and non-stationary behaviors, making them suitable for rigorous evaluation of multivariate time series forecasting models.

To ensure no overlap between training and test data, especially for temporal datasets such as ETT, the data splits are performed chronologically, preserving the temporal order to prevent information leakage. Specifically, the training, validation, and test sets correspond to contiguous non-overlapping time intervals. Furthermore, we adopt a 5-fold cross-validation strategy across all the datasets, where each fold respects this temporal split constraint. In each iteration, four folds are used for training and one for testing, with reported performance averaged over all folds to better reflect the model’s stability and generalization ability.

5.2. Evaluation Metrics

We employ two commonly used error metrics to measure forecasting performance comprehensively: Mean Squared Error (MSE) and Mean Absolute Error (MAE). MSE quantifies the average squared difference between predicted and true future values, emphasizing large deviations and providing a sensitive measure of prediction accuracy. MAE computes the average absolute difference, offering an interpretable assessment of overall forecasting errors. We report both MSE and MAE for each experiment on all forecasting horizons to ensure robust evaluation across short-, medium-, and long-term predictions. MSE and MAE are calculated as follows:

$$\begin{gathered} \mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{{\mathrm{T}}_{\mathrm{y}}}}\sum _{\mathrm{i}=1}^{{\mathrm{T}}_{\mathrm{y}}}{({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}})}^2, \\ \mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{{\mathrm{T}}_{\mathrm{y}}}}\sum _{\mathrm{i}=1}^{{\mathrm{T}}_{\mathrm{y}}}|({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}})|, \end{gathered}$$

(17)

where ${\mathrm{T}}_{\mathrm{y}}$ presents the length of the time series to be predicted, ${\mathrm{y}}_{\mathrm{i}}$ is the predicted value by TSGformer, and $\widehat{{\mathrm{y}}_{\mathrm{i}}}$ denotes the actual value.

5.3. Experimental Setup

All experiments are implemented using PyTorch 2.3.0. Models are trained and evaluated on an NVIDIA A100 GPU with 40 GB of memory to ensure consistent and fair comparisons. Each experimental setting is repeated three times with different random seeds, and we report the average results to reduce performance variance. For all methods, the input sequence length is fixed at $\mathrm{H}=96$ (for fair comparison), and we consider four standard forecasting horizons $\mathrm{T}=\left\{\mathrm{96,192,336,720}\right\}$, consistent with prior works. In addition, we conduct fine-tuning on the hyperparameters, including the learning rate and batch size on the validation set, and choose the settings with the best performance. The Adam optimizer is used with an initial learning rate of 0.0001, employing early stopping based on validation loss to prevent overfitting. The batch size is set to 32 for all experiments. We use mixed precision training with automatic loss scaling to accelerate convergence and improve stability. The code will be available upon the paper’s acceptance at https://github.com/cyyyyy100/TSGformer (accessed on 11 September 2025).

5.4. Baselines

We compare TSGformer with five strong baselines, representing the state of the art in Transformer-based and graph-enhanced time series forecasting. These include Informer [41], which proposes a sparse self-attention mechanism for long-sequence forecasting; Autoformer [42], which introduces deep decomposition for trend and seasonal patterns; Fedformer [43], a frequency-enhanced Transformer that decomposes time series in the frequency domain; MTGNN [44], a graph-based model capturing inter-variable dependencies; and Scaleformer [45], a recent architecture that explores multi-scale temporal patterns. All baseline implementations are obtained from the authors’ official repositories or standard open-source implementations, ensuring identical input settings, sequence lengths, and forecasting horizons for fair comparison.

To ensure an unbiased and fair evaluation, we conducted systematic hyperparameter tuning for all models. This tuning was performed via grid search or recommended procedures outlined in the original papers, focusing on key parameters such as learning rate, batch size, number of layers, and hidden dimensions. The best-performing hyperparameters were selected based on validation set performance for each dataset and forecasting horizon.

5.5. Experimental Results and Analysis

Table 2. Comparative experimental results of multivariate long time series prediction.

Models	TSGformer		Fedformer		Informer		Autoformer		MTGNN		Scaleformer		Crossformer		RLinear		ARIMA
Metrics	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETT (Avg)	0.377	0.391	0.408	0.428	1.960	1.016	0.465	0.459	0.585	0.534	0.415	0.435	0.685	0.578	0.380	0.392	0.419	0.487
Electric	0.207	0.288	0.214	0.327	0.310	0.396	0.227	0.338	0.242	0.334	0.449	0.458	0.244	0.334	0.219	0.298	0.214	0.326
Traffic	0.544	0.299	0.610	0.376	0.764	0.415	0.628	0.379	0.650	0.446	0.734	0.436	0.550	0.304	0.626	0.378	0.713	0.614
Exchange	0.354	0.428	0.519	0.429	1.550	0.998	0.613	0.539	0.725	0.634	0.520	0.491	0.940	0.707	0.378	0.417	1.485	1.056
Flight	0.205	0.320	0.211	0.327	0.391	0.439	0.237	0.344	0.279	0.378	0.517	0.523	0.265	0.372	0.233	0.345	0.581	0.553
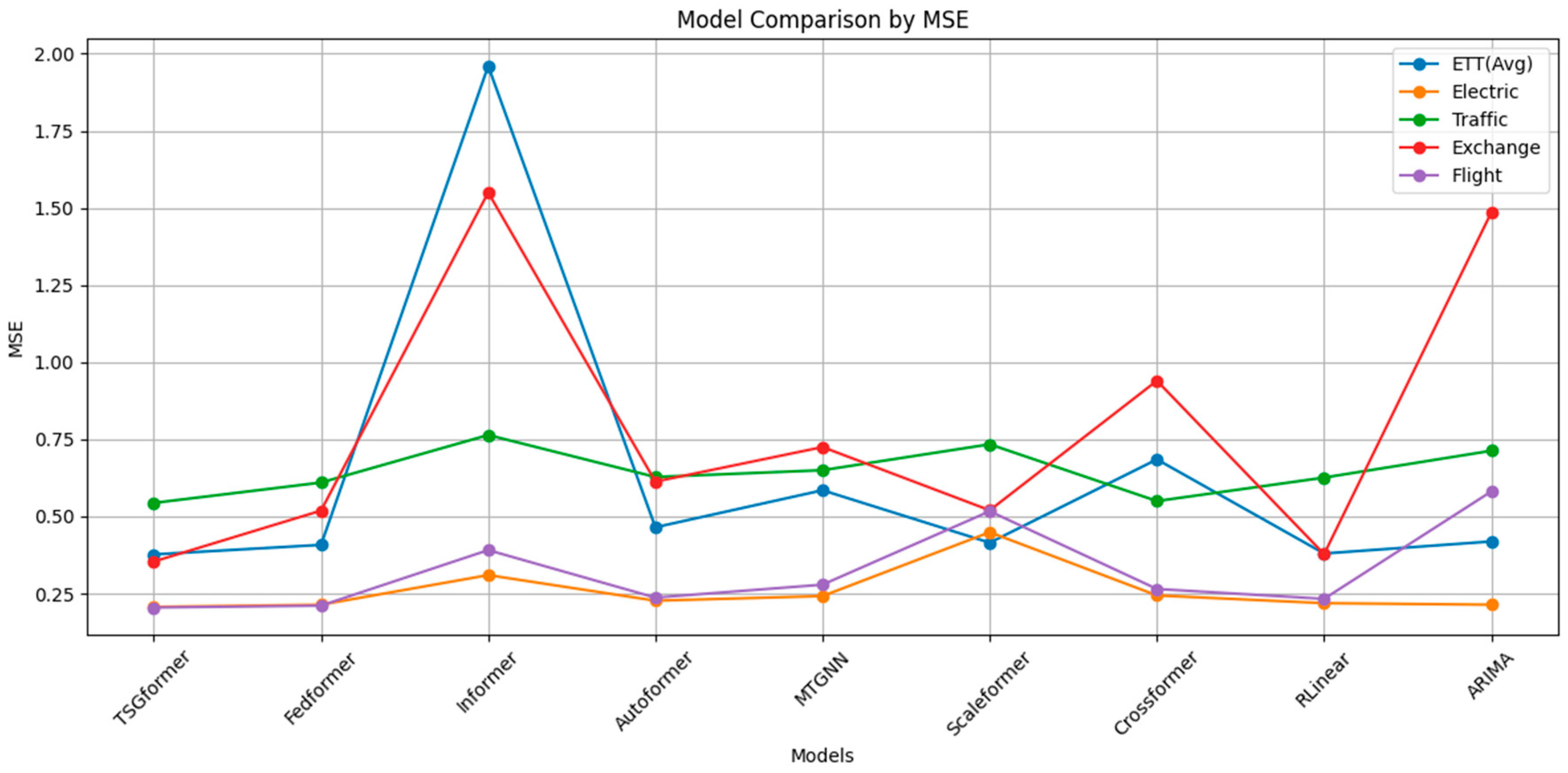
1st Rank	7		0		0		0		0		0		0		1		0

presents a comprehensive comparison of TSGformer against multiple state-of-the-art baselines across eight benchmark datasets and four forecasting horizons.

First, TSGformer exhibits a marked advantage in capturing complex periodic patterns and dynamically evolving temporal dependencies, particularly evident on the ETT datasets. It achieves the lowest average MSE and MAE, outperforming prominent models such as Fedformer and Autoformer by increasingly wider margins as the forecast horizon extends. This underscores the effectiveness of the proposed dynamic graph learning mechanism in modeling time-varying inter-series relationships, complemented by adaptive frequency-domain enhancements that robustly characterize non-stationary temporal dynamics. The widening performance gap at longer horizons indicates that the static attention mechanisms and fixed temporal dependencies employed by other models fail to adapt to complex shifting trends.

Second, in datasets characterized by pronounced periodicity intertwined with high-frequency noise—such as Electric and Traffic—TSGformer consistently delivers superior accuracy and stability. On the Electric dataset, it attains the lowest MSE and MAE, surpassing methods like Informer and Scaleformer, which suffer from pronounced error increases. The adaptive spectral filtering module effectively attenuates disruptive noise components while preserving critical periodic signals, thereby enhancing forecasting robustness. Despite the intrinsic volatility of Traffic data, TSGformer maintains the smallest MAE, demonstrating resilience to abrupt fluctuations and noisy perturbations.

Third, in scenarios involving high-dimensional multivariate series with complex and time-varying dependencies exemplified by Exchange and Flight, TSGformer’s strengths are further amplified. On the Exchange dataset, it achieves a substantial reduction in MSE, exceeding a 16% improvement over Fedformer. This performance gain is attributed to the model’s ability to dynamically construct and update adjacency matrices that accurately reflect evolving correlations, facilitating reliable long-term forecasting where fixed graph structures falter. Similarly, on Flight data, characterized by multifaceted interdependencies and external influences, TSGformer attains the smallest MSE, effectively capturing both short-term volatility and longer-term trends through progressive multi-scale feature aggregation.

Finally, an analysis of the error trajectories across increasing forecast lengths reveals that TSGformer maintains significantly more gradual error growth relative to competing methods. This stability reflects the synergistic integration of dynamic graph reasoning, temporal attention, and adaptive spectral decomposition, which collectively mitigate cumulative error propagation—a well-known challenge in long-horizon time series prediction. In contrast, models such as Informer and MTGNN exhibit pronounced error escalation, likely due to their reliance on static dependency assumptions and insufficient noise handling.

The empirical results detailed in Table 2, together with the illustrative visualizations in Figure 2 and Figure 3, provide compelling evidence of TSGformer’s robust capacity to jointly model multi-scale spatial, temporal, and spectral dependencies. This comprehensive modeling approach enables consistently superior forecasting accuracy and resilience across diverse real-world time series scenarios, highlighting its potential to overcome the limitations inherent in the existing state-of-the-art methods. In Table 2, bold data indicates the best-performing data among different models within the same dataset, while underlined data indicates the second-best-performing data.

5.6. Interpretability and Robustness Analysis Through Visualization

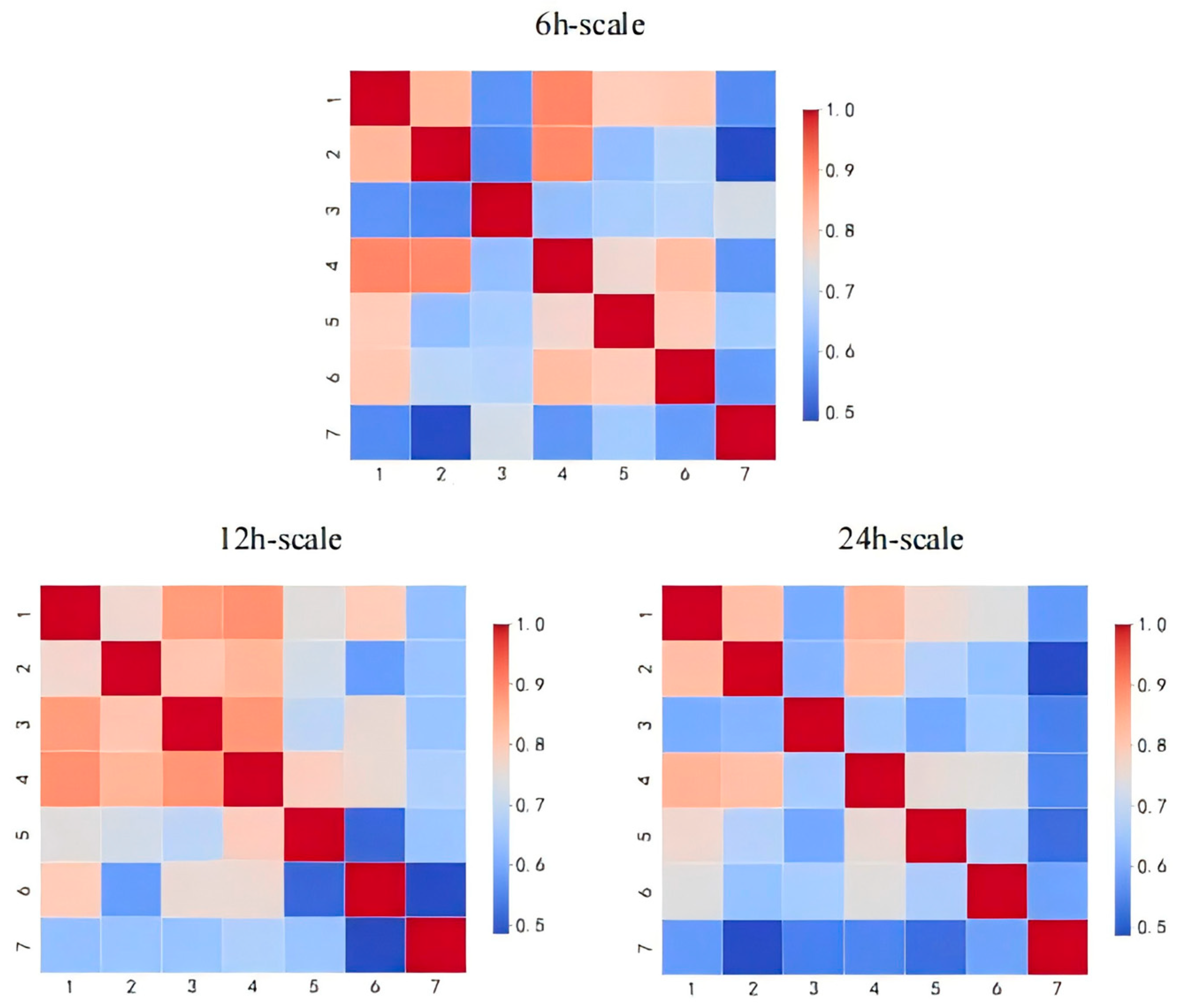
5.6.1. Visualization of Learned Inter-Series Dependencies

To elucidate the dynamic dependencies that TSGformer’s adaptive graph learning module captures, we visualize the learned adjacency matrices at three representative temporal scales: 6 h, 12 h, and 24 h, as illustrated in Figure 4. These adjacency matrices reveal the evolving interconnections among the seven airports in the Flight dataset, offering insights into how the model perceives temporal dependencies across different forecasting horizons.

First, at the short-term scale of 6 h, Airport 6 demonstrates a pronounced influence on Airport 1 and Airport 4, indicating strong immediate interactions likely driven by geographically localized flight scheduling patterns. However, as the temporal scale extends to 24 h, the strength of these connections attenuates significantly, reflecting the dissipating effect of short-lived dependencies over longer horizons. This temporal decay suggests that the model successfully adapts its relational modeling to the expected lifespan of operational interactions between airports.

Second, the persistent and consistently strong connections among Airport 1, Airport 2, and Airport 4 across all the time scales underscore the model’s ability to identify stable core structures in the air traffic network. The robustness of these learned connections aligns well with the actual geographical proximity of these airports, which form a central hub in the regional air transportation system. This observation provides qualitative evidence that the adaptive graph convolution component effectively extracts meaningful spatial dependencies critical to accurate multivariate forecasting.

5.6.2. Evaluation of Generalization Under Distribution Shifts

To rigorously assess the robustness and generalization ability of TSGformer in scenarios affected by external disruptions, we conduct a distribution shift experiment based on the COVID-19 outbreak. We partition the Flight dataset temporally into a training set strictly composed of pre-pandemic historical data, with the validation and test sets containing only data recorded during and after the onset of the pandemic. Two splitting strategies are employed: a standard 7:1:2 ratio and a distribution-shifted 4:4:2 ratio, designed to intensify exposure to out-of-distribution (OOD) conditions.

An analysis of the results in

Table 3. Experimental results of generalization performance of COVID-19.

Models	TSGformer		Fedformer		MTGnn		Autoformer
Metric	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
Flight (7:1:2)	0.205	0.321	0.211	0.328	0.280	0.378	0.238	0.344
Flight (4:4:2)	0.268	0.403	0.277	0.412	0.407	0.501	0.307	0.424
Decrease (%)	23.50	20.34	23.82	20.38	45.74	32.52	29.17	23.09

indicates that TSGformer maintains the lowest prediction errors across both splits, with its error fluctuation rate between the pre- and post-pandemic periods limited to just 20–24% of the baseline models. This significant robustness suggests that the multi-scale temporal, spatial, and spectral modeling capabilities of TSGformer effectively mitigate the impact of abrupt distribution changes. In particular, under the distribution-shifted 4:4:2 setting, TSGformer’s prediction error increases by only 23.5% relative to the standard split. In contrast, the corresponding increases for baselines like MTGnn and Autoformer exceed 29% and 30%, respectively. Such superior resilience can be attributed to the integrated three-dimensional analysis framework of TSGformer, which simultaneously leverages dynamic temporal propagation, graph-structured reasoning, and frequency-domain disentanglement. These components collectively empower the model to maintain predictive stability even under extreme external perturbations, highlighting its suitability for deployment in real-world forecasting scenarios subject to sudden unpredictable events.

5.7. Inference Efficiency

To further validate the efficiency of TSGformer, we compare the single-step inference time across representative baselines on the Electric dataset. As shown in

Table 4. Inference time comparison on the Electric dataset (single forward pass, in milliseconds).

Models	Inference Time (ms)
TSGformer	7.8
Fedformer	10.2
Informer	14.7
Autoformer	11.3
MTGNN	12.5
Scaleformer	9.9
Crossformer	13.4
RLinear	6.5
ARIMA	24.8

, TSGformer achieves a fast inference time of 7.8 ms, outperforming most deep learning-based models, including Informer (14.7 ms), Autoformer (11.3 ms), and Crossformer (13.4 ms), while being only slightly slower than RLinear (6.5 ms), a highly simplified linear baseline. This favorable trade-off is attributed to the lightweight temporal-slot guided attention mechanism, which reduces redundant computations without sacrificing accuracy.

z autoregressive models such as ARIMA (24.8 ms), which exhibit significantly higher latency due to iterative predictions, TSGformer offers consistent low-latency predictions, making it well-suited for real-time and large-scale time series applications. These results demonstrate the practical scalability of TSGformer in deployment scenarios where both forecasting accuracy and inference efficiency are critical.

5.8. Ablation Studies

To rigorously evaluate the contributions of each key component in TSGformer, we perform ablation studies by systematically disabling three modules: the dynamic multi-scale graph convolution block, the adaptive spectral decomposition block, and the cross-interactive convolution block. These ablated variants are evaluated on representative datasets ETTh1, Traffic, and Electric, covering diverse temporal patterns and noise levels. Specifically, we define three model variants: w/o-MAG, which removes the dynamic graph convolution module; w/o-ASD, which omits the adaptive spectral decomposition block; and w/o-CIF, which excludes the cross-interactive convolution mechanism. The quantitative results are summarized in

Table 5. Ablation experiment results on ETTh1, Traffic, and Electric.

Dataset	ETTh1		Traffic		Electric
Metric	MSE	MAE	MSE	MAE	MSE	MAE
TSGformer	0.428	0.451	0.607	0.374	0.207	0.320
w/o-MAG	0.435	0.455	0.608	0.375	0.209	0.322
w/o-ASD	0.434	0.455	0.608	0.375	0.209	0.323
w/o-CIF	0.440	0.460	0.610	0.377	0.214	0.327

.

First, on the ETTh1 dataset, characterized by long-term periodic signals and moderate trend shifts, the variant w/o-MAG consistently exhibits higher errors than the full TSGformer. The increased MSE and MAE reveal that removing the dynamic graph module leads to weaker modeling of evolving inter-variable dependencies. Without dynamically learned adjacency matrices, the model cannot adjust to shifting correlations across time, resulting in diminished predictive accuracy, particularly evident in the longer forecasting horizons. This confirms that dynamic spatial modeling is critical for effectively capturing cross-series dynamics in multivariate forecasting tasks.

Second, across all three datasets, the w/o-ASD variant demonstrates a marked degradation in performance relative to the complete model on ETTh1 and Electric, where the underlying signals exhibit strong periodicity interspersed with high-frequency noise, removing the adaptive spectral decomposition results in notably higher prediction errors. The consistent deterioration illustrates the importance of frequency-domain processing in TSGformer: adaptively filtering high-frequency noise and emphasizing relevant periodic components, the ASD block enhances the model’s ability to distinguish signal from noise, especially in datasets where periodicities are key predictors.

Third, examining the results of w/o-CIF, we observe performance deterioration on all the datasets, with the Electric dataset showing the largest relative increase in both MSE and MAE. The absence of the cross-interactive convolution block impairs the model’s ability to integrate multi-scale temporal features effectively. The model struggles to capture subtle yet important temporal cues without the bidirectional modulation of features across local and global convolutions. This leads to more error accumulation even on short-term forecasts. This highlights the CIF module’s role in refining feature interactions and enhancing the expressiveness of temporal patterns at different resolutions.

Overall, these ablation results demonstrate that each component of TSGformer makes distinct and essential contributions to the model’s predictive performance. Their synergistic integration enables TSGformer to robustly capture dynamic spatio-temporal dependencies, mitigate noise, and effectively model complex temporal structures, providing clear evidence of the design’s necessity and innovation.

6. Limitations and Future Work

While TSGformer introduces a novel integration of multi-scale adaptive graph learning, spectral decomposition, and cross-scale interactive fusion to enhance spatio-temporal representation, the added architectural sophistication inevitably leads to increased computational complexity. The layered design of multiple interdependent modules, especially those involving adaptive frequency operations and dynamic graph construction, may impose a higher computational burden during training and inference, raising concerns about scalability in resource-constrained or latency-sensitive applications.

In addition, the model assumes temporal stability in its decomposition and fusion processes, which may limit its responsiveness to non-stationary or rapidly evolving time series patterns. Although the adaptive mechanisms are designed to capture changing dynamics, their reliance on fixed-length windows and globally aggregated representations might constrain the model’s ability to react to abrupt transitions or localized anomalies. Further refinement is needed to incorporate context-sensitive decomposition bases and temporally aware graph modulation mechanisms that can respond more flexibly to such variations.

Finally, the current design implicitly treats spatial and spectral dependencies as orthogonal modeling dimensions without fully addressing their potential entanglement. This separation may hinder the model’s capacity to capture cross-domain interactions, particularly in real-world systems where spatial configurations and frequency characteristics evolve jointly. Future extensions could explore joint learning strategies that unify structural and spectral representations within a shared latent space, thereby improving the expressivity and coherence of the learned features.

7. Conclusions

In this work, we propose TSGformer, a novel Transformer-based architecture tailored for multivariate time series forecasting. By integrating adaptive graph convolutional modules, our model effectively captures dynamic spatial dependencies across series, while the adaptive frequency-domain enhancement module selectively amplifies informative spectral components and suppresses noise. The cross-domain interaction block further facilitates comprehensive fusion of temporal, spatial, and spectral features, addressing the key limitations of traditional Transformers in modeling evolving inter-variable relationships and managing non-stationary patterns. Extensive experiments on eight real-world benchmark datasets demonstrate that TSGformer consistently outperforms state-of-the-art Transformer-based and graph-augmented forecasting models across multiple prediction horizons and sequence lengths. Moreover, our robustness evaluations under distribution shifts, such as COVID-19-induced disruptions, confirm TSGformer’s generalization ability. For future work, we plan to extend TSGformer’s adaptability to cross-task scenarios, improve computational efficiency for ultra-long sequence forecasting, and investigate its potential integration with external knowledge graphs for further enhancing predictive performance in complex real-world systems.