Developing a Dynamic Simulation Model for Point-of-Care Ultrasound Assessment and Learning Curve Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. POCUS Assessment Framework
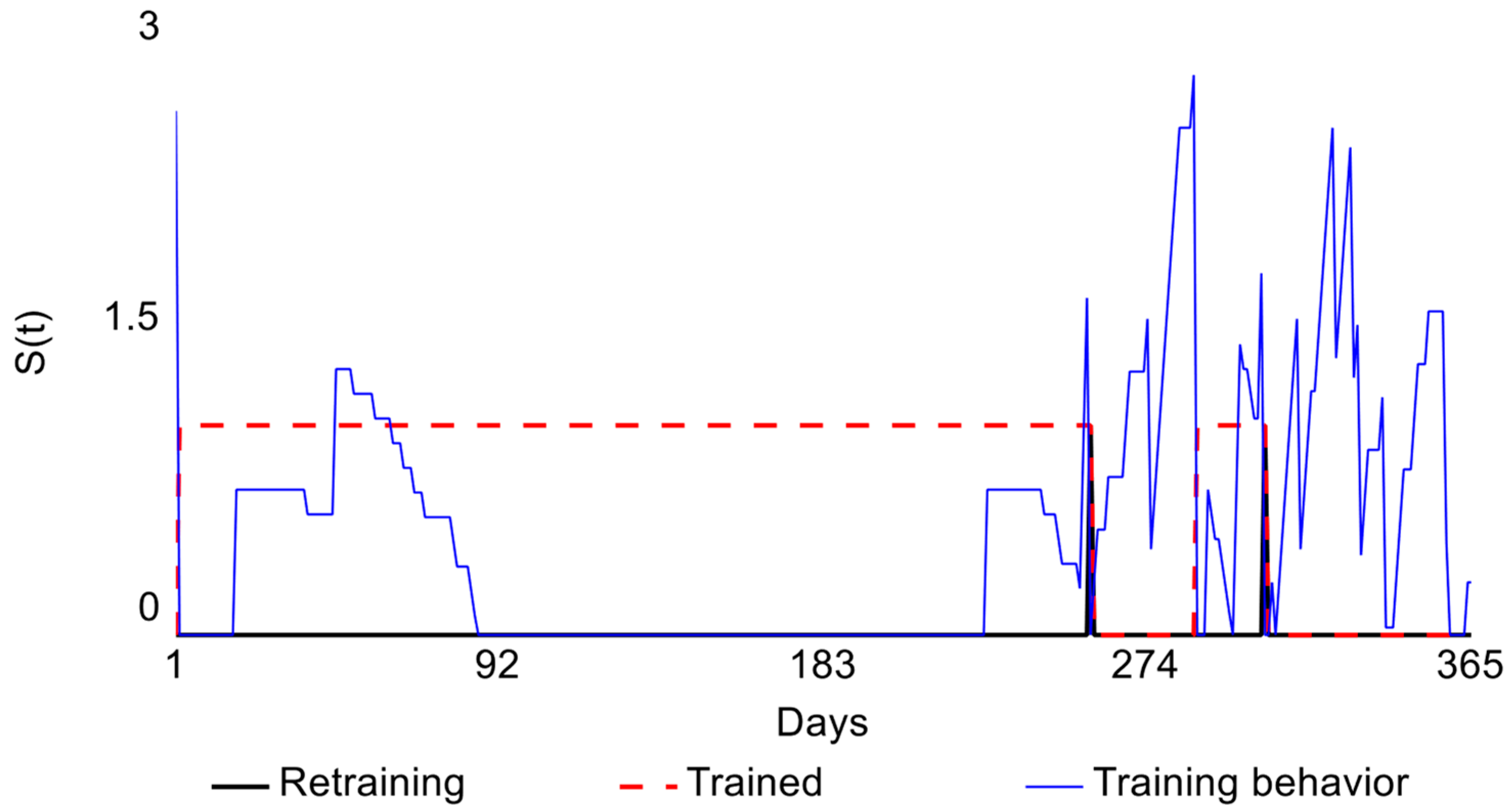
2.2. Learning Curve
2.3. Case Study
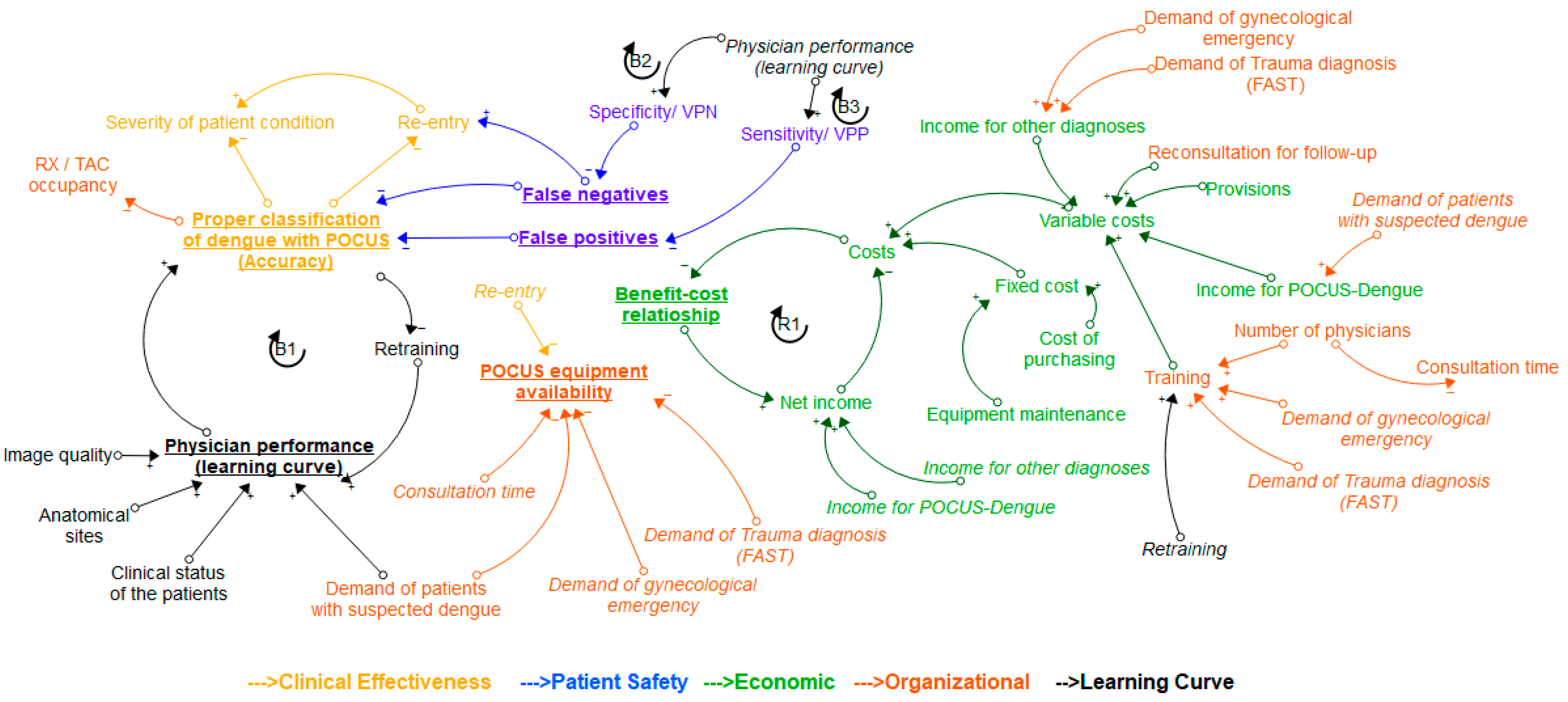
2.4. About the Conceptual Model
- Loop B1 (Balancing): It represents the relationship between proper classification of dengue with POCUS and physician performance (learning curve). When the physician’s performance improves, as evaluated and monitored through the learning curve, the number of patients properly diagnosed will increase, resulting in a lower amount of retraining. More retraining will lead to an improvement in the performance of the physician observed in the learning curve.
- Loop B2 (Balancing): As physician performance improves, specificity increases, and false negatives decrease. The more false negatives there are, the fewer patients are properly classified. Higher accuracy requires less training. The more training a physician receives, the better their performance becomes.
- Loop B3 (Balancing): As physician performance improves, sensitivity increases, and the number of false positives decreases. The more false positives there are, the fewer patients are properly classified. Higher accuracy requires less training. The more training a physician receives, the better their performance becomes.
- Loop R1 (Reinforcing): As total costs rise, the cost–benefit ratio falls, and as this ratio rises, net income also rises. To boost net income, costs need to decrease.
3. Results
3.1. About the Case Study
3.1.1. Patient Demand Module
3.1.2. Pocus Healthcare Module
3.1.3. Ponderation and Training Module
3.1.4. POCUS-Dengue Cost Module
3.1.5. Sensitivity Analyses
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SD | System Dynamics |
| POCUS | Point-of-Care Ultrasound |
References
- World Health Organization. Health Technology Assessment and Health Benefit Package Survey 2020/2021. 2021. Available online: https://www.who.int/teams/health-systems-governance-and-financing/economic-analysis/health-technology-assessment-and-benefit-package-design/survey-homepage (accessed on 1 March 2025).
- Dubromel, A.; Duvinage-Vonesch, M.A.; Geffroy, L.; Dussart, C. Organizational aspect in healthcare decision-making: A literature review. J. Mark. Access Health Policy 2020, 8, 1810905. [Google Scholar] [CrossRef]
- Kristensen, F.B.; Lampe, K.; Wild, C.; Cerbo, M.; Goettsch, W.; Becla, L. The HTA Core Model—10 Years of Developing an International Framework to Share Multidimensional Value Assessment. Value Health 2017, 20, 244–250. [Google Scholar] [CrossRef]
- Sampietro-Colom, L.; Lach, K.; Cicchetti, A.; Kidholm, K.; Pasternack, I.; Fure, B.; Rosenmöller, M.; Wild, C.; Kahveci, R.; Was-serfallen, J.B.; et al. The AdHopHTA handbook: A handbook of hospital-based Health Technology Assess-ment (HB-HTA); Public deliverable; The AdHopHTA Project (FP7/2007-13 grant agreement nr 305018); 2015. Available online: http://www.adhophta.eu/handbook (accessed on 5 July 2025).
- da Silva Galdino, J.P.; Camargo, E.B.; Silva Elias, F.T. Sedimentation of health technology assessment in hospitals: A scoping review. Cad. Saude Publica 2021, 37, e00352520. [Google Scholar] [CrossRef]
- Tarricone, R.; Torbica, A.; Drummond, M. Key Recommendations from the MedtecHTA Project. Health Econ. 2017, 26, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, S.; Olberg, B.; Panteli, D.; Perleth, M.; Busse, R. HTA of medical devices: Challenges and ideas for the future from a European perspective. Health Policy 2017, 121, 215–229. [Google Scholar] [CrossRef] [PubMed]
- Tarricone, R.; Torbica, A.; Drummond, M. Challenges in the Assessment of Medical Devices: The MedtecHTA Project. Health Econ. 2017, 26, 5–12. [Google Scholar] [CrossRef]
- Daubner-Bendes, R.; Kovács, S.; Niewada, M.; Huic, M.; Drummond, M.; Ciani, O.; Blankart, C.R.; Mandrik, O.; Torbica, A.; Yfantopoulos, J.; et al. Quo Vadis HTA for Medical Devices in Central and Eastern Europe? Recommendations to Address Methodological Challenges. Front. Public Health 2021, 8, 612410. [Google Scholar] [CrossRef]
- Sampietro-Colom, L.; Morilla-Bachs, I.; Gutierrez-Moreno, S.; Gallo, P. Development and Test of a Decision Support Tool for Hospital Health Technology Assessment. Int. J. Technol. Assess. Health Care 2012, 28, 460–465. [Google Scholar] [CrossRef]
- Miniati, R.; Frosini, F.; Cecconi, G.; Dori, F.; Gentili, G.B. Development of sustainable models for technology evaluation in hospital. Technol. Health Care 2014, 22, 729–739. [Google Scholar] [CrossRef]
- Ritrovato, M.; Faggiano, F.C.; Tedesco, G.; Derrico, P. Decision-oriented health technology assessment: One step forward in supporting the decision-making process in hospitals. Value Health 2015, 18, 505–511. [Google Scholar] [CrossRef]
- Miniati, R.; Frosini, F.; Cecconi, G.; Dori, F.; Gentili, G.B. Hospital-based expert model for health technology procurement planning in hospitals. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 3504–3507. [Google Scholar] [CrossRef]
- Frosini, F.; Miniati, R.; Grillone, S.; Dori, F.; Gentili, G.B.; Belardinelli, A. Integrated HTA-FMEA/FMECA methodology for the evaluation of robotic system in urology and general surgery. Technol. Health Care 2016, 24, 873–887. [Google Scholar] [CrossRef]
- Ivlev, I.; Vacek, J.; Kneppo, P. Multi-criteria decision analysis for supporting the selection of medical devices under uncertainty. Eur. J. Oper. Res. 2015, 247, 216–228. [Google Scholar] [CrossRef]
- Martelli, N.; Hansen, P.; Van Den Brink, H.; Boudard, A.; Cordonnier, A.L.; Devaux, C.; Pineau, J.; Prognon, P.; Borget, I. Combining multi-criteria decision analysis and mini-health technology assessment: A funding decision-support tool for medical devices in a university hospital setting. J. Biomed. Inform. 2016, 59, 201–208. [Google Scholar] [CrossRef] [PubMed]
- Martelli, N.; Devaux, C.; Van Den Brink, H.; Billaux, M.; Pineau, J.; Prognon, P.; Borget, I. Harmonizing health technology assessment practices in university hospitals: To what extent is the mini-hta model suitable in the French context? Int. J. Technol. Assess. Health Care 2017, 33, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Muñoz Tiznado, P.D.L.Á. Adquisición de Equipo Médicos Basada en AHP-Caso de Estudio de Servicio de Salud Maule (SSM). Ph.D. Thesis, Universidad de Concepción–CHILE, Concepción, Chile, 2016. [Google Scholar]
- Margotti, A.E.; Ferreira, F.B.; Santos, F.A.; Garcia, R.; Member, S. Health Technology Assessment to Improve the Medical Equipment Life Cycle Management. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 354–357. [Google Scholar]
- Grundy, Q. “Whether something cool is good enough”: The role of evidence, sales representatives and nurses’ expertise in hospital purchasing decisions. Soc. Sci. Med. 2016, 165, 82–91. [Google Scholar] [CrossRef]
- Pecchia, L.; Martin, J.L.; Ragozzino, A.; Vanzanella, C.; Scognamiglio, A.; Mirarchi, L.; Morgan, S.P. User needs elicitation via analytic hierarchy process. BMC Med. Inform. Decis. Mak. 2013, 13, 2. [Google Scholar] [CrossRef]
- Lasorsa, I.; Padoano, E.; Marceglia, S.; Accardo, A. Multi-criteria decision analysis for the assessment of non-clinical hospital services: Methodology and case study. Oper. Res. Health Care 2019, 23, 100171. [Google Scholar] [CrossRef]
- Hasegawa, M.; Komoto, S.; Shiroiwa, T.; Fukuda, T. Formal Implementation of Cost-Effectiveness Evaluations in Japan: A Unique Health Technology Assessment System. Value Health 2020, 23, 43–51. [Google Scholar] [CrossRef]
- Moshi, M.R.; Tooher, R.; Merlin, T. Development of a health technology assessment module for evaluating mobile medical applications. Int. J. Technol. Assess. Health Care 2020, 36, 252–261. [Google Scholar] [CrossRef]
- Schreier, J.; Genghi, A.; Laaksonen, H.; Morgas, T.; Haas, B. Clinical evaluation of a full-image deep segmentation algorithm for the male pelvis on cone-beam CT and CT. Radiother. Oncol. 2020, 145, 1–6. [Google Scholar] [CrossRef]
- Soneja, S.; Tsarouchi, G.; Lumbroso, D.; Tung, D.K. A Review of Dengue’s Historical and Future Health Risk from a Changing Climate. Curr. Environ. Health Rep. 2021, 8, 245–265. [Google Scholar] [CrossRef] [PubMed]
- Organización Mundial de la Salud [OMS]. Dengue. OMS. 2022. Available online: https://www.who.int/es/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 1 March 2025).
- Herath, H.M.M.T.B.; Udeshika, W.A.E.; Samarawickrama, S.S.M.; Yogendranathan, N.; Jayamali, W.D.; Kulatunga, A.; Rodrigo, C. Prediction of plasma leakage phase of dengue in resource limited settings. Clin. Epidemiol. Glob. Health 2019, 7, 279–282. [Google Scholar] [CrossRef]
- Dewan, N.; Zuluaga, D.; Osorio, L.; Krienke, M.-E.; Bakker, C.; Kirsch, J. Ultrasound in Dengue: A Scoping Review. Am. J. Trop. Med. Hyg. 2021, 104, 826–835. [Google Scholar] [CrossRef] [PubMed]
- Bélard, S.; Joekes, E.; Tamarozzi, F.; Heller, T.; Bustinduy, A.L.; Kuhn, W.; Brunetti, E.; Wallrauch, C.; Grobusch, M.P. Point-of-Care Ultrasound Assessment of Tropical Infectious Diseases—A Review of Applications and Perspectives. Am. J. Trop. Med. Hyg. 2015, 94, 8–21. [Google Scholar] [CrossRef]
- Brunetti, E.; Heller, T.; Richter, J.; Kaminstein, D.; Youkee, D.; Giordani, M.T.; Goblirsch, S.; Tamarozzi, F. Application of Ultrasonography in the Diagnosis of Infectious Diseases in Resource-Limited Settings. Curr. Infect. Dis. Rep. 2016, 18, 6. [Google Scholar] [CrossRef]
- Kaminstein, D.; Kuhn, W.T.; Huang, D.; Burleson, S.L. Perspectives on Point-of-Care Ultrasound Use in Pediatric Tropical Infectious Disease. Clin. Pediatr. Emerg. Med. 2019, 20, 128–140. [Google Scholar] [CrossRef]
- Díaz-Gómez, J.L.; Mayo, P.H.; Koenig, S.J. Point-of-Care Ultrasonography. N. Engl. J. Med. 2021, 385, 1593–1602. [Google Scholar] [CrossRef]
- Biau, D.J.; Williams, S.M.; Schlup, M.M.; Nizard, R.S.; Porcher, R. Quantitative and individualized assessment of the learning curve using LC-CUSUM. Br. J. Surg. 2008, 95, 925–929. [Google Scholar] [CrossRef]
- Woodall, W.H.; Rakovich, G.; Steiner, S.H. An overview and critique of the use of cumulative sum methods with surgical learning curve data. Stat. Med. 2020, 40, 1400–1413. [Google Scholar] [CrossRef]
- Fanta, G.B.; Pretorius, L. Sociotechnical factors of sustainable digital health systems: A system dynamics model. Health Policy Technol. 2023, 12, 100729. [Google Scholar] [CrossRef]
- Harrison, G.; Grant-Muller, S.M.; Hodgson, F.C. A review of transport-health system dynamics models. J. Transp. Health 2021, 22, 101138. [Google Scholar] [CrossRef]
- Nazarian-Jashnabadi, J.; Rahnamay Bonab, S.; Haseli, G.; Tomaskova, H.; Hajiaghaei-Keshteli, M. A dynamic expert system to increase patient satisfaction with an integrated approach of system dynamics, ISM, and ANP methods. Expert Syst. Appl. 2023, 234, 121210. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, T. Urban resilience under the COVID-19 pandemic: A quantitative assessment framework based on system dynamics. Cities 2023, 136, 104265. [Google Scholar] [CrossRef]
- Aminullah, E.; Erman, E. Policy innovation and emergence of innovative health technology: The system dynamics modelling of early COVID-19 handling in Indonesia. Technol. Soc. 2021, 66, 101682. [Google Scholar] [CrossRef]
- Ghazvini, A.; Shukur, Z. System Dynamics in E-health Policy Making and the “Glocal” Concept. Procedia Technol. 2013, 11, 155–160. [Google Scholar] [CrossRef]
- Newell, B.; Siri, J. A role for low-order system dynamics models in urban health policy making. Environ. Int. 2016, 95, 93–97. [Google Scholar] [CrossRef]
- Payne-Sturges, D.C.; Ballard, E.; Cory-Slechta, D.A.; Thomas, S.B.; Hovmand, P. Making the invisible visible: Using a qualitative system dynamics model to map disparities in cumulative environmental stressors and children’s neurodevelopment. Environ. Res. 2023, 221, 115295. [Google Scholar] [CrossRef]
- Manshadi, Z.D.; Parivar, P.; Sotoudeh, A.; Morovati Sharifabadi, A. Modeling urban growth effects on carrying capacity in arid and semi-arid regions using system dynamics. Ecol. Modell. 2024, 487, 110565. [Google Scholar] [CrossRef]
- Urban, R.C.; Nakada, L.Y.K.; de Lima Isaac, R. A system dynamics approach for large-scale water treatment plant sludge management: A case study in Brazil. J. Clean. Prod. 2023, 419, 138105. [Google Scholar] [CrossRef]
- Nahavandi, N.; Gorji, M.A. The impact of inspection policies on reducing disease prevalence in public buildings: A systems dynamics approach. Build. Environ. 2022, 223, 109398. [Google Scholar] [CrossRef]
- Cirone, J.; Bendix, P.; An, G. A System Dynamics Model of Violent Trauma and the Role of Violence Intervention Programs. J. Surg. Res. 2020, 247, 258–263. [Google Scholar] [CrossRef] [PubMed]
- Rashwan, W.; Abo-Hamad, W.; Arisha, A. A system dynamics view of the acute bed blockage problem in the Irish healthcare system. Eur. J. Oper. Res. 2015, 247, 276–293. [Google Scholar] [CrossRef]
- Lane, J.D.; Sterman, D.C. Profiles in Operations Research; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 9781441962805. [Google Scholar] [CrossRef]
- Cassidy, R.; Tomoaia-Cotisel, A.; Semwanga, A.R.; Binyaruka, P.; Chalabi, Z.; Blanchet, K.; Singh, N.S.; Maiba, J.; Borghi, J. Understanding the maternal and child health system response to payment for performance in Tanzania using a causal loop diagram approach. Soc. Sci. Med. 2021, 285, 114227. [Google Scholar] [CrossRef] [PubMed]
- Davahli, M.R.; Karwowski, W.; Taiar, R. A system dynamics simulation applied to healthcare: A systematic review. Int. J. Environ. Res. Public Health 2020, 17, 5741. [Google Scholar] [CrossRef] [PubMed]
- Barlas, Y. Formal aspects of model validity and validation in system dynamics. Syst. Dyn. Rev. 1996, 12, 183–210. [Google Scholar] [CrossRef]
- Cangelosi, M.; Chahar, A.; Eggington, S. Evolving Use of Health Technology Assessment in Medical Device Procurement—Global Systematic Review: An ISPOR Special Interest Group Report. Value Health 2023, 26, 1581–1589. [Google Scholar] [CrossRef]
- Biau, D.J.; Porcher, R. A method for monitoring a process from an out of control to an in control state: Application to the learning curve. Stat. Med. 2010, 29, 1900–1909. [Google Scholar] [CrossRef]
- Usaquén-Perilla, S.P.; Ropero-Rojas, D.; Mosquera-Restrepo, J.; Kirsch, J.D.; Kaltenborn, Z.P.; García-Melo, J.I.; Osorio-Amaya, L.E. Control charts to establish and monitor proficiency in the detection of pulmonary B-lines with Point of Care Ultrasound. Ing. y Univ. 2023, 27, 1–14. [Google Scholar] [CrossRef]
- Meadows, D.H.; Wright, D. Thinking in Systems: A Primer; Taylor & Francis: Milton Park, UK, 2008; Volume 2, ISBN 9781844077250. [Google Scholar] [CrossRef]
- Pusic, M.V.; Boutis, K.; Hatala, R.; Cook, D.A. Learning Curves in Health Professions Education. Acad. Med. 2015, 90, 1034–1042. [Google Scholar] [CrossRef]
- American College of Emergency Physicians. Emergency Ultrasound Standard Reporting Guidelines; ACEP: Irving, TX, USA, 2018. [Google Scholar]
- Balasubramanian, S.; Janakiraman, L.; Shiv Kumar, S.; Muralinath, S.; Shivbalan, S. A reappraisal of the criteria to diagnose plasma leakage in dengue hemorrhagic fever. Indian Pediatr. 2006, 43, 334–339. [Google Scholar]
- Ramsay, C.R.; Wallace, S.A.; Garthwaite, P.H.; Monk, A.F.; Russell, I.T.; Grant, A.M. Assessing the learning curve effect in health technologies. Lessons from the nonclinical literature. Int. J. Technol. Assess. Health Care 2002, 18, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Tolsgaard, M.G.; Todsen, T.; Sorensen, J.L.; Ringsted, C.; Lorentzen, T.; Ottesen, B.; Tabor, A. International Multispecialty Consensus on How to Evaluate Ultrasound Competence: A Delphi Consensus Survey. PLoS ONE 2013, 8, e57687. [Google Scholar] [CrossRef] [PubMed]
- Díez-Vidal, A.; Martínez-Martín, P.; González-Muñoz, B.; Tung-Chen, Y. Point-of-care ultrasound in infectious diseases: Current insights and future perspectives. Clin. Infect. Dis. 2024, 79, 420–429. [Google Scholar] [CrossRef] [PubMed]
- The Royal College of Radiologists RCR. Ultrasound Training Recommendations for Medical and Surgical Specialties Third Edition Board of the Faculty of Clinical Radiology; BMUS: London, UK, 2017. [Google Scholar]
- Perez-Sanchez, A.; Johnson, G.; Pucks, N.; Soni, R.N.; Lund, T.J.S.; Andrade, A.J.; Le, M.-P.T.; Solis-McCarthy, J.; Wong, T.; Ashraf, A.; et al. Comparison of 6 handheld ultrasound devices by point-of-care ultrasound experts: A cross-sectional study. Ultrasound J. 2024, 16, 45. [Google Scholar] [CrossRef]
- Andersen, C.A.; Brodersen, J.; Rudbæk, T.R.; Jensen, M.B. Patients’ experiences of the use of point-of-care ultrasound in general practice–a cross-sectional study. BMC Fam. Pract. 2021, 22, 116. [Google Scholar] [CrossRef]
- Balmuth, E.A.; Luan, D.; Jannat-Khah, D.; Evans, A.; Wong, T.; Scales, D.A. Point-of-care ultrasound (POCUS): Assessing patient satisfaction and socioemotional benefits in the hospital setting. PLoS ONE 2024, 19, e0298665. [Google Scholar] [CrossRef]

| Reference | Health Problems | Technical | Safety | Clinical Effectiveness | Economic | Ethical | Organization | Social | Legal | Training | Learning Curve |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HTA Core Model, [3] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| AdHopHTA Model, [4] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Sampietro-Colom et al., 2012, [10] | 1 | 1 | 1 | 1 | 1 | 1 | |||||
| Miniati et al., 2014, [11] | 1 | 1 | 1 | 1 | |||||||
| Ritrovato et al., 2015, [12] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Miniati et al., 2014, [13] | 1 | 1 | 1 | 1 | 1 | 1 | |||||
| Frosini et al., 2016, [14] | 1 | 1 | 1 | 1 | |||||||
| Ivlev et al., 2015, [15] | 1 | ||||||||||
| Martelli et al., 2016, [16] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| Martelli et al., 2017, [17] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| Muñoz 2016, [18] | 1 | 1 | |||||||||
| Margotti et al., 2013, [19] | 1 | 1 | 1 | ||||||||
| Grundy 2016, [20] | 1 | 1 | 1 | 1 | |||||||
| Pecchia et al., 2013, [21] | 1 | 1 | |||||||||
| Lasorsa et al., 2019, [22] | 1 | 1 | 1 | 1 | |||||||
| Hasegawa et al., 2020, [23] | 1 | ||||||||||
| Moshi et al., 2020, [24] | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Schreier et al., 2020, [25] | 1 | 1 | 1 | 1 | 1 | ||||||
| This study | 1 | 1 | 1 | 1 | 1 | 1 |
| Variable | Description | Representation in the Model |
|---|---|---|
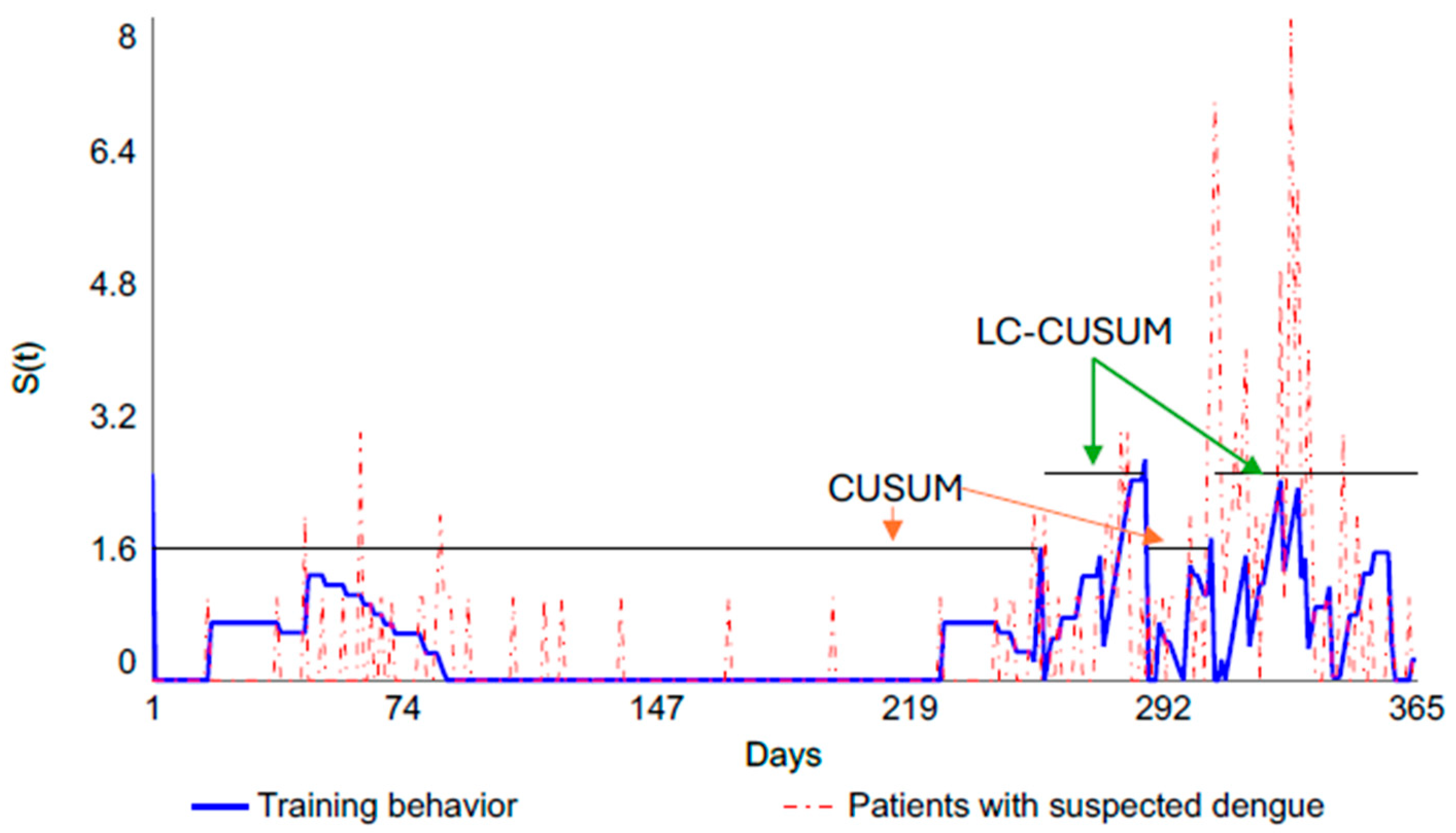
| Learning curve | Graphically represents the relationship between learning effort (example: time, repetitions) and learning outcomes [57]. | LC-CUSUM and CUSUM control charts. |
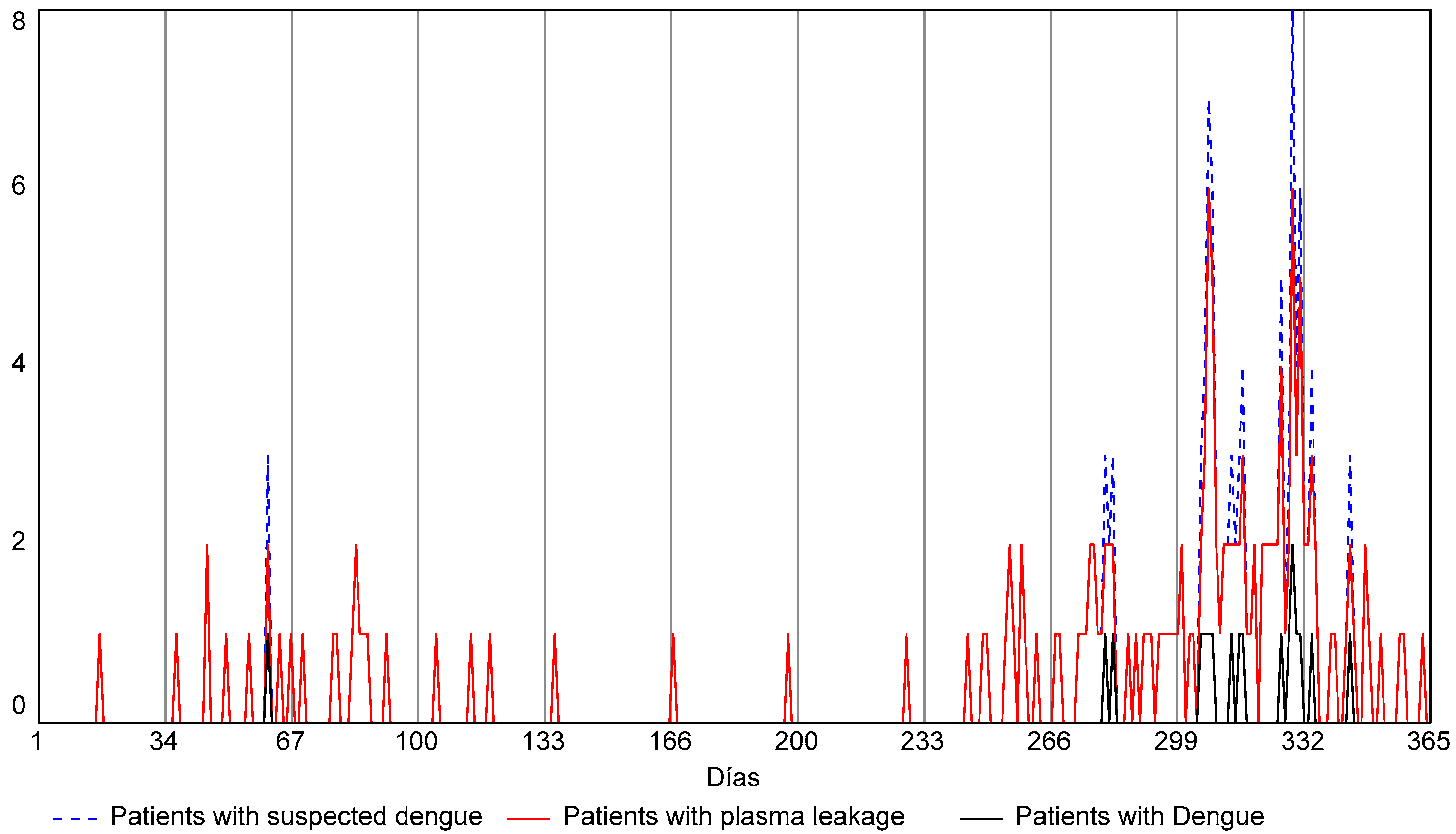
| Demand of patients with suspected dengue | Patients who are admitted to the emergency department with fever and whose attending physicians have considered a diagnosis of dengue virus disease. | Poisson distribution of the prospective cohort study data, in simulation time units of days. The function used in STELLA® generates a series of random numbers that fit a Poisson distribution. |
| Anatomical sites | It refers to the anatomical location for taking the image or video. | There is greater difficulty in achieving competence in certain anatomical points; in this sense, the model represents a single learning curve that should be the one that represents the highest degree of difficulty. |
| Image quality | It refers to the image quality measurement scale of American College of Emergency Physicians [58]. | Image quality influences the success or failure of image interpretation and, consequently, the construction of the learning curve. |
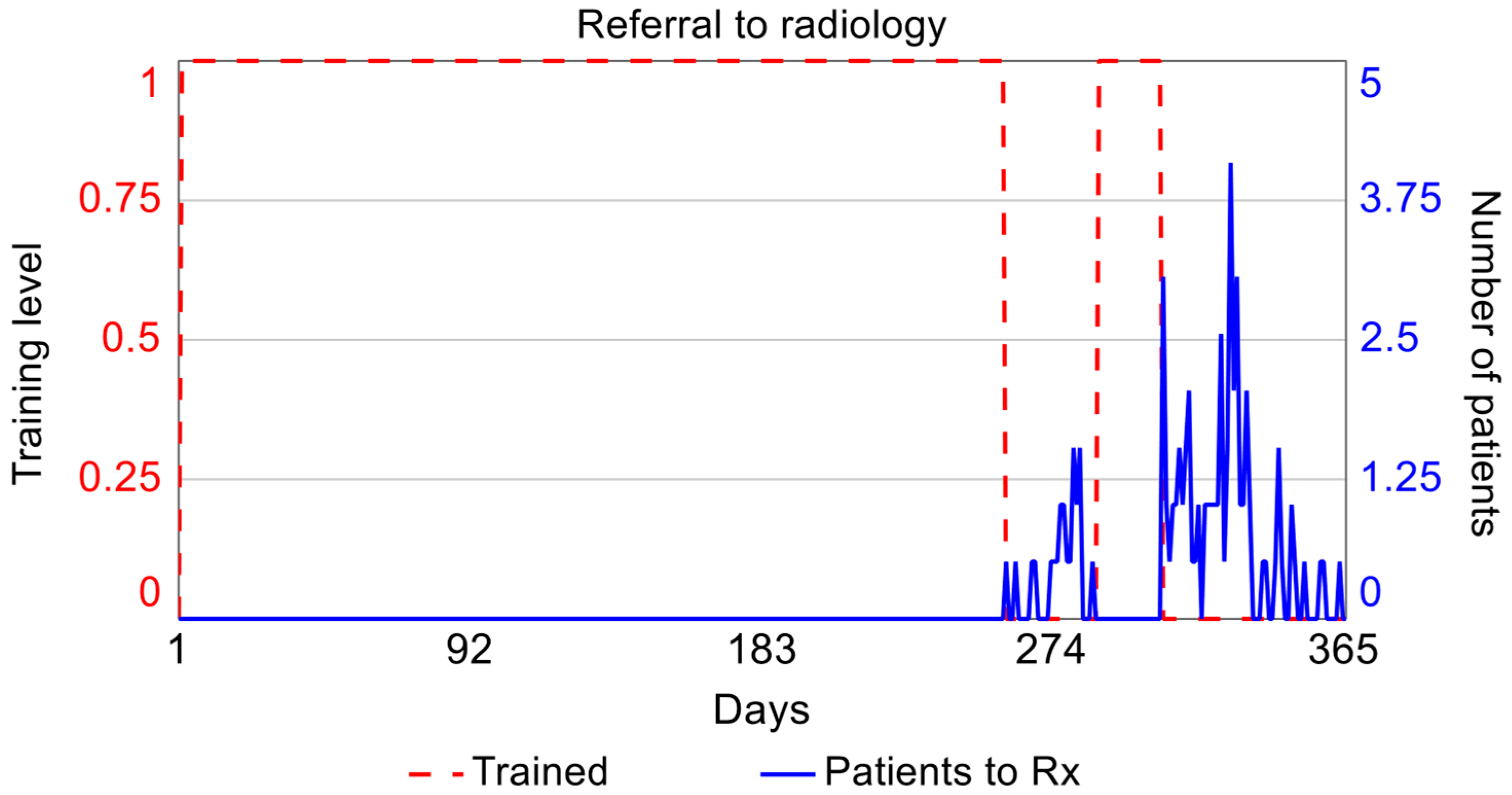
| Retraining | Moment at which the physician loses competence during the monitoring stage. | Point at which the limit (H) is exceeded on the CUSUM control chart. |
| Proper classification of dengue with POCUS | Represented by true negatives (POCUS diagnostic result as absence of plasma leak when the patient does not have this condition) and true positives (POCUS diagnostic result as presence of plasma leak when the patient actually has this condition). | Calculated from sensitivity and specificity values presented in the literature [59]; see Equations (4)–(7). |
| Re-entry reconsultation for follow-up | It is defined as patient admissions/visits to the emergency department for the same reason. Although the prospective cohort study did not include information on readmissions, the simulation allows the user to enter this parameter. | Proportion of consultations. |
| Severity of patient condition | This refers to the therapeutic approach followed for patients confirmed with IgM-positive dengue: - Recovered at home. - Recovered after hospitalization. - Immediately referred to another hospital with a higher level of complexity. - Recovered at another hospital. | Represented by means of the corresponding rates and flows taken from the cohort study. |
| Costs | Fixed costs: purchase price of equipment used in the emergency department, annual maintenance. Variable costs: costs of provisions needed for ultrasound, training courses and retraining, income from providing ultrasound procedures. | Reference values of the Colombian market. |
| Number of physicians | It refers to the number of emergency service physicians who will be trained. | Number of emergency department physicians who were trained. |
| Consultation time | Calculated as the reference time for performing POCUS-Dengue, FAST, and gynecological emergency ultrasounds. | Probability distribution according to the behavior of the cohort study times and reference values. |
| Demand of gynecological emergency | Demand from patients admitted to the emergency department with a diagnosis associated with gynecological emergencies. | Poisson distribution of data from prospective cohort study conducted at a first-level care Public Health Institution in Cali, in simulation time units of days. The function used in STELLA® generates a series of random numbers that fit a Poisson distribution. |
| Demand of trauma diagnosis (FAST) | Demand from patients admitted to the emergency department with diagnoses associated with abdominal trauma. | |
| Economic | Benefit–cost relationship summation of benefits, brought to the present, divided by the sum of the also discounted costs. | >1: means that revenues exceed costs, so the project is profitable. =1: means there are neither profits nor losses; the project is not viable. <1: indicates that costs exceed benefits, making the project unprofitable. |
| Patient safety | Relationship between false positives and false negatives within the total population. Although FP and FN are complementary indicators to specificity and sensitivity, they are considered patient safety indicators because adverse effects can occur from them. In other words, an FN could lead to an increase in the patient’s severity. | |
| Clinical effectiveness | Accuracy of POCUS technology. Sum of true negatives and true positives within the total population | |
| Organizational | POCUS equipment availability. Relationship between calendar hours minus equipment occupancy hours and calendar hours. The analysis was conducted in the emergency department, where the calendar hours are 24 h per day. |
| Variable | Scenario 0 No Learning Curve 177 Patients | Scenario 1 with Learning Curve 177 Patients | ||
|---|---|---|---|---|
| Learning Curve (Success Probability) | 50% | 80% | 100% | |
| Cost–Benefit Ratio | 0.54 | 0.02 | 0.2 | 0.78 |
| Number of Retrainings | 0 | 1 | 2 | 0 |
| Patient Safety (Total = FN + FP) | Cannot be determined for the hospital’s specific conditions | 109 | 43 | 0 |
| Clinical Effectiveness (Diagnostic Accuracy %) | Cannot be determined for the hospital’s specific conditions | 38.4% | 75.7% | 100% |
| Organizational (Availability of POCUS, (range)) | 95.1–99.9% | 95.1–99.9% | 95.1–99.9% | 95.1–99.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usaquén-Perilla, S.; Bocanegra-Villegas, L.V.; García-Melo, J.I. Developing a Dynamic Simulation Model for Point-of-Care Ultrasound Assessment and Learning Curve Analysis. Systems 2025, 13, 591. https://doi.org/10.3390/systems13070591
Usaquén-Perilla S, Bocanegra-Villegas LV, García-Melo JI. Developing a Dynamic Simulation Model for Point-of-Care Ultrasound Assessment and Learning Curve Analysis. Systems. 2025; 13(7):591. https://doi.org/10.3390/systems13070591
Chicago/Turabian StyleUsaquén-Perilla, Sandra, Laura Valentina Bocanegra-Villegas, and Jose Isidro García-Melo. 2025. "Developing a Dynamic Simulation Model for Point-of-Care Ultrasound Assessment and Learning Curve Analysis" Systems 13, no. 7: 591. https://doi.org/10.3390/systems13070591
APA StyleUsaquén-Perilla, S., Bocanegra-Villegas, L. V., & García-Melo, J. I. (2025). Developing a Dynamic Simulation Model for Point-of-Care Ultrasound Assessment and Learning Curve Analysis. Systems, 13(7), 591. https://doi.org/10.3390/systems13070591






