Micro-Driving Behavior Analysis of Drivers in Congested and Conflict Environments Using Graph Theory

Abstract

Many traffic conflicts on the roads are caused by a small proportion of drivers. Currently, there are few studies exploring the time-varying patterns of driving behavior among these drivers. This paper proposes a generic time-series analytical framework and uses it to analyze the driving behavior patterns of many high-risk drivers, which provides a theoretical and targeted basis for vehicle warning systems. Specifically, the natural trajectory time-series data in the rear-end conflict process from congested highway sections were first obtained. Secondly, K-medoid clustering was utilized to obtain the quantitative driving behavior sequence from the trajectory. Thirdly, the driving behavior sequence was transformed into a graph structure by the co-occurrence matrix. Graph theory and Markov theory were used to analyze the obtained graph to achieve the goal of analyzing the time-varying patterns of driving behavior. The analysis found that the driving behavior transition graph network of high-risk drivers on congested highway sections does not exhibit the small-world property and this suggests that during the conflict process, the driver is unable to quickly transition between states. Additionally, vehicles consistently evolve into a rear-end conflict state along a fixed driving behavior transition route, which indicates that the causes of conflicts in congested road sections are similar. Finally, the state change of the conflict process follows the Markov property, proving that the state during the conflict process can be predicted and controlled.

1. Introduction

The real-world traffic environment is highly complex, presenting significant challenges for conventional traffic management. Targeted traffic management policies offer a potential solution. However, developing effective policies requires detailed classification of traffic environments or driver types, enabling in-depth exploration and characterization of patterns associated with specific scenarios or driver cohorts.

Traditional traffic safety analysis and management have predominantly relied on crash data. Yet, such data are scarce and require extensive time to collect [1,2]. Studies have demonstrated the feasibility of using traffic conflict techniques for road safety analysis [3,4,5], as a strong correlation exists between conflicts and crashes [6]. Compared to crash data, traffic conflict data are significantly more accessible [6,7,8]. Consequently, an increasing number of researchers are investigating traffic safety through traffic conflict technologies.

Extensive research utilizing traffic conflict techniques has demonstrated significant correlations between traffic states on road segments—including traffic flow, occupancy, average speed, and vehicle composition—and environmental factors such as weather, with the occurrence of traffic conflicts [9,10,11,12]. Generally, higher traffic volumes and occupancies, coupled with greater fluctuations in average speed and increased traffic flow heterogeneity, are associated with a higher incidence of conflicts and potential accidents. While conflict frequency may rise under congested conditions, only a small proportion of vehicles are typically involved in such events. This suggests that deteriorating traffic conditions predominantly impact a limited subset of drivers. Consequently, analyzing the driving behaviors of those involved in rear-end conflicts offers valuable insights. Such investigations can elucidate characteristic behavioral patterns among these drivers and inform targeted traffic safety interventions.

Previous studies have examined conflict evolution from diverse perspectives. While investigations [13,14,15] have analyzed the propagation chain of inter-vehicle conflicts, they paid limited attention to the microscopic behavior of individual vehicles. In Ref. [9], the authors segmented road sections and examined risk evolution both within and between these segments. Similarly, the authors in [16] subdivided sections into finer spatial blocks to explore spatio-temporal risk evolution across blocks. A recent work [17,18] further investigated the influence of factors like speed variance and average speed of involved vehicles on conflict likelihood. However, these studies collectively failed to characterize the entire, fine-grained conflict process. Critically, existing research has primarily focused on conflict risk evolution within specific spatio-temporal road segments, overlooking the specific drivers involved in conflicts and the time-varying patterns of driving behavior among these high-risk drivers.

To address this research gap, we conducted a comprehensive investigation into the rear-end conflict process within congested highway segments. This study explicitly considers the temporal evolution of driver behavior throughout the entire conflict sequence and accounts for the heterogeneity inherent in congested traffic flows. The primary contributions of this work are summarized as follows:

• An explainable time-series analysis framework: We propose a novel framework designed for the explainable analysis of time-varying patterns, enabling fine-grained interpretation of temporal dynamics.
• Heterogeneity-aware conflict analysis under congestion: Leveraging the proposed framework, we analyzed a substantial dataset of conflict processes occurring under heterogeneous congested traffic conditions. The resulting actionable insights provide more detailed and targeted guidance for enhancing vehicle collision warning systems.
• A transferable analytical paradigm: The developed framework establishes a methodological paradigm that can be readily adapted to support time-series analysis challenges in other research domains.

The rest of this paper is organized as follows. Section 2 reviews some related works about traffic conflict technology. In Section 3, graph theory and Markov theory are briefly introduced. The proposed explainable analysis framework for rear-end conflicts is described in detail in Section 4. Section 5 conducts experiment on a real traffic dataset and presents discussions about the results. This paper is summarized, and some future directions are discussed in Section 6.

2. Related Work

Traffic conflict techniques have gained widespread recognition as valuable tools in traffic safety research. Current investigations into these techniques primarily focus on areas such as traffic conflict prediction, safety evaluation, and conflict analysis. Common methodological approaches include statistical models, machine learning, and deep learning. These methods universally rely on extensive datasets, extracting relevant features and employing suitable algorithms to address specific research challenges. Findings derived from such studies inform the formulation of evidence-based traffic management measures.

2.1. Statistical Methods

Traditional statistical models usually receive some traffic characteristics of a specific road section or period as input to the model and then obtain a classifier that can output a conflict probability. These methods include logistic regression, linear regression, and so forth. Sensitivity analysis and feature importance are often used to identify factors that cause conflict. Their advantage is that they have good interpretability, which is why they are often used for factor analysis [19,20,21,22,23,24]. Simultaneously, these methods are often employed to deal with macroscopic traffic features, as they are unable to handle high-dimensional microscopic traffic characteristics such as vehicle trajectories. Therefore, they are difficult to use for fine-grained time-varying pattern analysis, and another reason is that they cannot handle time-series data.

2.2. Machine Learning and Deep Learning Methods

Machine learning (ML) and deep learning (DL) methodologies aim to extract latent features or approximate data distributions from large-scale traffic datasets. These approaches are frequently employed for microscopic conflict prediction and analysis. For instance, studies leverage camera image data for real-time conflict probability prediction [25,26,27,28,29,30,31], while others utilize neural networks to model the data distribution of vehicle trajectories for conflict severity assessment and prediction [32,33,34]. However, ML and DL methods face practical challenges, including insufficient generalization capability and limited interpretability [6,35]. Although adept at processing high-dimensional data like vehicle trajectories, the specific factors driving model determinations often remain obscure.

Risk field theory (RFT) is commonly applied to assess the spatiotemporal evolution of risk for traffic conflict safety evaluation [21]. While RFT quantifies risk levels within defined spatiotemporal boundaries, it typically does not account for the specific microscopic evolution process of rear-end conflicts. Regarding conflict formation, some research has investigated the macro-scale spatial and temporal evolution of conflict risk [15,36,37]. Nevertheless, due to traffic flow heterogeneity, these findings may lack applicability in congested scenarios. Furthermore, these identified spatiotemporal risk patterns are derived from statistical aggregation across numerous vehicles, potentially overlooking the specific behavioral patterns of vehicles directly involved in conflicts.

As summarized in

Table 1. Summary of commonly used methods in related work and introduction.

	Input	Output
Statistical methods	Cross-sectional data	Conflict probability
Machine learning	Cross-sectional data	Conflict probability and number
Deep learning methods	Time series	Conflict probability and number
Spatial Markov	Time series	Conflict Probability distribution

, while numerous researchers have proposed novel methods addressing various traffic safety problems and employed technical means to infer the causative factors of conflicts, limited attention has been given to the precise microscopic details characterizing rear-end conflict processes. This includes, for example, the evolution of driver behavior patterns during the conflict event itself.

2.3. Analysis of the Causes of Conflict

A conflict causality analysis and risk prevention and control are core intelligent transport system research areas. In line with conventional car-following conflict modeling, the Random Parameters Logit Model (RPLM) was used at a two-way-stop controlled intersection in Aachen, Germany. It highlighted the significant impact of lead vehicle dynamic variables like speed and acceleration and first spotted the “unnecessary intentional deceleration” phenomenon, offering a theoretical basis for conflict intervention strategies [38].

To address rear-end collision risks, an evaluation framework combining deep neural networks and deep reinforcement learning was proposed. By dynamically adjusting the following vehicle speed, it effectively reduced rear-end collision probability, with its effectiveness verified by both simulation and real-vehicle data [39]. Further, an analytical approach based on time-to-collision (TTC) and its derivative (TTCD) was presented. It quantified the vehicle transition mechanism from safe to dangerous states, identified three typical transition modes, and confirmed that the following vehicle acceleration, speed difference, and acceleration difference between the two vehicles are significant TTCD-influencing factors [40].

To enhance the safety-distance model’s versatility, an improved car-following safety model introduced driver heterogeneity parameters. Using fuzzy theory to dynamically correct reaction time, it achieved precise safety-distance calculation under multiple traffic and driver-type conditions, underpinning active traffic-accident early warning [41].

In autonomous driving safety research, a pre-collision scenario classification method mapped and identified 24 high-incidence scenarios (98.1% accuracy), with rear-end and intersection conflicts identified as key risk scenarios. Causal- and correlation-based key-factor mining provided targeted paths for autonomous driving system optimization [42].

Special research on advanced driving systems (ADSs/ADASs) revealed that rear-end collisions accounted for 76.1% of cases in the NHTSA accident dataset. Ego vehicle speed, collision object motion state, and road type were identified as significant influencing factors. These findings are highly instructive for system design standards and road-user training [43].

For improved mixed-traffic-flow safety, a hybrid control framework was macro-simulated. It demonstrated a positive correlation between connected and automated vehicle (CAV) penetration rate and road capacity. Under high penetration rates, the framework effectively suppressed traffic oscillations and reduced collision risks [44].

Regarding lane-changing maneuver safety early warning, a hybrid model combining Mexican Hat Wavelet (MHW) transform and genetic-algorithm-optimized XGBoost (GA-XGBoost) achieved precise failed lane-changing detection (94.55% accuracy). It revealed a strong link between high collision risks of target-lane trailing vehicles and failed lane changes [45].

3. Preliminary

3.1. The Driving Behavior Time-Varying Pattern Analysis Based on a Graph

The purpose of the paper is to explore the patterns of vehicle state changes during rear-end collision processes. Our strategy involves converting the trajectory time-series data during conflicts into a network view structure. Initially, we utilize clustering methods on trajectory data to obtain quantified behavioral states of vehicles, followed by the analysis of transitions between these quantified behavioral states. In terms of constructing the graph structure, we represent the conflict process in the entire dataset by establishing a directed weighted graph, with the vehicle behavioral states as nodes, the transitions between behavioral states as edges, and the frequency of these transitions as edge weights.

Subsequently, we must analyze the obtained network graph, which includes assessing the significance of behavioral states, identifying patterns in state transitions, and examining the overall characteristics of the graph. Specifically, we employed complex network theory and Markov theory. Next, we will delve into the underlying technical principles.

Complex networks are commonly used to model the evolution process of systems. There are some concepts related to graph and edge property analysis in complex network theory:

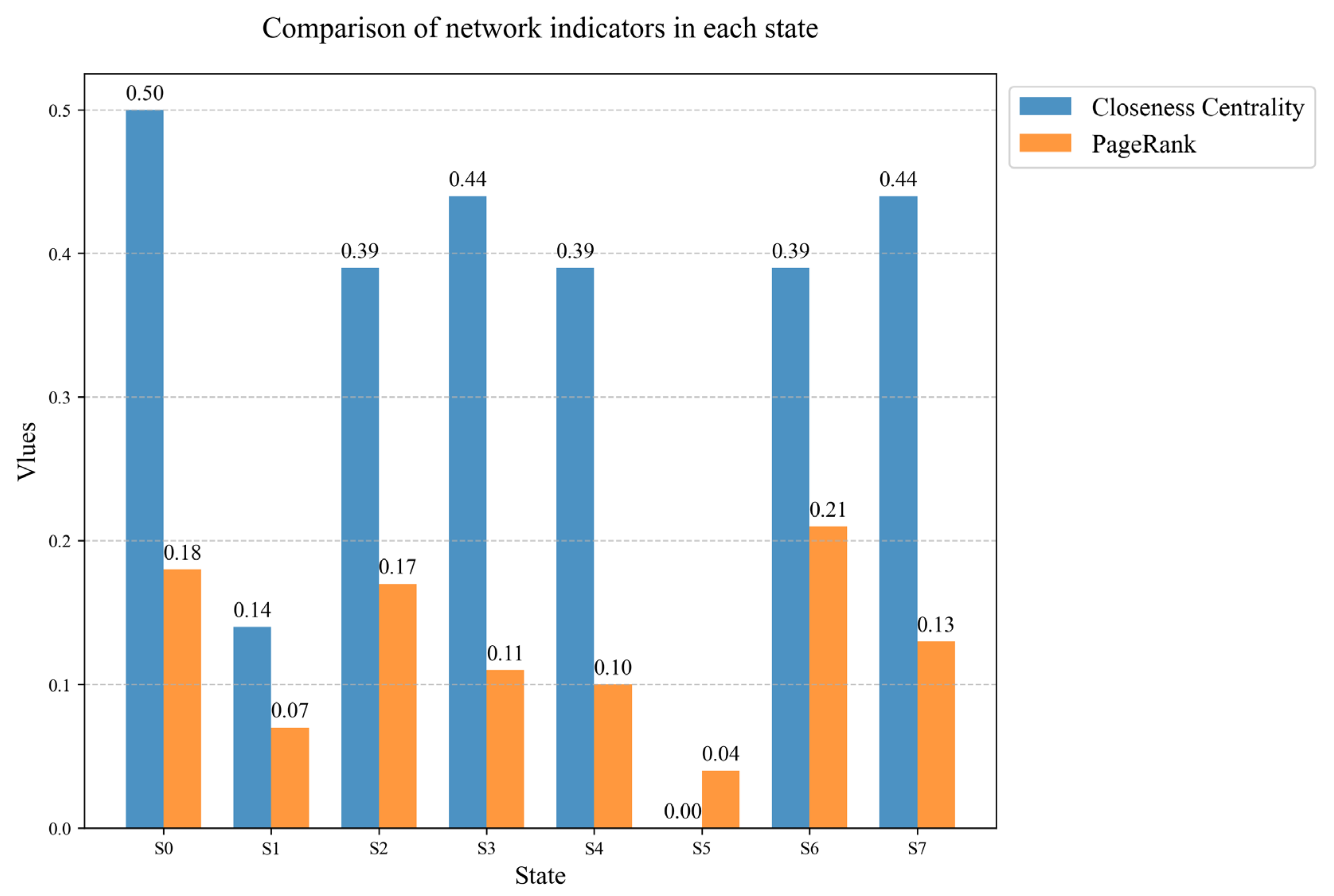
PageRank: The larger the PageRank value, the more important the node is. If a driving state node has a high PageRank score, it indicates that this driving state is crucial throughout the entire conflict process. Its formula is shown in (1).

$$PR\left(v_i\right)={\displaystyle \sum _{v_j\in M\left(v_i\right)}\frac{PR\left(v_j\right)}{L\left(v_j\right)}},i=1,2,\dots ,n$$

(1)

where $M\left(v_i\right)$ represents the set of nodes to node $v_i$, and $L\left(v_j\right)$ represents the number of directed edges connected by node $v_j$.

Closeness centrality: Its calculation formula is shown in (2). A driving behavior state node with a high closeness centrality can more quickly influence other driving states.

$$\left\{\begin{array}{l}{d}_i={\displaystyle \frac{1}{N-1}}{\displaystyle \sum _{j=1}^N{d}_{ij}}\\ C{C}_i={\displaystyle \frac{1}{d_i}}\end{array}\right.$$

(2)

where $d_i$ represents the average distance from node $v_i$ to the other node $v_j$.

Small-world property: The small-world characteristics are determined by the shortest path and the aggregation coefficient of graph. The shortest path is calculated by Formula (3) and it represents the average of paths between any two nodes in the network. The aggregation coefficient is calculated by Formula (4) and it indicates whether a node is densely connected to its neighboring nodes. When the shortest path is long and the aggregation coefficient is small, it indicates that the network does not have small-world characteristics. In this paper, we utilize these two metrics to determine whether the conflict process network exhibits small-world characteristics.

$$L={\displaystyle \frac{1}{n\left(n-1\right)}}{\displaystyle \sum _{i\ge j}{d}_{ij}}$$

(3)

where $n$ is node number and $d_{ij}$ is the shortest distance between any state nodes.

$$c{l}_T={\displaystyle \frac{{\left(A+A^T\right)}_{ii}^3}{2\left[d_i^{tot}\left(d_i^{tot}-1\right)-2{\left(A^2\right)}_{ii}\right]}}$$

(4)

where $c{l}_T$ is the aggregation coefficient, $A$ represents the adjacency matrix of the network and $d_i^{tot}$ represents the total degree of state node $i$.

Through these analysis methods, we can obtain the critical driving states during the conflict process and the transfer relationships between these states and conduct an explainable analysis of the conflict process accordingly.

3.2. Markov Property Analysis of Behavior Sequence

To explore the stochastic process of vehicle driving behavior during rear-end collisions, we conducted a statistical analysis of the changes in driving direction and frequency, resulting in the derivation of a co-occurrence matrix for driving behavior. The co-occurrence matrix, resembling a transition matrix, requires assessment to ascertain its adherence to Markovian properties. The Markov test can be used to analyze whether a discrete sequence satisfies a stochastic process, often using chi square statistics for testing.

Based on frequency transition matrix $F_{m\times m}$ and probability transition matrix $P_{m\times m}$, we can construct chi square statistics as Formula (5).

$${\chi }^2=2{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m{f}_{ij}\left|\log \frac{p_{ij}}{p_{.j}}\right|}}$$

(5)

where $m$ is the number of states, $f_{ij}$ and $p_{ij}$ are the transition probabilities and frequencies from state $i$ to state, respectively, and $p_{.j}$ is the boundary probability, which is calculated by Formula (6).

$$P_{.j}={\displaystyle \frac{{\displaystyle \sum _{j=1}^m{f}_{ij}}}{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m{f}_{ij}}}}}$$

(6)

If the chi square statistic of the driving behavior sequence during the conflict process is less than the $p$ value, it indicates that the conflict process satisfies the Markov property.

4. Methodology

4.1. Problem Definition

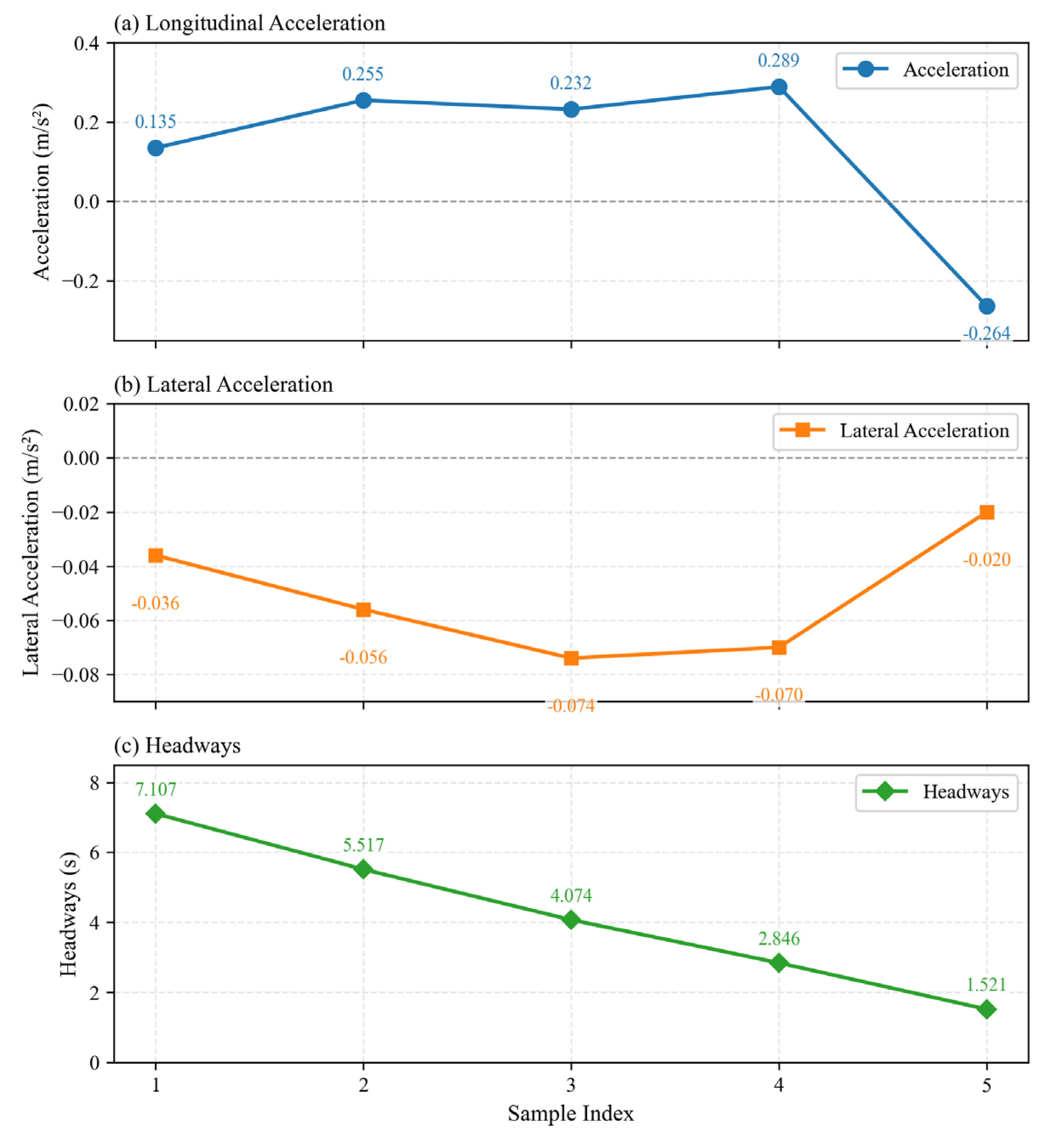
Analyzing conflict dynamic change mechanism under temporal effects can provide a better understanding of traffic conflict. Its purpose is to analyze the time-varying relationship during the process based on the natural trajectory times series data of vehicles before the conflict occurs by using relevant technical methods, such as to analyze the quantitative time-varying relationship of driving patterns. More specifically, the fine-grained variation patterns of headway, velocity, and acceleration in the time dimension during the conflict process are explored in this paper.

4.2. The Explainable Analysis Framework of Conflict Process

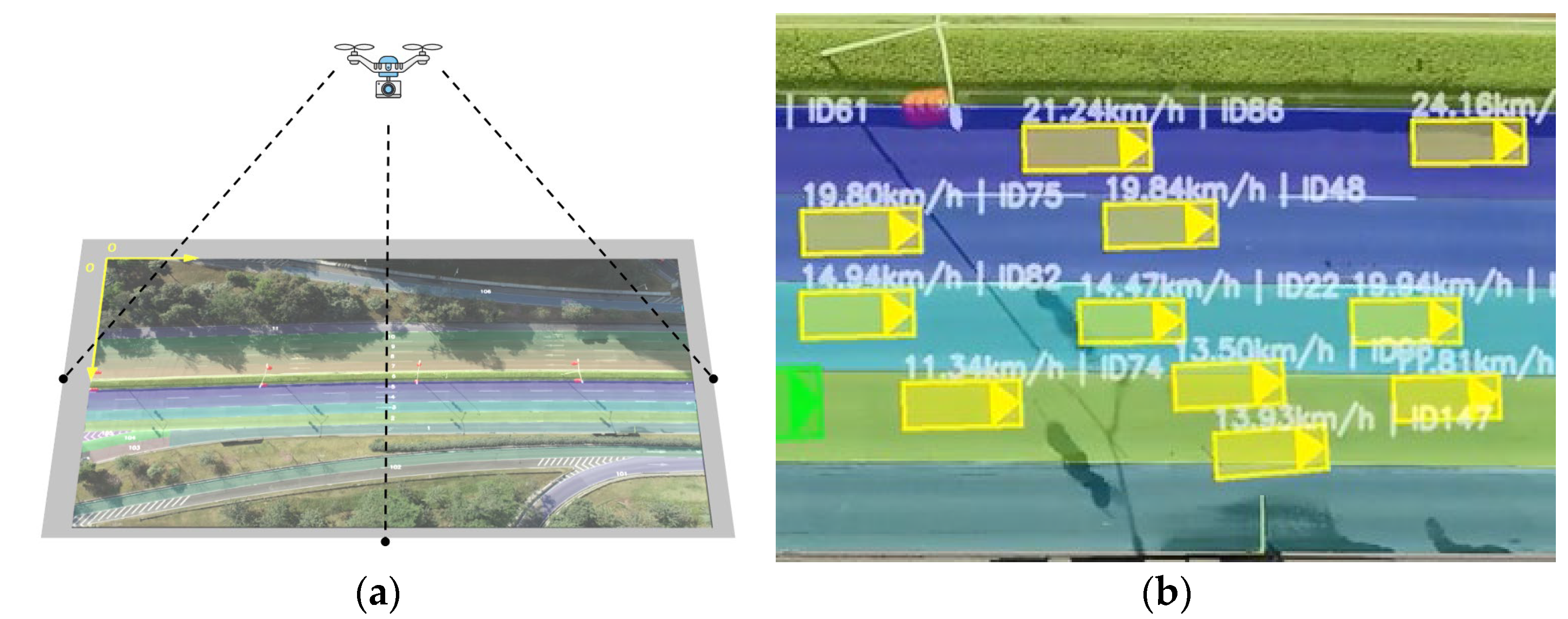
Figure 1 illustrates the conflict analysis framework proposed in this paper. The graph structure generation flowchart is shown in the left half, while the interpretability analysis of the driving state sequences and graph structure is shown in the right half.

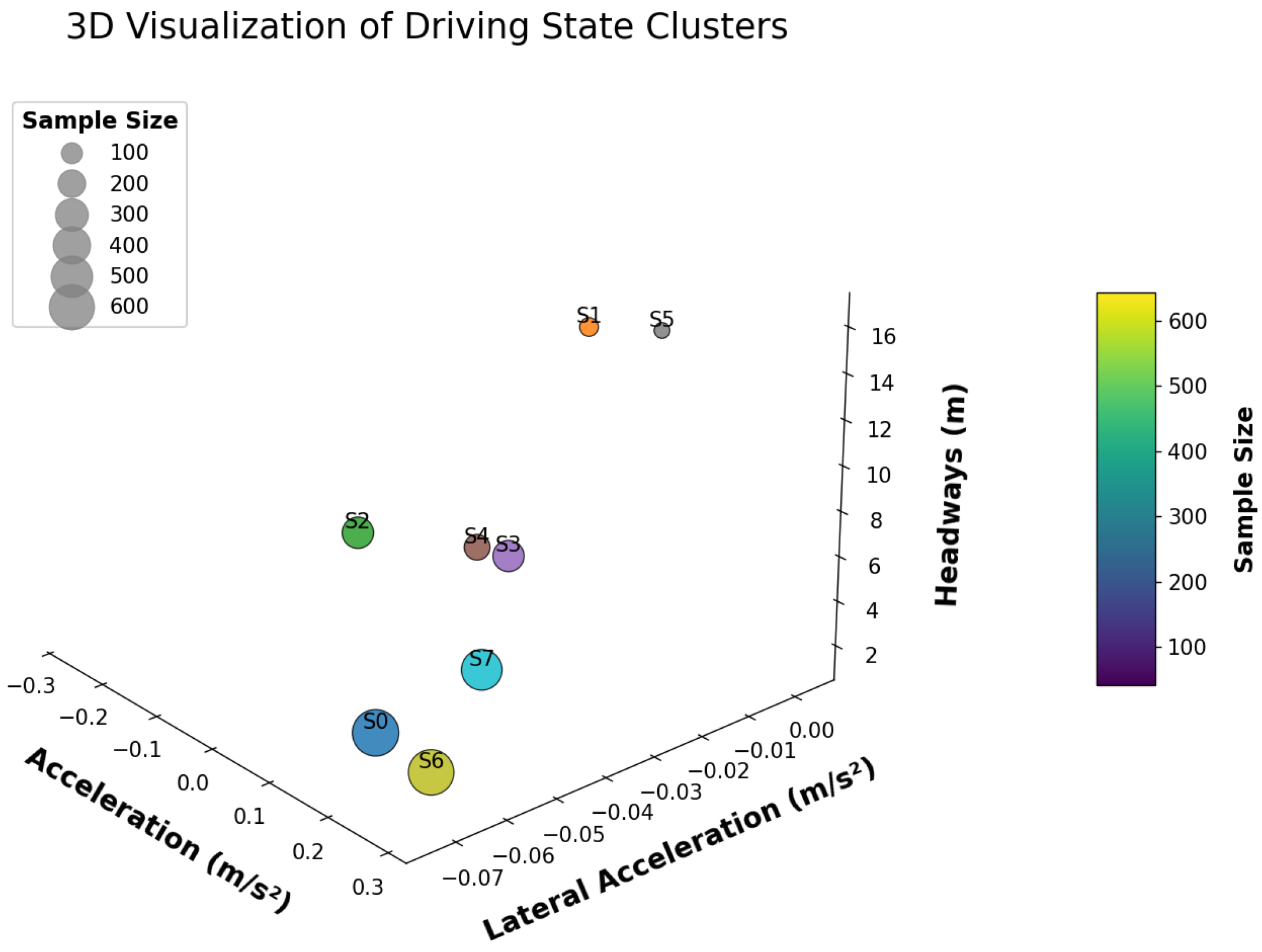
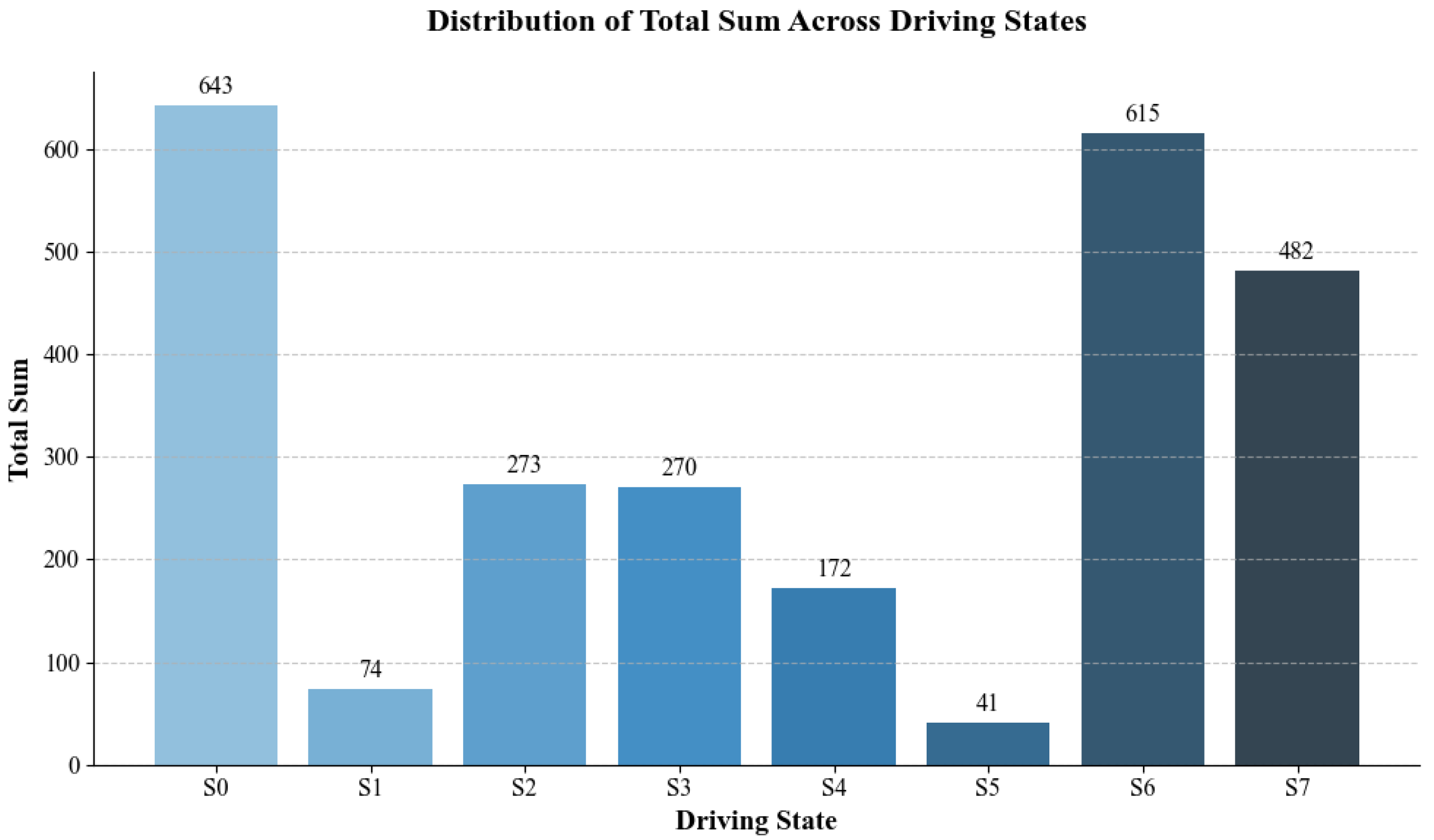
Upon identifying a conflict, we preserved the trajectories leading up to the conflict and systematically traversed the entire dataset, yielding hundreds of statistically significant trajectory records. Subsequently, we clustered the mean values of three features—vehicle speed, headway distance, and acceleration—within a 0.5 s time window to obtain quantitative driving behavior states for that time frame. Furthermore, by converting trajectory data into a sequence of driving states and conducting statistical analysis on this sequence, we derived a co-occurrence matrix. This matrix allowed us to construct the network structure of the conflict process in the dataset, unveiling its intricate complexity through a network graph. To obtain driving states during conflict processes, K-medoids are employed in unsupervised clustering. The ideal number of clusters is then ascertained using the Calinski–Harabasz score. Better clustering is indicated by a higher Calinski–Harabasz score.

On the right side of the illustration, the upper section features an analysis based on Markov theory, while the lower section presents an analysis rooted in complex network theory. These analyses primarily focus on the significant driving behavior states during the conflict process, the stochastic nature of driving behavior transitions, and the overall characteristics of these transitions. On the right side of the illustration, the upper section features an analysis based on Markov theory, while the lower section presents an analysis rooted in complex network theory. These analyses primarily focus on the significant driving behavior states during the conflict process, the stochastic nature of driving behavior transitions, and the overall characteristics of these transitions.

5. Experiments and Results

5.1. Dataset Introduction

DJI’s Aerial Dataset for China Congested Highway and Expressway (AD4CHE) provides detailed natural trajectory data of vehicles on multiple highways and expressways in China [46]. Its frame rate is 30 per second and the final distance error does not exceed 10 cm. It has been used by many scholars for research in areas such as trajectory prediction and traffic safety analysis.

Figure 2a shows a schematic diagram of the overhead shooting of drone, in which over 60 h of videos were captured in different locations using this method. In Figure 2b, a specific road section is shown, and the vehicles obtained through YOLO target recognition show dense traffic and slow vehicle speeds, indicating congestion on the road section.

Table 2. Partial fields of AD4CHE.

Frame	x Velocity	y Velocity	x Acceleration	y Acceleration	dhw	TTC
0	1.98	0.01	0.48	0.02	4.88	−37.65
1	1.98	0.01	0.48	0.02	4.95	−38.23
2	2.00	0.01	0.45	0.00	4.91	−41.08
3	2.01	0.01	0.45	0.00	4.91	−45.00
4	2.03	0.01	0.43	0.00	4.88	−49.09
5	2.04	0.01	0.41	0.00	4.72	−52.27

shows partial records of AD4CHE, which records various data of each frame of the vehicle and encompasses lateral and longitudinal velocity and acceleration (x is longitudinal and y is lateral), headway time and TTC. When TTC is less than 0, it indicates that the distance between the two vehicles is gradually widening.

For conflict identification, when TTC of vehicle is less than 1.5 s, we consider it a conflict [46]. In total, we obtained 257 rear-end conflicts from AD4CHE. We selected acceleration, headway, and lateral acceleration to describe driving behaviors of the rear vehicle. The reason is that they can fully record the following behavior during the conflict process, which was inspired by the car-following model. Finally, we take the moment of conflict occurrence as the zero-time point and then select the trajectory data within 5 s before the conflict [10].

5.2. Driving State Clustering

The optimal clustering number is determined by the Calinski–Harabasz score. Figure 3 shows the Calinski–Harabasz score of different clustering numbers. When the cluster number is 8, the Calinski–Harabasz score is the largest, which indicates that the optimal cluster number is 8. It means that the driving states during the conflict process can be roughly divided into 8 types. Therefore, we set the number of clusters for K-medoids to 8.

From Figure 4, it can be observed that the hierarchy between every cluster is clear, and the samples in each cluster are concentrated, proving that the clustering results are appropriate. Furthermore, the center of each cluster is shown in

Table 3. Cluster center for each driving state.

Driving State	Mean of Acceleration (m/s2)	Mean of Lateral Acceleration (m/s2)	Mean of Headways (m)	Total Sum
S0	0.232	−0.074	4.074	643
S1	−0.044	0.003	11.970	74
S2	−0.264	−0.020	1.521	273
S3	0.135	−0.036	7.107	270
S4	0.181	−0.048	9.096	172
S5	0.221	−0.016	16.354	41
S6	0.289	−0.070	2.846	615
S7	0.255	−0.056	5.517	482

.

In Figure 5, the characteristics of different driving states are significantly different: S2 has the strongest deceleration (median acceleration −0.264 m/s²) and S6 has the most obvious acceleration (0.289 m/s²); S5 has the largest headway (16.35 m) and S2 has the smallest (1.52 m); lateral acceleration is mostly negative, where only S1 is slightly positive (0.003 m/s²). The sample size varies greatly (S0/S6 has more than 600 cases, S5 has only 41 cases), and the box plot distribution is consistent with the cluster center, verifying the distinguishability of the state. S1 has the smallest lateral acceleration fluctuation and the most stable lateral movement. The distribution morphology of the box plots of each state is consistent with the cluster center, verifying the physical distinguishability of the driving state. Among them, the lateral acceleration of the S1 state has the smallest range of change, indicating that its lateral movement is the most stable.

Figure 6 shows the total number of each category, with S0 and S6 having the highest number. These two states are also the closest states to conflict, indicating that most drivers will experience these two states before a conflict occurs.

Figure 7 shows a bar chart of the average longitudinal acceleration, average lateral acceleration, and average distance between vehicles for each clustering state, which clearly shows the value size of each category. Among them, state 3 has the smallest headway and a larger deceleration, indicating that this state is closest to collision.

5.3. Graph Analysis Results

5.3.1. Graph Construction and State Node Transition Analysis

To conduct a detailed study of the conflict process, we can explore the transfer patterns of driving states during the conflict process. Firstly, we need to count the number of transitions between driving states and construct a state transition matrix. We conducted statistics on the state transitions of each driving state sequence. For example, if a sample transitions from state S1 to state S4, add 1 to the position corresponding to the co-occurrence matrix. Then, we obtain the transition matrix between driving states by a co-occurrence matrix that is obtained through statistics, which is shown in

Table 4. Driving state transition co-occurrence matrix.

	S0	S1	S2	S3	S4	S5	S6	S7
S0	437	0	8	0	0	0	120	20
S1	0	47	0	0	27	0	0	0
S2	0	0	194	0	0	0	19	0
S3	2	0	0	171	4	0	0	89
S4	0	0	0	53	118	0	0	0
S5	0	13	0	0	0	28	0	0
S6	32	0	47	0	0	0	426	0
S7	122	0	0	15	0	0	0	321

.

From Table 4, it can be observed that the key nodes (key driving states) are driving states 0, 2, 6, and 7. These key driving states are critical during conflict process because they have a more significant page rank and closeness centrality. During the conflict process, the driving state continues to change, and during the transformation process, it will either go through these critical key states or ultimately stay in them. Further, based on the state transition relationships in the co-occurrence matrix, we indirectly convert the conflict process into a graph structure.

In Figure 8, each node represents a driving state, and the weight of the edge is the number of transitions between two states. Next, we use complex network theory to analyze the graph structure to obtain key nodes (critical driving states) and determine whether the driving states’ transition process satisfies characteristics such as the small-world property.

In Figure 8, a thicker edge indicates more transitions, while a thinner edge indicates fewer transitions. We can also observe the patterns of state transitions. When the vehicle drives in the same state, the edge forms a self-loop. However, when the self-loop is broken and the current driving state transfers to another driving state, the driving state undergoes a sudden change. Here, “Free movement” generally refers to a vehicle moving slowly and steadily behind the vehicle ahead and “Sudden braking” refers to sudden emergency braking while following the vehicle ahead, which is often the result of congestion spreading from the lead vehicle to the rear.

From the thickness of the edges in Figure 6, S3–S7–S0–S6–S2 is the most prominent transition path. After maintaining S6 for a period, some vehicles transfer to S2, which is a state of emergency braking.

In this path, the headway continuously decreases. As the headway gradually decreases from 7 m to less than 1.5 m, it will likely transfer to a more dangerous driving state 2. This situation is often caused by incorrect acceleration behavior in the early stage (such as aggressive acceleration, cutting in, etc.), which leads to rapid deceleration in the later stage. Figure 9 shows the changing trends of the three variables in the state. It can be seen that as the front of the vehicle continues to decrease, the acceleration of the vehicle first increases and then decreases, and there is a trend of turning the steering wheel.

To prevent conflicts, this state transition path can be blocked in advance by always maintaining a headway of at least 6 m when following the front vehicle in a congested section on the highways.

5.3.2. Graph Node Importance and Small-World Characteristics

Through graph structure analysis, some key nodes (important driving states) and important state transition patterns can be obtained.

Table 5. Closeness centrality and page rank of driving status nodes.

	Closeness Centrality	Page Rank
S0	0.50	0.18
S1	0.14	0.07
S2	0.39	0.17
S3	0.44	0.11
S4	0.39	0.10
S5	0.00	0.04
S6	0.39	0.21
S7	0.44	0.13

shows the graph network characteristics of each driving state node.

Figure 10 shows the closeness centrality and page rank of each state, where S0, S2, and S3 are the states with higher closeness centrality and page rank, indicating that these states are crucial in the conflict process.

In addition, the state transition graph of the conflict process does not have a small-world property. So, the following conclusions can be inferred: the path of driving state transitions is lengthy, suggesting that multiple driving states must be experienced before reaching the final conflict. This indicates a slow transition between driving states, leading drivers unable to perceive dangerous headway early enough. Prior to the final conflict, the vehicle consistently remains in a self-loop state before abruptly entering the conflict state.

5.4. Markov Characteristic Analysis Results

Furthermore, we transform the driving state transition matrix (Table 4) into a state probability transition matrix, as shown in

Table 6. States’ probability transition matrix.

	S0	S1	S2	S3	S4	S5	S6	S7
S0	0.747	0.000	0.013	0.000	0.000	0.000	0.205	0.034
S1	0.000	0.635	0.000	0.000	0.365	0.000	0.000	0.000
S2	0.000	0.000	0.911	0.000	0.000	0.000	0.089	0.000
S3	0.007	0.000	0.000	0.643	0.015	0.000	0.000	0.335
S4	0.000	0.000	0.000	0.310	0.690	0.000	0.000	0.000
S5	0.000	0.317	0.000	0.000	0.000	0.683	0.000	0.000
S6	0.063	0.000	0.093	0.000	0.000	0.000	0.844	0.000
S7	0.266	0.000	0.000	0.033	0.000	0.000	0.000	0.701

.

Next, we calculate the power of this state transition matrix. After the 39th time, the matrix gradually reaches a stable state. The stable matrix is shown in

Table 7. Matrix under power stability.

	S0	S1	S2	S3	S4	S5	S6	S7
S0	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S1	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S2	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S3	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S4	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S5	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S6	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150
S7	0.1198	0.0000	0.4500	0.0015	0.0001	0.0000	0.4100	0.0150

.

This indicates that the driving state transition process during the conflict process corresponds to the Markov property, and the conflict process can be described using a Markov chain. Furthermore, when the power of the matrix reaches stability, it ultimately remains in the four key driving states analyzed above, i.e., 0, 2, 6, and 7, and it is most likely to stay in driving states 2 and states 6. And the calculated $p$ value of the chi square statistic is close to 0, which is much smaller than the given error probability $\alpha$ of 0.05. We can further reject the zero hypothesis; the conflict process satisfies Markov properties. This indicates that the driving state eventually tends to stabilize during the conflict process, and the driving state is predictable.

6. Conclusions

In this paper, a framework based on graph theory was proposed to analyze the time-varying patterns of time-series variables. And a fine-grained and detailed analysis of the rear-end conflict process on the congested highway sections was conducted using this framework. Specifically, we based our analysis on the micro-trajectory time series in the conflict process and used complex network theory to analyze the driving behavior switch time-varying patterns during the conflict process. The main results are as follows:

• The transition of driving behavior states during the conflict process conforms to the Markov property, which means that the driving behavior during the conflict process is predictable and can be altered.
• The network of the driving behavior state transition graph does not conform to the small-world property. This means that before the final conflict occurs, high-risk vehicles always continuously switch states between a few states or remain in a self-looping state until they abruptly transition into the final conflict state.
• On congested highway sections, rear-end collisions often transition to a conflict state along a fixed path within the graph structure, indicating that the majority of conflicts stem from similar causes.

Based on the careful analysis of traffic conflicts under congested traffic flow, these conclusions can be used to develop targeted vehicle auxiliary warning systems. In the future, research on vehicle collision avoidance control based on this process analysis is worth further exploration.