Group Stable Matching Problem in Freight Pooling Service of Vehicle–Cargo Matching Platform

Abstract

With the continuous advancement of the Internet and information technologies, the capacity for development and integration of vehicle and cargo resources has been significantly enhanced, driving the rapid emergence of vehicle–cargo matching platforms. Serving as critical intermediaries between vehicle owners and cargo owners, vehicle–cargo matching platforms effectively address key challenges in traditional logistics, such as low matching efficiency and information asymmetry. As a result, they significantly improve the intelligence and precision of logistics resource allocation. However, at the current stage, vehicle–cargo matching platforms rarely promote freight pooling services, leading to resource underutilization. Due to the freight pooling matching problem involving the combination and allocation of multiple vehicle owners and cargo owners, which is highly complex, few scholars have conducted research on such issues. The lack of coordinated optimization in matching models may result in inefficiencies, and the limited consideration of individual user preferences can lead to low user satisfaction. Therefore, this paper focuses on the freight pooling matching problem in vehicle–cargo matching platforms. To improve matching efficiency and fully consider user preferences, the theory of stable matching is introduced into the freight pooling matching problem. It defines the concepts of combination preferences and group stability based on combination preferences, establishes a group stable matching model for the freight pooling business of vehicle–cargo matching platforms, and verifies the stability of the model through theoretical proof. Since this model is a mixed-integer linear programming model with relatively few decision variables but a large number of constraints, this paper introduces the cutting-plane algorithm. Based on the characteristics of the problem, the algorithm is improved by removing ineffective constraints and only using key constraints, significantly reducing computational complexity, optimizing the solving process, and greatly improving the model’s solution efficiency. This approach aligns well with the characteristics of the vehicle–cargo freight-pooling matching model. The research results indicate that the group stable matching model significantly improves platform revenue, vehicle owners’ profits, and cargo owners’ satisfaction across various supply and demand scenarios. Additionally, the cutting-plane algorithm reduces computation time by 97% and decreases the number of constraints during the solving process by 99%. The stable matching theory and solution algorithm proposed in this paper can provide users with precise matching schemes, significantly improving matching efficiency, user satisfaction, platform revenue and platform competitiveness. It demonstrates high innovation and practical application value.

1. Introduction

In recent years, with the rapid development of the Internet and the continuous growth of economic demand, the freight market has been facing significant challenges in terms of freight capacity and efficiency. The information asymmetry between vehicles and cargoes has led to a significant waste of public transportation resources. For example, in the vast and highly fragmented road freight market, around 90% of participants are individual operators who lack complete information, making it difficult for them to find suitable orders [1]. As a result of limited access to return-trip information, most drivers return with empty vehicles, leading to high empty-load and return-empty rates, which in turn causes a sharp decline in their earnings [2].

In response to this issue, since 2015, a large number of vehicle–cargo matching platforms have emerged, such as Huolala, Yunniao, 58 Suyun, Yunmanman, Gogovan, and Trukkin, continuously attracting more platforms to enter this field. The core role of vehicle–cargo matching platforms is to serve as a bridge between vehicle owners and cargo owners, reducing and eliminating the information asymmetry between vehicles and cargoes. These platforms coordinate transportation arrangements for both parties, providing effective matching solutions to ensure that order allocation proceeds in an orderly manner at the right time and place [3,4]. Despite the large number of vehicle–cargo matching platforms, few have managed to truly survive and thrive. This is because these platforms face a range of new challenges in the process of integrating vehicle and cargo information, including but not limited to the need to further improve matching efficiency, the highly competitive nature of the freight market, and the acceptability of matching solutions [5,6]. Two particularly prominent challenges are that the platform’s matching efficiency still needs further improvement, and it must also meet the deeper needs of both vehicle owners and cargo owners. Therefore, how to improve vehicle–cargo matching efficiency and meet users’ deeper needs has become an urgent problem that every vehicle–cargo matching platform must solve in order to enhance its competitiveness.

Vehicle owners and cargo owners submit information related to their vehicles and cargoes to the vehicle–cargo matching platform in order to seek urban, intercity, or long-distance delivery services. For urban delivery services with transportation distances less than 50 km, due to the short distance and low transportation costs, as well as the high frequency of departures, the impact of short-distance empty driving and price fluctuations on cargo owners and drivers is relatively minor when submitting freight requests or accepting jobs. In contrast, for intercity delivery services with transportation distances between 50 and 500 km, as well as long-distance delivery services exceeding 500 km, the transportation distances are longer, costs are higher, and departures occur only once a day or even once every 2–5 days to complete the delivery. Therefore, cargo owners have certain demands regarding transportation price discounts and improvements in delivery timeliness. On the driver’s side, after completing a delivery, the high cost of long-distance empty driving means drivers spend a considerable amount of time searching for cargo, greatly reducing the empty driving rate and increasing their income. Vehicle–cargo matching platforms offer freight pooling services for long distance intercity delivery needs, which helps cargo owners save costs, increases vehicle utilization, and allows drivers to earn extra income. However, through comparative analysis of the operating models of numerous vehicle cargo platforms, it has been found that most platforms primarily offer truckload services, and freight pooling services for long distance transport have not been well promoted. Against this backdrop, most scholars have also focused their research on the more common truckload services provided by vehicle–cargo matching platform [7,8].

As a platform for publishing vehicle and cargo information, vehicle–cargo matching platform allow cargo owners and vehicle owners to submit their information. While waiting for matching results, both cargo owners and vehicle owners can view information about available carriers. Therefore, when the platform provides matching results, both cargo owners and vehicle owners may be motivated to reject the results in hopes of finding better matches. This not only affects matching efficiency but also leads to user dissatisfaction and a decline in platform revenue. To improve matching efficiency, a stable matching mechanism needs to be introduced during the matching process to ensure that, under the premise of voluntary acceptance by both vehicle owners and cargo owners, the platform can coordinate and optimize the vehicle–cargo matching scheme. The theory of two-sided stable matching was proposed in 1962 by Gale and Shapley in the context of problems such as marriage matching and college admissions. It aims to enable a third-party intermediary in a two-sided matching market to find a stable matching scheme which contains no “blocking pairs”. A blocking pair refers to a pair of individuals who are not matched with each other in the current scheme but could both benefit by rejecting the current matches and matching with each other instead [9]. If a stable matching scheme without any blocking pairs is found, none of the individuals on either side of the match will have an incentive to reject the scheme [10].

In summary, this paper focuses on the freight pooling matching problem in vehicle–cargo matching platforms for intercity and long-distance transportation services. It fully considers user preferences, introduces stable matching theory into the freight pooling matching problem, defines the concept of group stability based on combination preferences, and establishes the corresponding model. Additionally, an improved algorithm is proposed to enhance matching efficiency. The main contributions are as follows:

(1)

We introduced stable matching theory into the freight pooling matching problem on vehicle–cargo matching platforms, thereby improving platform matching efficiency, user satisfaction, and platform competitiveness. In the freight pooling transportation service scenario on vehicle–cargo matching platforms, cargo owners and vehicle owners submit relevant information such as transportation service requirements and carrying capacity to the platform. Within the carrying capacity range, a vehicle owner can provide transportation services to multiple cargo owners, with each cargo owner’s goods being allowed to be carried by only one vehicle owner. This constitutes a one-to-many stable matching problem under the vehicle–cargo matching platform.

(2)

Based on the characteristics of the freight pooling stable matching problem on vehicle–cargo matching platforms, we define the concepts of combination preferences and group stability based on combination preferences, establish a group stable matching model for the freight pooling business on vehicle–cargo matching platforms, and verify the stability of the model through theoretical proof.

(3)

Based on the characteristics of the model, an improved cutting-plane algorithm is designed to solve the model. The group stable matching model for the freight pooling business on vehicle–cargo matching platforms established in this paper is a mixed-integer linear programming model. Since the model is an NP-hard problem, the number of constraints reaches $O\left(m·2^{2n}\right)$, which severely impacts the solution efficiency of the group stable matching problem for the freight pooling business on vehicle–cargo matching platforms. At the same time, the model has only m⋅n decision variables, which is much smaller than the number of constraints, indicating that the majority of the constraints are ineffective. Therefore, this paper introduces the cutting-plane algorithm and improves it for the specific problem at hand. This modification allows for the removal of most ineffective constraints during the solving process, using only a subset of the model’s constraints to obtain the same solution as the original model. This significantly improves solving efficiency and is highly suited to the characteristics of the model.

(4)

Finally, through simulation experiments, we validate the advantages of the group stable matching model proposed in this paper over traditional matching models from the perspectives of the platform, vehicle owners, and cargo owners. Additionally, we verify the efficiency improvement of the cutting-plane algorithm in solving the group stable matching problem for vehicle–cargo matching platforms. The results show that this method has strong practicality and promotion value, as it can accurately push matching solutions for vehicle–cargo matching platforms in real-world operations, enhancing the platform’s matching efficiency and core competitiveness.

The remainder of this paper is organized as follows: Section 2 reviews the relevant literature. Section 3 describes the freight pooling matching problem on vehicle–cargo matching platforms, provides the definition of group stable matching, and establishes the relevant mathematical model along with the algorithm design. Section 4 provides numerical experiments and analysis to validate the proposed approach. Section 5 concludes the paper and discusses potential future extensions.

2. Literature Review

In light of the research content and methodology of this study, this section provides a brief overview of the existing literature from two perspectives: first, studies related to vehicle–cargo matching platforms, and second, research on stable matching theory. In addition, the final section clarifies the research gap by comparing this paper with existing studies.

2.1. Vehicle and Cargo Matching Platforms

As a critical component in the field of road freight transportation, vehicle–cargo matching directly impacts logistics efficiency and cost control. Research in this area has evolved from traditional intermediary-based matching to intelligent platform-based matching, progressively incorporating various technological approaches such as optimization algorithms, game theory, and machine learning.

Before the emergence of internet-based platforms, freight matching was primarily carried out by intermediaries or logistics hubs. Luisa et al. [11] focused on delivery tasks within fixed working days and employed the Lagrangian algorithm to solve the routing and scheduling problem, achieving transportation cost minimization. Kim et al. [12] developed a distributed scheduling model aimed at maximizing drivers’ profits and employed Lagrangian relaxation and subgradient methods for solution, demonstrating the model’s robustness under practical parameter fluctuations. Zhang and Wang [13] approached the problem from a multi-objective optimization perspective, integrating multiple indicators such as vehicle utilization and service level, and utilized a gray clustering method to evaluate and make decisions on loading schemes.

From an operational perspective, route optimization and cost control are the core objectives of matching platforms. Klundert and Otten [14] proposed a multi-model framework to address transportation optimization problems in freight exchange, achieving improved utilization and cost reduction. Sun et al. [3] developed a nonlinear mixed-integer programming model and employed the Expectation-Maximization algorithm to optimize vehicle allocation strategies, demonstrating the effectiveness of the algorithm in cost control. Badica et al. [4] focused on the efficient management of freight resource-sharing platforms and proposed a system architecture based on constraint logic programming, which can effectively generate feasible transportation routes and improve resource scheduling efficiency. Li et al. [15] further integrated matching, pricing, and route selection into a joint optimization strategy, proposing differentiated city-specific pricing mechanisms and tiered charging schemes, which effectively reduce platform operating costs and user waiting costs. Such studies emphasize resource utilization and cost control but do not identify the fundamental causes for improving platform efficiency.

With the development of machine learning, researchers have begun to focus on the intelligence of prediction and decision-making problems in vehicle–cargo matching. Kim et al. [16] proposed a deep learning-based cargo recommendation system. By creating a freight transaction dataset, they used natural language processing and text mining techniques to classify cargo categories and integrated external transportation distance data to reduce failed contracts on freight intermediary platforms and provide personalized services. The system aims to improve the efficiency of the freight market and enhance the long-term profit structure. Mallick et al. [5] modeled vehicle–cargo matching as a Markov decision process and employed the Neural Fitted Q-iteration algorithm to provide dynamic bidding decision support for transportation service providers, significantly enhancing the overall platform revenue. Deng et al. [17] proposed a vehicle–cargo matching probability prediction model based on static and dynamic Bayesian networks, incorporating temporal variations and business priorities, and implemented the prediction using a recursive algorithm. Meanwhile, Sganthi et al. [18] integrated blockchain and deep learning technologies to ensure the security and decentralization of the vehicle–cargo matching process, providing secure and trustworthy support for intelligent transportation systems. These studies demonstrate that prediction and learning techniques can significantly enhance the platform’s capability to handle uncertainties and dynamic changes. Chen et al. [19] addressed the problem of pallet loading of goods and heterogeneous vehicle allocation in less-than-truckload logistics. They proposed a two-stage hybrid heuristic algorithm: the first stage optimizes the three-dimensional loading layout of goods, and the second stage performs online matching of pallets to vehicles, considering time windows and cost control. Experimental results demonstrate that the method achieves 90% loading efficiency and 95% vehicle utilization and significantly reduces transportation costs, indicating strong practical applicability. However, existing intelligent algorithms often focus on improving accuracy while neglecting model interpretability and user acceptance.

Internet platforms have driven the digitization of freight information and the transformation of matching mechanisms, making matching efficiency and user behavior modeling key research focuses. Janssen and Verbraeck [20] employed an agent-based simulation approach to conduct both quantitative and qualitative comparative analyses of traditional matching mechanisms between vehicle owners and cargo owners versus internet-based electronic matching mechanisms in the transportation market. Their findings indicate that managing the transportation market through internet electronic intermediaries, which significantly reduce transaction time and costs, has gained favor among vehicle owners and cargo owners, making it the most effective method for managing their matching in the transportation market. Wang et al. [6] addressed the issues of information asymmetry and low matching efficiency in the freight market by employing prospect theory to characterize the discrepancies between the expected and actual values of both vehicle owners and cargo owners. They analyzed the loss aversion responses of the supply and demand sides in the freight market and used an evolutionary game model for solution. The study found that the platform’s service level, users’ initial acceptance probability, and waiting costs have positive and significant effects on the platform’s matching efficiency. Feng et al. [21] proposed a two-stage vehicle–cargo matching model for truck alliances and drop-and-hook transportation tasks, aiming to construct a comprehensive matching degree based on multiple criteria. They solved the model using a genetic algorithm. The results showed that truck alliances can effectively improve the matching between demand and capacity, thereby optimizing logistics resource allocation. Although this research enriches the design of matching mechanisms, most methods assume idealized user preferences and do not consider actual user demands, limiting the model’s adaptability in practical deployment.

2.2. Stable Matching Theory

Stability matching theory was first proposed by Nobel Prize winners Gale and Shapley in their 1962 paper titled “College Admissions and the Stability of Marriage” [9]. By studying the matching between two groups (such as males and females), they proposed an algorithm for solving stable matching and proved the existence of a stable matching solution, where no pair of participants can improve their satisfaction by swapping partners. The contributions of Gale and Shapley not only provided a method for solving the stable marriage problem, but their theoretical framework also has broad applications in various practical problems. Among them, one-to-one stable matching and one-to-many stable matching are two common matching models. The main difference between them lies in the number of matching participants and the definition of stability. In one-to-one stable matching, each member of one group can only be matched with one member from the other group; in one-to-many stable matching, a member of one group can be matched with multiple members from the other group. Roth et al. [22] established a mathematical model for one-to-one stable matching using mathematical programming techniques and formulated stability constraints and provided a simple proof of their model. Iwama et al. [23] and others studied the marriage stability matching problem under incomplete preferences and weak stability, proving that the marriage stability matching problem remains NP-hard even under incomplete preferences and weak stability. Wang et al. [24] applied the concept of approximate stability to study the dynamic carpooling problem, establishing stable and approximately stable mathematical programming models. These models ensure a slight decrease in system performance while significantly improving the stability of the carpooling system. Delorme et al. [25] and others studied the one-to-one orphan adoption problem and residency assignment problem under incomplete preferences and weak stability and provided the corresponding mathematical programming models. Roth and Gale [10,26,27], around 1985, systematically studied the college admissions problem and the marriage problem using game theory tools and proved that the two problems differ in their theoretical properties. Alvin Roth, by improving and extending the classic Gale–Shapley algorithm, proposed an algorithm specifically designed for medical matching. He demonstrated, through real-world cases, how to effectively match medical school graduates with hospital positions. Baïou et al. [28] proposed a study on the college admission problem and pointed out that it belongs to the category of one-to-many stable matching. They established a stable matching model for one-to-many matching.

The fairness and truthfulness of stable matching are also important considerations in this line of research. Fairness typically refers to the equitable treatment of all participants in the matching process, ensuring that no party is disadvantaged or treated unjustly. Sethurama et al. [29] characterizes a stable admission polyhedron using a system of linear inequalities, which shows that assigning each agent their “median” choice among all stable partners results in a stable match, which can be viewed as a “fair” compromise. Klimentova et al. [30] proposed a new fair integer programming model for multi-agent kidney exchange program (mKEP) in 2021. Extensive computational testing has shown that mKEPs have advantages over standalone KEPs in terms of potential increases in the number of migrations and consistently achieves more stable results than methods that do not use memory. The authenticity of stable matching focuses on whether the matching parties will provide their own real preferences. Teo et al. [31] proposed the optimal deception strategy of individuals in G-S algorithm and found that the party accepting the invitation in the G-S algorithm could benefit by lying about its preference, but in the example, it was found that in most cases, submitting the real preference list was still the best choice. Ehlers and Lars [32] studied women’s preference list truncation strategies in marriage matching problems in 2008, suggesting that women may gain by truncating their true preference list.

Dynamic matching is also one of the hot research issues at home and abroad. Xu et al. [33] designed matching algorithms for bilateral dynamic service market based on rematching and repair matching, respectively, in which only repairing the matching part affected by dynamic changes can better maintain the consistency of matching, and the generated matching solution is also stable. Alimudin and Ishida [34] studied stable marriages with dynamic preferences, where individuals can change their preferences at any stage, and found a mechanism to modify the original matching scheme at minimal cost when individual preferences change, rather than restarting the matching process. Kurino [35] introduced a dynamic framework to analyze bilateral matching interactions that occur repeatedly over time, proposed a dynamic concept of trusted group stability, and demonstrated that achieving an optimal stable match in each period is trusted group stable. Doval [36] proposed a new dynamic stability for two-sided one-to-one dynamic matching markets, in which matching opportunities arrive over time, not all individuals can match at the same time, and the expected returns of individuals maintaining mismatches are not independent of the matching results of other individuals of the same period. Considering dynamic stability ensures that individuals do not strategically delay their matching time, Sperisen and Wiseman [37] developed a stable matching model for an uncoordinated labor market, taking into account the dynamic incentives that matching outcomes impose on individuals, i.e., a firm cannot credibly threaten to fire an employee who is productive even with low effort, and proposed a new interpretation of pay for performance: The promise of higher wages increases the company’s willingness to fire, which in turn indirectly increases the incentive for employees to work hard.

In addition, the theory of bilateral stable matching also provides inspiration for some other fields of research. Gu et al. [38] found that stable matching theory can improve the performance of spectrum resource allocation in wireless networks. Pham et al. [39] applied the stable matching theory to server computing resource allocation, and the performance of their designed algorithm is close to that of the centralized heuristic algorithm, with a small optimality gap. Fenoaltea et al. [40] found the application of the marriage stability matching problem in the process of finding the ground state with the lowest energy of the system. In the case of negotiations between two participants, the stable solution and the ground state agree 78% of the time.

2.3. Research Gap

Based on the summary of the above research findings, the differences and contributions of this paper compared to existing studies are as follows:

(1)

Due to the high complexity of the freight pooling business on vehicle–cargo matching platforms, which involves matching the cargo of multiple cargo owners with vehicle owners, existing research predominantly focuses on the full-load business model of vehicle–cargo matching platforms. Research on the freight pooling business model, which can effectively improve transportation efficiency and vehicle utilization, is relatively scarce. This paper focuses on the freight pooling business on vehicle–cargo matching platforms, aiming to fill this research gap.

(2)

A review of the literature reveals that existing research predominantly focuses on pricing, route design, or the processing of basic information on vehicle–cargo matching platforms. However, the matching problem between vehicle owners and cargo owners on vehicle–cargo matching platforms is a critical task. It serves as a precursor to vehicle route planning and vehicle loading problems. Only by accurately matching vehicle owners with cargo owners can the matching efficiency of the platform be fundamentally improved. This paper focuses on the matching problem between vehicle owners and cargo owners in the freight pooling business of vehicle–cargo matching platforms. It fully considers user preferences and defines the concept of composite preferences, allowing the matching results to enhance user satisfaction.

(3)

While stable matching theory has been widely applied in areas such as one-to-one marriage stability matching, one-to-many admissions, medical resource allocation, and carpooling, research on one-to-many matching in the context of the freight pooling business on vehicle–cargo matching platforms remains a gap in the literature. This is primarily due to the fact that, compared to one-to-many stable matching problems with quantity constraints on one side, such as in university admissions [31] and medical resource allocation [33], the one-to-many stable matching problem in the freight pooling business of vehicle–cargo matching platforms involves quantity constraints on both sides (vehicle capacity constraints on the vehicle owner side and cargo capacity transportation demands on the cargo owner side). This significantly increases the complexity of the problem and the difficulty of solving it. To address this issue, this paper defines the concept of group stability based on composite preferences and establishes a group stable matching model for the freight pooling business on vehicle–cargo matching platforms. The stability of the model is then verified through theoretical proof.

(4)

Since the group stable matching model for the freight pooling business on vehicle–cargo matching platforms established in this paper is a mixed-integer linear programming model with relatively few decision variables but a large number of constraints, it significantly affects the solution efficiency of the group stable matching problem in the freight pooling business. This paper introduces the cutting-plane algorithm and improves it based on the characteristics of the problem. By utilizing only a subset of the constraints from the model, the algorithm achieves the same solution as the original model, significantly enhancing solution efficiency. This not only provides accurate matching solutions for vehicle owners and cargo owners but also effectively improves matching efficiency.

3. Problem Description, Model Setup, and Algorithm Design

This section will provide a detailed explanation of the group stable matching problem in the freight pooling business on vehicle–cargo matching platforms. It will define the concept and model of group stability and offer a thorough proof of the model’s stability. Finally, the section will present the solution algorithm and improvement strategies in detail.

3.1. Problem Description

This section will provide a detailed introduction to the specific operation of the freight pooling stability matching problem on vehicle–cargo matching platform from the perspectives of vehicle owners, cargo owners, and the platform. Based on the characteristics of the problem, the concept of stability in this context will also be defined.

From the perspective of the cargo owner, the cargo owner reports the required transportation capacity of their goods to the vehicle–cargo matching platform, seeks a suitable vehicle owner traveling the same route to transport their goods to the destination, and pays the vehicle owner a fee. In addition, each cargo owner has unique preferences for different logistics attributes: some may prioritize transportation time, while others may place more emphasis on quality assurance. Cargo owners also need to provide the platform with their respective levels of importance for these logistics’ attributes.

From the vehicle owner’s perspective, each vehicle owner can be matched with multiple cargo owners simultaneously, but the total matched cargo volume must not exceed the vehicle’s maximum carrying capacity. Upon completing the transportation tasks, the vehicle owner can receive payment provided by the cargo owners from the platform. Vehicle owners always aim to maximize their total earnings. Although all vehicle owners participating in the matching have the same origin and destination, they still possess different characteristics. For example, based on each vehicle owner’s schedule and habits, factors such as transportation time and quality assurance during the journey vary among different vehicle owners.

From the platform’s perspective, its role is to reasonably match vehicle owners and cargo owners and to earn revenue by taking a fixed percentage commission from the payments. When formulating a matching scheme, the platform needs to consider whether the proposed scheme will be accepted by both vehicle owners and cargo owners. If either party rejects the matching scheme for their own benefit, the platform may suffer a loss of revenue as a result. To ensure stable matching, the platform needs to accurately capture the preferences of both parties. Therefore, vehicle owners are required to provide information on their transportation time and quality assurance attributes, while cargo owners need to specify their level of importance for these two attributes to describe their preferences for vehicle owners.

The notations and their physical meanings used in this paper are shown in

Table 1. Notations and physical meanings.

Type	Notation	Physical Meaning
Platform	$\mathsf{\partial }$	The commission rate that the platform takes from the payment made by the cargo owner to the vehicle owner
Vehicle owner	$m$	Number of vehicle owners
	$h_i$	The $i$-th vehicle
	$H$	Set of vehicle owners, $H={\left\{h_i\right\}}_{i=1}^m$
	$c_i$	The maximum transportation capacity of vehicle owner $h_i$’s vehicle
	$o_i^1$	The transportation time rating of vehicle owner $h_i$, $o_i^1\in \left(\mathrm{0,1}\right)$; the closer it is to 1, the better the rating
	$o_i^2$	The quality assurance rating of vehicle owner $h_i$, $o_i^2\in \left(\mathrm{0,1}\right)$; the closer it is to 1, the better the rating
Cargo owner	$n$	Number of cargo owners
	$r_j$	The $j$-th vehicle
	$R$	Set of cargo owners, $R={\left\{r_j\right\}}_{j=1}^n$
	$s_j$	The transportation capacity required by the cargo owner $r_j$
	$P_j$	The payment that cargo owner $r_j$ is willing to offer
	$p_j$	The payment that a vehicle owner receives when matched with cargo owner $r_j$, $p_j=\left(1-\mathsf{\partial }\right)P_j$
	${\gamma }_j^1$	The importance level that cargo owner $r_j$ assigns to the $o_i^1$ attribute of the vehicle owner, ${\gamma }_j^1\in \left(\mathrm{0,1}\right)$
	${\gamma }_j^2$	The importance level that cargo owner $r_j$ assigns to the $o_i^2$ attribute of the vehicle owner, ${\gamma }_j^2=1-{\gamma }_j^1$
	${\mathsf{\Gamma }}_{h_i}^{\left[r_j\right]}$	The satisfaction level of cargo owner $r_j$ with vehicle owner $h_i$, ${\mathsf{\Gamma }}_{h_i}^{\left[r_j\right]}={\gamma }_j^1·o_i^1+{\gamma }_j^2·o_i^2$
Vehicle–cargo matching	$\mu$	A one-to-many relationship between elements of the vehicle owner set $H$ and the cargo owner set $R$.

.

Here, $\mu$ as a mapping must satisfy that $\mu \left(r_j\right)=h_i$ if and only if $r_j\in \mu \left(h_i\right)$, and for all $\forall h_i\in H$, the capacity constraint $c_i\ge {\sum }_{r_j\in \mu \left(h_i\right)}^j{s}_j$ holds. In other words, $\mu$ represents a matching relationship where each vehicle owner is matched with one or more cargo owners, and the total cargo volume matched to a vehicle owner does not exceed their maximum carrying capacity.

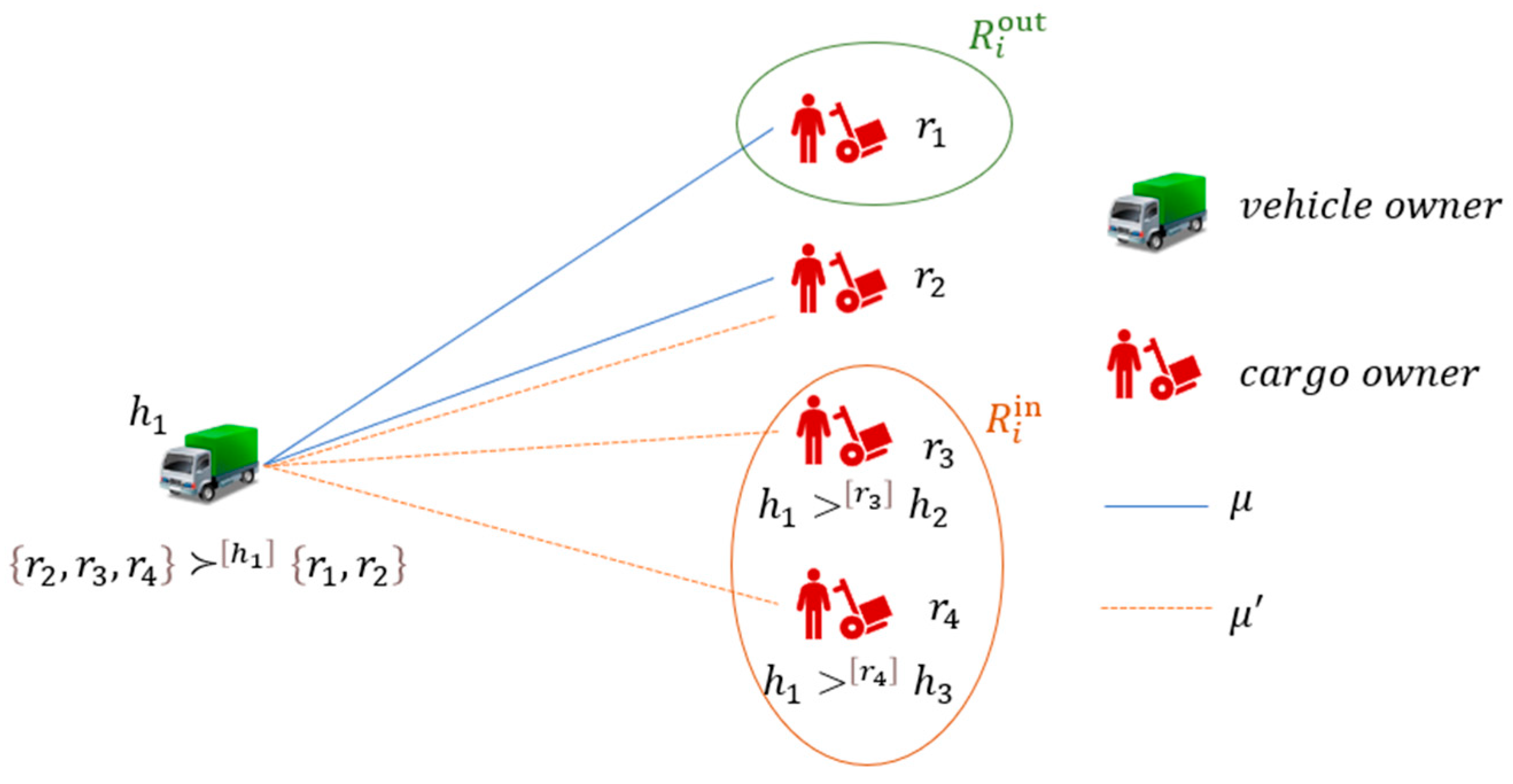
3.2. Group Stability Definition

In the freight pooling matching problem on vehicle–cargo matching platforms, each cargo owner entrusts their cargo to a single vehicle owner for transportation, while each vehicle owner can transport cargoes for multiple cargo owners simultaneously. Cargo owners rank vehicle owners in descending order based on their satisfaction levels to form preference lists. Vehicle owners compare different combinations of matched cargo owners, favoring the combinations that yield higher total earnings. In this paper, such preferences of a vehicle owner over different sets of cargo owners are defined as combinatorial preferences.

The cargo owner’s preference for vehicle owners is represented as follows:

$${\mathsf{\Gamma }}_{h_{i1}}^{\left[r_j\right]}>{\mathsf{\Gamma }}_{h_{i2}}^{\left[r_j\right]}\iff h_{i1}{>}^{\left[r_j\right]}{h}_{i2}$$

(1)

$${\mathsf{\Gamma }}_{h_{i1}}^{\left[r_j\right]}={\mathsf{\Gamma }}_{h_{i2}}^{\left[r_j\right]}\iff h_{i1}{=}^{\left[r_j\right]}{h}_{i2}$$

(2)

$${\mathsf{\Gamma }}_{h_{i1}}^{\left[r_j\right]}\ge {\mathsf{\Gamma }}_{h_{i2}}^{\left[r_j\right]}\iff h_{i1}{\ge }^{\left[r_j\right]}{h}_{i2}$$

(3)

Equation (1) indicates that cargo owner $r_j$ strictly prefers being matched with vehicle owner $h_{i1}$ over $h_{i2}$. Equation (2) indicates that cargo owner $r_j$ is indifferent between being matched with $h_{i1}$ and $h_{i2}$. Equation (3) indicates that cargo owner $r_j$ weakly prefers being matched with $h_{i1}$ over $h_{i2}$.

Similarly, the vehicle owner’s preference for cargo owners is represented as follows:

$${\sum }_{r_j\in R_2}^j{p}_j>{\sum }_{r_j\in R_1}^j{p}_j\iff R_2{>}^{\left[h_i\right]}{R}_1$$

(4)

$${\sum }_{r_j\in R_2}^j{p}_j={\sum }_{r_j\in R_1}^j{p}_j\iff R_2{=}^{\left[h_i\right]}{R}_1$$

(5)

$${\sum }_{r_j\in R_2}^j{p}_j\ge {\sum }_{r_j\in R_1}^j{p}_j\iff R_2{\ge }^{\left[h_i\right]}{R}_1$$

(6)

Here, $R_1,R_2\subseteq R$ and $R_2{>}^{\left[h_i\right]}{R}_1$ mean that vehicle owner $h_i$ prefers serving the group of cargo owners in $R_2$ over those in $R_1$. Under combinatorial preferences, vehicle owners no longer rank individual cargo owners according to some rule; instead, they evaluate which combinations of cargo owners within their capacity constraints will yield a higher total payment.

In addition, both vehicle owners and cargo owners consider being matched as strictly better than not being matched at all, that is,

$$\begin{array}{cc}{R}_j{>}^{\left[h_i\right]}\varnothing ,& \forall h_i\in H, \forall R_j\in R\end{array}$$

(7)

$$\begin{array}{cc}{h}_i{>}^{\left[r_j\right]}\varnothing ,& \forall h_i\in H, \forall r_j\in R\end{array}$$

(8)

After obtaining the preferences of vehicle owners and cargo owners, the group stability based on combinatorial preferences is defined as follows:

Definition 1.

For a given matching $\mu$, if there exists a subset $U$ and another matching ${\mu }^{\prime }$ such that $\exists \left(U,{\mu }^{\prime }\right)$ satisfies conditions (9)–(13), then $U$ is called a blocking coalition of matching $\mu$, and ${\mu }^{\prime }$ is referred to as the blocking scheme of $U$ under $\mu$.

$$U\subseteq H\cup R,U\cap H\ne \varnothing ,U\cap R\ne \varnothing$$

(9)

$$\begin{array}{ccc}{\mu }^{\prime }\left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left(U\cap R\right)& ,& \forall h_i\in U\end{array}$$

(10)

$$\begin{array}{ccc}{\mu }^{\prime }\left(r_j\right)\in U\cap H& ,& \forall r_j\in U\end{array}$$

(11)

$$\begin{array}{ccc}{\mu }^{\prime }\left(h_i\right){>}^{\left[h_i\right]}\mu \left(h_i\right)& ,& \forall h_i\in U\end{array}$$

(12)

$$\begin{array}{ccc}{\mu }^{\prime }\left(r_j\right){>}^{\left[r_j\right]}\mu \left(r_j\right)& ,& \forall r_j\in U\end{array}$$

(13)

Definition 2.

A matching $\mu$ that has no blocking coalition is said to possess group stability based on combinatorial preferences, denoted as $S_{group}$.

Equation (9) requires that the set $U$ contains at least one vehicle owner and one cargo owner. Equation (10) stipulates that in ${\mu }^{\prime }$, each vehicle owner in $U$ can only be matched with cargo owners in $U\cap R$ and those already matched to them in $\mu \left(h_i\right)$. Equation (11) requires that cargo owners in $U$ can only be matched with vehicle owners within $U$. Equations (12) and (13) require that all individuals in $U$ prefer their matches in ${\mu }^{\prime }$ over those in $\mu$.

Example 1:

Figure 1 below illustrates the blocking coalition that exists in the matching process.

In the original matching $\mu$, $\mu \left(h_1\right)=\left\{r_1,r_2\right\}$, meaning that vehicle owner $h_1$ is matched with cargo owners $r_1$ and $r_2$. $\mu \left(h_2\right)=\left\{r_3,r_6\right\}$, meaning that vehicle owner $h_2$ is matched with cargo owners $r_3$ and $r_6$. $\mu \left(h_3\right)=\left\{r_4,r_5,r_7\right\}$, meaning that vehicle owner $h_3$ is matched with cargo owners $r_4$, $r_5$ and $r_7$.

At this point, a coalition $U=\left\{h_1,h_2,r_3,r_4,r_5\right\}$ and a matching ${\mu }^{\prime }$ can be identified, where in ${\mu }^{\prime }$, ${\mu }^{\prime }\left(h_1\right)=\left\{r_2,r_3,r_4\right\}$, meaning that vehicle owner $h_1$ is matched with cargo owners $r_2$, $r_3$, and $r_4$. ${\mu }^{\prime }\left(h_2\right)=\left\{r_5\right\}$, meaning that vehicle owner $h_2$ is matched with cargo owners $r_5$. ${\mu }^{\prime }\left(h_3\right)=\varnothing$, meaning that vehicle owner $h_3$ is not matched with any cargo owner.

We can observe that for vehicle owner $h_1$, $\left\{r_2,r_3,r_4\right\}={\mu }^{\prime }\left(h_1\right){>}^{\left[h_1\right]}\mu \left(h_1\right)=\left\{r_1,r_2\right\}$. Therefore, vehicle owner $h_1$ can achieve a higher payoff through matching ${\mu }^{\prime }$ compared to matching $\mu$. As a result, vehicle owner $h_1$ will attempt to contact cargo owners $r_3$ and $r_4$, trying to persuade them to adopt matching ${\mu }^{\prime }$ instead of matching $\mu$. When cargo owner $r_3$ receives a call from vehicle owner $h_1$, they will realize that $h_1={{\mu }^{\prime }\left(r_3\right)>}^{\left[r_3\right]}\mu \left(r_3\right)=h_2$, meaning that vehicle owner $h_1$’s proposal ${\mu }^{\prime }$ is more favorable to them than the original matching $\mu$ (the same logic applies to cargo owner $r_4$). Therefore, vehicle owner $h_1$, cargo owner $r_3$, and cargo owner $r_4$ reach an agreement to adopt matching ${\mu }^{\prime }$ instead of matching $\mu$, while cargo owner $r_1$ is betrayed by vehicle owner $h_1$.

The situation for vehicle owner $h_2$ and cargo owner $r_5$ is similar, and readers can follow the same reasoning process as described above.

Therefore, once a pair $\left(U,{\mu }^{\prime }\right)$ that satisfies Definition 1 is found, all vehicle owners and cargo owners within the set $U$ will attempt to break the original matching $\mu$ and form the new matching ${\mu }^{\prime }$, as it is more beneficial to them (vehicle owners can obtain higher total earnings, and cargo owners can be matched with more preferred vehicle owners).

The matching ${\mu }^{\prime }$ can be divided into two parts: one part consists of new matchings formed between vehicle owners and cargo owners within the set $U$; the other part, as stated in Equation (10), allows vehicle owners in $U$ to retain their original matches with cargo owners from $\mu \left(h_i\right)$, even if those cargo owners are outside $U$. For these cargo owners outside $U$, being matched with the same vehicle owner in both ${\mu }^{\prime }$ and $\mu$ means there is no difference between the two matchings from their perspective. In other words, the vehicle owners and cargo owners within set $U$ can form the matching ${\mu }^{\prime }$ and collectively benefit from it solely through cooperation among themselves. The individuals who are involved in ${\mu }^{\prime }$ but are not part of $U$ remain unaffected and indifferent to this process, as their matching relationships do not change. Therefore, such a set $U$ constitutes a blocking coalition that can disrupt the matching $\mu$, as its members have both the incentive and the ability to deviate from the current matching. Only when all possible blocking coalitions are eliminated can the matching $\mu$ be considered stable, possessing group stability based on combinatorial preferences ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

Further observation of Example 1 reveals that $U=\left\{h_1,r_3,r_4\right\},{\mu }^{\prime }\left(h_1\right)=\left\{r_2,r_3,r_4\right\}$ also satisfies Equations (9)–(13), forming a smaller blocking coalition. Similarly, for $U=\left\{h_2,r_5\right\},{\mu }^{\prime }\left(h_2\right)=\left\{r_5\right\}$ holds true as well. In other words, in this example, the large blocking coalition that includes multiple vehicle owners is formed by combining several smaller blocking coalitions, each containing a single vehicle owner.

Corollary 1.

If a matching $\mu$ does not possess $S_{group}$, then there must exist a blocking coalition $U$ within $\mu$, and $U$ contains exactly one vehicle owner.

Proof. 

Given that matching $\mu$ does not possess ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, by Definition 2, there exists at least one blocking coalition $\widehat{U}$, with the corresponding blocking scheme denoted as $\widehat{{\mu }^{\prime }}$. From Equation (9), we know that $\widehat{U}\cap H\ne \varnothing$, meaning that there is at least one vehicle owner $h_i\in \widehat{U}$. Furthermore, from Equation (12), we know that $\widehat{{\mu }^{\prime }}\left(h_i\right){>}^{\left[h_i\right]}\mu \left(h_i\right)$, which implies that $h_i$ must be matched with at least one cargo owner in the blocking matching $\widehat{{\mu }^{\prime }}$ who was not matched in $\mu$. Moreover, according to Equation (10), $h_i$ is matched with at least one $r_j\in \left[\widehat{{\mu }^{\prime }}\left(h_i\right)\backslash \mu \left(h_i\right)\right]\subseteq \widehat{U}$. At this point, $U=\left\{h_i\right\}\cup \widehat{{\mu }^{\prime }}\left(h_i\right)\backslash \mu \left(h_i\right)$ also satisfies Definition 1 and forms a blocking coalition for $\widehat{{\mu }^{\prime }}$. First, $U$ contains at least one vehicle owner and cargo owner, satisfying Equation (9). Clearly, we have $\widehat{{\mu }^{\prime }}\left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left(\left\{h_i\right\}\cup \widehat{{\mu }^{\prime }}\left(h_i\right)\backslash \mu \left(h_i\right)\cap R\right)$, satisfying Equation (10). Since the set of shippers in $U$ is a subset of $\widehat{{\mu }^{\prime }}\left(h_i\right)$, Equation (11) also holds. Finally, $U$ is a subset of $U$, and $\widehat{U}$ satisfies Equations (12) and (13), which completes the proof. □

Corollary 2.

Matching $\mu$ possesses the $S_{group}$ property if and only if there is no blocking coalition in $\mu$ that contains only a single vehicle owner.

Proof. 

When there exists a blocking coalition in matching $\mu$ that contains only a single vehicle owner, it follows from Definition 2 that matching $\mu$ does not possess the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property. Conversely, if no such blocking coalition exists in $\mu$, then according to the contrapositive of Corollary 1, matching $\mu$ possesses the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property. This completes the proof. □

Corollary 3:

If there exists a blocking coalition $U$ in matching $\mu$ that contains only one vehicle owner $h_i$ and its blocking matching is ${\mu }^{\prime }$, then $U=\left\{h_i\right\}\cup {\mu }^{\prime }\left(h_i\right)\backslash \mu \left(h_i\right)$.

Proof. 

For the cargo owners newly matched to vehicle owner $h_i$ in the blocking matching ${\mu }^{\prime }$, $r_j\in {\mu }^{\prime }\left(h_i\right)\backslash \mu \left(h_i\right)$, according to Equation (10), we have $r_j\in U$. For the other cargo owners $r_j\in {\mu }^{\prime }\left(h_i\right)\cap \mu \left(h_i\right)$, matched to vehicle owner $h_i$ in the blocking matching ${\mu }^{\prime }$, it must hold that ${\mu }^{\prime }\left(r_j\right)=h_i{\nsucc }^{\left[r_j\right]}{h}_i=\mu \left(r_j\right)$, which does not satisfy Equation (13). For the cargo owners $r_j$ who are not matched to vehicle owner $h_i$ in the blocking matching ${\mu }^{\prime }$, that is, $r_j\notin {\mu }^{\prime }\left(h_i\right)$, we have ${\mu }^{\prime }\left(r_j\right)\ne h_i=U\cap H$, which does not satisfy Equation (11). This completes the proof. □

3.3. Mathematical Model

This section will utilize the inferences developed in the previous section to establish the group stable matching model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ based on composite preferences.

To ensure that the matching $\mu$ output by the model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ has ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, according to Inference 2, it is sufficient to ensure that no blocking coalition $U$ exists that contains only a single vehicle owner $h_i$. In other words, for each vehicle owner $h_i$, it is necessary to ensure that no matter how $h_i$ attempts to construct ${\mu }^{\prime }$, the coalition $U=\left\{h_i\right\}\cup {\mu }^{\prime }\left(h_i\right)\backslash \mu \left(h_i\right)$ cannot satisfy Definition 1. Therefore, the stability constraint must account for every possible attempt by each vehicle owner $h_i$ to construct ${\mu }^{\prime }$.

When vehicle owner $h_i$ attempts to construct ${\mu }^{\prime }$, they will first try to find additional cargo owners to include in ${\mu }^{\prime }$ based on $\mu \left(h_i\right)$. At the same time, due to their transportation capacity limitations, they will need to give up some of the cargo owners in $\mu \left(h_i\right)$. The set of additional cargo owners $h_i$ finds is denoted as $R_i^{\mathrm{i}\mathrm{n}}$, and the set of cargo owners $h_i$ gives up is denoted as $R_i^{out}$. Therefore, the matching $\mu \left(h_i\right)$ is given by ${\mu }^{\prime }\left(h_i\right)=\mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}$. In Example 1, the sets $R_i^{\mathrm{i}\mathrm{n}}$ and $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}$ found by vehicle owner $h_i$ are shown in the following Figure 2:

Only when $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$ can ${\mu }^{\prime }$ potentially be a blocking solution, because this is the only way for vehicle owner $h_i$ to achieve a higher payoff in ${\mu }^{\prime }$; that is, $\left(h_i\right){\prec }^{\left[h_i\right]}\mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}={\mu }^{\prime }\left(h_i\right)$.

When vehicle owner $h_i$ attempts to achieve a blocking solution by adding $R_i^{\mathrm{i}\mathrm{n}}$ and excluding $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}$, the following two conditions must also be satisfied for ${\mu }^{\prime }$ to constitute a blocking solution:

(1)

$c_i\ge {\sum }_{r_j\in \mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^j{s}_j$, meaning that the transportation capacity of vehicle owner $h_i$ is sufficient.

(2)

$h_i{>}^{\left[r_j\right]}\mu \left(r_j\right),\forall r_j\in R_i^{\mathrm{i}\mathrm{n}}$; that is, each cargo owner $r_j$ in $R_i^{\mathrm{i}\mathrm{n}}$ must consider vehicle owner $h_i$ to be preferred over their current matching partner $\mu \left(r_j\right)$.

Therefore, for all $\forall h_i\in H,\forall R_i^{\mathrm{i}\mathrm{n}}\subseteq R,\forall R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\subseteq R\backslash R_i^{\mathrm{i}\mathrm{n}},R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$, the constraints of the two points will not be satisfied simultaneously, thus ensuring that the matching $\mu$ output by model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ has ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. The model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ established based on this approach is as follows:

$$\begin{array}{cc}\mathrm{m}\mathrm{a}\mathrm{x}& {\sum }_{r_j\in R}^j{\sum }_{h_i\in H}^i\mathsf{\partial }·P_j·x_{i,j}\end{array}$$

(14)

$$\begin{array}{ccc}s.t.& {\sum }_{h_i\in H}^i{x}_{i,j}\le 1& \forall r_j\in R\end{array}$$

(15)

$$\begin{array}{cc}{\sum }_{r_j\in R}^j{x}_{i,j}·s_j\le c_i& \forall h_i\in H\end{array}$$

(16)

$$\begin{array}{c}M\left({\sum }_{r_l\in R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^l\left(1-x_{i,l}\right)+{\sum }_{r_j\in R_i^{\mathrm{i}\mathrm{n}}}^j{\sum }_{h_w{\ge }^{\left[r_j\right]}{h}_i}^w{x}_{w,j}\right)\\ +{\sum }_{r_t\in R\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^t{x}_{i,t}·s_t>c_i-{\sum }_{r_v\in R_i^{\mathrm{i}\mathrm{n}}}^v{s}_v\\ \forall h_i\in H,\forall R_i^{\mathrm{i}\mathrm{n}}\subseteq R,\forall R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\subseteq R\backslash R_i^{\mathrm{i}\mathrm{n}},R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}\end{array}$$

(17)

$$\begin{array}{cc}{x}_{i,j}\in \left\{\mathrm{0,1}\right\}& \forall h_i\in H,\forall r_j\in R\end{array}$$

(18)

Among them, Equation (14) serves as the objective function, aiming to maximize the platform’s commission revenue. Equation (15) indicates that each cargo owner can be matched with at most one vehicle owner. Equation (16) represents the vehicle owner’s transportation capacity constraint, meaning that the total weight of cargo transported by a vehicle owner must be within their transportation capacity. Equation (18) indicates that the decision variables in the model are binary (0–1) variables. Equation (17) is the stability constraint. In the following, we will break down Equation (17) step by step and explain its meaning.

For ease of explanation, we define $X_{\mu }$ as an $m\times n$ binary (0–1) matrix that satisfies Equations (15), (16), and (18). In other words, $X_{\mu }$ satisfies the variable type constraints and the one-to-many matching constraints of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, and therefore $X_{\mu }$ can represent a matching $\mu$. However, it does not guarantee that $\mu$ possesses the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

First, let us examine the indexing part of Equation (17). $\forall h_i\in H$ means that $h_i$ can be any element in the set $H$. $\forall R_i^{\mathrm{i}\mathrm{n}}\subseteq R$ means that $R_i^{\mathrm{i}\mathrm{n}}$ can be any subset of $R$. $\forall R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\subseteq R\backslash R_i^{\mathrm{i}\mathrm{n}},R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$ means that $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}$ can be any subset of the complement of $R_i^{\mathrm{i}\mathrm{n}}$ in $R$ that satisfies $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$.

Next, we will prove through two lemmas that a solution $X_{\mu }$ of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ satisfies the stability constraint (17) if and only if the matching $\mu$ represented by $X_{\mu }$ possesses the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property.

Lemma 1.

Suppose in the matching $\mu$ represented by $X_{\mu }$, there exists a blocking coalition $U$ that contains only one vehicle owner $U$, and its blocking matching is ${\mu }^{\prime }$. Then $X_{\mu }$ does not satisfy the constraint (17) indexed by $h_i=\widehat{h_i},R_i^{in}=U\cap R,R_i^{out}=\mu \left(\widehat{h_i}\right)\backslash \mu \prime \left(\widehat{h_i}\right)$.

Proof. 

First, we prove that the index itself must satisfy the requirement in constraint (17), namely $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$. □

According to Corollary 3 $U=\left\{\widehat{h_i}\right\}\cup {\mu }^{\prime }\left(\widehat{h_i}\right)\backslash \mu \left(\widehat{h_i}\right)$, and thus $R_i^{\mathrm{i}\mathrm{n}}=U\cap R={\mu }^{\prime }\left(\widehat{h_i}\right)\backslash \mu \left(\widehat{h_i}\right)$. By set operation rules, it is clear that $R_i^{\mathrm{i}\mathrm{n}}\cap R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\varnothing$, and ${\mu }^{\prime }\left(\widehat{h_i}\right)=\mu \left(\widehat{h_i}\right)\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\cup R_i^{\mathrm{i}\mathrm{n}}$. According to Equation (12), we have ${\mu }^{\prime }\left(\widehat{h_i}\right)=\mu \left(\widehat{h_i}\right)\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\cup R_i^{\mathrm{i}\mathrm{n}}{>}^{\left[\widehat{h_i}\right]}\mu \left(\widehat{h_i}\right)$. Then, by Equation (4), it follows that $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[\widehat{h_i}\right]}{R}_i^{\mathrm{i}\mathrm{n}}$.

Next, we prove that $X_{\mu }$ does not satisfy the constraint (17) indexed by these values.

Since $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\mu \left(\widehat{h_i}\right)\backslash \mu \prime \left(\widehat{h_i}\right)\subseteq \mu \left(\widehat{h_i}\right)$, we have ${\sum }_{r_l\in R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^l\left(1-x_{i,l}\right)=0$. Furthermore, since $R_i^{\mathrm{i}\mathrm{n}}=U\cap R$ and according to Equation (13), for all $\forall r_j\in R_i^{\mathrm{i}\mathrm{n}}$, we have $\widehat{h_i}={\mu }^{\prime }\left(r_j\right){>}^{\left[r_j\right]}\mu \left(r_j\right)$. That is, the cargo owners in $R_i^{\mathrm{i}\mathrm{n}}$ are not matched in $\mu$ to any vehicle owner better than or equal to $\widehat{h_i}$; therefore, ${\sum }_{r_j\in R_i^{\mathrm{i}\mathrm{n}}}^j{\sum }_{h_w{\ge }^{\left[r_j\right]}\widehat{h_i}}^w{x}_{w,j}=0$. Finally, since ${\mu }^{\prime }\left(\widehat{h_i}\right)=\mu \left(\widehat{h_i}\right)\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\cup R_i^{\mathrm{i}\mathrm{n}}$, the blocking matching ${\mu }^{\prime }$ itself requires that the vehicle owner does not exceed their maximum transportation capacity. Therefore, ${\sum }_{r_j\in {\mu }^{\prime }\left(\widehat{h_i}\right)}^j{s}_j={\sum }_{r_t\in R\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^t{x}_{i,t}·s_t+{\sum }_{r_v\in R_i^{\mathrm{i}\mathrm{n}}}^v{s}_v\le c_i$. It is clear that constraint (17) is not satisfied.

In summary, Lemma 1 is proved.

Based on the contrapositive of Lemma 1 and Corollary 2, any solution $X_{\mu }$ of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ that satisfies the stability constraint must represent a matching $\mu$ possessing the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property. In other words, constraint (17) can sufficiently guarantee that the matching solution obtained by ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ possesses the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property.

Next, we will prove that constraint (17) is also a necessary condition for the solution obtained by ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ to possess the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property.

Lemma 2.

Suppose the solution $X_{\mu }$ representing the matching $\mu$ violates constraint (17) indexed by $h_i,R_i^{in},R_i^{out}$. Then $U=\left\{h_i\right\}\cup R_i^{in}$ must form a blocking coalition of $\mu$, with the blocking matching defined as ${\mu }^{\prime }\left(h_i\right)=\mu \left(h_i\right)\cup R_i^{in}\backslash R_i^{out}$.

Proof. 

First, verify whether ${\mu }^{\prime }$ as a blocking matching exceeds the maximum transportation capacity of the vehicle owner $h_i$. Since constraint (17) itself requires that $R_i^{out}\subseteq R\backslash R_i^{in}$, it follows that $R_i^{\mathrm{i}\mathrm{n}}\cap R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\varnothing$. Therefore, ${\mu }^{\prime }\left(h_i\right)=\mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\mu \left(h_i\right)\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\cup R_i^{\mathrm{i}\mathrm{n}}$. Moreover, since constraint (17) is violated, the inequality ${\sum }_{r_t\in R\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^t{x}_{i,t}·s_t+{\sum }_{r_v\in R_i^{\mathrm{i}\mathrm{n}}}^v{s}_v\le c_i$ must not hold, indicating that ${\mu }^{\prime }$ does not exceed the maximum transportation capacity of vehicle owner $h_i$. □

Next, we directly use Equations (9)–(13) to verify whether $U$ and ${\mu }^{\prime }$ satisfy the definition of ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

Since $U=\left\{h_i\right\}\cup R_i^{\mathrm{i}\mathrm{n}}\subseteq H\cup R,U\cap H=\left\{h_i\right\}\ne \varnothing$, and the index of constraint (17) requires $\varnothing \preccurlyeq R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{in}\ne \varnothing$, it follows that $U$ and ${\mu }^{\prime }$ satisfy Equation (9). For all $\forall h_i\in U$, we have ${\mu }^{\prime }\left(h_i\right)=\mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\subseteq \mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}=\mu \left(h_i\right)\cup \left(U\cap R\right)$. Thus, $U$ and ${\mu }^{\prime }$ satisfy Equation (10). For all $r_j\in U$, as previously established $R_i^{\mathrm{i}\mathrm{n}}\cap R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\varnothing$, and since ${\mu }^{\prime }\left(h_i\right)=\mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}$, we have $R_i^{\mathrm{i}\mathrm{n}}\subseteq {\mu }^{\prime }\left(h_i\right)$. Therefore, for all $\forall r_j\in U\cap R=R_i^{\mathrm{i}\mathrm{n}}\subseteq {\mu }^{\prime }\left(h_i\right)$, we must have ${\mu }^{\prime }\left(r_j\right)=h_i\in \left\{h_i\right\}=U\cap H$. Thus, $U$ and ${\mu }^{\prime }$ satisfy Equation (11). For all $\forall h_i\in U$, constraint (17) itself requires that $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$, and as established above, $R_i^{\mathrm{i}\mathrm{n}}\cap R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\varnothing$. Therefore, according to the preference description in Equation (4), we have ${\mu }^{\prime }\left(h_i\right)=\mu \left(h_i\right)\cup R_i^{\mathrm{i}\mathrm{n}}\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{>}^{\left[h_i\right]}\mu \left(h_i\right)$. Thus, $U$ and ${\mu }^{\prime }$ satisfy Equation (12). For all $r_j\in U\cap R$, since constraint (17) is violated, we must have ${\sum }_{r_j\in R_i^{\mathrm{i}\mathrm{n}}}^j{\sum }_{h_w{\ge }^{\left[r_j\right]}{h}_i}^w{x}_{w,j}=0$, which means that for all $r_j\in R_i^{\mathrm{i}\mathrm{n}}$, we have ${\mu }^{\prime }\left(r_j\right)=h_i{>}^{\left[r_j\right]}\mu \left(r_j\right).$ Thus, $U$ and ${\mu }^{\prime }$ satisfy Equation (13).

In conclusion, Lemma 2 is proved.

According to Lemma 2, once the solution $X_{\mu }$ violates any stability constraint in ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, the matching $\mu$ represented by $X_{\mu }$ must contain a blocking coalition, and therefore does not possess the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property. In other words, satisfying constraint (17) is a necessary condition for the matching solution obtained by ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ to have the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property.

Thus, we have proven that the solution $X_{\mu }$ of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ satisfying the stability constraint (17) is a necessary and sufficient condition for the matching $\mu$ represented by $X_{\mu }$ to possess the ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ property. The model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ established in this section neither relaxes nor strengthens the stability requirements of ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

3.4. Cutting-Plane Method for Solving the Group Stable Matching Model Based on Combinational Preferences

Although the ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ model can address the one-to-many stable matching problem in vehicle–cargo matching platforms, its stability constraint (17) requires enumerating every vehicle owner $h_i$, every possible additional cargo owner set $R_i^{\mathrm{i}\mathrm{n}}$, and every possible dropout cargo owner set $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}$. As a result, when there are m vehicle owners and n cargo owners in the market, the number of constraints in the model grows at the order of $O\left(m·2^{2n}\right)$. Even without solving, the sheer number of constraints makes obtaining the complete model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ an NP-hard problem, which severely impacts the computational efficiency of solving the freight pooling stable matching problem on vehicle–cargo matching platforms. At the same time, the model has only $m·n$ decision variables, which is far fewer than the number of constraints. This means that ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ as a mixed-integer linear programming model contains a large majority of constraints that are inactive or redundant [41]. As a cutting-plane method, a type of row generation algorithm, it can eliminate most of the inactive constraints in the model during the solving process, using only a subset of the model’s constraints to obtain the same solution as the original model. This improves solving efficiency and fits very well with the characteristics of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ [42]. This section will introduce the cutting-plane method and propose a cutting-plane approach to solve the group stable matching model based on combinational preferences.

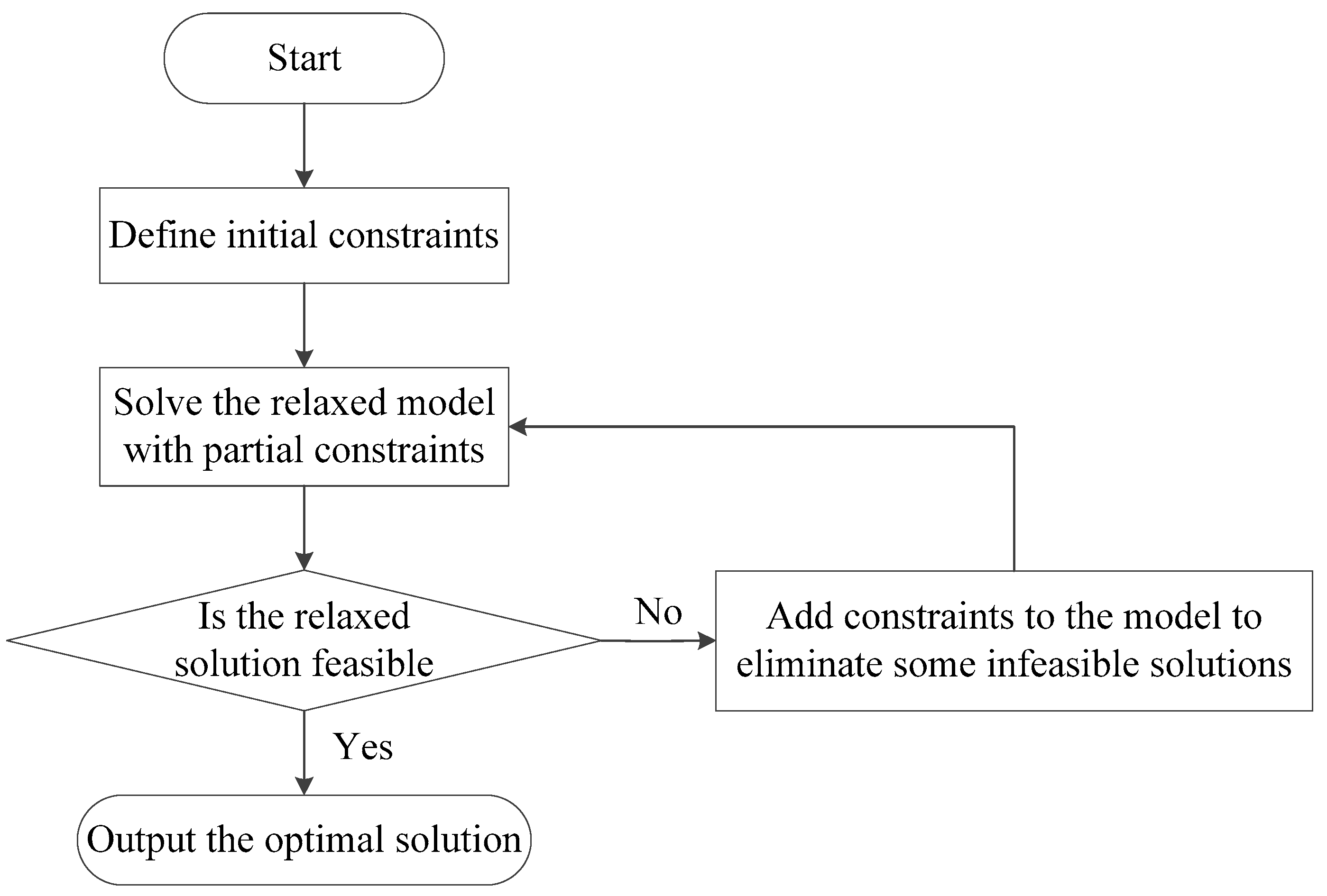
3.4.1. Introduction to the Cutting-Plane Method

The cutting-plane method is an iterative algorithm. Its general process (excluding cases of no solution or infeasibility) is shown in Figure 3. First, only a subset of the known constraints is added to the model to obtain the optimal solution of its relaxed problem. Then, other methods are used to check the feasibility of the relaxed solution. If the relaxed solution is feasible for the model, it is the optimal solution; otherwise, constraints that the current solution violates are identified from the known constraint set and added to the relaxed model for the next iteration [42].

From the process of the cutting-plane method, we can see that designing the cutting-plane method requires consideration of three parts:

(1)

How to determine the initial constraints;

(2)

How to determine the feasibility of the relaxed solution without checking all the constraints;

(3)

How to add effective cutting constraints when the relaxed solution is infeasible.

3.4.2. Selection of Initial Constraints

The exponential number of constraints in ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ originates from the stability constraint (17), while the one-to-many matching constraints (15)–(16) and the decision variable type constraint (18) are relatively few in number. Moreover, only when the one-to-many matching constraints are satisfied can the relaxed solution represent a matching $\mu$ and thus have physical meaning. Therefore, this chapter selects all constraints in ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ except for the stability constraint (17) as the initial constraints for the cutting-plane method designed for solving ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

3.4.3. Feasibility Check of the Relaxed Solution

Based on Lemma 1 and Lemma 2, for a solution $X_{\mu }$ that satisfies the one-to-many matching constraints and the decision variable type constraints, a necessary and sufficient condition for it to satisfy the stability constraint (17) and thus be a feasible solution to ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, is that the matching $\mu$ represented by the solution $X_{\mu }$ contains no blocking coalition. In other words, the matching $\mu$ possesses ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. Furthermore, based on Corollary 2 of ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, we can determine whether the solution $X_{\mu }$ is a feasible solution satisfying constraint (17) by checking whether for each vehicle owner $h_i\in H$ there exists a blocking plan ${\mu }^{\prime }$ that forms a blocking coalition containing only $U\cap H=\left\{h_i\right\}$.

According to the definition of a blocking coalition, ${\mu }^{\prime }\left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left(U\cap R\right)$, which means that in the blocking plan ${\mu }^{\prime }$, a vehicle owner can only be matched with the cargo owners who are either currently matched with them in $\mu$ or who belong to the blocking coalition $U$. For the latter case, where $r_j\in U$, it is required that $h_i={\mu }^{\prime }\left(r_j\right){>}^{\left[r_j\right]}\mu \left(r_j\right)$; that is, the cargo owner $r_j$ must prefer the vehicle owner $h_i$ over the vehicle owner they are matched with in $\mu$ for the condition of entering the blocking coalition to be satisfied.

Therefore, we have ${\mu }^{\prime }\left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left(U\cap R\right)\subseteq \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}$; in other words, the vehicle owner $h_i$ can construct a blocking plan ${\mu }^{\prime }$ arbitrarily within the set of cargo owners $\mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}$, since these rational cargo owners would not reject $h_i$ request. The goal of the vehicle owner $h_i$ is to maximize their total reward. Therefore, when constructing the blocking plan ${\mu }^{\prime }$, the vehicle owner $h_i$ essentially faces a 0–1 knapsack problem, which can be described using an integer programming model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ as follows:

$$\mathrm{m}\mathrm{a}\mathrm{x}{\sum }_{r_j\in \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}}^j{p}_j{·y}_{i,j}$$

(19)

$$\begin{array}{cc}s.t.& \sum _{r_j\in \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}}^j{s}_j{·y}_{i,j}\le c_i\end{array}$$

(20)

$$\begin{array}{cc}{y}_{i,j}\in \left\{\mathrm{0,1}\right\}& \forall r_j\in \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}\end{array}$$

(21)

The decision variables of model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ are binary variables $y_{i,j}$, where $y_{i,j}=1$ indicates $r_j\in {\mu }^{\prime }\left(h_i\right)$, and otherwise $r_j\notin {\mu }^{\prime }\left(h_i\right)$. Equation (19) aims to maximize the reward obtained by vehicle owner $h_i$. Constraint (20) is the capacity constraint of vehicle owner $h_i$. Constraint (21) is the variable type constraint.

Vehicle owner $h_i$ can obtain the optimal solution ${\mathit{y}}_{\mathit{i},\mathit{j}}^{*}$ by solving ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$, and the matching ${\mu }^{*}$ represented by ${\mathit{y}}_{\mathit{i},\mathit{j}}^{*}$ is the matching plan that allows $h_i$ to achieve the highest benefit when proposing a blocking plan. If vehicle owner $h_i$ can obtain a higher reward through ${\mu }^{*}$ than in the matching $\mu$, that is ${\mu }^{*}\left(h_i\right){>}^{\left[h_i\right]}\mu \left(h_i\right)$, then the proposed optimal blocking plan ${\mu }^{*}$ actually satisfies the definition of a blocking plan in ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, which further indicates that the matching $\mu$ does not possess ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

Lemma 3.

$\mu \left(h_i\right){=}^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$ is a necessary and sufficient condition for vehicle owner $h_i$ to find no blocking coalition containing only themselves in matching $\mu$.

Proof. 

First, prove the necessity of Lemma 3. □

Vehicle owner $h_i$ only selects all $r_j\in \mu \left(h_i\right)$, which constitute one feasible solution of the knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$; since ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ is a maximization model, it always holds that $\mu \left(h_i\right){\preccurlyeq }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$. When $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$, there exists $\exists \left(U=\left\{r_j|y_{i,j}^{*}=1\right\}\backslash \mu \left(h_i\right)\cup \left\{h_i\right\},{\mu }^{\prime }\left(h_i\right)=\left\{r_j|y_{i,j}^{*}=1\right\}\right)$ such that the following conditions are satisfied:

First, $U\cap H=\left\{h_i\right\}\ne \varnothing$; and since $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$, we have $U\cap R=\left\{r_j|y_{i,j}^{*}=1\right\}\backslash \mu \left(h_i\right)\ne \varnothing$, which means that $\left(U,{\mu }^{\prime }\right)$ satisfies Equation (9) in the definition of a blocking coalition.

For all $\forall h_i\in U\cap H$, we have ${\mu }^{\prime }\left(h_i\right)=\left\{r_j|y_{i,j}^{*}=1\right\}\subseteq U\cap R\subseteq \mu \left(h_i\right)\cup \left(U\cap R\right)$, which means that $\left(U,{\mu }^{\prime }\right)$ satisfies Equation (10) in the definition of a blocking coalition.

For all $\forall r_j\in U\cap R$, since $U\cap R=\left\{r_j|y_{i,j}^{*}=1\right\}\backslash \mu \left(h_i\right)\subseteq \left\{r_j|y_{i,j}^{*}=1\right\}={\mu }^{\prime }\left(h_i\right)$, it follows that $r_j\subseteq {\mu }^{\prime }\left(h_i\right)$; in other words, ${\mu }^{\prime }\left(r_j\right)=h_i\in U\cap H$, which means that $\left(U,{\mu }^{\prime }\right)$ satisfies Equation (11) in the definition of a blocking coalition.

For all $\forall h_i\in U\cap H$, we have ${\mu }^{\prime }\left(h_i\right)=\left\{r_j|y_{i,j}^{*}=1\right\}{>}^{\left[h_i\right]}\mu \left(h_i\right)$, which means that $\left(U,{\mu }^{\prime }\right)$ satisfies Equation (12) in the definition of a blocking coalition.

Since, in the knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$, all cargo owners come from the set $\mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}$, it follows that $r_j\in U\cap R=\left\{r_j|y_{i,j}^{*}=1\right\}\backslash \mu \left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}\backslash \mu \left(h_i\right)\subseteq \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}$. Hence, for every $\forall r_j\in U\cap R$ we have ${\mu }^{\prime }\left(r_j\right)=h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)$, which means that $\left(U,{\mu }^{\prime }\right)$ satisfies Equation (13) in the definition of a blocking coalition.

Therefore, when $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$, the matching $\mu$ does not satisfy ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

In summary, the necessity of Lemma 3 is proved.

Next, we proceed to prove the sufficiency of Lemma 3.

According to Corollary 3 of ${\mathrm{S}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, if there exists a blocking coalition in the matching $\mu$ that contains only one vehicle owner, denoted by the blocking coalition $U=\left\{h_i\right\}\cup {\mu }^{\prime }\left(h_i\right)\backslash \mu \left(h_i\right)$, with the corresponding blocking assignment ${\mu }^{\prime }\left(h_i\right)$, then according to Equation (12) in the definition of a blocking coalition, we have $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\mu \prime \left(h_i\right)$.

According to Equations (10) and (13), we have ${\mu }^{\prime }\left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left(U\cap R\right)\subseteq \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}$. At the same time, $\mu \prime \left(h_i\right)$ is also a matching. According to the requirements of a matching $\sum _{r_j\in \mu \prime \left(h_i\right)}^j{s}_j\le c_i$, thus, the solution ${\mathit{y}}_{\mathit{i},\mathit{j}}^{\prime }$ corresponding to $\mu \prime \left(h_i\right)$ satisfies all the constraints of the knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$, and is a feasible solution to the knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$.

Moreover, since ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ is a maximization model, the objective value of its optimal solution is not less than that of any feasible solution. Therefore, we have $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\mu \prime \left(h_i\right){\preccurlyeq }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$.

In summary, the sufficiency of Lemma 3 is proved.

Combining Lemmas 1 to 3 and Corollary 2, we can draw the following conclusion.

Lemma 4.

For a solution $X_{\mu }$ in $M_{group}$ that satisfies the one-to-many matching constraints and decision variable type constraints, the necessary and sufficient condition for satisfying the stability constraint (17) (i.e., for $X_{\mu }$ to be a feasible solution of $M_{group}$ is that, for every $\forall h_i\in H$, solving the knapsack model $M_{Knap}$ yields $\mu \left(h_i\right){=}^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$, where $\mu$ is the matching represented by the solution $X_{\mu }$.

Therefore, according to Lemma 4, we can avoid verifying all stability constraints and instead solve $m$ 0–1 knapsack problems to determine whether the relaxed solution generated by the cutting-plane method is a feasible solution of the model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

3.4.4. Method for Adding Cutting Constraints

During the feasibility check of the relaxed solution $X_{\mu }$, if there exists some $h_i\in H$ such that $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}$, that is, the relaxed solution $X_{\mu }$ is an infeasible solution of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. In this case, we can use the optimal solution $y_{i,j}^{*}$ of the knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ to identify which specific stability constraint among the many in ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ is violated by the relaxed solution $X_{\mu }$ and then add this constraint as a cutting constraint to the relaxed model.

Lemma 5.

For a solution $X_{\mu }$ in $M_{group}$ that satisfies the one-to-many matching constraints and decision variable type constraints, if there exists some $h_i\in H$ such that after solving the knapsack model $M_{Knap}$, $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\},$ then the stability constraint (17) in $M_{group}$ indexed by $h_i$, with $R_i^{in}=\left\{r_j|y_{i,j}^{*}=1\right\}\backslash \mu \left(h_i\right),R_i^{out}=\mu \left(h_i\right)\backslash \left\{r_j|y_{i,j}^{*}=1\right\}$ will be violated.

Proof. 

First $R_i^{\mathrm{i}\mathrm{n}}\cap R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}=\varnothing$, and $\mu \left(h_i\right){\prec }^{\left[h_i\right]}\left\{r_j|y_{i,j}^{*}=1\right\}=\mu \left(h_i\right)\backslash R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\cup R_i^{\mathrm{i}\mathrm{n}}$, and therefore, $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}{\prec }^{\left[h_i\right]}{R}_i^{\mathrm{i}\mathrm{n}}$, which satisfies the indexing requirements of the stability constraint (17) itself. □

Since $R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}\subseteq \mu \left(h_i\right)$, we have ${\sum }_{r_l\in R_i^{\mathrm{o}\mathrm{u}\mathrm{t}}}^l\left(1-x_{i,l}\right)=0$. Furthermore, because $R_i^{\mathrm{i}\mathrm{n}}=\left\{r_j|y_{i,j}^{*}=1\right\}\backslash \mu \left(h_i\right)\subseteq \mu \left(h_i\right)\cup \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}\backslash \mu \left(h_i\right)\subseteq \left\{r_j|h_i{>}^{\left[r_j\right]}\mu \left(r_j\right)\right\}$, we have ${\sum }_{r_j\in R_i^{\mathrm{i}\mathrm{n}}}^j{\sum }_{h_w{\ge }^{\left[r_j\right]}{h}_i}^w{x}_{w,j}=0$;

Finally, since ${\mathit{y}}_{\mathit{i},\mathit{j}}^{*}$ satisfies the capacity constraint of the knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$, we have $\sum _{r_j\in \left\{r_j|y_{i,j}^{*}=1\right\}}^j{s}_j={\sum }_{r_t\in R\backslash R_i^{out}}^t{x}_{i,t}·s_t+{\sum }_{r_v\in R_i^{in}}^v{s}_v\le c_i$.

In summary, stability constraint (17) is violated, and thus Lemma 5 is proved.

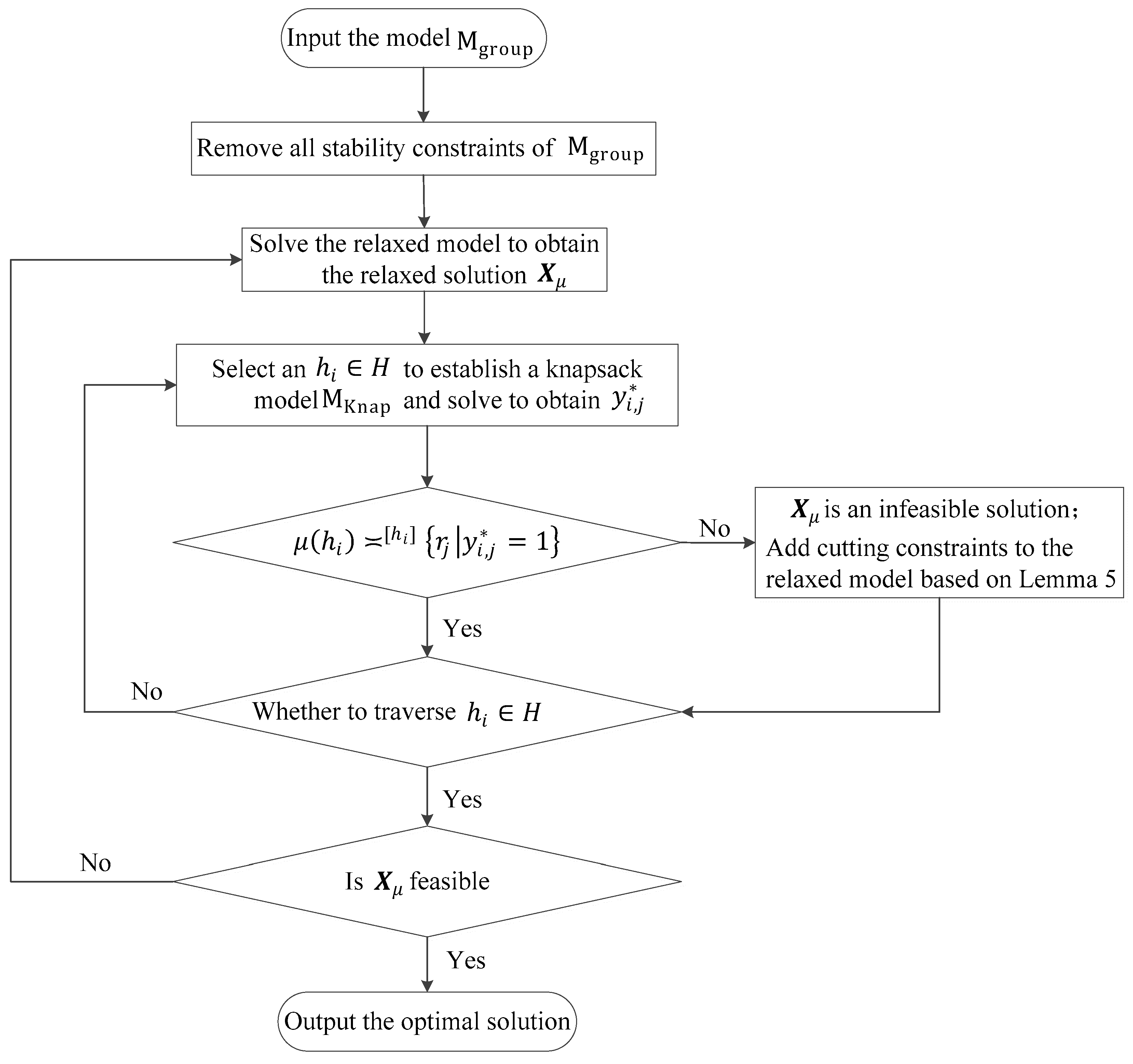
3.4.5. Cutting-Plane Method for Solving Group Stable Matching Models Based on Combinatorial Preferences

To summarize, the flowchart of the cutting-plane method developed for ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ is presented in Figure 4.

When using the cutting-plane method to solve model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, the relaxed model differs in feasible region from that of model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ due to the significant reduction in constraints. However, even though the feasible region of the model changes when using the cutting-plane method to solve model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, the method is still guaranteed to obtain the optimal solution of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. This conclusion can be drawn from the following points:

(1)

There are only a finite number of solutions in the solution space of model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. Since the decision variables $x_{i,j}$ are binary (0–1 variables), the number of possible solutions in the solution space is no more than $2^{mn}$.

(2)

The cutting-plane method will never produce an infeasible solution for model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. According to Lemma 4, by formulating and solving a knapsack model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ for each vehicle owner $\forall h_i\in H$, the solution of ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$ provides a necessary and sufficient condition to determine the feasibility of the relaxed solution of model ${\mathrm{M}}_{\mathrm{K}\mathrm{n}\mathrm{a}\mathrm{p}}$.

(3)

Infeasible relaxed solutions of model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ will not reappear repeatedly during the iterations. According to Lemma 5, at each iteration, constraints violated by infeasible relaxed solutions are added to the relaxed model. Therefore, these previously encountered relaxed solutions will not reoccur in the next iteration. Since the number of solutions is finite, the algorithm is guaranteed to terminate after a finite number of iterations.

(4)

The cutting-plane method will never produce a solution worse than the optimal solution of model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. Throughout the entire algorithm, the constraints added to the relaxed model are all present in model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. Therefore, the feasible region of the relaxed model is always at least as large as that of model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, ensuring that the solution obtained by the cutting-plane method is never worse than the optimal solution of model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

Therefore, the cutting-plane method designed for model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$ in this paper is guaranteed to obtain the optimal solution of ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. The validation of the algorithm’s efficiency improvement will be presented in the experimental analysis section later in the paper.

4. Numerical Experiment

In the previous sections, we provided a detailed introduction to the group stable matching problem in the freight pooling service of the vehicle–cargo matching platform. After defining the stability of this problem, we established the corresponding mathematical model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$. Subsequently, considering the large number of constraints in model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$, we designed a cutting-plane method to solve it. This section will analyze the advantages of the group stable matching model over existing matching models from the perspectives of the platform, vehicle owners, and cargo owners through simulation experiments, as well as examine the efficiency improvement brought by using the cutting-plane method to solve model ${\mathrm{M}}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}}$.

All experiments in this paper were conducted on a computer equipped with an Intel i7-8700 processor running at 3.20 GHz and 8 GB of RAM. The experimental program was written in Java 16.0, and IBM’s CPLEX 12.6.1 optimizer was used to solve the integer linear programming and mixed-integer linear programming models.

4.1. Example Parameters

This paper simulates the vehicle and cargo data submitted by vehicle owners and cargo owners based on the real operational conditions of the vehicle–cargo matching platform. The specific parameters are as follows:

The platform commission rate $\mathsf{\partial }=0.05$. The maximum transportation capacity $c_i$ of vehicle owner $h_i$ follows a uniform distribution $U\left(\mathrm{5,20}\right)$ tons. The transportation time evaluation score $o_i^1$ of vehicle owner $h_i$ follows a uniform distribution $U\left(\mathrm{0,1}\right)$. The service quality guarantee evaluation score $o_i^2$ of vehicle owner $h_i$ follows a uniform distribution $U\left(\mathrm{0,1}\right)$. The transportation capacity requirement $s_j$ of cargo owner $r_j$ follows a uniform distribution $U\left(\mathrm{1,10}\right)$ tons. The payment $P_j$ from cargo owner $r_j$ is related to the transportation demand $s_j$ by $P_j~U\left(\mathrm{0.8,1.2}\right)·s_j$. The importance weight ${\gamma }_j^1$ that cargo owner $r_j$ assigns to the vehicle owner’s transportation time $o_i^1$ follows a uniform distribution $U\left(\mathrm{0,1}\right)$. The importance weight ${\gamma }_j^2$ that cargo owner $r_j$ assigns to the vehicle owner’s service quality $o_i^2$ is given by ${\gamma }_j^2=1-{\gamma }_j^1$.

Based on the above parameters, simulation test cases with varying numbers of vehicle owners and cargo owners were generated to model different supply and demand environments in the vehicle–cargo matching market. For each test case of different sizes, 50 random trials were conducted and the results were averaged.

4.2. Comparative Analysis of Matching Models

When providing matching solutions for vehicle owners and cargo owners, traditional matching methods disregard their preference information and instead match them based solely on the basic attributes of vehicles and cargo. This paper introduces the concept of group stability and addressing the preference characteristics of vehicle owners in the vehicle–cargo matching problem and ensures group stability of the matching outcomes by defining and eliminating blocking coalitions that may include multiple vehicle owners and cargo owners. Therefore, this section conducts simulation experiments to comparatively verify the differences between the traditional matching model and the group stable matching model.

To compare the differences between the two matching schemes, this paper refers to the platform’s revenue obtained from the optimal solution of the matching scheme as the “ideal revenue”. However, in the traditional matching scheme, blocking coalitions composed of vehicle owners and cargo owners may still exist, enabling them to reject the matching scheme and mutually benefit, which leads to a loss of part of the platform’s commission revenue. Therefore, this paper defines the “actual revenue” to describe the platform’s remaining commission income after deducting the potential losses caused by such blocking coalitions. In other words, the ideal metric reflects the optimal scenario where all vehicle owners and cargo owners unconditionally comply with the platform’s scheme, whereas the actual metric reflects the real situation in which vehicle owners and cargo owners, motivated by their own interests, may disrupt the platform’s scheme.

For any cargo owner $r_j$ in a matching $\mu$, let $h_i$ be the vehicle owner matched with $r_j$ in $\mu$. If either of the following two conditions is satisfied, the platform excludes the commission revenue derived from the payment of this vehicle owner when calculating its total commission income:

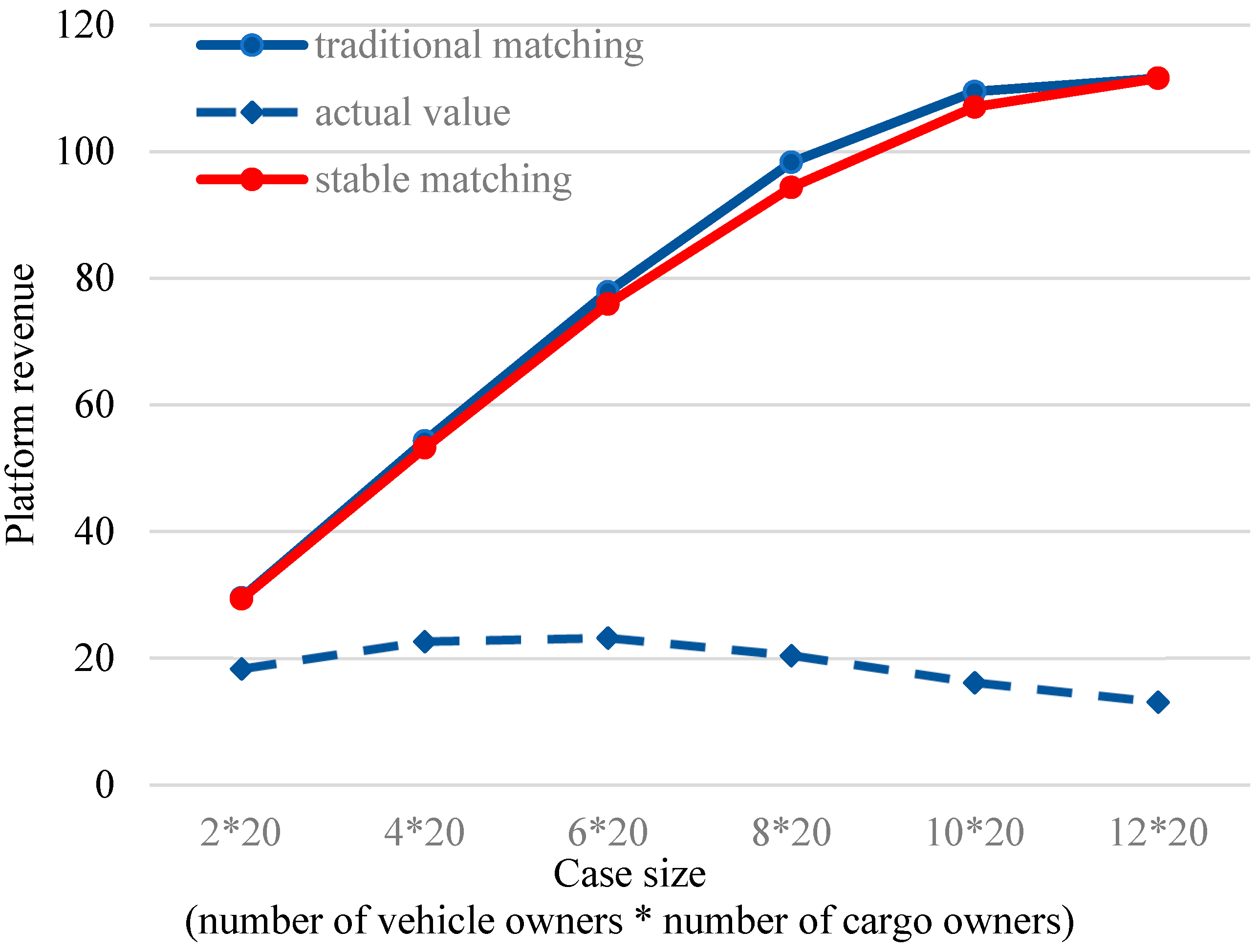
(1)

Vehicle owner $h_i$ can identify a blocking scheme ${\mu }^{\prime }\left(h_i\right)\not\ni r_j$ that does not include cargo owner $r_j$. In this case, cargo owner $r_j$ may be abandoned by vehicle owner $h_i$, resulting in a loss of the corresponding commission revenue for the platform.

(2)

Another vehicle owner $h_k$ is able to identify a blocking coalition ${\mu }^{\prime }\left(h_k\right)$ that includes cargo owner $r_j$. In this case, cargo owner $r_j$ may reject the original matching $\mu$ and instead choose to match independently with vehicle owner $h_k$ to obtain a more satisfactory outcome, resulting in the platform losing the corresponding portion of its commission revenue.

This section uses test cases consisting of 20 cargo owners and varying numbers of vehicle owners to simulate different market scenarios, ranging from supply shortage to supply surplus in terms of transportation capacity provided by vehicle owners. The resulting matching schemes are comparatively analyzed from multiple perspectives under different supply/demand conditions and matching models.

4.2.1. Comparison of Platform Revenue Under Different Supply/Demand Conditions and Matching Models

First, from the platform’s perspective, the commission revenue that the vehicle–cargo matching platform can obtain under different supply/demand environments using different matching models is analyzed (where the ideal revenue is represented by solid lines, and the actual revenue is represented by dashed lines in corresponding colors), as shown in Figure 5.

As shown in Figure 5, under the condition where the number of cargo owners remains constant and the vehicle owners’ capacity gradually exceeds demand, the platform’s ideal revenue continues to increase for both matching modes, with only a small difference. However, the issue of declining platform revenue in the traditional matching mode is particularly noteworthy. The core difference between the traditional matching mode and the stable matching mode lies in the stability of the matching solution and the handling of blocking coalitions. The traditional matching mode often involves a larger number of blocking coalitions, which means that in certain cases, the matching between cargo owners and vehicle owners may not be mutually optimal, leading to potential revenue loss. In contrast, the stable matching mode ensures matching stability, thereby avoiding such situations and aligning the platform’s ideal revenue with its actual revenue.

At the same time, it can be observed that as the vehicle owners’ capacity gradually exceeds demand, the platform’s actual revenue in the traditional matching mode decreases as the number of vehicle owners increases. The surplus of vehicle owners may alter the bargaining dynamics between vehicle owners and cargo owners. Cargo owner satisfaction gradually becomes a key factor influencing the matching outcome. As cargo owners become more selective in choosing matching solutions, more cargo owners are dissatisfied with the options provided by the platform in the traditional matching mode and thus opt out of the matching process. This leads to a reduced matching success rate and a decline in platform revenue. Therefore, when vehicle capacity exceeds demand, the platform faces the challenge of adjusting its pricing and resource allocation strategies to balance supply and demand and improve the matching success rate.

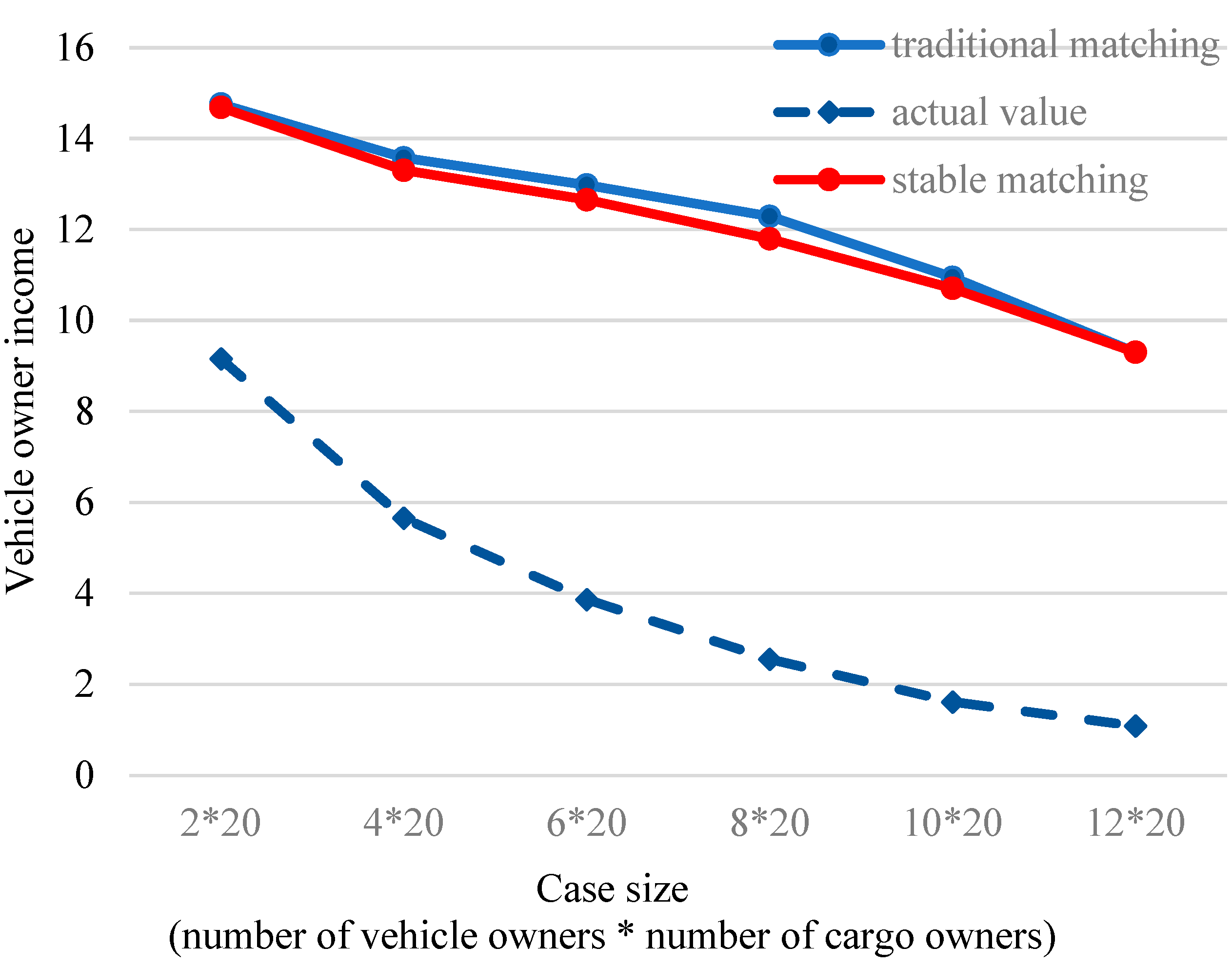
4.2.2. Comparison of Vehicle Owners’ Earnings Under Different Supply/Demand Conditions and Matching Models

Figure 6 illustrates the income variations of vehicle owners under different supply and demand environments when adopting different matching modes.

From the vehicle owner’s perspective, as the number of vehicle owners increases, the competitive pressure also rises, which directly leads to a decrease in the average ideal income of vehicle owners. However, although in the stable matching mode, the vehicle owner’s actual income is the same as the ideal income, in the traditional matching mode, vehicle owners face significant income loss. Moreover, in the traditional matching mode, as the number of vehicle owners increases, the income loss of vehicle owners becomes even more severe.

This phenomenon reflects the market’s “oversupply” condition. In this case, the platform’s matching algorithm needs to address the issue of supply/demand imbalance, and the traditional matching mode is clearly prone to failure under such conditions. As the number of vehicle owners exceeds demand, cargo owners have more options, leading to dissatisfaction with the solutions provided by the platform in the traditional mode. This results in a gradual decline in the matching efficiency between vehicle owners and cargo owners, which in turn affects the income of vehicle owners. This phenomenon also reflects potential flaws in the mechanism design of the traditional matching mode, which fails to effectively balance the needs and preferences of both supply and demand, especially in the case of market oversupply. The advantage of the stable matching mode lies in its ability to ensure that the vehicle owner’s actual income aligns with their ideal income. This indicates that the stable matching mode can effectively mitigate the adverse effects of market fluctuations on vehicle owners’ income. Its mechanism ensures bilateral stability between vehicle owners and cargo owners, reducing unnecessary income loss caused by intensified competition.

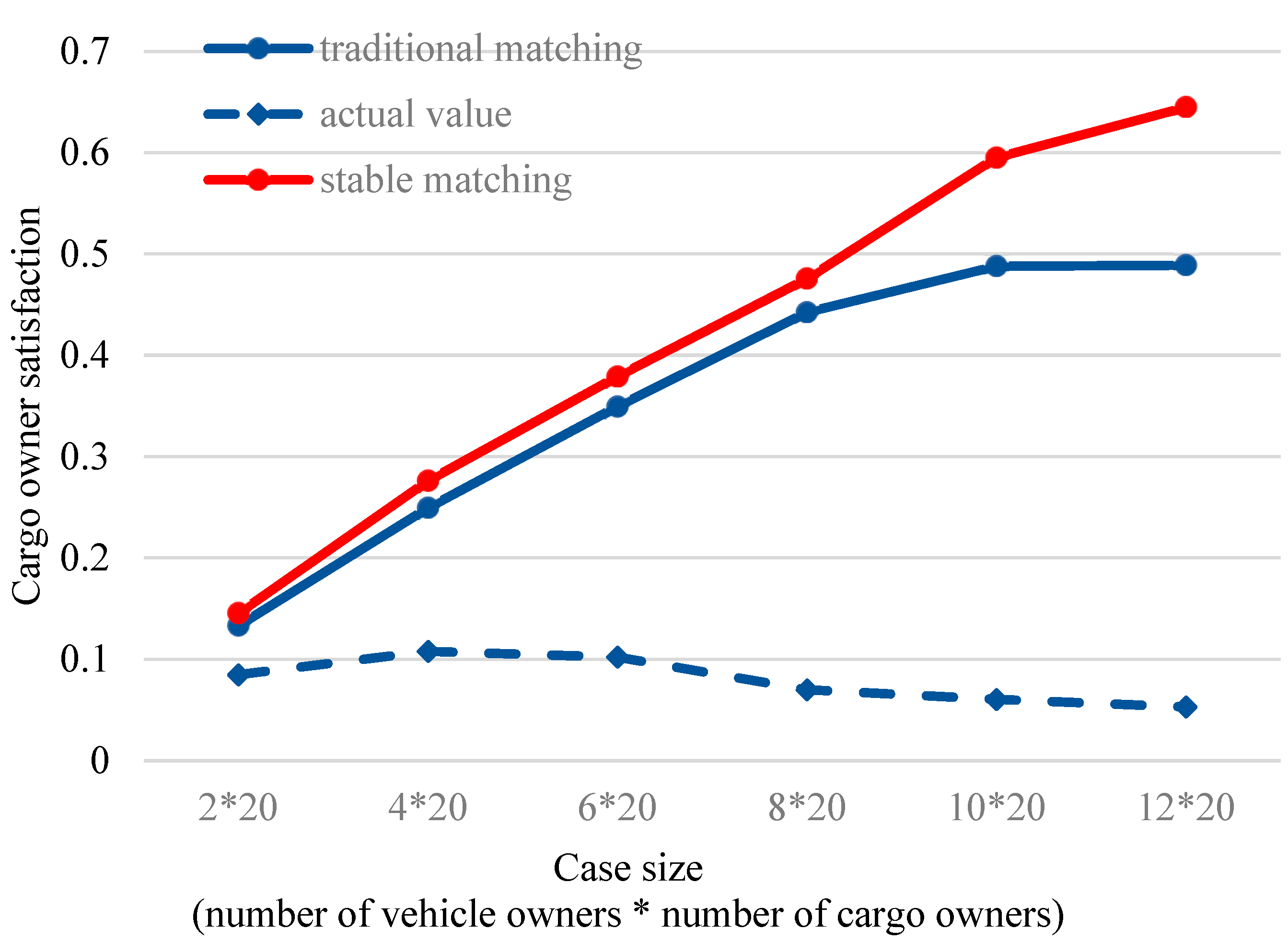
4.2.3. Comparison of Cargo Owners’ Satisfaction Under Different Supply/Demand Conditions and Matching Models

The difference between cargo owners’ “ideal satisfaction” and “actual satisfaction” is an important research issue. Ideal satisfaction represents the cargo owner’s expectations or ideal state regarding the matching solution, whereas actual satisfaction refers to the cargo owner’s perceived satisfaction during the actual matching process, influenced by factors such as matching quality, vehicle owner capability, and transportation costs.

Figure 7 reveals that as the number of vehicle owners gradually increases, cargo owners’ ideal satisfaction steadily rises, indicating that the increased market supply can better meet cargo owners’ demands for vehicle owners. However, changes in market supply and demand have a significant impact on cargo owners’ actual satisfaction. Due to its inability to ensure matching stability, the traditional matching mode may result in cargo owners facing mismatched solutions when there is an oversupply of vehicle owners, leading to a decline in actual satisfaction. The stable matching mode demonstrates a clear advantage in enhancing cargo owners’ actual satisfaction, particularly when the number of vehicle owners is large.

Platform strategies have a significant impact on cargo owner satisfaction, especially the resource allocation and scheduling strategies adopted by the platform during the matching process. One of the advantages of the stable matching mode over the traditional matching mode is its ability to enhance cargo owner satisfaction by ensuring stable resource allocation. However, how the platform can further optimize its strategies to adapt to market changes and improve cargo owner satisfaction remains an important issue.

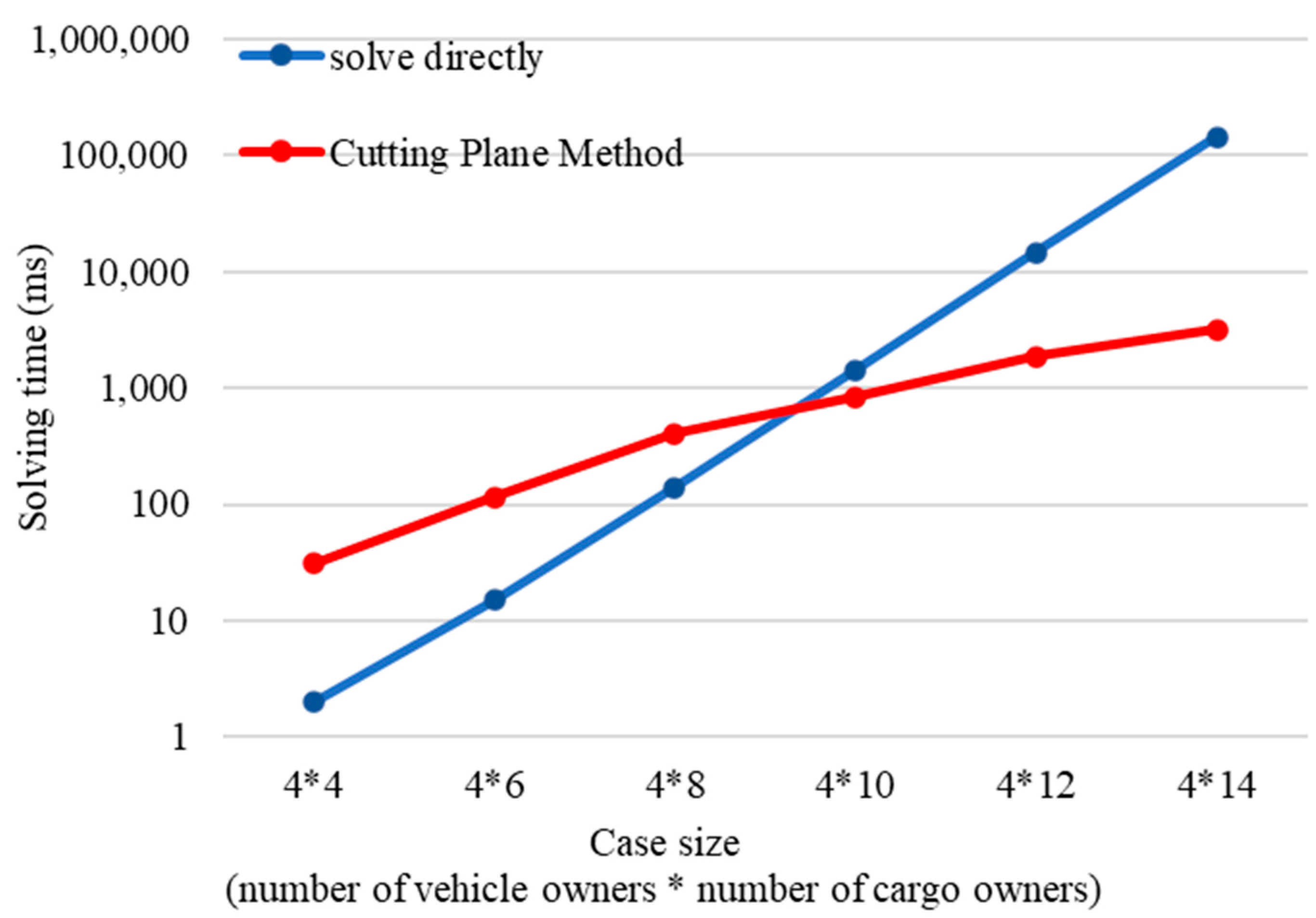
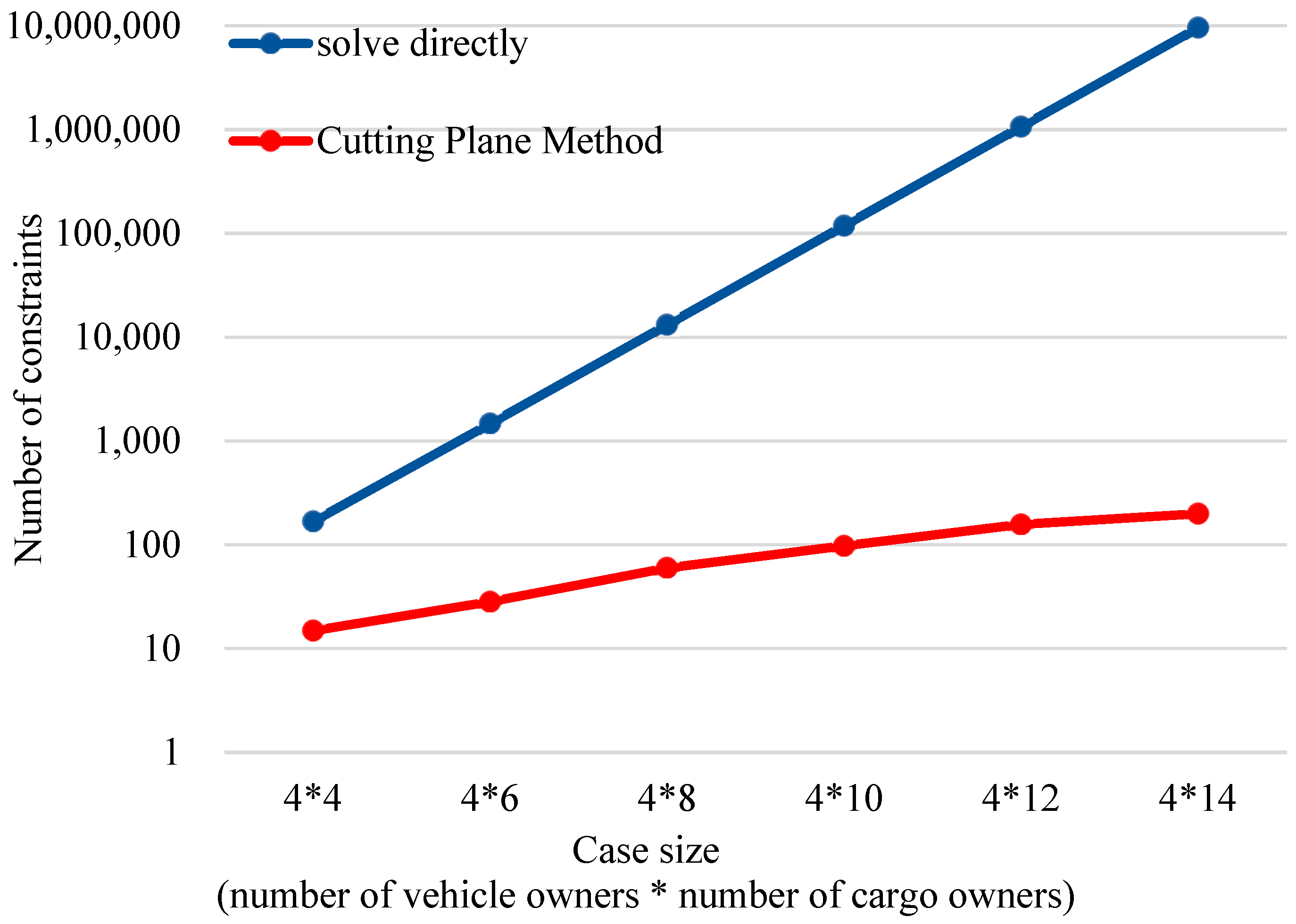
4.3. Efficiency Analysis of the Cutting-Plane Method

To validate the effectiveness of the proposed cutting-plane method in improving the computational efficiency of solving the group stable matching problem, this section conducts experiments on instances of varying sizes. Specifically, we compare two approaches: one that applies the cutting-plane method to solve a simplified version of the group stable matching model and another that directly formulates and solves the complete group stable matching model without employing the cutting-plane technique. Both approaches utilize the same optimization solver for solving the mixed-integer linear programming (MILP) models. The computational time and memory usage (measured by the number of constraints generated during the solution process) for solving the one-to-many stable matching problem on the vehicle–cargo matching platform using the two approaches are shown in Figure 8 and Figure 9, respectively. It is important to note that both figures use a logarithmic scale on the vertical axis.

As shown in Figure 6, when the instance size is small, directly solving the complete group stable matching model requires less computation time. However, as the instance size increases, the time required for the direct approach grows exponentially, quickly surpassing that of the cutting-plane method. Moreover, the gap between the two approaches continues to widen with increasing problem size.

In terms of memory usage, Figure 7 indicates that the number of constraints generated when directly solving the complete group stable matching model consistently exceeds that of the cutting-plane method. Furthermore, as the problem size increases, the number of constraints in the direct approach grows exponentially, resulting in a significantly higher order of magnitude compared to the cutting-plane method. For the largest instance in the experiment (4 × 14), the cutting-plane method reduced computation time by 97% and decreased the number of constraints generated during the solution process by 99%.

These results demonstrate that the cutting-plane method proposed in this study can effectively reduce both the computational time and memory requirements for obtaining the optimal solution to the group stable matching problem in vehicle–cargo matching platforms, thereby significantly improving the overall matching efficiency of the platform.

In summary, through simulation experiments from the perspectives of the platform, vehicle owners, and cargo owners, it has been verified that the group stable matching model for the carpooling business in vehicle–cargo matching platforms is highly adaptable. Additionally, the algorithm can significantly improve solution efficiency, especially in handling large-scale data and complex constraints on vehicle–cargo matching platforms. This model can enhance matching efficiency and platform competitiveness in practical operations, demonstrating good feasibility and promotional value.

5. Conclusions

This paper focuses on the freight pooling matching problem within vehicle–cargo matching platforms, incorporating stable matching theory in the process. To improve matching efficiency and fully consider user preferences, this paper defines the concepts of composite preference and group stability based on composite preferences, and establishes a group stable matching model. The model is a mixed-integer linear programming model, characterized by a small number of decision variables and a large number of constraints. To address the computational complexity, this paper introduces and improves the cutting-plane algorithm by removing redundant constraints and retaining only the essential ones, significantly enhancing the solution efficiency.

The main conclusions of this paper are as follows. (1) Advantages of the group stable matching model: The group stable matching model based on composite preferences significantly improves platform efficiency, vehicle owner revenue, and cargo owner satisfaction under different supply/demand conditions. Compared to traditional matching models, this approach better balances the supply/demand relationship, thereby optimizing platform resource allocation. (2) Efficiency of the cutting-plane algorithm: The cutting-plane algorithm saves 97% of the computation time and reduces 99% of the constraints during the solving process, significantly improving the solution efficiency of the model. This enables vehicle–cargo matching platforms to provide accurate matching solutions more quickly, greatly enhancing the response speed in practical applications. (3) Improvement in platform efficiency and user satisfaction: Through simulation experiments, this paper validates the significant advantages of the proposed group stable matching model in terms of platform efficiency, vehicle owner income, and cargo owner satisfaction, demonstrating the practicality and scalability of the method.

The main innovations of this paper are as follows: (1) Introduction of stable matching theory: This paper is the first to apply stable matching theory to the freight pooling matching problem in vehicle–cargo matching platforms, proposing the concept of group stability based on composite preferences, thereby overcoming the limitations of traditional matching models. (2) Algorithmic innovation and improvement: By introducing the cutting-plane algorithm and modifying it to suit the characteristics of the model, the solving efficiency is significantly improved. The algorithm removes redundant constraints and retains only the essential ones, greatly optimizing the solution process and demonstrating strong adaptability. (3) Comprehensive consideration of user preferences: The freight pooling matching problem fully takes into account the preferences of vehicle owners and cargo owners and establishes the corresponding group stable matching model, providing more personalized and accurate matching solutions for practical platforms.

The limitations and future research directions of this paper are as follows. (1) Model complexity: Although the mixed-integer linear programming model proposed in this paper offers high solving efficiency, due to the NP-hard nature of the problem, the model may still encounter computational bottlenecks under certain extreme supply/demand conditions. Future research could focus on designing more advanced algorithms to solve this problem. (2) Dynamic adaptability: This study primarily focuses on optimizing static matching models. Future research could further consider the impact of dynamic market demands on matching outcomes, such as fluctuations in demand or changes in vehicle owner and cargo owner preferences. Designing a flexible matching mechanism would enhance the platform’s adaptability and real-time response capability. (3) In this study, the price factor is primarily estimated by the cargo owner based on the weight of the cargo. Future research could consider introducing a personalized pricing mechanism and scheduling strategies based on reinforcement learning, which could further optimize the matching efficiency and income distribution for both vehicle owners and cargo owners.