The Hub Location and Flow Assignment Problem in the Intermodal Express Network of High-Speed Railways and Highways ^†

Abstract

The intermodal express network of high-speed railways and highways can fully utilize the flexibility of highways and the advantages of high-speed railways, such as low cost, high efficiency, and low carbon emission. This paper studies the hub location and flow assignment problem in the intermodal express network of high-speed railways and highways, which can not only increase the transportation efficiency but also provide door-to-door service. Considering the characteristics of multiple modes, flow balance, carbon emission, capacity constraints, and time constraints in the intermodal express network, a mixed-integer linear programming model is proposed with the objective of minimizing the total cost by determining the hub locations, allocations, mode selections, and flow assignments. Owing to the NP-hard computational complexity, an improved genetic algorithm with local search is designed by combining the genetic operators and two optimization strategies to solve the problem effectively. Lastly, numerical experiments are conducted to validate the feasibility of the model and the effectiveness of the algorithm.

1. Introduction

1.1. Motivations

Recently, the rapid development of e-commerce and cold chain logistics has significantly driven the growth of freight transportation and express delivery demands. Additionally, the rising demand for transporting high-value freight, including business documents, medical supplies, and perishable goods, has imposed stricter requirements on delivery speed, environmental control, and transportation reliability. This dynamic has energized the freight express market while creating new operational challenges. As a new mode of freight transportation, high-speed railway express (HRE) has gained widespread attention. Compared to air freight systems, HRE demonstrates superior load capacity and operational reliability independent of adverse weather conditions; compared to highway transportation, HRE has faster speed and is not influenced by traffic congestion. In addition, HRE is powered by electricity, whose carbon emissions per unit are much lower than those of transportation powered by traditional energy sources. Owing to its advantages of low cost, high efficiency, and low carbon emissions, HRE has become an ideal choice in medium–long-distance logistics.

Although HRE excels in medium–long-distance transportation, its coverage is inherently constrained by fixed railway routes and hub locations. Highway transportation, conversely, offers unparalleled flexibility in last-mile delivery, remote area accessibility, and time-sensitive regional distribution. Compared to HRE, the most significant advantage of highway transportation is its door-to-door service. This complementary relationship necessitates an intermodal network in which high-speed railways handle trunk line transportation between major hubs, while highways manage feeder distribution and regional connectivity. Such an intermodal express network can not only increase the transportation efficiency, but also facilitate door-to-door service. It was reported that 1 percentage increment of the intermodal transportation volume in China can reduce the total social logistics cost by approximately 0.9 percentage points, saving about 100 billion yuan, meanwhile 1 percentage increment of the railway volume reduces overall logistics cost by 0.2 to 0.5 percentage points [1]. This is the key motivation to study the intermodal express network of high-speed railway and highway transportation.

In the intermodal network, the critical challenge lies in the coordination of hub location and flow assignment, which are two complex and inter-related decisions. The integrated optimization of hub location and flow assignment is very meaningful for the intermodal express network. There are several key characteristics in the intermodal express network, mainly including transportation timeliness, hub and link capacities, and multiple transportation modes. Furthermore, the carbon emission is incorporated as a critical element into the modeling framework to evaluate the quality of the transportation. Therefore, this paper studies the intermodal express network of high-speed railway and highway transportation, and proposes an integrated optimization approach for the hub location and flow assignment problem to determine hub locations, demand node allocations, transport mode selections, and flow assignments.

1.2. Literature Review

The related literature will be reviewed in four main areas: the research of HRE, the hub location problem in the classical network, the hub location problem in the intermodal network, and the hub location and flow assignment problem in the intermodal network.

The research of HRE. With the development of high-speed railway networks, the research on HRE has grown significantly. Firstly, there has been a wave of research on the feasibility of HRE. Zhang and Qin [2] analyzed the development of HRE from both technical and economic aspects, and finally concluded that it is feasible to carry out HRE in China. Boehm et al. [3] investigated the development potential of HRE, revealing that replacing highway express with HRE could reduce carbon emissions by up to 80% and the operation cost can be mitigated by controlling the maximum speed of the high-speed railway. In addition, scholars have also proposed concrete strategies to support HRE development. Fang et al. [4] developed a multi-criteria decision-making model to address the pricing strategy for HRE in competitive markets, which can increase HRE operators’ revenue by 13%. Based on the integrated demand forecasting, Huang et al. [5] developed differentiated development strategies for HRE, concluding that the investment in high-demand areas should be prioritized and advocacy should be increased in low-demand areas. Recently, numerous studies on HRE have focused on its integration with other transportation modes. Wang et al. [6] proposed an intermodal network of high-speed railway and crowd-couriers to enhance the operational efficiency and cost-effectiveness of freight service. Sun [7] investigated the road–rail intermodal routing problem in a hub-and-spoke network and found that multiple time windows and truck operation optimization based on carbon cap-and-trade policies can reduce total costs and carbon emissions. Zhen et al. [8] focused on the intermodal network of high-speed railway and highway transportation to optimize the vehicle arrangement, station selection, and route planning of HRE. In addition, there are also a few studies involving the organizational mode [9] and scheduling optimization [10,11] of HRE.

The hub location problem in the classical network. Hub location constitutes a critical decision-making problem in both classical and intermodal networks. A review of classification, modeling, and solution methods for the hub location problem can be found in the existing literature, where the classical hub location problem can be divided into three categories: $p$-hub median problem, $p$-hub center problem, and hub covering problem [12,13,14]. Racunica and Wynter [15] analyzed the hub location problem for railway freight in a hub-and-spoke network and designed a heuristic algorithm to solve the problem. Gu et al. proposed a hub location model with multiple delivery time restrictions in the hub-and-spoke network [16]. Aloullal et al. [17] proposed a time-dependent hub location routing model, developing both exact and metaheuristic solution approaches to demonstrate how temporal decision-making improves adaptability to parameter changes. Wang et al. [18] proposed a hierarchical single-assignment $p$-hub median problem to cope with multilevel demand. Marand and Hoseinpour [19] focused on the congested hub location problem, aiming to optimize the total profit by determining the appropriate hub location and capacity.

The hub location problem in the intermodal network. O’kelly and Lao [20] pioneered the idea of mode selection optimization in air–truck intermodal networks. Ishfaq and Sox [21] extended the $p$-hub median model to intermodal networks. Alumur et al. [22] proposed a single-allocation intermodal network optimization problem, considering the integration of land and air transport, and designed a heuristic algorithm for solving it. Boucher and Fransoo [23] formulated a decision model to optimize terminal location and freight assignment across dedicated trucking transportation and intermodal networks, considering carbon emissions and mode transfer costs. Maiyar et al. [24] proposed an intermodal grain transportation model in the presence of hub disruption while incorporating environmental factors for sustainability. Jeong and Choi [25] introduced a multi-period capacitated hub location model to cope with the impacts of climate change and improve production sustainability. Ziar et al. [26] proposed a railway–highway intermodal $p$-hub median model for the dry port location problem, establishing inland intermodal terminals connected to dry port. Somsai et al. [27] focused on reducing energy consumption and emissions in intermodal networks by optimizing routes and using alternative transportation modes, proposing a general green vehicle routing model to identify optimal solutions for strategic decision-making.

The hub location and flow assignment problem in the intermodal network. Flow assignment is an important extension of the classic hub location problems. Serper and Alumur [28] demonstrated that the use of alternative transportation modes and different kinds of vehicles to transport goods in intermodal networks can better deal with flow assignment and optimize the total cost. Song et al. [29] focused on the transportation of hazardous goods and considered switching between railway, expressway, and ordinary transportation modes under traffic-constrained scenarios to optimize the freight services in the intermodal network of railways and trucks. Kovač et al. [30] focused on the intermodal network of highway, railway, and inland waterway transportation to rationalize the assignment of container flows and contribute to the development of dry port terminals to promote the sustainability of intermodal networks. Hu et al. [31] proposed a model for the intermodal network of an underground logistics system and highways to decide hub location, demand node allocation, and flow assignment.

To present the differences between this paper and the existing research more clearly,

Table 1. Summary of related studies.

Research	HRE	Hub Location	Flow Assignment	Intermodal Network	Carbon Emission
Ma and Liao [10]	√
Somsai et al. [27]				√	√
Zhen et al. [8]	√	√		√
Alumur et al. [22]		√	√
Fang et al. [4]	√
Hu et al. [31]		√	√	√
This study	√	√	√	√	√

provides a brief summary of related references. The existing research involves some issues related to HRE, hub location, flow assignment, and intermodal network. To the best of our knowledge, there has been no research considering the hub location and flow assignment problem in the intermodal express network of high-speed railways and highways, especially taking the carbon emissions into account.

1.3. Research Contributions and Outline

The contributions of this paper are as follows:

(1) This paper develops an integrated model for the hub location and flow assignment problem in the intermodal express network of high-speed railway and highway transportation, considering the characteristics of multiple transportation modes, flow balance, carbon emission, capacity limitations, and time constraints.

(2) Due to the computational complexity of the developed model, an improved GA is designed by integrating genetic operators with two optimization strategies. The genetic operators are primarily used to enhance the solution diversity, while the optimization strategies aim to accelerate convergence.

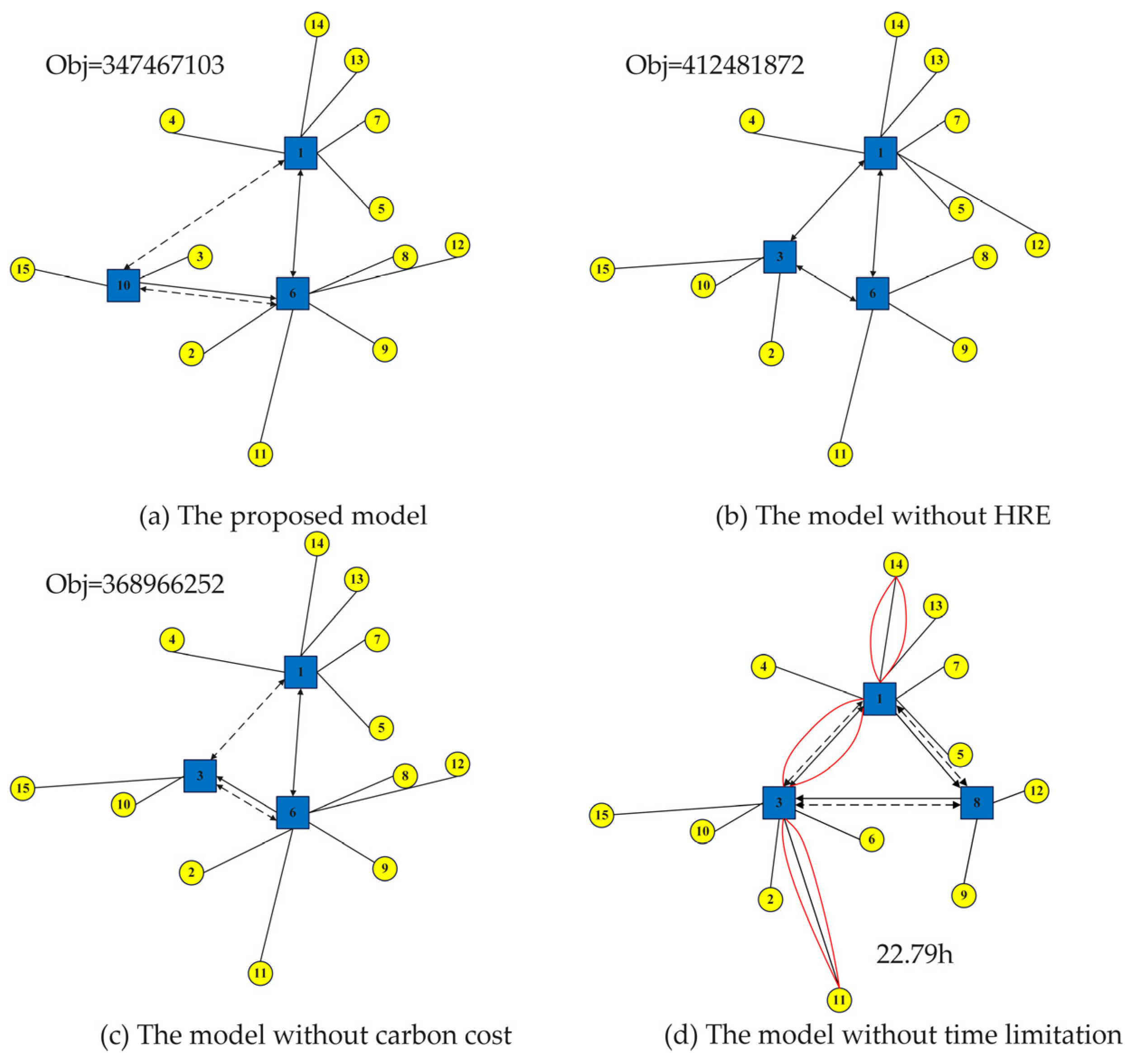
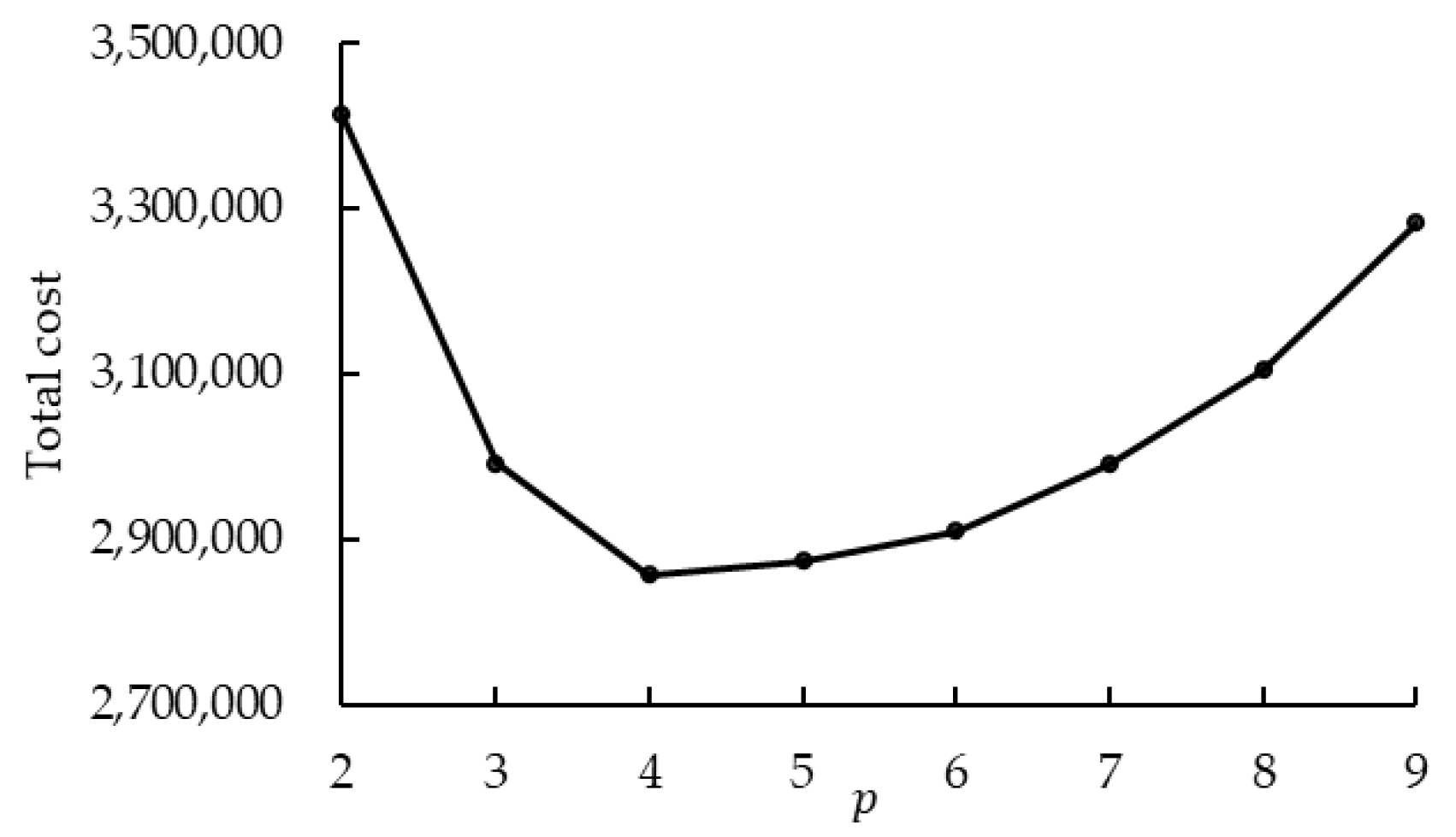
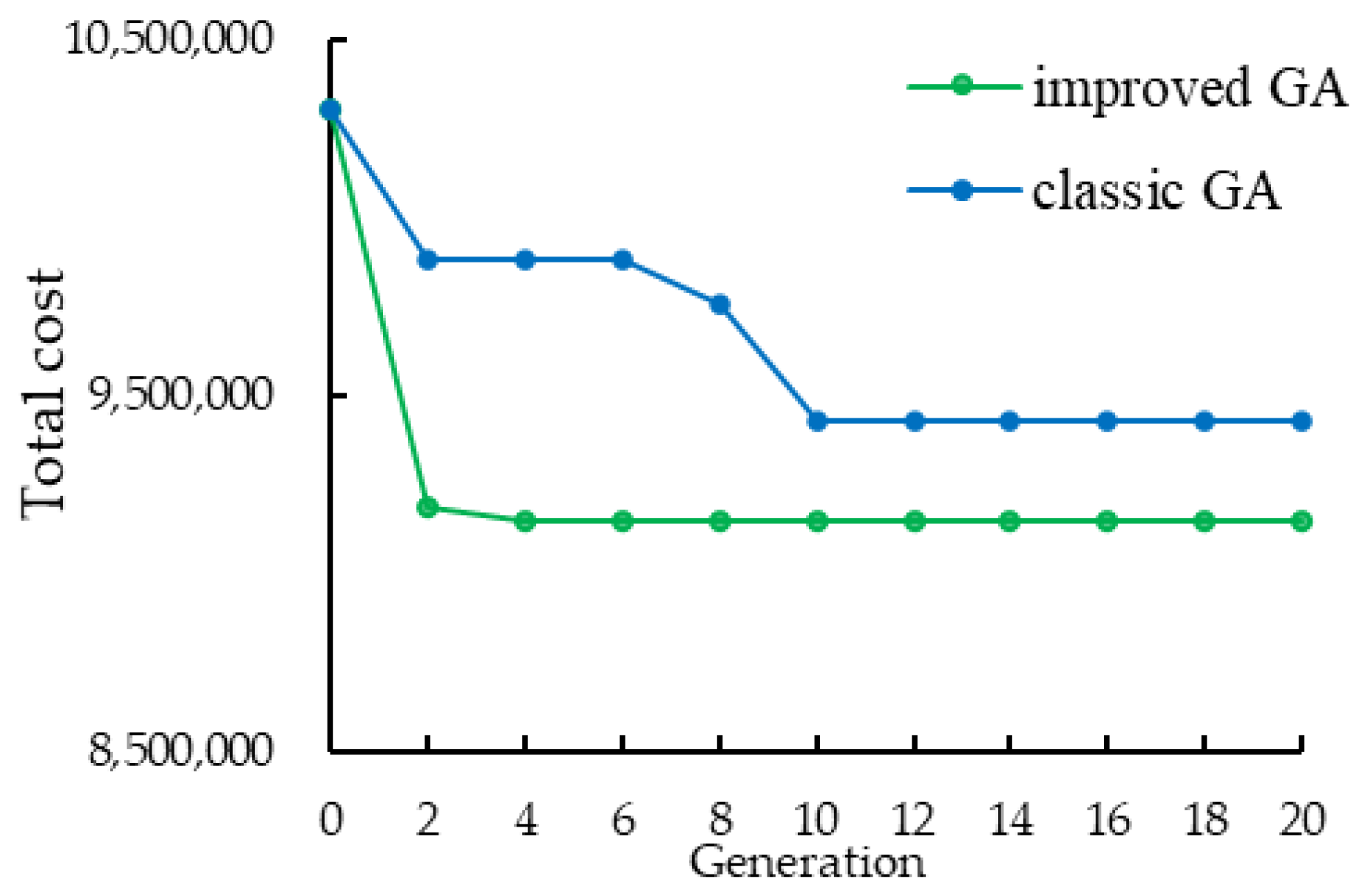
(3) Numerical experiments validate the advantages of the developed model compared with degenerated models and demonstrate the effectiveness of the proposed algorithm in terms of time and accuracy. Additionally, several insightful findings are discussed.

The remainder of this paper is organized as follows. Section 2 gives the problem description and model construction, and Section 3 designs improved GA. Section 4 gives the results of numerical experiments. Section 5 discusses the managerial implications, and finally, the conclusions and future studies are presented in Section 6.

2. Problem Description and Model Construction

2.1. Problem Description

In this problem, the intermodal express network of high-speed railway and highway transportation is a two-layer hub-and-spoke network. In the first layer, all hubs are connected by a complete network, and the links may be HRE, highway express, or both. In the second layer, all non-hubs are connected to hubs via a star network, and the link is highway transportation. Current high-speed railway hubs primarily focus on passenger transportation, with limited dedicated equipment and labors for freight express. Therefore, the capacity of hubs and links for freight express is considered.

Given all demand nodes and potential hubs, some potential nodes are selected to construct hubs, and each demand node is allocated to one selected hub. All express deliveries are transported by highway from the origin to the allocated hub, then transported by highway or HRE to another hub, and finally transported by highway to the destination. The transportation time from origin to destination shall be within the delivery period.

In the field of transportation, carbon emission is one of the core indicators for measuring environmental sustainability [32]. There are mainly two ways to considering carbon emission, the constraints of carbon emission cap [33] or the objective of carbon cost [34]. In this study, carbon emission is incorporated into the objective function as the saved carbon cost calculated by multiplying the saved carbon emissions by the carbon tax, which coincides with the focus on cost-effectiveness in traditional transportation planning. Moreover, considering the saved carbon cost is in line with the low-carbon feature of high-speed railway, which is conducive to the transformation of the highway express network into an intermodal express network of high-speed railway and highway transportation.

Figure 1 provides a simple example to illustrate the intermodal express network with ten nodes, all considered as potential hubs. A total of 3 of them (nodes 1–3) are selected to construct hubs; nodes 4, 5, and 8 are allocated to hub 1, nodes 6 and 7 are allocated to hub 2, and nodes 9 and 10 are allocated to hub 3. For the link between hubs 1 and 2, highway express is adopted; for the link between hubs 2 and 3, HRE is adopted; for the link between hubs 1 and 3, link 1→3 is connected by highway express and link 3→1 is connected by HRE.

2.2. Assumptions and Notations

Some necessary assumptions are made for modeling convenience.

(1) The total number of hubs to be constructed is predetermined, i.e., p-median hub location problem [12,35].

(2) The capacity limitations of hubs and links are considered, i.e., capacitated hub location problem.

(3) Due to economies of scale, the unit transportation cost between hubs is lower than that between demand nodes and hubs.

(4) The unit transportation cost of high-speed railway is lower than that of highway transportation.

(5) Carbon emissions are proportionally related to both transportation distance and flow volume, and the carbon emissions of HRE are significantly lower than those of highway express.

The following notations are introduced to facilitate the development of the mathematical models, where input parameters are defined in

Table 2. Input parameters and description.

Notations	Description
$N$	The set of demand nodes
$H$	The set of potential hubs
$p$	The number of hubs to be constructed
${ch}_k$	The fixed cost of constructing a hub at node $k$, $\forall k\in \mathrm{H}$
${hl}_{kl}$	The link cost of HRE from hub $k$ to hub $l$, $\forall k,l\in \mathrm{H}$
${hl}_{kl}^0$	The link cost of highway transportation from hub $k$ to hub $l$, $\forall k,l\in \mathrm{H}$
$d_{ij}$	The distance between demand nodes
$w_{ij}$	The freight demand from node $i$ to node $j$, and $O_i$ is the total volume originates from node $i$, $D_j$ is the total volume directs to node $j$, $i.e.$, $O_i={\sum }_j{w}_{ij},D_j={\sum }_i{w}_{ij},\forall i,j\in N$
$Q_{kl}$	The freight capacity from hub $k$ to hub $l$, $\forall k,l\in \mathrm{H}$
$V_k$	The capacity of hub $k$, $\forall k\in H$
$a$	The freight cost per distance and flow between non-hubs and hubs
$b^1$	The freight cost per distance and per flow of HRE between hubs
${\mathrm{b}}^2$	The freight cost per distance and per flow of highway between hubs
$\mathsf{\gamma }$	The carbon emissions saved per distance and per flow
$\theta$	The carbon tax per volume
$t_{ij}$	The transportation time from node $i$ to $j$ by highway express, $\forall i,j\in N$
$\mu$	The time discount factor for HRE
$t_k^0$	The operation time at hub $k$, $\forall k\in \mathrm{H}$
$T_1$	The time limitation for HRE
$T_2$	The time limitation for highway express
$M_0$	A sufficiently large constant

, and decision variables are specified in

Table 3. Decision variables and description.

Variables	Description
$x_{ik}$	Binary, equals to 1 if node $i$ is allocated to hub $k$, and 0 otherwise, note that if $x_{kk}$ equals to 1, node $k$ is a selected hub, $\forall i\in N,k\in H$
$z_{kl}$	Binary, equals to 1 if the HRE link is opened from hub $k$ to hub $l$, and 0 otherwise, $\forall k,l\in H$
$z_{kl}^0$	Binary, equals to 1 if the highway express is retained from hub $k$ to hub $l$, and 0 otherwise, $\forall k,l\in \mathrm{H}$
$f_{kl}^i$	Integer, the demand flow from node $i$ to hub $l$ via hub $k$, $\forall i\in N,k,l\in H$
$g_{kl}$	Integer, the demand flow by HRE from hub $k$ to hub $l$, $\forall k,l\in H$
$h_{kl}$	Integer, the demand flow by highway expresses from hub $k$ to hub $l$, $\forall k,l\in H$

.

2.3. Mixed-Integer Linear Programming Model

Based on the problem definition and notations, the following mixed-integer linear programming model is formulated.

$$\begin{array}{ll}\min & {\sum }_{k\in H}{ch}_k·x_{kk}+{\sum }_{k\in H}{\sum }_{l\in H}{hl}_{kl}·z_{kl}+{\sum }_{k\in H}{\sum }_{l\in H}{hl}_{kl}^0·z_{kl}^0\\ & +{\sum }_{k\in H}{\sum }_{i\in N}a·d_{ik}·O_i·x_{ik}+{\sum }_{k\in H}{\sum }_{i\in N}a·d_{ik}·D_i·x_{ik}\\ & +{\sum }_{k\in H}{\sum }_{l\in H}{b}^1·d_{kl}·g_{kl}+{\sum }_{k\in H}{\sum }_{l\in H}{b}^2·d_{kl}·h_{kl}-{\sum }_{k\in H}{\sum }_{l\in H}\theta ·\gamma ·d_{kl}·g_{kl}\end{array}$$

(1)

$$\mathrm{s}.\mathrm{t}.{\sum }_{k\in H}{x}_{kk}=p$$

(2)

$${\sum }_{k\in H}{x}_{ik}=1,\forall i\in N$$

(3)

$$x_{ik}\le x_{kk},\forall i\in N,k\in H$$

(4)

$${\sum }_{l\in H:l\ne k}{f}_{lk}^i+O_i·x_{ik}={\sum }_{l\in H:l\ne k}{f}_{kl}^i+{\sum }_j{w}_{ij}·x_{jk},\forall i\in N,k\in H$$

(5)

$$z_{kl}\le x_{kk},\forall k,l\in H$$

(6)

$$z_{kl}\le x_{ll},\forall k,l\in H$$

(7)

$$g_{kl}\le M_0·z_{kl},\forall k,l\in H$$

(8)

$${\sum }_{l\in H}{f}_{kl}^i\le M_0·x_{ik},\forall i\in N,k\in H$$

(9)

$$g_{kl}+h_{kl}={\sum }_{i\in N}{f}_{kl}^i,\forall k,l\in H$$

(10)

$$g_{kl}\le {\sum }_{i\in N}{f}_{kl}^i,\forall k,l\in H$$

(11)

$$g_{kl}\le Q_{kl},\forall k,l\in H$$

(12)

$${\sum }_{l\in H}{g}_{kl}+{\sum }_{l\in H}{g}_{lk}\le V_k,\forall k\in H$$

(13)

$$t_{ik}·x_{ik}+(t_k^0+\mu ·t_{kl}+t_l^0)·z_{kl}+t_{lj}·x_{jl}\le T_1,\forall i,j\in N,k,l\in H$$

(14)

$$t_{ik}·x_{ik}+t_{kl}·z_{kl}^0+t_{lj}·x_{jl}\le T_2,\forall i,j\in N,k,l\in H$$

(15)

$$x_{ik},z_{kl},z_{kl}^0\in \left\{\mathrm{0,1}\right\},f_{kl}^i,g_{kl},h_{kl}\ge 0,\forall i,j\in N,k,l\in H$$

(16)

Objective function (1) optimizes the total cost, where the first term is the construction cost of hubs; the second and third terms are the link connection cost; the fourth and fifth terms are the transportation cost between demand nodes and hubs; the sixth term is the HRE cost between hubs; the seventh term is the highway express cost between hubs; and the eighth term is the saved carbon cost [36]. Constraint (2) ensures that there are p nodes to be selected to construct hubs. Constraint (3) ensures the single allocation, i.e., every demand node is allocated to only one hub. Constraint (4) requires that the allocated node must be a selected hub. Constraint (5) maintains the balance of flows between hubs and ensures the resource allocation. Constraints (6)–(7) restrict that the link of HRE can only be opened when both the endpoints are hubs. Constraints (8)–(11) ensure flow balance throughout the network, where constraints (8)–(9) restrict the flow to exist only if the corresponding link is connected, and constraints (10)–(11) ensure that the sum of flows through hubs from all demand nodes is equal to the combined volume of HRE and highway express between hubs. Constraints (12)–(13) impose capacity limits for HRE of links and hubs, correspondingly. Constraints (14)–(15) ensure that delivery time limits are met for HRE and highway express. Constraint (16) defines variable domains.

The proposed model is a mixed-integer linear programming model with $O\left(\left|N\right|·{\left|H\right|}^2\right)$ decision variables and $O\left({\left|N\right|}^2·{\left|H\right|}^2\right)$ constraints, where $\left|N\right|$ and $\left|H\right|$ denote the number of demand nodes and alternative hubs, respectively. Obviously, with the increase in $\left|N\right|$ and $\left|H\right|$, the model contains a huge number of variables and constraints. Furthermore, the integration of hub location and flow assignment increases the computational complexity. Therefore, heuristic algorithms are designed to obtain the near-optimal solution within a short time.

3. Improved Genetic Algorithm

To address the inherent NP-hard complexity, we develop an improved GA with local search to obtain near-optimal solutions within reasonable computational time, which has been widely used in the fields of hub location problems [37]. The algorithm integrates genetic operators for global search with two optimization strategies for local search. The global search is responsible for maintaining population diversity and exploring the broader solution space, while the local search strategies focus on refining the solution quality. The flowchart of the proposed improved GA is illustrated in Figure 2.

3.1. Encoding and Decoding

The chromosome consists of three components: location gene, allocation gene, and HRE link connection gene. Based on these genes, the highway express links and flow assignments are determined. The location gene is composed of values “0” and “1”, with “0” indicating a non-hub and “1” indicating a selected hub. The allocation gene represents the allocated hub. The link connection gene also uses values “0” and “1”, where “1” indicates the HRE link is connected and “0” otherwise. It is noted that link “1→3” and link “3→1” might be different. Figure 3 provides an example of a chromosome with $\left|N\right|=10,\left|H\right|=5,p=3$. Note that the green parts of the chromosome indicate the location of hubs or link connections. Nodes 1, 2, and 3 are selected as hubs; nodes 4, 9, and 10 are allocated to hub 1; nodes 7 and 8 are allocated to hub 2; and nodes 5 and 6 are allocated to hub 3. The HRE links 1→3, 2→1, 2→3, and 3→1 are connected.

To calculate the objective function value, it is necessary to compute the construction cost, the link connection cost, the transportation cost, and the saved carbon cost. The construction cost can be calculated directly based on the location genes, i.e., the sum of construction cost corresponding to points with value “1”. Firstly, the flows of HRE, the highway express between hubs, and the flows between hubs, i.e., $g_{kl}$, $h_{kl}$, and $f_{kl}^i$, should be calculated. Then, the transportation cost, the saved carbon cost, and the link connection cost for highway transportation are calculated according to the obtained flows. Finally, the objective function value for each chromosome can be determined.

3.2. Initialization

The location and allocation genes are initialized randomly. For the location genes, $p$ points are randomly assigned a value of “1”, while the remaining points are assigned a value of “0”. The allocation genes are assigned to the points with a value of “1”. Notably, the allocation is initialized using a greedy strategy, that is to say the node is assigned to the nearest available hub.

The link connection genes depend on the balance between the link connection cost and the saved transportation cost, which is shown in Algorithm 1. The priority of links is determined based on the volume of demand flows, and the links with higher flows are given priority consideration for whether to open. The link will be established if the cost can be reduced and the remaining capacity is sufficient to meet the demand.

Algorithm 1. The initialization of link connection

Input: $x_{ik}$, $f_{kl}^i$, $V_k$, $Q_{kl}$

Output: $z_{kl}$

1. for all $k\in H,l\in H,k\ne l$

2.  if $k$ and $l$ are all hubs then

3.   calculate the total flow of the link $i.e.,sum{f}_{kl}={\sum }_i{f}_{kl}^i$

4.  end if

5. end for

6. determine the priority queue in descending order based on the total flow

7. for all links in the priority queue

8.  if cost savings exceed construction cost$\&\&$ hub capacity is enough then

9.   $z_{kl}\leftarrow 1$

10.  end if

11.end for

3.3. Genetic Operators

Selection operator. Roulette selection is widely adopted for screening high-performance individuals [38]. This study uses the roulette selection strategy to generate new populations, where the selection probability of each chromosome is based on its fitness.

Crossover operator. By exchanging gene fragments of parent individuals, the crossover operator generates offspring with new gene combinations, avoids premature convergence of the population to the local optima, and maintains diversity to explore a broader solution space [38]. Considering the characteristics of the chromosome, single-point crossover is applied to the location gene. Since the genes of allocation and HRE link depend on the genes of location, the crossover is performed only on the location part. First, a crossover point is randomly selected, and the gene segments before this point are exchanged between the two parent chromosomes. After the crossover, it is necessary to verify whether the number of hubs meets the requirement and the allocated nodes are legal hubs. If not, adjustments are made until the number of hubs and the allocation of demand nodes are legal. Concretely, the adjustment rules can be described as the two aspects. When the number of hubs is greater than p, randomly select a hub to make it a non-hub; when the number of hubs is less than p, randomly select a non-hub to make it a hub. This process continues until the number of hubs is p. Then, the check for the allocation is performed. If the assigned node is a non-hub or the assigned hub exceeds its capacity, the node is assigned to the nearest available hub. Figure 4 provides a simple example to illustrate the crossover operator. Node 4 is selected as the crossover point, and the gene segments before this point in these two paternal chromosomes are exchanged. After the exchange, the total hub number is violated; therefore, nodes 3 and 5 are randomly selected to adjust the number of hubs, and the demand nodes with invalid allocation genes marked with red crosses are reallocated to the nearest hub.

Mutation operator. Mutation operators can prevent population convergence to local optima by randomly altering individual genes. In this study, swap mutation is applied. Similarly to the crossover operator, the mutation is performed only on the location part. First, two points with different attribution are randomly selected, i.e., a hub and a non-hub, and then, their location genes are exchanged. After the crossover operation, illegal genes may occur after mutation. Therefore, necessary adjustments must be made to ensure the constraints are satisfied. Figure 5 provides a simple example to illustrate the mutation operator. Nodes 3 and 5 are selected as mutation points, and their properties are exchanged to obtain new location genes. The nodes marked with red crosses represent illegally allocated genes, which are then adjusted to become legal according to the adjustment rules mentioned in the cross operator.

3.4. Optimization Strategies

In this problem, location, allocation, and link connection are three important decisions, which jointly determine the quality of solutions. Therefore, two optimization strategies are developed with a focused goal, location and allocation optimization and link optimization, to systematically address the core elements of the hub location and flow assignment problem in the intermodal express network of high-speed railway and highway transportation.

Location and allocation Optimization. The location optimization aims to identify better hub positions, and its pseudocode is presented in Algorithm 2. For each hub, its gene is exchanged with that of a non-hub. After visiting all non-hubs, the location with the lowest cost is kept. This process is repeated until all hubs have been visited. Checks and adjustments are performed as described in Section 3.3. Figure 6 illustrates a simple example of the location and allocation optimization, in which the attribution of hub 8 is exchanged with non-hub 1, i.e., hub 8 is converted into a non-hub, and non-hub 1 is designated as a hub, resulting in a more balanced network configuration. Following the adjustment of the location gene, the corresponding allocation scheme must be updated to maintain feasibility. So, the allocation optimization is embedded within the location optimization process. Demand nodes are first allocated to the nearest hub; if the nearest hub violates any constraints, the allocation is sequentially assigned to the next closest feasible hub until all requirements are satisfied.

Algorithm 2. Location optimization

Input: $x_{ik}$

Output: $x_{ik}^{\prime }$

1. for all $k\in H,l\in H,k\ne l$

2.  if $k$ is a selected hub and $l$ is a non-hub $i.e.,x_{kk}=1\&\&x_{ll}=0$ then

3.   exchange the property of these two nodes, $i.e.,x_{kk}^1\leftarrow 0,x_{ll}^1\leftarrow 1$

4.   if the objective is better $i.e.,f\left(x_{ik}^1\right)<f\left(x_{ik}\right)$ then

5.    update: $x_{ik}^{\prime }\leftarrow x_{ik}^1$

6.   end if

7.  end if

8. end for

Link Optimization. The link optimization strategy focuses on fully utilizing the HRE capacity of hubs and searching for better links. The overall procedure is presented in Algorithm 3. When a link is closed, its occupied HRE capacity is released and becomes available for other links. For each opened link, its gene is exchanged with that of a closed link, and the one with the lowest cost is retained after visiting all links. This process is repeated until all open links have been visited. Figure 7 shows a simple example of link optimization, where link 3→1 was discontinued and link 1→2 was opened. This process is repeated to search for the optimal HRE network.

Algorithm 3. Link connection optimization

Input: $z_{kl},x_{ik},f_{kl}^i,V_k,Q_{kl}$

Output: $z_{kl}^{\prime }$

1. for all $k\in H,l\in H,k^{\prime }\in H,l^{\prime }\in H$

2.  if $z_{kl}+z_{k^{\prime }{l}^{\prime }}=1$ then

3.   exchange the property of these two links $i.e.z_{kl}^{\prime }\leftarrow z_{k^{\prime }{l}^{\prime }},z_{k^{\prime }{l}^{\prime }}^{\prime }\leftarrow z_{kl}$

4.   if $thecapacityisenough\&\&a·d_{k^{\prime }{l}^{\prime }}·g_{k^{\prime }·l^{\prime }}+{hl}_{k^{\prime }{l}^{\prime }}^{\prime }={hl}_{k^{\prime }{l}^{\prime }}$ then

5.    if the objective is better then

6.     update: $z_{kl}\leftarrow z_{kl}^{\prime },z_{k^{\prime }{l}^{\prime }}\leftarrow z_{k^{\prime }{l}^{\prime }}^{\prime }$

7.    end if

8.   end if

9.  end if

10. end for

4. Numerical Experiments

To assess the feasibility of the proposed model and the efficiency of the algorithm, a series of experiments were conducted. All experiments were performed on a personal laptop (13th Gen Intel^® Core™ i9-13900HX 2.20 GHz with 16.0 GB of RAM). The algorithm was compiled using Visual Studio Code 1.92.0 and CPLEX 12.6.3.0.

The data used in this section is a randomly generated dataset. The coordinates of all demand nodes are randomly generated. The distance between demand nodes is the Euclidean distance calculated based on coordinates, expressed in kilometers. The demand volumes, measured in tons, are randomly generated, while the construction costs of hubs are calculated in CNY based on capacities. The link connection costs are calculated in CNY based on capacities and distance. The unit carbon emission coefficients for HRE and highway express are different, with highway transportation exhibiting a higher coefficient. The specific parameter values are shown in

Table 4. The values of main parameters.

Parameter	$\mathit{p}$	$\mathit{\mu }$	$\mathit{\gamma }$	$\mathit{\theta }$	${\mathit{t}}_{\mathit{k}}^0$	${\mathit{T}}_1$	${\mathit{T}}_2$
Value	3	0.6	$7.68\times {10}^{-5}$ kg/ton.km	1500 yuan/kg	1 h	20 h	22 h

. It should be noted that the parameters $\gamma$ and $\theta$ are set according to the transformation method proposed by Li and Wang [34].

4.1. Model Comparison and Analysis

This paper proposed an optimization model for the intermodal express network of high-speed railway and highway transportation, considering the characteristics of carbon emission, capacity constraints, and time limitations. Comparative analyses with degenerated models are conducted to validate the effectiveness of the proposed model.

Figure 8 illustrates the networks obtained by the proposed model and the degenerated models, where Figure 8a represents the proposed model in this paper, Figure 8b represents a pure highway transportation network, Figure 8c represents the model without carbon cost, and Figure 8d represents the model without time constraints. The degenerated models select node 3 to construct a hub, while the proposed model selects node 10 to construct a hub owing to the transportation distance and the demand volume. Comparing the proposed model and the degenerated models, the hubs of the degenerated models are more crowded and inclined to distribute towards the center, while the hubs of the proposed model are more decentralized corresponding to longer transportation distances, increasing the advantages of HRE. In addition, the proposed model in Figure 8a achieves the lowest total cost of 347,467,103, which is 15.8% lower than the total cost of 412,481,872 in Figure 8b and 5.8% lower than that in Figure 8c, further confirming the cost-effectiveness of the proposed model. Comparing Figure 8a and Figure 8d, the network in Figure 8d has excessively long paths that fail to meet delivery deadlines. For instance, the highlighted path exhibits a delivery time of 22.79 h, which is 7.7% longer than the longest path in the proposed model.

4.2. Sensitivity Analyses

Sensitivity analyses are conducted to examine how different parameters impact the objective value and the network structure. In this study, parameters related to the number of hubs, time limitations, capacity limitations, and construction costs are critically important. Therefore, we test the influence of hub number ($p$), time limitation ($T_1$), hub capacity ($V_k$), the link cost of HRE (${hl}_{kl}$), and highway transportation (${hl}_{kl}^0$) on the total cost and the network structure.

Figure 9 and Figure 10 show the impact of the number of hubs ($p$) and the time limit ($T_1$) on the total cost. From Figure 9, the total cost initially decreases with the increase in the number of hubs, reaches its lowest point at $p=4$, and then rises as the number of hubs continues to grow. We also examined the effect of hub number on the total cost under other parameters, and the results showed the same trend, i.e., as the number of hubs increases, the total cost shows a decreasing and then an increasing trend, which means the local minimum of the curve is the optimal balance between the hub number and the total cost. From Figure 10, the total cost drops quickly as the time limit increases, then declines more gradually, and eventually stabilizes. This indicates that when the time limitation is tight, total cost is very sensitive to the time limitation; as the time limitation loosens, total cost becomes less sensitive to the time limitation. Therefore, an appropriate relaxation of the time constraint contributes to reduction in total cost. Figure 11 shows the impact of hub capacity ($V_k$) on the total cost; the total cost shows a decreasing and then an increasing trend, reaching its lowest value when $V_k=1400$. This indicates that hub capacity is not better the larger the hub, so a reasonable allocation of resources is crucial for achieving optimal cost-effectiveness. Figure 12 illustrates the impact of the HRE link cost (${hl}_{kl}$) and highway link cost (${hl}_{kl}^0$) on the number of opened HRE links. The number of HRE links decreases as the HRE opening cost rises, while it increases with higher highway opening cost. This indicates that the cost structure of different transportation modes significantly influences network configuration decisions. It is important to note that the horizontal axis in Figure 12 indicates the coefficients applied in the sensitivity analysis, not the actual values.

In order to show more clearly the effect of time and carbon emission constraints on the network design results, Figure 13 and Figure 14 present the network comparison between different values of time constraint $T_1$ and carbon tax $\theta$, respectively. Figure 13a represents the network with $T_1$=24 h, in which links 3→1 and 1→6 are connected by HRE; Figure 13b represents the network with $T_1$=20 h, in which links 1→3, 3→1 and 1→6 are connected by HRE. It can be seen that with the decrease in the time limit, there are more HRE links to open. Figure 14a–c represent the network under carbon tax of 1500, 2000, and 2500, respectively. In Figure 14a, links 3→1 and 1→6 are connected by HRE. In Figure 14b, links 3→1, 1→6 and 6→3 are connected by HRE. In Figure 14c, links 3→1, 1→6, 3→6 and 6→3 are connected by HRE. It is clear that as the carbon tax increases, the number of HRE openings in the network is increasing. This indicates that it is entirely possible for managers to consider carbon tax policies to promote the development of HRE. It is worth noting that the trend of the impact of changes in the carbon emissions saved per distance and per flow on the network is similar to that of carbon tax changes.

4.3. Algorithm Performance

To assess the performance of the proposed algorithm, a comparison is carried out between the proposed improved GA and the classic GA. In order to ensure the fairness and credibility of the comparison, the two algorithms used the same parameter configurations and were tested under the same computational conditions. Figure 15 presents the comparison of these two algorithms with the population size of 50, the crossover rate of 0.8, and the mutation rate of 0.4. We also experimented with other parameter configurations, and the results exhibited similar trends. It can be seen from the figure, with the increase in generation, the improved GA demonstrates rapid objective value reduction followed by asymptotic stabilization, whereas the classical GA exhibits slower convergence with premature local optimum entrapment.

In addition, we conducted numerical experiments on multiple test scales to compare the computational performance between the improved GA and the CPLEX software. In order to reasonably present the computational results at different scales, we followed the grouping of references [39,40] and divided the experiment into three groups: $\left|N\right|=15and\left|H\right|=10,\left|N\right|=30and\left|H\right|=15,\left|N\right|=50and\left|H\right|=30$.

Table 5. Computational results of the improved GA and CPLEX.

Scale	$\mathit{p}$	CPLEX				Improved GA
		UB	LB	Gap%	CPU (s)	${\mathit{f}}^{\prime }$	Gap *%	CPU (s)
$\left|N\right|=15$ $\left|H\right|=10$	3	240,429	240,429	0.00	0.20	240,429	0.00	0.55
	4	207,358	207,358	0.00	0.39	207,358	0.00	0.64
	5	189,329	189,329	0.00	1.80	189,329	0.00	0.71
	6	173,322	173,322	0.00	4.02	173,322	0.00	0.74
$\left|N\right|=30$ $\left|H\right|=15$	3	11,545,653	11,545,653	0.00	9.53	11,545,653	0.00	1.92
	4	10,287,601	10,287,601	0.00	100.66	10,294,134	0.06	2.86
	5	9,226,751	9,226,751	0.00	32.84	9,226,751	0.00	3.47
	6	9,142,812	9,142,812	0.00	107.84	9,142,812	0.00	4.04
$\left|N\right|=50$ $\left|H\right|=30$	3	728,874,785	487,248,335	49.59	3600.17	515,206,285	5.74	19.38
	4	879,901,565	543,921,348	61.77	3600.04	627,854,893	15.43	23.66
	5	1,188,385,502	663,754,190	74.09	3600.28	832,574,286	21.97	31.41
	6	2,119,803,206	1,135,102,118	86.75	3600.64	1,437,637,854	26.65	36.65
Average					1221.53			10.50

gives the comparison of computational results of these three scales. For the small-scale instances, i.e., $\left|N\right|=15and\left|H\right|=10$, the improved GA achieves optimal solutions for all cases, with an average computational time lower than CPLEX software. For the medium-scale instances, i.e., $\left|N\right|=30and\left|H\right|=15$, the improved GA provides optimal solutions for most cases and the average computational time of the improved GA is 10.50s, notably lower than the 1221.53s required by CPLEX software. For the large-scale instances, i.e., $\left|N\right|=50and\left|H\right|=30$, the CPLEX software fails to obtain optimal solutions within 1 h, so the upper bounds reached within this time are reported. In this group, the improved GA provides better solutions, with computational times all under 1 min. In conclusion, the proposed improved GA demonstrates high performance in both accuracy and speed.

5. Discussion

The findings of this paper offer actionable insights for transportation network design and policy formulation. The implications can enhance decision-making capabilities in infrastructure planning optimization and operational policy calibration.

Firstly, compared with other degradation models, the advantages of the proposed model in this paper highlight the importance of time constraints, capacity constraints, and the intermodal network. Incorporating time constraints yields better-balanced network configurations and high-quality service, while capacity constraints ensure infrastructure feasibility and avoid excessive congestion of partial hubs and links. The intermodal express network of high-speed railway and highway transportation can reduce the total cost by 5.8% through the saved carbon cost, improve the service quality by reducing the transportation time by 7.7%, and reduce the total cost by 15.8% compared to a single highway network. From a long-term perspective, the intermodal express network of high-speed railway and highway transportation will not only improve service efficiency and quality, but also reduce operating costs and promote the sustainable development of green logistics.

Secondly, the sensitivity analysis highlights the latent managerial implications for the intermodal express network of high-speed railway and highway transportation. The total cost exhibits sensitivity to both hub number $p$ and hub capacity $V_k$ with observable threshold effects, which is why determining the optimal number of hubs to construct and hub capacity is critical to controlling operating cost. It is very interesting to find that it is not true that the larger the number and capacity of hubs, the better. The local minimums of these two curves are the optimal balance between the number/capacity of hubs and the total cost, so this study can offer theoretical supports for the reasonable number and capacity of hubs required to achieve a more cost-effective network. Additionally, the total cost demonstrates phased sensitivity to time constraints, which indicates that an appropriate relaxation of the time constraint contributes to reduction in total cost. The opening cost of HRE and highway express significantly influences network configuration decisions; it highlights the necessity of dynamically adjusting cost parameters in response to market changes and policy shifts to maintain the optimal configuration of logistics networks. By adjusting the proportion of HRE in the intermodal network, the carbon emission and the service quality can be balanced.

Last but not least, the proposed heuristic algorithm can obtain high-quality solutions within short computational times. In realistic environments, the hub location and flow assignment problem require high computational complexity. The approach can avoid the high computational cost of the off-the-shelf solution software and enable the provision of high-quality solutions for more complex problems within short times.

6. Conclusions

This paper studied the hub location and flow assignment problem for the intermodal express network of high-speed railway and highway transportation. A mixed-integer linear programming model was developed, incorporating operational constraints such as location allocation, mode selection, flow balance, capacity limits, and time limits. An improved GA with local search was designed incorporating global search and local search, enabling the attainment of relatively optimal solutions within a short time frame. Lastly, numerical experiments were performed in terms of model comparison, sensitivity analyses, and algorithm performance.

The main results are as follows. For the model comparison, the proposed model can reduce the total cost by 15.8% compared to the degenerated model without HRE. The proposed model can reduce the total cost by 5.8% compared to the degenerated model without carbon cost. The proposed model can improve the service quality by reducing the transportation time by 7.7% compared to the degenerated model without time constraints. For the sensitivity analyses, the model shows high sensitivity to hub number and hub capacity and phased sensitivity to time constraints. The local minimums of the sensitivity curves are the optimal balance between the number/capacity of hubs and the total cost. An appropriate relaxation of the time constraint contributes to a reduction in total cost. For the algorithm performance, the improved GA performs better than the classical GA and the CPLEX software. For small- and medium-scale instances, the improved GA can obtain optimal solutions faster; for large-scale instances, the improved GA can obtain better solutions within short computational times.

While this paper advances the modeling of hub location problems in intermodal systems, several promising extensions merit further investigation. Future research could explore multilevel network architectures and consider demand uncertainty to enhance model robustness. Additionally, more precise calculation methods to measure carbon emission should be incorporated [41]. Moreover, the application of the model based on real-world networks and datasets will offer valuable validation and practical insights, further demonstrating its effectiveness and relevance in complex intermodal networks.