Probabilistic Linguistic Grey Target Group Decision-Making Method Considering Decision Makers’ Expected Information
Abstract
1. Introduction
2. Preliminaries
2.1. Interval Grey Number
- (1)
- (2)
- (3)
- (4)
2.2. Probabilistic Linguistic Term Set
- (1)
- If , then
- (2)
- If , then
- (i)
- If , then
- (ii)
- If , then
- (a)
- If , then
- (b)
- If , then .
2.3. Grey Target Decision-Making Method
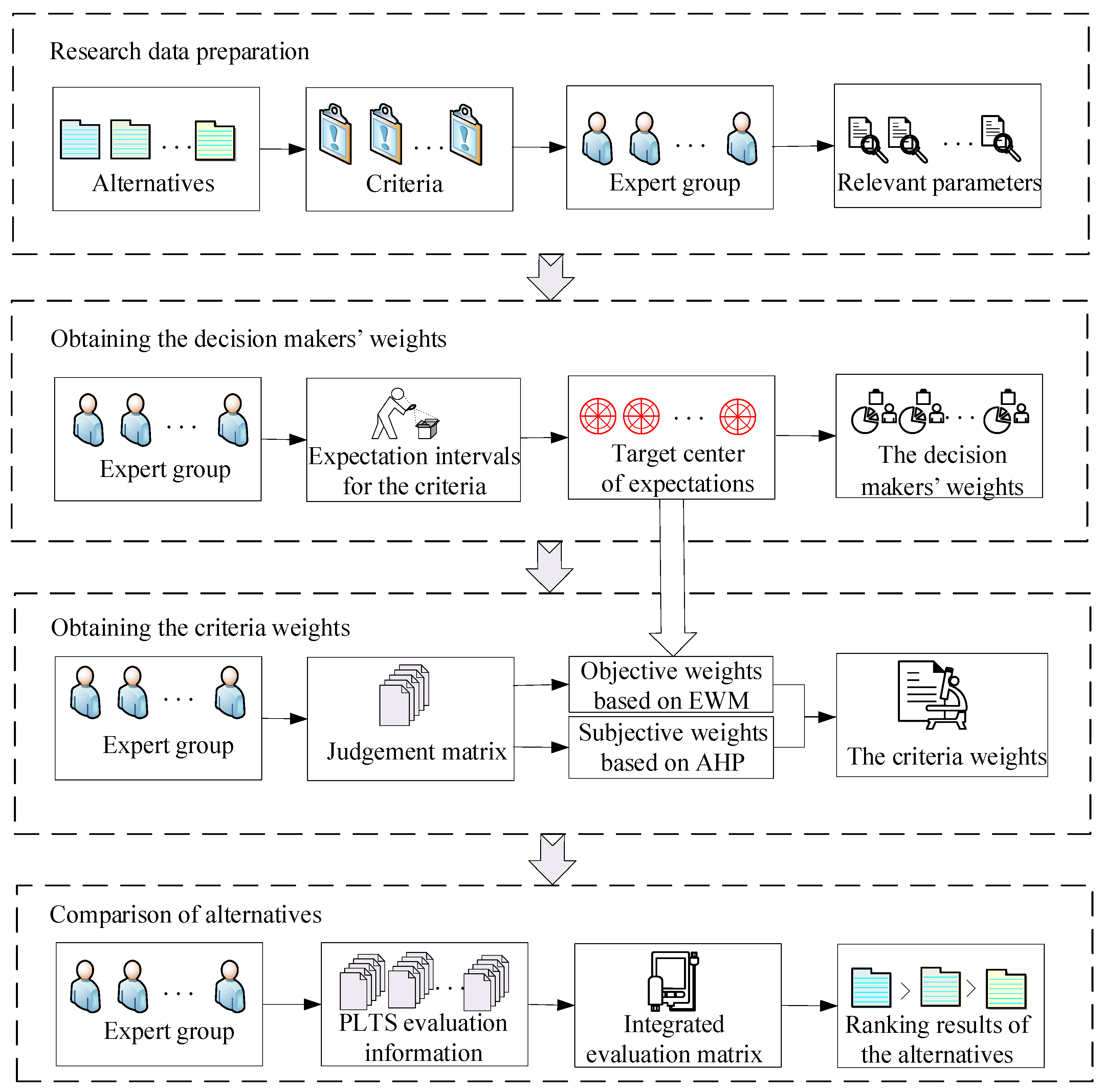
3. A Novel Grey Target Decision-Making Method Considering the Decision Makers’ Expected Information
3.1. Decision-Making Problem Description
3.2. Grey Target Decision-Making Method Considering the Decision Makers’ Expected Information
- (1)
- Obtaining the criteria weights
- (2)
- Obtaining the decision makers’ weights
- (3)
- Decision process and ranking alternatives
4. Case Study
4.1. Case Description
4.2. Decision Process
4.3. Comparison Analysis
- (1)
- Keeping the robustness of the results for obtaining criteria weights
- (2)
- Reflecting the preferences of experts and making the results of obtaining criteria weights reasonable
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kandakoglu, M.; Walther, G.; Ben Amor, S. The use of multi-criteria decision-making methods in project portfolio selection: A literature review and future research directions. Ann. Oper. Res. 2024, 332, 807–830. [Google Scholar] [CrossRef]
- Li, P.; Xu, Z.; Zhang, Z.; Li, Z.; Wei, C. Consensus reaching in multi-criteria social network group decision making: A stochastic multicriteria acceptability analysis-based method. Inf. Fusion 2023, 97, 101825. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, H.; Li, P.; Wei, C. Social network group decision-making method based on stochastic multi-criteria acceptability analysis for probabilistic linguistic term sets. Inf. Sci. 2024, 681, 121269. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Pedrycz, W. An incremental preference elicitation-based approach to learning potentially non-monotonic preferences in multi-criteria sorting. Eur. J. Oper. Res. 2024, 323, 553–570. [Google Scholar] [CrossRef]
- Hailiang, Z.; Khokhar, M.; Islam, T.; Sharma, A. A model for green-resilient supplier selection: Fuzzy best–worst multi-criteria decision-making method and its applications. Environ. Sci. Pollut. Res. 2023, 30, 54035–54058. [Google Scholar] [CrossRef]
- Bai, C.; Zhu, Q.; Sarkis, J. Circular economy and circularity supplier selection: A fuzzy group decision approach. Int. J. Prod. Res. 2024, 62, 2307–2330. [Google Scholar] [CrossRef]
- Khan, M.N.; Gupta, N.; Matharu, M.; Khan, M.F. Sustainable E-service quality in tourism: Drivers evaluation using AHP-TOPSIS technique. Sustainability 2023, 15, 7534. [Google Scholar] [CrossRef]
- Li, P.; Xu, Z.; Liu, J.; Wei, C. Social network group decision-making for probabilistic linguistic information based on GRA. Comput. Ind. Eng. 2023, 175, 108861. [Google Scholar] [CrossRef]
- Rafi-Ul-Shan, P.; Bashiri, M.; Kamal, M.M.; Mangla, S.K.; Tjahjono, B. An analysis of fuzzy group decision-making to adopt emerging technologies for fashion supply chain risk management. IEEE Trans. Eng. Manag. 2024, 71, 8469–8487. [Google Scholar] [CrossRef]
- Erfani, A.; Tavakolan, M. Risk evaluation model of wind energy investment projects using modified fuzzy group decision-making and monte carlo simulation. Arthaniti J. Econ. Theory Pract. 2023, 22, 7–33. [Google Scholar] [CrossRef]
- Li, P.; Xu, Z.; Wei, C.; Bai, Q.; Liu, J. A novel PROMETHEE method based on GRA-DEMATEL for PLTSs and its application in selecting renewable energies. Inf. Sci. 2022, 589, 142–161. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2011, 20, 109–119. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z. Probabilistic linguistic term sets in multi-attribute group decision making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Guo, Z.X.; Yang, Y.X.; He, Z.F. Evaluation of emergency logistics suppliers based on the improved TODIM method based on probabilistic linguistic term sets. Oper. Res. Manag. Sci. 2022, 31, 196–203. [Google Scholar]
- Wang, X.; Liang, X.D.; Li, X.Y.; Luo, P. Collaborative emergency decision-making for public health events: An integrated BWM-TODIM approach with multi-granularity extended probabilistic linguistic term sets. Appl. Soft Comput. 2023, 144, 110531. [Google Scholar] [CrossRef]
- Cui, C.S.; Wei, M.; Che, L.B.; Liu, J.D.; Wang, E.W. Research on the non-personalized recommendation algorithm based on probabilistic linguistic term sets. J. Syst. Sci. Math. Sci. 2023, 43, 2990–3010. [Google Scholar]
- Deng, J.L. Grey Control System; Huazhong University of Science and Technology Press: Wuhan, China, 1985. [Google Scholar]
- Liu, S.F. The Grey System Theory and Its Application; Science Press: Beijing, China, 2021. [Google Scholar]
- Dang, Y.G.; Liu, S.F.; Liu, B. Study on the multi-attribute decision model of grey target based on interval number. Eng. Sci. 2005, 7, 31–35. [Google Scholar]
- Wang, Z.X.; Dang, Y.G.; Yang, H. Improvements on decision method of grey target. Syst. Eng. Electron. 2009, 31, 2634–2636. [Google Scholar]
- Xiao, L.; Zhang, Q.J. Evaluation of rock burst level based on combination weighting-cobweb grey target model. Min. Res. Dev. 2024, 44, 149–155. [Google Scholar]
- Liu, Y.; Jiang, Q.; Huang, Z.H.; Forrest, J.Y.L. A multiobjective super conflict grey target negotiation consensus approach. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3934–3948. [Google Scholar] [CrossRef]
- Liu, Z.X.; Liu, S.F.; Jiang, S.Q. Study on the expansion of bidirectional projection grey target decision-making model based on general grey number. Syst. Eng. Theory Pract. 2019, 39, 776–782. [Google Scholar]
- Li, Q.; Liu, S.F. Grey target decision model for two-stage equipment maintenance strategy selection. Control Decis. 2023, 38, 1712–1720. [Google Scholar]
- Huang, B.; Miao, J.; Li, Q. A vetoed multi-objective grey target decision model with application in supplier choice. J. Grey Syst. 2022, 34, 15–27. [Google Scholar]
- Liu, S.F.; Fang, Z.; Yang, Y.; Forrest, J. General grey numbers and their operations. Grey Syst. Theory Appl. 2012, 2, 341–349. [Google Scholar] [CrossRef]
- Liu, S.F.; Fang, Z.G.; Xie, N.M. Algorithm rules of interval grey numbers based on the “Kernel” and the degree of greyness of grey numbers. Syst. Eng. Electron. 2010, 32, 313–316. [Google Scholar]
- Geng, X.L.; Pan, Y.H. Importance degree determination approach for product service system modules based on user experience. Comput. Integr. Manuf. Syst. 2020, 26, 1295–1303. [Google Scholar]
- Yuan, D.L.; Wang, Z.; Ren, L.W.; Zhang, J.S. Evaluation of application maturity of intelligent construction based on combinatorial empowerment-cloud model. Sci. Technol. Eng. 2024, 24, 8239–8247. [Google Scholar]
- Chen, W.; Xia, J.H. An optimal weights combination method considering both subjective and objective weight information. Math. Pract. Theory 2007, 37, 17–22. [Google Scholar]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Cao, A.P.; Ma, X.J.; Cheng, Z.N.; Zhang, J.W.; Hou, Y.X. Rated load state performance assessment and analysis of ultra-supercritical coal-fired power plant. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 4579–4592. [Google Scholar] [CrossRef]
- Xie, X.D.; Hu, M.L.; Yang, Y.J.; Zhang, Y.W. Grey target group decision model based on expected intervals of experts. J. Grey Syst. 2020, 32, 77–89. [Google Scholar]
- Estrada, E. Every nonsingular spherical Euclidean distance matrix is a resistance distance matrix. Linear Algebra Its Appl. 2023, 656, 198–209. [Google Scholar] [CrossRef]
- Zhang, K.; Dai, J. A novel TOPSIS method with decision-theoretic rough fuzzy sets. Inf. Sci. 2022, 608, 1221–1244. [Google Scholar] [CrossRef]
- Lin, M.W.; Chen, Z.Y.; Xu, Z.S.; Gou, X.J.; Herrera, F. Score function based on concentration degree for probabilistic linguistic term sets: An application to TOPSIS and VIKOR. Inf. Sci. 2021, 551, 270–290. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, Y.M.; Ding, S. Grey incidence quantile evaluation method and multidimensional relative poverty measurement. Stat. Decis. 2023, 39, 40–45. [Google Scholar]
- Zhang, Y.; Wang, L.; Lu, L.; Ye, Y.P.; Wan, L. PL-VIKOR group decision-making based on cumulative prospect theory and knowledge rating. Syst. Eng. Electron. 2023, 45, 1762–1771. [Google Scholar]
| Criteria | C1 | C2 | C3 | C4 | CR | ||
|---|---|---|---|---|---|---|---|
| C1 | 1 | 1 | 2 | 3 | 0.351 | 4.011 | 0.003 |
| C2 | 1 | 1 | 2 | 3 | 0.351 | ||
| C3 | 1/2 | 1/2 | 1 | 2 | 0.189 | ||
| C4 | 1/3 | 1/3 | 1/2 | 1 | 0.109 |
| Decision Method | The Best Alternative | Ranking Result |
|---|---|---|
| TOPSIS [37] | A4 | A4 > A2 > A1 > A3 |
| VIKOR [38] | A4 | A4 > A2 > A1 > A3 |
| Grey incidence method [39] | A4 | A4 > A2 > A1 > A3 |
| Modified VIKOR method [40] | A4 | A4 > A1 > A2 > A3 |
| Our proposed method | A4 | A4 > A2 > A1 > A3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhu, C. Probabilistic Linguistic Grey Target Group Decision-Making Method Considering Decision Makers’ Expected Information. Systems 2025, 13, 459. https://doi.org/10.3390/systems13060459
Li P, Zhu C. Probabilistic Linguistic Grey Target Group Decision-Making Method Considering Decision Makers’ Expected Information. Systems. 2025; 13(6):459. https://doi.org/10.3390/systems13060459
Chicago/Turabian StyleLi, Peng, and Chen Zhu. 2025. "Probabilistic Linguistic Grey Target Group Decision-Making Method Considering Decision Makers’ Expected Information" Systems 13, no. 6: 459. https://doi.org/10.3390/systems13060459
APA StyleLi, P., & Zhu, C. (2025). Probabilistic Linguistic Grey Target Group Decision-Making Method Considering Decision Makers’ Expected Information. Systems, 13(6), 459. https://doi.org/10.3390/systems13060459







