Abstract
With the rapid development of the Internet, businesses in the traditional catering industry are increasingly shifting toward the Online-to-Offline mode, as on-demand food delivery platforms continue to grow rapidly. Within these takeout systems, riders have a role throughout the order fulfillment process. Their behaviors involve multiple key time points, and accurately predicting these critical moments in advance is essential for enhancing both user retention and operational efficiency on such platforms. This paper first proposes a time chain simulation method, which simulates the order fulfillment in segments with an incremental process by combining dynamic and static information in the data. Subsequently, a GRU-Transformer architecture is presented, which is based on the Transformer incorporating the advantages of the Gated Recurrent Unit, thus working in concert with the time chain simulation and enabling efficient parallel prediction before order creation. Extensive experiments conducted on a real-world takeout food order dataset demonstrate that the Mean Squared Error of the prediction results of GRU-Transformer with time chain simulation is reduced by about 9.78% compared to the Transformer. Finally, according to the temporal inconsistency analysis, it can be seen that GRU-Transformer with time chain simulation still has a stable performance during peak periods, which is valuable for the intelligent takeout system.
1. Introduction
With the development of the Internet and the arrival of the post-epidemic era, more and more businesses in the traditional catering industry have launched the Online-to-Offline (O2O) business mode. The O2O business mode specifically refers to online order placing and offline delivery. On-demand Food Delivery (OFD) platforms have also taken advantage of the opportunity to develop, such as Meituan and Ele.me in China, Uber Eats and DoorDash in the United States, Just Eat and Deliveroo in Europe, etc. With the expansion of the delivery field, it is no longer just to deliver food, but also medicine, flowers and other items. The scale of the Internet delivery industry is growing steadily. According to data released by the China Internet Network Information Center (CNNCI), as of December 2024, the number of online takeout users in China reached 592 million, accounting for 53.4% of the total Internet users [1]. The development of China’s takeout industry is among the most advanced in the world [2]. According to Meituan’s 2024 financial report, as one of the largest O2O e-commerce platforms for local services in China, the company achieved an annual revenue of CNY 337.6 billion (Renminbi), the number of annual transaction users exceeded 770 million, and the number of annual active merchants increased to 14.5 million [3].
In the O2O business mode of a takeout system, four entities are involved: the OFD platform, merchant, rider, and user. The overall structure is shown in Figure 1, which has a triangular pyramid shape. The dotted lines show online communication, the solid lines represent offline interaction, and the arrows indicate the direction of communication or interaction.
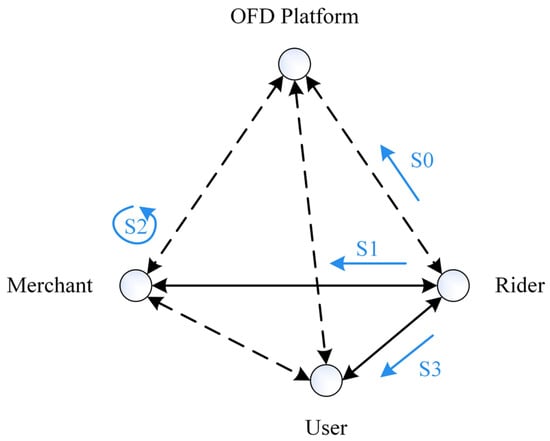
Figure 1.
O2O business mode structure of takeout system.
The whole process of order fulfillment consists of both online and offline components. In online fulfillment, the OFD platform typically acts as an intermediary, connecting the other three roles. Specifically, the user creates a takeout food order through the OFD platform, while the merchant and the rider receive the order information and confirm acceptance through the same platform. In offline fulfillment, the merchant prepares the food after the order is confirmed, while the rider picks up the order and delivers it to the user once ready. Under this mechanism, the rider is responsible for the offline transfer work, which plays a crucial role in the overall processes of takeout service. Therefore, the Order Fulfillment Cycle Time (OFCT, which refers to the time taken for an order from creation to delivery) is closely related to the time taken for activities, such as the rider accepting the order, arriving at the restaurant, picking up the food, and delivering it. These activities correspond to step S0, S1, S2, and S3 in Figure 1. Specifically, step S0 indicates that the rider is considering accepting the order after receiving the notification that the order has been created. Step S1 indicates that the rider is heading to the merchant’s restaurant after accepting the order. Step S2 indicates that the rider is waiting to pick up the food after arriving at the restaurant. Step S3 indicates that the rider is on the way to the user’s address after picking up the food.
A common challenge faced by e-commerce industries in the O2O mode is short delivery time, due to the fact that users want fast service and are sensitive to delays [4]. On the one hand, the time sensitivity of users is different for services in different industries. On the other hand, even within the same industry, users’ time sensitivity is heterogeneous [5]. Time sensitivity, specifically the degree to which a user is sensitive to the time it takes to purchase a product, has both high and low distinctions, as well as heterogeneous distinction between patience and impatience [6,7]. For example, order fulfillment in the express logistics industry is on a daily scale, meaning it typically displays the expected delivery date on the platform [8,9]. Order fulfillment in the housekeeping industry is on an hourly scale, meaning it usually has options for several hours of to-home service, and there are also hourly billing rules [10]. Order fulfillment in the takeout industry is on a minute scale, meaning it is displayed in minutes on the OFD platform’s merchant card and detail page for OFCT [11]. This is related to the particularity of the OFD platform, which requires fast delivery services to ensure the freshness of takeout food [5]. In contrast, the takeout industry has the highest time sensitivity. And the heterogeneous sensitivities of users make their tolerance for delay times different. Therefore, the estimated OFCT displayed on the OFD platform directly influences users’ choices and preferences for merchants when they are ready to place orders [12]. And after orders are placed, whether the food is delivered as soon as possible or on time can greatly affect users’ expectations and satisfaction. Based on these, in order to improve user retention rate and backend management efficiency, the OFD platform needs to accurately predict the OFCT.
In fact, the estimated time of takeout order falls within the scope of the Estimated Time of Arrival (ETA) problem [12]. ETA, which refers to the estimation of travel time from origin to destination, has been well studied in logistics and transportation [13,14,15,16]. However, existing studies of estimated time of takeout order still have the following limitations. First, many studies [12,17] treat order information as static, ignoring the fact that order status actually evolve dynamically. As order fulfillment is progressively completed, the dynamic information associated with it is constantly increasing [18]. As a result, the information on completed historical orders is both static and dynamic. The estimation of OFCT for a new order is usually performed before the order is created, when some of its key information is not available. This is because the OFCT displayed on the merchant card and detail page of the OFD platform usually exists before the order is created, and some of the order content and rider features are unknown at this time. Meanwhile, this is where estimated time of takeout order is different and difficult compared to other ETA problems. Second, while some studies [11,18] have achieved effective predictions of OFCT or other order times, there is still a lack of parallel prediction for multi-point time in orders. The OFD platform tends to improve the user experience by providing cross-entity transparency and interoperability through an intelligent takeout system [19]. Therefore, the parallel prediction of multi-point time will help to improve the management performance of the OFD platform. Third, the temporal inconsistency in the order data has not been further analyzed by many existing prediction methods. Temporal inconsistency, specifically the number of orders that are variable at different times of the day, is related to the fact that user demand fluctuates over time, and also means that there are peak and trough periods for orders [20].
To address these gaps, this paper uses deep learning to enable multi-point time prediction of food orders before creation, which provides new possibilities for takeout service optimization and backend management. The main contributions of this paper are summarized as follows.
- 1.
- This paper proposes a data processing method for time chain simulation. In order to simulate the order fulfillment process, the dynamic and static information involved in the fulfillment of takeout food order is innovatively integrated and divided into the form of time chains. Specifically, the values of features under different statuses are static if they do not change, and dynamic if they do. And the processes of the time chains contain features with different statuses, which makes their dynamic and static evolution evident. This method also makes the intervals and trends of the sequence data more visible through the principle of simulation, which can be adapted to subsequent GRU-Transformer recognize and capture. Additionally, time chains function as a method to expand the dimensionality of the data to enable a steady-state segmented simulation, which can increase the scalability of the data to some extent.
- 2.
- This paper proposes a GRU-Transformer architecture for sequence-to-sequence parallel prediction. Compared with the traditional Gated Recurrent Unit (GRU) and Transformer individually, the GRU-Transformer architecture combines the strengths of both. As a result, the new architecture effectively captures dependencies in time series while enabling feature enhancement learning. Moreover, thanks to the functionality of the GRU, it has a better ability to perceive the intervals and trends of sequences, which helps to improve its prediction performance.
- 3.
- In the takeout scenario, after implementing time chain simulation and GRU-Transformer architecture, it is able to effectively predict the multi-point time before order creation. The experimental results show that the Mean Squared Error (MSE) of the prediction results of the GRU-Transformer with time chain simulation is reduced by about 4.83% compared to the GRU-Transformer alone and by about 9.78% compared to Transformer. Moreover, the MSE of the prediction result of GRU-Transformer alone is reduced by about 5.20% compared to the Transformer. Finally, in the analysis of temporal inconsistency, GRU-Transformer with time chain simulation performs well in peak periods, but it slightly underperforms in trough periods.
The rest of this paper is organized as follows: Section 2 shows the related literature review. Section 3 introduces the method and architecture proposed in this paper in detail. Section 4 shows the experimental process and result analysis. Section 5 provides an in-depth discussion. Finally, Section 6 concludes this paper.
2. Literature Review
This section first describes many studies related to estimated time of takeout order, and then elaborates in detail on the development of time series prediction methods.
2.1. Estimated Time of Takeout Order
In recent years, time prediction of takeout order has become a hot topic in the field of e-commerce, attracting the attention of many scholars in algorithm research and machine learning.
Fulfillment-Time-Aware Personalized Ranking is a recommendation method proposed by Wang et al., and the OFCT prediction module mentioned in this method uses the Transformer architecture [11]. Compared with other models, the convergence and effectiveness of OFCT prediction module are proved. However, the module predicts the corresponding OFCT given the collection of historical orders and next time step feature vectors. This lacks consideration of the fact that some key information is unavailable before the order is created. After capturing the key features in the takeout fulfillment process, Zhu et al. input these features into a deep neural network (DNN), and then introduced a new post-processing layer to improve the convergence speed, thereby achieving effective prediction of OFCT [12]. Moreover, through an online A/B test deployed on Ele.me, it is demonstrated that the model reduced the average error in predicting OFCT by 9.8%. However, this approach does not take into account the fact that the order status is actually changing dynamically; it just treats the features all as static input of the model. Combined with probabilistic forecast, Gao et al. proposed a deep learning-based non-parametric method for predicting the food preparation time of takeout orders [21]. And based on the results of the online A/B test of Meituan, it can be seen that the method reduces the waiting time for picking up food among 2.17~4.57% of couriers. Although the non-parametric approach is more flexible, it can only output a finite number of prediction points and is limited in its ability to portray the tails or extremes of the distribution. In order to meet the surge in order demand during peak periods, Moghe et al. proposed a new system based on the collaborative work of multiple machine learning algorithms to enhance the estimation ability of batch order delivery time [22]. However, in practice, there are still many orders that cannot be batch delivered, and the method lacks a more in-depth consideration of this aspect. For multiple critical times in order fulfillment, Wang et al. present different methods used by Uber Eats to predict food preparation time, travel time, and delivery time, respectively [18]. But research on parallel prediction for these critical times is still missing. Şahin et al. applied the random forest algorithm in online food delivery service delay prediction to investigate compliance with fast delivery standards [17]. Since the method converts the prediction problem into a binary classification problem, although it is simple and convenient, it also sacrifices the fineness of the prediction.
Based on these, this paper identifies several research gaps regarding the estimated time of takeout orders. Therefore, the methods proposed in this paper innovatively address these gaps. First, this paper proposes a data processing method based on the concept of simulation. While conforming to the actual situation of order fulfillment, the method can realize the fusion of dynamic and static information in the order. Second, this paper builds a model architecture for parallel prediction in order to achieve effective prediction of multi-point time before order creation.
2.2. Time Series Prediction
In the takeout scenario, the system provides order service according to the “first created, first fulfilled” rule, and the rider resources available for scheduling are often fixed. Therefore, as a whole, after sorting by creation time, the OFCTs of historical orders have an impact on the OFCT of subsequent orders, which means that their OFCTs are correlated. Then, considering that different orders may involve the same entity, after grouping by entity, the OFCTs of the orders within the group tend to have a temporal dependency. For example, orders belonging to the same merchant are usually fulfilled based on temporality, which means that historical orders can impact the food preparation of subsequent orders. As a result, for orders characterized by significant temporality, this paper uses a model belonging to time series prediction to satisfy the forecasting needs.
With the increasing application of time series prediction, many scholars are constantly committed to model innovation to achieve more effective and accurate predictions. Time series prediction methods can be roughly divided into two categories, namely statistical methods and machine learning methods. First, methods based on traditional statistics mainly include Auto Regressive (AR) [23], Moving Average (MA) [24], Autoregressive Moving Average (ARMA) [25], Autoregressive Integrated Moving Average (ARIMA) [26], Hidden Markov Model (HMM) [27], etc. However, the predictive performance of these methods is limited. Second, methods based on machine learning mainly include Support Vector Machine (SVM) [28], Decision Tree [29], Random Forest [30], Feedforward Neural Network (FNN) [31], Multilayer Perceptron (MLP) [32], Recurrent Neural Network (RNN) [33], Long Short-Term Memory (LSTM) [34], Gated Recurrent Unit (GRU) [35], etc. Although these methods are more generalizable, there is still room for improvement in predictive accuracy.
Transformer, a more efficient and parallel computing architecture proposed by Vaswani et al. in 2017 [36]. It was originally designed for natural language processing tasks, especially machine translation. Inspired by the idea of Transformers, scholars have effectively improved the architecture and derived a series of new methods based on the Transformer for better application in time series prediction. By reversing the role of Attention Mechanism and Feed-Forward Network, Liu et al. proposed iTransformer to achieve better prediction performance [37]. However, when the feature variables are low dimensional, the predictive ability of iTransformer is still insufficient. Kitaev et al. proposed a Reformer with locality sensitive hashing (LSH) attention and reversible residual layers, which improves memory-efficiency and performs better on long sequence [38]. But its advantage in short sequence prediction is not obvious. To compensate for the cross-dimension dependency of the Transformer, Zhang et al. proposed a Crossformer with Dimension-Segment-Wise (DSW) embedding and Two-Stage Attention (TSA) layer [39]. However, the predictive ability of the Crossformer is limited to small-scale data. Tong et al. designed a multiscale residual sparse attention model RSMformer based on the Transformer architecture, and it performed well in long-sequence time series prediction tasks [40]. But RSMformer performs slightly less well on non-stationary time series that lack significant periodicity. Informer is an architecture proposed by Zhou et al. by designing the ProbSparse self-attention mechanism and refining operation, which solves the problems of Transformer’s quadratic time complexity and quadratic memory usage [41]. However, for shorter horizons, Informer’s prediction performance is not stable. Inspired by stochastic process theory, Autoformer is a new decomposition architecture with an autocorrelation mechanism based on sequence periodicity proposed by Wu et al. [42]. But its generalization ability on non-stationary data is still limited. The Block-Recurrent Transformer designed by Hutchins et al. applies transformer layers recursively along the sequence, and it utilizes parallel computing within the block to effectively utilize the accelerator hardware [43]. However, when its state space is too large, the Block-Recurrent Transformer struggles to effectively play its recurrent role.
Accordingly, after summarizing the shortcomings of the above studies, this paper chooses to combine the advantages of GRU and Transformer with each other, so as to propose a new architecture to achieve time series prediction in takeout scenarios.
3. Methodology
This section first introduces the methodological structure of the time chain simulation, and then describes the architectural design of the GRU-Transformer.
3.1. Time Chain Simulation
Numerical simulation is a technique for reproducing a system and behavior through a model or method, and it has been widely studied and applied across various fields [44,45]. Since there are multiple entities involved in the fulfillment of takeout orders, the simulation should match the actual situation in order to reflect the real and complex state of the features. On the one hand, this paper focuses on the fulfillment of takeout food orders from creation to delivery and the rider plays a key role throughout the entire process. On the other hand, considering that a comprehensive transient analysis is difficult to achieve, a steady-state segmented simulation is more suitable for the process of order fulfillment. As a result, based on the concept of simulation, this paper proposes a time chain simulation method from the rider’s perspective to be applied to the takeout system, and its specific structure is shown in Figure 2. This method is inspired by the route-based approach to solving the ETA problem and the Sequence Padding. Among them, the route-based approach to solving the ETA problem means that the total travel time is obtained by estimating the duration at each road segment and then summing it up [46]. Sequence Padding, which refers to shorter sequences are padded with zeros to ensure that all sequences are the same length [47].
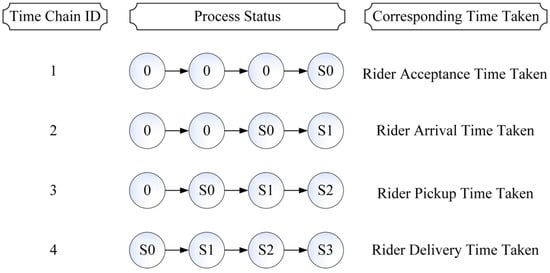
Figure 2.
Structure of time chain simulation.
Since order fulfillment can be summarized into four steps S0~S3 (see Figure 1 and its explanation for details), this paper concatenates them into four segments, respectively, based on the time chain form of route progression to simulate the entire process from online to offline. Specifically, four time chains simulate the progress of order fulfillment by segments, and the time taken of each time chain corresponds to the duration of its progress. Then, time chain sequences representing shorter progress are left padded using zeros, thus ensuring that the time chains are all of the same length. As a result, this method dynamically demonstrates order fulfillment through time chains, where each time chain contains four processes. And the rider’s status throughout the process is represented by 0, S0, S1, S2, and S3, as detailed in Table 1, and these statuses align with the steps shown in Figure 1. While each status has the same set of feature variables, the values of the same feature variables may differ across status. Based on these, this paper innovates the progression of processes within the time chains to indicate the advancement of order fulfillment corresponding to different Time Taken values.

Table 1.
Process status corresponding explanation.
3.1.1. Time Chain ID = 1
The first time chain represents the status evolution of the rider before accepting the order, corresponding to Time Chain ID = 1 in Figure 2. Specifically, the fourth process uses S0 to indicate the status of “The order has been created but the rider has not accepted the order”, and the status of the three preceding processes are all 0 to indicate “No status”. The Time Taken corresponding to this time chain is the Rider Acceptance Time Taken (i.e., , unit: second), and the calculation formula is as follows:
where is the moment when the rider accepts the order and is the moment when the order is created. And in this paper, T represents the period (unit: second), and t represents the time moment.
3.1.2. Time Chain ID = 2
The second time chain represents the status evolution of the rider before arriving at the restaurant, corresponding to Time Chain ID = 2 in Figure 2. Specifically, when transitioning from the third process to the fourth process, S0 to S1 represent the status change from “The order has been created but the rider has not accepted the order” to “The rider has accepted the order but it has not arrived at the restaurant”, and the statuses of the two preceding processes are all 0 to indicate “No status”. The Time Taken corresponding to this time chain is the Rider Arrival Time Taken (i.e., , unit: second), and the calculation formula is as follows:
where is the moment when the rider arrives at the restaurant.
3.1.3. Time Chain ID = 3
The third time chain represents the status evolution of the rider before picking up the food, corresponding to Time Chain ID = 3 in Figure 2. Specifically, when transitioning from the second process to the fourth process, S0 to S2 represent the status change from “The order has been created but the rider has not accepted the order” to “The rider has arrived at the restaurant but has not picked up the food”, and the status of the first process is 0 to indicate “No status”. The Time Taken corresponding to this time chain is the Rider Pickup Time Taken (i.e., , unit: second), and the calculation formula is as follows:
where is the moment when the rider picks up the food.
3.1.4. Time Chain ID = 4
The fourth time chain represents the status evolution of the rider before delivering, corresponding to Time Chain ID = 4 in Figure 2. Specifically, when transitioning from the first process to the fourth process, S0 to S3 represent the status change from “The order has been created but the rider has not accepted the order” to “The rider has picked up the food but it has not been delivered”. The Time Taken corresponding to this time chain is the Rider Delivery Time Taken (i.e., , unit: second), and the calculation formula is as follows:
where is the moment when the rider delivers the food to the user’s address.
In summary, the method of time chain simulation utilizes the change in features under different statuses and the gradual advancement of the process to realize the integration of the dynamic and static information therein, so as to simulate the entire process of order fulfillment. Therefore, the time chain simulation can also be extended to the solution of other ETA problems. Specifically, it can be applied to other transportation and delivery scenarios, such as express logistics and online car-hailing services, etc.
3.2. GRU-Transformer
For the parallel prediction of multi-point time before order creation, this paper synthesizes the following aspects. On the one hand, the fulfillment of takeout orders has a significant temporality. On the other hand, represents the OFCT, which needs to be displayed on the merchant card and detail page of the OFD platform. Based on these, this paper chooses to design architecture for parallel prediction based on temporal dependencies between orders from the same merchant. At the same time, this also means that the sequences modeled with this architecture must be previously grouped by merchants to ensure that there are temporal dependencies among the sequences. In addition, based on the actual situation before order creation, it can be known that in addition to the completed historical order information is known, a portion of the information about the new order is also known, such as merchant information and current time information, which are valuable for predicting multi-point time.
3.2.1. Transformer
Transformer implements parallel outputs in an Encoder–Decoder structure, and uses the Attention Mechanism to capture the dependence between different positions in the sequences. In the Seq-to-Seq task, the Encoder is responsible for encoding the input sequences into features, and the Decoder generates prediction sequences based on the output of the Encoder and the target sequences. In order to take the positional information in the sequences into account, Transformer uses Positional Encoding. This means that the output of the Positional Encoding is directly summed with the output of the Embedding Layer, and then fed into the Encoder or Decoder to ensure that the input sequences contain both features information and positional information. The Multi-Head Attention Mechanism in the Transformer utilizes different heads to focus on different parts of the key information, respectively, and the formulas are as follows [36].
where Q is query, K is key, V is value, is the K of dimension, H is the number of heads, and W is the weight. If , the calculation is Self-Attention. If , the calculation is Cross Attention.
Therefore, it is feasible to use the Transformer to focus on important sequence features and achieve parallel prediction. However, since the Transformer was originally an architecture for natural language processing, its Positional Encoding tends to lack time awareness. This limitation stems from the fact that Position Encoding is designed based on sine and cosine functions, which focuses mainly on the sequences’ positional information. As a result, it struggles to effectively capture time intervals, trends, and other temporal patterns within sequences. In contrast, GRU has a certain degree of time awareness, which can help compensate for this limitation in the Transformer.
3.2.2. Gated Recurrent Unit
Gated Recurrent Unit (GRU) is a variant of RNN, which similarly to LSTM also has gating mechanisms. As such, it can be an effective response to long-term dependency issues. It is through Reset Gate and Update Gate that GRU realizes the transfer and expression of long time series information, thus mitigating the gradient explosion or disappearance during training, which is calculated by the following formulas [48].
where z is the Update Gate mechanism, r is the Reset Gate mechanism, x is the sequence of inputs, h is the hidden state of outputs, t is the moment, and W is the weight.
In local temporality, the fulfillment time of a new order is often related to information from multiple historical orders. Thus, the ability of GRU to capture temporal dependencies between sequences is adapted to the task of predicting takeout order times.
3.2.3. Architecture Design
Combining the complementary advantages of GRU and Transformer, this paper proposes a new architecture of GRU-Transformer to be applied to parallel prediction of multi-point time and the specific structure is shown in Figure 3.
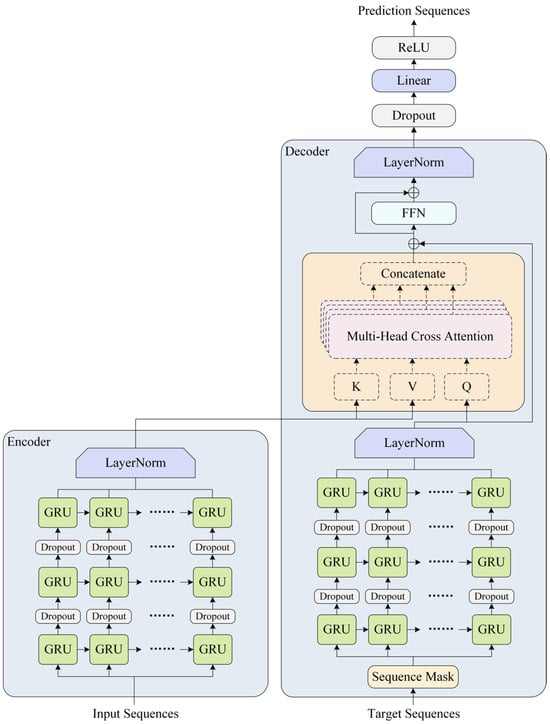
Figure 3.
GRU-Transformer architecture.
GRU-Transformer is an architecture with an Encoder–Decoder as its main structure. In its Encoder, the GRU network is used to capture the temporal dependencies of the input sequences, and then the encoded information is obtained after Layer Normalization. In its Decoder, Sequence Mask is used to mask the future information in the target sequences based on the fact that some key information is not available before the order is created. Secondly, the GRU network is used to capture the temporal dependency of the masked target sequences, and after Layer Normalization, the output of the encoder is combined to calculate the Multi-Head Cross Attention. Then, Residual Connection, Feed-Forward Networks (FFNs), and Layer Normalization are used to calculate the decoded information. Finally, a linear layer is connected to map out the prediction sequences. Among them, the gating mechanisms in the GRU network can flexibly choose to keep the important information or ignore the noise. Its Update Gate mechanism determines how much of the past information is retained, which makes it sensitive to long-term trends in the face of temporal inconsistencies in order data. Its Reset Gate mechanism enables it to capture new patterns of change in the short-term by resetting past information. In addition, Dropout is used to prevent overfitting and ReLU function ensures sparse activation.
In fact, users’ demand for purchasing takeout food tends to fluctuate over time [11]. This means that the number of takeout food orders is not consistent at different hours of the day. In this regard, the time-varying orders belonging to the same merchant are processed into the form of sequences based on temporality in this paper, and the corresponding input sequences, target sequences and prediction sequences are generated by combining the time window sliding. Among them, the input sequences contain all the information of the j-th to the (j + 2)-th order, the target sequences contain the feature information of the (j + 3)-th order, and the prediction sequences contain the 4 Time Taken values (i.e., ) of the (j + 3)-th order. Moreover, according to the method of time chain simulation described in the previous section, the information of each order can be extended and split into 4 time chain sequences. This means that the input sequences have 12 time chain sequences (i.e., ) and the target sequences have 4 time chain partial features sequences (i.e., ), and the step size of the sliding window is set to 4 to ensure that the 4 time chains of each order can be part of the sequences simultaneously and completely where the time chain consists of features and time taken together. The relevant formulas are as follows.
Accordingly, the specific calculation steps of the GRU-Transformer are as follows.
Step 1: Encode the input sequences.
where GRUs module refers to the network consisting of GRU Layer = N and Dropout.
Step 2: Decode the target sequences.
where
Moreover, mask is the matrix of Sequence Mask, which has the same shape as the target sequences but consists of 0–1. In this matrix, the positions of 1 indicates masking and the positions of 0 indicates no masking. As a result, the future information in the target sequences can be masked using this matrix, thus making the target sequences more realistic after the masking calculation.
Step 3: Output the prediction sequences.
In summary, GRU-Transformer learns the temporal dependencies and trends of historical order fulfillment by modeling and encoding the input sequences, and then computes the prediction sequences by querying based on the features in the target sequences.
4. Experiments and Results
In this section, this article demonstrates the effectiveness of time chain simulation and GRU-Transformer in parallel prediction of multi-point time through detailed experiments.
4.1. Dataset
The real-world takeout food order data from 6 July 2023 to 13 July 2023 is used in the experiments in this paper (data sourced from the OFD platform: Life Plus).
Life Plus is a local life digital comprehensive service platform with takeout business as its core and diversified county economy as one. As of now, the platform has a user base of 1.08 million, over 25 million service orders and an annual turnover of over CNY 210 million (Renminbi) [49]. Among them, the main location of the on-demand food delivery business is in Guizhou Province, China.
4.2. Data Preprocessing
Firstly, this paper filters the takeout food orders and retains only the data whose order status is completed. Secondly, due to the existence of a few special situations in which the users go to restaurants to pick up the takeout food by themselves, this means that the food for these takeout orders does not need to be delivered by riders. Therefore, these takeout records are directly excluded because these do not qualify as delivery orders.
In addition, takeout orders can be categorized into advance orders and normal orders. The delivery time of advance orders are set by the users, meaning they are not instantaneous deliveries. Therefore, this paper statistically finds that only 112 advance orders have a Rider Delivery Time Taken greater than 1.5 h (i.e., > 5400), accounting for about 0.28% of all valid orders. Because this proportion is very small, the advance orders with > 5400 will not have a large impact on the subsequent calculation after being excluded. After screening for outliers, a total of 39,735 orders were used for subsequent experiments, which involved 1404 merchants and 319 riders.
Then, in order to prove that there is a correlation between OFCTs in the overall order data, this paper conducts the Ljung–Box test () for the (i.e., OFCT, which is also the Rider Delivery Time Taken) after sorting the orders by creation time, and the results are shown in Table 2.

Table 2.
Ljung–Box test results.
The Ljung–Box test is a method for testing the overall autocorrelation of a time series over multiple lags [50]. Its null hypothesis (H0) is as follows: there is no autocorrelation in the top m lags of the time series, and its Q-statistic . Therefore, as can be seen from Table 2, the p-values for both the top 10 lags and the top 20 lags are less than 0.05 at the significance level of , which indicates that the Ljung–Box test results reject the null hypothesis. At the same time, this also implies that there is a significant autocorrelation in the series, thus indicating that the OFCTs of historical orders have an effect on the OFCT of subsequent orders.
Finally, the trend changes in the number of orders for the week of 6 July 2023 to 12 July 2023 are plotted in Figure 4. From Figure 4a, it can be observed that the number of orders is high on 8 and 9 July 2023, which indicates that the number of takeout food orders increases on weekends. From Figure 4b, it can be observed that the number of orders is high in the 12th, 13th, 18th, and 19th hour of a day, which indicates that the 12th, 13th, 18th, and 19th hour of the day are the peak periods for takeout food orders.
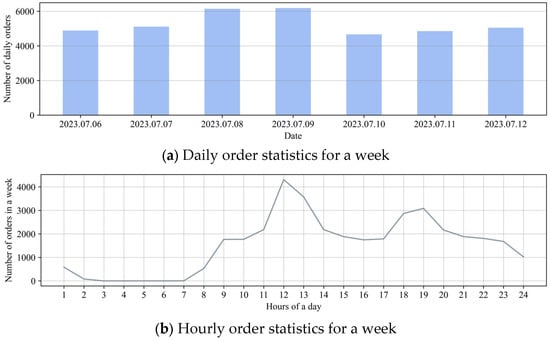
Figure 4.
Trend change in the number of orders in a week.
4.3. Feature Extraction and Time Chain Simulation
During the fulfillment process of a takeout order, a lot of features and information are generated. This paper extracts the following features from the perspectives of order, merchant, and rider.
- 1.
- Order time features: hour of a day, weekend, meal period, and peak period. Among them, meal periods are divided into breakfast, lunch, afternoon tea, dinner, midnight snack and other.
- 2.
- Order food features: order price, food quantity, and average food preparation time.
- 3.
- Merchant features: merchant identifier (i.e., merchant ID), distance from merchant to user, the average number of effective orders a month for the merchant, the current number of uncompleted orders by the merchant (MU), the current number of orders on the way by the merchant (MD) and merchant delivery ratio (MDR). The calculation formula of the merchant delivery ratio isand to prevent the denominator from being 0,The average number of effective orders a month for the merchant specifically refers to the average number of effective orders completed by merchants every day in June 2023, which is used to measure the delivery capabilities of the merchant.
- 4.
- Rider features: rider identifier (i.e., rider ID), the distance that the rider currently needs to go to the merchant (RTM), the distance that the rider currently needs to go to the user (RTU), cycling tool, rider level, the current number of uncompleted orders by the rider (RU), the current number of orders on the way by the rider (RD), rider delivery ratio (RDR) and the number of orders taken by a rider from the same merchant. Where the calculation formula of rider delivery ratio isand to prevent the denominator from being 0,
Combined with Table 1, it can be seen that in the S0 status, the rider has not accepted the order and does not need to go anywhere at this time, so RTM = RTU = 0. In the S1 status, the rider only needs to go to the merchant. The RTM corresponds to the distance between the rider and the merchant at the time of accepting the order, and RTU = 0. In the S2 status, the rider has arrived at the restaurant and is waiting to pick up the food. There is no need to go anywhere at this time, so RTM = RTU = 0. In the S3 status, the rider has picked up the food and only needs to go from the merchant to the user. So, at this point, RTM = 0, and the RTU corresponds to the distance between the rider and the user at the time of picking up the food.
In addition, in the first time chain, the rider’s features are unknown at this time since the time chain demonstrates the progress of the rider has not accepted the order. Specifically, the value of the rider’s features in the fourth process under S0 status should be set to 0. Finally, the above feature variables are concatenated in the form of the time chain processes in Figure 2. Among them, each process has all the feature variables, but the values of the feature variables are different in different statuses.
4.4. Experimental Details
In this paper, considering that orders are affected differently among different merchants, the order data from 6 July 2023 to 13 July 2023 are firstly grouped by merchant ID. Secondly, it is organized into the form of time chains and combined with time window sliding to generate samples with corresponding input sequences, target sequences and prediction sequences. Then, the samples from different groups are combined. Finally, the samples whose time belongs to the last 24 h are used as the test set, and the remaining samples before the last 24 h are randomly divided into training and validation sets in the ratio of 8:2.
Regarding the experimental setup, this paper uses Mean Squared Error (MSE) Loss as the loss function, Adam as the optimizer, and a learning rate of 0.0001. MSE Loss is chosen because it emphasizes reducing the larger prediction errors, making it suitable for the prediction task at hand. Adam is an optimization algorithm that adaptively adjusts the learning rate based on first and second moments estimation of the gradients. This means that Adam with its flexibility is suitable to optimize models with heterogeneity, such as the Transformer, which has a non-sequential stack of disparate parameter blocks [51]. Then, considering that the different modules of GRU-Transformer are stacked non-sequentially, which means that it is similarly heterogeneous to the Transformer, we choose Adam for model training. Moreover, we set the initial learning rate to 0.0001 is consistent with the relevant content in [37,52] which suggests that a lower learning rate can contribute to the stable convergence and more detailed tuning for GRU-Transformer. The loss of the validation set is used as the monitoring metric (i.e., Validation Loss), and the model is iteratively trained for 300 epochs. The model that minimizes the Validation Loss is selected as the optimal model. Moreover, all experiments are performed on a single NVIDIA GeForce RTX 2080 Ti.
To evaluate the effectiveness of time chain simulation, this paper notates the GRU-Transformer that incorporates time chain simulation sequences for the prediction task as GRU-Transformer-withTC, contrasting it with the standard GRU-Transformer without time chain simulation. The key parameters for GRU-Transformer are the number of GRU layers N and the number of Cross Attention heads H. The value of N determines the ability of the GRU-Transformer to capture sequence dependencies, but too many GRU layers may cause the gradient to vanish or explode. Similarly, the value of H affects the GRU-Transformer’s focus on important features, but too many Cross Attention heads may lead to overfitting or loss of focus. Therefore, this paper defines the selection space for N as [2, 3, 4] and for H as [2, 4, 8]. The minimum Validation Loss is used as the evaluation metric, and grid search is employed to find out the optimal combinations of these parameters. The specific results are shown in Figure 5.
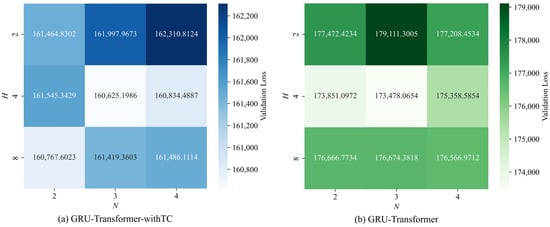
Figure 5.
Grid search result visualization.
As shown in Figure 5, the results from the grid search are visualized using heat maps, with evaluation metric values represented as the corresponding heat values. The key parameters corresponding to the grid cell with the smallest Validation Loss value are considered as the optimal combination. Specifically, the optimal combination of key parameters for GRU-Transformer is (N = 3, H = 4), i.e., the number of GRU layers is 3 and the number of Cross Attention heads is 4. Moreover, the comparison shows that the Validation Losses for GRU-Transformer-withTC are all smaller than GRU-Transformer. In summary, the search results in Figure 5 intuitively reflect the model performance for GRU-Transformer with different combinations of key parameters, thus contributing to finding the best combination (N = 3, H = 4).
4.5. Results and Analysis
In this section, in order to fully demonstrate the performance of GRU-Transformer and the effectiveness of the time chain simulation, the paper analyzes the comparison results, the results of temporal inconsistency, and the results of parameter sensitivity, respectively.
4.5.1. Comparative Analysis
First, multiple models are used for comparative analysis. The training iteration process of the models belonging to the neural network is shown in Figure 6. The evaluation results for all models are specified in Table 3.
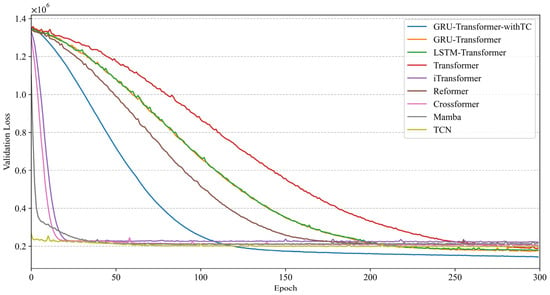
Figure 6.
Validation Loss in training iterations.

Table 3.
Evaluation and comparison of prediction results.
- 1.
- Module ablation: Transformer [36] and LSTM-Transformer are compared to demonstrate the role of the GRUs module in GRU-Transformer. Among them, LSTM-Transformer refers to the model obtained by replacing GRUs with LSTMs in GRU-Transformer. Additionally, GRU-Transformer-withTC using time chain sequences is used for comparison to demonstrate the impact of time chain simulation.
- 2.
- Transformer-based models: some highly efficient models are used for comparison to demonstrate the effectiveness of GRU-Transformer, such as iTransformer, Reformer, and Crossformer. Among them, iTransformer achieves higher prediction performance than Transformer through inverted attention and Feed-Forward Networks, and its stronger generalization ability is suitable for solving the problem at hand [37]. Reformer achieves comparable performance to Transformer through locality-sensitive hashing of attention and reversible residual layers, and it is more memory-efficient, which makes it suitable for solving the problem at hand [38]. With the ability to capture both cross-time and cross-dimension dependency, Crossformer is suitable for current multivariate time series forecasting [39].
- 3.
- Other architecture-based models: some state-of-the-art models are used for comparison to demonstrate the architecture performance of GRU-Transformer, such as Mamba and Temporal Convolutional Network (TCN). Among them, Mamba not only has linear scaling capability for sequence length, but also has a simpler architecture [52]. Moreover, Mamba performs significantly well in handling computations between relevant variables, which makes it suitable for solving the problem at hand. TCN is a unique architecture with causal convolutions and dilated convolutions and it performs well in the task of multiple time series prediction [53]. Moreover, TCN is able to capture long-term dependencies more effectively using cross-sequence modeling, which makes it suitable for solving the problem at hand.
- 4.
- Gradient boosting-based models: in order to demonstrate the superiority of the GRU-Transformer architecture, which belongs to the neural network, gradient boosting models that have good performance and belong to non-neural network are used for comparison, such as Gradient Boosting Decision Tree (GBDT) and eXtreme Gradient Boosting (XGBoost). Among them, GBDT has good robustness and flexibility [54], XGBoost has good prediction accuracy and can be trained quickly [55].
In Table 3, R-squared (R2), Mean Squared Error (MSE), Mean Absolute Error (MAE), and Root Mean Squared Error (RMSE) are used as evaluation indicators for the test set. The specific calculation formulae are as follows.
where is the g-th true value, and is the g-th predicted value.
Combining Figure 6 and Table 3, it can be seen that GRU-Transformer-withTC converges faster and predicts better than GRU-Transformer. Specifically, the Validation Loss of GRU-Transformer-withTC has reached the minimum at epoch = 246. Its MSE is reduced by about 4.83% compared to GRU-Transformer and 9.78% compared to Transformer. This shows that the feature changes and process advancement included in the time chains allow the sequence data to show the intervals and trends more prominently. This benefits the GRUs module in GRU-Transformer to capture temporal dependencies between sequences. Thus, time chain simulation can increase the scalability of the data and can assist the GRU-Transformer to recognize and integrate the evolution of dynamic and static information more easily. Moreover, the MSE of GRU-Transformer is reduced by about 5.20% compared to Transformer, which further proves that the GRUs module has a significant effect on improving performance. And, according to the prediction results of LSTM-Transformer, it can be seen that GRU-Transformer performs better. This is due to the fact that GRU has a simpler and more computationally efficient structure than LSTM. Then, GRU-Transformer also has better prediction performance compared to other Transformer-based models, which have about 2.3 times the total params of Transformer, but much less computational effort than Crossformer. In addition, although Mamba and TCN have faster convergence and fewer total params than GRU-Transformer, they have higher prediction errors. Specifically, the MSE of GRU-Transformer is reduced by about 18.70% compared to Mamba and 10.26% compared to TCN. This may be because Mamba struggles to capture complex time series patterns. As for TCN, despite enlarging its receptive field with dilated convolutions, it still faces limitations in this regard. Finally, although GBDT and XGBoost have very low computational costs, their prediction accuracy is lower compared to GRU-Transformer. This also means that the predictive ability of gradient boosting-based models is still limited. In summary, both prediction accuracy and convergence speed indicate that GRU-Transformer-withTC is the most effective model. Although it has more parameters due to the time chain simulation, this design choice results in superior prediction performance compared to other models.
Then, this paper also compares the computational overhead of GRU-Transformer and Transformer, as shown in Table 4.

Table 4.
Comparison of computational overhead.
Based on the time complexity of Transformer [36], the key difference with GRU-Transformer lies in the addition of the GRUs module. Specifically, the time complexity of GRU-Transformer becomes , where n is the sequence length and d is the dimension. The increased GPU memory usage of GRU-Transformer, compared to Transformer, is primarily due to the larger number of parameters in the GRUs module. However, GRUs perform faster when dealing with shorter sequences, which enables GRU-Transformer to utilize the GPU for less time than Transformer. This suggests that GRU-Transformer not only efficiently capture the temporal dependencies in sequences, but also focuses on the most important features in the sequences, thereby improving its prediction performance.
Finally, in order to analyze the model performance in depth, this paper calculates the Absolute Error (i.e., ) of all prediction results of GRU-Transformer-withTC, GRU-Transformer, and Transformer, respectively (i.e., and ). Then, and as one paired-sample, and as another paired-sample, and the differences within the paired-samples are calculated separately, i.e., and . For the normality of and , since the test set is a large sample, the Anderson–Darling test [56] adapted to them is used here. However, the test results show that both and do not follow a normal distribution at the significance level (). Therefore, this paper further uses the Wilcoxon test [57], which is a nonparametric method for determining whether differences in model performance are significant. Specifically, two-sided Wilcoxon tests are conducted for each of the two paired-samples, and their null hypothesis (H0) is that the model performance of the paired-sample is similar. The results are shown in Table 5.

Table 5.
Wilcoxon test results.
As can be seen in Table 5, the p-values for both paired-samples are less than 0.05, which means that both Wilcoxon tests reject the null hypothesis. Since the performance difference between GRU-Transformer-withTC and GRU-Transformer is significant, this again demonstrates the effectiveness of the time chain simulation. Since the performance difference between GRU-Transformer and Transformer is also significant, this again proves the importance of the GRUs module. Accordingly, combining all the above comparative analyses, the superiority of GRU-Transformer-withTC over other models is fully demonstrated.
4.5.2. Temporal Inconsistency Analysis
Considering that the prediction sequences contain the prediction results of four time points, their corresponding RMSE values are calculated in this paper to evaluate the prediction error of GRU-Transformer-withTC at each hour, as shown in Figure 7.
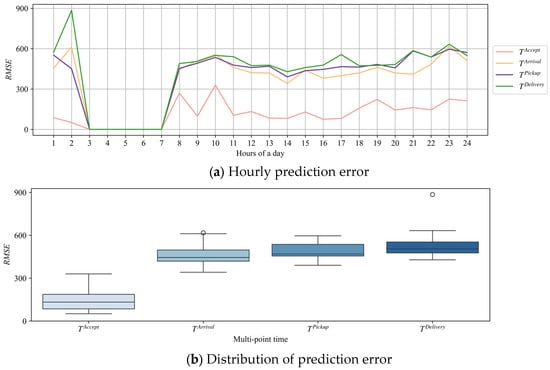
Figure 7.
Prediction error of GRU-Transformer-withTC.
For the existence of temporal inconsistency in order data, this paper calculates the prediction error (RMSE) of GRU-Transformer-withTC at different hours, as shown in Figure 7a. Among them, some RMSE values are 0 because there are no order data in the test set at the 3rd to 7th hours of the day. And RMSE values are higher in the 1st, 2nd, 23rd, and 24th hours of the day, which in combination with Figure 4b shows that these hours are trough periods for takeout. Trough periods refer to the times of day, such as early morning hours, when there are significantly fewer takeout orders. During these hours, demand for takeout food is low, resulting in fewer order samples. Additionally, with a very limited number of active riders in trough periods, there is a noticeable drop in delivery labor across the takeout system. This also means that the rider may be farther away from the merchant when accepting the order, and nighttime road conditions can further complicate the delivery. As a result, these challenges impact order fulfillment during trough periods, which in turn affects the prediction performance of GRU-Transformer-withTC at these times. Nevertheless, RMSE values of GRU-Transformer-withTC at all other hours are less than 10 min. And it is worth noting that takeout orders significantly increase during peak periods, which occurs when demand is higher, such as lunch time and dinner time. Specifically, peak periods correspond to the 12th, 13th, 18th, and 19th hours of the day. While the overall takeout system becomes busier during peak periods, it is also more difficult to accurately predict the multi-point time of food orders. Therefore, the stable performance of GRU-Transformer-withTC in peak periods is valuable for practical applications. Figure 7b illustrates the distribution of RMSE for and using box plot, where the outliers correspond to the larger prediction error during the trough periods. Among them, the outlier of corresponds to its RMSE in the 2nd hour of the day. Based on the actual takeout scenario, it is related to the complex situation of order fulfillment in the early morning, which leads to a larger prediction error. In addition, since the true value of is inherently smaller, the RMSE of its predicted results is generally smaller. The RMSE for has a wide range of fluctuations, which is related to the road conditions and the distance from the rider to the merchant at the moment the rider accepts the order. In summary, based on the RMSE patterns during trough periods, it is clear that special nighttime deliveries require the addition of more factors to be taken into account, such as active riders and road conditions. These factors may help the model to recognize complex situations, further improving the prediction performance during trough periods.
In order to further highlight the advantages and limitations of GRU-Transformer-withTC, this paper compares the prediction errors of other models for multi-point time at different periods. The specific results are shown in Figure 8 and Figure 9, respectively.
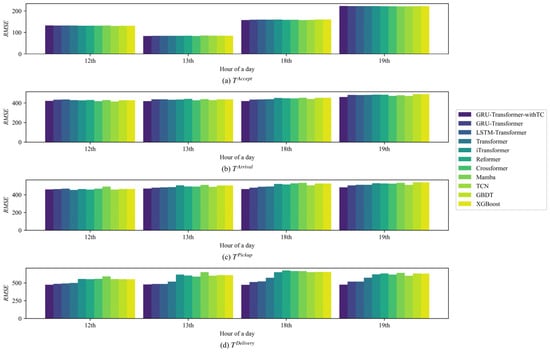
Figure 8.
Comparison of prediction errors for peak periods.
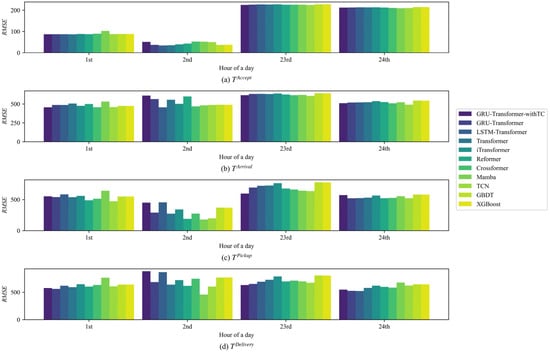
Figure 9.
Comparison of prediction errors for trough periods.
As can be seen from Figure 8, the prediction error of GRU-Transformer-withTC is generally lower in peak periods, and its performance advantage is more significant when predicting . This shows that the prediction performance of GRU-Transformer-withTC is stable for multi-point time with different sizes of time taken values. And it means that GRU-Transformer-withTC successfully recognizes the order fulfillment pattern in the busy state of the takeout system. Comparatively, the performance of Reformer and Crossformer in peak periods is less stable.
Then, as can be seen from Figure 9, GRU-Transformer occasionally outperforms GRU-Transformer-withTC during trough periods, such as at the second hour of the day. This suggests that the time chain simulation is somewhat less effective in the complex early morning conditions. Moreover, GRU-Transformer alone still generally performs better than LSTM-Transformer and Transformer most of the time.
4.5.3. Sensitivity Analysis
Finally, this paper performs a sensitivity analysis for the key parameters in GRU-Transformer-withTC, i.e., the prediction error of multi-point time for different combinations of GRU layers N and Cross Attention heads H is shown in Table 6.

Table 6.
Sensitivity analysis of GRU-Transformer-withTC.
According to Table 6, it can be seen that after different combinations of N and H, the RMSE of GRU-Transformer-withTC for predicting multi-point time does not change much. This indicates that GRU-Transformer-withTC has good robustness. Moreover, the optimal combination (N = 3, H = 4) predicts the overall RMSE of and as 159.2017, 450.9884, 486.9597, and 507.3490, respectively, where is the Order Fulfillment Cycle Time, and its overall error is not more than 8.5 min.
5. Discussion
Our research addresses the problem of parallel prediction of multi-point time in takeout scenarios when some important information is unknown before order creation. In this paper, we first propose a time chain simulation approach to achieve a steady-state segmented simulation of the order fulfillment process through the evolution of dynamic and static information, thus allowing the temporal dependencies between sequences to be more easily captured. Then, combining the respective strengths of GRU and Transformer, the GRU-Transformer architecture is designed to be used to better perceive the intervals and trends of sequences, so that it could enable more efficient parallel prediction. According to the results of many experiments, GRU-Transformer with time chain simulation has the best comprehensive performance. At the same time, we have gained some meaningful insights, as outlined below.
First, time chain simulation is able to reproduce the status of order fulfillment through changes in data. Based on the progressive structure of segmented processes, this method expands the feature dimensions so that the variation in dynamic and static information is more obvious. The MSE of the prediction results of GRU-Transformer with time chain simulation is reduced by about 4.83% when compared to GRU-Transformer using the original feature sequences. Moreover, the Wilcoxon test results of GRU-Transformer with time chain simulation and GRU-Transformer proved the significance of the performance difference. As a result, all these experiments validate the critical role of time chain simulation in fusing dynamic and static information in sequences.
Second, the GRU-Transformer architecture has a significant improvement in prediction performance compared to other models. Specifically, the performance of the architecture is improved by combining the GRU and Transformer, it reduces the MSE of the prediction results by about 5.20% compared to the Transformer. Moreover, the results of the Wilcoxon test for their paired sample indicate that there is a significant difference in performance between the two. All these results show that the simple GRUs module has an obvious benefit for GRU-Transformer in terms of improving its ability to capture temporal dependencies. In addition, it can also work in conjunction with the time chain simulation function to achieve effective parallel prediction of multi-point order time.
Third, for the temporal inconsistency in the order data, it not only reflects the changes in user demand at different times, but also demonstrates the model performance on unbalanced samples. In particular, the takeout system is in a busy state during peak periods, and a stable GRU-Transformer with time chain simulation is more useful at these times. During trough periods, although early morning complex situations can put pressure on the simulation effectiveness, it also means that the techniques used to balance the sample distribution have great potential in this regard.
In summary, the time chain simulation and GRU-Transformer proposed in this paper have achieved a significant improvement in the prediction accuracy of multi-point time before order creation. This not only has theoretical implications in terms of improving the model architecture for parallel prediction, but it also has practical implications for the application of intelligent takeout system.
6. Conclusions
This paper introduces a data processing method for time chain simulation that integrates dynamic and static information, and proposes a GRU-Transformer architecture to effectively predict the multi-point time of takeout food orders. The architecture is based on Encoder–Decoder as the main structure and incorporates the advantages of the GRU and Transformer, enabling it to capture both dependency relationships and focus on important features in the sequences. In addition, experiments are conducted using data from real-world takeout food orders. The experimental results show that GRU-Transformer performs well in the multi-point time prediction task, and the data processed in the form of time chains can be applied to capture the evolution of dynamic and static information more easily. However, when dealing with the temporal inconsistency of the data, GRU-Transformer shows less stable performance during trough periods. This suggests that there is room for improvement in its prediction accuracy during trough periods. To address this, future research can incorporate the over-sampling technique or other data augmentation methods, which balances the sample distribution by adding samples from underrepresented categories. This approach could help mitigate the temporal inconsistency of the data, ultimately improving the model’s ability to recognize and adapt to trough periods.
Finally, GRU-Transformer with time chain simulation predicts multi-point time that will help the OFD platform to control takeout food order fulfillment and can also be applied to the order allocation system to select the right rider for each order, thus improving the overall operational efficiency. Among them, the Rider Delivery Time Taken predicted in this paper can be applied to merchant cards and detail pages in the OFD platform, which can help to improve user retention rate. Moreover, the predicted Rider Arrival Time Taken and Rider Pickup Time Taken can be used to help riders plan their delivery schedules. Furthermore, when applying GRU-Transformer with time chain simulation to address the ETA problem in other domains, fine-tuning will be necessary. For instance, in online car-hailing services, passenger locations and traffic conditions vary across different times, leading to temporal inconsistency in the data. To address this, data augmentation techniques should be incorporated to mitigate the inconsistency and balance the data distribution. Additionally, new feature engineering should be applied to capture status changes in time chains under the new domain. Lastly, the Sequence Mask or other inner-architectures in GRU-Transformer should be modified to better suit the domain’s needs, ensuring proper masking of future information within sequences.
Author Contributions
Conceptualization, D.H. and W.D.; methodology, D.H. and W.D.; writing—original draft preparation, D.H.; writing—review and editing, W.D., Z.J. and Y.S.; supervision, W.D., Z.J. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 72231010, 71932008, and 72362004), the Guizhou Provincial Science and Technology Projects (grant numbers qiankehejichu[2024]Youth183, qiankehejichu-ZK[2022]yiban019 and qiankehezhichengDXGA[2025]yiban014) and the Research Foundation of Guizhou University of Finance and Economics (grant number 2020YJ045).
Data Availability Statement
The dataset presented in this paper cannot be freely accessed. Because it was obtained from the Life Plus platform of Guizhou Sunshine HaiNa Eco-Agriculature Co., Ltd. and the company does not allow authors to share its dataset.
Acknowledgments
The authors acknowledge the data support provided by the Life Plus platform for this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- The 55th Statistical Report on China’s Internet Development. Available online: https://www.cnnic.net.cn/n4/2025/0117/c88-11229.html (accessed on 10 April 2025). (In Chinese).
- Xia, T. The Use of Big Data in the Take-out and Delivery Market in China. Front. Manag. Sci. 2023, 2, 26–55. [Google Scholar] [CrossRef]
- Meituan’s 2024 Financial Report. Available online: https://www.meituan.com/news/NN250321082001991 (accessed on 12 April 2025). (In Chinese).
- Tao, J.; Dai, H.; Jiang, H.; Chen, W. Dispatch Optimisation in O2O On-Demand Service with Crowd-Sourced and in-House Drivers. Int. J. Prod. Res. 2021, 59, 6054–6068. [Google Scholar] [CrossRef]
- Wang, W.; Jiang, L. Two-Stage Solution for Meal Delivery Routing Optimization on Time-Sensitive Customer Satisfaction. J. Adv. Transp. 2022, 2022, 9711074. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, J. How Do Purchase Preferences Moderate the Impact of Time and Price Sensitivity on the Purchase Intention of Customers on Online-to-Offline (O2O) Delivery Platforms? Br. Food J. 2024, 126, 1510–1538. [Google Scholar] [CrossRef]
- Sainathan, A. Technical Note—Pricing and Prioritization in a Duopoly with Self-Selecting, Heterogeneous, Time-Sensitive Customers Under Low Utilization. Oper. Res. 2020, 68, 1364–1374. [Google Scholar] [CrossRef]
- Marino, G.; Zotteri, G.; Montagna, F. Consumer Sensitivity to Delivery Lead Time: A Furniture Retail Case. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 610–629. [Google Scholar] [CrossRef]
- Salari, N.; Liu, S.; Shen, Z.-J.M. Real-Time Delivery Time Forecasting and Promising in Online Retailing: When Will Your Package Arrive? Manuf. Serv. Oper. Manag. 2022, 24, 1421–1436. [Google Scholar] [CrossRef]
- Yu, J.; Fang, Y.; Zhong, Y.; Zhang, X.; Zhang, R. Pricing and Quality Strategies for an On-Demand Housekeeping Platform with Customer-Intensive Services. Transp. Res. E Logist. Transp. Rev. 2022, 164, 102760. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Liu, X.; Ding, D.; Hu, Z.; Zhang, P.; Zhou, C.; Bu, J. Fulfillment-Time-Aware Personalized Ranking for On-Demand Food Recommendation. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, QLD, Australia, 1–5 November 2021; ACM: New York, NY, USA, 2021; pp. 4184–4192. [Google Scholar]
- Zhu, L.; Yu, W.; Zhou, K.; Wang, X.; Feng, W.; Wang, P.; Chen, N.; Lee, P. Order Fulfillment Cycle Time Estimation for On-Demand Food Delivery. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 23–27 August 2020; ACM: New York, NY, USA, 2020; pp. 2571–2580. [Google Scholar]
- Wang, H.; Tang, X.; Kuo, Y.-H.; Kifer, D.; Li, Z. A Simple Baseline for Travel Time Estimation Using Large-Scale Trip Data. ACM Trans. Intell. Syst. Technol. 2019, 10, 19. [Google Scholar] [CrossRef]
- Zhang, C.; Yankov, D.; Karatzoglou, A.; Evans, M.; Sabau, F.; Dhifallah, O. A Post-Routing ETA Model Providing Confidence Feedback. In Proceedings of the 31st ACM International Conference on Advances in Geographic Information Systems, Hamburg, Germany, 13–16 November 2023; ACM: New York, NY, USA, 2023; pp. 1–4. [Google Scholar]
- Wang, Z.; Fu, K.; Ye, J. Learning to Estimate the Travel Time. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; ACM: New York, NY, USA, 2018; pp. 858–866. [Google Scholar]
- Li, Y.; Wu, X.; Wang, J.; Liu, Y.; Wang, X.; Deng, Y.; Miao, C. Unsupervised Categorical Representation Learning for Package Arrival Time Prediction. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, QLD, Australia, 1–5 November 2021; ACM: New York, NY, USA, 2021; pp. 3935–3944. [Google Scholar]
- Şahin, H.; İçen, D. Application of Random Forest Algorithm for the Prediction of Online Food Delivery Service Delay. Turk. J. Forecast. 2021, 5, 1–11. [Google Scholar] [CrossRef]
- Wang, Z. Predicting Time to Cook, Arrive, and Deliver at Uber Eats. Available online: https://www.infoq.com/articles/uber-eats-time-predictions/ (accessed on 20 March 2025).
- Gumzej, R. Intelligent Logistics Systems in E-Commerce and Transportation. Math. Biosci. Eng. 2023, 20, 2348–2363. [Google Scholar] [CrossRef] [PubMed]
- Xue, G.; Wang, Z.; Wang, G. Optimization of Rider Scheduling for a Food Delivery Service in O2O Business. J. Adv. Transp. 2021, 2021, 5515909. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, F.; Zhou, Y.; Feng, R.; Ru, Q.; Bian, K.; He, R.; Sun, Z. Applying Deep Learning Based Probabilistic Forecasting to Food Preparation Time for On-Demand Delivery Service. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; ACM: New York, NY, USA, 2022; pp. 2924–2934. [Google Scholar]
- Moghe, R.P.; Rathee, S.; Nayak, B.; Adusumilli, K.M. Machine Learning Based Batching Prediction System for Food Delivery. In Proceedings of the 3rd ACM India Joint International Conference on Data Science & Management of Data (8th ACM IKDD CODS & 26th COMAD), Bangalore, India, 2–4 January 2021; ACM: New York, NY, USA, 2021; pp. 316–322. [Google Scholar]
- Jafarova, H.; Aliyev, R. Applications of Autoregressive Process for Forecasting of Some Stock Indexes. In Recent Developments and the New Directions of Research, Foundations, and Applications; Shahbazova, S.N., Abbasov, A.M., Kreinovich, V., Kacprzyk, J., Batyrshin, I.Z., Eds.; Studies in Fuzziness and Soft Computing; Springer Nature: Cham, Switzerland, 2023; Volume 423, pp. 271–278. [Google Scholar]
- He, H.; He, Y.; Zhai, J.; Wang, X.; Wang, B. Predicting the Trend of the COVID-19 Outbreak and Timely Grading the Current Risk Level of Epidemic Based on Moving Average Prediction Limits. J. Shanghai Jiaotong Univ. Med. Sci. 2020, 40, 422–429. Available online: https://xuebao.shsmu.edu.cn/EN/10.3969/j.issn.1674-8115.2020.04.002 (accessed on 12 April 2025). (In Chinese).
- Hasan, M.; Wathodkar, G.; Muia, M. ARMA Model Development and Analysis for Global Temperature Uncertainty. Front. Astron. Space. Sci. 2023, 10, 1098345. [Google Scholar] [CrossRef]
- Liu, L. Stock Investment and Trading Strategy Model Based on Autoregressive Integrated Moving Average. In Proceedings of the 2022 IEEE Conference on Telecommunications, Optics and Computer Science (TOCS), Dalian, China, 11–12 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 732–736. [Google Scholar]
- Zhang, M.; Jiang, X.; Fang, Z.; Zeng, Y.; Xu, K. High-Order Hidden Markov Model for Trend Prediction in Financial Time Series. Phys. Stat. Mech. Appl. 2019, 517, 1–12. [Google Scholar] [CrossRef]
- Camastra, F.; Capone, V.; Ciaramella, A.; Riccio, A.; Staiano, A. Prediction of Environmental Missing Data Time Series by Support Vector Machine Regression and Correlation Dimension Estimation. Environ. Model. Softw. 2022, 150, 105343. [Google Scholar] [CrossRef]
- Ma, R.; Boubrahimi, S.F.; Hamdi, S.M.; Angryk, R.A. Solar Flare Prediction Using Multivariate Time Series Decision Trees. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2569–2578. [Google Scholar]
- Srinu Vasarao, P.; Chakkaravarthy, M. Time Series Analysis Using Random Forest for Predicting Stock Variances Efficiency. In Intelligent Systems and Sustainable Computing; Reddy, V.S., Prasad, V.K., Mallikarjuna Rao, D.N., Satapathy, S.C., Eds.; Springer Nature: Singapore, 2022; pp. 59–67. [Google Scholar]
- Rzayev, R.; Alizada, P. Dow Jones Index Time Series Forecasting Using Feedforward Neural Network Model. In Recent Developments and the New Directions of Research, Foundations, and Applications: Selected Papers of the 8th World Conference on Soft Computing, February 03–05, 2022, Baku, Azerbaijan, Vol. I.; Shahbazova, S.N., Abbasov, A.M., Kreinovich, V., Kacprzyk, J., Batyrshin, I.Z., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 329–337. [Google Scholar]
- Pardede, D.; Hayadi, B.H. Iskandar Kajian Literatur Multi Layer Perceptron Seberapa Baik Performa Algoritma Ini. J. ICT Apl. Syst. 2022, 1, 23–35. [Google Scholar] [CrossRef]
- Gjylapi, D.; Proko, E.; Hyso, A. Recurrent Neural Networks in Time Series Prediction. J. Multidiscip. Eng. Sci. Technol. 2018, 5, 8741–8746. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Saini, V.K.; Bhardwaj, B.; Gupta, V.; Kumar, R.; Mathur, A. Gated Recurrent Unit (GRU) Based Short Term Forecasting for Wind Energy Estimation. In Proceedings of the 2020 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 10–11 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7 May 2024; pp. 1–25. [Google Scholar]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020; pp. 1–12. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer Utilizing Cross-Dimension Dependency for Multivariate Time Series Forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023; pp. 1–21. [Google Scholar]
- Tong, G.; Ge, Z.; Peng, D. RSMformer: An Efficient Multiscale Transformer-Based Framework for Long Sequence Time-Series Forecasting. Appl. Intell. 2024, 54, 1275–1296. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of theAAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2021; Volume 34, pp. 22419–22430. [Google Scholar]
- Hutchins, D.; Schlag, I.; Wu, Y.; Dyer, E.; Neyshabur, B. Block-Recurrent Transformers. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 33248–33261. [Google Scholar]
- Singh, S.; Parmar, K.S.; Kumar, J. Development of Multi-Forecasting Model Using Monte Carlo Simulation Coupled with Wavelet Denoising-ARIMA Model. Math. Comput. Simul. 2025, 230, 517–540. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, J.; Xiang, J. Online Bearing Fault Diagnosis Using Numerical Simulation Models and Machine Learning Classifications. Reliab. Eng. Syst. Saf. 2023, 234, 109142. [Google Scholar] [CrossRef]
- Wei, J.; Ye, Z.; Yang, C.; Chen, C.; Ma, G. Process-Informed Deep Learning for Enhanced Order Fulfillment Cycle Time Prediction in On-Demand Grocery Retailing. In Proceedings of the 33rd ACM International Conference on Information and Knowledge Management, Boise, ID, USA, 21–25 October 2024; ACM: New York, NY, USA, 2024; pp. 4975–4982. [Google Scholar]
- Wang, F.; Li, J.; Deng, C.; Zhao, R. Fault Diagnosis for Ion Mill Etching Machine Cooling System Based on Omni-Dimensional Dynamic Convolution and Dynamic Spatial Pyramid Pooling. Nondestruct. Test. Eval. 2025, 1–32. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Guizhou Sunshine HaiNa Eco-Agriculature Co., Ltd. Available online: https://www.yangguanghaina.com/ (accessed on 10 April 2025). (In Chinese).
- Hassani, H.; Mashhad, L.M.; Royer-Carenzi, M.; Yeganegi, M.R.; Komendantova, N. White Noise and Its Misapplications: Impacts on Time Series Model Adequacy and Forecasting. Forecasting 2025, 7, 8. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Ding, T.; Li, Z.; Sun, R.; Luo, Z.-Q. Why Transformers Need Adam: A Hessian Perspective. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2024; Volume 37, pp. 131786–131823. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. In Proceedings of the First Conference on Language Modeling, Philadelphia, PA, USA, 7–9 October 2024; pp. 1–32. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Statist. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- González-Estrada, E. Computationally Efficient Tests for Multivariate Skew Normality. J. Stat. Theory Pract. 2025, 19, 43. [Google Scholar] [CrossRef]
- Pellitteri, F.; Calza, M.; Baldi, G.; De Maio, M.; Lombardo, L. Reproducibility and Accuracy of Two Facial Scanners: A 3D In Vivo Study. Appl. Sci. 2025, 15, 1191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).