A Hybrid Genetic Algorithm and Proximal Policy Optimization System for Efficient Multi-Agent Task Allocation
Abstract
1. Introduction
- We propose a Markov game formulation for the multi-agent task allocation problem, in which agents independently refine their strategies through continuous interaction with the environment. By relying on local observations to guide each agent’s decision-making, the proposed approach effectively supports coordinated and efficient task distribution throughout the swarm, thereby addressing scalability and resource allocation challenges in multi-agent systems.
- We propose the GAPPO algorithm, which integrates genetic algorithms with proximal policy optimization and incorporates an attention mechanism alongside an adaptive learning rate. This design enables agents to adjust to varying task requirements, enhancing learning stability and coordination efficiency.
- Numerical results validate the efficiency and scalability of the proposed method, highlighting its faster convergence and better adaptability compared to the prevailing reinforcement learning algorithms.
2. Problem Formulation
- State Estimation: At each time step t, the agent maintains a local state , comprising its spatial coordinates, surrounding occupancy information, and relevant task identifiers. This state is continuously updated and evolves according to a transition function . The Actor–Critic framework takes this state as input to support real-time motion planning, enabling effective navigation, obstacle circumvention, and target recognition.
- Task Allocation: To prevent agent congestion and redundant task assignments, a distributed allocation scheme is employed. Agents evaluate candidate tasks based on factors such as distance, priority level, and current workload. Decisions are dynamically adjusted through localized communication, promoting balanced task execution and optimal use of agent capabilities.
- Strategy: Agents refine their behavior through policy updates driven by local observations and rewards. In non-cooperative conditions, each agent adapts its policy independently. Under collaborative settings, shared policy gradients enhance collective learning. The GAPPO model incorporates attention mechanisms to facilitate both autonomous decision-making and inter-agent coordination.
2.1. System Model
2.2. State Action Model
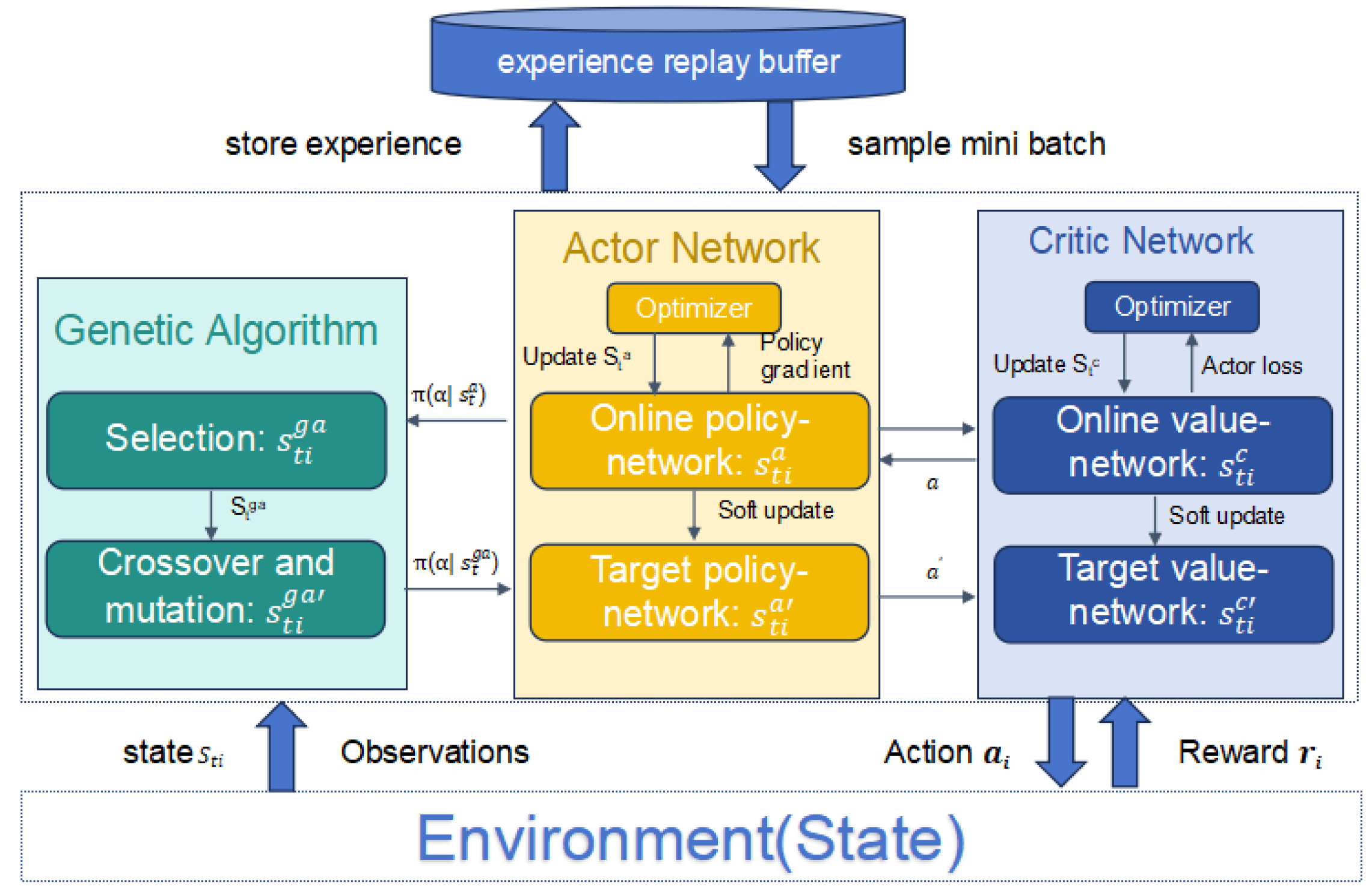
3. Learning Algorithm
| Algorithm 1 Proximal Policy Optimization Augmented With Genetic Algorithm. |
1: Initialize: Population of Actor–Critic networks , where each policy is encoded as a real-valued vector. Structural infeasibility, such as instability or divergence, is mitigated by bounding weight perturbations and incorporating penalty terms within the fitness evaluation to discourage infeasible policies; 2: Set hyperparameters: learning rate , discount factor , clip ratio , and KL divergence target ; 3: Initialize replay buffer with capacity ; 4: Set generation counter ; 5: while training do 6: for each individual do 7: Initialize trajectory T and observe initial state ; 8: for each time step to do 9: Select action using policy based on ; 10: Execute , observe reward and next state ; 11: Append transition to trajectory T; 12: if terminal state reached then 13: Break 14: end if 15: end for 16: Store trajectory T in replay buffer; 17: end for 18: if len(replay buffer) ≥ BATCH_SIZE then 19: Sample a batch of transitions from replay buffer; 20: for each transition in the batch do 21: Compute returns using ; 22: Compute advantages using Generalized Advantage Estimation (GAE); 23: Get action probabilities and state values ; 24: Calculate surrogate loss by (15); 25: Calculate value loss by (16); 26: Compute total loss ; 27: Update parameters using gradient descent by (17); 28: end for 29: end if 30: end while 31: Global Evolution via Genetic Algorithm 32: while g < max_generations do 33: for each individual do 34: Evaluate to obtain fitness score ; 35: end for 36: Select individuals based on fitness; 37: Select top 10% individuals based on fitness and retain them as elites; 38: Generate offspring to fill the remaining 90% of the population via: 39: Selection (e.g., tournament or roulette), 40: Crossover (with rate 0.8), and 41: Mutation (with rate 0.05); 42: Form new population ; 43: Update population and increment generation counter g; 44: end while 45: Periodically: Update target networks to stabilize training |
4. Experimental Results
- Advantage Actor–Critic (A2C) [29]: A2C integrates policy and value functions, with the advantage function defined aswhere is the expected return and is the baseline value, enhancing learning stability by reducing gradient variance.
- Proximal Policy Optimization (PPO) [30]: PPO balances exploration and exploitation by constraining policy updates, which enhances stability and sample efficiency.
- Deep Q-Network (DQN) [31]: The DQN approximates the optimal action-value function using deep neural networks, stabilizing learning through experience replay and a target network. The update rule is as follows:
- Deep Deterministic Policy Gradient (DDPG) [32]: The DDPG handles continuous action spaces with an Actor–Critic framework. The policy gradient update is as follows:
5. Conclusions and the Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Li, N.; Duan, J.; Qin, J.; Zhou, Y. Resource scheduling optimisation study considering both supply and demand sides of services under cloud manufacturing. Systems 2024, 12, 133. [Google Scholar] [CrossRef]
- Hou, Y.; Ma, Z.; Pan, Z. Online multi-agent task assignment and path finding with kinematic constraint in the federated internet of things. IEEE Trans. Consum. Electron. 2024, 70, 2586–2595. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, H. Intelligentcrowd: Mobile crowdsensing via multi-agent reinforcement learning. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 840–845. [Google Scholar] [CrossRef]
- Liu, W.; Liu, S.; Cao, J.; Wang, Q.; Lang, X.; Liu, Y. Learning communication for cooperation in dynamic agent-number environment. IEEE/ASME Trans. Mechatron. 2021, 26, 1846–1857. [Google Scholar] [CrossRef]
- Xiao, T.; Chen, C.; Dong, M.; Ota, K.; Liu, L.; Dustdar, S. Multi-agent reinforcement learning-based trading decision-making in platooning-assisted vehicular networks. IEEE/ACM Trans. Netw. 2024, 32, 2143–2158. [Google Scholar] [CrossRef]
- Dharmapriya, S.; Kiridena, S.; Shukla, N. Multiagent optimization approach to supply network configuration problems with varied product-market profiles. IEEE Trans. Eng. Manag. 2022, 69, 2707–2722. [Google Scholar] [CrossRef]
- Gao, G.; Wen, Y.; Tao, D. Distributed energy trading and scheduling among microgrids via multiagent reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 10638–10652. [Google Scholar] [CrossRef]
- Ramirez, C.A.; Agrawal, P.; Thompson, A.E. An approach integrating model-based systems engineering, iot, and digital twin for the design of electric unmanned autonomous vehicles. Systems 2025, 13, 73. [Google Scholar] [CrossRef]
- Rehman, A.U.; Usmani, Y.S.; Mian, S.H.; Abidi, M.H.; Alkhalefah, H. Simulation and goal programming approach to improve public hospital emergency department resource allocation. Systems 2023, 11, 467. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, S.; Li, F.; Trajanovski, S.; Zhou, P.; Hui, P.; Fu, X. Video content placement at the network edge: Centralized and distributed algorithms. IEEE Trans. Mob. Comput. 2023, 22, 6843–6859. [Google Scholar] [CrossRef]
- Jiang, X.; Zeng, X.; Sun, J.; Chen, J. Distributed synchronous and asynchronous algorithms for semidefinite programming with diagonal constraints. IEEE Trans. Autom. Control 2023, 68, 1007–1022. [Google Scholar] [CrossRef]
- Gao, A.; Wang, Q.; Liang, W.; Ding, Z. Game combined multi-agent reinforcement learning approach for uav assisted offloading. IEEE Trans. Veh. Technol. 2021, 70, 12888–12901. [Google Scholar] [CrossRef]
- Hu, T.; Luo, B.; Yang, C.; Huang, T. Mo-mix: Multi-objective multi-agent cooperative decision-making with deep reinforcement learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 12098–12112. [Google Scholar] [CrossRef] [PubMed]
- Jing, G.; Bai, H.; George, J.; Chakrabortty, A.; Sharma, P.K. Distributed multiagent reinforcement learning based on graph-induced local value functions. IEEE Trans. Autom. Control 2024, 69, 6636–6651. [Google Scholar] [CrossRef]
- Tian, L.; Ji, X.; Zhou, Y. Maximizing information dissemination in social network via a fast local search. Systems 2025, 13, 59. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Q.; Duan, Z. Optimal distributed leader-following consensus of linear multi-agent systems: A dynamic average consensus-based approach. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1208–1212. [Google Scholar] [CrossRef]
- Luo, Q.; Liu, S.; Wang, L.; Tian, E. Privacy-preserved distributed optimization for multi-agent systems with antagonistic interactions. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 1350–1360. [Google Scholar] [CrossRef]
- Zhang, M.; Pan, C. Hierarchical optimization scheduling algorithm for logistics transport vehicles based on multi-agent reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 3108–3117. [Google Scholar] [CrossRef]
- Zhou, J.; Lv, Y.; Wen, C.; Wen, G. Solving specified-time distributed optimization problem via sampled-data-based algorithm. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2747–2758. [Google Scholar] [CrossRef]
- Khdoudi, A.; Masrour, T.; Hassani, I.E.; Mazgualdi, C.E. A deep-reinforcement-learning-based digital twin for manufacturing process optimization. Systems 2024, 12, 38. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, S.-M.; Ni, Y.-Q. Cooperative control of maglev levitation system via hamilton–jacobi–bellman multi-agent deep reinforcement learning. IEEE Trans. Veh. Technol. 2024, 73, 12747–12759. [Google Scholar] [CrossRef]
- Ke, J.; Xiao, F.; Yang, H.; Ye, J. Learning to delay in ride-sourcing systems: A multi-agent deep reinforcement learning framework. IEEE Trans. Knowl. Data Eng. 2022, 34, 2280–2292. [Google Scholar] [CrossRef]
- Gao, S.; Xu, C.; Dong, H. Deterministic reinforcement learning consensus control of nonlinear multi-agent systems via autonomous convergence perception. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2229–2233. [Google Scholar] [CrossRef]
- Chang, Z.; Deng, H.; You, L.; Min, G.; Garg, S.; Kaddoum, G. Trajectory design and resource allocation for multi-uav networks: Deep reinforcement learning approaches. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2940–2951. [Google Scholar] [CrossRef]
- Guo, J.; Yao, H.; He, W.; Mai, T.; Ouyang, T.; Wang, F. Reinforcement learning-based genetic algorithm for differentiated traffic scheduling in industrial TSN-5G networks. In Proceedings of the 2024 International Wireless Communications and Mobile Computing (IWCMC), Ayia Napa, Cyprus, 27–31 May 2024; pp. 1283–1289. [Google Scholar]
- Ren, W.; Beard, R. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Low, C.B. A dynamic virtual structure formation control for fixed-wing uavs. In Proceedings of the 2011 9th IEEE International Conference on Control and Automation (ICCA), Santiago, Chile, 19–21 December 2011; pp. 627–632. [Google Scholar]
- Balch, T.; Arkin, R. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Konda, V.; Tsitsiklis, J. Actor-critic algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; Volume 12. [Google Scholar]
- Zhang, H.; Jiang, M.; Liu, X.; Wen, X.; Wang, N.; Long, K. Ppo-based pdacb traffic control scheme for massive iov communications. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1116–1125. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zheng, K.; Jia, X.; Chi, K.; Liu, X. Ddpg-based joint time and energy management in ambient backscatter-assisted hybrid underlay crns. IEEE Trans. Commun. 2023, 71, 441–456. [Google Scholar] [CrossRef]

| Technique | References | Year | Data Used |
|---|---|---|---|
| Distributed Optimization | [16] | 2022 | Wireless sensor networks |
| Mixed-Integer Programming | [11] | 2023 | Semidefinite programming |
| UAV Trajectory + Resource Allocation | [24] | 2024 | UAV data |
| MADDPG | [12] | 2021 | UAV trajectories |
| Combinatorial Optimization + RL | [22] | 2022 | Ride-sourcing data |
| MO-MIX (CTDE) | [13] | 2023 | Multi-objective optimization data |
| Autonomous Perception-based RL | [23] | 2024 | Autonomous perception data |
| GA + PPO for Traffic Scheduling | [25] | 2024 | TSN-5G traffic data |
| Component | Design Choice and Rationale |
|---|---|
| Encoding Scheme | Real-valued direct encoding of Actor–Critic network weights to ensure structural feasibility and smooth parameter space exploration. |
| Population Initialization | The population size N is scaled proportionally with the number of agents and tasks, ranging from 100 to 300 individuals. Each individual represents a complete Actor–Critic policy, encoded as a real-valued parameter vector. |
| Selection Strategy | Fitness-proportionate selection with soft penalty terms integrated to discourage unstable or divergent policies. |
| Crossover Mechanism | Uniform crossover applied with a rate of 0.8, enabling information exchange between high-performing individuals. |
| Mutation Strategy | Gaussian mutation with a probability of 0.05 per gene. Perturbations are clipped to ensure parameter validity and prevent instability. |
| Fitness Evaluation Function | , where : reward, : entropy, and : computational cost. |
| Fitness Weights | (performance), (exploration), and (efficiency). Tuned empirically for optimal balance. |
| Constraint Handling | Penalty of for infeasible allocations (capacity, range). Mutation range constraints enforce feasibility. |
| Generational Control | The population evolves for 500 generations. A generation counter tracks convergence trends. |
| Termination Criteria | Maximum of 500 generations or earlier if population fitness variance falls below a threshold, . |
| Reinsertion Strategy | Elitism is applied: the top 10% of individuals (based on fitness) are directly carried over to the next generation. The remaining 90% of the population is replaced by offspring generated via selection, crossover (rate 0.8), and mutation (rate 0.05). |
| Actor–Critic Network Structure | Actor: Two-layer MLP (256–128 units, ReLU), output via softmax. Critic: Two-layer MLP (256–128 units, ReLU), scalar output. Parameters are flattened for GA operations. |
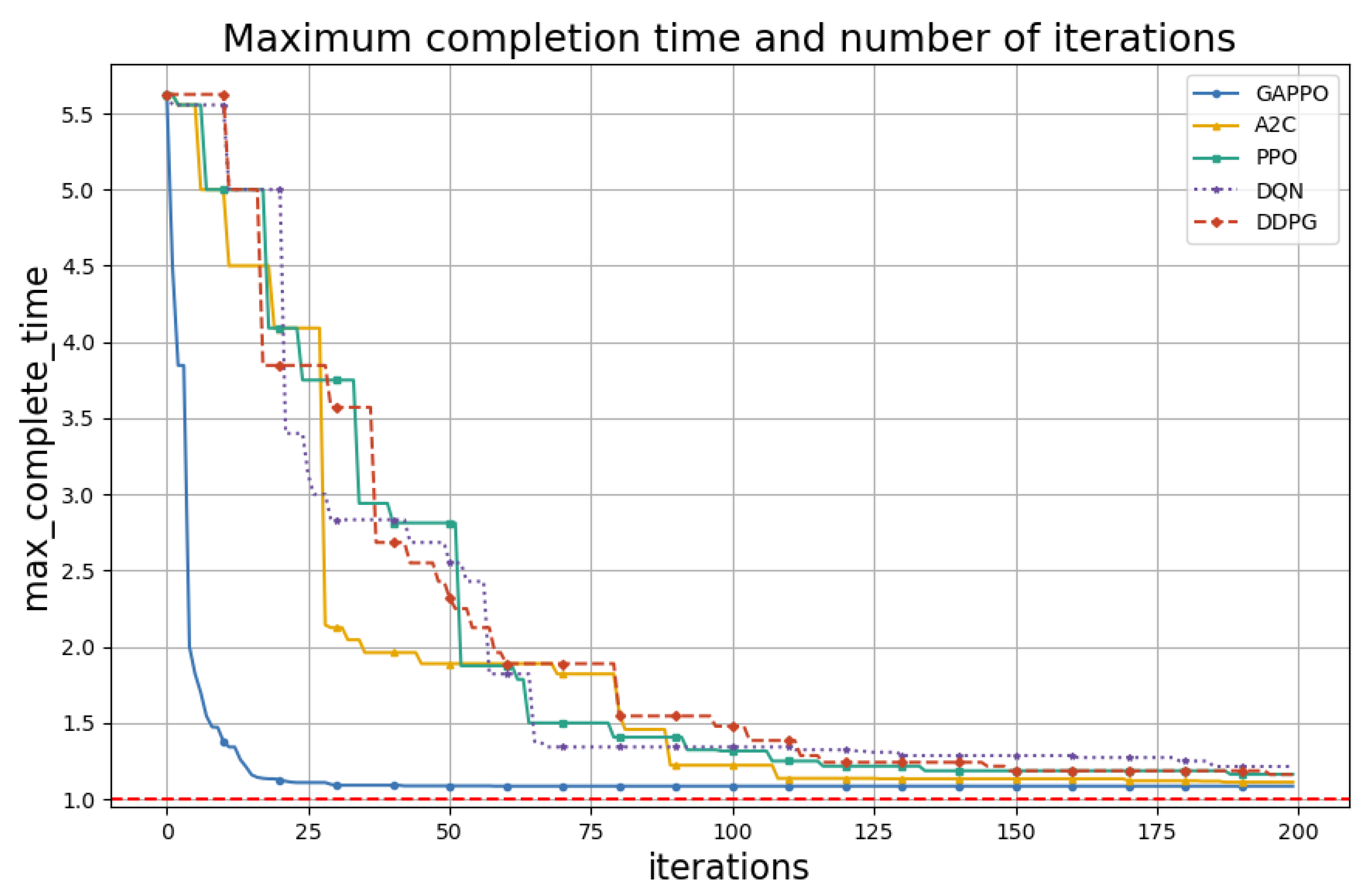
| Algorithm | T | min | ||
|---|---|---|---|---|
| GAPPO | 7.5% | 7.4% | 1.074 h | 45 |
| A2C | 6.8% | 8.8% | 1.088 h | 107 |
| PPO | 4.4% | 15.8% | 1.158 h | 186 |
| DQN | 2.2% | 22.1% | 1.221 h | 184 |
| DDPG | 4.5% | 16.2% | 1.162 h | 193 |
| Optimal | 100% | - | 1.0 h | - |
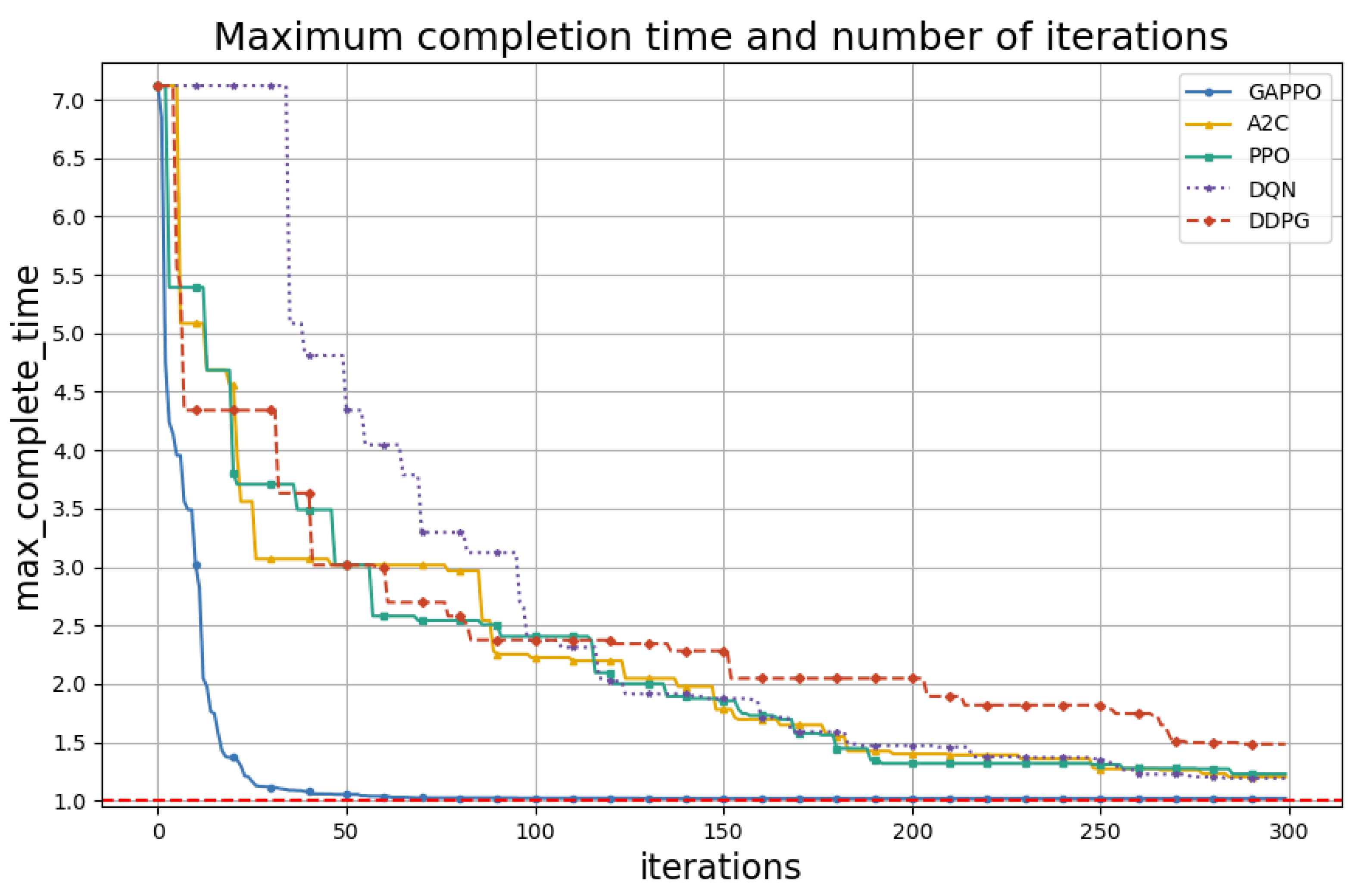
| Algorithm | T | min | ||
|---|---|---|---|---|
| GAPPO | 20.3% | 1.4% | 1.014 h | 86 |
| A2C | 2.6% | 23.4% | 1.234 h | 277 |
| PPO | 2.3% | 25.6% | 1.256 h | 281 |
| DQN | 2.1% | 21.2% | 1.212 h | 272 |
| DDPG | 1.2% | 50.2% | 1.502 h | 286 |
| Optimal | 100% | - | 1.0 h | - |
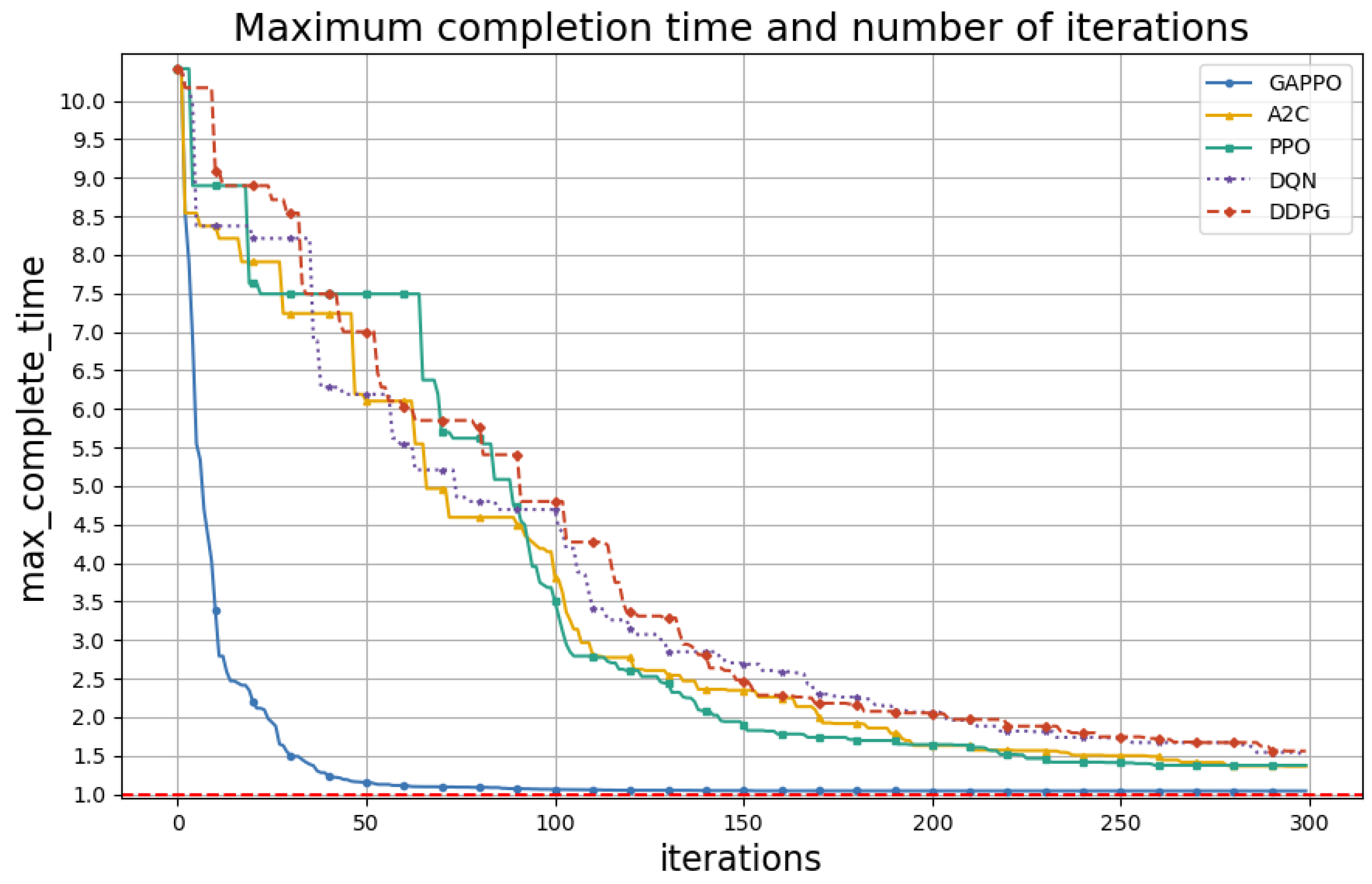
| Algorithm | T | min | ||
|---|---|---|---|---|
| GAPPO | 16.2% | 2.4% | 1.024 h | 220 |
| A2C | 3.2% | 40.2% | 1.402 h | 279 |
| PPO | 3.2% | 40.8% | 1.408 h | 263 |
| DQN | 2.6% | 51.1% | 1.511 h | 286 |
| DDPG | 2.6% | 51.8% | 1.518 h | 290 |
| Optimal | 100% | - | 1.0 h | - |
| Algorithm | T | min | ||
|---|---|---|---|---|
| GAPPO | 15.3% | 3.9% | 1.039 h | 261 |
| A2C | 3.1% | 43.6% | 1.436 h | 268 |
| PPO | 4.3% | 32.6% | 1.326 h | 290 |
| DQN | 3.8% | 37.3% | 1.373 h | 286 |
| DDPG | 2.4% | 51.8% | 1.518 h | 295 |
| Optimal | 100% | - | 1.0 h | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Yu, C.; Wang, J. A Hybrid Genetic Algorithm and Proximal Policy Optimization System for Efficient Multi-Agent Task Allocation. Systems 2025, 13, 453. https://doi.org/10.3390/systems13060453
Zhu Z, Yu C, Wang J. A Hybrid Genetic Algorithm and Proximal Policy Optimization System for Efficient Multi-Agent Task Allocation. Systems. 2025; 13(6):453. https://doi.org/10.3390/systems13060453
Chicago/Turabian StyleZhu, Zimo, Chuanqiang Yu, and Junti Wang. 2025. "A Hybrid Genetic Algorithm and Proximal Policy Optimization System for Efficient Multi-Agent Task Allocation" Systems 13, no. 6: 453. https://doi.org/10.3390/systems13060453
APA StyleZhu, Z., Yu, C., & Wang, J. (2025). A Hybrid Genetic Algorithm and Proximal Policy Optimization System for Efficient Multi-Agent Task Allocation. Systems, 13(6), 453. https://doi.org/10.3390/systems13060453






