A Novel Management Approach for Optimal Operation of Hybrid AC-DC Microgrid in the Presence of Wind and Load Uncertainties
Abstract
1. Introduction
- Examining the operational conditions of microgrids when functioning independently or interconnected.
- Analyzing microgrid performance when each AC or DC microgrid has its own central energy management system (MCEMS) versus when a single MCEMS is used.
- Incorporating uncertainty in renewable energy sources and loads across different connection and management scenarios.
- Minimizing microgrid operating costs by optimizing the MCEMS configuration and interconnection strategy.
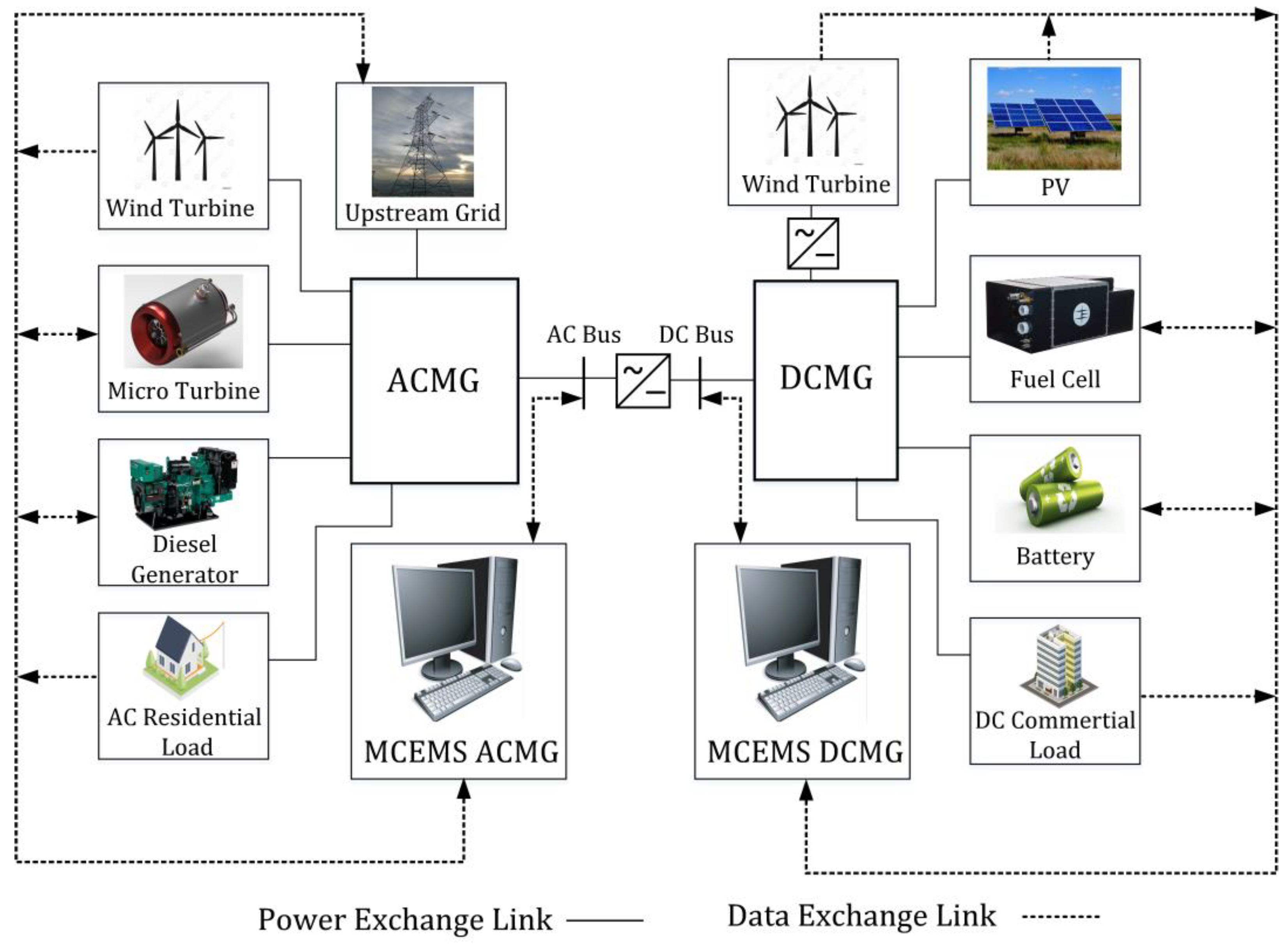
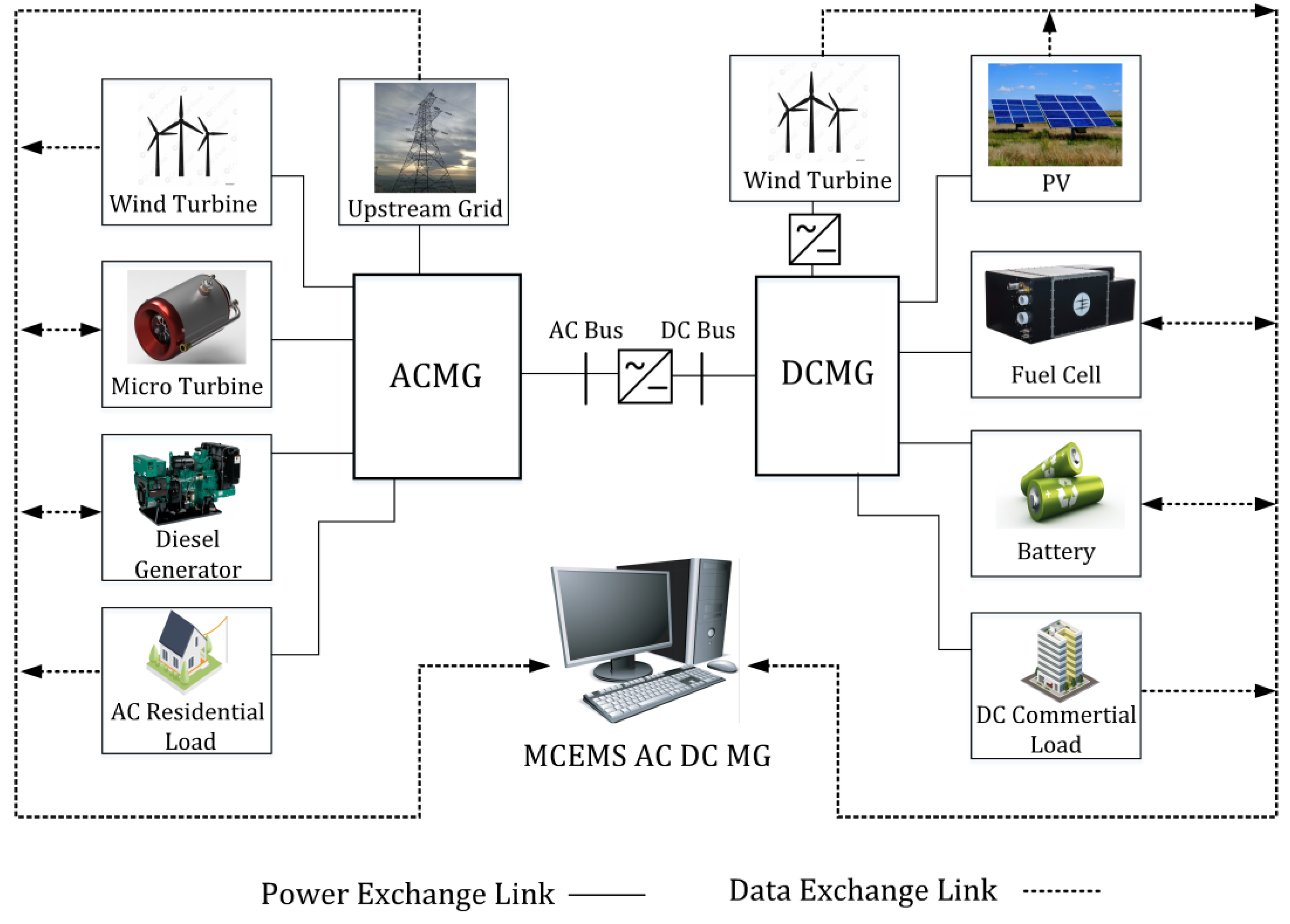
2. Microgrid Structures
3. Formulation of the Proposed Problem
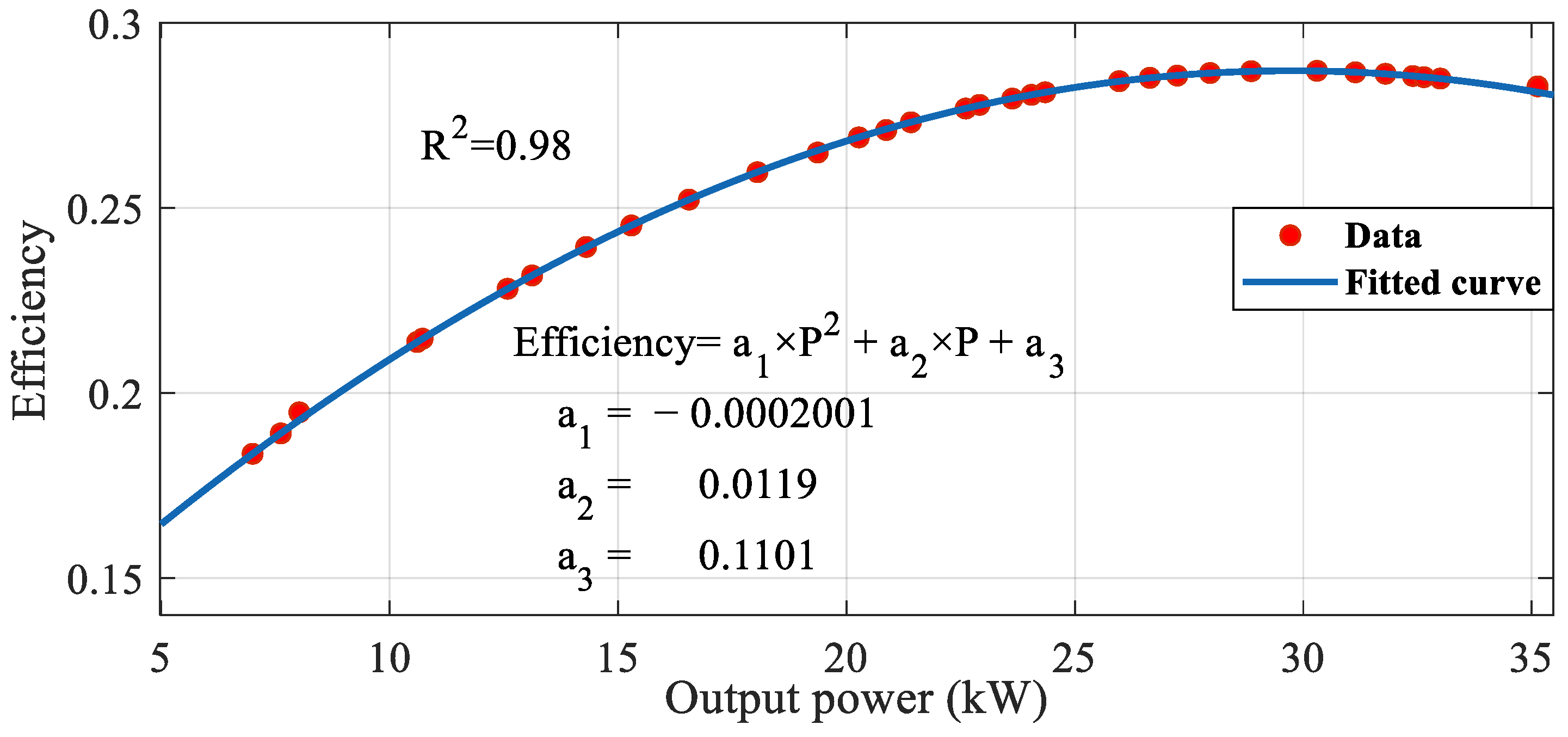
3.1. Power Generation Units
3.1.1. Probabilistic Model for Wind Speed and Demand Load
3.1.2. Generation Unit Cost Formulation
3.1.3. Constraints
3.2. Decision Variables
3.3. Objective Functions
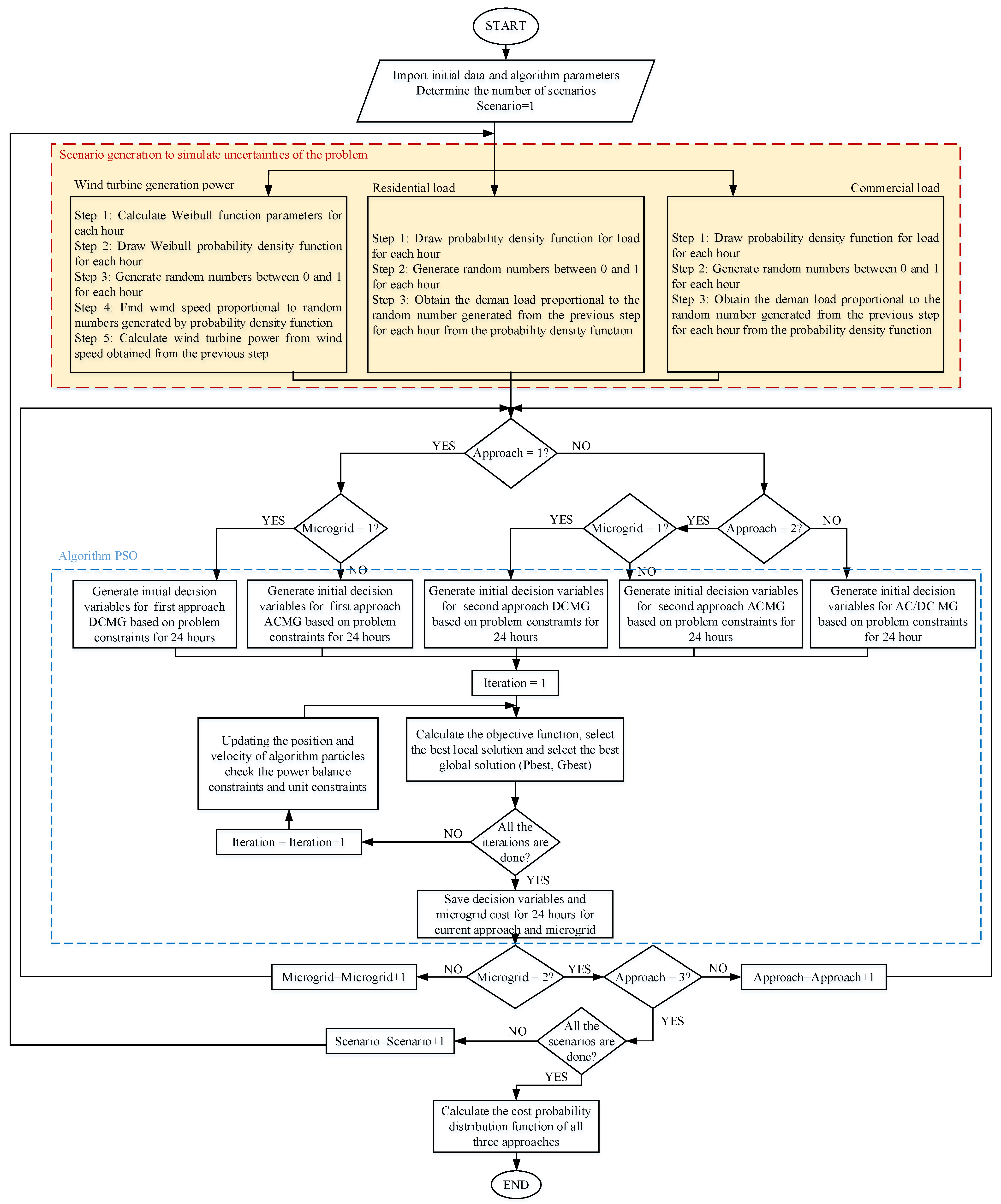
3.4. Proposed Method
4. Simulation Results
4.1. Input Data
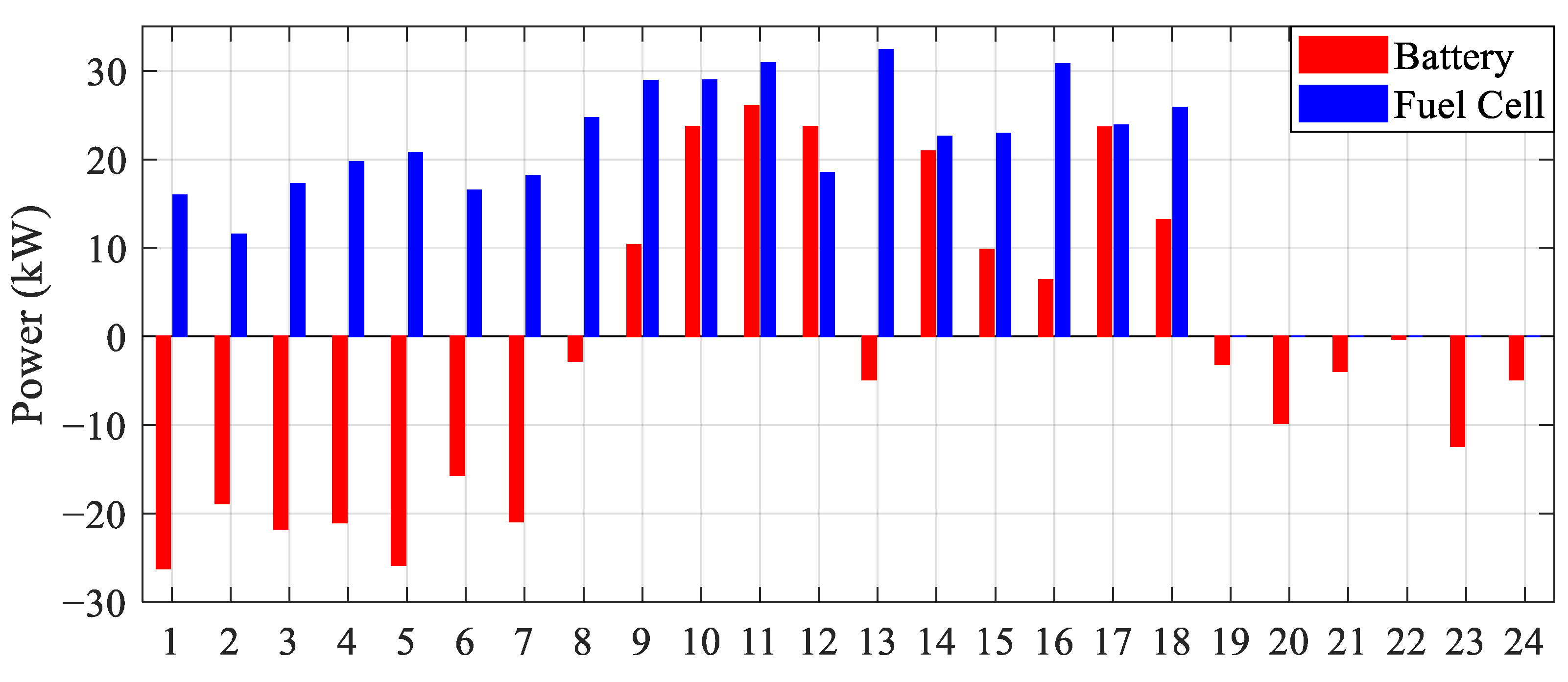
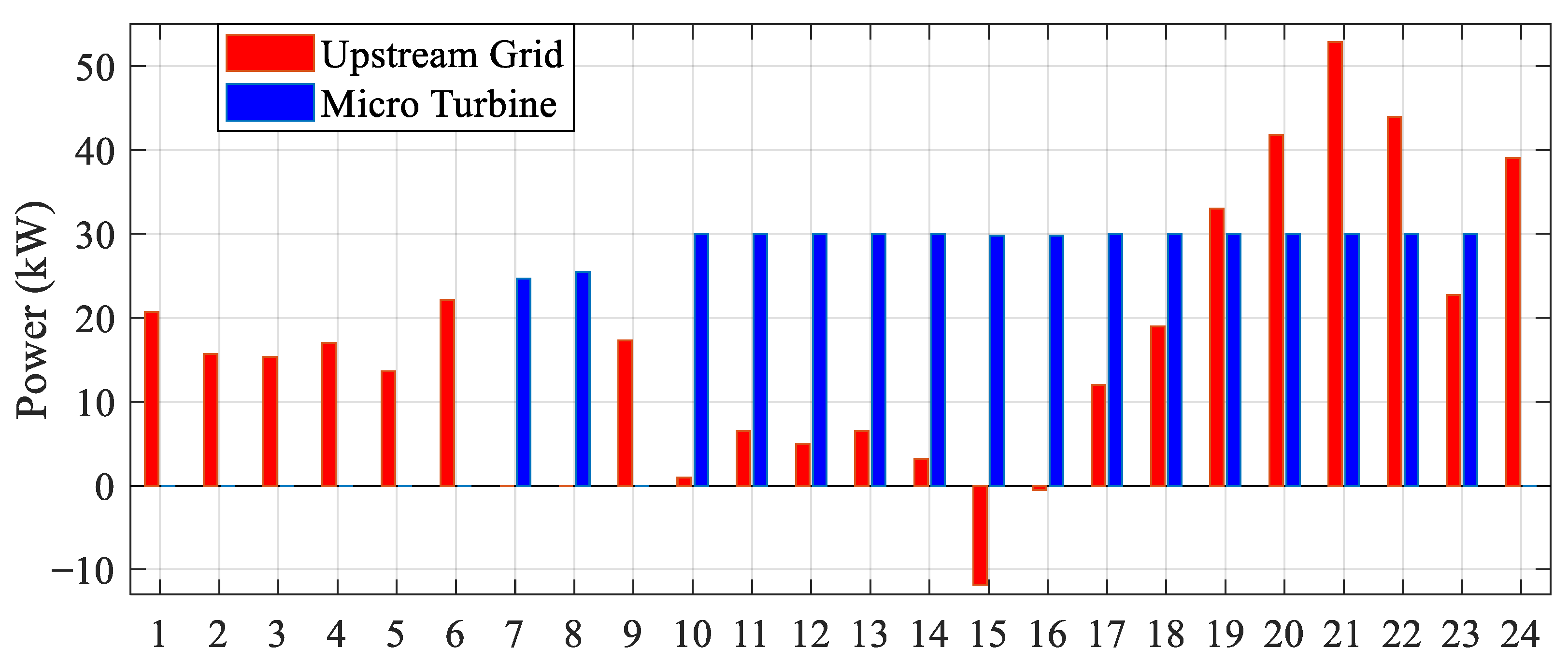
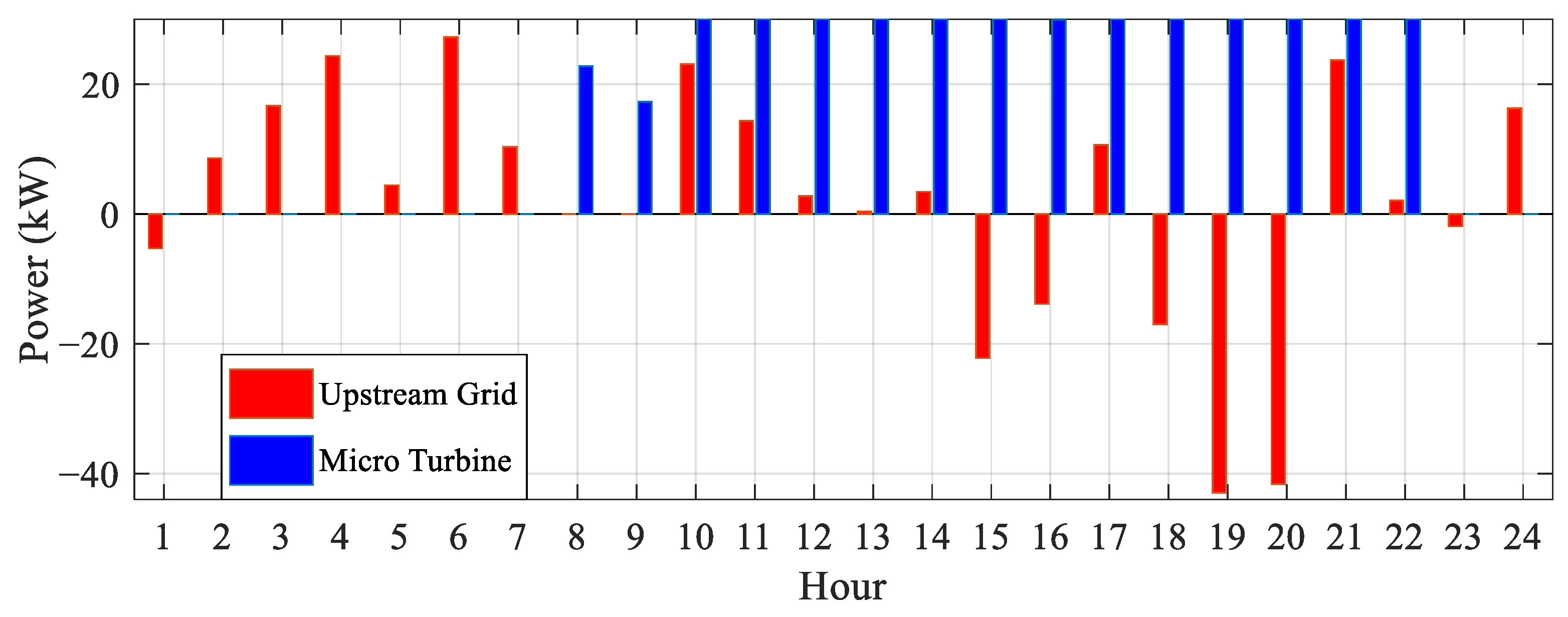
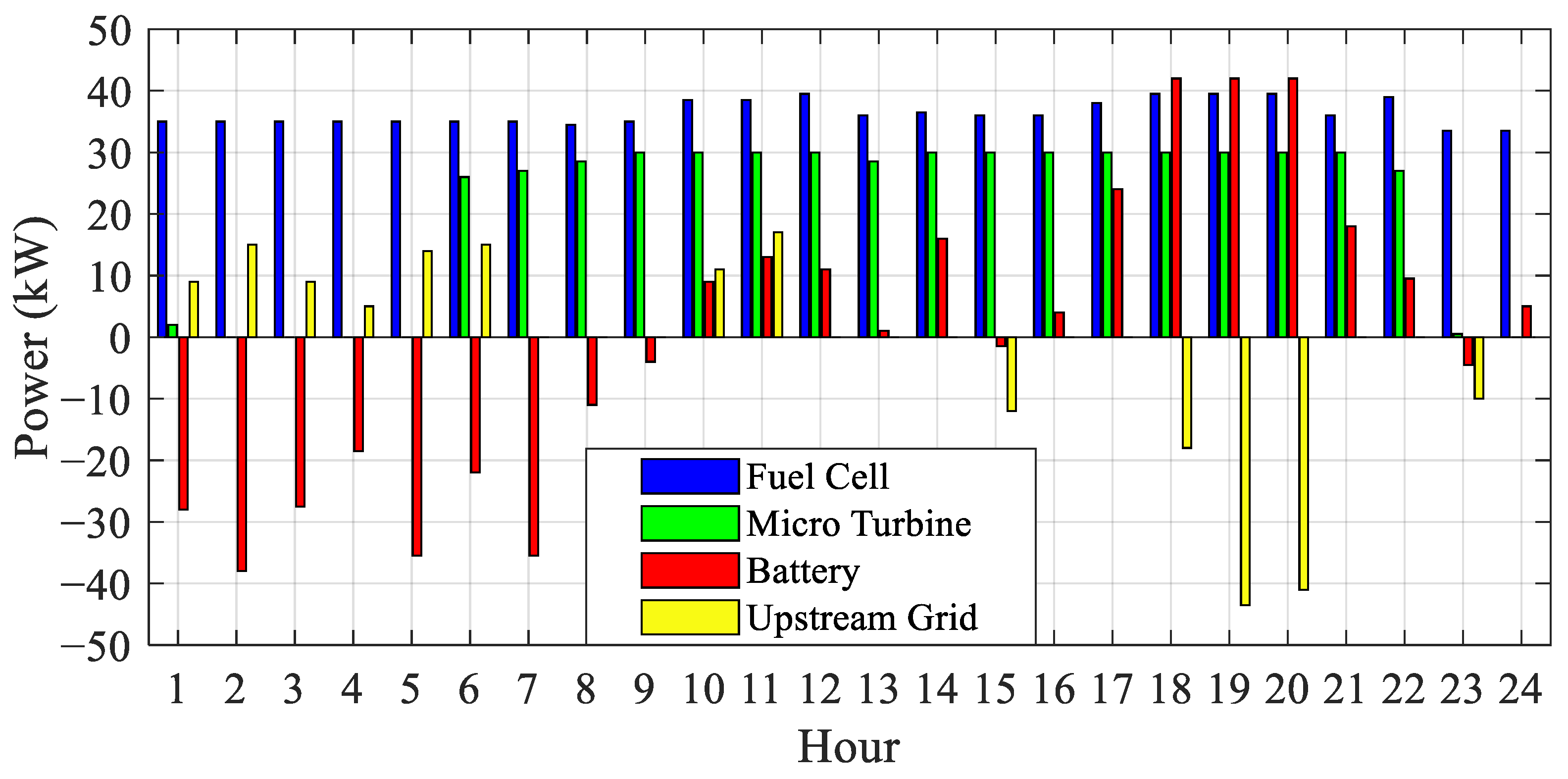
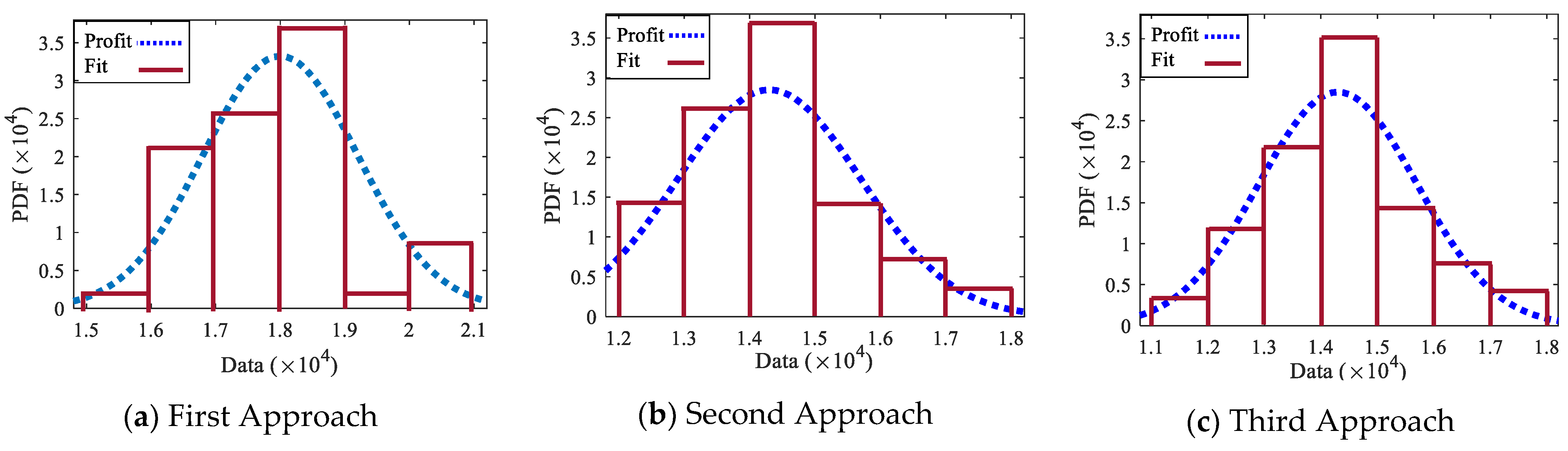
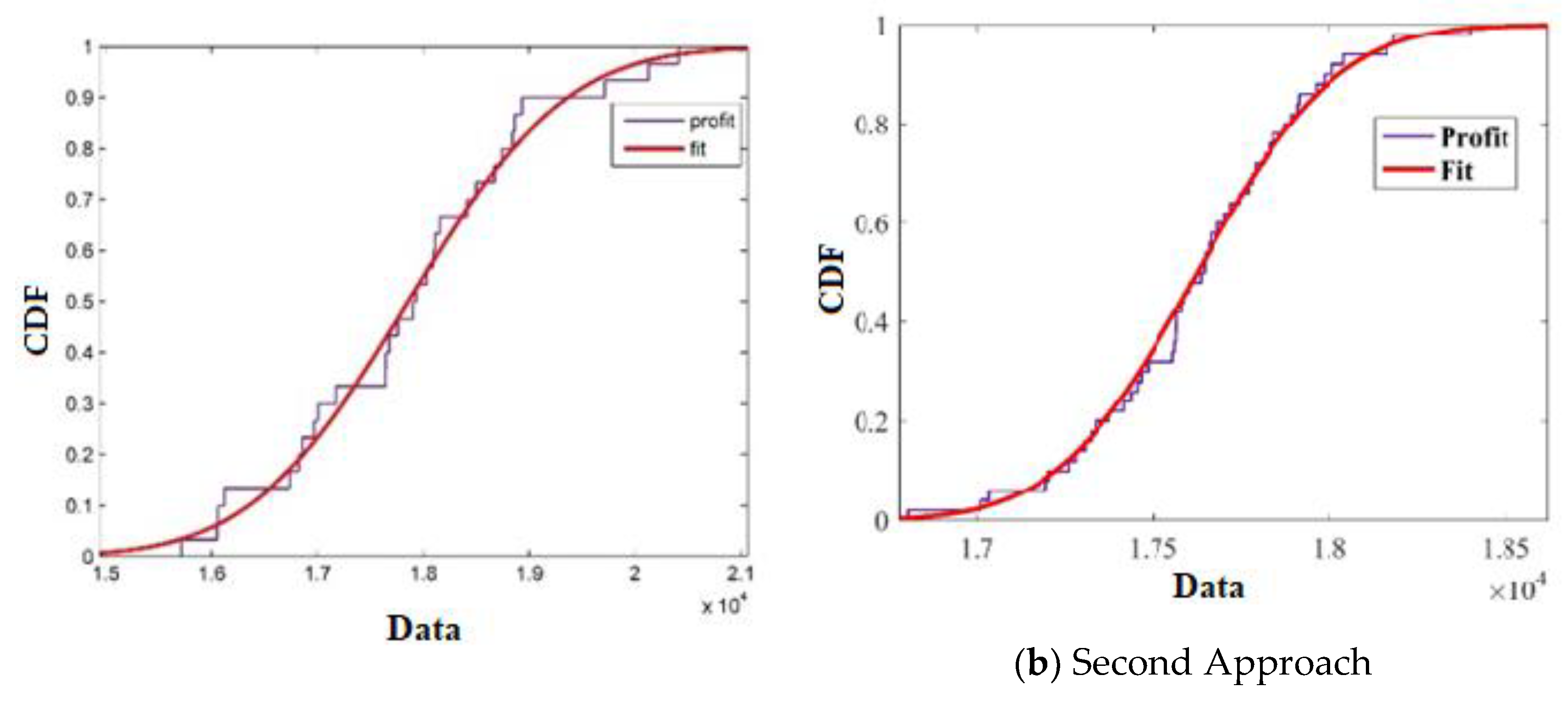
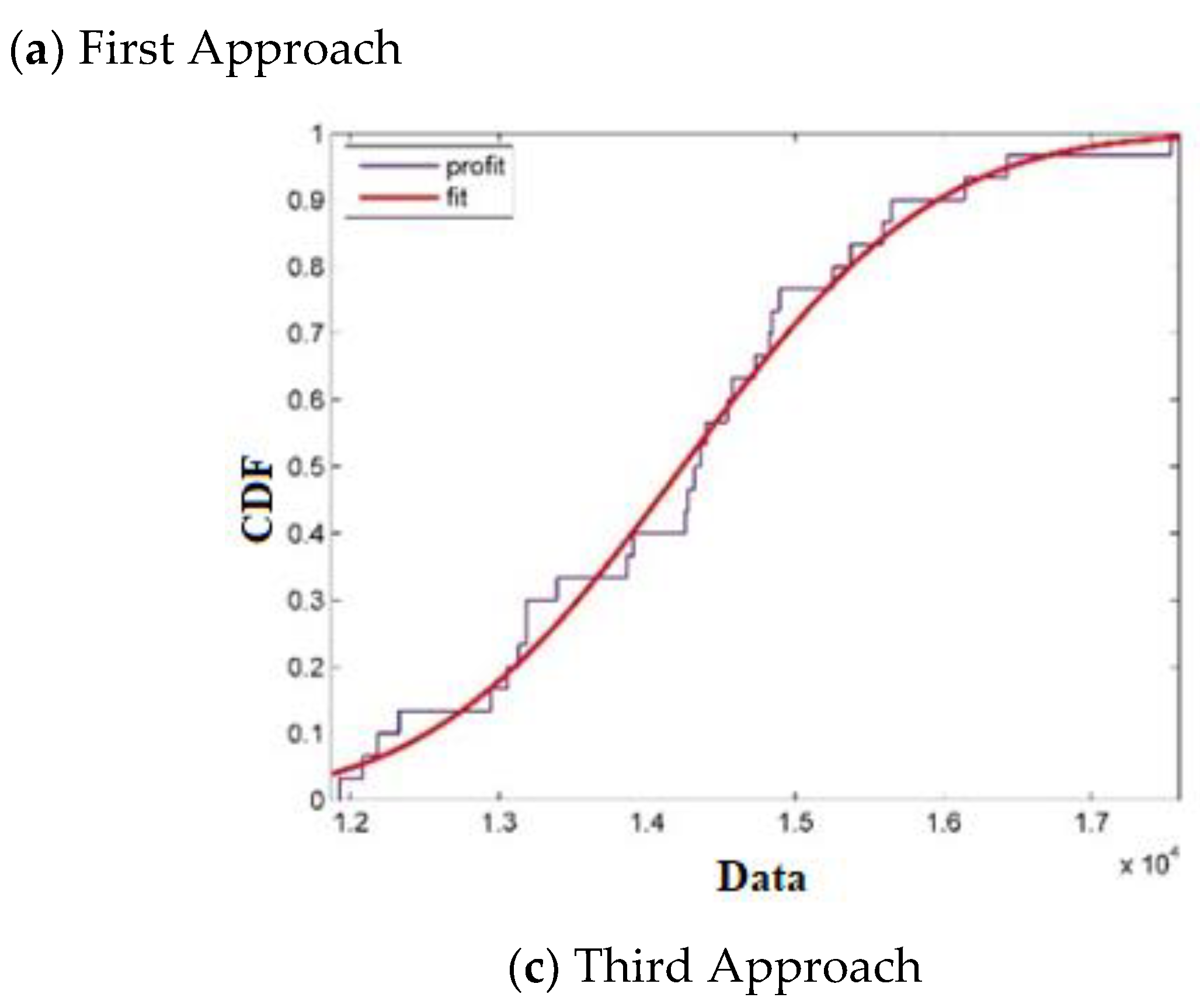
4.2. Results of Three Proposed Approaches
- Operating microgrids in islanded mode reduces the potential for distributed generation to fully meet the load demand.
- The battery’s performance differs between the islanded mode and grid-connected mode. In the islanded mode, the battery primarily functions as a regulator, maintaining the optimal operating point of programmable units.
- The presence of an MCEMS in microgrid connections enables power to be drawn from the main grid during early hours when energy prices are lower.
- During periods of higher energy prices and increased power generation from other sources, excess power consumed by the loads is sold back to the main grid.
- Applying multi-objective optimization methods in the operation of an AC/DC microgrid.
- Considering the presence of electric vehicles in the DC section.
- Evaluating the operation of an AC/DC microgrid while accounting for power losses.
- Analyzing unbalanced microgrids.
- Incorporating stochasticity in other parameters, such as energy costs or the state of charge (SOC) of the battery.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| ACMG | AC Microgrid |
| DCMG | DC Microgrid |
| DG | Diesel Generator |
| FC | Fuel Cell |
| Inv | Inverter |
| MCEMS | Microgrid Central Energy Management System |
| MT | Microturbine |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| SOC | State of Charge |
| WT | Wind Turbine |
References
- Wang, C.; Zhang, Z.; Abedinia, O.; Farkoush, S.G. Modeling and analysis of a microgrid considering the uncertainty in renewable energy resources, energy storage systems and demand management in electrical retail market. J. Energy Storage 2021, 33, 102111. [Google Scholar] [CrossRef]
- Niknam, T.; Zeinoddini-Meymand, H.; Mojarrad, H.D. A novel Multi-objective Fuzzy Adaptive Chaotic PSO algorithm for Optimal Operation Management of distribution network with regard to fuel cell power plants. Eur. Trans. Electr. Power 2011, 21, 1954–1983. [Google Scholar] [CrossRef]
- Safipour, R.; Oukati Sadegh, M. Optimal Planning of Energy Storage Systems in Microgrids for Improvement of Operation Indices. Int. J. Renew. Energy Res. 2018, 18, 1483–1498. [Google Scholar] [CrossRef]
- Prasad, T.N.; Devakirubakaran, S.; Mithubalaji, S.; Srinivasan, S.; Karthikeyan, B.; Palanisamy, R.; Bajaj, M.; Zawbaa, H.M.; Kamel, S. Power management in hybrid ANFIS PID based AC–DC microgrids with EHO based cost optimized droop control strategy. Energy Rep. 2022, 8, 15081–15094. [Google Scholar] [CrossRef]
- Modarresi, J. Coalitional game theory approach for multi-microgrid energy systems considering service charge and power losses. Sustain. Energy Grids Netw. 2022, 31, 100720. [Google Scholar] [CrossRef]
- García-Ceballos, S.P.-L.C.; Mora-Flórez Londono, S.P.J.; Ceballos, C.G.; Flórez, J.M. Stability analysis framework for isolated microgrids with energy resources integrated using voltage source converters. Results Eng. 2023, 19, 101252. [Google Scholar] [CrossRef]
- Raju, D.K.; Kumar, R.S.; Raghav, L.P.; Singh, A.R. Enhancement of loadability and voltage stability in grid-connected microgrid network. J. Clean. Prod. 2022, 374, 101252. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Gholami, M.; Mousavi, S.A. Development of new reliability metrics for microgrids: Integrating renewable energy sources and battery energy storage system. Energy Rep. 2023, 10, 2251–2259. [Google Scholar]
- Szilagyi, E.; Petreus, D.; Paulescu, M.; Patarau, T.; Hategan, S.M.; Sarbu, N.A. Cost-effective energy management of an islanded microgrid. Energy Rep. 2023, 10, 4516–4537. [Google Scholar] [CrossRef]
- Kassab, F.A.; Celik, B.; Locment, F.; Sechilariu, M.; Liaquat, S.; Hansen, T.M. Optimal sizing and energy management of a microgrid: A joint MILP approach for minimization of energy cost and carbon emission. Renew. Energy 2024, 224, 120186. [Google Scholar] [CrossRef]
- Caminiti, C.M.; Ragaini, E.; Barbieri, J.; Dimovski, A.; Merlo, M. Limited-Size BESS for Mitigating the Impact of RES Volatility in Grid-Tied Microgrids in Developing Countries: Focus on Lacor Hospital. In Proceedings of the 2024 IEEE PES/IAS PowerAfrica, Johannesburg, South Africa, 7–11 October 2024. [Google Scholar]
- Khajeh, A.; Modarress, H.; Zeinoddini-Meymand, H. Application of modified particle swarm optimization as an efficient variable selection strategy in QSAR/QSPR studies. J. Chemom. 2012, 26, 598–603. [Google Scholar]
- Nejabatkhah, F.; Li, Y.W. Overview of Power Management Strategies of Hybrid AC/DC Microgrid. IEEE Trans. Power Electron. 2015, 30, 7072–7089. [Google Scholar]
- Gupta, A.; Doolla, S.; Chatterjee, K. Hybrid AC–DC Microgrid: Systematic Evaluation of Control Strategies. IEEE Trans. Smart Grid 2018, 9, 3830–3843. [Google Scholar]
- Sohrabi-Tabar, V.; Jirdehi, M.A.; Hemmati, R. Energy management in microgrid based on the multi objective stochastic programming incorporating portable renewable energy resource as demand response option. Energy 2017, 118, 827–839. [Google Scholar] [CrossRef]
- Firouzi, B.; Zeinoddini-Meymand, H.; Niknam, T.; Mojarrad, H.D. A novel multi-objective Chaotic Crazy PSO algorithm for optimal operation management of distribution network with regard to fuel cell power plants. Int. J. Innov. Comput. Inf. Control 2011, 7, 6395–6409. [Google Scholar]
- Baziar, A.; Kavousi-Fard, A. Considering uncertainty in the optimal energy management of renewable micro-grids including storage devices. Renew. Energy 2013, 59, 158–166. [Google Scholar]
- Siahkali, H.; Vakilian, M. Stochastic unit commitment of wind farms integrated in power system. Electr. Power Syst. Res. 2010, 80, 1006–1017. [Google Scholar]
- Kumar, R.P.; Karthikeyan, G. A multi-objective optimization solution for distributed generation energy management in microgrids with hybrid energy sources and battery storage system. J. Energy Storage 2024, 75, 109702. [Google Scholar]
- Babu, V.V.; Roselyn, J.P.; Sundaravadivel, P. Multi-objective genetic algorithm based energy management system considering optimal utilization of grid and degradation of battery storage in microgrid. Energy Rep. 2023, 9, 5992–6005. [Google Scholar]
- Moradi, H.; Esfahanian, M.; Abtahi, A.; Zilouchian, A. Optimization and energy management of a standalone hybrid microgrid in the presence of battery storage system. Energy 2018, 147, 226–238. [Google Scholar]
- Li, Z.; Xie, X.; Cheng, Z.; Zhi, C.; Si, J. A novel two-stage energy management of hybrid AC/DC microgrid considering frequency security constraints. Electr. Power Energy Syst. 2023, 146, 108768. [Google Scholar] [CrossRef]
- Yuan, G.; Wang, H.; Khazaei, E.; Khan, B. Collaborative advanced machine learning techniques in optimal energy management of hybrid AC/DC IoT-based microgrids. Ad Hoc Netw. 2021, 122, 102657. [Google Scholar]
- Billah, M.; Yousif, M.; Numan, M.; Salam, I.U.; Kazmi, S.A.A.; Alghamdi, T.A.H. Decentralized Smart Energy Management in Hybrid Microgrids: Evaluating Operational Modes, Resources Optimization, and Environmental Impacts. IEEE Access 2023, 11, 143530–143548. [Google Scholar]
- Bacha, B.; Ghodbane, H.; Dahmani, H.; Betka, A.; Toumi, A.; Chouder, A. Optimal sizing of a hybrid microgrid system using solar, wind, diesel, and battery energy storage to alleviate energy poverty in a rural area of Biskra, Algeria. J. Energy Storage 2024, 84, 110651. [Google Scholar]
- Yang, F.; Ye, L.; Muyeen, S.M.; Li, D.; Lin, S.; Fang, C. Power management for hybrid AC/DC microgrid with multi-mode subgrid based on incremental costs. Electr. Power Energy Syst. 2022, 138, 107887. [Google Scholar]
- Cai, Y.; Lu, Z.; Pan, Y.; He, L.; Guo, X.; Zhang, J. Optimal scheduling of a hybrid AC/DC multi-energy microgrid considering uncertainties and Stackelberg game-based integrated demand response. Electr. Power Energy Syst. 2022, 142, 108341. [Google Scholar]
- Ahmed, H.M.A.; Sindi, H.F.; Azzouz, M.A.; Awad, A.S.A. An Energy Trading Framework for Interconnected AC–DC Hybrid Smart Microgrids. IEEE Trans. Smart Grid 2023, 14, 853–865. [Google Scholar]
- Valencia-Díaz, A.; Toro, E.M.; Hincapié, R.A. Optimal planning and management of the energy–water–carbon nexus in hybrid AC/DC microgrids for sustainable development of remote communities. Appl. Energy 2025, 377, 124517. [Google Scholar]
- Çimen, H.; Bazmohammadi, N.; Lashab, A.; Terriche, Y.; Vasquez, J.C.; Guerrero, J.M. An online energy management system for AC/DC residential microgrids supported by non-intrusive load monitoring. Appl. Energy 2022, 307, 118136. [Google Scholar]
- Wang, W.; Qin, C.; Zhang, J.; Wen, C.; Xu, G. Correlation analysis of three-parameter Weibull distribution parameters with wind energy characteristics in a semi-urban environment. Energy Rep. 2022, 8, 8480–8498. [Google Scholar]
- Solas, Á.F.; Romero, J.M.; Micheli, L.; Almonacid, F.; Fernandez, E.F. Estimation of soiling losses in photovoltaic modules of different technologies through analytical methods. Energy 2022, 244, 123173. [Google Scholar] [CrossRef]
- Jimenez, L.A.F.; Monteiro, C.; Rosado, I.J.R. Short-term probabilistic forecasting models using Beta distributions for photovoltaic plants. Energy Rep. 2023, 9, 495–502. [Google Scholar] [CrossRef]
- Nikmehr, N.; Najafi-Ravadanegh, S. Optimal operation of distributed generations in micro-grids under uncertainties in load and renewable power generation using heuristic algorithm. IET Renew. Power Gener. 2015, 9, 982–990. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Mirjalili, S.A. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 224, 113301. [Google Scholar] [CrossRef]
- Pourbehzadi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Shafie-Khah, M.; Catalao, J.P.S. Optimal operation of hybrid AC/DC microgrids under uncertainty of renewable energy resources: A comprehensive review. Electr. Power Energy Syst. 2019, 109, 139–159. [Google Scholar] [CrossRef]
- Jabbari-Sabet, R.; Tafreshi, S.M.M.; Mirhoseini, S.S. Microgrid operation and management using probabilistic reconfiguration and unit commitment. Int. J. Electr. Power Energy Syst. 2016, 75, 328–336. [Google Scholar] [CrossRef]
- Sun, H.; Cui, X.; Latifi, H. Optimal management of microgrid energy by considering demand side management plan and maintenance cost with developed particle swarm algorithm. Electr. Power Syst. Res. 2024, 231, 110312. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]




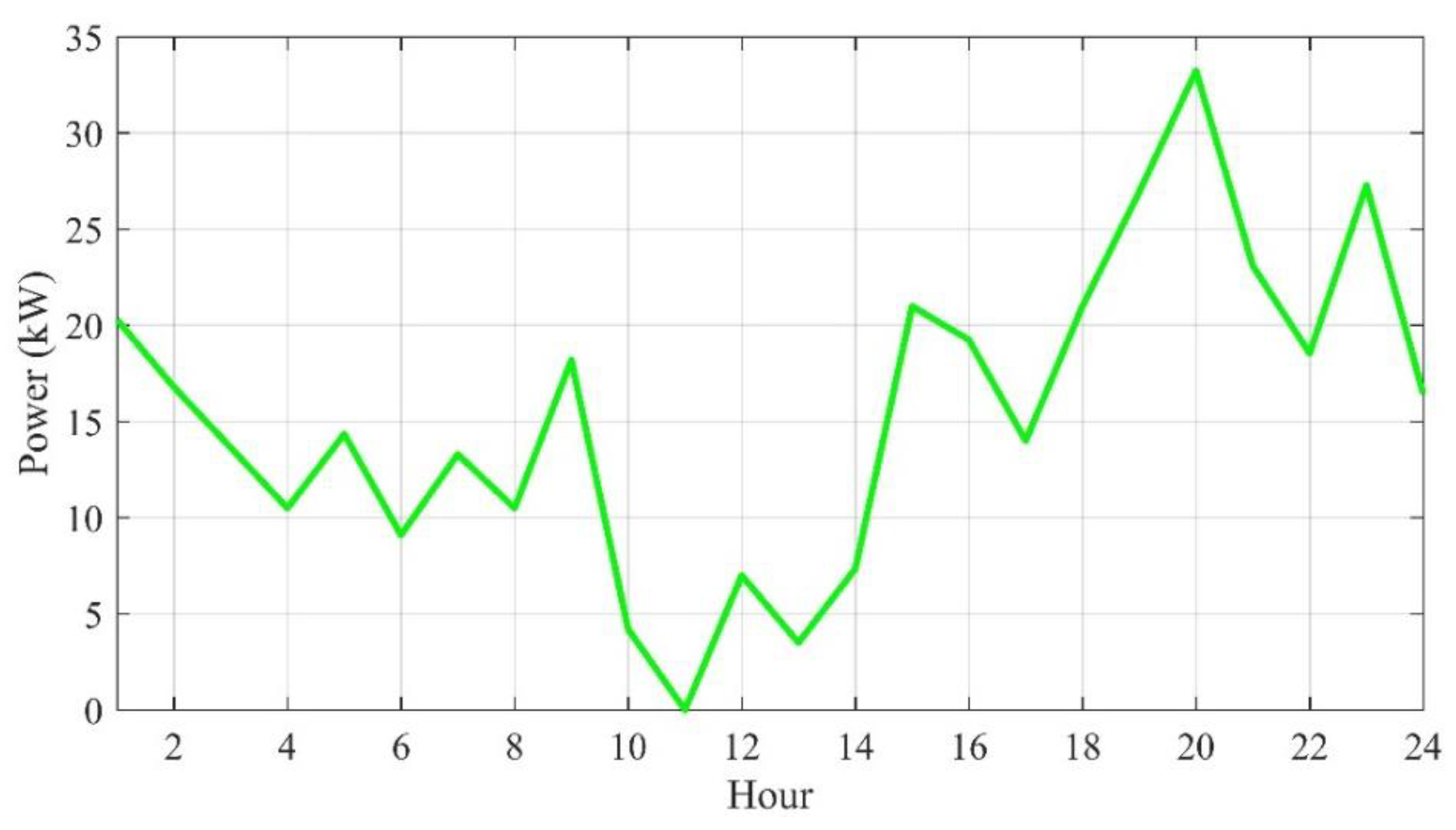
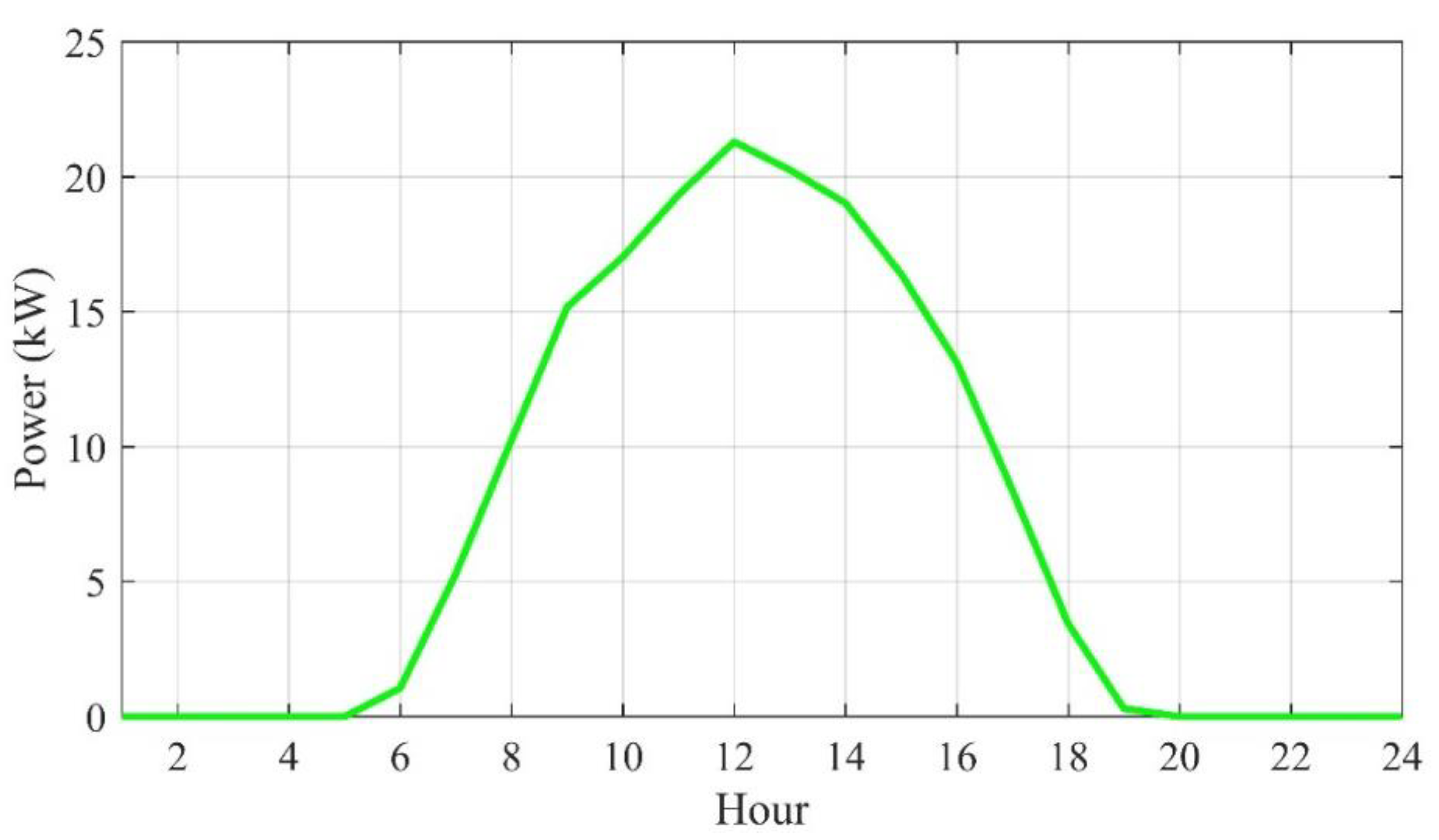
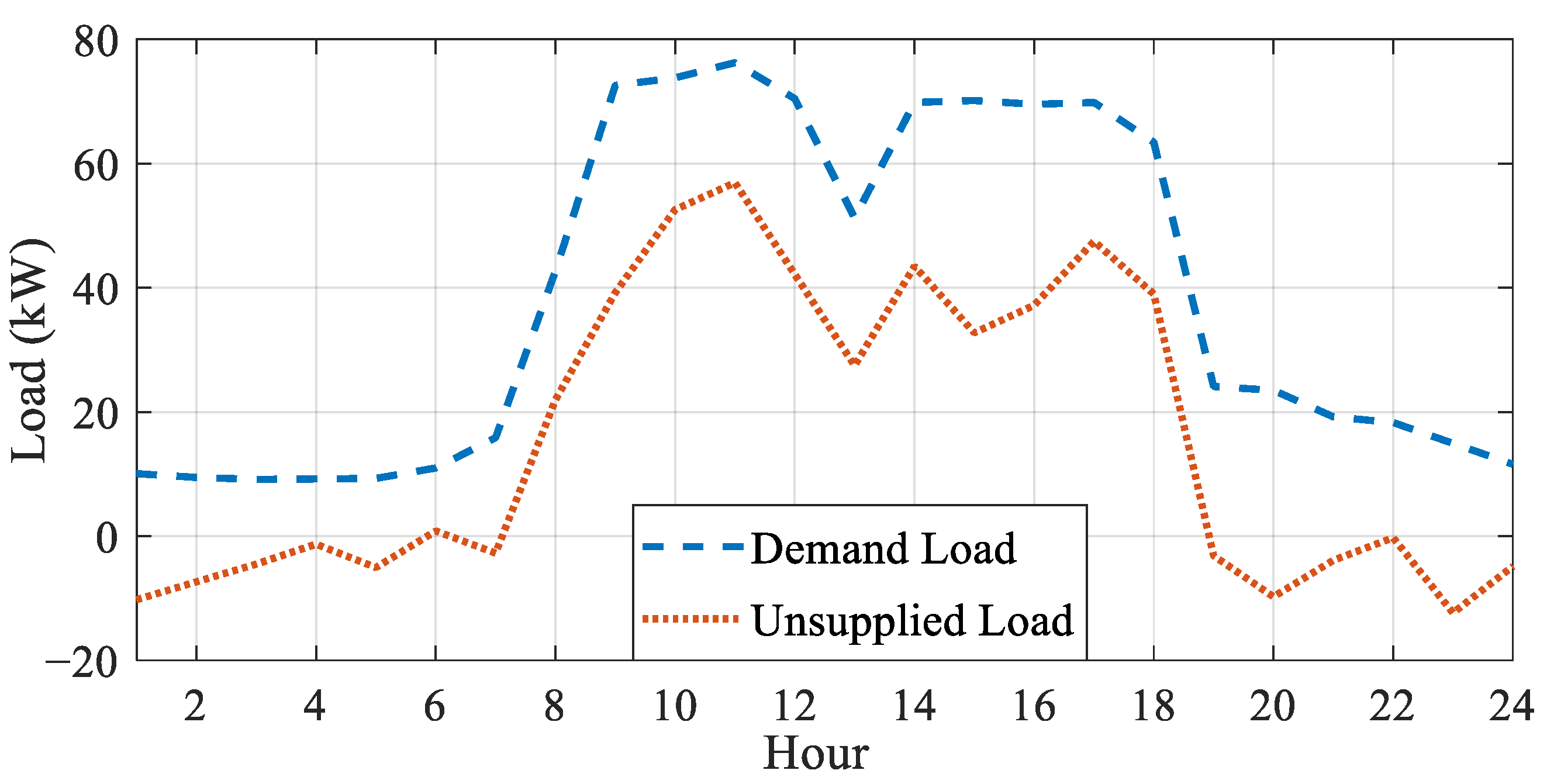
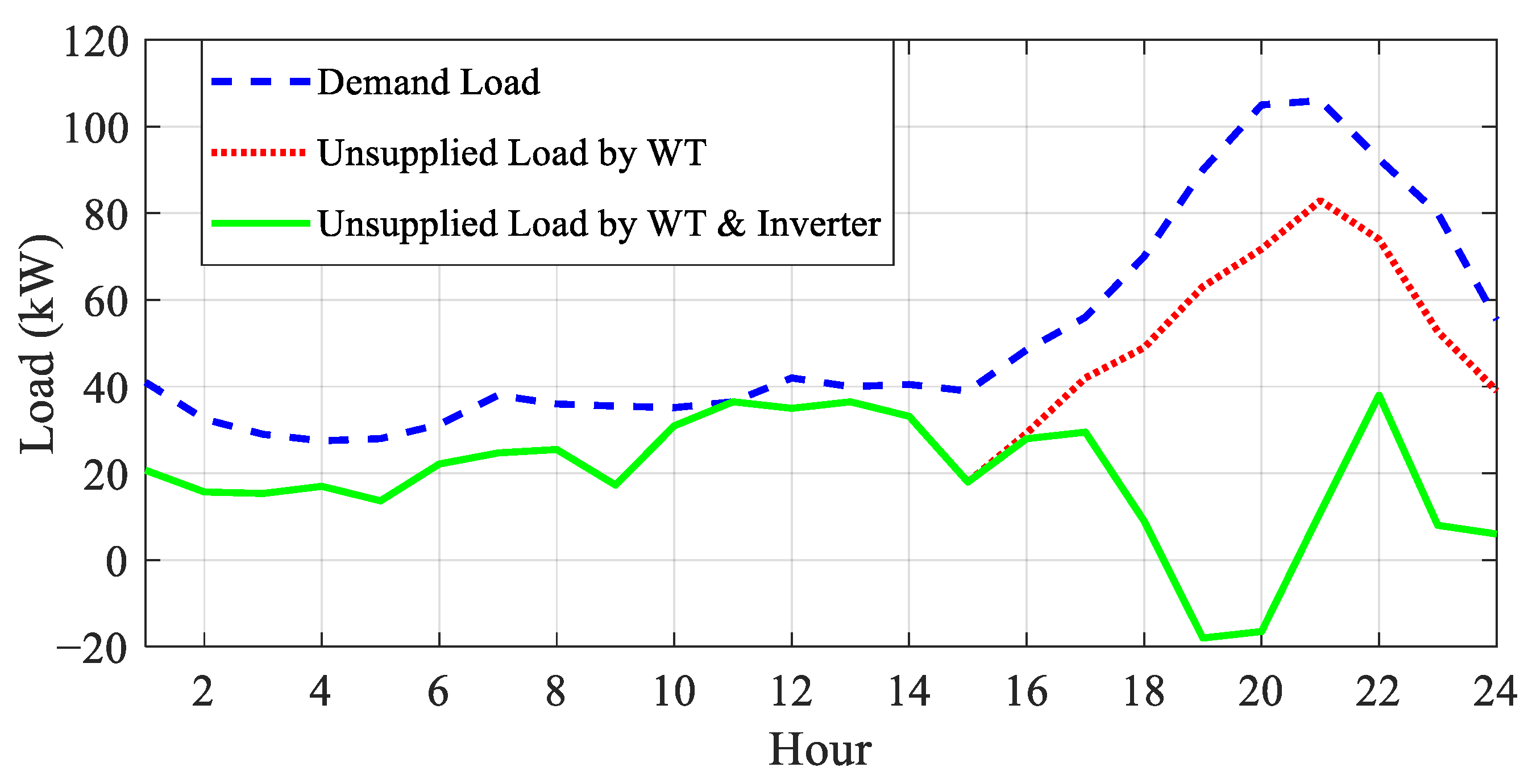







| SOCmin (kW) | SOCmax (kW) | Pmin (kW) | Pmax (kW) | COMB ($/year) | CRB ($) | LB (KWh) | NB |
|---|---|---|---|---|---|---|---|
| 30 | 250 | −40 | 40 | 10 | 900 | 10569 | 40 |
| Generation Unit | Lower Generated Power Limit (kW) | Upper Generated Power Limit (kW) |
|---|---|---|
| Microturbine | 9 | 30 |
| Fuel cell | 1.6 | 40 |
| Diesel generator | 15 | 50 |
| Wind turbine | 0 | 35 |
| Photovoltaic | 0 | 30 |
| Energy storage | −40 | 40 |
| Inverter output power | −150 | 150 |
| Main grid | −150 | 150 |
| Stored energy | 30 | 250 |
| Type of Pollutant | Penalty Factor | DG Emission Rate (kg/MWh) | FC Emission Rate (kg/MWh) | MT Emission Rate (kg/MWh) |
|---|---|---|---|---|
| NOx | 4.2 | 9.89 | 0.0136 | 0.199 |
| SO2 | 0.99 | 0.206 | 0.0027 | 0.0036 |
| CO2 | 0.014 | 0.649 | 0.489 | 0.724 |
| Generation Unit | DG ($/kWh) | FC ($/kWh) | MT ($/kWh) |
|---|---|---|---|
| CO&M | 0.01258 | 0.00587 | 0.00419 |
| Approach | DCMG Cost (Cents) | ACMG Cost (Cents) | Total Cost of Two Microgrids (Cents) |
|---|---|---|---|
| First approach | 3572.31 | 14,558.43 | 18,130.74 |
| Second approach | 914.22 | 12,789.4 | 13,703.26 |
| Third approach | 1145.75 | 12,493.78 | 13,639.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeinoddini-Meymand, H.; Safipour, R.; Namdari, F. A Novel Management Approach for Optimal Operation of Hybrid AC-DC Microgrid in the Presence of Wind and Load Uncertainties. Systems 2025, 13, 233. https://doi.org/10.3390/systems13040233
Zeinoddini-Meymand H, Safipour R, Namdari F. A Novel Management Approach for Optimal Operation of Hybrid AC-DC Microgrid in the Presence of Wind and Load Uncertainties. Systems. 2025; 13(4):233. https://doi.org/10.3390/systems13040233
Chicago/Turabian StyleZeinoddini-Meymand, Hamed, Reza Safipour, and Farhad Namdari. 2025. "A Novel Management Approach for Optimal Operation of Hybrid AC-DC Microgrid in the Presence of Wind and Load Uncertainties" Systems 13, no. 4: 233. https://doi.org/10.3390/systems13040233
APA StyleZeinoddini-Meymand, H., Safipour, R., & Namdari, F. (2025). A Novel Management Approach for Optimal Operation of Hybrid AC-DC Microgrid in the Presence of Wind and Load Uncertainties. Systems, 13(4), 233. https://doi.org/10.3390/systems13040233







