Reliable Process Tracking Under Incomplete Event Logs Using Timed Genetic-Inductive Process Mining
Abstract
1. Introduction
2. Related Research
2.1. Process Mining
2.2. Completeness of Event Log
- Data extraction limitations. Logs often capture events within specific timeframes, which may lead to truncated cases if a process started before or extended beyond the extraction period [8].
- Ongoing cases. Some processes remain active at the time of extraction, making them appear incomplete [8].
- Abandoned cases. Certain processes may never reach completion due to customer inaction, system failures, or external dependencies [8].
- Lack of system integration. Many organizations rely on periodic or asynchronous data entry systems, where activities may be logged with delays or not recorded at all due to system inefficiencies [13].
- Human factors. Manual data entry errors, workload pressures, and inconsistent recording practices often result in missing or incorrect timestamps, further exacerbating incompleteness [13].
2.3. Genetic Process Mining
2.4. Inductive Mining
2.5. Timed-Based Process Discovery
3. Timed Genetic-Inductive Process Mining
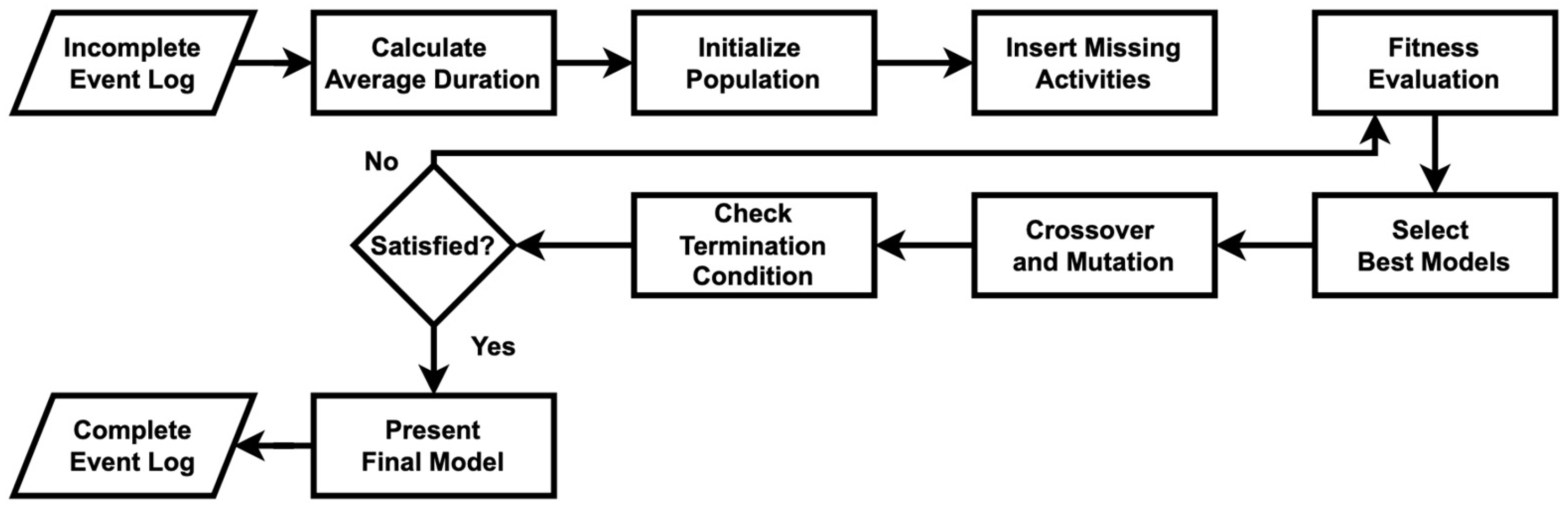
3.1. The Algorithm
3.2. Definition of Related Terms for TGIPM Algorithm
- Direct Succession: if activity is directly followed by in the same case, where and .
- Concurrency: if activities and can be executed in parallel in the same case, where or and .
- Choice: if either or directly occurs after the same activity , but not both, where ((, ( and . Here, operator means exclusive or relationship.
4. Experiment Evaluation
4.1. Experiment Purpose
- Qf is the fitness value.
- Qp is the precision value.
- Qg is the generalization value.
- Qs is the simplicity value.
- #casesCaptured is the number of processes depicted in the process model from the event log.
- #casesLog is the number of processes in the event log.
- #tracesCaptured is the number of traces recorded in the event log.
- #tracesModel is the number of traces that can be formed from the process model.
- #dupAct is the number of activities depicted as duplications in the tree model and the total number of duplications.
- #misAct is the number of activities in the event log that are not depicted in the tree model, and the activities that are depicted in the tree model but not in the event log.
- #exactNode is the number of nodes in the tree model traversed corresponds to the process in the event log.
- #nodeTree is the number of nodes contained in the tree model.
4.2. Experiment Setup
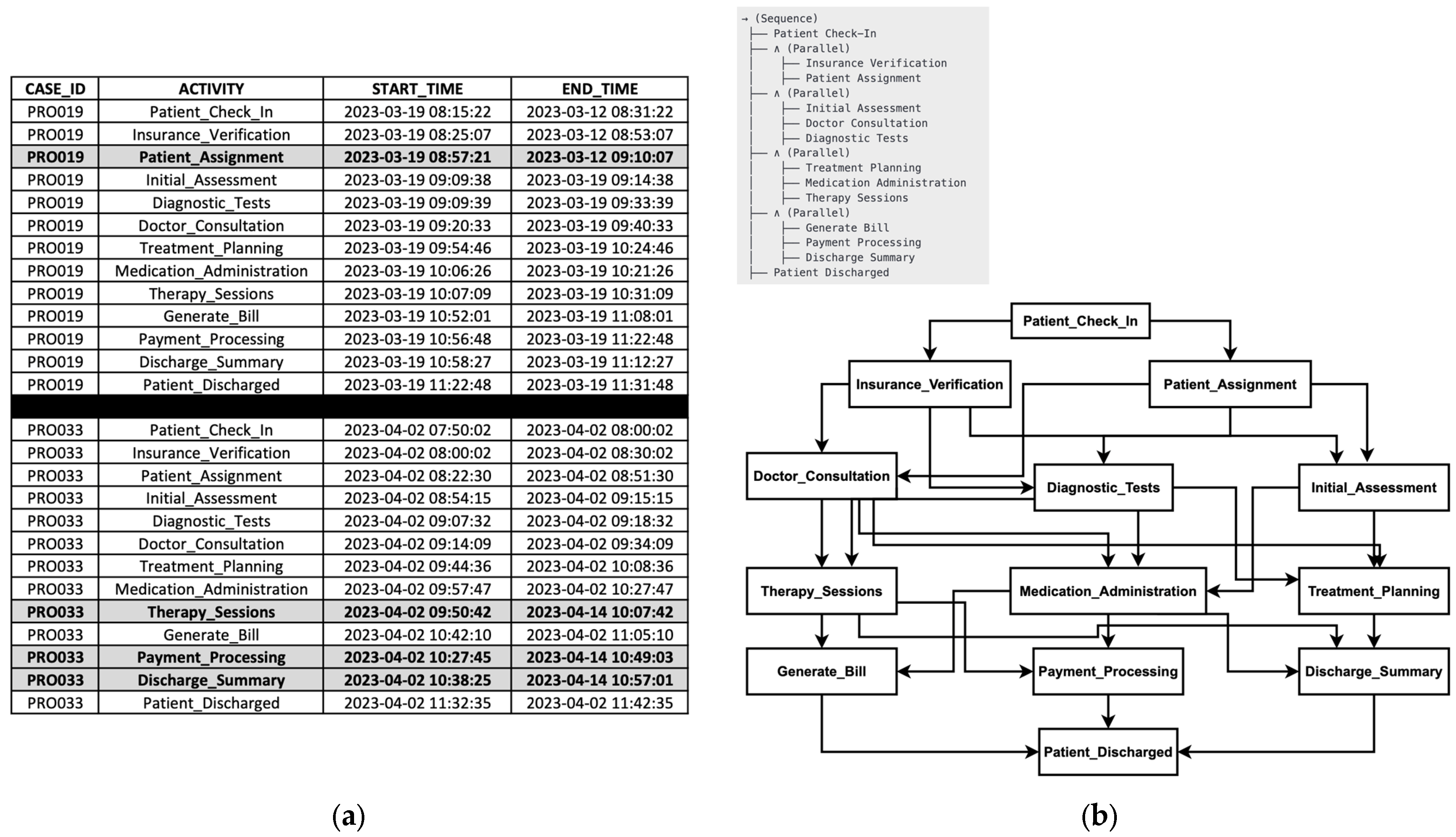
4.3. Experiment Results
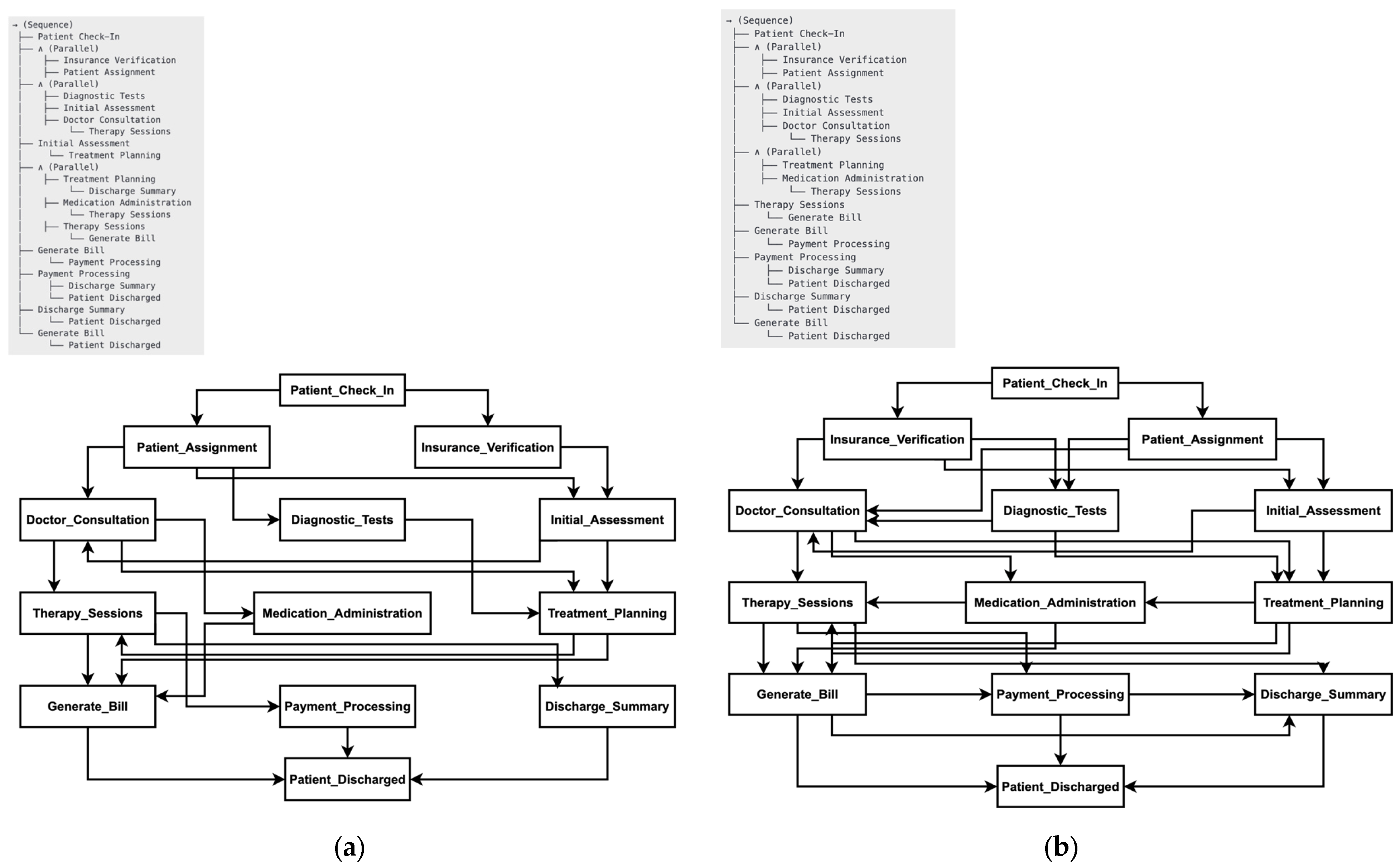
4.4. Comparison with Existing Genetic and Inductive Mining Approaches
- Dual timestamps integration, which improves missing activity reconstruction compared to [12]’s method.
- Genetic selection optimization, which refines process model fitness while preserving process structure, unlike [11]’s approach.
- Simultaneous recovery and discovery, ensuring that missing activities are reconstructed while the discovered process model remains structurally sound.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| GPM | Genetic Process Mining |
| IM | Inductive Mining |
| TGPM | Timed Genetic Process Mining |
| TGIPM | Timed Genetic-Inductive Process Mining |
| GSPNs | Generalized Stochastic Petri Nets |
| PIM | Probabilistic Inductive Miner |
| DPIM | Differentially Private Inductive Miner |
| IvM | Inductive Visual Miner |
| ERP | Enterprise Resource Planning |
| BPM | business process management |
| HIS | Hospital Information Systems |
Appendix A
| Algorithm A1. Pseudocode of TGIPM to recover missing activities and discover a process model |
| Input: EventLog: Event log containing CaseID, Activity, Start Time, End Time Generations: Number of generations for the genetic algorithm PopulationSize: Number of individuals in the genetic population Output: ProcessModel: A process model visualization # Step 1: Read and Preprocess Event Log Algorithm Read_Event_Log(file_path) Read event log from file_path Return event_log # Step 2: Calculate Average Activity Durations Algorithm Calculate_Average_Durations(event_log) Initialize average_durations as an empty dictionary Group event_log by Activity For each activity in grouped_event_log: Compute average_duration = Mean(End Time − Start Time) Store average_duration in average_durations dictionary Return average_durations # Step 3: Evaluate Fitness of an Activity Sequence Algorithm Evaluate_Fitness(sequence, start_times, end_times, average_durations) Initialize fitness_score = 0 For i = 1 to length(sequence) − 1: If i < length(start_times) − 1: expected_gap = average_durations(sequence [i + 1]) actual_gap = start_times [i + 1] − end_times [i] If actual_gap >= expected_gap: fitness_score += 1 Return fitness_score # Step 4: Genetic Operations (Crossover and Mutation) Algorithm Perform_Crossover(parent1, parent2) If length(parent1) > 2 AND length(parent2) > 2: Select crossover_point randomly from range(1, length(parent1) − 1) offspring1 = parent1[0:crossover_point] + parent2[crossover_point:end] offspring2 = parent2[0:crossover_point] + parent1[crossover_point:end] Else: offspring1, offspring2 = parent1, parent2 Return offspring1, offspring2 Algorithm Perform_Mutation(sequence, activity_pool) If length(sequence) > 1: Select mutation_index randomly from range (0, length(sequence) − 1) Replace sequence [mutation_index] with a random activity from activity_pool Return sequence # Step 5: Initialize Genetic Algorithm Population Algorithm Initialize_Population(size, missing_activities) Initialize empty population list For i = 1 to size: Generate a random sequence of missing_activities Add sequence to population Return population # Step 6: Genetic Process Mining for Recovering Missing Activities Algorithm Genetic_Process_Recovery (event_log, generations, population_size) Extract all unique activities from event_log Compute average_durations using Calculate_Average_Durations (event_log) Initialize recovered_log as an empty list For each case in event_log grouped by CaseID: Sort case events by Start Time Extract case_activities, start_times, and end_times Identify missing_activities = all_activities − case_activities Initialize population using Initialize_Population (population_size, missing_activities) For generation = 1 to generations: Compute fitness_scores for each individual in population Select individuals with maximum fitness Initialize new_population = empty list While length(new_population) < population_size: Select parent1, parent2 randomly from selected_population Generate offspring1, offspring2 using Perform_Crossover (parent1, parent2) Apply Perform_Mutation to offspring1 and offspring2 Add mutated offspring to new_population Update population = new_population Select best_individual with highest fitness Insert missing activities in chronological order based on average durations Store updated case in recovered_log Return recovered_log # Step 7: Compute Direct Succession Matrix Algorithm Compute_Direct_Succession (event_log, activities) Initialize direct_succession matrix with zeros for all activity pairs (a1, a2) For each trace in event_log grouped by CaseID: Sort trace by Start Time For i = 1 to length(trace) − 1: Increment direct_succession[trace[i], trace[i + 1]] Return direct_succession # Step 8: Identify Concurrency Matrix Algorithm Identify_Concurrency (direct_succession, activities) Initialize concurrency_matrix with zeros for all activity pairs (a1, a2) For each (a1, a2) in direct_succession: If direct_succession[a1, a2] > 0 OR direct_succession[a2, a1] > 0: concurrency_matrix[a1, a2] = 1 Return concurrency_matrix # Step 9: Remove Dummy Activities Based on Frequency Threshold Algorithm Remove_Dummy_Activities (event_log, threshold) Compute activity_counts = Frequency of each activity in event_log Identify dummy_activities = activities with count < threshold Remove dummy_activities from event_log Return cleaned_event_log # Step 10: Discover Process Model Using Inductive Mining Algorithm Discover_Process_Model (cleaned_event_log) Apply Inductive Mining on cleaned_event_log to generate a process tree Convert process tree into a process model visualization Return process_model |
References
- Gao, R.X.; Krüger, J.; Merklein, M.; Möhring, H.-C.; Váncza, J. Artificial Intelligence in Manufacturing: State of the Art, Perspectives, and Future Directions. CIRP Ann. 2024, 73, 723–749. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P. Process mining: Data science in action. In Process Mining: Data Science in Action, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 140–178. [Google Scholar] [CrossRef]
- Sjödin, D.; Parida, V.; Kohtamäki, M. Artificial intelligence enabling circular business model innovation in digital servitization: Conceptualizing dynamic capabilities, AI capacities, business models and effects. Technol. Forecast. Soc. Chang. 2023, 197, 122903. [Google Scholar] [CrossRef]
- Aldoseri, A.; Al-Khalifa, K.N.; Hamouda, A.M. AI-Powered Innovation in Digital Transformation: Key Pillars and Industry Impact. Sustainability 2024, 16, 1790. [Google Scholar] [CrossRef]
- Effendi, Y.A.; Minsoo, K. Refining Process Mining in Port Container Terminals Through Clarification of Activity Boundaries With Double-Point Timestamps. ICIC Express Lett. Part B Appl. 2024, 15, 61–70. [Google Scholar] [CrossRef]
- Bose, R.; Mans, R.; van der Aalst, W. Wanna improve process mining results? In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Singapore, 16–19 April 2013; Volume 2013, pp. 127–134. [Google Scholar]
- Pei, J.; Wen, L.; Yang, H.; Wang, J.; Ye, X. Estimating Global Completeness of Event Logs: A Comparative Study. IEEE Trans. Serv. Comput. 2018, 14, 441–457. [Google Scholar] [CrossRef]
- Process Mining Book. Available online: https://fluxicon.com/book/read/dataext/ (accessed on 1 December 2024).
- Laplante, P.A.; Ovaska, S.J. Real-Time Systems Design and Analysis; IEEE Press: Piscataway, NJ, USA, 2012; Volume 3, pp. 154–196. [Google Scholar]
- Barchard, K.A.; Pace, L.A. Preventing human error: The impact of data entry methods on data accuracy and statistical results. Comput. Hum. Behaviour. 2011, 27, 1834–1839. [Google Scholar] [CrossRef]
- De Medeiros, A.K.A.; Weijters, A.J.M.M.; van der Aalst, W.M.P. Genetic Process Mining: An Experimental Evaluation. Data Min. Knowl. Discov. 2007, 14, 245–304. [Google Scholar] [CrossRef]
- Buijs, J.C.A.M. Flexible Evolutionary Algorithms for Mining Structured Process Models. Ph.D. Thesis, Technische Universiteit, Eindhoven, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Effendi, Y.A.; Kim, M. Timed Genetic Process Mining for Robust Tracking of Processes under Incomplete Event Log Conditions. Electronics 2024, 13, 3752. [Google Scholar] [CrossRef]
- De Medeiros, A.; Weijters, A.; Van der Aalst, W.M.P. Using Genetic Algorithms to mine Process Models: Representation, Operators and Results; Beta Working Paper Series, WP 124; Eindhoven University of Technology: Eindhoven, The Netherlands, 2004. [Google Scholar]
- Pohl, T.; Pegoraro, M. An Inductive Miner Implementation for the PM4PY Framework. i9 Process and Data Science (PADS); RWTH Aachen University: Aachen, Germany, 2019. [Google Scholar]
- Sarker, I.H. AI-Based Modeling: Techniques, Applications and Research Issues Towards Automation, Intelligent and Smart Systems. SN Comput. Sci. 2022, 3, 158. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Z.; Chu, Y.; Chen, Z.; Xu, Z.; Wen, Q. Intelligent Cross-Organizational Process Mining: A Survey and New Perspectives. arXiv 2024, arXiv:2407.11280. [Google Scholar]
- Aldoseri, A.; Al-Khalifa, K.N.; Hamouda, A.M. Re-Thinking Data Strategy and Integration for Artificial Intelligence: Concepts, Opportunities, and Challenges. Appl. Sci. 2023, 13, 7082. [Google Scholar] [CrossRef]
- Effendi, Y.A.; Retrialisca, F. Transforming Timestamp of a CSV Database to an Event Log. In Proceedings of the 8th International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 22–23 June 2021; pp. 367–372. [Google Scholar] [CrossRef]
- Effendi, Y.A.; Kim, M. Transforming Event Log with Domain Knowledge: A Case Study in Port Container Terminals. ICIC Express Lett. 2025, 19, 291–299. [Google Scholar] [CrossRef]
- Huser, V. Process Mining: Discovery, Conformance and Enhancement of Business Processes. J. Biomed. Inform. 2012, 45, 1018–1019. [Google Scholar] [CrossRef]
- Jans, M.; De Weerdt, J.; Depaire, B.; Dumas, M.; Janssenswillen, G. Conformance Checking in Process Mining. Inf. Syst. 2021, 102, 101851. [Google Scholar] [CrossRef]
- De Leoni, M. Foundations of Process Enhancement. In Process Mining Handbook. Lecture Notes in Business Information Processing; Van der Aalst, W.M.P., Carmona, J., Eds.; Springer: Cham, Switzerland, 2022; Volume 448. [Google Scholar] [CrossRef]
- Yang, H.; van Dongen, B.F.; ter Hofstede, A.H.M.; Wynn, M.T.; Wang, J. Estimating completeness of event logs. BPM Rep. 2012, 1204, 1–23. [Google Scholar]
- Li, C.; Ge, J.; Wen, L.; Kong, L.; Chang, V.; Huang, L.; Luo, B. A novel completeness definition of event logs and corresponding generation algorithm. Expert Syst. 2020, 37, 12529. [Google Scholar] [CrossRef]
- Wang, L.; Fang, X.; Shao, C. Discovery of Business Process Models from Incomplete Logs. Electronics 2022, 11, 3179. [Google Scholar] [CrossRef]
- Bose, R.P.J.C.; van der Aalst, W.M.P. Discovering Signature Patterns from Event Logs. Knowl. Inf. Syst. 2013, 39, 491–526. [Google Scholar] [CrossRef]
- Suriadi, S.; Andrews, R.; ter Hofstede, A.H.M.; Wynn, M.T.; van der Aalst, W.M.P.; Budiyanto, M.A. Event Log Imperfection Patterns for Process Mining: Towards a Systematic Approach to Cleaning Event Logs. Inf. Syst. 2017, 64, 132–150. [Google Scholar] [CrossRef]
- Dakic, J.; La Rosa, M.; Polyvyanyy, A. Taxonomy and Classification of Event Log Imperfections in Process Mining. Inf. Syst. 2023, 113, 102122. [Google Scholar]
- Song, M.; Günther, C.W.; van der Aalst, W.M.P. Trace Clustering in Process Mining. In Business Process Management Workshops; Springer: Berlin/Heidelberg, Germany, 2009; pp. 109–120. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, Q.; Poon, S.K. A Deep Learning Approach for Repairing Missing Activity Labels in Event Logs for Process Mining. Information 2022, 13, 234. [Google Scholar] [CrossRef]
- Rogge-Solti, A.; Mans, R.S.; van der Aalst, W.M.P.; Weske, M. Repairing Event Logs Using Stochastic Process Models; Universitätsverlag Potsdam: Potsdam, Germany, 2013; p. 78. Available online: https://publishup.uni-potsdam.de/opus4-ubp/frontdoor/index/index/docId/6370 (accessed on 14 November 2024).
- Siek, M. Investigating inductive miner and fuzzy miner in automated business model generation. In Proceedings of the 3rd International Conference on Computer, Science, Engineering and Technology, Changchun, China, 22–24 September 2023; p. 2510. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Y.; Wen, L.; Wang, J. Cleaning Structured Event Logs: A Graph Repair Approach. Comput. Ind. 2015, 70, 194–205. [Google Scholar] [CrossRef]
- Brons, D.; Scheepens, R.; Fahland, D. Striking a New Balance in Accuracy and Simplicity with the Probabilistic Inductive Miner. In Proceedings of the 2021 3rd International Conference on Process Mining (ICPM), Eindhoven, The Netherlands, 31 October–4 November 2021; pp. 80–87. [Google Scholar] [CrossRef]
- Schulze, M.; Zisgen, Y.; Kirschte, M.; Mohammadi, E.; Koschmider, A. Differentially Private Inductive Miner. arXiv 2024, arXiv:2407.04595. [Google Scholar] [CrossRef]
- Leemans, S.J.J. Inductive Visual Miner Manual. ProM Tools. 2017. Available online: https://www.leemans.ch/publications/ivm.pdf (accessed on 14 February 2025).
- De Medeiros, A. Process Mining: Extending the α-Algorithm to Mine Short Loops; BETA Working Paper Series, WP 113; Eindhoven University of Technology: Eindhoven, The Netherlands, 2004. [Google Scholar]
- Mikolajczak, B.; Chen, J.L. Workflow Mining Alpha Algorithm—A Complexity Study. In Intelligent Information Processing and Web Mining: Proceedings of the International IIS: IIPWM’05 Conference, Gdansk, Poland, 13–16 June 2005; Kłopotek, M.A., Wierzchoń, S.T., Trojanowski, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 31. [Google Scholar] [CrossRef]
- Porouhan, P.; Jongsawat, N.; Premchaiswadi, W. Process and deviation exploration through Alpha-algorithm and Heuristic miner techniques. In Proceedings of the 2014 Twelfth International Conference on ICT and Knowledge Engineering, Bangkok, Thailand, 18–21 November 2014; pp. 83–89. [Google Scholar] [CrossRef]
- Burke, A.; Leemans, S.J.J.; Wynn, M.T. Stochastic Process Discovery by Weight Estimation. Lect. Notes Bus. Inf. Process. 2021, 406, 306–318. [Google Scholar] [CrossRef]
- Kaur, H.; Mendling, J.; Rubensson, C.; Kampik, T. Timeline-Based Process Discovery. arXiv 2024, arXiv:2401.04114. [Google Scholar]
- Sarno, R.; Wibowo, W.A.; Kartini, K.; Amelia, Y.; Rossa, K. Determining Process Model Using Time-Based Process Mining and Control-Flow Pattern. TELKOMNIKA 2016, 14, 349–360. [Google Scholar] [CrossRef]
- Sarno, R.; Kartini, W.; Wibowo, W.A.; Solichah, A. Time-Based Discovery of Parallel Business Processes. In Proceedings of the 2015 International Conference on Computer, Control, Informatics and its Applications (IC3INA), Bandung, Indonesia, 5–7 October 2015; pp. 28–33. [Google Scholar] [CrossRef]
- Fischer, M.; Küpper, T.; Bergener, K.; Räckers, M.; Becker, J. The Impact of Timestamp Granularity on Process Mining Insights: A Case Study. Inf. Syst. 2020, 92, 101531. [Google Scholar]
- Fracca, G.; De Leoni, M.; Ter Hofstede, A.H.M. Managing Missing Start Timestamps in Event Logs: A Probabilistic Approach. In Advanced Information Systems Engineering; Springer: Cham, Switzerland, 2022; pp. 273–288. [Google Scholar]
- Buijs, J.C.A.M.; van Dongen, B.F.; van der Aalst, W.M.P. On the role of fitness, precision, generalization and simplicity in process discovery. In On the Move to Meaningful Internet Systems: OTM 2012, 2nd ed.; Meersman, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7565, pp. 305–322. [Google Scholar]






| Scenario 1 | Scenario 2 | |
| Flow | Incomplete event log → TGPM → Complete Event Log → IM → Process Model | Incomplete event log → TGIPM → Complete Event Log and Process Model |
| Pros | Clear Separation of Tasks: Each algorithm performs a distinct function, allowing TGPM to focus solely on completing the event log and IM on model refinement. | Improved Log Quality: TGIPM appears to produce a slightly better complete event log, potentially capturing nuanced dependencies and context between tasks. |
| Control and Validation: Having a complete event log as an intermediate step allows us to validate it independently before proceeding to model generation, enhancing transparency. | Efficiency: Combining both steps into one phase can reduce processing time, as it minimizes redundancy in handling the data. | |
| Quality of Process Model: Since IM operates on a complete event log, it may generate a refined and optimized process model with minimal dummy activities. | Integrated Task: With both algorithms working together, the completion and model discovery tasks may complement each other, enhancing coherence in the event log and process model. | |
| Cons | Computational Cost: This approach may be computationally intensive and time-consuming, as each step is handled separately. | Less Intermediate Control: Without a separate complete event log as an output, validation between steps is limited, which could make debugging and quality assessment harder. |
| Slightly Lower Log Quality: The complete event log generated here is slightly less accurate than that in Scenario 2. | Potential Model Complexity: Depending on how well the combined algorithm handles both tasks, the process model could risk becoming more complex or less refined if the integration is not perfectly balanced. | |
| Potential Redundancy: Running two separate steps might introduce redundancy if the combined approach can achieve similar or better results. |
| Metric | Scenario 1 | Scenario 2 |
| Fitness | 0.85 | 0.92 |
| Precision | 0.88 | 0.91 |
| Simplicity | 0.90 | 0.87 |
| Generalization | 0.83 | 0.90 |
| Time Complexity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Effendi, Y.A.; Kim, M. Reliable Process Tracking Under Incomplete Event Logs Using Timed Genetic-Inductive Process Mining. Systems 2025, 13, 229. https://doi.org/10.3390/systems13040229
Effendi YA, Kim M. Reliable Process Tracking Under Incomplete Event Logs Using Timed Genetic-Inductive Process Mining. Systems. 2025; 13(4):229. https://doi.org/10.3390/systems13040229
Chicago/Turabian StyleEffendi, Yutika Amelia, and Minsoo Kim. 2025. "Reliable Process Tracking Under Incomplete Event Logs Using Timed Genetic-Inductive Process Mining" Systems 13, no. 4: 229. https://doi.org/10.3390/systems13040229
APA StyleEffendi, Y. A., & Kim, M. (2025). Reliable Process Tracking Under Incomplete Event Logs Using Timed Genetic-Inductive Process Mining. Systems, 13(4), 229. https://doi.org/10.3390/systems13040229








