Abstract
In the context of climate change, the implementation of education for sustainable development (ESD) is of particular importance in schools. Developing key competencies, such as systems thinking to understand complex relationships, is essential in teaching students how to solve sustainability-related problems through ESD. Previous research has shown that using system models in the classroom can foster systems thinking. This study investigated the effects of using alternative system models with varying visualization of temporal developments in developing different facets of systems thinking based on a heuristic structural competence model. Overall, 293 elementary school students were assigned to one of four groups (a qualitative system model without time representation vs. a qualitative system model with time representation vs. a quantitative system model with time representation vs. the control group) and participated in a five-lesson classroom intervention in pre-post-test design. The results showed a large effect of fostering systems thinking in all experimental groups compared to the control group. The qualitative system models led to higher learning gains than the quantitative system model, especially with system modeling and solving complex problems, which requires higher systems thinking skills. The results were interpreted by referring to situational interest in interacting with the respective system model.
1. Introduction
Climate change is considered one of the greatest challenges of our time and an even greater challenge for future generations. It poses severe threats to ecosystems, biodiversity, and human livelihoods. Counteracting climate change and protecting our ecological livelihoods is a prerequisite for ensuring social stability and economic prosperity for all generations worldwide [1]. To achieve this global aspiration for a sustainable society, the United Nations adopted the Sustainable Development Goals (SDGs) as part of the 2030 Agenda. These include the goal “Climate Action” (SDG 13), which directly emphasizes the need for urgent action to combat climate change and its impacts. In order to achieve this goal on an environmental, economic, and social dimension, quality education is needed to empower future generations. Accordingly, the need for Quality Education (SDG 4) was established in 2015, which includes the subgoal of promoting education for sustainable development (ESD), making schools responsible for its mandatory implementation. This subgoal also focuses on systems thinking, which UNESCO [2] (p. 10) defined as the ability “to recognize and understand relationships [and] to analyze complex systems”.
This type of thinking is considered to be a key competence for ESD [1,3,4,5] because it promotes the understanding of relationships in complex systems for the development of sustainable solutions in meeting the challenges mentioned above. Early age-appropriate development of this key competence is necessary, given that neither adults nor children demonstrate intuitive systems thinking skills [6]. However, research on systems thinking in elementary school (i.e., Grades 1 to 4 in most federal states in Germany and as it pertains to the current study) is limited compared to higher grade levels [7,8]. In their systematic review of empirical studies on systems thinking, Budak and Ceyhan [7] found only one relevant study out of 27 involving elementary school students, highlighting the need for further research in this age group.
One reason for this gap in the literature is the challenge of thematizing complex systems (such as the climate system) without mentally overloading elementary school students. The use of system models, whether analog, computational, or simulation, has proven to be a suitable approach for this in previous research [9,10,11,12,13,14,15,16], even in elementary school [3,17,18]. System models allow for the visualization of a variety of system elements (structure) and interactions (dynamics) within the system. However, it is unclear which type of system model is particularly conducive to optimally developing systems thinking in elementary school. Evidence supports the benefits of both qualitative (e.g., [9,19]) and quantitative system models (e.g., [10,20,21]), yet a direct comparison of these models within the same intervention has not been conducted. Furthermore, it is open whether time representations, which should be integrated into system models [22], given that students often lack an intuitive grasp of time dimensions [6], are conducive to learning for elementary school students or rather overwhelming.
Building on the evidence that the use of system models is conducive to learning, even at the elementary school level, the purpose of this study was to investigate whether there are advantages to a particular type of system model. Specifically, this study examined the effects of using alternative system models (qualitative vs. quantitative) with varying visualizations of temporal developments of climate change in the development of different facets of systems thinking in elementary school students. To answer our research questions, different system models (a qualitative system model without time representation vs. a qualitative system model with time representation vs. a quantitative system model with time representation vs. the control group) were used in a five-lesson classroom intervention study with fourth graders to foster systems thinking on climate change. We examined whether these models differ, in general, and whether differences exist between different facets of systems thinking. Additionally, we investigated whether any differences could be attributed to the situational interest in the system models and student interaction with the respective system model.
2. Theoretical Background
People interact daily in social, technical, economic, and ecological systems. Such systems are complex with interacting elements that form an organized unit (e.g., [5,23]). The actions that take place within them are often simultaneous and uncoordinated such that the effects are often not transparent. That is, systems can be complex and sometimes unpredictable in their behavior, for example, through feedback loops, dynamics, nonlinearities, and emergence [24,25]. Educating students to act responsibly in an increasingly complex world necessitates a systemic approach to the environment, given that students and even adults cannot intuitively recognize the just-mentioned properties of systems [6]. For this reason, systems thinking needs to be fostered and to be assigned a crucial role in science lessons [2,26].
Students should be enabled to understand not only superficial structural features but also deeper dynamic behaviors of systems, which experts are able to comprehend by including all components—structure, behavior, and function [27]. This level of understanding requires the identification of system elements as well as their properties and interrelationships [28,29,30]. An effective way to meet these requirements is systems thinking, which is not just a “coherent understanding” of systems but rather a way of thinking to explain, understand, and predict natural phenomena [10,31]. In line with this distinction, Mischo and Rieß [32] (p. 348f.) defined systems thinking as the cognitive “ability to recognize, describe, and model (e.g., to structure, to organize) complex aspects of reality as systems. This includes the ability to determine system elements and interrelationships, to grasp temporal dimensions (dynamics) and the ability to provide explanations, make predictions, and [derive recommendations for action] on the basis of one’s own modeling”.
An increasing number of empirical studies on systems thinking have been published, especially in recent years. Despite the substantial body of studies, no common terminology has yet been established. Different terminologies coexist, some of which are used synonymously but some of which arise from different conceptualizations of systems thinking [7,8,33]. One of the main reasons for this lack of common terms is the interdisciplinary nature of the respective research. Different disciplines analyze and interpret systems from different perspectives and with different focuses. In biology, topics range from microbiological systems, such as cells [34], to macroecological systems such as swamps [10], forests [11], and habitat models such as that of the stork [17]. However, geophysical systems, such as the water cycle [35] and economic systems such as the pizzeria [10] or chocolate from an economic–social perspective [3], have also been addressed. These disciplinary differences lead to different systemic perspectives. For example, biologists often focus on natural systems, whereas geographers, according to Rempfler and Uphues [4], integrate a socio–spatial perspective alongside the natural spatial perspective. Systems vary in their openness or closure as well as in their structural and behavioral complexity. Despite the different perspectives, a consensus exists among the disciplines on the fundamental characteristics of the construct. Specifically, the various disciplines agree on its multidimensional nature [36] as well as on the need to differentiate between a static representation of the system and the interactions among its individual components caused by interrelationships. This shared understanding of systems also results in a consensus about the skills required for effective systems thinking. Three core abilities are commonly recognized as follows: identifying system organization, analyzing system behavior, and system modeling [7,30].
Several competence models have been developed. The following chapter focuses on identifying a model that can be implemented in practice and is applicable for the purposes of this study. Subsequently, the results of intervention studies are presented, which clearly show the existing research gap.
2.1. Identification and Adaption of a Competence Model for Systems Thinking
For the purpose of this study, we had three requirements for the chosen competence model: (1) The competence model should account for modeling skills because elementary school students in particular need to be supported in their mental modeling when dealing with complex scientific phenomena that cannot be directly observed such as the climate system; (2) suitability for elementary school should exist or be achievable through minimal adaptations; and (3) the competence model should be suitable for use in intervention studies. We examined the competency model by Ossimitz [9], the structural model for systems competence by Sommer [17], the System Thinking Hierarchical (STH) Model by Assaraf and Orion [18,35], the Structure–Behavior–Function (SBF) Model by Hmelo-Silver and Liu [37] in combination with the Components–Mechanisms–Phenomena (CMP) Model by Hmelo-Silver et al. [12], the competence model for systems thinking by Bollmann-Zuberbühler et al. [19], the competence model for systems competence by Rempfler and Uphues [4], and the heuristic structural competence model by Rieß et al. [5].
After applying the three criteria, the heuristic structural competence model by Rieß et al. [5] resulted in the most suitable model. This model places a particular focus on the modeling of systems (requirement 1), which has been established in climate research and has shown to be conducive to learning in the above-mentioned intervention studies as well as in the overarching and pedagogical principles of developing systems thinking by Assaraf and Knippels [16]. In addition, this competence model addresses the entirety of systems thinking, from secondary school to adulthood, and can be easily adapted to the elementary school level (requirement 2). Following Yoon et al.’s [38] call for more comparative research on teaching and learning about complex systems in the sense of holistic spiral curricular teaching of science subjects, we intended to investigate if the model is also suitable for elementary school. Most recently, the heuristic structural competence model has shown to be practicable in intervention studies at the secondary school level [14,39], among student teachers [40,41], and in further teacher training [42] (requirement 3).
The version of the heuristic structural competence model [5] adapted to the elementary school target group is presented below (Table 1). The original competence model consists of four dimensions, each with four sub-capabilities. Given the focus on solving complex problems with the help of system models (dimension 3), we selected only the sub-capabilities that are central precursor capabilities for the target capabilities in dimension 3. Secondly, the time frame of this study of five lessons (each 45 min) would preclude the effective use of all sub-capabilities. For these reasons, we selected six sub-capabilities and adapted them for fourth graders in elementary school (Table 1). Note that the original version of the heuristic structural competence model of systems thinking [5] includes a fourth dimension, which focuses on the evaluation of system models. This competence is aimed at experts in systems science and is thus not relevant for elementary school students. We therefore omitted this dimension.

Table 1.
Selected competences of systems thinking adapted to the elementary school level (developed on the basis of the heuristic structural competence model of systems thinking [5]).
The requirements of each competence dimension are briefly described below, along with explanations of how they have been adapted to the elementary school level, accompanied by concrete examples that illustrate the level of requirements.
Dimension 1 addresses declarative, conceptual system knowledge, including basic knowledge of systems theory (e.g., [23]) as well as knowledge of areas of reality that can be considered as systems. Regarding the target group, it should be noted that this fundamental systems science approach is a basic knowledge. In an initial examination of systems at the elementary school level, aspects of complex systems such as multi-causality, feedback, dynamic complexity [9], nonlinearity, emergences, or dissipative structures [43] can only be addressed to a limited extent in favor of a basic understanding. For example, in this dimension, students should be able to describe a system in general terms by explaining that it consists of several elements that are connected to each other.
Dimension 2 is characterized by the ability to model systems and thus the ability to understand and construct different types of system models. Note that elementary school students should first be encouraged to understand before being able to construct system models, that is, starting with familiar forms of representation (e.g., text), then reducing features (e.g., word model), to finally understanding increasingly abstract system models (e.g., connection circle). For this study, the influence diagram method was replaced with the connection circle method because this method has already been established in elementary school [19]. A particular advantage over the influence diagram is the external structure of a circle, which is used for all system models and therefore simplifies system modeling. The system elements are arranged around the circle, and effect relationships are indicated by arrows with corresponding effect signs that denote the quality of the effect. For example, this dimension requires students to analyze information from a text and identify related arrow diagrams (as precursor models for qualitative and quantitative system models).
Dimension 3, which is the target dimension of this research, is characterized by solving complex problems (i.e., climate change in the current study) with the help of system models. The aim is to give simple explanations for system behavior, make predictions, and design simple technologies with either qualitative or quantitative system models. For example, this dimension requires students to explain how climate change affects sea levels over time using a qualitative or quantitative system model.
Many of the competency models presented have been used in intervention studies to evaluate which teaching–learning methods, tools, and teaching units are effective in developing systems thinking. In the following chapter, a selection of relevant studies is presented to highlight existing research approaches. Based on this review, the research gap is then identified, which is addressed by this study.
2.2. Fostering Systems Thinking
To understand complex systems, grasping the structure, behavior, relationships, interactions, feedback, and dynamics within the system is essential [44]. However, numerous studies have shown that students face cognitive challenges when dealing with complex systems [45] and have difficulties understanding interactive and especially dynamic aspects of complex systems beyond visible structures [46], particularly when cause and effect are spatially or temporally separated [6]. Given that systems thinking is not a natural development in students [6], it must be actively fostered to help students overcome these challenges and act appropriately within systems. Intervention studies have examined which approaches are particularly effective in developing systems thinking. Assaraf and Knippels [16] identified four overarching pedagogical guidelines and scaffold strategies from a variety of empirical studies that are particularly effective when embedded in a well-designed learning environment. Apart from the use of system language, cross-level reasoning, and authentic inquiry approach, modeling has emerged as a promising approach, which is the focus of this study. Models or modeling activities can exist in various forms: they can be mental, verbal, or qualitative, as seen in pen-and-paper modeling activities (e.g., concept map, connection circle, and causal loop diagram). They can also be formal, like most quantitative models, which utilize numerical data and systems of equations (e.g., (interactive) computer simulations) [9,16,22].
Studies have used qualitative system models or modeling activities to assess and to foster systems thinking. Concept maps and drawings are tools for modeling complex systems, and they offer the opportunity to visualize complex biological phenomena or problems and to explore system characteristics [16]. In this context, causal loop diagrams are considered a “standard tool” of systems thinking [9], whereas the connection circle has established itself as a simplified form of causal loop diagram in elementary schools [19]. Hogan [47] used a food web analysis task before and after a month-long, hands-on unit in which 11-year-old students constructed, observed, and manipulated mini-ecosystems. He found that students mostly considered direct effects and rarely indirect effects, a finding also reported by Grotzer [48]. In Sommer’s [17] 10 h intervention study on the white stork system in the third and fourth grade, students improved their system organization skills through classroom engagement with concept maps and a computer game (combination of qualitative and quantitative approaches), as evidenced by the significant increase in the number of system elements and the networking performance in concept maps. However, the students still showed a lack of understanding of system dynamics. Ben-Zvi Assaraf and Orion [18] also used concept maps in the fourth grade on the topic of the water cycle as part of a holistic teaching unit, in addition to experiments, outdoor activities, and knowledge integration activities. The study showed that students made significant progress in identifying system components and relationships after the intervention. The authors recommend that elementary schools should focus on recognizing relationships between system components and dynamic relationships as a basis for further development in secondary education.
In contrast to the qualitative models, the impact of quantitative system models (mainly in the form of simulations) on systems thinking has been examined. A simulation is a “tool used to explore a real-world […] system by approximating the behavior of the […] system” [49] (p. 2), which involves the manipulation of parameters to model the system. Research into the effectiveness of computer simulations in science education shows that the use of computer simulations in the classroom can be effective in science learning, depending on how they are used [20,21,50]. This finding also applies to the teaching of systems thinking with simulations. At this point, we would like to point out that there are just a few studies on quantitative system models to promote systems thinking in elementary education. In order to provide a broader overview, we have included relevant studies from higher grade levels. The findings from these studies can at least be partially transferred to the elementary level. Bergan-Roller et al. [13] demonstrated the effectiveness of a simulated computational model lesson on undergraduate biology students’ systems thinking skills and conceptual knowledge. The positive impact of simulations on systems thinking in learning environments was also examined in college students [51] and in secondary school students [9,11,12,14,15,52]. In the primary sector, Ceresia [53] developed the interactive learning environment Sunny Island, a comprehensive learning environment centered around a simulation, designed for fourth- and fifth-grade elementary school students. Initial qualitative analyses showed a positive effect on systems thinking, but the study was a pilot, and the final results have not yet been published. Evagorou et al. [10] investigated the impact of a simulation-based learning environment on the marsh ecosystem on the development of systems thinking in fifth and sixth graders. The results show that students improved in identifying the system’s structure and simple linear causal relationships. However, students showed low competence in considering the effects of elements on other elements beyond simple linear effects or on the whole system and in considering temporal perspectives.
Overall, we conclude that for the primary sector, (a) elementary school students as early as first grade can already be supported in developing systems thinking skills, (b) the use of system models (and modeling activities) has always been embedded within teaching units, (c) both types of system models have shown to be beneficial to learning; a comparative investigation (qualitative vs. quantitative) in the same teaching and learning environment has yet to be conducted. Furthermore, evidence has shown that (d) elementary school students, as well as novices in general, refer primarily to the structure and simple effects of a system but not to more complex properties such as temporal developments. Given that students show a lack of intuitive understanding of time dimensions [6], this temporal perspective should be considered in system models [22]. However, in elementary school it is open whether the additional representation of temporal development is conducive to learning or whether it is overwhelming [16].
2.3. The Present Study
As described in the previous chapter, interventions aimed at promoting systems thinking have been shown to be effective when embedded in teaching units. To ensure the effectiveness of the teaching unit in this study, it was designed using the Model of Problem-Oriented Teaching and Learning (MopoLL) by Rieß and Mischo [54]. Based on Van Merriënboer’s 4C/ID model [55,56] the authors developed a teaching method aimed at the evidence-based promotion of dynamic problem-solving competence and explicitly emphasized the model’s suitability for promoting systems thinking. The MopoLL consists of six strategically arranged and sequential phases, as shown in Figure 1.
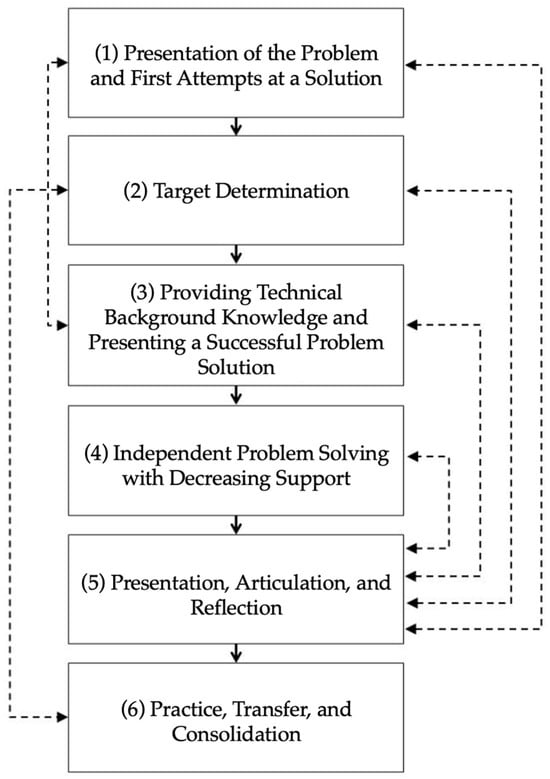
Figure 1.
Model of Problem-Oriented Teaching and Learning (MopoLL) [54].
In Phase (1), named Presentation of the Problem and First Attempts at a Solution, students are confronted with a scientific problem and attempt to generate a solution based on their prior knowledge. They recognize that the problem is theoretically solvable but requires additional or deeper competencies and knowledge. These target criteria (competencies, knowledge) are determined in Phase (2), named Target Determination, where an overview of the unit’s structure is made transparent. In Phase (3), named Providing Technical Background Knowledge and Presenting a Successful Problem Solution, instructive explanations are given to facilitate the knowledge construction process. Subsequently, in Phase (4), named Independent Problem Solving with Decreasing Support, students increasingly solve problems similar to the initial problem independently. In Phase (5), named Presentation, Articulation, and Reflection, students present their learning outcomes and reflect on the learning process in relation to the previous learning phases. Finally, in Phase (6), named Practice, Transfer, and Consolidation, the newly acquired skills and knowledge are applied to related problem-solving tasks.
2.4. Research Question and Hypotheses
There is evidence suggesting that system models foster systems thinking. However, to date, no fundamental research has been carried out at the elementary school level to determine whether qualitative or quantitative system models are more suitable, especially for the representation of time (dynamic processes) in complex systems such as the climate system. Consequently, the aim of this study was to investigate the effects of using alternative system models with varying visualizations of temporal developments in a problem-based teaching and learning environment on developing different facets of systems thinking in elementary school students.
We assumed the following after the intervention:
- All experimental groups would improve their general systems thinking in comparison to the control group.
- Students working with a quantitative system model (experimental group 3) would outperform students who work with a qualitative system model (experimental groups 1 and 2), especially in dimension 3 (solving problems using system models).
- Students working with a system model with time representation (experimental groups 2 and 3) would perform better in dimension 3 (solving problems using system models) than students who work with a system model without time representation (experimental group 1).
- Students working with a qualitative system model would perform better in dimension 2 (modeling systems).
3. Materials and Methods
3.1. Participants and Design
Based on previous studies [13,41] that found medium to high effect sizes in fostering systems thinking, we expected at least a medium effect size. Since four groups (three experimental groups and one control group) were investigated, an a priori power analysis (f = 0.25, α = 0.05, 1 − β = 0.90, ANOVA with four factor levels) revealed that at least 232 participants were needed. Overall, 293 fourth-grade students (56% female; 43.7% male; 0.3% not specified) from four elementary schools in Baden-Württemberg (Germany) participated in this quasi-experimental study. Given that the study took place over several days, direct randomization was not possible for organizational reasons. Thus, randomization took place at the class level, with classes randomly assigned to experimental or control conditions (a qualitative system model without time representation, a qualitative system model with time representation, a quantitative system model with time representation, and the control group). The following abbreviations are used: qualitative system model without time representation—QUAL_NT; qualitative system model with time representation—QUAL_T; quantitative system model with time representation—QUAN_T; and control group—CG. Initially, we considered a 2 × 2 research design (plus control condition), that is, we planned also a QUAN_NT condition. However, we did not realize this condition. As a key advantage of quantitative system models lies in the representation of temporal dynamics, not using this advantage would have been artificial and the practical benefit low. Of the 293 students, 75 students were assigned to the QUAL_NT condition, 78 students were assigned to the QUAL_T condition, 73 students were assigned to the QUAN_T condition, and 67 students were assigned to the CG.
For the experimental conditions, no significant differences existed in terms of climate knowledge before the intervention, F(3, 279) = 0.51, p = 0.68, prior interest in the topic, F(3, 279) = 1.32, p = 0.27, as well as the gender of the students χ2 = 10.57; p = 0.10. However, there were notable differences between the groups in the duration of the intervention. The requirement for participating schools was to complete the five lesson unit in 2.5 weeks, that is, to use all subject lessons per week for this topic. However, some schools only participated on the condition that the unit was implemented as part of a project week, which allowed us to generate a larger sample size. Other schools experienced technical problems; for example, the explanatory videos could not be played because of an internet outage. Consequently, the lesson was postponed, but it was extended by an additional week because of school vacation. The average number of days between pretest and post-test was 16.72 (SD = 7.51). The large mean difference from the other groups leads to a significant difference in the duration of the intervention between the groups, F(3, 289) = 29.06, p < 0.001. Thus, it was included as a covariate. In addition, a significant difference was found between the conditions in systems thinking before the intervention, F(3, 279) = 2.91; p = 0.04. To account for the difference in prior systems thinking knowledge, we created difference scores between the post and pretest.
3.2. Materials
The learner material focused on complex relations and interactions within the climate system. In addition to the content described in the heuristic structural competence model of systems thinking [5] the learning content included the basics of climate, factors influencing the climate (i.e., energy consumption, mobility, nutrition, power generation, leisure behavior, and packaging), the relationship between greenhouse gases and temperature (natural and anthropogenic greenhouse effect), and the effects of climate change (i.e., ice sheets, wildlife, harvest, and sea level). This learning content is addressed with system models, which are the core of the unit. A distinction is made between qualitative and quantitative system models. Qualitative system models, such as causal loop diagrams or connection circles, are mostly based on pen-and-paper methods and focus on the relationships and interactions between system elements [16]. They help to show the structure of a system and to make the effects visible. In contrast, quantitative system models use numerical data and mathematical equations, often through computer simulations. The interactivity helps to understand multi-causal relationships and to predict system behavior through the ability to simulate [9,22]. In the system models only selected aspects that are mostly relevant to the children’s lives and necessary for a basic understanding of climate change were considered. Complexity was thus reduced to essential features and simple interrelationships of the climate system, given the research findings showing the cognitive challenges of elementary school students [10,15,18]; for example, in identifying feedback loops (e.g., [10]). For the purpose of this article, we translated figures used in our materials from German to English.
3.2.1. Qualitative System Model Without Time Representation (QUAL_NT)
The QUAL_NT (Figure 2) was realized in a connection circle, which represents a simplified form of an influence diagram. The effect relationships between the elements of the system are represented by effect arrows, which indicate the direction of the effect. The effect signs (“+” and “−”) indicate the quality of the effect. The plus sign indicates an effect in the same direction (if more, then more; if less, then less), the minus sign indicates an effect in the opposite direction (if more, then less; if less, then more). An exemplary reading of the connection circle, starting from the fourth icon of the area “nutrition” is as follows: If more meat, then more greenhouse gases; if more greenhouse gases, then more temperature; if more temperature, then less ice sheets. This path of action can also be read with the opposite effect by starting with “if less”. The advantage of this system model is that the effect relationships are visible, and the quality of the effects can be read from the effect signs.
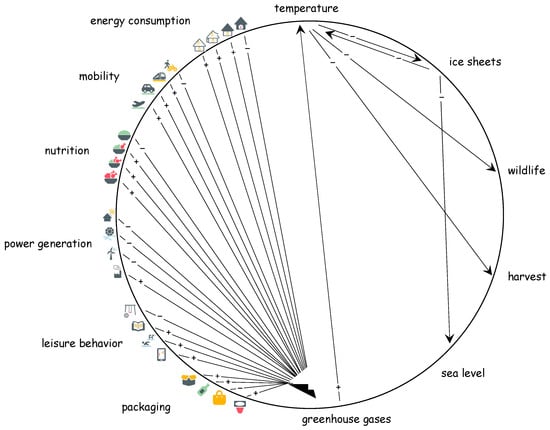
Figure 2.
Qualitative System Model (Connection Circle) without Time Representation (QUAL_NT).
3.2.2. Qualitative System Model with Time Representation (QUAL_T)
The QUAL_T (Figure 3) is identical to the QUAL_NT (Figure 2) in information, structure, and handling, it differs only in an additional representation of temporal developments. The advantage of this system model is that it supports mental modeling, as developments (today, in 10 years, in 50 years, in 100 years) are illustrated.
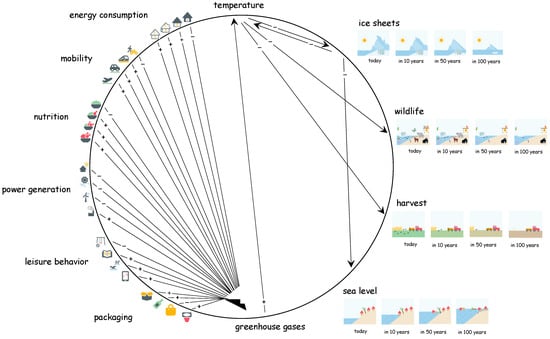
Figure 3.
Qualitative System Model (Connection Circle) with Time Representation (QUAL_T).
3.2.3. Quantitative System Model with Time Representation (QUAN_T)
THE QUAN_T (Figure 4) was realized in a computer simulation, which is a “tool used to explore a real world […] system by approximating the behavior of the […] system” [49] (p. 2), which involves the manipulation of parameters to model the system. For QUAN_T, we used the parameter simulation klimakids (freely available at https://klimakids.com). We developed this system model as a browser-based app, tailored to iPads to ensure easy accessibility [57]. The app addresses the same learning content as the QUAL_NT (Figure 2) and the QUAL_T (Figure 3) and the same time representation as the QUAL_T (Figure 3). It differs in the type of system model, that is, the quantity of effects within the system can be observed but not read off. Factors that influence the climate (e.g., energy consumption, mobility) can be changed by moving the sliders. Consequently, temperature changes can be observed in the thermometer and the arrow next to it. By using the drop-down menu (today, in 10 years, in 50 years, and in 100 years), time jumps are possible and changes in the affected dimensions (e.g., ice sheets, sea level) can be observed. The advantage lies in the quantitative representation of multi-causal relationships and the ability to simulate.
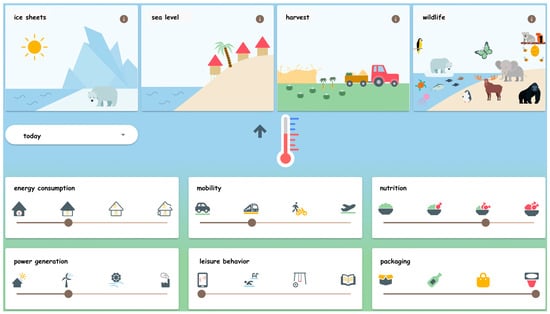
Figure 4.
Quantitative System Model (App) with Time Representation (QUAN_T).
3.2.4. Control Group (CG)
The control group received no treatment and only completed the tests. The purpose of the control group was not to control the benefits of modeling, but to control extracurricular influences on climate knowledge and consequently on systems thinking such as TV programs, the literature, peer groups, or actions weeks of associations. Those influences could have been high for this omnipresent topic.
3.3. Measures
3.3.1. Systems Thinking
According to the adapted heuristic structural competence model [5], systems thinking was measured with a test that was developed by Frey et al. [58]. The test measured systems thinking of three competence dimensions (see Table 1). Dimension 1 included declarative/conceptual systems knowledge. Dimension 2 included modeling systems. Dimension 3 comprised solving problems using system models. In line with Frey et al. [58], dimensions 1 and 2 are considered precursor skills for dimension 3. The main focus lies on problem solving using qualitative and quantitative system models (dimension 3). The effects of these two system models were examined in the present study. Consequently, dimension 1 was measured with three items, dimension 2 was measured with two items, and dimension 3 was measured with seven items. Dimension 3 was further divided into the competences: giving explanations (three items), making predictions (three items), and developing technologies (one item). Items were included as single-choice item (1 item), multiple-choice items (7 items), and open-answer items (4 items). Open-answer items were rated by three raters and inter-rater-reliability was satisfactory, ICC = 0.87–0.99 [59]. Since the experiment used a pre-post-test design, the test was implemented before (α = 0.67) and after (α = 0.73) the intervention. Example items for each dimension are provided in Appendix A (Figure A1, Figure A2, and Figure A3).
3.3.2. Climate Knowledge
An additional test on climate knowledge was implemented to not only assess general competences with regard to systems thinking but also on concrete factual climate knowledge. We developed this test by using nine multiple choice items (e.g., “What is the climate?”; “Which statements about the natural greenhouse effect are correct?”). Again, the test was implemented before (α = 0.61) and after (α = 0.66) the intervention.
3.3.3. Interest in and Practical Use of the System Model
Interest in learning activities with the system models was measured with five items, developed by Knogler et al. [60] and adapted to the present context. Three of the items measured whether interest was triggered (α = 0.84, e.g., “The connection circle/the app made me curious”.), and two items measured whether interest was maintained (α = 0.73, e.g., “I would like to investigate more things with the connection circle/the app”), to assess whether differences between the experimental groups in systems thinking were due to the nature of the respective system model. This interest scale was only included after the intervention and not in the control group because participants in the control group did not receive a system model. In addition to the interest in the system model, we investigated whether elementary school students can use an app intentionally to solve problems or whether they drift into the aimless play observed in previous research [61]. Although our procedure was designed to prevent aimless playing, this tendency may have emerged in some of the elementary school children. Therefore, the students in the QUAN_T group answered the additional item “Sometimes I played with the app and did not work on the tasks in the research booklet”.
3.4. Procedure
The investigation was based on the Model of Problem-Oriented Teaching and Learning (MopoLL) [54]. Of the six phases (see Figure 1), we decided to present only the first four phases: (1) Presentation of the problem and first attempts at a solution; (2) Target determination; (3) Providing technical background knowledge and presenting a successful problem solution; and (4) Independent problem solving with decreasing support. We omitted the last two phases, (5) Presentation, articulation, and reflection, and (6) Practice, transfer, and consolidation, because the intervention would have required a high degree of individual adaptation of the teaching process by the science teachers. This intervention would not have been possible to facilitate by videos, and we wanted to achieve the highest possible degree of standardization by providing all instructions via video. These phases were therefore not run in favor of video instruction to minimize the confound of the teacher variable throughout the entire intervention. Further actions to control the teacher variable were that the teachers conducting the unit were instructed to ensure the objectivity of the implementation by receiving a technical introduction to the topic and being presented with the teaching materials (test instrument, test manual, progress sketches, explanatory videos, system model, and research booklets) so that any related questions could be clarified directly. During the unit, they strictly followed the detailed progression sketches in which the wording for the transitions between individual teaching phases was specified. In order to check the teachers’ adherence to the sketches, they were asked to note and explain any necessary deviations in the progress sketches. Before the intervention started, participants fulfilled the pretest (demographics, interest, climate knowledge, and systems thinking). Afterward, the instructional phases took place (see Figure 5).
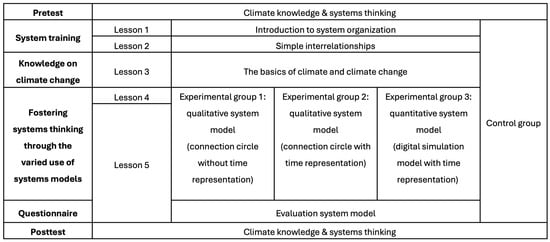
Figure 5.
Experimental procedure.
The intervention promoted systems thinking about climate change and consisted of five lessons of 45 min each. In the first two lessons (MopoLL phases 1–3), the students received systems training, which introduced them to systems organization, simple cause-and-effect relationships, and systems modeling. After teaching the technical basics of climate and climate change in the third lesson (MopoLL Phase 3), the last two lessons (MopoLL Phase 4) used the different system models described to promote systems thinking. To ensure comparability, experimental groups received the same lessons. The system model differed in only lessons four and five in which students worked in pairs. As stated above, the teacher variable was controlled to the extent that all instructions were presented via video. Hence, the teacher took on a relatively passive role. Independent work phases of the students were initiated by tasks in a research booklet that was identical for all experimental groups. The duration of the intervention varied between participating schools and classes. We took this into account when analyzing the data (see Section 3.5.).
3.5. Analysis Strategy
We first considered multilevel analyses because the experimental conditions were assigned by block randomization (at class level) for organizational reasons (see Section 3.1). However, initial multilevel analyses of the data revealed almost no class variance, which is why we decided to use variance analyses. The analyses were conducted with IBM SPSS 28.0 Statistics [62]. For the data collected on systems thinking and climate knowledge, we created difference scores between the post- and pretest, to show changes in competences and to constructively represent the variance between experimental groups in preintervention systems thinking in the data (see Section 3.1). By calculating analyses of covariance (ANCOVA), with the respective system model (QUAL_NT, QUAL_T, QUAN_T, and CG) as independent variable and the duration of the intervention as a covariate (see Section 3.1), differences between the experimental conditions could be analyzed. For systems thinking, the evaluation was carried out globally for all competences and for the respective sub-capabilities (at the dimensional level). For the situational interest in the system model (triggered and maintained), no difference scores between the post- and pretest were created, as the situational interest was only assessed after the intervention. Therefore, an ANCOVA was conducted with the overall score.
4. Results
4.1. Systems Thinking
This section presents the results on systems thinking. Furthermore, the formulated hypotheses will progressively be revisited and evaluated. Note that the hypotheses in this section are presented in a summarized form. For detailed descriptions see Section 2.4.
The data were analyzed according to the descriptions of the analysis strategy above (see Section 3.5). An ANCOVA with the overall score of systems thinking revealed a significant difference between all groups, F(3, 288) = 18.67, p < 0.001, ηp2 = 0.16. We found no significant influence of duration of intervention on systems thinking, p = 0.29. Post hoc tests (Sidak-corrected) revealed a significant difference between QUAL_NT and CG, Mdiff = 6.00, p < 0.001, d = 1.24; QUAL_T and CG, Mdiff = 6.10, p < 0.001, d = 1.13; and QUAN_T and CG, Mdiff = 4.29, p < 0.001, d = 0.84. No significant differences could be found across all competence dimensions between the three experimental groups. The corresponding hypothesis, Hypothesis 1, stated that “All experimental groups would improve their general systems thinking in comparison to the control group”. This hypothesis can be confirmed because all experimental groups differ significantly from the control group, with a large effect size across all dimensions. The key values for the individual competence dimensions are shown below (see Table 2) and described in the following.

Table 2.
Descriptives of systems thinking of the experimental groups and the control group.
In dimension 1 (declarative/conceptual system knowledge), a significant difference between all groups was found, F(3, 288) = 6.13, p < 0.001, ηp2 = 0.06. Post hoc tests (Sidak-corrected) revealed a significant difference between QUAL_NT and CG, Mdiff = 1.27, p = 0.002, d = 0.58; QUAL_T and CG, Mdiff = 1.25, p = 0.002, d = 0.64; and QUAN_T and CG, Mdiff = 1.21, p = 0.004, d = 0.59. No significant differences could be found between the three experimental groups.
In dimension 2 (modeling systems), a significant difference between all groups was found, F(3, 288) = 6.87, p < 0.001, ηp2 = 0.07. Post hoc tests (Sidak-corrected) revealed a significant difference between QUAL_NT and CG, Mdiff = 0.72, p = 0.029, d = 0.47, and QUAL_T and CG, Mdiff = 0.87, p = 0.004, d = 0.56, but not between QUAN_T and CG, Mdiff = 0.49, p = 0.233, d = 0.33. No significant differences could be found between the three experimental groups. The corresponding hypothesis, Hypothesis 4, stated that “Students working with a qualitative system model would perform better in dimension 2 (modelling systems)”. This hypothesis can be confirmed because the groups with the qualitative system models (QUAL_NT and QUAL_T) differed significantly from the control group on competence dimension 2, whereas no difference was found in the group with the quantitative system model (QUAN_T).
In dimension 3 (solving problems using system models), a significant difference between all groups was found, F(3, 288) = 7.39, p < 0.001, ηp2 = 0.07. As with dimension 2 (modeling systems), post hoc tests (Sidak-corrected) revealed a significant difference between QUAL_NT and CG, Mdiff = 2.45, p < 0.001, d = 1.07, and QUAL_T and CG, Mdiff = 1.90, p = 0.002, d = 0.52, but not between QUAN_T and CG, Mdiff = 1.25, p = 0.097, d = 0.48. No significant differences could be found between the three experimental groups. The first corresponding hypothesis, Hypothesis 2, stated that “Students who work with a quantitative system model (experimental group 3) would outperform students who work with a qualitative system model (experimental groups 1 & 2), especially in dimension 3 (solving problems using system models)”. This hypothesis must be rejected. Although no significant differences were found across all dimensions between participants who worked with a qualitative and participants who worked with a quantitative system model, differences occurred on a descriptive level. In addition, competence dimensions 2 (modeling systems) and 3 (solving problems using system models) showed that only the groups working with the qualitative system models differed significantly from the control group but not the group working with the quantitative system model. The second corresponding hypothesis, Hypothesis 3, stated that “Students who work with a system model with time representation (experimental groups 2 & 3) were expected to perform better in dimension 3 (solving problems using system models) than students who work with a system model without time representation (experimental group 1)”. This hypothesis must be rejected because the opposite occurred. The group that worked with the (qualitative) system model without time representation (QUAL_NT) differed significantly from the control group with a large effect. The groups that worked with system models with time representation performed worse. The qualitative system model (QUAL_T) differed significantly from the CG with a medium effect and the quantitative system model only at the descriptive level but not significantly.
4.2. Climate Knowledge
The data were analyzed according to the descriptions of the analysis strategy in Section 3.5. To calculate the differences in climate knowledge between the experimental conditions and the control group, an ANCOVA was conducted across all groups. The analysis revealed a significant difference in the overall score of climate knowledge between all groups, F(3, 288) = 26.08, p < 0.001, ηp2 = 0.21. Post hoc tests (Sidak-corrected) revealed a significant difference between QUAL_NT and CG, Mdiff = 5.25, p < 0.001, d = 1.31; QUAL_T and CG, Mdiff = 5.21, p < 0.001, d = 1.65; and QUAN_T and CG, Mdiff = 4.52, p < 0.001, d = 1.11. No significant differences could be found between the three experimental groups. The key values for the learning gains in climate knowledge are shown below (see Table 3).

Table 3.
Descriptives of climate knowledge of the experimental groups and the control group.
4.3. Interest in and Practical Use of the System Model
An ANCOVA with the overall score for the triggered situational interest in the system model revealed a significant difference between all experimental groups, F(2, 201) = 3.63, p = 0.028, ηp2 = 0.35. Post hoc tests (Sidak-corrected) revealed a significant difference between QUAL_NT and QUAN_T, Mdiff = 2.23, p = 0.032, d = 0.32, but not between QUAL_NT and QUAL_T and between QUAL_T and QUAN_T. No significant differences were observed in maintained interest between the experimental groups, F(2, 201) = 1.38, p = 0.254, ηp2 = 0.01. The key values for the interest triggered and maintained in the system model are shown below (see Table 4).

Table 4.
Descriptives of interest in the system model of the experimental groups immediately after the intervention.
The detailed results of an additional mediation analysis are not reported here because the nonsignificant mediation paths provide no additional information for interpreting the main effects (see Appendix B).
As described in Section 3.3.3, the QUAN_T group was given the additional item “Sometimes I played with the app and did not work on the tasks in the research booklet” and 14.1% answered “not true at all”, 21.9% answered “rather not true”, 15.6% answered “rather true”, and 48.4% answered “exactly right”.
5. Discussion
The goal of this study was to investigate the effects of using alternative system models (qualitative vs. quantitative) with varying illustrations of temporal developments (dynamics) on different facets of systems thinking about climate change in elementary school students. To measure learning effects, systems thinking based on the heuristic structural competence model [5] was measured before and after a five-lesson classroom intervention. Before discussing the results, the domain-specificity of systems thinking should be noted [63]. In the current study, we used the topic of climate change, with the requirement level adapted to fourth graders. The results presented should be interpreted in this way.
Our research has shown that all system models used, whether qualitative or quantitative, with or without time representation, have been successful in fostering systems thinking about climate change in elementary school students compared to the control group, which underlines the well-known benefits of system models for developing systems thinking [16], especially on sustainability issues of complex systems [64]. A closer look reveals differences between the system models on a descriptive level, but no clear advantage has been shown for one particular system model across all competence dimensions. All experimental groups in the current study improved relatively equally in declarative/conceptual system knowledge (dimension 1) between the two measurement times, but the connection circle, with and without time representation, showed advantages over the digital simulation model with time representation in modeling systems (dimension 2) and solving problems using system models (dimension 3). Overall, the connection circle with time representation led to the highest increase in competence. At this point, it is important to note that while time representation may be an important factor, there may also be potential confounding elements, such as better or more graphics in the system models with time representation and the additional interactivity in the quantitative system model, that influence the outcome. Future studies should consider isolating these variables to gain clearer insights. Comparison with other intervention studies reveals similarities: All of the models used were able to significantly improve systems thinking between measurement points. Similarly to our study, the simulation model performed worse in Brockmüller’s [14] study with students in grades 10–12. However, combining the simulation model with an analog model significantly increased its effectiveness. The effectiveness of combined learning strategies (simulation + lessons or analog models) is also highlighted by Rieß and Mischo [11] and Dierkes [20].
The results also showed that interest in all system models was very high. In particular, the digital simulation model with time representation was able to trigger short-term interest but could not be maintained over time to that extent. According to Eseryel et al. [65], a loss of interest is not necessarily equivalent to a decrease in engagement in problem solving. However, the advantage of the digital simulation in triggering interest is accompanied by a clear tendency to play aimlessly, an effect that was already reported in a review by de Jong and van Joolingen [61]. Ultimately, the results showed that this system model led to no increase in learning outcomes in systems thinking. Thus, interest in the system model has no explanatory power for the differences in systems thinking, as indicated by a mediation analysis that showed no significant effects.
The results suggest that no single system model optimally improves systems thinking across all dimensions. As the competence dimensions increase, especially in the challenging third dimension (solving problems using system models), a decrease in the complexity of the system model seems to be more conducive to learning. Evidence of this assumption is provided by the strong performance in dimension 3 (solving problems using system models) of the qualitative system model without time representation (low complexity), whereas the high standard deviation of the qualitative system model with time representation (medium complexity) suggests that the time representation benefits some students, yet proves to be a hindrance for others. This link is supported by Hmelo-Silver and Pfeffer’s [27] study, which shows that novices tend to focus on less complex, static components, suggesting that reduced complexity in the model enhances comprehension and problem-solving skills for learners of different levels of competence. Additionally, the quantitative system model with time representation (high complexity) achieved the poorest results. This finding is in line with the conclusions of Assaraf and Knippels [16], stating that computer-based simulations are conducive to learning, but the high cognitive load of simultaneous representations and information can be disadvantageous to learning. This effect seems to be particularly evident in fourth graders, given that the group in our study that worked with the computer-based simulation performed the worst, contrary to our hypothesis and to other promising studies on the use of simulations to foster systems thinking in older students (e.g., [10,13,15,51]). However, the real effect of this digital simulation model could also be masked by the way it was used (aimless play), which should be seen as a limitation of this study. Although our procedure tried to minimize aimless play (e.g., prior exploration phase, precise tasks), this effect still occurred. The way in which young students interact with digital system models could be investigated in future research, for example, by examining log files or screen recordings. Following the findings of Brockmüller [14], the extent to which an additive use of system models would be useful for elementary school students should also be investigated, for example, for the differentiated promotion of the different competence dimensions.
In line with previous research (e.g., [17,30,66]), we found comparable effects between subject knowledge and systems thinking. All experimental groups showed significant learning gains in climate knowledge. On a descriptive level, the connection circles, especially the connection circle with time representation, showed advantages identical to the results on systems thinking. Thus, domain-specific knowledge not only predicts the ability for systems thinking, but systems thinking also helps to structure and thereby retain newly acquired knowledge (here on climate change).
Finally, two practical limitations of the present intervention should be addressed. Firstly, for reasons of comparability, we refrained from going through the teaching processes initiated by the teacher. Specifically, this means that Phases 5 (presentation, articulation, and reflection) and 6 (practice, transfer, and consolidation) of MopoLL [54] were not part of the intervention (see Section 3.4). Yet, these phases are highly relevant for learning success because teachers can provide support in terms of structuring knowledge, and discussing the learning content can encourage in-depth exploration and lead to deeper understanding. Based on the findings of Grotzer and Bell Basca [67], the discussion of system models content would therefore be expected to lead to further learning gains than those shown in our study. It is likely that additional individual feedback during the use of the system model would also improve the performance of the digital simulation with time representation [21,50]. Secondly, for practical reasons, not all sub-capabilities of the heuristic structural competence model of systems thinking [5] could be addressed in this study. Future research could complete the sub-capabilities not considered here, given that the fourth competence dimension (evaluation of system models) is likely to be too complex for the elementary level.
Overall, our findings suggest that the qualitative system models of climate change were more effective than the quantitative system model on fostering systems thinking for elementary school students. The combination of the qualitative system model with time representation proved to be the most effective in the lower competence dimensions (declarative/conceptual system knowledge and modeling systems). For the higher competence requirements of solving complex problems, reducing the complexity of the qualitative system model (no time representation) seems to be more conducive to learning for fourth graders.
Author Contributions
Conceptualization, W.R., A.R. and S.F.; methodology, M.B.; software, M.B. and S.F.; validation, S.F., M.B. and W.R.; formal analysis, S.F. and M.B.; investigation, S.F.; resources, S.F. in cooperation with the Freiburg University of Education; data curation, S.F. and M.B.; writing—original draft preparation, S.F.; writing—review and editing, M.B., W.R. and A.R.; visualization, S.F.; supervision, W.R.; project administration, S.F. and W.R.; funding acquisition, W.R. and A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the MINISTRY OF SCIENCE, RESEARCH AND ARTS BADEN-WÜRTTEMBERG within the Research Training Group “Digitally supported teaching and learning environments for cognitive activation”, grant number 43-7742.35/24/1.
Institutional Review Board Statement
The study was conducted in accordance with the Ministry of Education, Youth and Sports of Stuttgart (protocol code: KM31-6499-3/64/3, date of approval: 20.12.2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The research data can be requested by emailing the first author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
Below example items for each dimension are shown. In Frey et al. [58] the test development and validation is thoroughly detailed, and item statistics are provided for all items.

Figure A1.
Example item from dimension 1 (declarative/conceptual system knowledge).
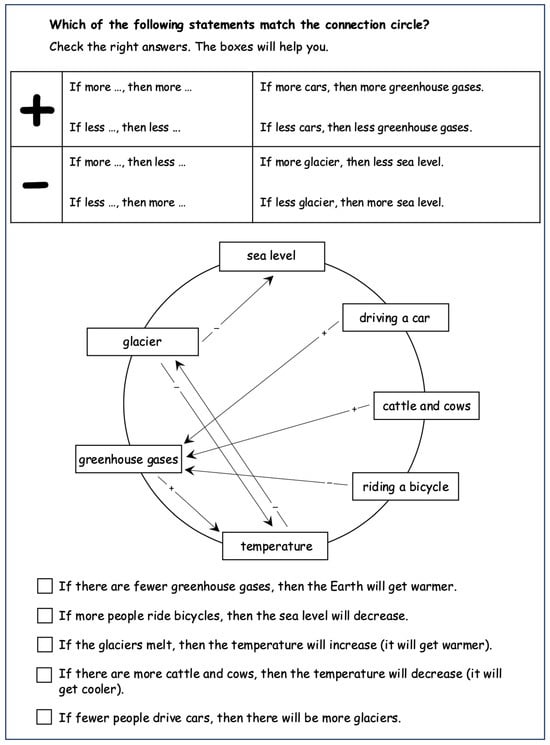
Figure A2.
Example item from dimension 2 (Understanding Qualitative System Models).
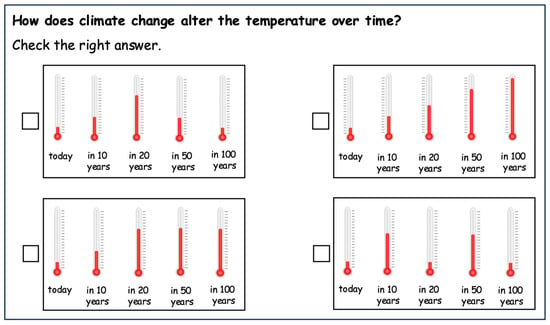
Figure A3.
Example item from dimension 3 (Making Predictions).
Appendix B
The JASP software (Version 0.19.3) [68] was used to conduct the mediation analyses mentioned in Section 4.3. The aim was to investigate whether the subjective ratings of triggered and maintained interest differ between the three system models and whether the beneficial effects on learning outcomes are mediated by potential effects on triggered and maintained interest. Experimental groups were included as predictors. Interest in the system model (triggered and maintained) was included as a mediator, and post-test systems thinking scores for all dimensions and climate knowledge were included as dependent variables. Since the control group was not included, three dummy variables were created (QUAL_NT vs. QUAL_T; QUAL_NT vs. QUAN_T; QUAL_T vs. QUAN_T).
The analysis of triggered interest in the system model generated the following results. Results for the QUAL_NT vs. QUAL_T comparison showed no indirect effects of dependent variables, ES = [0.01–0.05]; SE = [0.03–0.04]; z = [0.37–1.43]; p = [0.15–0.71]. Results for the QUAL_NT vs. QUAN_T comparison showed no indirect effects of the dependent variables, ES = [0.01–0.06]; SE = [0.03–0.04]; z = [0.50–1.44]; p = [0.15–0.62]. Results for the QUAL_T vs. QUAN_T comparison showed no indirect effects of the dependent variables, ES = [0.004–0.01]; SE = [0.01–0.03]; z = [0.27–0.28]; p = [0.78–0.79].
The analysis of maintained interest in the system model generated the following results. Results for the QUAL_NT vs. QUAL_T comparison showed no indirect effects of dependent variables, ES = [−0.02–0.02]; SE = [0.02–0.02]; z = [0.84–0.76]; p = [0.40–0.76]. Results for the QUAL_NT vs. QUAN_T comparison showed no indirect effects of dependent variables, ES = [−0.002–0.02]; SE = [0.02–0.02]; z = [−0.13–0.75]; p = [0.45–0.90]. Results for the QUAL_T vs. QUAN_T comparison showed no indirect effects of dependent variables, ES = < [0.001–0.002]; SE = [0.004–0.03]; z = [−0.19–−0.13]; p = [0.85–0.90].
References
- United Nations General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development (A/RES/70/1). 2015. Available online: https://documents.un.org/doc/undoc/gen/n15/291/89/pdf/n1529189.pdf (accessed on 11 December 2024).
- United Nations Educational, Scientific and Cultural Organization (UNESCO). Education for Sustainable Development Goals. Learning Objectives. 2017. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000247444 (accessed on 11 December 2024).
- Bertschy, F. Vernetztes Denken in der Grundschule fördern. Umweltpsychologie 2008, 12, 71–90. [Google Scholar]
- Rempfler, A.; Uphues, R. Systemkompetenz und ihre Förderung im Geographieunterricht. Geogr. Schule 2011, 33, 22–33. [Google Scholar]
- Rieß, W.; Schuler, S.; Hörsch, C. Wie lässt sich systemisches Denken vermitteln und fördern? Theoretische Grundlagen und praktische Umsetzung am Beispiel eines Seminars für Lehramtsstudierende. Geogr. Akt. Schule 2015, 37, 16–29. [Google Scholar]
- Sweeney, L.B.; Sterman, J. Thinking about systems: Student and teacher conceptions of natural and social systems. System Dyn. Rev. 2007, 23, 285–311. [Google Scholar] [CrossRef]
- Budak, U.; Ceyhan, G. Research trends on systems thinking approach in science education. Sociol. Methods Res. 2023, 21, 230–258. [Google Scholar]
- Bielik, T.; Delen, I.; Krell, M.; Ben-Zvi Assaraf, O. Characterising the literature on the teaching and learning of system thinking and complexity in STEM Education. J. STEM Educ. Res. 2023, 6, 199–231. [Google Scholar]
- Ossimitz, G. Entwicklung Systemischen Denkens. Theoretische Konzepte und Empirische Untersuchungen; Profil: München, Germany, 2000. [Google Scholar]
- Evagorou, M.; Korfiatis, K.; Nicolaou, C.; Constantinou, C. An investigation of the potential of interactive simulations for developing system thinking skills in elementary school: A case study with fifth-graders and sixth-graders. Int. J. Sci. Educ. 2009, 31, 655–674. [Google Scholar] [CrossRef]
- Rieß, W.; Mischo, C. Promoting systems thinking through biology lessons. Int. J. Sci. Educ. 2009, 32, 705–725. [Google Scholar]
- Hmelo-Silver, C.E.; Jordan, R.; Eberbach, C.; Sinha, S. Systems learning with a conceptual representation: A quasi experimental study. Instr. Sci. 2017, 45, 53–72. [Google Scholar] [CrossRef]
- Bergan-Roller, H.E.; Galt, N.J.; Chizinski, C.J.; Helikar, T.; Dauer, J.T. Simulated Computational Model Lesson Improves Foundational Systems Thinking Skills and Conceptual Knowledge in Biology Students. BioScience 2018, 68, 612–621. [Google Scholar] [CrossRef]
- Brockmüller, S. Erfassung und Entwicklung von Systemkompetenz—Empirische Befunde zu Kompetenzstruktur und Förderbarkeit durch den Einsatz Analoger und Digitaler Modelle im Kontext Raumwirksamer Mensch-Umwelt-Beziehungen. Doctoral Dissertation, Pädagogische Hochschule Heidelberg, Heidelberg, Germany, 2019. [Google Scholar]
- Haas, A.; Grapin, S.E.; Wendel, D.; Llosa, L.; Lee, O. How Fifth-Grade English Learners Engage in Systems Thinking Using Computational Models. Systems 2020, 8, 47. [Google Scholar] [CrossRef]
- Ben-Zvi Assaraf, O.; Knippels, M. Lessons learned: Synthesizing Approaches That Foster Understanding of Complex Biological Phenomena. In Fostering Understanding of Complex Systems in Biology Education; Ben-Zvi Assaraf, O., Knippels, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 249–278. [Google Scholar]
- Sommer, C. Untersuchung der Systemkompetenz von Grundschülern im Bereich Biologie. Doctoral Dissertation, Christian-Albrechts-Universität zu Kiel, Kiel, Germany, 2005. [Google Scholar]
- Ben-Zvi Assaraf, O.; Orion, N. System thinking skills at the elementary school level. J. Res. Sci. Teach. 2009, 47, 540–564. [Google Scholar] [CrossRef]
- Bollmann-Zuberbühler, B.; Frischknecht-Tobler, U.; Kunz, P.; Nagel, U.; Wilhelm Hamiti, S. Systemdenken Fördern. Systemtraining und Unterrichtsreihen zum Vernetzten Denken. 1.–9. Schuljahr; Schulverlag Plus AG: Bern, Switzerland, 2010. [Google Scholar]
- Dierkes, P. Computergestütztes Lernen im Biologieunterricht. Unterricht Biologie 2015, 402/403, 1–11. [Google Scholar]
- Smetana, L.K.; Bell, R.L. Computer Simulations to Support Science Instruction and Learning: A critical review of the literature. Int. J. Sci. Educ. 2012, 34, 1337–1370. [Google Scholar] [CrossRef]
- Sterman, J. System Dynamics: System Thinking and Modeling for a Complex World. Massachusetts Institute of Technology, Engineering Systems Division, ESD Working Papers, ESD-WP-2003-01.13, ESD Internal Symposium, 2002. Available online: http://hdl.handle.net/1721.1/102741 (accessed on 5 March 2025).
- von Bertalanffy, L. General System Theory. Foundations, Development, Applications; George Braziller: New York, NY, USA, 1968. [Google Scholar]
- Matthies, M. Einführung in die Systemwissenschaft. Lecture Script; Universität Osnabrück, Institut für Umweltsystemforschung: Osnabrück, Germany, 2010. [Google Scholar]
- Gilissen, M.G.R.; Knippels, M.-C.P.J.; Verhoeff, R.P.; van Joolingen, W.R. Teachers’ and educators’ perspectives on systems thinking and its implementation in Dutch biology education. J. Biol. Educ. 2020, 54, 485–496. [Google Scholar] [CrossRef]
- Next Generation Science Standards. Available online: https://www.nextgenscience.org/news/final-next-generation-science-standards-released (accessed on 10 December 2024).
- Hmelo-Silver, C.E.; Pfeffer, M.G. Comparing expert and novice understanding of a complex system from the perspective of structures, behaviors, and functions. Cogn. Sci. 2004, 28, 127–138. [Google Scholar] [CrossRef]
- Bossel, H. Simulation Dynamischer Systeme. Grundwissen, Methoden, Programme; Springer: Wiesbaden, Germany, 1992. [Google Scholar]
- Bräutigam, J. Systemisches Denken im Kontext einer Bildung für Nachhaltige Entwicklung. Konstruktion und Validierung eines Messinstruments zur Evaluation einer Unterrichtseinheit. Doctoral Dissertation, Pädagogische Hochschule Freiburg, Freiburg, Germany, 2014. [Google Scholar]
- Mambrey, S.; Timm, J.; Landskron, J.J.; Schmiemann, P. The impact of system specifics on systems thinking. J. Res. Sci. Teach. 2020, 57, 1632–1651. [Google Scholar] [CrossRef]
- Verhoeff, R.P.; Knippels, M.-C.P.J.; Gilissen, M.G.R.; Boersma, K.T. The theoretical nature of systems thinking. Perspectives on systems thinking in biology education. Front. Educ. 2018, 3, 1–11. [Google Scholar] [CrossRef]
- Mischo, C.; Rieß, W. Förderung systemischen Denkens im Bereich von Ökologie und Nachhaltigkeit. Unterrichtswissenschaft 2008, 36, 346–364. [Google Scholar]
- Boersma, K.; Waarlo, A.J.; Klaassen, K. The feasibility of systems thinking in biology education. J. Biol. Educ. 2011, 45, 190–197. [Google Scholar] [CrossRef]
- Verhoeff, R.P. Towards Systems Thinking in Cell Biology Education. Doctoral Dissertation, Universiteit Utrecht, Utrecht, The Netherlands, 2003. [Google Scholar]
- Ben-Zvi Assaraf, O.; Orion, N. Development of System Thinking Skills in the Context of Earth System Education. J. Res. Sci. Teach. 2005, 42, 518–560. [Google Scholar] [CrossRef]
- Mehren, R.; Rempfler, A.; Ullrich-Riedhammer, E.-M.; Buchholz, J.; Hartig, J. Systemkompetenz im Geographieunterricht. Ein theoretisch hergeleitetes und empirisch überprüftes Kompetenzstrukturmodell. Zeitschrift für Didaktik der Naturwissenschaften 2016, 22, 147–163. [Google Scholar] [CrossRef]
- Hmelo-Silver, C.E.; Liu, L. Fish swim, rocks sit, and lungs breathe: Expert-novice understanding of complex systems and designs for learning. J. Learn. Sci. 2007, 16, 307–331. [Google Scholar] [CrossRef]
- Yoon, S.A.; Goh, S.-E.; Park, M. Teaching and Learning About Complex Systems in K-12 Science Education: A Review of Empirical Studies 1995–2015. Rev. Educ. Res. 2018, 88, 285–325. [Google Scholar] [CrossRef]
- Brockmüller, S. Structure and measurement of system competence: Promoting systems thinking using analogue and digital models. In Fostering Scientific Citizenship in an Uncertain World; Carvalho, G.S., Afonso, A.S., Anastácio, Z., Eds.; Springer: Cham, Switzerland, 2023; pp. 79–94. [Google Scholar] [CrossRef]
- Fanta, D.; Bräutigam, J.; Greiff, S.; Rieß, W. Entwicklung und Validierung eines Messinstrumentes zur Erfassung von systemischem Denken bei Lehramtsstudierenden in ökologischen Kontexten. Z. Didakt. Nat. Wiss. 2017, 23, 241–259. [Google Scholar] [CrossRef]
- Fanta, D.; Bräutigam, J.; Rieß, W. Fostering systems thinking in student teachers of biology and geography—An intervention study. J. Biol. Educ. 2020, 54, 226–244. [Google Scholar] [CrossRef]
- Streiling, S.; Hörsch, C.; Rieß, W. Effects of Teacher Training in Systems Thinking on Biology Students—An Intervention Study. Sustainability 2021, 13, 7631. [Google Scholar] [CrossRef]
- Rosenkränzer, F.; Stahl, E.; Hörsch, C.; Schuler, S.; Rieß, W. Das Fachdidaktische Wissen von Lehramtsstudierenden zur Förderung von systemischem Denken: Konzeptualisierung, Operationalisierung und Erhebungsmethode. Z. Didakt. Nat. Wiss. 2016, 1, 109–121. [Google Scholar] [CrossRef]
- Dor-Haim, S.; Ben-Zvi Assaraf, O. Long Term Ecological Research as a Learning Environment: Evaluating Its Impact in Developing the Understanding of Ecological Systems Thinking—A Case Study. In Fostering Understanding of Complex Systems in Biology Education; Ben-Zvi Assaraf, O., Knippels, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 17–40. [Google Scholar] [CrossRef]
- Hmelo-Silver, C.E.; Azevedo, R. Understanding Complex Systems: Some Core Challenges. J. Learn. Sci. 2006, 15, 53–61. [Google Scholar] [CrossRef]
- Jacobsen, M.J.; Wilensky, U. Complex Systems in Education: Scientific and Educational Importance and Implications for the Learning Sciences. J. Learn. Sci. 2006, 15, 11–34. [Google Scholar] [CrossRef]
- Hogan, K. Assessing students’ systems reasoning in ecology. J. Biol. Educ. 2000, 35, 22–28. [Google Scholar] [CrossRef]
- Grotzer, T.A. Children’s Understanding of Complex Causal Relationships in Natural Systems: A Research Study. Doctoral Dissertation, Harvard University, Cambridge, MA, USA, 1993. [Google Scholar]
- D’Angelo, C.; Rutstein, D.; Harris, C.; Bernard, R.; Borokhovski, E.; Haertel, G. Simulations for STEM Learning: Systematic Review and Meta-Analysis; SRI International: Menlo Park, CA, USA, 2014. [Google Scholar]
- Rutten, N.; van Joolingen, W.R.; van der Veen, J.T. The learning effects of computer simulations in science education. Comput. Educ. 2012, 58, 136–153. [Google Scholar] [CrossRef]
- Waddington, D.I.; Fennewald, T. Grim FATE: Learning About Systems Thinking in an In-Depth Climate Change Simulation. Simul. Gaming 2018, 49, 168–194. [Google Scholar] [CrossRef]
- Maierhofer, M. Förderung des Systemischen Denkens Durch Computerunterstützten Biologieunterricht; GCA-Verlag: Herdecke, Germany, 2001. [Google Scholar]
- Ceresia, F. Sunny Island. An Interactive learning Environment to Promote Systems Thinking Education for Primary School Students. Procedia—Soc. Behav. Sci. 2017, 237, 980–985. [Google Scholar] [CrossRef]
- Rieß, W.; Mischo, C. The Model of problem oriented Teaching and Learning (MopoLL)—Towards an evidence-based teaching method for fostering complex and dynamic problem solving skills in biology. Z. Didakt. Biol. 2017, 21, 1–21. [Google Scholar]
- Van Merriënboer, J. Training Complex Cognitive Skills; Educational Technology Publications: Englewood Cliffs, NJ, USA, 1997. [Google Scholar]
- Van Merriënboer, J. Perspectives on problem solving and instruction. Comput. Educ. 2013, 64, 153–160. [Google Scholar] [CrossRef]
- Frey, S.; Tramowsky, N.; Rieß, W. Systemisches Denken lernen am Thema Klimawandel mit der App klimakids. In Naturwissenschaftlicher Sachunterricht Digital; Tramowsky, N., Meßinger-Koppelt, J., Irion, T., Eds.; Joachim Herz Stiftung: Hamburg, Germany, 2023; pp. 76–79. [Google Scholar]
- Frey, S.; Beege, M.; Tramowsky, N.; Rieß, W. Entwicklung und Validierung eines Messinstruments zur Erfassung systemischen Denkens zum Klimawandel bei Grundschülerinnen und Grundschülern. Zeitschrift für Didaktik der Biologie 2025, 31. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar]
- Knogler, M.; Harackiewicz, J.M.; Gegenfurtner, A.; Lewalter, D. How situational is situational interest? Investigating the longitudinal structure of situational interest. Contemp. Educ. Psychol. 2015, 43, 39–50. [Google Scholar] [CrossRef]
- de Jong, T.; van Joolingen, W.R. Scientific Discovery Learning With Computer Simulations of Conceptual Domains. Rev. Educ. Res. 1998, 68, 179–201. [Google Scholar]
- IBM Corp. IBM SPSS Statistics for Windows (Version 28.0) [Computer Software], IBM Corp.: Armonk, NY, USA, 2021.
- Klieme, E.; Maichle, U. Erprobung eines Modellbildungssystems im Unterricht; Institut für Test-und Begabungsforschung: Bonn, Germany, 1991. [Google Scholar]
- Galbraith, P.L.; Fisher, D.M. Addressing sustainability: Modelling to enhance participation as a global citizen. Eur. J. Sustain. Dev. Res. 2024, 8, em0274. [Google Scholar] [CrossRef] [PubMed]
- Eseryel, D.; Law, V.; Ifenthaler, D.; Ge, X.; Miller, R. An Investigation of the Interrelationships between Motivation, Engagement, and Complex Problem Solving in Game-based Learning. Educ. Technol. Soc. 2014, 17, 42–53. [Google Scholar]
- Sweeney, L.B.; Sterman, J.D. Bathtub dynamics: Initial results of a systems thinking inventory. Syst. Dyn. Rev. 2001, 16, 249–286. [Google Scholar] [CrossRef]
- Grotzer, T.A.; Bell Basca, B. How does grasping the underlying causal structures of ecosystems impact students’ understanding? J. Biol. Educ. 2003, 38, 16–29. [Google Scholar] [CrossRef]
- JASP Team. JASP (Version 0.19.3) [Computer Software], JASP Team: Amsterdam, The Netherlands, 2024.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).