Are Neural Networks Better than Machine Learning? A Comparative Study for Travel Mode Predictions
Abstract
1. Introduction
2. Literature Review
3. Data
- (1)
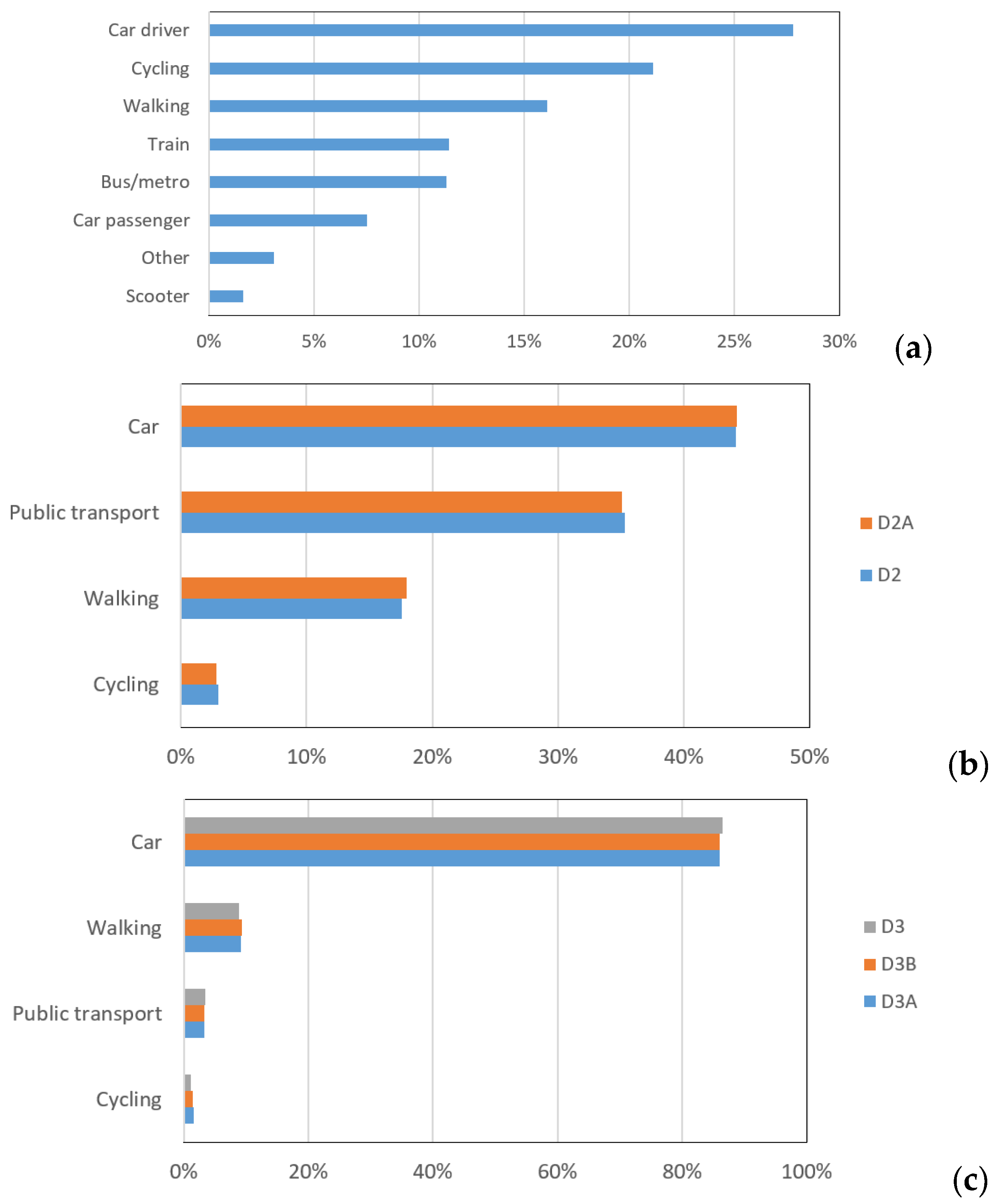
- There are some similarities in these datasets. For instance, the car is consistently the primary choice. Furthermore, the data imbalance in all datasets increases prediction difficulty.
- (2)
- For all the subsets, the proportions of all the travel modes are nearly the same as the original ones. Therefore, the performance differences between the subsets primarily result from the sample size.
- (3)
- Some differences in proportions mainly stem from the differences in typical national conditions. For example, the proportions of cycling in D1 (the Netherlands) are higher than that of walking. However, in D2 (the UK) and D3 (the US), the situation is just the opposite. In addition, the proportions of public transport in D3 (the US) are much lower than that of D1 (the Netherlands) and D2 (UK).
- (4)
- The imbalance is more prominent in D3. In Figure 1d, we only show the seven travel modes with a proportion greater than 1%. In other words, for 13 types in D3A/D3B/D3-20, their proportions are close to zero, and their influence on the final metrics of predictions will be little.
- (5)
- Note that the dependence of travel mode choices upon various variables is a complex topic, which cannot be quickly clarified merely through descriptive statistical charts. For this job, it is better to consider some other approaches, e.g., discrete choice models, which are out of the scope of this paper.
4. Methodology
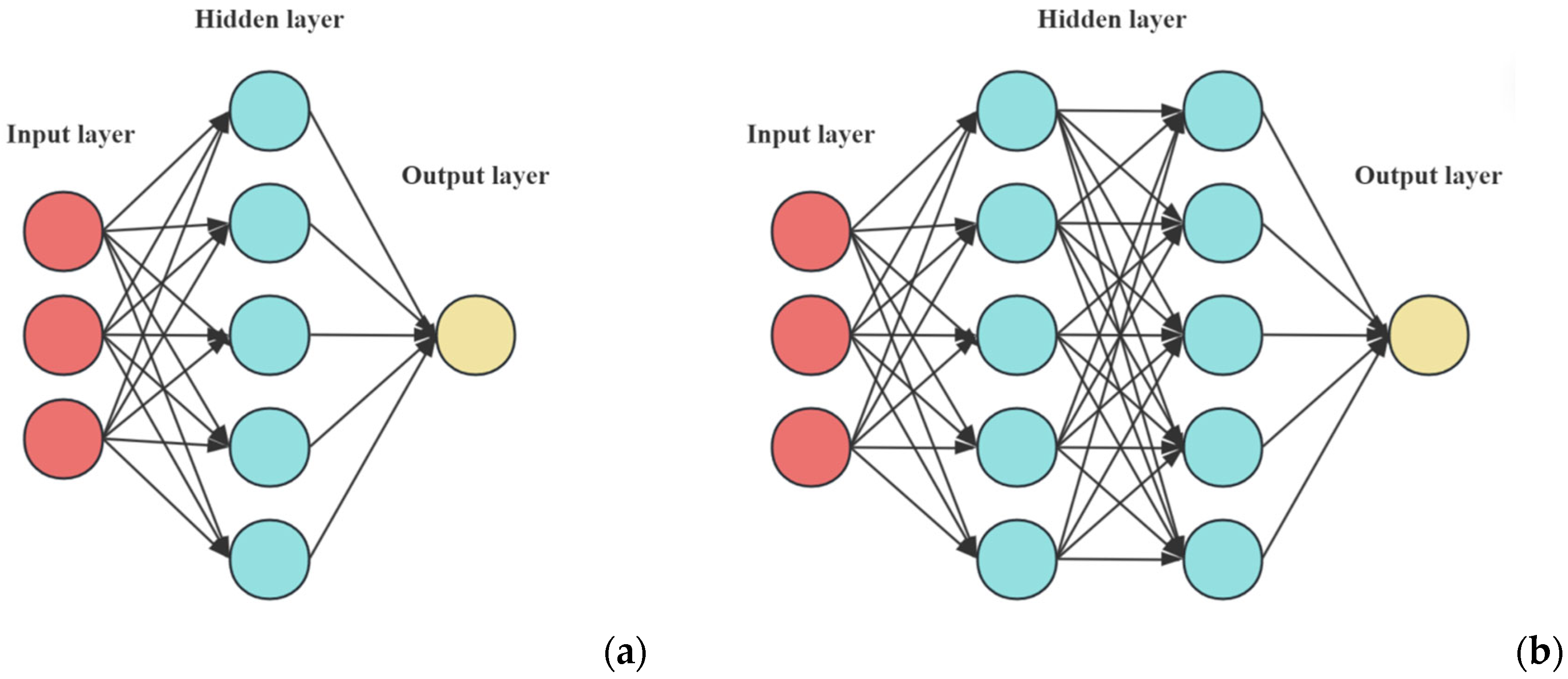
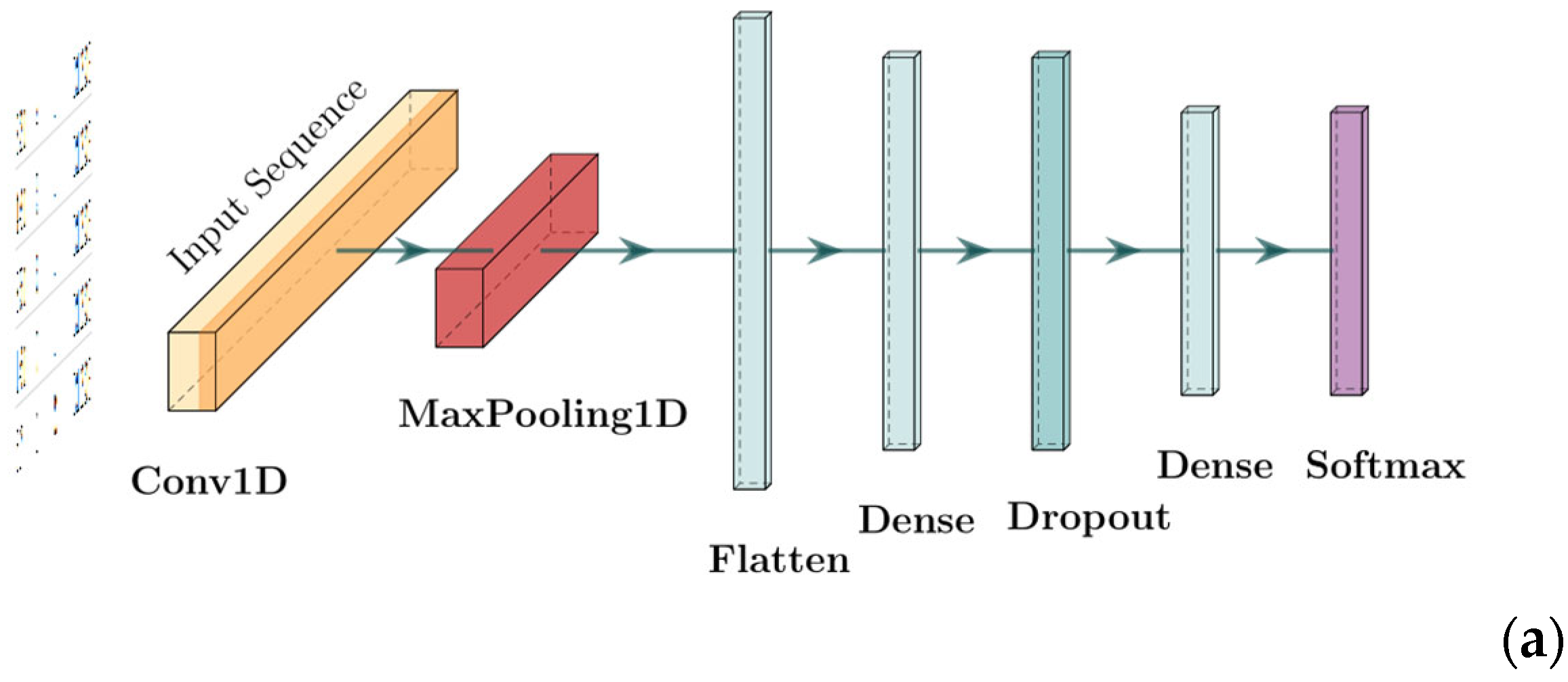
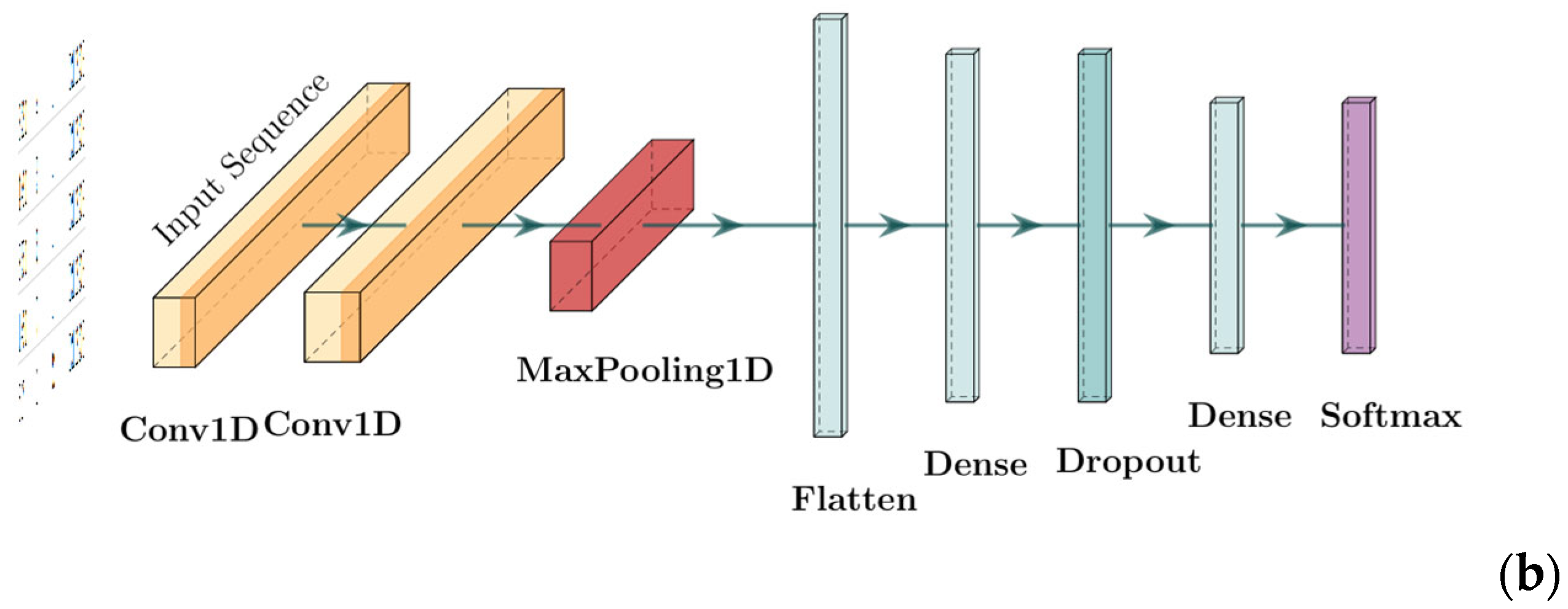
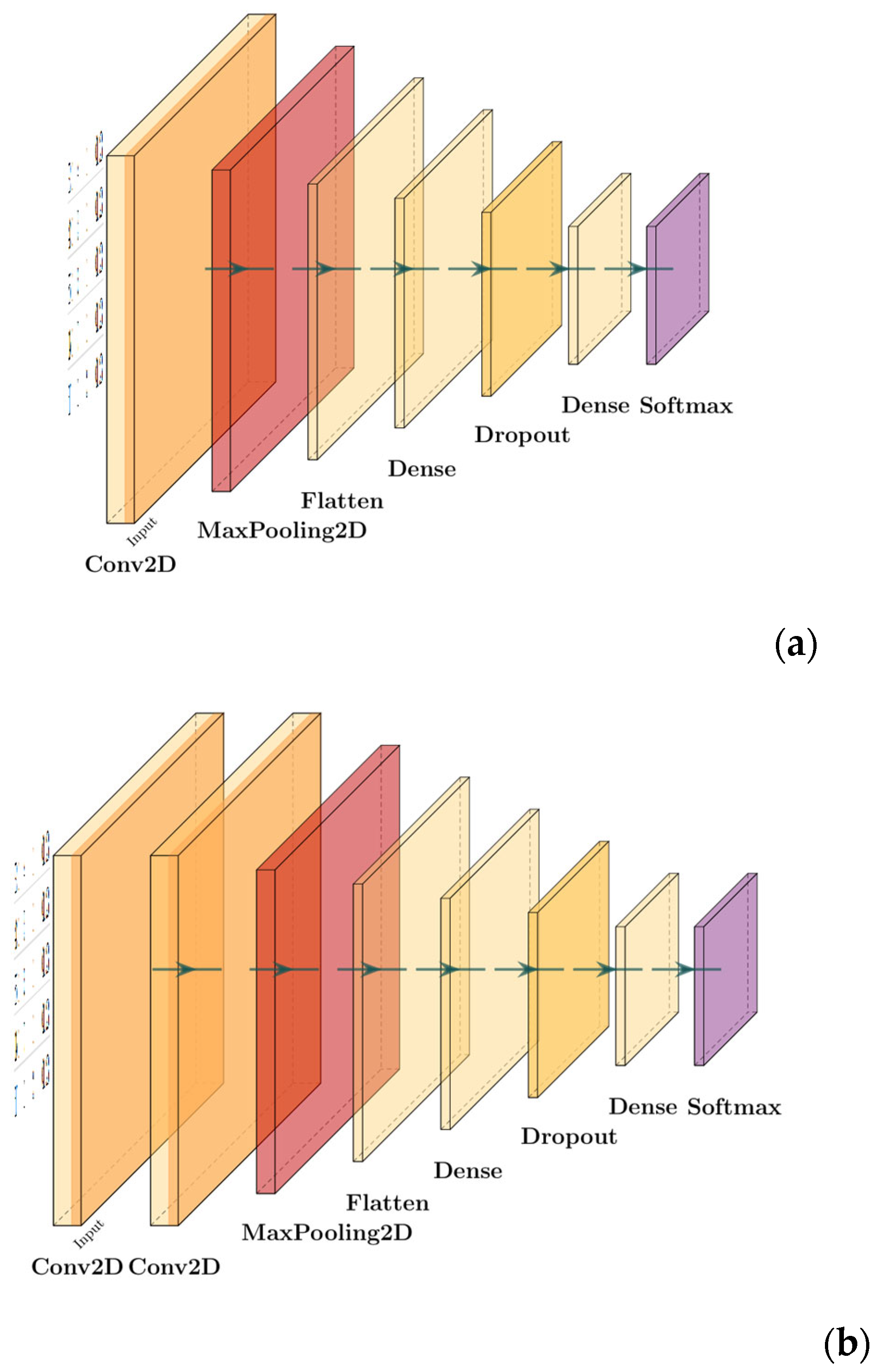
4.1. Models Used
4.2. Possible Methods for Improvement
- ▪
- SMOTE (synthetic minority over-sampling technique) is a synthetic minority over-sampling technique [32]. The algorithm flow is as follows:
- (1)
- For each sample x in the minority class, the Euclidean distance is used as the standard to calculate its distance to all the minority class samples, and its k-nearest neighbor is obtained.
- (2)
- A sampling ratio is set according to the sample imbalance ratio to determine the sampling rate N. For each minority sample X, a number of samples are randomly selected from its k-nearest neighbors, assuming that the selected nearest neighbors are Xn.
- (3)
- For each Xn, a new sample is constructed with the original sample according to the following formula:
- ▪
- Near-Miss is an under-sampling technique [33]. It aims to balance the class distribution by randomly eliminating most class examples. The basic intuitions are as follows:
- (1)
- Find the distance between all the majority class instances and minority ones. Here, most classes will be under-sampled.
- (2)
- The noun selects the majority class instance that has the smallest distance from the minority one.
- (3)
- If there are k instances of the minority class, the closest method will result in k × n instances of the majority class.
- (4)
- To find the n closest instances in most classes, there are several variations in the algorithm, including Version 1, Version 2, and Version 3. We selected Version 2 for its superior performance. This version identifies the minority sample that has the greatest distance to the k majority samples.
- ▪
- Focal loss is an innovation loss function for handling imbalanced samples, which was originally proposed by Lin et al. [34] when dealing with object detection. But it is also possible to be used for predictions of travel mode choices. The traditional cross-entropy loss function pays excessive attention to many easy negative samples, which may limit the model performance.
4.3. Optimization of the Parameters
5. Model Results
- (1)
- Generally speaking, when observing the F1 scores, the averaged performance of NN models is worse than ML models, as calculated in Table 10. This situation is not as expected as before, which will be discussed later. For the largest one (D3-20), the maximum F1 score of NN models is even smaller than the minimum value of ML models: 0.147 (GrowNet) < 0.192 (LR).
- (2)
- Among the five ML models, the performance of RF is the best for large datasets (D3, D3A, and D3B). The main reason is that RF is based on ensemble learning and incorporates random sampling and feature selection mechanisms. This increases the model diversity and makes it more robust against overfitting. However, for smaller datasets, the best choice is not so clear. In addition, LR is always the worst one among the ML models. Such a situation is easy to understand: the linear assumption of LR may lead to limitations when dealing with non-linear data.
- (3)
- The performance of six classic NN models are similar. For all the datasets, the differences between CNN-1D, CNN-2D, and MLP are not significant. This may be because there are no obvious local correlation patterns among the variables involved, or these local correlations are not key factors in this task. In addition, adding layers cannot improve the results for both CNN and MLP. For some situations (e.g., CNN-2D in D3A-20, MLP in D3B-4), the model with one layer could be better than that with two layers. In other words, increasing model complexity is not helpful for such a prediction problem.
- (4)
- The results of the ten new NN models are also unsatisfactory. It seems that they have better performance in a smaller dataset. For example, the best one among them in D1 (ResNet) is at least better than some ML models (LR and DT). However, with the increase in sample number, the advantages of new NN models gradually diminish. As shown in Table 10, in D2A/D2, their performances are similar to classic NN models, while in D3A/D3B/D3, they become even worse.
- (5)
- Differences between the datasets are observed. As introduced in Table 1 and Table 2, the sample sizes of D2 and D3A-4 are nearly the same, and their dependent variables (travel modes) and the five independent variables (age, sex, travel distance, number of family vehicles, and purpose of travel) are also the same. However, the metrics of the same models are different in Table 7, Table 8 and Table 9. For example, most accuracies in D3A-4 are higher than D2, while most F1 scores in D3A-4 are lower. In other words, the internal characteristics of the datasets selected in this paper actually vary significantly. This is also beneficial for us to fully examine and compare the characteristics of various models from different perspectives.
- (6)
- The sizes of datasets are also important. Generally speaking, smaller datasets are easier to predict. In addition, the simple problem with four types is easier than the difficult one with twenty types for all the datasets. This may be because the class imbalance problem is exacerbated in larger datasets, especially in D3.
- (1)
- The improvement in SMOTE is significant for many models. For some models, e.g., XGB and RF, the new F1 score is even more than two times the original value. At the same time, the improvement in F1 score by Near-Miss is also not too bad. Such phenomena coincide with what we can observe in some previous studies.
- (2)
- From Table 12 and Table 13, we can see that all the recalls have been increased, and the values of recalls and precisions have become nearly the same for the same model. Although the mechanisms of SMOTE and Near-Miss are not the same (e.g., the differences between under-sampling and over-sampling), similar results could be obtained, since both methods change the proportional relationship between FP and FN.
- (3)
- On the contrary, the effect of using focal loss is not ideal in Table 14. The marginal improvement can be nearly ignored. This may be because the imbalance in the weights of positive and negative samples is more severe, making it very difficult to find appropriate parameters.
- (4)
- For all the models, the improvement from SMOTE, Near-Miss, or using focal loss does not change the magnitude relationship between the results of ML models and NN models. In other words, regardless of using the conventional method or these improved methods, ML models are always better than NN models, including the new ones proposed in recent years. This conclusion seems a bit counterintuitive, but it is indeed the result after being tested.
6. Discussions
- ▪
- The type of input variables. For the travel mode predictions, many input variables are discrete. However, most NN models are typically based on the assumptions of continuity, such as gradient-based optimization methods. When faced with discrete variables, these methods may struggle to find optimal solutions because the discrete nature of the data does not allow for smooth gradients [35]. This makes it difficult for the models to capture complex relationships and patterns hidden within the data [36].
- ▪
- The importance of feature engineering. Typical machine learning models can better adapt to large databases through some traditional feature engineering methods. However, neural networks are restricted by the representation of the original data, and require more complex feature extraction and representation learning processes [37]. Recent studies also confirmed that without massive datasets, advanced gradient boosting models often outperform deep learning architectures on tabular travel data [38]. If the input layer and preprocessing steps of the neural network are not carefully designed (e.g., only five variables are directly input), it may not be able to effectively process this data.
- ▪
- The influence of local features. When the amount of data becomes large, the gradient descent process of the neural network may be inevitably affected by noise or local optimal solutions. This may result in overfitting to the local features of some samples, making its performance decline. In contrast, machine learning models can make better use of the newly added data to enhance generalization ability. For example, RF can construct multiple decision trees by randomly selecting features and samples. It is more robust to noise and local features, and the risk of overfitting can be reduced.
- ▪
- The lack of rotation invariance. As stated in Grinsztajn et al. [36], neural networks have rotation invariance because their learning process does not rely on the direction of features. This characteristic enables neural networks to perform outstandingly when processing data such as images. Since the orientation of an image can be arbitrary, neural networks are still able to recognize the same objects. However, the structured data (like tabular data) generally does not have rotational invariance. For example, each feature in the data of travel mode choice has a fixed position and direction. If they are rotated, the performance of the model will become worse. As a result, the advantages of neural networks cannot be fully utilized when dealing with residents’ travel mode data.
- ▪
- The possibility of overfitting. For some neural networks, especially the new NN models with complex structures, overfitting may be inevitable. Many papers about the new NN models did not mention the total parameter numbers of these models. But as introduced by NODE [26] and TabNet [29], their values could be higher than one million. However, even in the largest dataset of this paper (D3), the sample number is lower than one million. Under such conditions, the advantages of neural networks cannot be brought into play.
- ▪
- The object of comparisons: Many previous studies concentrate on the performance of discrete choice models (DCMs), and MNL/BL is usually considered as a typical benchmark. At the same time, some other studies considered different types of logit models. For example, Wang et al. [13], Salas et al. [14] studied the MMNL model when considering heterogeneity. Zhang et al. [7], Le and Teng [5] used the NL model, while Nam and Cho [12], Xia et al. [16], Püschel et al. [15] used both NL and CNL models. Wang et al. [19] studied an additional ten generalized linear models for a comprehensive comparison. Theoretically speaking, it is easy to understand that all of them can obtain the natural conclusion that “ML models are better than DCMs”. This is because the assumption of DCMs about utility norms is too simple and linear, and it has trouble handling categorical explanatory variables. However, this is different from the topic discussed in this paper.
- ▪
- The focus of studies: In many papers considering the comparison between different models, this topic is not the main concern. Instead, the main topic is about the proposal of one or more new models, e.g., DNN-A model in Nam and Cho [12], BMTM-DLP model in Lai et al. [39], RE-BNN model in Xia et al. [16], MTLDNN-M model in Bei et al. [40], “the optimized CNN model” in Wen and Chen [17], and several NN models in Kashifi et al. [8], etc. These authors tried to prove that their new models are better than the selected benchmark models (usually logit models, as mentioned in the last paragraph). In other words, the effects of many machine learning models are not fully considered.
- ▪
- The metrics for evaluations: In many previous studies, the metrics for evaluations differ. Some of them are related to specific problems, e.g., Nam and Cho [12], Le and Teng [5] and Xia et al. [16] chose to study the travel mode shares and their absolute values of errors when predicting. Similarly, Püschel et al. [15] considered the deviation in the predicted distributions. Some others focused on the losses or errors during the training, including Wang et al. [13] and Abulibdeh [9]. Martín–Baos et al. [18] studied some new indicators which were not widely used, e.g., the GMPCA. The only one metric considered by all the studies is accuracy. However, as shown in Table 10, for each dataset, the accuracy of the different models is always similar. If we only look at accuracy, it is too difficult to determine whether NN models are really better.
- ▪
- The size of datasets: In some papers, the metrics of NN models are significantly better than that of ML models, e.g., Wen and Chen [17]. However, since the sample number in this paper is only 1192, we think the “good performance” of NN models may be due to overfitting. Actually, similar situations could be seen in other studies considering more datasets. For example, in Table 4 of Salas et al. [14], when the sample size is 1000, the accuracy of NN model (0.840) is much better than all the ML models (max = 0.730). However, when the size increases to 3000 or 5000, that of NN model declines (0.755) and becomes very close to the other ones (max = 0.748). Therefore, to avoid overfitting, we think it is necessary to choose a dataset that is not too small.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | The original names of the travel modes in D2 are not exactly the same as that in D3, e.g., “public transport” vs. “public transit”. Nevertheless, we consider them as the same thing due to the similarities. |
| 2 | Since the classic neural networks used in this study are not very “deep”, we do not use the concept of “DNN” in this paper. In addition, we think the CNN and MLP models used in this paper belong to the scope of “ANN”, but we do not put emphasis on this concept. |
References
- McFadden, D. Conditional Logit Analysis of Qualitative Choice Behavior. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: New York, NY, USA, 1974; pp. 105–142. [Google Scholar]
- McFadden, D.; Train, K.E. Mixed MNL models for discrete response. J. Appl. Econom. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Naseri, H.; Waygood, E.O.D.; Patterson, Z.; Alousi-Jones, M.; Wang, B. Travel mode choice prediction: Developing new techniques to prioritize variables and interpret black-box machine learning techniques. Transp. Plan. Technol. 2025, 48, 582–605. [Google Scholar] [CrossRef]
- Li, W.; Kockelman, K.M. How does machine learning compare to conventional econometrics for transport data sets? A test of ML versus MLE. Growth Change 2022, 53, 342–376. [Google Scholar] [CrossRef]
- Le, J.; Teng, J. Understanding influencing factors of travel mode choice in urban-suburban travel: A case study in Shanghai. Urban Rail Transit 2023, 9, 127–146. [Google Scholar] [CrossRef] [PubMed]
- Benjdiya, O.; Rouky, N.; Benmoussa, O.; Fri, M. On the use of machine learning techniques and discrete choice models in mode choice analysis. LogForum Sci. J. Logist. 2023, 19, 331–345. [Google Scholar] [CrossRef]
- Zhang, Z.; Ji, C.; Wang, Y.; Yang, Y. A Customized Deep Neural Network Approach to Investigate Travel Mode Choice with Interpretable Utility Information. J. Adv. Transp. 2020, 2020, 5364252. [Google Scholar] [CrossRef]
- Kashifi, M.T.; Al-Rassas, A.M.; Bakar, K.A.; Al-Japairai, K.A.; Jamali, S.S. Predicting the travel mode choice with interpretable machine learning techniques: A comparative study. Travel Behav. Soc. 2022, 29, 279–296. [Google Scholar] [CrossRef]
- Abulibdeh, A. Analysis of mode choice affects from the introduction of Doha Metro using machine learning and statistical analysis. Transp. Res. Interdiscip. Perspect. 2023, 20, 100852. [Google Scholar] [CrossRef]
- Narayanan, S.; Tzenos, P.; Verani, E.; Vlahogianni, E.I. Can Bike-Sharing Reduce Car Use in Alexandroupolis? An Exploration through the Comparison of Discrete Choice and Machine Learning Models. Smart Cities 2023, 6, 1239–1253. [Google Scholar] [CrossRef]
- Kalantari, H.A.; Sabouri, S.; Brewer, S.; Ewing, R.; Tian, G. Machine learning in mode choice prediction as part of MPOs’ regional travel demand models: Is it time for change? Sustainability 2025, 17, 3580. [Google Scholar] [CrossRef]
- Nam, D.; Cho, J. Deep neural network design for modeling individual-level travel mode choice behavior. Sustainability 2020, 12, 7481. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; Lee, D.H. Deep neural networks for choice analysis: A statistical learning theory perspective. Transp. Res. Part B Methodol. 2021, 148, 60–81. [Google Scholar] [CrossRef]
- Salas, P.; Pezoa, R.; Oliveira, L.; Henríquez, G.; Raveau, S. A systematic comparative evaluation of machine learning classifiers and discrete choice models for travel mode choice in the presence of response heterogeneity. Expert Syst. Appl. 2022, 193, 116253. [Google Scholar] [CrossRef]
- Püschel, J.; Regue, R.; Gerike, R.; Nagel, K. Comparison of discrete choice and machine learning models for simultaneous modeling of mobility tool ownership in agent-based travel demand models. Transp. Res. Rec. 2024, 2678, 376–390. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, H.; Zimmermann, R. A random effect bayesian neural network (RE-BNN) for travel mode choice analysis across multiple regions. Travel Behav. Soc. 2023, 30, 118–134. [Google Scholar] [CrossRef]
- Wen, X.; Chen, X. A New Breakthrough in Travel Behavior Modeling Using Deep Learning: A High-Accuracy Prediction Method Based on a CNN. Sustainability 2025, 17, 738. [Google Scholar] [CrossRef]
- Martín-Baos, J.A.; Ros, L.G.; García-García, F.; López-Sánchez, A.D.; Soria-Olivas, E.; Pérez-Bernabeu, E. A prediction and behavioural analysis of machine learning methods for modelling travel mode choice. Transp. Res. Part C Emerg. Technol. 2023, 156, 104318. [Google Scholar] [CrossRef]
- Wang, S.; Kockelman, K.M.; Lemp, J.D. Comparing hundreds of machine learning and discrete choice models for travel demand modeling: An empirical benchmark. Transp. Res. Part B Methodol. 2024, 190, 103061. [Google Scholar] [CrossRef]
- Shahdah, U.E.; Elharoun, M.; Ali, E.K.; Elbany, M.; Elagamy, S.R. Stated preference survey for predicting eco-friendly transportation choices among Mansoura University students. Innov. Infrastruct. Solut. 2025, 10, 180. [Google Scholar] [CrossRef]
- Jin, C.; Luo, Y.; Wu, C.; Song, Y.; Li, D. Exploring the Pedestrian Route Choice Behaviors by Machine Learning Models. Int. J. Geo-Inf. 2024, 13, 146. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-Normalizing Neural Networks. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Song, W.; Shi, C.; Xiao, Z.; Wang, Z.; Sun, L.; Rossi, P. AutoInt: Automatic Feature Interaction Learning via Self-Attentive Neural Networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management (CIKM ‘19), Beijing, China, 3–7 November 2019; pp. 1161–1170. [Google Scholar]
- Badirli, S.; Tufan, A.; Kask, K.; Can, F.; User, H.B.; Yilmaz, A. Gradient Boosting Neural Networks: GrowNet. arXiv 2020, arXiv:2002.07971. [Google Scholar] [CrossRef]
- Popov, S.; Morozov, S.; Babenko, A. Neural Oblivious Decision Ensembles for Deep Learning on Tabular Data. In Proceedings of the International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Wang, R.; Fu, B.; Fu, G.; Wang, M. DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 1785–1797. [Google Scholar]
- Gorishniy, Y.; Rubachev, I.; Gulin, A.; Babenko, A. Revisiting Deep Learning Models for Tabular Data. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021. [Google Scholar]
- Arık, S.Ö.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. In Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI-21), Online, 2–9 February 2021; Volume 35, pp. 6679–6687. [Google Scholar]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction. arXiv 2017, arXiv:1703.04247. [Google Scholar]
- Yan, J.; Chen, J.; Wang, Q.; Chen, D.Z.; Wu, J. Team up GBDTs and DNNs: Advancing Efficient and Effective Tabular Prediction with Tree-hybrid MLPs. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ‘24), Barcelona, Spain, 25–29 August 2024. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Zhang, J.; Mani, I. KNN Approach to Unbalanced Data Distributions: A Case Study Involving Information Extraction. In Proceedings of the International Conference on Machine Learning (ICML), Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on tabular data? arXiv 2022, arXiv:2207.08815. [Google Scholar] [CrossRef]
- Borisov, V.; Leemann, T.; Seßler, K.; Haug, J.; Pawelczyk, M.; Kasneci, G. Deep Neural networks and tabular data: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7499–7519. [Google Scholar] [CrossRef]
- Banyong, C.; Hantanong, N.; Nanthawong, S.; Se, C.; Wisutwattanasak, P.; Champahom, T.; Ratanavaraha, V.; Jomnonkwao, S. Machine learning-based analysis of travel mode preferences: Neural and boosting model comparison using stated preference data from Thailand’s emerging high-speed rail network. Big Data Cogn. Comput. 2025, 9, 155. [Google Scholar] [CrossRef]
- Lai, Z.; Chen, C.; Wang, Y.; Wang, J.; Xu, Z. Travel mode choice prediction based on personalized recommendation model. IET Intell. Transp. Syst. 2023, 17, 667–677. [Google Scholar] [CrossRef]
- Bei, H.; Liu, J.; Zhang, Y.; Wang, W. Joint prediction of travel mode choice and purpose from travel surveys: A multitask deep learning approach. Travel Behav. Soc. 2023, 33, 100625. [Google Scholar] [CrossRef]

| Dataset | Source | Year | Country | Number of Samples | Number of Total Variables | Number of Types of Travel Modes |
|---|---|---|---|---|---|---|
| D1 | MPN | 2018 | The Netherlands | 7310 | 56 | 8 |
| D2A | LPMC | 2012–2015 | UK | 20,000 | 36 | 4 |
| D2 | LPMC | 2012–2015 | UK | 81,096 | 36 | 4 |
| D3A | NHTS | 2017 | US | 79,707 | 115 | 4, 20 |
| D3B | NHTS | 2017 | US | 149,445 | 115 | 4, 20 |
| D3 | NHTS | 2017 | US | 920,041 | 115 | 4, 20 |
| Dataset | Variables | Explanations | Statistics |
|---|---|---|---|
| D1 | ROLAUTO | Role in travel | Drivers: 78.8%; Passengers: 21.2% |
| KAFSTV | Travel distance | Mean: 13.00; Median: 4.35; Mode: 1.75; Std: 17.83 | |
| AANTRIT | Number of travels per day | Mean: 1.73; Median: 1.00; Mode: 1; Std: 1.35 | |
| VERPL | Travel features | No new trip: 19.1%; New trip: 79.3%; Trip abroad: 0.9%; Others: 0.7% | |
| KMOTIEF | Purpose of travel | Work: 21.2%; Business-related visit: 1.5%; Personal care: 3.0% Shopping: 19.4%; Education/courses: 6.4%; Visitation: 8.8% Social/recreational: 19.5%; Touring: 5.1%; Others: 15.0% | |
| D2A | AGE | Age | Mean: 39.60; Median: 38.00; Mode: 35; Std: 19.57 |
| SEX | Sex | Female: 53.2%; Male: 46.8% | |
| DISTANCE | Travel distance | Mean: 4515.34; Median: 2737.50; Mode: 1286; Std: 4770.33 | |
| OWNERSHIP | Number of family vehicles | Mean: 1.00; Median: 1.00; Mode: 1; Std: 0.75 | |
| PURPOSE | Purpose of travel | Work: 15.8%; Education: 11.0%; Employers’ business: 7.0%; Home-based other: 52.1%; Non-home-based other: 14.1% | |
| D2 | AGE | Age | Mean: 39.46; Median: 38.00; Mode: 35; Std: 19.23 |
| SEX | Sex | Female: 52.6%; Male: 47.4% | |
| DISTANCE | Travel distance | Mean: 4605.26; Median: 2814.00; Mode: 1309; Std: 4782.35 | |
| OWNERSHIP | Number of family vehicles | Mean: 0.98; Median: 1.00; Mode: 1; Std: 0.75 | |
| PURPOSE | Purpose of travel | Work: 16.7%; Education: 11.4%; Employers‘ business: 7.1%; Home-based other: 51.0%; Non-home-based other: 13.8% | |
| D3A | R_AGE | Age | Mean: 49.09; Median: 53.00; Mode: 65; Std: 20.55 |
| R_SEX | Sex | Female: 54.1%; Male: 45.9% | |
| TRPMILES | Travel distance | Mean: 11.73; Median: 3.45; Mode: 1.0; Std: 74.16 | |
| HHVEHCNT | Number of family vehicles | Mean: 2.24; Median: 2.00; Mode: 2; Std: 1.20 | |
| TRIPPURP | Purpose of travel | Work: 12.9%; Shopping: 21.3%; Social/recreational: 12.2%; Other: 20.0%; Not home-based: 33.6% | |
| D3B | R_AGE | Age | Mean: 49.03; Median: 53.00; Mode: 65; Std: 20.62 |
| R_SEX | Sex | Female: 53.1%; Male: 46.9% | |
| TRPMILES | Travel distance | Mean: 11.52; Median: 3.44; Mode: 1.0; Std: 82.56 | |
| HHVEHCNT | Number of family vehicles | Mean: 2.24; Median: 2.00; Mode: 2; Std: 1.22 | |
| TRIPPURP | Purpose of travel | Work: 12.7%; Shopping: 21.3%; Social/recreational: 12.4%; Other: 19.8%; Not home-based: 33.8% | |
| D3 | R_AGE | Age | Mean: 49.16; Median: 53.00; Mode: 65; Std: 20.64 |
| R_SEX | Sex | Female: 53.2%; Male: 46.8% | |
| TRPMILES | Travel distance | Mean: 11.36; Median: 3.44; Mode: 1.0; Std: 74.41 | |
| HHVEHCNT | Number of family vehicles | Mean: 2.23; Median: 2.00; Mode: 2; Std: 1.20 | |
| TRIPPURP | Purpose of travel | Work: 12.7%; Shopping: 20.6%; Social/recreational: 11.9%; Other: 20.6%; Not home-based: 33.6% |
| Model | Basic Feature | Design for Tabular Data |
|---|---|---|
| ResNet | It is a simple variation of the original ResNet. There is an almost clear path from the input to output. | It reuses well-established DL building blocks, which is beneficial for optimization. |
| SNN | It does not face vanishing or exploding gradient problems, since neuron activations automatically converge towards zero mean and unit variance. | It enables self-normalization by using the SELU activation function and specific weight initialization. |
| AutoInt | It can automatically learn high-order feature interactions, and the attention mechanism can show the correlations between different features. | It is designed for recommender systems where the features are sparse and contain high-dimensional tabular data. |
| GrowNet | It uses shallow neural networks as weak learners, and the final output is the weighted sum of all weak learners. | It is faster and easier to train, since it incorporates second-order statistics and a global corrective step for fine-tuning. |
| NODE | It is composed of differentiable oblivious decision trees (ODTs), which is a sequence of k NODE layers following the DenseNet model. | It is fully differentiable and allows constructing multi-layer architectures for end-to-end training. |
| DCN-V2 | It consists of an embedding layer, a cross network with multiple cross layers, and a deep network, which are helpful for learning explicit and implicit features. | The cross layers are designed to learn bounded-degree feature interactions, which are useful for tabular data where feature combinations are crucial. |
| FT—Transformer | It transforms all features (categorical and numerical) to embeddings, and applies a stack of transformer layers to these embeddings. | Based on the transformer, it uses multi-head self-attention and pre-normalization for better performance of tabular data. |
| TabNet | It consists of multiple decision steps. It uses a learnable mask for feature selection at each step, and processes the selected features through a transformer. | It employs sequential attention for instance-wise feature selection, which is beneficial for tabular data with redundant features. |
| DeepFM | It integrates the architectures of factorization machines (FMs) and deep neural networks (DNNs), sharing the same input to learn both low- and high-order feature interactions. | It is designed to capture both low- and high-order feature interactions from raw features without any feature engineering, effectively handling sparse categorical data. |
| GBDT + DNN | It incorporates a GBDT-based feature gate for sample-specific feature selection, followed by simplified sparse MLP blocks for prediction. | It integrates the advantages of GBDTs (efficient feature selection) and DNNs (smooth optimization) to address the model selection dilemma on tabular datasets. |
| Model | Hyper-Parameter | Search Range |
|---|---|---|
| LR | C | [0.001, 100] |
| solver | [‘liblinear’, ‘lbfgs’, ‘sag’, ‘saga’] | |
| KNN | n_neighbors | [3, 29] |
| weights | [‘uniform’, ‘distance’] | |
| p | [1, 2] | |
| DT | max_depth | [1, 11] |
| min_samples_split | [2, 10] | |
| min_samples_leaf | [1, 4] | |
| criterion | [‘gini’, ‘entropy’] | |
| max_features | [‘sqrt’, ‘log2’] | |
| RF | n_estimators | [10, 200] |
| max_depth | [1, 15] | |
| min_samples_split | [2, 10] | |
| min_samples_leaf | [1, 4] | |
| max_features | [‘sqrt’, ‘log2’] | |
| bootstrap | [True, False] | |
| criterion | [‘gini’, ‘entropy’] | |
| XGB | n_estimators | [10, 200] |
| max_depth | [1, 9] | |
| learning_rate | [0.01, 0.2] | |
| subsample | [0.6, 1.0] | |
| colsample_bytree | [0.6, 1.0] | |
| gamma | [0, 0.2] | |
| reg_alpha | [0, 0.5] | |
| reg_lambda | [0, 0.5] |
| Model | Hyper-Parameter | Search Range |
|---|---|---|
| MLP-1 | Number of neurons | [10, 500] |
| Dropout rate | [0, 0.3] | |
| Batch size | [4, 32] | |
| MLP-2 | Number of neurons in Layer 1, 2 | [10, 500] |
| Dropout rate | [0, 0.3] | |
| Batch size | [4, 32] | |
| CNN-1D-1 | Filters | [32, 512] |
| Kernel size | [3, 5] | |
| Number of neurons | [10, 500] | |
| Pooling size | [2, 3] | |
| Dropout rate | [0, 0.3] | |
| Batch size | [4, 32] | |
| CNN-1D-2 | Filters of Layer 1, 2 | [32, 512] |
| Kernel size of Layer 1, 2 | [3, 5] | |
| Number of neurons of Layer 1, 2 | [10, 500] | |
| Pooling size | [2, 3] | |
| Dropout rate | [0, 0.3] | |
| Batch size | [4, 32] | |
| CNN-2D-1 | Filters | [32, 512] |
| Kernel size | [(3,1), (5,1)] | |
| Number of neurons | [10, 500] | |
| Pooling size | [(2,1), (3,1)] | |
| Dropout rate | [0, 0.3] | |
| Batch size | [4, 32] | |
| CNN-2D-2 | Filters of Layer 1, 2 | [32, 512] |
| Kernel size of Layer 1, 2 | [(3,1), (5,1)] | |
| Number of neurons of Layer 1, 2 | [10, 500] | |
| Pooling size | [(2,1), (3,1)] | |
| Dropout rate | [0, 0.3] | |
| Batch size | [4, 32] |
| (a) The default and optimized parameters of D3B-4. | ||||||||
| Model | Hyper-parameter | Default value | Optimized value | |||||
| KNN | n_neighbors | 5 | 18 | |||||
| weights | uniform | distance | ||||||
| p | 2 | 1 | ||||||
| RF | n_estimators | 100 | 200 | |||||
| max_depth | None | None | ||||||
| min_samples_split | 2 | 2 | ||||||
| min_samples_leaf | 1 | 1 | ||||||
| max_features | auto | log2 | ||||||
| bootstrap | TRUE | TRUE | ||||||
| criterion | gini | entropy | ||||||
| MLP-2 | dense_units1 | 100 | 100 | |||||
| dense_units2 | 100 | 100 | ||||||
| dropout_rate | 0.2 | 0.1 | ||||||
| batch_size | 32 | 16 | ||||||
| CNN-1D-1 | filters | 64 | 128 | |||||
| kernel_size | 3 | 3 | ||||||
| pool_size | 2 | 2 | ||||||
| dense_units | 100 | 200 | ||||||
| dropout_rate | 0.2 | 0.01 | ||||||
| batch_size | 32 | 16 | ||||||
| (b) The default and optimized results of D3B-4. | ||||||||
| Model | KNN | RF | MLP-2 | CNN-1D-1 | ||||
| Statistics | Default result | Optimized result | Default result | Optimized result | Default result | Optimized result | Default result | Optimized result |
| Accuracy | 0.886 | 0.911 | 0.918 | 0.920 | 0.889 | 0.889 | 0.883 | 0.885 |
| Precision | 0.590 | 0.739 | 0.728 | 0.744 | 0.672 | 0.677 | 0.770 | 0.769 |
| Recall | 0.433 | 0.574 | 0.610 | 0.611 | 0.401 | 0.399 | 0.368 | 0.379 |
| F1 score | 0.471 | 0.630 | 0.655 | 0.658 | 0.434 | 0.459 | 0.402 | 0.416 |
| D1 | LR | KNN | DT | RF | XGB |
|---|---|---|---|---|---|
| Accuracy | 0.823 | 0.843 | 0.840 | 0.856 | 0.865 |
| Precision | 0.806 | 0.711 | 0.730 | 0.746 | 0.728 |
| Recall | 0.646 | 0.682 | 0.677 | 0.683 | 0.691 |
| F1 score | 0.637 | 0.808 | 0.741 | 0.784 | 0.818 |
| D2A | LR | KNN | DT | RF | XGB |
| Accuracy | 0.686 | 0.748 | 0.776 | 0.801 | 0.795 |
| Precision | 0.763 | 0.771 | 0.702 | 0.783 | 0.793 |
| Recall | 0.505 | 0.693 | 0.715 | 0.724 | 0.713 |
| F1 score | 0.507 | 0.723 | 0.708 | 0.748 | 0.743 |
| D2 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.651 | 0.752 | 0.757 | 0.782 | 0.744 |
| Precision | 0.733 | 0.795 | 0.690 | 0.747 | 0.708 |
| Recall | 0.454 | 0.697 | 0.702 | 0.720 | 0.612 |
| F1 score | 0.458 | 0.730 | 0.696 | 0.732 | 0.638 |
| D3A-4 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.871 | 0.906 | 0.888 | 0.914 | 0.910 |
| Precision | 0.605 | 0.711 | 0.590 | 0.723 | 0.729 |
| Recall | 0.301 | 0.579 | 0.610 | 0.605 | 0.572 |
| F1 score | 0.571 | 0.627 | 0.600 | 0.650 | 0.626 |
| D3A-20 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.438 | 0.481 | 0.529 | 0.564 | 0.552 |
| Precision | 0.769 | 0.251 | 0.357 | 0.426 | 0.520 |
| Recall | 0.076 | 0.182 | 0.407 | 0.422 | 0.337 |
| F1 score | 0.205 | 0.544 | 0.391 | 0.444 | 0.385 |
| D3B-4 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.864 | 0.911 | 0.891 | 0.920 | 0.909 |
| Precision | 0.639 | 0.739 | 0.584 | 0.744 | 0.727 |
| Recall | 0.263 | 0.574 | 0.613 | 0.609 | 0.535 |
| F1 score | 0.508 | 0.630 | 0.598 | 0.658 | 0.593 |
| D3B-20 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.428 | 0.539 | 0.503 | 0.543 | 0.526 |
| Precision | 0.835 | 0.485 | 0.353 | 0.436 | 0.504 |
| Recall | 0.067 | 0.300 | 0.378 | 0.381 | 0.272 |
| F1 score | 0.131 | 0.378 | 0.364 | 0.403 | 0.315 |
| D3-4 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.880 | 0.890 | 0.889 | 0.910 | 0.904 |
| Precision | 0.623 | 0.562 | 0.570 | 0.672 | 0.676 |
| Recall | 0.310 | 0.442 | 0.594 | 0.595 | 0.443 |
| F1 score | 0.334 | 0.472 | 0.581 | 0.625 | 0.476 |
| D3-20 | LR | KNN | DT | RF | XGB |
| Accuracy | 0.451 | 0.458 | 0.466 | 0.489 | 0.487 |
| Precision | 0.765 | 0.230 | 0.292 | 0.332 | 0.413 |
| Recall | 0.102 | 0.162 | 0.299 | 0.316 | 0.165 |
| F1 score | 0.192 | 0.221 | 0.295 | 0.323 | 0.211 |
| D1 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
|---|---|---|---|---|---|---|
| Accuracy | 0.821 | 0.854 | 0.822 | 0.851 | 0.833 | 0.852 |
| Precision | 0.807 | 0.835 | 0.808 | 0.819 | 0.818 | 0.833 |
| Recall | 0.649 | 0.679 | 0.651 | 0.678 | 0.661 | 0.676 |
| F1 score | 0.643 | 0.679 | 0.646 | 0.688 | 0.657 | 0.673 |
| D2A | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.708 | 0.712 | 0.710 | 0.711 | 0.708 | 0.710 |
| Precision | 0.781 | 0.768 | 0.779 | 0.756 | 0.781 | 0.631 |
| Recall | 0.525 | 0.529 | 0.530 | 0.530 | 0.527 | 0.531 |
| F1 score | 0.525 | 0.529 | 0.528 | 0.554 | 0.526 | 0.579 |
| D2 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.707 | 0.707 | 0.707 | 0.708 | 0.705 | 0.707 |
| Precision | 0.780 | 0.780 | 0.781 | 0.765 | 0.779 | 0.756 |
| Recall | 0.527 | 0.524 | 0.524 | 0.525 | 0.525 | 0.525 |
| F1 score | 0.526 | 0.524 | 0.524 | 0.525 | 0.524 | 0.550 |
| D3A-4 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.878 | 0.886 | 0.878 | 0.886 | 0.887 | 0.886 |
| Precision | 0.685 | 0.623 | 0.707 | 0.650 | 0.718 | 0.634 |
| Recall | 0.362 | 0.413 | 0.364 | 0.407 | 0.394 | 0.400 |
| F1 score | 0.469 | 0.442 | 0.447 | 0.440 | 0.453 | 0.459 |
| D3A-20 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.470 | 0.477 | 0.465 | 0.478 | 0.478 | 0.478 |
| Precision | 0.503 | 0.328 | 0.428 | 0.374 | 0.476 | 0.388 |
| Recall | 0.138 | 0.190 | 0.140 | 0.190 | 0.144 | 0.155 |
| F1 score | 0.294 | 0.364 | 0.326 | 0.279 | 0.348 | 0.378 |
| D3B-4 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.885 | 0.888 | 0.884 | 0.889 | 0.888 | 0.889 |
| Precision | 0.769 | 0.654 | 0.704 | 0.644 | 0.704 | 0.677 |
| Recall | 0.379 | 0.385 | 0.369 | 0.404 | 0.383 | 0.399 |
| F1 score | 0.416 | 0.427 | 0.430 | 0.440 | 0.466 | 0.459 |
| D3B-20 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.462 | 0.476 | 0.461 | 0.469 | 0.469 | 0.472 |
| Precision | 0.592 | 0.482 | 0.661 | 0.685 | 0.486 | 0.468 |
| Recall | 0.114 | 0.145 | 0.110 | 0.117 | 0.119 | 0.131 |
| F1 score | 0.249 | 0.311 | 0.235 | 0.243 | 0.322 | 0.338 |
| D3-4 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.890 | 0.895 | 0.890 | 0.895 | 0.895 | 0.895 |
| Precision | 0.820 | 0.751 | 0.826 | 0.705 | 0.725 | 0.726 |
| Recall | 0.369 | 0.395 | 0.369 | 0.406 | 0.401 | 0.403 |
| F1 score | 0.406 | 0.430 | 0.404 | 0.422 | 0.433 | 0.438 |
| D3-20 | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 |
| Accuracy | 0.468 | 0.475 | 0.471 | 0.474 | 0.472 | 0.475 |
| Precision | 0.779 | 0.766 | 0.743 | 0.764 | 0.721 | 0.737 |
| Recall | 0.126 | 0.138 | 0.129 | 0.133 | 0.130 | 0.141 |
| F1 score | 0.116 | 0.127 | 0.119 | 0.122 | 0.118 | 0.129 |
| D1 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.843 | 0.835 | 0.858 | 0.838 | 0.768 | 0.840 | 0.834 | 0.841 | 0.832 | 0.848 |
| Precision | 0.769 | 0.804 | 0.823 | 0.822 | 0.781 | 0.819 | 0.815 | 0.843 | 0.819 | 0.810 |
| Recall | 0.690 | 0.674 | 0.720 | 0.677 | 0.585 | 0.681 | 0.669 | 0.671 | 0.660 | 0.684 |
| F1 score | 0.756 | 0.688 | 0.732 | 0.678 | 0.591 | 0.696 | 0.693 | 0.673 | 0.656 | 0.683 |
| D2A | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.710 | 0.705 | 0.753 | 0.705 | 0.545 | 0.708 | 0.706 | 0.708 | 0.709 | 0.710 |
| Precision | 0.642 | 0.657 | 0.667 | 0.779 | 0.664 | 0.653 | 0.781 | 0.785 | 0.782 | 0.783 |
| Recall | 0.530 | 0.530 | 0.696 | 0.528 | 0.415 | 0.530 | 0.525 | 0.523 | 0.528 | 0.529 |
| F1 score | 0.629 | 0.553 | 0.678 | 0.526 | 0.408 | 0.579 | 0.524 | 0.525 | 0.528 | 0.529 |
| D2 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.708 | 0.705 | 0.746 | 0.707 | 0.539 | 0.707 | 0.702 | 0.703 | 0.705 | 0.708 |
| Precision | 0.708 | 0.757 | 0.671 | 0.750 | 0.671 | 0.685 | 0.779 | 0.783 | 0.780 | 0.781 |
| Recall | 0.525 | 0.521 | 0.684 | 0.526 | 0.402 | 0.527 | 0.520 | 0.517 | 0.525 | 0.527 |
| F1 score | 0.551 | 0.547 | 0.676 | 0.525 | 0.389 | 0.576 | 0.520 | 0.520 | 0.524 | 0.527 |
| D3A-4 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.880 | 0.886 | 0.881 | 0.888 | 0.859 | 0.888 | 0.879 | 0.860 | 0.886 | 0.888 |
| Precision | 0.649 | 0.691 | 0.639 | 0.721 | 0.894 | 0.633 | 0.782 | 0.791 | 0.809 | 0.747 |
| Recall | 0.347 | 0.391 | 0.396 | 0.395 | 0.251 | 0.405 | 0.379 | 0.273 | 0.387 | 0.413 |
| F1 score | 0.387 | 0.428 | 0.445 | 0.476 | 0.257 | 0.462 | 0.386 | 0.268 | 0.419 | 0.440 |
| D3A-20 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.473 | 0.475 | 0.485 | 0.481 | 0.476 | 0.481 | 0.474 | 0.439 | 0.479 | 0.480 |
| Precision | 0.524 | 0.551 | 0.506 | 0.620 | 0.602 | 0.487 | 0.796 | 0.870 | 0.743 | 0.715 |
| Recall | 0.146 | 0.143 | 0.171 | 0.142 | 0.148 | 0.157 | 0.124 | 0.066 | 0.127 | 0.152 |
| F1 score | 0.293 | 0.271 | 0.251 | 0.240 | 0.224 | 0.340 | 0.103 | 0.059 | 0.115 | 0.141 |
| D3B-4 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.884 | 0.885 | 0.883 | 0.887 | 0.860 | 0.889 | 0.877 | 0.861 | 0.888 | 0.889 |
| Precision | 0.648 | 0.630 | 0.658 | 0.670 | 0.834 | 0.661 | 0.758 | 0.806 | 0.738 | 0.690 |
| Recall | 0.374 | 0.391 | 0.385 | 0.377 | 0.262 | 0.409 | 0.386 | 0.282 | 0.380 | 0.421 |
| F1 score | 0.412 | 0.449 | 0.428 | 0.415 | 0.248 | 0.440 | 0.395 | 0.278 | 0.413 | 0.446 |
| D3B-20 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.469 | 0.887 | 0.477 | 0.477 | 0.431 | 0.478 | 0.469 | 0.439 | 0.477 | 0.481 |
| Precision | 0.624 | 0.637 | 0.504 | 0.639 | 0.858 | 0.433 | 0.800 | 0.870 | 0.699 | 0.727 |
| Recall | 0.120 | 0.406 | 0.133 | 0.137 | 0.067 | 0.149 | 0.116 | 0.066 | 0.129 | 0.160 |
| F1 score | 0.120 | 0.436 | 0.258 | 0.203 | 0.043 | 0.339 | 0.100 | 0.059 | 0.117 | 0.146 |
| D3-4 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.885 | 0.892 | 0.886 | 0.896 | 0.865 | 0.896 | 0.885 | 0.868 | 0.894 | 0.896 |
| Precision | 0.734 | 0.663 | 0.737 | 0.718 | 0.838 | 0.701 | 0.796 | 0.802 | 0.716 | 0.770 |
| Recall | 0.346 | 0.404 | 0.399 | 0.413 | 0.251 | 0.406 | 0.372 | 0.301 | 0.395 | 0.428 |
| F1 score | 0.383 | 0.436 | 0.399 | 0.445 | 0.233 | 0.443 | 0.394 | 0.298 | 0.432 | 0.459 |
| D3-20 | ResNet | SNN | AutoInt | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| Accuracy | 0.450 | 0.473 | 0.466 | 0.475 | 0.432 | 0.475 | 0.467 | 0.433 | 0.474 | 0.474 |
| Precision | 0.763 | 0.716 | 0.674 | 0.469 | 0.902 | 0.409 | 0.794 | 0.824 | 0.708 | 0.737 |
| Recall | 0.103 | 0.147 | 0.131 | 0.157 | 0.086 | 0.142 | 0.129 | 0.080 | 0.135 | 0.173 |
| F1 score | 0.103 | 0.134 | 0.125 | 0.147 | 0.053 | 0.135 | 0.114 | 0.067 | 0.124 | 0.146 |
| D1 | D2A | D2 | D3A-4 | D3A-20 | D3B-4 | D3B-20 | D3-4 | D3-20 | |
|---|---|---|---|---|---|---|---|---|---|
| ML | 0.758 | 0.686 | 0.651 | 0.615 | 0.394 | 0.597 | 0.318 | 0.498 | 0.248 |
| Classic NN | 0.664 | 0.557 | 0.529 | 0.452 | 0.332 | 0.440 | 0.283 | 0.422 | 0.122 |
| New NN | 0.685 | 0.548 | 0.536 | 0.397 | 0.204 | 0.392 | 0.182 | 0.392 | 0.115 |
| D3B-4 | DT | RF | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 | ResNet |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.000 | 0.000 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.006 |
| Precision | 0.001 | 0.002 | 0.013 | 0.075 | 0.025 | 0.085 | 0.064 | 0.079 | 0.024 |
| Recall | 0.001 | 0.000 | 0.012 | 0.013 | 0.018 | 0.040 | 0.010 | 0.014 | 0.036 |
| F1 score | 0.001 | 0.001 | 0.010 | 0.008 | 0.016 | 0.027 | 0.008 | 0.012 | 0.034 |
| D3B-4 | FT-Transformer | SNN | NODE | TabNet | GrowNet | DCN-V2 | AutoInt | DeepFM | GBDT + DNN |
| Accuracy | 0.010 | 0.004 | 0.003 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 | 0.004 |
| Precision | 0.057 | 0.063 | 0.115 | 0.007 | 0.077 | 0.032 | 0.011 | 0.095 | 0.103 |
| Recall | 0.058 | 0.026 | 0.029 | 0.011 | 0.008 | 0.020 | 0.003 | 0.014 | 0.020 |
| F1 score | 0.061 | 0.073 | 0.035 | 0.012 | 0.008 | 0.015 | 0.001 | 0.011 | 0.009 |
| D3B-20 | DT | RF | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | MLP-1 | MLP-2 | ResNet |
| Accuracy | 0.000 | 0.000 | 0.003 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.009 |
| Precision | 0.001 | 0.001 | 0.040 | 0.026 | 0.036 | 0.021 | 0.026 | 0.051 | 0.028 |
| Recall | 0.001 | 0.001 | 0.005 | 0.009 | 0.004 | 0.006 | 0.004 | 0.009 | 0.007 |
| F1 score | 0.001 | 0.001 | 0.006 | 0.010 | 0.005 | 0.006 | 0.003 | 0.006 | 0.007 |
| D3B-20 | FT-Transformer | SNN | NODE | TabNet | GrowNet | DCN-V2 | AutoInt | DeepFM | GBDT + DNN |
| Accuracy | 0.007 | 0.002 | 0.001 | 0.002 | 0.001 | 0.002 | 0.001 | 0.001 | 0.001 |
| Precision | 0.045 | 0.018 | 0.070 | 0.048 | 0.037 | 0.053 | 0.061 | 0.039 | 0.029 |
| Recall | 0.011 | 0.023 | 0.014 | 0.012 | 0.009 | 0.008 | 0.004 | 0.006 | 0.010 |
| F1 score | 0.011 | 0.020 | 0.009 | 0.026 | 0.018 | 0.068 | 0.056 | 0.006 | 0.006 |
| D3A-20 | XGB | RF | MLP-2 | CNN-2D-1 | DCN-V2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Original | SMOTE | Original | SMOTE | Original | SMOTE | Original | SMOTE | Original | SMOTE | |
| Accuracy | 0.552 | 0.827 | 0.564 | 0.909 | 0.480 | 0.676 | 0.471 | 0.593 | 0.481 | 0.699 |
| Precision | 0.520 | 0.804 | 0.426 | 0.907 | 0.685 | 0.639 | 0.428 | 0.559 | 0.487 | 0.673 |
| Recall | 0.337 | 0.827 | 0.422 | 0.909 | 0.142 | 0.675 | 0.140 | 0.593 | 0.157 | 0.700 |
| F1 score | 0.385 | 0.811 | 0.444 | 0.908 | 0.195 | 0.647 | 0.326 | 0.561 | 0.340 | 0.677 |
| D2 | LR | RF | MLP-1 | CNN-1D-1 | FT-Transformer | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Original | Near-Miss | Original | Near-Miss | Original | Near-Miss | Original | Near-Miss | Original | Near-Miss | |
| Accuracy | 0.651 | 0.607 | 0.782 | 0.855 | 0.705 | 0.741 | 0.707 | 0.763 | 0.702 | 0.747 |
| Precision | 0.733 | 0.599 | 0.747 | 0.855 | 0.779 | 0.745 | 0.780 | 0.766 | 0.779 | 0.767 |
| Recall | 0.454 | 0.607 | 0.720 | 0.855 | 0.525 | 0.741 | 0.527 | 0.762 | 0.520 | 0.747 |
| F1 score | 0.458 | 0.595 | 0.732 | 0.855 | 0.524 | 0.739 | 0.526 | 0.761 | 0.520 | 0.741 |
| D3B-20 | DT | RF | MLP-2 | CNN-2D-1 | ResNet | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Original | Focal Loss | Original | Focal Loss | Original | Focal Loss | Original | Focal Loss | Original | Focal Loss | |
| Accuracy | 0.503 | 0.499 | 0.543 | 0.545 | 0.472 | 0.478 | 0.461 | 0.468 | 0.469 | 0.467 |
| Precision | 0.353 | 0.332 | 0.436 | 0.448 | 0.468 | 0.717 | 0.661 | 0.647 | 0.624 | 0.420 |
| Recall | 0.378 | 0.379 | 0.381 | 0.377 | 0.131 | 0.134 | 0.110 | 0.132 | 0.120 | 0.122 |
| F1 score | 0.364 | 0.366 | 0.403 | 0.405 | 0.338 | 0.351 | 0.235 | 0.241 | 0.120 | 0.226 |
| Dataset | LR | KNN | DT | RF | XGB | MLP-1 | MLP-2 |
|---|---|---|---|---|---|---|---|
| D1 | <1 s | <1 s | <1 s | <1 s | <1 s | 15 s | 18 s |
| D3-20 | 30 s | 13 s | 4 s | 120 s | 30 s | 50 min | 54 min |
| Dataset | CNN-1D-1 | CNN-1D-2 | CNN-2D-1 | CNN-2D-2 | ResNet | SNN | AutoInt |
| D1 | 23 s | 26 s | 22 s | 26 s | 1 min 20 s | 22 s | 1 min 40 s |
| D3-20 | 1 h 18 min | 1 h 22 min | 1 h 03 min | 1 h 21 min | 4 h 59 min | 1 h 34 min | 4 h 19 min |
| Dataset | GrowNet | NODE | DCN-V2 | FT-Transformer | TabNet | DeepFM | GBDT + DNN |
| D1 | 15 s | 13 s | 19 s | 2 min 30 s | 2 min 14 s | 30 s | 26 s |
| D3-20 | 2 h 03 min | 1 h 35 min | 1 h 28 min | 9 h 21 min | 6 h 01 min | 2 h 50 min | 1 h 44 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Jin, C.-J.; Song, Y.; Li, D. Are Neural Networks Better than Machine Learning? A Comparative Study for Travel Mode Predictions. Systems 2025, 13, 1099. https://doi.org/10.3390/systems13121099
Zhang T, Jin C-J, Song Y, Li D. Are Neural Networks Better than Machine Learning? A Comparative Study for Travel Mode Predictions. Systems. 2025; 13(12):1099. https://doi.org/10.3390/systems13121099
Chicago/Turabian StyleZhang, Tongkai, Cheng-Jie Jin, Yuchen Song, and Dawei Li. 2025. "Are Neural Networks Better than Machine Learning? A Comparative Study for Travel Mode Predictions" Systems 13, no. 12: 1099. https://doi.org/10.3390/systems13121099
APA StyleZhang, T., Jin, C.-J., Song, Y., & Li, D. (2025). Are Neural Networks Better than Machine Learning? A Comparative Study for Travel Mode Predictions. Systems, 13(12), 1099. https://doi.org/10.3390/systems13121099






