Selection and Weight Determination of Factors for Price Adjustment Formulae Based on Bill of Quantities

Abstract

This study investigates the effectiveness of standard price adjustment formulae for construction contracts in Portugal. Price adjustment is a mechanism that aims to adjust contractual values to market price fluctuations in labor, materials, and equipment. Such formulae are often generalized and applied in contractual practices without being properly tailored to the specific characteristics of each project. To fill this gap, this study, informed by convergent proposals, builds on the argument that the use of different bill of quantities (BOQs)-based price adjustment formulae for the same contract is fairer, more equitable, and with greater capacity to cushion sudden variations in prices. Using a case study, consisting of a public construction contract, the study analyses price differences obtained through the application of the standard formula and compares them, over different periods, with those obtained through the use of two alternative calculation formulae specifically developed according to the project’s characteristics. The performance of all scenarios was evaluated against the evolution of the growth rate of the construction cost index (CCI). The results demonstrate that the standard formula, even when it is readjusted, provides disproportionate results. In contrast, the BOQ-based price adjustment formulae, developed according to different phases of the works, provide results that are very close to those obtained by CCI-based escalation. The behavior of these customized formulae, even during periods of high price indices increases, closely tracks that of inflation. The results of the study call for the enactment of a more comprehensive legal mechanism so that all cost elements of a construction project can be properly reflected in price adjustment methodologies.

1. Introduction

Every year, public authorities in the European Union (EU) spend around EUR 2.5 trillion (about 15% of GDP) on goods, services, and works [1]. Construction works constitute a large part of this total, making the construction industry one of the key sectors of the national economy due to its backward and forward linkages with other sectors of the economy [2]. However, the construction industry faces a number of challenges in both economic and technical spheres. Quantification of the construction industry’s resilience is, thus, essential for contributing to the sustainability of the built environment [3]. In the economic sphere, cost overruns have been recognized as one of the main constraints in construction projects in both developed and developing countries alike [4]. Many factors are responsible for cost overruns, one of them, which has been identified, is the upward movement in the prices of construction inputs [5]. As construction works generally take a long time to be carried out (months and/or years), there is a need to analyze whether prices have gone up or down in relation to the values stipulated in the contract. The prices of the most significant materials, labor, and equipment can fluctuate significantly due to various factors, such as inflation, supply chain constraints, or other unpredictable economic factors [6]. To manage this price variation in the costs of the production factors in the course of the works, price escalation clauses have been included in construction contracts, either as mandatory provisions enshrined by law in many national legal systems or as guidelines in professional associations’ standard forms of contracts. A detailed review of price escalation provisions under US-based, UK-based, and international standard forms of contracts is provided in [7]. This contractual mechanism allows the original price of a public or private works contract to be adjusted over time, in an attempt to compensate against the actual costs. Price adjustments of the initial amounts contained in the Payment Schedule are usually carried out on a monthly basis [8]. Without a price adjustment mechanism applied to construction contracts, there would be considerable exposure to excessive unilateral risks right from the bidding stage [9]. On the one hand, a substantial increase in the price of construction inputs could reduce the contractor’s margins significantly, affect the quality of works, lead to the termination of the contract and, ultimately, to the bankruptcy of the company [10,11]. On the other hand, if costs were to decrease dramatically, the contracting entity would overpay and the contractor would make abysmal profits. Moreover, the problem of price volatility in construction materials and components could lead to inflated tender prices on the part of the contractor, with the aim of protecting itself against potential price increases in the course of the works [12,13].

There are two main methods for determining price adjustment in construction contracts: (i) calculation formula, which will be dealt with later in this section and; (ii) index-based escalation, involving the use of indices, such as consumer price index (CPI) or construction price indices. Regarding the latter indices, it is important to clarify two concepts used in the literature [14]: (i) input price indices (also known as construction cost indices—CCI), which measure the evolution of the factors of production (labor, materials, and equipment) used in construction activity, and are usually used for regulating construction contracts and; (ii) output price indices, which tracks the evolution of the prices of the factors of production as well as changes in productivity and contractors’ profit margins. Output price indices are used for deflating construction sector components of nominal gross domestic product, as they track the actual prices paid by the client to the contractor. They are also used for capturing relative price changes in the construction industry for assessments and forecasting of market conditions [15]. Over the years, a considerable amount of research dealing with estimating and/or prediction of construction price indices has been developed. Techniques for predicting construction price indices include time series analyses, regression analyses, and techniques using machine learning algorithms [16]. Elfahham (2019) used traditional approaches and machine learning models, namely artificial neural networks (ANNs), time series, and regression models, with the goal of defining the best model to predict CCI values for concrete structures, based on data on key construction costs prevailing in the Egyptian construction industry [16]. This author concluded that ANN offer the highest accuracy due to their ability to model the complexity and non-linear nature of construction cost data. Dong et al. (2020) [17] proposed a framework based on Long Short-Term Memory (LSTM) to explore the possibility and optimization mechanisms of the algorithm in the area of construction cost index prediction. They found that the LSTM framework has advantages in forecasting CCI when compared with other advanced cost prediction models. Velumani & Nampoothiri (2021) [18] used smoothing techniques and machine learning techniques for forecasting CCI, based on data published by the Indian Construction Industry Development Council (CIDC). They concluded that smoothing techniques provide lower error and higher accuracy when compared with both ANN and support vector machine (SVM) techniques. Some studies have addressed CCI prediction for the highway segment of the construction market. Wang et al. (2025) proposed a hybrid model that combines variational mode decomposition (VMD), LSTM, and gated recurrent unit (GRU), and found that this approach represents a robust and adaptable forecasting tool for highway construction cost indices (HCCIs), capable of handling the multifaceted complexity of these data [19]. The LSTM framework was also used for predicting HCCI [20]. By using Texas HCCI as the raw data, the results were compared to the autoregressive integrated moving average model. The results show that the developed LSTM model outperformed the time series models in terms of providing more accurate prediction in all three forecasting scenarios: short-term, medium-term, and long-term prediction [21]. As pointed out in [14], construction price indices are marred by several uncertainties connected with the accuracy of the pricing and representativeness of the selected goods and of the weighting systems. Other reasons for questioning the accuracy of the indices have to do with changes in procurement routes and growing significance of mechanical, electrical, and telecommunications services, particularly in commercial and service buildings [15]. However, despite its flaws, the input price indices are used for regulating construction contracts and are mainly of interest to contractors [14]. It is worth noting that the indices are usually published by official institutions like national statistical agencies and reputable professional bodies with an established track record in the compilation of price indices, as is the case of Statistics Portugal. This aspect suggests that the input price indices tend to reflect the actual cost changes in construction inputs.

Research on price escalation in construction contracts and their volatility is related to the broader area of cost overruns, which has been extensively investigated over the years [20,22,23]. Zhu (2021) proposed a case-based reasoning (CBR) method for predicting the impact of country-related risks on cost overruns of overseas infrastructure projects [24]. Cost overruns in construction projects were also studied by Amini (2023), who identified poor management of the construction site, inadequate planning, variation in material prices, lack of experience, and poor economic conditions as the main reasons for cost overruns [25]. Lan (2025) describes the following causes for the failure of projects, namely inflation and price fluctuations, corruption, bureaucracy in project licenses and approvals, delays in receiving funds for payment, and use of low-quality materials [26]. These are linked to failure factors related to project execution and management dynamics, existing regulations, quality control requirements, project knowledge and leadership, and environmental challenges [27]. In the case of road projects, there are recommendations for flexible land acquisition policies and simplified compensation procedures, price adjustment mechanisms, and early stakeholder engagement to proactively address regulatory and environmental issues [28]. Some authors pointed out that the use of subcontractors and unskilled workers, delays in payments, economic factors such as inflation, price speculation, delays in ordering materials, delays in the completion of the works, and budget overruns are the most likely risks [29,30]. In contrast, floods, boycotts, landslides, attacks, hurricanes, and tornado hazards are considered rare hazards, with little manifestation. Poor management, application of damaged structural materials during storage, absence of material storage sites on site, lack of skillful operators in devices and equipment, changes in labor and material prices caused by political changes, absence of technical staff, duration of works, and incompatibility of works with change requests, can influence the effectiveness of the cost management practice of construction companies [25,31]. Nassar (2024) mentioned five main risks for delays and cost overruns, namely inflation, price variations (exchange rates, taxes, charges, interest rates on loans), contractor’s inexperience, inadequate planning and management of agreed schedules and the Payment Schedule, and contractor’s financial difficulties [32]. Ling (2021) advocated the adoption of productive technologies that aim to reduce labor dependence, based on empirically quantified project outcomes due to the COVID-19 pandemic, providing guiding insights for similar future events [33]. However, Altalhoni (2025) used an effective model for short-term forecasts in volatile conditions, providing important insights into the economic disturbances observed during the COVID-19 pandemic phase [34].

In Portugal, price adjustment provisions are applied to construction contracts through the calculation formula method, also known in Portugal as the polynomial formula, which has to be previously included in the contract clauses [8]. The standard formulae, similar to those provisioned by the International Federation of Consulting Engineers-FIDIC [35] and Regional Development Banks [36], are composed of coefficients corresponding to the components of labor, most significant materials, and equipment, whose weights represent the proportion of each component in the total cost of the works [37]. These coefficients are associated with published official price indices that reflect market price variations, thus allowing the initial price previously established in the contract to be adjusted to account for these variations [38]. There are specific algorithms that help in the calculation of unknown price indices when these are only known for some cost elements, for example, energy [39]. Tian et al. (2014) treated price escalation parameters using an input–output model and showed how coefficients and indices are used to contemplate price changes [39]. Jezzini (2024), proposed “dynamic” or “improved” models of price adjustment, with more variables and adjustable weightings, that allow comparison with (and criticism of) existing formulae [40]. In the same line, Mishra (2017) pointed out that incorporating accurate price indices in the price adjustment clauses can mitigate inflation risks in construction contracts and advocated for fair risk sharing between the contractor and the client, especially in periods of high inflation [41]. Problems of this order of magnitude are perceived by different stakeholders in a number of countries. This calls for changes to the basic legislation related to contract termination, price adjustment, late claims, performance-based compensation limits, and arbitration [42].

However, one of the common problems concerning price adjustment in contractual practices is how the composition of the calculation formula can be adjusted to the contract in question, as argued by Zhao (2007) [43]. It is common to opt for standard formulae published in legislation, but they are sometimes not the most appropriate ones, because the coefficients corresponding to the weights of labor, materials, and equipment are not the most expressive for specific typologies of works [44,45]. For example, for housing, there is a standard formula with a defined coefficient. If all residential building works use the same formula, it can be assumed that the quantities of materials, labor, and equipment are the same in all these works, as represented in the standard formula for housing, which is not always correct [44]. In other words, slight changes in the coefficients of a price adjustment formula can significantly affect the financial results of a contract. It is, thus, crucial that the contracting parties select adequately the coefficients, as well as their respective weightings, of the price adjustment formulae [46,47]. The lack of flexibility in the use of the formulae can result in a misalignment between actual price increases and the compensation provided through the traditional calculation formula [48]. Kayastha et al. (2023) delved into these issues, describing the impact that the use of unadjusted indices, such as those of unused or omitted materials, can have on price adjustment results [49,50]. The application of a single formula throughout the length of the contract is supported by some authors [51] and opposed by others [52]. However, the use of a single calculation formula does not seem to make sense, since the formulae are envisioned for the average structure of works. For example, a specific material is only used at the beginning of the works, and its corresponding coefficient continues nonetheless to be incorporated in the formula when the material is no longer used in the works [52].

The shortage of labor and the abnormal rise in material prices in the aftermath of COVID-19, partly exacerbated by the conflict in Ukraine, caused severe distortions of several orders of magnitude in the construction market [7]. To tackle this problem, the Portuguese government, through Decree-Law 36/2022 [53], enacted the “Exceptional and Temporary Price Revision” regime, with the ambition to minimize the severe losses incurred by contractors. This diploma was in force, in the first instance, until 31 December 2022, but was extended up to 31 December 2023 through Decree-Law No. 49-A/2023 [54]. The provisions of the aforementioned “Exceptional and Temporary Price Revision” regime were to be applied under certain conditions, but it states in its preamble that “there is widespread recourse to standard price adjustment formulae for public contracts which, by their nature, do not sufficiently reflect the impacts of abnormally intense and rapid variations in the prices of the various factors on the costs of actual and specific works included in the scope of these contracts” [53]. In other words, there were questions about the inadequacy of the standard formulae used in works contracts and whether the price adjustments in force would effectively express the updating of prices informed by market conditions [55].

It is, therefore, crucial to define real strategies that help those involved in the contracting process to work out price adjustment formulae that reflect the characteristics of the works that are the object of the contract, with the ambition of mitigating risks that can significantly affect the financial viability of the project [56]. In this line, this study builds on the argument that the use of different BOQ-based price adjustment formulae for the same contract is fairer, more equitable, and with greater capacity to cushion sudden variations in market prices [55]. Although not frequently used in contractual practices, the development of several price adjustment formulae for the same contract, based on the different phases of the work or on the nature of the various works, is contemplated in Portuguese legislation [37].

The paper represents a significant contribution to the area of construction management in Portugal, for it is, to the best of our knowledge, the first scholarly study concerning this country that presents a comparison between price adjustments obtained by calculation formula and those provided by CCI escalation. Thus, the results of this study might offer practical guidelines for all those involved in the contracting process, particularly in times of high volatility in the building materials market

The remaining part of the text is organized as follows: Section 2 presents the methodology adopted in the study; the results of the study are presented in Section 3; Section 4 analyzes the results and discusses the main findings; and finally, a concluding comment summarizes the results of the study, and some recommendations are put forward.

2. Materials and Methods

The aim of this study is to investigate the effectiveness of the standard price adjustment formula used in Portuguese public contracts and to compare it with two new constructed calculation formulae: (i) one derived from the standard formula and readjusted in a temporal basis according to the phases of the construction works; and (ii) the other formula is constructed from the information drawn from the Payment Schedule and bill of quantities (BOQs), again rearranged on a temporal basis according to the phases of the construction works. The method of analysis was based on the following:

-

A review of published literature on price adjustment mechanisms and publications from international organizations dealing with contractual arrangements of international construction projects.

-

A review of the Portuguese legal framework regarding price adjustment mechanisms and the Public Procurement Code (PPC) [57].

-

Analysis of data on price indices of construction inputs and on the Cost of Construction Index published by Statistics Portugal.

-

A case study consisting of a real construction contract (school building) promoted by a public entity, thus regulated by the PPC, used to show the results of the comparative analysis.

Section 2.1 and Section 2.2 present, respectively, the case study and the scenarios developed for the analysis, and the Portuguese context regarding price adjustment mechanisms.

2.1. Case Study and Scenario Development

The building consists of two floors and a partially underground floor (garage and storage), with a total gross area of 7800 m², with an estimated budget of EUR 11,963,904.30. The tender documents specified the use of the price adjustment formula F03 (see Section 2.2), as described in the Administrative Order No. 1592/2004 (2nd series) of 8 January [44]. Data and information presented by the awarded contractor were used in the calculation of price adjustments, namely those described in the Payment Schedule (

Table A1. Payment Schedule provided by the contractor and approved by the Owner.

Month	Initial Prices (€)	Accumulated Initial Prices (€)
1	139,584.30	139,584.30
2	134,439.90	274,024.20
3	211,222.10	485,246.30
4	520,432.20	1,005,678.40
5	774,664.90	1,780,343.40
6	655,382.90	2,435,726.30
7	450,404.10	2,886,130.40
8	161,012.20	3,047,142.60
9	271,743.50	3,318,886.20
10	513,638.00	3,832,524.20
11	892,814.80	4,725,339.00
12	1,389,964.80	6,115,303.70
13	1,328,868.20	7,444,172.00
14	1,271,894.70	8,716,066.70
15	723,947.50	9,440,014.20
16	609,228.90	10,049,243.10
17	439,928.70	10,489,171.80
18	399,983.60	10,889,155.40
19	541,577.70	11,430,733.20
20	197,136.10	11,627,869.30
21	82,646.70	11,710,516.00
22	56,220.70	11,766,736.70
23	86,819.90	11,853,556.70
24	110,347.60	11,963,904.30

in Appendix A), the respective Work Plan, and the BOQs. The construction works were expected to last 24 months.

Based on this information, the following three different scenarios were proposed for this study:

-

Scenario A—Use of the standard price adjustment formula F03 (provided for in the tender documents).

-

Scenario B—Division of the formula F03 into two new formulae, restructuring the coefficients of the cost elements according to whether they are assigned to the first or second phase of the construction works. The first formula is used for the first seven months of the work and refers to the building’s structural works. The second formula, involving the remaining coefficients not assigned to the first formula, is used for the remaining months of the contract period and refers to the finishing and installation components of the works.

-

Scenario C—Development of two price adjustment formulae based on the Payment Schedule and the bill of quantities (BOQs) [58]. These two formulae correspond to the phases of the work as described for Scenario B.

Each of these scenarios involved the calculations of price adjustments for the following periods, with base dates set two months before the beginning of each period considered in the study:

-

Period 01 (TP01)—April 2022 to March 2024 (base date—February 2022);

-

Period 02 (TP02)—October 2022 to September 2024 (base date—August 2022);

-

Period 03 (TP03)—April 2023 to March 2025 (base date—February 2023).

The time periods considered in this study cover up to March 2025, which coincided with the period in which the most recent data on price indices of construction inputs were available at the time of writing. They also cover the period from February 2022 onwards, in which the great majority of construction materials experienced a considerable increase in prices, which were reflected in the price indices. This striking increase in construction input prices, particularly in material prices, that followed in the period up to November 2022, even gave rise to the enactment of the “Extraordinary and Exceptional Price Revision” regime to mitigate the effects of this price escalation. This regime allowed the possibility of developing new price adjustment formulae for ongoing contracts when the cost of materials represented more than 3% of the contract price and the year-on-year growth rate in the cost of these materials was equal to or higher than 20% [53]. Thus, the consideration of different scenarios, time periods, and calculation formulae in this analysis gives a broad picture of real price situations in the event of crises of considerable price increases. The comparison of the different scenarios in the different periods will establish the conclusions of this study.

2.2. Price Adjustment Mechanisms in Portugal

Decree-Law No. 6/2004 of 6 January, as amended by Decree-Law No. 73/2021 of 18 August [37], which is considered an important instrument of Portuguese law applicable to administrative contracts, sets out the rules for price adjustment of public contracts [8]. This diploma has as its ambition the principle of equity in contractual relations, with the proviso that the economic viability of the works shall not be compromised by changes in economic conditions.

The price adjustment methodology involves some technical complexities, imperfections in the compensation mechanisms, propensity to litigation, and some bureaucracy. However, some of its benefits are also recognized, such as those related to the financial sustainability of companies, reduction in the risk of default (unbalanced contracts have a risk of default or abandonment), transparency, and price predictability for both parties involved in the contract [7]. The most significant provisions contained in Decree-Law No. 6/2004 [8] can be stated as follows:

-

The diploma applies to works contracts, contracts for the supply of goods, and contracts for the provision of services promoted by public entities, when the duration of the contract is expected to be equal to or greater than six months.

-

The principles and methodologies of this legislation are also deemed to be applicable as a reference to large private contracts.

-

It is mandatory for public contracts, striking a balance between the issues related to the financial sustainability of contracting companies and the principles favoring the maintenance of the contract.

-

Three methods for calculating price adjustments are provisioned in the legislation: Calculation Formula, Cost Compensation, and a mix of Formula and Cost Compensation.

-

Consideration of the base date with price indices referring to the month prior to that indicated for the submission of the proposals, and the current date with price indices corresponding to the months to which the measurement of the works refers.

-

Possibility of extraordinary price adjustments of contracts, in very limited cases, when there are significant and unpredictable changes in economic conditions, which make the use of price adjustment formula presented in the contract inadequate.

In turn, Decree-Law No. 73/2021 reinforced, clarified, and adjusted some of the provisions already existing in the former regime, the main ones stated below [37]:

-

Clarification of the conditions for the application of extraordinary revision of contracts by enumerating situations of abnormal and unpredictable changes in which the application of the calculation formulae is deemed to be inadequate.

-

Strengthening the articulation and complementarity with the PPC, ensuring consistency between these two pieces of legislation.

-

Introduction of some provisions of a technical and procedural nature, to reduce bureaucracy and speed up the calculation process, thereby reducing the margin of errors and possible litigation.

The calculation formula method, which is the one used in this study, has the following structure (Equation (1)):

$$\mathrm{P}n=\mathrm{a}\times {\displaystyle \frac{\mathrm{L}n}{\mathrm{L}\mathrm{o}}}+b \times {\displaystyle \frac{\mathrm{M}n}{\mathrm{M}o}}+ b^{\prime }\times {\displaystyle \frac{{\mathrm{M}}^{\prime }n}{{\mathrm{M}}^{\prime }o}}{+ b}^{″}\times {\displaystyle \frac{{\mathrm{M}}^{″}n}{{\mathrm{M}}^{″}o}}+\dots +c \times {\displaystyle \frac{\mathrm{E}n}{\mathrm{E}o}}+d$$

(1)

where

-

“Pn” is the price adjustment factor to be applied to the initial value of the works carried out in month “n”. It is obtained by the sum of the terms, rounded off to six decimal places.

-

“Ln” is the price index of labor for the month to which the price adjustment relates.

-

“Lo” is the same index, but relative to the month prior to that indicated for the submission of proposals.

-

“Mn”, “M′n”, “M″n”, … are the current price indices of the most significant materials for the month to which the price adjustment relates.

-

“Mo”, “M′o”, “M″o”, … are the same indices, but relating to the month prior to that indicated for the submission of proposals.

-

“En” is the price index of the cost of equipment, depending on the type of work, for the month to which the price adjustment relates.

-

“E0” is the same index, but relative to the month prior to that indicated for the submission of proposals.

-

“a”, “b”, “b′”, “b″”, …, c are the coefficients (rounded off to two decimals) corresponding to the estimated proportion of each cost element (labor, materials, and equipment) in the cost structure of the contract price.

-

“d” is a fixed coefficient (0.10) representing the non-adjustable part of the contract price.

In the development of the price adjustment formulae, the sum of the coefficients “a”, “b”, “b′”, “b″”…“c”, and “d” shall be equal to one. Each of these coefficients, to be included in the formulae, must represent a weight of at least 1% of the contract price. The coefficient “a” can be adapted to represent a polynomial with different occupational categories, provided that the weight of each category represents at least 1% of the contract price. The indices Sn and S0, mentioned above, as well as the other indices Mn, M0, … En, and E0 are made up of representative parcels of the various factors of production, and are published by the Portuguese Institute for Public Market, Real Estate, and Construction [59].

Considering that P0n is the initial price for a specific month “n” as specified in the Payment Schedule (Table A1, Appendix A), the corresponding price difference for month “n” payable to the contractor is calculated as follows (Equation (2)):

P1n = P0n × (Pn − 1)

(2)

where

“P1n”—Price difference for the month “n”;

“P0n”—Initial price for the month “n” as specified in the Payment Schedule;

“Pn”—Price Adjustment Factor for the month “n”.

The total price differences and the final contract price (total adjusted prices) payable to the contractor for the duration of the contract are calculated by applying Equations (3) and (4), respectively.

$$\mathrm{PD}={\sum }_{n=1}^{m}P1n$$

(3)

$$\mathrm{AP}={\sum }_{n=1}^{m}P1n +{\sum }_{n=1}^{m}P0n$$

(4)

where

“PD”—total price differences;

“AP”—total adjusted prices (final contract price);

“∑P0n”—total initial prices (initial contract price);

“m”—duration (in months) of the contract.

Price adjustments are only considered for situations in which the price adjustment factor is equal to or greater than 1.01, or when this factor is equal to or lower than 0.99. That is, when Pn is equal to or greater than 1.01, there is an adjustment amount (increase) payable to the contractor in addition to the initial prices. When Pn is equal to or lower than 0.99, there is an adjustment amount (decrease) deducted from the initial prices.

Decree-Law No. 73/2021 also considers the influence of work delay on price adjustment provisions. This diploma states that if there are delays that are attributable to the owner, the Work Plan and the Payment Schedule must be revised for later consideration in price adjustment calculations [37]. However, if the delay is attributable to the contractor, the Pn shall be calculated for the following two situations: (i) one corresponding to the month in which the works would be carried out if the initial Work Plan was followed; and (ii) the other corresponding to the month in which the works were effectively carried out. The Pn to be used in the calculations is the lowest of the two. As regards the consideration of advanced payment for specific materials and/or equipment and its effect on price adjustment, the higher the advanced payment provided, the lower the adjustment amount tends to be.

Administrative Order No. 1592/2004 (2nd series) of 8 January combined with Administrative Order No. 22 637/2004 (2nd series) of 12 October, considers as a whole 23 standard price adjustment formulae, thus defining the weights of the coefficients “a”, “b”, “b′”, “b″”, …, “c”, according to the specificities of each type of work [36,37]. These standard formulae correspond to the following types of work:

• Standard formulae for works prescribed in Administrative Order No. 1592/2004 (2nd series) of 8 January [44]: F01—residential buildings; F02—administrative buildings; F03—school buildings; F04—buildings for the health sector; F05—light rehabilitation of buildings; F06—medium rehabilitation of buildings; F07—deep rehabilitation of buildings; F08—playing fields with changing rooms; F09—exterior arrangements; F10—roads; F11—tunnels; F12—bridges of reinforced or prestressed concrete; F13—reinforced or prestressed concrete viaducts; and F14—uneven crossings of reinforced or prestressed concrete.
• Standard formulae for works prescribed in Administrative Order No. 22637/2004 (2nd series) of 12 October [45]: F15—road repairs; F16—road maintenance; F17—road pavement; F18—reinforced concrete structures; F19—metal structures; F20—electrical installations; F21—water supply and wastewater networks; F22—earth dams; and F23—irrigation and drainage networks.

As an example,

Table 1. Weights and coefficients of the standard price adjustment formula F03.

Coefficient	Weight	Coefficient	Weight	Coefficient	Weight	Coefficient	Weight
a	0.43	b18	0.02	b26	0.01	b43	0.04
b03	0.03	b20	0.05	b29	0.01	b45	0.01
b06	0.03	b23	0.01	b32	0.02	b46	0.05
b09	0.03	b24	0.05	b40	0.04	c	0.02
b10	0.02	b25	0.01	b42	0.02	d	0.10

shows the coefficients and respective weights of the standard price adjustment formula F03 (school buildings).

As already mentioned, Portuguese legislation allows for some flexibility in the use of the standard formulae, or for their consideration when they are omitted in the contract. However, the consideration of changing the weights of the different factors provided for in the standard formulae, in a way to adjust them to the work’s specificities, can be a risky endeavor, especially in very volatile market price conditions [47,60]. Some writers suggest that new technologies, such as BIM can be used to fine-tune the selection and weight determination of factors for price adjustment formulae [61]. Other authors propose the adoption of best practices in the development of specific formulae that can be applied to international engineering contracts [43].

3. Results

3.1. Results from Scenario A

Scenario A involved the use of the standard price adjustment formula F03 mentioned above. The price adjustment factors for the different months of the contract period, and for the three time periods, are calculated as follows (Equation (5)):

$$\begin{array}{cc}\hfill Pn=0.43\times {\displaystyle \frac{\mathrm{L}\left(\mathrm{n}\right)}{\mathrm{L}\left(\mathrm{o}\right)}}& +0.03\times {\displaystyle \frac{\mathrm{M}03\left(\mathrm{n}\right)}{\mathrm{M}03\left(\mathrm{o}\right)}}+ 0.03\times {\displaystyle \frac{\mathrm{M}06\left(n\right)}{\mathrm{M}06\left(\mathrm{o}\right)}}+0.03\times {\displaystyle \frac{\mathrm{M}09\left(n\right)}{M09\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}10\left(n\right)}{M10\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}18\left(n\right)}{M18\left(\mathrm{o}\right)}}\hfill \\ & +0.05\times {\displaystyle \frac{\mathrm{M}20\left(n\right)}{M20\left(\mathrm{o}\right)}}+0.01\times {\displaystyle \frac{\mathrm{M}23\left(n\right)}{M23\left(\mathrm{o}\right)}}+0.05\times {\displaystyle \frac{\mathrm{M}24\left(n\right)}{M24\left(\mathrm{o}\right)}}+0.01\times {\displaystyle \frac{\mathrm{M}25\left(n\right)}{M25\left(\mathrm{o}\right)}}+0.01\times {\displaystyle \frac{\mathrm{M}26\left(n\right)}{M26\left(\mathrm{o}\right)}}\hfill \\ & +0.01\times {\displaystyle \frac{\mathrm{M}29\left(n\right)}{M29\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}32\left(n\right)}{M32\left(\mathrm{o}\right)}}+0.04\times {\displaystyle \frac{\mathrm{M}40\left(n\right)}{M40\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}42\left(n\right)}{M42\left(\mathrm{o}\right)}}+0.04\times {\displaystyle \frac{\mathrm{M}43\left(n\right)}{M43\left(\mathrm{o}\right)}}\hfill \\ & +0.01\times {\displaystyle \frac{\mathrm{M}45\left(n\right)}{M45\left(\mathrm{o}\right)}}+0.05\times {\displaystyle \frac{\mathrm{M}46\left(n\right)}{M46\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{E}\left(n\right)}{\mathrm{E}\left(\mathrm{o}\right)}}+0.10\hfill \end{array}$$

(5)

The different materials’ price indices presented in Equation (4) correspond to the following materials: M03—inert; M06—limestone and granite tiles and stonework; M09—red ceramic products; M10—tiles and mosaics; M18—bulk bitumen; M20—bagged cement; M23—glass; M24—pine wood; M25—special or exotic wood; M26—wood-based products; M29—paints for construction; M32—PVC pipe; M40—thermolacquered aluminum frames; M42—steel piping and plumbing apparatus; M43—steel for reinforced concrete; M45—heavy and light profiles; and M46—products for electrical installations.

Table A2. Price adjustment factors (months 1 to 24) for TP01, TP02, and TP03 of scenario A.

TP	1	2	3	4	5	6	7	8	9	10	11	12
01	1.061594	1.064884	1.058990	1.052860	1.053057	1.060963	1.064297	1.066132	1.066422	1.103009	1.104972	1.104244
02	1.010737	1.011983	1.012069	1.047446	1.049015	1.048467	1.044328	1.042486	1.042741	1.043859	1.042354	1.042358
03	0.995825	0.994206	0.994047	0.995008	0.993940	0.994258	1.006491	1.005378	1.002017	1.041249	1.042785	1.044339
TP	13	14	15	16	17	18	19	20	21	22	23	24
01	1.100233	1.098315	1.098622	1.099734	1.098076	1.098144	1.110912	1.110282	1.106869	1.150425	1.152242	1.153495
02	1.055047	1.054422	1.051463	1.094373	1.096074	1.097269	1.107765	1.110831	1.109249	1.111215	1.113801	1.107970
03	1.053939	1.057132	1.055732	1.057712	1.060446	1.054363	1.051986	1.054271	1.054985	1.074758	1.076243	1.077762

(Appendix A) presents the monthly price adjustment factors (Pn) for the different months of the course of the works and for the three different time periods of this scenario.

Following Equation (2), the procedure for calculating price differences is as follows: each monthly initial price (as presented in the Payment Schedule) is multiplied by the price adjustment factor of the corresponding month presented in Table A2 (Appendix A), taking into account the value of Pn that exceeds the legal threshold of price invariability. The expression (Pn − 1) multiplied by the initial price (P0n) gives the price differences for month n. As can be seen in Table A2, the values of the Pn for the first nine months of TP03 fall within the threshold of price invariability (0.99 < Pn < 1.01). So, for these months of this time period, the contractor is entitled to be paid the initial prices only. Total price differences and total adjusted prices are calculated by applying Equations (3) and (4), respectively. These values and the contract price increase (%) are shown in

Table 2. Total adjusted prices, total price differences, and contract price increase for scenario A.

TP	Total Price Differences (€)	Total Adjusted Prices (€)	Contract Price Increase (%)
01	1,089,583.60	13,053,487.90	9.11%
02	693,306.70	12,657,211.00	5.79%
03	452,003.40	12,415,907.70	3.78%

.

3.2. Results from Scenario B

3.2.1. Price Adjustment Formula for the Building’s Structural Works Phase in Scenario B

For the structural works phase (months 1 to 7), the coefficients b03, b06, b10, b20, b32, b43, and b45 of the materials’ component were considered, and the remaining coefficients of the construction materials’ component of the standard formula were assigned to the formula for the finishing works phase. The combined weight of the coefficients b03, b06, b10, b20, b32, b43, and b45 for the standard formula is 0.20. The proportion of materials’ component in the cost structure of the works, as specified in the standard formula F03, is set up at 0.45. Thus, the procedure for calculating the weights of the coefficients of the formula for the structural phase of the building was as follows: the weights of the corresponding coefficients of the standard formula are multiplied by the factor 0.45/0.20 = 2.25. For example, the weight of the coefficient b03 for the standard formula is 0.03. Then, the weight of the coefficient b03 of the formula for the structural works phase is 0.03×2.25 = 0.068, which is rounded off to 0.07. The rounding off the coefficients is made in a way that the sum of the weights of the coefficients “a” (0.43), “b”, “b′” …, c (0.02), and “d” (0.10) shall be equal to 1 (one).

The price adjustment formula for the building’s structural works phase, developed from the standard formula F03, is given by Equation (6).

$$\begin{array}{cc}\hfill \mathrm{P}n=0.43\times {\displaystyle \frac{L \left(n\right)}{L \left(o\right)}}& +0.07\times {\displaystyle \frac{M03 \left(n\right)}{M03 \left(o\right)}}+0.07\times {\displaystyle \frac{M06\left(n\right)}{M06\left(o\right)}}+0.04\times {\displaystyle \frac{M10\left(n\right)}{M10\left(o\right)}}+0.12\times {\displaystyle \frac{M20\left(n\right)}{M20\left(o\right)}}+0.04\times {\displaystyle \frac{M32\left(n\right)}{M32\left(o\right)}}\hfill \\ & +0.09\times {\displaystyle \frac{M43\left(n\right)}{M43\left(o\right)}}+0.02\times {\displaystyle \frac{M45\left(n\right)}{M45\left(o\right)}}+0.02\times {\displaystyle \frac{E \left(n\right)}{E \left(o\right)}}+0.10\hfill \end{array}$$

(6)

3.2.2. Development of the Price Adjustment Formula for the Building’s Finishing Works Phase in Scenario B

For the finishing works phase, the coefficients b09, b18, b20, b23, b24, b25, b26, b29, b40, b42, and b46 of the materials’ components were considered. These coefficients were not considered in the formula for structural works, except for coefficient b20 (bagged cement). The combined weight of the coefficients b09, b18, b20, b23, b24, b25, b26, b29, b40, b42, and b46 of the standard formula is 0.30. Doing the same procedure as that described in Section 3.2.1, the weights of the corresponding coefficients of the standard formula are multiplied by the factor 0.45/0.30 = 1.50.

The price adjustment formula for the building’s finishing works phase, developed from the standard formula F03, is given by Equation (7).

$$\begin{array}{cc}\hfill \mathrm{P}n=0.43\times {\displaystyle \frac{\mathrm{L}\left(\mathrm{n}\right)}{\mathrm{L}\left(\mathrm{o}\right)}}& +0.04\times {\displaystyle \frac{\mathrm{M}09\left(\mathrm{n}\right)}{\mathrm{M}09\left(\mathrm{o}\right)}}+0.03\times {\displaystyle \frac{\mathrm{M}18\left(n\right)}{\mathrm{M}18\left(\mathrm{o}\right)}}+0.07\times {\displaystyle \frac{\mathrm{M}20\left(n\right)}{M20\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}23\left(n\right)}{M23\left(\mathrm{o}\right)}}+0.07\times {\displaystyle \frac{\mathrm{M}24\left(\mathrm{n}\right)}{M24\left(\mathrm{o}\right)}}\hfill \\ & +0.02\times {\displaystyle \frac{\mathrm{M}25\left(n\right)}{M25\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}26\left(n\right)}{M26\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}29\left(n\right)}{M29\left(\mathrm{o}\right)}}+0.06\times {\displaystyle \frac{\mathrm{M}40\left(\mathrm{t}\right)}{M40\left(\mathrm{o}\right)}}+0.03\times {\displaystyle \frac{\mathrm{M}42\left(\mathrm{t}\right)}{M42\left(\mathrm{o}\right)}}\hfill \\ & +0.07\times {\displaystyle \frac{\mathrm{M}46\left(\mathrm{t}\right)}{M46\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{E}\left(\mathrm{t}\right)}{\mathrm{E}\left(\mathrm{o}\right)}}+0.10\hfill \end{array}$$

(7)

3.2.3. Price Differences, Adjusted Prices, and Contract Price Increase for Scenario B

For the calculation of the price adjustment factors, the formula presented in Equation (6) was used for the first seven months of the work, which corresponds to the structural phase of the building. Equation (7) was used to calculate the Pn for the remaining works of the course of the contract, corresponding to the building’s finishing works phase. The Pn for this scenario is presented in

Table A3. Price adjustment factors (months 1 to 24) for TP01, TP02, and TP03 of scenario B.

TP	1	2	3	4	5	6	7	8	9	10	11	12
01	1.069982	1.075563	1.058543	1.049479	1.054280	1.069873	1.075716	1.072075	1.075484	1.112064	1.116644	1.116561
02	1.019938	1.019484	1.019181	1.063902	1.064842	1.060991	1.055067	1.054492	1.052343	1.054725	1.053924	1.055530
03	0.990545	0.982989	0.986326	0.986833	0.981967	0.979688	0.991377	1.013328	1.009715	1.048004	1.049580	1.053536
TP	13	14	15	16	17	18	19	20	21	22	23	24
01	1.115552	1.118314	1.115994	1.118525	1.117510	1.119279	1.131698	1.129480	1.126217	1.169173	1.170887	1.174707
02	1.067835	1.065770	1.062835	1.105067	1.106687	1.110241	1.120109	1.123247	1.120268	1.121555	1.123176	1.115974
03	1.062609	1.065883	1.063122	1.064496	1.066299	1.058724	1.056469	1.060950	1.060950	1.081277	1.082183	1.085362

(Appendix A). The procedures for calculating price differences, adjusted prices, and contract price increase are the same as those described in Section 3.1. Again, as can be seen in Table A3, the Pn for the months 1, 7, and 9 of the TP03 falls within the threshold of price invariability. The Pn for months 2 to 6 is lower than 0.99; that is, the amounts of price differences for months 2 to 6 are negative and are deductible from the initial prices payable to the contractor in the corresponding months.

Table 3. Total price differences, total adjusted prices and contract price increase for scenario B.

TP	Total Price Differences (€)	Total Adjusted Prices (€)	Contract Price Increase (%)
1	1,246,354.90	13,210,259.20	10.42%
2	838,087.20	12,801,991.50	7.01%
3	478,329.10	12,442,233.40	4.00%

presents total price differences, total adjusted prices, and contract price increase for scenario B.

3.3. Results from Scenario C

Scenario C involved the development of two price adjustment formulae [50], based on the previously agreed Payment Schedule and BOQs, with the weights of the different cost components adjusted to the reality of the works, as suggested by different independent experts [62].

3.3.1. Development of the Price Adjustment Formula for the Building’s Structural Works Phase in Scenario C

For the development of the formula for the structural works (months 1 to 7), the following materials were considered: M03—inert; M09—red ceramic products; M20—bagged cement; and M43—steel for reinforced concrete. For determining the weights of the coefficients representing different cost elements, the following procedures were adopted:

-

Coefficient “a” (labor)—As proposed in [63], the proportion of labor in the cost structure of building’s structural works ranges from 30% to 50%. The structure of the building is simple, in which prefabricated elements are regularly utilized. Thus, the proportion of 30% considered for the cost of labor seems to be acceptable [64].

-

Coefficient “c” (equipment)—The proportion of equipment in the cost structure of building structures ranges from 5% to 15% [65]. A weight of 0.05 for the coefficient “c” was adopted, which is nonetheless greater than that established for the standard formula F03 (0.02);

-

Coefficients “b” (materials)—The estimated values of materials were constructed from data presented in the Payment Schedule and the BOQs, they are as follows: M03 (EUR 297,271.43); M09 (EUR 314,588.21); M20 (EUR 207,801.39); and M43 (EUR 773,482.95). The accumulated initial prices for the first seven months, according to the Payment Schedule, are EUR 2,886,130.40. Taking into account that the sum of the coefficients “a”, “b”, “b′”……, “c”, and “d” shall be equal to 1 (one), the weights of the coefficients corresponding to the materials’ components were determined according to the proportion of each construction material in the total costs of the building’s structural works phase.

Table 4. Cost elements, coefficients, and weights of the price adjustment formula for the building’s structural works phase of scenario C.

Cost Element	Cost Elements Value (€)	Coefficient	Weight
Labor	865,839.12	a	0.30
Inert	292,797.93	b03	0.10
Red ceramic products	315,252.02	b09	0.11
Bagged cement	204,799.81	b20	0.07
Steel for reinforced concrete	774,521.96	b43	0.27
Equipment	144,306.52	c	0.05
Constant	288,613.04	d	0.10
Total (Σ)	2,886,130.40		1

presents the cost elements, coefficients, and weights of the price adjustment formula for the structural works phase of scenario C.

The price adjustment formula for the structural works phase of Scenario C is given by Equation (8).

$$\mathrm{P}\mathrm{n}=0.30\times {\displaystyle \frac{\mathrm{L}\left(\mathrm{n}\right)}{\mathrm{L}\left(\mathrm{o}\right)}}+0.10\times {\displaystyle \frac{\mathrm{M}03\left(\mathrm{n}\right)}{\mathrm{M}03\left(\mathrm{o}\right)}}+0.11\times {\displaystyle \frac{\mathrm{M}09\left(n\right)}{\mathrm{M}09\left(\mathrm{o}\right)}}+0.07\times {\displaystyle \frac{\mathrm{M}20\left(n\right)}{M20\left(\mathrm{o}\right)}}+0.27\times {\displaystyle \frac{\mathrm{M}43\left(n\right)}{M43\left(\mathrm{o}\right)}}+0.05\times {\displaystyle \frac{\mathrm{E}\left(n\right)}{\mathrm{E}\left(\mathrm{o}\right)}}+0.10$$

(8)

3.3.2. Development of the Price Adjustment Formula for the Building’s Finishing Works Phase in Scenario C

For the development of the formula for the finishing phase of the building (months 8 to 24), the following materials were considered for this part of the works: M03—inert; M20—bagged cement; M29—paints for construction; M31—bituminous membrane; M40—thermolacquered aluminum frames; M46—products for electrical installations; M53—piping and accessories for water distribution networks; M54—products based on pre-dosed mineral binders for coatings; M57—thermal and acoustic insulation; and M09—red ceramic products. For determining the weights of the coefficients representing different cost elements, in a manner similar to that described in Section 3.3.1, the following procedures were adopted:

-

Coefficient “a” (labor)—as proposed in [63], the proportion of labor in the cost structure of the works pertaining to the finishing phase of building construction is in a range from 30% to 50%, which depends on the quality level of the works. The finishing of the building is simple, regular, and in which prefabricated elements that are regularly utilized. Thus, the proportion of 40% considered for the cost of labor seems to be reasonable [64];

-

Coefficient “c” (equipment)—the weight of 0.02 was adopted for this coefficient, which is equal to that established for the standard formula F03;

-

Coefficients “b” (materials)—The estimated values of materials were constructed from data presented in the Payment Schedule and the BOQs, they are as follows: M03 (EUR 190,633.25); M20 (EUR 108,933.28); M26 (EUR 172,477.70); M29 (EUR 88,962.18); M31 (EUR 199,711.02); M40 (EUR 290,488.76), M46 (EUR 2,414,687.78), M53 (EUR 83,515.52), M54 (EUR 453,888.68), and M57 (EUR 354,033.17); M03 (EUR 297,271.43); M09 (EUR 314,588.21); M20 (EUR 207,801.39) and; M43 (EUR 773,482.95). The accumulated initial prices from months 8 to 24, as per the Payment Schedule, total EUR 9,077,773.60. It should be noted that for some materials and components, such as HVAC, telecommunications, active safety, fire safety, and centralized management, there are no price indices available in the Portuguese statistical system. These materials were embedded in the heading “Products for electrical installations”. The weights of the coefficients corresponding to the materials’ components were determined according to the same procedure of that described in Section 3.3.1.

Table 5. Cost elements, coefficients and weights of the price adjustment formula for the structural phase of Scenario C.

Cost Element	Cost Element Value (€)	Coefficient	Weight
Labor	3,631,109.44	a	0.4
Inert (floor and wall coverings)	190,633.25	b03	0.02
Bagged cement	108,933.28	b20	0.01
Derived wood (carpentry, furniture)	172,477.70	b26	0.02
Paints for construction	88,962.18	b29	0.01
Bituminous membrane (Asphalt screens)	199,711.02	b31	0.02
Thermolacquered aluminum frames	290,488.76	b40	0.03
Products for electrical installations (Considered: Electricity, telecommunications, Active safety, Fire safety, HVAC, Elevators, Centralized Security Equipment Management) *	2,414,687.78	b46	0.27
Pipes and fittings for water distribution networks (water networks)	83,515.52	b53	0.01
Products based on pre-dosed mineral binders for coatings (wall coatings)	453,888.68	b54	0.05
Products based on pre-dosed mineral binders for coatings (wall coatings)	354,033.17	b57	0.04
Equipment	181,555.47	c	0.02
Constant	907,777.36	d	0.1
Total (Σ)	9,077,773.60		1

(*) All these cost elements were aggregated into the heading “products for electrical installations”.

presents the cost elements, coefficients, and weights of the price adjustment formula for the finishing works phase of Scenario C.

The price adjustment formula for the building’s finishing works of Scenario C is given by Equation (9).

$$\begin{array}{cc}\hfill \mathrm{P}\mathrm{n}=0.40\times {\displaystyle \frac{\mathrm{L}\left(n\right)}{\mathrm{L}\left(\mathrm{o}\right)}}& +0.02\times {\displaystyle \frac{\mathrm{M}03\left(n\right)}{\mathrm{M}03\left(\mathrm{o}\right)}}+0.01\times {\displaystyle \frac{\mathrm{M}20\left(n\right)}{\mathrm{M}20\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}26\left(n\right)}{M26\left(\mathrm{o}\right)}}+0.01\times {\displaystyle \frac{\mathrm{M}29\left(n\right)}{M29\left(\mathrm{o}\right)}}+0.02\times {\displaystyle \frac{\mathrm{M}31\left(n\right)}{M31\left(\mathrm{o}\right)}}\hfill \\ & +0.03\times {\displaystyle \frac{\mathrm{M}40\left(n\right)}{M40\left(\mathrm{o}\right)}}+0.27\times {\displaystyle \frac{\mathrm{M}46\left(n\right)}{M46\left(\mathrm{o}\right)}}+0.01\times {\displaystyle \frac{\mathrm{M}53\left(n\right)}{M53\left(\mathrm{o}\right)}}+0.05\times {\displaystyle \frac{\mathrm{M}54\left(n\right)}{M54\left(\mathrm{o}\right)}}+0.04\times {\displaystyle \frac{\mathrm{M}57\left(n\right)}{M57\left(\mathrm{o}\right)}}\hfill \\ & +0.02\times {\displaystyle \frac{\mathrm{E}\left(n\right)}{\mathrm{E}\left(\mathrm{o}\right)}}+0.10\hfill \end{array}$$

(9)

3.3.3. Price Differences, Adjusted Prices, and Contract Price Increase for Scenario C

For the calculation of the price adjustment factors, the formula presented in Equation (7) was used for the first seven months of the work, which correspond to the building’s structural works. Equation (6) was used to calculate the Pn for the remaining works of the course of the works, corresponding to the building’s finishing works phase. The Pn for this scenario is presented in

Table A4. Price adjustment factors (months 1 to 24) for TP01, TP02, and TP03 of scenario C.

TP	1	2	3	4	5	6	7	8	9	10	11	12
01	1.141469	1.132718	1.072537	1.041621	1.048567	1.088661	1.072994	1.041184	1.044138	1.076176	1.083841	1.083253
02	1.023058	1.003005	0.999667	1.027255	1.026946	1.027723	1.018402	1.039468	1.038140	1.044326	1.045193	1.045355
03	0.990779	0.978362	0.976423	0.978250	0.966743	0.962001	0.971829	1.005952	1.008695	1.039799	1.044685	1.046747
TP	13	14	15	16	17	18	19	20	21	22	23	24
01	1.078248	1.075898	1.074502	1.080825	1.082058	1.082247	1.091279	1.090208	1.093280	1.127086	1.132404	1.134683
02	1.054173	1.053201	1.056078	1.089726	1.094759	1.096871	1.102197	1.105351	1.104893	1.105690	1.105572	1.099812
03	1.051826	1.054981	1.054441	1.054879	1.054826	1.049226	1.051051	1.050240	1.049487	1.073593	1.079096	1.082304

(Appendix A). The procedures for calculating adjusted prices, price differences, and contract price increase are the same as those described in Section 3.1. As can be seen in Table A4, the Pn for the months 1, 8, and 9 of the TP03 falls within the threshold of price invariability, and the Pn for months 2 to 7 is lower than 0.99. That is, the amounts of price differences for the months 2 to 7 are negative. These amounts are deductible to the initial prices payable to the contractor in the corresponding months.

Table 6. Total adjusted prices, total price differences and contract price increase for scenario C.

TP	Total Adjusted Prices (€)	Total Price Differences (€)	Contract Price Increase (%)
1	932,622.20	12,896,526.5	7.80%
2	633,868.20	12,597,772.5	5.30%
3	359,936.70	12,323,841.0	3.01%

presents total price differences, total adjusted prices, and contract price increase for scenario C.

3.4. Calculation of Price Differences by Construction Cost Index-Based Escalation

The construction cost index (CCI) is an important economic tool that tracks costs in the construction industry in Portugal as well as in the European Union [66,67]. In Portugal, this index is published by the Portuguese National Institute of Statistics. It measures the changes in prices of construction inputs (labor, materials, and energy) used in residential building construction. In Portugal, the index is calculated on the basis of the average structure of the works and is published for the total cost, materials cost, and labor cost, with 2021 as the base year [68]. In constructing the total index, the weighting is 56% for materials cost and 44% for labor cost [69].

Table A5. Evolution of construction cost index (CCI): February 2022–March 2025.

Month and Year	CCI	Month and Year	CCI
February 2022	106.49	September 2023	116.85
March 2022	109.69	October 2023	116.37
April 2022	112.67	November 2023	117.6
May 2022	113.13	December 2023	116.8
June 2022	113.12	January 2024	118.89
July 2022	113.98	February 2024	119.4
August 2022	113.62	March 2024	119.21
September 2022	114.43	April 2024	120.08
October 2022	114.59	May 2024	120.4
November 2022	114.81	June 2024	120.58
December 2022	114.79	July 2024	120.31
January 2023	116.13	August 2024	120.95
February 2023	116.4	September 2024	120.7
March 2023	116.55	October 2024	121.22
April 2023	116.19	November 2024	121.52
May 2023	116.29	December 2024	121.7
June 2023	116.36	January 2025	123.03
July 2023	116.39	February 2025	123.02
August 2023	116.33	March 2025	123.68

(Appendix A) presents the evolution of CCI in Portugal for the period from February 2022 to March 2025. Figure 1, Figure 2 and Figure 3 present the evolution of CCI for TP01 (April 2022–March 2024), TP02 (October 2022–September 2024), and TP03 (April 2023–March 2025), respectively. Figure 1 shows that CCI for TP01 (base date–February 2022) increased markedly from 112.67 in April 2022 to 119.21 in March 2024. CCI at the base date was 106.49. Figure 2 shows that CCI for TP02 (base date–August 2022) increased slightly from 114.59 in October 2022 to 116.55 in March 2023, flatlined in the period March 2023–September 2023, followed by a somewhat marked increase between September 2023 and September 2024. CCI at the base date was 113.62. Figure 3 shows that CCI for TP03 (base date–February 2023) remained practically stagnant in the period April 2023–September 2023, increased markedly from 116.85 in September 2023 to 119.21 in March 2024, and then increased slightly to 123.68 in March 2025. However, a steep increase in the last three months of TP03 is apparent. The CCI at the base date was 116.40.

The CCI can also be used for calculating price adjustments for construction contracts. Equation (10) shows how the index of price difference is calculated on the basis of the index for the current date and the index for the base date. The calculation of price differences by this method is given by applying Equation (11), which is similar to Equation (2), in which P1n and P0n have the same meanings as those in Equation (2). The total price differences and total adjusted prices (final contract price) are calculated by applying Equations (3) and (4), respectively.

IPDn = (CCIn/CCIo − 1)

(10)

P1n = P0n × IPDn

(11)

where

“IPDn”—index of price difference for the month “n”;

“CCIn”—construction cost index for the month “n” (current date);

“CCIo”—construction cost index for the base date.

As already mentioned, the base date for TP02 is August 2022, and the base date for TP03 is February 2023. It is worth noting, however, that the average of the indices for February 2022 and March 2022 was taken as the base date for TP01. As can be seen in Table A5 (Appendix A), the CCI increased abnormally in the two-month period February 2022–April 2022 (a growth rate of 5.80%). So, the averaging method was used to smooth the base date for this time period. Some implications of “base effects”, which occur when the base or initial month of a growth rate is unusually low or high, are discussed in [70]. The initial prices of the contract are presented in Table A1. The calculations of the price difference for the month “n” are given by applying Equations (10) and (11). The calculations of price differences for the first month of TP01, TP02, and TP03 are shown here for illustrative purposes:

-

Price difference for April 2022 of TP01

IPDn = (112.67/108.9 − 1) = 0.04237

P0n = EUR 139,584.30

P1n = 139,584.30 × 0.04237 = EUR 5914.19

-

Price difference for October 2022 of TP02

IPDn = (114.67/113.62 − 1) = 0.008537

P0n = EUR 139,584.30

P1n = 139,584.30 × 0.008537 = EUR 1191.66

-

Price difference for February 2023 of TP03

IPDn = (116.19/116.40 − 1) = −0.001804

P0n = EUR 139,584.30

P1n = 139,584.30 × (−0.001804) = EUR −251.83

The total price differences and the final contract price (total adjusted prices) payable to the contractor for the duration of the contract are calculated by applying Equations (3) and (4), respectively.

Table 7. Total price differences, total adjusted prices, and contract price increase by CCI escalation.

TP	Total Price Differences (€)	Total Adjusted Prices (€)	Contract Price Increase (%)
01	853,760.40	12,817,664.70	7.14%
02	376,682.70	12,340,587.00	3.15%
03	285,659.00	12,249,563.30	2.39%

presents total price differences, total adjusted prices, and the contract price increase calculated through CCI-based escalation.

In order to check the robustness of the calculations of the contract price increase for TP01, the average annual growth rate (AAGR) of the index for the period from March 2022 to March 2024 was calculated, based on data reported in [68]. The AAGR was considered because it was assumed that half of the works were carried out in the first year, and the other half of the works occurred in the second year of the contract period. The AAGR is 6.90%, which is close to the figure for TP01 presented in Table 7.

3.5. Summary of Results

This subsection briefly summarizes the results of price adjustments obtained for scenario A, scenario B, and scenario C, analyzed in Section 3.1, Section 3.2 and Section 3.3, as well as those obtained by CCI escalation, analyzed in Section 3.4. The calculations of price adjustments for the three scenarios, as well as those informed by CCI escalation, covered the same three different time periods: TP01 (April 2022–March 2024), TP02 (October 2022–September 2024), and TP03 (April 2023–March 2025). Figure 4 presents the contract price increases for TP01, TP02, and TP03, as well as the averages of TP01, TP02, and TP03 of scenarios A, B, and C, and CCI-based escalation.

In order to quantify the statistical uncertainties of the results (price adjustment factors–Pn), presented in Table A2, Table A3 and Table A4, the margins of error of the mean (24 observations) were calculated at the 95% confidence level for all time periods of scenario A, scenario B, and scenario C (Equation (12)).

MOE = µ ± Z × σ/√n

(12)

where

“MOE”—margin of error;

“µ”—mean;

“Z”—Z-value for the chosen confidence level (1.960);

“σ”—standard deviation;

“n”—number of observations = 24.

For scenario A, the margins of error are 1.0933 ± (1.11%), 1.0645 ± (1.31%), and 1.0350 ± (1.19%) for TP01, TP02, and TP03, respectively. For scenario B, the margins of error are 1.1064 ± (1.31%), 1.0757 ± (1.30%), and 1.0369 ± (1.45%) for TP01, TP02, and TP03, respectively. For scenario C, the margins of error are 1.0862 ± (1.31%), 1.0586 ± (1.36%), and 1.0282 ± (1.52%) for TP01, TP02, and TP03, respectively. Thus, the margins of error of all scenarios, and for all time periods are lower than 2%, which is considered good.

4. Analysis of Results and Discussion

The three price adjustment formulae corresponding to the three scenarios were developed in compliance with the provisions stated in Portuguese law. A real example of a construction contract was used to show price adjustment behaviors for three time periods. These time periods (TP01, TP02, and TP03), each lasting two years and separated by six months to cover changing market situations, spanned the period from April 2022 to March 2025. The approach adopted in this study, based on information drawn from the contract documents, namely, the Payment Schedule and BOQs, is similar to the one developed by Sharma (2016) [71]. Price differences in the contract value were also calculated through CCI-based escalation for the same three time periods, using the monthly indices published by Statistics Portugal. The choice of CCI instead of the most well-known consumer price index (CPI) is that the latter, which tracks changes in the prices of consumer goods and services paid by consumers over time, is not considered an adequate measure of price movements in construction inputs [72].

TP01 coincided with a high inflationary period across different sectors of the economy, which started in March 2022 and continued up to the first semester of 2023, which was spearheaded by rocketing energy prices and supply chain constraints derived from the conflict between Russia and Ukraine [73]. This was reflected in a high increase in construction materials, labor, and equipment prices [74,75]. 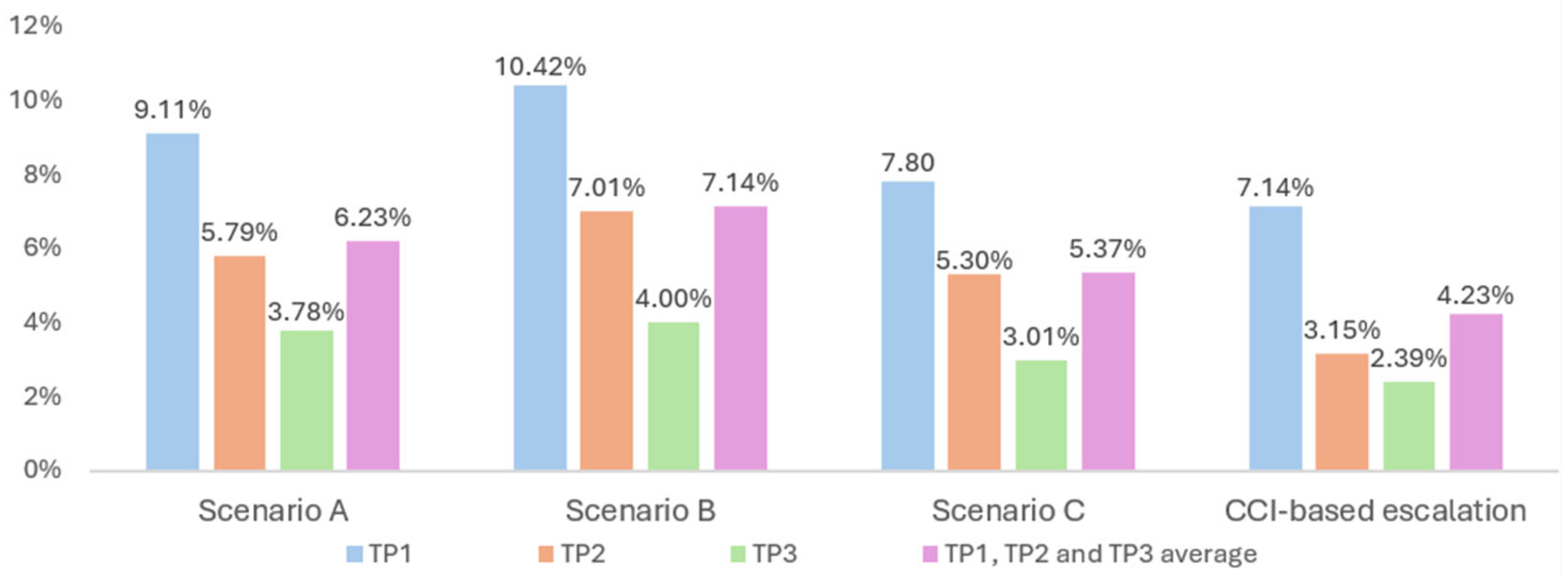As can be seen in Table A5, construction inputs (particularly construction materials) experienced a considerable increase in the period between March 2002 up to February 2023, flatlined through 2023, and increased slightly from February 2023 onwards, hovering around a 3% annualized growth rate. Thus, it is not surprising that TP01 was the period in which the increase in the contract price for all scenarios was most pronounced. As shown in Figure 4, for TP01, the contract price for scenarios A, B, C, and CCI-based escalation increased by 9.11%, 10.42%, 7.80%, and 7.14%, respectively. For TP03, in the same order as that of TP01, the contract price increase were 3.78%, 4.00%, 3.01%, and 2.39%, respectively. Figure 4 also shows that the averages of contract price increase in TP01, TP02, and TP03 were 6.23%, 7.14%, 5.37%, and 4.23% for scenarios A, B, C, and CCI-based escalation, respectively. That is, the average contract price increase for scenario A is 47.3% higher than that informed by CCI escalation. The average contract price increase for scenario B is 68.8% higher than that informed by CCI escalation. The average contract price increase for scenario C is 27.0% higher than that informed by CCI escalation. However, for TP01, the contract increase for scenario C is only 9.24% higher than that of CCI-based escalation.

In general, all scenarios, as well as those calculated through CCI-based escalation, experienced similar patterns of variation in contract price increase amongst the three time periods analyzed. However, scenario B provided the highest contract price increase for all three time periods, while the lowest increase, again for all time periods, occurred in scenario C. The contract price increase informed by CCI escalation, for all time periods, was lower than those for all the scenarios, but close to those obtained for scenario C. These results keep up with those of Kayastha (2024), who pointed out that several mistakes regarding price adjustment clauses are made by both parties involved in the contracting process, such as the use of standard formulae that are not adjusted to the reality of the works [49]. According to Lederer (2024), who used an ARIMA model for price escalation forecasting, price adjustments calculated by calculation formula, broken down according to different phases of works, contribute to a fairer risk attribution [10,43], a situation that seems to be reflected in scenario C. The results provided here, however, suggest that by merely breaking down calculation formulae according to different phase of the works, while maintaining the coefficients of the standard formulae and readjusting their weights at the same time, can provide disproportionate price adjustments, a situation that seems to be manifested in scenario B. The calculation formula for scenario C, in which the selection of factors and weight determination were informed by the Payment Schedule and BOQs seemed to be the most adequate and adjusted to the reality of the works [62,76]. This approach is consistent with the idea that each construction project is unique, and that calculation formulae reflecting more realistic cost elements [76] and correct weights tend to be more accurate [52,77]. The results also revealed that, in situations of risinge and falling (or the reverse) price indices of construction inputs, the monthly price differences are reflected in the final contract price of scenario C in a way very similar to that calculated through CCI-based escalation (TP01 and TP03). On the contrary, in situations of relative volatility in the price indices, the final contract price of scenario C is less convergent with that informed by CCI escalation (TP02). However, a note of caution is needed regarding the use of CCI for calculating price escalation. The index used in the calculation was that for the total, although the indices of materials and labor costs are also reported in [68]. In situations of high price volatility, particularly that of energy-intensive construction materials, price differences calculated by CCI-based escalation may not reflect the true characteristics of the works.

This study has limitations. For all the scenarios analyzed, the calculation formulae do not completely reflect the reality of the works in question, as there are a number of very expressive materials such as HVAC systems, fire safety measures, telecommunications, centralized management, and elevators, among others, whose corresponding coefficients are not included in the price adjustment formulae. Kamran Hafeez (2014) pointed out that standard price adjustment formulae are limited to a few construction parameters and recommended the inclusion of parameters related to energy (as in the case of international civil engineering contracts), since this is a resource with recurrent price fluctuations [6]. The construction materials mentioned above, combined, represented about 25% of the total value of the contract, but there are no specific coefficients for these presumed cost elements. For this study, in scenario C, the coefficients corresponding to these materials’ components were embedded, in coefficient b46 (products for electrical installations); however, this aspect might have brought some distortions in the effective and functional values expected for price adjustments. Another limitation has to do with the index used in the calculation of price adjustments. The CCI values reported in [68] refer to the new residential housing segment of the construction market. Refining the weighting of construction materials and labor costs for constructing the index for the total could possibly provide more accurate results.

5. Conclusions and Recommendations

This study involved the use of a real construction contract, whose expected duration was 24 months, to show price adjustment behaviors across three different scenarios (A, B, and C), which were developed based on the Payment Schedule, Work Plan, BOQs, and the standard calculation formula presented in the contract documents [71]. The analysis of these different scenarios, as well as that informed by CCI escalation, was tested in three different time periods to simulate different market conditions [78]. These different periods allowed a greater perception of the different market price fluctuations, which were translated into rises and falls of price indices, and ultimately reflected in the price adjustment values of the contract. For the different time periods considered, the different scenarios, as well as CCI-based escalation, revealed similar patterns of variation in contract price increase. For different time periods, the results for scenario A are higher than those of scenario C, and those of scenario B are the highest values obtained amongst all the scenarios. The results also revealed that the contract price increases in scenario C, for all three time periods considered, were close to those informed by CCI escalation, whereas the contract price increases in the latter were much lower than those of scenarios A and B. These results suggest that the calculation formula for scenario C (developed on the basis of the budget and BOQs, according to different phases of the works) is the one that better captures the reality of the works. These results are in line with those reported in [79], especially when the coefficients’ weights accurately reflect in the proportion of each cost element in the overall cost structure [71].

The variations in the price indices of the different components of construction inputs (labor, materials, and equipment) are often more pronounced than that of inflation measured by CPI [80]. This may represent a novel pattern in the costs of construction inputs, which, in the case of labor cost, may be partly explained by recurrent labor shortage. However, even with readjusted formulae, the price adjustments obtained by the calculation formula respond directly to immediate rises in the inflation rate, but the same does not happen with sudden falls, whose effects are translated more slowly in the price indices, as is the case of TP02.

The results of the study also suggest that a better approach for calculating price escalation in construction contracts would be the development of three price adjustment formulae for the same contract, namely for structural works, finishing works, and installation works. Regarding installation components, the standard formula contains coefficients for water networks and electrical installations only, which demonstrates the inexistence of a formula suitable for all situations [81]. Telecommunications, air conditioning, centralized management, elevators (electromechanical installations), and fire safety, among others, are not represented in the standard formula. These materials often represent a significant proportion of the cost structure in total building construction works, particularly in modern commercial and service buildings. Thus, the results of the study call for amendments to national legislation concerning price adjustment regimes, by introducing new calculation formulae (or by amending the existing ones) that better capture the characteristics of different typologies of works [82].

As a final contribution, the study calls for the development of material price indices for specific infrastructure typologies, to be published monthly specifically for price adjustment purposes. This would reflect the growing importance of electrical and mechanical services in modern building markets. With such data, it would be possible to develop three or more calculation formulas for the same contract, instead of two, as developed in the study. Price adjustments obtained by these calculation formulae, based on BOQs, would then be compared with those based on CCI escalation. We believe that this would be of interest to all stakeholders involved in the contracting process.