Advancing Digital Project Management Through AI: An Interpretable POA-LightGBM Framework for Cost Overrun Prediction
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Pelican Optimization Algorithm
3.2. Light Gradient Boosting Machine (LGBM)
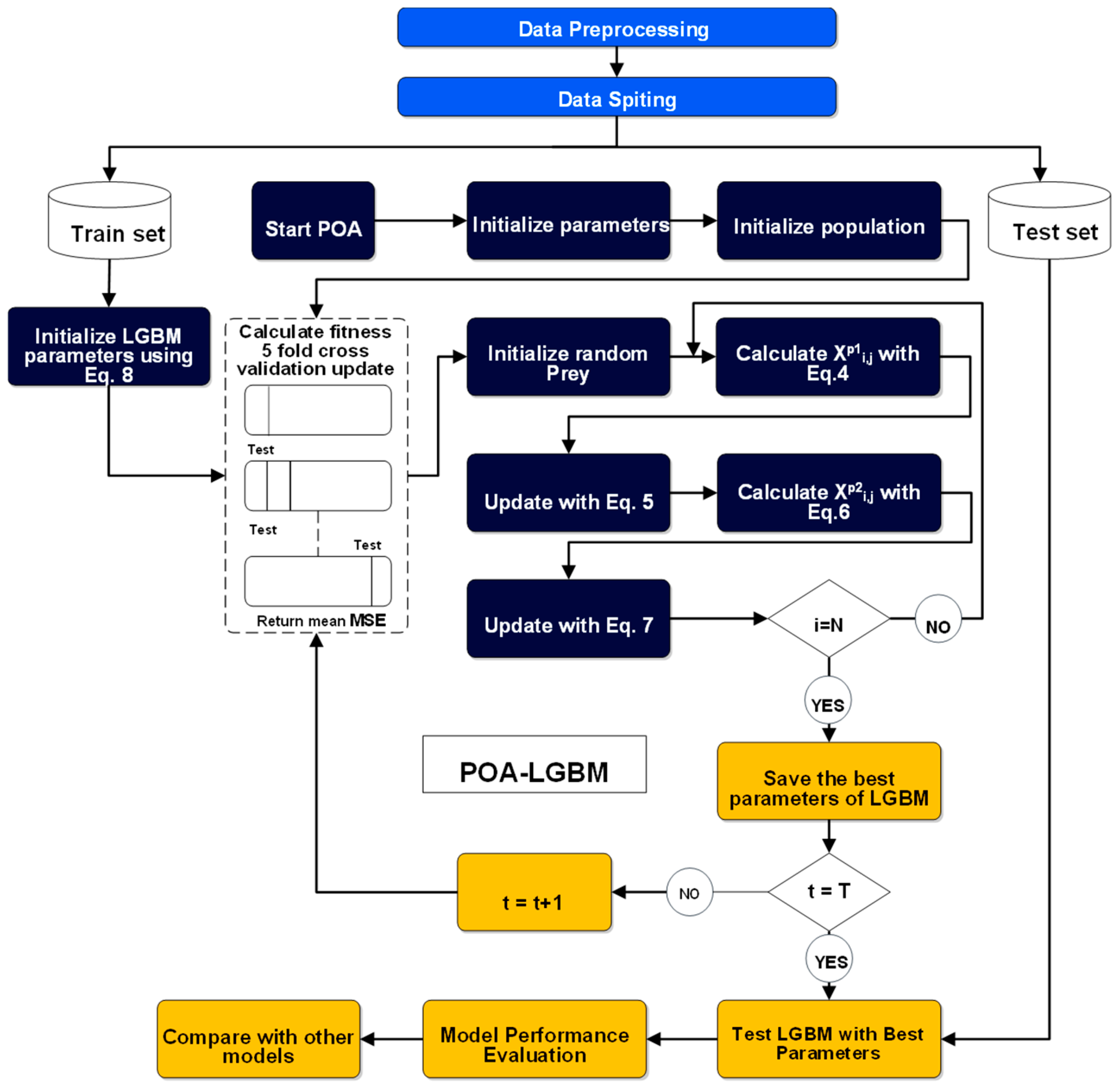
3.3. Proposed Framework
3.3.1. Data Partitioning and Initialization
3.3.2. POA for Hyperparameter Tuning
- Initialization: The POA process begins by initializing a population of pelicans, where each pelican represents a candidate solution. Each candidate solution corresponds to a unique set of LGBM hyperparameters. The positions of the pelicans are randomly initialized within predefined search boundaries for each hyperparameter. Also, the LGBM model is initialized using Equation (8).
- Fitness Evaluation: The fitness of each pelican (each set of hyperparameters) is evaluated using a fitness function. This function trains an LGBM model on the training data using the specified hyperparameters and calculates the model’s performance. In the proposed framework, the fitness of pelicans is measured by Mean Squared Error (MSE) through a 5-fold cross-validation procedure. Cross-validation ensures a robust and generalizable fitness score by mitigating the risk of overfitting to a specific subset of the training data. The objective is to minimize this error metric.
- Population Update: The POA iteratively updates the positions of the pelicans through two primary phases, mirroring pelican hunting strategies:
- ○
- Moving Towards Prey (Exploration Phase): In this phase, pelicans explore the search space to locate promising areas (prey). The position of each pelican is updated based on the location of randomly selected prey, as described by the POA’s mathematical model (Equation (4)). Afterwards, the update rule in Equation (5) is adopted if the new position is better or worse.
- ○
- Winging on the Water Surface (Exploitation Phase): Once a promising region is identified, pelicans exploit the area to converge on the best solution. This phase involves a more localized search around the current best solutions to refine the hyperparameter values (Equation (6)). Afterwards, the update rule in Equation (7) is adopted if the new position is better or worse.
- Iteration and Termination: The fitness evaluation and population update steps are repeated for a predetermined number of iterations (T). Throughout this process, the algorithm records the best set of hyperparameters found so far (best solution). The iterative process terminates when the maximum number of iterations is reached.
3.3.3. Final Model Training and Evaluation
3.4. Data
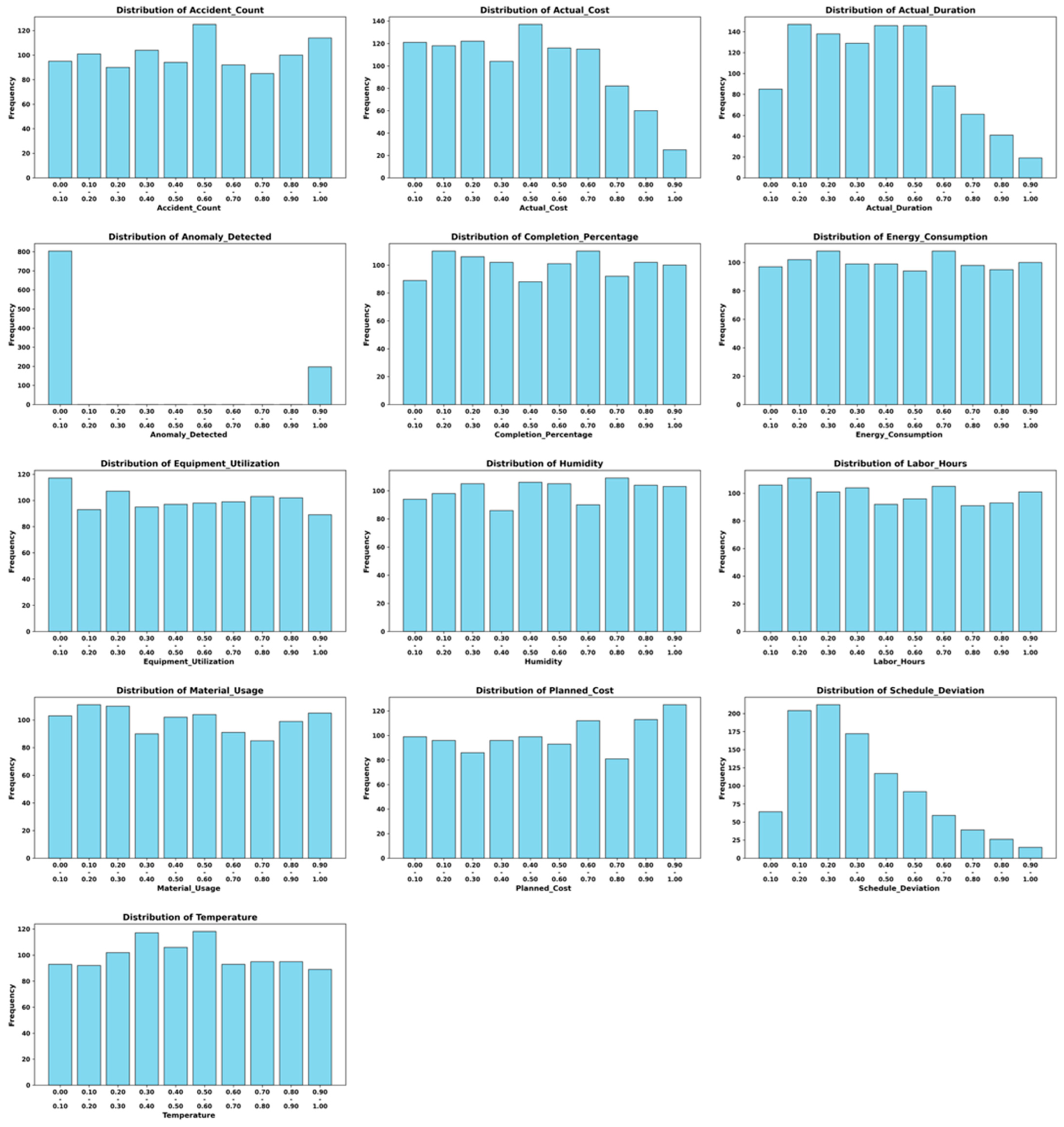
3.4.1. Dataset Description
3.4.2. Data Characteristics and Feature Selection
3.4.3. Data Preprocessing and Transformation
3.4.4. Feature Scaling and Normalization
3.5. Evaluation Metrics
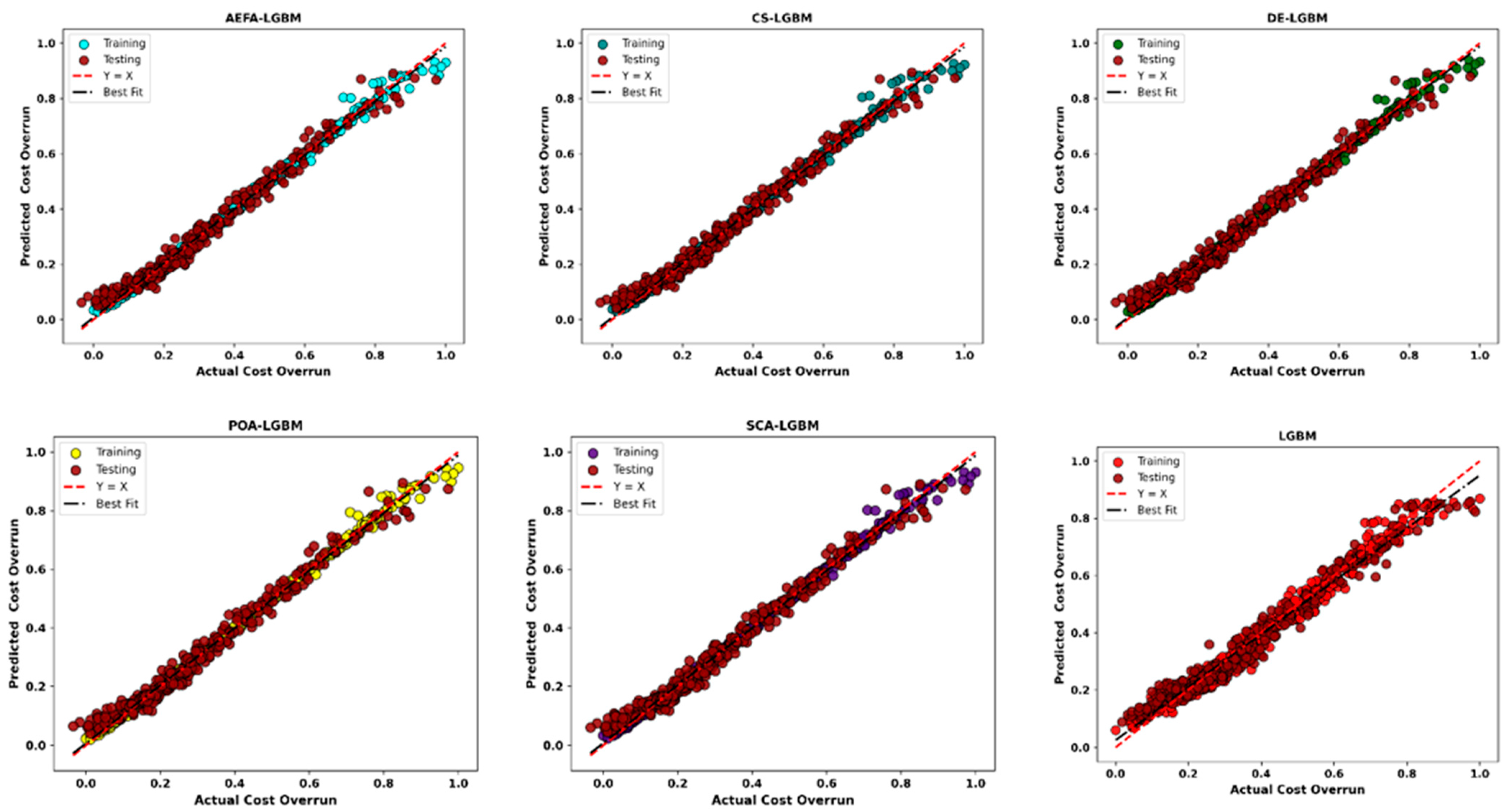
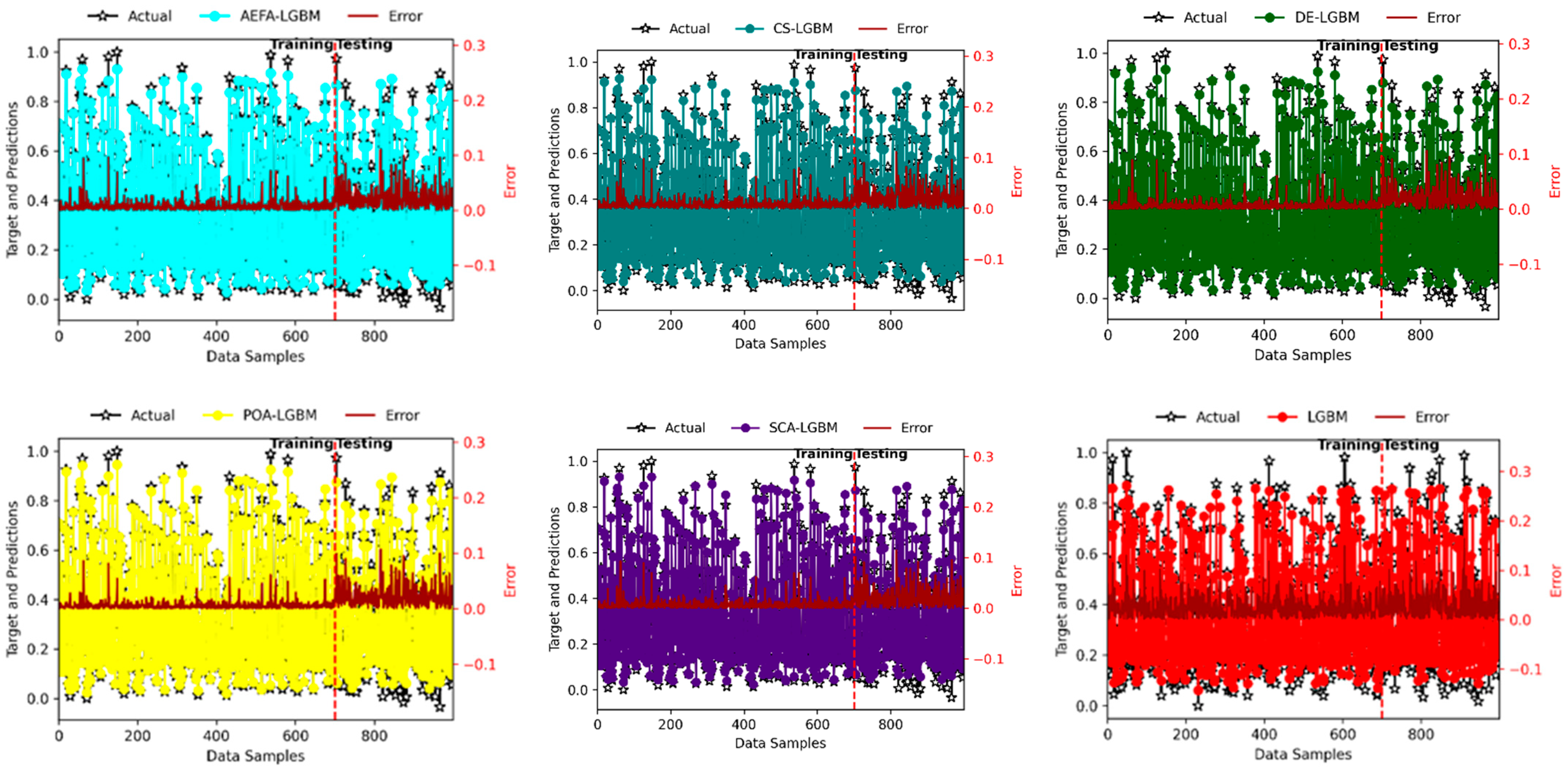
4. Experimental Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atkinson, R. Project management: Cost, time and quality, two best guesses and a phenomenon, its time to accept other success criteria. Int. J. Proj. Manag. 1999, 17, 337–342. [Google Scholar] [CrossRef]
- Bryde, D.J.; Brown, D. The Influence of a Project Performance Measurement System on the Success of a Contract for Maintaining Motorways and Trunk Roads. Proj. Manag. J. 2004, 35, 57–65. [Google Scholar] [CrossRef]
- Ahiaga-Dagbui, D.D.; Smith, S.D. Dealing with construction cost overruns using data mining. Constr. Manag. Econ. 2014, 32, 682–694. [Google Scholar] [CrossRef]
- Osei-Asibey, D.; Ayarkwa, J.; Baah, B.; Afful, A.E.; Anokye, G.; Nkrumah, P.A. Impact of time-based delay on public-private partnership (PPP) construction project delivery: Construction stakeholders’ perspective. J. Financ. Manag. Prop. Constr. 2024, 30, 88–110. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Liu, J.; Zhou, C. Investors’ exit timing of PPP projects based on escalation of commitment. PLoS ONE 2021, 16, e0253394. [Google Scholar] [CrossRef]
- Love, P.E.D.; Sing, M.C.P.; Ika, L.A.; Newton, S. The cost performance of transportation projects: The fallacy of the Planning Fallacy account. Transp. Res. Part. A Policy Pract. 2019, 122, 1–20. [Google Scholar] [CrossRef]
- Melaku Belay, S.; Tilahun, S.; Yehualaw, M.; Matos, J.; Sousa, H.; Workneh, E.T. Analysis of Cost Overrun and Schedule Delays of Infrastructure Projects in Low Income Economies: Case Studies in Ethiopia. Adv. Civ. Eng. 2021, 2021, 4991204. [Google Scholar] [CrossRef]
- Terrill, M.; Emslie, O.; Moran, G. The Rise of Mega-Projects: Counting the Costs. 2020. Available online: https://trid.trb.org/View/1756433 (accessed on 16 September 2025).
- Kadiri, D.S.; Onabanjo, B.O. Cost and Time Overruns in Building Projects Procured Using Traditional Contracts in Nigeria. J. Sustain. Dev. 2017, 10, p234. [Google Scholar] [CrossRef]
- Andrić, J.M.; Lin, S.; Cheng, Y.; Sun, B. Determining Cost and Causes of Overruns in Infrastructure Projects in South Asia. Sustainability 2024, 16, 11159. [Google Scholar] [CrossRef]
- Flyvbjerg, B.; Holm, M.S.; Buhl, S. Underestimating Costs in Public Works Projects: Error or Lie? J. Am. Plan. Assoc. 2002, 68, 279–295. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Yoon, S.; Weidner, T.J.; Hastak, M. Purdue Index for Construction Analytics: Prediction and Forecasting Model Development. J. Manag. Eng. 2021, 37, 04021052. [Google Scholar] [CrossRef]
- Coffie, G.H.; Cudjoe, S.K.F. Toward predictive modelling of construction cost overruns using support vector machine techniques. Cogent Eng. 2023, 10, 2269656. [Google Scholar] [CrossRef]
- Plebankiewicz, E. Model of Predicting Cost Overrun in Construction Projects. Sustainability 2018, 10, 4387. [Google Scholar] [CrossRef]
- ForouzeshNejad, A.A.; Arabikhan, F.; Aheleroff, S. Optimizing Project Time and Cost Prediction Using a Hybrid XGBoost and Simulated Annealing Algorithm. Machines 2024, 12, 867. [Google Scholar] [CrossRef]
- Shreena Global Construction Futures. Oxford Economics 2023. Available online: https://www.oxfordeconomics.com/resource/global-construction-futures/ (accessed on 16 September 2025).
- Shamim, M.M.I.; Hamid, A.B.B.A.; Nyamasvisva, T.E.; Rafi, N.S.B. Advancement of Artificial Intelligence in Cost Estimation for Project Management Success: A Systematic Review of Machine Learning, Deep Learning, Regression, and Hybrid Models. Modelling 2025, 6, 35. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (accessed on 5 September 2025).
- Anonto, H.Z.; Hossain, M.I.; Momo, M.; Shufian, A.; Kumar Roy, A.; Ashraf, M.S.; Islam, R. Optimizing Energy Consumption Prediction Using Hybrid LightGBM and XGBoost: Integrating Heterogeneous Data for Smart Grid Management. In Proceedings of the 2025 IEEE Region 10 Symposium (TENSYMP), Christchurch, New Zealand, 10 July 2025; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, J.; Mucs, D.; Norinder, U.; Svensson, F. LightGBM: An Effective and Scalable Algorithm for Prediction of Chemical Toxicity-Application to the Tox21 and Mutagenicity Data Sets. J. Chem. Inf. Model. 2019, 59, 4150–4158. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Duan, S.; Huang, S.; Bu, W.; Ge, X.; Chen, H.; Liu, J.; Luo, J. LightGBM Low-Temperature Prediction Model Based on LassoCV Feature Selection. Math. Probl. Eng. 2021, 2021, 1776805. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, S.; Du, X.; Wan, X.; Lu, Z.; Wu, J. Lidom: A Disease Risk Prediction Model Based on LightGBM Applied to Nursing Homes. Electronics 2023, 12, 1009. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, W.; Wang, K.; Song, J. Application of LightGBM Algorithm in the Initial Design of a Library in the Cold Area of China Based on Comprehensive Performance. Buildings 2022, 12, 1309. [Google Scholar] [CrossRef]
- Budak, İ. Prediction of Water Quality’s pH value using Random Forest and LightGBM Algorithms. MEMBA Su Bilim. Derg. 2025, 11, 42–49. [Google Scholar] [CrossRef]
- Xi, X. The role of LightGBM model in management efficiency enhancement of listed agricultural companies. Appl. Math. Nonlinear Sci. 2023, 9, 1–14. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Y.; Zhao, Y. LightGBM: An Effective miRNA Classification Method in Breast Cancer Patients. In Proceedings of the 2017 International Conference on Computational Biology and Bioinformatics, in ICCBB ’17, Newark, NJ, USA, 18–20 October 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 7–11. [Google Scholar] [CrossRef]
- Li, S.; Jin, N.; Dogani, A.; Yang, Y.; Zhang, M.; Gu, X. Enhancing LightGBM for Industrial Fault Warning: An Innovative Hybrid Algorithm. Processes 2024, 12, 221. [Google Scholar] [CrossRef]
- Shirali, M.; Hatamiafkoueieh, J.; Razoumny, Y.; Olegovich, D.D. Accuracy enhancement in land subsidence prediction using lightgbm and metaheuristic optimization. Earth Sci. Inf. 2025, 18, 435. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf (accessed on 5 September 2025).
- Janizadeh, S.; Thi Kieu Tran, T.; Bateni, S.M.; Jun, C.; Kim, D.; Trauernicht, C.; Heggy, E. Advancing the LightGBM approach with three novel nature-inspired optimizers for predicting wildfire susceptibility in Kauaʻi and Molokaʻi Islands, Hawaii. Expert. Syst. Appl. 2024, 258, 124963. [Google Scholar] [CrossRef]
- Nazier, M.M.; Gomaa, M.M.; Abdallah, M.M.; Sayed, A. Arabic Sentiment Analysis Using Optuna Hyperparameter Optimization and Metaheuristics Feature Selection to Improve Performance of LightGBM. Int. J. Adv. Comput. Sci. Appl. 2025, 16, 553. [Google Scholar] [CrossRef]
- Akinola, I.T.; Sun, Y.; Adebayo, I.G.; Wang, Z. Daily peak demand forecasting using Pelican Algorithm optimised Support Vector Machine (POA-SVM). Energy Rep. 2024, 12, 4438–4448. [Google Scholar] [CrossRef]
- Al mnaseer, R.; Al-Smadi, S.; Al-Bdour, H. Machine learning-aided time and cost overrun prediction in construction projects: Application of artificial neural network. Asian J. Civ. Eng. 2023, 24, 2583–2593. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Vu, Q.-T.; Gosal, F.E. Hybrid deep learning model for accurate cost and schedule estimation in construction projects using sequential and non-sequential data. Autom. Constr. 2025, 170, 105904. [Google Scholar] [CrossRef]
- Elmasry, N.H.; Elshaarawy, M.K. Hybrid metaheuristic optimized Catboost models for construction cost estimation of concrete solid slabs. Sci. Rep. 2025, 15, 21612. [Google Scholar] [CrossRef] [PubMed]
- Coffie, G.H.; Cudjoe, S.K.F. Using extreme gradient boosting (XGBoost) machine learning to predict construction cost overruns. Int. J. Constr. Manag. 2024, 24, 1742–1750. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Nejati, H.R.; Mohammadi, M. Optimized machine learning modelling for predicting the construction cost and duration of tunnelling projects. Autom. Constr. 2022, 139, 104305. [Google Scholar] [CrossRef]
- Doulabi, R.Z. A Hybrid Machine Learning and Metaheuristic Framework for Optimizing Time and Cost in Hospital Construction Projects. Int. J. Intell. Syst. Appl. Eng. 2025, 13, 385–394. [Google Scholar]
- Han, K.; Wang, T.; Liu, W.; Li, C.; Xian, X.; Yang, Y. Construction cost prediction model for agricultural water conservancy engineering based on BIM and neural network. Sci. Rep. 2025, 15, 24271. [Google Scholar] [CrossRef]
- Almahameed, B.A.; Bisharah, M. Applying Machine Learning and Particle Swarm Optimization for predictive modeling and cost optimization in construction project management. Asian J. Civ. Eng. 2024, 25, 1281–1294. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Mahmoudzadeh, A.; Amiri-Ramsheh, B.; Atashrouz, S.; Abedi, A.; Abuswer, M.A.; Ostadhassan, M.; Mohaddespour, A.; Hemmati-Sarapardeh, A. Modeling CO2 solubility in water using gradient boosting and light gradient boosting machine. Sci. Rep. 2024, 14, 13511. [Google Scholar] [CrossRef]
- Sun, X. Application of an improved LightGBM hybrid integration model combining gradient harmonization and Jacobian regularization for breast cancer diagnosis. Sci. Rep. 2025, 15, 2569. [Google Scholar] [CrossRef] [PubMed]
- BIM-AI Integrated Dataset. Available online: https://www.kaggle.com/datasets/ziya07/bim-ai-integrated-dataset (accessed on 4 September 2025).
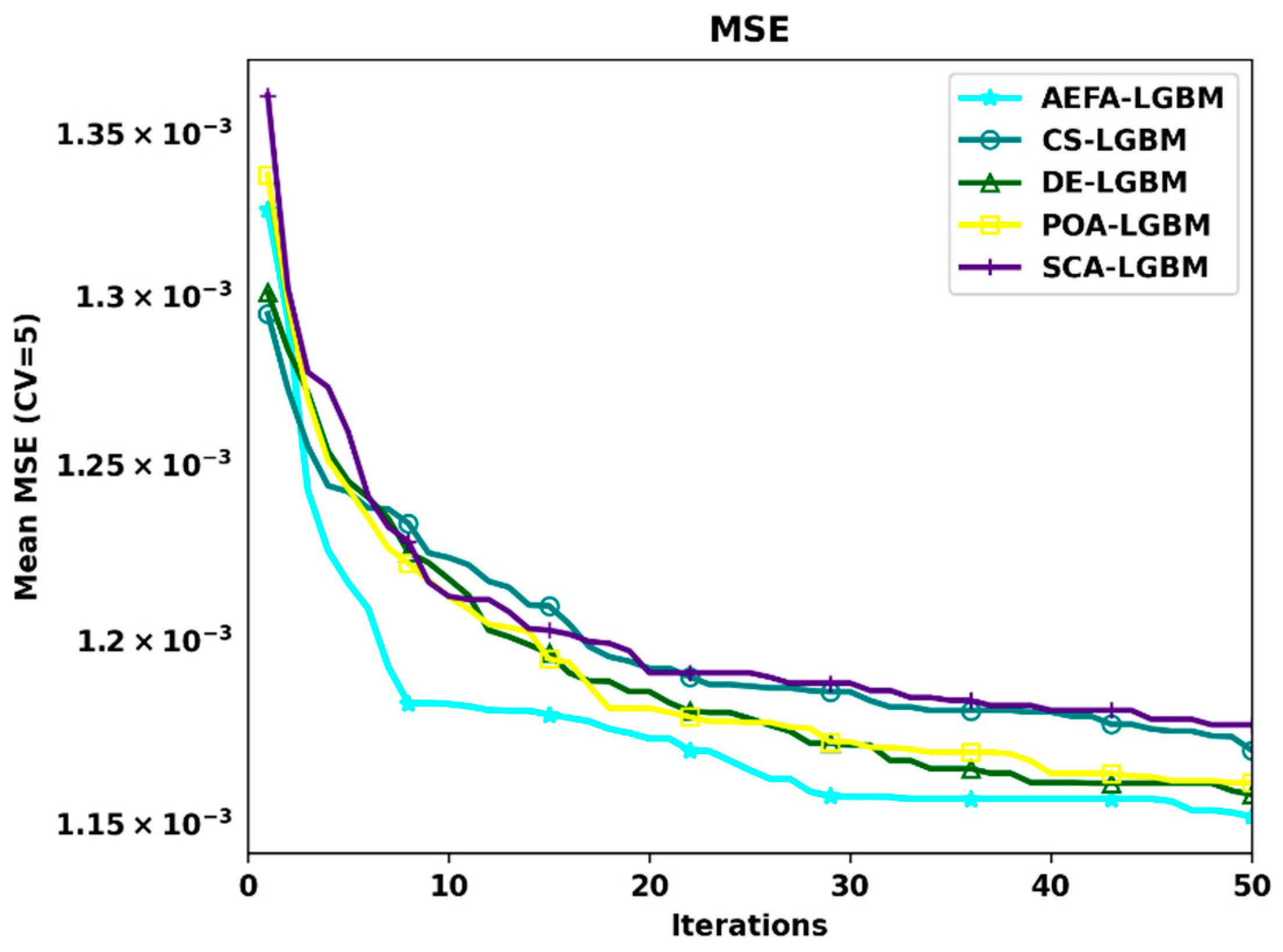

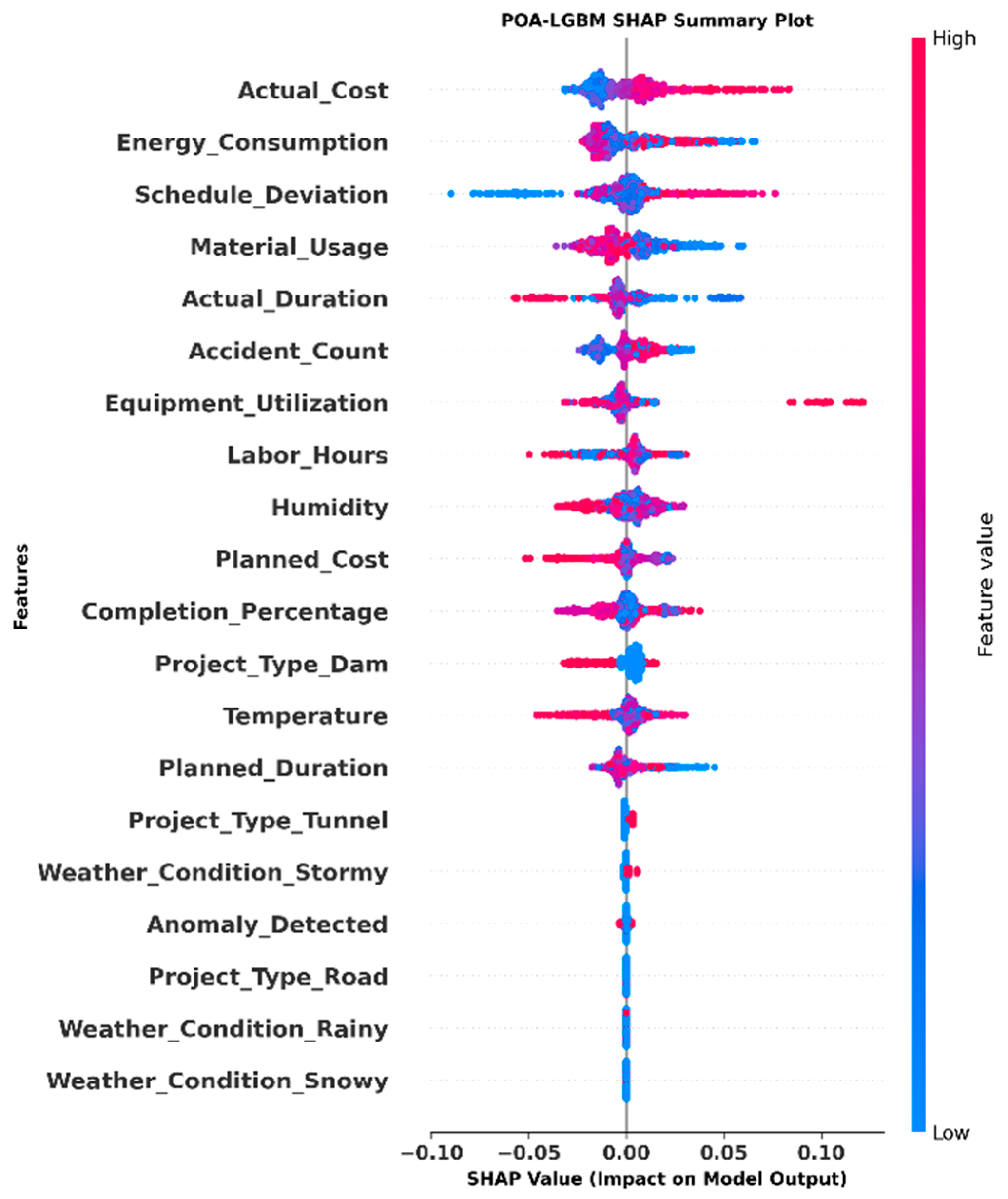
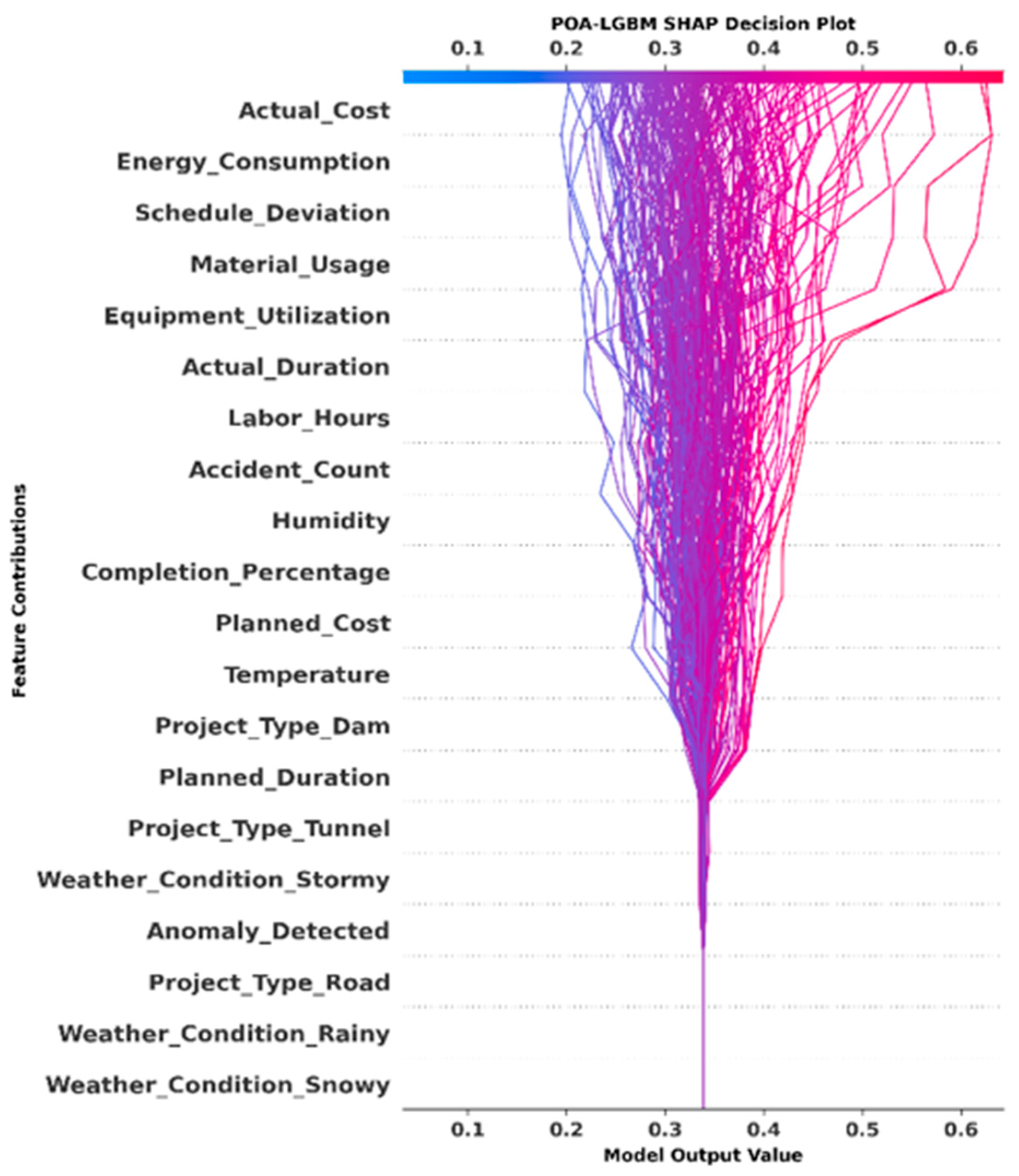
| Metric | Mathematical Formulation | Typical Range & Note |
|---|---|---|
| (values < 0 occur when the model underperforms the mean predictor) | ||
| RMSE (Root-Mean-Squared Error) | ; lower is better | |
| MAE (Mean Absolute Error) | ; lower is better | |
| MAPE (Mean Absolute Percentage Error) | ; lower is better |
| Algorithms | Parameter Setting |
|---|---|
| AEFA | , |
| CS | , |
| DE | |
| POA | R = 0.2 |
| SCA |
| AEFA-LGBM | CS-LGBM | DE-LGBM | POA-LGBM | SCA-LGBM | LGBM | ||
|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.99560 | 0.99714 | 0.99722 | 0.99711 | 0.99717 | 0.97683 |
| STD | 9.6721 × 10−4 | 1.2766 × 10−3 | 8.1976 × 10−4 | 9.7025 × 10−4 | 1.6715 × 10−3 | 1.6387 × 10−3 | |
| Best | 0.99751 | 0.99918 | 0.99854 | 0.99852 | 0.99942 | 0.97984 | |
| RMSE | AVG | 1.4254 × 10−2 | 1.1258 × 10−2 | 1.1265 × 10−2 | 1.1472 × 10−2 | 1.1014 × 10−2 | 3.1964 × 10−2 |
| STD | 1.5742 × 10−3 | 2.5896 × 10−3 | 1.6884 × 10−3 | 1.8294 × 10−3 | 3.2976 × 10−3 | 9.4009 × 10−4 | |
| Best | 1.0778 × 10−2 | 6.1850 × 10−3 | 8.2730 × 10−3 | 8.3130 × 10−3 | 5.2050 × 10−3 | 3.0067 × 10−2 | |
| MAE | AVG | 9.2692 × 10−3 | 7.0936 × 10−3 | 7.0767 × 10−3 | 7.1763 × 10−3 | 6.8588 × 10−3 | 2.4781 × 10−2 |
| STD | 1.1983 × 10−3 | 1.9636 × 10−3 | 1.3036 × 10−3 | 1.4814 × 10−3 | 2.6748 × 10−3 | 6.6421 × 10−4 | |
| Best | 6.5610 × 10−3 | 3.2520 × 10−3 | 4.6230 × 10−3 | 4.6130 × 10−3 | 2.3110 × 10−3 | 2.3480 × 10−2 | |
| MAPE | AVG | 6.4322 | 4.6809 | 4.6034 | 4.7092 | 4.4852 | 1.3997 × 101 |
| STD | 9.4115 × 10−1 | 1.5075 | 1.0321 | 1.1219 | 2.0236 | 2.8684 | |
| Best | 4.2945 | 1.8143 | 2.7754 | 2.7495 | 1.1217 | 1.1578 × 101 |
| AEFA-LGBM | CS-LGBM | DE-LGBM | POA-LGBM | SCA-LGBM | LGBM | ||
|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.97848 | 0.97837 | 0.97845 | 0.97856 | 0.97822 | 0.95919 |
| STD | 7.7721 × 10−5 | 7.0533 × 10−4 | 6.3666 × 10−4 | 3.8363 × 10−4 | 7.1151 × 10−4 | 4.6021 × 10−3 | |
| Best | 0.97827 | 0.97669 | 0.97683 | 0.97794 | 0.97637 | 0.95019 | |
| RMSE | AVG | 3.0493 × 10−2 | 3.0566 × 10−2 | 3.0513 × 10−2 | 3.0432 × 10−2 | 3.0671 × 10−2 | 4.2477 × 10−2 |
| STD | 5.4949 × 10−5 | 4.9664 × 10−4 | 4.4780 × 10−4 | 2.7326 × 10−4 | 4.9791 × 10−4 | 2.9544 × 10−3 | |
| Best | 3.0415 × 10−2 | 2.9673 × 10−2 | 2.9956 × 10−2 | 2.9762 × 10−2 | 2.9799 × 10−2 | 3.7379 × 10−2 | |
| MAE | AVG | 2.3193 × 10−2 | 2.3427 × 10−2 | 2.3414 × 10−2 | 2.3267 × 10−2 | 2.3482 × 10−2 | 3.3356 × 10−2 |
| STD | 5.6641 × 10−5 | 4.6134 × 10−4 | 4.5545 × 10−4 | 2.3405 × 10−4 | 4.5953 × 10−4 | 2.4926 × 10−3 | |
| Best | 2.3104 × 10−2 | 2.2732 × 10−2 | 2.2902 × 10−2 | 2.2804 × 10−2 | 2.2655 × 10−2 | 2.8801 × 10−2 | |
| MAPE | AVG | 3.0828 × 101 | 3.0661 × 101 | 3.0439 × 101 | 3.0567 × 101 | 3.0702 × 101 | 2.0975 × 101 |
| STD | 1.3558 × 10−1 | 6.4876 × 10−1 | 4.4589 × 10−1 | 5.2025 × 10−1 | 7.9319 × 10−1 | 7.9711 | |
| Best | 3.0639 × 101 | 2.9467 × 101 | 2.9813 × 101 | 2.9165 × 101 | 2.9413 × 101 | 1.2617 × 101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lekraik, J.M.M.; Ojekemi, O.S. Advancing Digital Project Management Through AI: An Interpretable POA-LightGBM Framework for Cost Overrun Prediction. Systems 2025, 13, 1047. https://doi.org/10.3390/systems13121047
Lekraik JMM, Ojekemi OS. Advancing Digital Project Management Through AI: An Interpretable POA-LightGBM Framework for Cost Overrun Prediction. Systems. 2025; 13(12):1047. https://doi.org/10.3390/systems13121047
Chicago/Turabian StyleLekraik, Jalal Meftah Mohamed, and Opeoluwa Seun Ojekemi. 2025. "Advancing Digital Project Management Through AI: An Interpretable POA-LightGBM Framework for Cost Overrun Prediction" Systems 13, no. 12: 1047. https://doi.org/10.3390/systems13121047
APA StyleLekraik, J. M. M., & Ojekemi, O. S. (2025). Advancing Digital Project Management Through AI: An Interpretable POA-LightGBM Framework for Cost Overrun Prediction. Systems, 13(12), 1047. https://doi.org/10.3390/systems13121047






