Evolutionary Game Analysis for Regional Collaborative Supply Chain Innovation Under Geospatial Restructuring
Abstract
1. Introduction
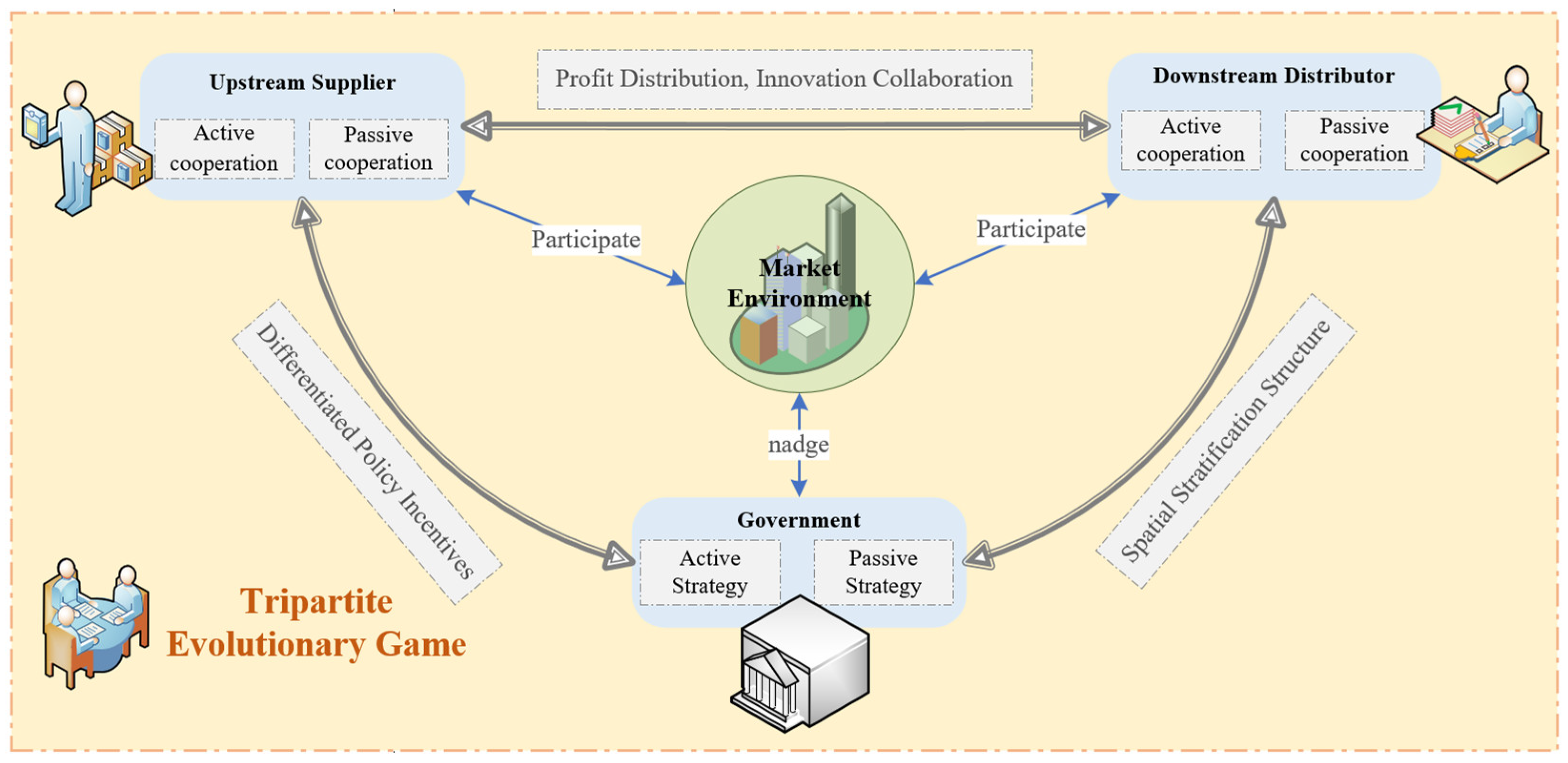
2. Problem Statement and Model Construction
- (1)
- Industrial concentration (LQ), measured by the location quotient of major manufacturing and logistics industries in each region;
- (2)
- Logistics network density, calculated as the ratio of freight flow volume to total transportation capacity, representing intercity connectivity;
- (3)
- Regional GDP share, indicating the relative economic strength of each spatial unit.
3. Tripartite Evolutionarily Stable Strategy Analysis
3.1. Replicator Dynamics Analysis of Upstream Suppliers
- (1)
- When , is non-positive or non-negative over the interval [0, 1], and any value of x can be stable. This implies that the upstream supplier’s strategy tends to remain unchanged over time regardless of its initial value. The strategy of choosing innovation investment does not evolve dynamically.
- (2)
- When , both x = 0 and x = 1 are potential equilibrium strategies. The stability of each depends on the relative payoff conditions. We consider two sub-cases:
- (i)
- If , substituting x = 0 and x = 1 into the replicator dynamic equation yields . This indicates that x = 0 is a locally stable strategy. That is, when the probability that downstream retailers adopt an innovation investment strategy is below a critical threshold , upstream suppliers are more likely to evolve toward the “non-innovation investment” strategy.
- (ii)
- If , similarly, substituting into the replicator dynamic equation gives and . In this case, x = 0, x = 1 becomes the evolutionarily stable point . This implies that when the probability of downstream retailers choosing innovation exceeds the threshold , upstream suppliers tend to evolve toward the “innovation investment” strategy.
3.2. Replicator Dynamics Analysis of Downstream Retailers
- (1)
- When , it follows that , and the strategy of adopting collaborative innovation remains dynamically stable regardless of its initial probability. That is, the probability of downstream retailers adopting collaborative innovation remains unchanged over time.
- (2)
- When , two pure strategies exist at y = 0 and y = 1. The stability of each can be examined under the following conditions:
- (i)
- If , then plugging in y = 0 and y = 1 into the replicator dynamic yields . This indicates that y = 0 is an evolutionarily stable strategy. That is, if the likelihood of upstream suppliers assuming collaborative innovation falls below some threshold, , downstream retailers are more likely to take a non-collaborative approach.
- (ii)
- If , then substituting y = 0 and y = 1 yields . In this case, y = 1 becomes the evolutionarily stable point, indicating that when the probability of upstream suppliers engaging in collaborative innovation exceeds a certain threshold , downstream retailers tend to adopt collaborative innovation strategies.
3.3. Government Replicator Dynamics Analysis
- (i)
- If , substituting z = 0 and z = 1 into the replicator dynamic equation yields , indicating that z = 1 is the evolutionarily stable strategy for the government. This implies that if the probability of upstream suppliers engaging in collaborative innovation falls below , the government will prefer the “active regulation” strategy.
- (ii)
- If , substituting z = 0 and z = 1 into the replicator dynamic equation yields and , indicating that z = 0 is the evolutionarily stable strategy. In this scenario, when the probability of upstream suppliers engaging in collaborative innovation exceeds , the government will adopt the “passive regulation” strategy.
4. Simulation Analysis
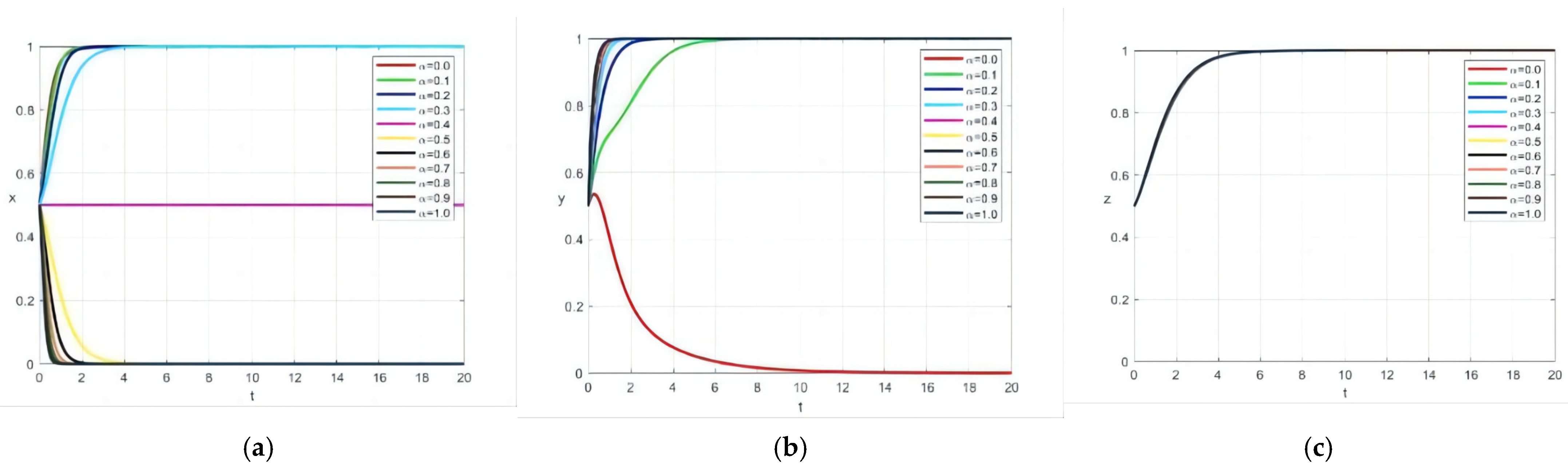
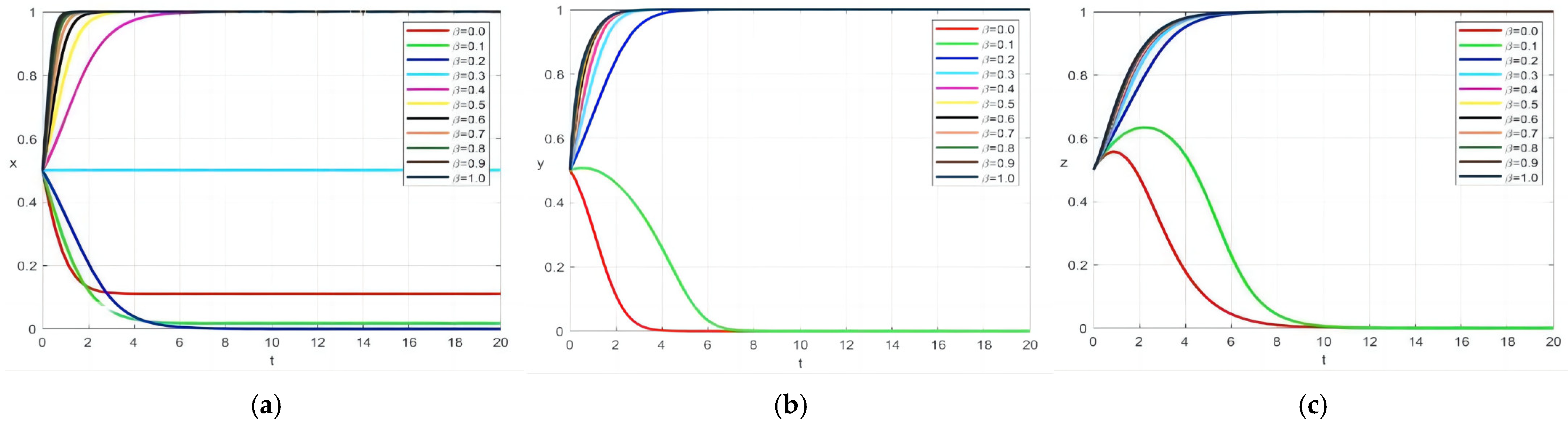
4.1. Impact of the Benefit Conversion Efficiency Coefficient on System Evolution
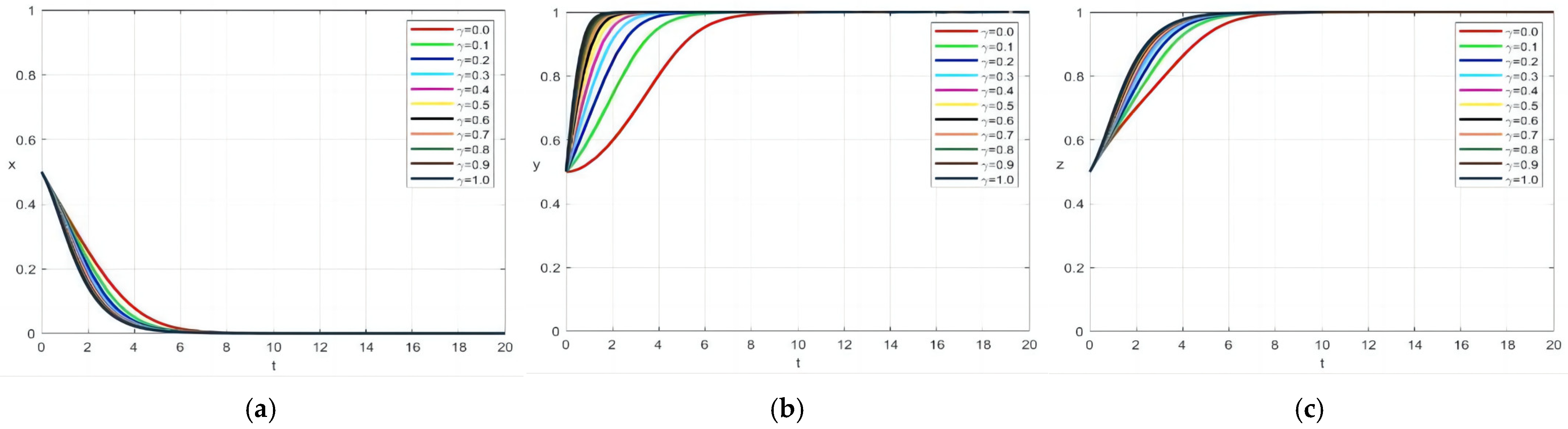
4.2. Impact of Information Sharing Coefficient on System Evolution
4.3. Impact of Mutual Trust Coefficient on System Evolution
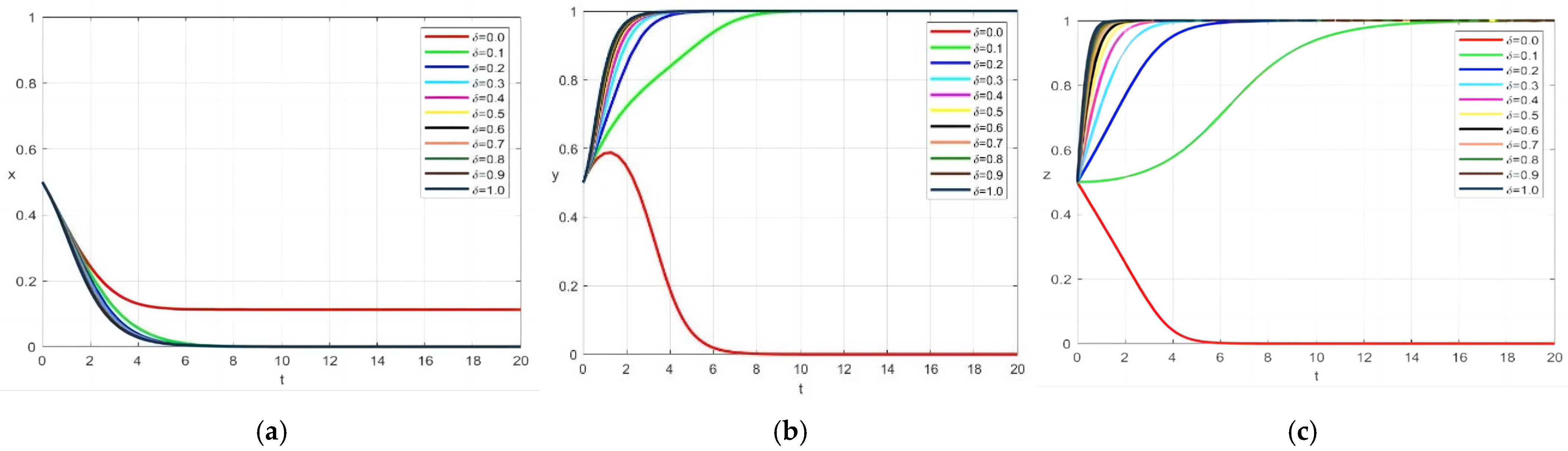
4.4. Impact of Fiscal Subsidy Coefficient on System Evolution
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Xu, J.; Zhang, G. An Evolutionary Game Study of Collaborative Innovation across the Whole Industry Chain of Rural E-Commerce under Digital Empowerment. Systems 2024, 12, 353. [Google Scholar] [CrossRef]
- Ciarli, T.; Kenney, M.; Massini, S.; Piscitello, L. Digital technologies, innovation, and skills: Emerging trajectories and challenges. Res. Policy 2021, 50, 104289. [Google Scholar] [CrossRef]
- Chen, X.; Wang, C.; Li, S. The impact of supply chain finance on corporate social responsibility and creating shared value: A case from the emerging economy. Supply Chain Manag. 2023, 28, 324–346. [Google Scholar] [CrossRef]
- Feng, K.; Han, S.; Feng, M.; Szolnoki, A. An evolutionary game with reputation-based imitation-mutation dynamics. Appl. Math. Comput. 2024, 472, 128618. [Google Scholar] [CrossRef]
- Han, J.; Guo, J.E.; Cai, X.; Lv, C.; Lev, B. An analysis on strategy evolution of research & development in cooperative innovation network of new energy vehicle within policy transition period. Omega 2022, 112, 102686. [Google Scholar] [CrossRef]
- Hashemi, V.; Taleai, M.; Abolhasani, S. Enhancing agricultural land valuation in land consolidation projects through cooperative game theory and genetic algorithm optimization. Habitat Int. 2024, 152, 103157. [Google Scholar] [CrossRef]
- He, Y.; Yang, Y.; Wang, S. Network and mechanism of China’s new energy vehicle industry from the perspective of value chain. J. Geogr. Sci. 2024, 34, 779–803. [Google Scholar] [CrossRef]
- Hendriksen, C. Artificial intelligence for supply chain management: Disruptive innovation or innovative disruption? J. Supply Chain Manag. 2023, 59, 65–76. [Google Scholar] [CrossRef]
- Iftikhar, A.; Ali, I.; Arslan, A.; Tarba, S. Digital innovation, data analytics, and supply chain resiliency: A bibliometric-based systematic literature review. Ann. Oper. Res. 2024, 333, 825–848. [Google Scholar] [CrossRef]
- Isaksen, A.; Jakobsen, S.-E.; Njøs, R.; Normann, R. Regional industrial restructuring resulting from individual and system agency. Innov. Eur. J. Soc. Sci. Res. 2019, 32, 48–65. [Google Scholar] [CrossRef]
- Lingfan, Y.; Mi, T.; Xiaolong, L.; Xiaolong, L. Inter-city cooperation fever’ in China: Its trajectory, mechanisms and adjustment strategy. Habitat Int. 2025, 158, 103355. [Google Scholar] [CrossRef]
- Qiu, L.; Xia, W.; Wei, S.; Hu, H.; Yang, L.; Chen, Y.; Zhou, H.; Hu, F. Collaborative management of environmental pollution and carbon emissions drives local green growth: An analysis based on spatial effects. Environ. Res. 2024, 259, 119546. [Google Scholar] [CrossRef]
- Rahmanzadeh, S.; Pishvaee, M.S.; Govindan, K. Emergence of open supply chain management: The role of open innovation in the future smart industry using digital twin network. Ann. Oper. Res. 2023, 329, 979–1007. [Google Scholar] [CrossRef]
- Richey, R.G.; Chowdhury, S.; Davis-Sramek, B.; Giannakis, M.; Dwivedi, Y.K. Artificial intelligence in logistics and supply chain management: A primer and roadmap for research. J. Bus. Logist. 2023, 44, 532–549. [Google Scholar] [CrossRef]
- Shi, T.; Han, F.; Chen, L.; Shi, J.; Xiao, H. Study on value co-creation and evolution game of low-carbon technological innovation ecosystem. J. Clean. Prod. 2023, 414, 137720. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Q.; Zou, L. Spatial-temporal evolution and driving mechanism of rural production-living-ecological space in Pingtan islands, China. Habitat Int. 2023, 137, 102833. [Google Scholar] [CrossRef]
- Belhadi, A.; Mani, V.; Kamble, S.S.; Khan, S.A.R.; Verma, S. Artificial intelligence-driven innovation for enhancing supply chain resilience and performance under the effect of supply chain dynamism: An empirical investigation. Ann. Oper. Res. 2024, 333, 627–652. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Yang, Z.; Yan, H.; Zhao, Y. How to reduce construction risks in rural areas: An evolutionary game analysis. Eng. Constr. Archit. Manag. 2024, 32, 4495–4521. [Google Scholar] [CrossRef]
- Hellström, D.; Olsson, J. Let’s Go Thrift Shopping: Exploring Circular Business Model Innovation in Fashion Retail. Technol. Forecast. Soc. Change 2024, 198, 123000. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, X.; Wang, Y.; Xu, J. A Tripartite Evolutionary Game for the Regional Green Logistics: The Roles of Government Subsidy and Platform’s Cost-Sharing. Kybernetes 2024, 53, 216–237. [Google Scholar] [CrossRef]
- Huang, F.; Fan, H.; Shang, Y.; Wei, Y.; Almutairi, S.Z.; Alharbi, A.M.; Ma, H.; Wang, H. Research on Renewable Energy Trading Strategies Based on Evolutionary Game Theory. Sustainability 2024, 16, 2671. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, L.; Cao, B.; Fan, X. Benefit distribution and stability analysis of enterprises’ technological innovation cooperation alliance. Comput. Ind. Eng. 2021, 161, 107637. [Google Scholar] [CrossRef]
- Liu, H.; Wu, Q. Evolutionary game analysis on technological innovation strategies of marine ranching enterprises considering government’s incentive policies and consumer preferences. Front. Mar. Sci. 2024, 11, 1470846. [Google Scholar] [CrossRef]
- Cai, M.; Hu, S.; Wang, Y.; Xiao, J. A Dynamic Social Network Matching Model for Virtual Power Plants and Distributed Energy Resources with Probabilistic Linguistic Information. Sustainability 2022, 14, 14920. [Google Scholar] [CrossRef]
- Zou, H.; Qin, H.; He, D.; Sun, J. Research on an enterprise green innovation ecosystem from the vulnerability perspective: Evolutionary game and simulation. IEEE Access 2021, 9, 140809–140823. [Google Scholar] [CrossRef]
- Shakiba, H.; Belitski, M. A game theory analysis of regional innovation ecosystems. J. Technol. Transf. 2025, 50, 797–820. [Google Scholar] [CrossRef]
- Zhao, X.; Zou, Z.; Li, J.; Yuan, X.; He, X. Monitoring Policy-Driven Urban Restructuring and Logistics Agglomeration in Zhengzhou Through Multi-Source Remote Sensing: An NTL-POI Integrated Spatiotemporal Analysis. Remote Sens. 2025, 17, 3107. [Google Scholar] [CrossRef]
- Hao, Q.; Chen, C.; Xu, Q.; Lou, F.; Li, Y.; Yan, R.; Fang, J. Analysis of the evolutionary game of energy-saving retrofit of residential buildings in urban villages under the background of urban renewal. J. Hous. Built Environ. 2025, 40, 1715–1747. [Google Scholar] [CrossRef]
- Paula, I.C.; Campos, E.A.R.; Pagani, R.N.; Guarnieri, P.; Kaviani, M.A. Are collaboration and trust sources for innovation in the reverse logistics? Insights from a systematic literature review. Supply Chain Manag. Int. J. 2020, 25, 176–222. [Google Scholar] [CrossRef]
- Hulke, C.; Diez, J.R. Understanding regional value chain evolution in peripheral areas through governance interactions-An institutional layering approach. Appl. Geogr. 2022, 139, 102640. [Google Scholar] [CrossRef]
- Jakobsen, S.E.; Uyarra, E.; Njøs, R.; Fløysand, A. Policy action for green restructuring in specialized industrial regions. Eur. Urban Reg. Stud. 2022, 29, 312–331. [Google Scholar] [CrossRef]
- Wang, N.; Weng, G. Spatiotemporal Evolution of and Regional Differences in Consumer Disputes in the Tourism System: Empirical Evidence from the Yangtze River Economic Belt, China. Systems 2025, 13, 473. [Google Scholar] [CrossRef]
- Xu, J.; Liu, S. Current status, evolutionary path, and development trends of low-carbon technology innovation: A bibliometric analysis. Environ. Dev. Sustain. 2024, 26, 24151–24182. [Google Scholar] [CrossRef]
- Yeung, H.W. Regional worlds: From related variety in regional diversification to strategic coupling in global production networks. Reg. Stud. 2021, 55, 989–1010. [Google Scholar] [CrossRef]
- Xue, L.; Yao, F.; Liang, J. Study on the spatial and temporal evolution characteristics and future trends of China’s coal mining and dressing industry green total factor productivity. Environ. Dev. Sustain. 2025, 27, 19025–19066. [Google Scholar] [CrossRef]
- Liu, J.; Dong, C. Understanding the complex adaptive characteristics of cross-regional emergency collaboration in china: A stochastic evolutionary game approach. Fractal Fract. 2024, 8, 98. [Google Scholar] [CrossRef]
- Tang, Q.; Wang, C.; Feng, T. Research on the Group Innovation Information-Sharing Strategy of the Industry–University-Research Innovation Alliance Based on an Evolutionary Game. Mathematics 2023, 11, 4161. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997; Volume 3, pp. 190–196. [Google Scholar]
- Shi, J.; Lu, H.; Liu, W. Tripartite Evolutionary Game Analysis for Manufacturing Firms, Service Providers and Consumers in Collaborative Innovation Systems. Mathematics 2025, 13, 2227–7390. [Google Scholar] [CrossRef]
- Ding, X.; Ren, J.; Lu, H.; Hussain, J.; Zhou, R. Strategic dynamics of local governments in regional collaborative governance: An evolutionary game theory analysis of haze pollution response in the Fen-Wei Plain, China. Heliyon 2024, 10, 2405–8440. [Google Scholar] [CrossRef]
- Peng, D.; Wu, H.; Wang, L. Comprehensive energy cooperative optimization model based on energy conversion efficiency considering investment benefit. Int. J. Energy Res. 2021, 45, 2997–3015. [Google Scholar] [CrossRef]
- Zha, Y.; Li, Q.; Huang, T.; Yu, Y. Strategic information sharing of online platforms as resellers or marketplaces. Mark. Sci. 2023, 42, 659–678. [Google Scholar] [CrossRef]
- Singh, A.; Chatterjee, K. An adaptive mutual trust based access control model for electronic healthcare system. J. Ambient. Intell. Hum. Comput. 2020, 11, 2117–2136. [Google Scholar] [CrossRef]
- Zhou, C.; Leng, M.; Liu, Z.; Cui, X.; Yu, J. The impact of recommender systems and pricing strategies on brand competition and consumer search. Electron. Commer. Res. Appl. 2022, 53, 101144. [Google Scholar] [CrossRef]
| Game Participant | Government | ||
|---|---|---|---|
| Active Strategy (z) | Passive Strategy (1 − z) | ||
| Innovation Investment (x) | Collaborative Innovation (y) | ||
| No Collaborative Innovation (1 − y) | |||
| No Innovation Investment (1 − x) | Collaborative Innovation (y) | ||
| No Collaborative Innovation (1 − y) | |||
| Equilibrium Point | λ1 | λ2 | λ3 |
|---|---|---|---|
| E1(0, 0, 0) | |||
| E2(0, 0, 1) | |||
| E3(0, 1, 0) | |||
| E4(0, 1, 1) | |||
| E5(1, 0, 0) | |||
| E6(1, 0, 1) | |||
| E7(1, 1, 0) | |||
| E8(1, 1, 1) |
| Equilibrium Point | Situation 1 | Situation 2 | Situation 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ1 | λ2 | λ3 | Stability | λ1 | λ2 | λ3 | Stability | λ1 | λ2 | λ3 | Stability | |
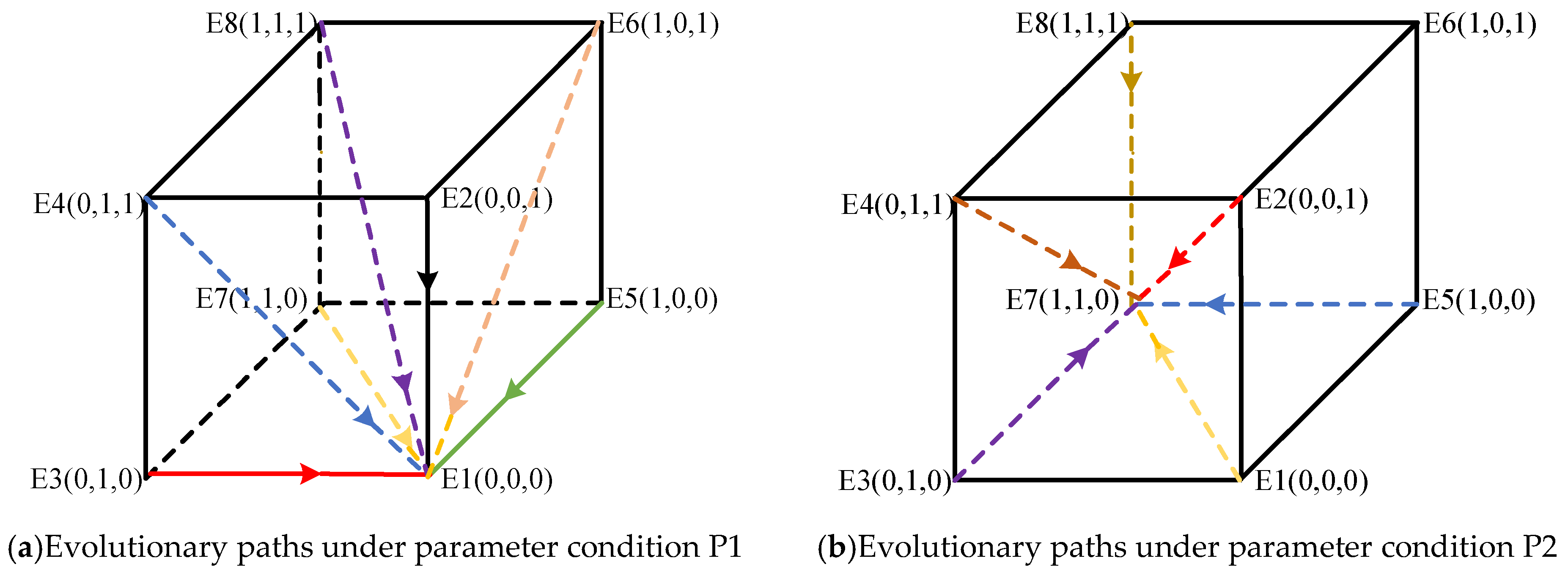
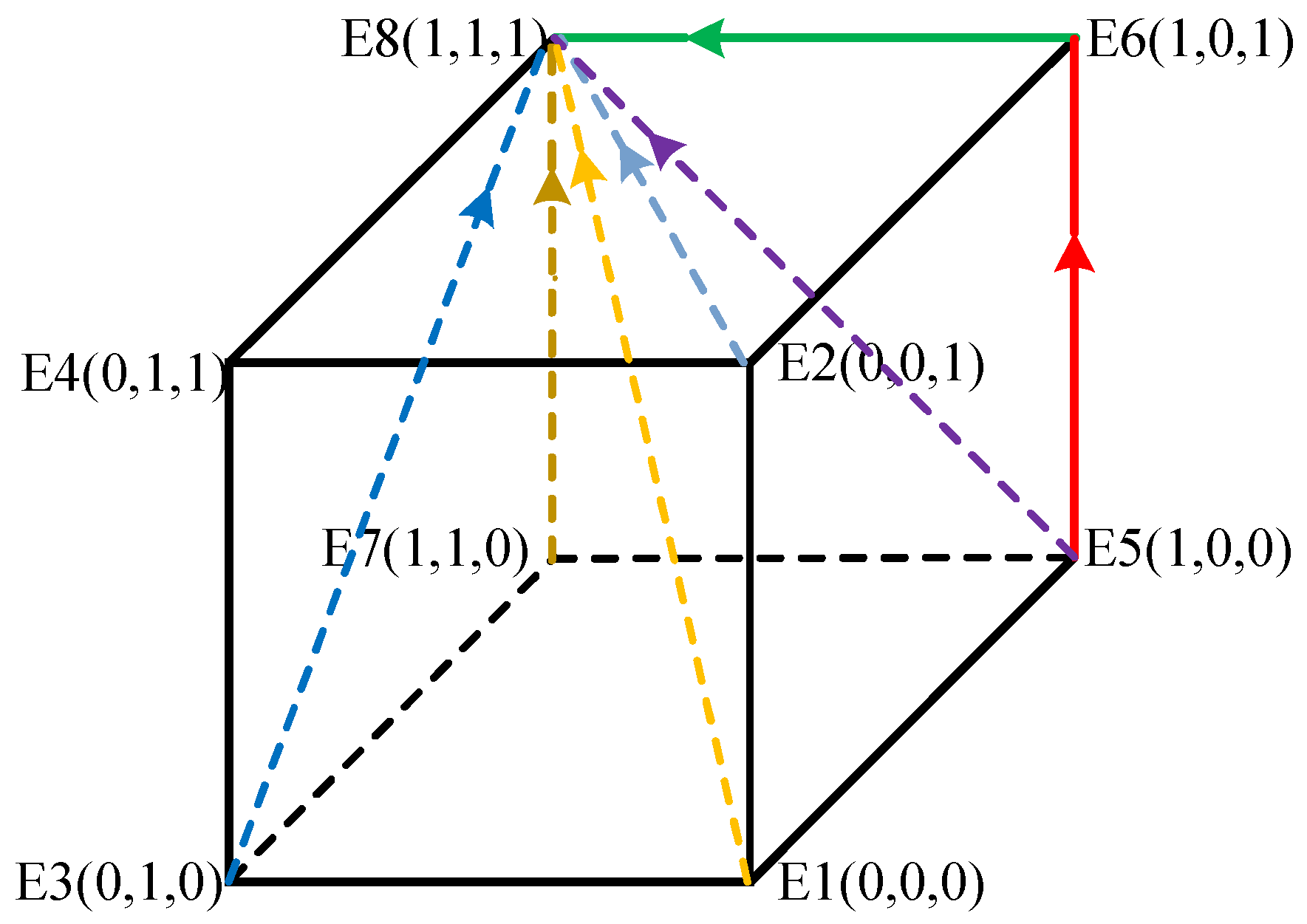
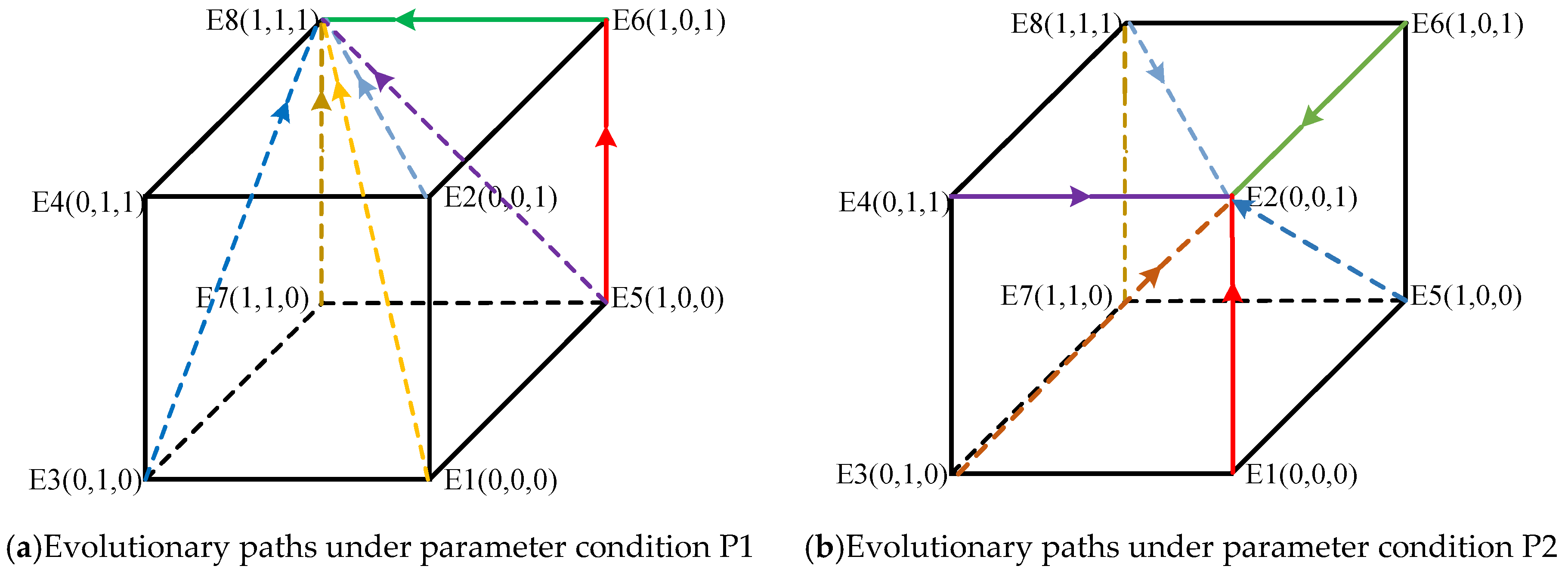
| E1(0, 0, 0) | − | − | − | ESS | + | + | + | instability | − | − | + | saddle point |
| E2(0, 0, 1) | ± | ± | + | saddle point | + | + | − | saddle point | − | − | − | ESS |
| E3(0, 1, 0) | + | + | − | saddle point | + | − | + | saddle point | + | + | + | instability |
| E4(0, 1, 1) | + | ± | + | saddle point | + | − | − | saddle point | + | + | − | saddle point |
| E5(1, 0, 0) | + | + | − | saddle point | − | + | + | saddle point | + | + | + | instability |
| E6(1, 0, 1) | ± | + | + | saddle point | − | + | − | saddle point | + | + | − | saddle point |
| E7(1, 1, 0) | − | − | − | ESS | − | − | + | saddle point | − | − | + | saddle point |
| E8(1, 1, 1) | − | − | + | saddle point | − | − | − | ESS | − | − | − | ESS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Li, C.; Zhang, J. Evolutionary Game Analysis for Regional Collaborative Supply Chain Innovation Under Geospatial Restructuring. Systems 2025, 13, 1044. https://doi.org/10.3390/systems13121044
Li R, Li C, Zhang J. Evolutionary Game Analysis for Regional Collaborative Supply Chain Innovation Under Geospatial Restructuring. Systems. 2025; 13(12):1044. https://doi.org/10.3390/systems13121044
Chicago/Turabian StyleLi, Ruiqian, Chunfa Li, and Jun Zhang. 2025. "Evolutionary Game Analysis for Regional Collaborative Supply Chain Innovation Under Geospatial Restructuring" Systems 13, no. 12: 1044. https://doi.org/10.3390/systems13121044
APA StyleLi, R., Li, C., & Zhang, J. (2025). Evolutionary Game Analysis for Regional Collaborative Supply Chain Innovation Under Geospatial Restructuring. Systems, 13(12), 1044. https://doi.org/10.3390/systems13121044






