Enhancing E-Commerce RMFS Order Fulfillment Through Pod Positioning with Jointly Optimized Task Allocation

Abstract

Robotic mobile fulfillment systems have become an integral part of e-commerce warehouses. The pod repositioning problem, due to its interdependence with robot task allocation strategies, poses a significant challenge that constrains system performance. In this paper, we aim to jointly optimize the two interrelated problems of pod repositioning and task allocation. A multi-objective mixed-integer planning model is developed to minimize the maximum completion time of robots and the deviation between the pod position and the expected position. To tackle the challenges of decision coupling and a vast solution space, an adaptive genetic-neighborhood search algorithm guided by pod heat maps is designed. Additionally, to promptly correct expected layout deviations and avoid layout instability, a progressive storage mechanism is designed to update the expected layout. The numerical experiments show that compared to the staged optimization strategy, the joint optimization strategy proposed in this paper can reduce the maximum completion time by approximately 48%, and that the strategy reduces the maximum completion time by 9% to 16% compared to the nearest allocation strategy, which is commonly used and performs best in practice.

1. Introduction

The rapid development of e-commerce for the warehouse operation and management has brought a lot of challenges, customer demand for a wide range of stock-keeping unit (SKU) varieties, orders in small batches and other new features prompted the logistics industry to put forward new solutions. In the traditional “person-to-goods” order picking model, order pickers need to frequently walk through the aisles of the warehouse storage area to manually pick SKUs, and their walking time accounts for more than 60% of the total picking time, which results in high operating costs and low picking efficiency. In recent years, the robotic mobile fulfillment system (RMFS) as a new type of automated warehousing system in e-commerce warehouses has been widely put into use by some large-scale e-commerce companies such as Amazon, JD Logistics, and Alibaba, and extensively applied in medicine, clothing, and many other industries in logistics warehouses [1]. Its picking efficiency is 2~3 times that of the traditional “person-to-goods” mode, and has a high degree of flexibility and scalability. RMFS mainly consists of three parts: mobile robots, movable pods and workstations; the mobile robots can move the movable pods to be picked from the storage area to the designated workstations, and the pickers only need to pick the SKUs out of the workstations. The picker only needs to pick out the SKUs at the workstation to complete the order picking task. Compared with traditional manual picking, this “goods-to-person” mode significantly reduces the walking time consumed by order pickers when picking goods, reduces labor costs, and significantly improves the order picking efficiency of the warehousing system [2].

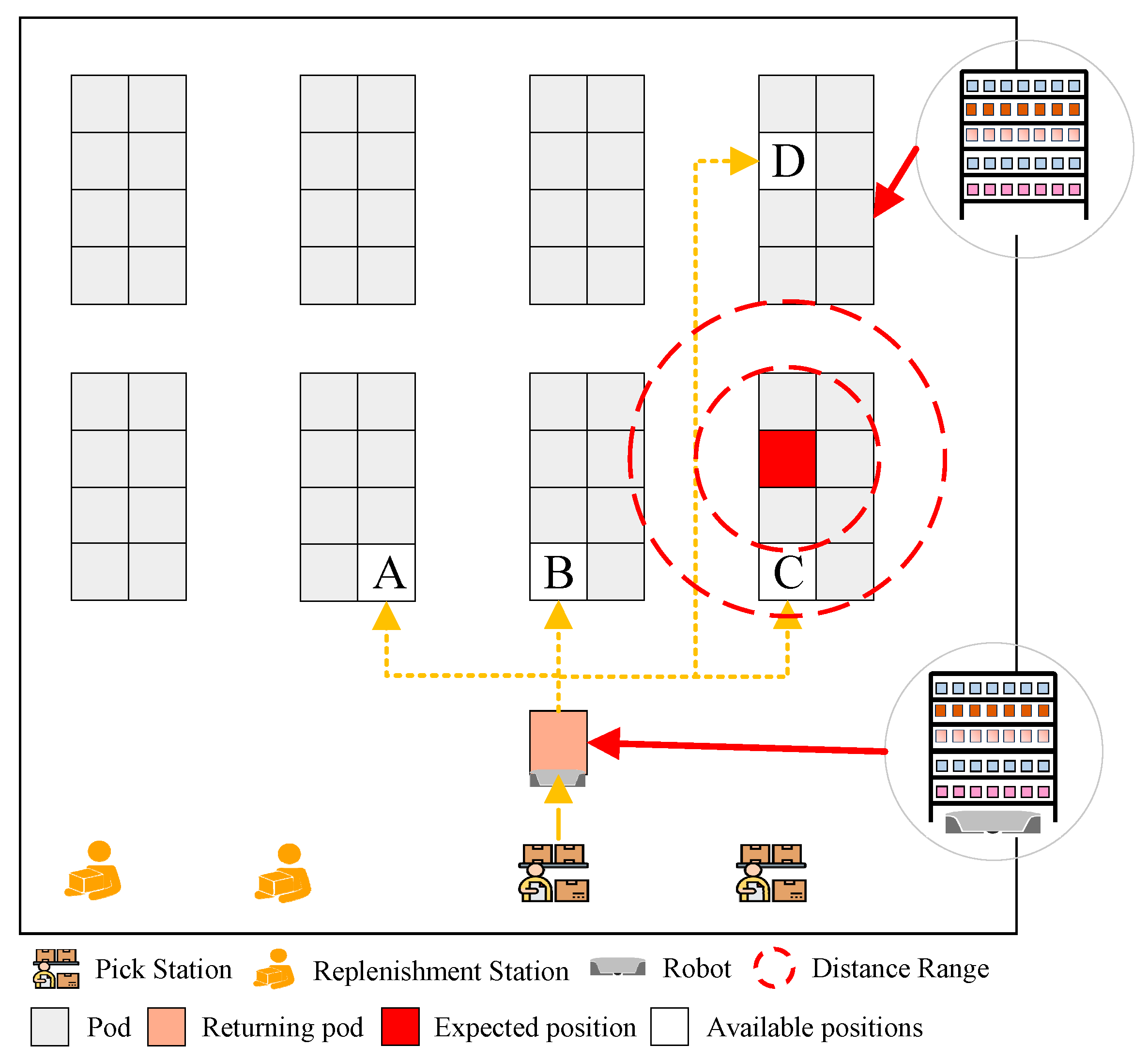
Pod repositioning serves as a core mechanism for achieving dynamic warehouse optimization in RMFS, and its execution is closely interrelated with robot task allocation. As shown in Figure 1, workstations (picking stations/replenishment stations) in RMFSs are typically fixed along one side of the warehouse. When pods are returned to the storage area, the system selects its new location from available positions (e.g., A–D in Figure 1) under the guidance of the expected layout, which integrates multiple operational factors. This process inherently involves a fundamental conflict between optimizing pod layout and controlling robot travel costs. Specifically, the selection of pod locations influences both the future warehouse layout structure and the execution efficiency of subsequent robot tasks. These two aspects form a structural interdependence and mutual constraint through handling activities. Pursuing an optimal layout requires increasing the frequency of pod adjustments, whereas reducing operating costs demands minimizing handling operations. This inherent competitive relationship makes it difficult to achieve overall system performance optimization through unilateral improvements, thereby constituting the core challenge in the joint optimization of pod repositioning and task allocation.

The expected layout in this article is based on pod picking frequency, pod replenishment frequency, and pod inter-association. Among these, pod picking frequency and pod inter-association have been proven to be important factors influencing warehouse layout. Additionally, high-frequency picking operations result in rapid depletion of SKUs on the pods, and when there are not enough SKUs on the pods to satisfy order picking needs, the pods need to be carried by robots to replenishment stations to replenish the out-of-stock SKUs [3]. During replenishment, pods are unable to perform picking tasks, which directly affects the efficiency of picking operations. Therefore, it is important to consider the replenishment frequency of pods. In addition, since the picking frequency of pods in the RMFS is significantly higher than the replenishment frequency, it is also important to balance the robot’s picking and replenishment tasks through reasonable task allocation planning.

This paper focuses on studying the pod repositioning strategy considering joint optimization with task allocation, and proposes a mixed-integer programming model to minimize the maximum completion time of robots and the distance between the pod position and the expected position. The maximum completion time of robots refers to the longest picking completion time required for robots to complete the set of orders at all workstations. In order to solve this complex model effectively, an improved genetic algorithm, i.e., adaptive genetic-variable neighborhood search algorithm (AGA-VNS), is developed, which provides a feasible solution to improve the efficiency of the RMFS. Meanwhile, in order to realize the flexible response of the pod layout to the order demand, a progressive storage mechanism is proposed based on the idea of “predictive guidance, progressive movement”, so that the warehouse layout is gradually close to the theoretically optimal expected layout during the pod repositioning process.

In this paper, we design instances of different scales to verify the feasibility of the joint optimization algorithm and progressive storage mechanism proposed in this paper. Since the RMFS is highly scalable and the number of robots, pods and workstations can be flexibly adjusted with the change in business volume, this paper analyzes the factors affecting the performance of the system through sensitivity experiments, which provides theoretical guidance and practical enlightenment for logistics centers to realize the rational scheduling of warehouse resources.

In summary, the contributions of this paper are as follows:

(1)

A joint optimization strategy based on the heat guidance of pod repositioning and task allocation is proposed, which expands the scope of the pod repositioning problem and has important theoretical significance;

(2)

A generative order-guided progressive storage mechanism is proposed to update the expected layout, which further improves the matching of the warehouse layout with the expected layout while reducing the maximum completion time of robots;

(3)

An adaptive genetic-variable neighborhood search algorithm is designed, in which an adaptive strategy is introduced into the genetic algorithm to accelerate the speed of population searching, and three target-oriented local search operators are designed for VNS perturbation, which can effectively improve the local development ability of the algorithm.

The rest of the paper is structured as follows: Section 2 outlines the relevant literature review. Section 3 details the background of the problem. Section 4 and Section 5 present the mathematical models and algorithms. Section 6 performs numerical experiments and sensitivity analysis. Section 7 summarizes and gives concluding remarks.

2. Literature Review

Optimization of the RMFS has been studied in detail in different fields, and this section provides a detailed description of the two main research directions in the RMFS, i.e., pod repositioning and robot task allocation, and analyzes the current research progress in joint optimization.

2.1. Pod Repositioning Problem

Pod repositioning strategies can greatly utilize the flexibility of RMFSs and are a key component that directly impacts the efficiency and responsiveness of warehouse operations. Lamballais et al. take into account the unique characteristics of RMFS warehouses, noting that robots can move pods between storage areas and workstations, and can continually reposition them during operations [4]. Therefore, the pod repositioning problem is a special kind of pod position allocation problem, which is still essentially a storage location allocation problem, and thus strategies for the storage location allocation problem, such as nearest storage [5], original storage, and turnover-based storage [6], can be naturally applied to solve the pod repositioning problem. Krenzler et al. solved binary, proximity, fixed-position, randomized-position, genetic, and Tetris algorithms under a deterministic model and found the Russian algorithm to be more efficient [7]. This shows that a reasonable pod location allocation strategy can effectively improve the efficiency of pod repositioning. Weidinger et al. further transformed the pod repositioning problem into a special interval scheduling problem and solved it using an adaptive programming approach [8]. Guan et al. constructed a pod similarity matrix and Laplacian matrix, partitioned the pods according to the historical pickup frequency, and proposed a pod repositioning strategy for the same-zone distribution strategy [9]. After that, some scholars began to study the problem of pod repositioning in a complex context. Ji et al. divided the pod repositioning problem into two types of problems, assigning to one pod at a time and assigning to multiple pods at a time, and established an optimization model considering the future handling distance of the pods [10]. Li et al. investigated task allocation, path planning, and blocking problem solving for high-density storage warehouses [11].

In the process of research, storage strategies based on pod turnover rate have gradually become a hot direction of research. Yuan et al. proposed a new storage strategy based on pod turnover rate, and found that having two or three types of storage zones has more benefits when partitioning pods with different turnover rates for storage by fluid modeling [12]. Li et al. proposed a new decentralized storage strategy based on turnover rate considering that turnover rate-based storage is prone to congestion, based on item association rule analysis and a clustering method [13]. Xu et al. took into account the continuous dynamic change relationship of the warehouse layout, designed the matching degree index by the ratio of pod turnover rate and the distance from the storage location to the picking station, and solved the dynamic pod repositioning strategy considering the matching degree of the pod and the storage location by using the single-moment exchange simulated annealing algorithm [14]. Ding studied the approach of dynamically adjusting pod positions based on SKU sales and correlations [15]. Tian et al. proposed a dynamic pod position allocation strategy that takes into account real-time changes in commodity demand and balanced tasks at picking stations, and designed a hybrid algorithm combining a greedy algorithm and improved adaptive genetic algorithm to solve the problem [16]. Some scholars have redefined the pod turnover rate and analyzed pod heat as a key indicator, and the pod heat is essentially a derivation of the pod turnover rate. Based on customer orders, Wang et al. established a model to generate pod picking heat and inter-pod correlation, and proposed a new idea of “customer orders → pod usage frequency → pod location optimization” to obtain a pod repositioning scheme considering pod heat and correlation degree [17]. Zhai designed a mathematical algorithm, MABBD, based on Benders decomposition by considering the hot-start strategy and the main variable fixing strategy [18].

Due to the simultaneous existence of picking and replenishment operations in RMFS warehouses, some scholars have considered the impact of replenishment on pod repositioning, and Jiang et al. proposed a novel synchronization mechanism for picking and replenishment that can balance replenishment work and picking efficiency [19]. Wang et al. considered both order splitting cost and replenishment cost minimization to develop a hybrid algorithm using alternating large-neighborhood and local searches to solve the pod repositioning problem [20]. Li et al. designed a weighted double-Q learning algorithm to form a dynamic optimization strategy for pod position allocation under picking and replenishment operations by integrating factors such as pod hotness, inter-pod correlation, and existing pod position, which can adapt to the fluctuation of order status [21]. Zhang et al. considered joint storage allocation and pod positioning in the replenishment stage with channel workload equalization, and designed a decentralized pod storage allocation strategy that is conducive to the realization of channel workload equalization [22].

2.2. Robot Task Allocation Problem

Robot task allocation is a very complex combinatorial optimization problem, and reasonable scheduling of multiple robots to meet the rapid transportation needs of task pods plays an important role in improving system efficiency and reducing costs. Merschformann et al., in their study of the impact of task allocation, pod selection, and pod location optimization problems on system operation metrics, noted that the task allocation strategy had the greatest impact on system throughput metrics [23].

In early research on robot task allocation, scholars worked to reveal the correlation laws between influencing factors and allocation strategies in RMFSs. Jin et al. simulated warehouse environments through computer modeling and used a variety of pod selection rules and task allocation rules, pointing out the link between robot task allocation and warehouse square footage [24]. Zou et al. considered the relationship between the picking speed of the picking table and the assignment of picking tasks, and pointed out that assigning pod tasks according to the picking speed is more efficient than randomly assigning tasks to pods [25]. Yuan et al. analyzed the two operation modes of synchronous and asynchronous picking with multiple picking stations, and with the goal of achieving the shortest possible time for the robot to complete all the tasks, the robot task scheduling scheme was obtained using co-evolutionary genetic algorithms for synchronous and asynchronous picking modes [26]. Roy et al. categorized the robots into shared and dedicated types, analyzed the application of the two types of robots in the picking and replenishment scenarios of RMFSs, and found that the shared robot is more effective than random picking of pods in terms of picking speed. The application was analyzed and it was found that the order picking time can be reduced to one-third of the original time with shared robots [27].

Some scholars have considered the dynamic nature of RMFS warehouses by taking into account the effects of task changes, path conflicts, and other situations on robot task allocation during robot movement. Yoshitake et al. established a real-time scheduling method that takes into account both pod and robot states, which allows for task allocation of robots while pods are in the process of picking [28]. Zhang et al. modeled the robot task allocation problem as a resource-constrained project scheduling problem with transfer time, and proposed a dedicated serial scheduling generation scheme and a genetic algorithm based on the building block crossover operator to solve the problem, which can realize the dynamic scheduling of robots [29]. Gharehgozli et al. studied the task allocation problem considering pod access constraints and pointed out that multi-position selection is the key to reducing traveling time [30]. Li et al. designed a two-stage algorithm based on pod priority to obtain a multi-robot scheduling scheme considering the path planning of a single robot and collision avoidance among multiple robots [31]. Yuan et al. designed a four-stage balanced heuristic auction algorithm to solve the multi-robot task allocation model considering the balance between task relevance and picking workstations with the objective of minimizing the overall sorting time [32]. Sun et al. proposed a dynamic scheduling method to dynamically solve robot task allocation through a forbidden search algorithm with the objective of minimizing the completion time [33]. Zhang et al. designed an improved adaptive large neighborhood search algorithm for solving the problem with the objective of minimizing the maximum completion time by taking into account the dynamic task time-consuming characteristics of the system and the capacity constraints of the picking station’s seeding wall [34]. Tian et al. proposed a two-layer planning model for robot task allocation considering load quantity equalization for system congestion, and utilized an improved adaptive genetic algorithm introducing a sigmoid function to solve the problem [35]. Zhao et al. established a mixed-integer linear programming model with the objective of minimizing the order picking time for the cooperative optimization problem of robot task allocation and charging scheduling, and designed a genetic algorithm embedded with reinforcement learning to solve it [36].

In order to explore the coupling relationship between different influencing factors in RMFSs, some scholars have built multi-objective optimization models. Wang et al. constructed a multi-objective optimization model with the objectives of minimizing the maximum completion time, workshop energy consumption and the number of robots used to solve the sustainable optimal scheduling problem of a flexible job shop [37]. Wang constructed a multi-objective optimization mathematical model with the matching relationship between robots and tasks as the decision variable, and effectively solved the multi-robot multi-task assignment problem using a dynamic parameter-adaptive adjustment strategy adjusted from both local and global perspectives [38]. Zhang et al. solved the problem using the NSGA-II algorithm that introduces variable neighborhood search with the objective of minimizing the maximum completion time, total energy consumption, and the delivery penalty value of the workpiece [39].

2.3. Joint Optimization Problem for Pod Repositioning and Robot Task Allocation

More and more studies focus on joint optimization problems in RMFSs, which help to improve the overall efficiency of warehousing. On pod position optimization as well as joint optimization for path planning problems, Cai et al. proposed a pod location allocation strategy based on pod turnover rate by setting robot operation rules using a reservation table mechanism [40]. Lai et al. used movable pods as storage units, established a two-layer optimization model with the objective of minimizing the sum of optimized picking paths and pod movement costs for the warehouse layout in the upper layer, as well as the total picking paths in the lower layer, and designed a two-layer meta-heuristic algorithm to solve the problem [41]. Shi et al. proposed a three-item hybrid heuristic algorithm based on product supply relationships for solving order allocation and pod location optimization problems [42]. Wang et al. jointly optimized pod repositioning and pod sorting and designed a logic-based Benders decomposition exact solution algorithm (LBBD) [43].

A few scholars have considered the interaction between task allocation and pod repositioning. Bao et al. proposed a strategy that considers both task allocation and pod repositioning, i.e., a strategy in which pods are returned to the location that minimizes the sum of the distances between the assigned location and the next task position [44]. Shi et al. followed up by studying a pod scheduling problem with multiple types of storage locations by solving the storage location allocation problem in the upper tier, and a two-layer optimization method in the lower layer that determines the optimal order of picking up pods based on the given storage locations and performs joint optimization of pod repositioning and robot task allocation [45]. Zhuang et al. considered that the decisions of “stocking pod” and “picking pod” scheduling jointly determine the traveling distance of the robots, and with the goal of reducing the total traveling distance of the robots, they made a joint decision on pod repositioning and robot task allocation, constructed a multi-robot “storage–retrieval pod” scheduling optimization model, and designed an adaptive mathematical planning heuristic algorithm to solve the problem [46]. Li et al. also considered the impact of robot task allocation, and with the objective of minimizing the cost of robots to complete the task, they constructed a mathematical model that takes into account the difference in the cost of heavy load and no load, and proposed a joint optimization strategy that takes into account pod repositioning and task allocation [47].

In summary, current research focuses on decision optimization in picking situations, and the efficiency and cost increase caused by replenishment situations have not been fully considered in the joint optimization of pod repositioning and robot task allocation. In this paper, we focus on the impact of picking and replenishment on the pod repositioning and task allocation strategies, and construct a multi-objective pod repositioning and robot task allocation joint optimization model, with the aim of proposing a pod repositioning and robot allocation scheme that takes into account the replenishment situation and maximizes the picking efficiency.

3. Problem Description

Due to increased customer demand and shorter delivery times in modern e-commerce, orders fluctuate dramatically [48]. The method of pre-planning warehouse layout based on historical orders in traditional warehousing systems lacks dynamic adaptability and, when used for a long time, can easily lead to mismatches between pod demand patterns and pod positions. At the same time, each link in the warehouse operation is complementary to each other: workstations, pods and robots operate together to determine the order picking efficiency. The positions of the pods determine the distance that the robot needs to move when handling the pods, and the order of tasks assigned to the robot when handling the pods also affects the storage location allocation strategy of the pods. Therefore, the positions of pods are updated in real time as order patterns change, requiring dynamic adjustments in the reasonable allocation of robot tasks.

In this study, we first use historical order data to continuously predict future order demand and then solve for the corresponding expected layout based on future orders. On this basis, we dynamically update the expected layout according to the progressive storage mechanism to achieve the theoretical optimum of the expected layout. Guided by this expected layout, we jointly optimize the robot task allocation and the pod repositioning. That is, for each batch of operational tasks, it is necessary to complete the robot and pod task matching at the same time, based on the expected position of the optimal available positions for the return pod assignment. Through this collaborative decision-making model, we can effectively reduce the layout deviation, increase the storage system resource utilization efficiency, and reduce the order response speed due to the double enhancement.

The research problem of this paper can be described as follows: simulate order picking based on the future order set obtained from the historical order set prediction, obtain the picking hotness, replenishment hotness and inter-pod correlation of pods, accordingly plan the layout of the warehouse, obtain the expected layout, and guide the joint optimization of pod repositioning and robot task allocation. With the incoming orders, the historical order set changes and the expected layout needs to be adjusted. If each pod handling process is considered as a task, then decisions need to be made about which robot in the set of robots R will handle the pod, and the available positions l on the return trip after the pod has been handled, i.e., task allocation of the robots and repositioning of the pod. The pod repositioning decision affects the total distance moved by the robots, and the distance traveled by the robots affects the efficiency of the system, so in this paper, we make a joint decision on the pod repositioning and task allocation.

Based on the observation of the actual operation process in the picking center of a large online retailer and the related literature, this paper makes the following assumptions for the joint optimization problem of pod repositioning and robot task allocation:

(1)

Using wave picking and first-come-first-served strategies, orders are picked over a period of time in batches, and the order of order picking is consistent with the order in which the orders are passed to the picking station.

(2)

The types and quantities of SKUs stored in the initial pods are known and are stored using a decentralized storage strategy.

(3)

Task processing at the picking and replenishment stations is completed immediately.

(4)

Robot traveling distance is calculated according to the Manhattan distance.

(5)

After a pod completes a task, the pod always returns to the storage area before the next task can be performed.

(6)

Future orders can be predicted.

(7)

Congestion, acceleration/deceleration, and charging of robots are not considered.

4. Mathematical Model

In this paper, a joint optimization model is proposed to solve the complex operations in RMFSs. The symbolic parameters are defined as shown in

Table 1. Notation declaration of mathematical formulation.

Parameter	Description
$L$	Set of positions
$l$	Number of positions
$S$	Set of expected positions
$s$	Number of expected positions
$M$	Set of current positions, $M\in L$
$N$	Set of free positions, $N\in L$
$P$	Set of pods
$p$	Number of pods
$I$	Set of task pods, $I\in P$
$K$	Set of workstations, including picking stations and replenishment stations
$R$	Set of robots
$r$	Number of robots
${\mu }_r$	The position of robot $r$
$v_1$	The no-load speed of robot
$v_2$	The heavy-load speed of robot
$d_{p{p}^{\prime }}$	Distance traveled by the robot from position $l$, where pod $p$ is located, to position $l^{\prime }$, where pod $p^{\prime }$ is located, when the robot is no-loaded
$d_{lk}$	Distance traveled by a robot carrying pods from position $l$ to workstation $k$(or from workstation $k$ to position $l$)
${\pi }_i$	Workstations that carry out picking/replenishment operations on task pods, ${\pi }_i\in K$
$x_{mn}^{ri}$	If the task pod $i$ is carried by robot $r$ from position $m$ to complete the task and then stored in position $n$, the value is 1; otherwise, it is 0

.

In order to obtain the maximum time required for the robot to complete the task, the overall process affecting the distance traveled by the robot is first divided into three parts based on the storage-and-retrieve pod scheduling decisions in the warehouse.

(1)

No-load distance D₁: The distance the robot travels to the position of the task pod to carry the pod, and the distance the robot travels to the position of the next task pod after completing the storage of the previous task pod.

$$D_1={\displaystyle \sum _{r\in R}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{m\in M}{\displaystyle \sum _{n\in N}{d}_{{\mu }_{r}m}{x}_{mn}^{ri}}}}}$$

(1)

(2)

Carrying distance D₂: The distance a robot carries a task pod from a position to a workstation that needs to perform a picking/replenishment task on the pod.

$$D_2={\displaystyle \sum _{r\in R}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{m\in M}{\displaystyle \sum _{n\in N}{d}_{m{\pi }_i}{x}_{mn}^{ri}}}}}$$

(2)

(3)

Return distance D₃: The distance the robot carries the pod from the task workstation to the available positions.

$$D_3={\displaystyle \sum _{r\in R}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{m\in M}{\displaystyle \sum _{n\in N}{d}_{{\pi }_{i}n}{x}_{mn}^{ri}}}}}$$

(3)

From this, the distance required for the robot to complete the task can be obtained, which leads to the joint optimization model of this paper:

$$min{Z}_1=max({\displaystyle \frac{D_1}{v_1}}+{\displaystyle \frac{D_2+D_3}{v_2}})$$

(4)

$$min{Z}_2={\displaystyle \sum _{r\in R}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{m\in M}{\displaystyle \sum _{n\in N}{\displaystyle \sum _{s\in S}{d}_{l_i{s}_i}{x}_{mn}^{ri}}}}}}$$

(5)

$${\displaystyle \sum _{i\in I}{x}_{mn}^{ri}=1\hspace{1em}}\forall r\in R,m\in M,n\in N$$

(6)

$${\displaystyle \sum _{r\in R}{x}_{mn}^{ri}=1\hspace{1em}}\forall i\in I,m\in M,n\in N$$

(7)

$${\displaystyle \sum _{n\in N}{x}_{mn}^{ri}=1\hspace{1em}}\forall r\in R,i\in I,m\in M$$

(8)

$$x_{mn}^{ri}\in \left\{0,1\right\}\hspace{1em}\forall r\in R,i\in I,m\in M,n\in N$$

(9)

Objective function (4) minimizes the maximum completion time of robots. Objective function (5) denotes the minimization of the deviation between the task pod position and the expected position. Constraint (6) denotes that each task can only be performed by one robot; constraint (7) denotes that each robot can only carry one task pod at a time; constraint (8) denotes that each pod can only be stored in one position; and constraint (9) is the decision variable value constraint.

5. Algorithm Design

As mentioned earlier, this joint optimization problem is NP-hard, and the proposed joint optimization model for pod repositioning and task allocation can be solved using commercial solvers. However, the solvers have difficulty in efficiently handling large-scale problems in an acceptable time.

5.1. Introduction to the General Framework

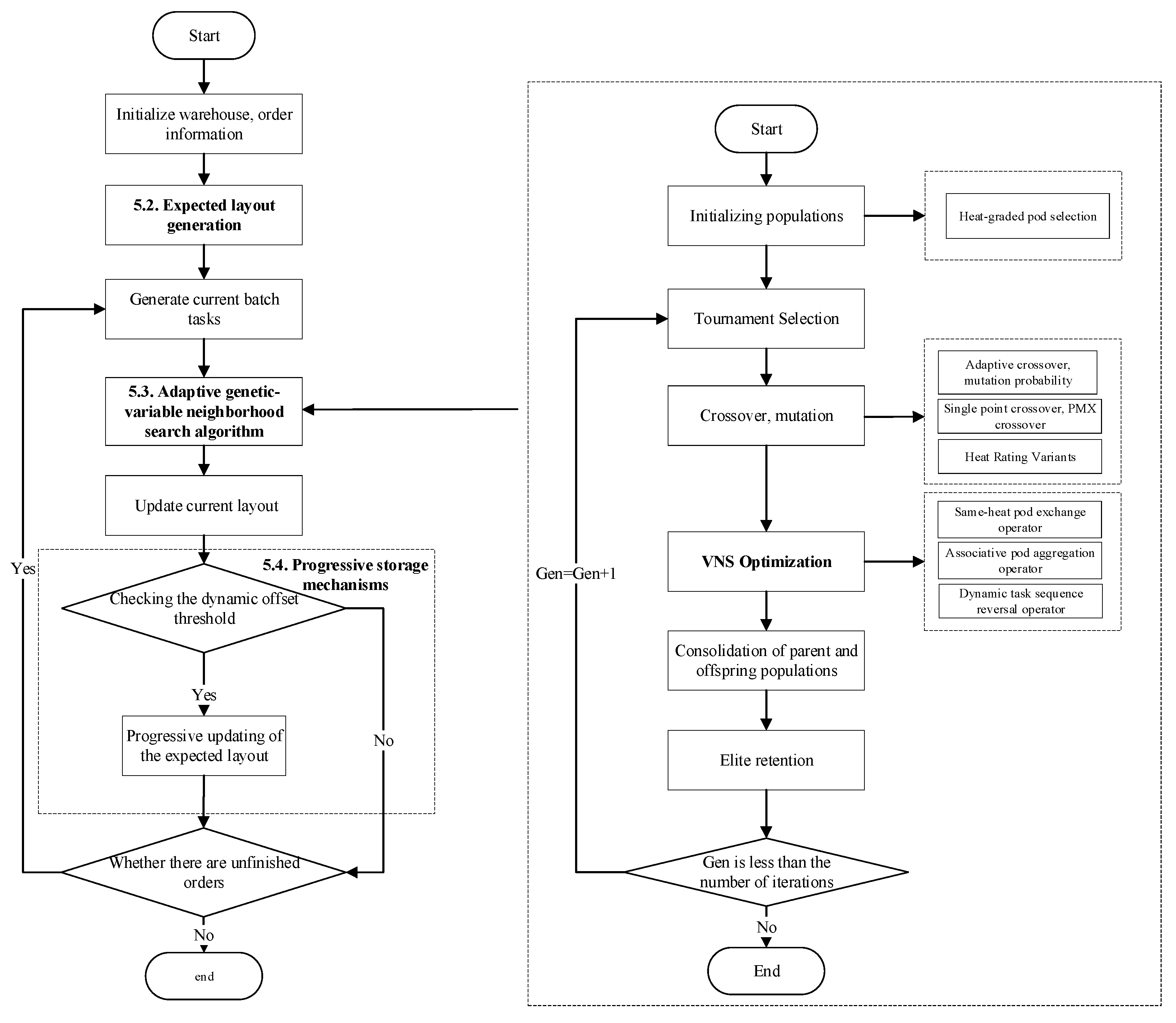
In this paper, we propose a joint optimization strategy of pod repositioning and task allocation based on pod heat guidance, which takes the expected layout of the system as the guide, and makes a joint decision on the robot task sequence and the target position allocation scheme of the return pod. At the same time, a progressive storage mechanism is introduced so that the expected layout can be continuously adjusted with the order update, forming a progressive optimization system of “prediction–layout–execution”.

With the changes in customer order requirements, future orders continue to update, the expected layout continuously iterates, the pod position dynamically adjusts, and each pod handling operation promotes the overall layout of the warehouse to the expected optimal state of gradual convergence, thereby effectively improving the utilization of warehouse layout and operational efficiency. The overall framework of this study is shown in Figure 2.

5.2. Predictive Layout Generation

5.2.1. Predictive Order Generation Strategy

Before the picking process starts, orders in the future period are predicted based on historical order data. In this paper, we adopt an order generation strategy that combines the Apriori algorithm and Monte Carlo simulation, which guides the predictive order generation by mining the commodity-associated features in the historical orders, and has better adaptability and accuracy compared to the traditional methods. The specific implementation is divided into two core phases:

• Merchandise association feature extraction based on the Apriori algorithm.

The Apriori algorithm is utilized to mine the association law between SKUs from historical order data to extract customers’ purchasing habits. Firstly, the frequency of each SKU appearing individually is counted to screen out high-frequency SKUs; then the combination relationship between SKUs is analyzed, and the strength of SKU association is quantified by support degree, as in Equation (10), to find the combination of SKUs that are often purchased at the same time. By setting a reasonable support threshold, the Apriori algorithm can automatically filter out the chance combinations and retain the truly meaningful association rules.

$$support\left(X\right)={\displaystyle \frac{O_x}{O}}$$

(10)

In the above equation, O is the total number of orders, and $O_X$ is the number of orders containing item set X.

2.

Order generation based on Monte Carlo simulation.

Monte Carlo simulation utilizes the association features extracted by Apriori to generate predicted orders that match the real scenario through random sampling. In the generation process, the order law proposed in the literature is followed [49]: about 60% of the orders contain only a single item, and 40% contain 2–3 items; when generating multi-item orders, as shown in Equation (11), priority is given to selecting historical high-frequency combinations, and the rest of the scenarios are randomly paired according to the hotness of the SKUs. The number of SKUs purchased follows the Pareto distribution; 80% of the orders are only 1 item, and a small number of orders contain 2–5 items.

$$P(X|S)=\beta U(F_{\left|S\right|})+(1-\beta ){\displaystyle \prod _{i\in X}\frac{f_i^{\alpha }}{{\displaystyle \sum f_k^{\alpha }}}}$$

(11)

In the above equation, $\beta$ is the frequent itemset selection probability, $F_n$ is a collection of n-frequent term sets, $U\left(\cdot \right)$ is a uniformly distributed sampling function, $f_i$ is the historical frequency of occurrence of commodity $i$, and $\alpha$ is the frequency weighting index.

This stratified sampling approach ensures a reasonable frequency of occurrence of high-frequency SKUs and popular combinations, while simulating uncertain behavior in real shopping through controlled randomness. The final generated order retains the historical core features while flexibly adapting to the changing needs of the business.

5.2.2. Priority-Based Pod Selection Method

To fulfill orders, pods are selected for picking operations and replenished when necessary. An efficient pod selection operation ensures that the picking station meets the items required for the order and minimizes the maximum completion time of robots. As shown in Figure 3, the pod selection process consists of two parts: the matching of orders and pods, and the picking and replenishment operations of pods. On the one hand, the matching of orders and pods as well as the replenishment plan of pods affects the heat and correlation of pods, which plays an important role in calculating the expected position of the current pod. On the other hand, when the quantity of a product on a pod reaches the replenishment threshold and needs to be replenished, the pod is not available for the next batch of task allocations, which reduces the options available in the pod selection group, and replenishment needs to be assigned to be carried by the robot to the replenishment station, which takes up robot resources and improves the robot’s operation cost.

The pod selection problem is modeled as follows:

$$\min {\displaystyle \sum _{p\in P}{\displaystyle \sum _{o\in O}{\mathrm{y}}_{op}+z_{op}}}$$

(12)

$${\displaystyle \sum _{p\in P}{x}_{opi}\ge }{r}_{oi}\hspace{1em}\forall o\in O,i\in I$$

(13)

$$x_{opi}\le {\mathrm{q}}_{pi}\hspace{1em}\forall o\in O,i\in I$$

(14)

$$M{y}_{op}\ge {\displaystyle \sum _{i\in I}{x}_{opi}}\hspace{1em}\forall o\in O,p\in P$$

(15)

$${\displaystyle \sum _{k\in K}{\omega }_{ok}}\le 1 \hspace{1em}\forall o\in O$$

(16)

$${\displaystyle \sum _{p\in P}\ln \left(z_{op}+\alpha \right)\left[(q_{pi}-x_{opi})-{\mathrm{e}}_i\right]}<0 \hspace{1em}\forall o\in O,i\in I,\alpha \in (0,1)$$

(17)

$$x_{opi}\in Z^{+},y_{op}\in \{0,1\}$$

(18)

In the above equation, objective function (12) represents the minimization of the number of pod movements, which contains both picking and replenishment movements. $y_{op}$ is 1 if pod $p$ has been used in the picking process that satisfies the set of orders $O$, and 0 otherwise, and $z_{op}$ is 1 if it has been used in the replenishment process. Constraint (13) denotes that the customer demand of a picking order for a particular item must be satisfied, and the total quantity $x_{opi}$ of pods $p$ to provide picking for SKU $i$ in the order set $O$ cannot be smaller than the total quantity $r_{oi}$ of SKU $i$ needed in the order set $O$. Constraint (14) is a SKU availability constraint that indicates that each SKU in the picking order can be picked from the position and $x_{opi}$ cannot be greater than the total number $q_{pi}$ of stored SKUs $i$ on pod $p$. Constraint (15) defines the relationship between the variables x and y. The number of SKUs offered for picking must be zero when the number of pod $p$ moves is zero. Constraint (16) indicates that each order can be processed by at most one workstation, and the value of ${\omega }_{ok}$ is 1 if the set of orders $O$ is processed by picking station $K$, and 0 otherwise. Constraint (17) defines the relationship between the replenishment threshold and replenishment, when the pod provides the number of items $x_{opi}$ for order picking, resulting in the quantity $q_{pi}$ of SKU $i$ stored on pod $p$ being less than the replenishment threshold $e_i$, the pod needs to be replenished, and the number of replenishments should be increased. Constraint (18) defines the domains of the variables.

The resulting picking heat and replenishment heat of the pod are shown in Equation (19) and Equation (20), respectively:

$$m_p={\displaystyle \sum _{o\in O}{\mathrm{y}}_{op}\hspace{1em}\forall p\in P}$$

(19)

$$n_p={\displaystyle \sum _{o\in O}{z}_{op}\hspace{1em}\forall p\in P}$$

(20)

And combined with the idea of pod prioritization proposed in the literature [50], the replenishment process is added to the picking operation, considering the change in the remaining quantity of SKUs in the case of replenishment, and designing the greedy picking algorithm based on pod prioritization for solving.

5.2.3. Bi-Level Position Optimization Algorithm

Pod location optimization is performed according to the pod heat and inter-pod correlation obtained from the pod selection algorithm. Since the positions of the picking and replenishment stations in the RMFS warehouse are fixed, the position of the pods determines the distance that the robot needs to move when handling the pods. By arranging the pods in suitable locations, the demand pattern of the pods is matched with the positions in the warehouse. As shown in Figure 4, the time and distance traveled by the robot can be reduced by placing the high heat pods closer to the workstations and the high picking pods closer to the picking tables in the expected layout.

The pod location optimization problem is modeled as follows:

$$\min {\displaystyle \sum _{p\in P}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K}{m}_p{d}_{lk}{x}_{pl}}}}+{\displaystyle \sum _{p\in P}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{s\in S}{n}_p{d}_{ls}{x}_{pl}}}}+{\displaystyle \sum _{p\in P}{\displaystyle \sum _{p^{\prime }\in P}{r}_{p{p}^{\prime }}{d}_{p{p}^{\prime }}}}$$

(21)

$${\displaystyle \sum _{l\in L}{x}_{pl}=1\hspace{1em}\forall p\in }P$$

(22)

$${\displaystyle \sum _{p\in P}{x}_{pl}\le 1\hspace{1em}\forall l\in L}$$

(23)

$$x_{pl}\in \left\{\left.0,1\right\}\right.$$

(24)

In the above equation, objective function (21) represents minimizing the total distance traveled by the robot. The objective function contains three parts. The first part is the distance of the robot carrying pods to the picking station; $x_{pl}$ indicates that the value is 1 if the pod $p$ is stored on the storage position $l$ and 0 otherwise, and the total distance of the pod $p$ to the picking station in the whole picking process is obtained by the pod picking heat $m_p$ and the distance traveled by the robot carrying pods from the storage position $l$ to the picking station $k$ (or from the picking station $k$ to the storage position $l$). In the second part, similarly, the total distance of pod $p$ to the replenishment station during the whole replenishment process is obtained by the pod replenishment heat $n_p$ and the distance traveled by the robot to carry the pod from the storage position $l$ to the replenishment station $s$ (or from the replenishment station $s$ to the storage position $l$). The third part is the no-load distance; $d_{p{p}^{\prime }}$ denotes the distance traveled when arriving from pod $p$ to another pod $p^{\prime }$, and $r_{p{p}^{\prime }}$ denotes the correlation between the two pods. Constraint (22) indicates that a pod can only be placed in one position; constraint (23) indicates that at most one pod can be placed in one position; and constraint (24) is a variable-value constraint.

5.3. Adaptive Genetic-Variable Neighborhood Search Algorithm

Considering that the genetic algorithm has a strong global search capability but has the disadvantage of early convergence in the early stage and slow convergence in the late stage, this paper proposes an improved genetic algorithm, namely, adaptive genetic-variable neighborhood search algorithm (AGA-VNS). By introducing adaptive transform probability and local search process in GA, a hybrid optimization algorithm of global generalization and local refinement is developed. Firstly, the initial population is generated according to the greedy idea to improve the randomness and diversity of the first-generation population; then, a combination of elite retention and roulette is used to select individuals and construct crossover and mutation operators with adaptive transformation probabilities to obtain the new population; finally, finer local operations are carried out on the sub-generation mid-population from each individual to improve the overall performance of the algorithm. The improved genetic algorithm process has been demonstrated in Figure 1, and the main steps are as follows:

5.3.1. Chromosome Code

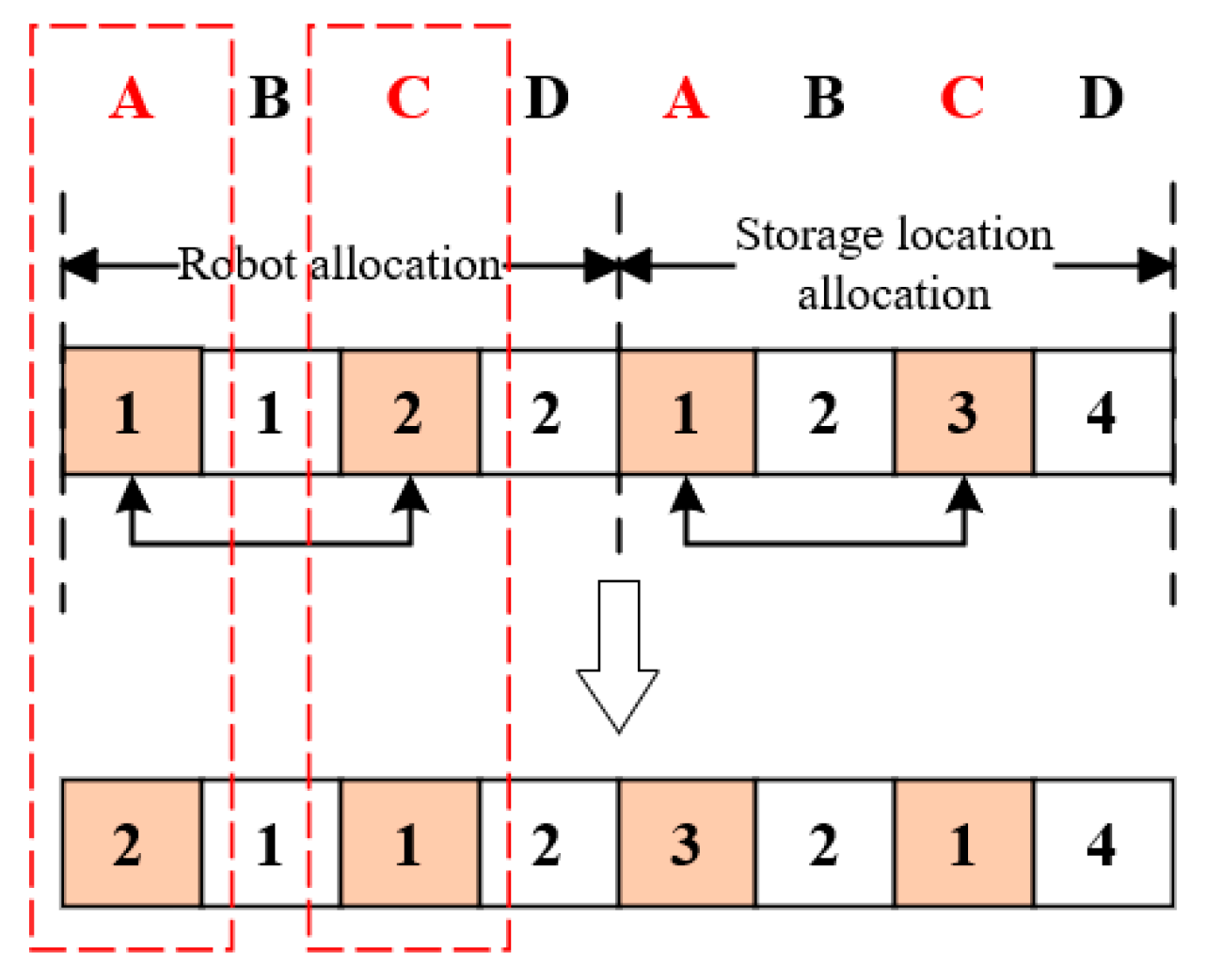
In order to jointly optimize the task allocation and pod repositioning operations, a chromosome is designed, as shown in Figure 5. The left half of the chromosome is the robot task allocation sequence, and each gene bit represents a robot number, the right half of the chromosome is the storage location allocation for pod repositioning, and each gene bit represents a position number; the number of gene bits is the number of tasks to be accomplished in the current batch, and the gene order is the current task order. This encoding method allows direct visualization of the direct matching of tasks to robots and pods to positions; for example, in Figure 4, the total number of tasks in the batch is 4, and task pod 1 is carried by robot 2 and reassigned to location 4.

5.3.2. Multi-Objective Processing

In practical pod repositioning problems, the direct trade-off between the two objective functions is challenging due to their varying importance. Furthermore, significant differences exist in both the units of measurement and magnitudes of the two objectives, making simple linear weighting methods inadequate for handling these multiple objectives.

A multi-objective model with the objectives of maximizing the completion time required for the robot to complete the task and minimizing the deviation of the pods from the expected positions is developed. In the actual pod repositioning problem, it is difficult to coordinate the two objective functions due to their different importance. Furthermore, significant differences exist in both the units of measurement and magnitudes of the two objectives, making simple linear weighting methods inadequate for handling these multiple objectives [51]. The specific steps of multi-objective processing in this paper are as follows.

Step 1: Convert the multi-objective model into two objective models and solve them. These two optimal objective values are defined as $f_1^{*}$ and $f_2^{*}$.

Step 2: Calculate the new target values $F_1$ and $F_2$ by Equations (25) and (26). Obviously, this step not only eliminates the differences in the units of measure of the three targets, but also restricts them to the same order of magnitude.

$$F_1=f_1/f_1^{*}$$

(25)

$$F_2=f_2/f_2^{*}$$

(26)

Step 3: Propose the weights for each of the three objectives. The two weight parameters are defined as ${\omega }_1$ and ${\omega }_2$ and satisfy the following constraints:

$${\omega }_1+{\omega }_2=1$$

(27)

$${\omega }_1,{\omega }_2\ge 0$$

(28)

Step 4: Calculate the integrated objective value. The new objective function of the multi-objective model is defined as Equation (29).

$$\min F={\omega }_1{F}_1+{\omega }_2{F}_2$$

(29)

5.3.3. A Strategy for Pod Selection Based on Heat Grading

In order to obtain a high-quality solution quickly and optimize the optimization search process, this paper proposes a pod selection method under the consideration of heat grading. By setting the maximum offset of the pods, the high-heat-degree pods are prioritized to select the location closer to the expected location.

5.3.4. Adaptive Crossover and Variational Operators

The setting of the crossover and mutation probability values has a great influence on the optimization process of the solution; the crossover probability and mutation probability of traditional genetic algorithms are set to a fixed value according to the experience and subjective judgment; if they are set to a smaller value, it will make the individual evolution slower and increase the algorithm’s solution time, and if they are set to a larger value, it will be easy to destroy the excellent individuals in the late stage of the algorithm’s solution, so that the algorithm will fall into the locally optimal solution. In order to accelerate the speed of population optimization search, this paper refers to the crossover and mutation operator design ideas proposed in the literature [52]. The population is highly explored with a large crossover variance probability in the early stage to increase the diversity of solutions, and the crossover variance probability gradually becomes smaller in the late stage to avoid destroying the excellent individuals and to avoid premature convergence while maintaining the diversity of the population. The adaptive crossover and variance probability formulas are shown in Equations (30) and (31).

$$P_c=\left\{\begin{array}{l}{P}_{c\text{\_}\max }-{\displaystyle \frac{\left(P_{c\text{\_}\max }-P_{c\text{\_}\min }\right)\left(f^{\prime }-f_{avg}\right)}{f_{\max }-f_{avg}}},f^{\prime }\ge f_{avg}\hfill \\ P_{c\text{\_}\max },f^{\prime }<f_{avg}\hfill \end{array}\right.$$

(30)

$$P_m=\left\{\begin{array}{l}{P}_{m\text{\_}\max }-{\displaystyle \frac{\left(P_{m\text{\_}\max }-P_{m\text{\_}\min }\right)\left(f^{\prime }-f_{avg}\right)}{f_{\max }-f_{avg}}},f^{\prime }\ge f_{avg}\hfill \\ P_{m\text{\_}\max },f^{\prime }<f_{avg}\hfill \end{array}\right.$$

(31)

In the above equation, $P_{c\text{\_}max}$, $P_{m\text{\_}max}$ are the maximum values of the crossover and variance probability intervals, respectively; $P_{c\text{\_}min}$, $P_{m\text{\_}max}$ are the minimum values of the crossover and variational probability intervals, respectively; $f$ is the individual fitness value; $f^{\prime }$ is the fitness value of the optimal individual in the parent that performed the crossover; $f_{max}$ is the maximum of all individual fitness values; $f_{avg}$ is the average fitness value for all individuals.

Considering that there is a one-to-one correspondence between pods and positions in the warehouse, if the operation is carried out according to the traditional crossover and mutation, it will destroy the original feasible solution and produce a large number of infeasible solutions, which will require a large amount of time to repair. In this regard, we design the crossover and mutation operators.

• Crossover operator.

Task allocation part: Randomly select multiple crossover points, exchange the genes at the corresponding positions of the two parent individuals, and obtain two new offspring. Pod repositioning part: For pod number, since the encoding of the pod number array is unique, this paper adopts the Partial Matching Crossover (PMX) to ensure that each pod gene is unique among the offspring.

2.

Mutation operator.

A single point mutation at even randomized positions was used to randomly select two pod number exchange genes on the chromosome.

5.3.5. Introduction to the VNS Operator

In order to improve the local search capability of AGA, this paper designs three neighborhood search operators oriented to two different optimization objectives, namely the maximum robot completion time and the total layout deviation, so as to ensure that each objective can be quickly and accurately approached to the optimal solution in the iterative process.

• Same-heat pod exchange operator.

Since the same-heat pod has similar access frequency and optimization needs, the exchange of positions will not destroy the overall heat distribution pattern; as shown in Figure 6, the letter indicates the pod number, the number indicates the solution, while colors denote changes during the update process. Assuming that pods A and C are the same-heat pods (marked by red dotted lines), the two corresponding robot allocation numbers and storage location allocation numbers can be exchanged. In addition, the exchange of high-heat pods can fine-tune the position to reduce the deviation, and the exchange of low-heat pods can increase the flexibility of the warehouse layout.

2.

Associative pod aggregation operator.

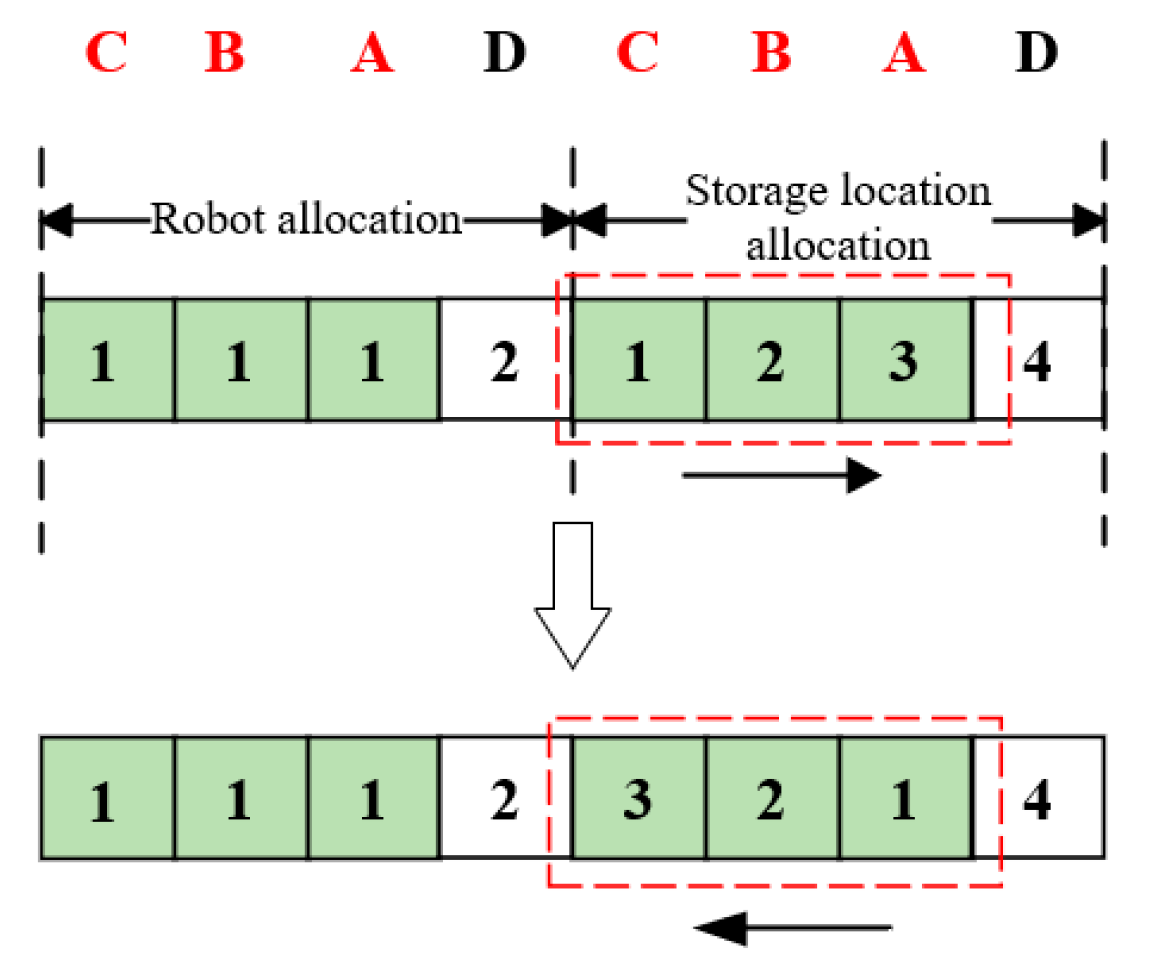
Aggregation of frequently co-visited pod positions that are continuously handled by the same robot. The proximity of associated pods (e.g., frequently present in the same order) can significantly reduce the cross-zone travel distance for future handling. Continuous execution by the same robot avoids empty trips due to task splitting. As shown in Figure 7, the letter indicates the pod number, the number indicates the solution, while colors denote changes during the update process. Assuming that B and D are associated pods and that pod D is hotter, pod D is used as the center to find the nearest available positions, e.g., C (marked by red dotted lines). The pre-reassigned positions of B and C are swapped, and pod B will be handled by Robot 2 that is handling pod D.

3.

Dynamic task sequence reversal operator.

The task order directly affects the robot path length, and the optimal handling sequence for the robot is found by dynamically adjusting the task order. The insertion operation can jump out of the local optimum and explore more compact path combinations. As shown in Figure 8, the letter indicates the pod number, the number indicates the solution, while colors denote changes during the update process. For a batch of task pods A–D, task points A and C are selected as the basis for reverse operations. By altering the sequence between these two task points (marked by red dotted lines), the optimal sequence for the robot to complete the task is determined.

5.4. Progressive Storage Mechanism

Since the expected layout plays a guiding role in the joint optimization strategy proposed in this paper, and the wrong expectation will make the warehouse layout gradually change in the direction of inefficiency, the expected layout needs to be continuously updated with the incoming orders to maintain the advancement. However, frequent updating of the expected layout will not only increase unnecessary pod handling operations, but also waste a lot of arithmetic power in the warehouse management system. Therefore, this paper designs a novel progressive storage mechanism. The mechanism contains two parts, the dynamic offset threshold and the expected layout update mechanism, as shown in Figure 2, with the dynamic offset threshold as the judgment criterion. When the overall pod offset of the standardized warehouse exceeds the dynamic offset threshold, it indicates that the current expected layout has deviated too much from the actual situation, and it needs to be updated by using the predictive layout update mechanism, or else it can continue to maintain the original expected layout.

5.4.1. Dynamic Offset Threshold

The deviation threshold is dynamically adjusted by an exponential decay function, as shown in Equation (32), where a higher threshold is set at the initial stage to accommodate fluctuations during the initialization phase of the system and then gradually lowered to the steady-state threshold by the decay coefficient with the increase in picking batches. This nonlinear decay characteristic accurately simulates the progressive optimization process of warehouse operation: at the initial stage, a large positional deviation is allowed to accumulate to reduce the cost of frequent adjustments, and at the later stage, the deviation growth is responded to by tightening the threshold value in time to ensure that the system always operates near the optimal state.

$$e(t)={\theta }_{init}\times e^{-kt}+{\theta }_{stable}$$

(32)

In the above equation, $t$ is the number of batches processed, ${\theta }_{init}$ is the initial threshold, $k$ is the decay rate, and ${\theta }_{stable}$ is the steady-state threshold. When the normalized deviation is greater than the dynamic offset threshold, the update of the expected layout is performed. The values of parameters ${\theta }_{init}$, $k$ and ${\theta }_{stable}$ were determined using a systematic Taguchi method through Minitab 21 software. This optimization employed the signal-to-noise ratio (S/N) as the metric, aiming to ensure the robustness of the proposed mechanism across different operational scenarios.

5.4.2. Mechanisms for Updating the Expected Layout

Directly updating the expected layout is likely to cause turbulence in the warehouse layout, so the expected layout is updated by adopting a greedy idea of “Stronger animals prey on weaker ones”. Since the high-heat-level pods are handled frequently, they have a greater impact on the system performance. Therefore, the high-heat pods are defined as “strong” and the low-heat pods are defined as “weak”, and the high-heat pods have a higher priority in the selection of pod locations.

As shown in Figure 9, this diagram illustrates the adjustment process from original to new expected layout for 20 pods. The first row shows pod numbers, the second row displays original expected position numbers, and the third row indicates new expected position numbers. Under this mechanism, high-temperature pods (marked with red circles in the first row) will prioritize the new expected position, while the original expected positions for low-temperature pods will be retained. The final adjustment results are shown in the last row, clearly reflecting the mechanism.

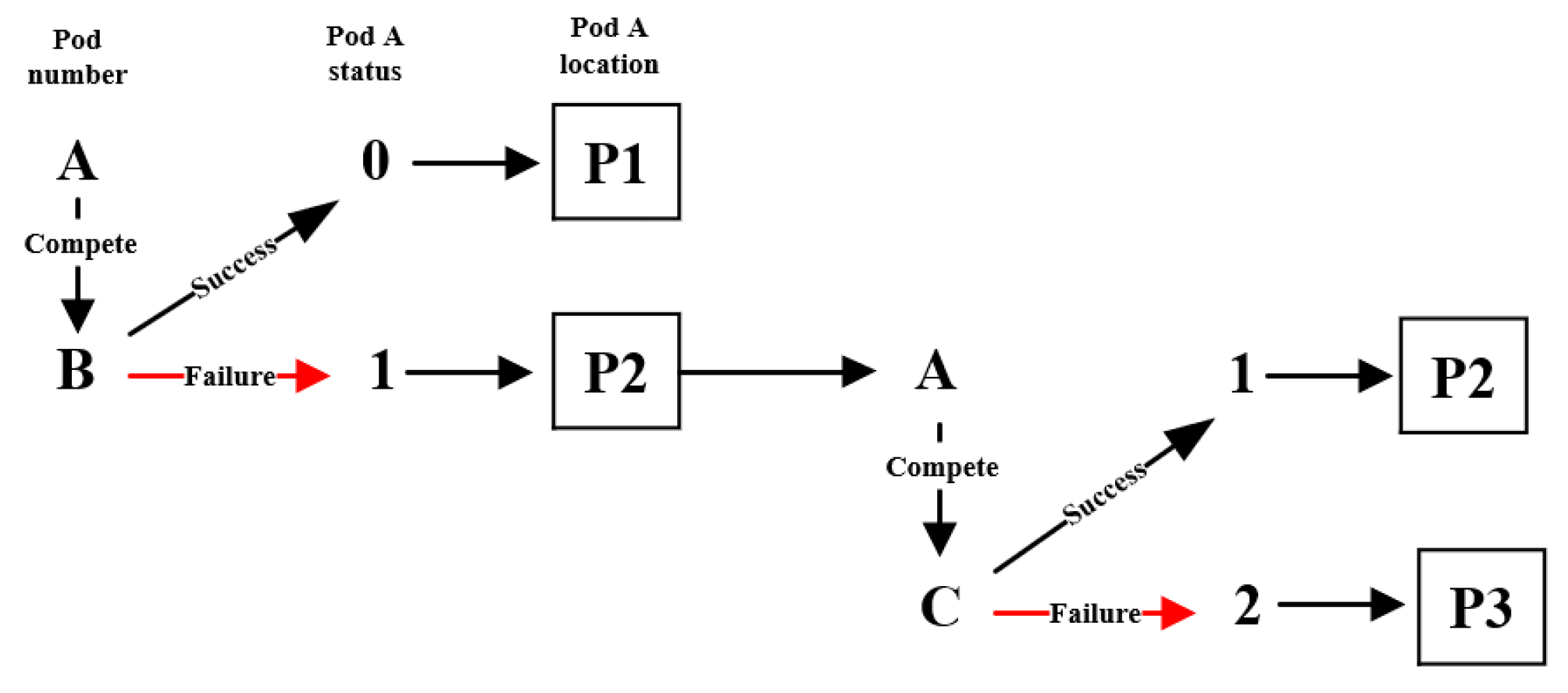
For conflict resolution, a novel “Double-elimination” mechanism is designed based on the recursive idea, which utilizes three levels of states to mark the pods (0: not updated; 1: updated; 2: need to be optimized), so that when the low-heat pods fail in the conflict competition, they have one opportunity to choose to force the pods to be updated to the expected position; otherwise, they can only choose a closer position to their original expected position from among the remaining locations. Otherwise, it can only choose the position that is closer to its original expected position from the remaining storage positions.

As shown in Figure 10, assume that pod A and pod B have a position conflict, with both currently having the expected position P1. If pod A’s original expected position was P2, then after pod A loses the competition with pod B, its status is marked as “1,” and its expected position reverts from P1 back to its original expected position P2. If the conflict remains unresolved, and pod A subsequently loses a competition with another pod C, its status updates to “2”. At this point, the system abandons the expected position strategy and instead executes the nearest match strategy, forcibly assigning pod A to the nearest available position P3.

6. Numerical Study

6.1. Instance Generation and Parameter Setting

In this paper, we refer to the data of a large e-commerce warehouse used in the literature [49] for the simulation of order, product and pod information. According to the existing literature and survey data, the heavy-load speed of the robot is set to 0.8 m/s, and the no-load speed to 1.6 m/s. In order to verify the effectiveness of the joint optimization strategy, the progressive storage strategy, and the improved genetic algorithm proposed in this paper, this paper consists of designing three different scales of the instances (I, II, and III) in accordance with the scales of the warehouses in the literature [18], from small to large. The specific characteristics of the arithmetic examples are shown in

Table 2. Parameters for instance generation.

Instance	No.	P	O	I	K	S	R
I	1	8	80	40	1	1	2
	2	10	100	50			2
	3	16	160	80			2
	4	20	180	90			2
II	5	30	280	140	2	2	3
	6	32	320	160			3
	7	40	400	200			3
	8	48	480	240			3
	9	60	560	280			3
	10	64	600	300			3
III	11	100	900	450	3	2	5
	12	144	1440	720			5
	13	200	1800	900			5
	14	250	2400	1200			8
	15	288	2700	1350			8
	16	320	3000	1500			8
	17	350	3300	1650			10
	18	432	3900	1950			10

. The algorithms are programmed using MATLAB R2022 a on a computer with the Windows 10 operating system, 8 GB of memory, and an Intel (R) Core (TM) i5- 8250 U CPU. The main frequency is 1.80 GHz.

6.2. Comparison of Experimental Results

6.2.1. Comparison of the Different Strategies

In order to validate the effectiveness of the joint optimization strategy of pod repositioning and robot task allocation based on pod heat dominance, this paper, based on the staged optimization method designed in the literature [46], similarly designs three staged optimization strategies for pod repositioning and robot task allocation: (1) nearby storage location assignment and nearby robot allocation (NN); (2) nearby storage location assignment and random robot allocation (NR); and (3) fixed storage location allocation and nearby robot allocation (FN). Under the progressive layout strategy, the proposed method in this paper is compared with the above three staged optimization strategies, and the results are shown in

Table 3. Comparison of different strategies in the instances.

No.	Joint Optimization		NN		NR		FN		GAP
	f1	f2	f1	f2	f1	f2	f1	f2	NN	NR	FN
1	696.875	5	763.75	9	876.875	11	757.5	8	8.76%	20.53%	8.00%
2	975.625	8	1096.25	14	1346.875	22	1091.875	16	11.00%	27.56%	10.65%
3	1725.625	37	1897.5	54	2156.875	49	1938.125	53	9.06%	19.99%	10.96%
4	2152.5	52	2415.63	51	2798.75	70	2458.125	82	10.89%	23.09%	12.43%
Average									9.93%	22.79%	10.51%
5	2683.125	99	3041.88	125	3704.375	110	3094.375	135	11.79%	27.57%	13.29%
6	3205.625	110	3790.63	175	4981.25	187	3750.625	177	15.43%	35.65%	14.53%
7	4661.875	177	5313.75	214	6604.375	229	5326.25	242	12.27%	29.41%	12.47%
8	6491.25	263	7651.88	293	9516.875	300	7526.875	302	15.17%	31.79%	13.76%
9	8113.75	405	9703.13	421	12251.25	446	9921.25	455	16.38%	33.77%	18.22%
10	8778.125	441	10503.8	431	12184.38	458	10275.625	479	16.43%	27.96%	14.57%
Average									14.58%	31.02%	14.47%
11	9362.5	715	10633.8	845	14636.25	850	10931.875	870	11.95%	36.03%	14.36%
12	19599.38	1532	23175.6	1535	31521.88	1543	23630	1542	15.43%	37.82%	17.06%
13	33405	2439	38031.9	2560	50943.75	2670	38575.625	2730	12.17%	34.43%	13.40%
14	35432.5	3750	43188.1	3894	65063.75	3863	44173.125	3780	17.96%	45.54%	19.79%
15	39550.63	4379	48185.6	4444	72523.75	4469	49272.5	4346	17.92%	45.47%	19.73%
16	57484.38	5866	69009.4	6070	102561.9	6176	69773.75	5928	16.70%	43.95%	17.61%
17	53645	6694	67215.6	6887	104468.1	6795	68026.875	6950	20.19%	48.65%	21.14%
18	67336.25	8442	82298.1	8767	129371.9	8792	82821.875	8850	18.18%	47.95%	18.70%
Average									16.31%	42.48%	17.72%

. The metrics that determine the performance of an RMFS are f1, which is the maximum completion time required for the robot to complete the task, and f2, which is the optimization of the overall warehouse layout; these are idealized metrics, so the warehouse layout can only be close to the expected layout due to the correlation relationship between the access pods. Therefore, in Table 3, only the optimized gap for f1 is shown.

Several findings can be drawn from Table 3.

(1)

The optimization objective f1 solved by the joint optimization strategy proposed in this paper outperforms the staged optimization strategy in all the instances, while the optimization objective f2 is mostly better than the other three strategies, thus verifying its effectiveness.

(2)

The joint optimization strategy also achieves considerable improvement in the optimization ratio, which covers the range of 8% to 48.65% in different cases, and the performance advantage is very significant. When the scale increases, the optimization ratio of the joint optimization strategy also shows a continuous and obvious growth trend; for example, in the case of NN, the average value of gap is also increased from 9.93% in instance I to 16.31% in instance III, which fully demonstrates that the joint optimization strategy has a scalable advantage in dealing with large-scale and high-complexity problems, and its performance advantage is even more prominent in the more challenging real-world scenarios.

(3)

Among the three phased scheduling optimization strategies, the nearest storage and random robot task assignment (NR) strategy achieves the worst results, and the average gap with the joint optimization method at the third arithmetic scale reaches 42.48%, which indicates that there are inherent limitations in random robot task assignment, which can produce strong negative effects, and that a reasonable robot assignment rule can help to improve the pod repositioning effectiveness and help companies improve their operational efficiency faster.

6.2.2. Comparison of the Two Mechanisms

In order to verify the effectiveness of the progressive storage mechanism proposed in this paper, the performance differences between the processes using the progressive storage mechanism and those not using the progressive mechanism in different instances are compared under the same joint optimization strategy, and the results are shown in

Table 4. Comparison of progressive and non-progressive storage mechanisms in instances.

No.	Progressive		Non-Progressive		GAP
	f1	f2	f1	f2	f1	f2
1	696.875	5	715.625	7	2.62%	28.57%
2	975.625	8	1003.125	8	2.74%	0.00%
3	1725.625	37	1776.875	44	2.88%	15.91%
4	2152.5	41	2268.75	52	5.12%	26.83%
Average					3.34%	17.83%
5	2683.125	99	2817.5	104	4.77%	4.81%
6	3205.625	110	3427.5	120	6.47%	8.33%
7	4661.875	177	4936.875	191	5.57%	7.33%
8	6491.25	263	6996.875	249	7.23%	−5.62%
9	8113.75	373	8977.5	405	9.62%	8.58%
10	8778.125	441	9523.75	404	7.83%	−9.16%
Average					6.91%	2.38%
11	9362.5	715	10931.875	828	14.36%	13.65%
12	19599.375	1532	23593.125	1522	16.93%	−0.66%
13	33405	2439	38571.875	2550	13.40%	4.35%
14	35432.5	3750	44162.5	3902	19.77%	3.90%
15	39550.625	4379	49246.25	4388	19.69%	0.21%
16	57484.375	5866	69761.25	6069	17.60%	3.34%
17	53645	6694	68036.25	6878	21.15%	2.68%
18	67336.25	8442	82813.75	8811	18.69%	4.19%
Average					17.70%	3.96%

.

From Table 4, the following can be seen:

(1)

The progressive storage mechanism is superior to the non-progressive mechanism in solving f1 in different instances, and most of the optimization objectives f2 are better than the non-progressive mechanism, which is enough to prove the effectiveness of the progressive mechanism.

(2)

The enhancement value of the optimization objective f1 of the progressive mechanism compared to the non-progressive mechanism becomes bigger with the scale increases, and there is more than 3% enhancement for the optimization objective f2 in instance II and instance III, indicating that the progressive mechanism has excellent scale adaptability and can meet the needs of real enterprise large-scale warehouse operation.

6.2.3. Algorithm Performance Comparison

In order to verify the performance of the AGA-VNS algorithm proposed in this paper, AGA and VNS are applied to solve the joint optimization strategy in this paper. The above three algorithms are run under three instances, and the results are shown in the table, still focusing on the maximum completion time f1.

Table 5. Comparison of algorithm experimental results.

No.	AGA		VNS		AGA-VNS		GAP
	f1	f2	f1	f2	f1	f2	AGA	VNS
1	712.5	5	721.25	6	696.875	5	2.19%	3.38%
2	1003.75	12	1067.5	9	975.625	8	2.80%	8.61%
3	1814.375	39	1834.375	49	1725.625	37	4.89%	5.93%
4	2270	52	2306.875	69	2152.5	52	5.18%	6.69%
Average							3.77%	6.15%
5	2793.75	93	3184.375	110	2683.125	99	3.96%	15.74%
6	3401.875	144	3650.625	136	3205.625	110	5.77%	12.19%
7	4846.875	191	5305	177	4661.875	177	4.92%	12.12%
8	6731.25	263	7439.375	245	6491.25	263	4.57%	12.74%
9	8621	362	9854.375	356	8113.75	405	5.88%	17.66%
10	9085	479	9825.625	435	8778.125	441	3.38%	10.66%
Average							4.75%	13.52%
11	9983.125	816	11887.5	793	9362.5	715	6.22%	21.24%
12	22011.15	1433	25025	1483	19599.38	1532	10.96%	21.68%
13	35913.125	2437	38422.5	2466	33405	2439	6.98%	13.06%
14	39934.375	3758	47560	3534	35432.5	3750	11.27%	25.50%
15	45298.75	4379	52200	4116	39550.63	4379	12.69%	24.23%
16	62541.875	6035	72536.875	5729	57484.37	5866	8.09%	20.75%
17	62106.25	6677	74310	6761	53645	6694	13.62%	27.81%
18	75651.875	8629	91301.875	8310	67336.25	8442	10.99%	26.25%
Average							10.10%	22.57%

shows the experimental results of the algorithm performance comparison.

As can be seen from Table 5,

(1)

AGA-VNS has obvious advantages in terms of solution quality compared with both AGA and VNS, and thus AGA-VNS is able to solve the joint optimization problems better.

(2)

The enhancement of AGA-VNS with respect to AGA and VNS also shows a strong scale dependence, and compared to AGA, as the scale of the instances increases, AGA-VNS can further reduce the maximum completion time by 6.33% (10.10–3.77%), indicating that AGA-VNS has outstanding advantages in dealing with large-scale problems, fully integrating the global search capability of AGA and the local development mechanism of VNS.

(3)

The enhancement magnitude of AGA-VNS compared to VNS is significantly higher than that of the enhancement to AGA, which suggests that AGA provides a key support for VNS, and by consistently providing high-quality and diversified initial solutions, it significantly improves the search starting point of VNS.

6.3. Sensitivity Analysis

From the Section 6.2, it can be seen that the index to judge the efficiency in the RMFS is mainly f1, and f2 focuses more on adjusting the pod position towards the expected warehouse layout, which is an idealized state. Therefore, in this paper, we mainly analyze the sensitivity of f1, and show the results of f1 in terms of the number of free positions and the number of robots.

6.3.1. Analysis of the Effect of the Number of Free Positions on the Maximum Completion Time

Companies usually design a certain number of free positions in RMFSs as a way to increase the flexibility of the warehouse. In order to investigate the effect of the number of free positions on the objective of the maximum completion time, this paper generates five sets of randomized instances with P = 100, O = 900, I = 450, R = 5, and the number of free positions in each set is increased from 2 to 20, resulting in eight different numbers of free positions. Using the method proposed in this paper to solve each of the instances, and taking the average of the 5 groups of instances in order to observe the change in the maximum completion time with the free position, the results are shown in Figure 11.

The following two conclusions can be obtained from Figure 11.

(1)

With the increase in the number of free positions, the maximum completion time shows a gradual decrease. This indicates that keeping a certain number of free positions in the RMFS warehouse can help improve the operational efficiency of the warehouse.

(2)

After the number of free positions increases to 15, the decrease in the maximum completion time tends to level off, i.e., there is an upper limit on the benefit brought by the increase in the number of free positions. When the number of free positions in the system reaches a certain value, even if the number of free positions is increased, the maximum completion time will not be reduced.

6.3.2. Analysis of the Effect of the Number of Robots on the Maximum Completion Time

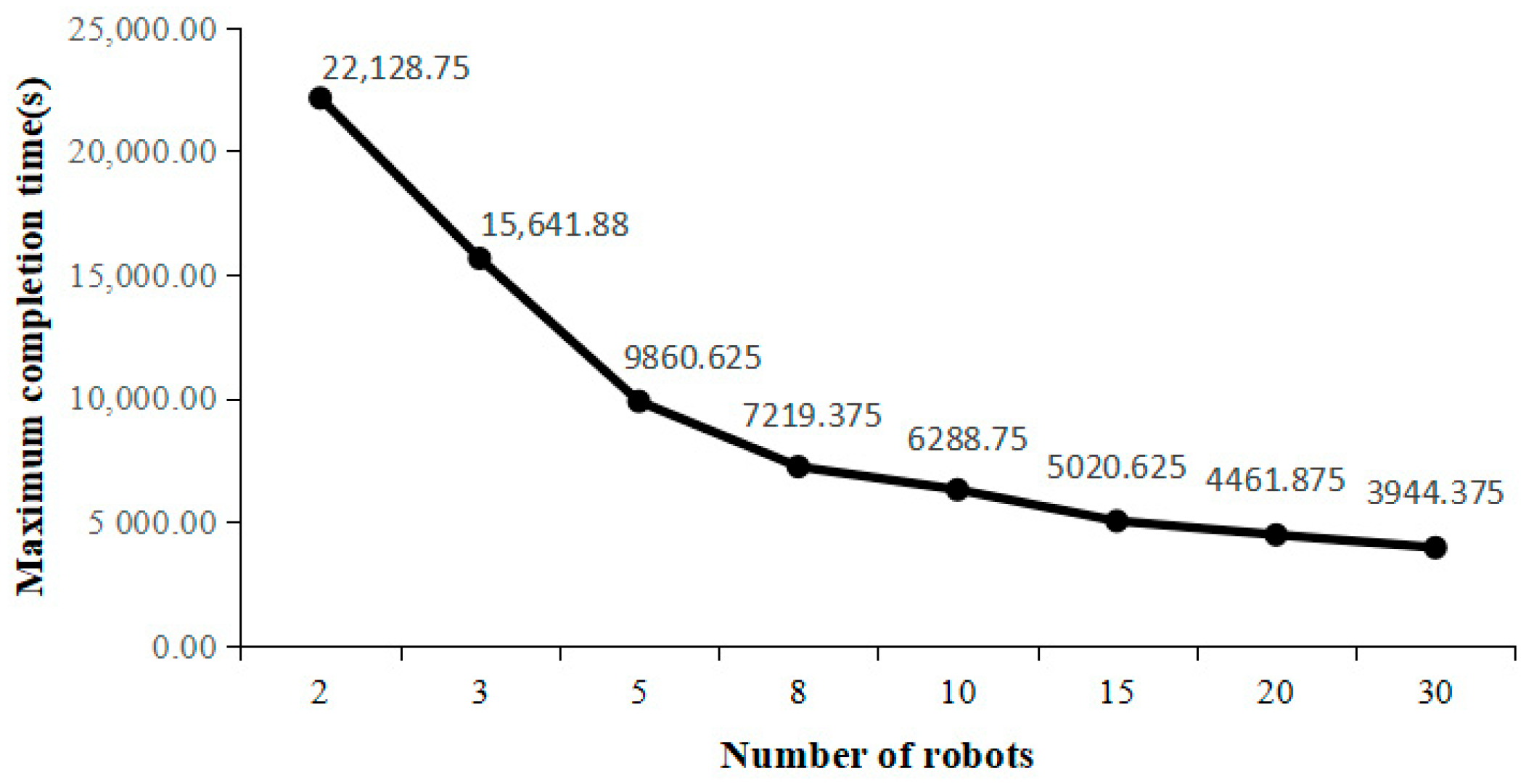
Robots are one of the most expensive equipment resources in RMFSs. In order to analyze the effect of the number of robots on the maximum completion time, this paper randomly generates 5 sets of arithmetic instances with P = 100, O = 900, I = 450, and R = 5, and the number of robots in each set is increased from 2 to 30 to obtain 8 different numbers of robots. The 5 arithmetic instances are solved and averaged using the method proposed in this paper and the results are shown in Figure 12.

From Figure 12, it can be found that

(1)

With the increase in the number of robots, the maximum completion time will be reduced, indicating that the number of robots has a positive effect on the improvement of the operational efficiency of the warehouse.

(2)

In the early stage of the growth, the number of robots can significantly reduce the maximum completion time, and the rate of change reaches 55.44% in the process of growth from 2 to 5 robots, but with the increase in the robot number, the decreasing trend tends to slow down, indicating that there is an optimal number of robots under different scales of warehouses, and beyond this optimal boundary, although a large number of additional robots will reduce the time required, the reduction is very low and is not even enough to offset the cost of the robot’s input.

As shown in Figure 12, system efficiency peaks when the number of robots reaches five units. Beyond this threshold, efficiency actually declines. This finding suggests that managers should seek an optimal balance between cost and efficiency to avoid blind investment.

7. Conclusions

7.1. Summary of Research Findings

RMFSs are widely used in high-frequency scenarios, and the study of the pod repositioning problem considering joint optimization with task allocation is of great practical significance for improving the operational responsiveness of e-commerce warehouses and accelerating the fulfillment process of e-commerce orders. The key to solving this problem lies in simultaneously realizing the optimal matching between pods and positions, as well as robots and task points.

In order to further improve the operational efficiency of the robot and the scientific layout of the warehouse, this paper constructs a joint optimization model of pod repositioning and task allocation with the objectives of minimizing the robot task completion time and the deviation between the pod position and the expected position. Aiming to realize the proposed model, a joint optimization strategy of pod repositioning and task allocation based on pod heat dominance is designed, and an improved genetic algorithm is used to solve the pod and task allocation scheme. Based on this joint optimization strategy, an incremental storage mechanism guided by generative orders is designed to incrementally update the expected layout of the RMFS repository through the idea of “predictive guidance, incremental movement”. Through numerical experiments, the results of the study are as follows:

(1)

From the perspective of joint optimization, while considering the influence of the replenishment situation on the selection of pod position, the problems of pod repositioning and robot task allocation are combined into one optimization problem, which realizes the coordination between the two related problems and provides theoretical references for the solution of the pod repositioning problem.

(2)

A progressive storage mechanism is proposed and compared with the traditional non-progressive process. Through the analysis, it is concluded that the progressive storage strategy can guide the movement of pods to more promising locations and effectively improve the quality of the expected layout of the warehouse.

(3)

Combining AGA and VNS has excellent synergistic effects and can utilize the advantages of both in search capabilities while having excellent stability.

7.2. Limitations and Future Research

Although this study provides an effective solution for the joint optimization of pod repositioning and task allocation in RMFSs, certain limitations remain. First, the model assumes robots operate under ideal conditions, neglecting practical constraints that may arise in real-world environments, such as robot congestion, dynamic obstacle avoidance, battery charging, and workstation waiting times. Second, the study focuses solely on robot-side optimization without incorporating human factors related to pickers, which limits the model’s direct applicability in complex real-world warehouse environments.

Future research can explore the following directions: first, integrating congestion, obstacle avoidance mechanisms, and charging scheduling into the existing joint optimization framework to enhance system robustness and practicality; second, incorporating human factors engineering principles to establish a human–robot collaborative optimization model centered on “robot-picker” coordination efficiency, thereby comprehensively improving the overall system performance.