Research on the Analysis of Influential Factors of Short-Period Passenger Flow of Urban Rail Transit Based on Spatio-Temporal Heterogeneity

Abstract

Urban Rail Transit (URT), as an important part of the modern urban transportation system, undertakes a large number of daily commuter passenger flow transportation needs. In this context, the in-depth analysis of influential factors of URT passenger flow has become an important issue in transportation management and optimization. This paper selects 13 POI (Point of Interest) types and the surrounding demographic data as the independent variables, and constructs a multi-scale spatio-temporal geographically weighted regression (MGTWR) model with the daily morning peak inbound traffic of the URT station as the dependent variable. The results of the study show that the positive effect of the business and residential variables on the URT morning peak inbound passenger flow is the most significant, reflecting the fact that the increase in these variables promotes the morning peak inbound passenger flow; relatively speaking, the scenic spot variables have a negative effect on the URT morning peak inbound passenger flow, indicating that the increase in these variables inhibits the morning peak inbound passenger flow. In addition, the corporate variables have a negative effect on the morning peak inbound passenger flow, and the company variables have a negative effect on the daily peak inbound passenger flow of URT. URT morning peak inbound passenger flow is non-stationary, i.e., the degree of its influence fluctuates greatly in different spatial and temporal scales. In order to further understand these influence mechanisms, this paper conducts an in-depth analysis of the spatio-temporal characteristics of the above three types of variables, revealing the influence of their spatio-temporal heterogeneity on URT passenger flow.

1. Introduction

With the rapid growth of the urban population leading to an increase in urban transportation demand, the urban rail transit (URT) system has developed into a key solution to improve urban mobility and accessibility due to its large capacity, high reliability and efficiency.

With the widespread adoption of the Automatic Fare Collection System (AFC) [1], easy access to historical travel data has become possible. Meanwhile, the rapid development of big data and deep learning technologies has provided theoretical frameworks that effectively support the analysis of URT influencing factors.

In recent years, the URT industry has increasingly focused on analyzing the spatiotemporal heterogeneity of passenger flow in built environments, considering factors such as population distribution and land use characteristics. However, existing studies lack detailed categorization of influencing factors and employ regression models (e.g., Geographically and Temporally Weighted Regression, GTWR) inadequately to examine their spatiotemporal impacts on URT passenger flow. This highlights the urgent need to refine factor classifications and select appropriate models to quantify these elements’ effects on spatiotemporal heterogeneity in URT passenger flow.

In view of the existing problems, this paper uses the POI data and population distribution data of rail transit, and analyzes the influencing factors of three subway lines in Hangzhou with GTWR and MGTWR as research models, respectively. The fitting accuracy and other indicators of the two models are compared, and the interpretation analysis is carried out in time and space dimensions according to the regression coefficients.

The main contributions of this paper are as follows:

• This study proposes a Multi-Scale Geographically and Temporally Weighted Regression (MGTWR) model to analyze the spatio-temporal heterogeneity of influencing factors on Urban Rail Transit (URT) morning peak passenger flow. By integrating 13 types of Point of Interest (POI) data and population distribution around stations, the model effectively captures the non-stationary and multi-scale characteristics of passenger flow influences, providing a more refined and accurate analytical framework compared to traditional GTWR models.
• Through rigorous multicollinearity and spatial autocorrelation tests, this study identifies and addresses the strong collinearity among four key variables (catering services, life services, commercial housing, and government agencies) using ridge regression. This preprocessing step enhances the interpretability and stability of the MGTWR model, ensuring more reliable estimation of variable impacts across different spatio-temporal scales.
• The study reveals the complex dual effects and spatio-temporal heterogeneity of various built environment factors on URT passenger flow. Specifically, business and residential variables show the most significant positive impact, while scenic spots exhibit a strong inhibitory effect. Corporate variables demonstrate non-stationary behavior, positively influencing passenger flow on weekdays but negatively influencing passenger flow on weekends. These findings provide valuable insights for urban planning and URT operation optimization, especially during peak hours.

The subsequent parts of the paper are organized as follows: Section 2 provides a comprehensive literature review on factors influencing URT passenger flow and the evolution of regression models from GWR to GTWR and MGTWR. Section 3 outlines the data sources and variable selection process, including POI categorization and spatial correlation analysis. Section 4 details the methodology, including the GTWR and MGTWR models, variable testing, and evaluation metrics. Section 5 presents a case study using Hangzhou URT data, including variable tests, model fitting, and spatio-temporal analysis of influencing factors. Finally, Section 6 summarizes the research findings, discusses implications for URT management, and suggests directions for future research.

2. Literature Review

China’s urban rail transit system is currently in a critical phase of rapid development, making research on passenger flow characteristics and influencing factors particularly crucial. In recent years, advancements in computer technology and information systems have driven extensive studies by scholars worldwide on factors affecting passenger flow in URT (Urban Rail Transit) systems. These influencing factors can generally be categorized into internal and external elements. Internal factors relate to train operation scheduling, including departure intervals and fare structures. External factors primarily involve the characteristics of URT station areas. Wang et al. [2] developed an evaluation method that analyzes how fixed-fare policies transition to distance-based pricing through smart card data analysis. This approach enables examination of fare adjustments’ impacts on demand, travel distance, and price elasticity across different time periods and distance intervals. Chen et al. [3] conducted comprehensive analyses using a control method for three Chinese cities—Hangzhou, Ningbo, and Xiamen—that implemented free public transportation policies, evaluating the effects of three distinct free transit strategies on daily subway passenger flows.

Regarding external influencing factors, most studies focus on the impact of the built environment on urban rail passenger flow. Li Guoqiang et al. [4] analyzed passenger flow influencing factors at subway stations by mining AFC and urban POI data. Based on analyzing station passenger flow characteristics, they comprehensively considered the quantity and proportion of various types of POIs within service areas, categorizing all stations into four typical types and establishing a station influencing factor set. Pan et al. [5] utilized IC card data from subway passenger volume and cellular signaling data on human activity spatial distribution in Shanghai. Their explanatory variables included station area employment and population distribution, commuting distance, subway network accessibility, transfer station status, and integration with commercial activity centers. Through regression analysis using station passenger flow as the dependent variable, they identified variations in passenger flow between rail transit stations. Zhu et al. [6] developed a Bayesian negative binomial regression model to identify key influencing factors related to daily peak and off-peak passenger flows. Based on this model, they established a geographically weighted model to analyze the spatial dependencies of these influences across different periods. Using Beijing station passenger flow data, they explored the spatiotemporal relationship between station passenger flow and the built environment.

With the introduction of the Geographical Weighted Regression (GWR) model, Calvo et al. [7] adopted this framework to analyze spatial heterogeneity relationships between daily subway trips and socioeconomic variables, including population, land use, accessibility, and transportation systems. Cardozo et al. [8] conducted spatial analyses of Madrid’s metro passenger flow using both GWR and ordinary least squares regression models, demonstrating that GWR models exhibit superior analytical performance. Chen et al. [9] utilized Shenzhen’s Metro AFC data, incorporating the Minkowski Distance (MD) metric to measure geographical distance and refine weighted matrix calibration. They employed exponential distance decay weighting functions to quantify spatial correlations among independent variables, thereby constructing a GWR model to address spatial autocorrelation and non-stationary issues in station-level metro passenger flow. Gao et al. [10] proposed a Network Distance-Based Geographical Weighted Regression (ND-GWR) model, calculating spatial impacts of demographic, land use, network, transfer, and station characteristics on metro passenger flow. The study compared these effects across weekdays, weekends, and holidays.

With continuous advancements in spatiotemporal data analysis methods, research models have gradually transitioned from traditional geographically weighted regression (GWR) to spatiotemporal geographically weighted regression (GTWR). Unlike GWR models that only consider spatial heterogeneity, GTWR introduces a temporal dimension. By simultaneously accounting for both temporal and spatial weighting effects, GTWR models can more accurately capture the dynamic characteristics of traffic flow and other socioeconomic variables over time. Wang et al. [11] developed spatiotemporal geographically weighted regression (GTWR) to explore how changes in land use, transfer connection facilities, and station attributes affect the spatiotemporal heterogeneity of passenger flow at subway stations. Results indicate that GTWR outperforms ordinary least squares (OLS) and geographically weighted regression (GWR) models. Ma Junze et al. [12] focused on the urban built environment around Shenzhen Metro station entrances/exits, employing the Tyson polygon analysis method to construct a transit travel recognition model. They analyzed station entry/exit passenger flow variations during weekday morning and evening rush hours and combined spatiotemporal geographically weighted regression models to investigate the spatial impact of built environment characteristics on transit demand. Shao et al. [13] developed a gradient boosting decision tree model to calculate the relative importance of land use variables and their thresholds and moderating effects on passenger flow. Xu Xinyue et al. [14] investigated the impacts of four built environment characteristics—demographic–economic, station, external transportation, and land use—on passenger flow at transportation hubs. By integrating Geographical Weighted Regression (GTWR) with Random Forest (RF), they developed a combined model called Geographical Weighted Random Forest (GTWR RF). This approach aims to reveal the spatiotemporal heterogeneity and nonlinear effects of built environment features on passenger flow patterns around transportation hubs.

In studies analyzing influencing factors around URT sites, GTWR effectively reveals the temporal and spatial variability of environmental factors across different stations by incorporating geospatial and temporal weights. The GTWR model has become a crucial tool for researchers to analyze surrounding factors due to its capability in handling spatial heterogeneity and temporal dynamics. However, despite its notable achievements in various applications, the model still demonstrates limitations when addressing complex spatiotemporal interactions, particularly under multi-scale and multi-level analysis requirements. In contrast, the Multi-Scale Spatiotemporal Geographical Weighted Regression (MGTWR) model introduces greater flexibility by simultaneously processing spatial heterogeneity and temporal dynamic changes at multiple scales, significantly enhancing its capacity to capture intricate spatiotemporal relationships. By optimizing regression coefficients across multiple scales, MGTWR provides more detailed spatiotemporal patterns and regional variations. This makes it particularly effective in accurately reflecting the unique characteristics of different stations when analyzing multi-layered and multi-dimensional influencing factors. Furthermore, the infrastructure design of railway lines and stations themselves constitutes another crucial dimension. The configuration of tracks (single, double, or multiple tracks) and station types (e.g., junctions, terminals) fundamentally determine capacity and operational performance, forming the physical backbone upon which passenger flow characteristics emerge [15]. Ref. [15] For URT passenger flow prediction, recent studies have adopted deep learning approaches. Sun et al. [16] proposed a Bi-graph Graph Convolutional Spatio-Temporal Feature Fusion Network (BGCSTFFN) that integrates POI data and station topology through graph convolutional networks and a Transformer, demonstrating superior performance in multi-step prediction tasks.

This study focuses on analyzing factors influencing urban rail transit passenger flow. By selecting 13 types of Points of Interest (POIs) and population distribution around stations as independent variables, we constructed a Multi-Scale Temporal-Spatial Geometric Weighted Regression Model (MGTWR) with morning rush hour station entry passenger flow as the dependent variable. The model aims to investigate how station characteristics and surrounding environments affect the spatiotemporal heterogeneity of passenger flow across different spatial scales and temporal dimensions. To evaluate the model’s superiority, this paper systematically compares MGTWR with traditional Geometric Weighted Regression (GTWR) models.

3. Problem Statement

3.1. Data Source of URT Station Card Swipe

The data used in this study originates from the Tianchi Big Data Competition, specifically including card-swiping records from three subway lines and 81 URT stations in Hangzhou, spanning from 1 January to 25 January 2019 [17]. Each record contains passenger swipe details, documenting boarding and alighting events that provide detailed insights into rail transit system mobility. These card-swiping datasets encompass critical information such as boarding/alighting times, station locations, and swipe methods. Selected AFC data can be referenced in

Table 1. Examples of some AFC swipe data.

Time	Line Id	Station Id	Device Id	Status	User Id	Pay Type
5 January 2019 8:15	A	73	3332	0	C35ff……25246	2
5 January 2019 8:15	B	24	1235	0	D2821……41526	3
5 January 2019 8:15	B	4	158	0	A91aec……a9e93	0
5 January 2019 8:15	C	41	1919	1	Bbb3a……d6357	1
5 January 2019 8:15	B	24	1221	0	B1426……61853	1
5 January 2019 8:15	B	15	782	1	B1576……db5e0	1

. Before data analysis, we cleaned and processed the raw AFC data to ensure data quality:

• Data Cleaning: Identified and removed invalid values and inconsistent records, including handling duplicate entries, outliers, and missing values.
• Data Transformation: This study primarily focuses on predicting passenger flow during the URT morning peak period (6:30–9:30). Therefore, the passenger flow sequence for the URT morning peak period was extracted from 25 CSV files containing historical AFC passenger flow data recorded from 1 January to 25 January 2019, using 5 min and 15 min intervals. Two datasets were obtained: 5 min and 15 min intervals. URT passenger flow $Y_i^t$ represents the passenger volume entering the station i during the t-th time period. $Y^t\in R^{N\times 1}$ denotes the total passenger volume across all URT stations during the t-th time period. N indicates the total number of stations on the URT line. Furthermore, prior to inputting the data into the prediction model, the URT passenger flow data undergoes normalization processing.

3.2. Variable Selection

Based on the daily passenger flow correlation rankings of station POIs in

Table 2. Results of POI correlation analysis between Station 7 and selected stations.

Site	3	5	6	7	15	43	68
POI Relativity	0.9394	0.912	0.9320	1	0.9059	0.8747	0.8876
Related Rankings	1	3	2	-	4	6	5
Daily Passenger Flow Correlation	0.9267	0.9153	0.9247	1	0.8072	0.9151	0.8884
Related Rankings	1	3	2	-	6	4	5

and the proximity rankings of selected stations to Station 7’s POI counts in

Table 3. Ranking of the number of POIs in each category at selected sites and their proximity to the number of POIs at Station 7.

Site	3	Ranking	5	Ranking	6	Ranking	7
Automobile Service	35	4	37	5	28	1	23
Car Sales	14	3	0	2	0	2	2
Vehicle Maintenance and Repair	8	1	8	1	9	2	8
Motorcycle Service	0	2	0	2	0	2	2
Food Service	366	2	295	3	211	4	345
Shopping Services	378	1	343	2	296	3	439
Service For Life	405	2	436	1	284	4	470
Sports and Leisure Services	83	5	80	4	44	2	56
Medical and Health Services	105	1	75	2	64	3	135
Accommodation Services	62	2	27	5	38	4	252
Famous Scenery	3	2	4	1	2	3	13
Commercial Housing	31	4	47	1	45	2	94
Government Agencies and Social Organizations	63	3	151	2	118	1	124
Science, Education and Cultural Services	112	3	132	6	57	1	77
Transportation Facilities Services	152	1	210	3	170	2	153
Financial And Insurance Services	20	4	84	2	50	1	60
Incorporated Business	115	4	153	2	153	2	199
Road Ancillary Facilities	0	2	0	2	1	1	1
Location Address Information	55	1	47	2	39	3	60
Communal Facilities	22	2	57	3	24	1	36
Event Activities	0	1	0	1	0	1	0
Transportation Facilities	0	1	0	1	0	1	0
Site	15	Ranking	43	Ranking	68	Ranking
Automobile Service	49	6	13	3	17	2
Car Sales	4	2	1	1	1	1
Vehicle Maintenance and Repair	2	4	2	4	3	3
Motorcycle Service	0	2	0	2	1	1
Food Service	355	1	158	5	145	6
Shopping Services	243	4	125	6	215	5
Service For Life	329	3	146	6	150	5
Sports and Leisure Services	51	1	43	3	26	6
Medical and Health Services	51	4	32	6	37	5
Accommodation Services	232	1	40	3	26	6
Famous Scenery	3	2	2	3	3	2
Commercial Housing	35	3	30	5	26	6
Government Agencies and Social Organizations	46	4	28	6	43	5
Science, Education and Cultural Services	44	2	30	4	29	5
Transportation Facilities Services	260	6	61	4	59	5
Financial and Insurance Services	22	3	10	6	19	5
Incorporated Business	140	3	163	1	72	5
Road Ancillary Facilities	0	2	0	2	0	2
Location Address Information	33	5	34	4	11	6
Communal Facilities	81	6	1	5	4	4
Event Activities	0	1	0	1	0	1
Transportation Facilities	0	1	0	1	0	1

, we selected 13 POI categories with non-zero values and similar daily passenger flow correlation rankings. Drawing from prior research, we added the surrounding population size as the 14th variable. These 14 variables are: Food & Beverage Services, Shopping Services, Daily Living Services, Sports & Leisure Services, Healthcare Services, Lodging Services, Scenic Spots, Commercial Residential Areas, Government Agencies & Social Organizations, Science, Education & Cultural Services, Transportation Facilities Services, Financial & Insurance Services, Corporate Enterprises, and Station Surrounding Population. These variables were selected by synthesizing existing research findings to ensure comprehensive coverage of station-related factors.

POI Relativity: The overall similarity in the distribution of all types of POIs surrounding different transit stations. Daily Passenger Flow Correlation: The degree of consistency in daily passenger flow fluctuation trends between different stations. Table 2 presents the analysis results for a selected group of sites (3, 5, 6, 15, 43, 68) exhibiting high POI correlation with Site 7. Building upon this, Table 3 further selects the top three ranked sites (3, 5, 6).

3.3. Variable Testing

3.3.1. Multiple Linear Test of Variables

Multiple collinearity testing serves as the foundation for ensuring the validity and accuracy of model estimation results in spatiotemporal regression analysis. Commonly referred to as multicollinearity testing, this method aims to identify whether explanatory variables exhibit high correlation. If strong collinearity exists among these variables, the economic interpretation of regression coefficients may become distorted, meaning their actual impact cannot be accurately reflected [18]. The estimated values of regression coefficients might deviate, thereby compromising the model’s reliability and stability, which in turn weakens its interpretative power and predictive precision. Therefore, by employing diagnostic tools such as variance inflation factors (VIF), we can effectively detect collinearity issues among independent variables, ensuring the model’s reliability and stability [19].

The formula for calculating the variance expansion factor (VIF) is shown as follows:

$$VI{F}_i={\displaystyle \frac{1}{1-R_i^2}}$$

(1)

where $X_i$ is used as the dependent variable for regression, and all other explanatory variables are used as independent variables for regression analysis. In this regression analysis, the obtained $R_i^2$ refers to the explainable portion of $X_i$ under the influence of other independent variables (i.e., the squared correlation value between the regression model and all other independent variables).

3.3.2. Autocorrelation Test of Variables

Global Moran’s Index (GMI), a key metric for assessing the spatial clustering or dispersion of variables across a study area, serves as a quantitative tool to evaluate spatial autocorrelation. By calculating this index for specific variables, researchers can determine whether significant spatial correlations exist within the region [20]. The GMI calculation process is as follows:

$$I={\displaystyle \frac{n{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{ij}(x_i-\overline{x})(x_j-\overline{x})}}}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{ij}{\displaystyle \sum _{i=1}^n{(x_i-\overline{x})}^2}}}}}$$

(2)

where $n$ is the number of spatial units; $w_{ij}$ is the weight between location $i$ and location $j$; $x_i$ and $x_j$ respectively denote the attribute values selected at location $i$ and location $j$; $\overline{x}$ is the average value of all observed values.

In the spatial autocorrelation analysis, the spatial weight matrix $w_{ij}$ is used to measure the spatial relationship between the attribute $x_i$ at location $i$ and the attribute $x_j$ at location $j$ When the distance between the two locations is relatively short, it is assigned a value of 1, indicating that there is a significant spatial correlation between these two locations; while when the distance between the locations is relatively long, it is assigned a value of 0, meaning that the spatial relationship between these two locations is weak or does not exist.

In addition to the global Moran’s Index (Moran’s I), spatial autocorrelation can also be tested through the standardized statistic Z. The calculation process of the standardized statistic Z is shown in Equation (3):

$$Z(I)={\displaystyle \frac{I-E(I)}{\sqrt{Var(I})}}$$

(3)

where $E(I)$ and $Var(I)$ represents the expected value and variance.

Z is a method to further process Moran’s index. Standardizing the expected value and standard deviation of Moran’s index provides more accurate statistical tests to evaluate the degree of autocorrelation of spatial data.

4. Methodology

The multiscale geospatial time-weighted regression (MGTWR) model employed in this paper traces its theoretical evolution back to geographic weighted regression (GWR). Serving as the starting point for this series of studies, GWR’s core objective is to address the issue of “spatial non-stationarity” in variable relationships. Subsequently, by incorporating a temporal dimension, the research model evolved from GWR to the spatiotemporal geographically weighted regression (GTWR), enabling the simultaneous capture of spatial and temporal heterogeneity in variables.

4.1. GTWR Model

Before introducing the MGTWR model, it is essential to first explain its theoretical foundation—the GTWR model—which enhances our understanding of spatiotemporal modeling processes. Building upon the GWR model’s consideration of local spatial heterogeneity, the GTWR model incorporates a temporal dimension [21]. By utilizing adjacent sample points in both time and space domains to calibrate regression coefficients for local observation points, it achieves analysis of spatiotemporal non-stationarity. The specific calculation formula is shown in Equation (4):

$$Y_i={\beta }_0\left(u_i,v_i,t_i\right)+{\displaystyle \sum _{k=1}^m{\beta }_k\left(u_i,v_i,t_i\right)x_{ik}}+{\epsilon }_i$$

(4)

where $\left(u_i,v_i,t_i\right)$ is the sample point $i$ with spatial coordinates and time coordinates; $m$ is the sample size; ${\epsilon }_i$ is the random error term; ${\beta }_k\left(u_i,v_i,t_i\right)$ is the estimated local regression coefficient.

In order to simplify the analysis process, some of the geographical factors directly related to time and space are usually omitted to make the expression more concise.

$$Y_i={\beta }_0+{\displaystyle \sum _{k=1}^m{\beta }_k{x}_{ik}}+{\epsilon }_i$$

(5)

Expand it as shown in Equation (6):

$$\left\{\begin{array}{c}{y}_1={\beta }_{10}+{\beta }_{11}{x}_{11}+{\beta }_{12}{x}_{12}+\dots +{\beta }_{1m}{x}_{1m}+{\epsilon }_1\\ y_2={\beta }_{20}+{\beta }_{21}{x}_{21}+{\beta }_{22}{x}_{22}+\dots +{\beta }_{2m}{x}_{2m}+{\epsilon }_2\\ ⋮\\ y_n={\beta }_{n0}+{\beta }_{n1}{x}_{n1}+{\beta }_{n2}{x}_{n2}+\dots +{\beta }_{nm}{x}_{nm}+{\epsilon }_n\end{array}\right.$$

(6)

The matrix expression is $W_i$$Y=\left(X\otimes \beta \right)I+\epsilon$

$$Y=\left[\begin{array}{c}\begin{array}{l}{y}_1\\ y_2\end{array}\\ ⋮\\ y_n\end{array}\right],X=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \dots & x_{1m}\\ 1& x_{21}& x_{22}& \dots & x_{2m}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_{n1}& x_{n2}& \dots & x_{nm}\end{array}\right],\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ ⋮\\ {\epsilon }_n\end{array}\right]$$

(7)

The $i$ estimated coefficient of the first variable is obtained by weighted least squares, and its calculation matrix expression is shown in Equation (8):

$${\widehat{\beta }}_i={(X^T{W}_{i}X)}^{-1}{X}^T{W}_{i}Y$$

(8)

where $X$ represents the $n\times m$ design matrix, where the values in the first column are all 1, representing the intercept term; $W_i$ is an $n\times n$ diagonal matrix determined by spatial variables, that is, $W_i=diag\left(W_{i1},W_{i2},\dots ,W_{ij},\dots ,W_{in}\right)$ all elements of $W_i$ determined by the dependent variable.

4.2. MGTWR Model

The Multi-Scale Spatio-temporal Geographical Weighted Regression (MGTWR) model, as an extension of the Geospatial Weighted Regression (GTWR) model, addresses some limitations of the latter. The traditional GTWR model assumes all explanatory variables share identical spatiotemporal bandwidths, meaning that in regression analysis, each influencing factor’s spatiotemporal effects on the dependent variable are confined to the same scale. However, this assumption overlooks the possibility that variables may exhibit different influence intensities and ranges across different spatial and temporal scales, potentially leading to overestimation or underestimation of variable effects. Therefore, the MGTWR model introduces variable-specific spatiotemporal bandwidths, allowing each explanatory variable to possess independent spatiotemporal stability and enabling more precise capture of factors’ impacts on the dependent variable across different scales [22]. The specific calculation formula is shown in Equation (9):

$$\begin{array}{l}{Y}_i={\beta }_{best(0)}\left(u_i,v_i,t_i\right)+{\displaystyle \sum _{j=1}^k{\beta }_{best(j)}\left(u_i,v_i,t_i\right)x_{ij}}+{\epsilon }_i\\ ={\displaystyle \sum _{j=0}^k{f}_j}+{\epsilon }_i\end{array}$$

(9)

where $k$ is the number of explanatory variables; $best(j)$ is the specific spatio-temporal bandwidth of explanatory variable $j$; ${\beta }_{best(j)}$ is the regression coefficient of explanatory variable $j$ under the specific spatio-temporal bandwidth; $f_j={\beta }_{bes(j)}\left(u_i,v_i,t_i\right)x_{ij}$ is the additive term of explanatory variables.

The MGTWR model can be regarded as a generalized additive model. During the modeling process, to determine the optimal spatiotemporal bandwidth, the GTWR model is used to initialize the additive $\widehat{\epsilon }=y-{\displaystyle \sum _{j=0}^k{f}_j}$ term vector, yielding an initial value. The error term is defined as follows: unlike the GTWR model, the MGTWR model employs a backfitting algorithm to iteratively update and gradually adjust the bandwidth of each variable until it meets predefined convergence criteria, ultimately terminating parameter updates.

The backfitting steps are as follows [23,24]:

Step 1: View the MGTWR model as a generalized additive model as a whole:

$$Y={\displaystyle \sum _{j=0}^k{f}_j}+\epsilon ,\begin{array}{cc}& f_j\end{array}={\beta }_{best(j)}{x}_j$$

(10)

Step 2: Initialization is obtained ${\beta }_{best(0)},{\beta }_{best(1)}\otimes x_1,{\beta }_{best(2)}\otimes x_2,\dots ,{\beta }_{best(j)}\otimes x_j$, that is $f_0^{(0)},f_1^{(0)},f_2^{(0)},\dots ,f_j^{(0)}$, the initial residual term ${\epsilon }^{(0)}=Y-f_0^{(0)}-f_1^{(0)}-f_2^{(0)}-\dots -f_k^{(0)}$ is calculated.

Step 3: Use the GTWR model to perform a regression operation on the intercept term $x_0$, calibrate to generate the optimal spatial bandwidth and time bandwidth, and update to obtain $f_0^{(1)}={\beta }_0^{(1)}{x}_0$, ${\epsilon }_0^{(1)}=f_0^{(1)}-f_1^{(0)}-\dots -f_k^{(0)}$;

Step 4: Use the GTWR model to perform regression operation on the explanatory variables $x_1$, calibrate to generate the optimal spatial bandwidth and time bandwidth, and update to obtain $f_1^{(1)}={\beta }_1^{(1)}{x}_1$, ${\epsilon }_1^{(1)}=f_0^{(1)}-f_1^{(1)}-\dots -f_k^{(0)}$;

Step 5: Perform regression operations on each of the $k$ explanatory variables one by one to obtain the first parameter estimation values ${\beta }_0^{(1)},{\beta }_1^{(1)},\dots ,{\beta }_k^{(1)}$ and repeat steps 3–5 until the convergence criterion is met.

The convergence criterion adopts the classical SOC criterion [25], whose termination condition is less than or equal to, as shown below:

$$SO{C}_f^{p+1}=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{j=1}^k\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left({\widehat{f}}_{ij}^{\left(p+1\right)}-{\widehat{f}}_{ij}^{\left(p\right)}\right)}^2}}}{{\displaystyle \sum _{i=1}^n{\left({\displaystyle \sum _{j=1}^k{\widehat{f}}_{ij}^{\left(p+1\right)}}\right)}^2}}}}<\delta$$

(11)

In this case $\delta$, we usually take the negative of 10 to the power of, the sum of the squared residuals $RSS={\displaystyle \sum _{i=1}^n{\left({\displaystyle \sum _{j=1}^k{\widehat{f}}_{ij}^{\left(p+1\right)}}\right)}^2}$.

4.3. Evaluating Indicator

(1)

Residual sum of squares

$$RSS={\displaystyle \sum _{i=1}^n{\left({\displaystyle \sum _{j=1}^k{\widehat{f}}_{ij}^{\left(p+1\right)}}\right)}^2}$$

(12)

(2)

Information criteria (AICc)

The Akaike Information Criterion (AICc) is a statistical measure used to evaluate model fit and select parameters. These criteria also play a crucial role in bandwidth selection, as they emphasize that optimizing models requires not only considering fitting accuracy but also imposing penalties for model complexity factors such as the number of parameters.

$$AICc=2n\ln \left(\widehat{\delta }\right)+2n\ln (2\pi )+n\left[{\displaystyle \frac{n+tr\left(s\right)}{n-2-tr\left(s\right)}}\right]$$

(13)

where $\widehat{\delta }$ is the estimated standard deviation of the error term, $\widehat{\delta }=RSS/n-tr(s)$, where $tr\left(S\right)$ is the trace of $S$, and $S$ is the hat matrix of GTWR. The rows of the $i$-th sample can be expressed as follows:

$$S_i=X_i{\left(X^T{W}_{i}X\right)}^{-1}{X}^T{W}_i$$

(14)

Finally, the bandwidth combination with the smallest AICc value is selected as the optimal bandwidth combination.

(3)

Goodness of fit (R²):

$$R^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}}{{\displaystyle {\sum }_{i=1}^N{(y_i-\overline{y})}^2}}}$$

(15)

Among them, $y_i$, ${\widehat{y}}_i$ and ${\overline{y}}_i$ are the real value, predicted value and mean of passenger flow of URT stations $i$, and $N$ is the total number of URT stations.

5. Case Study

In the experimental design, 14 independent variables were initially selected, with the dependent variable being daily morning rush hour passenger flow from 1 January to 25. First, multiple collinearity tests and spatial correlation analyses were conducted on the independent variables to evaluate their linear relationships and spatial data interdependencies. Based on these findings, a Multi-Scale Geographical Weighted Regression (MGTWR) model was further developed to reveal the spatiotemporal heterogeneity effects of each variable on the dependent variable.

5.1. Variable Collinearity Test Results

In this regression analysis, we employed Variance Inflation Factors (VIF) to assess multicollinearity among independent variables. As shown in

Table 4. VIF values for each variable.

Argument	VIF
Food Service	10.34668186
Shopping Services	7.032731489
Service For Life	23.82167605
Sports and Leisure Services	6.554564789
Medical and Health Services	4.078520572
Accommodation Services	4.399362948
Famous Scenery	4.462307008
Commercial Housing	11.88041137
Government Agencies and Social Organizations	13.31520142
Science, Education and Cultural Services	4.877289223
Transportation Facilities Services	3.670111891
Financial and Insurance Services	3.733694487
Incorporated Business	1.828769161
Population Distribution	2.975139216

, the VIF values of four variables—catering services, life services, commercial housing, and government agencies/social organizations—all exceeded 10, indicating strong multicollinearity. However, most variables maintained VIF values well below 10. To mitigate multicollinearity in these four variables, ridge regression was first applied to the independent variables before their inclusion in the MGTWR model, thereby enhancing the interpretability of the model’s estimated parameters.

Ridge Regression works by adding a regularization term (or penalty term) to the objective function that minimizes the sum of squared residuals. This term multiplies the sum of squared regression coefficients by a regularization parameter, thereby reducing the absolute values of the coefficients and preventing overfitting or instability caused by multicollinearity.

The loss function expression of ridge regression is shown in Equation (16):

$$L(\beta )={{\displaystyle \sum _{i-1}^n\left(y_i-x_i^T{\beta }_j\right)}}^2+\lambda {\displaystyle \sum _{j-1}^p{\beta }_j^2}$$

(16)

where $n$ is the number of samples; $y_i$ is the target value of the $i$-th sample; $x_i$ is the feature vector of the $i$-th sample; ${\beta }_j$ is the regression coefficient of the $j$-th feature; $\lambda$ is the regularization parameter, which controls the intensity of the penalty term.

5.2. Variable Correlation Test Results

Spatial autocorrelation analysis serves as the final step in examining independent variables before regression analysis, aiming to identify spatial clustering patterns among variables. To ensure spatial autocorrelation among variables, this study employed a Python-programmed algorithm (Programming language: Python 3.9. Editor: Pycharm. Model is built using the deep learning framework of Pytorch.) to calculate Moran’s I index for spatial autocorrelation testing. The correlation analysis results are presented in

Table 5. Results of the spatial correlation test for each variable.

Argument	Moran’s I	E(I)	Var(I)	z-Value	p-Value
Food service	0.303251889	−0.0125	6.37 × 10−6	125.134	0
Shopping services	0.497486103	−0.0125	1.04 × 10−5	157.7971	0
Service for life	0.468983164	−0.0125	9.85 × 10−6	153.4383	0
Sports and leisure services	0.246757545	−0.0125	5.18 × 10−6	113.901	0
Medical and health services	0.506598145	−0.0125	1.06 × 10−5	159.1655	0
Accommodation services	0.429375709	−0.0125	9.02 × 10−6	147.1677	0
Famous scenery	0.576883604	−0.0125	1.21 × 10−5	169.35	0
Commercial housing	0.955530334	−0.0125	2.01 × 10−5	216.1215	0
Government agencies and social organizations	0.93230677	−0.0125	1.96 × 10−5	213.5476	0
Science, education and cultural services	0.544384151	−0.0125	1.14 × 10−5	164.7188	0
Transportation facilities services	0.467177063	−0.0125	9.81 × 10−6	153.1579	0
Financial and insurance services	0.614376574	−0.0125	1.29 × 10−5	174.5404	0
Incorporated business	0.206291487	−0.0125	4.33 × 10−6	105.1286	0
Population distribution	0.993669173	−0.0125	2.09 × 10−5	220.2831	0

.

The analysis of the table reveals that both Moran’s I and z-values are positive, with all Moran’s I values remaining below 1. This indicates significant spatial autocorrelation among all independent variables. Furthermore, the significance levels (p-values) for each variable are all below 0.05, further confirming spatial correlations among all 14 independent variables. Notably, the clustered characteristic value z maintains positive values, demonstrating significant spatial clustering among these variables. Consequently, these 14 independent variables were selected as foundational variables for the study. Overall, the independent variable data meet the essential requirements for constructing the MGTWR model.

5.3. Results of the MGTWR Model at URT Site

Based on the selected 14 independent variables and 1 dependent variable, we constructed the MGTWR combined model (MGTWR). The exponential spatiotemporal weight function was selected, with the parameter $\delta$ in the convergence criterion SOC set to ${10}^{-4}$. The influence coefficients of each variable in the model are shown below. The statistics in

Table 6. Fitting parameters for the MGTWR model of morning peak inbound passenger flow.

Argument	Least Value	The Last Four Digits	Median	Lower Quartile	Crest Value
The Intercept Term	553.7797	821.6143	1214.1688	1261.4603	1347.7401
Food Service	6.7665	10.1378	13.5146	14.3634	17.8539
Shopping Services	−1.6585	−1.1661	−0.7152	−0.6078	−0.3245
Service For Life	3.2319	4.3188	5.4752	5.8761	6.1308
Sports and Leisure Services	−33.1797	−30.2744	−29.3012	−28.3353	−26.4028
Medical and Health Services	12.0856	14.0070	17.7617	19.1660	21.5747
Accommodation Services	3.2178	3.9127	4.3618	5.2461	8.9824
Famous Scenery	−54.5313	−48.9200	−45.8257	−23.6494	−11.6348
Commercial Housing	13.9447	17.2068	18.5939	19.6171	20.7198
Government Agencies and Social Organizations	−30.2892	−29.6214	−28.7856	−27.1498	−24.7318
Science, Education and Cultural Services	−4.9256	−4.0762	−3.7593	−3.3391	−2.5871
Transportation Facilities Services	1.4142	3.7231	4.1307	4.7995	6.7697
Financial and Insurance Services	−20.1579	−18.3932	−16.8708	−10.9467	−8.1135
Incorporated Business	−2.4580	−1.2893	−0.2972	0.2815	1.0551
Population Distribution	0.0585	0.0682	0.0891	0.0953	0.1027

include: minimum value, lower quartile, median, upper quartile, and maximum value.

The regression results of the model reveal that all eight independent variables—catering services, living services, accommodation services, healthcare services, business residences, transportation facilities, and population distribution—display positive parameter estimates. Notably, business residences exhibit the highest values across all indicators, indicating their significant positive correlation with morning rush hour passenger flow. This demonstrates that expanded availability of these service facilities enhances regional appeal and functionality, thereby driving increased passenger traffic during peak hours.

Contrary to expectations, the parameter estimates for five independent variables—shopping services, sports and leisure facilities, scenic attractions, government agencies and social organizations, as well as science, education, culture, and financial insurance services—all showed negative correlations. Notably, all indicators related to scenic attractions ranked lowest, indicating that increased availability of these services had a suppressive effect on morning rush hour passenger flow, with scenic attractions demonstrating the most significant impact. This inverse relationship suggests that expanding these service types may not effectively boost passenger numbers during peak hours under specific spatiotemporal conditions. Furthermore, variations in regional distribution patterns or differences in passenger demand patterns could potentially lead to reduced traffic volumes.

Furthermore, the parameter estimates of the corporate enterprise variable exhibit both positive and negative values under different scenarios, indicating a complex dual effect on morning rush hour passenger flow. This bidirectional influence may stem from significant temporal and spatial variations in the corporate enterprise’s impact, reflecting how its role in passenger flow dynamics shifts across contexts. This demonstrates the spatiotemporal heterogeneity inherent in the model.

In conclusion, these regression results not only reveal the complex relationship between independent variables and dependent variables, but also emphasize that the influence of variables may be nonstationary or heterogeneous when considering the time-space dimension.

To investigate the spatiotemporal heterogeneity of morning rush-hour passenger flow at URT stations in built environments, this study analyzes three representative influencing factors: First, commercial-residential properties demonstrate significant positive effects on station entry passenger flow; second, scenic attractions exhibit strong inhibitory effects on passenger flow; third, corporate entities show complex spatiotemporal variations due to their non-stationary characteristics across different time periods. Through temporal-spatial analysis of these variables’ coefficients, we aim to reveal the spatiotemporal differences and underlying mechanisms of built environment elements affecting URT passenger flow during peak hours.

(1)

Time characteristic analysis of the influence coefficient of specific variables

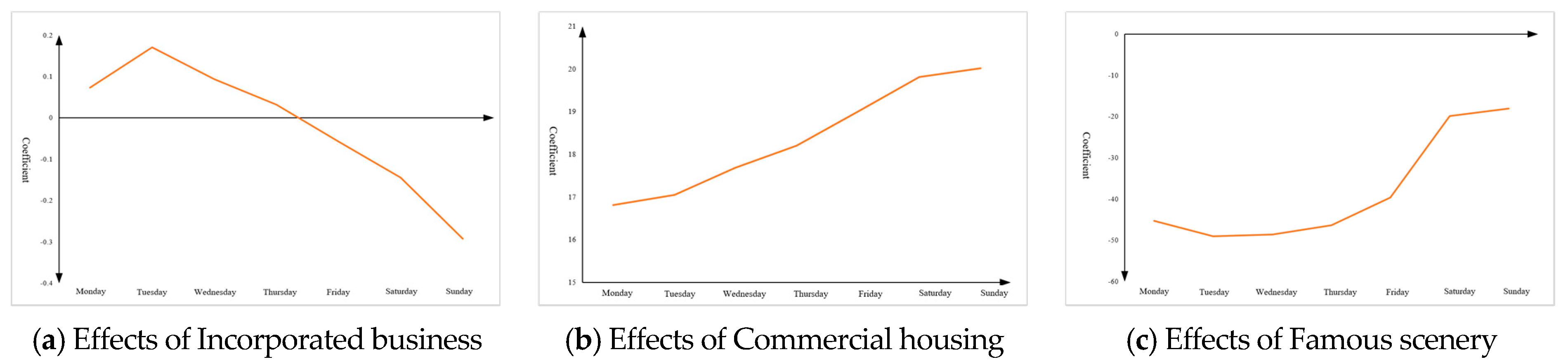
In order to explore the variation trend of the influence coefficient of the independent variable company enterprise over different times, the average coefficient values of each station from 7 January (Monday) to 13 January (Sunday) were selected, and the results are shown in Figure 1:

As shown in Figure 1a, the corporate presence variable exhibits positive coefficients from Monday to Thursday, with its impact peaking on Tuesday. The weekday coefficient significantly outperforms weekend levels, demonstrating that corporate establishments around stations substantially boost morning rush hour passenger flow during these hours. However, the coefficient turns negative and shows a continuous decline from Friday to Sunday, indicating that corporate presence acts as a counterforce during weekends. Most companies are closed during weekends, reducing commuting demand and causing a sharp drop in URT morning peak passenger numbers. Weekend travel patterns predominantly consist of non-work-related activities like leisure, socializing, and shopping. These dispersed demands lack the concentration seen during weekdays, thus failing to effectively drive morning peak traffic.

As shown in Figure 1b, commercial residential variables demonstrate significant positive impacts on both weekday and weekend morning rush hour station passenger flows. Specifically, the influential coefficients of commercial residential variables show a gradual upward trend throughout the week, reaching their peak on Sundays. This phenomenon reflects the continuous and time-sensitive effects of commercial residential areas as built environment elements on public transportation demand across different periods. During weekdays, residents in commercial residential zones exhibit regular commuting patterns, leading to a gradual increase in morning rush hour passenger flows over time, demonstrating strong connectivity with surrounding transportation systems. On weekends, despite most workplaces being closed, residents within these zones maintain robust travel demands for leisure, entertainment, and social activities, driving increased passenger flow. Particularly on Sundays, when influencing factors reach their maximum value, this may be closely related to intensified weekend activity concentration and higher frequency of outings, highlighting the unique role of commercial residential areas in URT (Urban Rail Transit) passenger flow during non-working days. Overall, commercial residential variables not only significantly impact morning rush hour commuter flows during weekdays but also amplify URT passenger demand through diversified resident activities during weekend hours. This pattern reveals the complex influence of commercial residential variables on URT morning rush hour station passenger flows.

As shown in Figure 1c, scenic area variables exhibit a negative impact on both weekday and weekend passenger flows. Specifically, the negative coefficient of scenic area variables on passenger flow reaches its minimum value on Tuesday, indicating that during this period, the variable exerts the most significant suppression effect on URT morning peak passenger flow. Moreover, the influential coefficient on weekdays is significantly lower than that on weekends, suggesting that scenic area variables have a more pronounced suppressive effect on weekday traffic demand. Furthermore, the degree of negative impact on the URT morning peak passenger flow shows notable temporal variations across different periods.

This phenomenon can be analyzed from multiple perspectives. Firstly, scenic area variables significantly influence passenger leisure and tourism activities. During weekdays, when most people are engaged in regular work routines, travel demand remains relatively stable and limited, resulting in a smaller negative impact of scenic area variables on URT morning peak passenger flow. In contrast, weekends, characterized by widespread rest periods, see concentrated travel demands from residents, particularly increased tourism demand for scenic areas. This heightened demand volatility amplifies weekend URT morning peak passenger flow, thereby weakening the negative impact of scenic area variables on passenger traffic.

It is worth noting that Tuesday, being the mid-point of the week, typically sees relatively stable passenger flow during most weekdays with sparse tourism demand and lower visitor numbers at scenic spots. This could explain why the negative impact coefficient of scenic spot variables shows minimal influence on passenger flow during this period. The varying negative coefficients across different time periods reflect shifts in residents’ travel habits, social activity patterns, and transportation demands.

(2)

Spatial characteristic analysis of influence coefficients of specific variables

ArcGIS 10.2 was employed to conduct spatial visualization analysis of morning rush hour passenger flow patterns at stations during weekday and non-working day periods. As shown in Figure 2a,b, corporate variables significantly boost URT (Urban Rail Transit) ridership at most stations during weekdays. However, during non-working days, these corporate variables suppress morning rush hour passenger flow across all stations, with the suppression intensity gradually decreasing from central to peripheral areas, reaching its minimum at northeastern regional stations. Spatially, the impact of corporate variables shows distinct gradient characteristics across different regions. Stations located in urban centers and commercial hubs demonstrate more pronounced effects from corporate variables, particularly during working hours. During non-working days, while passenger flow decreases substantially at these stations, the inhibitory effect diminishes as the distance from the city center increases. This indicates that travel patterns in peripheral areas may be more influenced by alternative factors such as leisure activities.

In terms of spatial dimensions, there are significant differences in passenger travel patterns between working and non-working days. Specifically, as shown in Figure 3a,b, the promoting effect of commercial residential variables on URT (urban rail transit) trips during morning rush hours exhibits distinct spatiotemporal variations across different time periods and regions.

During weekday hours, the business residential variables show weaker boosting effects on morning rush hour passenger flow in urban core areas, while demonstrating more significant positive impacts at stations farther from central districts—particularly at terminal line endpoints. Specifically, stations located at the northernmost positions exhibit the most pronounced effects. This phenomenon likely stems from commuting demands during weekdays, especially for office workers residing in peripheral areas whose travel needs peak during morning rush hours. Consequently, business residential variables around these stations exert stronger demand stimulation effects on URTs (Urban Transport Rides).

During non-working days, the spatial distribution of business residential variables’ impact on URT morning rush hour passenger flow shows a reverse pattern compared to working days. Compared with weekdays, the positive influence coefficient of business residential variables on morning rush hour passenger flow at eastern regional stations is relatively smaller, while the positive influence coefficient at central regional stations reaches its peak. This indicates that during non-working days, the promotional effect of business residential variables on morning rush hour passenger flow at central regional stations is stronger than in other areas. This is because passenger mobility during non-working days is more driven by leisure activities, shopping, and other social engagements, which exhibit greater dispersion and lack of concentration.

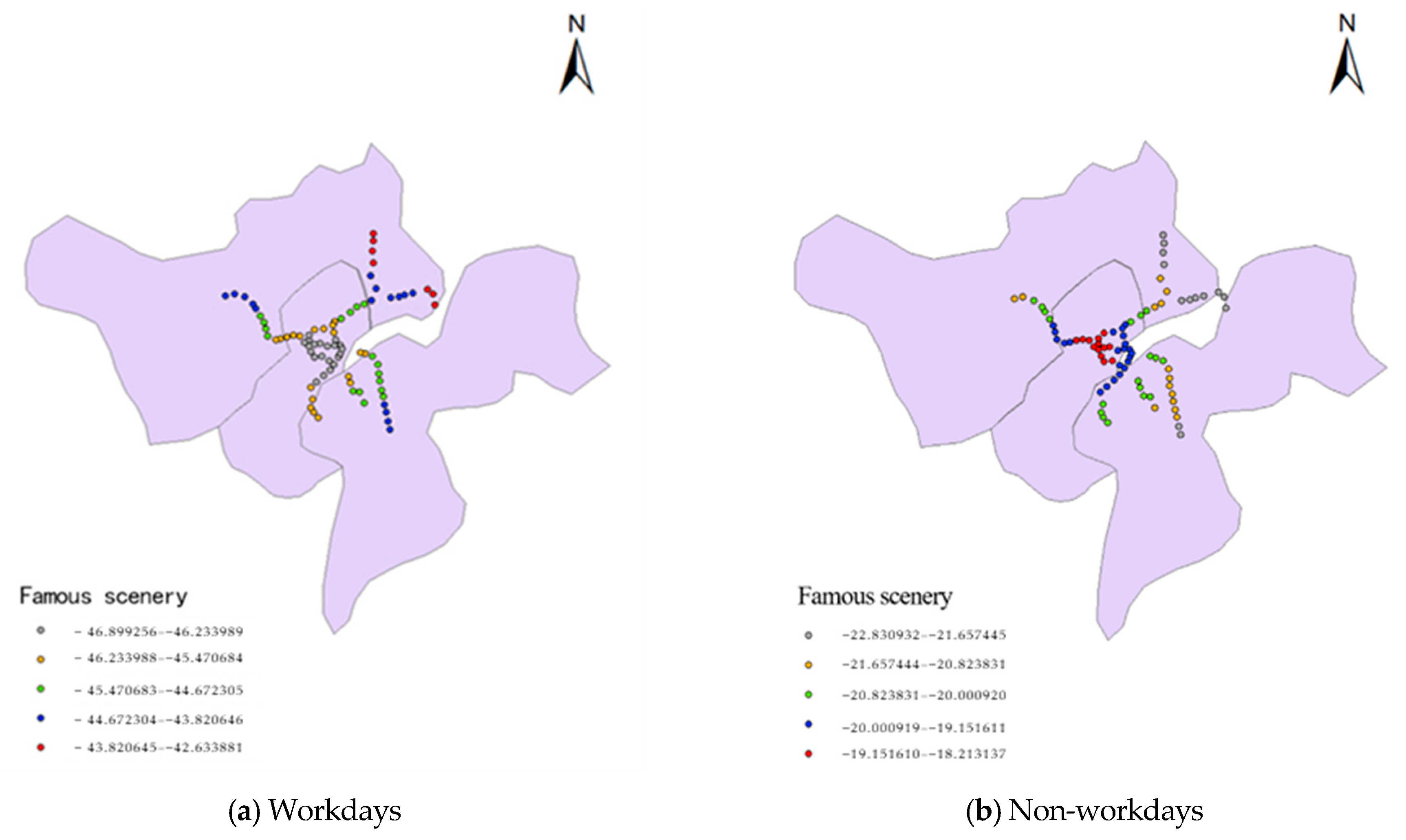
From a spatial perspective, the impact of scenic spots on URT’s morning rush hour station passenger flow demonstrates significant spatiotemporal variations, with distinct differences observed between weekdays and non-working days. As shown in Figure 4a,b, scenic areas exhibit a suppressive effect on station passenger flow across all stations during both working and non-working periods. However, the spatial distribution patterns of this inhibitory effect show notable temporal variations.

During weekday hours, scenic area variables exhibit strong spatial heterogeneity in morning rush hour passenger flow at stations. As commuting demands weekday travel, the inhibitory effect of scenic area variables on morning peak passenger flow is most pronounced in urban center areas, particularly around tourist attractions. During weekdays, morning peak passenger flow tends to be more dispersed, primarily consisting of commuters rather than tourists. In contrast, stations farther from city centers—especially those located at route endpoints—show weaker inhibitory effects. Particularly at the northernmost sections of routes, the impact of scenic area variables on passenger flow remains relatively minimal. This phenomenon reflects differences in commuting patterns during workdays.

During non-working days, the impact of scenic area variables shows a completely different trend. Particularly in central areas of tourist attractions like West Lake, the negative influence coefficient of scenic area variables on morning rush hour passenger flow at regional stations peaks and gradually increases toward peripheral areas, reaching its maximum in the northeastern route regions. This indicates that during non-working days, scenic area variables suppress morning rush hour passenger flow across all stations, with weakening intensity from the center outward, and minimal impact on northeastern regional stations. This phenomenon closely aligns with the characteristics of non-working day travel demand: passenger flow primarily depends on the appeal of scenic centers, while peripheral areas exhibit relatively weaker attractiveness, resulting in limited passenger growth at terminal stations.

(3)

Model comparison

To verify the performance advantages of the constructed MGTWR model over other models, this study selected the GTWR model and conducted a systematic comparison using three metrics: R², AICc, and RSS. As shown in

Table 7. Comparison of results from different models.

Model	R2	AICc	RSS
GTWR	62.16%	35,926	4,134,135,268
MGTWR	65.10%	35,615	3,992,430,828

, the MGTWR model demonstrated a 2.94% improvement in R² compared to the GTWR model, indicating its significant advantage in data fitting and ability to accurately capture underlying patterns. Additionally, the MGTWR model showed a 311-point reduction in AICc compared to the GTWR model, highlighting its higher efficiency in data interpretation and better balance between model complexity and fit. Furthermore, the MGTWR model reduced RSS by 14,170,4440 points compared to the GTWR model, significantly lowering the sum of squared residuals and further validating its improved prediction accuracy. In conclusion, considering these metrics comprehensively, the MGTWR model not only exhibits remarkable improvements in fitting, model interpretability, and prediction accuracy compared to the GTWR model but also demonstrates stronger adaptability and higher effectiveness when handling spatiotemporal data.

6. Conclusions

To balance passenger flow throughout the week, differentiated planning for station surroundings can be implemented based on the spatiotemporal heterogeneity of variables affecting commercial residences, scenic attractions, and corporate enterprises. This study first conducted multicollinearity and spatial autocorrelation tests on selected variables, identifying multicollinearity issues among four variables. Subsequently, ridge regression was applied to the data before inputting it into the Multi-Geospatial Temporal Geographical Weighted Regression (MGTWR) model. Through this approach, we conducted an in-depth analysis of how the characteristics of built environments around stations influence URT morning rush hour passenger flow. The findings indicate the following:

(1)

There are 8 independent variables that have a positive impact on the morning rush hour station passenger flow, among which the business residential variable has the biggest impact; while there are 5 independent variables that have a negative impact on the passenger flow, among which the scenic spot has the biggest impact the corporate enterprise shows a complex double effect, reflecting non-stationary spatiotemporal heterogeneity.

(2)

Business residential properties demonstrate the most significant positive impact on morning rush hour passenger flow, particularly during weekends. Scenic attractions exhibit negative effects during weekdays, though this adverse effect diminishes due to concentrated tourism demand on weekends. Corporate entities show marked non-stationary patterns in passenger flow dynamics: they boost traffic during workdays while exerting a restraining effect on weekends.

(3)

Corporate variables boost URT travel in urban centers and commercial hubs during weekdays, while showing inhibitory effects on non-working days, with diminished impact on peripheral areas. Business residential variables and scenic attraction variables exhibit significant spatiotemporal differences in their influence on URT travel: the former stimulates commuting demand in peripheral regions, whereas the latter intensifies leisure demand in central scenic area clusters during off-workdays.