Charging Decision Optimization Strategy for Shared Autonomous Electric Vehicles Considering Multi-Objective Conflicts: An Integrated Solution Process Combining Multi-Agent Simulation Model and Genetic Algorithm

Abstract

There is a lack of systematic research on the behavioral design of charging decision-making for Shared Autonomous Electric Vehicles (ASEVs), and the thresholds of “when to charge and where to charge” have not been clarified. Therefore, this paper investigates the optimization of charging decisions of SAEVs and the impact of different decision-making objectives to provide theoretical support and practical guidance for intelligent operation. A multi-agent simulation model (which accurately simulates complex interaction systems) is constructed to simulate the operation and charging behavior of SAEVs. Four charging decision optimization objective functions are defined, and a weighted multi-objective optimization method is adopted. A comprehensive solution process combining the multi-agent simulation model and genetic algorithm (efficiently solving complex objective optimization problems) is applied to approximate the global optimal solution among 35 scenarios through 100 iterative runs. In this paper, factors such as passenger demand (e.g., average remaining battery power, demand response time) and operator demand (e.g., empty vehicle mileage, charging cost) are considered, and the impacts of different objectives and decision variables are analyzed. The optimization results show that (1) when a single optimization objective is selected, minimizing the total charging cost effectively balances the overall fleet operation; (2) there are trade-offs between different objectives, such as the conflict between the remaining battery power and charging cost, and the balance between the demand response time and the empty vehicle mileage; and (3) in order to satisfy the operational requirements, the weight distribution, charging probability, stopping probability, and recommended battery power should be adjusted. In conclusion, this study provides optimal charging decision strategies for the intelligent operation of SAEVs in different scenarios, which can optimize target weights and charging parameters, and achieve dynamic, balanced fleet management.

1. Introduction

Shared Autonomous Electric Vehicles (SAEVs) have emerged as an innovative smart mobility solution, bringing significant benefits to transportation systems through rapid technological advancements. These vehicles reduce labor costs while ensuring uninterrupted round-the-clock operation. Moreover, their electrification significantly lowers energy consumption and emissions, making them an environmentally friendly alternative [1]. In practice, several companies, including Waymo, Cruise, Zoox, and Motional, have already started exploring autonomous ride-hailing services. To enhance the operational efficiency of SAEVs, optimizing charging decisions has become a critical challenge. Charging decisions involve more than simply determining whether to charge; they also include complex operational choices such as parking, idle waiting, and cruise scheduling. These decisions directly impact vehicle utilization, energy consumption, and user satisfaction. Specifically, each SAEV must continuously assess in real time: Should it charge immediately or continue accepting ride requests? When the battery level is sufficient, should it charge in advance, wait in place, or continue cruising? These decisions influence two key performance indicators: (1) vehicle utilization and energy consumption, which determine the profitability of fleet operators [2,3]; and (2) demand response time, which directly affects user experience and market competitiveness [4]. However, most current SAEV operators adopt a “low-battery forced charging” strategy, which has significant limitations. Charging only when battery levels are low can lead to congestion at charging stations, increased response times, and excessive empty vehicle mileage [4]. In other words, conventional approaches—such as charging only when necessary—fail to effectively address the multi-objective optimization challenges in SAEV charging decisions. These methods struggle to balance key factors such as response time, empty vehicle mileage, charging costs, and remaining battery levels. Therefore, an intelligent charging decision-making system is urgently needed—one that can comprehensively consider charging costs, response time, and empty vehicle travel distance while analyzing the trade-offs between these objectives. Achieving truly optimal decision-making in this context is the key challenge that this paper aims to address.

Based on the above content, this paper proposes a charging decision optimization model based on multi-agent simulation and genetic algorithm, aimed at solving the dynamic decision optimization problem of SAEVs between charging, parking, and continuing to accept ride requests. On one hand, multi-agent simulation studies the dynamic characteristics of SAEV operations by simulating the interactions of multiple agents. On the other hand, genetic algorithms, with their powerful global search capability and adaptability to complex problems, offer a novel approach to optimizing SAEV charging decisions. This paper will focus on exploring SAEV charging decision optimization, including model development, objective function construction, and result analysis. The emphasis will be placed on analyzing the impact of different decision objectives, providing theoretical support and methodological guidance for the efficient operation of SAEV systems.

First, based on multi-agent simulation technology, this paper constructs a model capable of accurately simulating the entire SAEV operation and charging process, including key stages such as ride request fulfillment, charging decisions, and parking. In terms of optimization strategy, a multi-objective optimization framework is developed, incorporating four distinct optimization objectives, which are combined using a weighted approach to achieve balanced optimization. Second, a genetic algorithm is employed to iteratively compute 35 different weight combinations, effectively obtaining the globally optimal strategy. Finally, this paper comprehensively considers key indicators from two perspectives: passenger demand (e.g., average remaining battery level, average demand response time) and operator demand (e.g., average empty vehicle mileage, average total charging cost). The paper reveals the impact of different optimization objectives on these indicators and analyzes how variations in decision variables influence operational performance.

The primary contributions of this study lie in the integrated simulation–optimization framework and the in-depth investigation of multi-objective conflicts in SAEV charging. Unlike existing approaches that predominantly focus on single objectives, this research constructs a charging decision optimization model based on the joint solution of multi-agent simulation and genetic algorithms. Furthermore, the introduction of segmented charging probability and globally recommended charge levels represents a key contribution in providing dynamic strategies for diverse operational scenarios.

The structure of this paper is organized as follows. Section 1 provides an introduction. Section 2 presents a review of existing research. Section 3 describes the multi-agent simulation model, including its structure and operational logic. Section 4 constructs the charging decision optimization model with four different optimization objectives. Section 5 develops the charging decision optimization model by integrating the multi-agent simulation and the genetic algorithm, covering algorithm logic and data processing. Section 6 presents and discusses the optimization results. Finally, Section 7 concludes the paper.

2. Literature Review

The optimization of vehicle charging decisions involves diverse modeling assumptions and methodologies, leading to varied outcomes and policy implications. Current research predominantly employs optimization-based or reinforcement learning approaches to enhance electric vehicle (EV) fleet performance through allocation, scheduling, and charging strategies [5,6]. For example, Xiaolong Yang et al. [7] developed a bi-level optimization framework integrating pricing and load models to derive optimal EV charging control strategies. However, their work focused narrowly on private EVs, emphasizing charging costs and grid load while neglecting shared mobility contexts. This limitation reflects broader trends in earlier studies, which prioritized private EVs due to insufficient data and infrastructure for SAEVs during their nascent stages. Recent advancements in SAEV research increasingly leverage simulation-based methods. Matthew D. Dean et al. [8] utilized an agent-based POLARIS model to simulate charging and repositioning behaviors, quantifying fleet utilization and deadhead mileage. Similarly, Benjamin Loeb et al. [9] employed MATSim to evaluate SAEV operational efficiency, identifying key factors such as passenger wait times and vehicle occupancy rates. These studies demonstrate the efficacy of simulation in capturing SAEV dynamics and cost-performance trade-offs. Meanwhile, Francesco Strati et al. [10] combined the genetic algorithm with optimal Monte Carlo simulation to obtain the desired statistical properties. Their research inspired us to explore whether integrating the genetic algorithm with a multi-agent simulation model could help achieve our objectives.

In this paper, we also reviewed many articles to explore the factors involved in charging decision optimization. Qiujun Qian et al. [11] applied reinforcement learning to optimize charging schedules for long-distance and low-range EVs, demonstrating significant cost reductions. Qian et al. [12] highlighted the critical role of charging initiation timing in load distribution, emphasizing its inclusion as a decision variable. Beyond cost and load considerations, Ana S. Vasconcelos et al. [13] evaluated car-sharing systems through multi-stakeholder metrics, balancing operator profits, and user costs. Zewei Zhong et al. [14] investigated multi-objective charging strategies, considering economic costs and CO₂ emissions. Their study explored the societal benefits of intelligent EV charging from the perspective of system operators. Zonggen Yi et al. [15] examined the charging decisions of autonomous electric taxi fleets, focusing on energy consumption and charging demand. Their research provided valuable insights for our analysis. Furthermore, with the increasing connectivity and intelligence of vehicles, the deep integration of electric vehicles with the power grid (V2G) has emerged as a cutting-edge research focus. In the field of microgrid frequency stabilization, Sahu et al. [16] proposed an advanced intelligent control strategy to address challenges posed by electric vehicle integration and renewable energy fluctuations. Their research demonstrates that the designed fractional-order fuzzy power system stabilizer (FO-Fuzzy PSS), optimized using an improved sine-cosine algorithm (a-SCA), significantly outperforms traditional controllers in frequency regulation. It reduces frequency stabilization time by over 98%, providing an effective solution for addressing dynamic frequency stability issues in microgrids. However, there are also several limitations. First, many prioritize operator-centric factors (e.g., grid stability) while overlooking passenger-centric metrics like wait times. Second, SAEV-specific variables—such as dynamic repositioning and shared demand patterns—remain underexplored. Third, single-objective optimization dominates the field, neglecting the inherent trade-offs between sub-objectives. For instance, minimizing charging costs risks insufficient battery replenishment, while reducing deadhead mileage may prolong passenger wait times. Similarly, maximizing vehicle utilization through continuous cruising increases energy consumption, whereas high parking rates lower operational efficiency. These contradictions underscore the necessity for multi-objective frameworks capable of dynamically balancing competing priorities across operational scenarios. Accordingly, this paper primarily focuses on addressing these limitations. To more clearly illustrate the limitations of existing research and define the positioning and contributions of this study,

Table 1. Comparison of related studies in methodologies and objectives.

References	Core Methodology	Optimization Objective	Similarities and Differences with This Study
[5] Idle vehicle relocation strategy through deep learning for shared autonomous electric vehicle system optimization. Journal of Cleaner Production	Deep Learning	Vehicle downtime, system efficiency	Focus on SAEV scheduling but emphasize idle vehicle scheduling through deep learning.
[6] Mendoza (2021) Dynamic Ride-Hailing with Electric Vehicles.	Dynamic Optimization	Operating profit	Regarding the optimization of electric vehicle operations, the core challenge lies in dynamic ride-hailing, with operational profitability as the primary objective.
[8] Synergies between repositioning and charging strategies for shared autonomous electric vehicle fleets	Agent-based Simulation	Fleet performance	The SAEV fleet conducts simulation studies to explore the synergistic effects of repositioning and charging.
[9] Fleet performance and cost evaluation of a shared autonomous electric vehicle (SAEV) fleet: A case study for Austin, Texas	Simulation	Cost, service metrics	Evaluate the performance and cost of SAEV fleets through simulation, focusing on case study assessments of cost and service metrics.
[14] The social benefits resulting from electric vehicle smart charging balancing economy and decarbonization. Transport Policy	Multi-objective Optimization	Cost, response time, empty mileage, fleet power consumption (multi-objective trade-off)	The study considers multiple objectives but adopts a macro-level model, examining the societal benefits of smart charging for electric vehicles from the perspective of system operators.
Charging Decision Optimization Strategy for Shared Autonomous Electric Vehicles Considering Multi-Objective Conflicts: An Integrated Solution Process Combining Multi-Agent Simulation Model and Genetic Algorithm	Integrated Simulation-Optimization	Trade-offs under multiple conflicting objectives (e.g., charging cost, remaining battery capacity, demand response time, empty-running mileage)	This study proposes an integrated solution process combining multi-agent simulation models and genetic algorithms to approximate global optimal solutions across 35 scenarios. It specifically addresses trade-offs between different objectives—such as passenger demand and operator requirements—and provides optimal charging decision strategies for diverse scenarios.

provides a systematic comparison of relevant representative studies across dimensions such as core methodologies and optimization objectives.

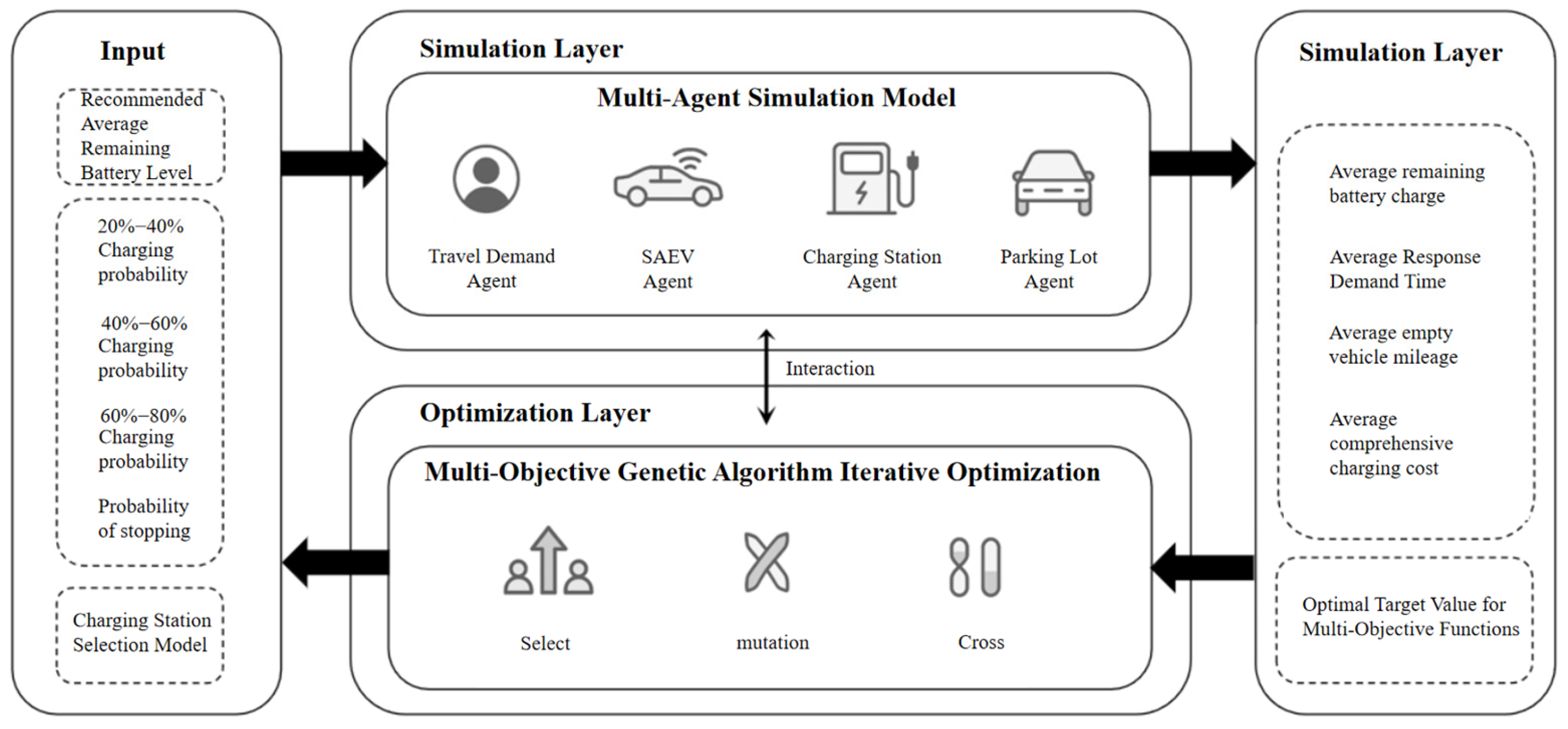
3. Design of a Multi-Agent Simulation Framework for Shared Autonomous Electric Vehicle Charging Decision-Making

The Multi-Agent Model, a distributed artificial intelligence-based simulation approach, investigates the dynamic behaviors of complex systems by emulating interactions among autonomous agents. An agent is defined as an autonomous entity capable of perceiving its environment, processing information, and executing actions to achieve predefined objectives. Each agent exhibits autonomy, reactivity, and social adaptability, enabling decision-making through environmental feedback and inter-agent collaboration.

To evaluate the systemic impacts of SAEV charging behaviors, the proposed simulation framework integrates realistic interactions among SAEVs, passengers, charging stations, and parking lots. The SAEV operational workflow comprises the following stages: (1) passengers submit travel requests, which the system matches to optimal SAEVs; (2) dispatched SAEVs navigate to passengers via shortest-path routing; (3) post-travel, SAEVs dynamically assess their State of Charge (SOC), charging station availability, parking resources, and electricity pricing to autonomously select immediate charging, parking, or continued service; (4) vehicles requiring charging navigate to optimal stations, recharge, and re-enter service, while others proceed to subsequent tasks. This process is simulated through agent-based modeling, enabling granular adjustments to demand patterns, route optimization, charging strategies, and parking decisions. The framework, developed on the AnyLogic platform, incorporates four agent classes: Travel Demand Agent, SAEV Agent, Charging Station Agent, and Parking Lot Agent.

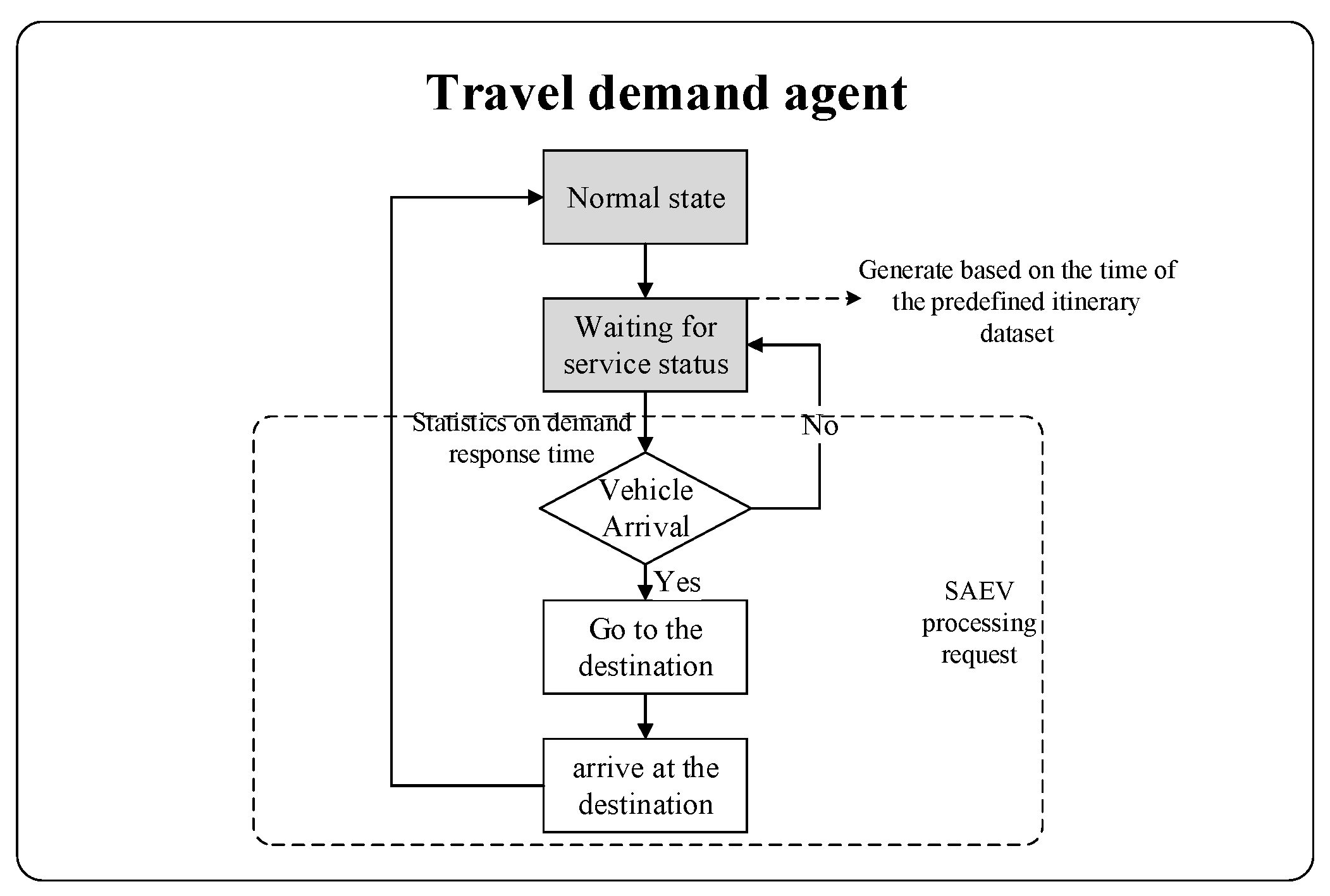
3.1. Travel Demand Agent

The Travel Demand Agent generates trip requests at predefined intervals using a historical travel dataset. Upon initiating a request, the agent transmits an order signal to the SAEV Agent, appends the request to a prioritized waiting queue, and enters a service-pending state. The system allocates the nearest available SAEV with sufficient battery capacity (>20% SOC) to fulfill the request. Upon SAEV arrival, the agent records critical metrics, including unserviced request counts and demand response times. The specific state changes are shown in Figure 1. To ensure temporal precision, the agent executes the dataset’s chronological sequence at one-minute intervals. Prioritization is given to proximate SAEVs with adequate charge; if none are available, response time accrual commences until vehicle assignment.

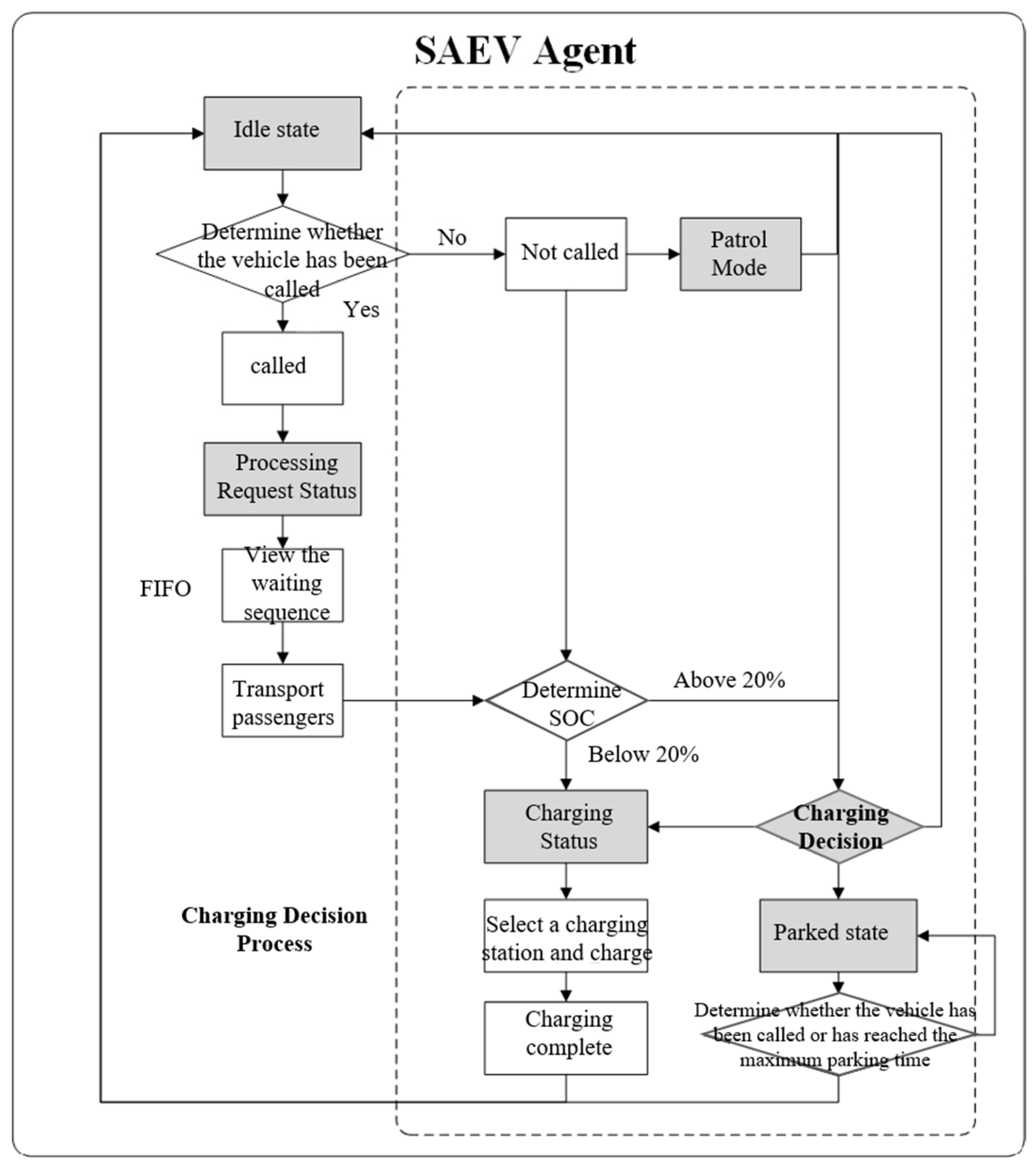
3.2. SAEV Agent

In idle mode, the SAEV Agent continuously monitors local ride-hailing demand and State of Charge (SOC) levels. For incoming orders, the system prioritizes the nearest SAEV with >20% SOC. During inactive periods, SAEVs autonomously select cruising or charging based on SOC thresholds. Post-travel, vehicles with >20% SOC employ a charging decision optimization model (detailed in subsequent sections) to determine immediate charging needs. SAEVs with ≤20% SOC autonomously route to charging stations, queue, recharge, and return to idle status. The specific state change flow is shown in Figure 2. Initial SOC levels are randomized between 20% and 80% to emulate real-world variability. Key operational parameters, derived from commercial EVs (e.g., BYD Qin EV300), are outlined in

Table 2. SAEV parameters.

Parameter Name	Value
Speed	60 km/h
Maximum Driving Range	300 km, 5 h (60 kWh consumption)
80% State of Charge (SOC)	240 km, 4 h (48 kWh consumption)
20% State of Charge (SOC)	60 km, 1 h (12 kWh consumption)

.

The SAEV Agent outputs include vehicle queuing time, charging time, and empty-travel distance. Relevant formulas are shown below:

$$t_{vc}^{wait}=t_{vc}^{arrive}-t_{\mathit{charge}}^{start}$$

(1)

$$t_{vc}^{\mathit{charge}}=t_{\mathit{charge}}^{start}-t_{\mathit{charge}}^{end}$$

(2)

$$eVMT=(T-t_{vc}^{\mathit{charge}}-t_v^{occupied}-t_{vp})v_s$$

(3)

where V is the set of all SAEVs, $v\in V$, C denotes the set of all charging stations, $c\in C$, $t_{vc}^{wait}$ denote the waiting time of vehicle v at charging station c, $t_{vc}^{\mathit{charge}}$ denotes the queuing time of vehicle v at charging station c, $t_{vc}^{arrive}$ denotes the arrival time at the station, $t_{\mathit{charge}}^{start}$ denotes the charging start time, $t_{\mathit{charge}}^{end}$ denotes the charging end time, $eVMT$ denotes the empty-travel distance, $T$ denotes the total simulation duration, $t_v^{occupied}$ denotes the time vehicle v spends transporting passengers (i.e., pickup and drop-off time), $t_{vp}$ denotes the parking time of vehicle v, and $v_s$ denotes the vehicle speed, which is 60 km/h in this study.

As can be seen from Figure 2, SAEV charging station selection is also an important part of the charging decision-making process, which is related to the reliability and response efficiency of the operating system, and can make SAEV charging decision-making more flexible; therefore, based on the passenger demand and the reality of commercial operations, this section sets the SAEVs’ charging station selection behaviors around the four core objectives in a detailed and quantitative manner: distance minimization, time minimization, integrated charging cost minimization, and demand response time minimization. Among them, distance minimization ensures that SAEVs can reach charging stations quickly, reduce the risk of driving with low battery, and find the nearest charging station to charge; time minimization improves charging efficiency by choosing charging stations with less driving distance and shorter queuing time; comprehensive charging cost minimization considers charging and time costs to help operators save money; and demand response time minimization can dynamically respond to the future demand of travel, for example, high orders. Minimizing demand response time enables a dynamic response to future travel demand; for example, charging in high-order areas can prepare for future orders in advance and reduce unnecessary empty vehicle miles.

(1)

Distance Minimization

In this scenario, SAEVs are selected based only on the distance to the charging station, with preference given to the nearest charging station, as in the following equation. Vehicles return to the nearest charging station within the range that the vehicle can travel to reach. The intelligences are placed on the GIS map, and the distance between the intelligences is calculated using the Dijkstra bidirectional algorithm, which performs the shortest path optimization after searching to the complete path by bidirectional search.

$$\underset{c\in C}{\min } d_{vc},v\in V,c\in C$$

(4)

$$\underset{c\in C}{\min } d_{vc}<R_v,v\in V,c\in C$$

(5)

$$R_v=5E_v^{remain},v\in V$$

(6)

where V is the set of all SAEVs, $v\in V$, C is the set of all charging stations, $c\in C$, and $d_{vc}$ is the distance that vehicle v travels to the charging station c. $R_v$ is the current drivable range of vehicle v. $E_v^{total}$ is the total battery capacity (kWh) of vehicle v.

(2)

Time Minimization

Considering the travel time of the SAEVs to the charging station and the expected queuing time at the charging station, the model selects the charging station with the shortest total time within the travel range of the SAEVs, i.e., the one with the smallest total time to return to the charging station.

$$\underset{c\in C}{\min }(d_{vc}/v_s+t_{vc}^{wait}),v\in V,c\in C$$

(7)

$$\underset{c\in C}{\min } d_{vc}<R_v,v\in V,c\in C$$

(8)

$$R_v=5E_v^{remain},v\in V$$

(9)

where $t_{vc}^{wait}$ is the queuing waiting time of vehicle v at charging station c, and $v_s$ denotes the traveling speed of the vehicle, which takes the value of 60 km/h in this paper.

(3)

Minimization of integrated charging cost

Integrated charging cost is divided into charging economic cost and charging time cost. Charging economic cost is the cost paid by SAEVs during the charging process, which is affected by the charging price at the charging station, i.e., the charging price multiplied by the charging time. The charging time cost is the sum of the three-time costs, including the time SAEVs drive to the charging station, the queuing time, and the charging duration. Considering the charging price, charging station location, driving time to the charging station, charging time, and queuing time, the cost function U is calculated for all charging stations within the driving range of the SAEVs, and the charging station with the smallest combined charging cost is returned.

$$\underset{c\in C}{\min } \mathrm{U}=\underset{\mathrm{c}\in C}{\min }\{{\displaystyle \sum _{v\in V}{\displaystyle \sum _{c\in C}{x}_{vc}{m}_c{t}_{vc}^{\mathit{charge}}}}{P}_c+k\times {\displaystyle \sum _{v\in V}{\displaystyle \sum _{c\in C}{x}_{vc}(t_{vc}+t_{vc}^{wait}+t_{vc}^{\mathit{charge}})}}\}$$

(10)

$$t_{vc}^{\mathit{charge}}=(E_v^{total}-E_v^{remain})/P_c$$

(11)

$$t_{vc}=d_{vc}/v_s$$

(12)

$$d_{vc}<R_v,v\in V,c\in C$$

(13)

$$R_v=5E_v^{remain},v\in V$$

(14)

where $t_{vc}^{\mathit{charge}}$ is the time spent by vehicle v charging at charging station c, $E_v^{total}$ is the total battery capacity of vehicle v, $E_v^{remain}$ is the remaining power of vehicle v, $P_c$ is the charging power of charging station c, $\mathrm{U}$ is the cost function, $x_{vc}$ is the decision variable of vehicle v going to charging station c, $m_c$ is the charging price of charging station c, $k$ is the time-cost conversion coefficient, which is taken as the value of RMB 7.25/h in this paper [17,18], $t_{vc}$ is the traveling time of vehicle v to charging station c, $t_{vc}^{wait}$ is the queuing waiting time of vehicle v at charging station c, and $v_s$ denotes the traveling speed of the vehicle. This objective is achieved by minimizing the cost function U (Equation (10)), which is a weighted sum of the economic cost of charging and the total time cost.

(4)

Demand Response Time Minimization

Priority is given to charging stations that are reachable within range and are located within an area of high outgoing demand during the next t + 1 time period. After locking the region, the closest charging station within the region is randomly returned.

Since the focus of this paper is not on predicting travel demand, the high travel demand region is determined from historical data. Based on the distribution of travel locations, the entire region is divided into 0.5 km × 0.5 km areas, as shown in Figure 3. Then, this paper uses historical data to rank the number of travel demands in each area. SAEVs search for charging stations with the highest future travel demand in the adjacent area with a radius of 1.5 km.

$$c\in R_{highdemand}^{t+1},c\in C$$

(15)

$$d_{vc}<R_v,v\in V,c\in C$$

(16)

$$R_v=5E_v^{remain},v\in V$$

(17)

where $R_{highdemand}^{t+1}$ is the high demand region in time period t + 1. This objective is achieved through a three-step screening process: 1. delineate high-demand zones for the next time period (Formula (15)); 2. screen charging stations accessible to vehicles within these zones (Formulas (16) and (17)); and 3. randomly select the nearest station to enable rapid response to potential orders after vehicle charging.

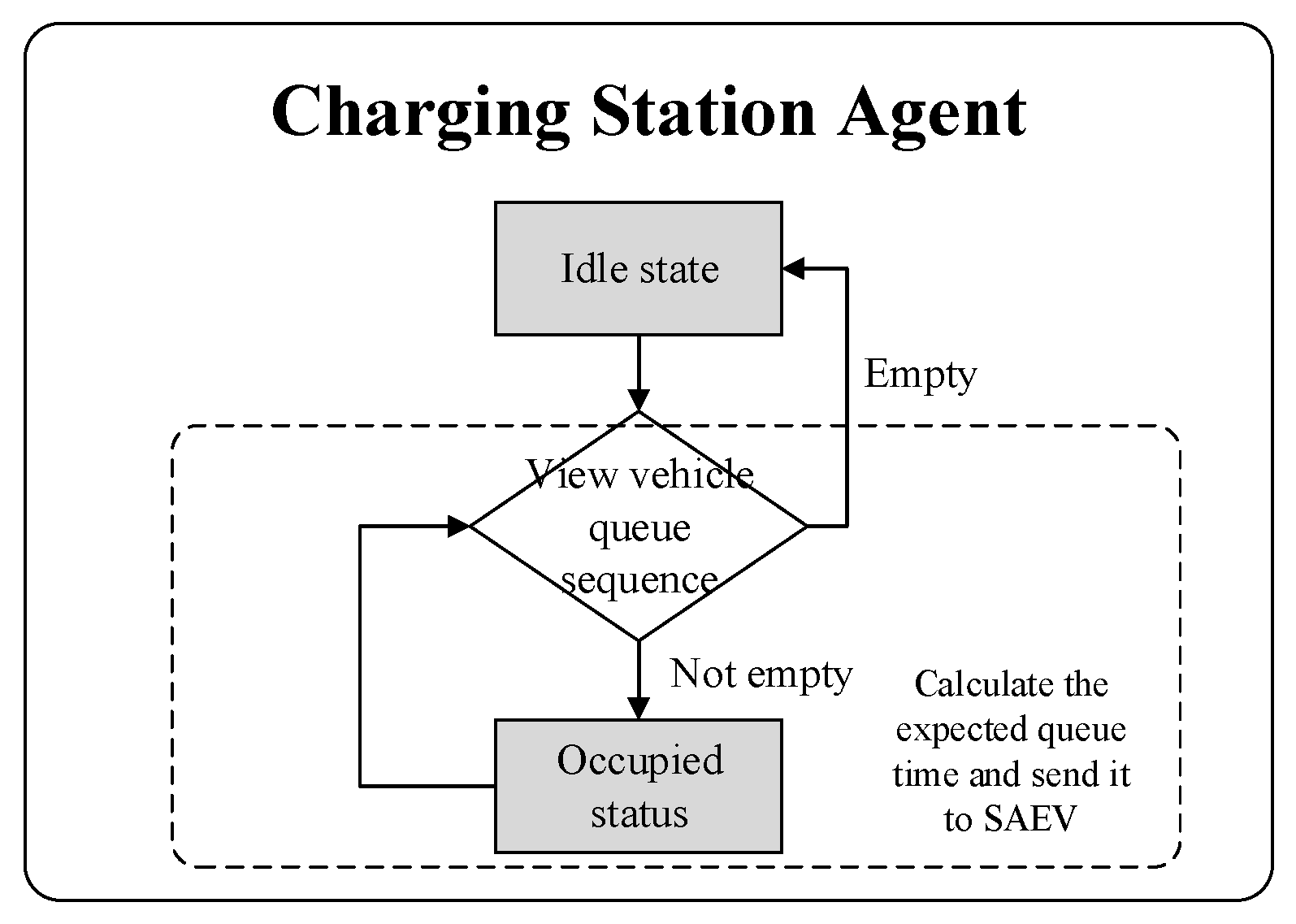
3.3. Charging Station Agent

This agent manages charging infrastructure by simulating station occupancy states (idle or occupied) and resource allocation. The states of the Charging Station Agent include idle state and occupied state, as shown in Figure 4: Idle stations provide immediate service, while occupied stations dynamically update queuing sequences based on SAEV arrivals and departures. Each station is uniquely identified, geolocated, and subject to capacity constraints. Real-time queue lengths and estimated wait times are broadcast to SAEV Agents to inform charging decisions.

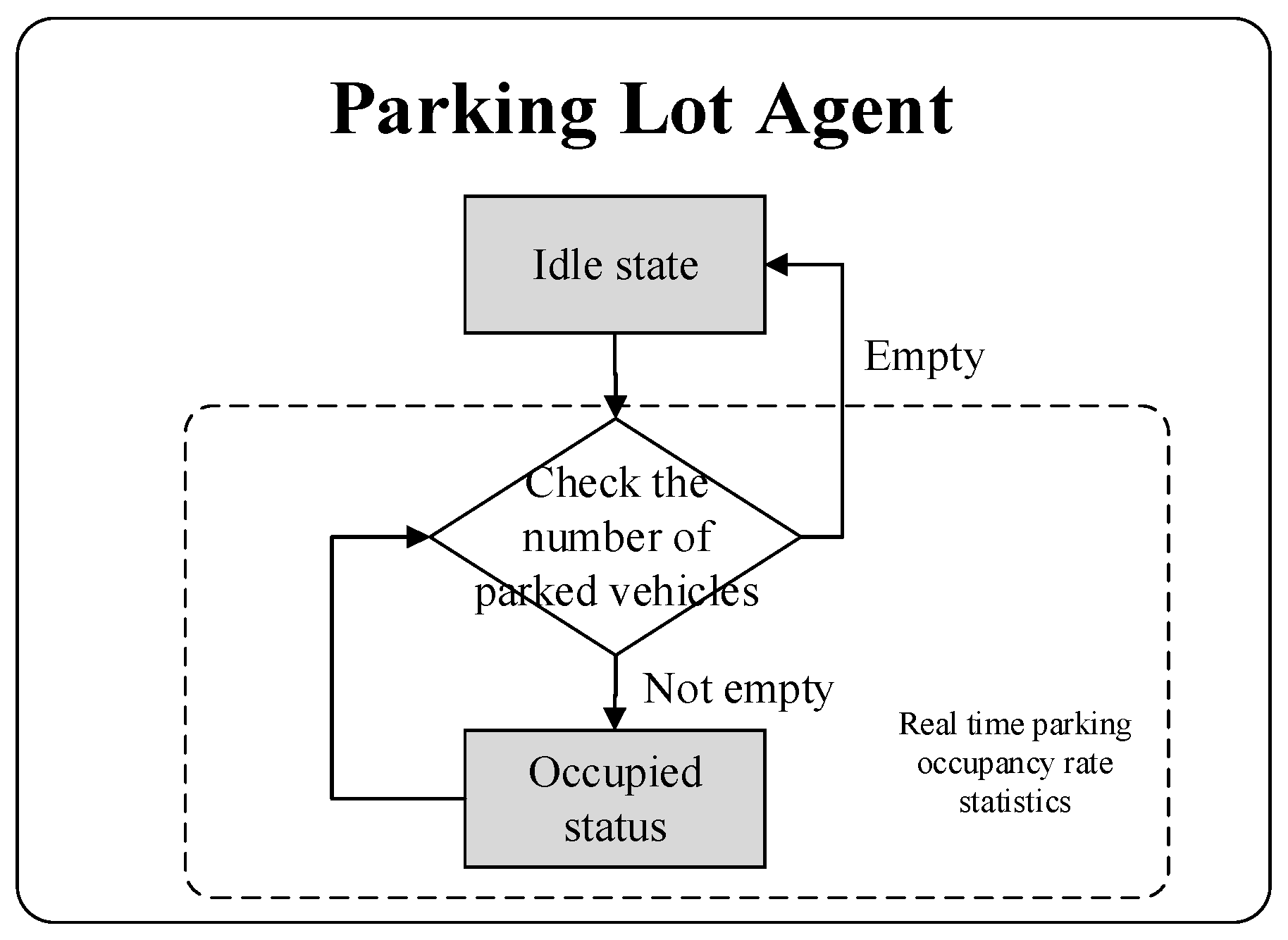
3.4. Parking Lot Agent

The parking lot agent manages parking resources and primarily simulates the operational status of the parking lot and the resource allocation process. The states of the Parking Lot Agent include the idle state and the occupied state, as shown in Figure 5: In the idle state, the parking lot has enough parking spaces available for vehicles; in the occupied state, the parking spaces in the parking lot have been partially or fully occupied. Continuous occupancy monitoring enables real-time data transmission to SAEV Agents, supporting parking strategy optimization.

4. Construction of the Multi-Objective Optimization Model for Charging Decision Strategy

In the optimization of SAEV charging decision strategies, constructing a scientifically sound objective function is key to improving system performance. This paper focuses on four core optimization objectives: remaining battery level optimization, demand response time optimization, empty vehicle mileage optimization, and total charging cost optimization.

4.1. Objective Function for Maximizing Average Remaining Battery Level

$$f_{energy}={\displaystyle \sum _{v\in V}(E_v-E_v^d+{\displaystyle \sum _{c\in C}{P}_c{t}_{vc}^{\mathit{charge}}})}/50$$

(18)

$$E_v^d=d_v/5$$

(19)

where V is the set of all SAEVs, $v\in V$, C is the set of all charging stations, $c\in C$. $E_{\mathrm{v}}$ represents the battery state of vehicle v at the decision time step t. $E_v^d$ is the energy consumed by vehicle v during its travel, and $d_v$ is the distance traveled by vehicle v, where it is assumed that 1 kWh of energy allows the vehicle to travel 5 km. $P_c$ represents the charging speed of charging station c, and $t_{vc}^{\mathit{charge}}$ denotes the charging time of vehicle v at station c. The denominator “50” in the formula serves as a normalization factor to balance the numerical magnitudes of different terms in the objective function.

$f_{energy}$ represents the objective function for the average remaining battery level of the SAEV fleet. The optimization process aims to maximize the overall battery state of the fleet, ensuring that there is always enough energy to meet passengers’ travel demand, thereby achieving a higher service level. The optimization process seeks to maximize this criterion.

4.2. Objective Function for Minimizing Average Demand Response Time

$$f_{request}={\displaystyle \sum _{o\in O}{t}_o^{wait}}/R$$

(20)

where O is the set of all travel demands, i.e., the set of all passengers, $o\in O$. $t_o^{wait}$ is the waiting time for passenger o from initiating the travel request to boarding the vehicle. R is the amount of travel demand.

$f_{request}$ represents the objective function for minimizing passenger demand response time. The optimization process aims to minimize the waiting time for passengers, ensuring that each passenger’s travel demand is met in a timely manner. This will reduce passenger waiting time as much as possible and improve service level. The optimization process seeks to minimize this criterion.

4.3. Objective Function for Minimizing Average Empty Vehicle Mileage

$$f_{evmt}=v_s{\displaystyle \sum _{v\in V}({\displaystyle \sum _{o\in O}{t}_{vo}}+{\displaystyle \sum _{c\in C}{t}_{vc}}+{\displaystyle \sum _{p\in P}{t}_{vp}}+t_{vi})}/50$$

(21)

where O is the set of all travel demands, i.e., the set of all passengers, $o\in O$. C is the set of all charging stations, $c\in C$. P is the set of all parking lots, $p\in P$. $v_s$ represents the vehicle’s driving speed. $t_{vo}$ is the travel time for vehicle v to pick up the passenger after receiving the ride request. $t_{vc}$ is the travel time for vehicle v to reach charging station c. $t_{vp}$ is the travel time for vehicle v to reach parking lot p. $t_{vi}$ is the total cruising time when vehicle v is idle.

$f_{evmt}$ represents the objective function for minimizing the overall empty vehicle mileage of the SAEV fleet. The optimization process aims to minimize the fleet’s overall empty vehicle mileage, avoiding unnecessary travel, reducing unnecessary vehicle wear and tear, and improving vehicle operational efficiency. The optimization process seeks to minimize this criterion.

4.4. Objective Function for Minimizing Total Charging Cost

$$f_{cost}=[{\displaystyle \sum _{v\in V}{\displaystyle \sum _{c\in C}{x}_{vc}{m}_c{t}_{vc}^{\mathit{charge}}}}{P}_c+k\times {\displaystyle \sum _{v\in V}{\displaystyle \sum _{c\in C}{x}_{vc}(t_{vc}+t_{vc}^{wait}+t_{vc}^{\mathit{charge}})}}]/50$$

(22)

where $t_{vc}^{\mathit{charge}}$ represents the charging time of vehicle v at charging station c, $P_c$ represents the charging speed of charging station c, and $x_{vc}$ is the decision variable indicating whether vehicle v chooses charging station c. $m_c$ represents the charging price at station c, and $k$ is the time cost conversion factor, which is 7.25 CNY/h in this study [17,18]. $t_{vc}$ is the driving time for vehicle v to reach charging station c, and $t_{vc}^{wait}$ represents the queueing time of vehicle v at charging station c.

$f_{cost}$ represents the objective function for minimizing the average total charging cost of the SAEV fleet. The total charging cost includes both the economic cost and the time cost during the charging process. The economic cost refers to the electricity cost based on the charging price, charging rate, and the remaining battery level of the vehicle. The time cost includes the time spent traveling to the charging station, queueing for charging, and the actual charging time. The optimization process aims to minimize the operational cost of fleet charging. The optimization process seeks to minimize this criterion.

4.5. Multi-Objective Optimization Function

The weighted objective function contains the previous four objective functions, in order to reduce the computational complexity of solving the multi-objective optimization problem; the overall objective function in the optimization model is a weighted linear combination of the four objective functions. Because of the different indicators of different units and different quantities (such as “demand response time” is hours, “charging cost” is yuan, “empty vehicle mileage” is kilometers), it does not make sense to add or compare them directly. The study first normalizes each metric, which maps all metrics to a dimensionless range of 0 to 1, allowing for a fair comparison of different metrics. On the basis of normalization (eliminating the influence of dimension) for remaining power, demand response time, empty vehicle mileage and charging cost indicators, the total target value in the range of 0 to 1 is obtained through weighted summation, and the smaller the total target value, the better.

$$\min \begin{array}{cc}& \end{array}\beta f_{request}+\gamma f_{evmt}+\delta f_{cost}-\alpha f_{energy}$$

(23)

$$\alpha +\beta +\lambda +\delta =1$$

(24)

$$\begin{array}{l}0\le \alpha \le 1\\ 0\le \beta \le 1\\ 0\le \lambda \le 1\\ 0\le \delta \le 1\end{array}$$

(25)

where $\alpha ,\beta ,\lambda ,\delta$ are weight coefficients between 0 and 1, and the sum of all coefficients equals 1.

Adjusting the weight coefficients in the objective function is a crucial approach for optimizing SAEV charging decisions. It directly affects the trade-offs between different operational objectives. By modifying the weight coefficients, the system can flexibly balance charging efficiency, response time, empty vehicle mileage, and operational costs. This adaptability allows the optimization model to accommodate various fleet operation scenarios and priority objectives. Section 6 will analyze in detail how adjustments to the weight coefficients influence vehicle charging decisions and charging behavior.

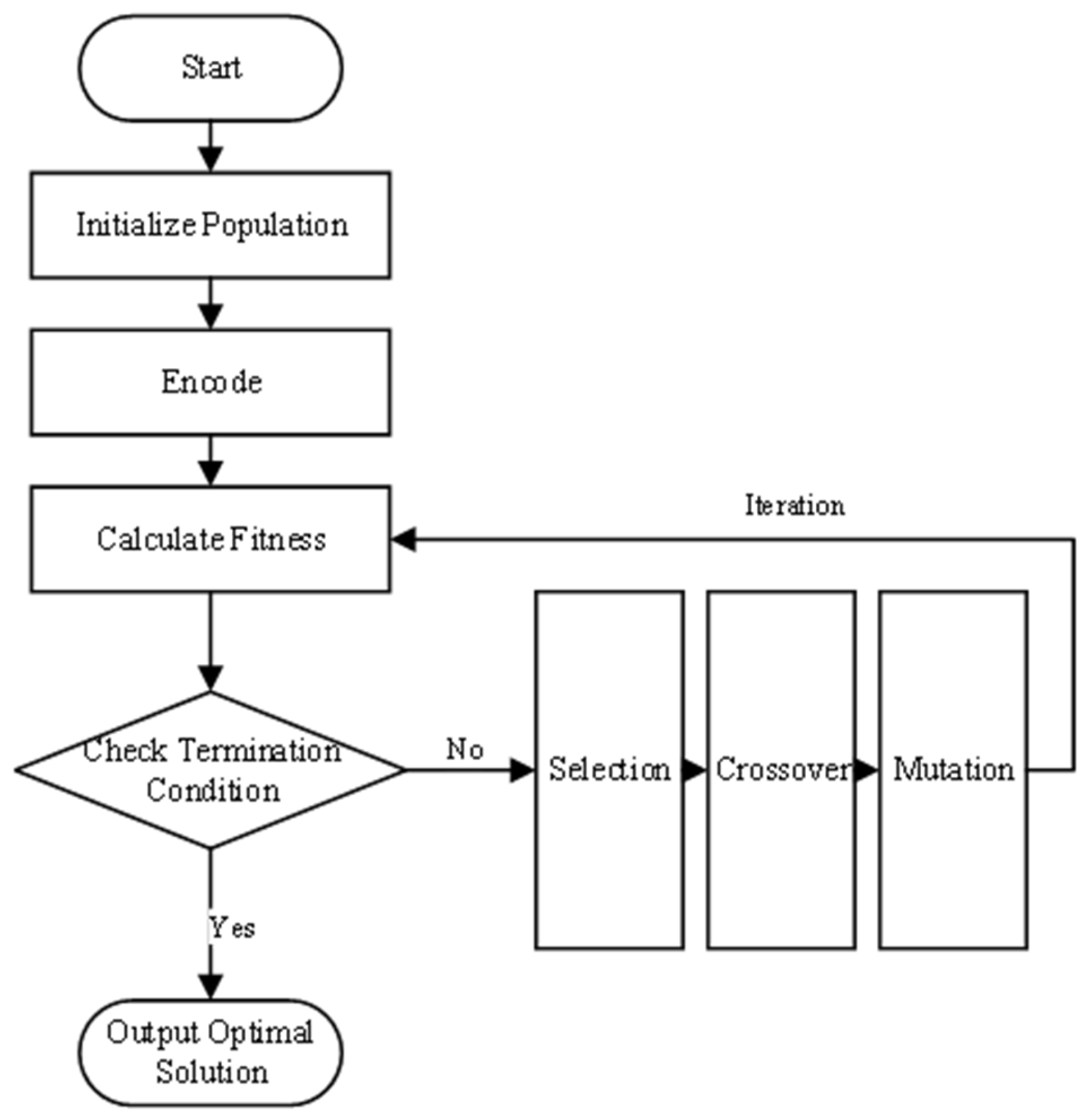
5. Integrated Solution Process Combining Multi-Agent Simulation Models and Genetic Algorithms

5.1. Agent Simulation Model and Genetic Algorithm Joint Solution

In order to study the optimization problem of SAEVs charging decision in depth, a joint solution framework of Agent simulation and genetic algorithm is constructed, including two parts, the simulation layer and the optimization layer. Among them, the simulation layer simulates the whole process operation of SAEVs through discrete-event simulation, while the optimization layer adopts genetic algorithm to optimize the relevant variables such as charging probability and the charging station selection model, so as to realize the comprehensive evaluation and optimization of the charging decision of SAEVs, and the overall architecture is shown in Figure 6.

The model adopts an iterative optimization framework, and its core process includes the coupling mechanism of simulation and optimization: firstly, a set of input parameter combinations are generated and input into the simulation layer, and the simulation system will output the results including the optimal objective values and the performance of each sub-objective; these results are then fed back to the optimization layer for archiving and analysis, and at the same time, the optimization layer generates a new generation of input parameters based on the mechanism of genetic algorithms by selecting, crossover, and mutation. The resulting closed-loop optimization system drives the parameter combinations to converge to the global optimal solution through continuous iteration and finally realizes the multi-objective collaborative optimization.

Inputs are decision variables in the decision-making process, and a set of input data is generated each time before the model starts running, including the recommended average remaining power, charging probabilities for different power intervals, parking probabilities, and charging station selection models. The recommended average remaining power is a global influencing factor for the SAEVs fleet to ensure that the overall power of the fleet is maintained within a reasonable range, which has a constraining effect on the charging decision of the vehicles, and the range of values of the recommended average remaining power is limited to between 3.6 kWh and 14.4 kWh (set according to the parameters of the SAEVs); the charging probability is divided into different power intervals, low power interval (20–40%), medium power interval (40–60%), and high power interval (60–80%), which is used to accurately control the charging behaviors of SAEVs under different power levels and make the charging decision more detailed and the range of the charging probability is set from 0 to 1. The parking probability is used as a probabilistic parameter to assist the charging decision, which is used for the balancing of charging and order-taking behaviors, and the range of the parking probability is set from 0 to 1. The charging station selection model is specialized in regulating the station selection behavior after the vehicle enters the charging state, forming a multi-dimensional decision-making system with each probability in the previous section, and then perfecting the overall process of when to charge and where to charge in charging decision-making, and the charging station selection model is the charging station selection set in the previous Section 3.2.

The outputs are the sub-objective results of passenger demand (including average remaining power and average demand response time) and operator demand (including average empty vehicle driving mileage and average comprehensive charging cost), as well as the optimal objective value of the multi-objective function.

In the simulation layer, a multi-intelligence body model containing Travel Demand Agent, SAEVs Agent, Charging Station Agent, and Parking Lot Agent is constructed to simulate the whole process of SAEVs operation through discrete event simulation. Among them, the data used by the Travel Demand Agent is the travel demand in the central area of Luohu District, Shenzhen City, as the data source; the SAEVs Agent is able to make dynamic decisions between charging, parking, and continuing to take orders, and is also able to charge according to the charging station selection model; the Charging Station Agent and Parking Garage Agent both contain basic parameters such as coordinates and capacity. The specific Agent operation behavior is described in detail in Section 3.

At the optimization layer, a multi-objective genetic algorithm is designed to emulate principles of natural selection and genetics. Its core evolutionary operations include selection, crossover, and mutation. The selection operation probabilistically chooses high-fitness individuals from the population to form a new breeding pool for the next generation. An individual’s selection probability is directly proportional to its fitness value. This paper employs roulette wheel selection (fitness-proportionate selection), where each individual’s reproduction probability is calculated based on normalized fitness values, followed by stochastic sampling to construct the offspring population. The crossover operation involves randomly selecting two parent individuals from the population and exchanging segments of their chromosomes to produce offspring. This genetic recombination transfers high-performance traits from parents to children, generating new high-quality solutions. The mutation operation randomly selects individuals from the population and modifies their genetic material based on a predefined mutation probability, introducing controlled diversity to prevent premature convergence. The complete workflow is illustrated in Figure 7. The algorithm parameters in this study are configured as follows: population size = 50, maximum iterations = 100, selection method = roulette wheel, crossover probability = 0.5, and mutation probability = 0.4.

To integrate multi-Agent simulation with genetic algorithms, this study implements an optimization module within the simulation platform. The module is designed to deploy a genetic algorithm framework, enabling the discovery of optimal solutions for the target objective function. For the integrated system, the decision variables are defined as charging probabilities for distinct SOC intervals, parking probabilities, and recommended remaining battery level. These variables are iteratively adjusted by the optimization algorithm to extremize the objective function. These variables were selected because they holistically capture the charging behavior, resource utilization, and system-wide coordination requirements of SAEV operations. Specifically, segmented charging probability thresholds enable granular control over charging initiation at different SOC levels, effectively preventing both premature charging (which wastes grid resources) and deep discharge scenarios (that cause service interruptions). Parking probability directly governs vehicle idle time and empty vehicle mileage, serving as the critical control variable for optimizing resource utilization efficiency. The recommended remaining battery level enables system-wide energy coordination, maintaining the fleet’s overall battery capacity within an optimal range to prevent concentrated surges in charging demand.

The optimization module in the agent-based simulation platform (implemented using AnyLogic in this paper) automatically executes the configured genetic algorithm to iteratively evaluate the model under different decision variable values, calculating corresponding objective function values and identifying the optimal solution. This paper minimizes the objective function. An optimization module is implemented in AnyLogic, which utilizes “root.ObjectiveFunction” to call the pre-configured multi-objective optimization model [19]. The iterative parameters are set as follows: A total of 100 generations with 1 simulation run per generation (i.e., each iteration executes one full 120 h model simulation and outputs the corresponding objective value). After 100 iterations, the global optimal solution is exported. The maximum allocated memory is 8192 MB, and a fixed random seed is applied to ensure experimental reproducibility. Additionally, relevant variable parameters are configured by specifying the decision variables as discrete numerical types, with defined minimum/maximum values and step sizes to control search space precision. This reduces computational demands and improves model efficiency. Before execution, initialize the objective value statistical dataset using functions such as “datasetCurrentObjective.reset()”. Secondly, configure real-time updates for the global optimal solution. The code for Algorithm 1 is as follows:

Algorithm 1 Optimal solution update process.

Input: Current solution, optimal solution Output: optimal solution if (isBestSolutionFeasible()) then     datasetBestFeasibleObjective.update(); end if if (!isCurrentSolutionFeasible()) then     bestInfeasibleObjective = min(bestInfeasibleObjective, getCurrentObjectiveValue()); end if

In order to realize the visual analysis of the optimization process and results, the target value changes are monitored through convergence curves and tables, and the following figure shows the optimization model running diagram. In order to realize the visual analysis of the optimization process and results, the target value changes are monitored through iteration curves and tables, and Figure 8 below shows Optimization model execution results, and the scene settings are shown in the next section. As seen in Figure 8, after 100 iterations of optimization of the model, the resultant iteration curves all show a convergence trend, indicating that the model has good stability and reliability.

5.2. Experimental Design

The experimental design, firstly, designs 35 scenarios according to different weight combinations; secondly, it presets the assumptions of the simulation to make the simulation easier to realize and analyze; and finally, it preprocesses the simulation data that will be used in the experimental process, so that it can be initialized to ensure the rigor and repeatability of the data in each iteration.

The weight coefficients of the objective function will be adjusted in increments of 0.25, resulting in a total of 35 scenarios, as shown in

Table 3. Weight of the objective functions for each scenario.

Number	Weight				Number	Weight
	Maximizing Remaining Battery	Minimizing Demand Response Time	Minimizing Empty Vehicle Mileage	Minimizing Total Charging Cost		Maximizing Remaining Battery	Minimizing Demand Response Time	Minimizing Empty Vehicle Mileage	Minimizing Total Charging Cost
1	1	0	0	0	19	0.5	0.25	0	0.25
2	0	1	0	0	20	0.5	0	0.25	0.25
3	0	0	1	0	21	0.25	0.5	0.25	0
4	0	0	0	1	22	0.25	0.5	0	0.25
5	0.25	0.25	0.25	0.25	23	0	0.5	0.25	0.25
6	0.75	0.25	0	0	24	0.25	0.25	0.5	0
7	0.75	0	0.25	0	25	0.25	0	0.5	0.25
8	0.75	0	0	0.25	26	0	0.25	0.5	0.25
9	0.25	0.75	0	0	27	0.25	0.25	0	0.5
10	0	0.75	0.25	0	28	0.25	0	0.25	0.5
11	0	0.75	0	0.25	29	0	0.25	0.25	0.5
12	0.25	0	0.75	0	30	0.5	0.5	0	0
13	0	0.25	0.75	0	31	0.5	0	0.5	0
14	0	0	0.75	0.25	32	0.5	0	0	0.5
15	0.25	0	0	0.75	33	0	0.5	0.5	0
16	0	0.25	0	0.75	34	0	0.5	0	0.5
17	0	0	0.25	0.75	35	0	0	0.5	0.5
18	0.5	0.25	0.25	0	—	——	——	——	——

below. This paper explores their impact on charging decisions and four key metrics. These metrics are categorized into passenger demand (average remaining battery level, average demand response time) and operator demand (average idle driving distance, average total charging cost).

Among them, 35 scenarios are analyzed using the control variable method to explore the impact mechanisms of different optimization objectives on SAEV operations. Scenarios 1–4 represent single-objective optimization, separately examining the extreme cases of maximizing remaining battery level (Scenario 1), minimizing demand response time (Scenario 2), minimizing idle driving distance (Scenario 3), and minimizing total charging cost (Scenario 4). Scenario 5 serves as a balanced reference, assigning equal weights (0.25 each) to all four objectives. Scenarios 6–35 adopt mixed weights, optimizing for two or three primary and secondary objectives to study their interactions. Each scenario runs 100 iterations, and the global optimal solution is obtained at the end of the iterations.

The decision variables of this model include the following key parameters: probability of charging at 20% to 40% of the power interval, probability of charging at 40% to 60% of the power interval, probability of charging at 60% to 80% of the power interval, probability of stopping, and the recommended average level of remaining power.

(1)

The recommended average residual power level is set to ensure that the overall power of the fleet is maintained within a reasonable range through global coordination to avoid a concentrated outbreak of large-scale charging demand. This is because in the simulation process, each SAEVs is an independently operating intelligence that is able to make decisions autonomously based on its own state, such as choosing to charge, take orders, or cruise. This independence allows each vehicle to respond flexibly to dynamic travel demands and changes, thus improving the overall efficiency of the system. However, the independence of vehicles is not completely unconstrained; so, in this paper, the recommended average remaining power level is used as a global optimization aspect objective, which exerts a certain amount of influence on the charging decisions of vehicles. For example, when the system detects a low overall average residual power level, it may prioritize the charging behavior of vehicles to ensure the overall operational continuity of the fleet. The recommended range of values for average residual power is limited to between 3.6 kWh and 14.4 kWh (set according to SAEVs parameters).

(2)

Setting the charging probability in segments can finely control the charging decision of vehicles at different power levels, avoiding the waste of resources or service interruption caused by charging too early or too late. The power interval is divided into low power interval (20–40%), medium power interval (40–60%), and high power interval (60–80%), and the charging behavior of the vehicle is precisely regulated by setting differentiated charging probabilities for different power intervals. Charging in the low power interval avoids stopping driving due to low power; charging in the medium power interval is more flexible, which can better respond to future demand and also charge in advance to avoid large power consumption; charging in the high power interval is preventive charging. The value range of charging probability is set between 0 and 1.

(3)

As a variable of auxiliary charging behavior, parking probability directly affects vehicle idle time and empty vehicle mileage, balancing power consumption and order-taking behavior, which is the key to reducing vehicle charging frequency and optimizing charging resource utilization. The value range of parking probability is set between 0 and 1.

(4)

The role of the charging station selection model is to be able to join the charging station selection behavior under the decision-making of the probability parameter, to be able to make the whole charging decision-making process more complete, and to select the most appropriate charging station selection model under the current scenario, so as to make the optimization strategy more complete, to strengthen the analysis of the multi-dimensional factor changes in charging decision-making, and to explore the optimal strategy under different scenarios. The charging station selection model is the charging station selection set in Section 3.2.

These variables are dynamically adjusted during the iterative process of the algorithm as the core dimensions of the search space, aiming to achieve the global optimal solution of the objective function by optimizing their values. Specifically, the algorithm evaluates the impact of different combinations of these variables on the system performance by exploring different combinations of these variables to find the parameter configuration that maximizes the value of the objective function.

5.3. Simulation Data Preprocessing

(1)

Simulation Environment Initialization: Load road network, charging station locations, and travel demand data. Initialize operational parameters, including charging prices, queuing rules, and service capacity. Reset simulation time with a total duration of 120 h and a time step size of one minute.

(2)

Vehicle Model Initialization: Configure initial vehicle parameters, positions, speeds, and behavioral patterns, including fleet size, battery capacity, maximum driving range, and energy consumption rate.

(3)

Data Logging System Initialization: Initialize the data recording system comprising statistical, storage, and analytical modules. Configure the system to capture critical simulation data (e.g., vehicle status, charging station states, charging events), preload real-time monitoring datasets and post-processing tools, and deploy visualization modules for live simulation monitoring and result analysis.

The entire initialization process is automated through scripting, ensuring experimental reproducibility and consistency. The system also provides parameter adjustment capabilities to enable flexible scenario configuration and testing.

5.4. Additional Simulation Assumptions

(1)

Real-time Information Exchange. SAEVs maintain seamless connectivity with all charging stations, enabling dynamic sharing of critical operational data, including station locations, available charging points, charging prices, real-time queue lengths, and estimated waiting times.

(2)

Charging Station Facilities. All stations are publicly accessible and equipped with infrastructure meeting SAEV charging requirements, including compatible charging interfaces and adequate power supply. Each station is configured such that the number of vehicle parking spaces matches that of charging points.

(3)

Road Network Assumptions. The road network is assumed to operate under ideal free-flow conditions, with traffic signals, congestion phenomena, and other external disturbances explicitly excluded from the simulation scope.

(4)

Charging Protocol. SAEVs adopt a “Full-Charge Departure” policy at charging stations, immediately vacating the station upon reaching full battery capacity.

(5)

Parking Behavior Policy. SAEVs implement a flexible parking strategy, immediately departing the parking facility when either the parking duration reaches a preset threshold or a new mobility request is received.

6. Optimization Results Analysis

This section analyzes the analysis of the change rule of the optimal objective value, the results of the sub-objectives, including the average remaining power, the average demand response time, the average empty vehicle mileage, and the average comprehensive charging cost, and the paradoxical relationship that exists between the sub-objectives. This study clearly defines scenario 5 (weighting coefficients: 0.25, 0.25, 0.25, 0.25) as the baseline scenario, and the performance analysis of all subsequent scenarios is based on this baseline. In Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 below, the baseline scenario is highlighted in gray.

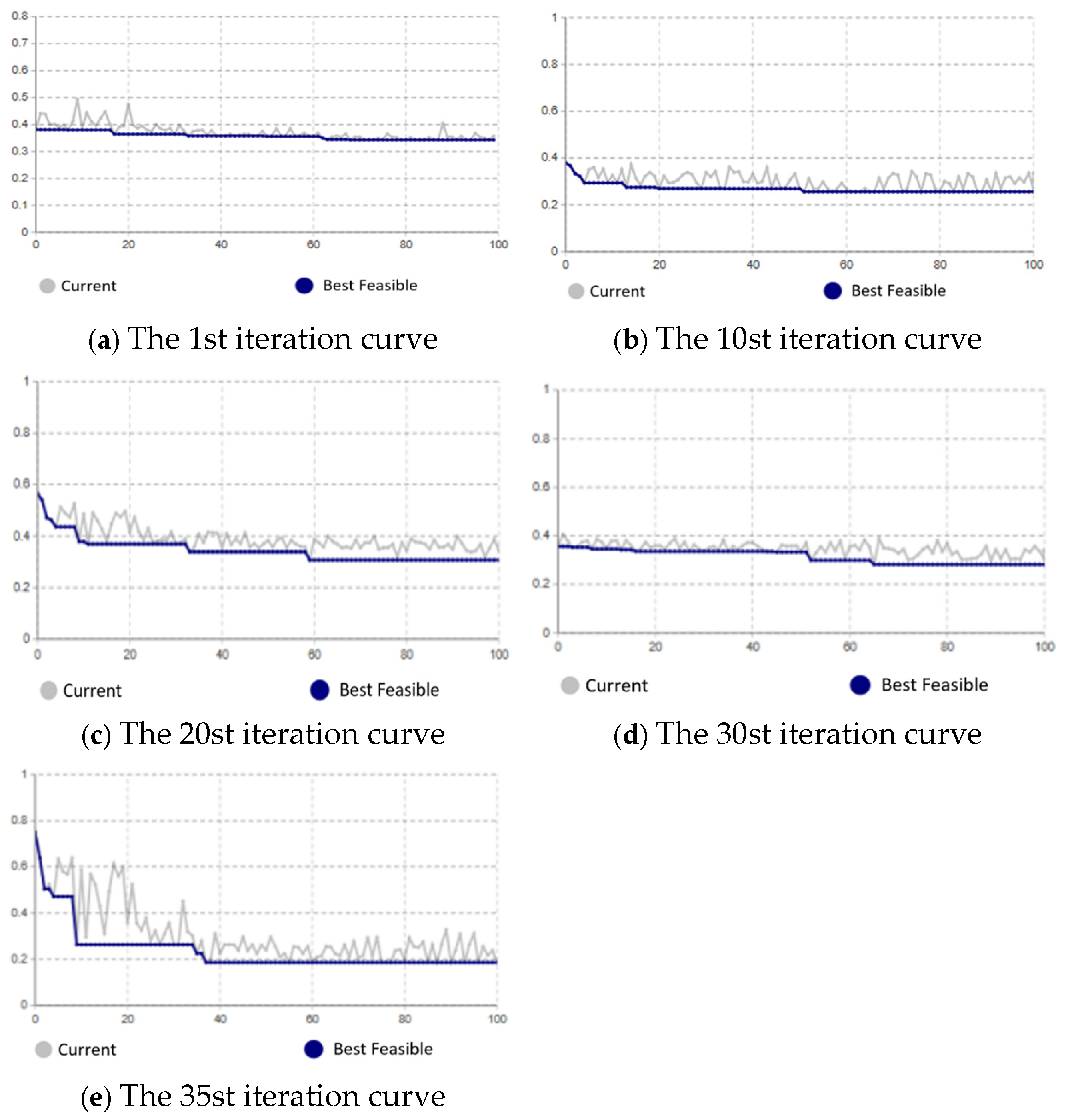
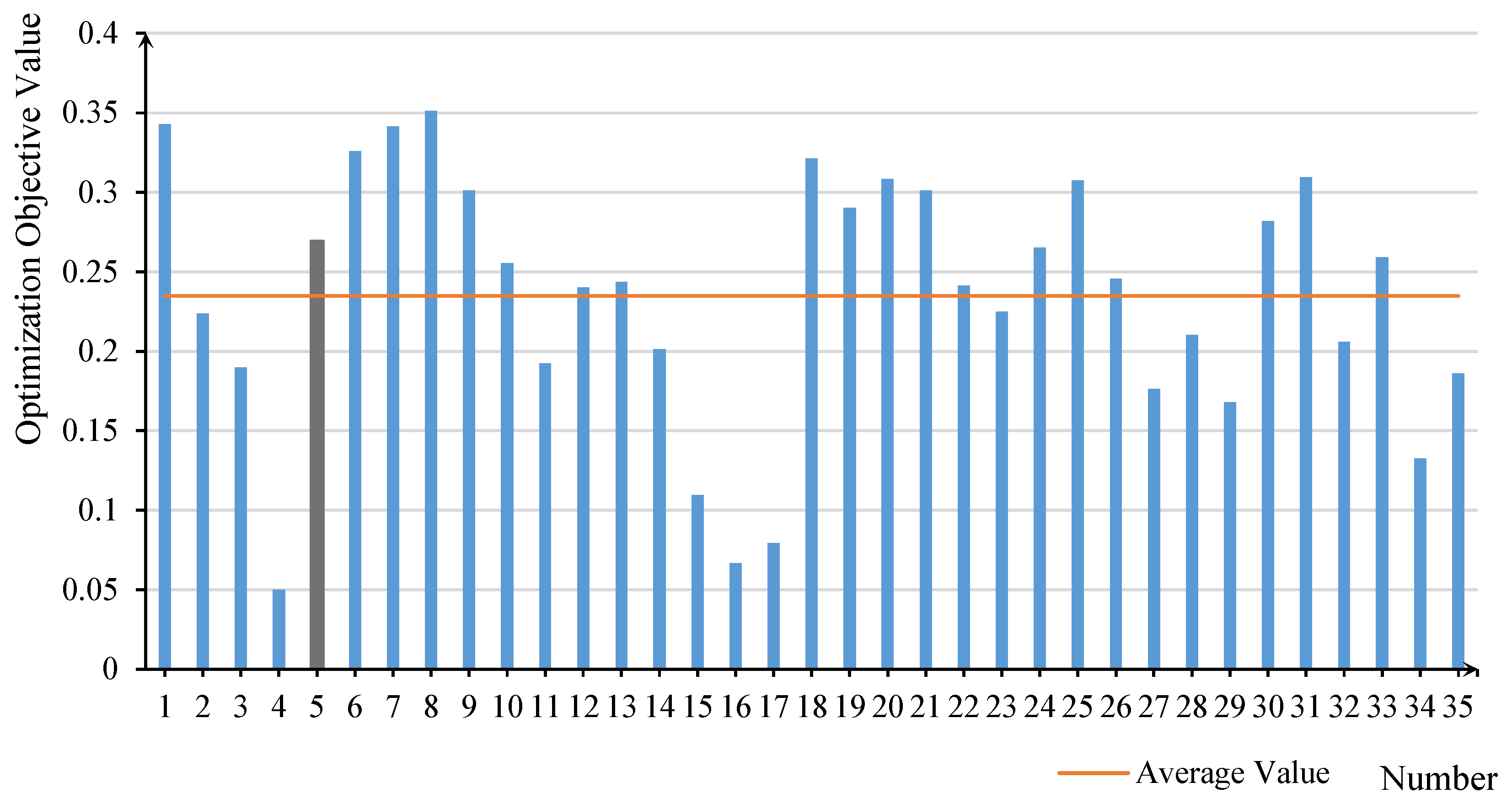
6.1. Analysis of the Variation Pattern of Optimal Objective Values Under Different Scenarios

The optimization objective value is a normalized composite score between 0 and 1, used to evaluate the overall performance of different decision variable combinations in the multi-objective optimization problem. Since different indicators have different units and dimensions (e.g., “demand response time” is measured in hours, “charging cost” is measured in CNY, and “empty vehicle mileage” is measured in kilometers), direct summation or comparison is meaningless. Normalization maps are all indicators to a range from 0 to 1, allowing for fair comparison across different indicators. It is calculated by normalizing indicators such as demand response time, empty vehicle mileage, and charging cost (eliminating the impact of units) and then applying weighted computation. A smaller value indicates better performance.

After multiple iterations of the algorithm model optimization, the optimal objective value for each scenario is obtained, as shown in Figure 9 below. This process involves continuously changing the decision variables to find the global optimal solution for the optimization objectives.

From Figure 9, by comparing the first four Scenarios, where a single objective is used for optimization, it can be seen that when minimizing total charging cost (i.e., Scenario 4) is the sole criterion, its overall objective value is significantly lower than the others. This indicates that minimizing total charging cost has the greatest influence on the optimization objective value, dominating the overall optimization process. This is because total charging cost typically encompasses several key factors, including the economic cost of charging and the time cost (such as the time spent traveling to the charging station and waiting). The combination of these factors results in its greatest contribution to the optimization objective value. In contrast, other single-objective optimization scenarios (such as maximizing remaining battery, minimizing demand response time, and minimizing empty vehicle mileage) have higher optimization objective values, suggesting that they cannot fully account for the overall system when optimized individually. However, single-objective optimization still has limitations, which can be observed in Section 6.2. Therefore, unless in special cases, it is recommended to consider a weighted approach that takes different objectives into account, rather than focusing solely on single-objective optimization. If only one optimization objective can be chosen, minimizing total charging cost can be selected as the objective function to balance the overall SAEV fleet as much as possible.

Scenario 5 (weight: 0.25, 0.25, 0.25, 0.25) has the most balanced weight distribution. However, its optimization objective value is slightly higher than the average, making it not the optimal solution.

From Scenario 6 to Scenario 17, the optimization is performed by selecting only two primary and secondary objectives for charging decision-making. In each case, one primary objective has a weight of 0.75, while the secondary objective has a weight of 0.25. Regardless of which secondary objective is chosen, the overall optimization effectiveness of the primary objectives, ranked from best to worst, is as follows: total charging cost, empty vehicle mileage, demand response time, and remaining battery level. Additionally, the best-performing secondary objectives for each primary objective are as follows: When the primary objective is remaining battery level, the best secondary objective is demand response time. When the primary objective is demand response time, the best secondary objective is total charging cost. When the primary objective is empty vehicle mileage, the best secondary objective is total charging cost. When the primary objective is total charging cost, the best secondary objective is demand response time. In summary, when only two objectives can be selected with a primary-secondary structure, the weight distribution can be set based on these findings. Adjustments can also be made according to real-world conditions.

From Scenario 18 to Scenario 29, three objectives are selected for charging decision optimization, with one primary objective (weight of 0.5) and two secondary objectives (each with a weight of 0.25). This approach evaluates the impact of three objectives on the optimization results. From the result chart, it is evident that when total charging cost is chosen as the primary objective (Scenario 27–29), the overall optimization value is significantly lower than other categories. Therefore, total charging cost should be prioritized as the primary objective. Additionally, when selecting three objectives, prioritizing demand response time, empty vehicle mileage, and total charging cost yields better optimization results, as observed in Scenarios 23, 26, and 29.

From Scenario 30 to Scenario 35, two objectives are selected for charging decision optimization, with equal importance and a balanced weight distribution of 0.5 for each. The most recommended combination is demand response time and total charging cost (Scenario 34), while the least recommended is remaining battery level and empty vehicle mileage (Scenario 31). Additionally, when total charging cost is included as one of the optimization objectives, the other objective can be either empty vehicle mileage or remaining battery level, in addition to demand response time. The optimization values for the latter two combinations are relatively similar, allowing for selection based on real-world conditions.

In summary, when selecting optimization objectives for the charging decisions of shared autonomous electric vehicles, it is best to assign a higher weight to total charging cost optimization. In other words, to effectively balance passenger demand and operator requirements, total charging cost should be included in the objective function. This ensures that the overall optimization results achieve a more desirable balance across all key factors.

6.2. Analysis of Conflicting Sub-Objectives

In addition to the overall optimized objective value, this paper also focuses on the independent numerical performance of four key sub-objectives: average remaining battery level, demand response time, empty vehicle mileage, and total charging cost.

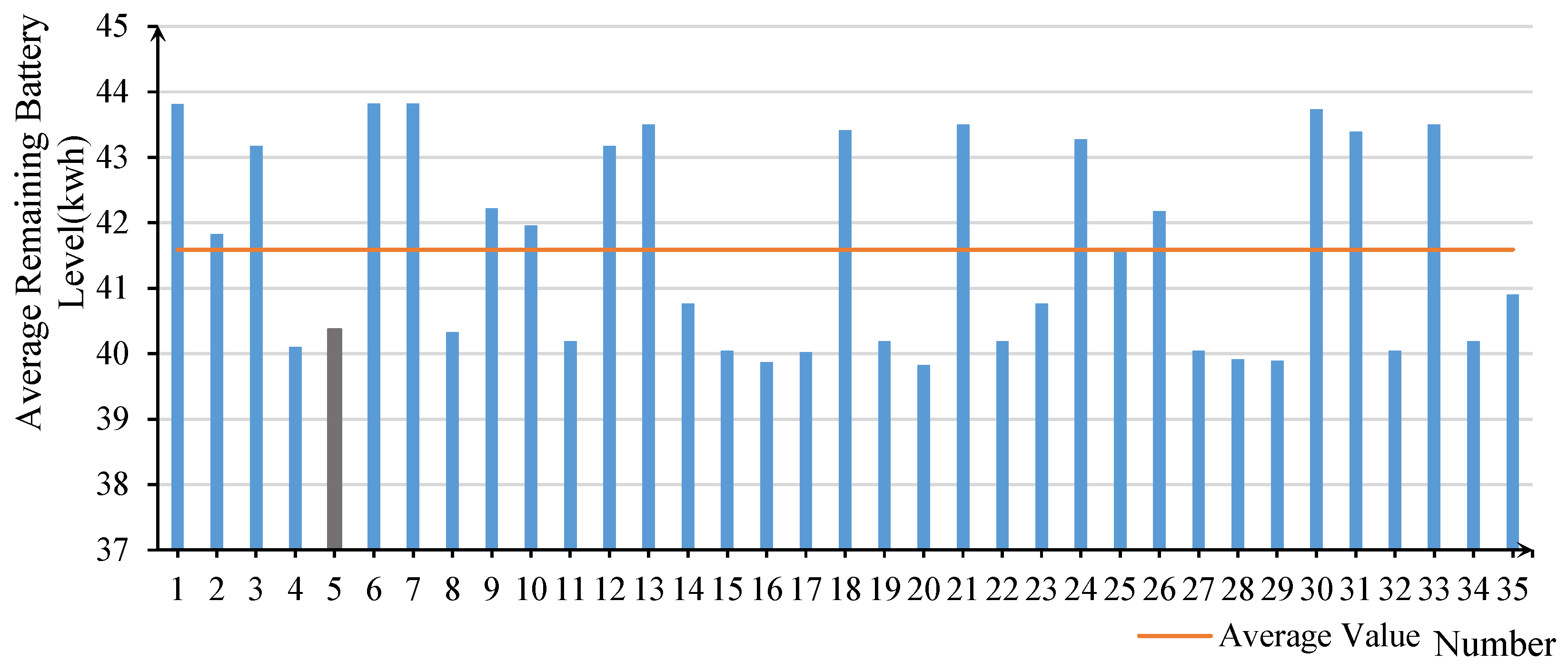
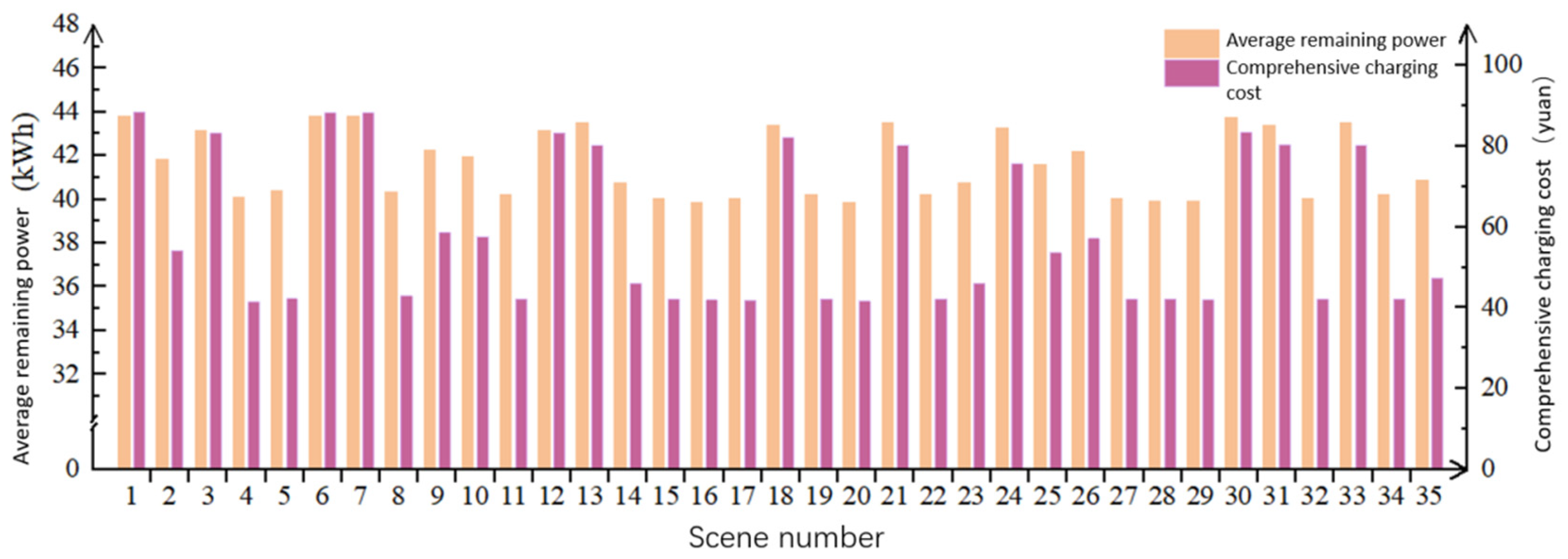
6.2.1. Average Remaining Battery Level

The average remaining battery level refers to the average remaining battery percentage of all SAEVs at a given time, used to assess the overall battery level of the fleet. The higher this value, the better. In the model, it is calculated once per minute, and the global average remaining battery level per vehicle is obtained at the end. A higher average remaining battery level ensures that the SAEV fleet maintains a sufficient charge to remain operational and respond to passenger demand more effectively. This is particularly important for shared mobility services, as SAEVs must be able to quickly respond to passenger requests during peak demand periods (such as rush hours) while avoiding service disruptions or efficiency losses due to insufficient battery charge.

From Figure 10, it can be observed that maximizing remaining battery level is crucial for improving vehicle battery levels and should be given higher weight. On the other hand, minimizing total charging cost should be controlled appropriately, as assigning too much weight to it will significantly lower the battery level. For example, in Scenario 20 (weight 0.5, 0, 0.25, 0.25), the average remaining battery level is 39.830 kWh, indicating that balancing remaining battery level and total charging cost, while also considering empty vehicle mileage, leads to a good balance. If the primary operational goal focuses solely on the average remaining battery level, the weight distribution should prioritize maximizing the remaining battery level (weights of 0.5 to 0.75) to ensure that vehicles maintain a higher battery level, supporting longer driving distances and more tasks. The weight of minimizing total charging cost should not be too high (suggested 0.25 to 0.5) to avoid significantly reducing the battery level. Meanwhile, the weights for demand response time and empty vehicle mileage can be flexibly adjusted according to actual needs (suggested 0.25 to 0.5) to improve battery levels while optimizing user experience and operational efficiency.

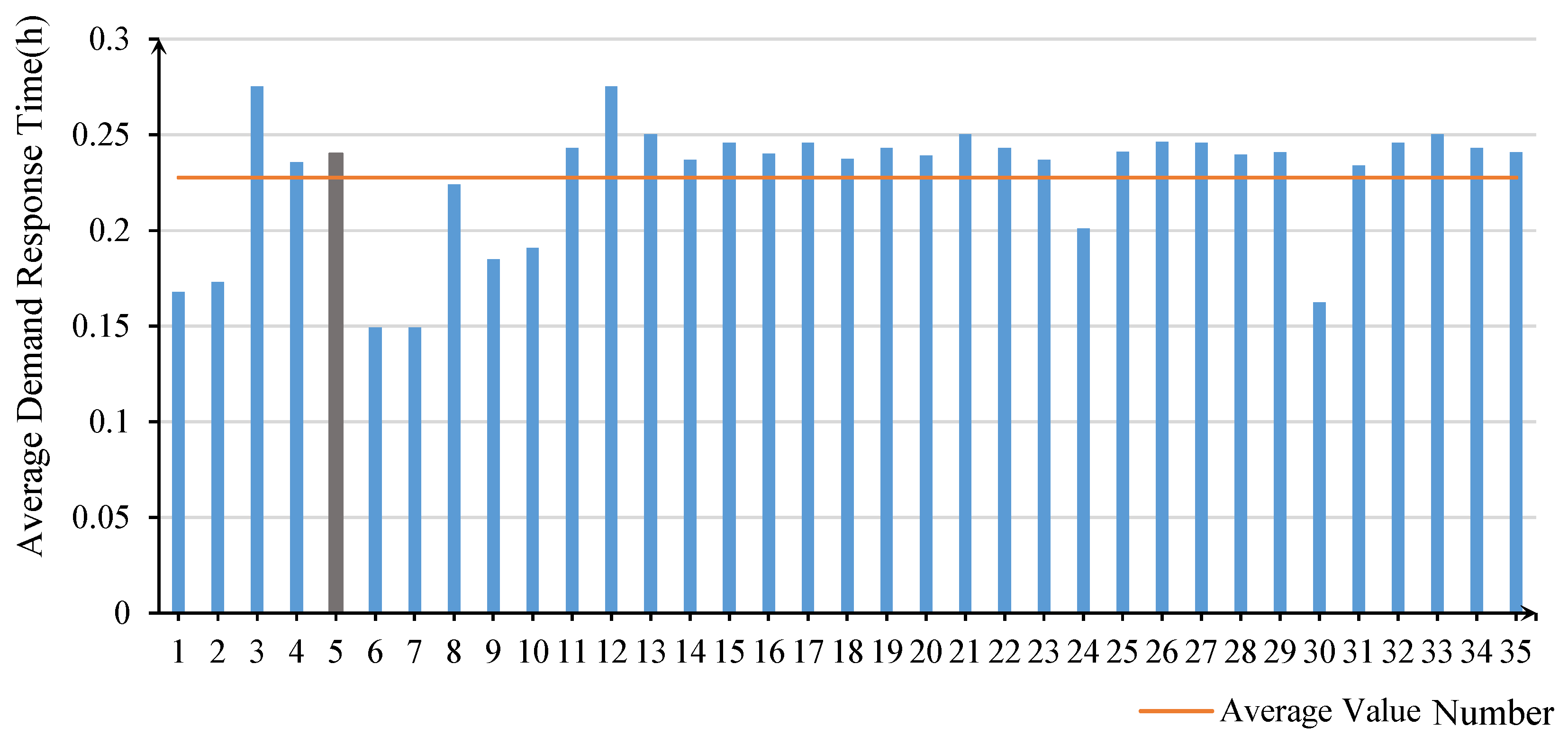
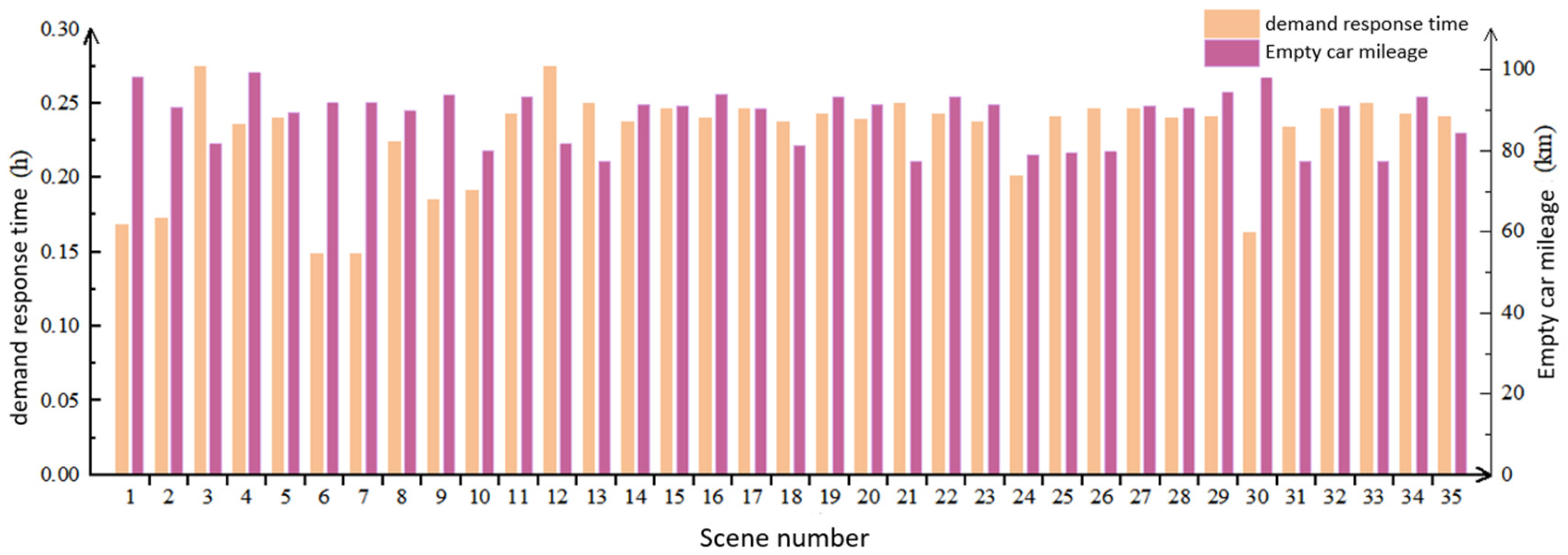
6.2.2. Average Demand Response Time

Average demand response time refers to the average waiting time from when a passenger initiates a ride request to when they board the vehicle and begin the trip. The smaller this value, the better. Average demand response time is directly related to user experience, service efficiency, and operational revenue. In real-world operations, longer response times can decrease passenger satisfaction, potentially leading to user attrition or a shift to alternative transportation modes, thereby reducing the number of orders and revenue.

From Figure 11, it can be seen that maximizing remaining battery level and minimizing demand response time are key to reducing demand response time and should be given higher weights. On the other hand, giving too much weight to minimizing empty vehicle mileage and minimizing total charging cost can increase demand response time and should be appropriately controlled. For example, in Scenario 24 (weights 0.25, 0.25, 0.5, 0), the response time is 0.201 h, which indicates that while focusing on minimizing empty vehicle mileage, appropriately considering remaining battery level and demand response time can achieve a good balance. If the actual operational goal prioritizes minimizing demand response time, the weight distribution should prioritize maximizing remaining battery level (weights 0.5–0.75) and minimizing demand response time (weights 0.5–0.75) to significantly reduce response time while improving battery level. At the same time, the weights for minimizing empty vehicle mileage and total charging cost should not be too high (suggested 0.25–0.5) to avoid significantly increasing demand response time.

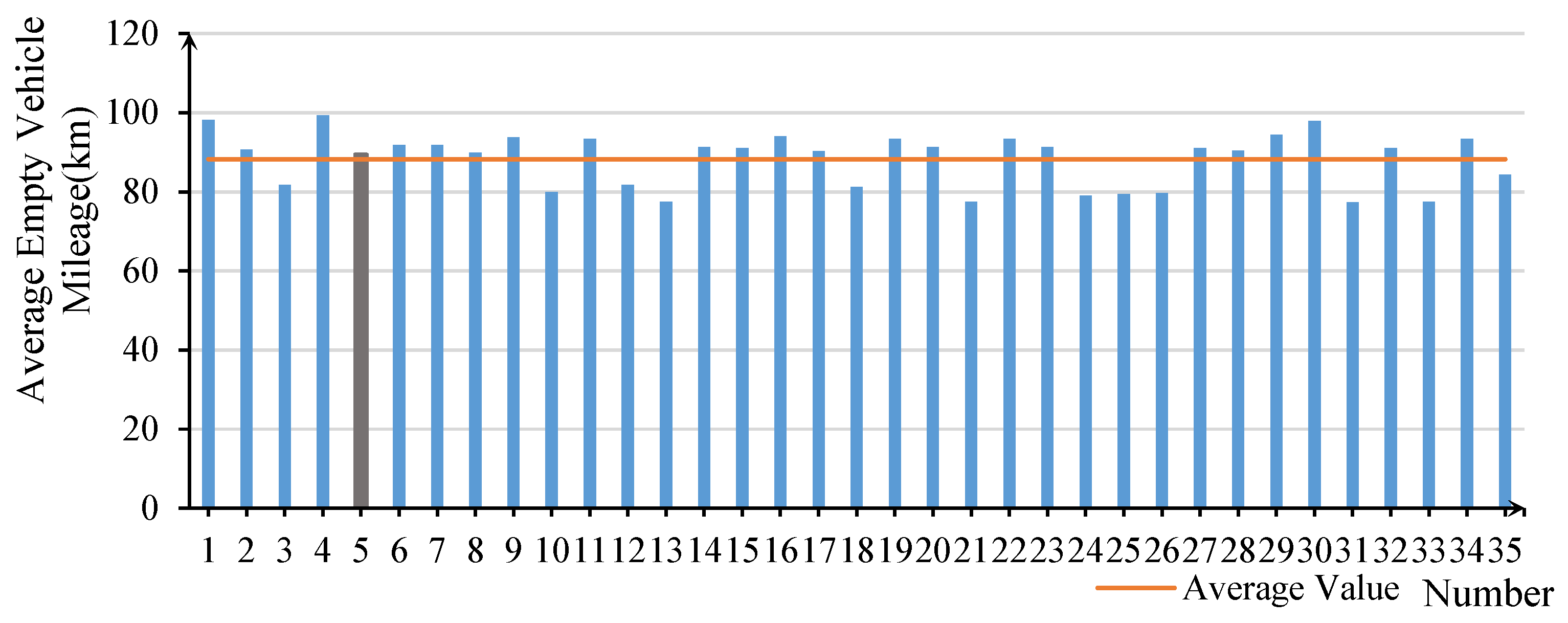
6.2.3. Average Empty Vehicle Mileage

The average empty vehicle mileage refers to the driving distance of the vehicle excluding charging, parking, and picking up or dropping off passengers. To provide a more intuitive understanding, this value is represented as the empty vehicle mileage of a single vehicle per day, with smaller values being better. A higher average empty vehicle mileage means that the vehicle drives longer distances without passengers, which not only increases energy consumption and charging demand but also raises operational costs. In addition, the increase in average empty vehicle mileage leads to higher carbon emissions, which is contrary to environmental sustainability goals.

From Figure 12, it can be observed that minimizing empty vehicle mileage and minimizing demand response time should be assigned higher weights. In contrast, the weights for maximizing remaining battery level and minimizing total charging cost should be controlled, as excessively high weights for these objectives may lead to longer cruising times and increased travel distances to charging stations, resulting in higher empty vehicle mileage. If the primary operational objective is to minimize average empty vehicle mileage, the weight distribution should prioritize minimizing demand response time (weight 0.5–0.75) and minimizing empty vehicle mileage (weight 0.5–0.75) to significantly reduce this metric. Meanwhile, the weights for remaining battery level and total charging cost should not be too high (recommended range: 0.25–0.5). In practical applications, it is suggested that during high-demand periods, priority should be given to minimizing demand response time and empty vehicle mileage. During low-demand periods, more consideration can be given to maximizing remaining battery level and minimizing total charging cost.

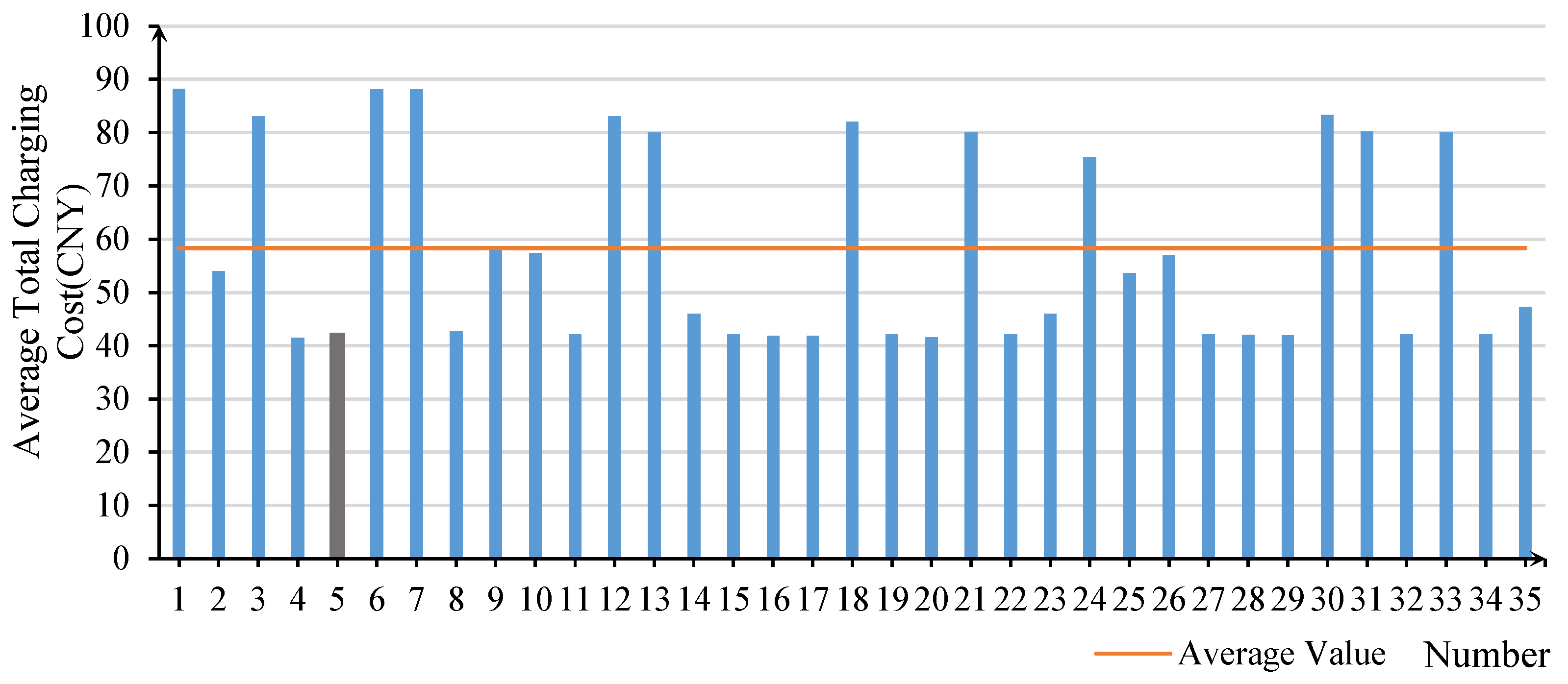
6.2.4. Average Total Charging Cost

From Figure 13, it can be observed that minimizing total charging cost and minimizing demand response time should be assigned higher weights, while maximizing remaining battery level and minimizing empty vehicle mileage should be moderately controlled. For example, when the weight of total charging cost is high (e.g., in Scenarios 4 and 15–17), the total charging cost is the lowest (41.490–42.127 CNY), indicating that a high weight allocation to total charging cost can significantly reduce charging expenses. If the primary operational objective is to minimize total charging cost, the weight distribution should prioritize minimizing total charging cost (0.5–0.75) and minimizing demand response time (0.5–0.75) to achieve significant cost reductions. Meanwhile, the weights of remaining battery level and empty vehicle mileage should not be too high (recommended at 0.25–0.5) to avoid significantly increasing charging costs.

6.2.5. Sub-Objective Relationships

By comparing the numerical changes in each sub-objective under different weight combinations, a typical trade-off phenomenon in multi-objective optimization can be clearly observed. When one sub-objective performs optimally, it often leads to a significant deterioration in the performance of other sub-objectives.

(1)

Trade-off Between Surplus Power And Charging Costs

Although remaining power maximization and charging cost minimization are contradictory in terms of optimization objectives, the two actually show significant synergistic change characteristics, as shown in Figure 14. Scenario 1 (residual power maximization weight 1.0), although achieving the advantage of the highest average residual power (43.812 kWh), is accompanied by the problem of excessive cost (USD 88.244). Scenario 4 (combined charging cost minimization weight 1.0), although achieving the lowest cost (USD 41.409), results in a reduction in the remaining power to 40.105 kWh.

(2)

Trade-off Between Demand Response Time and Empty Vehicle Mileage

Demand response time exhibits a negative correlation with empty-running mileage, as shown in Figure 15.Scenario 2 (weight of minimizing demand response time = 1.0) achieves the shortest response time (0.173 h) but results in an empty vehicle mileage of 90.680 km. Scenario 3 (weight of minimizing empty vehicle mileage = 1.0) achieves the optimal empty vehicle mileage (71.767 km) but extends response time to 0.275 h.

(3)

Recommended Multi-Objective Optimization Strategies

Based on the above results, the following optimal weight combinations are recommended:

• Cost-Control Strategy (Scenario 17, weights: 0, 0, 0.25, 0.75): Achieves the second-lowest cost of 41.810 CNY but at the expense of higher empty vehicle mileage (90.327 km, 10.5% higher than the optimal value). Suitable for peak electricity price periods.
• Emergency Response Strategy (Scenario 10, weights: 0, 0.75, 0.25, 0): Ensures a low demand response time of 0.191 h (third lowest across all scenarios) while maintaining relatively optimal empty vehicle mileage of 79.944 km. Suitable for peak travel demand periods.
• Balanced Strategy (Scenario 5, weights: 0.25, 0.25, 0.25, 0.25): All objectives deviate less than 15% from their optimal values, making it a viable baseline strategy.

6.3. Decision Variable Sensitivity Analysis and Optimal Strategy Analysis

The decision variables in this chapter include the following key parameters: the charging probabilities for the battery level ranges of 20% to 40%, 40% to 60%, and 60% to 80%, parking probability, and the recommended average remaining battery level.

This paper defines 35 scenarios, iteratively changing the decision variables to seek the global optimal solution. The optimal results of the decision variables are shown in

Table 4. Optimization results of decision variables.

Number	Decision Variables
	Recommended Average Remaining Battery Level (kwh)	Charging Probability for the Battery Level Between 20% and 40%	Charging Probability for the Battery Level Between 40% and 60%	Charging Probability for the Battery Level Between 60% and 80%	Parking Probability	Charging Station Selection Model
1	13.2	0.75	0.7	0.4	0	Time Minimization
2	30	0.3	0.65	0.2	0.4	Demand Response Time Minimization
3	36.6	0.2	0.65	0.85	0.65	Distance minimization
4	38.4	0.25	0.75	0.1	0.85	Minimize comprehensive Charging Costs
5	31.8	0.25	0.9	0.1	0.9	Minimize Comprehensive Charging Costs
6	16.2	0.9	0.75	0.35	0	Time Minimization
7	12	0.8	0.75	0.35	0	Time Minimization
8	30	0.15	0.85	0.1	0.75	Time Minimization
9	18.6	0.3	0.65	0.25	0.45	Demand Response Time Minimization
10	27.6	0.3	0.5	0.25	0.45	Demand Response Time Minimization
11	33.6	0.1	0.9	0.1	0.9	Demand Response Time Minimization
12	36.6	0.2	0.65	0.85	0.65	Distance Minimization
13	12.6	0.7	0.7	0.65	0.45	Distance Minimization
14	22.2	0.1	0.8	0.15	0.85	Distance Minimization
15	39.6	0.1	0.8	0.1	0.95	Minimize Comprehensive Charging Costs
16	34.2	0.1	0.6	0.1	0.9	Minimize Comprehensive Charging costs
17	28.2	0.2	0.85	0.1	0.95	Minimize Comprehensive Charging Costs
18	35.4	0.25	0.7	0.65	0.3	Time Minimization
19	32.4	0.1	0.9	0.1	0.9	Minimize Comprehensive Charging Costs
20	13.2	0.7	0.6	0.1	0.85	Minimize Comprehensive Charging Costs
21	18.6	0.7	0.7	0.65	0.45	Demand Response Time Minimization
22	39.6	0.1	0.9	0.1	0.9	Minimize Comprehensive Charging Costs
23	30.6	0.1	0.8	0.15	0.85	Minimize Comprehensive Charging costs
24	18	0.2	0.55	0.45	0.3	Distance Minimization
25	30.6	0.1	0.6	0.25	0.9	Minimize Comprehensive Charging Costs
26	15	0.7	0.7	0.3	0.9	Minimize Comprehensive Charging Costs
27	42.6	0.1	0.8	0.1	0.95	Minimize Comprehensive Charging Costs
28	31.2	0.15	0.85	0.1	0.9	Minimize Comprehensive Charging Costs
29	17.4	0.1	0.7	0.1	0.9	Minimize Comprehensive Charging Costs
30	16.2	0.25	0.75	0.35	0	Demand Response Time Minimization
31	26.4	0.7	0.7	0.65	0.4	Time Minimization
32	39.6	0.1	0.8	0.1	0.95	Minimize Comprehensive Charging Costs
33	40.2	0.7	0.7	0.65	0.45	Time Minimization
31	26.4	0.7	0.7	0.65	0.4	Time Minimization
32	39.6	0.1	0.8	0.1	0.95	Minimize Comprehensive Charging Costs
33	40.2	0.7	0.7	0.65	0.45	Time Minimization
34	13.2	0.1	0.9	0.1	0.9	Minimize Comprehensive Charging Costs
35	18	0.15	0.75	0.15	0.9	Minimize Comprehensive Charging Costs

, and the following section provides a detailed analysis of the impact of changes in the decision variables on the results.

(1)

Charging Probability:

This is divided into three battery level intervals (20–40%, 40–60%, and 60–80%), with significant differences in charging probability across different scenarios. From a strategic perspective, charging in the low battery interval (20–40%) is highly urgent, preventing SAEVs from ceasing operation due to low battery levels. Charging in the medium battery interval (40–60%) offers greater flexibility, allowing for better response to future demand while also preventing excessive battery depletion. Charging in the high battery interval (60–80%) is a preventive measure, ensuring sufficient energy reserves for future high-demand periods.

In general, if the overall charging probability is relatively high (e.g., in Scenarios 1, 6, and 7), this may lead to high average total charging costs (approximately 88 CNY) and long empty travel distances (91–98 km). If the overall charging probability is relatively low (e.g., in Scenarios 15, 27, and 32), the parking probability tends to be higher (0.9–0.95), and the average total charging cost is minimized (approximately 42 CNY). Specifically, we categorize the range of charging probabilities into several strategic approaches, as shown in

Table 5. Charging probability distribution strategies.

Strategy Type	Charging Probability Range	Advantages and Disadvantages	Representative Scenarios
Passive Charging	High probability in low battery interval (>0.7)	Short response time but extremely high cost	1, 6, 7
Conservative Charging + High Parking	High probability in medium battery interval (~0.8) + high parking probability (≥0.9)	Lowest cost but long response time	15, 27, 32
Balanced	Moderate charging probability in medium battery interval(0.5–0.7), moderate parking probability (0.4–0.6)	Balanced cost, response time, and empty mileage	10, 26
Preventive Charging	High probability in high battery interval (≥0.8)	Stable battery interval but potential overcharging	3, 12, 18

:

In summary, passive charging is suitable for short-term peak demand, making it ideal for high-density travel order periods where ensuring operational capacity is the priority, albeit at a very high cost. Conservative charging + high parking is well-suited for cost-sensitive operations, particularly during off-peak hours or low electricity price periods, but it comes at the cost of slower vehicle response times, potentially leading to longer demand response times. Balanced charging does not exhibit significant drawbacks, making it applicable to general scenarios. Preventive charging is best suited for scenarios with consistently high travel demand, such as airports and stations, where vehicles need to remain on standby for extended periods.

(2)

Parking Probability:

The role of parking probability is primarily to balance charging and responding to travel demand, influencing vehicle distribution and battery status while preventing unnecessary empty vehicle travel. Generally, when the SAEV parking probability is high (≥0.85, such as in Scenarios 4, 5, 11, and 15), it significantly reduces charging costs (41–45 CNY) but may increase demand response time (0.236–0.246 h). Conversely, when the parking probability is low (≤0.2, such as in Scenarios 6 and 7), vehicles continuously cruise or charge, leading to higher charging costs (around 88 CNY). Specifically, we categorize the range of parking probability into several strategic approaches, as shown in

Table 6. Parking probability distribution strategies.

Strategy Type	Parking Probability Range	Advantages and Disadvantages	Representative Scenarios
Zero Parking	0	Short response time, but high cost	1, 6, 7
High Parking + Low Charging	≥0.8	Lowest cost, but long response time	4, 15, 27
Balanced	0.4–0.6	Balanced cost, response time, and empty mileage	2, 9, 26
High Parking + High Charging	≥0.8 + High charging probability	Stable battery interval but cost may increase	3, 12

:

In summary, zero parking is suitable for peak travel periods or high-demand areas, where back-and-forth scheduling and long-term charging are required to ensure operational capacity. High parking + low charging is suitable for low-demand periods or cost-sensitive operations, as it minimizes costs but may result in longer passenger response times. The balanced strategy is applicable to general scenarios, as the results are relatively moderate across various factors. High parking + high charging is suitable for areas with dense charging facilities or low electricity price periods, as it reduces the mileage caused by back-and-forth scheduling to parking lots while minimizing the impact of excessively high costs.

(3)

Recommended Average Remaining Battery Level:

The recommended average remaining battery level refers to the suggested average battery level for the current state. Only when the remaining battery level of the SAEV is lower than this value will a certain charging probability be triggered to determine whether charging is needed, thus controlling the overall fleet’s battery status. Generally, when the recommended average remaining battery level is higher (≥36 kWh, as in Scenario 15 and 27), the total charging cost is lower (around 42 CNY), but a balance with demand response time needs to be maintained. When the recommended average remaining battery level is lower (≤18 kWh, as in Scenario 1, 6, and 7), the demand response time significantly decreases (0.14–0.17 h), but there is a risk of overcharging, and the total charging cost becomes significantly higher (around 88 CNY). Specifically, we categorize the range of recommended average remaining battery levels into several strategic approaches, as shown in

Table 7. Recommended average remaining battery level distribution strategies.

Strategy Type	Recommended Average Remaining Battery Level Range (kwh)	Advantages and Disadvantages	Representative Scenarios
Low Battery	≤18	High charging cost, but the shortest response time	1, 6, 7
High Battery	≥36	Low cost, but long response time and stable battery level	15, 27, 32
Balanced	18–30	Balanced cost, response time, and battery level	2, 9, 10
Preventive Charging	≥30 + High Charging Probability	Maintains high battery level, but may increase empty driving distance and cost	3, 12, 18

.

In conclusion, a higher battery level is not always better. Low battery levels are suitable for areas or time periods with high order density, such as emergency evacuations or peak hours, where supply is insufficient. High battery levels are more appropriate for areas with scarce charging facilities or long-distance orders, such as airport pickups or intercity orders. The balanced type is more versatile and fits general scenarios. Preventive charging is suitable for cities with uneven distribution of charging stations. It helps reduce the risk of not finding a charging station and ensures a stable high battery level. However, excessive charging may lead to resource waste.

(4)

Charging station selection model

In this section, on the basis of probabilistic parameter optimization, a charging station selection model for SAEVs is also introduced to achieve optimality through double regulation, which not only improves the completeness of the charging decision-making process, but also, more importantly, is able to filter out the charging station selection strategy that best matches the current combination of weights.

In general, the system exhibits strong convergence when the weight of a single objective is ≥0.75, e.g., maximization of remaining power (weight 0.75) has a high probability of leading to a time-minimizing charging station selection strategy (e.g., Scenarios 6–8), and the objective of minimizing the integrated charging cost exhibits the strongest convergence, which dominates the decision-making when the weight is ≥0.25 (e.g., Scenarios 19–29). The cost optimization strategy dominates with balanced weights (0.25 weights each) (Scenario 5).

In particular, the weight combination of demand response time (weight ≤ 0.25) + empty vehicle mileage (weight ≥ 0.5) is preferred to the “distance minimization charging station selection model” (e.g., Scenarios 13 and 24), which is due to the fact that the weight of the empty vehicle mileage minimization objective is higher, the more stringent the distance requirement is, and the other is that the distance minimization charging station selection model has a greater negative impact on the demand response time. On the other hand, although the negative impact of the distance minimization charging station selection model on the demand response time is large, under the constraints of charging probability and parking probability, the phenomenon of excessive queuing is reduced, and thus the distance minimization charging station selection model is chosen as the optimal choice for such scenarios.

In more detail, this chapter will distribute the corresponding strategies according to the charging station selection model, as shown in

Table 8. Distribution strategy of charging station selection model.

Type of Strategy	Selection Criteria	Advantages and Disadvantages	Representative Strategy
Distance minimization	Applicable to high empty mileage weights	Reduces operational losses, but may be more costly	3, 12, 13
Time minimization	Applicable to high residual power weights	Fast response but high cost, suitable for emergency power replenishment	1, 6, 18
Minimize comprehensive charging costs	Suitable for high consolidated cost weights	Minimal cost, limited response time	4, 15, 17
Demand response time minimization	Suitable for high response time weighting	Good user experience at the expense of some economics	2, 9, 30

:

In summary, the distance-minimizing charging station selection model is suitable for urban capillary road sections, which can significantly reduce the empty driving mileage. The time-minimized charging station selection model is particularly suitable for peak travel times or high demand areas, where fast chargers are preferred to ensure operational capacity, but at a higher charging cost; the integrated charging cost-minimized charging station selection model is preferred for low peak times or cost-sensitive operations, but with moderately longer response times. The Demand Response Time Minimized Charging Station Selection Model is designed for high-quality-of-service scenarios and ensures the passenger experience but increases charging costs by 20–25%.

7. Conclusions and Discussions

This paper investigates the charging decisions of the SAEV fleet and the potential impacts of different decision objectives. The paper aims to build and simulate the specific operations and charging behaviors of the SAEVs through a multi-agent simulation model. Four charging decision optimization objective functions are set, and multi-objective optimization is conducted using weighted approaches. At the same time, an integrated solution process combining multi-agent simulation model and genetic algorithm is used to iteratively calculate the global optimal solution under different weight coefficients (a total of 35 scenarios). To examine the overall operation of the SAEV fleet, various factors are introduced and analyzed, including passenger demand (average remaining battery level, average demand response time) and operator demand (average empty vehicle mileage, total charging cost). This enables an analysis of how different objective priorities and decision variables influence these data.

The results indicate the following:

(1)

In single-objective optimization, the goal of minimizing comprehensive charging costs best balances overall fleet performance. In multi-objective optimization, adjusting its weight to 0.5–0.75 effectively coordinates passenger demand with operator requirements.

(2)

Significant trade-offs exist between sub-objectives: increasing average remaining battery level raises charging costs, while shortening demand response time may increase empty-run mileage.

(3)

For different operational scenarios, weight distributions, charging probabilities, parking probabilities, and recommended charge levels must be adjusted. In general scenarios, the recommended charging probability for the medium charge range is 0.5–0.7. During short-term peak periods prioritizing response speed, the charging probability for the low charge range should be increased to above 0.7. During off-peak or low-tariff periods, cost-effectiveness takes precedence, recommending a medium-level charging probability of 0.8. In areas with sustained long-term demand or uneven charging infrastructure distribution, appropriately increase the high-level charging probability while maintaining average remaining energy above 30 kWh.

The above strategy recommendations provide SAEV fleet operators with a smart charging decision-making framework. By adjusting target weights, balanced fleet management can be achieved, continuously optimizing overall performance in complex and changing operating environments. However, this study still has several limitations and areas for improvement: (1) The road network modeling employs simplified assumptions and does not account for real-world traffic congestion or traffic light conditions. (2) It does not address the issue of coordinated scheduling for mixed fleets (SAEVs and conventional vehicles). (3) It does not investigate the impact of SAEVs’ charging and discharging behavior as distributed energy storage units during peak and off-peak electricity pricing periods on the power grid, nor does it perform coordinated optimization of the transportation and energy systems.

In conclusion, it is hoped that the findings of this study will contribute to more scientific and reasonable SAEV operations. By adjusting the weights of different objectives and parameters such as charging probability and parking probability in response to changes in future operational goals, dynamic optimization can be achieved, providing reliable theoretical support and practical guidance for the intelligent operation and management of SAEVs.