System Dynamics Modeling and Multicriteria Analysis Methods for Selecting Scenarios in a Harness Assembling Plant

Abstract

The global automotive industry faces significant challenges with respect to its supply chain, particularly component scarcity and the increasing complexity of modern vehicles, which have severely impacted the production of high-tech harnesses. This study addresses the issues faced by a leading automotive harness manufacturing company in Ciudad Obregón, Mexico (an international company that requested confidentiality), which has suffered considerable economic losses (over USD 2870) and production downtime due to component scarcity and delivery delays in component deliveries, affecting “Crew Grande” harness production. This proposal aims to develop a technological solution with a graphical interface to support decision-making in the face of this scarcity. The methodology employed system dynamics to model the supply chain’s complexity, using software such as Stella^® Architect for Forrester diagrams and equations and Vensim^® PLE for causal diagrams. The model was validated with a relative error, confirming its reliability. Multicriteria decision-making (MCDM) was performed using the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) and Faire Un Choix Adequate (FUCA) methods to evaluate 15 scenarios (normal, pessimistic, and optimistic), identifying the four most favorable scenarios for optimizing operational performance. The results demonstrate these solutions’ potential to mitigate losses, improve operational efficiency, and strengthen the company’s position against market and demand fluctuations, especially for its main client, Ford Motor Company, using a graphical user interface (GUI) to support analysis and decision-making.

1. Introduction

The car industry is transforming globally; thus, its importance lies in its capacity to increase economic, technological, and social progress, although it also faces significant challenges in its route toward continuous sustainability and innovation. The growing complexity of modern vehicles—driven by megatrends such as autonomous electrification and autonomous driving—has exponentially increased the demand for electronic components, particularly high-technology harnesses. However, this sophistication also exposes significant vulnerabilities in the industry with respect to its supply chain. Recent examples underline the urgency to develop supply chain strategies, as the global scarcity of semiconductors has deeply affected automotive production. For example, studies have demonstrated that dynamic simulation has been used to model the supply chain of automotive semiconductors and analyze the impact of interruptions, revealing challenges not only during contingencies but also in a later period [1,2]. This situation highlights the need to support decision-making solutions in the automotive sector, exploring its technological evolution, socioeconomic impacts, challenges, and opportunities within a contemporary context marked by digitalization, sustainability, and innovation [3].

The automotive industry in Mexico is considered a success story because of the manufacturing sector’s contribution, 18%, to the gross domestic product (GDP); furthermore, it generates 824 thousand jobs in direct employment, which represents 20% of Mexico’s manufacturing activity. Currently, cars are no longer simple objects for mobility, having been transformed into efficient machines that offer new digital and driving experiences. Electric cars are profiled to be the future of the industry globally since their boom started due to greater yields granted by new technologies [4].

Megatrends in the automotive sector are significant large-scale changes modifying the industry and its future direction. Taking advantage of opportunities, automotive companies should be willing to adapt quickly, invest in innovation, and collaborate with strategic partners to drive mobility transformation. By understanding and anticipating these megatrends, which usually cover technological, social, economic, and environmental aspects, companies can position themselves effectively to lead change and guarantee long-term success in an ever-evolving market. Vehicle electrification not only alters power trains but also requires a total supply chain reconfiguration of electronic components, including harnesses that must now support high voltages and greater complexity for electric vehicle functions [5].

According to Clemetson [6], the automotive electronics market is rapidly expanding, and this is associated with five key megatrends: autonomous driving, infotainment (information and entertainment), electrification, connectivity, and security. Industrial analysts predict that the demand for automobile semiconductors may triple in the next eight years. These next-generation automobile applications require greater storage for advanced functions and recording events. Universal Flash Storage (UFS) has turned out to be the preferred solution for In-Vehicle Infotainment (IVI) and Advanced Driver Assistance Systems (ADAS) memory applications. By 2025, more than half of these automotive applications will be using UFS devices, and the majority are expected to switch from eMMC (embedded multi-media card) to UFS by 2030.

This change is driven by a notable increase in programmable content and faster processing speeds for reading/writing operations that adapt to these new advanced flash memory requirements. The size of the automotive wiring harness market was estimated to be USD 1,98 thousand million in 2023, and it is expected to reach USD 2,43 thousand million in 2028, growing at a compound annual rate of 4.19% during the forecast period (2023–2028) [7]. Growth is attributed to several factors, such as the increase in new vehicle demand, the development of innovative technologies in automobile manufacturing, and transport infrastructure expansion in emerging markets. The name of the company under study has been omitted due to confidentiality; hereafter, it is designated as the “company”—an independent manufacturer of automotive components established in Japan in 1941 and a world leader in research, development, and delivery of data solutions and vehicle energy for automotive applications. The company produces wire harnesses, distribution products, energy control systems, information systems for drivers, and products and sensors for hybrid and electric vehicles. With more than 300,000 employees in 46 countries, the company under study is one of the largest private automation providers in the world.

The product made by the company is a harness, which is a set of circuits designed to transmit electric signals to all vehicle systems: for example, the cabling for motor engine ignition, front lights, power windows, air conditioning, airbags, alarms, command boards, stop lights, car ceiling lights, and sensors, among others.

This study was conducted at the company under review, focusing on the areas of supply and production, with an emphasis on production line 16, model 2024. The analysis focused on the components used in this line and covered the period from January to August 2024, with the first data collection beginning on 30 October 2023.

The data were obtained from various internal sources, including SAP system records used by the company for operational management; internal reports in Excel format, which consolidate information on production and losses; daily and monthly production reports; and maintenance logs for the period of analysis.

In addition to the documentary sources, a complementary qualitative validation was carried out via consultations with line supervisors and production managers, with the aim of clarifying and contextualizing certain recorded events.

The information used was provided with the formal authorization of the company in compliance with previously established confidentiality and academic use guidelines.

This study addresses a robust methodological process based on the proposal by Forrester and Sterman and adapted by Lagarda, which includes two aspects that have been little addressed by other authors: the incorporation of FUCA and TOPSIS MCMs, in addition to a section that incorporates a GUI to support data-driven decision-making.

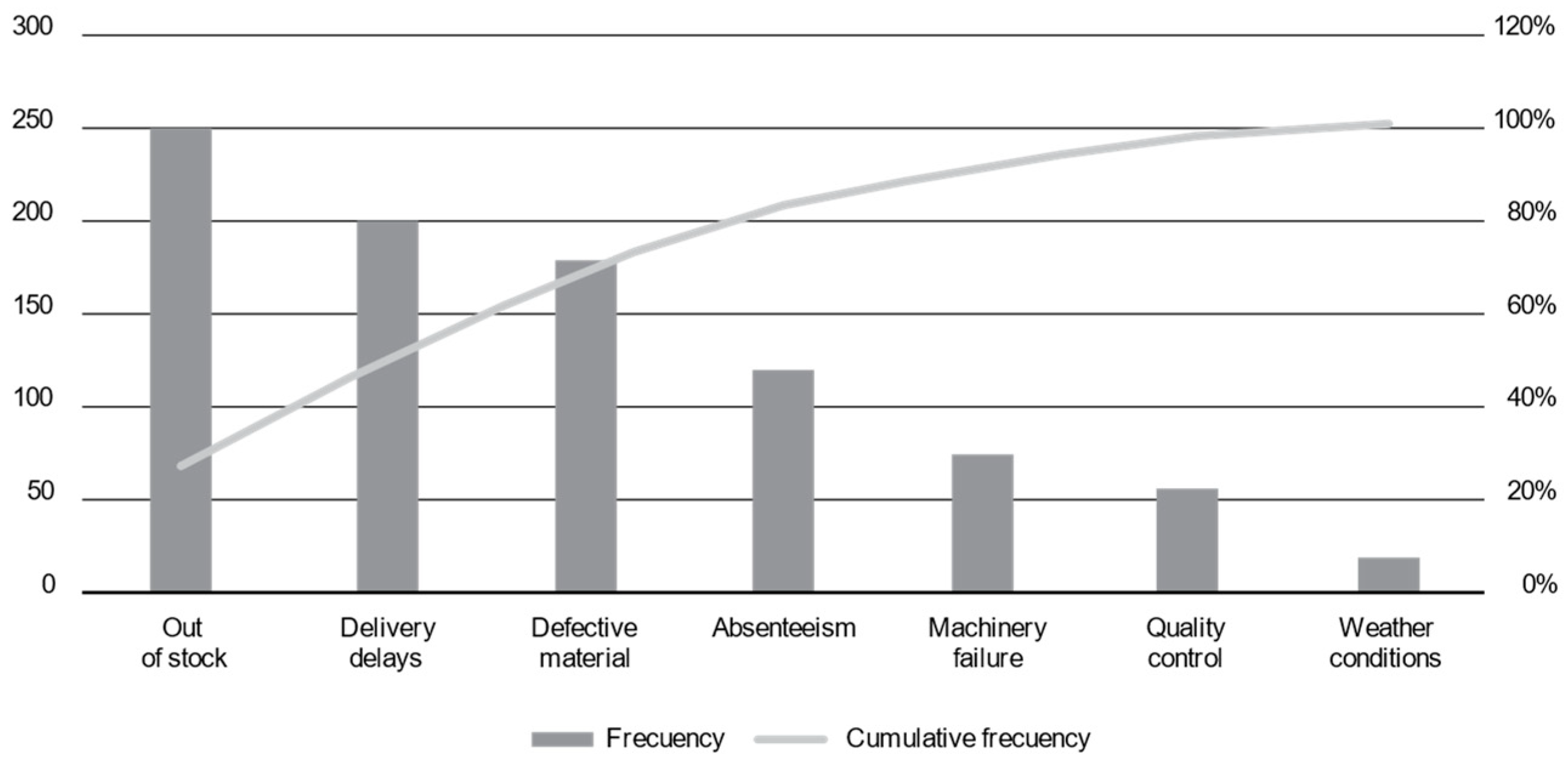
The company under study—located in Ciudad Obregón, México—is important in the automotive industry, and it specializes in vehicle harness manufacturing. Nevertheless, the company has been facing significant challenges due to a shortage of components. This situation has generated concerns surrounding the company’s capacity to maintain production and satisfy the international market demand. As mentioned, the scarcity of components in the company surged as a result of diverse factors, some of which include the following: (1) interruptions in the supply chain and (2) raw material fluctuations due to market demand. These challenges have directly impacted the enterprise’s capacity to maintain its harness production efficiently and promptly. The lack of components in the production line has generated a series of negative consequences, among which are customer product delivery delays, loss of income due to the inability to satisfy the demand, and deterioration of the company’s reputation in the market. Moreover, this situation has placed additional pressure on the company’s staff and resources to develop effective solutions. For this purpose, a Pareto diagram is shown in Figure 1, along with its production program.

The previous figure shows three main problems in descending order from the most to the least frequent. For example, firstly, the lack of variety affects production and may cause delays or interruptions in the assembly line. On the other hand, delays in deliveries may take place: for example, failure to meet production deadlines and the risk of fines imposed by customers. Lastly, defective materials may generate additional costs due to reprocessing, material waste, and possible damage to the company’s reputation. Supply chains and production processes are examined, taking into account the current demand of approximately 110 units per shift for the main clients (Ford Motor Company, USA).

For example, in production model line 16, specifically in the section designated “Crew Grande”, which refers to harness size, a problem related to harness loss was identified for the 2024 model. Considering data analyses from 30 October 2023 to 18 June 2024, the period during which the latest data for the present study were collected, there was an accumulated loss of production time totaling 71.04 h. The economic losses in USD for line 16 highlight the importance of efficiently identifying and resolving problems in car harness production. These losses not only affect the company’s profitability but might also have a significant impact on competitiveness and client perception with respect to the final product’s quality. This temporary loss translates into an economic depreciation equivalent to USD 2875 (from 30 October 2023 to 18 June 2024).

These numbers not only have an impact on the company’s financial state but also highlight the need to implement effective strategies to minimize losses and optimize operational efficiency in all manufacturing stages. Thus, the present study aims to identify the actions needed to address how the shortage of components affects the Crew Grande harness production process. In response, the following objective is established: to develop a technological solution based on a graphical interface and support decision-making with respect to identifying the shortage of assortment components affecting harness production for Crew Grande using system dynamics.

2. Literature Review

The automotive industry is undergoing an unprecedented transformation, driven by the widespread adoption of electric vehicles (EVs) and advances toward autonomous driving. These megatrends not only redefine the concept of mobility but also require a profound reengineering of internal vehicle architecture. Salari et al. [8] analyzed how this era of electrical/electronic autonomous vehicles results in significant challenges and opportunities for automotive architecture. Harness systems are capable of supporting greater potential demands, high-velocity data transmission, and the integration of denser components. However, harness engineering faces increasingly shorter program launch cycles and growing price pressures, alongside rising product and configuration complexity, highlighting the critical need for advanced tools to optimize design and manufacturing [9]. The scarcity problem of components is exacerbated due to the inherent complexity of the automotive industry, particularly in harness manufacturing. A contemporary vehicle may incorporate kilometers of wiring and hundreds of connectors, requiring intricate designs. Despite technological advances, harness manufacturing continues to be a highly manual process, with scarce opportunities for complete automation due to the high configuration variability of each vehicle model [10].

It is important to note that the harness industry has previously been studied in various contexts. In this regard, other studies have identified and analyzed automation concepts in harness manufacturing, highlighting the need for transparent and reproducible processes. Although automation in harness manufacturing has been a topic of interest, most processes still rely heavily on manual labor [11].

Similarly, Liu and Lu [12] applied lean manufacturing principles to the assembly process of the A9815086 automotive harness. Using industrial engineering methods, they reduced handling times by 42%; decreased transport distances by 32%; and increased the production line’s balance rate from 69.29% to 91.47%.

On the other hand, Reis et al. [13] conducted a comprehensive review of innovations in automotive harnesses, addressing aspects such as reliability, safety, simulation, and manufacturing. They highlighted the evolution of materials and technologies, the importance of using simulations in product development, and the need for efficient manufacturing processes and quality control.

Popa et al. [14] proposed an innovative assembly line structure to optimize the logistics flow of harnesses in response to growing production demands. Their approach highlighted the importance of efficiency in component distribution and adaptability to customer needs.

Finally, Górny [15] explored how Industry 5.0 can improve production efficiency by focusing on human–machine interactions, customization, and sustainability. This approach seeks to integrate advanced production capabilities with a human-centered approach.

Supply chain resilience has emerged as a fundamental pillar for the automotive industry’s sustainability. Diverse investigations have explored how companies strengthen investigations before disruptive events. For example, the collaboration between Ford Motor Company and academics has demonstrated the value of innovative risk-based models using simulations to evaluate the impact of disruptions at any point in its complex supply chain. This approach enables the identification of previously unrecognized risks and the development of optimal contingency plans [16]. The global automotive industry has proven to be particularly vulnerable to supply chain disruptions, as evidenced by the recent scarcity of components.

This fragility is accentuated in critical segments such as semiconductors, where disruptions can cause significant losses and global delays in vehicle production. To understand the dynamics of these crises, mitigation strategies and tools have turned out to be essential for developing effective simulation dynamics. Afridi et al. [17] modeled an automotive semiconductor supply chain at multiple levels, demonstrating how system dynamics enable the analysis of supply chain behavior with respect to disruptive market scenarios and revealing persistent challenges not only during but also after the interruption period. This type of analysis underlines the critical proactive technological solutions needed to guarantee operational continuity and resilience in harness production.

As the automotive industry requires new methodologies, its inherent decision-making capacity in volatile supply chain environments must integrate multiple criteria and effectively cope with uncertainty. These defects affect product quality, generate waste, and reduce competitiveness. Although quality tools are used, such as cause–effect diagrams or verification sheets, they do not allow for analyzing the complex dynamics and system feedback loops that contribute to defect appearance.

In this context, multicriteria decision-making (MCDM) is positioned as a fundamental tool for evaluating and prioritizing alternatives. For example, Rezaei and Fazel-Zarandi [18] proposed an MCDM focus for selecting sustainable providers in the automotive industry, emphasizing how these techniques allow considering not only economic factors but also environmental, social, and risk factors. The study of Ivanov [19] established that the automotive industry—despite its strategic and economic importance—confronts constant challenges: the presence of defects in manufacturing processes; ensuring both economic and technical goals are reached: for example, high productivity, lowest material consumption, lowest labor costs, etc. In order to achieve multiple goals at the same time, it is necessary to solve the multi-objective optimization problem.

FUCA is known to be a multicriteria decision-making method that does not require data normalization [20,21]. Although it was developed recently, this method has already been applied to select optimal alternatives in various fields [22].

The multicriteria nature of selecting the best alternative from the ones proposed is addressed using multicriteria decision-making techniques. In this manner, the decision-maker can consider the various criteria defined, establish their preferences (what interests them the most, depending on the case), and receive guidance in selecting the best alternative among the proposals. The techniques used to address the decision problem posed in this study are FUCA and TOPSIS. These techniques are chosen due to their ease of use, widespread adoption, and proven effectiveness. For example, Baydas et al. [23] used these techniques to evaluate economic and financial data [24]. These techniques can also be used to evaluate quantitative data and consider a large number of criteria. An additional point to mention about FUCA is that this technique does not require data normalization, which greatly benefits from the loss of information due to the same requirement in other methods. Both techniques are used to evaluate a decision matrix, which is shown in

Table 1. Decision matrix developed from the criteria, alternatives, preferences, and objectives of the decision-making situation.

	Weight 1	Weight 2	Weight 3		Weight m
	Max/Min	Max/Min	Max/Min	…	Max/Min
	Criterion 1	Criterion 2	Criterion 3	…	Criterion n
Alternative 1	Result11	Result12	Result13		Result1n
Alternative 2	Result21	Result22	Result23		Result2n
Alternative 3	Result31	Result32	Result33		Result3n
…
Alternative m	Resultm1	Resultm2	Resultm3		Resultmn

Source: Own elaboration, 2025.

.

The FUCA method [25] uses three steps to rank alternatives:

• The alternatives are ranked for a given criterion (columns of the decision matrix). Suppose that there are m alternatives, the worst alternative is ranked in the m-th place, and the best alternative is ranked as the first.
• A weighted summation (the weights representing the preferences) of each alternative (rows of the decision matrix) is calculated.
• The alternatives are ranked according to the values of the weighted sum. The best alternative is the alternative with the smallest value, and vice versa.

The basic operation of TOPSIS [26] is a comparison of Euclidean distances to select the best alternative. To carry this out, the distance between the available alternatives and the ideal reference alternative is calculated. The ideal alternative is a theoretical point. TOPSIS is used to evaluate a decision matrix, as described in Table 1, and the vector of weights representing the decision-maker’s preferences is considered. A normalized decision matrix is then calculated, and the ideal negative and positive alternatives are determined from the normalized matrix. Subsequently, the distances between the alternatives in the decision matrix and the ideal alternatives are calculated, and these distances are used to calculate a ratio for each alternative. Finally, the alternatives in the decision matrix are ranked according to the calculated ratio.

Therefore, the objective of the present study is to demonstrate how the system dynamics methodology [27,28,29] may be applied efficiently to understand the complexity of creation dynamics and defect reduction, focusing on simulating the manufacturing system’s behavior by means of causal and stock flow diagrams. Training and personal motivation improvement policies are evaluated, in addition to planned maintenance. With respect to the results, the system dynamics model was constructed via five phases (articulation of the problem, dynamic hypothesis, simulation, tests, and policy formulation) using Stella^® Architect (version 3.8, Isee systems Inc., Lebanon, NH, USA, 2025) software. The model identified six key defects: dents, stains, sealing and paint damage, dirt, and bad fit. The customer satisfaction level decreased as the multiplicity of defects increased, which in turn increased the need for resources to improve the process. Evidently, customer satisfaction levels decreased as the number of defects increased, raising the need for additional resources to improve the process.

After simulating an improvement policy (training, maintenance, and incentives), the creation rate of the defect reduced from 160 to 83 in three months. On the other hand, Lindow et al. [30] established that the automotive industry is evolving toward digital services based on vehicle data. Nevertheless, great uncertainty exists with respect to whether these services may be consolidated in the market and how they can be carried out. Moreover, what factors influence the adoption of new services is still not understood due to ecosystem complexity (regulators, means, users, etc.). Thus, this study’s objective is to develop a system dynamics model to simulate automotive service adoption based on data. For this purpose, the ecosystem’s behavior was explored by considering key actors (conductors, manufacturers, means, and regulators), in addition to performing a scenario analysis to evaluate future conditions and support strategic decisions. With respect to the results, a model was built based on the extended Bass diffusion model to include variables such as mediatic coverage, social pressure, and regulatory opening of interfacing. Two scenarios were analyzed. The first is the favorable scenario, with high mediatic coverage, low privacy (more available data), and open regulation. The results are as follows: 47.1 million adoptions in 29 months, and EUR 1130 million (euros) in profits. The second is the unfavorable scenario: low coverage, high privacy, and no regulation. The result is as follows: only 40.3 million in adoptions in 60 months and EUR 419 million in profits. The model showed how the decisions of ecosystem actors (especially means and regulators) may accelerate or curb service adoption drastically.

Al-Dhaafri and Al-Marri [31] developed a system dynamics model specifically designed to improve supply chain resilience in the automotive industry, showing the capacity of this methodology to evaluate the impact of interruptions and the effectiveness of mitigation strategies. Component shortage scenarios were explored, and the technological solutions holistically proposed to optimize harness production were evaluated. In this context, the system dynamics simulation was consolidated as an invaluable tool for optimizing and managing complex supply chains. These risks are seen as all factors that may interrupt the flow of material through the supply chain, including scarcity periods [32]. Likewise, recent investigations endorse the use of dynamic simulations for resilient supply chain design in the automotive sector, providing a framework for evaluating mitigation strategies for supply disruptions or interruptions [33].

Rahmawati et al. [34] studied the challenges that Taiwan faces in increasing the adoption of electric vehicles (EVs) as part of their strategy to achieve net-zero emissions by 2050. Although advances have taken place, the objective is to eliminate fossil fuel combustion vehicles by 2040, following countries as South Korea and Canada, in addition to the European Union. This situation requires a deeper understanding of the factors that affect EV market growth. Moreover, the objective of their study was to develop a system dynamics model to evaluate the impact of different factors on EV market participation in Taiwan. For this purpose, market behavior was simulated using variables such as consumer preferences; access to charging infrastructure; EV yield; and financial and social availability. The model was calibrated with historical data (2010–2021) and current governmental policies to validate scenarios and design effective interventions. The main results show that critical EV determinant market growth factors include accessible charging stations and manageable financial costs. Governmental subsidies significantly increase consumers’ purchase intentions. Vehicle yields (autonomy) and environmental awareness also influence adoption positively. With respect to model validation, minor simulation errors were observed at 5%, indicating high pressure.

The most recent studies have expanded the use of this methodology to advanced sustainability and production areas. Olivares-Aguila and ElMaraghy [35] used system dynamics to understand how supply chains behave when confronting disruptions. One of their most relevant conclusions was that problems occurring closer to the end customer (in the downstream section) tend to substantially impact the overall chain behavior than those arising at earlier stages. Moreover, proactive solutions were found: For example, maintaining partial installation operations instead of closing them completely may be more effective than reactive measures, such as accelerating production (expediting), which increases costs without offering great benefits. Their study also demonstrated the importance of coordinating decision-making among the different supply chain levels, as acting separately may generate unintended consequences. These findings demonstrate how system dynamics may be a useful tool for simulating scenarios and design strategies that help confront disruptions better in complex environments. Rodríguez et al. [36] simulated various conventional production contexts—centralized and distributed—to evaluate the additive production effect in the supply chain. Their findings indicate that distributed configurations with 3D delivery reduce delivery times and logistics costs, enhancing operational flexibility.

Other research performed by Kaur and Kander [37] used system dynamics to simulate manufacturing materials made with reinforced polymers with artificial hemp, proving that the application of circular practices (such as recycling and reusing materials) decreases waste and CO₂ emissions. Likewise, inventory administration and production pacing are crucial elements for preserving an environmental–economic balance. Moreover, Rodríguez-Aguilá and ElMaraghy [38] developed a model for analyzing disruptions in multiple layers, concluding that rapid recovery strategies have a fast short-term impact, but they require structural adjustments in order to be sustainable. Huang and Zhang [39] offer exhaustive bibliometrics, establishing that risk management had not been evaluated in the field of automobile supply chain disruption. The results allow identifying the following risks: external issues, time, information, financial issues, supply, operation, and demand. At the same time, after 2011, there was an increasing trend with respect to the focus on resilience, sustainability, and technological integration. The current challenges are recognized in the theoretical research domain, particularly due to low business participation and scarce collaboration. Finally, future directions point to blockchain integration, IA, the circular economy, greater practical application, and multidisciplinary approaches.

3. Materials and Methods

The objective of this study is to support the manufacturing of automotive harnesses for the “company”, focusing on supply chain and production processes within an organization located in southern Sonora, México.

3.1. Materials

The software Stella^® Architect, (version 3.8, 2, Isee systems Inc., Lebanon, NH, USA, 2025) was used to build the model implemented by the company under study. A Forrester model was constructed, including equations to simulate process behavior; a sensitivity analysis under pessimistic, current, and optimistic scenarios; and a dynamic user interface that allows data interaction and modification for simulation purposes. Software Vensim^® PLE (version 8.2.1, Ventana Systems, Inc., Harvard, MA, USA, 2021) was used to elaborate the causal diagram of the studied process, in which variables and graphical parameters were established with greater relevance, creating balance loops and key system reinforcement for evaluating the relationship between them. An Excel Macro for MCDM of FUCA and TOPSIS was used for selecting the best scenarios according to their type.

3.2. Method

A detailed procedure is outlined as follows, complying with the objective of this study.

Analyze the Context in Which the Organization Under Study Operates: The initial stage begins by elaborating supply chain mappings using a visual representation. These processes were performed using previously collected data, with the purpose of analyzing the organization integrally as an interconnected system. A systemic focus was adopted to understand how each supply chain link affects the rest of the links.

Elaborate on the Causal Diagram: Once the most relevant variables and parameters were identified, a causal diagram was created, representing the supply chain links. Based on this, the interactions between the variables and parameters are illustrated. The product generated is a causal diagram composed of archetypes that combine reinforcing (R) and balancing (B) loops. The Vensim^® PLE software was needed to develop this diagram, which allowed the design of the causal model object of study.

Formulate the Simulation Model Using a Forrester Diagram and Mathematical Equations: Based on the causal diagram and process mapping as references, the Forrester diagram was elaborated, starting with the classification of four supply chain links: provision, production, distribution, and inverse logistics. Next, the most relevant processes were schematized in these links with respect to their input and output stocks, taking into account all exogenous and endogenous variables and previously identified parameters. Lastly, mathematical equations were developed, including research on formulas and concepts to understand the process’s logic; for this purpose, Stella^® Architect was used.

Validate the Current Model: After finalizing the dynamic simulation, its validation proceeded via a series of tests, which covered the consistency check of units and extremes, allowing the evaluation of the structure and model parameters. Moreover, a comparison was performed between the real structure system and that of the model, which was carried out jointly with a dimensional consistency revision of the mathematical equations and parameters. Lastly, a test under extreme conditions was performed to ensure the model’s robustness in different scenarios.

Select Current, Pessimistic, and Optimistic Scenarios: This step elaborated three quantitative scenarios that represent different conditions via a maximization and minimization multicriteria analysis of the critical variables; five scenario runs were carried out with respect to the type: current, pessimistic, and optimistic. These scenarios were analyzed and compared using FUCA and TOPSIS multicriteria decision-making tests to select the most adequate option according to the comparison of the two methods. As a result, 15 scenarios were generated, and they were divided equally among the three types. Furthermore, a sensitivity analysis was performed, considering diverse variation policies in the parameters to evaluate the system’s response when facing changes. Finally, the creation of normal, pessimistic, and optimistic scenarios was carried out in accordance with priorities (1, 2, and 3) according to the multicriteria decision-making TOPSIS and FUCA.

Construct the Graphical User Interface for Decision-Making: In the final stage, the graphical user interface was developed, where the most relevant variables were incorporated for decision-making; those more susceptible to change were characterized by the most sensitive parameters. This interface includes elements such as buttons, graphics, tables, and images alluding to the company, which were designed to facilitate user interactions with the simulation model and provide useful information for decision-making. As a result, a developed graphical interface was developed in the Stella^® Architect software.

4. Results

This section analyzes the obtained results, with the objective of developing a technological supply and production link solution for decision-making using MCMD FUCA and TOPSIS as a part of the SD methodology.

This study faced the following limitations in achieving its objective, which are as follows:

• The proposed supply chain study is limited to specific supply and production areas for decision-making.
• The production line considered for the case study is line 16, model 2024.
• The object under study is the components of the production line.
• The data were obtained on 30 October 2023.
• This study was conducted during the period from January to August 2024.
• Restrictions on access to internal company data were in place, limiting the depth of the analysis and our understanding of certain operational aspects.
• Sensitive information could not be disclosed, affecting the completeness of the results.
• Internal changes in the company during the research period could affect the validity and applicability of the results, as the company is dynamic and its structure may evolve.
• External factors beyond the control of the project also affected this study.

MCMD has been used in the automotive sector in various contexts, such as those described by Shahroudi and Rouydel [40], who analyzed supplier selection in the Iranian automotive industry. The ANP–TOPSIS method allowed them to evaluate the interdependence between criteria such as logistics costs, environmental compliance, and reliability. For management, this implies that managers must not only weigh each factor but also analyze how they interact with each other. The results of this approach can guide strategic purchasing decisions and reduce risks in the supply chain.

On the other hand, Mirzaaliyan [41] applied a hybrid methodology that integrates discrete event simulation with TOPSIS to evaluate resilience strategies in automotive supply chains. Managers who adopt this approach can simulate disruption scenarios and use the results as inputs for multicriteria analyses, thus choosing strategies that maximize operational continuity at the lowest cost. This is especially relevant in the face of logistical crises or fluctuations in demand.

Similarly, Ghosh et al. [42] showed that by integrating quantitative data and expert judgments into and FUCA model, managers can identify more robust sourcing options, even when there is uncertainty in the information. This strategy renders it easier to prioritize suppliers that provide greater long-term value beyond the immediate price.

4.1. Context Analysis in Which the Organization Under Study Operates

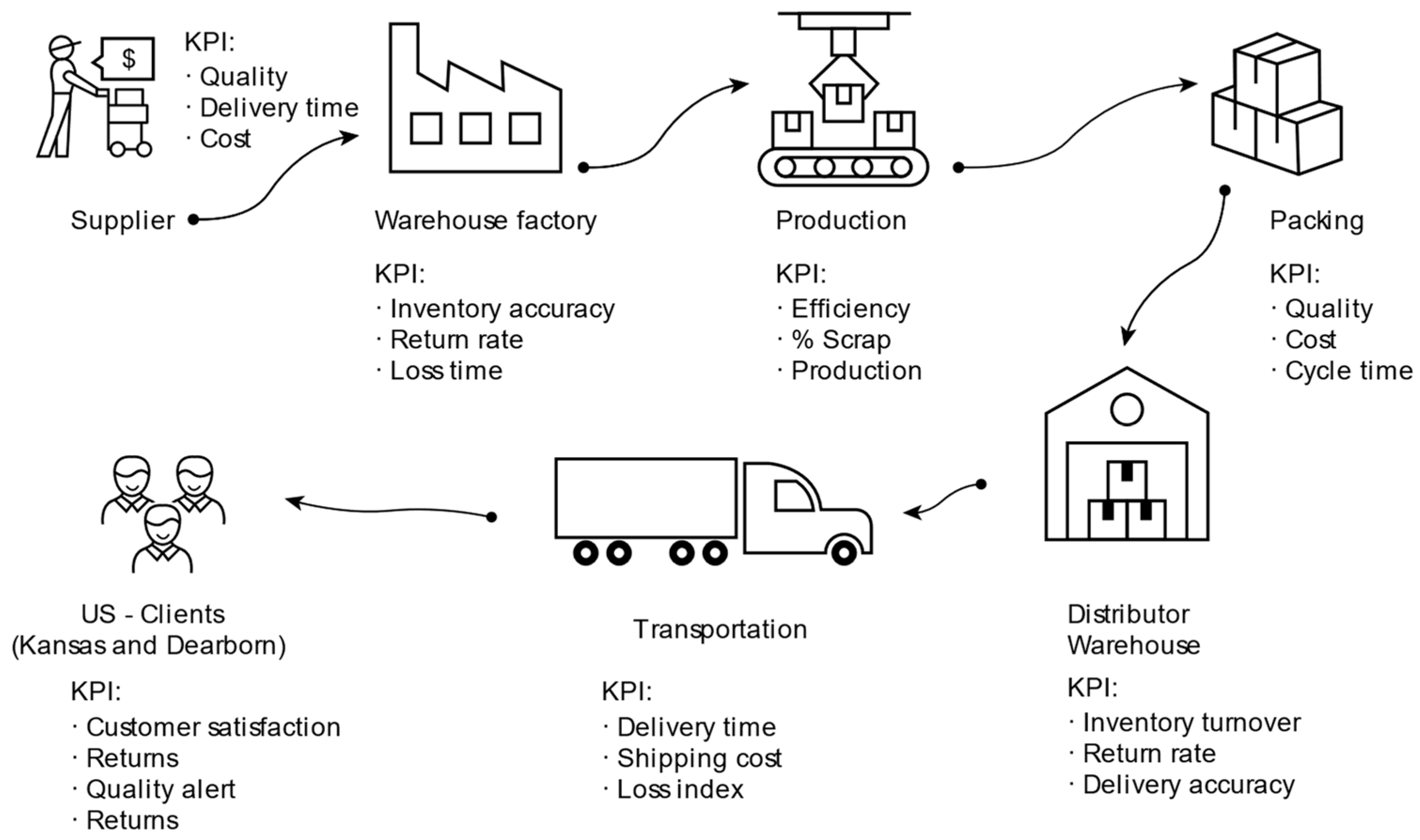
As part of the organizational context, Figure 2 was constructed to illustrate the logic that symbolizes the organizational structure of the company under study. The figure represents different integral and general organizational processes, encompassing relevant elements in the supply chain and considering its key performance indicators (KPI).

The image represents each process and its interrelations, accompanied by its respective KPI in detail. As an example, the supply chain starts with the supplier phase, followed by production, packaging, distribution to the warehouse (Ford Motor Company), transportation, and delivery to the customer.

Additionally, an end-customer phase is integrated, which corresponds to the individuals who buy the manufactured product. Each phase has performance indicators, which help evaluate yield and process success. The process begins with the delivery of raw materials related to the components of the harnesses. This then proceeds to the production process with respect to the assigned production lines. Once completed, the finished products are packaged and sent to the final product warehouse for distribution to the US market via the highway connecting the state of Sonora in Mexico with the state of Arizona in Nogales. After this stage, all final products are shipped to Kansas and Dearborn in the USA.

4.2. Causal Diagram Elaboration

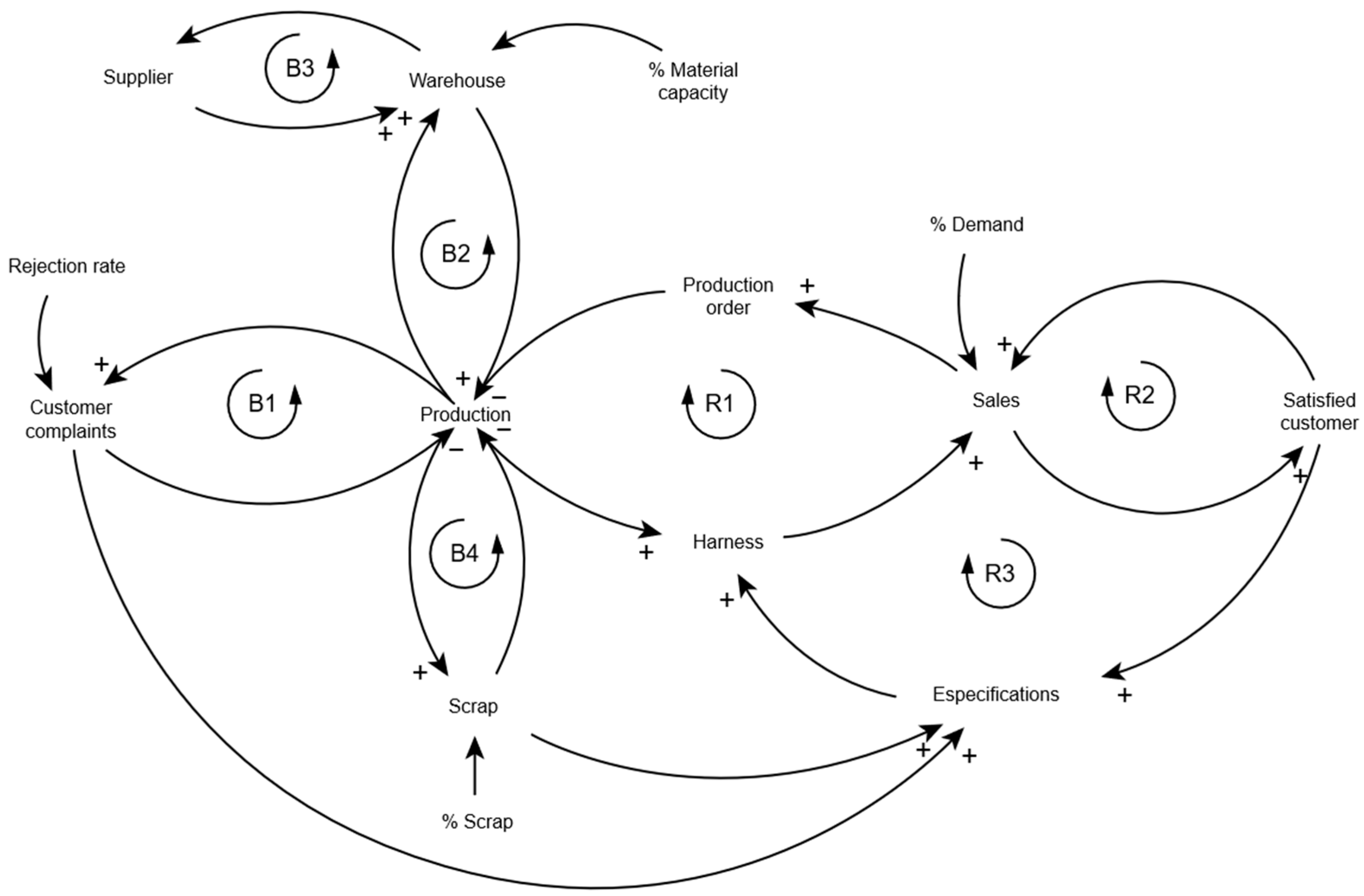
Figure 3 represents the cause–effect relationship of the variables that comprise the company under study, with the objective to analyze how it functions, its behavior, and its relationship with its surroundings. The elements known as reinforcing (R) and balancing (B) loops help maintain equilibrium and support understanding of the system.

Reinforcement loops reveal the processes of exponential growth or accelerated decline, where the effects amplify the original causes, generating virtuous or vicious circles that can result in dramatic changes in the system. Balance loops, on the other hand, identify self-regulating mechanisms that seek to maintain stability or specific objectives, acting as stabilizing forces that counteract deviations. In this sense, this study allows us to observe that there are four balance loops and three reinforcement loops, which—via visual representation—facilitate the understanding of nonlinear interactions and help identify leverage points in the model.

The previous structure exhibits the causal diagram process, for which its objective is to represent the system’s relationships—starting from the elements that comprise them. The diagram has four balance loops, and three reinforced loops are described as follows:

Balance loops:

B1: The first balance loop determines that a production increase results in a complaint increase due to a greater rejection rate percentage. These complaints, in turn, cause a slowdown in production.

B2: The second balance loop accumulates more inventory by increasing production. Once the inventory reaches its maximum capacity, production stops, maintaining an adequate level of raw material capacity.

B3: As a consequence of the B2 loop, it is observed that when inventory levels are higher, less supply is required from the providers. However, by increasing the number of providers, the available inventory increases.

B4: Finally, the fourth balance loop determines that by increasing production, the amount of scrap material generated also increases. Production decreases as a consequence of scrap generation.

Reinforcing loops

R1: The first reinforcing loop establishes that an increase in production generates more harnesses, which results in an increase in sales and production orders. Sales are linked to a demand percentage.

R2: The second reinforcing loop is found in the sales area, where an increase in sales results in greater customer satisfaction, which generates even more sales.

R3: The third reinforcing loop determines that in scrap generation, customer complaints or satisfaction carry greater product specifications. As a result, an increase in harness production is needed to comply with these specifications.

This type of diagram is widely used in system understanding processes [28] to analyze recovery options for electronic parts used in the automotive industry, particularly with respect to SD in the supply chain of this sector. It employs structures to demonstrate the relationships of R and B types, illustrating how variables are interconnected, as discussed by the authors of [43,44].

4.3. Simulation Model Formulation Using Forrester Diagrams and Formulated Mathematical Equations

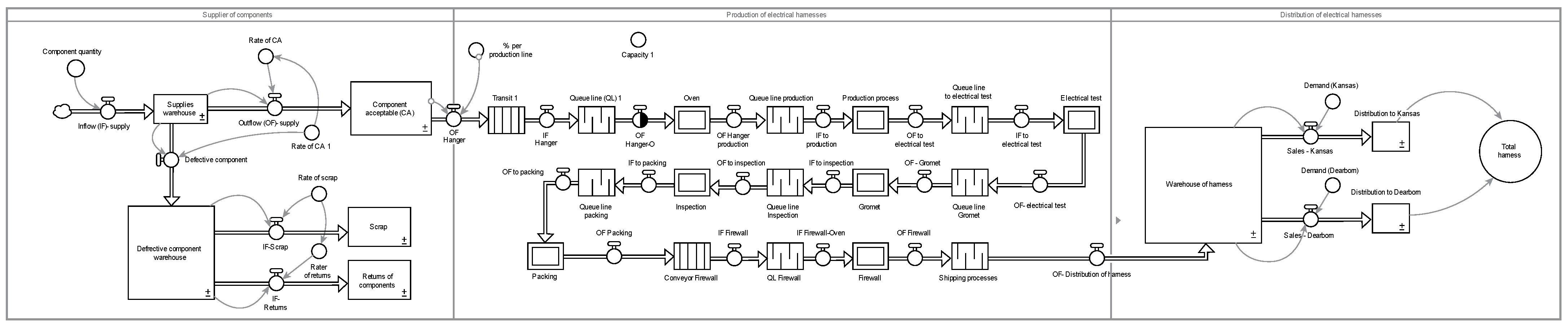
Starting from the causal diagram, the variables and parameters were classified to construct the Forrester diagram by means of Stella^® Architect software. This diagram is organized into the main system components: storage, production, and distribution. The model illustrated the complete process, starting from the reception of 32,000 pieces of components per shift, ending with the shipment to the final customers, which are Kansas and Dearborn, as detailed in Figure 4.

The Forrester diagram for process simulations of the company under study encompasses three key loops: storage, production, and distribution. The storage loop manages the reception and storage of the components. The production loop is centered on harness making, transforming acceptable components into finished products (considering time and capacities). Finally, the distribution link manages the shipment of finished products to Kansas and Dearborn for Ford Motor Company—the final customer—which allows for analyzing and optimizing the material and product flow along the supply chain. The diagram shows the first process loop of the storage stage, which includes the reception of the necessary components—approximately 32,000—for production and storage lines. The components are classified into two categories: acceptable and defective. Inverse logistics plays an important role in this process, as the defective components are managed in two ways: one part is sent to the waste area, while the other is returned to be replaced or repaired.

In the production structure, the line includes diverse activities necessary for manufacturing the final product, which is the harness in this case. The diagram describes the processes involved in harness manufacturing, starting from the perch, where the circuits are performed. Then, taping is performed in the production band. The electricity test ensures that circuits are connected correctly, while a detailed inspection of the components is performed in the grommet. Subsequently, the geometric conformity of the harness is verified in accordance with an inspection table. Packing is performed using pallets. Finally, an additional inspection is performed on the firewall (at 200%). The production line has a capacity of approximately 1250 pieces of components, producing around 15 harnesses per hour, although only 4% of the components stored were used for this line.

Finally, the distribution loop shows the projected demand for the two main destinations. This process ensures that the finished products arrive on time and in good condition at the planned destinations, complying with Ford Motor Company’s requirements. This distribution structure shows how the harnesses are delivered to different destinations: Kansas and Dearborn. Each destination has a specific demand that varies weekly with respect to customer requirements. This fluctuating demand requires detailed planning and adjustments in the distribution process to ensure that the necessary volumes arrive at each destination. These variations are managed to satisfy customer needs efficiently in order to guarantee a continuous flow of products and prices at both destinations. As derived from previous results, they are compared with empirical studies that use flow and level diagrams to create formal logical structures [45,46,47], where the importance of developing these models lies in using specialized Vensim^® PLE, USA, and Power Sim^® software, Norway.

4.4. Model Equations

The model uses levels, inflows and outflows, auxiliary conveyors, ovens, and queues, as well as parameters. To illustrate these, some equations are presented by type (see

Table 2. Equations by type used in the dynamic model for harness production in line 16.

Types of Equations Presented in the Dynamic Model
Stocks: Represents an accumulation or quantity that exists at a given moment, such as inventory of parts, order volume, or capital.
$$\begin{gathered} \mathrm{A}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \mathrm{A}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\left(\mathrm{t} - \mathrm{d}\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+ \left(\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} - \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y} - \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{\%}\mathrm{H}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{r}\right) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(1)
$$\begin{gathered} \mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s} \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s} \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} - \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y} - \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y} - \mathrm{D}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(2)
$\mathrm{S}\mathrm{c}\mathrm{r}\mathrm{a}\mathrm{p}\left(\mathrm{t}\right) = \mathrm{S}\mathrm{c}\mathrm{r}\mathrm{a}\mathrm{p}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} - \mathrm{S}\mathrm{c}\mathrm{r}\mathrm{a}\mathrm{p}) \times \mathrm{d}\mathrm{t}$	(3)
Conveyors: These are a special type of flow that transports material or information with a fixed transit time from an entry point to an exit point, without allowing any intermediate accumulation.
$\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t} 1\left(\mathrm{t}\right)$ $\hspace{1em}\hspace{1em}\hspace{1em}=\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}1(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{\%}\mathrm{H}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{r} - \mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} - \mathrm{H}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{r}) \times \mathrm{d}\mathrm{t}$	(4)
$$\begin{gathered} \mathrm{R}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \mathrm{R}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{F}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l} - \mathrm{O}\mathrm{F} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{f} \mathrm{H}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(5)
$$\begin{gathered} \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{y}\mathrm{o}\mathrm{r} \mathrm{F}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{y}\mathrm{o}\mathrm{r} \mathrm{F}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{P}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{g} - \mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{F}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(6)
Ovens: Element that models processes with fixed retention times during which the quantity remains unchanged for a specified period before moving on to the next stage.
$$\begin{gathered} \mathrm{E}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{T}\mathrm{e}\mathrm{s}\mathrm{t}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \mathrm{E}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{T}\mathrm{e}\mathrm{s}\mathrm{t}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(7)
$$\begin{gathered} \mathrm{I}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(\mathrm{t}\right) = \mathrm{I}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{i}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} - \mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{t}\mathrm{o} \mathrm{p}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(8)
$\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{t}\left(\mathrm{t}\right) = \mathrm{G}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{t}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} - \mathrm{G}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{t} - \mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{i}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}) \times \mathrm{d}\mathrm{t}$	(9)
Queues: Components representing a queue where entities remain until capacity becomes available in the subsequent process.
$$\begin{gathered} \mathrm{Queue}\mathrm{line}\mathrm{production}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \mathrm{Q}\mathrm{u}\mathrm{e}\mathrm{u}\mathrm{e} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{H}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{r} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} - \mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{P}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(10)
$$\begin{gathered} \mathrm{Queue}\mathrm{line}\mathrm{Inspection}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\mathrm{Queue}\mathrm{line}\mathrm{Inspection}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{i}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{i}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(11)
$$\begin{gathered} \mathrm{Queue}\mathrm{line}\mathrm{Packaging}\left(\mathrm{t}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\mathrm{Queue}\mathrm{line}\mathrm{Packaging}(\mathrm{t} - \mathrm{d}\mathrm{t}) + (\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{p}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}- \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{p}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g}) \times \mathrm{d}\mathrm{t} \end{gathered}$$	(12)
Inflow: This is the rate of change that increases or decreases a stock, such as production speed, sales pace, or waste rate.
$\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{s}\mathrm{c}\mathrm{r}\mathrm{a}\mathrm{p}=$ $\mathrm{D}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e} \times \mathrm{T}\mathrm{i}\mathrm{m}\mathrm{e} \mathrm{t}\mathrm{o} \mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{S}\mathrm{c}\mathrm{r}\mathrm{a}\mathrm{p}$	(13)
$\mathrm{D}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t} = \mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s} \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e} \times \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\mathrm{s}$	(14)
$\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{H}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{r} = \mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{A}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \times \mathrm{\%}\mathrm{p}\mathrm{e}\mathrm{r} \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}$	(15)
Outflow: This is the rate of change that increases or decreases a stock, such as production speed, sales pace, or waste rate.
$$\begin{gathered} \hspace{1em}\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w} \mathrm{t}\mathrm{o} \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y} \\ \hspace{1em}= \mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s} \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e} \mathrm{x} \mathrm{T}\mathrm{i}\mathrm{m}\mathrm{e} \mathrm{t}\mathrm{o} \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y} \mathrm{a}\mathrm{t} \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{a}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \end{gathered}$$	(16)
$\mathrm{S}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{s} \mathrm{D}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{r}\mathrm{n} = \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{h}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \times \mathrm{D}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{o} \mathrm{D}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{r}\mathrm{n}$	(17)
$\mathrm{S}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{s} \mathrm{K}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{a}\mathrm{s} = \mathrm{W}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{h}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \times \mathrm{D}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{o} \mathrm{K}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{a}\mathrm{s}$	(18)
Auxiliary: These are intermediate or supporting variables that calculate values needed to determine flows or stocks, such as machine efficiency, demand coefficients, or quality indices.
$\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{H}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} = \mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{t}\mathrm{o} \mathrm{K}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{a}\mathrm{s} + \mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{t}\mathrm{o} \mathrm{D}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{r}\mathrm{n}$	(19)
Key Parameters: A key parameter is a fixed value or input function that represents the structural characteristics, policies, or external conditions of the system.
% per production line = 0.4 Component quantity = RANDOM (28,100, 32,100) Demand (Dearborn) = RANDOM (0.6, 0.8, 0.7528) Demand (Kansas) = RANDOM (0.6, 0.8, 0.7528)

Source: Own elaboration based on a sample of the equations used in the model.

).

In an SD, stocks store the system’s history (state). Flows describe the actions that change that state, and elements such as conveyor, oven, and queue add realism by modeling transport, processing, or waiting times. Auxiliary variables act as “logical bridges” that connect policies, parameters, and feedback, ensuring that simulations reflect real interactions between production, inventory, logistics, and demand.

4.5. Current Model Validation

According to Sargent [48], model validation aims to verify that a model is sufficiently representative and useful for the specific purposes for which it was created. The model’s evolution depends on the context and objectives for which it will be used. On the other hand, according to Banks, Carson, and Nelson [49], validation implies the process of demonstrating that a model reflects—in a precise and adequate manner—the phenomenon it is designed to represent, ensuring that the model is adequate for the applications it is designed for.

Thus, Barlas and Carpenter [50] applied a mean error test, which consisted of analyzing the mean error test generated from real data in absolute values against those that are simulated, and they are divided between real data in absolute values. The model is valid and reliable if the error rate is smaller than or equal to 5%. The comparison of data that the company has registered is associated with the amount distributed to Kansas City and Dearborn in the USA. The data were confirmed by the company—an average of 220 harnesses per turn (firewall)—and the relative error test is applied as follows:

%ER = |(Simulated Data-Real data real)/Real data| × 100%

(20)

where

ER = relative error.

By calculating the % of relative error for each type of customer error, we obtain the following (foreign customer 1 (CE1)):

% relative error = |(230 − 220)/220| × 100% = 4.54%

As 4.54% ≤ 5%, this complies with the validation criteria.

By calculating the % of the relative error for each type of customer error, we obtain the following (foreign customer 2 (CE2)):

% relative error = |(228 − 220)/220| × 100% = 3.63%

As 3.63% ≤ 5%, this complies with the validation criteria.

To conclude, the model complies with the relative error test; thus, it may be inferred that the model represents reality. The data associated with the production of harnesses on the production line under study (16) were collected from 30 October 2023 to 18 June 2024, when the final data for this study were collected.

On the other hand, Sterman [27] researched other methods for validating models that were applied in this case. Below are the two methods used in the model developed.

Dimensional Consistency: In this test, all units of measurement were checked to ensure consistency to align the model’s operating logic with reality. All units were verified during the equation’s construction process.

Extreme Conditions: This test consists of assigning a value of zero to an input parameter, in which case the model does not exhibit forward behavior.

4.6. Selection of the Pessimistic, Current, and Optimistic Scenarios

The sensitivity analysis was performed by identifying the most critical parameters of the model. For this purpose, six scenarios were developed for each type—five current (C), five pessimistic (P), and five optimistic (O) scenarios—with the objective of evaluating the most relevant variables. The difference between the scenarios was established based on three basic parameters: (a) part capacity; (b) % of demand for Dearborn; and (c) % of demand for Kansas City. Based on this, the scenarios explained below are simulated:

Current Scenario: This establishes how line 16 produces the harnesses during the period under study, and the data reflects the reality at that time.

Pessimistic Scenario: This scenario considers the modification of the three most sensitive parameters, where part capacity and demand are critical, i.e., they are reduced.

Optimistic Scenario: This is the most favorable scenario and considers the modification of the three most sensitive parameters, where part capacity and demand are improved, i.e., they increase in line with demand.

The selection and valuation of the most adequate scenarios are performed via FUCA and TOPSIS multicriteria decision-making, which allows for carrying out an optimization multiple-criterion analysis. The following tables show the macros related to TOPSIS and FUCA (see

Table 3. Scenarios starting from multicriteria decision-making (TOPSIS).

			CA	CD	FW	DK	DD	DT
			Max	Min	Max	Max	Max	Max
Scenario	VG	Rank	0.25	0.05	0.3	0.1	0.1	0.2
Current 1	0.13278	12	695	12	135	609	849	1458
Current 2	0.189	10	688	17	150	667	930	1597
Current 3	0.222	7	682	16	150	726	1013	1739
Current 4	0.26055	4	685	16	150	789	1100	1888
Current 5	0.98174	1	723	3	216	1548	2156	3705
Pessimist 1	0.09314	14	682	17	135	556	774	1329
Pessimist 2	0.13811	11	683	11	135	610	851	1461
Pessimist 3	0.19772	9	681	14	150	668	932	1600
Pessimist 4	0.2345	6	691	12	150	727	1015	1742
Pessimist 5	0.20399	8	698	15	120	790	1102	1892
Optimist 1	0.07692	15	675	23	135	557	776	1333
Optimist 2	0.09618	13	681	20	135	612	853	1465
Optimist 3	0.24822	5	680	2	150	670	935	1605
Optimist 4	0.27855	2	682	1	150	730	1019	1749
Optimist 5	0.26833	3	684	14	150	794	1106	1900

Notes: AC = Acceptable component; DC = defective component; FW = firewall; KD = Kansas distribution; DD = Dearborn distribution; TD = total demand; VG = general value. Source: Own elaboration, 2025.

and

Table 4. Scenarios starting from multicriteria decision-making (FUCA).

			AC	DC	FW	KD	DD	TD
			Max	Min	Max	Max	Max	Max
Scenario	VG	Rank	0.25	0.05	0.3	0.1	0.1	0.2
Current 1	7.45	9	695	12	135	609	849	1458
Current 2	5.2	2	688	17	150	667	930	1597
Current 3	6.3	6	682	16	150	726	1013	1739
Current 4	5.55	4	685	16	150	789	1100	1888
Current 5	4.4	1	723	3	216	1548	2156	3705
Pessimist 1	8.6	12	682	17	135	556	774	1329
Pessimist 2	8.8	13	683	11	135	610	851	1461
Pessimist 3	7.2	8	681	14	150	668	932	1600
Pessimist 4	5.3	3	691	12	150	727	1015	1742
Pessimist 5	8.55	11	698	15	120	790	1102	1892
Optimist 1	10	15	675	23	135	557	776	1333
Optimist 2	9.3	14	681	20	135	612	853	1465
Optimist 3	8	10	680	2	150	670	935	1605
Optimist 4	6.8	7	682	1	150	730	1019	1749
Optimist 5	5.95	5	684	14	150	794	1106	1900

Notes: AC = Acceptable component; DC = defective component; FW = firewall; KD = Kansas distribution; DD = Dearborn distribution; TD = total demand; GV = general value. Source: Own elaboration, 2025.

, respectively).

The weighted values for each of the six optimization criteria were defined based on the experience of the supervisor of production line 16 (obtained from a conducted interview): acceptable component (0.25%); defective component (0.05); firewall (0.3); Kansas distribution (0.1); Dearborn distribution (0.1); and total demand (0.2). Adding these values results in a value of 1 (100%).

Five current scenarios are compared with five pessimistic and five optimistic scenarios using TOPSIS and FUCA multicriteria decision-making. This comparison is fundamental for the analysis of data, which allows identifying the best four scenarios.

Table 5. Comparative scenarios using MCMD FUCA and TOPSIS.

Ranking with	Relative Proximal Value	Scenarios	Ranking with	Valor General
TOPSIS			FUCA
12	0.132784	Current 1	9	7.45
10	0.189002	Current 2	2	5.2
7	0.222003	Current 3	6	6.3
4	0.260547	Current 4	4	5.55
1	0.981742	Current 5	1	4.4
14	0.093139	Pessimist 1	12	8.6
11	0.138108	Pessimist 2	13	8.8
9	0.197715	Pessimist 3	8	7.2
6	0.234504	Pessimist 4	3	5.3
8	0.203994	Pessimist 5	11	8.55
15	0.076922	Optimist 1	15	10
13	0.09618	Optimist 2	14	9.3
5	0.248216	Optimist 3	10	8
2	0.278554	Optimist 4	7	6.8
3	0.268331	Optimist 5	5	5.95

Note: FUCA and TOPSIS scenarios. Source: Own elaboration, 2025.

shows a comparison of the 15 analyzed scenarios.

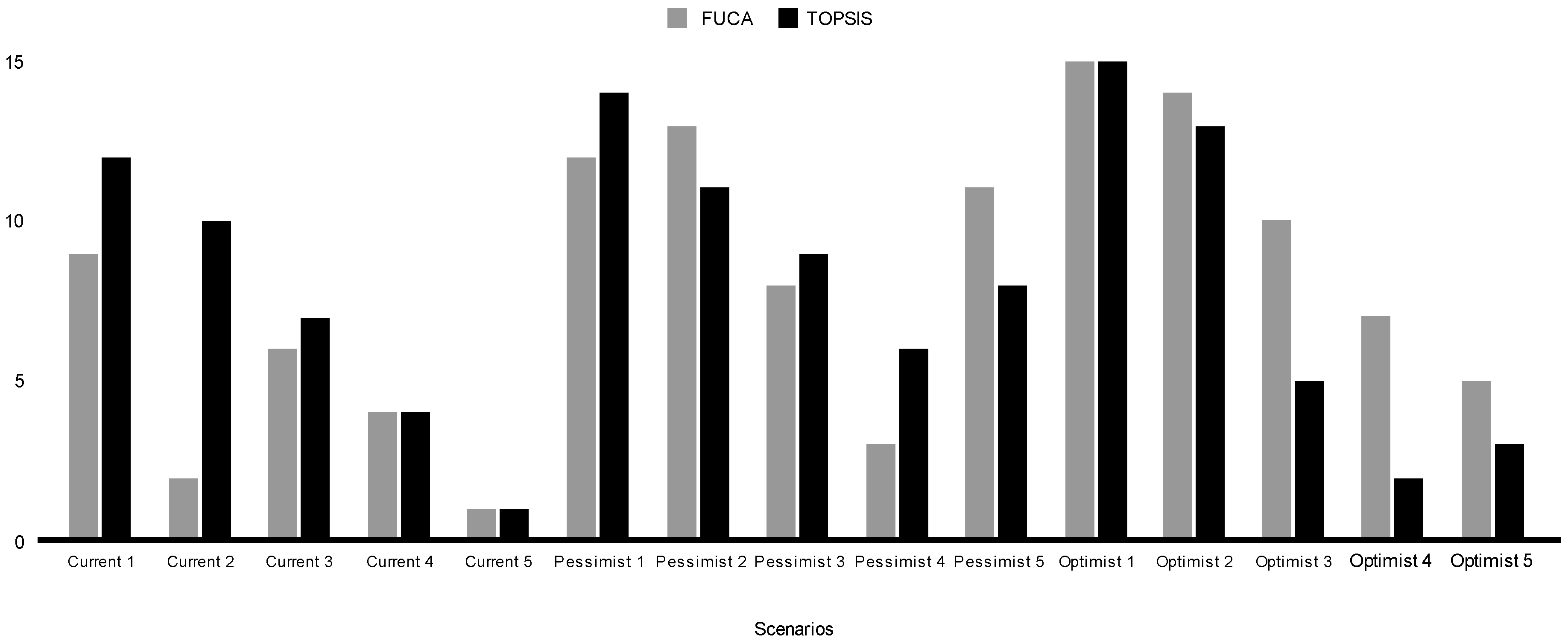
Figure 5 shows the comparison in terms of the position achieved according to the scenario analyzed using FUCA and TOPSIS multicriteria decision-making (MCDM).

It can be seen that the two methods produce very similar results, considering the same optimization criteria under analysis: acceptable component; defective component; firewall; Kansas distribution; Dearborn distribution; total demand; general value.

With respect to the most favorable results according to MCMD TOPSIS and FUCA, the following findings are observed:

Current Scenario: Number 5 exhibits the highest value and is considered the best, reaching a value of 0.981742. It is ranked first in both FUCA and TOPSIS in MCMD.

Optimistic Scenario: Number 4 exhibits the second-highest value, particularly reaching a value of 0.278554. It is ranked second.

Optimistic Scenario: Number 3 exhibits the third-highest value, reaching a value of 0.268331. It is ranked third.

Current Scenario: Number 4 exhibits the fourth-highest value, reaching a value of 0.260547, and it is ranked fourth.

Using MCMD to evaluate different objectives allows FUCA and TOPSIS to be used in complex processes; both techniques are especially important when multiple objectives that converge in a complex system exist, as they are required to be valued at the same time in order to make the best decision [51,52].

The joint application of multicriteria analysis tools, such as FUCA and TOPSIS, within the system dynamics approach provides an effective method for addressing the complex challenges of the automotive sector, characterized by the interaction of factors related to the main variables selected: demand, inventories, associated costs, waste, etc. While system dynamics allows for the representation of cause–effect relationships, feedback loops, and nonlinear behaviors, the FUCA and TOPSIS methods support the selection and prioritization of alternatives considering quantitative indicators. This combination provides decision-makers with a comprehensive perspective: First, different scenarios are modeled and simulated to analyze their evolution and the dependencies between variables. Then, they are evaluated using a multicriteria weighting scheme. Thus, managers can define production or supply policies that are not only feasible in the dynamic model but also aligned with the organization’s strategic objectives.

4.7. Graphical User Interface Construction for Decision-Making

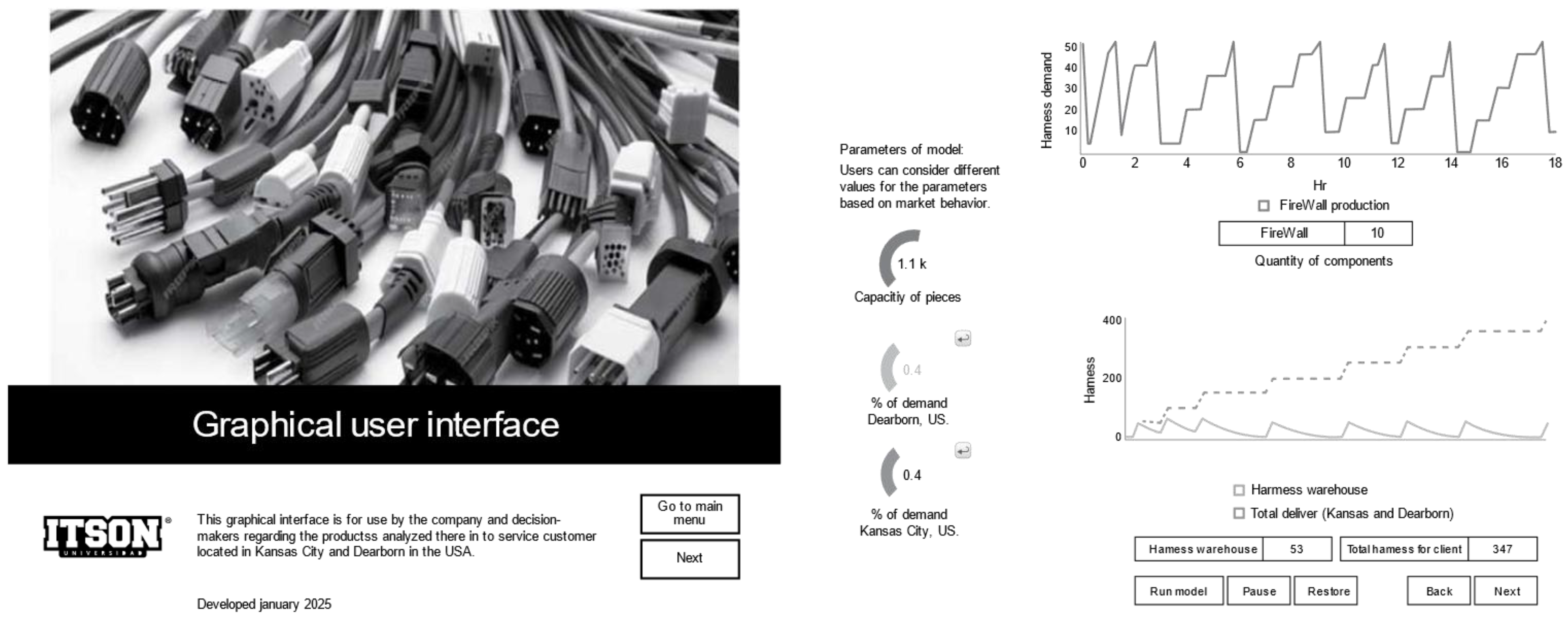
A graphical user interface (GUI) allows decision-makers to systematically follow behaviors according to company information. Figure 6 shows two screens that interact with individuals who have access to the GUI.

By having information containing concentrated data and tendencies, companies have greater decision-making capacities and may—starting from policies—predict the effects of demands during critical moments; moreover, high certainty is achieved when knowing the consequent effects that will impact current and potential customers.

This section of the graphical interface allows users to initiate firewall simulation as a key component and monitor the number of harnesses available in storage, taking into account the total deliveries made with respect to Dearborn and Kansas City in the USA. In this sense, the decision-maker can apply policies in different scenarios (what-if scenarios) based on three key indicators: part capacity, the % of demand allocated to customers (Dearborn and Kansas City), and the ability to modify these values either simultaneously or individually, depending on the conditions that may arise. This allows for multiple simulations to be run in order to observe behaviors over an 18 h time horizon (a two-shift day).

Using a graphical interface is now more important for companies than using information concentrated in data tables, as reported by Lagarda et al. [53] (for a production company in the food sector); in their study, a graphical interface was developed by small fig producers using Stella^® Architect software. The development of technological solutions involving a graphical user interface has been applied using various methods since 1991, with over 230 published articles to date. This highlights the relevance of this type of solution in supporting decision-making within organizations [54].

5. Discussion

The procedure used in this study provides a method that can support future research in the automotive sector using system dynamics, with results discussed in comparison with other studies based on the contributions made at each stage.

The development of flowcharts to understand variable and parameter relationships proved to be essential for constructing causal diagrams. This preliminary analysis approach was validated by Mirzaaliyan, Rahman, and Sepehri [41]—who developed process flowcharts to describe automotive supply chain dynamics under different resilience strategies—and by Zupan [55]—who used process flow diagrams to map production stages before building system dynamics models. Similarly, Barrera-Díaz [56] applied detailed flowcharts to represent material handling sequences in automotive parts manufacturing plants.

The translation of the causal model into flow and stock diagrams, divided into three sectors representing the supply, production, and distribution of harnesses, allows for the proper structuring of stock equations, conveyors, ovens, and queues connected by input and output flows. This approach aligns with studies that use stock and flow diagrams to model inventory behavior, helping automotive managers determine optimal stock policies that balance high availability with low inventory maintenance costs [57,58].

The application of multicriteria analysis methods (FUCA and TOPSIS) for scenario selection represents a significant methodological contribution. Li et al. [59] demonstrated that combining system dynamics with TOPSIS facilitates the objective evaluation of sustainability strategies in automotive supply chains, while Jato-Espino et al. [60] applied both FUCA and TOPSIS within simulation frameworks to support decision-making in complex industrial systems.

The convergence of results between FUCA and TOPSIS methods reinforces decision-making confidence, as demonstrated by Yazdani et al. [61] in strategic manufacturing planning. When both methods yield similar results, managers can proceed with greater certainty and reduce the risks associated with adopting new operational policies.

The technological solution based on a graphical user interface represents the main contribution of this study. This GUI consolidates all previous analytical stages into a user-friendly platform designed for company personnel involved in harness transformation processes who may not be system dynamics experts [62].

The interface addresses the critical need for timely information to evaluate various scenarios when facing uncontrollable exogenous changes in demand, internal processes, and supplier conditions [63]. By offering accessible simulation capabilities, the GUI enables users to interpret data and trends from graphical outputs, supporting informed decision-making during supply shortages and operational disruptions.

This technological solution fills a gap in the automotive industry by democratizing access to sophisticated analytical tools, allowing operational managers to leverage system dynamics modeling without requiring specialized technical expertise and ultimately improving response times and decision quality in dynamic supply chain environments.

6. Conclusions

This study demonstrates the effectiveness of a technological solution that integrates system dynamics (SD) with multicriteria analysis methods (MCDMs) to address component shortages in an automotive harness assembly plant. This study not only validates a model for mitigating economic losses and downtime but also offers significant theoretical contributions, practical management implications, and clear directions for future research.

The main theoretical contribution of this study is the innovative methodological hybridization of system dynamics using FUCA and TOPSIS techniques. While SD allows for capturing the complexity, interdependencies, and feedback loops (such as the identified B1-B4 and R1-R3 loops) inherent in a supply chain, MCDMs provide a quantitative and objective framework for prioritizing operational scenarios. This approach fills a gap in the literature, where traditional quality tools fail to analyze the dynamic nature of production problems in such a complex sector. Additionally, this study highlights the theoretical importance of graphical user interfaces (GUIs) as a bridge between complex simulation models and managerial decision-making, facilitating the adoption of these tools by non-expert users.

On a practical level, the developed technological solution offers managers a powerful tool for proactive, data-driven decision-making. The graphical interface allows them to simulate “what if?” scenarios and predict, within an 18 h horizon, the impact of variations in critical parameters, such as part capacity and customer demand. This transforms crisis management into informed strategic planning.

The analysis of 15 scenarios (current, pessimistic, and optimistic) and the identification of the four most favorable configurations using FUCA and TOPSIS provide a clear roadmap for optimizing operational performance. Managers can implement policies corresponding to “Current Scenario 5,” which was ranked the most favorable using both methods. This implementation can be carried out with confidence, as it is aligned with the multiple weighted performance criteria, including acceptable component levels and total demand. Ultimately, this tool strengthens supply chain resilience, allowing the company to respond more nimbly to market fluctuations and consolidate its position as a key supplier to customers such as Ford Motor Company.

We acknowledge the limitations of this study, which include the focus on a single production line (line 16, “Crew Grande” model) and a specific analysis period. The confidentiality of certain internal data may have also limited the depth of some analyses.

These limitations open the door to valuable future research directions. We propose replicating the solution’s operational logic across other product lines within the same company, using real-time data to validate its scalability. Likewise, it would be beneficial to conduct a benchmarking study with other plants within the company that manufacture the same product to evaluate the model’s effectiveness in different operating contexts. Finally, future research could explore the integration of emerging technologies such as artificial intelligence (AI) and blockchain, enriching the model to address sustainability and resilience challenges in the automotive supply chain, a trend that is identified in the literature.