Trajectory Prediction for Powered Two-Wheelers in Mixed Traffic Scenes: An Enhanced Social-GAT Approach
Abstract
1. Introduction
- This study specifically focuses on PTWs, capturing their unique motion patterns in mixed traffic scenarios. This fine-grained analysis enhances behavioral prediction accuracy, contributing to improved safety for autonomous vehicles.
- A reinforced LSTM encoder–decoder framework integrated with graph attention is proposed. It effectively captures long-term temporal dependencies and complex interactions, achieving high-precision trajectory prediction in intricate traffic scenarios.
- An absolute coordinate correction module is introduced to mitigate the starting point drift caused by relative coordinate output. This method significantly improves prediction accuracy on the rounD dataset.
2. Related Works
2.1. Current Research Status in Trajectory Prediction
2.2. Current Research Status in Interaction Modeling
3. Methodology
3.1. Problem Description
3.2. Trajectory Characteristics Analyse
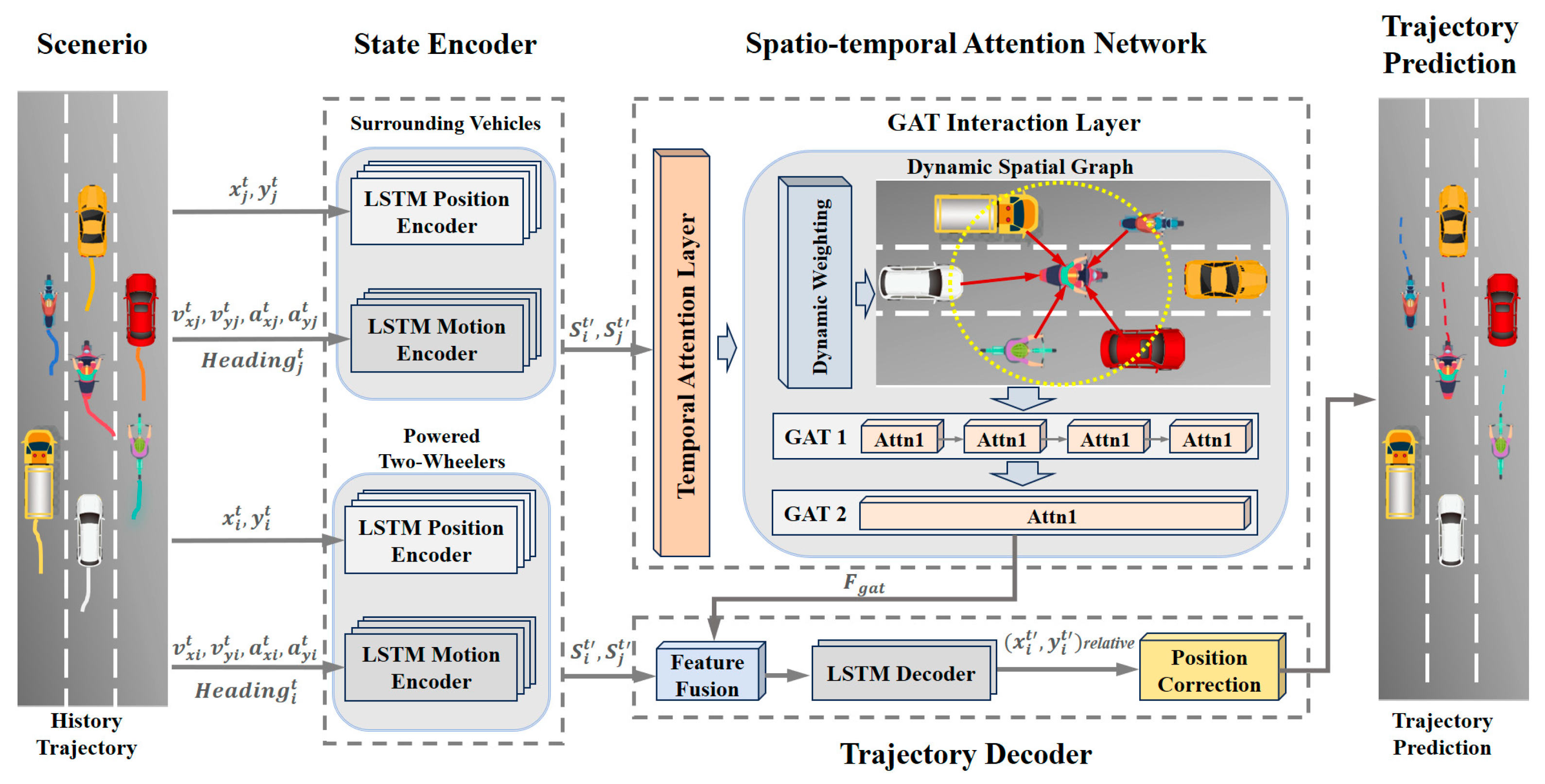
3.3. Model Architecture
3.3.1. Trajectory State Encoder
3.3.2. Spatiotemporal Attention Network
Temporal Attention Layer
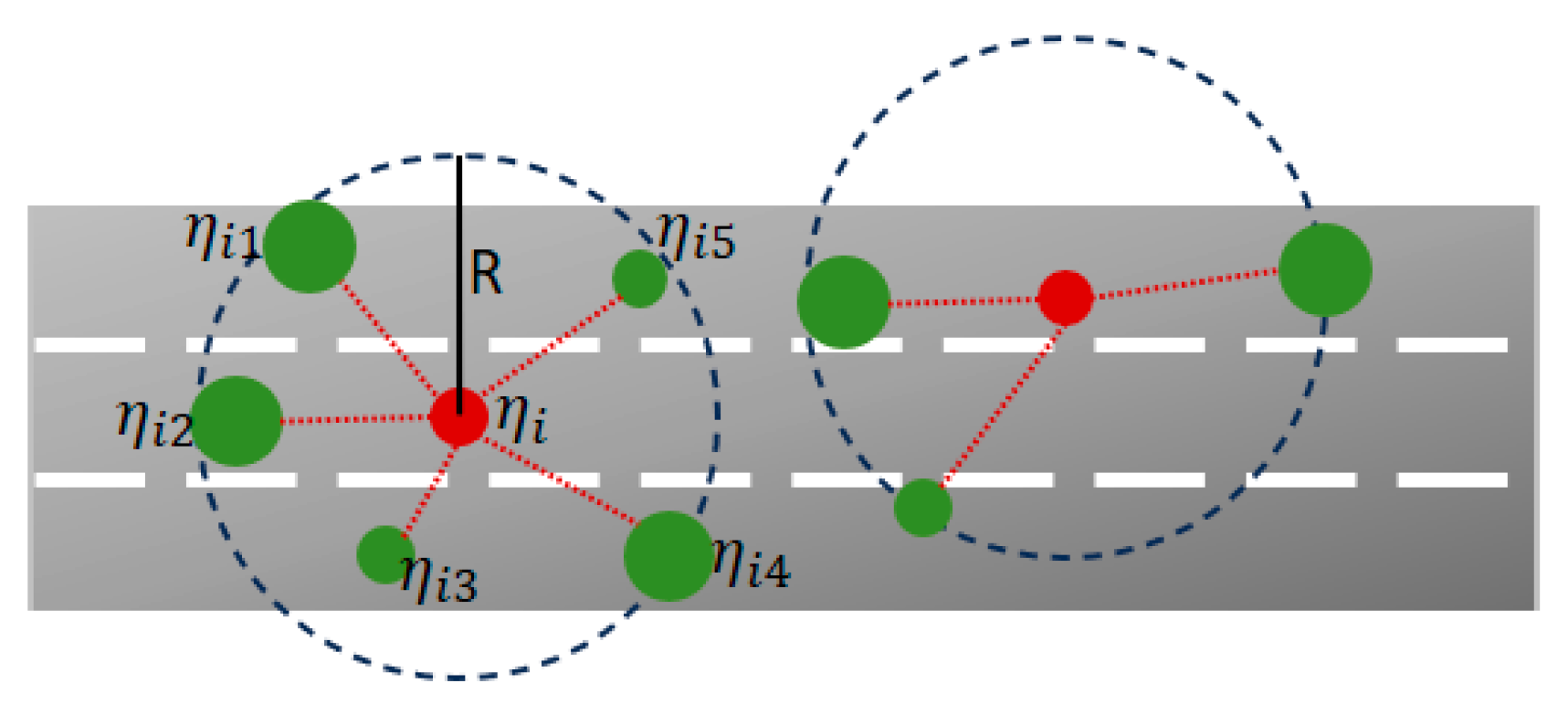
GAT Interaction Layer
3.3.3. Trajectory Decoder
4. Experiments and Analysis
4.1. Dataset
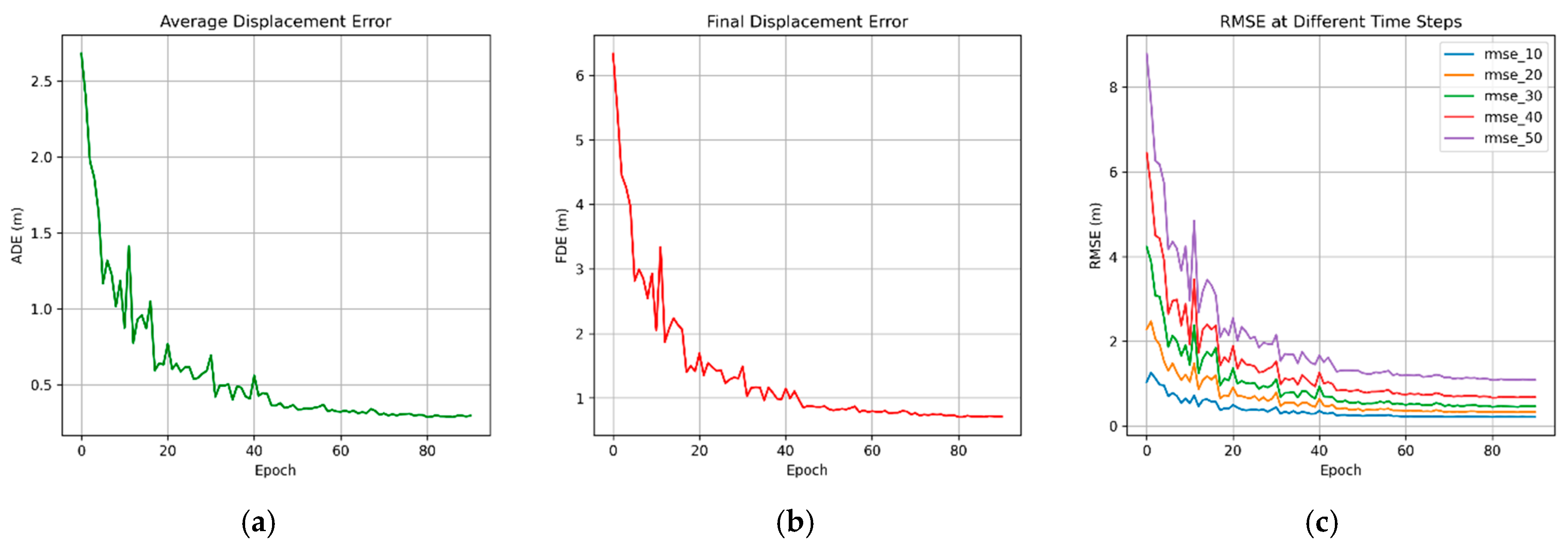
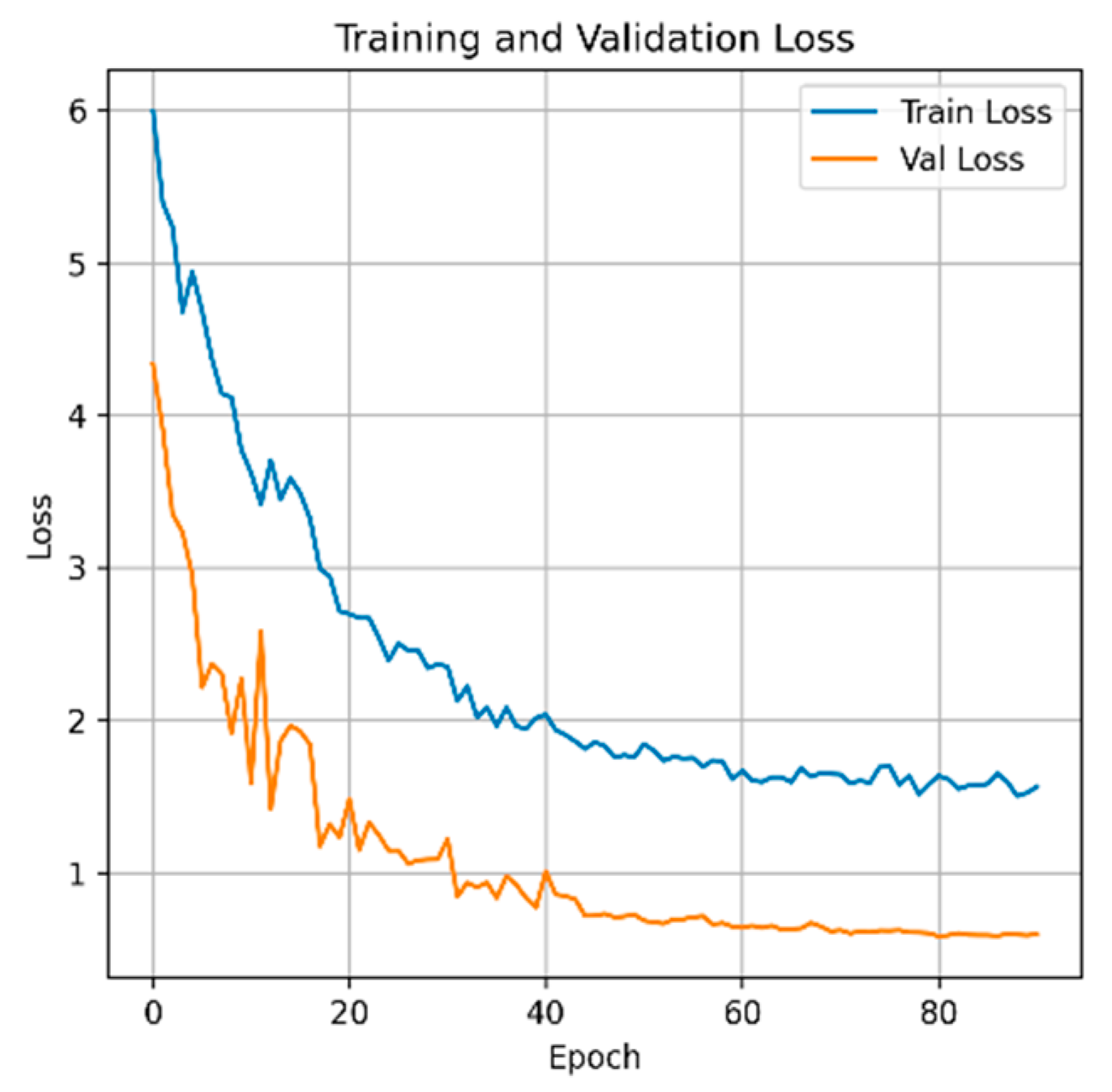
4.2. Evaluation Metrics and Implementation Details
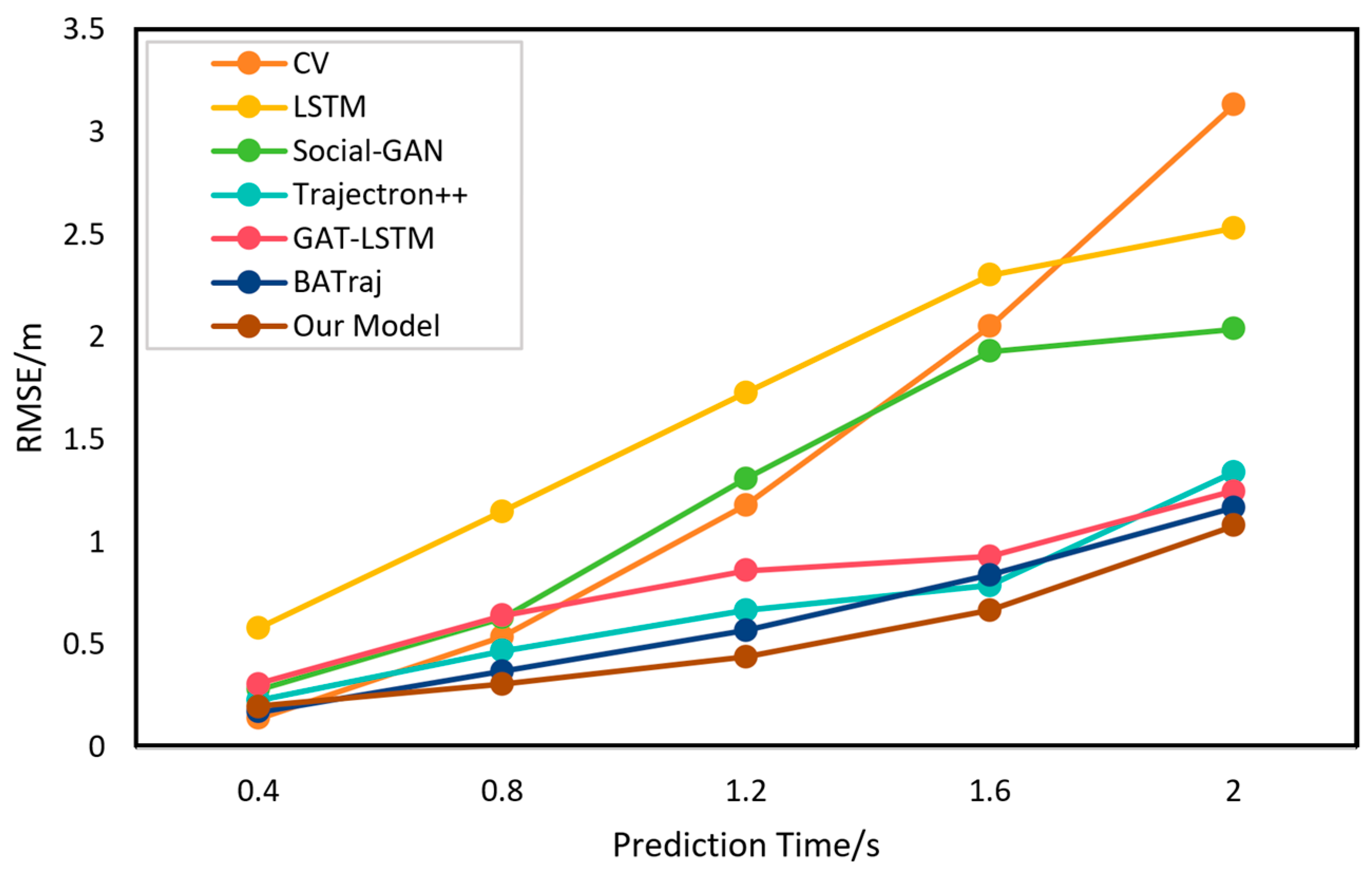
4.3. Model Comparison Experimental Results and Analysis
4.4. Ablation Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Y.; Du, J.; Yang, Z.; Zhou, Z.; Zhang, L.; Chen, H. A survey on trajectory-prediction methods for autonomous driving. IEEE Trans. Intell. Veh. 2022, 7, 652–674. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, J.; Tian, Y.; Ni, Y.; Yu, S. Modeling and simulation of nonmotorized vehicles’ dispersion at mixed flow intersections. J. Adv. Transp. 2019, 2019, 9127062. [Google Scholar] [CrossRef]
- Li, J.; Ni, Y.; Sun, J. A Two-layer integrated model for cyclist trajectory prediction considering multiple interactions with the environment. Transp. Res. Part C Emerg. Technol. 2023, 155, 104304. [Google Scholar] [CrossRef]
- Maurer, L.F.; Meister, A.; Axhausen, K.W. Cycling speed profiles from GPS data: Insights for conventional and electrified bicycles in Switzerland. J. Cycl. Micromobil. Res. 2025, 5, 100077. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Li, J.; Yang, L.; Chen, Y.; Jin, Y. MFAN: Mixing feature attention network for trajectory prediction. Pattern Recognit. 2024, 146, 109997. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, B.; Li, C. A networked multi-agent reinforcement learning approach for cooperative FemtoCaching assisted wireless heterogeneous networks. Comput. Netw. 2023, 220, 109513. [Google Scholar] [CrossRef]
- Leigh, A.; Pineau, J.; Olmedo, N.; Zhang, H. Person tracking and following with 2D laser scanners. In Proceedings of the International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 726–733. [Google Scholar] [CrossRef]
- Schöller, C.; Aravantinos, V.; Lay, F.; Knoll, A. What the constant velocity model can teach us about pedestrian motion prediction. IEEE Robot. Autom. Lett. 2020, 5, 1696–1703. [Google Scholar] [CrossRef]
- Liu, K.; Wang, W.; Gong, J. Dynamic modeling and trajectory tracking of intelligent vehicles in off-road terrain. J. Beijing Inst. Technol. 2019, 39, 933–937. [Google Scholar] [CrossRef]
- Liao, J.H. Research on LiDAR/IMU Integrated Navigation and Positioning Method. Ph.D. Theis, Nanchang University, Nanchang, China, 6 June 2020. [Google Scholar] [CrossRef]
- Lefkopoulos, V.; Menner, M.; Domahidi, A.; Zeilinger, M.N. Interaction-aware motion prediction for autonomous driving: A multiple model Kalman filtering scheme. IEEE Robot. Autom. Lett. 2020, 6, 80–87. [Google Scholar] [CrossRef]
- Li, X.; Rosman, G.; Gilitschenski, I.; Vasile, C.I.; DeCastro, J.A.; Karaman, S.; Rus, D. Vehicle trajectory prediction using generative adversarial network with temporal logic syntax tree features. IEEE Robot. Autom. Lett. 2021, 6, 3459–3466. [Google Scholar] [CrossRef]
- Zhang, S.; Zhi, Y.; He, R.; Li, J. Research on traffic vehicle behavior prediction method based on game theory and HMM. IEEE Access 2020, 8, 30210–30222. [Google Scholar] [CrossRef]
- Huang, L.; Wu, J.; You, F.; Lv, Z.; Song, H. Cyclist social force model at unsignalized intersections with heterogeneous traffic. IEEE Trans. Ind. Inform. 2017, 13, 782–792. [Google Scholar] [CrossRef]
- Yan, Z.; Yue, L.; Sun, J. High-resolution reconstruction of non-motorized trajectory in shared space: A new approach integrating the social force model and particle filtering. Expert Syst. Appl. 2023, 233, 120753. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, J.; Pi, L.; Song, X.; Yang, L. LSTM based trajectory prediction model for cyclist utilizing multiple interactions with environment. Pattern Recognit. 2021, 112, 107800. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Ship trajectory uncertainty prediction based on a Gaussian process model. Ocean Eng. 2019, 182, 499–511. [Google Scholar] [CrossRef]
- Mandalia, H.; Salvucci, D. Using support vector machines for lane-change detection. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Orlando, FL, USA, 26–30 September 2005; Volume 49, pp. 1965–1969. [Google Scholar] [CrossRef]
- He, G.; Li, X.; Lv, Y.; Gao, B.; Chen, H. Probabilistic intention prediction and trajectory generation based on dynamic Bayesian networks. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 2646–2651. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J. Vehicle trajectory prediction model based on graph attention Kolmogorov-Arnold networks and multiple attention. Eng. Appl. Artif. Intell. 2025, 159, 111804. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Dong, Q.; Guo, G. DSTAnet: A trajectory distribution-aware spatio-temporal attention network for vehicle trajectory prediction. IEEE Trans. Veh. Technol. 2025, 74, 10187–10197. [Google Scholar] [CrossRef]
- Pool, E.A.I.; Kooij, J.F.P.; Gavrila, D.M. Context-based cyclist path prediction using recurrent neural networks. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 824–830. [Google Scholar] [CrossRef]
- Scheel, O.; Nagaraja, N.S.; Schwarz, L.; Navab, N.; Tombari, F. Attention-based lane change prediction. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 8655–8661. [Google Scholar] [CrossRef]
- Sun, J.; Qi, X.; Xu, Y.; Tian, Y. Vehicle turning behavior modeling at conflicting areas of mixed-flow intersections based on deep learning. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3674–3685. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, G.; Shi, J.; Xu, B.; Zheng, L. SRAI-LSTM: A social relation attention-based interaction-aware LSTM for human trajectory prediction. Neurocomputing 2022, 490, 258–268. [Google Scholar] [CrossRef]
- Helbing, D.; Molnár, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Li, F.F.; Savarese, S. Social LSTM: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar] [CrossRef]
- Chandra, R.; Bhattacharya, U.; Bera, A.; Manocha, D. TraPHic: Trajectory prediction in dense and heterogeneous traffic using weighted interactions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8483–8492. [Google Scholar] [CrossRef]
- Jia, X.; Wu, P.; Chen, L.; Liu, Y.; Li, H.; Yan, J. HDGT: Heterogeneous driving graph transformer for multi-agent trajectory prediction via scene encoding. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13860–13875. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar] [CrossRef]
- Zhou, Z.; Ye, L.; Wang, J.; Wu, K.; Lu, K. HiVT: Hierarchical vector transformer for multi-agent motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8813–8823. [Google Scholar] [CrossRef]
- Li, Q.; Ou, B.; Liang, Y.; Wang, Y.; Yang, X.; Li, L. TCN-SA: A Social attention network based on temporal convolutional network for vehicle trajectory prediction. J. Adv. Transp. 2023, 2023, 1286977. [Google Scholar] [CrossRef]
- Zhan, T.; Zhang, Q.; Chen, G.; Cheng, J. VRR-Net: Learning vehicle-road relationships for vehicle trajectory prediction on highways. Mathematics 2023, 11, 1293. [Google Scholar] [CrossRef]
- Li, R.; Qin, Y.; Wang, J.; Wang, H. AMGB: Trajectory prediction using attention-based mechanism GCN-BiLSTM in IOV. Pattern Recognit. Lett. 2023, 169, 17–27. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, X.; Jia, Y. Vehicle trajectory prediction based on GAT and LSTM networks in urban environments. Promet-Traffic Transp. 2024, 36, 867–884. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L.; Wang, G.; Yu, J.; Zheng, X.; Mei, Y.; Han, B. A dual-level graph attention network and transformer for enhanced trajectory prediction under road network constraints. Expert Syst. Appl. 2025, 261, 125510. [Google Scholar] [CrossRef]
- Shi, S.; Jiang, L.; Dai, D.; Schiele, B. MTR++: Multi-agent motion prediction with symmetric scene modeling and guided intention querying. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 3955–3971. [Google Scholar] [CrossRef] [PubMed]
- Jo, E.; Sunwoo, M.; Lee, M. Vehicle trajectory prediction using hierarchical graph neural network for considering interaction among multimodal maneuvers. Sensors 2021, 21, 5354. [Google Scholar] [CrossRef] [PubMed]
- Salzmann, T. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 683–700. [Google Scholar] [CrossRef]
- Krajewski, R.; Moers, T.; Bock, J.; Vater, L.; Eckstein, L. The round dataset: A drone dataset of road user trajectories at roundabouts in Germany. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Saleh, K.; Hossny, M.; Nahavandi, S. Cyclist trajectory prediction using bidirectional recurrent neural networks. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Wellington, New Zealand, 11–14 December 2018; Volume 11320, pp. 284–295. [Google Scholar] [CrossRef]
- Gupta, A.; Johnson, J.; Li, F.F.; Savarese, S.; Alahi, A. Social GAN: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2255–2264. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Li, H. LSTM-based graph attention network for vehicle trajectory prediction. Comput. Netw. 2024, 248, 110477. [Google Scholar] [CrossRef]
- Liao, H.; Li, Z.; Shen, H.; Zeng, W.; Liao, D.; Li, G.; Xu, C. BAT: Behavior-aware human-like trajectory prediction for autonomous driving. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2024; Volume 38, pp. 10332–10340. [Google Scholar] [CrossRef]
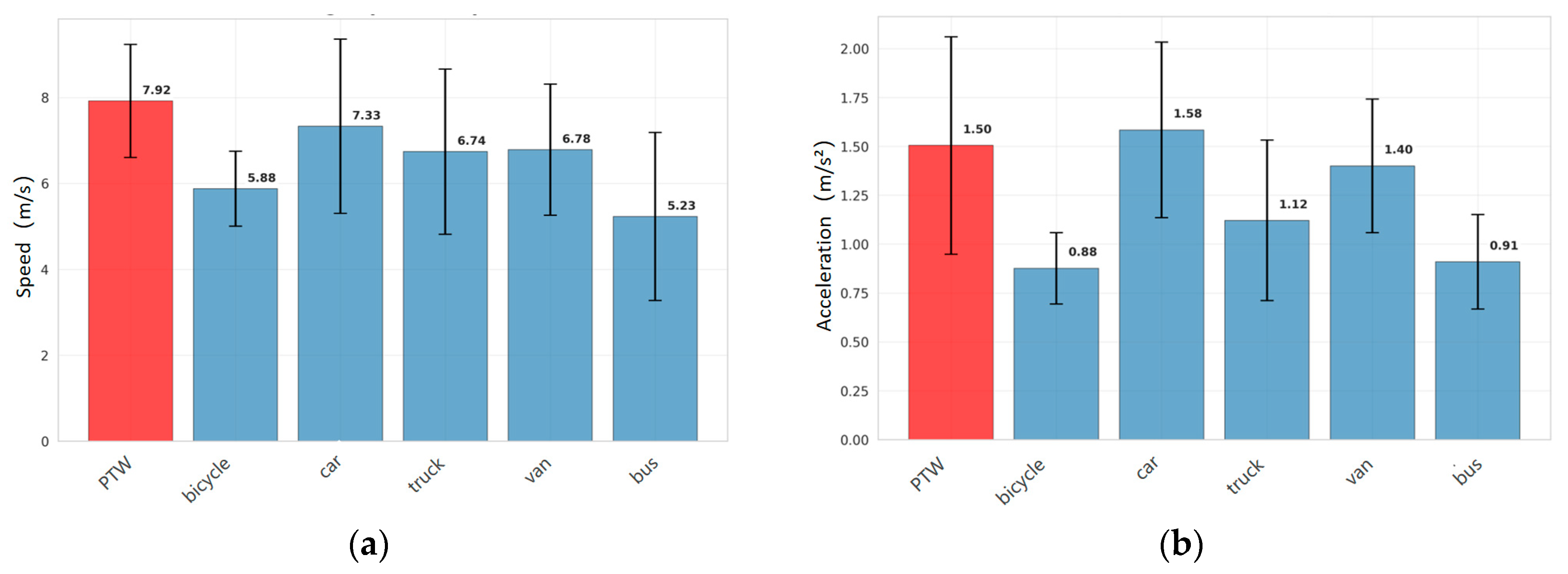
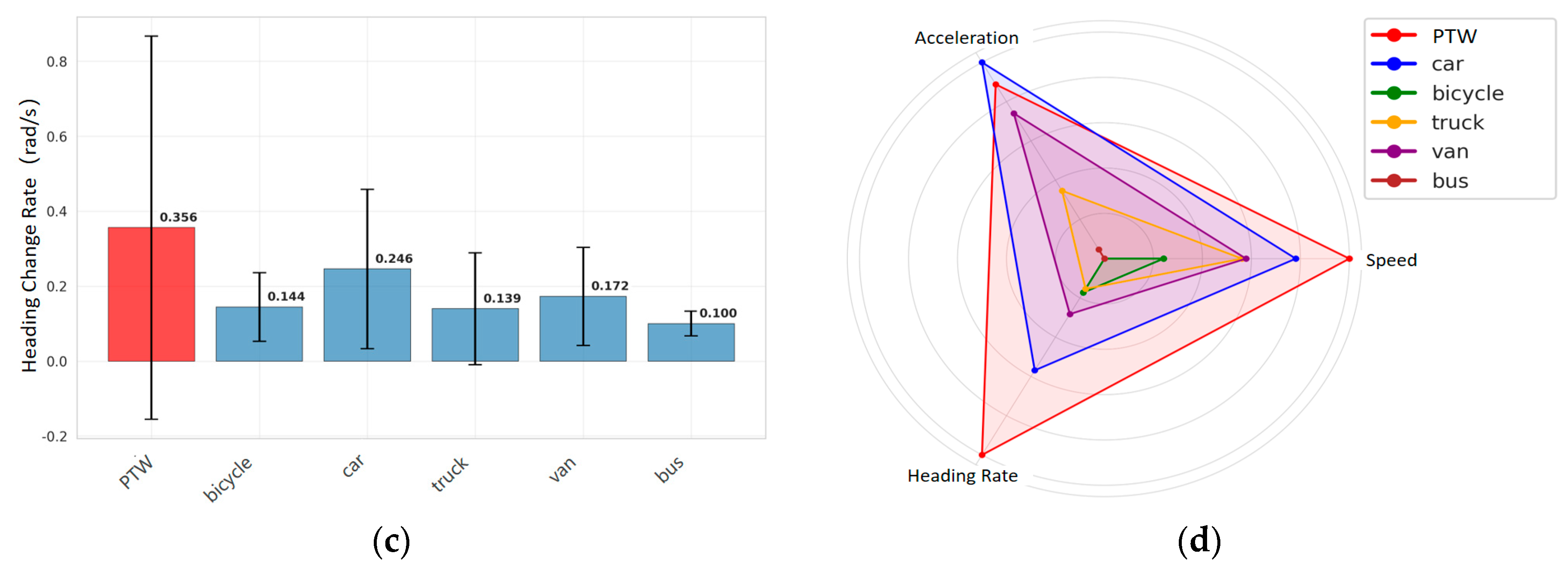
 indicates the data collection location of the rounD dataset)).
indicates the data collection location of the rounD dataset)).
 indicates the data collection location of the rounD dataset)).
indicates the data collection location of the rounD dataset)).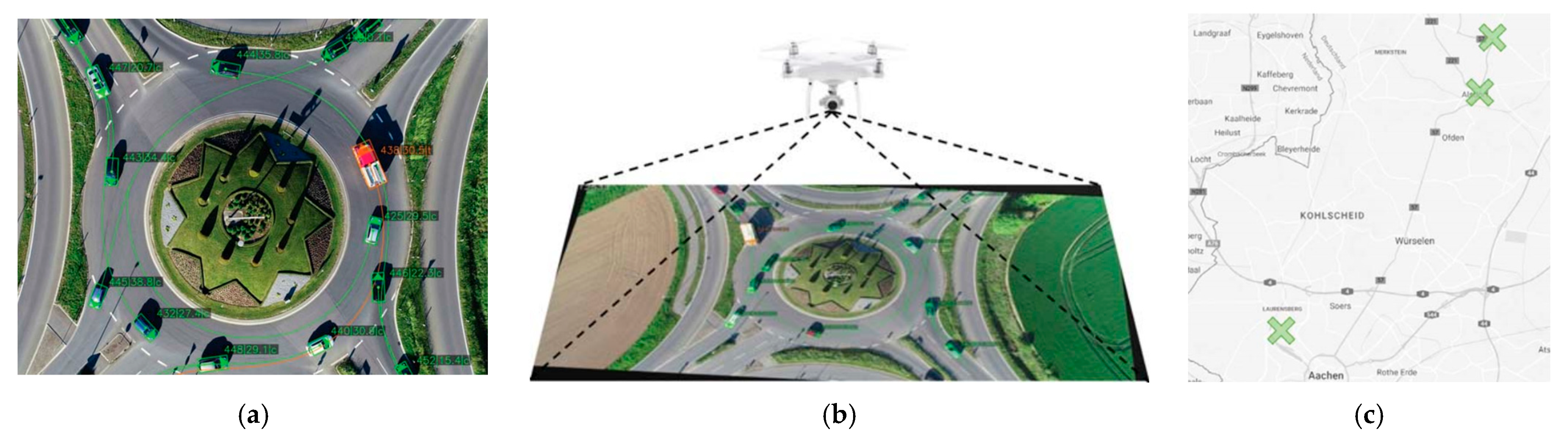
| Variable | Definition |
|---|---|
| The set of historical states of powered two-wheelers (PTWs) in a mixed traffic scenario. . | |
| The set of time steps for trajectory data. . | |
| The total length of historical time steps input to the trajectory prediction model. | |
| powered two-wheelers (PTWs). | |
| Surrounding vehicles, mainly including motor vehicles and bicycles. | |
| The historical state of the PTW at time step input to the model. . | |
| The historical state of surrounding vehicles at time step input to the model. . | |
| The position coordinates of the PTW and surrounding vehicles at time step , including the horizontal and vertical coordinates. Among these, . | |
| The velocity information of the PTW and surrounding vehicles at time step , including the lateral and longitudinal velocities. Among these, . | |
| The acceleration information of the PTW and surrounding vehicles at time step , including the lateral and longitudinal accelerations. Among these, . | |
| The heading angle of the PTW and surrounding vehicles at time step . | |
| The identity codes of the PTW and surrounding vehicles, used for trajectory tracking and organization. | |
| The type identifiers of the PTW and surrounding vehicles, used for categorizing and processing trajectory characteristics of different vehicles in the dataset. Among these, . |
| Models | Evaluation Metrics | ||||||
|---|---|---|---|---|---|---|---|
| RMSE | ADE (m) | FDE (m) | |||||
| 0.4 s | 0.8 s | 1.2 s | 1.6 s | 2.0 s | |||
| CV | 0.14 | 0.54 | 1.18 | 2.05 | 3.13 | 0.78 | 2.23 |
| LSTM | 0.58 | 1.15 | 1.73 | 2.30 | 2.53 | 1.90 | 2.53 |
| Social-GAN | 0.28 | 0.63 | 1.31 | 1.93 | 2.04 | 0.91 | 1.58 |
| Trajectron++ | 0.23 | 0.47 | 0.67 | 0.79 | 1.34 | 0.31 | 0.89 |
| GAT-LSTM | 0.31 | 0.64 | 0.86 | 0.93 | 1.25 | 0.37 | 0.76 |
| BATraj | 0.17 | 0.37 | 0.57 | 0.84 | 1.17 | 0.59 | 0.67 |
| Our Model | 0.20 | 0.31 | 0.44 | 0.67 | 1.08 | 0.28 | 0.70 |
| Modules | Evaluation Metrics | ||||
|---|---|---|---|---|---|
| Time Attention Layer | GAT Interaction Layer | Feature Fusion | Position Correction | ADE (m) | FDE (m) |
| × | √ | √ | √ | 0.36 | 0.83 |
| √ | × | √ | √ | 0.53 | 0.95 |
| √ | √ | × | √ | 0.45 | 0.86 |
| √ | √ | √ | × | 0.48 | 0.88 |
| × | × | √ | √ | 0.65 | 1.23 |
| √ | √ | × | × | 0.39 | 0.98 |
| √ | √ | √ | √ | 0.28 | 0.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Chen, F.; Li, J.; Wang, H.; Li, Y.; Zhai, Z. Trajectory Prediction for Powered Two-Wheelers in Mixed Traffic Scenes: An Enhanced Social-GAT Approach. Systems 2025, 13, 1036. https://doi.org/10.3390/systems13111036
Zeng L, Chen F, Li J, Wang H, Li Y, Zhai Z. Trajectory Prediction for Powered Two-Wheelers in Mixed Traffic Scenes: An Enhanced Social-GAT Approach. Systems. 2025; 13(11):1036. https://doi.org/10.3390/systems13111036
Chicago/Turabian StyleZeng, Longxin, Fujian Chen, Jiangfeng Li, Haiquan Wang, Yujie Li, and Zhongyi Zhai. 2025. "Trajectory Prediction for Powered Two-Wheelers in Mixed Traffic Scenes: An Enhanced Social-GAT Approach" Systems 13, no. 11: 1036. https://doi.org/10.3390/systems13111036
APA StyleZeng, L., Chen, F., Li, J., Wang, H., Li, Y., & Zhai, Z. (2025). Trajectory Prediction for Powered Two-Wheelers in Mixed Traffic Scenes: An Enhanced Social-GAT Approach. Systems, 13(11), 1036. https://doi.org/10.3390/systems13111036





