Hybrid Supply Chain Model for Wheat Market
Abstract
1. Introduction
- We propose a hybrid model that combines a graph transformer and recurrent network architectures to tackle the problems above. This model utilizes the transformer to catch the interdependence between wheat export quantities in different countries. As a recurrent network, the proposed model also generates hidden embeddings for each country and export direction and utilizes these embeddings from the previous step to forecast exports. This way, the model summarizes the trading history via the hidden embeddings and uses them to perform accurate export predictions.
- We show how the proposed model can be applied to implement if–then scenarios in a multi-agent-like setting.
2. Related Work
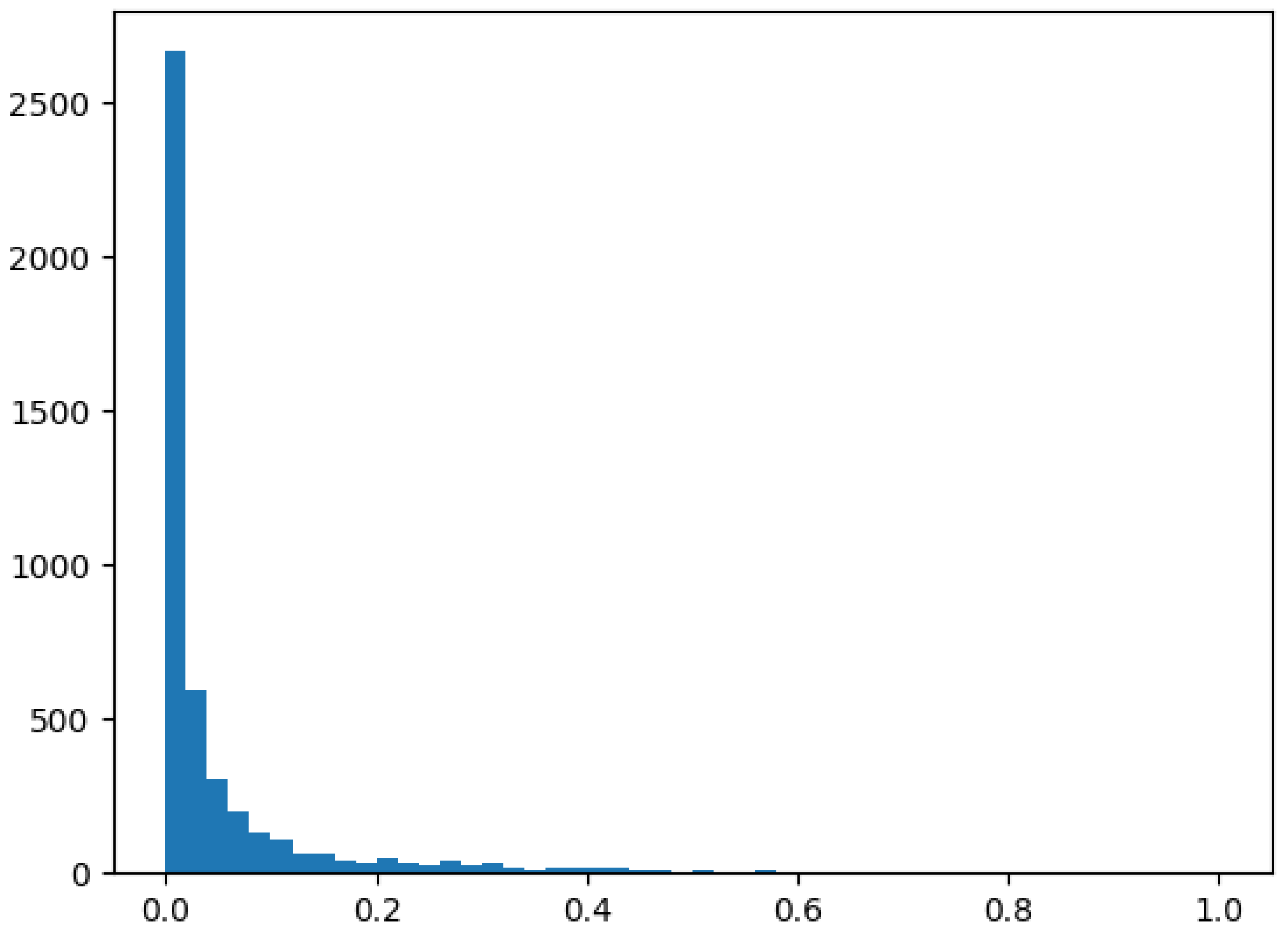
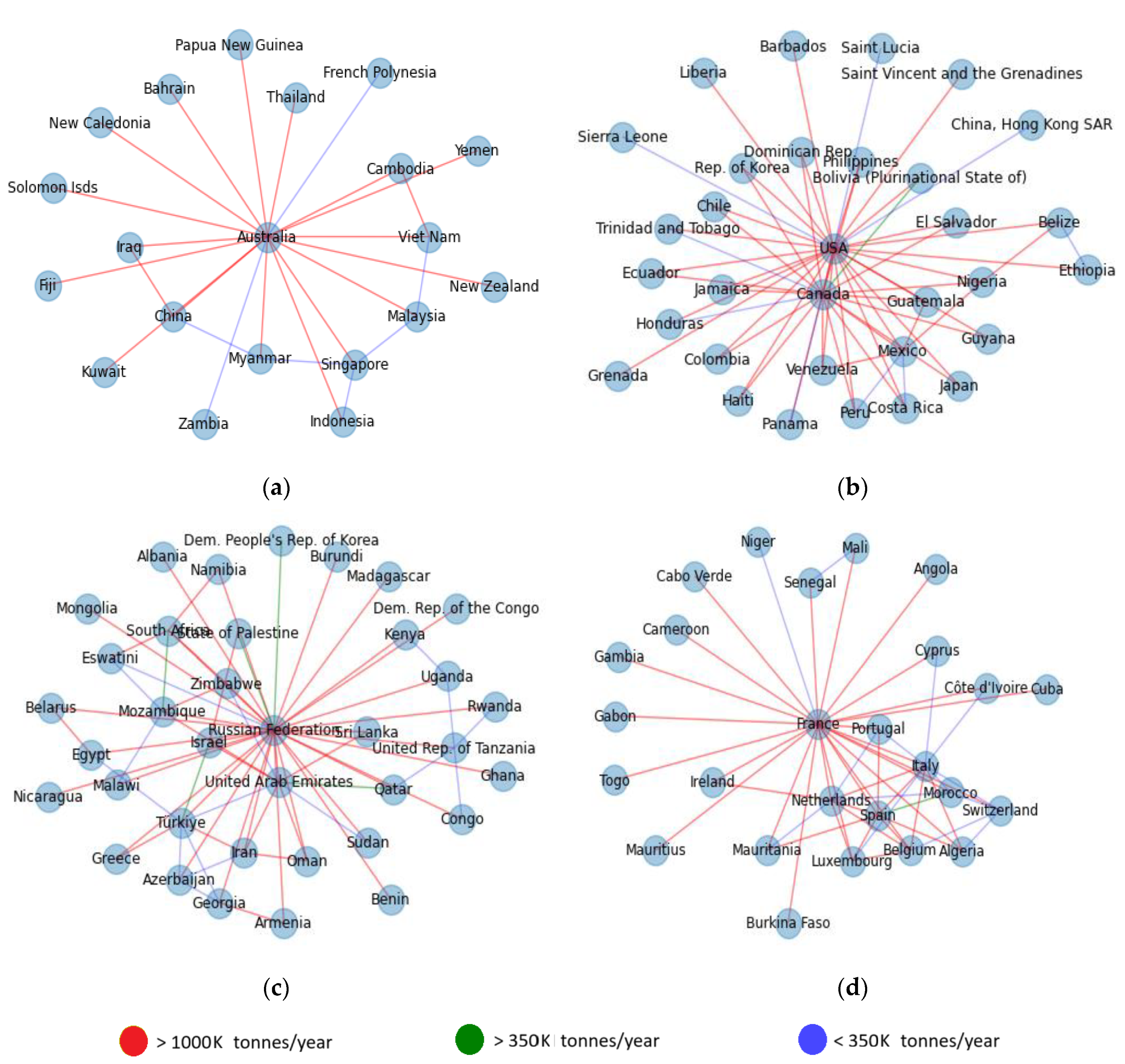
3. Dataset
4. Forecast Models
4.1. Baseline Regression Models
4.2. Recurrent Graph Transformer Model
4.3. Recurrent Graph Transformer Encoder–Decoder Model
5. Experiment Results
- Forecast of wheat grain exports without any limitations.
- Forecast of wheat grain exports, providing the limitation on the sale of grain to one of the importers.
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Model | Imputation | Loss | MSE, ×1017, kg2 | MAE, ×108, kg | MAPEall | MAPElarge | R2 |
|---|---|---|---|---|---|---|---|
| TKAN | Forward fill | BCE | 1.38 ± 0.40 | 1.73 ± 0.58 | 41.80 ± 71.80 | 0.35 ± 0.09 | 0.76 ± 0.11 |
| TKAN | Forward fill | MSE(logit) | 3.41 ± 3.02 | 2.14 ± 1.10 | 6.47 ± 9.36 | 0.43 ± 0.23 | 0.58 ± 0.36 |
| LSTM | Forward fill | BCE | 1.76 ± 0.18 | 1.57 ± 0.06 | 10.28 ± 3.54 | 0.36 ± 0.02 | 0.73 ± 0.07 |
| LSTM | Forward fill | MSE(logit) | 1.97 ± 0.24 | 1.76 ± 0.17 | 2.56 ± 0.14 | 0.40 ± 0.03 | 0.74 ± 0.03 |
| GRU | Forward fill | BCE | 1.57 ± 0.57 | 1.53 ± 0.18 | 13.88 ± 7.52 | 0.33 ± 0.02 | 0.77 ± 0.04 |
| GRU | Forward fill | MSE(logit) | 2.33 ± 0.71 | 1.85 ± 0.24 | 2.64 ± 0.72 | 0.46 ± 0.02 | 0.65 ± 0.04 |
| TKAN | Interpolation | BCE | 1.61 ± 0.47 | 1.60 ± 0.16 | 7.06 ± 2.53 | 0.33 ± 0.02 | 0.78 ± 0.05 |
| TKAN | Interpolation | MSE(logit) | 1.85 ± 0.53 | 1.53 ± 0.19 | 2.28 ± 0.66 | 0.31 ± 0.02 | 0.74 ± 0.05 |
| LSTM | Interpolation | BCE | 1.37 ± 0.34 | 1.52 ± 0.15 | 5.97 ± 3.47 | 0.32 ± 0.02 | 0.80 ± 0.03 |
| LSTM | Interpolation | MSE(logit) | 2.31 ± 0.55 | 1.87 ± 0.19 | 3.02 ± 1.31 | 0.43 ± 0.06 | 0.67 ± 0.09 |
| GRU | Interpolation | BCE | 1.53 ± 0.45 | 1.53 ± 0.15 | 11.34 ± 5.31 | 0.33 ± 0.03 | 0.78 ± 0.05 |
| GRU | Interpolation | MSE(logit) | 2.54 ± 1.03 | 1.93 ± 0.32 | 3.19 ± 1.71 | 0.48 ± 0.08 | 0.65 ± 0.11 |
| TKAN | Model-based | BCE | 1.71 ± 0.29 | 1.60 ± 0.13 | 7.91 ± 2.32 | 0.33 ± 0.01 | 0.77 ± 0.04 |
| TKAN | Model-based | MSE(logit) | 3.23 ± 2.09 | 2.12 ± 0.93 | 10.59 ± 16.22 | 0.44 ± 0.21 | 0.52 ± 0.33 |
| LSTM | Model-based | BCE | 1.23 ± 0.39 | 1.54 ± 0.20 | 13.67 ± 6.05 | 0.34 ± 0.03 | 0.80 ± 0.03 |
| LSTM | Model-based | MSE(logit) | 2.48 ± 0.42 | 2.01 ± 0.16 | 2.29 ± 0.92 | 0.51 ± 0.03 | 0.64 ± 0.04 |
| GRU | Model-based | BCE | 1.94 ± 0.22 | 1.79 ± 0.12 | 13.39 ± 3.22 | 0.35 ± 0.02 | 0.76 ± 0.02 |
| GRU | Model-based | MSE(logit) | 2.14 ± 0.48 | 1.80 ± 0.21 | 3.27 ± 0.93 | 0.46 ± 0.10 | 0.70 ± 0.06 |
| TKAN | ARIMA | BCE | 1.47 ± 0.35 | 1.52 ± 0.13 | 5.55 ± 2.71 | 0.32 ± 0.02 | 0.79 ± 0.03 |
| TKAN | ARIMA | MSE(logit) | 2.32 ± 1.88 | 1.70 ± 0.76 | 3.58 ± 5.64 | 0.35 ± 0.12 | 0.68 ± 0.21 |
| LSTM | ARIMA | BCE | 1.39 ± 0.38 | 1.49 ± 0.13 | 7.61 ± 4.22 | 0.33 ± 0.03 | 0.79 ± 0.06 |
| LSTM | ARIMA | MSE(logit) | 2.67 ± 0.64 | 1.99 ± 0.24 | 2.66 ± 1.08 | 0.47 ± 0.05 | 0.63 ± 0.06 |
| GRU | ARIMA | BCE | 1.53 ± 0.41 | 1.58 ± 0.18 | 10.17 ± 3.56 | 0.34 ± 0.03 | 0.77 ± 0.05 |
| GRU | ARIMA | MSE(logit) | 2.50 ± 0.57 | 1.89 ± 0.20 | 2.63 ± 0.98 | 0.46 ± 0.05 | 0.65 ± 0.06 |
| Imputation | Loss | Layers | Attn. Heads | FFT | Recurrent Embeddings | MSE, ×1017, kg2 | MAE, ×108, kg | MAPEall | MAPElarge | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Forward fill | MSE(logit) | 1 | 1 | + | + | 1.60 ± 0.37 | 1.48 ± 0.18 | 1.03 ± 0.13 | 0.34 ± 0.08 | 0.74 ± 0.08 |
| Forward fill | BCE | 1 | 1 | + | + | 1.03 ± 0.46 | 1.28 ± 0.22 | 12.94 ± 5.73 | 0.30 ± 0.05 | 0.84 ± 0.06 |
| Forward fill | MSE(logit) | 1 | 1 | + | - | 6.68 ± 1.46 | 3.61 ± 0.40 | 3.40 ± 1.22 | 0.69 ± 0.08 | 0.15 ± 0.13 |
| Forward fill | BCE | 1 | 1 | + | - | 6.01 ± 2.07 | 4.41 ± 0.42 | 93.55 ± 97.00 | 0.59 ± 0.07 | 0.20 ± 0.15 |
| Forward fill | MSE(logit) | 1 | 2 | + | + | 2.18 ± 0.62 | 1.73 ± 0.24 | 1.04 ± 0.18 | 0.38 ± 0.05 | 0.69 ± 0.08 |
| Forward fill | BCE | 1 | 2 | + | + | 1.01 ± 0.40 | 1.32 ± 0.15 | 13.37 ± 12.45 | 0.28 ± 0.02 | 0.86 ± 0.04 |
| Forward fill | MSE(logit) | 1 | 2 | + | - | 6.22 ± 1.83 | 3.50 ± 0.55 | 3.92 ± 1.41 | 0.70 ± 0.07 | 0.25 ± 0.13 |
| Forward fill | BCE | 1 | 2 | + | - | 7.66 ± 1.28 | 5.22 ± 0.13 | 158.10 ± 65.71 | 0.52 ± 0.05 | −0.02 ± 0.02 |
| Forward fill | MSE(logit) | 1 | 4 | + | + | 2.63 ± 1.00 | 1.70 ± 0.50 | 1.21 ± 0.26 | 0.44 ± 0.05 | 0.57 ± 0.10 |
| Forward fill | BCE | 1 | 4 | + | + | 0.79 ± 0.39 | 1.13 ± 0.26 | 6.32 ± 3.95 | 0.25 ± 0.05 | 0.88 ± 0.05 |
| Forward fill | MSE(logit) | 1 | 4 | + | - | 5.97 ± 1.61 | 3.31 ± 0.49 | 5.69 ± 2.05 | 0.71 ± 0.09 | 0.15 ± 0.16 |
| Forward fill | BCE | 1 | 4 | + | - | 5.33 ± 1.59 | 4.18 ± 0.48 | 82.81 ± 75.30 | 0.57 ± 0.07 | 0.26 ± 0.14 |
| Forward fill | MSE(logit) | 2 | 1 | + | + | 2.71 ± 1.11 | 1.69 ± 0.41 | 1.11 ± 0.18 | 0.37 ± 0.03 | 0.59 ± 0.12 |
| Forward fill | BCE | 2 | 1 | + | + | 1.25 ± 0.45 | 1.33 ± 0.32 | 8.34 ± 6.38 | 0.30 ± 0.03 | 0.82 ± 0.02 |
| Forward fill | MSE(logit) | 2 | 1 | + | - | 5.43 ± 1.59 | 3.20 ± 0.38 | 4.32 ± 1.71 | 0.67 ± 0.04 | 0.31 ± 0.15 |
| Forward fill | BCE | 2 | 1 | + | - | 6.53 ± 1.98 | 4.12 ± 0.54 | 84.29 ± 110.03 | 0.59 ± 0.07 | 0.24 ± 0.14 |
| Forward fill | MSE(logit) | 2 | 2 | + | + | 2.11 ± 1.13 | 1.69 ± 0.57 | 1.17 ± 0.32 | 0.37 ± 0.08 | 0.69 ± 0.21 |
| Forward fill | BCE | 2 | 2 | + | + | 1.83 ± 0.57 | 1.69 ± 0.23 | 8.14 ± 2.85 | 0.32 ± 0.04 | 0.76 ± 0.06 |
| Forward fill | MSE(logit) | 2 | 2 | + | - | 6.84 ± 3.34 | 3.54 ± 0.80 | 4.81 ± 2.68 | 0.68 ± 0.07 | 0.20 ± 0.14 |
| Forward fill | BCE | 2 | 2 | + | - | 5.17 ± 1.32 | 3.59 ± 0.68 | 102.70 ± 88.77 | 0.60 ± 0.02 | 0.25 ± 0.19 |
| Forward fill | MSE(logit) | 2 | 4 | + | + | 1.54 ± 0.86 | 1.43 ± 0.26 | 0.87 ± 0.06 | 0.32 ± 0.03 | 0.79 ± 0.12 |
| Forward fill | BCE | 2 | 4 | + | + | 0.84 ± 0.32 | 1.15 ± 0.21 | 6.48 ± 2.33 | 0.27 ± 0.05 | 0.86 ± 0.04 |
| Forward fill | MSE(logit) | 2 | 4 | + | - | 4.70 ± 1.50 | 2.81 ± 0.53 | 4.81 ± 1.39 | 0.67 ± 0.05 | 0.23 ± 0.12 |
| Forward fill | BCE | 2 | 4 | + | - | 6.13 ± 1.59 | 3.81 ± 0.56 | 47.83 ± 25.29 | 0.63 ± 0.05 | 0.11 ± 0.07 |
| Forward fill | MSE(logit) | 3 | 1 | + | + | 2.30 ± 0.79 | 1.68 ± 0.31 | 1.07 ± 0.08 | 0.34 ± 0.04 | 0.70 ± 0.05 |
| Forward fill | BCE | 3 | 1 | + | + | 1.90 ± 0.64 | 1.62 ± 0.29 | 5.52 ± 3.09 | 0.32 ± 0.02 | 0.78 ± 0.04 |
| Forward fill | MSE(logit) | 3 | 1 | + | - | 5.10 ± 0.47 | 3.09 ± 0.34 | 4.33 ± 1.30 | 0.67 ± 0.11 | 0.35 ± 0.02 |
| Forward fill | BCE | 3 | 1 | + | - | 5.15 ± 1.20 | 3.57 ± 0.51 | 29.56 ± 9.89 | 0.61 ± 0.07 | 0.26 ± 0.12 |
| Forward fill | MSE(logit) | 3 | 2 | + | + | 2.82 ± 0.47 | 1.75 ± 0.26 | 1.14 ± 0.31 | 0.38 ± 0.05 | 0.57 ± 0.05 |
| Forward fill | BCE | 3 | 2 | + | + | 0.95 ± 0.36 | 1.13 ± 0.20 | 6.73 ± 2.38 | 0.28 ± 0.05 | 0.85 ± 0.06 |
| Forward fill | MSE(logit) | 3 | 2 | + | - | 4.35 ± 0.63 | 2.98 ± 0.32 | 3.24 ± 0.71 | 0.66 ± 0.08 | 0.40 ± 0.05 |
| Forward fill | BCE | 3 | 2 | + | - | 4.45 ± 0.76 | 3.24 ± 0.19 | 28.82 ± 6.16 | 0.60 ± 0.06 | 0.29 ± 0.10 |
| Forward fill | MSE(logit) | 3 | 4 | + | + | 1.61 ± 0.99 | 1.48 ± 0.35 | 0.98 ± 0.15 | 0.31 ± 0.07 | 0.78 ± 0.14 |
| Forward fill | BCE | 3 | 4 | + | + | 1.55 ± 0.68 | 1.41 ± 0.36 | 12.02 ± 8.30 | 0.36 ± 0.12 | 0.77 ± 0.09 |
| Forward fill | MSE(logit) | 3 | 4 | + | - | 4.93 ± 1.37 | 3.19 ± 0.55 | 3.91 ± 1.08 | 0.67 ± 0.09 | 0.31 ± 0.09 |
| Forward fill | BCE | 3 | 4 | + | - | 6.69 ± 0.78 | 4.12 ± 0.28 | 40.27 ± 22.37 | 0.60 ± 0.06 | 0.11 ± 0.12 |
| Forward fill | MSE(logit) | 4 | 1 | + | + | 1.36 ± 0.42 | 1.35 ± 0.23 | 0.90 ± 0.05 | 0.33 ± 0.02 | 0.77 ± 0.06 |
| Forward fill | BCE | 4 | 1 | + | + | 1.15 ± 0.46 | 1.38 ± 0.29 | 5.12 ± 2.22 | 0.29 ± 0.03 | 0.85 ± 0.04 |
| Forward fill | MSE(logit) | 4 | 1 | + | - | 5.16 ± 1.71 | 3.24 ± 0.55 | 10.54 ± 11.46 | 0.62 ± 0.04 | 0.24 ± 0.06 |
| Forward fill | BCE | 4 | 1 | + | - | 3.78 ± 1.04 | 3.06 ± 0.46 | 27.06 ± 10.96 | 0.57 ± 0.05 | 0.37 ± 0.04 |
| Forward fill | MSE(logit) | 4 | 2 | + | + | 2.82 ± 0.97 | 1.68 ± 0.23 | 1.17 ± 0.10 | 0.35 ± 0.05 | 0.62 ± 0.09 |
| Forward fill | BCE | 4 | 2 | + | + | 1.03 ± 0.21 | 1.33 ± 0.14 | 7.41 ± 1.35 | 0.30 ± 0.02 | 0.84 ± 0.03 |
| Forward fill | MSE(logit) | 4 | 2 | + | - | 5.10 ± 1.73 | 2.94 ± 0.47 | 9.61 ± 6.62 | 0.66 ± 0.06 | 0.28 ± 0.18 |
| Forward fill | BCE | 4 | 2 | + | - | 5.52 ± 1.25 | 3.71 ± 0.45 | 46.39 ± 31.38 | 0.62 ± 0.07 | 0.20 ± 0.12 |
| Forward fill | MSE(logit) | 4 | 4 | + | + | 112.40 ± 3.00 | 32.89 ± 0.56 | 467.51 ± 67.11 | 3.38 ± 0.12 | −17.69 ± 4.11 |
| Forward fill | BCE | 4 | 4 | + | + | 1.96 ± 1.54 | 1.95 ± 1.06 | 19.35 ± 32.26 | 0.32 ± 0.12 | 0.71 ± 0.29 |
| Forward fill | MSE(logit) | 4 | 4 | + | - | 4.95 ± 1.32 | 3.01 ± 0.44 | 4.65 ± 1.97 | 0.66 ± 0.05 | 0.34 ± 0.06 |
| Forward fill | BCE | 4 | 4 | + | - | 5.52 ± 1.43 | 3.69 ± 0.44 | 37.92 ± 33.77 | 0.65 ± 0.10 | 0.25 ± 0.15 |
| Interpolation | MSE(logit) | 1 | 1 | + | + | 1.71 ± 0.64 | 1.51 ± 0.24 | 0.96 ± 0.13 | 0.33 ± 0.01 | 0.75 ± 0.11 |
| Interpolation | BCE | 1 | 1 | + | + | 1.27 ± 0.41 | 1.46 ± 0.30 | 13.12 ± 11.63 | 0.30 ± 0.03 | 0.84 ± 0.03 |
| Interpolation | MSE(logit) | 1 | 1 | + | - | 5.42 ± 1.41 | 3.09 ± 0.53 | 3.56 ± 0.47 | 0.65 ± 0.09 | 0.26 ± 0.15 |
| Interpolation | BCE | 1 | 1 | + | - | 6.69 ± 2.37 | 4.42 ± 0.82 | 55.59 ± 29.87 | 0.53 ± 0.04 | 0.18 ± 0.16 |
| Interpolation | MSE(logit) | 1 | 2 | + | + | 3.91 ± 1.35 | 2.17 ± 0.45 | 1.23 ± 0.21 | 0.38 ± 0.05 | 0.52 ± 0.15 |
| Interpolation | BCE | 1 | 2 | + | + | 1.07 ± 0.40 | 1.34 ± 0.23 | 9.12 ± 7.63 | 0.29 ± 0.05 | 0.85 ± 0.05 |
| Interpolation | MSE(logit) | 1 | 2 | + | - | 4.91 ± 1.22 | 3.08 ± 0.40 | 4.63 ± 2.56 | 0.68 ± 0.12 | 0.19 ± 0.11 |
| Interpolation | BCE | 1 | 2 | + | - | 5.82 ± 1.61 | 4.50 ± 0.40 | 73.48 ± 19.07 | 0.52 ± 0.04 | 0.12 ± 0.06 |
| Interpolation | MSE(logit) | 1 | 4 | + | + | 2.46 ± 0.48 | 1.68 ± 0.16 | 1.11 ± 0.06 | 0.38 ± 0.04 | 0.63 ± 0.04 |
| Interpolation | BCE | 1 | 4 | + | + | 1.12 ± 0.39 | 1.21 ± 0.22 | 10.15 ± 4.52 | 0.32 ± 0.04 | 0.81 ± 0.04 |
| Interpolation | MSE(logit) | 1 | 4 | + | - | 5.97 ± 0.90 | 3.14 ± 0.22 | 2.89 ± 1.02 | 0.66 ± 0.08 | 0.21 ± 0.13 |
| Interpolation | BCE | 1 | 4 | + | - | 7.18 ± 1.20 | 5.10 ± 0.28 | 157.29 ± 71.37 | 0.51 ± 0.01 | −0.00 ± 0.00 |
| Interpolation | MSE(logit) | 2 | 1 | + | + | 3.66 ± 1.14 | 2.11 ± 0.40 | 1.07 ± 0.11 | 0.39 ± 0.05 | 0.58 ± 0.08 |
| Interpolation | BCE | 2 | 1 | + | + | 1.21 ± 0.42 | 1.33 ± 0.29 | 7.55 ± 4.62 | 0.29 ± 0.03 | 0.82 ± 0.05 |
| Interpolation | MSE(logit) | 2 | 1 | + | - | 4.38 ± 1.04 | 2.89 ± 0.45 | 3.34 ± 0.71 | 0.62 ± 0.03 | 0.35 ± 0.07 |
| Interpolation | BCE | 2 | 1 | + | - | 4.22 ± 0.87 | 3.25 ± 0.59 | 24.27 ± 7.63 | 0.61 ± 0.08 | 0.31 ± 0.13 |
| Interpolation | MSE(logit) | 2 | 2 | + | + | 2.22 ± 1.08 | 1.59 ± 0.23 | 1.11 ± 0.11 | 0.34 ± 0.03 | 0.68 ± 0.16 |
| Interpolation | BCE | 2 | 2 | + | + | 1.20 ± 0.46 | 1.30 ± 0.25 | 3.81 ± 1.56 | 0.30 ± 0.05 | 0.83 ± 0.04 |
| Interpolation | MSE(logit) | 2 | 2 | + | - | 4.32 ± 1.44 | 2.90 ± 0.49 | 3.14 ± 0.73 | 0.60 ± 0.08 | 0.36 ± 0.09 |
| Interpolation | BCE | 2 | 2 | + | - | 4.37 ± 1.40 | 3.44 ± 0.47 | 31.59 ± 17.69 | 0.57 ± 0.03 | 0.35 ± 0.10 |
| Interpolation | MSE(logit) | 2 | 4 | + | + | 2.16 ± 0.90 | 1.56 ± 0.23 | 1.23 ± 0.13 | 0.37 ± 0.02 | 0.68 ± 0.13 |
| Interpolation | BCE | 2 | 4 | + | + | 1.43 ± 0.28 | 1.41 ± 0.06 | 5.24 ± 1.38 | 0.32 ± 0.02 | 0.81 ± 0.03 |
| Interpolation | MSE(logit) | 2 | 4 | + | - | 6.45 ± 1.49 | 3.46 ± 0.49 | 6.82 ± 2.65 | 0.81 ± 0.12 | 0.03 ± 0.23 |
| Interpolation | BCE | 2 | 4 | + | - | 4.20 ± 1.03 | 2.97 ± 0.46 | 25.45 ± 6.85 | 0.73 ± 0.09 | 0.32 ± 0.07 |
| Interpolation | MSE(logit) | 3 | 1 | + | + | 1.76 ± 0.89 | 1.53 ± 0.38 | 1.21 ± 0.34 | 0.36 ± 0.08 | 0.76 ± 0.07 |
| Interpolation | BCE | 3 | 1 | + | + | 0.91 ± 0.34 | 1.20 ± 0.16 | 3.97 ± 2.88 | 0.28 ± 0.03 | 0.86 ± 0.05 |
| Interpolation | MSE(logit) | 3 | 1 | + | - | 5.19 ± 0.95 | 3.03 ± 0.28 | 4.63 ± 1.72 | 0.68 ± 0.07 | 0.23 ± 0.14 |
| Interpolation | BCE | 3 | 1 | + | - | 4.80 ± 0.54 | 3.55 ± 0.23 | 50.16 ± 47.81 | 0.66 ± 0.05 | 0.25 ± 0.11 |
| Interpolation | MSE(logit) | 3 | 2 | + | + | 3.48 ± 1.64 | 2.02 ± 0.48 | 1.21 ± 0.08 | 0.39 ± 0.07 | 0.51 ± 0.20 |
| Interpolation | BCE | 3 | 2 | + | + | 0.94 ± 0.25 | 1.23 ± 0.14 | 7.29 ± 2.85 | 0.25 ± 0.01 | 0.87 ± 0.02 |
| Interpolation | MSE(logit) | 3 | 2 | + | - | 4.56 ± 1.10 | 2.92 ± 0.51 | 4.54 ± 2.57 | 0.65 ± 0.07 | 0.33 ± 0.13 |
| Interpolation | BCE | 3 | 2 | + | - | 5.80 ± 1.20 | 4.05 ± 0.45 | 35.55 ± 22.95 | 0.60 ± 0.05 | 0.25 ± 0.12 |
| Interpolation | MSE(logit) | 3 | 4 | + | + | 2.33 ± 0.79 | 1.68 ± 0.32 | 1.07 ± 0.18 | 0.32 ± 0.03 | 0.70 ± 0.04 |
| Interpolation | BCE | 3 | 4 | + | + | 0.91 ± 0.36 | 1.17 ± 0.23 | 4.46 ± 1.36 | 0.27 ± 0.03 | 0.87 ± 0.03 |
| Interpolation | MSE(logit) | 3 | 4 | + | - | 4.59 ± 1.38 | 2.98 ± 0.54 | 4.19 ± 1.45 | 0.65 ± 0.09 | 0.30 ± 0.08 |
| Interpolation | BCE | 3 | 4 | + | - | 5.80 ± 1.71 | 3.74 ± 0.82 | 55.00 ± 22.26 | 0.59 ± 0.07 | 0.19 ± 0.15 |
| Interpolation | MSE(logit) | 4 | 1 | + | + | 8.08 ± 2.56 | 3.98 ± 0.95 | 9.69 ± 2.58 | 0.89 ± 0.01 | −0.17 ± 0.06 |
| Interpolation | BCE | 4 | 1 | + | + | 0.91 ± 0.46 | 1.20 ± 0.24 | 4.20 ± 1.19 | 0.26 ± 0.04 | 0.87 ± 0.05 |
| Interpolation | MSE(logit) | 4 | 1 | + | - | 7.08 ± 2.78 | 3.75 ± 0.90 | 6.25 ± 2.09 | 0.81 ± 0.15 | 0.02 ± 0.28 |
| Interpolation | BCE | 4 | 1 | + | - | 5.93 ± 2.15 | 3.58 ± 0.78 | 37.12 ± 21.17 | 0.66 ± 0.05 | 0.25 ± 0.13 |
| Interpolation | MSE(logit) | 4 | 2 | + | + | 2.89 ± 0.89 | 1.83 ± 0.24 | 0.97 ± 0.07 | 0.36 ± 0.04 | 0.63 ± 0.11 |
| Interpolation | BCE | 4 | 2 | + | + | 1.03 ± 0.45 | 1.26 ± 0.25 | 6.66 ± 2.96 | 0.31 ± 0.05 | 0.85 ± 0.03 |
| Interpolation | MSE(logit) | 4 | 2 | + | - | 5.65 ± 1.66 | 3.22 ± 0.60 | 5.64 ± 2.72 | 0.67 ± 0.08 | 0.27 ± 0.07 |
| Interpolation | BCE | 4 | 2 | + | - | 6.04 ± 1.73 | 3.79 ± 0.52 | 26.44 ± 12.15 | 0.67 ± 0.09 | 0.14 ± 0.14 |
| Interpolation | MSE(logit) | 4 | 4 | + | + | 19.49 ± 28.13 | 7.68 ± 9.84 | 81.31 ± 138.85 | 0.92 ± 0.99 | −1.63 ± 3.83 |
| Model-based | MSE(logit) | 1 | 1 | + | + | 2.31 ± 0.49 | 1.73 ± 0.32 | 1.03 ± 0.18 | 0.40 ± 0.10 | 0.68 ± 0.04 |
| Model-based | BCE | 1 | 1 | + | + | 1.63 ± 0.89 | 1.59 ± 0.43 | 3.78 ± 1.43 | 0.31 ± 0.05 | 0.81 ± 0.08 |
| Model-based | MSE(logit) | 1 | 1 | + | - | 4.52 ± 1.69 | 2.87 ± 0.64 | 7.49 ± 5.39 | 0.74 ± 0.06 | 0.20 ± 0.15 |
| Model-based | BCE | 1 | 1 | + | - | 6.42 ± 0.68 | 4.50 ± 0.47 | 112.95 ± 81.72 | 0.53 ± 0.04 | 0.08 ± 0.18 |
| Model-based | MSE(logit) | 1 | 2 | + | + | 2.48 ± 0.89 | 1.60 ± 0.25 | 1.25 ± 0.33 | 0.37 ± 0.03 | 0.65 ± 0.11 |
| Model-based | BCE | 1 | 2 | + | + | 3.96 ± 2.98 | 3.10 ± 1.80 | 81.01 ± 76.31 | 0.37 ± 0.10 | 0.48 ± 0.39 |
| Model-based | MSE(logit) | 1 | 2 | + | - | 6.04 ± 1.76 | 3.44 ± 0.52 | 3.92 ± 0.83 | 0.68 ± 0.05 | 0.22 ± 0.08 |
| Model-based | BCE | 1 | 2 | + | - | 5.83 ± 0.60 | 4.47 ± 0.31 | 135.05 ± 31.64 | 0.55 ± 0.04 | 0.15 ± 0.05 |
| Model-based | MSE(logit) | 1 | 4 | + | + | 1.58 ± 0.58 | 1.43 ± 0.28 | 1.01 ± 0.20 | 0.38 ± 0.10 | 0.78 ± 0.08 |
| Model-based | BCE | 1 | 4 | + | + | 1.99 ± 1.50 | 1.72 ± 0.87 | 14.34 ± 10.81 | 0.33 ± 0.04 | 0.73 ± 0.18 |
| Model-based | MSE(logit) | 1 | 4 | + | - | 6.78 ± 1.93 | 3.44 ± 0.78 | 7.69 ± 4.01 | 0.74 ± 0.04 | 0.10 ± 0.10 |
| Model-based | BCE | 1 | 4 | + | - | 10.17 ± 8.31 | 5.30 ± 2.37 | 102.72 ± 130.70 | 0.65 ± 0.08 | −0.36 ± 1.05 |
| Model-based | MSE(logit) | 2 | 1 | + | + | 2.90 ± 0.27 | 1.86 ± 0.21 | 0.94 ± 0.07 | 0.37 ± 0.02 | 0.63 ± 0.02 |
| Model-based | BCE | 2 | 1 | + | + | 1.61 ± 0.68 | 1.50 ± 0.17 | 11.31 ± 7.10 | 0.30 ± 0.04 | 0.81 ± 0.09 |
| Model-based | MSE(logit) | 2 | 1 | + | - | 6.68 ± 1.43 | 3.51 ± 0.57 | 3.79 ± 1.21 | 0.76 ± 0.11 | 0.14 ± 0.23 |
| Model-based | BCE | 2 | 1 | + | - | 4.15 ± 0.52 | 3.67 ± 0.26 | 121.03 ± 38.99 | 0.56 ± 0.03 | 0.27 ± 0.07 |
| Model-based | MSE(logit) | 2 | 2 | + | + | 2.12 ± 1.24 | 1.64 ± 0.53 | 0.96 ± 0.08 | 0.35 ± 0.06 | 0.69 ± 0.17 |
| Model-based | BCE | 2 | 2 | + | + | 1.27 ± 0.53 | 1.45 ± 0.36 | 5.05 ± 3.46 | 0.32 ± 0.07 | 0.84 ± 0.04 |
| Model-based | MSE(logit) | 2 | 2 | + | - | 5.86 ± 1.01 | 3.47 ± 0.22 | 4.79 ± 2.55 | 0.75 ± 0.04 | 0.14 ± 0.09 |
| Model-based | BCE | 2 | 2 | + | - | 6.55 ± 1.28 | 4.39 ± 0.66 | 73.56 ± 77.17 | 0.61 ± 0.06 | 0.08 ± 0.07 |
| Model-based | MSE(logit) | 2 | 4 | + | + | 3.57 ± 2.66 | 2.17 ± 0.73 | 3.91 ± 5.18 | 0.47 ± 0.21 | 0.56 ± 0.33 |
| Model-based | BCE | 2 | 4 | + | + | 1.29 ± 0.49 | 1.44 ± 0.30 | 5.68 ± 3.96 | 0.31 ± 0.04 | 0.83 ± 0.04 |
| Model-based | MSE(logit) | 2 | 4 | + | - | 3.99 ± 0.68 | 2.77 ± 0.43 | 3.77 ± 1.89 | 0.67 ± 0.09 | 0.33 ± 0.13 |
| Model-based | BCE | 2 | 4 | + | - | 4.70 ± 1.15 | 3.48 ± 0.26 | 29.98 ± 9.99 | 0.60 ± 0.06 | 0.30 ± 0.12 |
| Model-based | MSE(logit) | 3 | 1 | + | + | 2.49 ± 1.39 | 1.70 ± 0.57 | 1.09 ± 0.16 | 0.36 ± 0.05 | 0.63 ± 0.11 |
| Model-based | BCE | 3 | 1 | + | + | 0.81 ± 0.30 | 1.20 ± 0.17 | 4.66 ± 2.20 | 0.27 ± 0.02 | 0.87 ± 0.03 |
| Model-based | MSE(logit) | 3 | 1 | + | - | 5.46 ± 0.85 | 2.89 ± 0.35 | 4.04 ± 1.48 | 0.70 ± 0.04 | 0.29 ± 0.06 |
| Model-based | BCE | 3 | 1 | + | - | 5.23 ± 1.25 | 3.47 ± 0.62 | 19.87 ± 2.74 | 0.66 ± 0.08 | 0.27 ± 0.13 |
| Model-based | MSE(logit) | 3 | 2 | + | + | 1.69 ± 0.30 | 1.58 ± 0.16 | 1.16 ± 0.14 | 0.37 ± 0.04 | 0.73 ± 0.05 |
| Model-based | BCE | 3 | 2 | + | + | 1.42 ± 0.56 | 1.40 ± 0.21 | 12.40 ± 4.94 | 0.32 ± 0.04 | 0.78 ± 0.07 |
| Model-based | MSE(logit) | 3 | 2 | + | - | 6.67 ± 1.20 | 3.69 ± 0.53 | 10.97 ± 8.26 | 0.80 ± 0.13 | −0.13 ± 0.44 |
| Model-based | BCE | 3 | 2 | + | - | 9.48 ± 9.17 | 4.23 ± 1.89 | 72.63 ± 106.58 | 0.78 ± 0.18 | −0.61 ± 1.83 |
| Model-based | MSE(logit) | 3 | 4 | + | + | 2.43 ± 0.69 | 1.77 ± 0.32 | 1.22 ± 0.22 | 0.38 ± 0.04 | 0.67 ± 0.08 |
| Model-based | BCE | 3 | 4 | + | + | 2.59 ± 1.92 | 2.18 ± 1.44 | 17.61 ± 6.42 | 0.37 ± 0.12 | 0.64 ± 0.26 |
| Model-based | MSE(logit) | 3 | 4 | + | - | 5.53 ± 1.56 | 3.51 ± 0.46 | 7.47 ± 5.62 | 0.71 ± 0.07 | 0.20 ± 0.12 |
| Model-based | BCE | 3 | 4 | + | - | 5.03 ± 1.33 | 3.68 ± 0.59 | 40.47 ± 11.99 | 0.61 ± 0.06 | 0.19 ± 0.14 |
| Model-based | MSE(logit) | 4 | 1 | + | + | 46.73 ± 55.32 | 14.17 ± 15.61 | 208.27 ± 254.44 | 1.60 ± 1.56 | −5.31 ± 7.45 |
| Model-based | BCE | 4 | 1 | + | + | 1.42 ± 0.63 | 1.41 ± 0.35 | 4.71 ± 1.91 | 0.31 ± 0.06 | 0.81 ± 0.08 |
| Model-based | MSE(logit) | 4 | 1 | + | - | 4.11 ± 1.29 | 3.00 ± 0.46 | 3.45 ± 0.91 | 0.65 ± 0.07 | 0.35 ± 0.15 |
| Model-based | BCE | 4 | 1 | + | - | 6.56 ± 1.93 | 4.26 ± 0.75 | 263.20 ± 446.90 | 0.67 ± 0.07 | −0.05 ± 0.19 |
| Model-based | MSE(logit) | 4 | 2 | + | + | 3.05 ± 1.33 | 2.09 ± 0.62 | 1.19 ± 0.14 | 0.41 ± 0.04 | 0.57 ± 0.18 |
| Model-based | BCE | 4 | 2 | + | + | 1.10 ± 0.57 | 1.26 ± 0.32 | 7.37 ± 5.68 | 0.29 ± 0.07 | 0.84 ± 0.05 |
| Model-based | MSE(logit) | 4 | 2 | + | - | 4.74 ± 0.80 | 2.88 ± 0.46 | 5.14 ± 2.53 | 0.69 ± 0.09 | 0.22 ± 0.15 |
| Model-based | BCE | 4 | 2 | + | - | 5.12 ± 0.97 | 3.57 ± 0.42 | 51.89 ± 32.71 | 0.66 ± 0.11 | 0.25 ± 0.08 |
| Model-based | MSE(logit) | 4 | 4 | + | + | 2.13 ± 0.64 | 1.71 ± 0.41 | 1.04 ± 0.22 | 0.36 ± 0.03 | 0.69 ± 0.05 |
| Model-based | BCE | 4 | 4 | + | + | 1.74 ± 1.22 | 1.71 ± 0.78 | 10.18 ± 12.19 | 0.34 ± 0.15 | 0.78 ± 0.16 |
| Model-based | MSE(logit) | 4 | 4 | + | - | 6.02 ± 2.33 | 3.43 ± 1.06 | 6.31 ± 3.82 | 0.71 ± 0.04 | 0.22 ± 0.12 |
| Model-based | BCE | 4 | 4 | + | - | 5.37 ± 0.43 | 3.70 ± 0.31 | 38.21 ± 32.85 | 0.68 ± 0.05 | 0.30 ± 0.05 |
| ARIMA | MSE(logit) | 1 | 1 | + | + | 2.82 ± 0.68 | 1.72 ± 0.21 | 1.11 ± 0.32 | 0.38 ± 0.03 | 0.61 ± 0.08 |
| ARIMA | BCE | 1 | 1 | + | + | 1.43 ± 0.46 | 1.66 ± 0.36 | 4.93 ± 5.15 | 0.30 ± 0.03 | 0.84 ± 0.03 |
| ARIMA | MSE(logit) | 1 | 1 | + | - | 7.46 ± 1.70 | 3.92 ± 0.64 | 7.10 ± 2.79 | 0.79 ± 0.06 | 0.09 ± 0.19 |
| ARIMA | BCE | 1 | 1 | + | - | 6.87 ± 1.96 | 4.31 ± 0.75 | 37.82 ± 12.43 | 0.58 ± 0.03 | 0.19 ± 0.13 |
| ARIMA | MSE(logit) | 1 | 2 | + | + | 1.83 ± 0.35 | 1.67 ± 0.24 | 1.07 ± 0.10 | 0.33 ± 0.02 | 0.74 ± 0.04 |
| ARIMA | BCE | 1 | 2 | + | + | 1.13 ± 0.51 | 1.25 ± 0.22 | 5.81 ± 2.84 | 0.28 ± 0.04 | 0.85 ± 0.04 |
| ARIMA | MSE(logit) | 1 | 2 | + | - | 4.29 ± 0.73 | 2.77 ± 0.70 | 4.50 ± 1.30 | 0.65 ± 0.07 | 0.27 ± 0.08 |
| ARIMA | BCE | 1 | 2 | + | - | 4.48 ± 0.68 | 3.65 ± 0.37 | 61.71 ± 18.07 | 0.58 ± 0.10 | 0.30 ± 0.13 |
| ARIMA | MSE(logit) | 1 | 4 | + | + | 2.13 ± 0.64 | 1.55 ± 0.27 | 1.19 ± 0.17 | 0.34 ± 0.03 | 0.68 ± 0.02 |
| ARIMA | BCE | 1 | 4 | + | + | 1.36 ± 0.53 | 1.45 ± 0.30 | 5.02 ± 3.51 | 0.28 ± 0.03 | 0.83 ± 0.06 |
| ARIMA | MSE(logit) | 1 | 4 | + | - | 5.11 ± 2.06 | 3.03 ± 0.78 | 4.60 ± 2.12 | 0.72 ± 0.08 | 0.18 ± 0.13 |
| ARIMA | BCE | 1 | 4 | + | - | 5.18 ± 0.37 | 4.06 ± 0.52 | 103.04 ± 71.29 | 0.59 ± 0.10 | 0.23 ± 0.12 |
| ARIMA | MSE(logit) | 2 | 1 | + | + | 2.26 ± 0.55 | 1.64 ± 0.22 | 1.18 ± 0.27 | 0.36 ± 0.05 | 0.66 ± 0.06 |
| ARIMA | BCE | 2 | 1 | + | + | 1.31 ± 0.35 | 1.54 ± 0.33 | 4.90 ± 2.21 | 0.31 ± 0.05 | 0.84 ± 0.02 |
| ARIMA | MSE(logit) | 2 | 1 | + | - | 4.80 ± 0.65 | 3.08 ± 0.29 | 2.98 ± 0.56 | 0.71 ± 0.10 | 0.29 ± 0.11 |
| ARIMA | BCE | 2 | 1 | + | - | 4.37 ± 0.61 | 3.33 ± 0.23 | 20.57 ± 12.20 | 0.62 ± 0.02 | 0.34 ± 0.08 |
| ARIMA | MSE(logit) | 2 | 2 | + | + | 1.60 ± 0.70 | 1.37 ± 0.30 | 1.09 ± 0.21 | 0.31 ± 0.05 | 0.74 ± 0.08 |
| ARIMA | BCE | 2 | 2 | + | + | 1.18 ± 0.31 | 1.35 ± 0.28 | 3.71 ± 1.08 | 0.28 ± 0.03 | 0.83 ± 0.05 |
| ARIMA | MSE(logit) | 2 | 2 | + | - | 5.69 ± 0.84 | 3.28 ± 0.20 | 4.15 ± 2.24 | 0.65 ± 0.04 | 0.22 ± 0.09 |
| ARIMA | BCE | 2 | 2 | + | - | 5.58 ± 3.10 | 3.85 ± 0.96 | 33.48 ± 13.82 | 0.59 ± 0.04 | 0.32 ± 0.13 |
| ARIMA | MSE(logit) | 2 | 4 | + | + | 2.22 ± 0.65 | 1.75 ± 0.39 | 0.89 ± 0.13 | 0.36 ± 0.07 | 0.71 ± 0.07 |
| ARIMA | BCE | 2 | 4 | + | + | 1.14 ± 0.47 | 1.33 ± 0.27 | 7.47 ± 4.63 | 0.29 ± 0.05 | 0.82 ± 0.07 |
| ARIMA | MSE(logit) | 2 | 4 | + | - | 5.63 ± 1.24 | 3.26 ± 0.62 | 4.74 ± 1.95 | 0.66 ± 0.07 | 0.23 ± 0.15 |
| ARIMA | BCE | 2 | 4 | + | - | 6.03 ± 0.21 | 4.97 ± 0.12 | 165.61 ± 19.61 | 0.52 ± 0.02 | −0.00 ± 0.00 |
| ARIMA | MSE(logit) | 3 | 1 | + | + | 1.88 ± 1.10 | 1.53 ± 0.40 | 0.91 ± 0.07 | 0.32 ± 0.04 | 0.75 ± 0.10 |
| ARIMA | BCE | 3 | 1 | + | + | 1.10 ± 0.28 | 1.29 ± 0.12 | 2.83 ± 1.15 | 0.28 ± 0.02 | 0.85 ± 0.02 |
| ARIMA | MSE(logit) | 3 | 1 | + | - | 5.09 ± 1.56 | 3.19 ± 0.57 | 6.22 ± 2.54 | 0.74 ± 0.07 | 0.27 ± 0.04 |
| ARIMA | BCE | 3 | 1 | + | - | 5.57 ± 1.87 | 4.11 ± 0.80 | 45.67 ± 13.26 | 0.62 ± 0.10 | 0.04 ± 0.26 |
| ARIMA | MSE(logit) | 3 | 2 | + | + | 1.52 ± 0.40 | 1.34 ± 0.31 | 0.95 ± 0.07 | 0.33 ± 0.06 | 0.76 ± 0.05 |
| ARIMA | BCE | 3 | 2 | + | + | 1.28 ± 0.34 | 1.40 ± 0.16 | 4.33 ± 3.43 | 0.29 ± 0.01 | 0.83 ± 0.02 |
| ARIMA | MSE(logit) | 3 | 2 | + | - | 6.15 ± 1.71 | 3.38 ± 0.65 | 6.42 ± 4.26 | 0.74 ± 0.09 | 0.20 ± 0.17 |
| ARIMA | BCE | 3 | 2 | + | - | 5.71 ± 1.51 | 3.88 ± 0.41 | 59.30 ± 27.34 | 0.64 ± 0.06 | 0.17 ± 0.12 |
| ARIMA | MSE(logit) | 3 | 4 | + | + | 2.47 ± 0.94 | 1.76 ± 0.37 | 1.06 ± 0.21 | 0.35 ± 0.05 | 0.68 ± 0.10 |
| ARIMA | BCE | 3 | 4 | + | + | 1.18 ± 0.35 | 1.31 ± 0.20 | 8.88 ± 1.92 | 0.31 ± 0.02 | 0.83 ± 0.02 |
| ARIMA | MSE(logit) | 3 | 4 | + | - | 6.67 ± 1.12 | 3.66 ± 0.45 | 5.23 ± 1.56 | 0.67 ± 0.08 | 0.17 ± 0.14 |
| ARIMA | BCE | 3 | 4 | + | - | 5.56 ± 1.26 | 3.96 ± 0.46 | 42.09 ± 22.79 | 0.61 ± 0.08 | 0.17 ± 0.06 |
| ARIMA | MSE(logit) | 4 | 1 | + | + | 2.46 ± 1.10 | 1.75 ± 0.47 | 1.19 ± 0.22 | 0.34 ± 0.02 | 0.68 ± 0.06 |
| ARIMA | BCE | 4 | 1 | + | + | 1.14 ± 0.35 | 1.36 ± 0.24 | 5.56 ± 2.55 | 0.31 ± 0.04 | 0.83 ± 0.04 |
| ARIMA | MSE(logit) | 4 | 1 | + | - | 4.19 ± 1.12 | 2.77 ± 0.45 | 3.37 ± 0.64 | 0.68 ± 0.10 | 0.26 ± 0.14 |
| ARIMA | BCE | 4 | 1 | + | - | 5.69 ± 1.94 | 3.48 ± 0.60 | 28.93 ± 8.54 | 0.71 ± 0.13 | 0.18 ± 0.17 |
| ARIMA | MSE(logit) | 4 | 2 | + | + | 1.96 ± 0.80 | 1.46 ± 0.32 | 1.08 ± 0.23 | 0.34 ± 0.07 | 0.68 ± 0.10 |
| ARIMA | BCE | 4 | 2 | + | + | 1.34 ± 0.50 | 1.33 ± 0.23 | 9.42 ± 13.70 | 0.28 ± 0.03 | 0.82 ± 0.04 |
| ARIMA | MSE(logit) | 4 | 2 | + | - | 4.32 ± 0.67 | 2.70 ± 0.21 | 4.91 ± 1.34 | 0.67 ± 0.08 | 0.30 ± 0.07 |
| ARIMA | BCE | 4 | 2 | + | - | 5.71 ± 1.48 | 3.65 ± 0.57 | 39.23 ± 24.22 | 0.59 ± 0.06 | 0.22 ± 0.11 |
| ARIMA | MSE(logit) | 4 | 4 | + | + | 2.93 ± 1.47 | 2.02 ± 0.49 | 1.26 ± 0.28 | 0.39 ± 0.05 | 0.63 ± 0.12 |
| ARIMA | BCE | 4 | 4 | + | + | 1.43 ± 0.65 | 1.45 ± 0.33 | 7.75 ± 4.61 | 0.31 ± 0.04 | 0.80 ± 0.05 |
| ARIMA | MSE(logit) | 4 | 4 | + | - | 5.30 ± 0.72 | 2.96 ± 0.39 | 7.09 ± 4.87 | 0.65 ± 0.04 | 0.30 ± 0.09 |
| ARIMA | BCE | 4 | 4 | + | - | 5.02 ± 1.93 | 3.49 ± 0.67 | 28.37 ± 15.94 | 0.61 ± 0.08 | 0.23 ± 0.21 |
| ARIMA | MSE(logit) | 1 | 1 | - | + | 1.94 ± 0.50 | 1.59 ± 0.22 | 1.26 ± 0.19 | 0.36 ± 0.06 | 0.74 ± 0.09 |
| ARIMA | BCE | 1 | 1 | - | + | 1.15 ± 0.28 | 1.28 ± 0.19 | 7.44 ± 0.99 | 0.32 ± 0.02 | 0.82 ± 0.02 |
| ARIMA | MSE(logit) | 1 | 1 | - | - | 1.01 ± 0.75 | 1.26 ± 0.34 | 1.35 ± 0.10 | 0.31 ± 0.04 | 0.85 ± 0.09 |
| ARIMA | BCE | 1 | 1 | - | - | 1.08 ± 0.42 | 1.35 ± 0.26 | 10.39 ± 2.99 | 0.30 ± 0.02 | 0.83 ± 0.05 |
| ARIMA | MSE(logit) | 1 | 2 | - | + | 2.23 ± 0.53 | 1.66 ± 0.24 | 1.19 ± 0.18 | 0.34 ± 0.02 | 0.69 ± 0.06 |
| ARIMA | BCE | 1 | 2 | - | + | 1.01 ± 0.59 | 1.20 ± 0.18 | 9.77 ± 2.42 | 0.29 ± 0.03 | 0.85 ± 0.06 |
| ARIMA | MSE(logit) | 1 | 2 | - | - | 1.17 ± 0.55 | 1.25 ± 0.19 | 1.37 ± 0.16 | 0.32 ± 0.04 | 0.81 ± 0.05 |
| ARIMA | BCE | 1 | 2 | - | - | 1.34 ± 0.37 | 1.45 ± 0.11 | 7.49 ± 4.18 | 0.29 ± 0.02 | 0.84 ± 0.03 |
| ARIMA | MSE(logit) | 1 | 4 | - | + | 2.08 ± 0.73 | 1.53 ± 0.24 | 1.14 ± 0.08 | 0.31 ± 0.04 | 0.74 ± 0.07 |
| ARIMA | BCE | 1 | 4 | - | + | 1.36 ± 0.41 | 1.44 ± 0.24 | 8.82 ± 5.09 | 0.30 ± 0.01 | 0.81 ± 0.03 |
| ARIMA | MSE(logit) | 1 | 4 | - | - | 1.59 ± 0.41 | 1.41 ± 0.16 | 1.21 ± 0.10 | 0.31 ± 0.03 | 0.79 ± 0.04 |
| ARIMA | BCE | 1 | 4 | - | - | 1.35 ± 0.46 | 1.33 ± 0.12 | 10.27 ± 2.82 | 0.31 ± 0.02 | 0.82 ± 0.05 |
| ARIMA | MSE(logit) | 2 | 1 | - | + | 1.70 ± 0.53 | 1.54 ± 0.23 | 1.48 ± 0.38 | 0.33 ± 0.02 | 0.77 ± 0.05 |
| ARIMA | BCE | 2 | 1 | - | + | 1.33 ± 0.57 | 1.44 ± 0.21 | 5.52 ± 2.16 | 0.30 ± 0.03 | 0.83 ± 0.05 |
| ARIMA | MSE(logit) | 2 | 1 | - | - | 1.72 ± 0.99 | 1.39 ± 0.24 | 1.36 ± 0.16 | 0.33 ± 0.04 | 0.77 ± 0.07 |
| ARIMA | BCE | 2 | 1 | - | - | 1.69 ± 0.67 | 1.42 ± 0.11 | 7.03 ± 2.51 | 0.31 ± 0.02 | 0.77 ± 0.08 |
| ARIMA | MSE(logit) | 2 | 2 | - | + | 2.17 ± 0.42 | 1.59 ± 0.10 | 1.16 ± 0.07 | 0.35 ± 0.03 | 0.72 ± 0.05 |
| ARIMA | BCE | 2 | 2 | - | + | 1.17 ± 0.30 | 1.33 ± 0.15 | 6.51 ± 3.28 | 0.28 ± 0.02 | 0.83 ± 0.03 |
| ARIMA | MSE(logit) | 2 | 2 | - | - | 1.93 ± 1.17 | 1.61 ± 0.42 | 1.45 ± 0.19 | 0.31 ± 0.02 | 0.76 ± 0.07 |
| ARIMA | BCE | 2 | 2 | - | - | 1.90 ± 0.90 | 1.50 ± 0.36 | 7.16 ± 2.52 | 0.32 ± 0.04 | 0.76 ± 0.10 |
| ARIMA | MSE(logit) | 2 | 4 | - | + | 2.62 ± 0.69 | 1.65 ± 0.18 | 1.34 ± 0.15 | 0.37 ± 0.03 | 0.60 ± 0.07 |
| ARIMA | BCE | 2 | 4 | - | + | 1.91 ± 0.43 | 1.64 ± 0.28 | 8.38 ± 5.63 | 0.31 ± 0.03 | 0.75 ± 0.05 |
| ARIMA | MSE(logit) | 2 | 4 | - | - | 1.65 ± 0.42 | 1.56 ± 0.22 | 1.26 ± 0.23 | 0.35 ± 0.04 | 0.79 ± 0.04 |
| ARIMA | BCE | 2 | 4 | - | - | 1.26 ± 0.33 | 1.43 ± 0.14 | 7.09 ± 3.06 | 0.28 ± 0.03 | 0.82 ± 0.03 |
| ARIMA | MSE(logit) | 3 | 1 | - | + | 1.16 ± 0.36 | 1.25 ± 0.10 | 1.21 ± 0.13 | 0.32 ± 0.02 | 0.81 ± 0.04 |
| ARIMA | BCE | 3 | 1 | - | + | 1.81 ± 0.47 | 1.47 ± 0.24 | 6.81 ± 2.72 | 0.32 ± 0.03 | 0.76 ± 0.05 |
| ARIMA | MSE(logit) | 3 | 1 | - | - | 1.72 ± 0.81 | 1.62 ± 0.52 | 1.53 ± 0.48 | 0.37 ± 0.11 | 0.78 ± 0.09 |
| ARIMA | BCE | 3 | 1 | - | - | 1.52 ± 0.69 | 1.53 ± 0.37 | 7.38 ± 2.11 | 0.29 ± 0.02 | 0.80 ± 0.05 |
| ARIMA | MSE(logit) | 3 | 2 | - | + | 1.45 ± 0.40 | 1.39 ± 0.16 | 1.67 ± 0.33 | 0.32 ± 0.04 | 0.79 ± 0.04 |
| ARIMA | BCE | 3 | 2 | - | + | 1.56 ± 0.75 | 1.58 ± 0.41 | 9.16 ± 8.66 | 0.30 ± 0.03 | 0.80 ± 0.06 |
| ARIMA | MSE(logit) | 3 | 2 | - | - | 1.30 ± 0.00 | 1.14 ± 0.00 | 1.47 ± 0.00 | 0.30 ± 0.00 | 0.82 ± 0.00 |
| Imputation | Loss | FFT | Recurrent Embeddings | Masked Ratio | MSE, ×1017, kg2 | MAE, ×108, kg | MAPEall | MAPElarge | R2 |
|---|---|---|---|---|---|---|---|---|---|
| Forward fill | MSE(logit) | + | - | 0.1 | 8.82 ± 2.53 | 4.22 ± 0.82 | 10.25 ± 0.99 | 0.88 ± 0.02 | −0.17 ± 0.04 |
| Forward fill | BCE | + | - | 0.1 | 1.35 ± 0.67 | 1.76 ± 0.44 | 12.53 ± 9.51 | 0.35 ± 0.03 | 0.82 ± 0.05 |
| Forward fill | MSE(logit) | + | + | 0.1 | 2.53 ± 0.63 | 1.92 ± 0.33 | 1.92 ± 0.41 | 0.37 ± 0.05 | 0.70 ± 0.04 |
| Forward fill | BCE | + | + | 0.1 | 1.69 ± 0.22 | 1.89 ± 0.09 | 7.73 ± 1.56 | 0.38 ± 0.06 | 0.79 ± 0.04 |
| Forward fill | MSE(logit) | + | + | 0.5 | 1.58 ± 0.18 | 1.46 ± 0.11 | 1.10 ± 0.15 | 0.32 ± 0.03 | 0.73 ± 0.04 |
| Forward fill | BCE | + | + | 0.5 | 0.71 ± 0.16 | 1.13 ± 0.12 | 17.46 ± 2.06 | 0.26 ± 0.05 | 0.88 ± 0.04 |
| Model-based | MSE(logit) | + | - | 0.1 | 8.78 ± 0.00 | 4.56 ± 0.00 | 6.88 ± 0.00 | 0.80 ± 0.00 | −0.13 ± 0.00 |
| Model-based | MSE(logit) | + | + | 0.1 | 2.91 ± 1.39 | 1.92 ± 0.37 | 1.45 ± 0.16 | 0.37 ± 0.03 | 0.63 ± 0.06 |
| ARIMA | MSE(logit) | + | + | 0.1 | 1.86 ± 1.04 | 1.77 ± 0.51 | 2.79 ± 0.75 | 0.35 ± 0.05 | 0.73 ± 0.13 |
| ARIMA | BCE | + | + | 0.1 | 1.35 ± 0.38 | 1.64 ± 0.26 | 10.90 ± 4.18 | 0.35 ± 0.02 | 0.81 ± 0.03 |
| Interpolation | MSE(logit) | - | + | 0.1 | 2.02 ± 0.96 | 1.71 ± 0.31 | 1.98 ± 0.50 | 0.37 ± 0.07 | 0.68 ± 0.16 |
| Interpolation | BCE | - | + | 0.1 | 2.40 ± 0.41 | 2.21 ± 0.16 | 5.44 ± 2.36 | 0.40 ± 0.05 | 0.74 ± 0.03 |
| Interpolation | MSE(logit) | - | - | 0.1 | 2.28 ± 1.28 | 2.12 ± 0.64 | 3.27 ± 1.20 | 0.62 ± 0.18 | 0.66 ± 0.13 |
| Interpolation | BCE | - | - | 0.1 | 1.97 ± 0.39 | 1.64 ± 0.19 | 6.67 ± 2.65 | 0.34 ± 0.03 | 0.76 ± 0.03 |
| Interpolation | MSE(logit) | - | + | 0.3 | 1.68 ± 0.43 | 1.50 ± 0.17 | 1.46 ± 0.38 | 0.34 ± 0.04 | 0.73 ± 0.08 |
| Interpolation | BCE | - | + | 0.3 | 3.33 ± 1.82 | 2.82 ± 1.47 | 76.73 ± 90.06 | 0.38 ± 0.10 | 0.50 ± 0.36 |
References
- Food and Agriculture Organisation. World Food and Agriculture; FAO: Rome, Italy, 2015. [Google Scholar]
- Caparas, M.; Zobel, Z.; Castanho, A.D.; Schwalm, C.R. Increasing risks of crop failure and water scarcity in global breadbaskets by 2030. Environ. Res. Lett. 2021, 16, 104013. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Zhou, W.-X. Structural evolution of international crop trade networks. Front. Phys. 2022, 10, 926764. [Google Scholar] [CrossRef]
- Duan, J.; Nie, C.; Wang, Y.; Yan, D.; Xiong, W. Research on Global Grain Trade Network Pattern and Its Driving Factors. Sustainability 2022, 14, 245. [Google Scholar] [CrossRef]
- Food and Agriculture Organisation. The State of Agricultural Commodity Markets; FAO: Rome, Italy, 2022. [Google Scholar]
- Burkholz, R.; Schweitzer, F. International crop trade networks: The impact of shocks and cascades. Environ. Res. Lett. 2019, 14, 114013. [Google Scholar] [CrossRef]
- Seekell, D.; Carr, J.; Dell’Angelo, J.; D’Odorico, P.; Fader, M.; Gephart, J.; Kummu, M.; Magliocca, N.; Porkka, M.; Puma, M. Resilience in the global food system. Environ. Res. Lett. 2017, 12, 025010. [Google Scholar] [CrossRef] [PubMed]
- Burkholz, R.; Garas, A.; Schweitzer, F. How damage diversification can reduce systemic risk. Phys. Rev. E 2016, 93, 042313. [Google Scholar] [CrossRef]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef]
- Cabell, J.F.; Myles, O. An indicator framework for assessing agroecosystem resilience. Ecol. Soc. 2012, 17, 1–13. [Google Scholar] [CrossRef]
- Schipanski, M.E.; MacDonald, G.K.; Rosenzweig, S.; Chappell, M.J.; Bennett, E.M.; Kerr, R.B.; Blesh, J.; Crews, T.; Drinkwater, L.; Lundgren, J.G.; et al. Realizing resilient food systems. BioScience 2016, 66, 600–610. [Google Scholar] [CrossRef]
- Robu, R.G.; Alexoaei, A.P.; Cojanu, V.; Miron, D. The cereal network: A baseline approach to current configurations of trade communities. Agric. Food Econ. 2024, 12, 24. [Google Scholar] [CrossRef]
- Schoenherr, T.; Kanak, G.; Montalbano, A.; Patel, S.; Bourlakis, M.; Sawyerr, E.; Cong, W.F. Frontiers in Agri-Food Supply Chains: Frameworks and Case Studies; Burleigh Dodds Science Publishing: Cambridge, UK, 2024. [Google Scholar]
- Davide, M. S-MARL: An Algorithm for Single-To-Multi-Agent Reinforcement Learning: Case Study: Formula 1 Race Strategies. Available online: https://www.diva-portal.org/smash/get/diva2:1763095/FULLTEXT01.pdf (accessed on 2 August 2025).
- Ahmar, A.S.; Singh, P.K.; Ruliana, R.; Pandey, A.K.; Gupta, S. Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India. Forecasting 2023, 5, 138–152. [Google Scholar] [CrossRef]
- Qader, S.H.; Utazi, C.E.; Priyatikanto, R.; Najmaddin, P.; Hama-Ali, E.O.; Khwarahm, N.R.; Dash, J. Exploring the use of Sentinel-2 datasets and environmental variables to model wheat crop yield in smallholder arid and semi-arid farming systems. Sci. Total Environ. 2023, 869, 161716. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Leucci, A.C.; Ghinoi, S.; Sgargi, D.; Wesz Junior, V.J. VAR models for dynamic analysis of prices in the agri-food system. In Agricultural Cooperative Management and Policy: New Robust, Reliable and Coherent Modelling Tools; Springer International Publishing: Cham, Switzerland, 2014; pp. 3–21. [Google Scholar]
- Lutkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Li, X.; Yuan, J. DeepVARwT: Deep learning for a VAR model with trend. J. Appl. Stat. 2025, 52, 1–27. [Google Scholar] [CrossRef]
- Rumánková, L. Evaluation of market relations in soft milling wheat agri-food chain. AGRIS on-line. Pap. Econ. Inform. 2016, 8, 133–141. [Google Scholar]
- Zhao, Y.; Ye, L.; Pinson, P.; Tang, Y.; Lu, P. Correlation-constrained and sparsity-controlled vector autoregressive model for spatio-temporal wind power forecasting. IEEE Trans. Power Syst. 2018, 33, 5029–5040. [Google Scholar] [CrossRef]
- Han, K.; Leem, K.; Choi, Y.R.; Chung, K. What drives a country’s fish consumption? Market growth phase and the causal relations among fish consumption, production and income growth. Fish. Res. 2022, 254, 106435. [Google Scholar] [CrossRef]
- Xiong, T.; Li, C.; Bao, Y.; Hu, Z.; Zhang, L. A combination method for interval forecasting of agricultural commodity futures prices. Knowl. Based Syst. 2015, 77, 92–102. [Google Scholar] [CrossRef]
- Iniyan, S.; Varma, V.A.; Naidu, C.T. Crop yield prediction using machine learning techniques. Adv. Eng. Softw. 2023, 175, 103326. [Google Scholar] [CrossRef]
- Panda, S.K.; Mohanty, S.N. Time series forecasting and modeling of food demand supply chain based on regressors analysis. IEEE Access 2023, 11, 42679–42700. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-Arnold networks. In Proceedings of the Thirteenth International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Xu, K.; Chen, L.; Wang, S. Kolmogorov-Arnold networks for time series: Bridging predictive power and interpretability. arXiv 2024, arXiv:2406.02496. [Google Scholar] [CrossRef]
- Genet, R.; Inzirillo, H. A Temporal Kolmogorov-Arnold Transformer for Time Series Forecasting. arXiv 2024, arXiv:2406.02486. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Mukherjee, T. EleKAN: Temporal Kolmogorov-Arnold Networks for Price and Demand Forecasting Framework in Smart Cities. In Proceedings of the International Conference on Frontiers of Electronics, Information and Computation Technologies, Singapore, 22–24 June 2024; pp. 182–192. [Google Scholar]
- Le, D.; Rajasegarar, S.; Luo, W.; Nguyen, T.T.; Angelova, M. Navigating Uncertainty: Gold Price Forecasting with Kolmogorov-Arnold Networks in Volatile Markets. In Proceedings of the 2024 IEEE Conference on Engineering Informatics (ICEI), Melbourne, Australia, 20–21 November 2024; pp. 1–9. [Google Scholar]
- Ibañez, S.C.; Monterola, C.P. A Global Forecasting Approach to Large-Scale Crop Production Prediction with Time Series Transformers. Agriculture 2023, 13, 1855. [Google Scholar] [CrossRef]
- Ma, B.; Xue, Y.; Chen, J.; Sun, F. Meta-Learning Enhanced Trade Forecasting: A Neural Framework Leveraging Efficient Multicommodity STL Decomposition. Int. J. Intell. Syst. 2024, 2024, 6176898. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Buchholz, T.O.; Jug, F. Fourier image transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1846–1854. [Google Scholar]
- He, S.; Lin, G.; Li, T.; Chen, Y. Frequency-Domain Fusion Transformer for Image Inpainting. arXiv 2025, arXiv:2506.18437. [Google Scholar] [CrossRef]
- Li, Z.; Liu, T.; Peng, W.; Yuan, Z.; Wang, J. A transformer-based neural operator for large-eddy simulation of turbulence. Phys. Fluids 2024, 36, 065167. [Google Scholar] [CrossRef]
- Woo, G.; Liu, C.; Sahoo, D.; Kumar, A.; Hoi, S. Learning deep time-index models for time series forecasting. In Proceedings of the 14th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Li, H. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Li, Y.; Moura, J.M.F. Forecaster: A Graph Transformer for Forecasting Spatial and Time-Dependent Data. In Proceedings of the European Conference on Artificial Intelligence, Santiago de Compostela, Spain, 31 August–8 September 2020. [Google Scholar]
- Banerjee, S.; Dong, M.; Shi, W. Spatial–temporal synchronous graph transformer network (stsgt) for COVID-19 forecasting. Smart Health 2022, 26, 100348. [Google Scholar] [CrossRef]
- Liu, H.; Dong, Z.; Jiang, R.; Deng, J.; Chen, Q.; Song, X. Spatio-temporal adaptive embedding makes vanilla transformer SOTA for traffic forecasting. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023. [Google Scholar]
- Wang, H.; Chen, J.; Pan, T.; Dong, Z. STGformer: Efficient Spatiotemporal Graph Transformer for Traffic Forecasting. arXiv 2024, arXiv:2410.00385. [Google Scholar] [CrossRef]
- Hu, S.; Zou, G.; Lin, S.; Wu, L.; Zhou, C.; Zhang, B.; Chen, Y. Recurrent transformer for dynamic graph representation learning with edge temporal states. arXiv 2023, arXiv:2304.10079. [Google Scholar]
- Lee, J.; Xu, C.; Xie, Y. Transformer Conformal Prediction for Time Series. In Proceedings of the ICML 2024 Workshop on Structured Probabilistic Inference and Generative Modeling, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Caliendo, L.; Parro, F. Gains from Trade: A Model for Counterfactual Trade Policy Analysis; The University of Chicago Working Papers; The University of Chicago: Chicago, IL, USA, 2009. [Google Scholar]
- Yu, Z.; Han, J.; Shi, X.; Yang, Y. Estimates of the trade and global value chain (GVC) effects of China’s Pilot Free Trade Zones: A research based on the quantitative trade model. J. Asia Pac. Econ. 2025, 30, 1255–1302. [Google Scholar] [CrossRef]
- Roningen, V.O.; Dixit, P.M. Economic Implications of Agricultural Policy Reform in Industrial Market Economics; Rapport Techniques de I’USDA, Ages 80–36; United States Department of Agriculture, Economic Research Service: Washington, DC, USA, 1989.
- Hertel, T.W. Global Trade Analysis: Modeling and Applications; Cambridge University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Parikh, K.S.; Fisher, G.; Frohberg, K.; Gulbrandsen, O. Towards Free Trade in Agriculture; Martinus Mijhoff Publishers: Laxemburg, Austria, 1988. [Google Scholar]
- Keeney, R.M.; Hertel, T. GTAP-AGR: A Framework for Assessing the Implications of Multilateral Changes in Agricultural Policies: GTAP Technical Paper; Purdue University: West Lafayette, IN, USA, 2005. [Google Scholar]
- Britz, W.; Leip, A. Development of marginal emission factors for N losses from agricultural soils with the DNDC-CAPRI meta-model. Agric. Ecosyst. Environ. 2009, 133, 267–279. [Google Scholar] [CrossRef]
- Gong, X.; Xu, J. Geopolitical risk and dynamic connectedness between commodity markets. Energy Econ. 2022, 110, 106028. [Google Scholar] [CrossRef]
- Mashkova, A.; Bakhtizin, A. Algorithm and data structures of the agent-based model of trade wars. In Proceedings of the 2021 IEEE 15th International Conference on Application of Information and Communication Technologies (AICT), Baku, Azerbaijan, 13–15 October 2021; pp. 1–6. [Google Scholar]
- Poledna, S.; Miess, M.G.; Hommes, C.; Rabitsch, K. Economic forecasting with an agent-based model. Eur. Econ. Rev. 2023, 151, 104306. [Google Scholar] [CrossRef]
- Butler, K.; Iloska, M.; Djurić, P.M. On counterfactual interventions in vector autoregressive models. In Proceedings of the 2024 32nd European Signal Processing Conference (EUSIPCO), Lyon, France, 26–30 August 2024; IEEE: Piscataway, NJ, USA; pp. 1987–1991. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/faostat/en/ (accessed on 2 August 2025).
- UN Comtrade: International Trade Statistics. Available online: https://comtradeplus.un.org/TradeFlow (accessed on 2 August 2025).
- Hodel, F.; Booth, J. The Beta-Binomial Distribution; Cornell University: Ithaca, NY, USA, 2023. [Google Scholar]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. In Proceedings of the 30th Advances in Neural Information Processing Systems, Long Beach, CA, USA, 7–9 December 2017. [Google Scholar]
- Dwivedi, V.P.; Bresson, X. A generalization of transformer networks to graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Dueck, D. Affinity Propagation: Clustering Data by Passing Messages. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]




| Feature Set | Frequency | For | Features | Unit |
|---|---|---|---|---|
| Trade flows | Annual | Pair of countries | Export quantity | |
| Import quantity | Kilograms | |||
| Re-export quantity Re-import quantity | ||||
| Production | Annual | Country | Production quantity | Tonnes |
| Model | MSE, ×1017 kg2 | MAE, ×108 kg | MAPEall | MAPElarge | R2 |
|---|---|---|---|---|---|
| ARIMA | 1.99 ± 0.13 | 1.82 ± 0.09 | (3.03 ± 0.03) × 1021 | 0.46 ± 0.02 | 0.72 ± 0.03 |
| GRU | 1.57 ± 0.57 | 1.53 ± 0.18 | 13.88 ± 7.52 | 0.33 ± 0.02 | 0.77 ± 0.04 |
| LSTM | 1.37 ± 0.34 | 1.52 ± 0.15 | 5.97 ± 3.47 | 0.32 ± 0.02 | 0.80 ± 0.03 |
| TKAN | 1.47 ± 0.35 | 1.52 ± 0.13 | 5.55 ± 2.71 | 0.32 ± 0.02 | 0.79 ± 0.03 |
| Model | MSE, ×1017 kg2 | MAE, ×108 kg | MAPEall | MAPElarge | R2 |
|---|---|---|---|---|---|
| Recurrent graph transformer | 1.01 ± 0.75 | 1.26 ± 0.34 | 1.35 ± 0.10 | 0.31 ± 0.04 | 0.85 ± 0.09 |
| Recurrent graph transformer + spectral features | 0.79 ± 0.39 | 1.13 ± 0.26 | 6.32 ± 3.95 | 0.25 ± 0.05 | 0.88 ± 0.05 |
| Recurrent graph transformer (Encoder-Decoder) | 0.71± 0.16 | 1.13± 0.12 | 17.46 ± 2.06 | 0.26 ± 0.05 | 0.88 ± 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otmakhova, Y.; Devyatkin, D.; Zhou, H. Hybrid Supply Chain Model for Wheat Market. Systems 2025, 13, 1026. https://doi.org/10.3390/systems13111026
Otmakhova Y, Devyatkin D, Zhou H. Hybrid Supply Chain Model for Wheat Market. Systems. 2025; 13(11):1026. https://doi.org/10.3390/systems13111026
Chicago/Turabian StyleOtmakhova, Yulia, Dmitry Devyatkin, and He Zhou. 2025. "Hybrid Supply Chain Model for Wheat Market" Systems 13, no. 11: 1026. https://doi.org/10.3390/systems13111026
APA StyleOtmakhova, Y., Devyatkin, D., & Zhou, H. (2025). Hybrid Supply Chain Model for Wheat Market. Systems, 13(11), 1026. https://doi.org/10.3390/systems13111026








