How Competing Retailers Invest in ESG: Strategic Behavior Under Heterogeneous Consumer Preferences

Abstract

As environmental and social sustainability become an increasingly critical concern, retailers are under rising pressure from both eco-conscious consumers and evolving regulatory frameworks to enhance the environmental, social, and governance (ESG) performance of their supply chains. Given that most ESG-related violations originate from upstream suppliers, downstream retailers are compelled to invest in promoting responsible practices beyond their immediate operations. To capture this dynamic, we develop a two-tier supply chain model in which a single supplier distributes products to multiple retailers engaged in Cournot competition. Each retailer independently determines its level of investment aimed at improving the supplier’s ESG outcomes while accounting for heterogeneous consumer preferences between supplier-driven and retailer-driven sustainability efforts. Our findings reveal that retailers are only incentivized to invest when the number of market participants falls below a critical threshold. We further extend the analysis to an asymmetric setting, where only a subset of retailers engage in ESG investments and pay a premium wholesale price. In contrast to the baseline scenario, this structure may encourage higher investment levels among participating retailers when more of them are involved. Moreover, under conditions of strong consumer preference heterogeneity, a larger number of investing retailers can incentivize the supplier to reduce the wholesale price, thereby reinforcing investment incentives and facilitating improved ESG performance across the supply chain. In summary, the results provide valuable managerial implications for retailers, suppliers, and policymakers seeking to foster coordinated and sustainable ESG investment within supply chains.

1. Introduction

The escalating convergence of climate-related risks and social equity imperatives has catalyzed the unprecedented adoption of environmental, social, and governance (ESG) frameworks across global supply chains [1,2]. In particular, the implementation of EU sustainability regulations has significantly raised the bar for ESG compliance. Crucially, ESG violations predominantly originate from lower-tier suppliers, making their practices a pivotal determinant of overall chain-wide sustainability performance [3]. For example, Xiaomi, a leading consumer electronics firm, suffered a delay in its initial public offering (IPO) due to reports of suppliers with repeated environmental violations [4]. Tesla’s upstream component suppliers were accused of repeatedly exceeding standards and regulations, which starkly contrasts with Tesla’s long-standing environmental image, and the sales of Tesla’s new energy vehicles have been seriously affected [5]. These cases illustrate a recurring challenge in supply chain sustainability: although ESG violations typically arise from upstream suppliers, the reputational, regulatory, and market consequences are disproportionately borne by downstream retailers. As a result, investing in suppliers’ ESG performance has become a pivotal yet highly complex strategic decision for retailers.

While retailers are increasingly compelled to invest in improving suppliers’ ESG performance, the effectiveness and incentives of such investments critically depend on how consumers perceive ESG efforts along the supply chain [6]. It is widely recognized that the impact of ESG initiatives is more pronounced for firms closer to end consumers, suggesting that retailers may obtain greater market benefits from ESG investment compared to upstream suppliers [7,8]. However, advances in digital technologies have substantially increased supply chain transparency, enabling consumers to directly observe and evaluate suppliers’ ESG credibility [9]. As a result, the relative benefits of ESG efforts at different supply chain tiers have become heterogeneous and uncertain. In particular, whether consumers attribute greater ESG value to the supplier or to the retailer remains unclear, and this heterogeneity can fundamentally alter retailers’ incentives to invest in supplier ESG performance.

In practice, heterogeneous investment behaviors among retailers are widely observed across industries, even when they share common upstream suppliers. For example, according to the Green Supply Chain CITI Index report, the electronics manufacturing industry scored high in terms of ESG performance, and Apple consistently topped the green supply chain list for six consecutive years [10]. Similarly, following the Rana Plaza collapse in Bangladesh, 25 of the 29 apparel brands involved in the incident jointly signed an agreement to invest in a five-year program aimed at improving fire safety in Bangladeshi factories [11]. ESG investments in the new energy vehicle industry, however, fared poorly. Numerous prominent new energy vehicle retailers, including Tesla, BYD, Honda, and Toyota, were accused of claiming that their new energy vehicles were "environmentally friendly and superior” despite the severely negative environmental impact from the production processes of their common auto-part suppliers [12]. These contrasting patterns suggest that the number of competing retailers may significantly shape investment incentives. On the one hand, a larger downstream market amplifies the positive spillover effects of ESG investments, encouraging retailers to invest when their efforts collectively enhance supplier compliance [13,14]. On the other hand, intensified competition erodes retailers’ marginal revenues, which can weaken their willingness to undertake cost-reducing ESG investments [15,16]. The coexistence of these opposing forces implies that the relationship between retailer competition and ESG investment is theoretically ambiguous and remains insufficiently understood.

A growing body of research has examined ESG investment decisions in sustainable supply chains, typically using competitive models to analyze retailers’ incentives. However, two major limitations remain. First, most existing studies rely on duopoly settings involving only two retailers [17,18], which restrict their ability to capture the strategic dynamics present in industries where multiple retailers simultaneously source from common suppliers. As a result, these models fail to reflect the strategic complexity of multi-retailer competition and the underlying micro-mechanisms of free-riding. Second, prior work often assumes that the number of retailers does not influence wholesale pricing decisions [19,20]. Such assumptions neglect the role of heterogeneous consumer ESG preferences, which can induce threshold-based shifts in retailers’ investment behavior and potentially grant retailers substantial market power to influence supplier pricing. Collectively, these gaps limit our understanding of how competition intensity interacts with ESG preference heterogeneity to shape retailers’ optimal investment decisions.

Motivated by these practical observations and theoretical gaps, this study examines how competition intensity and heterogeneous consumer ESG preferences jointly shape retailers’ incentives to invest in improving the supplier’s ESG performance. Accordingly, we focus on the following research questions. (i) Under what conditions will multiple retailers choose to invest in enhancing the supplier’s ESG performance? (ii) How do heterogeneous consumer ESG preferences influence retailers’ optimal investment decisions? (iii) How will equilibrium investment decisions change when only a subset of retailers engages in ESG investment while others free-ride?

To this end, we develop a two-tier supply chain model in which a single supplier distributes products to multiple competing retailers engaged in Cournot competition. Each retailer makes a cost-reducing investment to enhance the supplier’s ESG performance, taking into account the heterogeneous preferences of consumers for ESG attributes. In practice, only parts of the downstream retailers of non-ESG-compliant suppliers are prepared to engage in investment activities. For this reason, we first consider the scenario where all retailers make symmetric investments and then extend our study to the asymmetric investment scenario where there are two types of retailers: those who invest and those who do not. Furthermore, to maintain sufficient downstream competition and incentivize retailer investment, we assume that the supplier offers a wholesale price premium exclusively for retailers that invest.

The contributions of this study are threefold. First, we develop a game-theoretic model of a sustainable supply chain that explicitly incorporates multiple competing retailers, enabling us to examine how competition intensity shapes suppliers’ ESG efforts and downstream retailers’ equilibrium decisions. This extends prior work that predominantly relies on duopoly structures and therefore cannot capture strategic dynamics in more realistic multi-retailer markets. Second, we incorporate heterogeneous consumer ESG preferences toward the supplier and the retailer, departing from the common assumption of homogeneous ESG perceptions. This allows us to analytically identify how preference asymmetry interacts with competition to influence wholesale pricing and retailers’ investment incentives. Third, we uncover the micro-mechanisms underlying ESG investment behavior in environments where only a subset of retailers chooses to invest. This analysis clarifies how retailer heterogeneity and free-riding behavior emerge endogenously in multi-retailer competition and how these dynamics reshape equilibrium outcomes.

The remainder of this paper is structured as follows. Section 2 summarizes the relevant literature. Section 3 describes our model’s setup. Section 4 solves the equilibrium for the supplier and retailer separately and then analyzes the optimal investment decision of the retailer. Section 5 expands the benchmark to the asymmetric investment scenario. Section 6 examines two extensions and conducts numerical simulations to check the robustness of our main results. Section 7 provides concluding remarks and gives possible future directions. Figure 1 illustrates the research process, research questions, and research contents to present the overall research framework of this study.

2. Literature Review

Our paper is closely related to the ESG management of suppliers in supply chains. Studies have been conducted from a variety of perspectives, including ESG audits to reduce suppliers’ non-compliance risk [21,22]; design of information sharing and disclosure mechanisms under incomplete supply chain transparency [23,24]; strategic sourcing considering supplier diversification and vertical integration [25,26]; lower-level supplier management [27,28]; incentive strategies for green technology selection and adoption [29]; etc. Our study is closely related to the literature on retailers’ investment strategies that enhance suppliers’ ESG performance and capabilities.

Most of the investment strategy-related studies typically examine one of two topics: (1) the investment motivation of retailers and (2) the allocation of ESG responsibilities between suppliers and retailers. For the first topic, earlier studies have explored retailers’ investment motives in terms of government regulations, such as investment subsidies [30,31], environmental and social standards [32,33], and carbon tax regulations [34,35]. Recently, the role of consumer preferences in retailers’ investment decisions has received significant attention [36]. Kraft et al. [37] design a motivational human-subject experimental approach to explore how supply chain transparency affects consumers’ perceptions of corporate social responsibility (CSR). Based on the theoretical framework, Kraft et al. [38] extend the analysis to construct a game model that examines how ENGO disclosures affect consumers’ valuations of the supplier’s sustainability and the brand’s investment strategies. They reveal that higher transparency can effectively help the buyer better align their investments. Panda [39] and Khodoomi et al. [40] explore the effectiveness of various incentive mechanisms, i.e., revenue sharing, cost sharing, and wholesale price premium, in encouraging suppliers to reduce emissions or engage in green innovation. In their model, consumer preferences for the ESG initiatives of the supplier and the retailer are assumed to be homogeneous. Thus, the supplier and retailer have homogeneous marginal benefits related to the improved supplier’s SR performance. For the second topic, researchers prove that a retailer undertaking more ESG responsibilities than a supplier can be more conducive to improving the total ESG effort [41]. Notably, several recent papers have expanded their focus from studying interactions between one supplier and one retailer to examining interactions among multiple firms within one tier. Ref. [42] develop a game-theoretic model consisting of one retailer and multiple suppliers to characterize equilibrium coalition structures. They found that although forming supplier coalitions can benefit all stakeholders, achieving such a win–win–win outcome hinges on the proportion of socially conscious consumers and the efficiency gains from coalition formations. Gopalakrishnan et al. [43] adopt the framework of the Shapley value to study the allocation of carbon reduction responsibilities among multiple firms. They demonstrate that when abatement costs comprise private information, an allocation based on the Shapley value incentivizes firms to exert optimal effort. Feng et al. [4] explore the coordination of firms’ ESG investments in complex supply networks using a multilateral bargaining framework. They demonstrate that the initiator’s strategy implementation hinges on suppliers’ bargaining power and the supply network’s complexity. As these studies focus more on competitive and cooperative interactions of supply chain members’ investment efforts to improve the supplier’s SR, they do not explicitly characterize prices or quantities.

Similarly to Gopalakrishnan et al. [43] and Feng et al. [4], we analyze the retailer’s investment incentives based on a complex sourcing network in which multiple retailers source from one supplier. Yet, our paper is different from theirs in two aspects: First, our model captures endogenous wholesale prices and discusses the effect of a wholesale price premium mechanism on mitigating retailer competition. Second, based on observations in practice, it is obvious that the supplier and the retailer may derive different benefits from the improvement in the supplier’s ESG performance. However, few studies investigate how the heterogeneity of marginal SR benefits between the supplier and retailer influences wholesale pricing. Our study adds to this gap. In contrast to their result that the changes in the number of retailers do not alter the magnitude of wholesale prices, we demonstrate that when the marginal ESG benefit of the supplier is more significant than that of the retailer, the supplier is prone to cut down the wholesale price with the growing number of retailers.

Our study also relates to the impact of competition on retailers’ operational decisions. Previous research typically adopts a competition model for sustainable supply chains involving mainly one supplier and two retailers or two suppliers and one retailer. Zhu and He [44] investigate the influence of two forms of competition, product competition and greenness competition, on green product design. They found that price competition raises product greenness, yet greenness competition lowers product greenness. Similarly, Shi et al. [17] examine that, compared to the duopoly situation, monopoly competition always undermines the investment effort of retailers and the overall ESG level. Caro et al. [21] investigate how two buyers enhance the supplier’s environmental performance with a collective penalty mechanism. They find that implementing an audit-penalty mechanism (i.e., the two buyers jointly sharing the total audit costs) results in increased environmental efforts from the buyers compared to auditing independently. Orsdemir et al. [26] assess the conditions under which CSR promotes vertical integration in two supply chain competition scenarios and show that firms do not need to integrate, despite higher risks of environmental violations and greater demand externalities. These papers primarily focus on the price or greenness competition and the pursuit of an agreement between the two sides rather than industry-wide competition.

Note that existing research in economics and operations management has adopted the Cournot model to study how multiple downstream firms’ competition affects wholesale prices, quantities, or supply chain efficiency [15,19,45]. These studies demonstrate that multiple competitive firms generate different questions or insights that two competitive firms may not capture. Yet, despite growing attention to ESG compliance in supply chains, limited research addresses the role of competition among multiple retailers. Wang et al. [18] investigate the interplay between the probability of government regulation and the voluntary adoption decision of green technology among multiple competing firms. Interestingly, they uncover that while stricter government regulations will incentivize firms’ green technology adoption, higher competition for environmental efforts will discourage firms from adopting it. However, their studies were not extended to the supply chain setting. Considering the effects of externalities (positive or negative) among retailers caused by suppliers’ SR violations, Fang et al. [13] extend the model of Caro et al. [21] to a more general situation in which multiple retailers compete. Differing from the result of Caro et al. [21], they find that externalities do not necessarily lead to the cooperative strategy improving the supplier’s CSR level.

As in the study of Fang et al. [13], the above papers mostly adopt a cooperative game framework that captures the competition of SR compliance effort between retailers, whereas we adopt a Cournot model that captures multiple retailers’ quantity competition to highlight the significant role of numbers in incentivizing the retailers’ investment. In particular, we consider how the competition and externality effects among multiple retailers influence their optimal investment decisions in improving the supplier’s SR. Interestingly, we discover that a critical mass of retailers exists, which serves as an incentive for retailers to exert the optimal investment effort. Moreover, we derive conditions that contribute to a “win-win” outcome for both invested and non-invested retailers.

To highlight the differences between our study and previous related studies, we include a comparison table, as shown in

Table 1. Overview of previous studies and the unresolved gaps addressed in this research.

Literature	Supply Chain Setting		Investment Strategies		Endogenous Wholesale Price
	SC Structure	Competition Mode	Multiple Retailers	Heterogeneous SR Benefits
[43]	network	Quantity	✗	✓	✗
[4]	2S + R	Quantity	✗	✓	✗
[17]	S + 2R	Price	✗	✗	✓
[21]	M + 2R	ESG effort	✗	✗	✗
[26]	2S + 2R	ESG effort	✗	✗	✗
[18]	nR	Quantity	✓	✗	✗
[13]	S + nR	ESG effort	✓	✗	✗
Our study	S + nR	Quantity	✓	✓	✓

Note: “S”, “R”, and “M” stand for supplier, retailer, and manufacturer, respectively. The second column of the table lists different supply chain structures. For example, 2S + 2R represents a supply chain structure that includes two upstream suppliers and two downstream retailers.

.

3. Model Setting

We consider a two-echelon supply chain containing one supplier (S) and multiple retailers ($i\in I$, $i=1,2,\dots ,n$), where the supplier sells a product to n retailers and charges the uniform wholesale price w. The retailers compete in the same market, and each retailer simultaneously decides on an order quantity $q_i$. Then, $Q={\displaystyle \sum _{i\in I}}{q}_i$ denotes the total quantity the supplier provides to the n retailers. Suppose that retailers compete á la Cournot and the market-clearing price follows an inverse demand function

$$\begin{array}{c}{p}_i=a-q_i-b\sum _{i^{\prime }\in I,i^{\prime }\ne i}{q}_{i^{\prime }},\end{array}$$

(1)

where b$(0<b\le 1)$ measures the substitution rate of n retailers’ products and can also represent the intensity of product competition (the larger the b, the more intense the competition). The fundamental market potential a is normalized to be 1. This normalization eliminates the units of demand, allowing for scale-free comparisons of price and quantity—an approach commonly adopted in Cournot models (see Singh and Vives [46] and Adida and DeMiguel [47]).

The supplier determines its effort x to increase the ESG level. The cost of the supplier’s ESG effort is $k{x}^2$, where $k>0$ is the coefficient of the increasing marginal cost of the ESG effort. A larger k represents a relatively lower efficiency of the supplier’s ESG effort. Retailers cannot directly affect the suppliers’ ESG, but they can indirectly affect the suppliers’ decision-making x by investing in their capabilities [38]. In industrial practices, the retailer’s investment activities often refer to investment in the supplier’s development projects, the adoption of green technology, or the implementation of environmental standards and codes of conduct [48]. The investment decision of each retailer is modeled as $\lambda \in [0,1)$, which indicates that the degree of supplier’s ESG effort cost is reduced owing to the enhanced capability [28]. The retailer’s investment decision is supposed to be fixed, and each retailer exerts the same level of investment effort. To some extent, this hypothesis is reasonable for two reasons: First, our focus is on the effect of the increasing number of retailers on their incentives to invest in supplier’s ESG rather than on the previously well-studied mechanisms of cooperation among retailers based on cost or revenue sharing [39]; second, this assumption is consistent with the observation in practice that, in the presence of multiple competing retailers in a market, these retailers usually enter into agreements voluntarily to determine a fixed investment level. For instance, following the outbreak of the Rana Plaza collapse in Bangladesh, the 25 apparel retailers involved signed an agreement to invest in the establishment of a collective five-year building fire safety program [11]. Furthermore, when the total investment level of multiple retailers exceeds the supplier’s ESG costs (i.e., $n\lambda \ge 1$), the supplier’s marginal ESG cost becomes non-positive, eliminating the incentive to engage in ESG initiatives and undermining the core logic that retailers’ costly investments indirectly drive the supplier’s ESG improvement. Therefore, we assume that $n\lambda <1$, meaning that the total investment by n retailers is not sufficient to cover the supplier’s SR costs completely.

The supplier’s ESG effort x can reduce violation risk and improve brand image for supply chain firms, which will increase the ESG benefits ${\tau }_{S}xQ$ and ${\tau }_{R}x{q}_i$ for each supplier and each retailer, where ${\tau }_S$ and ${\tau }_R>0$ denote the degree of the marginal ESG benefits of the supplier and the retailer. This formulation of the ESG benefit is similar to the social responsibility objective in the study of Jiang et al. [49] and Wu et al. [50]. Differentiating from the previous literature, we extend this setting to the context of supply chains and suppose that the ESG preferences of the supplier and the retailers are heterogeneous; that is, ${\tau }_R$ may be either larger or smaller than ${\tau }_S$. Then, the profit functions of each supplier and retailer can be, respectively, written as

$$\begin{array}{c}{\pi }_S=wQ+{\tau }_{S}xQ-(1-n\lambda )k{x}^2,\end{array}$$

(2)

$$\begin{array}{c}{\pi }_{Ri}=(p_i-w)q_i+{\tau }_{R}x{q}_i-\lambda k{x}^2.\end{array}$$

(3)

According to Equations (2) and (3), the supply chain profit is given by

$$\begin{array}{c}\mathrm{\Pi }={\pi }_S+\sum _{i\in I}{\pi }_{Ri}.\end{array}$$

(4)

Following the study of [46], using a similar utility function for a representative consumer, we have the consumer surplus

$$\begin{array}{c}CS=\sum _{i\in I}(q_i-{\displaystyle \frac{1}{2}}{q}_i^2)-b\sum _{i\in I,i\ne i^{\prime }}{q}_i{q}_{i^{\prime }}-\sum _{i\in I}{q}_i{p}_i.\end{array}$$

(5)

where the first term ${\displaystyle \sum _{i\in I}}(q_i-{\displaystyle \frac{1}{2}}{q}_i^2)$ represents the total intrinsic utility obtained from all products, the second term $b{\displaystyle \sum _{i\in I,i\ne i^{\prime }}}{q}_i{q}_{i^{\prime }}$ reflects the disutility arising from product substitutability, and the last term ${\displaystyle \sum _{i\in I}}{q}_i{p}_i$ corresponds to consumers’ total payment.

We adopt the ESG level of total quantity in the supply chain as the total ESG benefit, which is represented by

$$\begin{array}{c}E=xQ.\end{array}$$

(6)

This formulation captures the idea that the overall ESG benefit depends jointly on the supplier’s ESG effort and the total output in the supply chain, which reflects the aggregated impact of ESG practices on production and consumption activities. This definition is consistent with prior studies on environmental and social benefit modeling [33,51], where the total benefit increases with both the intensity of ESG effort and the scale of production.

According to Equations (4)–(6), social welfare is

$$\begin{array}{c}SW=\mathrm{\Pi }+CS.\end{array}$$

(7)

The notations used in this paper are listed in

Table 2. Definition of notations.

Notation	Description
w	The supplier’s wholesale price
$q_i$	The retailer i’s order quantity
x	The supplier’s ESG effort, $x\in \{0,1\}$
$\lambda$	The retailer’s investment level
b	The substitution rate of n retailers’ products, $b\in (0,1)$
${\tau }_S$	The marginal ESG benefits of the supplier
${\tau }_R$	The marginal ESG benefits of the retailer
k	The coefficient of the marginal cost of the supplier’s ESG effort
N	The total number of retailers
n	The number of invested retailers
d	The wholesale price premium offered by the supplier

.

The decision sequence, illustrated in Figure 2, for this game problem is illustrated as follows. At time 1, the retailer decides the ESG investment level $\lambda$ (in the following analysis, we determine the optimal investment strategies that maximize the retailer’s profit, mainly for the sake of analysis. This processing is also adopted in the study of Zhou et al. [52] and Wang et al. [53]). At time 2, for any given retailer’s investment $\lambda$, the supplier determines its ESG effort x. At time 3, the supplier determines its wholesale price w. At time 4, each retailer i determines its order quantity $q_i$ simultaneously.

4. Equilibrium Analysis

We highlight the role of retailer competition in influencing market outcomes. We then compare the insights from classic models with one or two retailers to those obtained when multiple retailers compete simultaneously. In Section 4.1, we first derive the supplier’s ESG effort, wholesale price, retailer’s order quantity, and their corresponding profits in equilibrium. Anticipating their equilibrium decisions, in Section 4.2, we further examine the investment incentive of the retailer under multiple retailer competition, and we investigate the impacts of the retailer’s investment on total ESG benefits, supply chain profits, and social welfare.

4.1. Equilibrium Characteristics

Solving the game problem between the supplier and multiple retailers, the equilibrium results obtained are shown in Theorem 1.

Theorem 1.

The equilibrium decisions and profits of the supplier and the retailer are summarized as follows:

(i) 

The supplier’s optimal ESG effort is $x^{*}={\displaystyle \frac{n({\tau }_S+{\tau }_R)}{4(2-b+bn)(1-n\lambda )k-n{({\tau }_S+{\tau }_R)}^2}}$, and the optimal wholesale price is $w^{*}={\displaystyle \frac{2(2-b+bn)(1-n\lambda )k-n({\tau }_S+{\tau }_R){\tau }_S}{4(2-b+bn)(1-n\lambda )k-n{({\tau }_S+{\tau }_R)}^2}}$. The retailer’s optimal order quantity is $q_i^{*}={\displaystyle \frac{2(1-n\lambda )}{4(2-b+bn)(1-n\lambda )k-n{({\tau }_S+{\tau }_R)}^2}}$.

(ii) 

The supplier’s optimal profit is ${\pi }_S^{*}={\displaystyle \frac{n(1-n\lambda )}{4(2-b+bn)(1-n\lambda )k-n{({\tau }_S+{\tau }_R)}^2}}$. The retailer’s optimal profit is ${\pi }_{Ri}^{*}={\displaystyle \frac{k[4{(1-n\lambda )}^{2}k-n^2{({\tau }_S+{\tau }_R)}^2\lambda ]}{{[4(2-b+bn)(1-n\lambda )k-n{({\tau }_S+{\tau }_R)}^2]}^2}}.$

Theorem 1 indicates that when retailers are symmetric, the equilibrium order quantity $q_i^{*}$ and profit ${\pi }_{Ri}^{*}$ of any two retailers are equal. Notably, the marginal ESG benefits of the supplier and the retailer ${\tau }_S$ and ${\tau }_R$ have different effects on the wholesale price w. As we all know, the supplier’s profit comes from two parts: One is product sales revenue, and the other is the ESG benefit. Hence, the supplier will weigh its own ESG benefit and that of the retailer to determine its wholesale price. Moreover, the profit of the supplier is greater than the total profits of the retailers, i.e., ${\pi }_S^{*}>n{\pi }_{Ri}^{*}$, which signifies that the supplier makes a higher profit than the retailer. Consequently, to prevent retailers from reducing their investments and withdrawing from the market, the supplier is incentivized to reduce its wholesale prices when its marginal ESG benefit is larger than that of the retailer.

Then, we restrict our attention to Theorem 1 to derive comparative static outcomes regarding how product competition intensity and the retailers’ number affect the expected ESG effort, order quantity, and wholesale price decisions, as shown in Lemma 1.

Lemma 1.

At equilibrium, the supplier’s ESG effort $x^{*}$, wholesale price $w^{*}$, quantity $Q^{*}$, and the retailer’s order quantity $q_i^{*}$ possess the following properties:

(i) 

$x^{*}$ is decreasing in b; $x^{*}$ is increasing in n.

(ii) 

$q_i^{*}$ and $Q^{*}$ are decreasing in b; $Q^{*}$ is increasing in n, and $q_i^{*}$ is decreasing in n if and only if $n<n_r$.

(iii) 

$w^{*}$ is increasing in b if and only if ${\tau }_S>{\tau }_R$; $w^{*}$ is decreasing in n if and only if ${\tau }_S>{\tau }_R$, where $n_r={\displaystyle \frac{1}{n}}-{\displaystyle \frac{{\tau }_S+{\tau }_R}{n\sqrt{4bk}}}$.

Lemma 1 (i) reveals that the increased product competition intensity b leads to a reduced product demand, inhibiting the supplier from increasing its ESG effort. In contrast, although the growing number of retailers will intensify horizontal competition and decrease product orders, the increased retailers’ number n incentivizes the supplier’s ESG effort. It occurs because the growing number of retailers enables the supplier to generate more cost savings in the supplier’s ESG effort. Lemma 1 (ii) shows that the increased product competition b has a dampening effect on the order quantity. Because the total demand Q is driven by $q_i$ ($Q=nq$), the effects of b on $Q^{*}$ are congruent with the effects on $q_i^{*}$. Moreover, as the number of retailers n increases, the total demand Q becomes more prominent because of the strategic competition effect among multiple retailers [15]. On the other hand, we find that the growing number of retailers n may induce each retailer to order more. This result seems to contradict the prevailing view that the growing number of retailers n always leads to a lower order quantity [15,45,54]. Nevertheless, we justify our result because if the retailers’ number is sufficiently large, i.e., $n\ge n_r$, each retailer’s externality benefit generated by other retailers’ investments can compensate for the losses caused by retailer competition. Thus, each retailer is willing to increase its order quantity to gain a higher ESG benefit.

Extant studies related to the Cournot model reveal that the wholesale price is unaffected by the increased retailers’ number [19]. However, as shown in Lemma 1 (iii), we demonstrate that the heterogeneity of ESG benefits among the supplier and the retailer acts a vital role in determining the wholesale price. The reason is mainly because, as the retailers’ numbers increase, the ESG effort of the supplier and total demand from all retailers increase; however, each retailer reacts and orders less to avoid the intensified horizontal competition. Therefore, when the supplier’s marginal ESG benefit is larger than that of the retailer, i.e., ${\tau }_S>{\tau }_R$, the increase in ESG benefit ${\tau }_{S}xQ$ with respect to the supplier is greater than that with respect to the retailer ${\tau }_{R}x{q}_i$. Then, in order to avoid an excessive reduction in product sales $wQ$, the supplier reacts to reduce the wholesale price to stimulate each retailer’s order quantity $q_i$. The logic behind the impact of the product competition b on the wholesale price decision is similar to that of n, which we will omit here. This result implies that when considering the heterogeneity of marginal environmental benefit between the supplier and retailer, the retailer may accrue market power to drive down the wholesale price by investing more or purchasing less.

4.2. The Retailer’s Optimal Investment Decision

In this section, we focus on the optimal investment decision of the retailer in the context of multiple retailer competition. Although retailers’ investments bring ESG benefits for them, profit-driven retailers treat ESG initiatives as pure cost items, which will reduce their production and operational performance. However, we demonstrate that, under certain conditions, retailers are motivated to invest not only for the increase in ESG benefits but also for the increase in sales revenue, as given in Proposition 1.

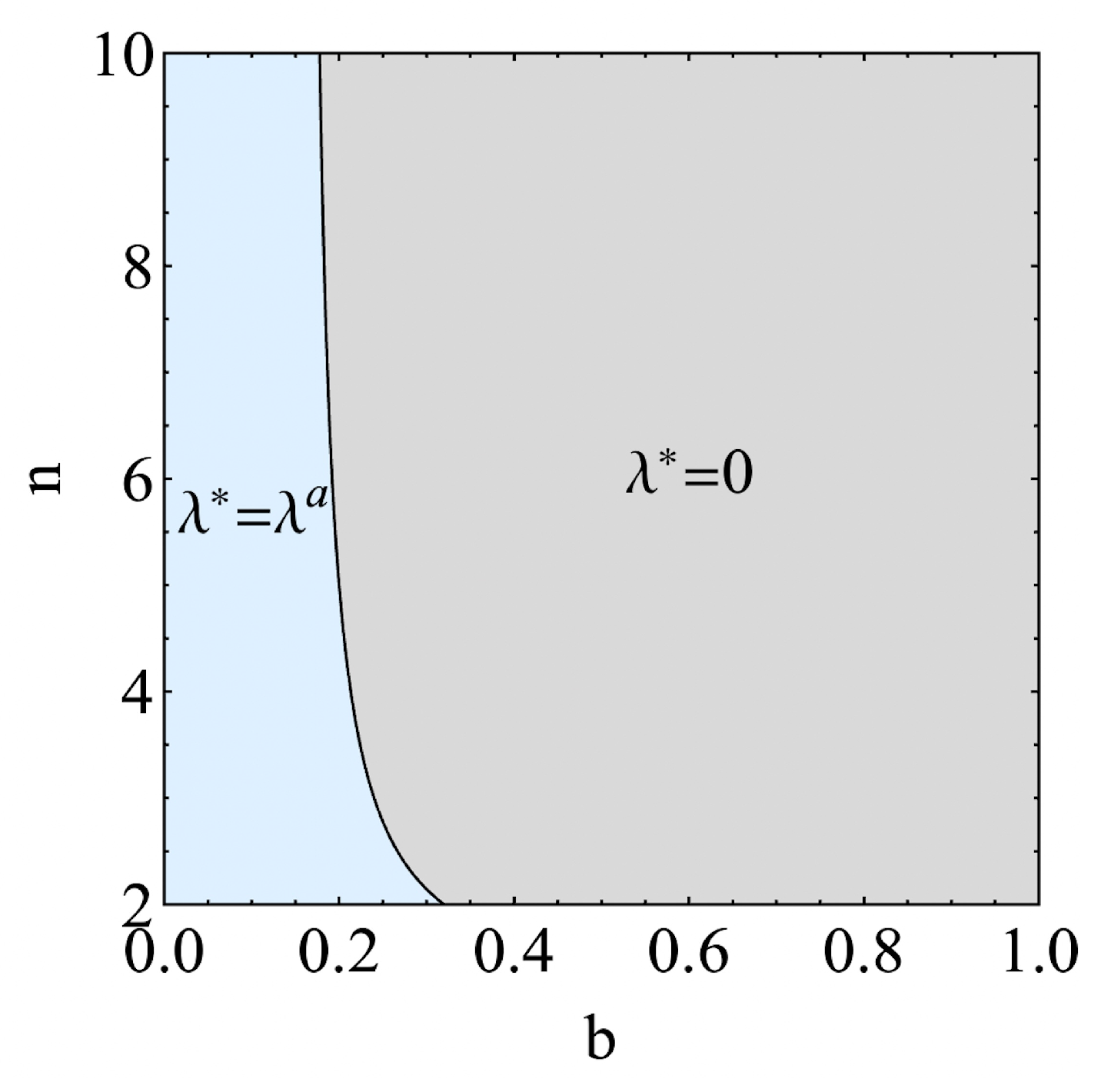
Proposition 1.

The retailer’s optimal investment decision ${\lambda }^{*}$ is as follows:

(i) 

The retailer’s optimal investment decision is ${\lambda }^{*}={\lambda }^a$ if $b<{\displaystyle \frac{{({\tau }_S+{\tau }_R)}^2}{4k}}$ or $b\ge {\displaystyle \frac{{({\tau }_S+{\tau }_R)}^2}{4k}}$ and $n<n^a$.

(ii) 

The retailer’s optimal investment decision is ${\lambda }^{*}=0$ if $b\ge {\displaystyle \frac{{({\tau }_S+{\tau }_R)}^2}{4k}}$ and $n\ge n^a$, where $n^a={\displaystyle \frac{4bk}{4bk-{({\tau }_S+{\tau }_R)}^2}}$, ${\lambda }^a={\displaystyle \frac{n{({\tau }_S+{\tau }_R)}^2-4b(n-1)k}{4nk(4-b+bn)}}$.

Note that, by simple calculation, we can conclude that the supplier can always benefit from the retailer’s investment, as the supplier’s ESG benefit is enough to cover the potential revenue loss. However, Proposition 1 reveals that the retailer does not necessarily benefit from its investment depending on the product competition intensity b and the number of retailers n. Caro et al. [21] show that an audit mechanism by which two buyers audit their upstream supplier jointly and share the total audit costs induces the buyers to exert their ESG effort than if they audit independently. The underlying reason for this result is that two buyers can afford a higher ESG effort cost through cost-sharing. However, we demonstrate that the retailer may be reluctant to make investments when the number of retailers exceeds a certain threshold.

The increased number of retailers produces two conflicting effects on each retailer’s investment incentive. On the one hand, it improves the retailers’ total investment level, motivating the supplier to increase its ESG effort, and thus, each retailer can gain more positive externality benefits from the other retailers’ investments: That is to say that the increased number of retailers captures the fact that each retailer can gain an enlarged ESG benefit through the cost-sharing mechanism. On the other hand, recall from Lemma 1 (i) that a more significant number of retailers induces the retailers to order more, which can lead to a significant drop in sales prices. Consequently, the growing number of retailers intensifies horizontal competition and undermines the sales revenue of the retailer, which, in turn, reduces the retailer’s investment incentive. When the product’s competition intensity is low, i.e., $b<{\displaystyle \frac{{({\tau }_S+{\tau }_R)}^2}{4k}}$, a growing number of retailers makes nearly no contribution to exacerbating the product’s competition. Thus, no matter the number of retailers, the retailer’s optimal investment level is ${\lambda }^a$. In contrast, when the product competition becomes intense, i.e., $b\ge {\displaystyle \frac{{({\tau }_S+{\tau }_R)}^2}{4k}}$, the retailer’s optimal decision is constrained by the retailers’ number n.

In the case where competing retailers’ numbers are small, i.e., $n<n^a$, the benefit from the ESG effort is substantial compared to the sales loss from the intensified competition among retailers, so the retailer can benefit from the increased investment if and only if $\lambda <{\lambda }^a$. This result contributes to explaining why there is always an optimal ESG effort in the study of Caro et al. [21], in which two retailers compete. However, in the case where the competing retailers’ numbers are large, i.e., $n\ge n^a$, the internal competition among retailers becomes more intense such that the damaging sales loss is more significant than the positive ESG benefit. Hence, the retailer will be reluctant to make an investment.

The results in Proposition 1 suggest that, in addition to the intensity of product competition, the number of competing retailers is an essential driving factor in the choices of investment strategy of the retailer, a factor that has often been underestimated in previous studies. In essence, regardless of product competitiveness, retailers are encouraged to invest as long as the number of retailers is manageable.

Furthermore, we examine how the retailer’s investment $\lambda$ affects the total ESG benefit, the supply chain profit, and the social welfare, as shown in Corollary 1.

Corollary 1.

The impacts of the retailer’s investment λ on the total ESG benefit $E^{*}$, the supply chain profit ${\mathrm{\Pi }}^{*}$, and social welfare $S{W}^{*}$ are as follows:

(i) 

$E^{*}$ is increasing in λ.

(ii) 

If $\lambda <{\lambda }_T^{*}$, ${\mathrm{\Pi }}^{*}$ is increasing in λ; otherwise, ${\mathrm{\Pi }}^{*}$ is decreasing in λ.

(ii) 

If $\lambda <{\lambda }_w^{*}$, $S{W}^{*}$ is increasing in λ; otherwise, $S{W}^{*}$ is decreasing in λ, where ${\lambda }_T^{*}={\displaystyle \frac{1}{n(3-b+bn)}}$ and ${\lambda }_W^{*}={\displaystyle \frac{3-b+bn}{7-3b+3bn}}$.

Corollary 1 shows that the total ESG level $E^{*}$ always increases with the retailer’s investment, since the retailer’s investment raises the total demand Q and ESG effort x. However, when the investment level is high, i.e., $\lambda \ge {\lambda }_T^{*}$, the rising supplier’s profit cannot fully compensate for the total retailer’s potential loss, and hence, the supply chain profit ${\mathrm{\Pi }}^{*}$ decreases as investment increases. Similarly, social welfare $S{W}^{*}$ also increases with the number of retailers when the investment level is low, i.e., $\lambda <{\lambda }_W^{*}$. The reason is mainly because, although the investment can positively affect the total ESG level and consumer surplus, the negative effect of decreased supply chain profit is enlarged by the increased investment level. Moreover, when $\lambda <{\lambda }_T^{*}$, the total ESG, the supply chain profit, and the social welfare can be aligned.

5. Asymmetric Investment Scenario

In practice, due to the existence of free-riding behavior, not all retailers are willing to invest in their common suppliers. Therefore, in this section, we consider the heterogeneous retailer scenario where competing retailers make asymmetric investments. Suppose that there are N competing retailers, where the number of retailers i in set I who invests (invested retailer) is n and the number of retailers u in set U who do not invest (non-invested retailer) is $N-n$. We assume ${\tau }_R={\tau }_{Ri}={\tau }_{Ru}$, which means that all retailers have identical ESG benefits regardless of whether they invest or not, since all retailers with identical market shares purchase the same products from the supplier. A similar assumption is made by Zhu et al. [44] and Guo et al. [55]. In Section 6.1.2, we relax this assumption by considering another heterogeneous retailer scenario with asymmetric market shares, in which retailers’ ESG benefits positively correlate with their market shares. Our results demonstrate that the main conclusions remain unchanged. Additionally, to incentivize retailers to exert a higher level of investment, the supplier offers the retailer i a fixed wholesale price premium d. Then, the profit functions of the supplier, retailer i, and retailer u are

$$\begin{array}{c}{\pi }_S=(w-d)\sum _{i\in I}{q}_i+w\sum _{u\in U}{q}_u+{\tau }_{S}x(\sum _{i\in I}{q}_i+\sum _{u\in U}{q}_u)-(1-n\lambda )k{x}^2,\end{array}$$

(8)

$$\begin{array}{c}{\pi }_{Ri}=(p_i-w+d)q_i+{\tau }_{R}x{q}_i-\lambda k{x}^2,\end{array}$$

(9)

$$\begin{array}{c}{\pi }_{Ru}=(p_u-w)q_u+{\tau }_{R}x{q}_u.\end{array}$$

(10)

Solving the above game problem, Theorem 2 characterizes the equilibrium results under the heterogeneous retailer scenario.

Theorem 2.

Under the asymmetric investment scenario, the equilibrium decisions and profits of the supplier and the retailer are summarized as follows:

(i) 

The supplier’s optimal ESG effort is $x^{A*}={\displaystyle \frac{N({\tau }_S+{\tau }_R)}{T}}$, and the optimal wholesale price is $w^{A*}={\displaystyle \frac{2(2-b+bn)(N+2dn)(1-n\lambda )k-N({\tau }_S+{\tau }_R)[{\tau }_{S}N+({\tau }_S+{\tau }_R)dn]}{(2-b)NT}}$. The retailer u’s optimal order quantity is $q_u^{A*}={\displaystyle \frac{2[(2-b)N-2(2-b+bn)dn](1-n\lambda )k+dnN{({\tau }_S+{\tau }_R)}^2}{(2-b)NT}}$, and the retailer i’s optimal order quantity is $q_i^{A*}={\displaystyle \frac{2[(2-b)N-2(2-b+bn)dn](1-n\lambda )k+dnN{({\tau }_S+{\tau }_R)}^2+dNT}{(2-b)NT}}$.

(ii) 

The supplier’s optimal profit is ${\pi }_S^{A*}={\displaystyle \frac{d^{2}nN(N-n){({\tau }_S+{\tau }_R)}^2+[(b-2)N^2+4d^{2}n(2-b+bN)(N-n)](n\lambda -1)k}{(b-2)NT}}$. The retailer u’s optimal profit is ${\pi }_{Ru}^{A*}={\left(q_u^{A*}\right)}^2$ and the retailer i’s optimal profit is ${\pi }_{Ri}^{A*}={\left(q_u^{A*}\right)}^2+{\displaystyle \frac{d^2(N-2n)T^2+4(2-b)dN(1-n\lambda )T-{(2-b)}^2{N}^3{({\tau }_S+{\tau }_R)}^{2}k\lambda }{{(2-b)}^{2}N{T}^2}}$, where $T=4(2-b+bN)(1-n\lambda )k-N{({\tau }_S+{\tau }_R)}^2$.

Theorem 2 presents the asymmetrical equilibrium decisions and profits of retailer i and retailer u. By simple calculations, we can obtain $q_i^{A*}-q_u^{A*}={\displaystyle \frac{d}{2-b}}$. This result implies that wholesale price premium d can play a role in coordinating the order quantity among retailers. First, when the supplier charges the same wholesale price for different retailers, i.e., $d=0$, we can easily observe that $q_i^{A*}=q_u^{A*}$, so all retailers will respond to the wholesale price in the same manner: That is, no retailer invests, which will be detrimental to the supplier. Second, when $d>0$, retailer i can intuitively enjoy lower wholesale prices than retailer u and thus is motivated to increase investments and order quantities. Meanwhile, a competition effect exists among retailers, whereby the underlying competition among retailers causes retailer u to perceive an aggravated disadvantage in their wholesale price. Thus, anticipating the increase in wholesale price premium d of retailer i, retailer u reacts and holds back its order quantity.

Furthermore, we performed a comparative static analysis of the equilibrium results in the heterogeneous retailer scenario with the same relevant parameters as in Lemma 1. The analysis results are similar to Lemma 1, so we will not repeat them here. Notably, due to the positive externality effect caused by each retailer i ’s investment, the profit of retailer i may not be higher than that of retailer u. The details are provided in Lemma 2.

Lemma 2.

Under the asymmetric investment scenario, the profit comparison of the retailer i and the retailer u is as follows:

(i) 

When the number of retailer u is larger than that of retailer i, i.e., $N-n\ge n$, if $d>{\underline{d}}_1$, ${\pi }_{Ri}^{A*}>{\pi }_{Ru}^{A*}$; otherwise, ${\pi }_{Ri}^{A*}\le {\pi }_{Ru}^{A*}$.

(ii) 

When the number of retailer u is smaller than that of retailer i, i.e., $N-n<n$, we have the following:

a. If $n>{\underline{n}}_1$, ${\pi }_{Ri}^{A*}\le {\pi }_{Ru}^{A*}$;

b. If $n\le {\underline{n}}_1$ and $d>{\underline{d}}_1$, ${\pi }_{Ri}^{A*}>{\pi }_{Ru}^{A*}$; otherwise, ${\pi }_{Ri}^{A*}\le {\pi }_{Ru}^{A*}$, where the expressions of ${\underline{n}}_1$ and ${\underline{d}}_1$ are defined in Appendix A.

Lemma 2 reveals how the relative number of invested retailers and non-invested retailers in the market affects the wholesale price premium d on the retailers’ profits. It is acknowledged that since the order quantity of retailer i is more significant than that of retailer u, the greater the number of retailer i among a total of N retailers, the more intense the competition among retailers. When $N-n\ge n$, the internal competition among retailers is mild, and a higher wholesale price premium effect, i.e., $d>d_1$, can provide the retailer i a competitive advantage such that ${\pi }_{Ri}^{A*}>{\pi }_{Ru}^{A*}$. In contrast, when $N-n\le n$, the wholesale price premium advantage of retailer i is disputed by retailer competition. Thus, a sizeable wholesale price premium d does not guarantee that retailer i’s profit is more significant than that of retailer u. That is to say that the suppliers offering wholesale price premiums more widely among retailers can trigger a crowding-out effect: As the number of retailer i increases, the wholesale price advantage of each retailer i is reduced. Thus, the retailer i can benefit greatly from a higher wholesale price only when the number of retailer i is below a threshold value, i.e., $n\le {\underline{n}}_1$.

We then analyze the impact of investment on retailer i’s profit, as shown in Proposition 2.

Proposition 2.

Under the asymmetric investment scenario, the retailer i’s optimal investment decision ${\lambda }^{A*}$ is as follows:

(i) 

The retailer i’s optimal investment decision is ${\lambda }^{A*}={\lambda }^h$ if $d>{\underline{d}}_2$ and $n>{\underline{n}}_2$.

(ii) 

The retailer i’s optimal investment decision is ${\lambda }^{A*}=0$ if $d\le {\underline{d}}_2$ or $n\le {\underline{n}}_2$, where the expressions of ${\underline{d}}_2$, ${\underline{n}}_2$ and ${\lambda }^h$ are defined in Appendix A.

Proposition 2 indicates that the retailer i may be motivated to increase its investment by a higher number of invested retailers, which is different from the result in the asymmetric investment scenario. Notably, Proposition 2 reflects the fact that, compared with the scenario where all retailers make investments, the competition among retailers in the scenario where only part of the retailers make investments is alleviated, as explained in Lemma 3. When the wholesale price premium is sufficiently high, i.e., $d\ge {\underline{d}}_2$, as the number of retailers i increases, the wholesale price premium cannot coordinate the order quantities such that each retailer i will order more; thus, the increase in the number of retailer i is detrimental to retailer’s sales revenue. Nevertheless, each retailer i can gain larger ESG benefit $x{q}_i$ due to a larger order quantity. Consequently, when the number of retailer i is large, the ESG benefit is more significant than the sales loss, inducing the retailer i to increase its investment. That is to say that despite the intense competition, the retailer is supposed to make the investment when the wholesale price premium is sufficiently large.

By comparing the conclusion of Proposition 2 with that of Proposition 1, we can conclude that the retailer should consider not only the market competition structure but also the investment structure when making investment decisions. Moreover, for the supplier, what is essential is to understand the competition structure of the downstream industry and strategically set wholesale price premiums to coordinate profits between the invested retailer and the non-invested retailer.

6. Discussion and Numerical Simulation

In this section, we examine the two extensions and conduct numerical simulations to validate the robustness of our main results.

6.1. Discussion

In Section 6.1.1, we extend our examination to the scenario with competing retailer source products from multiple suppliers; in Section 6.1.2, we consider another heterogeneous retailer scenario with asymmetric market shares.

6.1.1. Multiple Suppliers

In the base model, we demonstrate that a supplier always benefits from multiple retailer competition. However, as suggested by Korpeoglu et al. [20], an increase in the suppliers’ number may weaken each supplier’s power and further affect the retailer’s investment decision. For this reason, we extend the base model to allow multiple competing retailers to source products from multiple suppliers. We assume that the number of suppliers and retailers is m and n, respectively. Each supplier j sells $q_j$ to retailers at a wholesale price $w_j$, and each retailer orders the quantity $q_i$ from the suppliers. Hence, ${\displaystyle \sum _{j=1}^m}{q}_j={\displaystyle \sum _{i=1}^n}{q}_i$. Following the study of Corbett and Karmarkar [19], the wholesale price is determined by the market-clearing conditions in a market with multiple suppliers and multiple retailers. Thus, in this section, the supplier is assumed to decide on the production quantity at time 3 by anticipating its impact on the wholesale price. The remaining model setting is the same as that in Section 6.2. By analyzing and comparing the equilibrium solution (see Appendix B for details), we find that the retailer is motivated to make the investment when the number of retailers is sufficiently high, which proves that our result in Proposition 1 is robust. Moreover, we demonstrate that the increased number of suppliers weakens the selling power of each supplier, which in turn lowers the supplier’s wholesale price and improves the retailer’s investment motivation.

6.1.2. Asymmetric Market Share

Recall the assumption in Section 6 that the invested and non-invested retailers have symmetric market share. In essence, the size of the retailer’s market share, to some extent, represents different market power, i.e., bargaining power or consumers’ perceived brand strength. Apparently, in practice, the invested retailer may have stronger market power than the non-invested retailer (Wu et al. [56]). To that end, we relax the assumption in Section 6 and consider that the invested retailer and the non-invested retailer have asymmetric market shares. Without loss of generality, we assume that the invested retailer and non-invested retailer are 1 and $\theta$ ($\theta <1$), respectively. We adopt a Cournot competition model consistent with the base model, and the inverse demand functions of the invested retailer and the non-invested retailer are given by

$$\begin{array}{c}{p}_i=1-q_i-b\sum _{i^{\prime }\in I,i^{\prime }\ne i}{q}_{i^{\prime }}-b\sum _{u\in U}{q}_u,\\ p_u=\theta -q_u-b\sum _{u^{\prime }\in I,u^{\prime }\ne u}{q}_{u^{\prime }}-b\sum _{i\in I}{q}_i.\end{array}$$

Moreover, the retailers’ ESG benefits are positively related to their market shares. That is to say that the invested and non-invested retailers are ${\tau }_{S}x{q}_i$ and $\theta {\tau }_{R}x{q}_u$, respectively. In this case, a larger market share represents that the retailer can gain a larger ESG benefit from the improved ESG performance of the supplier. Consequently, the supplier does not necessarily set different wholesale prices for retailers to incentivize retailers to invest. The settings of the rest of the model are consistent with those of Section 6.

We next derive the equilibrium results under the asymmetric market share scenario (see Appendix B for details). Due to the complexity of the model analysis, the numerical analysis is performed to investigate the optimal investment decision of the retailer. We show that the optimal investment decision of the retailer i depends on the size of the retailer u’s market share $\theta$ and retailer i’s number n. First, for any given n, the larger the $\theta$, the more reluctant retailer i is in making investments. In particular, when $\theta$ is sufficiently large, the retailer is willing to invest only when the number of retailer i is large enough. This finding is consistent with that of Section 6 and proves the robustness of the main findings. Second, when $\theta$ is small, regardless of the number of retailers, the retailer is willing to invest. This is because the intensified competition among retailers caused by the increased number of retailers induces the supplier to set a lower wholesale price for the retailers. In this context, the invested retailers who dominate the share market can reap greater benefits. This result implies that a relatively small market share of the non-invested retailer contributes to a “win-win” outcome for both invested and non-invested retailers.

6.2. Sensitivity Analysis

To make the mathematical derivations clearer and easier to understand, we conducted numerical simulations in MATLAB version 2021a under the assumptions specified in the theoretical model. All parameters were calibrated based on field investigations of retail and manufacturing enterprises, complemented by empirical evidence from academic and industrial reports. The calibration logic and rationale for each key parameter are summarized below. The investment cost coefficient k reflects the relative marginal cost of ESG investment. The retailer’s ESG investment cost k is generally high. For example, according to the China Environmental Statistics Yearbook (2024) and the Report on the State of the Ecology and Environment in China (2024), environmental protection investments generally account for 1–3% of fixed-asset investments in manufacturing sectors and exceed 5% in highly polluting industries such as chemicals and steel [57]. Therefore, based on the proportional relationship in the profit function and a reasonable estimation of the firm’s revenue, the baseline level of this parameter is set relatively high at 50. To maintain numerical comparability with the benefit coefficients, k was normalized to the interval [50, 200], where lower values represent low-cost industries and higher values correspond to high-pollution, high-cost sectors. The marginal ESG benefit coefficients measure the incremental environmental or social benefit obtained per unit of ESG investment by the supplier and the retailer, respectively. Following the research of Zhang and Qin [58] regarding consumers’ environmental preference and the studies of Lee and Park [59] and Cao et al. [1] regarding the effect of ESG investments on the environmental returns of upstream and downstream firms, we set ${\tau }_S$ and ${\tau }_R$ within [0, 8] to reflect the heterogeneity of ESG benefit distributions across the supply chain. The product substitutability coefficient b captures market-competition intensity and was set within [0, 1], consistent with standard Cournot-type competition models [46,47]. All parameters were proportionally normalized to ensure that simulation outcomes remained realistic and comparable without altering the intrinsic functional relationships among variables. This calibration ensures both the empirical relevance and theoretical consistency of the simulation analysis.

6.2.1. The Impact of Retailer’s Number and Marginal ESG Benefit on Retailer’s Optimal Investment Decision

As shown in Figure 3, in the baseline model, retailers are willing to invest in improving the upstream supplier’s ESG performance only when the number of retailers is not too large and the product competition is not too intense. We further examine the effects of the increase in retailer number and the heterogeneity of marginal ESG benefits on the retailers’ optimal ESG investment decisions. As illustrated in Figure 4a, the retailer’s optimal ESG investment level decreases with an increase in the number of retailers. This occurs because the losses caused by intensified competition outweigh the additional ESG benefits, thereby discouraging retailers from investing. By comparing Figure 4a and Figure 4b,c, an increase in marginal ESG benefits significantly enhances the supplier’s optimal ESG investment level. However, the results show that the effect of n on the retailer’s optimal ESG investment level remains robust to changes in the marginal benefit ratio ${\tau }_S/{\tau }_R$. More interestingly, as shown in Figure 4d, the ratio ${\tau }_S/{\tau }_R$ affects how n influences the optimal wholesale price decision. When ${\tau }_S/{\tau }_R>1$, the supplier gains higher ESG benefits and tends to lower the wholesale price to stimulate demand as the number of retailers increases. In contrast, when ${\tau }_S/{\tau }_R<1$, the retailers gain higher ESG benefits, prompting the supplier to raise the wholesale price to increase its own sales revenue.

We further explore the effect of the number of retailer i on their optimal investment decisions ${\lambda }_h$ in an asymmetric investment scenario. The results indicate that retailers are motivated to raise their investment levels only under moderate competition—when the number of retailers remains small—and when a generous wholesale discount is offered (see Figure 5b). Specifically, as shown in Figure 5b, there exists an optimal retailer number that motivates the retailer i to exert the highest level of investment effort. When retailer i’s number is small, the optimal investment level ${\lambda }^h$ increases with the growing number of invested retailers n because the competition among retailers is moderate and the value of the wholesale price premium d is significant for retailer i. Conversely, when the retailer i’s number is large, the horizontal competition is intense, and the value of wholesale price premium effect d of each retailer i is reduced because of the crowding-out effect that is explained in Lemma 2. As a result, the optimal investment level ${\lambda }^h$ decreases as the number of invested retailers n increases. Hence, to mitigate the crowding-out effect, the supplier is advised to carefully use the wholesale price premium mechanism: that is, do not offer excessively high wholesale price premiums to invested retailers to limit the number of invested retailers entering the market.

6.2.2. The Profit Comparison of Invested and Non-Invested Retailers Under Asymmetric Investment Scenario

Figure 6 illustrates how the wholesale price subsidy d and the number of investing retailers n jointly influence the profits of investing and non-investing retailers, which is consistent with the conclusions of Lemma 2. When the number of investing retailers is smaller than that of non-investing retailers, i.e., $N-n\ge n$, the overall ESG benefit of the system remains relatively low. In this case, when the wholesale price subsidy exceeds a certain threshold $d>\underline{d_1}$, non-investing retailers suffer from a greater wholesale price disadvantage, and the free-riding gains are diluted by the large number of non-investors. Consequently, their profits become lower than those of the investing retailers. Conversely, when the subsidy level is small, the free-riding ESG benefits can offset the wholesale price disadvantage, allowing non-invested retailers to earn higher profits, as shown in Figure 6a. In contrast, when the number of investing retailers exceeds that of non-invested ones, i.e., $N-n<n$, the total ESG benefit of the supply chain increases significantly. In this situation, only when the number of investing retailers is relatively small and the subsidy level is sufficiently high, i.e., $n\ge \underline{n_1}$ and $d<\underline{d_1}$, will the investing retailers achieve higher profits than the non-invested retailers. As the number of investing retailers increases, the crowding-out effect reduces their wholesale price advantage, whereas non-invested retailers can still obtain considerable ESG gains through free-riding. Thus, the profits of investing retailers become lower than those of non-invested ones, as shown in Figure 6b.

Overall, the results in Figure 6 demonstrates that the relative profitability of investing versus non-invested retailers depends on the interaction between the number of investors and the level of the wholesale price subsidy. Excessive subsidies or excessive numbers of investing retailers both weaken investment incentives, whereas a moderate subsidy and balanced investment participation help sustain the profitability advantage of investing retailers.

7. Conclusions

This paper examines how the profit-driven retailer employs its investment to motivate the supplier’s ESG in a market where multiple retailers compete and the supplier and retailer have heterogeneous ESG benefits. To investigate the conditions that prompt the retailer to invest, we first examine the base model where multiple retailers make symmetric investments and then carry out extensions to analyze heterogeneous retailers with different investment decisions. Our results reveal that the number of competing retailers may be an essential driving factor in the investment strategy choices of the retailer. Our work provides valuable managerial insights for competing retailers to optimize their investment decisions.

7.1. Main Findings

First, our analysis reveals that the retailer may be incentivized to increase investments when the retailer’s number falls below a certain threshold. In contrast to classic research that considers two retailers [17,21], we develop a model that incorporates competition among multiple retailers, enabling us to analyze how the number of retailers and the amount of investment jointly determine the decisions of the supplier and the retailer. Regardless of the retailers’ number, as expected, with an increase in the retailer’s investment, the supplier is motivated to increase its ESG effort because of the increased total order quantity and decreased ESG effort cost. However, in addition to the effects of product competition intensity, which have been extensively studied in the previous literature, our analysis reveals that the number of retailers restricts the optimal retailer’s investment decision. Specifically, when the retailers’ number is sufficiently large, the negative competition loss outweighs the positive SR benefit of the retailer, which inhibits their willingness to invest. Moreover, when there are a relatively small number of competing retailers, driven by the improved supplier’s ESG level and the increased total quantity, the increase in retailers’ investment can concurrently improve the total ESG benefit, supply chain profit, and social welfare.

Second, in the asymmetric investment scenario where only parts of retailers invest, we find that when the invested retailers is substantial, the retailer may be willing to increase its investment, which complements the results in the base model. Intuitively, the non-invested retailer always benefits from the invested retailer’s investment since it can free-ride on the positive externality effect created by the invested retailer’s investment. More interestingly, when the number of retailers is large, despite intense horizontal competition, the retailer remains incentivized to invest due to the presence of a wholesale price premium that alleviates internal competitive pressures. Consequently, the wholesale price premium by the supplier can serve as a coordination mechanism to align the profits of both the invested retailer and the non-invested retailer.

Third, we illustrate that the increased retailer number may prompt the supplier to reduce its wholesale price, indirectly increasing the retailer’s investment willingness. In previous studies, the marginal ESG benefits of the supplier and the retailer are assumed to be homogeneous and show that the changes in the number of retailers do not alter the magnitude of wholesale prices [15,45,60]. We relax this assumption and demonstrate that the heterogeneity of marginal ESG benefits between supplier and retailer grants the retailer market power to influence the wholesale price. This is because, as retailers’ numbers increase, the supplier weighs the increased ESG benefit brought by multiple retailers’ investment against the decreased sales revenue caused by intensified competition to determine the wholesale price. When the marginal ESG benefit of the supplier is more significant than that of the retailer, the supplier is prone to cut down its wholesale price to avoid a substantial decline in retailers’ total demand and attract more investment. This finding highlights the importance of the heterogeneity of the marginal ESG benefit in driving the retailer’s investment and mitigating retailer competition.

7.2. Management Insights

Our study provides the following managerial implications for retailers, suppliers, and policy makers. Firstly, retailers are supposed to keep the coalition size of investing members below the critical threshold to prevent excessive competition from eroding investment returns. When the supplier’s marginal ESG benefit exceeds that of the retailer, retailers are advised to negotiate wholesale-premium menus that align ESG incentives between both parties. Retailers operating in industries with existing ESG investment practices (e.g., IT and textiles) may benefit from joining such coalitions, whereas in emerging industries like new energy vehicles, where few retailers have yet to invest, excessive horizontal competition may discourage investment. Second, suppliers can use the wholesale price subsidy as a coordination mechanism to align ESG incentives across the supply chain. However, they should cap the number of premium recipients to avoid the crowding-out effect that diminishes the price advantage of investing retailers. When designed properly, a moderate subsidy structure can sustain long-term cooperation and enhance collective ESG performance. Third, governments should consider both the number of investing retailers and the overall industry scale when designing ESG promotion policies. In highly competitive industries, investment subsidies should be complemented by transparency mandates rather than direct wholesale price controls. Improving information transparency in multi-tier supply chains can help mitigate free-riding behaviors and strengthen retailers’ motivation to invest in ESG initiatives.

7.3. Limitations

This study has several limitations that should be acknowledged. First, the analysis mainly focused on supply chain structures involving a single retailer and multiple retailers, with an extension to settings where multiple retailers invest in multiple suppliers. However, real-world supply chain networks are often more intricate. For instance, some retailers may share suppliers while others have exclusive ones, leading to mixed network structures that are not captured in this model. Second, due to the limited transparency in sustainable supply chains, retailers may have incomplete information about their suppliers’ ESG investment costs, particularly in multi-tier supply chain hierarchies [28,61]. This lack of transparency poses challenges for retailers in accurately assessing the true costs and effectiveness of suppliers’ ESG initiatives. Third, the model assumes equal bargaining power between the supplier and retailers. In reality, the bargaining power over wholesale pricing and profit allocation often differs across participants, which could significantly affect the strategic behavior and outcomes of the supply chain [4,62]. Finally, consumers’ ESG preferences are treated as deterministic in this study, while, in practice, they are often uncertain and vary across segments. Moreover, retailers may possess more accurate or updated information about consumer preferences than suppliers, which may influence decision-making processes.

7.4. Future Research Directions

Building upon these limitations, several promising directions can be explored in future research. First, extending the model to hybrid supply chain structures—where some suppliers are shared among retailers while others remain exclusive—would help reveal new strategic dynamics and coordination challenges in ESG investment. Second, future work could incorporate incomplete or asymmetric information into the model, particularly concerning suppliers’ ESG investment costs and consumer ESG preferences. Investigating how such information asymmetry affects investment incentives, disclosure strategies, and contract design in multi-tier supply chains would provide deeper insights. Third, introducing heterogeneous bargaining power among supply chain members would allow for a more realistic exploration of price negotiation, profit sharing, and investment decisions under power asymmetry. Finally, considering consumer preference uncertainty through stochastic modeling or behavioral frameworks could enrich the understanding of market responses and improve the robustness of firms’ ESG investment and disclosure strategies.