Adaptive Deployment of Fixed Traffic Detectors Based on Attention Mechanism

Abstract

In urban intelligent transportation systems, the real-time acquisition of network-wide traffic states is constrained by limited sensor density and high deployment costs. To address this challenge, this paper proposes a learnable Detection Point Selection Module (DPSM), which adaptively determines the most informative observation points through an end-to-end attention mechanism to support full-map traffic state estimation. Distinct from conventional fixed deployment strategies, DPSM provides an adaptive detector configuration that, under the same number of loop sensors, achieves significantly higher estimation accuracy by intelligently optimizing their placement. Specifically, the module takes normalized spatial and temporal information as input and generates an attention-based distribution to identify critical traffic flow readings, which are subsequently fed into various backbone prediction models, including fully connected networks, convolutional neural networks, and long short-term memory networks. Experiments on the real-world NGSIM-US101 dataset demonstrate that three variants—DPSM-NN, DPSM-CNN, and DPSM-LSTM—consistently outperform their corresponding baselines, with notable robustness under sparse observation scenarios. These results highlight the advantage of adaptive detector placement in maximizing the utility of limited sensors, effectively mitigating information loss from sparse deployments and offering a cost-efficient, scalable solution for urban traffic monitoring and control.

1. Introduction

With the acceleration of global urbanization, traffic congestion has become one of the major challenges faced by large cities. The continuous increase in urban populations has placed growing pressure on transportation networks, thereby raising the demand for accurate traffic flow estimation. Precise traffic state estimation not only provides a decision-making basis for real-time traffic control, signal optimization, and travel prediction, but also offers critical support for emergency response and intelligent dispatching systems [1]. Therefore, accurately estimating the global state of urban traffic under conditions of limited observation data and sparse sensor deployment has become a core issue in the field of intelligent transportation systems.

However, current traffic monitoring systems in practice often suffer from insufficient numbers of sensors and uneven spatial distribution. Traditional monitoring equipment mainly relies on fixed traffic detectors, whose quantity and placement typically fail to cover the entire road network, resulting in detection blind spots and limited ability to capture dynamic traffic variations [2]. Hence, how to make full use of a limited number of sensor readings to accurately estimate the overall traffic state remains an urgent problem to be solved in traffic flow prediction.

In recent years, benefiting from the development of traffic big data and computing technologies, model-driven approaches based on deep learning have been widely applied to traffic flow modeling and prediction, yielding remarkable progress [3]. For example, in highway traffic state estimation, deep learning has achieved impressive results in predicting traffic flow, travel time, and road network conditions [4,5,6]. Nevertheless, most existing methods still rely on fixed or manually designed observation point configurations, which generally suffer from poor generalization. In particular, under conditions of highly volatile traffic flows or uneven sensor distribution, the prediction performance of such models often degrades significantly [7]. Against this background, dynamically selecting the most representative detectors from all available observation points has become crucial for reducing deployment cost and discovering more generalizable sensor configuration strategies.

Although many existing studies have improved traffic state estimation accuracy, they typically rely on fixed or manually designed detector layouts, which are difficult to generalize under real-world deployment constraints. This limitation creates a significant research gap: how to make full use of a limited number of sensors to capture the most informative traffic observations. To address this gap, the present work focuses on adaptive detector selection. By leveraging an attention-based learnable module, we aim to maximize the utility of limited sensors and guarantee estimation accuracy under varying deployment densities, thus providing a practical and scalable solution for real-world transportation systems.

To address the above problem, this paper proposes a Detection Point Selection Module (DPSM) based on an attention mechanism. Unlike traditional static sensor placement strategies, the DPSM is trained in an end-to-end manner and integrates the spatiotemporal features of traffic conditions to adaptively select the most representative observation points based on the actual variation in traffic flow. Specifically, the DPSM dynamically selects traffic flow inputs based on the learned attention weights, which are then used by subsequent models to predict the global traffic state. This dynamic selection mechanism effectively addresses the problem of sparse or uneven sensor deployment and significantly improves prediction accuracy under different observation point configurations. The main contributions of this paper are as follows:

• A DPSM is proposed to overcome the limitations of traditional static sensor placement, and it significantly enhances traffic state estimation accuracy by dynamically selecting the most representative observation points.
• Three DPSM-based models are constructed by incorporating spatiotemporal features of traffic flow, and their superior performance under various observation configurations is validated.
• Experiments on the real-world NGSIM-US101 traffic dataset demonstrate that the DPSM achieves strong robustness and high prediction accuracy under low-observation-point scenarios.

The structure of this paper is arranged as follows: Section 2 provides a literature review on traffic state estimation and fixed detector placement; Section 3 describes the proposed adaptive deployment method and the DPSM; Section 4 presents the experimental evaluation; Section 5 concludes the paper and discusses future work.

2. Related Work

2.1. Traffic State Estimation

Traffic state estimation is one of the core problems in intelligent transportation systems. It aims to accurately reconstruct and predict parameters such as traffic flow, speed, and density at present or in the future based on existing observation data. Existing traffic state estimation methods can be broadly categorized into model-driven and data-driven approaches [8]. Model-driven approaches are primarily based on physical traffic flow models and use real-time data as input for estimation. Typical methods include first-order Lighthill–Whitham–Richards (LWR) models, the cell transmission model (CTM), and Kalman filtering [9,10,11]. For example, Liu et al. proposed a Multi-layer Multiclass Cell Transmission Model (MMCTM) with multi-size cells, which overcomes numerical diffusion in conventional MCTMs and more accurately models heterogeneous traffic with different free-flow speeds [12]. Wang et al. developed a real-time freeway traffic state estimator based on stochastic macroscopic modeling and extended Kalman filtering, which adaptively estimates both model parameters and traffic states and has been successfully validated with a real dataset [13]. However, model-driven methods often rely on a series of assumptions, and improper model selection or insufficient calibration may lead to biased estimations. They also tend to perform poorly in noisy environments or under sudden traffic changes [14].

In recent years, with the rapid development of deep neural networks, data-driven approaches have shown remarkable advantages in traffic state estimation. These methods can learn from massive traffic datasets to capture complex spatiotemporal patterns and provide more accurate predictions. Common deep learning models include fully connected neural networks (NN), convolutional neural networks (CNN), recurrent neural networks (RNN), and long short-term memory networks (LSTM) [15,16,17,18,19]. Van Lint et al. proposed a highway travel time prediction method based on RNNs, significantly improving prediction accuracy [17]. Cui et al. combined the strengths of RNNs in prediction and designed a stacked unidirectional and bidirectional LSTM-RNN model for network-wide traffic state prediction, demonstrating strong robustness [20]. Ma et al. introduced LSTM to traffic flow prediction, effectively modeling temporal features and further improving forecasting accuracy [21]. In addition, Tisljaric et al. transformed speed information extracted from GPS data into curve images and applied convolutional neural networks to identify traffic states of road segments, achieving prediction accuracy over 90% [22]. To address the problem of sparse data in training, Dai et al. proposed a deformable convolutional neural network that introduces positional offsets in the receptive field, enabling adaptive extraction of deformation features [23]. Liang et al. used generative adversarial networks (GANs) to further explore traffic data characteristics. By generating data resembling real labels, the network achieved higher prediction accuracy during training [24].

Although these studies have demonstrated the strong capacity of deep learning in mining spatiotemporal features of traffic flow, most of them still rely on fixed or static sensor configurations and lack the ability to dynamically model and adaptively optimize observation point distributions. Current research focuses more on improving prediction performance, while relatively little attention has been paid to learning and optimizing sensor placement strategies. Therefore, under real-world constraints of limited observation and rapidly changing traffic conditions, existing methods lack sufficient robustness and flexibility.

2.2. Fixed Traffic Detector Deployment

Detector deployment has long been an important research topic in traffic state estimation and prediction. Traditional methods often adopt a hybrid numerical-graphical approach to optimize detector placement within a road network and enhance estimation accuracy. Guo et al. proposed an observability analysis algorithm based on multiple source mixed traffic sensors, which constructs an output matrix to study traffic system observability and optimizes the placement of both single-type and multi-type sensors to improve the coverage and representativeness of the sensor network [25]. Fu et al. proposed a multi-type traffic sensor location model that integrates multi-source data and considers link travel time covariance to enhance the accuracy of network-wide travel time estimation [26]. Tascikaraoglu et al. proposed a quadratic programming-based method for sensor location and link flow reconstruction, which determines the minimum number of measurements and sensor locations via a graphical approach and incorporates turn ratio sensors to achieve full network observability and accurate flow estimation [27].

With the development of simulation technologies, recent studies have adopted a “deploy-then-model” strategy, where various sensor layout schemes are preset, and estimation models are built to compare prediction performance. Hong et al. proposed an ensemble Kalman filtering method, which evaluates multiple sensor deployment schemes to identify the optimal layout. Experiments showed that deploying a detector every 300 m on Tokyo highways leads to better estimation results [28]. Eisenman et al. analyzed the impact of detector locations and quantities on prediction results from the perspective of state estimation and forecasting [29]. Cao et al. proposed an optimal sensor deployment method for freeways that incorporates the temporal-spatial effects of accident risk, formulates the deployment as a risk coverage problem, and applies particle swarm optimization to improve the accuracy and timeliness of traffic accident detection [30].

Although these traditional methods may achieve certain optimization under fixed layouts, they typically depend on prior knowledge or static strategies and lack adaptability to dynamic environments. As traffic conditions become increasingly complex, traditional approaches face growing challenges in real-world applications. In contrast, attention-based detector selection methods can automatically adjust the focus area according to input data, offering greater adaptability and flexibility. For example, Liu et al. leveraged the power of heterogeneous graph neural networks and proposed a novel end-to-end surrogate model for traffic assignment, which integrates adaptive graph attention with virtual links between origin–destination pairs to capture spatial patterns and ensure flow conservation [31]. Inspired by this line of research, the DPSM proposed in this study is grounded in the same concept. By leveraging attention mechanisms in neural networks, it dynamically selects the most representative observation points across the entire spatial domain, effectively addressing the limitations of existing methods in terms of flexibility and generalization capability.

3. Methodology

3.1. Problem Definition

In real-world traffic management systems, the limited density of sensor deployment and the high cost of installation often hinder real-time access to complete traffic state information across the entire network. Consequently, one of the core challenges in traffic state estimation is how to accurately reconstruct or predict the global traffic state using only partial observations from a small number of detectors.

This study focuses on the problem of optimal detector selection under limited observation. The goal is to reduce system costs while ensuring high-precision estimation of the global traffic state, thereby providing reliable data support for traffic optimization and control.

Assume that there are D fixed detectors deployed along a certain road segment. At the current time step t, the system is only able to collect flow information from k (k < D) observation points. The objective is to learn a function ${\mathrm{M}}_{\mathsf{\theta }}$ based on a deep learning model, which takes the following inputs and outputs the estimated global traffic state at time t:

$${\hat{\mathrm{F}}}_{\mathrm{t}}={\mathrm{M}}_{\mathsf{\theta }}({\mathrm{F}}_{\mathrm{t},{\mathrm{S}}_{\mathrm{k}}},{\mathrm{S}}_{\mathrm{k}},{\mathrm{d}}_{\mathrm{norm}},{\mathrm{t}}_{\mathrm{norm}})\in {\mathrm{R}}^{\mathrm{D}}$$

(1)

where ${\hat{\mathrm{F}}}_{\mathrm{t}}$ represents the observed traffic flow values from selected detectors. ${\mathrm{F}}_{\mathrm{t},{\mathrm{S}}_{\mathrm{k}}}$ is the observed flow values from selected detectors. ${\mathrm{S}}_{\mathrm{k}}$ is the index set of the selected k observation points. ${\mathrm{d}}_{\mathrm{norm}}$ is the normalized spatial position of detectors and ${\mathrm{t}}_{\mathrm{norm}}$ is the normalized temporal information.

3.2. Detection Point Selection Module (DPSM)

In real-world traffic systems, factors such as sparse sensor deployment, data collection costs, and system latency make it infeasible to access complete traffic state information at every time step.

To effectively address this challenge, we propose a learnable module called the Detection Point Selection Module (DPSM), designed to automatically identify and select the most representative detectors based on full-map input information. This module is placed at the front of the overall model pipeline and is responsible for selecting k representative detectors to assist downstream models in estimating the global traffic state, as illustrated in Figure 1.

Beyond conventional attention-based feature selection, the design of DPSM explicitly accounts for the unique characteristics of traffic systems. First, it incorporates spatial topology awareness by leveraging the structural dependencies between detectors in the road network, ensuring that selected points capture critical bottlenecks such as highway junctions or arterial corridors. Second, DPSM adapts to the temporal dynamics of traffic by learning time-varying importance weights, which allows the module to flexibly adjust detector selection under different patterns such as peak hours versus off-peak periods. Third, DPSM enhances robustness under sparse and incomplete observations, ensuring that even with limited detectors, the module can still reconstruct representative global states.

The core mechanism of the DPSM is based on a learnable attention network, enabling the model to dynamically select observation points according to real-time traffic conditions, instead of relying on static or manually configured detectors. The module can be seamlessly integrated into any traffic state estimation framework and jointly trained with downstream components in an end-to-end fashion. This traffic-specific design enhances the model’s flexibility and adaptability, while significantly improving estimation accuracy under sparse observation settings. It is important to emphasize that our proposed detector selection module is not a straightforward application of attention to the sensor placement problem, but a tailored design for traffic state prediction. Compared with entropy-based approaches, our method does not rely on manually computing global uncertainty but adaptively learns the importance of observation points through end-to-end training. Unlike traditional greedy placement strategies, our approach avoids iterative heuristic selection and is able to obtain a more globally consistent set of detectors within a single forward pass. In comparison with GNN-based selection methods, our module does not require additional graph convolutional propagation, thereby reducing computational overhead, while still leveraging interpretable attention scores to capture the contribution of each detector within the spatiotemporal traffic topology. These design choices improve the flexibility and efficiency of modeling complex spatiotemporal dependencies, while alleviating the scalability and efficiency issues faced by conventional methods.

3.3. Detailed Module Design

3.3.1. Input Preparation

During training, the DPSM receives inputs from the traffic system, including the ground-truth global flow map ${\hat{\mathrm{F}}}_{\mathrm{t}}$, normalized spatial locations ${\mathrm{d}}_{\mathrm{norm}}$, and normalized time information ${\mathrm{t}}_{\mathrm{norm}}$, which are then passed into the feature construction stage. The flow map ${\hat{\mathrm{F}}}_{\mathrm{t}}$ provides a comprehensive representation of the network-wide traffic state, allowing the module to capture correlations between different road segments. The normalized spatial locations ${\mathrm{d}}_{\mathrm{norm}}$ encode the position of each detector in a scale-invariant manner, enabling the network to recognize spatial patterns such as congestion hotspots or high-flow corridors. The normalized temporal information ${\mathrm{t}}_{\mathrm{norm}}$ captures the time-of-day and periodic variations in traffic, which is essential for distinguishing between recurring peak and off-peak traffic conditions. Prior to feature construction, these inputs are concatenated and optionally projected into a shared latent space through linear transformations, which helps the network learn more expressive representations and facilitates stable training. It should be emphasized that the global flow map is only used during training to supervise DPSM in learning the importance of each detector; during inference, the module relies solely on locally observable information and the learned topology embeddings, ensuring feasibility in real-world deployment. This preparation ensures that the DPSM has access to both local detector-level and global network-level information, forming a solid foundation for subsequent feature extraction and attention-based scoring.

3.3.2. Feature Vector Construction

To accurately estimate the traffic state, the DPSM constructs an input feature vector for each detector, incorporating the observed flow ${\mathrm{F}}_{\mathrm{t},\mathrm{i}}$ normalized spatial location ${\mathrm{d}}_{\mathrm{norm}}$, and normalized temporal information ${\mathrm{t}}_{\mathrm{norm}}$:

$${\mathrm{x}}_{\mathrm{i}}=[{\mathrm{F}}_{\mathrm{t},\mathrm{i}},{\mathrm{d}}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}},{\mathrm{t}}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}]$$

(2)

This design allows the network to evaluate each detector not only based on its local traffic observations but also considering its spatial-temporal context in the entire network. The feature vectors serve as the critical input for the scoring and selection process, providing rich information for assessing the relative importance of each detector. To enhance the representational power, the feature vectors can optionally be transformed through embedding layers with linear and non-linear operations, which help capture complex interactions between flow, location, and time. By structuring input features in this way, the module ensures that downstream scoring mechanisms have sufficient and consistent information to identify the most informative detectors for traffic state estimation.

3.3.3. Attention-Based Scoring

Scoring is a key component of the DPSM, aimed at evaluating the relative importance of each detector under current traffic conditions. An attention mechanism is employed to model all detector feature vectors within a shared-parameter network, allowing the module to learn which detectors contribute most to accurate traffic estimation. For each detector, the attention network computes a score:

$$s_{\mathrm{i}}={\mathrm{f}}_{\mathsf{\theta }}\left({\mathrm{x}}_{\mathrm{i}}\right)$$

(3)

where ${\mathrm{f}}_{\mathsf{\theta }}$ denotes the attention network and $s_{\mathrm{i}}$ is the attention score for detector ${\mathrm{x}}_{\mathrm{i}}$. All individual scores are aggregated into a vector $\mathrm{s}=\left[s_1,s_2,\dots ,s_{\mathrm{D}}\right]$, providing a complete importance profile for the entire network. The attention mechanism enables the module to dynamically adjust the weighting of each detector according to the current traffic state, capturing temporal fluctuations and spatial correlations simultaneously. This approach allows the model to prioritize detectors that are both representative and informative, forming the foundation for the normalized selection stage.

3.3.4. Normalized Selection

The DPSM applies a softmax function to normalize the score vector into an attention distribution, making the scores directly comparable across detectors:

$${\mathsf{\alpha }}_{\mathrm{i}}={\displaystyle \frac{\exp \left({\mathrm{s}}_{\mathrm{i}}\right)}{\sum _{\mathrm{j}=1}^{\mathrm{D}}\exp \left({\mathrm{s}}_{\mathrm{j}}\right)}}$$

(4)

The normalized scores enable direct comparison across detectors, highlighting the most critical sensors for the current time step. Based on these attention weights, the top k detectors with the highest values are selected to form the observation set ${\mathrm{S}}_{\mathrm{k}}=\mathrm{TopK}\left(\mathsf{\alpha },\mathrm{k}\right)$. This process ensures that only the most representative detectors are retained for downstream traffic state estimation, effectively reducing redundancy while maintaining comprehensive network coverage. By dynamically adjusting the selection at each time step, the module can respond to changing traffic conditions in real time, capturing emerging congestion or flow variations efficiently.

3.3.5. Output of Selected Detectors

Finally, the DPSM outputs the indices of the selected detectors ${\mathrm{S}}_{\mathrm{k}}$ and their corresponding observed flows ${\mathrm{F}}_{\mathrm{t},{\mathrm{S}}_{\mathrm{k}}}$, which are used as inputs for downstream traffic state estimation models. This design maintains a clear interface between the selection module and the estimation network, enabling end-to-end training where gradients from the prediction loss can propagate back to DPSM. Through joint optimization, the module learns to select detectors that maximize global prediction accuracy while adapting to varying traffic patterns. During inference, this output allows real-time detector selection and ensures that downstream models receive the most informative observations at each time step, forming a robust and adaptive pipeline for high-precision traffic state reconstruction.

The overall workflow of the Detection Point Selection Module (DPSM), including input preparation, feature construction, attention-based scoring, normalized selection, and detector output, is summarized in Algorithm 1.

Algorithm 1: Detection Point Selection Module (DPSM)

Input:

Ground-truth global flow map ${\hat{\mathrm{F}}}_{\mathrm{t}}$

Normalized spatial coordinates ${\mathrm{d}}_{\mathrm{norm}}$

Normalized temporal features ${\mathrm{t}}_{\mathrm{norm}}$

Number of detectors to select k

Output:

Indices of selected detectors ${\mathrm{S}}_{\mathrm{k}}$

Observed flows of selected detectors ${\mathrm{F}}_{\mathrm{t},{\mathrm{S}}_{\mathrm{k}}}$

1: # Step 1: Input Preparation

2: for i = 1 to D do

3:       ${\mathrm{x}}_{\mathrm{i}}=[{\mathrm{F}}_{\mathrm{t},\mathrm{i}},{\mathrm{d}}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}},{\mathrm{t}}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}]$ # Construct feature vector for each detector

4: end for

5: # Step 2: Attention-based Scoring

6: for i = 1 to D do

7:      $s_{\mathrm{i}}$ = AttentionNetwork (${\mathrm{x}}_{\mathrm{i}}$) # Compute attention score for each detector

8: end for

9: $\mathrm{s}=[s_1,s_2,\dots ,s_{\mathrm{D}}]$ # Aggregate scores into a vector

10: # Step 3: Normalized Selection

11: alpha = softmax(s) # Normalize scores to obtain attention weights

12: # Step 4: Top-k Detector Selection

13: ${\mathrm{S}}_{\mathrm{k}}=\mathrm{TopK}\left(\mathsf{\alpha },\mathrm{k}\right)$ # Select top k detectors based on attention weights

14: # Step 5: Output Selected Detectors

15: ${\mathrm{F}}_{\mathrm{t},{\mathrm{S}}_{\mathrm{k}}}={\mathrm{F}}_{\mathrm{t}}\left[{\mathrm{S}}_{\mathrm{k}}\right]$ # Extract observed flows of selected detectors

16: return ${\mathrm{S}}_{\mathrm{k}},{\mathrm{F}}_{\mathrm{t},{\mathrm{S}}_{\mathrm{k}}}$

4. Experiment

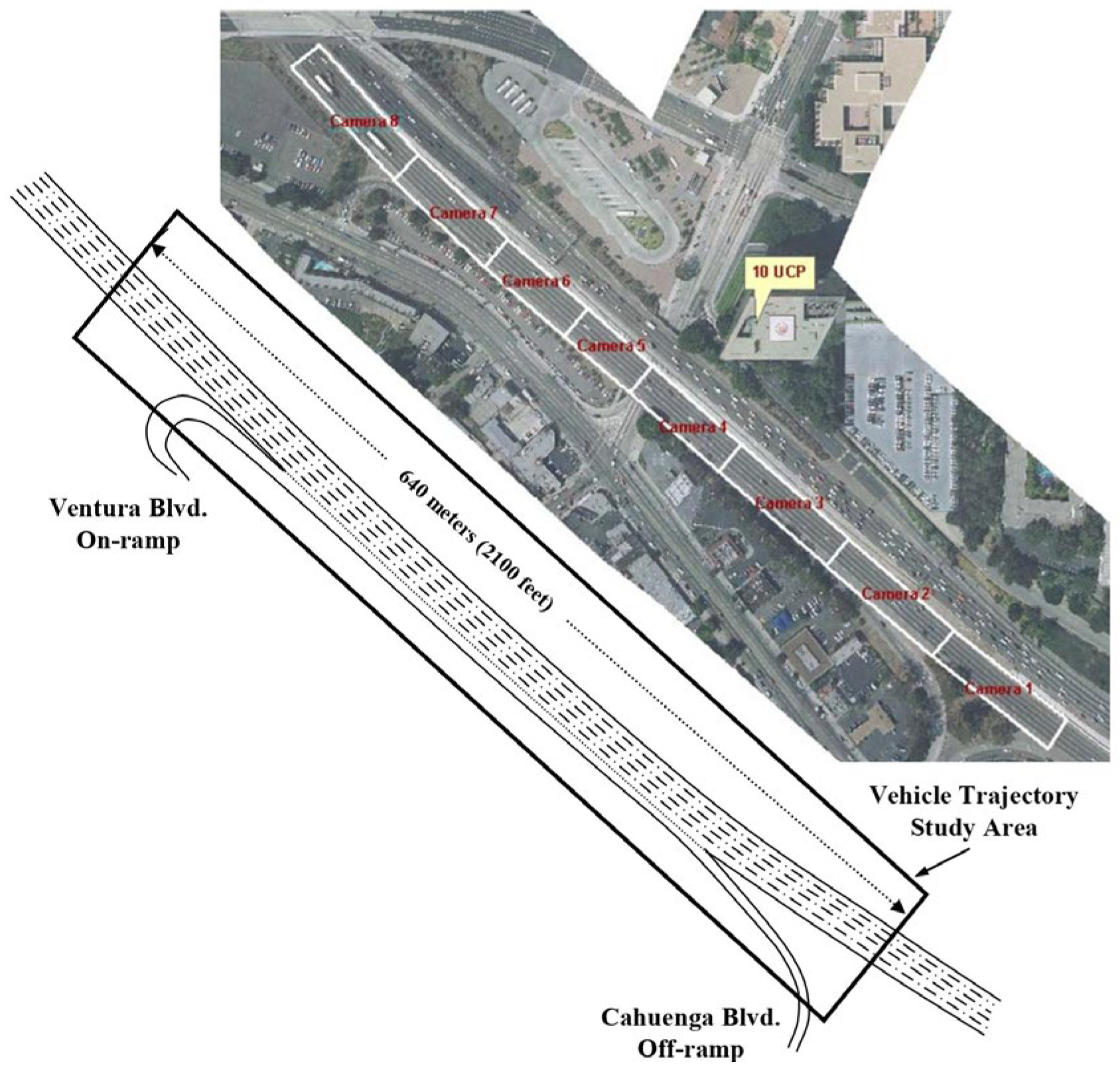
4.1. Dataset Description

This study uses the Next Generation Simulation (NGSIM) dataset, which gathers vehicle trajectories and traffic flow parameters from urban roads and highways via high-definition video recordings. The NGSIM data records traffic conditions on segments such as US101 and I-80 freeways, with a sampling rate of 10 Hz, enabling detailed capture of spatiotemporal dynamics. As can be seen from Figure 2, the data collection range of US101 is rectangular in shape. It is approximately 640 m (2100 feet) in the vertical direction and includes a total of 6 lanes (Lane 1 to Lane 6) in the horizontal direction. Among them, Lanes 1 to 5 are the main lanes of the road, while Lane 6 is an auxiliary lane connecting the on-ramp entrance and off-ramp exit. We selected a section of approximately 2000 ft (600 m) on US101 as the study area. The data cover April 13, 2005, from 07:50 to 08:05 am, corresponding to the morning peak period and featuring typical traffic flow patterns [32].

For spatiotemporal modeling and analysis, this study divides the segment into spatial intervals of 6 m and discretizes time into 5 s intervals. Consequently, the space is divided into 100 equal-length segments (each representing a detector location), and time into 540 steps. Based on this discretization, the raw vehicle trajectories are converted into a 2D traffic flow matrix, as shown in Figure 3. The vertical axis represents spatial positions, the horizontal axis represents time steps, and each cell contains the observed flow at that spatiotemporal location.

This matrix intuitively reflects spatiotemporal evolution trends of traffic flow and captures characteristic fluctuations during the morning peak. It provides a solid data foundation for subsequent traffic state estimation and detector selection method development and validation. In the experiment, we considered a freeway segment of approximately 600 m on US101, which was divided into 100 evenly spaced intervals, each corresponding to a potential detector location. To simulate different deployment conditions, four sensor densities were configured by selecting k = 6, 11, 21, and 26 detectors, corresponding to spacings of 120 m, 60 m, 30 m, and 24 m, respectively. For each configuration, the DPSM adaptively determined the most representative detectors, while the baseline models used evenly spaced detectors at fixed intervals. The underlying traffic data were obtained from the NGSIM dataset, which records vehicle trajectories with a sampling frequency of 10 Hz using high-resolution video cameras. These trajectories were then processed to compute traffic flows for each spatial interval and aggregated at 5 s intervals, forming a spatiotemporal flow matrix. This setting ensures that both sensor placement and traffic state estimation are evaluated under realistic conditions with limited observation resources.

4.2. Baseline Models and Evaluation Metrics

To validate the effectiveness of the proposed detector selection method and traffic state estimation models, experiments were conducted on the NGSIM-US101 dataset. The selected data span April 13, 2005, from 07:50 to 08:05 with a 10 Hz sampling rate. The raw trajectory data were preprocessed and aggregated at 5 s intervals; spatially, the segment was partitioned into equal 10 m grids to form a continuous spatiotemporal traffic flow map. In the experimental setup, data from 07:50 to 08:00 were used as the training set, and data from 08:00 to 08:05 as the test set. All data were normalized in both spatial and temporal dimensions to improve model convergence and generalization performance.

To systematically evaluate the effectiveness and generalizability of the proposed DPSM across different prediction frameworks, three deep learning–based traffic state estimation models were designed: the DPSM-NN model (using fully connected layers), the DPSM-CNN model (using convolutional layers), and the DPSM-LSTM model (incorporating temporal sequence modeling). These three models cover typical deep learning architectures for traffic state modeling—from static mapping through spatial feature extraction to temporal dynamic modeling—making them highly representative.

1.

DPSM-NN: Fully connected Prediction Model

The DPSM-NN model employs a multilayer fully connected network as its backbone. It first receives normalized spatial locations and temporal information of detectors, concatenates them, and inputs them into the DPSM to generate importance scores. After softmax normalization, the top k detectors are selected as the current observation set. The selected detectors’ flow values, along with their normalized spatial and temporal features, form the input features, which are fed into the fully connected network for full-map traffic state regression. This model’s simple structure and computational efficiency make it suitable for validating DPSM’s selection capability and deploying in resource-constrained environments.

2.

DPSM-CNN: Convolutional Prediction Model

The DPSM-CNN model introduces convolutional neural networks in the prediction module to further evaluate DPSM’s spatial modeling capabilities. Similarly based on normalized spatial and temporal information, only flow values at selected detector locations are retained while other positions are zero-padded, creating a sparse “traffic image.” This image is then fed into the convolutional module to capture spatial flow distribution features via local receptive fields and shared parameters, generating the full-map traffic state prediction.

3.

DPSM-LSTM: LSTM Prediction Model

The DPSM-LSTM model addresses the temporal dependency of traffic states by using a Long Short-Term Memory (LSTM) network as the prediction module. DPSM first selects k key detectors and extracts their corresponding flow observations. These flow values, along with normalized spatial and temporal features, form an input sequence fed to a single-layer LSTM for temporal modeling. Finally, the LSTM’s hidden state is mapped to generate the predicted full-map traffic state at the current time.

Based on the above models, three baseline models with identical structures but without the DPSM were constructed, enabling ablation studies to analyze DPSM’s effectiveness and contribution across different neural network architectures. To comprehensively evaluate model performance, we use Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE), measuring prediction bias, error variability, and relative error, respectively. All evaluation results are based on test set statistics and visual analysis to validate the generalization and practical potential of the proposed methods. This matrix intuitively reflects spatiotemporal evolution trends of traffic flow and captures characteristic fluctuations during the morning peak. It provides a solid data foundation for subsequent traffic state estimation and detector selection method development and validation.

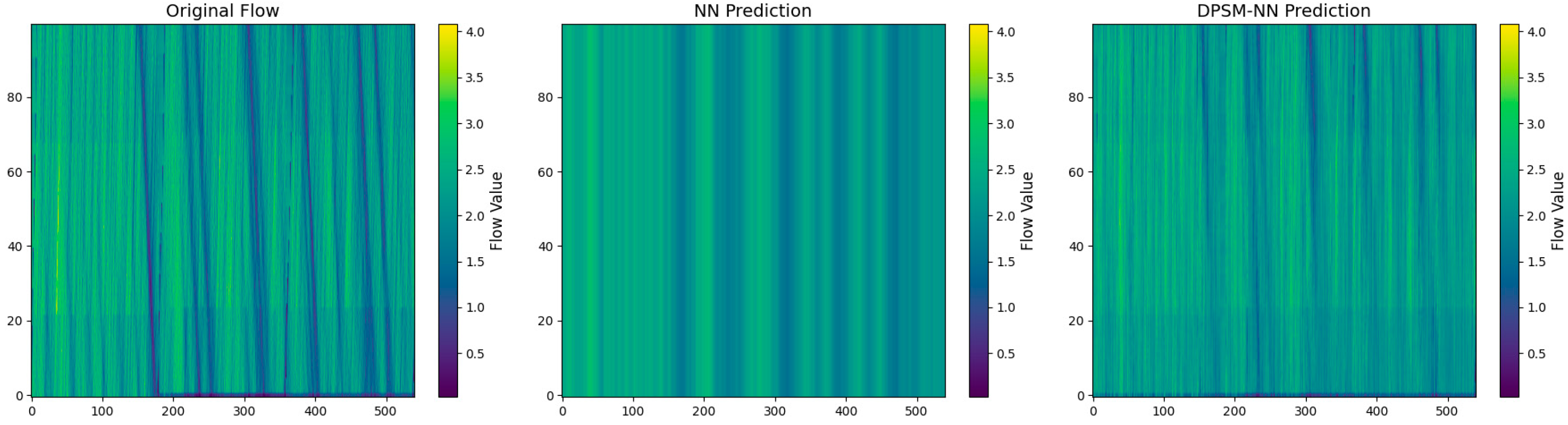
4.3. Experimental Results

As shown in

Table 1. Performance Comparison of Models. The black bolded parts in the table represent the optimal results of this study.

Model	d = 120 (k = 6)			d = 60 (k = 11)			d = 30 (k = 21)			d = 24 (k = 26)
	MAE	RMSE	MAPE	MAE	RMSE	MAPE	MAE	RMSE	MAPE	MAE	RMSE	MAPE
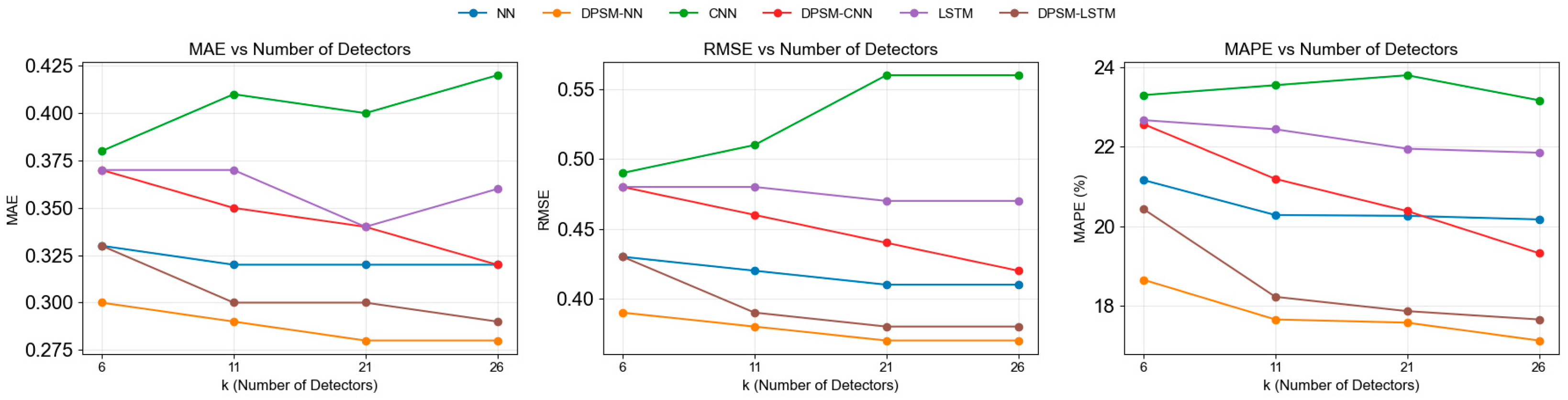
NN	0.33	0.43	21.16	0.32	0.42	20.28	0.32	0.41	20.26	0.32	0.41	20.17
DPSM-NN	0.30	0.39	18.65	0.29	0.38	17.65	0.28	0.37	17.57	0.28	0.37	17.12
GAIN (%)	9.09	9.30	11.86	9.38	9.52	12.97	12.50	9.76	13.2	12.5	9.76	15.12
CNN	0.38	0.49	23.3	0.41	0.51	23.55	0.40	0.56	23.80	0.42	0.56	23.17
DPSM-CNN	0.37	0.48	22.57	0.35	0.46	21.19	0.34	0.44	20.38	0.32	0.42	19.32
GAIN (%)	2.63	2.04	3.40	14.63	9.80	10.02	15.00	14.29	14.37	23.81	25.00	16.62
LSTM	0.37	0.48	22.67	0.37	0.48	22.44	0.34	0.47	21.95	0.36	0.47	21.85
DPSM-LSTM	0.33	0.43	20.43	0.30	0.39	18.22	0.30	0.38	17.86	0.29	0.38	17.65
GAIN (%)	10.81	10.42	9.88	18.92	18.75	18.81	11.76	19.15	18.63	19.44	19.15	19.22

, we systematically compare the performance of different models under various detector deployment densities for the traffic state estimation task. The proposed DPSM-NN, DPSM-CNN, and DPSM-LSTM models integrate an automatic detector selection module, which dynamically chooses observation points based on the current traffic state. In contrast, the baseline models (NN, CNN, LSTM) use fixed, evenly spaced detectors; for example, with a spacing of 120 m, the selected positions are [0, 120, 240, 360, 480, 600]. Table 1 reports the prediction errors of all models, where MAE, RMSE, and MAPE quantify deviations in traffic flow intensity, defined as the number of vehicles per 5 s interval, from the ground truth. The three evaluation metrics are formally defined as follows:

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N|{\hat{y}}_i-y_i|$$

(5)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N({\hat{y}}_i-y_i{)}^2}$$

(6)

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{N}}{\displaystyle \frac{{\sum }_{i=1}^N|{\hat{y}}_i-y_i|}{y_i}}\times 100\mathrm{\%}$$

(7)

where ${\hat{y}}_i$ and $y_i$ denote the predicted and ground-truth values at index i, and N represents the total number of samples.

To comprehensively evaluate the adaptability and effectiveness of the detector selection module across different network architectures, we incorporated DPSM into three deep learning models—DPSM-NN, DPSM-CNN, and DPSM-LSTM—and compared them with their respective baselines. Four detector deployment densities were considered, corresponding to one detector every 120, 60, 30, and 24 m (k = 6, 11, 21, and 26, respectively), simulating scenarios from extremely sparse to relatively dense sensor coverage. For each deployment density, model performance was evaluated using three metrics: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE).

Experimental results demonstrate that the detector selection module consistently enhances prediction accuracy across all model structures and deployment densities. Detailed findings are as follows:

Fully connected architecture: The DPSM-NN model outperforms the NN baseline under all configurations. Under the sparsest setting, MAE drops from 0.33 to 0.30 and RMSE from 0.43 to 0.39, with respective reductions of 9.09% and 9.30%. Under the densest setting, MAPE decreases from 20.17% to 17.12%, achieving a 15.12% improvement.

Convolutional architecture: DPSM-CNN achieves stable performance improvements across all settings. At a 10 m spacing, MAE decreases from 0.41 to 0.35, RMSE drops by 0.05, and MAPE reduces by over 10%. Under the densest deployment, RMSE drops by 25% and MAPE by 16.62%.

Temporal architecture: DPSM-LSTM also yields significant performance gains. At 10 m spacing, MAE reduces from 0.37 to 0.30 (an 18.92% drop), and MAPE decreases from 22.44% to 18.22%. Even under the sparsest deployment, MAPE improves by 9.88%.

This study compares the prediction error trends of different models under varying numbers of observation points. As the number of observation points increases from 6 to 26, all models exhibit a consistent decrease in three key metrics: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE). This indicates that additional observation information enhances the model’s ability to reconstruct the full-map traffic state. Further comparisons reveal that models integrated with the detector selection module—namely DPSM-NN, DPSM-CNN, and DPSM-LSTM—consistently outperform their corresponding baseline models across all observation point settings. This performance advantage is especially prominent in scenarios with fewer observation points. Notably, the improvement is most significant in the MAPE metric, suggesting that the module not only enhances overall prediction accuracy but also improves the model’s responsiveness to sudden traffic changes and abnormal flow patterns. Moreover, from the overall trend of error curves, models with the integrated detector selection module show smoother and more stable declines, indicating lower dependency on the number of observation points. Even under sparse observation conditions, they maintain strong predictive performance, demonstrating the robustness and generalizability of the module. As shown in Figure 4, all models benefit from an increasing number of observation points, but DPSM-based models consistently outperform baselines across all densities, particularly under sparse conditions. This indicates that adaptive detector selection provides stronger resilience when resources are limited.

Under the configuration with 11 observation points, this study compares the performance differences between the traditional fully connected neural network model and the DPSM-NN model enhanced with the detector selection module in estimating the full-map traffic state. By comparing the predicted results and the ground truth flow map in the form of heatmaps, the accuracy and detail restoration capabilities of each model in reproducing traffic conditions can be observed. The real flow map exhibits typical spatiotemporal evolution characteristics of traffic flow, including congestion build-up areas, the spatial movement of high-flow bands, and the sparse distribution in low-flow regions. These features collectively reflect the complex traffic dynamics during the morning peak period. In the baseline model, that is, the traditional fully connected neural network, the predicted map captures the overall trend to some extent but shows noticeable deviations in local details. Particularly in congested areas, the model struggles to accurately delineate clear boundaries and the development process. This is reflected in the heatmap as unclear slopes and fuzzy transitions in congested zones, failing to effectively capture the spatial boundaries of congestion and its temporal propagation patterns—thereby significantly weakening the model’s ability to depict dynamic changes in congestion. In contrast, the DPSM-NN model with the detector selection module produces prediction results that more closely resemble the actual traffic state map. This model not only accurately captures the spatial position and morphological characteristics of high-flow bands but also shows smoother and more continuous transitions in regions of changing flow. Furthermore, in modeling congestion areas, the DPSM-NN model is able to more clearly reconstruct their spatial extents and temporal evolution paths, demonstrating higher sensitivity and accuracy in spatiotemporal modeling. Figure 5 further illustrates that DPSM-NN not only captures overall flow patterns but also restores local congestion boundaries more accurately, which is essential for real-world traffic management.

As shown in

Table 2. Detector Selection Results of DPSM in Different Models.

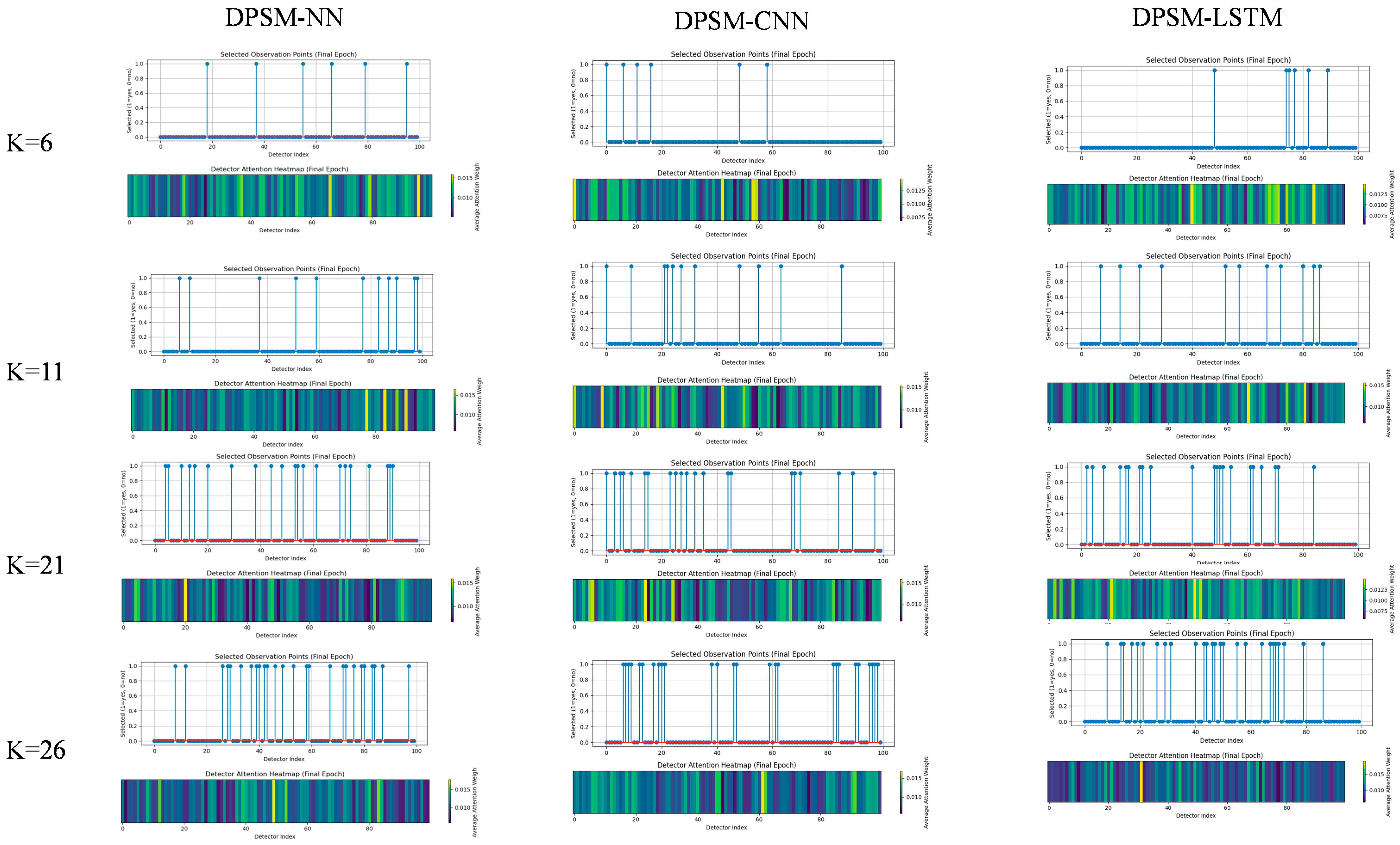
k	Model	Selected Detectors	Distribution Pattern Analysis
6	DPSM-NN	[18, 37, 55, 66, 79, 95]	Covers front, middle, and rear sections; strong global representativeness.
	DPSM-CNN	[0, 6, 11, 16, 48, 58]	Dense selection in the front and middle; reflects CNN sensitivity to edges and local spatial features.
	DPSM-LSTM	[48, 74, 75, 77, 82, 89]	Concentrated in middle and rear; more compact layout; aligned with temporal dependency modeling.
11	DPSM-NN	[6, 10, 37, 51, 59, 77, 83, 87, 90, 97, 98]	Dense selections at the rear; indicates tail section’s importance for global traffic state prediction.
	DPSM-CNN	[0, 9, 21, 22, 24, 27, 32, 48, 55, 63, 85]	Fairly uniform from front to rear; denser in the middle, enabling multi-level spatial feature extraction.
	DPSM-LSTM	[7, 14, 21, 29, 52, 57, 67, 72, 80, 84, 86]	Focuses on middle and rear with more dispersed layout; helps capture temporal evolution patterns.
21	DPSM-NN	[4, 5, 10, 13, 15, 20, 29, 38, 44, 48, 53, 54, 56, 61, 70, 72, 74, 81, 88, 89, 90]	Broad coverage with emphasis on middle and rear; builds robust spatial perception.
	DPSM-CNN	[0, 3, 5, 6, 9, 14, 15, 23, 25, 27, 29, 32, 35, 44, 45, 67, 68, 70, 84, 89, 97]	Mostly concentrated in the middle and edge zones; loose structure reflecting CNN’s locality.
	DPSM-LSTM	[2, 4, 8, 16, 17, 21, 22, 25, 40, 48, 49, 50, 51, 54, 61, 62, 65, 70, 71, 84]	Clear middle focus with endpoints added; supports modeling of long-range dependencies.
26	DPSM-NN	[8, 12, 26, 28, 29, 33, 37, 39, 40, 42, 43, 46, 49, 53, 58, 59, 67, 72, 73, 76, 79, 80, 83, 84, 87, 97]	Dense in middle-rear; balanced layout enhances congestion observation.
	DPSM-CNN	[6, 7, 8, 9, 12, 13, 17, 19, 20, 21, 38, 40, 46, 47, 59, 61, 62, 82, 83, 84, 90, 91, 95, 96, 97, 98]	Dispersed and broad spatial coverage; aligns with CNN’s multi-scale feature needs.
	DPSM-LSTM	[8, 13, 14, 17, 19, 21, 26, 29, 31, 40, 43, 44, 46, 47, 49, 50, 55, 58, 64, 67, 68, 69, 70, 72, 79, 86]	Middle-preferred with rear support; forms a temporal backbone for sequence modeling.

, we report the detectors selected by the DPSM across different prediction models. The corresponding attention weight distributions are illustrated in Figure 6. In Figure 6, the attention weight distributions reveal different selection strategies across NN, CNN, and LSTM, suggesting that DPSM can adaptively adjust to the underlying model architecture while maintaining strong spatial representativeness. These results collectively demonstrate the practical value of DPSM in guiding cost-effective detector placement and improving traffic monitoring robustness. Under sparse deployment settings, the three models exhibit distinct selection strategies: DPSM-NN demonstrates strong global representativeness, with selections spanning low, mid, and high indices, capturing spatial structure even under highly constrained observation resources; DPSM-CNN tends to select detectors in the front and middle segments, reflecting CNN’s sensitivity to local spatial continuity and its preference for stable, generalizable patterns; DPSM-LSTM primarily selects from the middle to rear regions, suggesting its reliance on capturing later-stage traffic evolution in temporal modeling.

As the number of observation points increases, each model exhibits more distinct regional preferences in its detector selection strategy. DPSM-NN model significantly intensifies its focus on the downstream segment of the road, with selected detectors concentrated in higher-indexed positions. This indicates that the model considers downstream traffic states to contribute more informative cues for reconstructing the full traffic map; DPSM-CNN model adopts a relatively uniform distribution, though with a central-region preference, forming a continuous spatial feature path that improves the model’s capacity for stable and expressive spatial representation; DPSM-LSTM model shows a more scattered selection pattern, still biased toward the mid-to-rear segments. Such a layout better aligns with the need to capture critical temporal dynamics in sequential modeling.

Under dense deployment settings, the structural differences in detector selection strategies among the three models become more pronounced. DPSM-NN model maintains a mid-to-rear-centered selection while ensuring a degree of spatial uniformity, aiming to build a detector layout that balances representativeness and coverage; DPSM-CNN model presents a sparser and point-wise multi-scale selection pattern, which enhances its ability to model fine-grained local traffic variations. The selected detectors are evenly distributed across the middle and at both ends of the road segment, reflecting the model’s dual emphasis on spatial breadth and depth. In contrast, DPSM-LSTM model adopts a “temporal backbone with peripheral reinforcement” strategy, forming a core selection path along the central segment while incorporating detectors at the rear or symmetrically at both ends. This strategy is designed to strengthen the model’s ability to capture long-term dependencies in traffic dynamics.

5. Conclusions

To address the challenges of “sparse observation points” and “static deployment” in traffic state estimation, this study proposes a Detector Point Selection Module (DPSM) based on a learnable attention mechanism and integrates it into three types of neural network architectures for systematic experimentation. Experimental results demonstrate that the DPSM consistently and significantly improves model performance across different observation point settings and backbone networks.

The proposed DPSM provides a practical framework for transportation agencies to maximize the value of limited sensors by adaptively selecting the most informative detectors. This capability is particularly important under budget constraints or in large-scale urban networks where dense deployment is infeasible. The main strengths of the model lie in its adaptability, generalizability across different backbone networks, and robustness under sparse observation settings. These advantages make DPSM well-suited for real-world deployment scenarios, such as highway traffic monitoring, congestion management, and intelligent control.

Nevertheless, some limitations remain. First, the current model relies on supervised training with full-map data during the learning phase, which may limit its direct applicability in cases where the global ground truth is unavailable. Second, in real-world traffic scenarios, sensor measurements may be noisy or missing due to failures, adverse weather, or transmission errors. Such imperfect data can affect the attention-based detector selection in DPSM, potentially leading to suboptimal observation point choices. To mitigate this, techniques such as Kalman filtering or other preprocessing methods can be applied to reconstruct or smooth the traffic measurements before input to DPSM. Third, DPSM is primarily designed to capture general traffic trends, and sudden events such as accidents or abrupt congestion spikes may not be fully captured by the attention mechanism, which could delay or reduce estimation accuracy. Future work will focus on addressing these limitations by integrating unsupervised or semi-supervised learning strategies, extending to multi-objective optimization, validating the framework in real-time edge computing environments, and enhancing robustness under noisy, incomplete, or highly dynamic traffic conditions, possibly through event-detection modules or anomaly detection techniques. Finally, the end-to-end attention mechanism increases computational load, which may pose challenges for real-time deployment in resource-constrained edge computing environments. Future work will focus on integrating unsupervised or semi-supervised learning strategies, extending to multi-objective optimization, enhancing robustness under noisy, incomplete, or highly dynamic traffic data, and exploring model compression, pruning, quantization, or hybrid architectures to enable practical edge deployment.