A Chaos-Driven Fuzzy Neural Approach for Modeling Customer Preferences with Self-Explanatory Nonlinearity

Abstract

Online customer reviews contain rich sentimental expressions of customer preferences on products, which is valuable information for analyzing customer preferences in product design. The adaptive neuro fuzzy inference system (ANFIS) was applied to the establishment of customer preference models based on online reviews, which can address the fuzziness of customers’ emotional responses in comments and the nonlinearity of modeling. However, due to the black box problem in ANFIS, the nonlinearity of the modeling cannot be shown explicitly. To solve the above problems, a chaos-driven ANFIS approach is proposed to develop customer preference models using online comments. The model’s nonlinear relationships are represented transparently through the fuzzy rules obtained, which provide human-readable equations. In the proposed approach, online reviews are analyzed using sentiment analysis to extract the information that will be used as the data sets for modeling. After that, the chaos optimization algorithm (COA) is applied to determine the polynomial structure of the fuzzy rules in ANFIS to model the customer preferences. Using laptop products as a case study, several approaches are evaluated for validation, including fuzzy regression, fuzzy least-squares regression, ANFIS, ANFIS with subtractive cluster, and ANFIS with K-means. Compared to the other five approaches, the values of mean relative error, variance of error, and confidence interval of validation error are improved based on the proposed approach.

1. Introduction

Understanding customer preferences for products is an essential task in the customer-centric design of products, as the preferences of customers can be mapped into optimal design [1]. Commonly used methods to analyze customer preferences are questionnaires or participant interviews. However, only scores in questionnaires or answers to the predefined questions can be obtained. Also, not much sentimental expression is contained in the collected survey data. Comparatively, online reviews include rich information about customer preferences, which are generated freely by customers after using products. They are important data for product design and studying customer preferences. By using comments on products, sentiment analysis can be introduced to understand customer preferences and collect effective data sets, which is almost cost-free. Next, a modeling method will be developed to assess the relationship between design characteristics and customer preferences. Recently, the adaptive neuro fuzzy inference system (ANFIS) has been frequently applied to develop customer preference models using online reviews. It can deal with the fuzzy nature of sentimental expression from customers and the nonlinearity of relationships. However, ANFIS cannot provide an interpretation of the nonlinear relationship transparently, and no visible nonlinear equations between inputs and outputs can be obtained. There is also a lack of clarity about its inner working, which is called black box modeling. The only transparent information generated from the ANFIS is the fuzzy rules, in which the internal models are in the linear function, and the nonlinear relationship cannot be shown. As explainable artificial intelligence develops, exhibiting explicit and understandable nonlinearity in ANFIS becomes increasingly important. In order to solve the above limitations of ANFIS, this paper proposes a chaos-driven ANFIS approach to model customer preferences with nonlinear fuzzy rules. First, the proposed approach conducts sentiment analysis, which involves analyzing online reviews, extracting dimensions of customer preferences, and computing sentiment scores. Based on the extracted information and settings of the product’s design characteristics, a chaos optimization algorithm (COA) is integrated into the ANFIS to generate the customer preference models. To solve the black box issue of ANFIS, we propose transforming the linear internal models into fuzzy rules for a nonlinear structure, including higher-order or interaction terms. Some stochastic optimization algorithms accept poor solutions to escaping from the local minimum based on a certain probability. In contrast, COA provides better solutions because it can avoid local minima by examining the regularity in chaotic motions [2]. It can provide more diverse solutions and has a fast convergence speed. Furthermore, the chaotic search technique is well known for simulating the dynamic behavior of the nonlinear systems [3]. COA and ANFIS are combined to create customer preference models that can handle the fuzziness and nonlinearity of the relationship, and they are transparent for readers.

Following is a list of the rest of the paper’s contents. A description of related works is provided in Section 2. The proposed chaos-driven ANFIS approach is discussed in Section 3, and its implementation in a laptop case study is discussed in Section 4. Validations of the proposed approach are presented in Section 5 along with a comparison with five other approaches. Section 6 provides the conclusions of the study.

2. Related Works

The contents of this section mainly include details of the existing sentiment analysis methods based on online reviews and the modeling approaches used for customer preferences in previous studies.

2.1. Sentiment Analysis for Product Design

Qualitative analysis of text content is called sentiment analysis, which includes an intelligent search for and retrieval of the features of text, including keywords and phrases in their content [4]. Based on the extracted dimensions of features, their sentimental polarity and sentimental scores are identified. In online comments created by customers, customers’ opinions and emotions can be analyzed by sentiment analysis. The mined features, including customer preferences and design characteristics, can be obtained. Some previous research has been conducted on using sentiment analysis for designing products. Information about customer needs has been mined using an ontology learning system in product development [5]. Zhou et al. [6] used case analogical reasoning and sentiment analysis to analyze online product reviews to discover latent preferences of customers. By analyzing social media data, an automated method was proposed for discovering implicit product features and leading customers [7]. The authors also applied a data mining-driven approach to obtain the product characteristics and customer preferences by using social media networks [8].

A framework called OPINSTREAM was proposed for mining product characteristics and determining the polarity in the reviews of different products [9]. For a large amount of textual data, an approach for mining product features based on Bayesian sampling has been proposed [10]. Zhang et al. [11] employed a sentiment analysis algorithm to identify the product characteristics and analyzed their opinion intensity. Online comments were used to identify product features using a rule-based method [12]. Zhou et al. [13] used a hybrid sentiment analysis to incorporate information about customer preferences with feature models and augment the feature models by combining the positive and negative customers’ opinions. At the conceptual design stage, Chiu and Lin [14] combined text mining with Kansei engineering to mine customer preferences. The online voices of customers were analyzed to determine real-time customer needs using patent mining and social media [15]. Review-based online methods were used to identify the characteristics of products that need to be changed or improved for product redesign [16]. Ali et al. [17] developed an ontology-based reasoning method to mine design characteristics from online comments. Also, some research was carried out on establishing models for relating customer preferences to design characteristics. Chung and Tseng [18] proposed a rule-induction framework to establish the link between customer ratings and product reviews. For affective design, an approach to obtaining association rules using multi-objective particle swarm optimization (PSO) has been proposed to relate design characteristics with customer preferences based on online comments [19]. However, for the determination of the optimal settings of design characteristics, the generated if–then rules are not suitable to be used.

2.2. Modeling Approach for Customer Preferences

To generate the models of the relationship between design characteristics and customer preferences, a number of previous studies have been conducted. Using the generated models, new products’ design characteristics can be better determined. In the study of automotive interior materials, You et al. [20] utilized the quantification I analysis to build customer satisfaction models. Kohonen self-organizing maps were used to correlate the affective requirements of customers with design characteristics [21]. A rule-based belief methodology was developed to show the association between product characteristics and consumer preferences [22]. The above approaches cannot, however, account for fuzziness in customer responses. To handle fuzziness, the fuzzy inference method was adopted to map customer preferences onto the relevant design attributes in quality function deployment [23]. Park and Han [24] designed a fuzzy rule-based approach to modeling affective customer preferences which is applied in the office chair design. A possibilistic regression approach with nonlinear programming was introduced for product functional design [25]. Sekkeli et al. [26] used Tanaka’s fuzzy linear regression approach to develop classification models by using survey data, which included information about customer preferences. However, these models were developed as linear architectures, which failed to address the nonlinear features of the data.

Considering both the nonlinearity and fuzzy aspects of the modeling, Chan et al. [27] proposed an approach based on genetic programming and fuzzy regression to address the nonlinearity and fuzziness of affective modeling for product design. They also designed a stepwise-based fuzzy regression method [28] and a forward selection-based fuzzy regression method [29] to correlate design attributes with consumer preferences in new product development. In product design, a fuzzy regression with the COA approach was designed for developing nonlinear customer preference models [30]. In the process of modeling for affective product design, a PSO-based ANFIS method was introduced to deal with the nonlinearity and fuzziness [31]. However, the nonlinearity is not interpretable in the developed customer preferences models because of the black box problem of ANFIS.

In summary, there is a gap in the comprehensive application of online reviews in product design, and their integration into quantitative design models remains undeveloped. Moreover, in the development of customer preference models, three critical issues need to be managed: inherent fuzziness in the data, nonlinearity in the relationship, and transparently showing the above two features in the models. However, a review of prior research indicates that existing approaches have typically addressed only one or two of these challenges. For instance, some studies manage fuzziness but assume linear relationships, while others capture nonlinearity through black-box models that lack transparency. Therefore, it is necessary to propose a novel approach to simultaneously resolve the three issues in the modeling process by leveraging the full potential of online reviews.

3. A Chaos-Driven ANFIS Approach

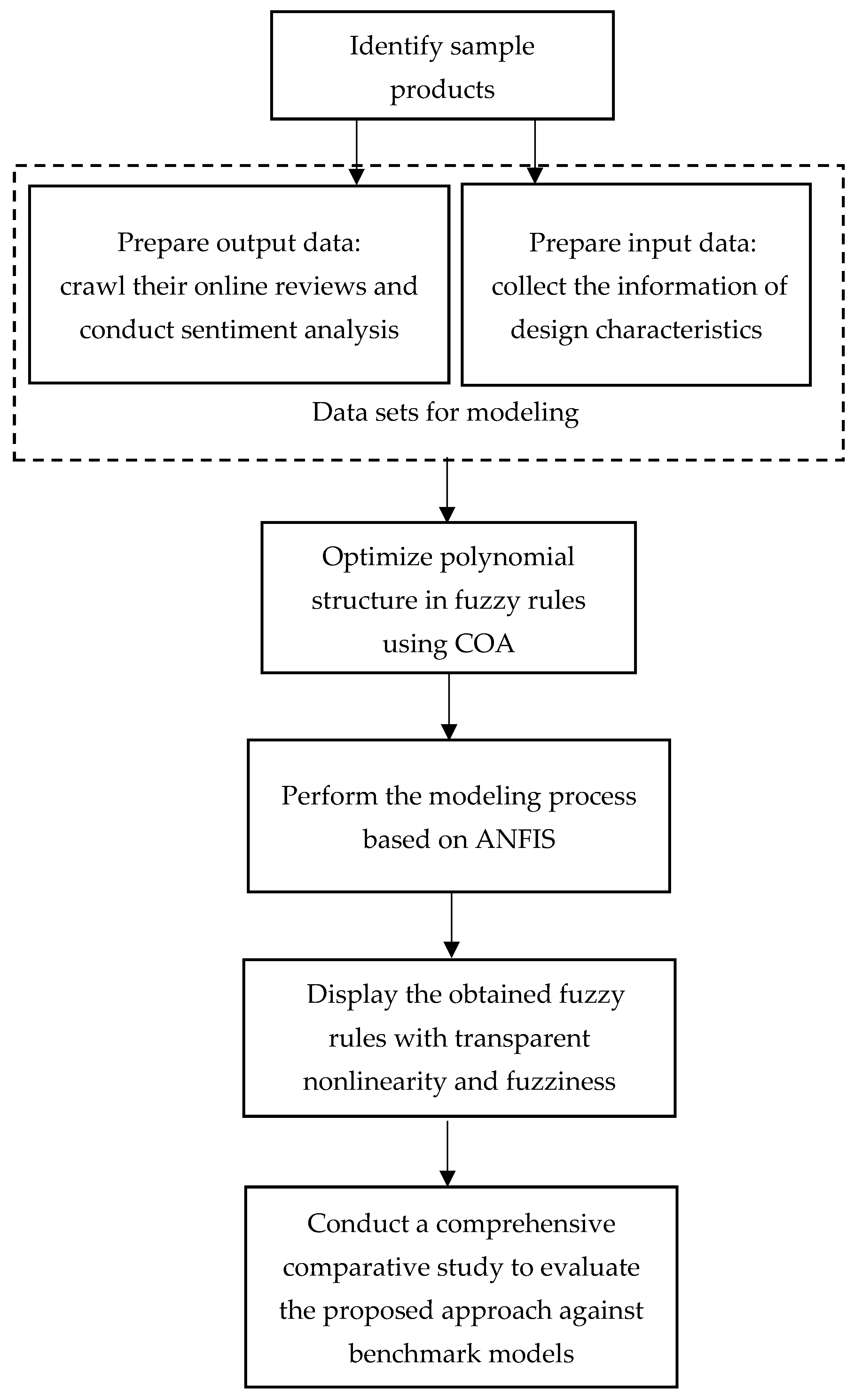
The data sets used for modeling in a chaos-driven ANFIS approach are the design characteristics of products and the sentiment scores of customer preferences. According to the information about the products, the design characteristics are collected. Customer preference sentiment scores are derived from online reviews using sentiment analysis. To determine the nonlinear structure of fuzzy rules in ANFIS, COA is used. In the developed models, the nonlinearity and fuzziness of the relationships are explicit and explainable, which are shown in the generated fuzzy rules. The procedure used in the proposed approach is described in Figure 1.

3.1. Subsection Sentiment Analysis Based on Customer Reviews

The products used for the research are determined as samples first. Lexalytics’ text and sentiment analysis, called Semantria API, is introduced to analyze customer reviews, identify customer preferences, and determine the corresponding sentimental scores. To collect online reviews, a web crawler with Python 3.12.9 is used by requesting the URL of the websites. An Excel file is used to store the collected customer reviews as a data source for sentiment analysis. The procedure of sentiment analysis in Semantria includes the following six steps. First, the review content is cleaned, from which punctuation, stop words, and non-alphanumeric symbols are removed. Second, the words in online reviews are categorized using part-of-speech tagging. In this paper, nouns describe the dimensions of customer preferences, while adjectives and adverbs refer to related emotions. Third, the expressions of the emotions related to customer preferences are extracted. Fourth, by using feature pruning, redundancy and incorrect features are deleted. Fifth, the synonymous keywords or phrases are grouped and provided as the settings of Semantria. For example, the words “weight”, “heavy”, “light”, and “comfortable to carry” have similar meaning as the customer preference “easy carrying”, which are the settings in Semantria. Finally, the semantic scores and polarity of customer presences are determined based on SentiWordNet, which is an opinion lexicon that assigns three numerical scores indicating positivity, negativity, and objectivity to each synset [32].

3.2. Generation of Nonlinear Fuzzy Rules

In the original ANFIS, the expression of the fuzzy rules with two inputs is shown as follows.

$$R_{ij}:If x_1 is {\mu }_i and x_2 is {\lambda }_j, Then f_{ij}=p_{ij}{x}_1+q_{ij}{x}_2+r_{ij}\hspace{1em}(\forall i=1,2, j=1,2)$$

(1)

where $R_{ij}$ represents the fuzzy rules; ${\mu }_i$ and ${\lambda }_j$ denote the ith and jth membership functions for the input $x_1$ and $x_2$, respectively; and $p_{ij}$, $q_{ij}$, and $r_{ij}$ are the consequent parameters in the internal model $f_{ij}$. The above internal models in the fuzzy rules only involve linear terms and demonstrate a linear relationship between customer preference and design characteristics. To interpret the nonlinear relationship transparently, in this research, the nonlinear fuzzy rules in polynomial structure are proposed for ANFIS, which are expressed in (2).

$$\begin{gathered} R_{ij}:If x_1 is {\mu }_i and x_2 is {\lambda }_j, Then \\ {f}_{ij}={\sum }_{t_1=1}^2{C}_{ij}^{t_1}{x}_{t_1}+{\sum }_{t_1=1}^2{\sum }_{t_2=1}^2{C}_{ij}^{t_1{t}_2}{x}_{t_1}{x}_{t_2}+ \\ {\sum }_{t_1=1}^2{\sum }_{t_2=1}^2{\sum }_{t_3=1}^2{C}_{ij}^{t_1{t}_2{t}_3}{x}_{t_1}{x}_{t_2}{x}_{t_3}+\cdots \cdots +C_{ij} \end{gathered}$$

(2)

$f_{ij}$ is the nonlinear model for $R_{ij}$; $C_{ij}^{t_1}$, $C_{ij}^{t_1{t}_2}$ and $C_{ij}^{t_1{t}_2{t}_3}$ are the coefficients of items in the polynomial structure. $C_{ij}$ is the constant in the model. In (2), the polynomial structure is determined based on the COA by minimizing the mean relative error (MRE) as shown in (3).

$$MRE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\displaystyle \frac{\left|{\widehat{y}}_i-y_i\right|}{y_i}}$$

(3)

where n denotes the size of the data set; $y_i$ and ${\widehat{y}}_i$ represent the ith actual and the predicted sentiment score of customer preference, respectively.

3.3. Chaos Optimization Algorithm (COA)

COA is characterized by employing chaotic dynamics to search for the optimal regions instead of random searches and find the optimal solution for the problems at the global level [33]. The process of searching in COA includes two phases, which are the global search and the local search. To identify the good states, a global search is first conducted using the ergodic trace of the entire searching area. If the termination requirement is met, then the good states are achieved, which implies that the best solution is near. Then local search is started in accordance with these results. The deeper search is conducted in the local space by using a small disturbance term. When the criterion of the final terminated state is satisfied, the best solution is found. In chaotic dynamics, variables are transformed from chaotic space to solution space, which determines the solution ranges. The process is described as follows.

In this paper, COA employs the logic model. By iterating the calculation according to (4), chaotic variables are obtained.

$${ c}_{m+1}=f\left(c_m\right)=\mu c_m(1-c_m)$$

(4)

where m represents the iteration number; $c_m$ is the value of the chaotic variable c at the mth iteration, and the range is [0, 1]; $\mu$ is commonly equal to 4 to reach all the chaotic states. For example, if $c_m=0.2$, then ${ c}_{m+1}=4\times 0.2\times \left(1-0.2\right)=0.64$. By utilizing (4), the chaos variables are generated by the successive iterations. In the optimization process, the search for optimal solutions is performed using the generated chaos variables through their own locomotion law.

Based on (5), the optimization variable $q_m$ is obtained by transferring the chaos variable $c_m$ using the linear mapping.

$$q_m=a+(b-a)c_m$$

(5)

where a and b are the lower and upper limits of the elements in $q_m$. Based on (4) and (5), the chaos variable $c_m$ traverses between 0 and 1, while the optimization variable $q_m$ traverses between a and b. For example, if the values of a and b are 1 and 4, respectively, and $c_m=0.5$, then the value of the element in $q_m$ is 1 + (4 − 1) × 0.5 = 2.5 which is between 1 and 4.

The values of $q_m$ determine the nonlinear structure of the fuzzy rules. The elements in $q_m$ involve the inputs of ANFIS, which are denoted as $x_1,x_2,\cdots x_N$, and the mathematical operations between each two inputs. In fuzzy rule (2), there are two types of mathematical operations, which are addition, “+” and multiplication, “×”. The following (6) is the expression of $q_m$.

$$q_m=[{\mathrm{q}}_m^1,{\mathrm{q}}_m^2,\cdots ,{\mathrm{q}}_m^{No}]$$

(6)

where $No$ should be an odd value, which represents the element number in $q_m$. Also, it is the length of $c_m$.

Table 1. The settings of $q_m$.

Items	${\mathbf{q}}_{\mathit{m}}^1$	${\mathbf{q}}_{\mathit{m}}^2$	${\mathbf{q}}_{\mathit{m}}^3$	${\mathbf{q}}_{\mathit{m}}^4$	${\mathbf{q}}_{\mathit{m}}^5$	$\dots$	${\mathbf{q}}_{\mathit{m}}^{\mathit{N}\mathit{o}}$
Settings	Integer ${\mathrm{q}}_m^1\in [a,b]$	0 or 1	Integer ${\mathrm{q}}_m^3\in [a,b]$	0 or 1	Integer ${\mathrm{q}}_m^5\in [a,b]$	$\dots$	Integer ${\mathrm{q}}_m^{No}\in [a,b]$

shows the structure of $q_{m }$.

For the items at the odd positions ${\mathrm{q}}_m^1, {\mathrm{q}}_m^3,\cdots ,{\mathrm{q}}_m^{No}$, their rounded values denote the numerical sequence of inputs. For example, if ${\mathrm{q}}_m^1$ = 2, then the input $x_2$ is determined as the first position in the $q_m$. For the items at the even positions, the values are either 0 or 1. 0 denotes the mathematical operation “+” while 1 denotes the operation “×” between the two inputs. For example, if the item number in $q_m$ is 5 and it is obtained as $q_m=[\mathrm{2,0},\mathrm{3,1},1]$, the polynomial structure of the fuzzy rule is translated as $x_2+x_3{x}_1$. There are two items, $x_2$ and $x_3{x}_1$, in the structure and the coefficients are determined by the least square estimation (LSE) method in the learning process of ANFIS. Therefore, nonlinear structures are generated for the fuzzy rules.

3.4. Chaos-Driven ANFIS

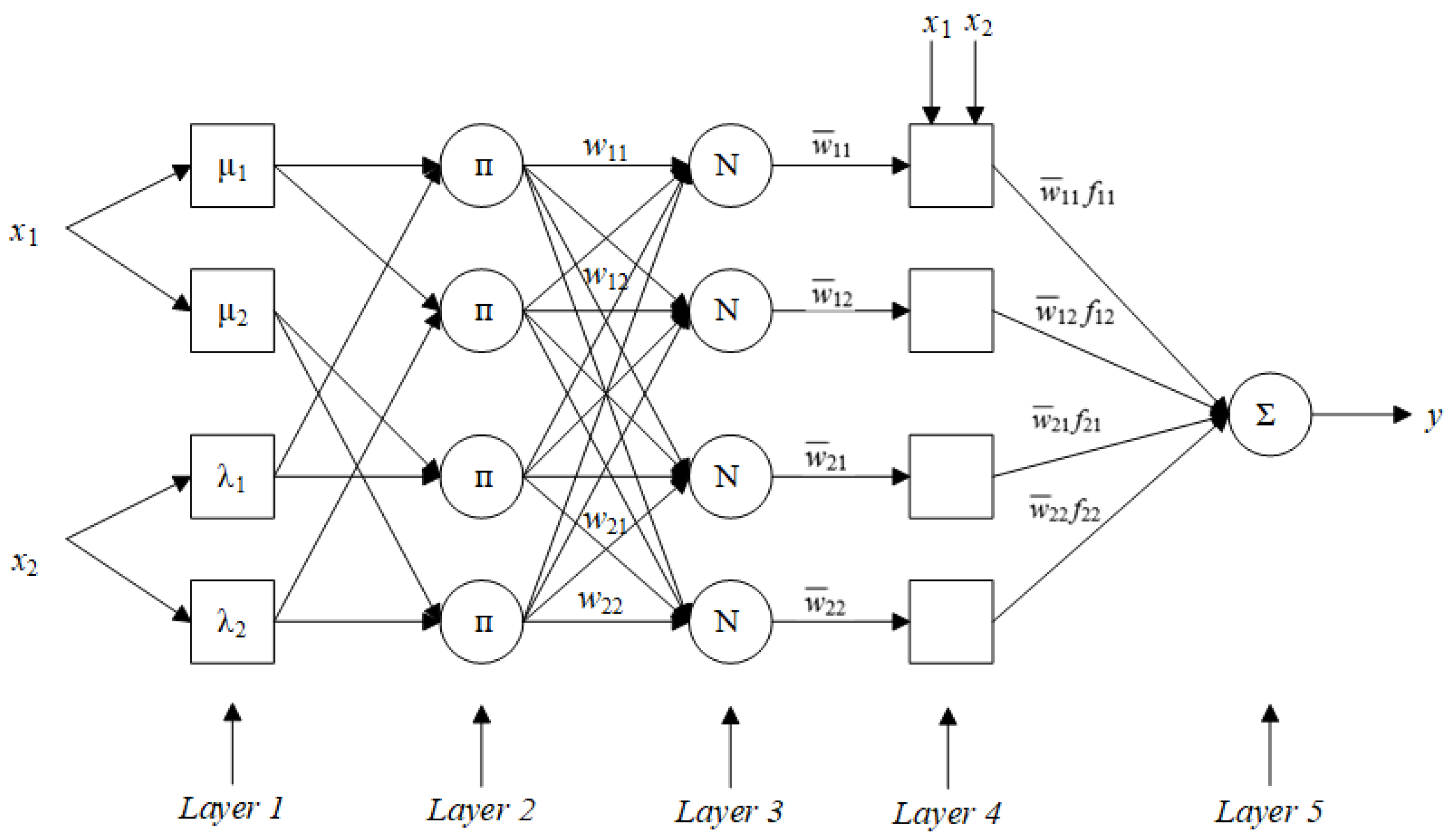
ANFIS integrates a multi-layer feedforward neural network with fuzzy reasoning and maps inputs into an output [34]. An example of an ANFIS structure can be seen in Figure 2, which consists of two inputs and one output, and two membership functions are associated with each input.

In the first layer, ${\mu }_i$ and ${\lambda }_j$, $i=1, 2$ and $j=1, 2$, represent the membership function of the ith and jth linguistic explanation of $x_1$ and $x_2$, respectively. In this study, the triangle membership function is applied, and is shown as follows:

$${\mu }_i=\left\{\begin{array}{cc}{\displaystyle \frac{x_1-a_i}{b_i-a_i}}& a_i\le x_1\le b_i\\ {\displaystyle \frac{c_i-x_1}{c_i-b_i}}& b_i\le x_1\le c_i\\ 0& Otherwise\end{array}\right.$$

and

$${\lambda }_j=\left\{\begin{array}{cc}{\displaystyle \frac{x_2-s_j}{t_j-s_j}}& s_j\le x_2\le t_j\\ {\displaystyle \frac{u_j-x_2}{u_j-t_j}}& t_j\le x_2\le u_j\\ 0& Otherwise\end{array}\right.$$

(7)

where $(a_i, b_i, c_i)$ and $(s_j, t_j, u_j)$ are the antecedent parameters in ANFIS which are the fuzzy numbers in the shape of a triangle. Their values are determined based on the grid partition method.

The second layer consists of four nodes determined by the membership function of the inputs. The outputs of this layer are the firing strength and are calculated as follows.

$$w_{ij}={\mu }_i{\lambda }_j\hspace{1em}(\forall i=1,2 j=1,2)$$

(8)

In the third layer, the normalized firing strength ${\overline{w}}_{ij}$ is defined by (9).

$${\overline{w}}_{ij}={\displaystyle \frac{w_{ij}}{W}} where W={\sum }_i{\sum }_j{w}_{ij}\hspace{1em}(\forall i=1,2, j=1,2)$$

(9)

Each combination of membership functions of $x_1$ with $x_2$ is indicated by one fuzzy rule. Therefore, the fourth layer consists of 4 fuzzy rules. The importance of fuzzy rule $R_{ij}$ is measured by the value of ${\overline{w}}_{ij}$. The larger value of ${\overline{w}}_{ij}$ means more importance of $R_{ij}$. The fuzzy rules are proposed in (2), and in a fuzzy rule, $f_{ij}$ is the internal model with the nonlinear structure.

A single node in the fifth layer represents the final output, which is computed using (10).

$$\widehat{y}={\sum }_{i=1}^2{\sum }_{j=1}^2{\overline{w}}_{ij}{f}_{ij}={\sum }_{i=1}^2{\sum }_{j=1}^2{\overline{w}}_{ij}({\sum }_{t_1=1}^2{C}_{ij}^{t_1}{x}_{t_1}+{\sum }_{t_1=1}^2{\sum }_{t_2=1}^2{C}_{ij}^{t_1{t}_2}{x}_{t_1}{x}_{t_2}+{\sum }_{t_1=1}^2{\sum }_{t_2=1}^2{\sum }_{t_3=1}^2{C}_{ij}^{t_1{t}_2{t}_3}{x}_{t_1}{x}_{t_2}{x}_{t_3}+\cdots \cdots +C_{ij})$$

(10)

In (10), $C_{ij}^{t_1}$, $C_{ij}^{t_1{t}_2}$, $C_{ij}^{t_1{t}_2{t}_3}$ and $C_{ij}$ are the consequent parameters of ANFIS, which are defined by the LSE method. The output (10) can be transformed into the following equation.

$$\begin{gathered} \widehat{y}=\sum _{i=1}^2\sum _{j=1}^2{\overline{w}}_{ij}(\sum _{t_1=1}^2{C}_{ij}^{t_1}{x}_{t_1}+\sum _{t_1=1}^2\sum _{t_2=1}^2{C}_{ij}^{t_1{t}_2}{x}_{t_1}{x}_{t_2}+\sum _{t_1=1}^2\sum _{t_2=1}^2\sum _{t_3=1}^2{C}_{ij}^{t_1{t}_2{t}_3}{x}_{t_1}{x}_{t_2}{x}_{t_3}+\cdots \cdots +C_{ij}) \\ \begin{array}{l}={\overline{w}}_{11}(C_{11}^1{x}_1+C_{11}^2{x}_2+C_{11}^{11}{x}_1^2+C_{11}^{12}{x}_1{x}_2+C_{11}^{21}{x}_2{x}_1+C_{11}^{22}{x}_2^2+\cdots \cdots +C_{11})+\\ {\overline{w}}_{12}\left(C_{12}^1{x}_1+C_{12}^2{x}_2+C_{12}^{11}{x}_1^2+C_{12}^{12}{x}_1{x}_2+C_{12}^{21}{x}_2{x}_1+C_{12}^{22}{x}_2^2+\cdots \cdots +C_{12}\right)+\\ {\overline{w}}_{21}\left(C_{21}^1{x}_1+C_{21}^2{x}_2+C_{21}^{11}{x}_1^2+C_{21}^{12}{x}_1{x}_2+C_{21}^{21}{x}_2{x}_1+C_{21}^{22}{x}_2^2+\cdots \cdots +C_{21}\right)+\\ {\overline{w}}_{22}\left(C_{22}^1{x}_1+C_{22}^2{x}_2+C_{22}^{11}{x}_1^2+C_{22}^{12}{x}_1{x}_2+C_{22}^{21}{x}_2{x}_1+C_{22}^{22}{x}_2^2+\cdots \cdots +C_{11}\right)\end{array} \\ \begin{array}{l}={(\overline{w}}_{11}{x}_1)C_{11}^1+{{(\overline{w}}_{11}x}_2)C_{11}^2+{{(\overline{w}}_{11}x}_1^2)C_{11}^{11}+{{{(\overline{w}}_{11}x}_1{x}_2)C}_{11}^{12}+{{{(\overline{w}}_{11}x}_2{x}_1)C}_{11}^{21}+{{(\overline{w}}_{11}x}_2^2)C_{11}^{22}+\cdots \cdots +{(\overline{w}}_{11})C_{11}\\ {+(\overline{w}}_{12}{x}_1)C_{12}^1+\left({\overline{w}}_{12}{x}_2)C_{12}^2+{( {\overline{w}}_{12}{x}_1^2)C}_{12}^{11}+{( {\overline{w}}_{12}{x}_1{x}_2)C}_{12}^{12}+{( {\overline{w}}_{12}{x}_2{x}_1)C}_{12}^{21}+{( {\overline{w}}_{12}{x}_2^2)C}_{12}^{22}+\cdots \cdots +{( {\overline{w}}_{12})C}_{12}\right)\\ +{(\overline{w}}_{21}{x}_1)C_{21}^1+{(\overline{w}}_{21}{x}_2{)C}_{21}^2+{{(\overline{w}}_{21}{x}_1^2)C}_{21}^{11}+{(\overline{w}}_{21}{x}_1{x}_2)C_{21}^{12}+{{(\overline{w}}_{21}{x}_2{x}_1)C}_{21}^{21}+{{(\overline{w}}_{21}{x}_2^2)C}_{21}^{22}+\cdots \cdots +{(\overline{w}}_{21})C_{21}\\ {+(\overline{w}}_{22}{x}_1)C_{22}^1+{(\overline{w}}_{22}{x_2)C}_{22}^2+{ {(\overline{w}}_{22}{x}_1^2)C}_{22}^{11}+{(\overline{w}}_{22}{x}_1{x}_2)C_{22}^{12}+{(\overline{w}}_{22}{x_2{x}_1)C}_{22}^{21}+{{(\overline{w}}_{22}{x}_2^2)C}_{22}^{22}+\cdots \cdots +{{(\overline{w}}_{22})C}_{11}\\ =A\theta \end{array} \end{gathered}$$

(11)

where $A=({\overline{w}}_{11}{x}_1,{{\overline{w}}_{11}x}_2, {{\overline{w}}_{11}x}_1^2,{{\overline{w}}_{11}x}_1{x}_2, {{\overline{w}}_{11}x}_2{x}_1, {{\overline{w}}_{11}x}_2^2{,\overline{w}}_{11}, {\overline{w}}_{12}{x}_1, {\overline{w}}_{12}{x}_2, {\overline{w}}_{12}{x}_1^2, {\overline{w}}_{12}{x}_1{x}_2, {\overline{w}}_{12}{x}_2{x}_1,{\overline{w}}_{12}{x}_2^2, {\overline{w}}_{12},{\overline{w}}_{21}{x}_1,{\overline{w}}_{21}{x}_2,{\overline{w}}_{21}{x}_1^2,{\overline{w}}_{21}{x}_1{x}_2,{\overline{w}}_{21}{x}_2{x}_1,{\overline{w}}_{21}{x}_2^2,{\overline{w}}_{21}$, ${\overline{w}}_{22}{x}_1,{\overline{w}}_{22}{x}_2,{\overline{w}}_{22}{x}_1^2,{\overline{w}}_{22}{x}_1^2,{\overline{w}}_{22}{x}_1{x}_2,{\overline{w}}_{22}{x}_2{x}_1,{\overline{w}}_{22}{x}_2^2,{\overline{w}}_{22})$ and $\theta =(C_{11}^1,C_{11}^2,C_{11}^{11},C_{11}^{12},C_{11}^{21},C_{11}^{22},\cdots ,C_{11},C_{12}^1,C_{12}^2,C_{12}^{11},C_{12}^{12}{,C}_{12}^{21},C_{12}^{22},\cdots$, $C_{12}{, C}_{21}^1,C_{21}^2,C_{21}^{11},C_{21}^{12},C_{21}^{21},C_{21}^{22},\cdots ,C_{21}, C_{22}^1,C_{22}^2,{ C}_{22}^{11},C_{22}^{12},C_{22}^{21},C_{22}^{22},{\cdots ,C}_{11})$. Based on the process of ANFIS, matrix A is obtained. An estimated value of $\theta$, denoted as $\widehat{\theta }$, is obtained by minimizing the following squared error ${‖A\theta -y‖}^2$, which is updated and calculated based on the following equations.

$$\stackrel{\wedge }{{\theta }_{i+1}}=\stackrel{\wedge }{{\theta }_i}+{\displaystyle \frac{S_{i+1}{a}_{i+1}({b_{i+1}}^T-{a_{i+1}}^T\stackrel{\wedge }{{\theta }_i})}{1+{a_{i+1}}^T{S}_{i+1}{a}_{i+1}}}$$

(12)

$$S_{i+1}=S_i-{\displaystyle \frac{S_i{a}_{i+1}{a_{i+1}}^T{S}_i}{1+{a_{i+1}}^T{S}_i{a}_{i+1}}}$$

(13)

where $S_i$ represents the covariance matrix and $S_0=\gamma I$; $\gamma$ should be set as a positive and large number; $I$ denotes the identity matrix; $a_i^T$ denotes the $ith$ row of the matrix $A$; and $b_i^T$ is the $ith$ element of $y$; Based on $\widehat{\theta }$, the predicted output $\stackrel{\wedge }{y}$ can also be calculated using (14).

$$\stackrel{\wedge }{y}=A\stackrel{\wedge }{\theta }$$

(14)

where $\widehat{y}$ is the predicted customer preference’s sentiment score.

3.5. The Procedure of the Proposed Approach

The following is a description of the chaos-driven ANFIS method to model customer preferences with the explainable nonlinearity derived from online comments.

Step 1. Based on the defined samples of products, the data sets for modeling are first prepared. Sentiment analysis is conducted according to Section 3.1 to extract the customer preferences and calculate their sentiment scores, which are the outputs of the datasets. The inputs, which are the settings of the relevant design characteristics, are obtained from the products’ information.

Step 2. The initialization for the parameters used in the proposed approach is performed, such as the iteration number of COA, the length of the chaos variable $c_m$, the number of fuzzy rules, the initial value for $c_1$, and the values of a and b in (5).

Step 3. The iteration of COA starts (m = 1). Based on (4), the chaos variable $c_{m+1}$ is computed. Using (5), the corresponding $q_{m+1}$ is obtained. Based on the generated $q_{m+1}$, the items at the odd positions are substituted by the values of corresponding inputs, and the items at the even positions are replaced by the operations, “+” or “×”.

Step 4. Using the generated polynomial structure, the models are built following (7)~(10), and the coefficients of nonlinear fuzzy rules are trained and obtained using (11)~(13). The predicted customer preference’s sentiment scores ${\widehat{y}}_i$ are calculated based on (14). Then, in each iteration, the fitness value of COA, MRE, is computed using (3).

Step 5. The iteration goes on m + 1 $\to$ m, and the processes are repeated from Step 3. When the iteration number achieves the predefined number, the iteration is stopped. The smallest MRE is found, and a record is made for the corresponding iteration number. Therefore, the best customer preference model is the model generated in this iteration.

4. Implementation

To assess the effectiveness of the chaos-driven ANFIS approach, a case study of laptop products is introduced in this research. Ten laptops from different brands are selected as samples, and their customer reviews are compiled from the Amazon website. The number of online reviews collected is 4990, 630, 590, 1100, 610, 590, 1980, 500, 412, and 370 for products 1 to 10, respectively. As a result of sentiment analysis using Semantria, four categories of customer preferences are identified, which are easy carrying, exterior design, quality, and performance. In this study, the customer preference, easy carrying, is selected for the illustration and is denoted as y. Its sentiment score is obtained and shown in the last column of

Table 2. Data sets for modeling.

Product Number	Display Size (x1)	Weight (x2)	Easy Carrying (y)
1	15.6	3.97	0.2470
2	15.6	3.75	0.9187
3	13.5	2.83	0.1533
4	14	3.63	0.6009
5	14	2.65	0.4097
6	15.6	5.07	0.1221
7	11.6	2.64	0.3779
8	14	3.3	0.3838
9	14	3.17	0.3777
10	15.6	4.19	0.4830

. Display size and weight are two design characteristics related to easy carrying, which are denoted by $x_1$ and $x_2$, respectively. Their settings are found in the description of the products and are shown in Table 2.

To model customer preferences, the proposed approach is applied to the above data sets. For the two inputs, each input has three membership functions. Therefore, the total number of fuzzy rules is nine. To include all the inputs in the polynomial structure of fuzzy rules, the number of items in the optimization variable, $No$, is set as 5. The initial values of $c_1$ are the random values between 0 and 1. For the odd number of chaos variables, the value of a is 1, and the value of b is set as the total number of inputs. For an even number of chaos variables, the values of a and b are equal to 0 and 1, respectively. In COA, the number of iterations is set to 200. Extensive experimental tests were conducted over a range of iterations from 50 to 5000. The selection of 200 iterations is justified by its ability to achieve an optimal balance between computational time and models’ accuracy. Assuming that there are n data sets, the number of clusters will be ≤$\sqrt{n}$ [35]. Therefore, the number of membership functions for each input is set to 3 for each input in ANFIS. Based on the description in Section 3.4, the number of fuzzy rules in the proposed approach is 3 ×3 = 9. To describe the modeling results, the following training example is used. Products 1 and 2 are used as the validation data, while products 3~10 are used as the training data sets. MATLAB software with version R2023a was installed on a Lenovo-XiaoXinPro 16 ARP8 laptop with a 64-bit operating system. They are utilized to implement the process of modeling using the proposed approach.

The parameters $(a_i, b_i, c_i)$ of the three membership functions for $x_1$ are obtained as (9.6, 11.6, 13.6), (11.6, 13.6, 15.6), and (13.6, 15.6, 17.6). And the values of $(s_j, t_j, u_j)$ for $x_2$ are determined as (1.425, 2.64, 3.855), (2.64, 3.855, 5.07), and (3.855, 5.07, 6.285). By introducing the above antecedent parameters into Equation (7), the membership functions in ANFIS are generated. Using the data set of product 3 as an example, ${\mu }_1={\displaystyle \frac{c_i-x_1}{c_i-b_i}}={\displaystyle \frac{13.6-13.5}{13.6-11.6}}=0.05$ and ${\lambda }_1={\displaystyle \frac{u_j-x_2}{u_j-t_j}}={\displaystyle \frac{3.855-2.83}{3.855-2.64}}$ = 0.8436. Based on (8), $w_{11}={\mu }_1{\lambda }_1=0.05\times 0.8436=0.0422$. Following the same calculations, all the values of $w_{ij}$ can be obtained and then ${\overline{w}}_{ij}$ can be determined using (9).

The optimal solution for the optimization variable $q_m$ is obtained as follows.

$$q=[\mathrm{1,0},\mathrm{1,1}, 2]$$

(15)

Therefore, the generated nonlinear structure of the nine fuzzy rules in this example is transformed as follows.

$$x_1+x_1{x}_2+c$$

(16)

where c is a constant in the fuzzy rule.

Based on the LSE method, the coefficients for the items in the above structure are calculated and shown in

Table 3. The generated nonlinear fuzzy rules for validation 1.

Rule Number	Fuzzy Rules in Validation 1
Rule 1	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then {f_{11}=-0.0649x}_1+0.0095x_1{x}_2$+ 0.8753
Rule 2	$If x_1 is {\mu }_1 and x_2 is {\lambda }_2, Then {f_{12}=0.9717x}_1+0.8812x_1{x}_2$+ 0.9065
Rule 3	$If x_1 is {\mu }_1 and x_2 is {\lambda }_3, Then {f_{13}=0.7586x}_1+0.0518x_1{x}_{2 }$+ 0.9603
Rule 4	$If x_1 is {\mu }_2 and x_2 is {\lambda }_1, Then {f_{21}=0.1592x}_1-0.0797x_1{x}_{2 }$+ 0.3083
Rule 5	$If x_1 is {\mu }_2 and x_2 is {\lambda }_2, Then {f_{22}=0.0012x}_1-0.0027x_1{x}_2$+ 0.9806
Rule 6	$If x_1 is {\mu }_2 and x_2 is {\lambda }_3, Then {f_{23}=0.9124x}_1+{0.4901x}_1{x}_2$+ 0.6482
Rule 7	$If x_1 is {\mu }_3 and x_2 is {\lambda }_1, Then {f_{31}=-0.1259x}_1+0.1429x_1{x}_2$+ 0.5063
Rule 8	$If x_1 is {\mu }_3 and x_2 is {\lambda }_2, Then {f_{32}=-0.1546x}_1+0.0352x_1{x}_2$+ 0.4445
Rule 9	$If x_1 is {\mu }_3 and x_2 is {\lambda }_3, Then {f_{33}=0.2683x}_1-0.0583 x_1{x}_2$+ 0.5559

. Using the data set of product 1 in validation 1 as an example,

if $x_1 is {\mu }_1 and x_2 is {\lambda }_1,then f_{11}=-0.0649\times 15.6+0.0095\times 15.6\times 3.97$ + 0.8753 = 0.4512.

By using the proposed approach, the establishment of a customer preference model for easy carrying is completed. The nonlinear fuzzy rules in Table 3 are explainable as the equations can show the relationship between the inputs and the output.

5. Validation

To further evaluate the proposed chaos-driven ANFIS approach, five validation tests were performed on a case study of laptop products. In the process of training and validation, no repeated data sets were used. In validation tests 1 to 5, as validation data sets, product 1 and 2, product 3 and 4, product 5 and 6, product 7 and 8, and product 9 and 10 have been chosen. Training data sets were derived from the remaining 8 products. In each validation, a comparison is made between the proposed approach and the other five approaches, which are fuzzy regression (FR), fuzzy least-squares regression (FLSR), ANFIS, ANFIS with subtractive cluster (ANFIS with SC), and ANFIS with K-means. In ANFIS with SC and ANFIS with K-means, ANFIS is combined with the methods of subtractive clustering and K-means to identify the membership function of inputs. All six approaches were tested using the same data sets. For the purpose of comparing the validation results based on the six approaches, the values of MRE in (3) and the variance of errors (VoE) in (17) were applied.

$$VoE={\displaystyle \frac{1}{n-1}}{\sum }_{i=1}^n{({\displaystyle \frac{\left|{\widehat{y}}_i-y_i\right|}{y_i}}-MRE)}^2$$

(17)

Further information about parameter settings in the chaos-driven ANFIS approach can be found in Section 4. A comparison of the MRE and VoE values based on the six approaches in the five validations is presented in

Table 4. The validation results based on the six approaches.

Validation Number	FR	FLSR	ANFIS	ANFIS with SC	ANFIS with K-Means	Chaos-Driven ANFIS
	MRE
1	0.4203	0.7530	0.6403	0.5261	0.8111	0.2379
2	1.3421	1.1654	2.9822	0.9662	0.1853	0.1496
3	3.3718	2.5441	1.9400	3.4929	4.3322	0.4866
4	0.5911	0.2657	0.2322	0.1257	0.1279	0.1098
5	0.1508	0.2479	0.7024	1.0312	0.8874	0.1233
	VoE
1	0.2629	0.1744	0.0434	0.2998	0.5853	0.0008
2	2.4549	2.1798	14.4430	0.6439	0.0048	2.0337 × 10−5
3	18.9518	10.0461	4.2043	14.8020	21.2967	0.0069
4	0.4791	0.0086	0.0420	0.0290	0.0209	0.0003
5	0.0009	0.0135	0.7282	1.4385	0.1352	4.3746 × 10−5

. From Table 4, it can be seen that the values of MRE and VoE are the smallest based on the proposed approach compared with those based on the other five approaches.

Based on all the validation errors from the five tests, the confidence intervals of the six approaches with a 95% level of confidence were calculated and are compared in

Table 5. The confidence intervals of validation errors based on the six approaches.

Approaches	Confidence Interval	Interval Width	Center Point
FR	[−0.4453, 2.7957]	3.2410	1.1752
FLSR	[−0.1790, 2.1695]	2.3485	0.9953
ANFIS	[−0.1125, 2.7113]	2.8238	1.2994
ANFIS With SC	[−0.4077, 2.8645]	3.2722	1.2284
ANFIS with K-means	[−0.9010, 3.4386]	4.3396	1.2688
Chaos-drive ANFIS	[0.0273, 0.4156]	0.3883	0.2215

. The comparison analysis shows that the proposed approach has both the narrowest interval and the lowest center point, which indicates the proposed approach yields significantly more robust and stable models than the other five approaches.

The generated explainable nonlinear fuzzy rules for validation 1 are given in Table 3, and

Table 6. The generated nonlinear fuzzy rules for validations 2~5.

Rule Number	Validation 2
Rule 1	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then f_{11}={{0.0010x}_{1}x}_2^2+0.3002$
Rule 2	$If x_1 is {\mu }_1 and x_2 is {\lambda }_2, Then f_{12}={{0.3772x}_{1}x}_2^2+0.8303$
Rule 3	$If x_1 is {\mu }_1 and x_2 is {\lambda }_3, Then f_{13}={{0.1600x}_{1}x}_2^2+0.3123$
Rule 4	$If x_1 is {\mu }_2 and x_2 is {\lambda }_1, Then f_{21}={-0.0119x_{1}x}_2^2+0.9267$
Rule 5	$If x_1 is {\mu }_2 and x_2 is {\lambda }_2, Then f_{22}={{0.0020x}_{1}x}_2^2+0.3002$
Rule 6	$If x_1 is {\mu }_2 and x_2 is {\lambda }_3, Then{ f}_{23}={{0.5391x}_{1}x}_2^2+0.4112$
Rule 7	$If x_1 is {\mu }_3 and x_2 is {\lambda }_1, Then{ f}_{31}={{0.0294x}_{1}x}_2^2+0.1189$
Rule 8	$If x_1 is {\mu }_3 and x_2 is {\lambda }_2, Then f_{32}={{0.0004x}_{1}x}_2^2+0.2969$
Rule 9	$If x_1 is {\mu }_3 and x_2 is {\lambda }_3, Then f_{33}={{-0.0001x}_{1}x}_2^2+0.1880$
Rule number	Validation 3
Rule 1	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then f_{11}={0.0122x}_2-0.0017x_1^2+0.5914$
Rule 2	$If x_1 is {\mu }_1 and x_2 is {\lambda }_2, Then f_{12}={0.7506x}_2+0.1737x_1^2+0.2083$
Rule 3	$If x_1 is {\mu }_1 and x_2 is {\lambda }_3, Then f_{13}={0.3025x}_2+{0.6986x}_1^2+0.8159$
Rule 4	$If x_1 is {\mu }_2 and x_2 is {\lambda }_1, Then f_{21}={0.8486x}_2-0.0178x_1^2+0.5115$
Rule 5	$If x_1 is {\mu }_2 and x_2 is {\lambda }_2, Then f_{22}={0.0575x}_2-0.0013x_1^2+0.3265$
Rule 6	$If x_1 is {\mu }_2 and x_2 is {\lambda }_3, Then f_{23}={0.4757x}_2+{0.5916x}_1^2+0.5225$
Rule 7	$If x_1 is {\mu }_3 and x_2 is {\lambda }_1, Then{ f}_{31}={0.4199x}_2+{0.0116x}_1^2+0.6771$
Rule 8	$If x_1 is {\mu }_3 and x_2 is {\lambda }_2, Then f_{32}={0.5146x}_2-0.0092x_1^2+0.6649$
Rule 9	$If x_1 is {\mu }_3 and x_2 is {\lambda }_3, Then{ f}_{33}=0.0465x_2-0.0040x_1^2+0.7873$
Rule number	Validation 4
Rule 1	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then f_{11}={{0.0036x}_{1}x}_2^2+0.0407$
Rule 2	$If x_1 is {\mu }_1 and x_2 is {\lambda }_2, Then f_{12}={0.9001x_{1}x}_2^2+0.3555$
Rule 3	$If x_1 is {\mu }_1 and x_2 is {\lambda }_3, Then f_{13}={0.3580x_{1}x}_2^2+0.8713$
Rule 4	$If x_1 is {\mu }_2 and x_2 is {\lambda }_1, Then f_{21}={-0.0154x_{1}x}_2^2+0.8499$
Rule 5	$If x_1 is {\mu }_2 and x_2 is {\lambda }_2, Then f_{22}={{0.0009x}_{1}x}_2^2+0.7051$
Rule 6	$If x_1 is {\mu }_2 and x_2 is {\lambda }_3, Then f_{23}={{0.0298x}_{1}x}_2^2+0.5198$
Rule 7	$If x_1 is {\mu }_3 and x_2 is {\lambda }_1, Then{ f}_{31}={{0.0398x}_{1}x}_2^2+0.3269$
Rule 8	$If x_1 is {\mu }_3 and x_2 is {\lambda }_2, Then{ f}_{32}={{0.0010x}_{1}x}_2^2+0.0357$
Rule 9	${If x_1 is {\mu }_3 and x_2 is {\lambda }_3, Then f}_{33}={{-0.0016x}_{1}x}_2^2+0.7828$
Rule number	Validation 5
Rule 1	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then {f_{11}=0.2223x}_1-0.0986x_1{x}_2$+ 0.8485
Rule 2	$If x_1 is {\mu }_1 and x_2 is {\lambda }_2, Then {f_{12}=0.0847x}_1+0.1865x_1{x}_2$+ 0.8760
Rule 3	$If x_1 is {\mu }_1 and x_2 is {\lambda }_3, Then {f_{13}=0.7847x}_1+0.3442x_1{x}_2$+ 0.7873
Rule 4	${{If x_1 is {\mu }_2 and x_2 is {\lambda }_1, Then f}_{21}=0.5121x}_1-0.2104x_1{x}_2$+ 0.5136
Rule 5	$If x_1 is {\mu }_2 and x_2 is {\lambda }_2, Then {f_{22}=0.5978x}_1-0.1389x_1{x}_2-$0.0035
Rule 6	$If x_1 is {\mu }_2 and x_2 is {\lambda }_3, Then {f_{23}=0.8223x}_1+{0.3537x}_1{x}_2$+ 0.1425
Rule 7	$If x_1 is {\mu }_3 and x_2 is {\lambda }_1, Then{{ f}_{31}=0.3251x}_1-0.0459x_1{x}_2$+ 0.3380
Rule 8	$If x_1 is {\mu }_3 and x_2 is {\lambda }_2, Then {f_{32}=0.1761x}_1-0.0499x_1{x}_2$+ 0.7044
Rule 9	$If x_1 is {\mu }_3 and x_2 is {\lambda }_3, Then{{ f}_{33}=0.2985x}_1-0.0685 x_1{x}_2$+ 0.8697

shows the nonlinear fuzzy rules in different polynomial structures for validations 2~5.

Using validation 5 as a reference, the customer preference models developed based on FR and FLSR are expressed in (18) and (19), respectively. And nine examples of fuzzy rules derived from ANFIS, ANFIS with SC, and ANFIS with K-means are shown in

Table 7. The examples of fuzzy rules based on ANFIS, ANFIS with SC, and ANFIS with K-means in validation 5.

Example Number	The Examples of Fuzzy Rules
1	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then {f_{11}=0.05259x}_1-0.07x_2-0.05085$
2	$If x_1 is {\mu }_1 and x_2 is {\lambda }_2, Then {f_{12}=0.8419x}_1+0.1765x_2+0.06235$
3	$If x_1 is {\mu }_2 and x_2 is {\lambda }_1, Then {f_{21}=0.0819x}_1-0.4573x_2+0.1787$
4	$If x_1 is {\mu }_2 and x_2 is {\lambda }_2, Then {f_{22}=-0.2089x}_1+1.025x_2+0.01703$
5	$If x_1 is {\mu }_3 and x_2 is {\lambda }_1, Then{{ f}_{31}=0.0584x}_1+0.3712x_2-0.1077$
6	$If x_1 is {\mu }_3 and x_2 is {\lambda }_2, Then{{ f}_{32}=0.3505x}_1-1.256x_1+0.001492$
7	$If x_1 is {\mu }_3 and x_2 is {\lambda }_3, Then {f_{33}=-0.3874x}_1+1.221x_2-0.02483$
8	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then {f_{11}=-0.2200x}_1+0.6708x_2+0.1526$
9	$If x_1 is {\mu }_1 and x_2 is {\lambda }_1, Then {f_{11}=-0.7336x}_1-0.2215x_2+0.4026$

.

$${\widehat{y}=\left(-1.1080, 0.8354\right)+(0.1365, 0.0336)x}_1+(-0.1135, 0)x_2$$

(18)

$${\widehat{y}=\left(0.1946, 0.0790\right)+(0.0132, 0.0076)x}_1+(0.0386, 0.0651)x_2$$

(19)

Based on the above six methods, the customer preference models for easy carrying are developed. The models based on FR and FLSR are transparent linear models with fuzzy coefficients but lack nonlinear capability. The methods of ANFIS, ANFIS with SC, ANFIS with K-means, and chaos-driven ANFIS can deal with both the fuzziness and nonlinearity of the models. However, from Table 7, it can be observed that the methods of ANFIS, ANFIS with SC, and ANFIS with K-means cannot solve the black box problems of ANFIS, as the fuzzy rules generated are linear models, which are only transparent information from the modeling process, and the nonlinearity is obscured. Comparatively, the fuzzy rules derived from the chaos-driven ANFIS approach, as shown in Table 6, are explained in nonlinear equations, and the nonlinearity in the relationship between the customer preferences and design characteristics can be interpreted directly and explicitly. Therefore, only the proposed approach can mitigate the black-box problem of ANFIS by explicitly revealing the model construction and processes involved in nonlinear modeling.

6. Conclusions

In modeling customer preferences based on customer comments, ANFIS is an effective approach to associate customer preferences with design characteristics. By using ANFIS, the fuzziness and nonlinearity of the modeling can be addressed. ANFIS, however, has black box issues. Its internal decision-making process is buried within complex, interconnected layers of nodes and membership functions that are difficult for a human to decipher. To solve the above problem, a chaos-driven ANFIS approach is introduced to develop models with nonlinearity that can be explained transparently. As an illustration of the modeling process of the proposed approach, a case study of laptop products is introduced in the study. And the modeling of customer preference, easy carrying, is selected as an example. Five validation tests were performed to further evaluate the chaos-driven ANFIS approach, along with comparisons to FR, FLSR, ANFIS, ANFIS with SC, and ANFIS with K-means. Based on the comparison results, it can be shown that the proposed approach has smaller mean relative errors, variance in errors, and confidence intervals of validation errors than the other five approaches. While all established models from the ANFIS-based approaches capably capture the model’s fuzziness and nonlinearity, only the proposed approach solves the inherent black-box issue of ANFIS. The proposed method revolutionizes this by structuring the “THEN” part of its fuzzy rules as interpretable polynomials. Each rule now represents a clear, nonlinear relationship that is valid within a specific fuzzy-defined region of the input space. This means the entire model can be broken down into a set of human-readable equations. Each governs the system’s behavior under certain conditions, which allow the model’s nonlinearity to be addressed explicitly and its logic to be directly interpreted.

By mapping sentiment-based customer preferences directly to design characteristics, the transparent ANFIS model provides product designers with a useful decision-support tool. The designers move beyond knowing what is happening to understand precisely why it is happening. In product strategy and development, designers are no longer left guessing which feature to improve. Instead, they can strategically reallocate resources. They can proactively adjust the settings of key design characteristics, such as battery life, weight, or screen size, to refine existing products or blueprint entirely new ones. This data-driven alignment ensures that resources are invested in features that directly drive customer satisfaction, dramatically increasing the likelihood of market success. Also, this transparent ANFIS model provides product designers with a critical bridge between powerful AI capability and human-centric design. It converts abstract data into tangible and explainable logic and can empower designers to create products aligned with the changing needs of customers.

The limitation of the proposed chaos-driven ANFIS approach is the complexity of the ANFIS structure, which increases with the number of input variables of a given data set. As inputs are added, the number of nodes in layers 2~4 of ANFIS increases exponentially, leading to a massive increase in the number of parameters that must be tuned during training. Consequently, the computational time required for modeling becomes longer, or even fails to converge to a solution. To mitigate the limitation and enhance the model’s practicality, future research will be conducted on the reduction of the input dimensionality in ANFIS. The methods of optimal feature selection or identifying the nonlinear combination of the variables can be employed by introducing advanced optimization algorithms, such as evolutionary or swarm intelligence techniques. Furthermore, future research work will include the involvement of the higher-degree polynomial terms within the fuzzy rules in the modeling process to investigate their influence on the performance of the models. Also, the development of adaptive polynomials with variable degrees in the models can be performed using advanced artificial intelligence techniques. On the other hand, the dynamic trends in customer preferences will be captured by modeling time series customer preferences using customer reviews.