Improving Transfer Connectivity in Railway Timetables Based on Closeness Centrality: The Case of the European International Network
Abstract
1. Introduction
2. Literature Review
3. Methodology
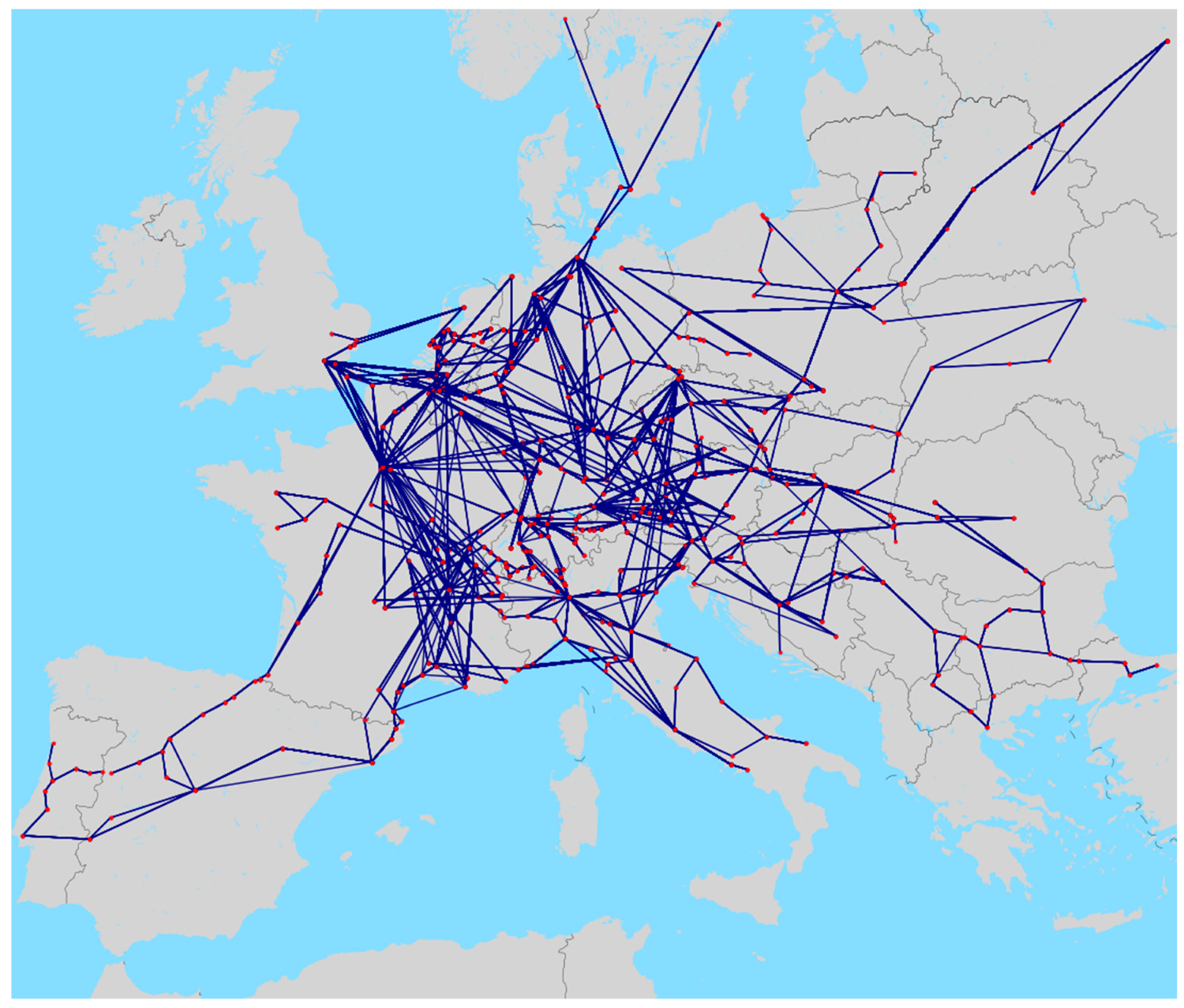
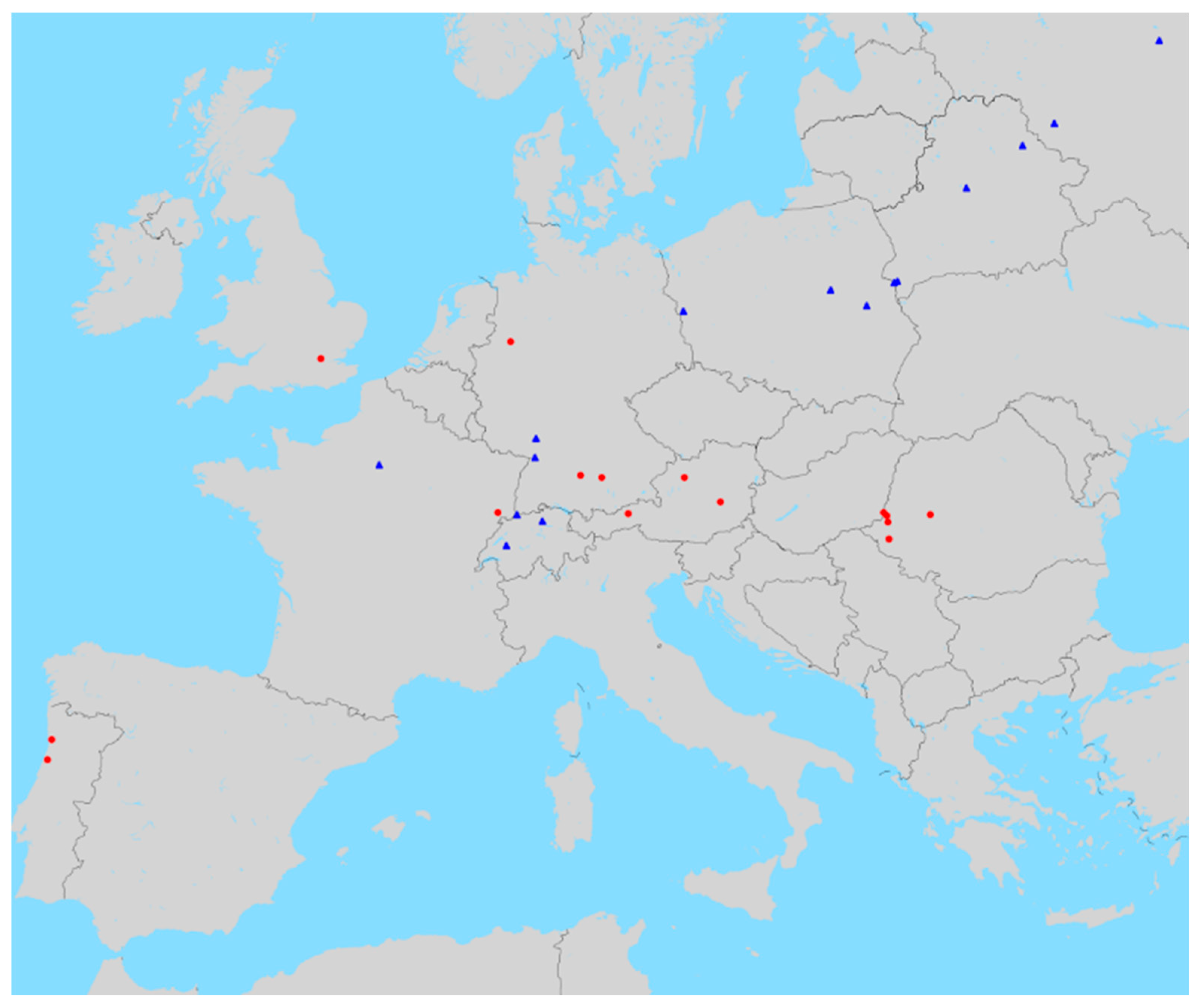
3.1. The European Railway Network
3.2. Algorithm to Find Better Schedules
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Li, X.; Li, H. A quantitative approach for assessing the critical nodal and linear elements of a railway infrastructure. Int. J. Crit. Infrastruct. Prot. 2015, 8, 3–15. [Google Scholar] [CrossRef]
- European Commision. Priorities for 2021–2027. Available online: https://ec.europa.eu/regional_policy/policy/how/priorities_en?etrans=hr (accessed on 8 February 2022).
- European Commission. Cohesion Policy Investments on Track for Rail Transport. 2021. Available online: https://ec.europa.eu/regional_policy/en/newsroom/panorama/2021/03/03-12-2021-cohesion-policy-investments-on-track-for-rail-transport (accessed on 19 August 2024).
- EUROSTAT. Energy, Transport and Environment Statistics: 2020 Edition; European Union: Luxembourg, 2020. [Google Scholar]
- Debrezion, G.; Pels, E.; Rietveld, P. Modelling the joint access mode and railway station choice. Transp. Res. Part E 2009, 45, 270–283. [Google Scholar] [CrossRef]
- Chowdhury, S.; Ceder, A. Definition of Planned and Unplanned Transfer of Public Transport Service and User Decisions to Use Routes with Transfers. J. Public Transp. 2013, 16, 1–20. [Google Scholar] [CrossRef]
- Etgen, B. Connecting with Transit: Using Connectivity to Align and Schedule Transit Service. J. Public Transp. 2022, 24, 100012. [Google Scholar] [CrossRef]
- Hu, Y.; Li, S.; Dessouky, M.M.; Yang, L.; Gao, Z. Computationally efficient train timetable generation of metro networks with uncertain transfer walking time to reduce passenger waiting time: A generalized Benders decomposition-based method. Transp. Res. Part B 2022, 163, 210–231. [Google Scholar] [CrossRef]
- Roy, S.; Maji, A. High-Speed Rail Station Location Optimization Using Customized Utility Functions. IEEE Intell. Transp. Syst. Mag. 2023, 15, 26–35. [Google Scholar] [CrossRef]
- Liu, T.; Cats, O.; Gkiotsalitis, K. A review of public transport transfer coordination at the tactical planning phase. Transp. Res. Part C Emerg. Technol. 2021, 133, 103450. [Google Scholar] [CrossRef]
- Calzada-Infante, L.; Adenso-Díaz, B.; García Carbajal, S. Analysis of the European international railway network and passenger transfers. Chaos Solitons Fractals 2020, 141, 110357. [Google Scholar] [CrossRef]
- Bhatia, U.; Kumar, D.; Kodra, E.; Ganguly, A.R. Network science based quantification of resilience demonstrated on the indian railways network. PLoS ONE 2015, 10, e0141890. [Google Scholar] [CrossRef]
- Wang, W.; Cai, K.; Du, W.; Wu, X.; Tong, L.C.; Zhu, X.; Cao, X. Analysis of the Chinese railway system as a complex network. Chaos Solitons Fractals 2020, 130, 1–13. [Google Scholar] [CrossRef]
- Xu, W.A.; Zhou, J.; Qiu, G. China’s high-speed rail network construction and planning over time: A network analysis. J. Transp. Geogr. 2018, 70, 40–54. [Google Scholar] [CrossRef]
- But, T.; Prokhorchenko, A. Investigation into Train Flow System on Ukraine’s Railways with Methods of Complex Network Analysis. Am. J. Ind. Eng. 2013, 1, 41–45. [Google Scholar]
- Feng, X.; He, S.; Li, G.; Chi, J. Transfer network of high-speed rail and aviation: Structure and critical components. Phys. A Stat. Mech. Its Appl. 2021, 581, 126197. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Complex Network Topology of Transportation Systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Kinder, M. Models for Periodic Timetabling. Master’s Thesis, Technische Universität Berlin, Berlin, Germany, 2008. [Google Scholar]
- Li, Y.; Han, B.; Zhao, P.; Yang, R. Collaborative optimization for train stop planning and train timetabling on high-speed railways based on passenger demand. PLoS ONE 2023, 18, e0284747. [Google Scholar] [CrossRef] [PubMed]
- Serafini, P.; Ukovich, W. A mathematical model for periodic scheduling problems. SIAM J. Discret. Math. 1989, 2, 550–581. [Google Scholar] [CrossRef]
- Polinder, G.J.; Schmidt, M.; Huisman, D. Timetabling for strategic passenger railway planning. Transp. Res. Part B Methodol. 2021, 146, 111–135. [Google Scholar] [CrossRef]
- Liebchen, C. The First Optimized Railway Timetable in Practice. Transp. Sci. 2008, 42, 420–435. [Google Scholar] [CrossRef]
- Drábek, M.; Mazel, D.; Pospíšil, J. High-speed rail network and periodic timetable: A comparative analysis of operational concepts. Acta Polytech. CTU Proc. 2021, 31, 5–9. [Google Scholar] [CrossRef]
- Cacchiani, V.; Huisman, D.; Kidd, M.; Kroon, L.; Toth, P.; Veelenturf, L.; Wagenaar, J. An overview of recovery models and algorithms for real-time railway rescheduling. Transp. Res. Part B Methodol. 2014, 63, 15–37. [Google Scholar] [CrossRef]
- Caprara, A.; Monaci, M.; Toth, P.; Guida, P.L. A Lagrangian heuristic algorithm for a real-world train timetabling problem. Discret. Appl. Math. 2006, 154, 738–753. [Google Scholar] [CrossRef]
- Huan, N.; Hess, S.; Yao, E. Understanding the effects of travel demand management on metro commuters’ behavioural loyalty: A hybrid choice modelling approach. Transportation. 2022, 49, 343–372. [Google Scholar] [CrossRef]
- Schakenbos, R.; Paix, L.L.; Nijenstein, S.; Geurs, K.T. Valuation of a Transfer in a Multimodal Public Transport Trip. Transp. Policy 2016, 46, 72–81. [Google Scholar] [CrossRef]
- Park, J.; Chowdhury, S. Investigating the Needs of People with Disabilities to Ride Public Transport Routes Involving Transfers. J. Public Transp. 2022, 24, 100010. [Google Scholar] [CrossRef]
- Yu, D.; Xu, H.; Chen, W.; Yao, J. Synchronized optimization of last trains’ timetables in mass rail transit networks based on extra dwell time. J. Phys. Conf. Ser. 2019, 1176, 052034. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Van Oudheusden, D. Decreasing the passenger waiting time for an intercity rail network. Transp. Res. Part B Methodol. 2007, 41, 478–492. [Google Scholar] [CrossRef]
- Potter, J. European Rail Timetable Limited; Woodcock, C., Ed.; Issue May; CPI Group (UK) Ltd.: Croydon, UK, 2018. [Google Scholar]
- Das, K.; Samanta, S.; Pal, M. Study on centrality measures in social networks: A survey. Soc. Netw. Anal. Min. 2018, 8, 13. [Google Scholar] [CrossRef]
- Prabhakar, N.; Anbarasi, L.J. Exploration of the global air transport network using social network analysis. Soc. Netw. Anal. Min. 2021, 11, 12. [Google Scholar] [CrossRef]
- Jiao, J.; Wang, J.; Jin, F. Impacts of high-speed rail lines on the city network in China. J. Transp. Geogr. 2017, 60, 257–266. [Google Scholar] [CrossRef]
- Wei, S.; Teng, S.N.; Li, H.J.; Xu, J.; Ma, H.; Luan, X.L.; Yang, X.; Shen, D.; Liu, M.; Huang, Z.Y.X.; et al. Hierarchical structure in the world’s largest high-speed rail network. PLoS ONE 2019, 14, e0211052. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, C.; Wang, F.; Yao, S. The impact of high-speed railway on urban housing prices in China: A network accessibility perspective. Transp. Res. Part A Policy Pract. 2021, 152, 84–99. [Google Scholar] [CrossRef]
- Chen, J.; Li, W.; Wu, B.; Yu, Z. Does High-Speed Railway Promote the Quality of Urbanization? From a Dynamic Network Perspective. Systems 2023, 11, 523. [Google Scholar] [CrossRef]
- Dangalchev, C. Residual closeness in networks. Phys. A Stat. Mech. Its Appl. 2006, 365, 556–564. [Google Scholar] [CrossRef]
- Wheat, P.; Wardman, M. Effects of timetable related service quality on rail demand. Transp. Res. Part A 2017, 95, 96–108. [Google Scholar] [CrossRef]
- Hoos, A.H.; Stützle, T. Stochastic Local Search Foundations and Applications; Morgan Kaufmann Pub.: San Francisco, CA, USA, 2005. [Google Scholar]
- Pons, P.; Latapy, M. Computing communities in large networks using random walks. J. Graph Algorithms Appl. 2006, 10, 191–218. [Google Scholar] [CrossRef]
- Perennes, P. Use of combinatorial auctions in the railway industry: Can the ‘invisible hand’ draw the railway timetable? Transp. Res. Part A 2014, 67, 175–187. [Google Scholar] [CrossRef]

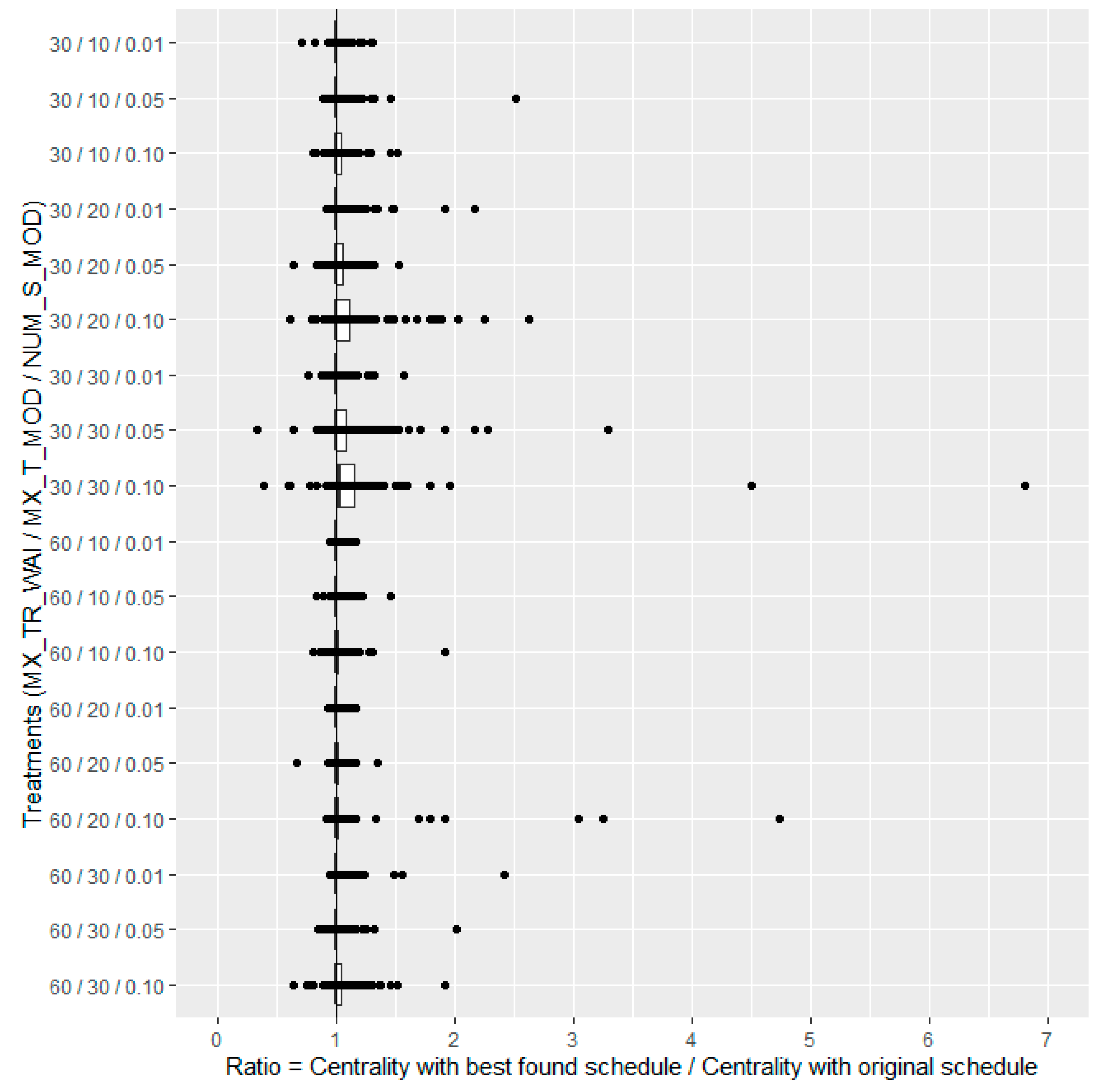

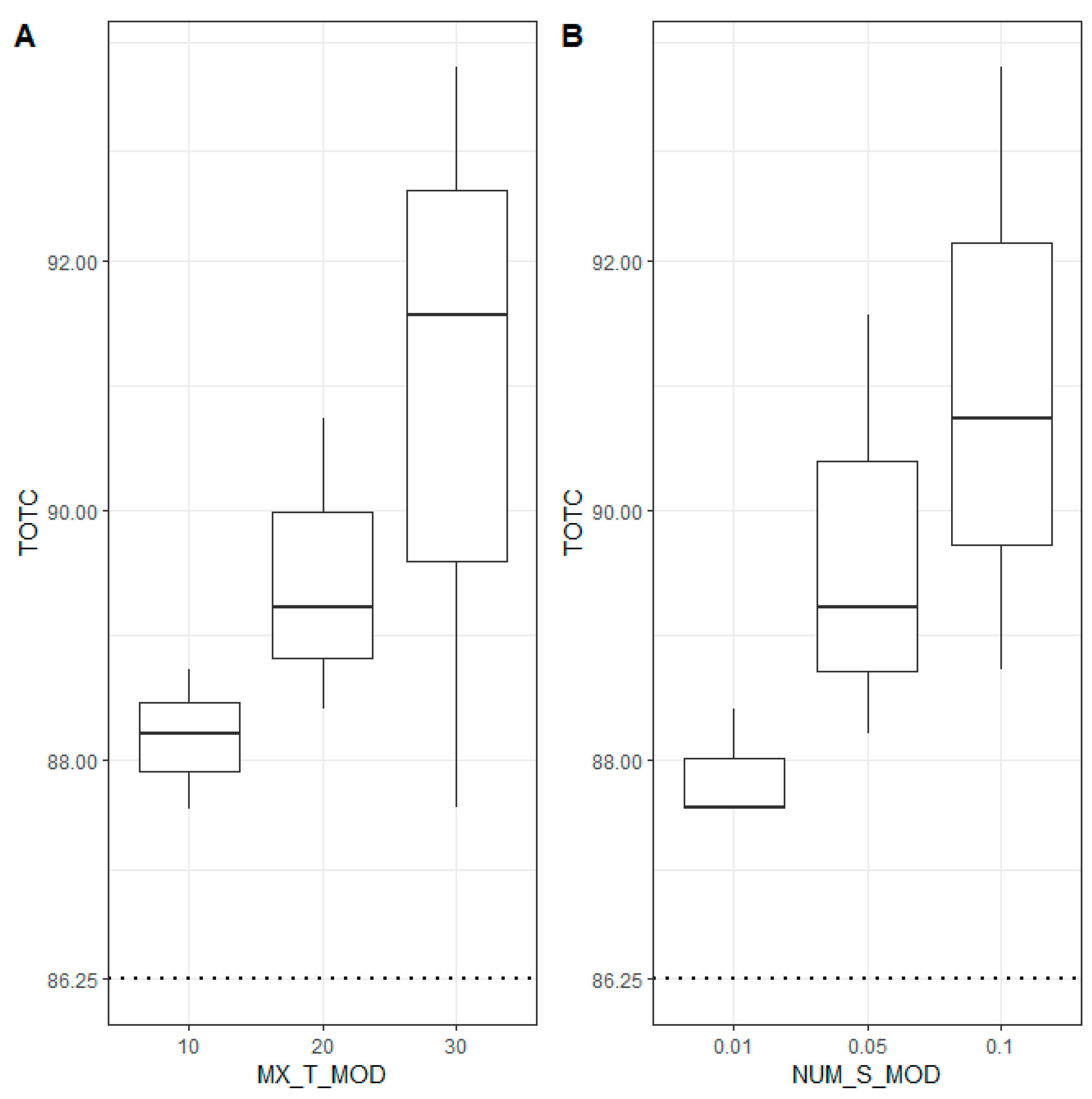
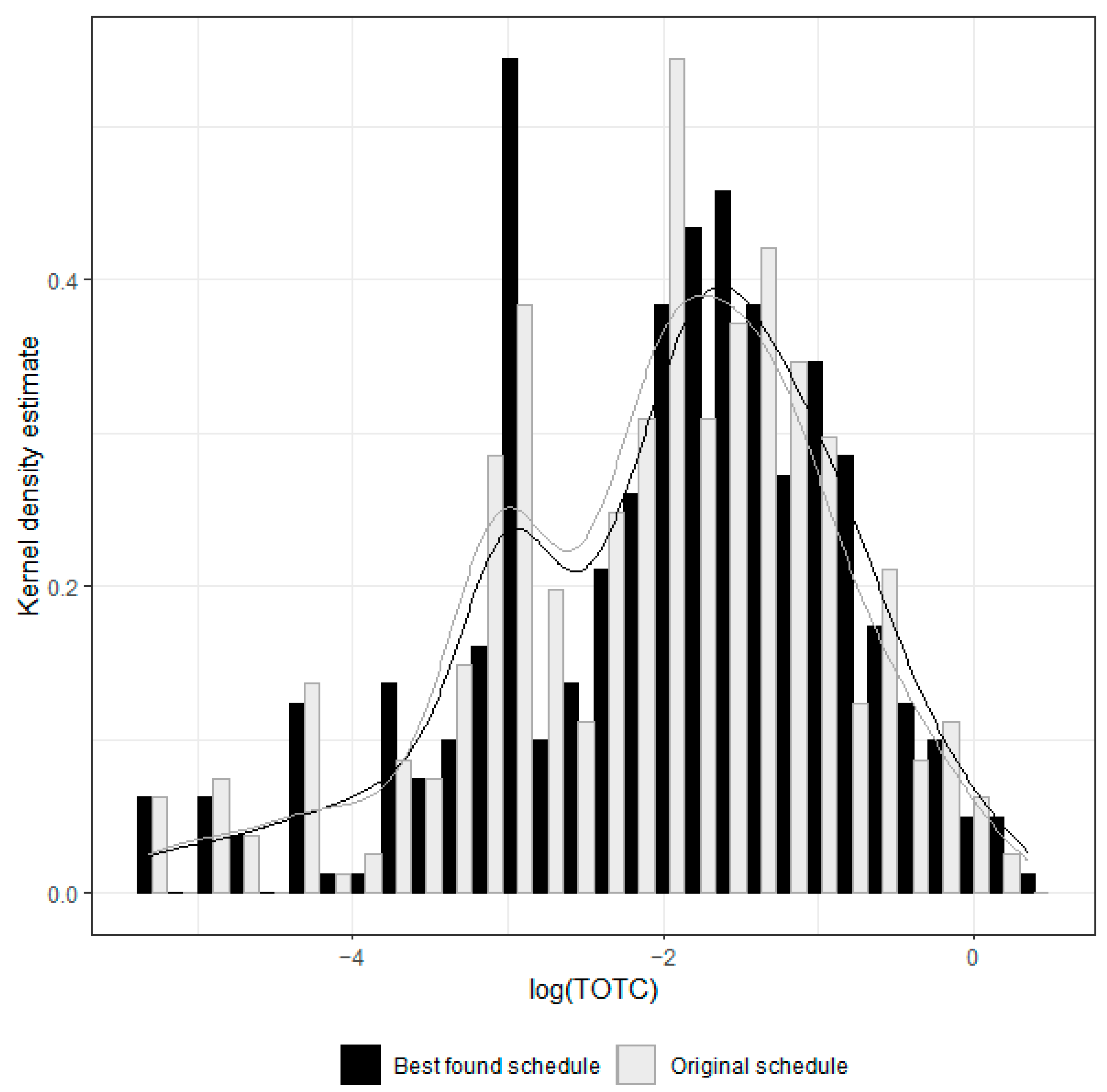
| MX_ TR_ WAI | MX_ T_ MOD | NUM_ S_ MOD | Original Schedule | Best Schedule Found | ||||
|---|---|---|---|---|---|---|---|---|
| TOTC | Pairs of Cities Connected | C (*) | TOTC | Pairs of Cities Connected | C (*) | |||
| 30 | 10 | 0.01 | 86.25 | 27,449 | 26 | 87.60 [1.57%] | 27,853 [1.47%] | 26 |
| 0.05 | “ | “ | 26 | 88.21 [2.27%] | 27,961 [1.87%] | 26 | ||
| 0.10 | “ | “ | 26 | 88.72 [2.86%] | 28,133 [2.49%] | 25 | ||
| 20 | 0.01 | “ | “ | 26 | 88.41 [2.50%] | 28,055 [2.21%] | 26 | |
| 0.05 | “ | “ | 26 | 89.22 [3.44%] | 28,303 [3.11%] | 26 | ||
| 0.10 | “ | “ | 26 | 90.73 [5.19%] | 28,804 [4.94%] | 25 | ||
| 30 | 0.01 | “ | “ | 26 | 87.63 [1.60%] | 27,804 [1.29%] | 26 | |
| 0.05 | “ | “ | 26 | 91.57 [6.17%] | 28,957 [5.49%] | 26 | ||
| 0.10 | “ | “ | 26 | 93.55 [8.46%] | 29,453 [7.30%] | 27 | ||
| 60 | 10 | 0.01 | 117.66 | 35,005 | 25 | 118.80 [0.97%] | 35,290 [0.81%] | 25 |
| 0.05 | “ | “ | 25 | 118.74 [0.92%] | 35,249 [0.70%] | 24 | ||
| 0.10 | “ | “ | 25 | 119.49 [1.56%] | 35,447 [1.26%] | 23 | ||
| 20 | 0.01 | “ | “ | 25 | 118.84 [1.00%] | 35,287 [0.81%] | 25 | |
| 0.05 | “ | “ | 25 | 119.70 [1.73%] | 35,466 [1.32%] | 24 | ||
| 0.10 | “ | “ | 25 | 119.90 [1.90%] | 35,538 [1.52%] | 23 | ||
| 30 | 0.01 | “ | “ | 25 | 119.16 [1.27%] | 35,400 [1.13%] | 24 | |
| 0.05 | “ | “ | 25 | 119.86 [1.87%] | 35,490 [1.39%] | 24 | ||
| 0.10 | “ | “ | 25 | 120.90 [2.75%] | 35,767 [2.18%] | 25 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calzada-Infante, L.; Adenso-Díaz, B.; Carbajal, S.G. Improving Transfer Connectivity in Railway Timetables Based on Closeness Centrality: The Case of the European International Network. Systems 2024, 12, 327. https://doi.org/10.3390/systems12090327
Calzada-Infante L, Adenso-Díaz B, Carbajal SG. Improving Transfer Connectivity in Railway Timetables Based on Closeness Centrality: The Case of the European International Network. Systems. 2024; 12(9):327. https://doi.org/10.3390/systems12090327
Chicago/Turabian StyleCalzada-Infante, Laura, Belarmino Adenso-Díaz, and Santiago García Carbajal. 2024. "Improving Transfer Connectivity in Railway Timetables Based on Closeness Centrality: The Case of the European International Network" Systems 12, no. 9: 327. https://doi.org/10.3390/systems12090327
APA StyleCalzada-Infante, L., Adenso-Díaz, B., & Carbajal, S. G. (2024). Improving Transfer Connectivity in Railway Timetables Based on Closeness Centrality: The Case of the European International Network. Systems, 12(9), 327. https://doi.org/10.3390/systems12090327








