Evolutionary Game Analysis of Government–Enterprise Collaboration in Coping with Natech Risks
Abstract
1. Introduction
- (1)
- Digital-intelligence-driven emergency collaboration aims to improve the multi-agent cooperation ability in responding to emergencies through the integration and application of digital and intelligent technologies. The existing research is conducted through two paradigms of “it is” and “it should be”. For example, based on the general model of safety information cognition, Zhang et al. built a big data-driven emergency information collaboration mechanism with a power mechanism, operation mechanism, and action mechanism as the core [20]. By analyzing typical cases, Zhang et al. made it clear that the construction of a multi-channel emergency rescue information smooth mechanism could promote the diversification of knowledge transfer methods, and the construction of an emergency rescue information integration mechanism based on a digital platform could enhance the knowledge integration ability, thus improving the performance level of emergency management [21].
- (2)
- Organizational network analysis is an important way to reflect the effectiveness of emergency collaboration. Existing studies were carried out through the horizontal comparison of time slices and the longitudinal comparison across cases. For example, Chen et al. found the trend or rule of emergency collaboration by comparing the collaboration network of emergency organizations in Wenchuan, Yushu, Lushan, and Ludian earthquick in China [22]. Yang et al. analyzed the collaboration network of emergency organizations in different stages of COVID-19 prevention and control in Wuhan to identify the characteristics of collaboration at different stages and the evolutionary mechanism of emergency collaboration [23].
- (3)
- The dynamics of government–enterprises interaction have also been explored through the lens of evolutionary game theory, which examines various facets of disaster management collaboration. These aspects include enterprise engagement in disaster management [24], governmental mobilization of enterprise resources post-disaster [25], corporate involvement in emergency rescue operations [26], contributions to post-disaster reconstruction [27], government and enterprises’ collaborative governance [28,29], and the provision of emergency supplies by enterprises [30,31].
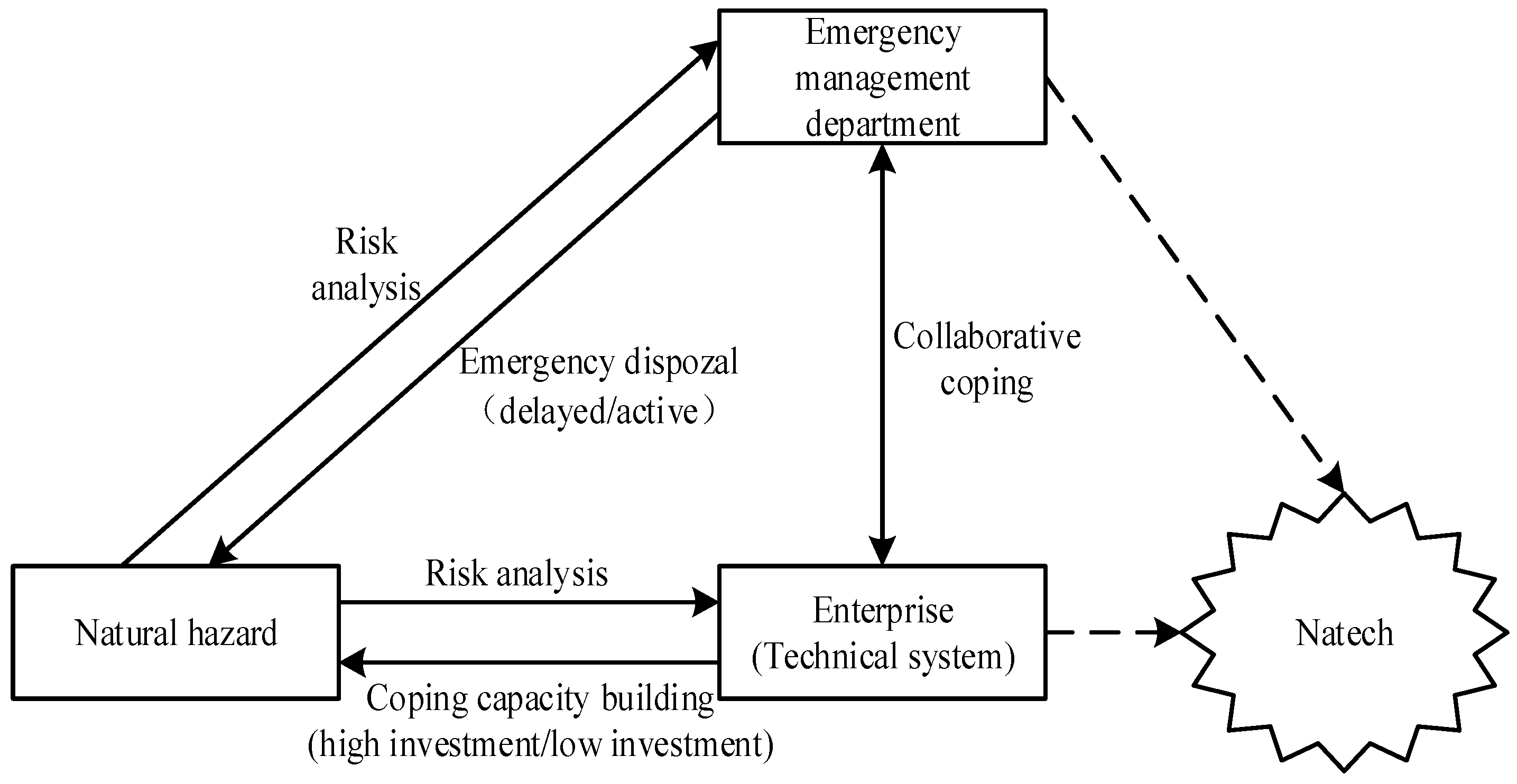
2. Establishment of an Evolutionary Game Model of Government–Enterprise Collaboration in Coping with Natech Risks
2.1. Theoretical Model
2.2. Interest Matrix Construction of Government–Enterprise Collaboration in Coping with Natech Risk
3. The Solution of ESS of Government–Enterprise Collaboration in Coping with Natech Risk
3.1. Revenue Expectation Function Construction
3.2. ESS Analysis
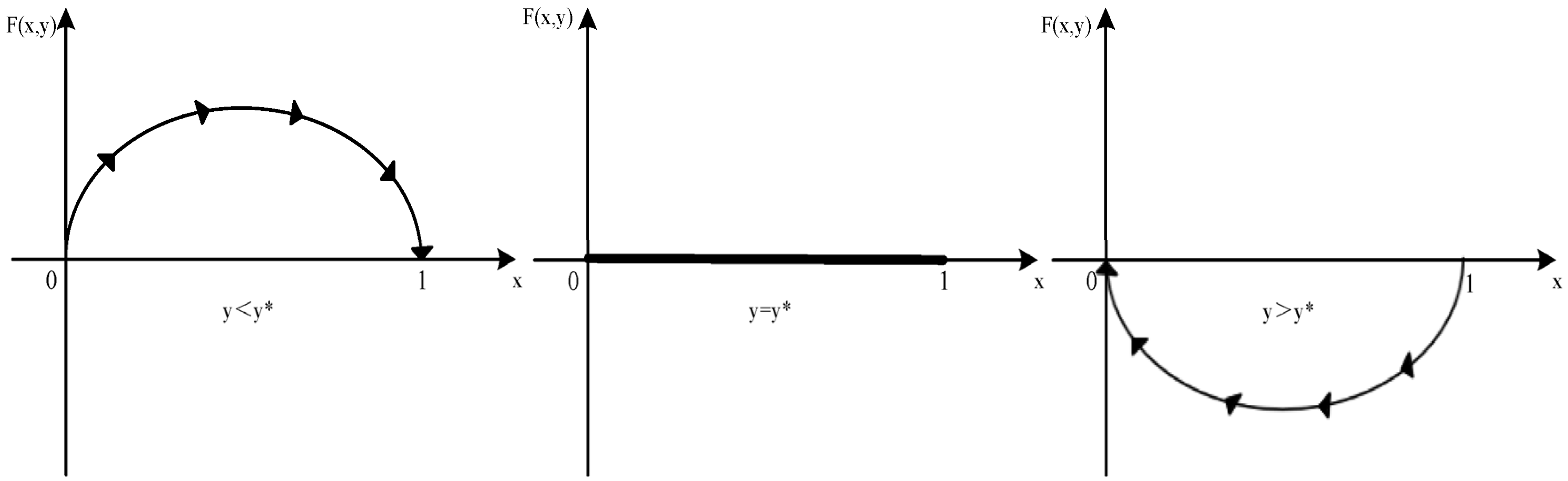
3.2.1. ESS Analysis of Enterprise
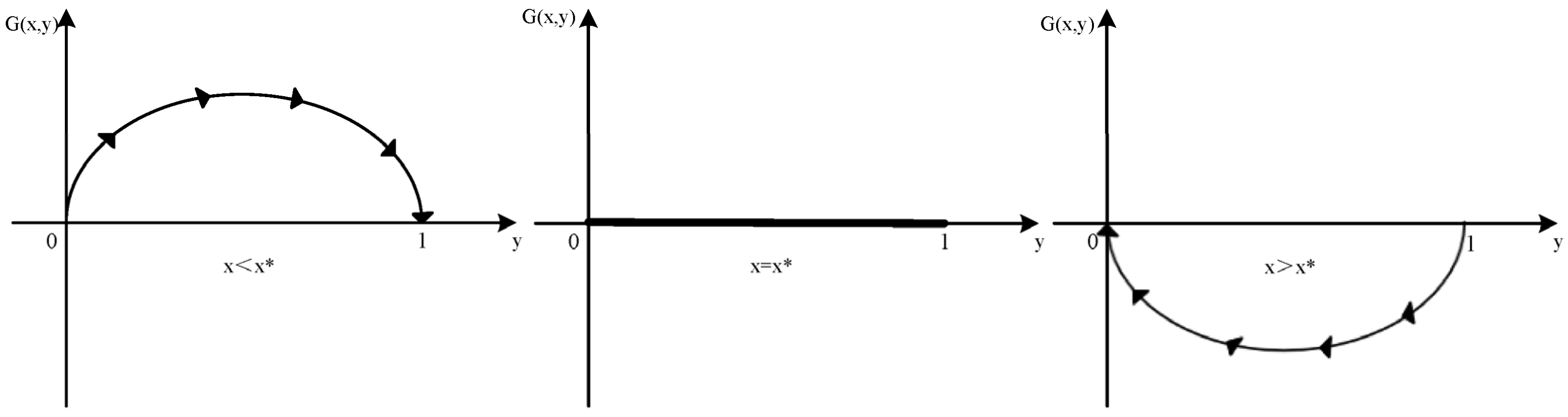
3.2.2. ESS Analysis of Emergency Management Department
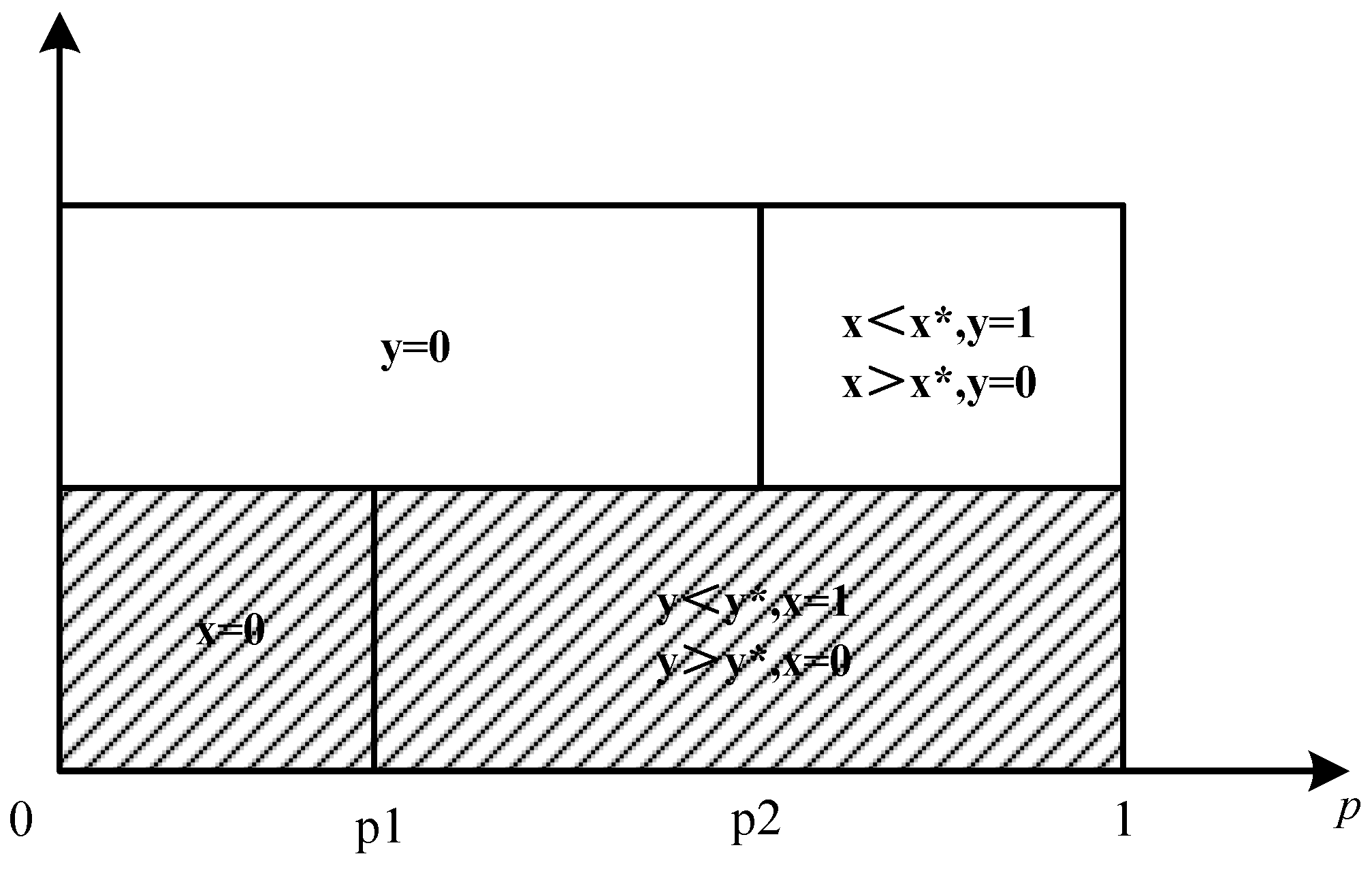
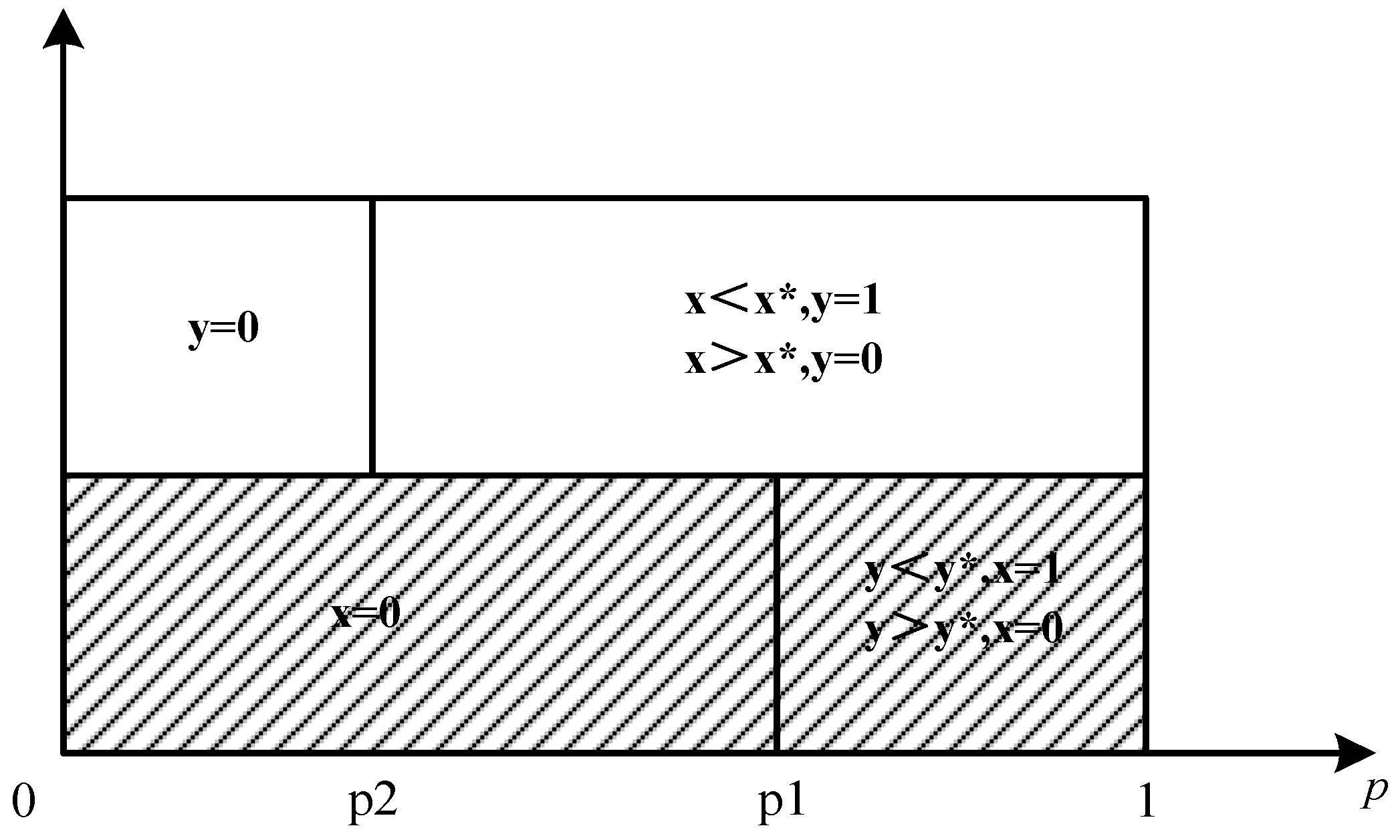
3.2.3. ESS Analysis Based on Natech Risk Level
4. Numerical Simulation
4.1. Parameter Assumptions
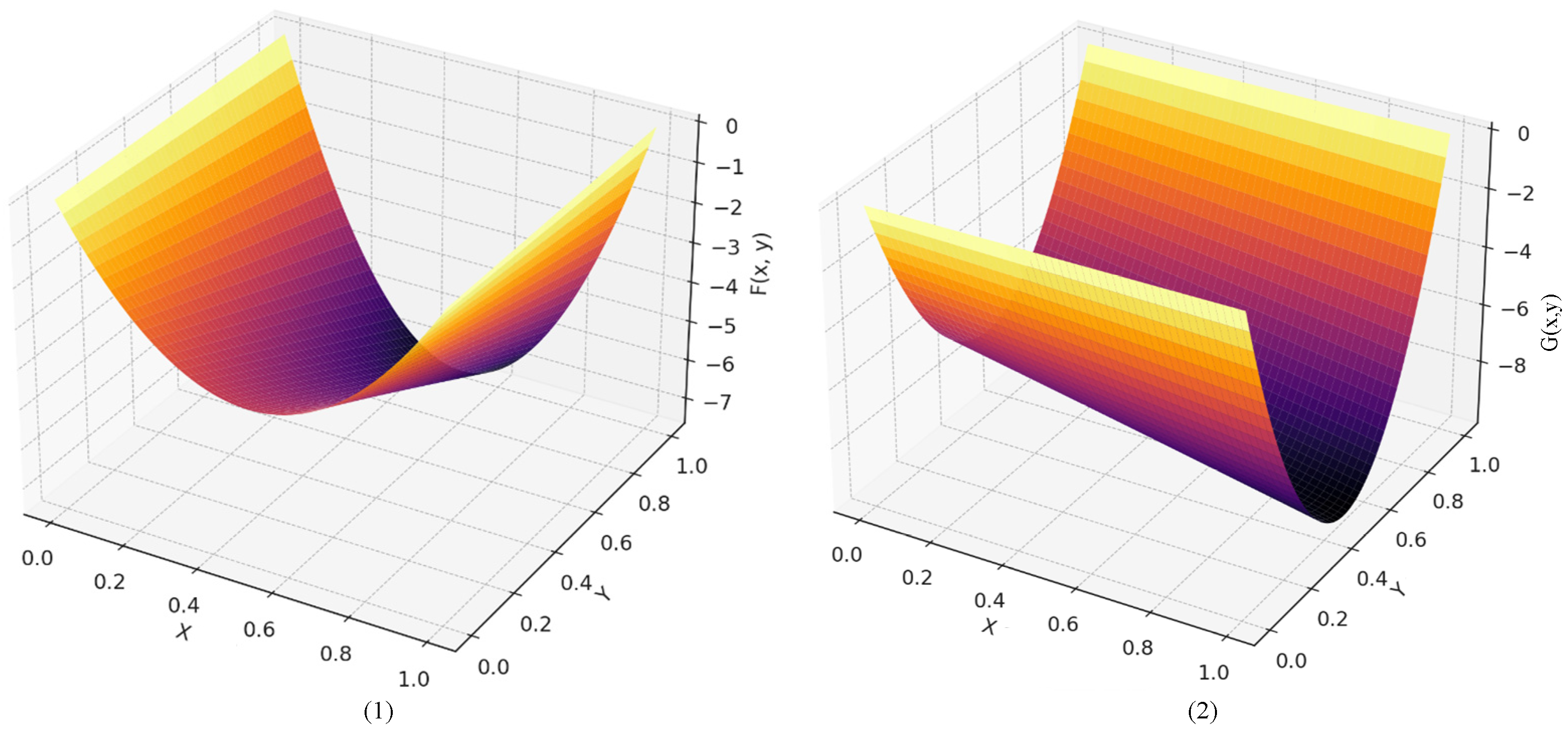
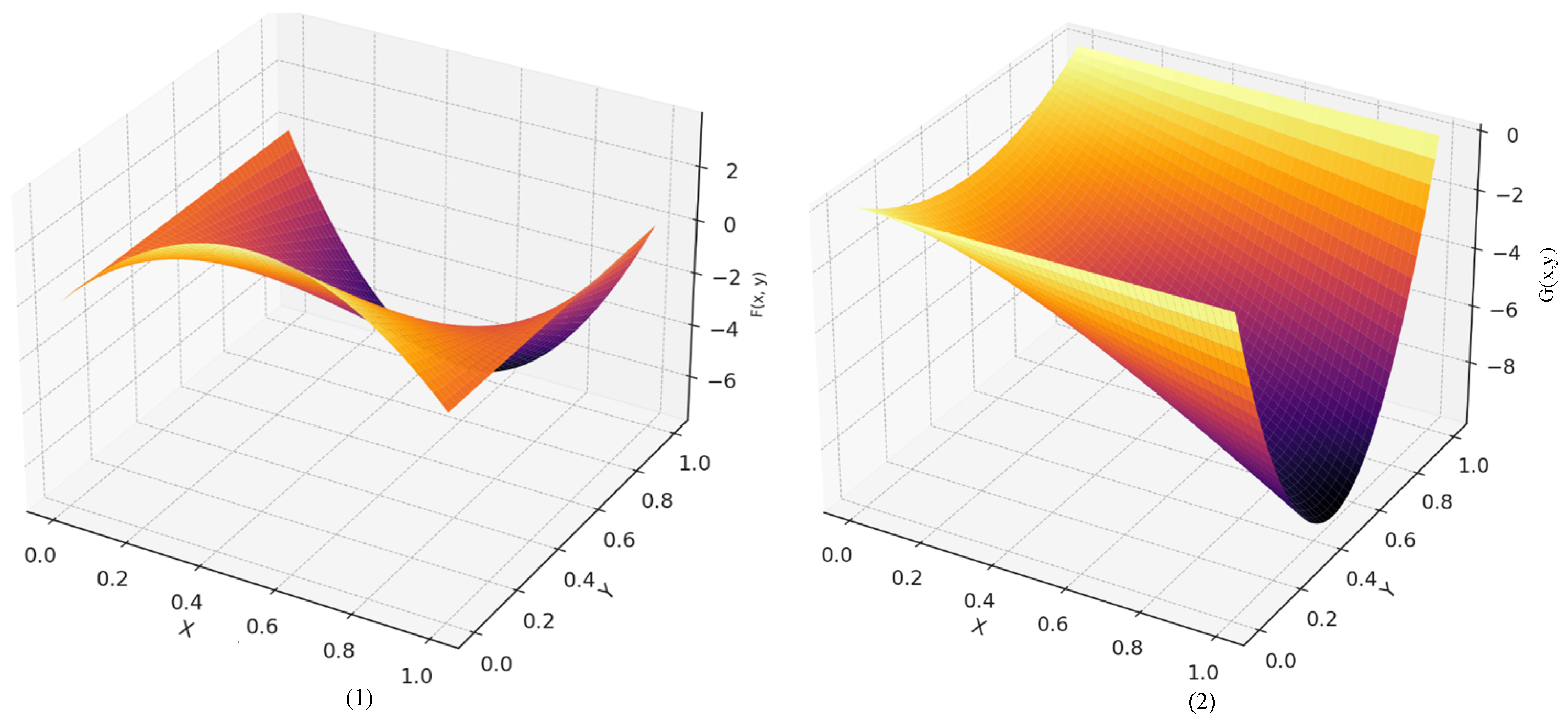
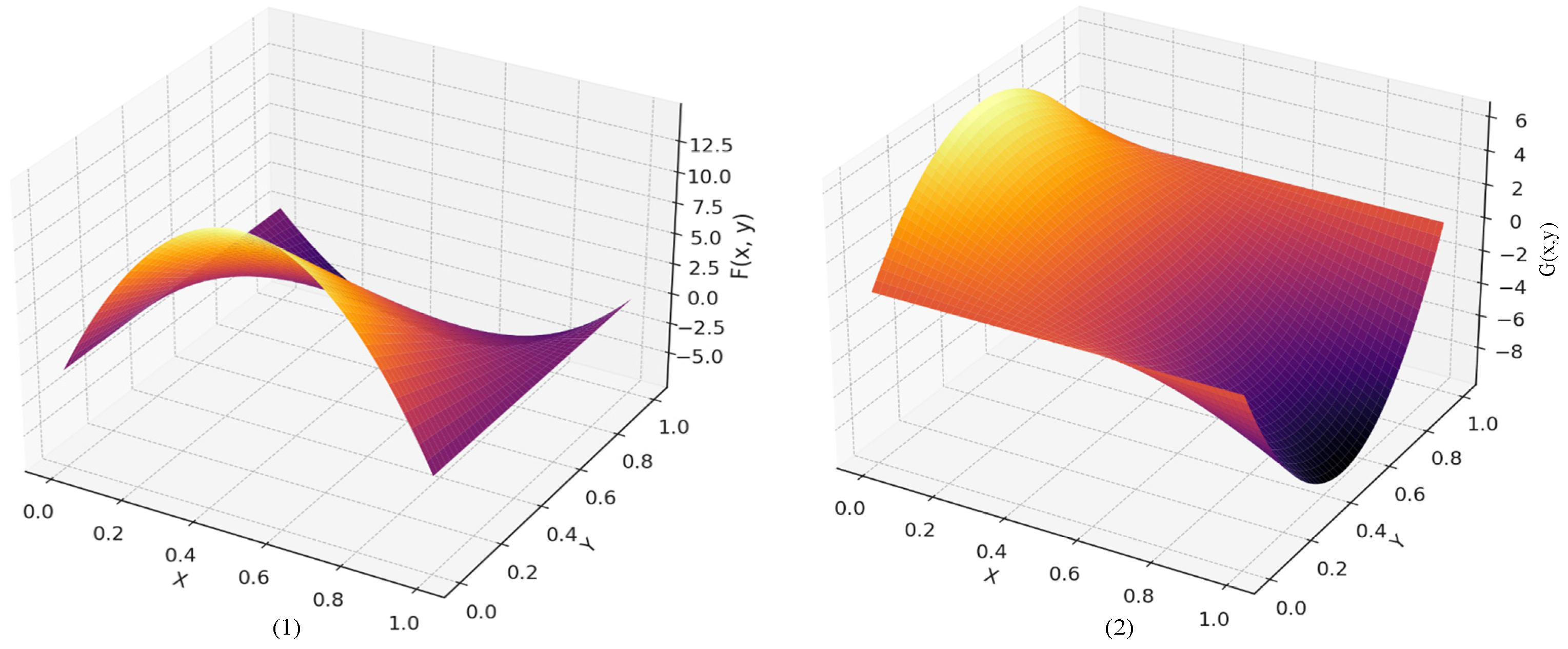
4.2. Analysis of Evolutionary Results
5. Results Discussion
5.1. Impact Analysis of the Evolution Game of Government–Enterprise Collaboration in Coping with Natech Risks
- (1)
- Failure of Natech risk analysis will lead to the failure of government–enterprise collaboration in coping with Natech risks
- (2)
- Insufficient ability of government–enterprise collaboration in coping with Natech risk in extreme disaster situations
5.2. Impact Reduction Strategy for the Evolution Game of Government–Enterprise Collaboration in Coping with Natech Risks
- (1)
- Improve Natech risk analysis ability
- (2)
- Establish an integrated mechanism of Natech risk information sharing and response
- (3)
- Strengthen coping capacity building for Natech
6. Conclusions and Discussion
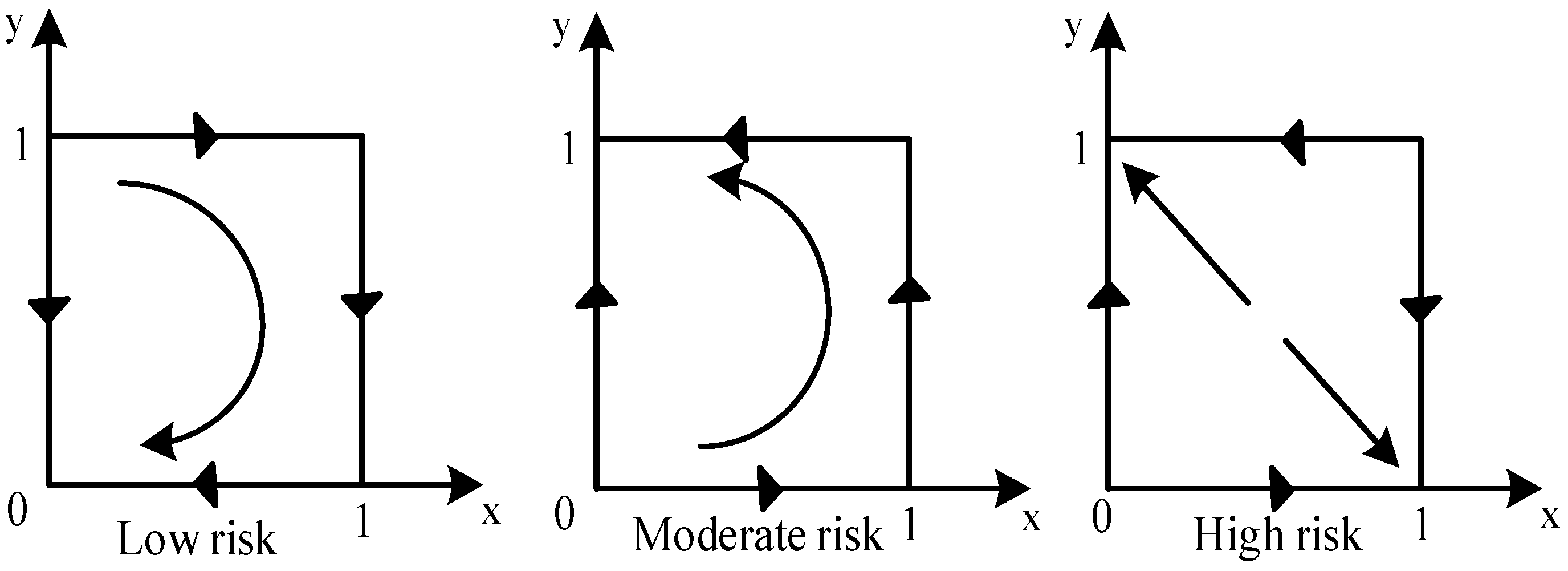
- (1)
- Under Natech’s low risk, enterprises will choose low investment in response capacity building, and emergency management departments will choose delayed disposal.
- (2)
- Under the moderate risk of Natech, when the emergency management department only chooses delayed disposal, the enterprise will choose high response capacity building investment according to the behavioral strategy of the emergency management department. When the enterprise chooses only low response capacity building investment, the emergency management department will choose active disposal according to the behavior strategy of the enterprise.
- (3)
- Under high Natech risk, enterprises and emergency management departments make misplaced choices based on each other’s behavior and eventually form a stable state. When enterprises choose to invest in high coping capacity, emergency management departments will choose delayed disposal; when enterprises choose low coping capacity input, emergency management departments will choose active disposal.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cruz, A.M. Challenges in Natech Risk Reduction. Rev. Ing. 2012, 79–86. [Google Scholar] [CrossRef]
- Krausmann, E.; Necci, A. Thinking the unthinkable: A perspective on Natech risks and Black Swans. Saf. Sci. 2021, 139, 105255. [Google Scholar] [CrossRef]
- Cruz, A.M.; Suarez-Paba, M.C. Advances in Natech research: An overview. Prog. Disaster Sci. 2019, 1, 100013. [Google Scholar] [CrossRef]
- Li, P.; Wang, T.; Qie, Z. Collaborative Relationship Modeling and Analysis of Natech Emergency Response Organizations Based on Stochastic Petri Net. Nat. Hazards Rev. 2024, 25, 04024009. [Google Scholar] [CrossRef]
- Suarez-Paba, M.C.; Cruz, A.M.; Munoz, F. Emerging Natech risk management in Colombia: A survey of governmental organizations. Saf. Sci. 2020, 128, 104777. [Google Scholar] [CrossRef]
- Kumasaki, M.; King, M. Three cases in Japan occurred by natural hazards and lessons for Natech disaster management. Int. J. Disaster Risk Reduct. 2020, 51, 101855. [Google Scholar] [CrossRef] [PubMed]
- Girgin, S.; Necci, A.; Krausmann, E. Dealing with cascading multi-hazard risks in national risk assessment: The case of Natech accidents. Int. J. Disaster Risk Reduct. 2019, 35, 101072. [Google Scholar] [CrossRef]
- Krausmann, E.; Baranzini, D. Natech risk reduction in the European Union. J. Risk Res. 2012, 15, 1027–1047. [Google Scholar] [CrossRef]
- Pilone, E.; Moreno, V.C.; Cozzani, V.; Demichela, M. Climate change and NaTech events: A step towards local-scale awareness and preparedness. Saf. Sci. 2021, 139, 105264. [Google Scholar] [CrossRef]
- Krausmann, E.; Girgin, S.; Necci, A. Natural hazard impacts on industry and critical infrastructure: Natech risk drivers and risk management performance indicators. Int. J. Disaster Risk Reduct. 2019, 40, 101163. [Google Scholar] [CrossRef]
- Zhang, G.; Feng, W.; Lei, Y.; Wang, S. Generation and evolution mechanism of systemic risk (SR) induced by extreme precipitation in Chinese Urban system: A case study of Zhengzhou “7 20” incident. Int. J. Disaster Risk Reduct. 2022, 83, 103401. [Google Scholar] [CrossRef]
- Santella, N.; Steinberg, L.J.; Aguirra, G.A. Empirical Estimation of the Conditional Probability of Natech Events Within the United States. Risk Anal. 2011, 31, 951–968. [Google Scholar] [CrossRef] [PubMed]
- Khakzad, N.; Cozzani, V. Special issue: Quantitative assessment and risk management of Natech accidents. Reliab. Eng. Syst. Saf. 2020, 203, 107198. [Google Scholar] [CrossRef]
- Damle, S.; Mani, S.K.; Balamurugan, G. Natech guide words: A new approach to assess and manage natech risk to ensure business continuity. J. Loss Prev. Process Ind. 2021, 72, 104564. [Google Scholar] [CrossRef]
- Cai, M.; Marson, S.M. A regional Natech risk assessment based on a Natech-prone facility network for dependent events. Nat. Hazards 2021, 107, 2155–2174. [Google Scholar] [CrossRef]
- O’Reilly, G.J.; Shahnazaryan, D.; Dubini, P.; Brunesi, E.; Rosti, A.; Dacarro, F.; Gotti, A.; Silvestri, D.; Mascetti, S.; Ducci, M.; et al. Risk-aware navigation in industrial plants at risk of NaTech accidents. Int. J. Disaster Risk Reduct. 2023, 88, 103620. [Google Scholar] [CrossRef]
- Luo, X.; Tzioutzios, D.; Tong, Z.; Cruz, A.M. Find-Natech: A GIS-based spatial management system for Natech events. Int. J. Disaster Risk Reduct. 2022, 76, 103028. [Google Scholar] [CrossRef]
- Mesa-Gomez, A.; Casal, J.; Munoz, F. Risk analysis in Natech events: State of the art. J. Loss Prev. Process Ind. 2020, 64, 104071. [Google Scholar] [CrossRef]
- Luo, X.; Cruz, A.M.; Tzioutzios, D. Extracting Natech Reports from Large Databases: Development of a Semi-Intelligent Natech Identification Framework. Int. J. Disaster Risk Sci. 2020, 11, 735–750. [Google Scholar] [CrossRef]
- Guirong, Z.; Yu, L.; Wei, F. Research on coordination mechanism of emergency information driven by big data. J. Intell. 2022, 41, 181–185+201. [Google Scholar]
- Zhang, L.; Wang, J.; Wang, X.; Gao, Y. Research on cross-city emergency management collaboration mechanism in major emergencies: Insights from a knowledge management perspective. J. Knowl. Manag. 2024. ahead-of-print. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, H.; Comfort, L.K.; Tao, Z. Exploring complex adaptive networks in the aftermath of the 2008 Wenchuan earthquake in China. Saf. Sci. 2020, 125, 104607. [Google Scholar] [CrossRef]
- Yang, L.; Lou, J.; Zhou, J.; Zhao, X.; Jiang, Z. Complex network-based research on organization collaboration and cooperation governance responding to COVID-19. Eng. Constr. Archit. Manag. 2023, 30, 3749–3779. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, N.; Liu, D. Complex disaster management: A dynamic game among the government, enterprises, and residents. J. Clean. Prod. 2020, 266, 122091. [Google Scholar] [CrossRef]
- Du, L.; Qian, L. The government’s mobilization strategy following a disaster in the Chinese context: An evolutionary game theory analysis. Nat. Hazards 2016, 80, 1411–1424. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, C.; Li, H. Evolutionary game analysis of emergency rescuer dispatching under bounded rationality. Int. J. Disaster Risk Reduct. 2023, 96, 103927. [Google Scholar] [CrossRef]
- Peng, Y.; Gu, X.; Wang, Z.; Li, Q.; Jiang, S. Behavior of Rural Victims and Local Government during Post-Disaster Reconstruction: Agent-Based Simulation. Nat. Hazards Rev. 2021, 22, 04021051. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Tadikamalla, P.R.; Qu, M.; Wang, Y. Evolutionary game analysis for multi-level collaborative governance under public crisis in China: From a value perception perspective. Risk Anal. 2024, 44, 582–611. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, H.; Gu, X. A Two-Stage Evolutionary Game Model for Collaborative Emergency Management Between Local Governments and Enterprises. Int. J. Disaster Risk Sci. 2023, 14, 1029–1043. [Google Scholar] [CrossRef]
- Li, C.; Zhang, F.; Cao, C.; Liu, Y.; Qu, T. Organizational coordination in sustainable humanitarian supply chain: An evolutionary game approach. J. Clean. Prod. 2019, 219, 291–303. [Google Scholar] [CrossRef]
- Wu, X.; Yang, M.; Wu, C.; Liang, L. How to avoid source disruption of emergency supplies in emergency supply chains: A subsidy perspective. Int. J. Disaster Risk Reduct. 2024, 102, 104303. [Google Scholar] [CrossRef]
- Ma, X. Research on disaster collaborative management from the perspective of government, market, and society cooperation. Econ. Probl. 2020, 1, 18–22. [Google Scholar] [CrossRef]
- Amaducci, F.; Misuri, A.; Bonvicini, S.; Salzano, E.; Cozzani, V. Quantitative risk assessment of Natech scenarios triggered by earthquakes involving pipelines. Reliab. Eng. Syst. Saf. 2024, 245, 109993. [Google Scholar] [CrossRef]
- Antonioni, G.; Landucci, G.; Necci, A.; Gheorghiu, D.; Cozzani, V. Quantitative assessment of risk due to NaTech scenarios caused by floods. Reliab. Eng. Syst. Saf. 2015, 142, 334–345. [Google Scholar] [CrossRef]
- Cozzani, V.; Antonioni, G.; Landucci, G.; Tugnoli, A.; Bonvicini, S.; Spadoni, G. Quantitative assessment of domino and NaTech scenarios in complex industrial areas. J. Loss Prev. Process Ind. 2014, 28, 10–22. [Google Scholar] [CrossRef]
- Kabir, G.; Suda, H.; Cruz, A.M.; Munoz Giraldo, F.; Tesfamariam, S. Earthquake-related Natech risk assessment using a Bayesian belief network model. Struct. Infrastruct. Eng. 2019, 15, 725–739. [Google Scholar] [CrossRef]
- Congress SCotNPs. Law of the People’s Republic of China on Production Safety; Congress SCotNPs, Ed.; Beijing, China, 2021. [Google Scholar]
- Zhang, H.; Tong, X. Public crisis governance and accountability. Political Stud. 2010, 02, 50–55. [Google Scholar]
- Liu, J.-G.; Wang, J.-J.; Zhou, H.; Zhang, Y. Research on supervision problems of port hazardous chemicals base on security risk level. Syst. Eng. Theory Pract. 2018, 38, 1141–1152. [Google Scholar]

| Enterprise | Emergency Management Department | |
|---|---|---|
| Active Disposal (y) | Delayed Disposal (1 − y) | |
| High investment in emergency capacity building (x) | c − a, d − b | c − a, d |
| Low investment in emergency capacity building (1 − x) | c − e, d − b | (1 − p) × (c − e) − p × f, (1 − p) × d − p × g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Feng, W.; Zhang, G.; Wen, Y. Evolutionary Game Analysis of Government–Enterprise Collaboration in Coping with Natech Risks. Systems 2024, 12, 275. https://doi.org/10.3390/systems12080275
Guo S, Feng W, Zhang G, Wen Y. Evolutionary Game Analysis of Government–Enterprise Collaboration in Coping with Natech Risks. Systems. 2024; 12(8):275. https://doi.org/10.3390/systems12080275
Chicago/Turabian StyleGuo, Shaojun, Wei Feng, Guirong Zhang, and Ying Wen. 2024. "Evolutionary Game Analysis of Government–Enterprise Collaboration in Coping with Natech Risks" Systems 12, no. 8: 275. https://doi.org/10.3390/systems12080275
APA StyleGuo, S., Feng, W., Zhang, G., & Wen, Y. (2024). Evolutionary Game Analysis of Government–Enterprise Collaboration in Coping with Natech Risks. Systems, 12(8), 275. https://doi.org/10.3390/systems12080275





