Abstract
In this study, a tripartite decision-making parking pricing model was developed based on Game Theory to comprehensively reflect the impact of parking pricing on private car travelers, parking lot operators, and traffic managers. Utility theory is introduced to analyze the behavioral characteristics of the tripartite participants in parking pricing. A parking behavior model for private car travelers, an operating profit model for parking lot operators, and a social negative utility model for traffic managers are established. This article presents an analysis of the mutual influence between them based on a game theory perspective and introduces parking saturation and road saturation as new factors influencing parking pricing to address the interactive relationship among the tripartite participants. A parking pricing model based on tripartite games is established, and a solution algorithm is designed. The results indicate that when the parking fee rates for the two public parking lots in the scenario are 8.5 CNY/h and 9 CNY/h, respectively, the parking demand is 300, and the sum of the total travel costs of private car travelers and the total operating profits are CNY 20,589 and 2187.9, respectively. The parking saturation of the public parking lot and the difference between the expected value is minimized to 0.25, and the road saturation and the difference between the expected value are minimized to 1.48, which is the parking pricing plan that minimizes the conflicts of interest among the tripartite stakeholders in the tripartite game. The parking pricing model of a public parking lot provides a reference for formulating parking fee strategies that comprehensively reflect the needs of the three parties involved in the public parking lot.
1. Introduction
In response to the increasingly prominent urban parking issues, parking fees represent an effective traffic management method for enhancing the utilization of parking resources and alleviating parking problems. Reasonable pricing for parking fees facilitates appropriate parking behavior choices by private vehicle users, increases profits for parking facility operators, and promotes the rational distribution of parking demand in terms of time and space. The “Opinions on Promoting the Development of Urban Parking Facilities” issued in 2021 by the National Development and Reform Commission and other four ministries proposed to “improve parking fee policies, enhance the parking fee mechanism mainly determined by the market, and gradually narrow the range of government pricing”. Currently, in some cities in China, there exists loose management and blanket pricing by operators for parking fee pricing. This situation makes it difficult to reach a consensus among private vehicle users, parking lot operators, and traffic managers. How to coordinate the interests of the three parties, formulate reasonable parking pricing, and meet the objectives of saving travel costs for private vehicle users, maximizing profits for parking lot operators, and minimizing negative social impacts for traffic managers has become an important research question.
Research on the impact of parking fee pricing on private vehicle users, parking lot operators, and traffic managers has mainly focused on changing parking behaviors, enhancing parking facility operational profits, and increasing public transit modal share. He Kangkang et al. [1] constructed a nested Logit model based on data including dynamic pricing parking reservation intentions and driver personal attributes, revealing significant influences of parking reservation fees on driver travel behavior choices. Li Hao et al. [2] investigated the combined management strategies of flexible working hours and dynamic parking fees, establishing a bi-level planning model based on travel distribution and dynamic parking fee rates, with results indicating that combined strategies are more effective in alleviating traffic congestion. Hensher et al. [3] surveyed some parking facilities in the Sydney CBD area, suggesting that raising parking fees would increase the proportion of public transit usage and significantly affect private vehicle users’ parking location choices. Xu Hongli et al. [4] constructed a parking fee model based on traffic flow distribution considering ridesharing incentives, proposing that reasonable parking fees and ridesharing incentives can significantly increase travelers’ willingness to participate in ridesharing and increase the number of successful ridesharing matches. Hu Xiaowei et al. [5] analyzed the interests of various stakeholders in urban parking PPP projects, constructing target planning models under different expected pricing for PPP project companies, government entities, and parking users. Proulx et al. [6], through a survey of commuting behaviors at the University of California, argued that both public transit fares and parking fee rates influence travel behavior choices, with parking fee rates having the greatest impact. Wang Jianjun et al. [7] proposed that parking pricing methods should not only consider the interests of parkers and operators but also address the needs of the general public, based on studies of public transit modal share, to analyze optimal pricing mechanisms. Research indicates that parking fee rates have significant effects on travelers’ mode choice, travel behavior selection, and overall transportation demand.
In recent years, the application of game theory in transportation research has become increasingly widespread [8,9,10,11,12,13,14,15]. Research on game models mainly includes studies on solution algorithms for game models, application research on public transportation systems, application research on congestion pricing, and application research on parking fees, among others. In the research on formulating parking fee strategies using game theory, the objectives of travelers or parking operators are usually selected. By reasonably setting the relative weights of each objective and constructing the management objectives of traffic managers, the balance of parking supply and demand is adjusted. Tsai et al. [8] constructed a parking fee pricing game model and studied the pricing problem of parking lots jointly operated by government management departments and parking operators when the government management department owns parking spaces. Qian et al. [9,10] analyzed the characteristics of private parking lots from an economic perspective, established four equilibria based on peak-hour travel parking fee management under perfect market conditions, and discussed how parking fee policies through market competition can minimize social costs to the greatest extent. Zhu Chengjuan et al. [11] considered the characteristics of private operators pursuing maximum operational profits and governments pursuing minimum total social costs and constructed a game model to study parking space allocation strategies and parking fee pricing problems. The dynamic Stackelberg leader-follower game was developed to set parking prices in real-time for effective parking access and space utilization [12]. This model allowed a parking agency to set system optimal pricing policies while considering user competition and market equilibrium. Both the theories of the Stackelberg game and the Nash equilibrium were used to build a two-level parking pricing model, which can determine the optimal parking rate and thus balance the temporal and spatial distribution of the parking demand in urban areas [13]. Wang Yuqiong et al. [14] established a three-stage parking fee game model based on the FSC utility function to solve the bargaining range between fee collectors and parkers during the parking fee process. Karri and Dhabu [15] proposed a pricing strategy using a multistage game model where the two players—drivers and parking lot owners—try to maximize their benefits, and the model finds a Nash equilibrium between these two players regarding the prices of the parking slots. Previous studies have shown that the participants involved in parking fee pricing can adjust parking fee rates by establishing game models to achieve their own interests.
In summary, some scholars, both domestically and internationally, have examined the effects of parking fee rates on travelers’ travel choices, parking lot operational profits, the proportion of public transportation usage, and other aspects. They have analyzed the impact of parking fee pricing on private car travelers. Investigating the relationships and respective interest demands among private car travelers, parking lot operators, and traffic managers in parking fee pricing can provide a reference basis for formulating parking fee strategies for public parking lots. Previous studies of parking pricing always took parking agencies and individual drivers as the participants of the game, while traffic managers, such as the government management department, were also important participants in deciding parking pricing. At the same time, shared parking is developing rapidly in China, so it is significant to study this new intelligent parking mode. For the bi-level game theory models built in previous studies, the iterative solutions of the Nash equilibrium can be acquired, while the trilateral game in our paper makes it difficult to deduce the Nash equilibrium solutions. Therefore, a new method to calculate the optimal solution for a trilateral game needs to be researched.
This paper takes into account the interests of private car travelers, parking lot operators, and traffic managers, respectively, and analyzes the interactive relationships among the three parking participants from the perspective of game theory. Also, the coefficient of variation method for obtaining the optimal solutions is proposed to determine the deviation. It constructs a parking fee pricing model for public parking lots and explores the globally optimal parking fee pricing strategy under the condition of the three parties jointly participating in parking fee pricing.
2. Materials and Methods
2.1. Parking Pricing Tripartite Participant Gaming Relationships
The pricing of public parking lots involves decision-making by three stakeholders: private car travelers, parking lot operators, and traffic managers. In parking price decisions, these three participants typically opt for decisions that minimize their own costs or maximize their benefits, aiming to find solutions that optimize their respective interests. Addressing the minimal conflicts of interest among the stakeholders is the key issue that needs to be resolved in parking fee pricing.
Utility theory is a typical decision theory in economics, representing the subjective evaluation of decision outcomes by decision-makers, quantifying their satisfaction with the consequences of their decisions through mathematical functions [16]. In the parking system, traffic managers formulate parking fee schemes, parking lot operators provide parking services, and private car travelers choose routes and parking lots. Based on the decision-making behavior of the three parties, this paper simulates the psychological activities of parking fee pricing participants, assigns a utility value to each decision-making behavior, assumes that participants choose the decision-making behavior with the maximum utility value, i.e., the highest satisfaction, providing a basis for constructing parking fee pricing models using game theory.
Game theory is a theoretical framework and methodology for studying the interactive decision-making of two or more decision-making entities, as well as the issues of decision equilibrium [17]. The constituent elements of game theory include the set of participants, the set of strategies, and the set of payoff functions. In the context of studying parking pricing issues, the set of participants consists of the three parties involved in public parking fee pricing, namely private car travelers (drivers), parking lot operators (enterprises), and traffic managers (administrative authorities). Based on utility theory, the set of strategies represents the optimal strategies chosen by the three parties participating in parking fee pricing, while the set of payoff functions quantifies the benefits of each party’s strategies.
The three parties involved in the parking service chain exhibit both adversarial and cooperative relationships. The interactions among them necessitate considerations of overall benefits, aiming to maximize relative interests while minimizing the overall losses in the entire parking service chain due to conflicts among the participants. The game problem at hand pertains to the optimization of parking fee rates under the game played by the three parties, as illustrated in Figure 1, depicting the game relationships among the three participants.
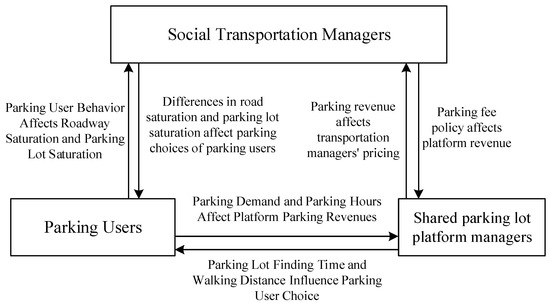
Figure 1.
Game relationship between three participants.
From the perspective of parking fee pricing participants, private car travelers constitute the lower tier of the tripartite game. Metrics such as parking rates and search time reflect the economic and time costs incurred by private car travelers. Private car travelers make parking decisions with the goal of maximizing their travel utility and providing feedback on decision information to parking lot operators and traffic managers.
Parking lot operators occupy the intermediate tier in the tripartite game, engaging with private car travelers in an ordered yet non-cooperative manner and influencing each other within the tripartite game hierarchy. They adhere to parking fee policies issued by traffic managers while providing feedback to them for policy improvement.
Traffic managers represent the upper tier in the tripartite game, utilizing indicators such as road saturation and parking saturation to assess the rational utilization of traffic resources. They formulate parking fee schemes to guide or constrain the decision-making behaviors of private car travelers and parking lot operators based on social factors.
The tripartite game process entails private car travelers, parking lot operators, and traffic managers influencing each other’s actions directly or indirectly through parking fee prices, with the aim of achieving the most favorable outcome for themselves. This paper reconstructs this dynamic process based on utility theory and applies game theory to elucidate the interactions among the involved parties.
2.2. Decision-Making Behavior of Parking Lot Participants
Under the premise that each tripartite participant solely considers their own interest indicators, all parties involved will engage in decision-making behaviors aimed at maximizing their respective benefits. Utilizing utility theory, models are constructed to depict the maximization of individual interests by each tripartite participant, providing a theoretical foundation for the game of pricing parking fees among the tripartite participants.
2.2.1. A Model of Travelers’ Parking Behavioral Choices
The act of parking entails a series of decision-making behaviors by private car travelers in the process of seeking and selecting parking spaces for their vehicles. After driving from the starting point to the vicinity of the destination, private car travelers have multiple parking lots to choose from, resulting in multiple paths to different parking lots from the starting point. For private car travelers, three processes are involved: driving on the road, approaching the destination to choose a parking lot for parking, and walking from the parking lot to the destination after parking.
The decision-making process of parking users can be divided into four components and three stages. The four components consist of the origin, road network, shared parking facilities, and destination. The three stages involve the parking user departing from the origin and entering the road network, selecting a specific shared parking facility within the road network, and finally walking to the destination to complete the entire process. The process of selecting a shared parking facility within the road network entails a series of decision-making behaviors, as illustrated in Figure 2. Parking users depart from a certain origin point , select a driving route with relatively low time costs, park at a specific shared parking facility within the shared parking domain and ultimately walk to the destination . The relevant parameters utilized in the following model are presented in Table 1.
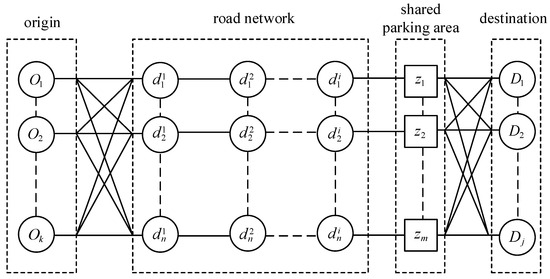
Figure 2.
Parking decision-making process.

Table 1.
Definitions of parameters and variables.
From Figure 1, it can be observed that parking users choose different routes based on their destination and traffic delays, resulting in varying parking costs Cm. Therefore, the objective of the parking user’s parking decision model is to minimize the total parking cost. The objective function is formulated as follows:
The parking cost Cm comprises two stages: the journey from the origin to the shared parking facility (OZ) and from the shared parking facility to the destination (ZD). In the OZ stage, the driving time and the search time within the shared parking facility are considered travel costs, while the walking time in the ZD stage is regarded as pedestrian costs. Therefore, the expression for Cm is as follows:
2.2.2. Shared Parking Operating Platform Revenue Model
Determining parking pricing is a process that comprehensively considers factors such as supply and demand dynamics, geographical location, types and quality of parking facilities, market competition, as well as policies and regulations. The aim of reasonable parking pricing is to balance the interests of parking facility operators and vehicle owners while adhering to market competition rules, policies, and regulations to ensure fair, equitable, and sustainable parking services. As an intermediary player in the game, the profit of shared parking operation platforms is the sole criterion for meeting their requirements. The platform’s operational profit is determined by subtracting operating costs from parking fee revenue. Therefore, it is necessary to establish a reasonable shared parking fee rate to maximize profit. Based on this, the objective function for maximizing the total operational profit of the platform is as follows:
2.2.3. Shared Parking Operating Platform Revenue Model
The benefits of traffic management are reflected in various aspects, such as improving road utilization efficiency, reducing traffic congestion, enhancing traffic safety, reducing environmental pollution, and promoting socio-economic development. Through scientific traffic management, traffic flow can be optimized, and road resources can be allocated reasonably, thereby reducing ineffective driving and traffic congestion and improving road capacity and utilization efficiency. Additionally, traffic management can enhance traffic safety, reduce the incidence of traffic accidents, and mitigate environmental pollution, providing strong support for urban sustainable development and residents’ travel. In the context of shared parking systems, the benefits of traffic management are reflected in whether the road saturation and shared parking facility saturation within the shared parking domain are within the optimal saturation range. The objective function for this is as follows:
Equation (4) describes the road saturation, where represents the number of parking users in a shared parking lot z, represents the number of shared parking spaces in a shared parking lot z, and represents the upper and lower limits for optimal parking saturation in shared parking lots, respectively. Equation (5) describes the shared parking facility saturation, where represents actual traffic on section d, represents the actual capacity of road section d, and represents the upper and lower limits of optimal road saturation, respectively.
2.3. Shared Parking Charge Pricing Model
In game theory models, parties engage in continuous dynamic optimization to achieve their individual optimal states. The process of dynamic optimization involves the continual mutual influence among the participants in the game, which is reflected in the model by establishing multi-level models to seek the optimal solution. In the research model of this paper, the three parties involved are the upper-level traffic management efficiency model, the middle-level shared parking platform revenue model, and the lower-level parking user decision-making model. These parties coordinate their conflicting interests by continually reducing their respective costs and increasing their respective revenues, aiming to approach the overall optimum.
2.3.1. A Multi-Tier Pricing Model in Shared Parking Domains Based on Game Theory
In this multi-level optimization model, the upper level aims to maximize traffic management efficiency, the middle level strives to maximize the shared parking platform revenue, and the lower level parking user decision-making seeks to minimize costs. By adjusting pricing, the three parties in the game can regulate their costs and revenues to achieve the overall optimum. The specific model is as follows:
The first objective is to minimize the parking costs for shared parking users, which contains the costs from the origin to the shared parking facility and from the shared parking facility to the destination. Where the charge rate , parking user travel time , parking users seeking time in a shared parking lot , and walking time are control variables. The second objective is to maximize the profit for a shared parking operating platform, which is the difference between operating costs and parking fee revenue. Where the charge rate and the number of parking users in a shared parking lot are control variables. The third objective is to minimize the management utility within a shared parking system for the traffic management department, which is measured by road saturation and shared parking facility saturation. Where the actual traffic in a section and the number of parking users in a shared parking lot are control variables. , , and are the utility functions of parking users, the operating platform of shared parking, and the management department of shared parking, respectively.
The characteristic of this model lies in its consideration of the optimization not only for individual participants but also in coordinating multiple participants to achieve a balanced equilibrium in which all parties approach optimality. The solution to this model entails finding a balance point that satisfies all three parties, thus achieving equilibrium in the game.
2.3.2. Determination of Weights
In a shared parking system, owing to the involvement of complex issues across multiple aspects and the fact that the parties involved in the game are not in the same dimension and do not consider the same factors, various indicators exhibit conflicting or mutually constraining relationships. Moreover, the process of mutual coordination is rather ambiguous, which may ultimately lead to an inability to achieve ideal results. Therefore, this paper simplifies the multi-level model for ease of resolution using the coefficient of variation method.
The coefficient of variation method is a statistical approach for determining weights that measure the dispersion of different datasets and mitigate the influence of units of measurement [18]. It is suitable for use in a multi-index evaluation system when the dimensions of various evaluation indicators differ significantly or when there is substantial variability. The advantages of the coefficient of variation method mainly lie in its operability, objectivity, repeatability, wide applicability, and simplicity. The specific steps are as follows:
The formula for calculating the coefficient of variation is as follows:
where “”, “”, and “” represent the standard deviation, mean, and coefficient of variation for the j-th indicator, respectively.
Normalizing the coefficients of variation for each indicator, we obtain the weights “” for each indicator as follows:
Unlike bi-level game theory models, it is difficult to deduce the Nash equilibrium solutions for the trilateral game in our paper. Therefore, the coefficient of variation method is used to obtain the optimal solutions, and the deviation is the criteria for evaluating the proposed model. Based on the determined weights for each indicator and the normalized results, the deviation for each indicator is obtained by weighted summation. The expression for determining the deviation is:
2.3.3. Determination of Parameters
- (1)
- Parking User Unit Trip Costs
The unit travel cost for parking users comprises time and fuel costs. Therefore, the total travel cost is represented by the sum of fuel consumption cost and time cost. The time cost serves as the cost of walking to the destination. Additionally, existing research indicates that fuel consumption expressions during peak and off-peak hours differ [19]. As this research focuses on peak hours, the fuel consumption cost expression during peak hours is utilized as follows:
The time value of travel for transportation users is influenced by various factors, including their income level, consumption level, consumption structure, and value orientation. In this study, the ratio of annual income to annual working hours for parking users is selected as a determinant [20]. The expression is as follows:
where AI represents the annual average income (CNY) of parking users within the shared parking domain, while AWH signifies the annual average working hours (hours) of parking users within the shared parking domain.
- (2)
- Driving time from the starting point to the shared parking lot
The driving time from the origin to the shared parking lot comprises two components: one is the travel time within the road section, and the other is the time spent passing through intersections along the road section [21]. The expression is as follows:
where D represents the total number of road sections within the shared parking domain, while J signifies the number of intersections within the shared parking domain.
The travel time of road sections within the shared parking domain, denoted as , is calculated using the BPR (Bureau of Public Roads) traffic impedance model as expressed in reference [22,23,24]:
where a represents the free-flow travel time of given road section d, while and are undetermined parameters of the model, typically set at 0.15 and 4, respectively.
The calculation of intersection passage time “” is divided into two parts: one part is uniform delay time, and the other part is oversaturated delay time. The combined expression of the two is provided in reference [25]:
where C represents the cycle length, denotes the green time ratio, x signifies the lane saturation flow, e represents the correction coefficient for the type of signal control at a single intersection, CAP denotes the calculated lane capacity (pcu/h), and T represents the duration of the analysis period.
- (3)
- Finding shared berth times
The search time for parking users in a shared parking lot can be expressed through the occupancy rate of parking spaces, as detailed in reference [26]:
where represents the parking duration for users under free flow conditions (in hours), equals to 1, and equals to 1.
- (4)
- Walking time from the shared parking to the destination for parking users
The walking time of parking users is jointly determined by the distance from the shared parking space to the destination and the walking speed of the parking user, expressed as follows:
2.3.4. Model Solution
The fundamental solution approach of game theory involves analyzing the rules of the game and the strategy selection of the participants to identify the equilibrium state of the game. Throughout this process, it is necessary to consider the anticipatory and actual behaviors of the participants, as well as their interactions and influences. By resolving the equilibrium state of the game, it becomes feasible to anticipate the behaviors and outcomes of the participants, thereby determining the optimal solution. In this study, by providing a given parking pricing range, simultaneously and iteratively calculating the costs for parking users, the revenue of the sharing platform, and the traffic management benefits to achieve a three-party equilibrium result, the algorithm proceeds as follows:
Step 1: Input parameters: comprising parking user information, traffic flow information within the shared parking domain, intersection details, shared parking lot information, and destination information.
Step 2: Initialization: setting the maximum and minimum values for parking pricing, as well as the iteration increment; iteration count i = 1.
Step 3: Parking user’s parking decision: based on the pricing set by the upper-level traffic manager for various parking lots within the shared parking domain. Parking users’ parking demands lead to choosing the most favorable parking path and shared parking lot, resulting in an incurred parking cost . Updating the parameters based on this parking path affects the overall parking domain’s traffic distribution, prompting parking users to make new parking decisions based on the updated parameters, repeating until all parking users have completed parking.
Step 4: Result determination: yielding the three-party game outcomes under the pricing scenario parking user parking decision costs , shared parking operation platform revenue , and traffic management benefits .
Step 5: Iterative update: if , then the iteration count is i = i + 1, redefining the shared parking fees based on the iteration increment set in Step 2, proceeding to Step 3 for a new round of parking fee pricing. If , proceed to Step 6.
Step 6: Output results: after completing all iterations, obtain the parking cost matrix for parking users as in Equation (19), the profit matrix for the shared parking platform as in Equation (20), and the traffic management benefit matrix as in Equation (21).
Step 7: Weight determination: calculate the standard deviation and average value for each indicator based on the results matrix of these three indicators. Compute the coefficient of variation for each indicator, normalize the coefficients of variation, and derive the weightings for each indicator.
Step 8: Stable point identification: utilize the calculated weights determined in Step 7 to perform weighted calculations on the elements of matrices , , , and using Equation (11). Identify the value with minimal deviation, signifying that the three-party game within the shared parking domain has reached a stable state.
3. Case Study
As illustrated in Figure 3, this study selects the central urban area of the Heping District, Tianjin City, focusing on the “Three Verticals and Three Horizontals” main roads, which include Hebei Road, Xinhua Road, Jianshe Road, Tangshan Road, Baoding Road, and Yantai Road. This area boasts a prime geographical location, encompassing densely populated residential areas such as Wuhu Li, Wenquan West Garden, and Sande Li, as well as large commercial centers such as Xinhua Building and commercial office locations like the Haizhu Building and Hongda Building. Survey results indicate a significant overflow of parking demand within the region, along with intersecting parking demands, thus rendering it suitable for use as a shared parking domain.
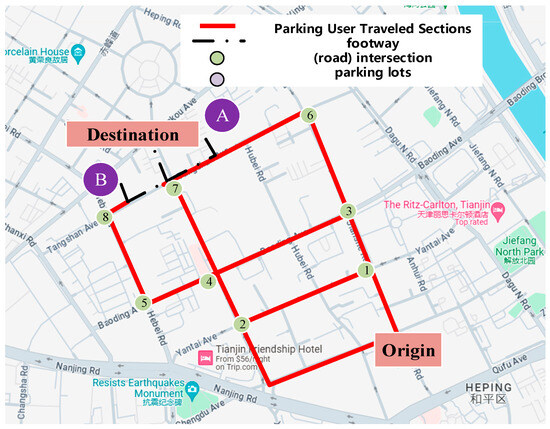
Figure 3.
Road network within shared parking areas.
3.1. Parameter Input
Due to the proximity requirement for shared parking lots within the shared parking domain, locations A and B have been chosen as two such facilities, both servicing the endpoint D. Additionally, a high-traffic intersection has been selected as the starting point O. Within the shared parking domain, there are a total of eight intersections and eleven road segments. Parking users depart from the starting point O and select different routes based on the traffic flow of each road segment and the occupancy rate of parking spaces at lots A and B in order to complete parking.
A survey was conducted on the traffic conditions within the designated shared parking domain. The traffic parameters for road segments are presented in Table 2. Intersection information within the survey domain includes traffic details such as signal cycle length, green signal ratio, and the number of inbound lanes, as shown in Table 3. The routes available for parking users between origin and destination (OD) are outlined in Table 4, while the computational parameters for shared parking lots A and B are provided in Table 5.

Table 2.
Road network parameters.

Table 3.
Intersection parameters.

Table 4.
Parking path.

Table 5.
Parking lot parameters.
The remaining parameters are shown in Table 6. According to the survey conducted in December 2023, the average price of 92# gasoline in Tianjin City is 7.82 CNY/L. The average cruising speed of parking users in the city center is 45 km/h. Substituting the data into Equation (10) yields the unit fuel consumption cost (c1) for parking users as 28 CNY/h. In 2023, the per capita disposable income of residents in Tianjin City, denoted as (AI), is CNY 51,271, with 250 statutory working days in a year and assuming an 8 h working day, resulting in an annual average working hours for residents (AWH) of 200 h. Based on Equation (11), the unit time cost for parking users (wc) is determined to be 22 CNY/h. In order to better compare the merits and demerits of various parking strategies, this paper does not consider the situation where parking demand exceeds the number of shared parking spaces. Thus, the total parking demand is set as a fixed value of 300. It should be noted that the exceeded parking demand will be allocated to regular public parking, and the proposed model can also deal with this situation.

Table 6.
Other parking parameters.
The pricing of shared parking facilities is influenced by operational costs, which encompass labor costs, equipment maintenance costs, land rent, and insurance expenses. Additionally, operational costs may include utilities, taxes, and other fees. Specific operational costs are affected by various factors such as the scale of the parking facility, geographic location, condition of equipment, and service quality. Based on the survey of parking prices in nearby parking facilities within the selected shared parking area, this study sets the pricing range for shared parking spaces from a minimum of 1 CNY/hour to a maximum of 9 CNY/hour, considering the operational costs of shared parking spaces and average parking durations.
The road traffic saturation level “x” is commonly used to describe the congestion level of road traffic. Typically, when “x” is between 0 and 60%, the traffic is considered relatively smooth-flowing. When “x” ranges from 60 to 80%, the traffic condition is generally regarded as congested. When “x” exceeds 80%, the traffic is considered heavily congested, with vehicles unable to maintain normal speeds, resulting in almost stagnant traffic flow. This study selects values “” and “” as 0.6 and 0.4, respectively. Simultaneously, according to surveys, there exists an optimal parking saturation within shared parking facilities. Insufficient parking spaces lead to the wastage of parking resources, while excessive parking spaces cause overcrowding and traffic congestion, affecting parking experiences and potentially increasing risks of vehicle damage and scratches. Moreover, excessive parking spaces increase management difficulties of parking facilities. Based on surveys of surrounding parking facilities, this study sets the optimal parking saturation between 0.7 and 0.8. Deviations below or above this range result in operational losses for parking facilities. Therefore, values “” and “” are set to 0.8 and 0.7, respectively.
3.2. Comparison and Analysis
3.2.1. Programmatic Comparison
Following the solution process outlined in Section 2.3.4, a MATLAB (R2019b) program was developed to solve the game-theory-based pricing model for shared parking domains. The program iteratively evaluates parking prices ranging from 1 CNY/hour to 9 CNY/hour for Parking Facility A (Site 1) and Parking Facility B (Site 2) within the selected area, with an iteration step of 0.1. The computed results were imported into Origin for three-dimensional plotting. Figure 4 illustrates the relationship between travel costs for parking users and the pricing rates of the two shared parking facilities. In the context of game theory, the optimal point for parking users corresponds to the minimum parking cost point.
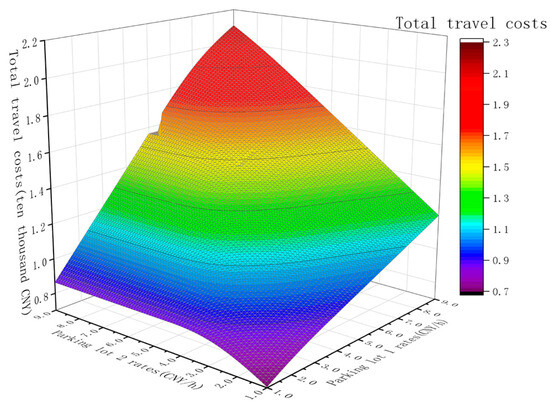
Figure 4.
The relationship between travel costs and parking rates.
According to Figure 4, under constant total parking demand, when the parking rates at Shared Parking Facility 1 (Site 1) and Shared Parking Facility 2 (Site 2) are both set at 1 CNY per hour, the minimum parking cost for users is CNY 7038.28. Specifically, the demand at Site 1 is 145 vehicles, and at Site 2 is 155 vehicles. Additionally, from the figure, it can be observed that if the parking rates at Site 1 and Site 2 are maintained constant while ensuring that the rate of fee increase at the other shared parking facility remains consistent, the rate of increase in travel costs for parking users accelerates more rapidly with increases in the parking fee at Site 1. This phenomenon arises because users at Site 1 have longer average parking durations and a larger number of shared parking spaces. Therefore, due to varying intrinsic conditions among the shared parking facilities within the domain, the impact of price changes on parking users varies in magnitude.
The total operational profit calculations for two shared parking facilities are depicted in Figure 5, with all parking fees directly attributed to the shared parking management platform without intermediary commissions. The peak point in the figure represents the most advantageous position for the shared parking management platform in game theory terms. At a shared parking rate of 9 CNY per hour for both Parking Facility 1 and Parking Facility 2, the maximum total operational profit amounts to CNY 2265.12, with Parking Facility 1 accommodating 145 vehicles and Parking Facility 2 accommodating 155 vehicles. In comparison to Figure 4, under ideal conditions, there exists an absolute antagonistic relationship between the operational profit of the platform and the benefits to parking users. Each party’s optimal point corresponds to the maximum point of the other’s loss, which aligns more closely with real-world scenarios. Consideration of costs incurred by the platform for leasing shared parking spaces would further diminish profits. This study assumes compliance by parking users with established agreements, parking exclusively during shared space availability. In reality, the users can use the shared parking within a set time period, which, over time, will influence the use by the parking owner. Therefore, the platform offers fixed leasing fees to providers of shared parking spaces, which does not affect the outcomes of this research. Hence, to determine the optimal solution for the overall shared parking system, transportation managers need to evaluate its traffic benefits.
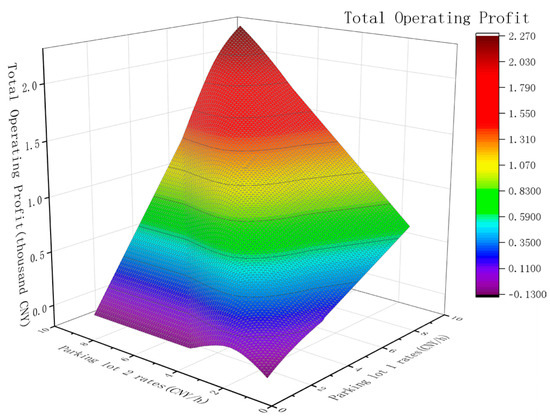
Figure 5.
The relationship between total operating profit and parking rates.
In the shared parking system, the saturation level index of shared parking facilities in the upper-tier transportation management benefits is illustrated in Figure 6. When Parking Facility 1 charges 2.7 CNY per hour and Parking Facility 2 charges 3.2 CNY per hour, the minimum value of “” is 0.2457, with a total travel cost of CNY 10,443 for parking users and a profit of CNY 457.3 for the shared parking platform. It can be observed from Figure 6 that the region with minimal discrepancy between the saturation level and the expected value lies at points where the charging rates of the two shared parking facilities are close. In other words, the closer the pricing of shared parking facilities within the shared parking domain, the greater the enhancement in transportation management benefits.
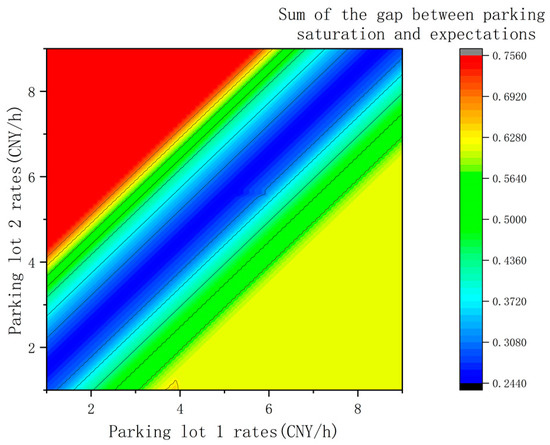
Figure 6.
The relationship between parking saturation and expected value gap and parking rate.
As shown in Figure 7, another metric of transportation management effectiveness, the sum of road saturation deviation from the expected value, reaches its minimum when Parking Facility 1 charges 1 CNY per hour and Parking Facility 2 charges 1.6 CNY per hour, with a value of 1.4827. The travel cost for parking users is CNY 7551, the shared parking platform incurs a loss of CNY −41.9, and the sum of parking saturation deviation from the expected value is 0.2521. Similar to the parking saturation trend, areas where the charging rates of two shared parking facilities are close exhibit smaller deviations between road saturation and the expected value. However, when Parking Facility 2 charges higher and Parking Facility 1 charges lower, the deviations in both saturations from the expected values are larger. Unlike the parking saturation trend, when Parking Facility 1 charges higher and Parking Facility 2 charges lower, road saturation is closer to the expected value compared to parking saturation. This divergence is attributed to parking saturation being more influenced by parking prices, whereas road saturation correlates more closely with traffic conditions within the shared parking domain.
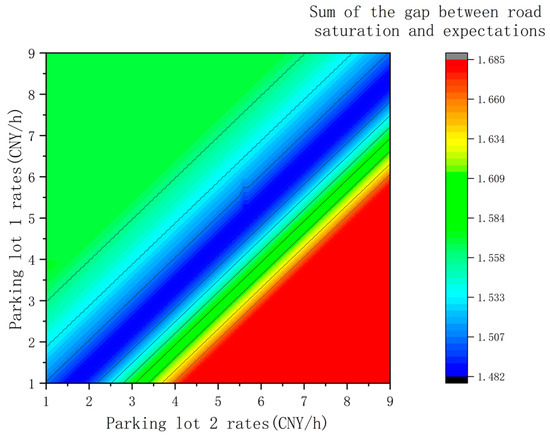
Figure 7.
The relationship between road saturation and expected value gap and parking rate.
3.2.2. Weighting Calculations
Based on the calculation results of four indicators, travel cost for parking users, total operational profit of the shared platform, parking saturation, and road saturation, and utilizing the coefficient of variation method for weight determination as described in Section 2.3.3, the computed results are presented in Table 7.

Table 7.
Game parameters.
3.2.3. Model Solution
According to the weights determined by substituting into Equation (9) to obtain the optimal solution of the objective function, the stable equilibrium point in tripartite game theory is identified. The model’s computational results are illustrated in Figure 8. Following the principle that a lower deviation indicates better game effectiveness, the point with the lowest deviation represents the optimal solution of this objective function. When Parking Lot 1 charges 8.5 CNY per hour and Parking Lot 2 charges 9 CNY per hour, the game tends towards equilibrium, reaching a stable point with a deviation of 0.8155. At this point, Parking Lot 1 accommodates 160 vehicles, Parking Lot 2 accommodates 140 vehicles, and the parking costs for the users total CNY 20,589, the platform operational profit amounts to CNY 2,187.9, the deviation of parking saturation from the expected value is 0.2457, and road saturation deviation from the expected value is 1.4847.
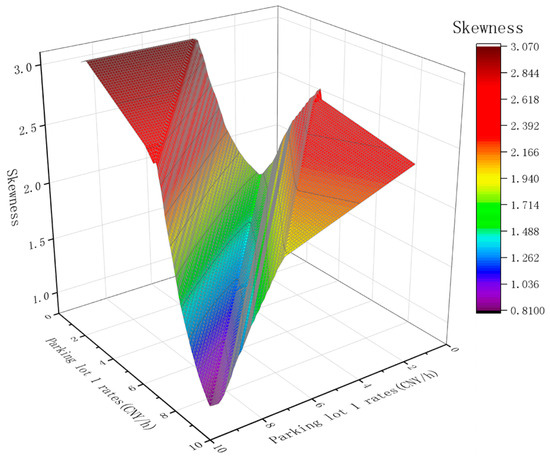
Figure 8.
The relationship between deviation degree and parking rate.
3.2.4. Analysis of Results
Based on the obtained results, the scenarios with minimal user parking costs, maximal shared parking platform revenue, and optimal transportation management effectiveness are compared individually with the outcomes of the game equilibrium points, as presented in Table 8.

Table 8.
Strategy comparison.
When the scenario minimizes user parking costs, the operational profit of the shared parking platform, deviation from expected parking saturation, and deviation from expected road saturation are relatively large, resulting in a total deviation of 1.7504. In contrast, maximizing operational profit significantly increases user parking costs, but since the parking rates in both shared parking facilities remain unchanged, there is no alteration in parking or road saturation. Due to the higher weighting of operational profit over travel costs, the expected deviation of this scenario is lower than that of the scenario minimizing user parking costs, amounting to 0.8982. When minimizing the deviation from expected parking saturation, user parking costs tend towards an intermediate value. Although operational profit is positive, it is comparatively lower, and the deviation from expected road saturation is also reduced, resulting in a total deviation of 1.4998. Alternatively, when minimizing the deviation from the expected road saturation, the operational profit of the shared platform is smaller and negative, leading to a total deviation of 1.6789. The total deviation in reference [13] is 0.8831. Compared with our model, it has a lower travel cost but a higher operating profit. In summary, adopting the pricing strategy with the minimum deviation of 0.8155, while not individually optimal for all parties in the game, represents the optimal solution for the shared parking system within the shared parking domain. This minimizes conflicts among stakeholders, achieving equilibrium as per game theory principles.
4. Conclusions
This chapter, based on game theory, establishes multi-objective functions considering the tripartite game relationship among parking users, shared parking operators, and traffic managers in domains with overlapping parking demands. The decision-making processes of participants in shared parking domains incorporate parking choices by users, revenue objectives of shared parking operators, and traffic management benefits. The parking decisions of users, as the lower layer in the game, involve selecting parking routes and walking distances, considering fuel consumption and time costs, with the objective of minimizing total parking costs. Shared parking platforms, positioned as the middle layer in the game, aim to maximize revenue. Traffic managers, as the upper layer in the game, prioritize enhancing traffic efficiency in the network, using road saturation and parking saturation as evaluation metrics with the goal of minimizing deviations from expected values. Due to differing objectives among game participants, weights are determined using the coefficient of variation method. Finally, through case studies involving varied pricing strategies at different shared parking facilities, scenarios optimizing for minimum total travel costs, maximum shared parking platform revenue, minimum deviation in parking saturation from expected values, and minimum deviation in road saturation from expected values are analyzed and compared against the scenario with the lowest deviation. This verification demonstrates that the highest overall benefits of the shared parking system are achieved only when deviation is minimized, indicating equilibrium in the game. The numerical experiment shows that 8.5 CNY per hour for Parking Lot 1 and 9 CNY per hour for Parking Lot 2 charges are the optimal solutions. Under this policy, parking costs for users total CNY 20,589, platform operational profits amount to CNY 2187.9, the deviation of parking saturation from the expected value is 0.2457, the road saturation deviation from the expected value is 1.4847, and the model deviation is 0.8155.
This provides a solid theoretical basis for traffic managers to formulate shared parking pricing strategies within shared parking domains. The research is of benefit for balancing parking occupancy, reducing parking difficulty, and potentially increasing parking revenue. This work can also provide a reference for formulating parking fee strategies that comprehensively reflect the needs of the three parties involved in the shared parking lot.
In the future, we aim to evaluate our model on a large traffic network, and the shared parking lots and urban traffic conditions will be more comprehensive. At the same time, the dynamic parking pricing is more significant in alleviating parking difficulty and traffic congestion, and this is also our future research emphasis.
Author Contributions
Conceptualization by C.S.; Methodology by C.S. and H.J.; Software and Data curation by H.J.; Formal analysis by H.J. and H.Y.; Writing—original draft by H.J. and H.Y.; Writing—review and editing by C.S.; Supervision by C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Humanities and Social Sciences Foundation of the Ministry of Education of China (22YJCZH153) and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (SJCX23_2050).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- He, K.; Ren, G. Travel behavior choice under the condition of dynamic reservation parking pricing. J. Transp. Eng. Inf. 2020, 18, 53–60. [Google Scholar]
- Li, H.; Ning, X.; Yu, L.; Chen, H. Combined flexible working arrangements and time-dependent parking charges. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 1–7. [Google Scholar]
- Hensher, D.A.; King, J. Parking demand and responsiveness to supply, pricing and location in the Sydney central business district. Transp. Res. Part A Policy Pract. 2001, 35, 177–196. [Google Scholar] [CrossRef]
- Xu, H.; Yu, J.; Xu, W.; Zhang, K. Charging strategy of park-and-ride facilities with consideration to ride-sharing incentive and heterogeneous cost-sharing proportion. Syst. Eng.-Theory Pract. 2023, 43, 1220–1231. [Google Scholar]
- Hu, X.; Li, C.; An, S. Pricing model of urban parking project in public-private partnership mode considering interests of multiple participants. J. Transp. Eng. Inf. 2023, 21, 113–124. [Google Scholar]
- Proulx, F.R.; Cavagnolo, B.; Torres-Montoya, M. Impact of parking prices and transit fares on mode choice at the university of California, Berkeley. Transp. Res. Rec. J. Transp. Res. Board 2014, 2469, 41–48. [Google Scholar] [CrossRef]
- Wang, J.; Jin, S.; Li, W.; Chen, F. Parking pricing method of public parking lots based on multi-aspect comprehensive benefit maximization. J. Traffic Transp. Eng. 2017, 17, 126–135. [Google Scholar]
- Tsai, J.F.; Chu, C.-P. Economic analysis of collecting parking fees by a private firm. Transp. Res. Part A Policy Pract. 2006, 40, 690–697. [Google Scholar] [CrossRef]
- Qian, Z.; Xiao, F.; Zhang, H.M. The economics of parking provision for the morning commute. Transp. Res. Part A Policy Pract. 2011, 45, 861–879. [Google Scholar] [CrossRef]
- Qian, Z.; Xiao, F.; Zhang, H.M. Managing morning commute traffic with parking. Transp. Res. Part B Methodol. 2012, 46, 894–916. [Google Scholar] [CrossRef]
- Zhu, C.; Jia, B.; Han, L. Parking space allocation and pricing based on Stackelberg game. J. Transp. Syst. Eng. Inf. Technol. 2015, 15, 19–24. [Google Scholar]
- Daniel, M.; Bai, Y.; Ouyang, Y. Parking space management via dynamic performance-based pricing. Transp. Res. Procedia 2015, 7, 170–191. [Google Scholar]
- Zong, F.; He, Y.; Yuan, Y. Dependence of parking pricing on land use and time of day. Sustainability 2015, 7, 9587–9607. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, S.; Li, J.; Wei, R. A model of network assignment for multi-mode travel considering roadside parking charge game. J. Transp. Inf. Saf. 2019, 37, 88–94. [Google Scholar]
- Sowmya, K.; Dhabu, M.M. Multistage game model based dynamic pricing for car parking slot to control congestion. Sustainability 2022, 14, 11808. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, C.; Chen, Y. A study on data pricing model using utility method. Price Theory Pract. 2022, 11, 164–167. [Google Scholar]
- Shao, Z. Game theory application in traffic management. Road Traffic Saf. 2006, 6, 8–10. [Google Scholar]
- Zahra, J.; Amirhossein, A.; Philippe, C.; Khoo, M.B.C. Monitoring the coefficient of variation: A literature review. Comput. Ind. Eng. 2021, 161, 107600. [Google Scholar]
- Kui, H.; Wang, J.; Wang, Y.; E, W.; Gao, L. Vehicle fuel consumption model based on urban road operations. J. Jilin Univ. Eng. Technol. Ed. 2009, 39, 1146–1150. [Google Scholar]
- Zong, F.; Juan, Z.; Zhang, H.; Jia, H. Calculation and application of value of travel time. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 114–119. [Google Scholar]
- Zhou, Z. Study on Functional Design and Key Models of Urban Parking Guidance Information System. Ph.D. Thesis, Southeast University, Nanjing, China, 2004. [Google Scholar]
- Feng, H.; Zhu, C. Model of curb parking pricing in urban center district of China. J. Transp. Syst. Eng. Inf. Technol. 2008, 8, 129–135. [Google Scholar]
- Sun, C.; Zhang, P.; Shi, Y.; Chang, Y. Sensor location strategy and scaling rate inference for origin-destination demand estimation. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3455–3467. [Google Scholar] [CrossRef]
- Sun, C.; Chu, Z.; Zhang, P.; Chang, Y. Day-to-day traffic user equilibrium model considering influence of intelligent highways and advanced traveler information systems. J. Cent. South Univ. 2022, 29, 1376–1388. [Google Scholar] [CrossRef]
- An, S.; Ma, T.; Yin, J. Parking fee pricing model for urban cities in China. J. Harbin Inst. Technol. 2000, 32, 65–69. [Google Scholar]
- Shin, J.H.; Jun, H.B.; Kim, J.G. Dynamic control of intelligent parking guidance using neural network predictive control. Comput. Ind. Eng. 2018, 120, 15–30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).