Framework for Assessing the Sustainability Impacts of Truck Routing Strategies

Abstract

The impact of freight on the transportation system is accentuated by the fact that trucks consume a greater roadway capacity than other vehicles and therefore cause more significant problems including traffic congestion, traffic delays, crashes, and pavement damage. Evaluating the actual repercussions of truck traffic becomes paramount in locales where roadway expansion is unfeasible. Trucks are vital to the economy, providing essential services to commerce and industry, and yet it is crucial that their operation does not contribute to the deterioration of infrastructural quality or compromise public safety. Currently, we lack methodologies in practice for the real-time management of traffic, specifically for truck routing, to minimize travel times and prevent delays due to non-recurrent congestion, such as traffic incidents. Accordingly, this study aimed to devise a truck routing strategy utilizing a traffic micro-simulation model (VISSIM) and to assess its effects on reducing travel delays. This involved the development of real-time truck re-routing simulation models that take into account non-recurrent congestion and the resulting travel delays and fuel consumption. The VISSIM model was applied to the I-75 corridor in Marion County, Florida, focusing on non-recurrent congestion effects on travel delays and fuel consumption. The initial findings suggest that the implementation of a dynamic truck re-routing system can significantly alleviate traffic congestion, resulting in a marked decrease in travel delays and fuel usage, demonstrating the potential for such strategies to enhance the overall efficiency of the transportation system.

1. Introduction

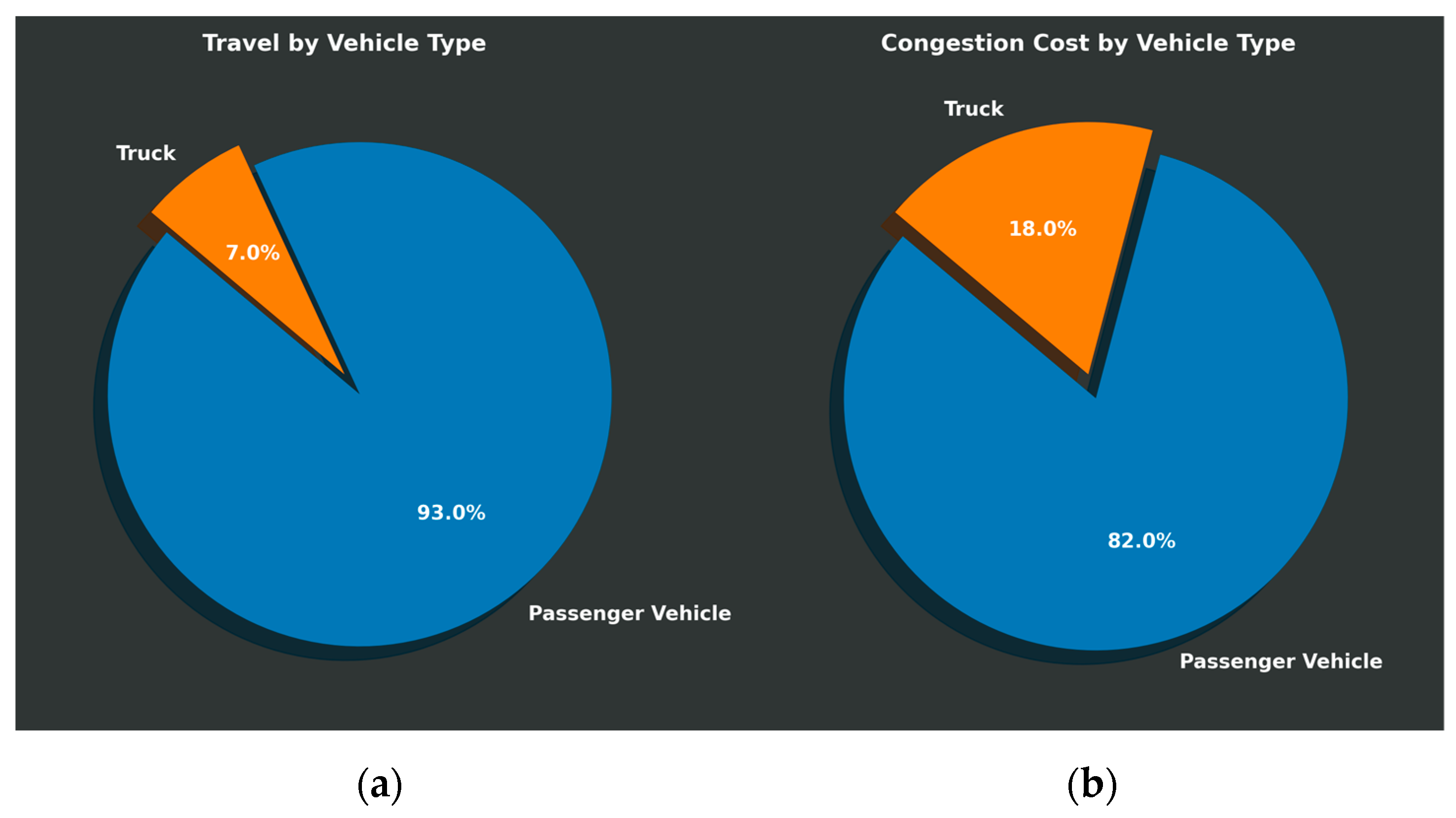
Traffic congestion causes a significant problem with numerous implications. In 2014, congestion caused urban Americans to travel an extra 6.9 billion hours and consume an additional 3.1 billion gallons of fuel, resulting in a congestion cost of USD 160 billion. Trucks account for 17 percent (USD 28 billion) of that cost, which is disproportionate to their 7 percent share of road traffic (see Figure 1). Truck traffic is the most considerable component among freight transport modes. Consequently, freight demand is a growing cause of traffic in the transportation network, which has historically increased at a faster rate compared to the growth of personal travel demand. To meet the needs of individuals and businesses, the shipment of materials and products is a primary component of travel demand on the transportation system. In terms of vehicle miles traveled on the roadway system, trucks involved in freight transportation rank third, only after personal travel for daily activities and tourist travel. Since trucks consume more roadway capacity than other vehicles and they are not only larger but also heavier, the impact of freight must be further assessed, including congestion, delays, crashes, pollution, energy consumption, and road damage in many regions.

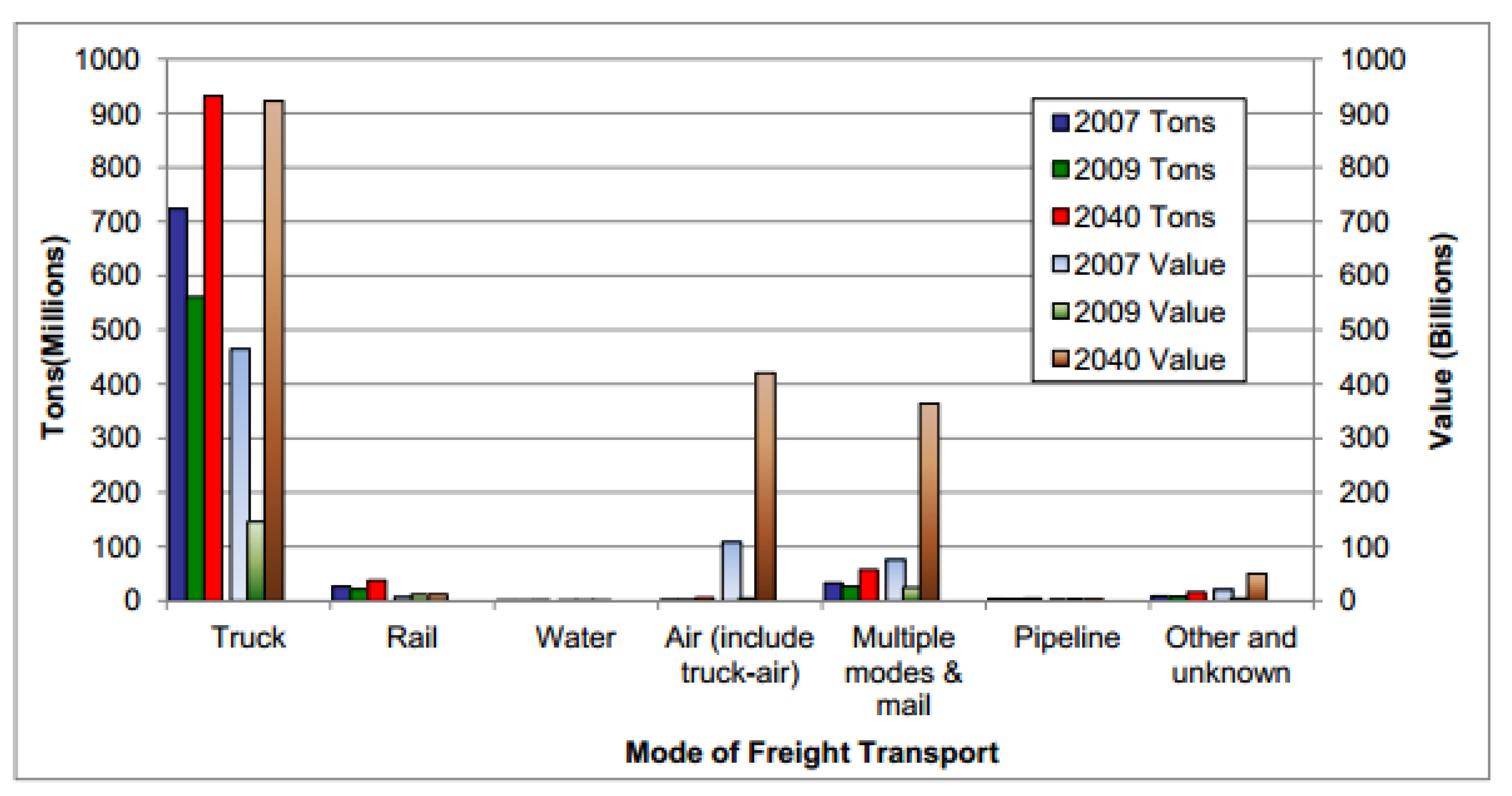
Florida ranks as the fourth most populous state in the nation. It also boasts an annual tourist population exceeding 80 million. In addition, the state is a prolific producer of various products that are distributed both domestically and internationally. Consequently, Florida has become a principal hub for freight activity. According to the 2003 Florida Statewide Freight and Goods Mobility Plan, freight totaling 848 million tons and valued at over USD 939 billion was transported to, from, within, and through Florida using truck, rail, air, and water modes. Of this, approximately 597 million tons was conveyed by truck. When considering shipment values, the proportion attributable to truck transport becomes even more significant, reaching approximately 80 percent.

In Figure 2, the value and tonnage of Florida’s freight shipments by mode are presented. As the figure illustrates, trucks continue to be the dominant mode of freight transportation and are predicted to increase in both value and tonnage until 2040. We wish to highlight that the decrease in tonnage and value from 2007 to 2009 was primarily due to the economic downturn at the time.

There is a growing need to quantify the actual effects of trucks on traffic, to support the ability to move goods and people safely and efficiently in areas where the expansion of roadways is generally not an option. Accordingly, this research aimed to formulate operational strategies for truck routing that will improve travel efficiency and to examine the effects of truck movements, focusing on congestion costs, safety, and sustainability.

2. Related Research

Traffic congestion due to incidents has a large number of impacts on freeway traffic delays. There have been numerous research studies on how to minimize the effect of traffic incidents, and many have developed different methods for determining how incidents form. Some have used artificial neural networks [2], an approach based on loop occupancy, and the wavelet technique [2]. Those methods helped reduce the time required for the detection of incidents and, therefore, decreased the effect of incidents on traffic delays and other phenomena that they cause.

In a USDOT research project, an incident-induced delay (IDD) model was developed by Wang in 2008 [3]. Current methods use either deterministic queuing theory or shockwave analysis. The queuing-theory-based procedures calculate the IID by using a queuing diagram formed from the cumulative vehicle arrivals and departures. These methods examine the area under the curve to calculate the delay in units of vehicle-hours [3]. Using the queuing diagram, Morales [4] created a method for determining the IDD by implementing in a computer spreadsheet. Doing so makes it easier to compute the delay, time to normal flow, and maximum queue in the wake of a freeway incident. Similar to this method, Lindley created the FREWAY model [5]. After 10 years, another method was proposed by Sullivan, which involved using a two-level approach [6]—combining the queuing diagram and FREWAY—called IMPACT. This method forecasts the incident rate severity and duration in level one, and for the second level, it forecasts the traffic delay caused by the incident. In another study, Skabardonis et al. used the queuing diagram to reveal the IDD, and Fu and Rilet created a model to estimate the delay in an incident region by using the real-time traffic conditions [7,8]. Soon after, Fu and Hellinga used fuzzy queuing to estimate the future delay in an incident situation.

Cohen and Southworth utilized the queuing model and developed a methodology for forecasting the time delay following an incident on a freeway [9], where an estimation is provided with the mean and variance following the incident time. Since a traffic model has some similarities with fluid flow, some researchers have proposed using kinematic wave theory to explain traffic flow. This idea helps in shockwave effect analysis of the IDD. The first attempt to explain the shockwave effect was by Lighthill and Whitham [10]. At the same time, Richards created a model for traffic flow, with the idea of replacing single vehicles with continuous fluid density [11]. In the literature on traffic engineering, the first shockwave-based model was called the LWR model.

Nam and Drew proposed that “deterministic queuing analysis always underestimates the overall magnitude of delays compared to shockwave analysis” [12]. Nonetheless, Hurdle and Son along with Rakha and Zhang supposed that for better results [13,14], both methods should be used together to gain additional knowledge about traffic congestion.

Hallenbeck et al. used Seattle’s metropolitan freeways to understand the nature of traffic congestion [15]. A comparison was made of the normal use of a lane versus usage during incident occurrence. An estimation was then performed by looking at the difference between the two profiles. This method opened the door to incident detection and delay estimation in Washington State, even though the estimations of traffic congestion were questionable due to a failure to account for movement from upstream to downstream locations.

The importance of considering the variability in travel times as a source of traveler costs have been noted in previous studies [16,17,18,19,20]. The estimation of passengers’ reactions to changes in their average daily travel time, which represents their everyday commute, formed the basis for a large proportion of these evaluation studies. One popular approach for these studies was to use logit models for route selection. These models showed that the choices made by a sample of commuters were related to differences between driving times and out-of-road travel times for these individuals. The various monetary costs associated with each mode or route alternative selected were also included. In order to derive the monetary value of savings related to time, a ratio between the resulting parameter values assigned to travel times and those relating to costs was used in these models [15]. Alternatively, to derive the value of time spent in travel for work or leisure purposes, a number of travel behavior studies were carried out based on consumer choice models. This perspective of economic theory includes the avoidable time spent traveling as a nonproductive activity against which there is an opportunity cost. Delays in the daily commute may lead to lost working time, for example. The assessment of value for these hours lost, multiplied by some percentage of gross hourly wages, including vacation benefits paid for by employers, is a common approach to determining the cost of this extra time spent on travel [21]. These studies, however, show that significant benefits for passengers can be obtained under the right conditions, in particular, in congested peak periods, by reducing variability and, therefore, uncertainty associated with travel times. This is important because it is usual for travel time savings to dominate the benefits assigned to major transportation improvement projects [22].

Recent advancements in traffic management strategies emphasize the integration of simulation models and dynamic routing to enhance network robustness and reduce congestion impacts. Yildirim demonstrated that implementing buffer stacks combined with Truck Restriction Time Window policies at the Port of Izmir significantly alleviated congestion and emissions by optimizing truck flows during peak periods [23]. Similarly, Li and Khattak explored the effectiveness of en route diversions during incidents on freeway corridors, suggesting that real-time traffic management systems can substantially improve the routing of commercial traffic under connected and automated vehicle conditions [24]. Further, Madar, Maoh, and Anderson utilized the Network Robustness Index (NRI) to evaluate the resilience of the Ontario truck road network to capacity reductions, highlighting the necessity of strategic planning in infrastructure to maintain commerce flow during disruptions [25]. Collectively, these studies underline the pivotal role of innovative traffic management solutions in sustaining efficient and environmentally friendly transportation networks.

3. Technical Objectives and Modeling Procedure

The seamless flow of goods through our transportation networks is a linchpin of economic stability and growth. Trucks, as the lifeblood of land freight, navigate the arteries of these networks, where efficiency and sustainability are paramount. This section delineates a sophisticated research methodology aimed at optimizing truck routing strategies. The ultimate goal is to enhance travel efficiency and rigorously assess the multifaceted impacts of truck movements, particularly focusing on the cost implications of congestion, safety considerations, and environmental sustainability.

This section propels our narrative forward, charting the course for a series of methodical steps to address the pressing challenges faced in freight transportation management.

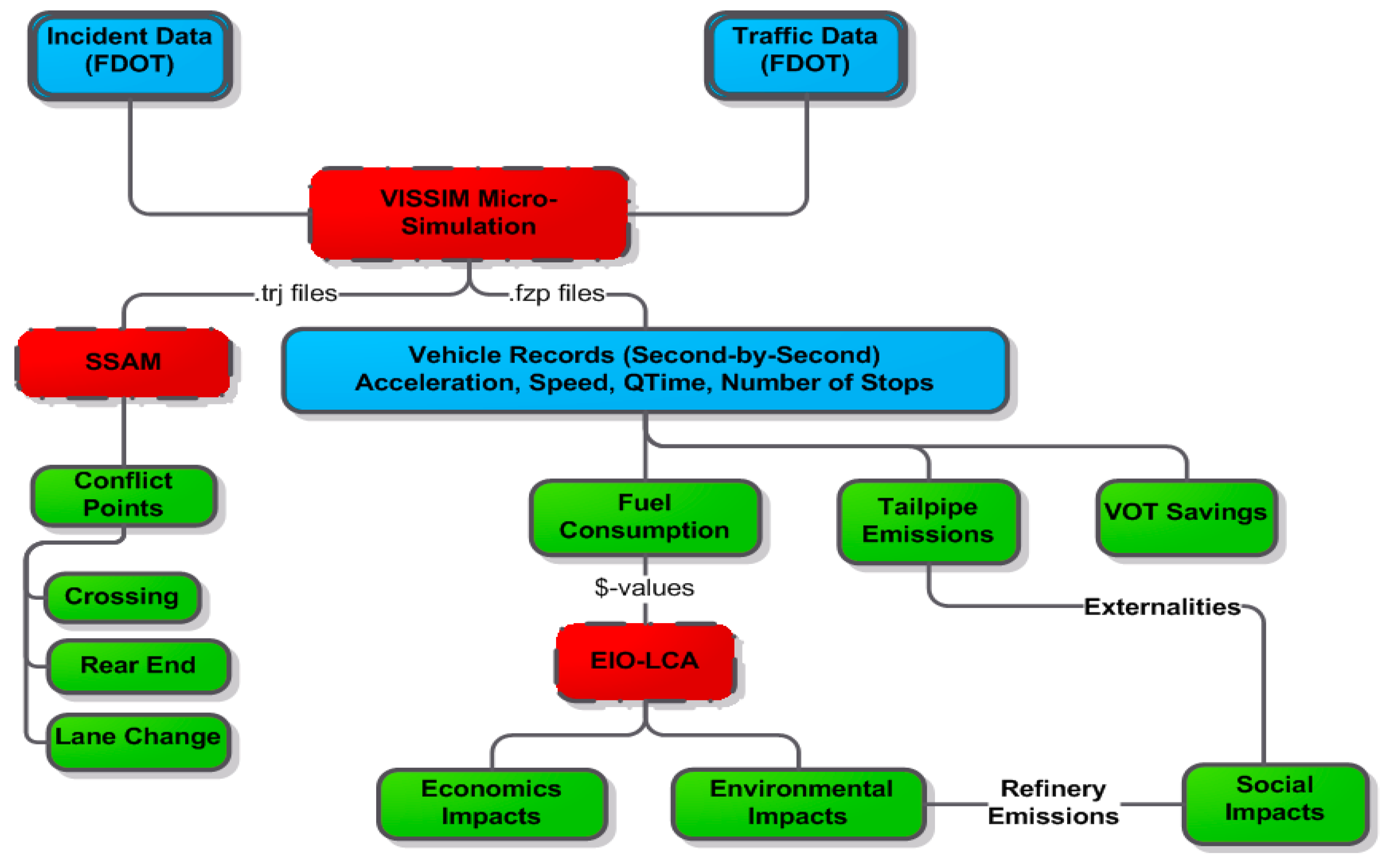
The principal aim of our research was to devise operational strategies that bolster travel efficiency on truck routes and evaluate the resultant impacts of these movements in terms of congestion costs, safety, and sustainability. Our methodology, meticulously developed and described in this paper, lays out a systematic approach to achieving this aim. A framework of the research methodology is presented in Figure 3.

• Regional and Corridor Analysis: We began by identifying key regions, facilities, and corridors integral to freight movement. This targeted approach allows for an accurate estimation of congestion-based travel delays and fuel consumption, utilizing detailed truck routing models for micro-level operational analysis. The financial quantification of these impacts is a crucial step toward informing the formulation of cost-effective strategies.
• Fuel Consumption and Re-routing Estimation: This research methodologically determined the fuel consumption associated with current truck routing practices. By estimating potential re-routing scenarios, this study extrapolated the effects of strategic changes to standard routes, aiming to reduce the incidence of stops and idling that contribute to excess fuel usage.
• Traffic Flow and Crash Rate Analysis: A thorough examination of the effects on traffic flow, with a keen focus on the impacts on crash rates, was performed. Conflict points such as rear-end, crossing, and lane change incidents were analyzed to understand how improved truck routing could mitigate these safety risks.

The data-driven approach taken here was not only designed to further our understanding of the current state of truck travel efficiency and sustainability impacts but also to lay a foundational framework for real-time traffic management. By closely examining how these strategies affect various facets of the transportation ecosystem, we were able to formulate concrete recommendations for operational improvements.

Thus, our research methodology was geared toward achieving the dual objectives of enhancing travel efficiency and conducting a thorough investigation into the economic, environmental, and societal impacts of truck movements. Although our results provide a strong basis for the development of strategic operational adjustments, we acknowledge certain limitations. Quantifying the full spectrum of social impacts, especially the monetization of safety implications, remains a complex task that our current study only begins to address. Additionally, while we suggest that a reduction in stop-and-go traffic of loaded trucks may lead to less pavement damage, future research should focus on the long-term effects and benefits of these routing changes on roadway infrastructure.

We propose that subsequent studies expand upon our findings, using our methodology as a steppingstone towards gaining an even more nuanced understanding of the implications of truck routing strategies. Potential areas of further investigation include the development of more sophisticated models for safety impact monetization and a more detailed analysis of the effects of optimized truck routing on road maintenance cycles and costs.

4. Data Preparation

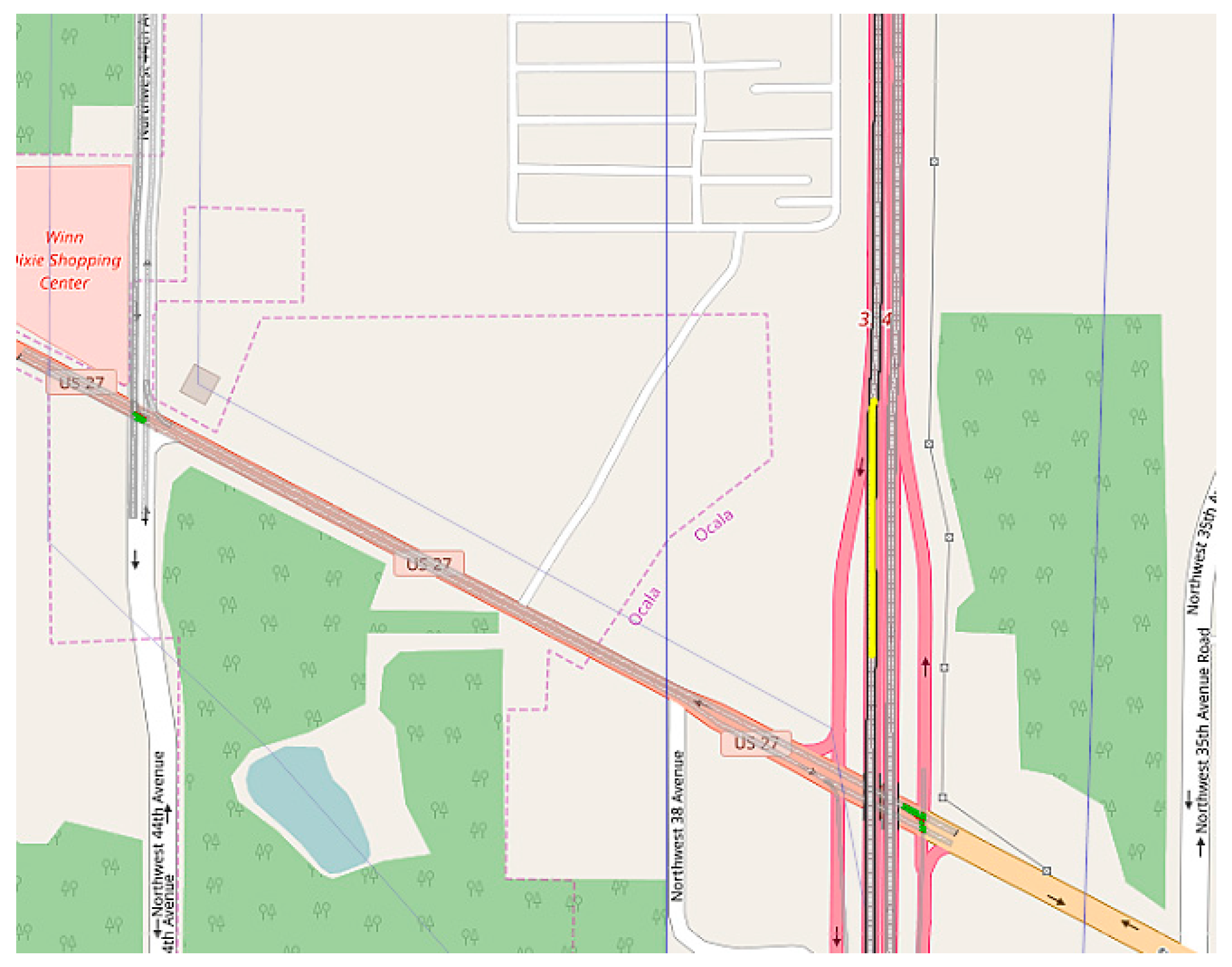
In order to study non-recurrent-incident-induced truck travel delays, a busy highway corridor with a high truck percentage was selected by examining the truck percentages as well as the AADT levels on both Interstate-75 and Interstate-95. Another specification that affected the decision was the presence of an easy by-pass route. After trials of many busy corridors with high truck percentages, the site location was selected on I-75 at one mile north of US-27. 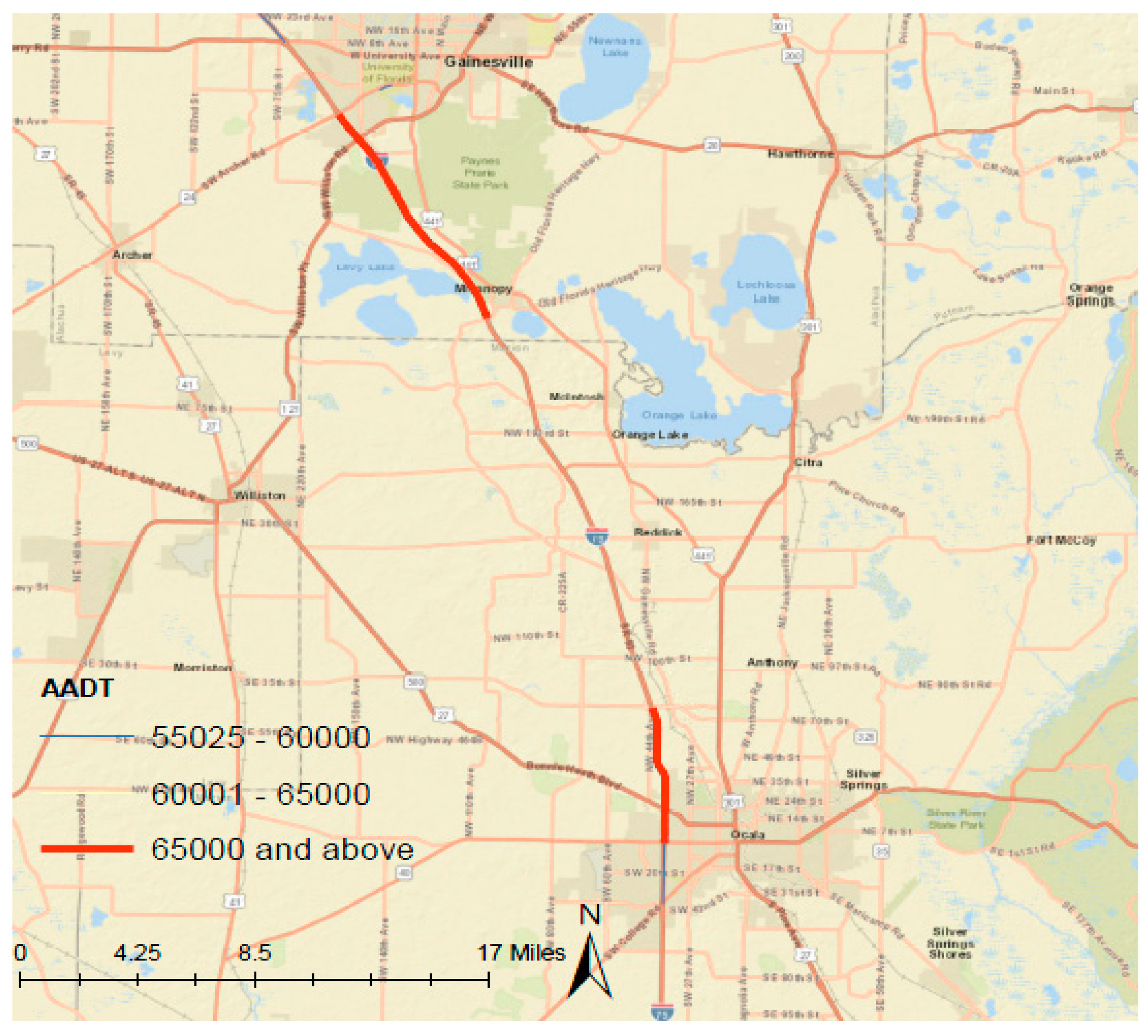Figure 4 illustrates the truck percentage categories on Florida highways and Figure 5 provides the high AADT levels. The site location’s truck percentage (T factor) is 24.2% while the AADT is 65,500. The traffic collecting system (Portable Telemetered System) site information is as follows: site number 360438, which is situated on I-75, approximately 0.986 miles north of US-27 (RCLP) in Marion County. The specific section of the highway is recorded at mile point 18.809, which is noted for its substantial traffic volumes, as evidenced by the annual average daily traffic (AADT) figure of 65,500 vehicles. The data collection at this site is facilitated through a portable device, ensuring the flexibility of traffic monitoring. Although class data were not gathered at this location, essential traffic composition factors were calculated: the K factor, which represents the proportion of daily traffic in the peak hour, was 10.6; the D factor, indicating the directional distribution of peak hour traffic, stood at 54.5; and the T factor, which describes the percentage of trucks in the traffic stream, was 24.2. This detailed traffic information is pivotal for informed decision-making regarding transportation planning and infrastructural management in the area.

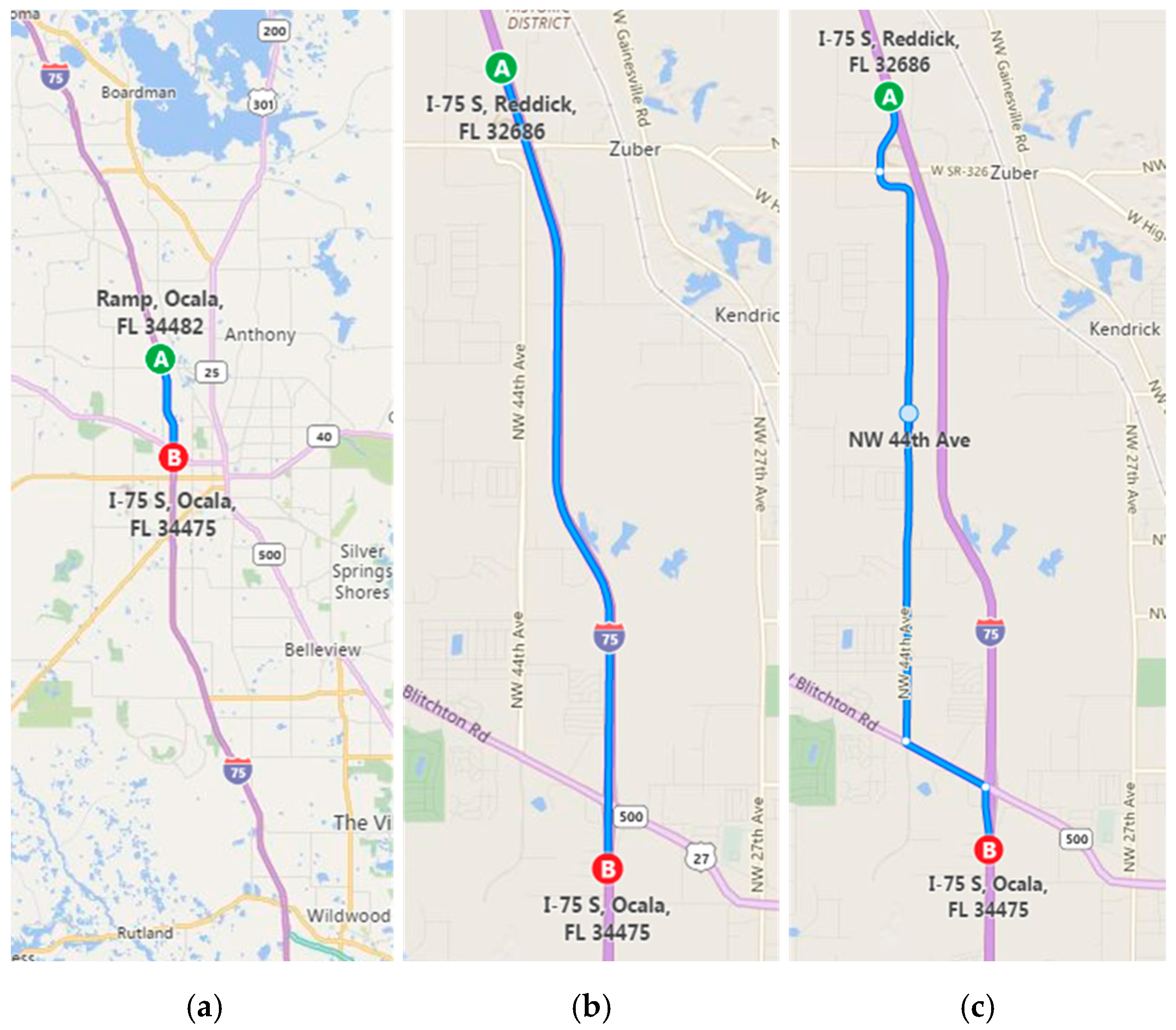
The selected corridor has an alternative route of 5.8 miles (while the main route is 5.4 miles). The travel time difference is approximately 5 min in non-congestion conditions. For this study, micro-simulation models of incidents were calibrated only on the southbound direction of the study corridor. Main and alternative routes are shown in Figure 6. This section of the article, divided by subheadings, provides a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

Incident Data (FDOT)

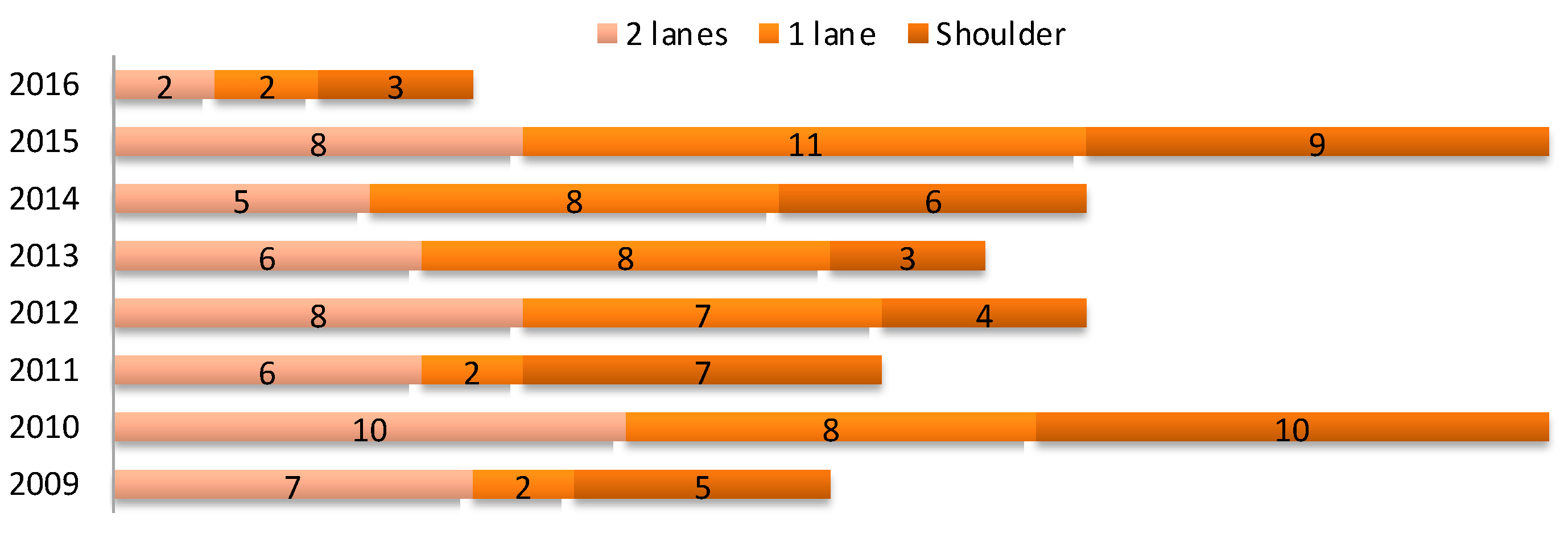
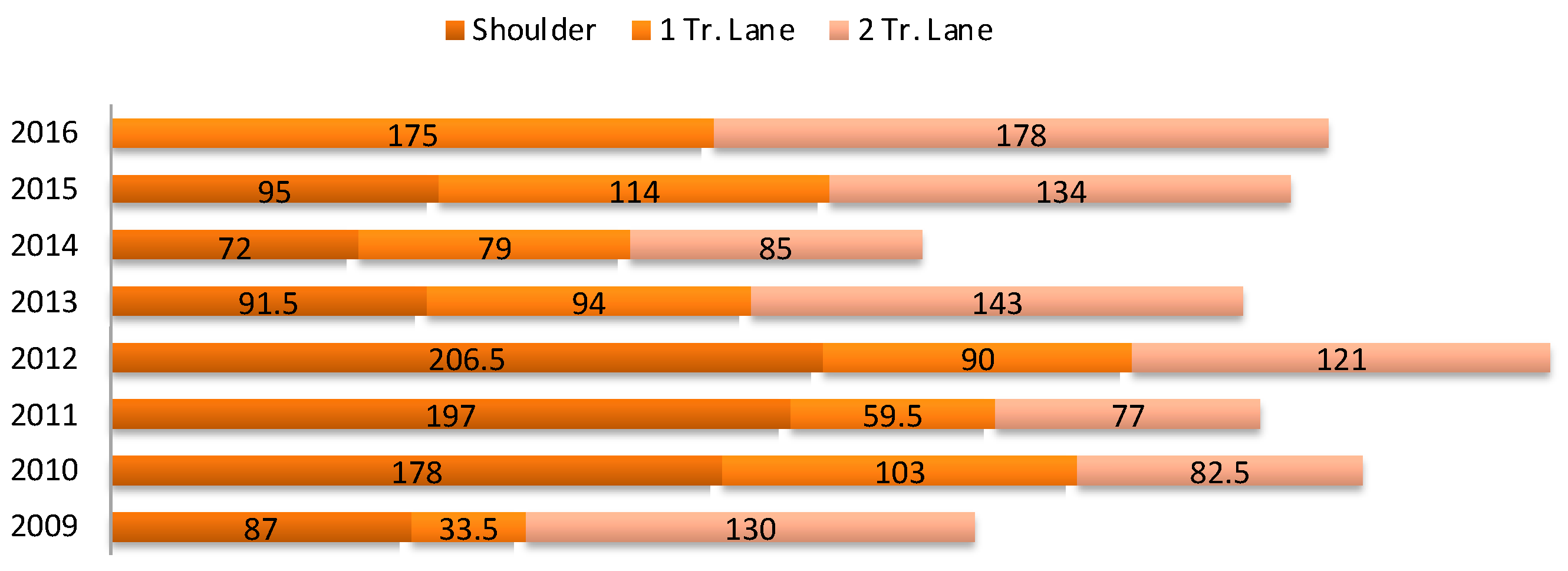
Traffic incident data of the Central Florida Area collected by the Florida Department of Transportation were utilized to assess the traffic event history of the study corridor. A traffic events dataset was collected from October 2009 to February 2016. The data features include but are not limited to the type of event, level of closure, incident duration, date and time, geo-location, etc. Given the aforementioned information, traffic incidents were categorized by their level of closure. Events that caused at least one shoulder closure were selected for the evaluation. Annual incident frequencies and mean durations are illustrated in Figure 7 and Figure 8. The years 2009 and 2016 are not complete due to the data collection period.

The incident history of the study corridor was utilized to compute the annual impacts of the micro-simulation models. Furthermore, mean durations were used to choose the best possible simulation period.

A wide range of factors affects truck speed and travel time reliability, including the terrain, infrastructural design and capacity, weather, incidents, work zones, and time of travel.

Highway incidents are a major impediment to the free flow of traffic, causing an estimated one-quarter of highway delays [23]. Major crashes are a significant source of incident-related delays, but just as important are less intense incidents such as vehicle breakdowns, road debris, etc.

A model was developed to find the incident-induced truck travel delays. A scenario site was determined by examining truck origin–destination data from Tennessee provided by Productivity Apex, Inc.(Winter Park, FL, USA) In the data file, the following variables were present: (1) start date and time and end date and time; (2) duration of the trip; (3) standstill time (duration of idling); (4) start/end odometer; (5) distance of the trip; (6) start latitude/longitude (origin); (7) end latitude/longitude (destination).

Individual incident-based analysis was also used for estimating the fuel consumption and monetizing.

Travel delay savings were assumed to be idling savings in order to convert them into fuel costs. Information on fuel consumption due to idling was found from the US Department of Energy Argonne National Laboratory. Loaded diesel trucks were found to consume 1.15 gal/h. In addition to 1.15 gal/h, we took the annual truck VMT and multiplied that by the travel delay savings matrix in order to find the annual cost of idling savings.

5. Methodology

In most traffic assignment methods, the effect of road capacity on travel times is specified by means of volume–delay functions t(v), used to express the travel time (or cost) on a road link as a function of the traffic volume v. Usually these functions are expressed as the product of the free-flow time multiplied by a normalized congestion function f(x), where the argument of the delay function is the v/c ratio, with c being a measure of the capacity of the road.

Many different types of volume–delay functions have been proposed and used in practice in the past. By far the most widely used are the BPR functions (Bureau of Public Roads, 1964), which are defined as

$$T={\mathrm{T}}_0(1+\mathsf{\alpha }{\left(\frac{\mathrm{V}}{\mathrm{C}}\right)}^{\mathsf{\beta }})$$

where

T = travel time (minutes);

T₀ = free-flow travel time (minutes);

V = traffic volume (vehicles per hour);

C = capacity (vehicles per hour);

α, β = parameter.

The coefficient, α, in the BPR function was determined by forcing the curve to fit the speed/volume data at zero volumes (free speed) and at capacity (LOS E). The second coefficient, β, was found by nonlinear regression.

For this model, there are reduction factors added to the capacity and free-flow travel times in BPR functions. The capacity and free-flow speed adjustment factors are provided in HCM-2010, as shown in

Table 1. VISSIM stochastic model data.

Routes	Shoulder Closure		1-Lane Closure		2-Lane Closure
	Main	Alternate	Main	Alternate	Main	Alternate
Vehicle Input (Volume)	4500	930	3450	930	3450	930
Desired Speed Distribution	70 mph	45 mph	70 mph	45 mph	70 mph	45 mph
Link Type	Freeway	Urban	Freeway	Urban	Freeway	Urban
Truck Percentage	20%	5%	20%	5%	20%	5%
Simulation Period (s)	7500	7501	7500	7500	7500	7500
Incident Period	6500		5500		5500
Priority rules		2		2		2

. In this table, incidents are grouped in five categories for a variety of roadway segments divided by the number of lanes. In addition to the adjustment factors, sample occurrence probabilities of the incident groups are provided in

Table 2. The default per open lane CAFs based on HCM-2010.

Number of Lanes (1 Direction)	No Incident	Shoulder Closure	1-Lane Closure	2-Lane Closure	3-Lane Closure	4-Lane Closure
2	1.00	0.81	0.70	-	-	-
3	1.00	0.83	0.74	0.51	-	-
4	1.00	0.85	0.77	0.50	0.52	-
5	1.00	0.87	0.81	0.67	0.50	0.50
6	1.00	0.89	0.85	0.75	0.52	0.52
7	1.00	0.91	0.88	0.80	0.63	0.63
8	1.00	0.93	0.89	0.84	0.66	0.66
Average Incident Duration (min)	-	32.00	34.00	53.00	69.00	69.00
FFS Adjustment Factors	-	0.86	0.79	0.61	0.61	0.61
Probability of Occurrence	91.91%	5.75%	1.62%	0.40%	0.32%	0.00%

. Average durations for each incident type are also given in Table 1.

Vehicles per hour is how the queue growth length is measured during an incident. The rate is determined by the number of vehicles arriving at the end of the queue (V) while subtracting the number of vehicles that move past the incident (rC). If the volume of the measured traffic zone—in this case, the freeway capacity (V)—is greater than the capacity of the traffic zone during the incident, this will create an increasing queue until the incident is cleared. This incident reporting is measured in hours (Ti Hours) and, to determine the maximum queue length, which occurs at some point in time during the traffic incident before the queue is cleared, is calculated as follows [26]:

Q = (V − rC)Ti

where

Q = maximum queue length (vehicles);

r = capacity reduction factor due to incident;

Ti = incident duration (hours).

Because the queue grows from a length of zero (when the incident occurs) to a length of Q (when the incident is cleared), the average length of the queue during the incident is Q/2 [26].

The model calculates the travel times for a range of volume-to-capacity ratios from 0.4 to 1.1. If the travel cost for the shortest path exceeds the travel cost for the alternative path, then the model makes a change on the route and diverts the truck from the ramp at Location A. The travel cost calculations are as follows:

$$\begin{array}{l}\mathit{If} \left(\right(T_0)1+TQ)\ast (\mathit{Avg}. \mathit{Truck} \mathit{Value} \mathit{of} \mathit{Time})<\\ (D2-D1)\ast (\mathit{Avg}. \mathit{Cost} \mathit{of} \mathit{Fuel} \mathit{per} \mathit{mile}) \mathit{then} “\mathrm{Keep}”\end{array}$$

(1)

$$\begin{array}{l}\mathit{If} \left(\right(T_0)1+TQ)\ast (\mathit{Avg}. \mathit{Truck} \mathit{Value} \mathit{of} \mathit{Time})>\\ (D2-D1)\ast (\mathit{Avg}. \mathit{Cost} \mathit{of} \mathit{Fuel} \mathit{per} \mathit{mile}) \mathit{then} “\mathrm{Change}”\end{array}$$

(2)

where

(T₀)1 = free-flow travel time on shortest path (minutes);

TQ = travel time delay (time in Q) (minutes);

D1 = shortest route distance (7.4 miles);

D2 = alternative route distance (9.5 miles);

Avg. truck value of time = USD 1.55 per min.; USD 93 per hour (TTI 2012 Urban Mobility Report);

Avg. cost of fuel = USD 0.69 (per mile);

Average miles traveled per gallon: 5.8 miles;

Yearly average diesel price: USD 4.00 per gallon.

The distance from the exit ramp to the incident location is also considered in the model. The variation in the distance from the incident location will change the travel delay since the travel time formula changes from when the truck arrives at the back of the queue. Distances of from 1 mile to 7 miles (with 1-mile intervals) are considered in the model. Last but not least, the travel time savings by changing routes are multiplied by the corresponding probability, given in Table 1, of each type of incident.

The probabilities of occurrence of the incident types are applied to the travel time matrix and the results are divided by 7.4 miles, which is the distance of the shortest path, in order to find the travel time savings per mile. These numbers are monetized by multiplying them by the average loaded truck value of time, which is USD 93.00. The daily truck VMT of the section is calculated as follows:

Avg. Daily Truck VMT = (Truck AADT)*(Distance in shortest path) × (365 days)

The results of the travel time savings per mile matrix are multiplied by the daily truck VMT and daily delay cost savings based on the incident scenarios matrix. In addition, the daily cost saving matrix is multiplied by 365 days in order to find the average annual delay cost savings.

Individual Incident Analysis Based on Generated Scenarios

In this section, the scenarios generated in the previous model are individually analyzed. The number of trucks affected by the incidents is found and multiplied by the travel delay savings for each scenario. These trucks are found by traffic flow calculations. Traffic densities for both “in the queue” and “before the queue” are calculated. The findings for each scenario are as follows:

Fuel Consumption

In this section, the output from the estimated model in the previous section is used to calculate the fuel consumption of extra miles traveled due to route changes on trips. Furthermore, the fuel consumption of idling due to travel delay savings in the incident scenarios will be determined. For the routes where a change in route found necessary, trucks will be traveling extra miles since the alternative route is 2.1 miles longer in distance than the shortest route. Therefore, the fuel consumption needs be determined. Moreover, the changed routes are saving travel delays. The delays due to the incident-based congestion are considered as savings in terms of idling fuel consumption.

Micro-Simulation Model Development with VISSIM

VISSIM 7.0 is a stochastic and behavior-based micro-simulation tool developed by PTV to model traffic and public transit operations. VISSIM can be applied as a powerful tool in a variety of transportation problem settings to model multimodal transport operations.

It can analyze traffic operations under constraints such as lane configurations, traffic compositions, traffic signals, etc. Therefore, it is a useful tool for the evaluation of various alternatives based on ITS-based transportation engineering and effective planning measures (www.ptvamerica.com, access date: 11 October 2023). In this model, there are three types of scenarios to simulate non-recurrent congestion (i.e., an incident has induced). The first one is a “shoulder-only” closure, the second is a “one out of three lanes closure”, and the last scenario is a “two out of three lanes closure”. Truck re-routing is applied depending on second-by-second travel delay comparisons. In order to determine the impacts of truck diversion strategies, each of these scenarios has a base case where no truck re-routing is applied.

In the calibration process, assessing the network geometry, including horizontal curves, grades, and ramp locations, is a critical step. Accordingly, the geometric boundaries of the I-75 corridor were coded in VISSIM, as shown in Figure 9. Based on southbound traffic data and incident statistics, the time of day of the study period (7500 s) was chosen to be within the Wednesday evening peak hours (i.e., 6:00 p.m. to 8:05 p.m.).

Parameter calibration is performed to minimalize the misfit between observed data as much as possible from the actual network. The program user can assess the results from a visual or from a numerical point of view while the simulation is running. Accordingly, a visual inspection can be made to observe movements on the screen visualization, slowing the user to check for the network geometry, which reflects whether the traffic movements are realistically simulated. For example, unexpected decelerations can cause shockwaves leading to disruptions in the traffic flow. This highlights the importance of geometric coding.

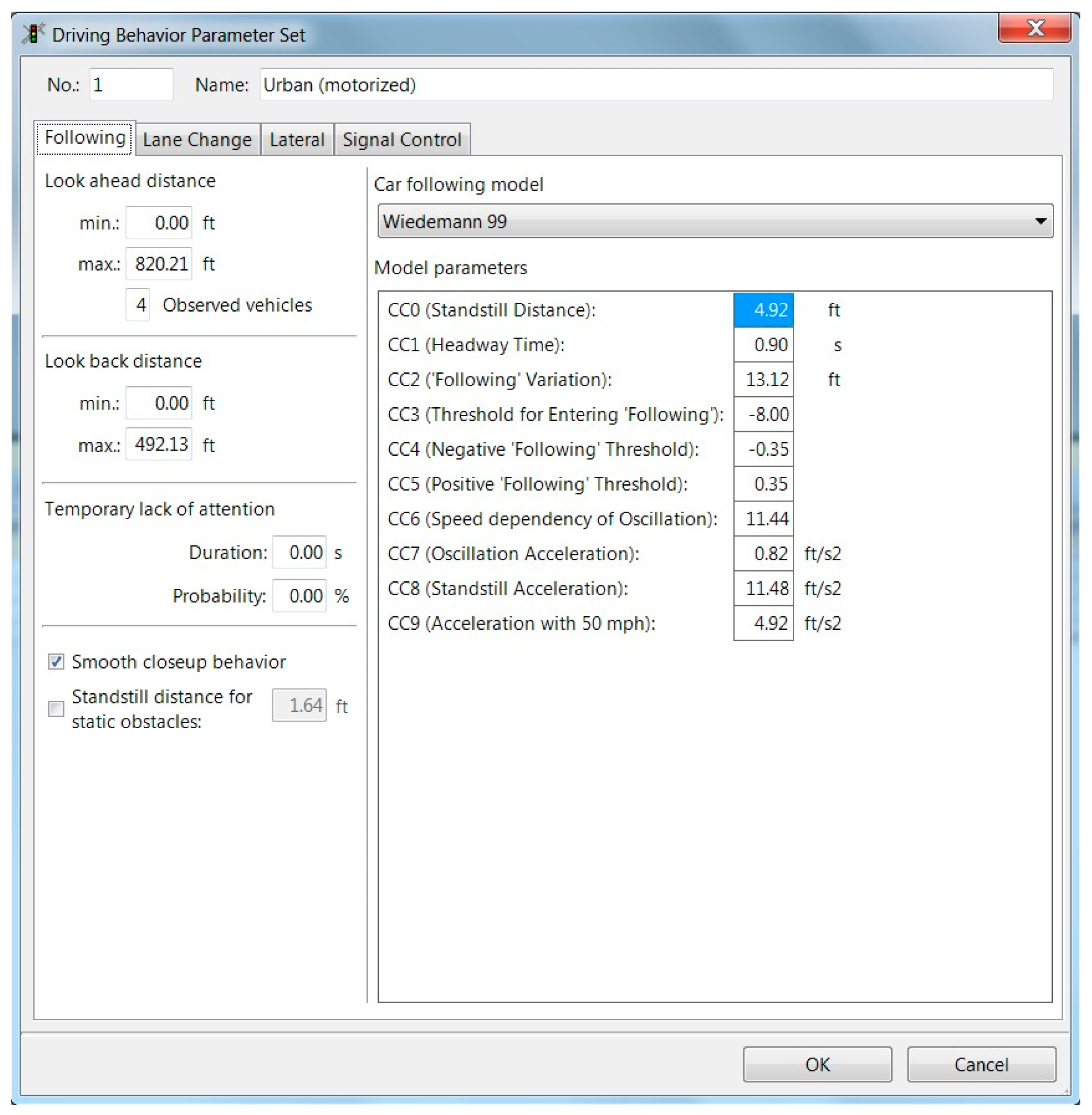
Traffic simulation models consist of various parameters and variables to define. VISSIM uses two main types of models: car-following models and lane change models. Car-following models are related to vehicle-following behaviors, which affect flow rates depending on the selected car-following model. These models are as follows: Wiedemann 74, which is mainly suitable for urban traffic (arterials), and Wiedemann 99, which is primarily suitable for freeways. The lane-changing models affect the driving behavior based on an extensive range of parameters. These parameters are presented in Figure 10. The driving behavior parameters can be defined for each link as well as for each vehicle class.

The first step in the calibration process is to make a set of runs with different seed numbers. Since VISSIM is a stochastic model, a random number generator is used for all types of parameters. The seed number is a starting point for the generator, which is called by the program and used to analyze many different parameters for the simulation. The parameters that use a random number generator include car following, lane changing, driver’s behavior, and release of demand volume.

Incidents were simulated by using reduced speed areas on the affected lanes. According to HCM, the capacity reduction factor due to shoulder closures is 81% and the FFS reduction factor is 86%. Due to the high volume (V/C = 1) in shoulder closure scenarios, a reduced speed area with 55 mph was placed towards the end of the main route to imitate a shoulder blockage case (see Figure 11). To simulate a one-lane closure, a reduced speed area with 0 mph speed on right lane was coded. Since HCM suggests a 79% FFS reduction factor, reduced speed areas of 55 mph for the remaining two lanes were also placed. Finally, a two-lane closure was simulated by implementing 0 mph reduced speed areas for the right two lanes for 5500 s. The left lane speed was also reduced to 40 mph to follow HCM’s 61% FFS reduction factor.

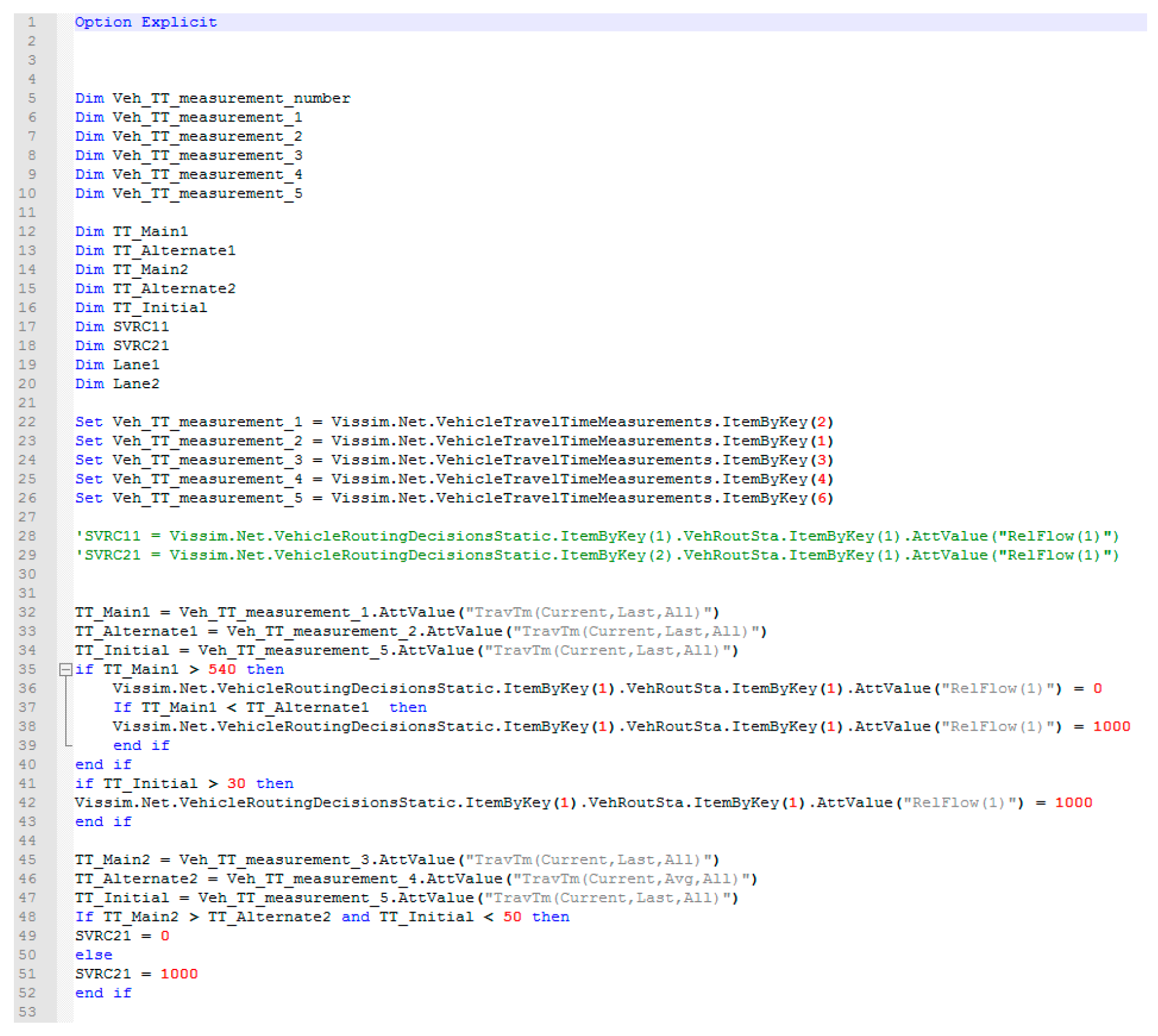
A visual basic (VB) code was written to make the routing decisions based on incident-induced travel delay comparisons between main and alternative routes in each scenario. For base scenarios, the script was not used. Another run was utilized with the script running at the start of every time step. The VB code is illustrated in Figure 12. When the VB script is activated for each time step, a decision is made in each simulation second based on the travel time comparison of both routes.

6. Results

Vehicle Record Outputs

One of the VISSIM direct output datasets is the vehicle record file with an FZP extension. The simulation output provides a suite of parameters crucial for evaluating vehicle performance and traffic flow characteristics. Each vehicle in the simulation is tagged with a unique ID number and associated with a specific Lane Link ID and Lane Index, which define its position in the traffic stream, including latitudinal and longitudinal placement. The output records the vehicle’s total simulation seconds and tracks key metrics such as the delay time and the time spent in a queue, which is instrumental in assessing traffic congestion. Additional data points include the total distance traveled, speed, vehicle weight, and vehicle type, offering detailed insights into traffic composition and mobility patterns. The simulation also measures acceleration, the number of stops a vehicle makes, the power it exerts, and fuel consumption, providing a comprehensive view of vehicular dynamics and the environmental impact. For public transport vehicles, the dwell time is monitored. Finally, the output includes economic metrics such as the total cost and total travel time, which are essential for cost–benefit analyses and for optimizing traffic management strategies.

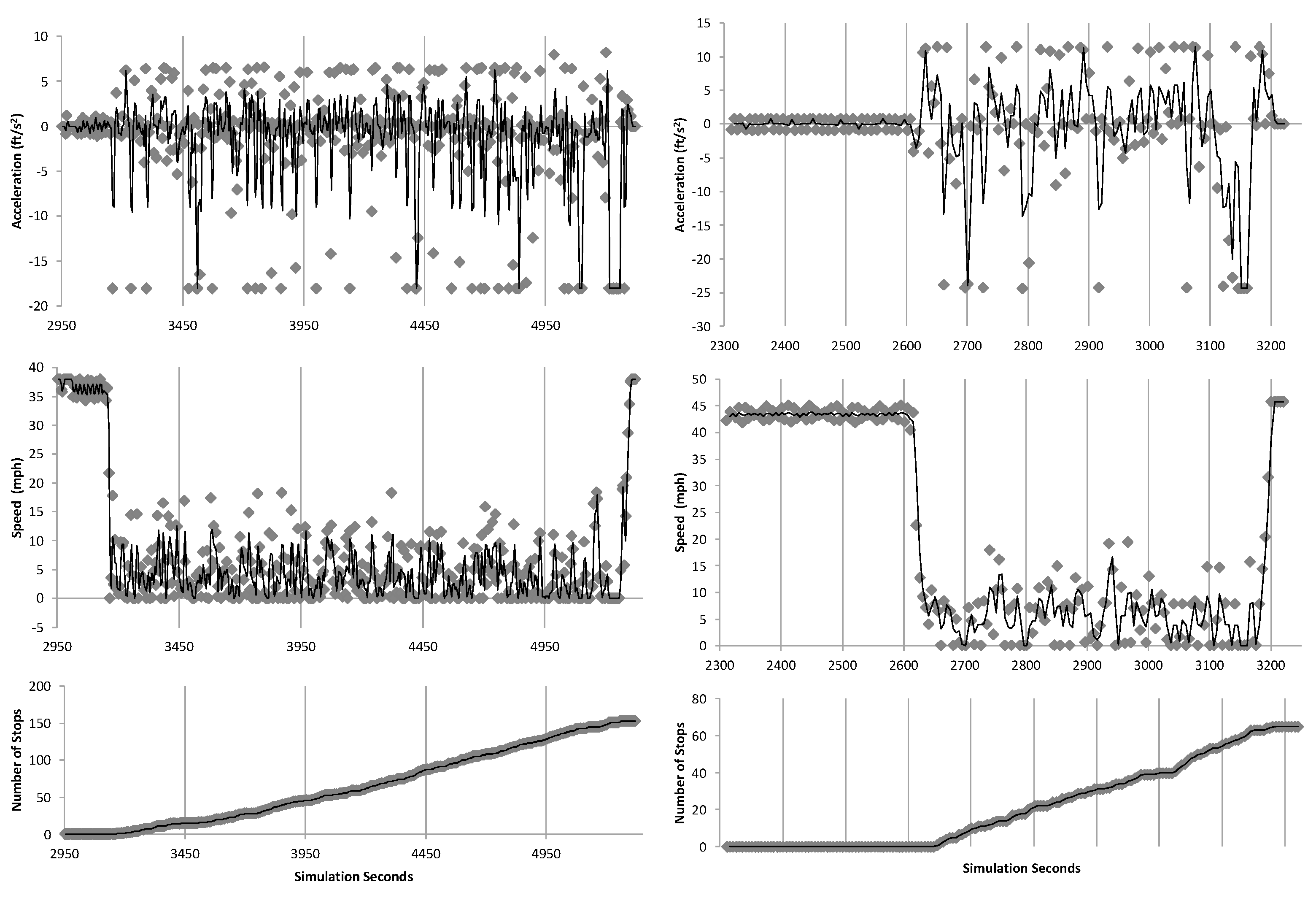
The detailed second-by-second vehicle record attributes in our simulation offer a granular view of network dynamics, crucial for calculating the value of time (VOT) savings accurately. By aggregating total travel times and delays based on vehicle and link IDs, we gain precise insights into the efficiency gains across various scenarios. Our methodical evaluation of randomly selected vehicles from key routes revealed significant improvements when we compared baseline scenarios to those with the implemented scripts. Notably, there was a marked reduction in acceleration–deceleration cycles, the number of stops, and speed variability, as evidenced in Figure 13, Figure 14 and Figure 15.

These findings are significant as they suggest that the application of advanced routing scripts has the potential to streamline traffic flow and reduce erratic driving behavior, which is a common contributor to traffic congestion and accidents. These behavioral changes not only enhance the overall travel experience by minimizing stress and unpredictability for drivers but also suggest broader implications for road safety and infrastructure wear-and-tear. Moreover, the observed improvements in vehicular movement patterns could lead to a decline in fuel consumption and emissions, advancing the sustainability objectives of transportation management. The results underscore the value of incorporating intelligent transportation systems into traffic management to foster a safer and more efficient transportation network.

Queue lengths for each scenario are provided in

Table 3. Queue lengths of each scenario.

(miles)	V/C Ratio
Blocked	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1	1.1
Shoulder	0.00	0.00	0.00	0.00	0.00	0.00	0.28	0.68	1.07
1-Lane	0.00	0.00	0.04	0.46	0.89	1.31	1.73	2.16	2.58
2-Lane	0.86	1.52	2.17	2.83	3.49	4.15	4.81	5.47	6.13

.

The results of the decisions based on travel costs are provided in

Table 4. Decisions for route change based on travel cost.

	V/C Ratio
	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1	1.1
Shoulder	No Q	No Q	No Q	No Q	No Q	No Q	Keep	Keep	Keep
1-Lane	No Q	No Q	Keep	Keep	Keep	Keep	Change	Change	Change
2-Lane	Keep	Change	Change	Change	Change	Change	Change	Change	Change

, where each cell represents the decision made in an individual scenario. The change decisions are where the incident-induced congestion cost is more than the difference in distance of the two routes. These scenarios are highlighted.

Table 5. Travel time differences with the alternative route (minutes).

	V/C Ratio
	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1	1.1
Shoulder	−7.00	−7.00	−7.00	−7.00	−7.00	−7.00	−6.62	−5.86	−4.77
1-Lane	−7.00	−7.00	−6.94	−6.07	−4.54	−2.15	1.35	6.20	12.66
2-Lane	−1.84	10.17	34.01	74.70	137.70	150.00	150.00	150.00	150.00

provides the travel time differences between the shortest path and alternative path based on the scenarios generated. The highlighted cells are positive, which means that there will be travel time savings but not necessarily travel cost savings.

An assumption in the travel time delay calculations is that the trucks are at Location A exactly 5 min prior to the incident occurrence time. So, with this assumption, the travel delays are set not to exceed {Incident duration—5 min} in order to avoid the queue length exceeding Location A.

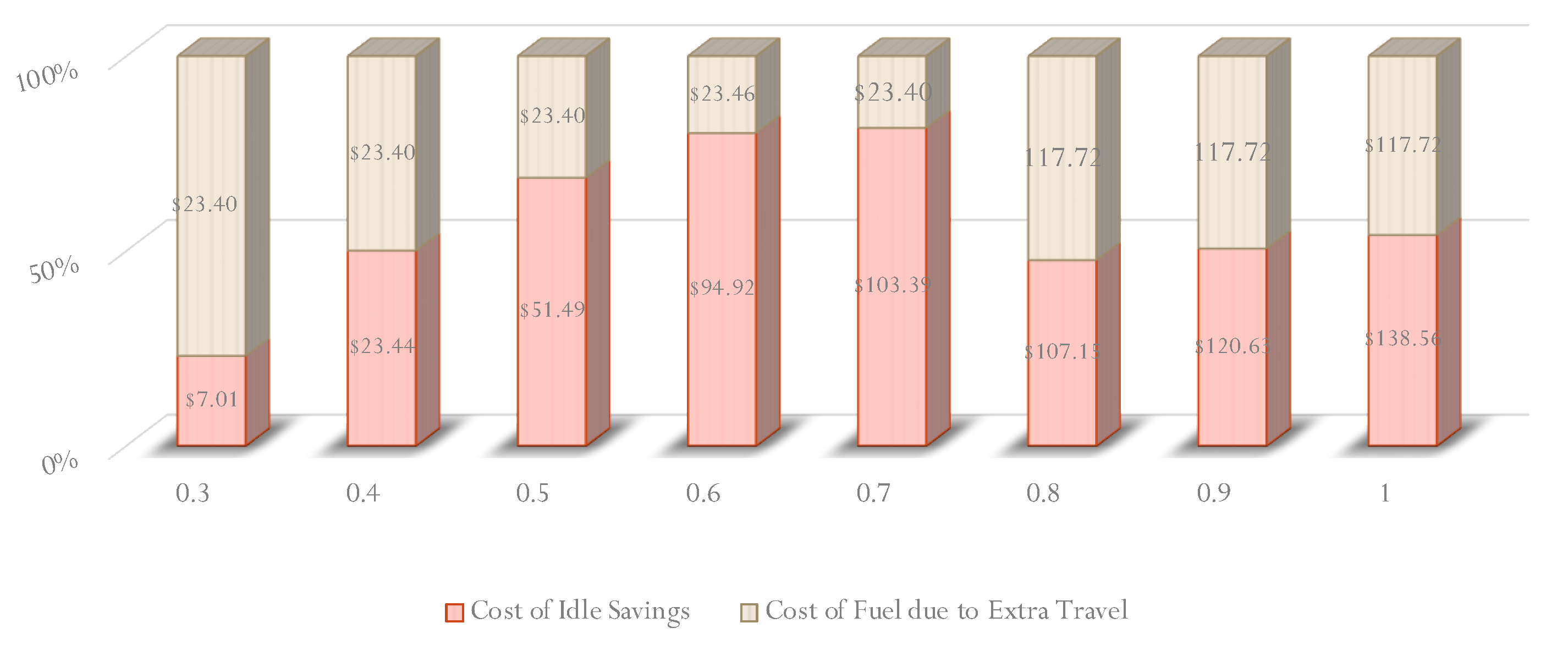
Cost of Fuel Savings

The number of “change” decisions in each incident category in Table 3 is considered as 2.1 miles of fuel consumption by a diesel truck engine. The extra miles matrix is multiplied by the incident category probabilities. This matrix is also divided by the distance of the shortest path in order to use the unit of extra miles traveled per mile. The average miles traveled per gallon for diesel trucks is 5.8. So, each figure is divided by 5.8 and multiplied by the annual truck VMT in order to find the annual fuel consumption in gallons due to extra miles traveled. The results are shown in Figure 16.

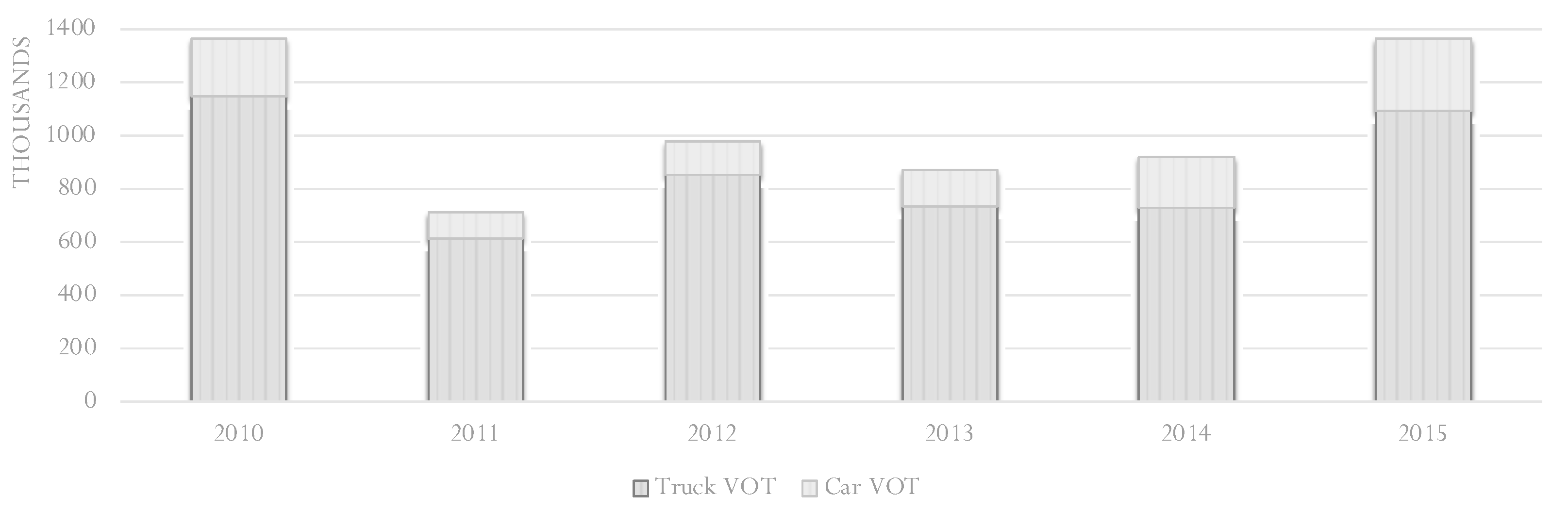
Value of Time Savings

The VISSIM output called the vehicle record has been described in detail. As mentioned in the aforementioned section, one of the attributes of FZP files is the travel time. Total travel times are compared between base and “with routing” scenarios. The differences are considered as travel delay savings. Aggregation of total travel times by vehicle types provides the total time of each vehicle type spent on the main route. According to the Texas A&M Transportation Institute (TTI), the costs of congestion are as follows; USD 17.67 per person-hour and USD 94.04 per truck. Travel time monetary values were multiplied by the travel times in each scenario and the results are provided in Figure 17. A value of time savings for each year from 2009 to 2016 is also presented in Figure 18.

7. Conclusions and Future Recommendations

The paramount objectives of this study were to devise a truck routing strategy to enhance travel time efficiency and to rigorously quantify its impacts on emissions, assessing subsequent effects on the economy and environment. By utilizing real-time truck routing simulation models (VISSIM) on critical corridors characterized by high truck traffic and volumes, we aimed to estimate non-recurrent congestion-based travel delays and fuel consumption. The economic dimension was approached through congestion cost studies, which indicated significant potential for the annual value of time savings.

However, our study is not without limitations. While we have made strides in quantifying the economic and environmental impacts of optimized truck routing, monetizing the safety impacts—including the social costs associated with traffic incidents—remains a complex challenge due to the multifaceted nature of these events. Additionally, while we postulate that fewer stop-and-go cycles of loaded trucks can reduce pavement wear, quantifying the precise changes in pavement damage requires a more intricate approach that accounts for a multitude of stress factors affecting road infrastructure.

For future studies, we recommend the development of comprehensive models that can accurately account for the social impacts of traffic safety improvements. These models should strive to monetize the full spectrum of safety implications, offering a more holistic view of the benefits of traffic management innovations. Further research should also focus on the long-term infrastructural savings from reduced pavement damage, drawing from a wider dataset that encapsulates various vehicle types and traffic conditions. Lastly, extending this study to incorporate emerging technologies such as connected and autonomous vehicles could yield insights into the future landscape of freight transportation and its interplay with urban development and roadway design [27].